- 1College of Physics and Electronic Engineering, Qilu Normal University, Jinan, China
- 2College of Physics and Astronomy, China West Normal University, Nanchong, China
The Lorentz symmetry breaking theory not only affects the space–time background but also the dynamic behavior of bosons and fermions in curved space–time. Therefore, the Lorentz symmetry breaking theory will affect the quantum tunneling rate, Hawking temperature, black hole entropy, and other physical quantities of black holes. According to the modification of the space–time background and the modification of the particle dynamic equations, the quantum tunneling radiation of the Kerr–Sen-like black hole in bumblebee gravitational theory and its related contents are deeply studied. The research methods and a series of new results obtained in this paper are discussed. This makes the research methods and conclusions in this paper of more astrophysical significance and reference value.
1 Introduction
Lorentz symmetry is the basic relationship of general relativity and quantum field theory. General relativity is a gravity theory that cannot be renormalized. Therefore, researchers put forward string theory, M-theory, and loop quantum gravity theory for studying quantum gravity theory. The studies on string theory and quantum gravity theory show that the Lorentz symmetry needs to be modified on the Planck scale in the case of high energy. The theory of Lorentz symmetry breaking in high energy physics includes the Horava–Lifshitz theory proposed by Horava in 2009. Another Lorentz symmetry breaking theory of gravity is the Einstein-aether theory. Since Einstein gravity theory cannot be renormalized, the quantum gravity theory combined with gravity theory and quantum theory as well as the grand unified theory in physics cannot be constructed so far. On the other hand, significant amounts of dark matter and dark energy are observed in cosmology, but these results still cannot be reasonably explained by current gravity theory. Since the publication of general relativity more than 100 years ago, researchers of physics and astronomy have always been studying Einstein’s gravity theory and the modified gravity theory. The supersymmetry theory, scalar tensor gravity theory, f(R) theory, f (R, T) gravity theory, Rastall gravity theory, and Finsler gravity theory are all gravity theories with modification. This paper studies the modification of Bekenstein–Hawking entropy in the Kerr–Sen-like black hole in the bumblebee gravity theory and its related projects [1, 2]. We consider two impacts of Lorentz symmetry breaking in curved space–time, namely, the impact on the space–time background and the influence on the dynamic equations of bosons and fermions in curved space–time. Without the Lorentz-breaking modification for the space–time background, people have modified the dynamic equations of bosons and fermions in static, stationary, and non-stationary black hole space–time with Lorentz-breaking modification and carried out a series of meaningful research works on related topics [3–16]. [1, 2] show that in the Einstein–bumblebee gravity theory, due to the influence of Lorentz-breaking on the space–time background, the space–time metric of the stationary Kerr–Sen-like black hole is modified to a certain extent. In this modified space–time background, the modifications to the dynamic equation of fermions by Lorentz-breaking and related projects are studied. Section 2 introduces the modification of space–time background and the modified dynamic equation of fermions. Section 3 describes the modified form of black hole entropy. The final section presents the research results.
2 The dynamic equation of fermions in Einstein–bumblebee gravity and Kerr–Sen-like black hole space–time
The Einstein–bumblebee gravity action including the term Lorentz-breaking is expressed as follows [1, 2].
In Eq. 1, λ is a non-minimal coupling constant between gravity and the bumblebee vector field Bμ. Obviously, when Bμ = 0, Eq. 1 is back to the action of the Einstein gravitational field. Bμν in Eq. 1 and the following Eq. 2 is the field strength tensor corresponding to the bumblebee field reads [1, 2].
where b2 is a real positive constant and b2 provides field Bμ, a non-vanishing vacuum expectation value (VEV). Eq. 3 is assumed to have a minimum through the condition BμBμ ± b2 = 0, which ensures a non-zero VEV.
where
In the above Eqs 4–7, M is the mass of such a black hole, a = J/M is the angular momentum per unit mass, J is the angular momentum, and ℓ and b are expressed in the above content. Equation 4 is the form in the Boyer–Lindquist coordinate and the space–time metric of the stationary axisymmetric Kerr–Sen-like black hole after the Lorentz-breaking modification. Such space–time background is not only the modification of the stationary Kerr–Sen black hole but also the development of Kerr–Sen metric. When ℓ = 0 and b = 0, Kerr–Sen-like metric is back to Kerr metric. According to Eq. 4, the components of non-zero covariant metric tensors are shown as follows, respectively:
Then, the metric determinant g corresponding to gμν is expressed as
According to Eqs 8, 9, we can calculate the components of the non-zero inverse metric tensors as follows:
With the expression gμν, according to a hypersurface equation
Substituting Eq. 10 into Eq. 11, it can be concluded that
namely,
This is the equation that is satisfied by the event horizon of the Kerr–Sen-like black hole. From this equation, it can be seen that the outer horizon of this black hole, the event horizon, is expressed as
According to Eqs 12–14, the event horizon rH of the black hole is modified due to the influence of Lorentz-breaking on the space–time background.
In order to research the quantum tunneling radiation characteristics of the Kerr–Sen-like black hole, we can consider the expression of the action quantity of spin 1/2 fermions, which has been modified by Lorentz-breaking theory. Due to the particularity of spin 1/2 fermions, one of the action modification terms is the chiral, and the other two are aether-like field vector and Carroll–Field–Jackiw (CFJ). In fact, the first discovered Lorentz-breaking term is the CFJ term [20–22]. In the later research process, researchers proposed the aether-like vector modification term uμ for the scalar field. For the spinor field, the chiral term and the aether-like term were proposed. The Lorentz-breaking modification of field theory models has attracted widespread attention [23–29]. There have been some reports on the use of Lorentz-breaking theory to modify fermion dynamic equations in flat and curved space–time [30–33]. Now, based on the particularity of the Kerr–Sen-like black hole metric and considering the fermions of spin 1/2, we can express the modified spinor field action as [29–32]
where Ωμ and Ων are spinor contacts,
we can obtain
Due to
Multiplying by
This is the modified form of the dynamic equation of spin 1/2 fermions, also known as a matrix equation. According to the WKB approximation theory, the wave function ψ is expressed as
where S is the action of spin 1/2 fermions. Substituting Eq. 20 into Eq. 19, an equation in the matrix form can be obtained as follows:
where ℏΩμ and ℏΩν are omitted. Equation 21 is a matrix equation, which is actually an eigenmatrix. Accordingly, the condition for nontrivial solutions in Eq. 21 is that the value of the determinant corresponding to the matrix is 0.
where γμ is the gamma matrix in curved space–time, γ5 is the matrix in the chiral modification term, and
where I in Eq. 23 is a unit matrix. After multiplying both sides of Eq. 22 by γν∂νS and omitting the higher-order small quantities, the following field equation is obtained:
This is the spinor field equation for fermions with spin 1/2 in Kern–Sen-like black hole space–time. Calculate S from Eq. 25; then, according to the WKB approximation theory and the black hole quantum tunneling radiation theory, we can research the quantum tunneling radiation characteristics of such black holes.
3 Modification of the Kerr–Sen-like black hole entropy by Lorentz-breaking theory
To solve the field in Eq. 25 in the Kerr–Sen-like space–time background, the four components of the aether-like field vector uμ are selected as follows:
Obviously, uμuμ is a constant and meets the basic conditions of the aether-liker field vector. In Eq. 25,
where σ1, σ2, σ3 are Pauli matrices, namely,
Equations 23 and 29 are completely consistent. According to Eq. 27 and the Kerr–Sen-like metric feature, we can construct γ5 as follows:
where γ5 is a Hermitian matrix. From Eqs 27, 30, we can obtain
Obviously, γ5 in Eq. 31 completely meets the requirements of Eq. 24, and correct γ5 is merely constructed by correctly choosing γμ. By substituting Eq. 26 and gμν into Eq. 25, Eq. 25 can be simplified as
where the modification term corresponding to Kerr–Sen-like space–time is expressed as
Killing vector
By substituting Eqs 10, 33, 34 into Eq. 32 and multiplying both sides of Eq. 32 by
we can get the radial dynamic equation of Eq. 32 at rH as follows:
From this Eqs 35, 36, we can obtain
where
Taking square roots on both sides of Eq. 37, we can obtain
In the above Eq. 39, ω0 is shown in Eq. 38. Using the residue theorem integrals, we can obtain
According to the WKB approximation theory and the quantum tunneling radiation theory, we can get that the quantum tunneling rate of the spin 1/2 fermions at the event horizon of the black hole is
where
This is the modified expression for Hawking temperature, where ℓ and b are the modification terms due to the influence of Lorentz-breaking on the space–time background. d is the modification term of the CFJ term. c, Ct, and Cr are modification terms caused by the aether-like field vector. The new significance of Eqs 41, 42 is including the modification for background and also for the dynamic behavior of spin 1/2 fermions in the curved space–time backgrounds, where ω0 is the chemical potential, due to the rotation of the black hole; a ≠ 0; and ω0 ≠ 0. So ω0 is related to ℓ and b and also to a = J/M. This is the basic feature of the stationary Kerr–Sen-like black hole thermodynamics.
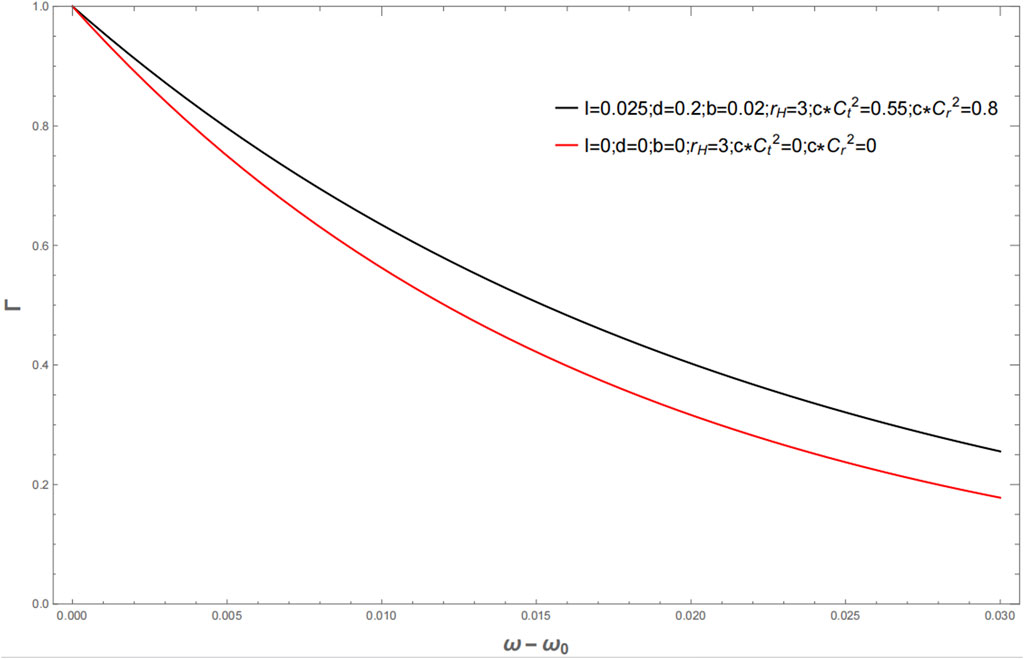
In order to more intuitively represent the influence of ℓ, b, d, c, Cr, and Ct on the quantum tunneling rate of the Kerr–Sen-like black hole, the figures Γ − (ω − ω0) are drawn.
As can be seen from Figures 1, 2, the Lorentz-breaking bumblebee gravity theory has modified the space–time background of the Kerr–Sen-like black hole. After the correction, the Kerr–Sen black hole space–time background becomes the Kerr–Sen-like black hole. Figure 1 shows the comparison of the quantum tunneling rates of the Kerr–Sen-like black hole and Kerr-Sen black hole. Figure 2 shows a schematic diagram of the quantum tunneling rate of the Kerr–Sen-like black hole affected by the CFJ and the aether-like correction terms.
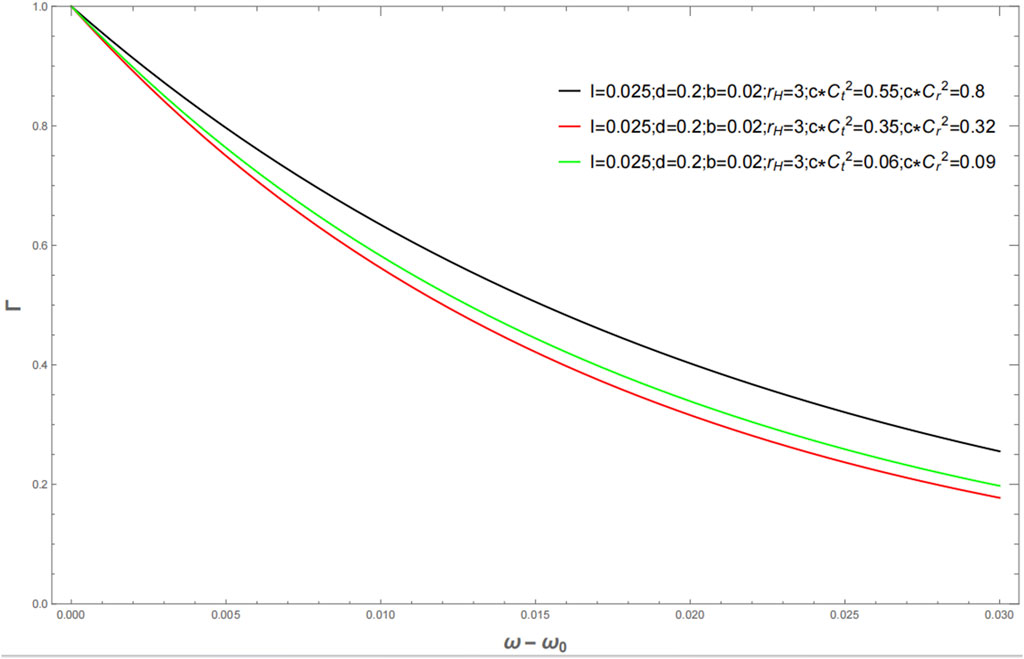
Figure 2. Variation of the quantum tunneling rate for different parameters such as d, c, Cr, and Ct.
Another major physical quantity in black hole thermodynamics is black hole entropy. The entropy of black holes is closely related to Hawking temperature. Due to the modified Hawking temperature expressed in Eq. 42, there should be corresponding modified black hole entropy. According to the first law of black hole thermodynamics, the Bekenstein–Hawking entropy SBH of the black hole is related to the Hawking temperature of the black hole as
where Ω is the rotational angular velocity. From Eq. 43, we obtain the following equation:
From Eq. 44, we obtain the following equation:
In the above Eq. 45, Th is the Hawking temperature at the event horizon of the Kerr black hole before modification, so Eq. 44 with the integral is
where
The metric determinant corresponding to Eq. 47 is
Therefore, according to Eq. 48, the event horizon area AH of such a black hole is
Then,
Substituting Eq. 50 into Eq. 46, the expression of the modification entropy of such a black hole is
It can be seen that the modified entropy SBH of the black hole is related to d, b, ℓ, c, Ct, and Cr. If using ΔSBH to express the Bekenstein–Hawking entropy transformation, then the expression of the quantum tunneling rate, as shown in Eq. 41, can be rewritten as
Eqs 40–42, 49–52 indicate that due to Lorentz-breaking, both the space–time background and quantum tunneling radiation are affected to some extent. A series of conclusions obtained above are of certain practical significance for research on black hole thermodynamics.
4 Conclusion
First, it should be noted that this term containing f in Eq. 25 does not appear in the abovementioned series of results, which is because
In the previous literature on the modification of the quantum tunneling radiation of the black hole by Lorentz-breaking, the modification of the space–time background by Lorentz-breaking was generally not considered [12–15]. Therefore, the novelty of the abovementioned research content is that the Lorentz-breaking modification of space–time background and the fermion dynamics equation are taken into account at the same time, and a series of novel outcomes are obtained. In a future in-depth research process, we should consider the effects of Lorentz-breaking theory on the space–time background of static, stationary, and non-stationary black holes. In the process of measuring the shadow of the black hole, for example, we should take into account the effect of Lorentz-breaking theory. All these research contents should continuously enrich the content of quantum gravity theory research.
For bosons, the abovementioned methods cannot be used to research the dynamic characteristics of bosons, and it is necessary to research the dynamic behavior of bosons from the modified form of the scalar field equation. For other static, stationary, and non-stationary black holes, the abovementioned research methods can be used to study the quantum tunneling radiation characteristics of fermions and the physical significance of black hole temperature and black hole entropy modification. We need to deeply understand the conclusions mentioned above, especially the profound meaning of black hole entropy. Black hole entropy is one of the important physical quantities in black hole physics, and it is directly proportional to the area of the black hole. According to the second law of black hole thermodynamics, the area of a black hole will never decrease in the clockwise direction, which means that black hole entropy will not decrease. When we explore black hole entropy from the perspective of quantum theory, black hole entropy is directly proportional to the area of the event horizon measured in the Planck area, which is a scientific project worthy of in-depth research.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
XT: formal analysis, software, validation, writing–original draft, and writing–review and editing. CW: software and writing–review and editing. S-ZY: conceptualization, data curation, methodology, and writing–original draft.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (No. 12373109).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Jha SK, Rahaman A. Bumblebee gravity with a kerr-sen like solution and its shadow. Eur Phys J C (2021). 81:345. doi:10.1140/epjc/s10052-021-09132-6
2. Carleo A, Lambiase G, Mastrototaro L. Energy extraction via magnetic reconnection in lorentz breaking kerr-sen and kiselev black holes. Eur Phys J C (2022). 82:776. doi:10.1140/epjc/s10052-022-10751-w
3. Banerjee R, Majhi BR. Connecting anomaly and tunneling methods for the hawking effect through chirality. Phys Rev D (2009). 79:064024. doi:10.1103/physrevd.79.064024
4. Kruglov SI. Modified Dirac equation with lorentz invariance violation and its solutions for particles in an external magnetic field. Phys Lett B (2012). 718:228–31. doi:10.1016/j.physletb.2012.10.037
5. Amelino-Camelia G. Phenomenology of planck-scale lorentz-symmetry test theories. New J Phys (2004). 6:188. doi:10.1088/1367-2630/6/1/188
6. Magueijo J, Smolin L. Generalized lorentz invariance with an invariant energy scale. Phys Rev D (2003). 67:044017. doi:10.1103/physrevd.67.044017
7. Ellis JR, Mavromatos NE, Sakharov VS. Synchrotron radiation from the crab nebula discriminates between models of space-time foam. Astropart Phys (2004). 20:669–82. doi:10.1016/j.astropartphys.2003.12.001
8. Kruglov SI. Modified wave equation for spinless particles and its solutions in an external magnetic field. Mod Phys Lett A (2013). 28:1350014. doi:10.1142/s0217732313500144
9. Yang SZ, Chen DY. A new method to study hawking tunneling radiation of the charged particles from ressiner-nordström black hole. Int J Theor Phys (2007). 46:1747–52. doi:10.1007/s10773-006-9306-x
10. Yang SZ, Lin K. Hawking tunneling radiation in lorentz-violating scalar field theory. Acta Phys Sin (2019). 68:060401. doi:10.7498/aps.68.20182050
11. Li R, Yu ZH, Yang SZ. Modification of bekenstein-hawking entropy of cylindrical symmetric black hole by lorentz breaking theory. EPL (2023). 141:50001. doi:10.1209/0295-5075/acbb9b
12. Tan X, Zhang J, Li R. Correction of lorentz breaking theory to quantum tunneling radiation and entropy of black hole in gravity’s rainbow. Phys Scripta (2023). 98:105015. doi:10.1088/1402-4896/acf810
13. Tan X, Liu YZ, Liu ZE, Sha B, Zhang J, Yang S. Modification of the dynamic equation and tunneling radiation of fermions with arbitrary spin in kerr-newman-kasuya black hole space-time. Mod Phys Lett A (2020). 35:2050168. doi:10.1142/s0217732320501680
14. Zhang J, Liu ZE, Sha B. Influence of lorentz invariation violation on arbitrarily spin fermions tunneling radiation in the vaidya-bonner spacetime. Adv High Energ Phys. (2020). 2020:2742091. doi:10.48550/arXiv.2002.05946
15. Sha B, Liu ZE, Liu YZ, Tan X, Zhang J, Yang SZ. Accurate correction of arbitrary spin fermion quantum tunneling from non-stationary kerr-de sitter black hole based on corrected lorentz dispersion relation. Chin Phys C (2020). 44:125104. doi:10.1088/1674-1137/abb4d6
16. Liu ZE, Tan X, Liu YZ, Sha B, Zhang J, Yang SZ. Hawking radiation of reissner-nordström-de sitter black hole with a global monopole der ived from modified hamilton-jacobi equation. Can J Phys (2021). 99:451–4. doi:10.1139/cjp-2020-0402
17. Javed F, Mustafa G, Mumtaz S, Atamurotov F. Thermal analysis with emission energy of perturbed black hole in f(Q) gravity. Nucl Phys B (2023). 990:116180. doi:10.1016/j.nuclphysb.2023.116180
18. Rakhimova G, Atamurotov F, Javed F, Abdujabbarov A, Mustafa G. Thermodynamical analysis of charged rotating black hole surrounded by perfect fluid dark matter. Nucl Phys B (2023). 996:116363. doi:10.1016/j.nuclphysb.2023.116363
19. Abbas G, Ali RH, Mustafa G. Thermodynamical analysis with extended phase transition of ads hairy black hole in gravitational decoupling theory. Phys Scr (2024). 99:045025. doi:10.1088/1402-4896/ad340a
20. Carrol S, Field G, Jackiw R. Limits on a lorentz-and parity-violating modification of electrodynamics. Phys Rev D (1990). 41:1231–40. doi:10.1103/physrevd.41.1231
21. Jackiw R, Kostelecky VA. Radiatively induced lorentz and violation in electrodynamics. Phys.Rev.Lett. (1999). 82:3572–5. doi:10.1103/physrevlett.82.3572
22. Coleman S, Glashow SL. High-energy tests of lorentz invariance. Phys Rev D (1999). 59:116008. doi:10.1103/physrevd.59.116008
23. Kostelecky VA. Gravity, lorentz violation, and the standard model. Phys Rev D (2004). 69:105009. doi:10.1103/physrevd.69.105009
24. Belich H, Costa-Soares T, Ferreira MM, Helayel-Neto JA. Non-minimal coupling to a Lorentz-violating background and topological implications. Eur Phys J C (2005). 41:421–6. doi:10.1140/epjc/s2005-02240-y
25. Belich H, Colatto LP, Costa-Soares J, Helayël-Neto JA, Orlando MTD. Magnetic moment generation from non-minimal couplings in a scenario with lorentz-symmetry violation. Eur Phys J C (2009). 62:425–32. doi:10.1140/epjc/s10052-009-1017-z
26. Klinkhammer FR, Schrec KM. Consistency of isotropic modified maxwell theory: microcausality and unitarity. Nucl Phys B (2011). 848:90–107. doi:10.1016/j.nuclphysb.2011.02.011
27. Klinkhammer FR, Schrec KM. Models for low-energy lorentz violation in the photon sector: addendum to ’consistency of isotropic modified maxwell theory. Nucl Phys B (2012). 856:666–9. doi:10.1016/j.nuclphysb.2011.11.019
28. Nascimento JR, Passos E, Petrov AY, Brito FA. Lorentz-cpt violation, radiative corrections and finite temperature. JHEP (2007). 0706:016. doi:10.1088/1126-6708/2007/06/016
29. Gomes M, Nascimento JR, Petrov AY, da Silva AJ. Aetherlike lorentz-breaking actions. Phys Rev D (2010). 81:045018. doi:10.1103/physrevd.81.045018
30. Nascimento JR, Yu Petrov A, Reyes CM. Lorentz-breaking theory with higher derivatives in spinor sector. Phys Rev D (2015). 92:045030. doi:10.1103/physrevd.92.045030
31. Pu J, Yang SZ, Lin K. Lorentz-violating theory and tunneling radiation characteristics of Dirac particles in curved spacetime of vaidya black hole. Acta Phys Sin (2019). 68:190401. doi:10.7498/aps.68.20190437
32. Yang SZ, Lin K. Modified fermions tunneling radiation from Kerr-Newman-de Sitter black hole. Sci Sin-phy Mech Astron (2019). 49:019503. doi:10.1360/sspma2018-00307
Keywords: bumblebee gravity, Lorentz-breaking, Kerr–Sen-like black hole, Hawking temperature, black hole entropy
Citation: Tan X, Wang C and Yang S-Z (2024) Modification entropy of Kerr–Sen-like black hole in Lorentz-breaking bumblebee gravity. Front. Phys. 12:1415418. doi: 10.3389/fphy.2024.1415418
Received: 10 April 2024; Accepted: 21 May 2024;
Published: 12 June 2024.
Edited by:
Pradyumn Kumar Sahoo, Birla Institute of Technology and Science, IndiaReviewed by:
Piyali Bhar, Government General Degree College, IndiaGhulam Mustafa, Zhejiang Normal University, China
Copyright © 2024 Tan, Wang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xia Tan, dGFueGlhQHFsbnUuZWR1LmNu
 Xia Tan
Xia Tan Cong Wang1
Cong Wang1