Global particle buildup simulations with gas puff scan: application to WEST discharge

This paper deals with the distribution of sources, transport, and exhaust of particles in a tokamak. Knowledge and understanding of all the physical phenomena involved in the global particle buildup are necessary to study and predict density regimes and subsequently to develop optimized scenarios for tokamak operation in order to control heat and particle exhaust. Neutral particles and their interactions with plasma are central in this perspective. This paper discusses the impact of varying the intensity of particle fueling in 2D transport simulations of a WEST discharge. Simulations are performed with an updated version of SOLEDGE-HDG that allows a more realistic transport of neutrals using a self-consistent diffusive model based on charge exchange and ionization processes. New code capabilities allow the entire WEST poloidal cross section to be simulated in a realistic configuration for both geometry and the range of control parameters. A gas puff scan illustrates the main features of the sheath-limited, high-recycling, and detached regimes, such as the buildup of the temperature gradient and the pressure drop in the scrape-off layer (SOL), the target temperature falling to 1 eV, and the ionization source moving away from the targets, as well as the particle flux rollover. A crude estimate of wall erosion is also provided, showing the respective role of each plasma wall component in each of these regimes.

1 Introduction

With targeted self-sustained burning plasmas in ITER [1], the issue of power exhaust and the control of heat fluxes onto the tokamak walls in high-energy confinement configurations remains critical to successfully run future ITER experiments [2]. This calls for the design of scenarios in ITER that are able to mitigate heat fluxes on the dedicated wall components [3]. Since the mid-1990s, reduced divertor heat flux scenarios have been successfully carried out in experiments, reducing the peak power and erosion of divertor components to an acceptable level. They are mostly based on highly dissipative boundary plasmas in divertor tokamaks where divertor radiation is significantly increased through additional gas fueling to raise the density and lower divertor plasma temperature (see results of some of the initial experiments in, for example, JET [4], ASDEX-Upgrade [5], and DIII-D [6]). These divertor plasmas were labeled as “detached” because the primary plasma boundary interaction moved upstream off the divertor target surface. Other attempts were also based on a stochastic boundary, as proposed, for example, in Tore Supra [7]. In the latter, the ergodic divertor configuration demonstrated the capability to control energy and particle deposition while providing both screening of impurities and stable radiating layers.

In order to prepare for the successful operation of ITER, the design of these optimized operations and the prediction of the power load at the wall still require an improvement in our understanding of the mechanisms involved, resulting from the complex interaction of transport processes in the plasma, losses at the wall, and complex atomic and molecular interactions. Together with experimental measurements and theoretical modeling, numerical codes have become powerful interpretation tools for current tokamak operation, with the longer-term objective of becoming predictive. A chain of models is being developed, ranging from simplified models for optimization and uncertainty propagation to state-of-the-art, first principal models of plasma turbulence transport in relevant plasma conditions. As mentioned recently in the review article by Schwander et al. [8], transport codes based on reduced fluid models—in which the turbulence has been smoothed by averaging—remain the current workhorse of physicists, particularly in studies closely linked to operational aspects, aiming to explore and design optimal scenarios for reactor performance. Some of the state-of-the-art transport codes widely used in the community are EDGE2D-EIRENE [9, 10], EMC3-EIRENE [11], SOLEDGE3X-EIRENE [12], SOLPS-ITER [13], and UEDGE-DEGAS2 [14, 15]. It should be highlighted, however, that significant physics can be lost from the model reduction. This, in particular, concerns both cross-field transport, which has proven not to be able to be described convectively [16], and the interaction between fluctuating plasma fields and neutrals [17, 18].

One of the key ingredients in high-fidelity plasma simulations is understanding the global particle buildup, which requires knowledge of the distribution of sources, transport, and exhaust of particles. Neutral particles and their interaction with the ionized species are, therefore, central. The volumetric losses of momentum and energy associated with their recycling back into plasma are the main drivers for accessing the detached conditions mentioned above. Experimental evidence demonstrates an impact of density regimes on the transverse plasma transport, which might, in turn, influence the access to detachment and its stability [19]. These effects can be modeled using averaged plasma and neutral fluid fields. However, employing such an approach hides interactions between blobs and neutrals, which may lead to overestimating density fluxes across the last closed flux surface (LCFS) [20]. The influence of the blobs on the plasma sources is extensively studied in 2D slab turbulent simulations performed by the HESEL group [18, 21, 22]. A more accurate way to simulate neutral transport is based on a Monte Carlo algorithm and is widely used by coupling transport solvers with EIRENE [10] and DEGAS2 [15]. This method generally introduces statistical noise that deteriorates the convergence of the plasma solver and is also computationally expensive, especially in highly collisional regions such as the divertor. The described issues are partially dealt with in [21] by considering neutral-plasma interactions stochastically, while transport of neutrals deterministically with an extensive parallelization of the code and additional smoothening of the sources. Nonetheless, the fluid approach remains attractive with varying degrees of refinement, being fully deterministic and reducing the real computational time. Despite its relative simplicity, the latter can provide a good approximation of the plasma source generated by recycling and the radiation power losses in the divertor, as shown in recent transport studies [23, 24].

The resolution of the conservation equations for mean plasma quantities remains particularly challenging and stressful for the numerical methods. The marked anisotropy linked to the strong magnetization of the plasma in the tokamak and the complex geometry of both the tokamak wall and magnetic equilibrium remain important issues that limit the capabilities of many solvers. As an attempt to solve all these issues, we have been developing SOLEDGE-HDG [25] in the SOLEDGE suite of codes for transport simulations. This code is based on high-order finite elements, where the entire plasma volume, including the core and the scrape-off layer (SOL) plasma up to the wall, is meshed with triangles. This discretization allows the mesh to be magnetic equilibrium free. In addition, a combination with an implicit time integrator using Newton–Raphson iterations allows fast convergence of the code towards plasma equilibrium, enabling parametric studies to be carried out at reasonable computational cost.

This paper deals with the distribution of sources, transport, and exhaust of particles in WEST [26] using SOLEDGE-HDG simulations. These latter are performed with an updated version of the code, which allows a more realistic transport of neutrals using a self-consistent diffusive model based on charge-exchange and ionization processes inspired by [27, 28] and already implemented into SOLPS-ITER [29]. Unlike the state-of-the-art plasma fluid codes mentioned above, which are usually based on the magnetic-field-aligned approach, the SOLEDGE-HDG numerical scheme and mesh are well suited to dealing with neutrals, whose transport is non-aligned with the magnetic field and provide an accurate description of the tokamak wall, with a detailed description of the gas puff region in particular. For example, in the recent work in SOLPS-ITER [29], fluid neutrals require mesh simplification even for the “extended grid” version of the code.

The paper is organized as follows. Section 3 presents the computational domain, describing the complete poloidal cross section of the realistic geometry of the WEST tokamak. In Section 4, the mathematical model is introduced, focusing on the updated fluid neutral model with a self-consistent diffusion based on charge-exchange and ionization processes. A comparison with the former model with constant diffusion is made in Section 5. A gas puff scan illustrates how the main features of the sheath-limited, high-recycling, and detached regimes are recovered in Section 6. Finally, Section 7 concludes the paper and provides some interesting perspectives on this work.

2 A realistic WEST tokamak geometry

The 2D computational domain corresponds to the entire plasma volume in the WEST poloidal cross section, going from the core up to the wall, as shown in Figure 1, and providing a realistic geometrical description.

Figure 1

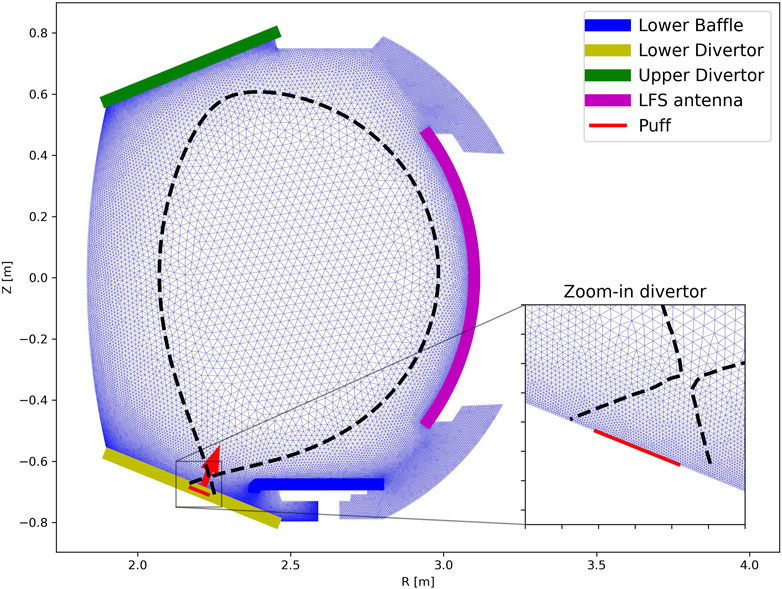
Figure 1. Poloidal cross section of the WEST tokamak operated at CEA-IRFM. The various plasma-facing components are shown with thick colored lines. The puff (red) region is shown with a thin line and an arrow. The separatrix location for the t = 4.73 s of shot #54487 is shown as a dashed black line. The zoomed-in lower divertor mesh is shown in the inset figure. Triangles of a typical mesh show the capability of the numerical scheme to discretize the entire plasma domain.

The axisymmetric equilibrium magnetic field $\mathit{B}$ is assigned from the experimental reconstruction (see numerical details in Section 3.3) of the WEST Ohmic discharge #54487 at $t$ = 4.73 s after ignition. The configuration corresponds to the so-called single null semi-open divertor configuration. It includes closed flux surfaces in the center and open flux surfaces with field lines impacting the wall at the edge, both of which are separated by the separatrix. The distance from the X-point to the targets (as well as from baffle to separatrix) is about $d_{\text{X}-\text{point}}\approx$6 cm, which is comparable with characteristic mean free path (mfp) of the neutrals escaping from the surface, as will be shown in Sections 3.2, 5, 6.

The strong difference of intensity between the toroidal and poloidal components $\Vert B_p\Vert \ll \Vert B_t\Vert$ defines a privileged direction denoted as the parallel direction, with reference to the direction along the magnetic field lines. To take advantage of this flow anisotropy, the plasma equations (in Supplementary Appendix A) are projected along the magnetic field lines using the differential operators ${\mathbf{\nabla }}_{\Vert }=\mathit{b}\cdot \mathbf{\nabla }$ and ${\mathbf{\nabla }}_{\perp }=\mathbf{\nabla }-\mathit{b}\cdot {\mathbf{\nabla }}_{\Vert }$, where $\mathit{b}=\frac{\mathit{B}}{\Vert \mathit{B}\Vert }$ is the unitary vector in the parallel direction.

3 SOLEDGE-HDG mathematical model

The model is based on the 2D drift-reduced Braginskii conservative fluid equations for a deuterium plasma introduced in [25]. These equations are listed in Supplementary Appendix A together with the boundary conditions in Supplementary Appendix B for the sake of completeness of the paper. $n,u,T_{\mathrm{e}},T_{\mathrm{i}}$ denote the electron density, the ion parallel velocity, and the electron and ion temperatures, respectively. Neutral transport is assumed to be purely diffusive. The model is inspired by the work of Horsten et al. [27], where the diffusion is self-consistently determined using atomic data, as detailed below. Despite its overall simplicity, it has shown to be appropriate for understanding the effect of the ionization source on the plasma flows on the divertor target [23, 24]. The neutral diffusion model provides a self-consistent source of particles due to recycling at the wall, and a rather realistic description of the plasma in front of the targets is achieved.

3.1 A self-consistent neutrals diffusion model

The equation representing the neutral density $n_{\text{n}}$ in the model is as follows:

${\partial }_t{n}_{\text{n}}-\nabla \cdot \left(D_{n_{\text{n}}}{\nabla }_{\perp }{n}_{\text{n}}\right)=-n_{\text{n}}n\langle \sigma {v\rangle }_{\text{iz}}+n^2\langle \sigma {v\rangle }_{\text{rec}},(1)$

with a non-uniform diffusion coefficient $D_{n_{\text{n}}}$ defined as in [27]:

$D_{n_{\text{n}}}=\frac{e{T}_{\text{i}}\left[\text{eV}\right]}{m_{\text{i}}n\left(\langle \sigma {v\rangle }_{\text{cx}}+\langle \sigma {v\rangle }_{\text{iz}}\right)},(2)$

where $T_{\text{i}},m_{\text{i}}$ are the main ion temperature and mass, $n$ is the plasma density (in case of quasi-neutrality and pure deuterium plasma $n_{\text{i}}=n_{\text{e}}=n$), and ${⟨\sigma v⟩}_{\text{cx}}$ and ${⟨\sigma v⟩}_{\text{iz}}$ are the effective rates of charge exchange and ionization. In the current version of the code, they can be estimated using splines from one of three articles [30–32]. Details on atomic data are discussed below in Section 3.2. Note that in the absence of a neutral energy equation, neutrals are assumed to be thermalized $(T_{\text{n}}=T_{\text{i}})$.

$D_{n_{\text{n}}}$ can be interpreted through mean free paths of neutrals so that Eq. 2 equivalently reads as:

$D_{n_{\text{n}}}=\frac{c_{\text{s,i}}}{2}{\lambda }_{\text{neut}}=\frac{c_{\text{s,i}}}{2}{\left(\frac{1}{{\lambda }_{\text{cx}}}+\frac{1}{{\lambda }_{\text{iz}}}\right)}^{-1},(3)$

where $c_{\text{s,i}}=\sqrt{2k_{\text{b}}{T}_{\text{i}}/m_{\text{i}}}$ is the ion sound speed and ${\lambda }_{\text{cx,iz}}=c_{\text{s,i}}/(n{⟨\sigma v⟩}_{\text{cx,iz}})$

This fluid modeling is theoretically limited to highly collisional, charge-exchange-dominated plasma regions (i.e., divertor targets). Therefore, $D_{n_{\text{n}}}$ requires being bounded to maintain numerical stability. Indeed, when the plasma temperature and density become too low, Eq. 2 leads to unphysical values (up to $D_{n_{\text{n}}}=10^{12}$ ${\text{m}}^2$/s) that lead to computation overflow. Therefore, in all present computations, $D_{n_{\text{n}}}$ has been bounded to $D_{n_{\text{n}},\text{\hspace{0.17em}max}}=20000{\text{m}}^2/\text{s}$ and $D_{n_{\text{n}},\text{\hspace{0.17em}min}}=10D$, where $D$ is the value of plasma diffusion. A smoothing function, softplus $f_{\text{sp}}$, has been applied on both limits with:

$f_{\text{sp}}\left(D_{n_{\text{n}}}\right)=\left\{\begin{array}{c}{D}_{n_{\text{n}},\text{\hspace{0.17em}max}},{\mathrm{D}}_{n_{\text{n}}}\ge D_{n_{\text{n}},\text{\hspace{0.17em}max}}+kw\hfill \\ D_{n_{\text{n}},\text{\hspace{0.17em}max}}-w\text{ln}\left(1+{\text{e}}^{-\frac{D-D_{n_{\text{n}},\text{\hspace{0.17em}max}}}{w}}\right),D_{n_{\text{n}},\text{\hspace{0.17em}max}}-kw\le {\mathrm{D}}_{n_{\text{n}}}<D_{n_{\text{n}},\text{\hspace{0.17em}max}}+kw\hfill \\ {\mathrm{D}}_{n_{\text{n}}},D_{n_{\text{n}},\text{\hspace{0.17em}min}}+kw\le {\mathrm{D}}_{n_{\text{n}}}<D_{n_{\text{n}},\text{\hspace{0.17em}max}}-kw\hfill \\ D_{n_{\text{n}},\text{\hspace{0.17em}min}}+w\text{ln}\left(1+{\text{e}}^{-\frac{D-D_{n_{\text{n}},\text{\hspace{0.17em}max}}}{w}}\right),D_{n_{\text{n}},\text{\hspace{0.17em}min}}-kw\le {\mathrm{D}}_{n_{\text{n}}}<D_{n_{\text{n}},\text{\hspace{0.17em}min}}+kw\hfill \\ D_{n_{\text{n}},\text{\hspace{0.17em}min}},{\mathrm{D}}_{n_{\text{n}}}\le D_{n_{\text{n}},\text{\hspace{0.17em}min}}-kw.\hfill \end{array}\right.(4)$

The two free parameters in Eq. 4 $w$ and $k$ are chosen arbitrarily to ensure a reasonable transition region. Here, $w=0.01\cdot D_{\text{max,\hspace{0.17em}min}}$ and $k=10$. This also makes the linearization of Eq. 2 required to improve convergence of the Newton–Raphson iterations easier [33].

The model is associated with an appropriate boundary condition at the plasma-facing components that takes into account recycling onto the walls and also includes a puff term in the private flux region (PFR) (Figure 1). The following boundary condition is imposed:

$-D_{n_{\text{n}}}\mathrm{\nabla }{n}_{\text{n}}\cdot \mathbf{n}=-R\left(-D{\mathrm{\nabla }}_{\perp }n\cdot \mathbf{n}+nu\mathbf{b}\cdot \mathbf{n}\right)-{\mathrm{\Gamma }}_{\text{puff}},(5)$

where $\mathbf{n}$ is outside normal to the boundary vector, and $R$ is the recycling coefficient, which can take different values depending on the plasma-facing components (PFCs). ${\mathrm{\Gamma }}_{\text{puff}}$ in Eq. 5 is defined by the following expression:

${\mathrm{\Gamma }}_{\text{puff}}=\left\{\begin{array}{c}\frac{N}{A_{\text{puff}}},\text{on}\partial {\mathrm{\Omega }}_{\text{puff}}\hfill \\ 0,\text{on}\partial \mathrm{\Omega }/{\mathrm{\Omega }}_{\text{puff}},\hfill \end{array}\right.(6)$

where $N$ is the intensity of the puff (particles/s), and $A_{\text{puff}}$ is the area of the puff region. $\mathrm{\Omega }$ in Eq. 6 denotes the boundary of the computational domain, while ${\mathrm{\Omega }}_{\text{puff}}$ corresponds to the puff region defined in Figure 1.

3.2 Temperature and density-dependent atomic processes: data sources and implications

Only deuterium is considered in this work, both as plasma ions and neutrals. Even in such a simplified model, the choice of atomic data is crucial for the quality of the obtained solutions. They atomic processes define the interactions between plasma and neutrals as well as radiation processes, hence governing the sources and sinks of particles, energy, and momentum in the system. 1D and 2D atomic data are currently available in the code to determine the charge exchange, ionization, and recombination rate coefficients.

For the ionization and recombination rate coefficients, 1D and 2D expressions are respectively extracted from the Naval Research Laboratory (NRL) Plasma formulary in [30] and from the AMJUEL database [32], such as the following:

- 1D expressions of the ionization and recombination rates are functions of the electron temperature only and are expressed as follows [30]:

${⟨\sigma v⟩}_{\text{iz}}\left(T_{\mathrm{e}}\right)=10^{-11}\frac{{\left(\frac{T_{\mathrm{e}}}{E_{\text{Ry}}}\right)}^{1/2}}{E_{\text{Ry}}^{3/2}\left(6.0+\frac{T_{\mathrm{e}}}{E_{\text{Ry}}}\right)}\text{exp}\left(-\frac{E_{\text{Ry}}}{T_{\mathrm{e}}}\right){\text{m}}^3/s(7)$

${⟨\sigma v⟩}_{\text{rec}}\left(T_{\mathrm{e}}\right)=5.2\times 10^{-20}\frac{E_{\text{Ry}}}{T_{\mathrm{e}}}\left[0.43+\frac{1}{2}\text{ln}\left(\frac{E_{\text{Ry}}}{T_{\mathrm{e}}}\right)+0.469{\left(\frac{E_{\text{Ry}}}{T_{\mathrm{e}}}\right)}^{-1/3}\right]{\text{m}}^3/s,(8)$

with $E_{\text{Ry}}$ = 13.6 eV, $T_{\mathrm{e}}$ in eV.

- 2D expressions use splines in log-log space and write in a generalized form [32]:

$\text{ln}\left({⟨\sigma v⟩}_{\text{iz}}\right)\left(T_{\mathrm{e}},n_{\mathrm{e}}\right)={\displaystyle \sum _{i=0}^8}{\displaystyle \sum _{j=0}^8}{\alpha }_{i,j}\text{ln}{\left(T_{\mathrm{e}}\right)}^i\text{ln}{\left(n_{\mathrm{e}}\right)}^j,(9)$

where ${\alpha }_{i,j}$ are determined from the AMJUEL database. Here, we implemented AMJUEL 2.1.5JH for ionization and 2.1.8JH or 2.1.8a for recombination. Note that AMUJEL2.1.8a does not include three-body recombination.

The introduction of 2D atomic data splines can introduce some issues on the numerical stability of the solution. Furthermore, atomic data are only defined over a given range of temperatures and electron densities, whilst values outside these ranges can be encountered in simulations, making it necessary to extrapolate the atomic data. Thus, for the electron density, atomic rates are assumed to be constant for $n_e>10^{22}{\text{m}}^{-3}$ or $n_e<10^{14}{\text{m}}^{-3}$. For the temperature, NRL expression atomic rates are assumed to be constant for $T_e<0.05$eV for ionization and $T_e<0.1$ eV for recombination. The AMJUEL expressions are extrapolated linearly in log-log space for $T_e<0.1$ eV and $T_e>20$ keV (the latter, however, were never reached in the discussed simulations). The difference in the extrapolation is maintained for the sake of backward compatibility and usually leads to minor changes in the results.

An approximation of OpenADAS [31] thermal charge-exchange rates from adf11 files is used for charge-exchange rate coefficients because neutrals are assumed to be thermalized. As in Eq. 9, a similar spline of the given atomic data is made but for the electron temperature only, such as

$\text{ln}\left({⟨\sigma v⟩}_{\text{cx}}\left[{\text{m}}^3/\text{s}\right]\right)={\displaystyle \sum _{i=0}^4}{\alpha }_i{\left(\text{ln}\left(T_{\mathrm{e}}\left[\text{eV}\right]\right)\right)}^i,(10)$

with ${\alpha }_i$ = $[32.59,0.4518,0.0358,8\times 10^{-3},6.837\times 10^{-4}]$. For $T_{\mathrm{e}}<0.1$ eV, the spline is linearly extrapolated in log-log space.

Comparisons of the evolution of the ionization, charge-exchange, and recombination atomic rate coefficients using 1D and 2D expressions as a function of electron temperature are shown in Figure 2 for different values of density. The rate coefficients computed from the NRL expressions (magenta lines for both ionization and recombination rates in Figure 2) are similar to those obtained using data from AMJUEL 2.1.5JH for ionization and from AMJUEL 2.1.8a for recombination. As a consequence, in problems where three-body recombination is not of interest, NRL atomic data will be preferred because of their lower computational cost. However, in low-temperature and high-density regions like the divertor region, three-body recombination becomes crucial, and the AMJUEL database must be preferred. Figure 2B shows the large difference between NRL and AMJUEL predictions for $T_{\text{e}}<$ 1 eV: the AMJUEL database predicts a large increase of the recombination rate coefficient as soon as the density increases. In this paper, we will use AMJUEL 2.1.5JH and 2.1.8JH data.

Figure 2

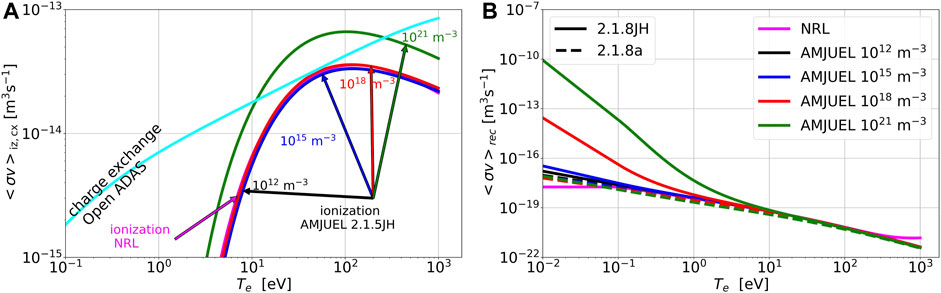
Figure 2. Comparisons of ionization and charge-exchange (A) and recombination (B) atomic rate evolutions as a function of electron temperature for different values of density. (A) Ionization rates from NRL [30] (Eq. 7) and AMJUEL 2.1.5JH [32] (Eq. 9) and charge-exchange atomic rates from OpenADAS [31] (Eq. 10). (B) Recombination atomic rates from NRL [30] (Eq. 8) and AMJUEL 2.1.8JH and 2.1.8a [32] (Eq. 10).

3.2.1 Neutral diffusion model validity

With the given charge-exchange and ionization atomic rate coefficients, we can now estimate the neutrals’ mean free path dependency on plasma density and temperature from Eqs 2, 3. For simplicity, we assume here $T_{\text{i}}=T_{\text{e}}$. Figure 3 shows that electron density has more impact on the mean free path of neutrals than plasma temperature. Therefore, if plasma density at the vicinity of LCFS is lower than 2–3 $\times 10^{19}$ ${\text{m}}^{-3}$, the fluid model Eq. 1 predicts almost free penetration of neutrals up to the separatrix. In addition, this model is valid in the charge-exchange dominated regimes, where ${\lambda }_{\text{cx}}<{\lambda }_{\text{iz}}$. We can see that this condition is confirmed for most of the $(n_{\text{e}},T)$ space. Moreover, the conditions where the model fails correspond to quite dense and moderately hot plasma regions, which can be seen in SOL for a sheath-limited regime, although this regime is not of great interest for the operation of modern tokamaks. This combination of plasma density and temperature directly reflects the parameter space where the charge-exchange rate is lower than the ionization rate, as shown in Figure 2A. As it will be shown in Section 6.1, the condition ${\lambda }_{\text{cx}}<{\lambda }_{\text{iz}}$ may also fail at the vicinity of the LCFS (second row of Figure 11). However, the ionization mean free path is only slightly lower than the charge exchange one, and the neutral density is already rather negligible at the same locations.

Figure 3

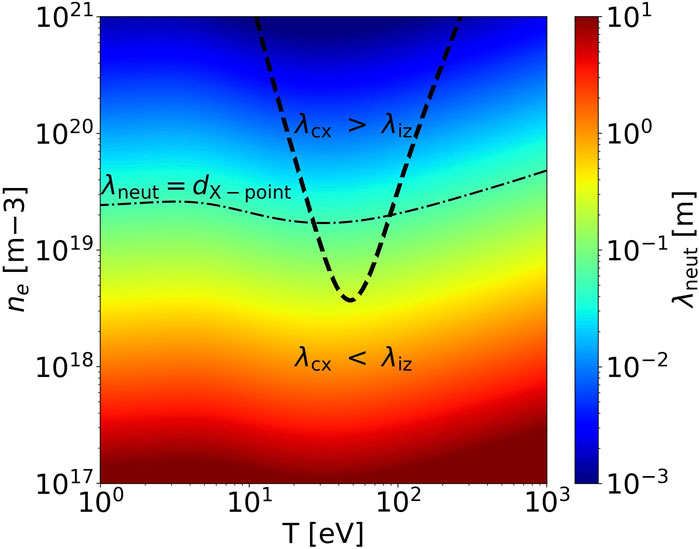
Figure 3. Mean free path of neutrals ${\lambda }_{\text{neut}}={(1/{\lambda }_{\text{cx}}+1/{\lambda }_{\text{iz}})}^{-1}$ as a function of plasma density and temperature ($T_{\text{i}}=T_{\text{e}}$ assumed). The dashed line shows the edge between ionization and charge-exchange dominant regions. The dash-dotted line shows the distance from the lower divertor and baffle to the LCFS.

We also neglect the impact of molecules in the model; that is, we suppose that neutral deuterium enters the computational domain in the form of atoms. Although this simplification might be important in the case of puff located in the far SOL [17], in this work, this is believed to have a smaller impact because the source of neutral particles is close to the strike points in the private flux region (Figure 1). In addition, for all simulations considered in this work, the total particle source due to recycling was 2–3 orders of magnitude higher than the puff rate. In addition, the front of the charge-exchange rate in most simulations, except for the lowest density one, was located in the vicinity of the strike points. This also supports the validity of the assumption of thermalized neutrals. Moreover, the total charge-exchange source was generally higher than the recycling one by 5%–30% for lower and average puff rates, reaching about an order of magnitude larger value for the most detached simulation considered further.

Therefore, we can state here that the employed neutral model assumptions hold rather well in the discussed simulation range, being most applicable for the highest density, charge-exchange dominant regimes, which also correspond to the hypothesis assumed in [27]. Readers interested in a more general discussion of the validity of neutral fluid models may refer to the recent publication by Kvist et al. [21], which also provides a good overview of state-of-the-art neutral fluid models.

3.3 Numerical and simulation setup

3.3.1 Numerical setup

The equations introduced in Supplementary Appendix A, together with the neutral model described in Section 3.1, are resolved using the high-order finite-elements code SOLEDGE-HDG [25, 33]. The space discretization is based on the hybrid discontinuous Galerkin method on an unstructured triangle mesh, as shown in Figure 1. It is composed of approximately 80,000 triangular elements with interpolation polynomial of degree $p$ = 4 (resulting in approximately 1,200,000 nodes) partitioned into eight subdomains. It is refined at the upper and lower divertors, lower baffle, and low-field side (LFS) limiters to deal with the stiff gradients occurring in these plasma regions. Simulations are run on 32 CPUs, and reaching a steady state takes a few hours, thanks to the very efficient time-marching procedure implemented in the code [25, 33].

3.3.2 Magnetic equilibrium and plasma current reconstruction

Given that the experimental magnetic equilibrium is reconstructed using a simplified rectangular grid, it has significant numerical artifacts (i.e., non-zero magnetic field divergence or noise at the edge of the computational domain). These artifacts necessitate post-processing to adapt the equilibrium for utilization on the refined mesh required by the simulations.

The 2D profile of the poloidal flux is approximated employing a bi-variate cubic spline with a small smoothing factor chosen to reasonably damp out spurious irregularities in the magnetic field at the wall. Using the given spline, the poloidal component of the magnetic field is thus calculated according to [34] as

$B_R=-\frac{1}{2\pi R}\frac{\partial \psi }{\partial Z},(11)$

$B_Z=\frac{1}{2\pi R}\frac{\partial \psi }{\partial R},(12)$

where $(R,Z)$ are the radial and vertical coordinates in a cylindrical coordinate system, $(B_R,B_Z)$ are the radial and vertical components of the magnetic field, and $\psi$ is the poloidal flux. The comparison between the bi-linear interpolation of $B_Z$ obtained experimentally and after the smoothing procedure mentioned above (Eqs 11–12) is shown in Figure 4. The initial $B_Z$ component obtained experimentally shows rather noisy iso-lines, especially in the far SOL, at the LFS antenna, and beyond. Because the poloidal magnetic field is crucial to evaluate transport operators (see Supplementary Appendix A), such noise leads to irregularities in the plasma solution (i.e., multiple stagnation points on LFS antennas) and also reduces the numerical stability of the code. The toroidal component of the magnetic field $B_{\varphi }$ is simply interpolated using a bi-variate cubic spline on the computational mesh. Finally, the plasma current is interpolated bi-linearly because it only occurs into the Ohmic heat source and, hence, does not affect the numerical stability too much.

Figure 4

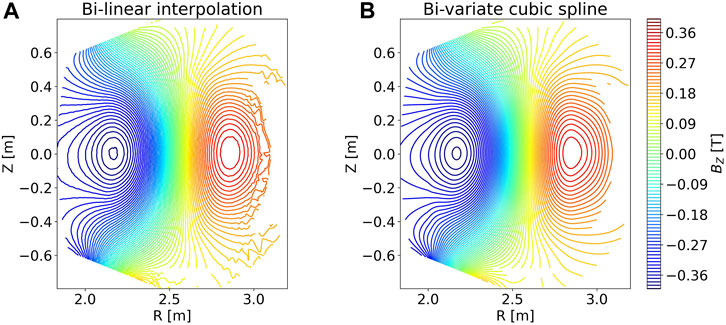
Figure 4. Comparison of the magnetic field component $B_Z$ isolines obtained using bi-linear interpolation of experimental data (A) and a bi-variate cubic spline and Eq. 12 onto the computational mesh (B).

3.3.3 Simulation setup

$•$ The plasma is assumed to be a pure deuterium plasma with $Z_{\text{eff}}$ = 1 with corresponding self-consistent Ohmic heating source. The latter was the only heating source in the discussed simulations. The details on the Ohmic source expression are discussed in Supplementary Appendix A.

$•$ All perpendicular diffusion and conduction coefficients $\mu$, $D$, ${\chi }_{\mathrm{i}}$ and ${\chi }_{\mathrm{e}}$ are constant and equal to $1{\text{m}}^2/\text{s}$, which leads to a reasonable match to the experimental density profiles (which are demonstrated in [25, 35]), while maintaining the code numerical stability. The implementation of a self-consistent turbulent model to define perpendicular transport properties of plasma is ongoing work that is beyond the scope of the current article.

$•$ Recycling on the wall in this work is set constant and equal to $R_{\text{wall}}$ = 0.998, which corresponds to 99.8% of the ions re-emitted as neutrals on the wall. This value showed the best match of the average plasma density evolution during the full discharge simulation in [25].

$•$ Parallel diffusion coefficients are chosen such that $k_{\Vert \mathrm{i}}=60[{\text{Wm}}^{-1}{\text{eV}}^{-7/2}]$ and $k_{\Vert \mathrm{e}}=2000[{\text{Wm}}^{-1}{\text{eV}}^{-7/2}]$ according to [36].

$•$ Sheath-transition coefficients are kept constant for the whole boundary with ${\gamma }_{\mathrm{i}}=2.5$, ${\gamma }_{\mathrm{e}}=4.5$.

$•$ Neutrals are also generated at gas puff locations with a prescribed flow rate that has been varied between $3\times 10^{19}$ and $3.25\times 10^{20}$ in the range of experimental values [25].

In the simulations, the gas valve is located in the private flux region of the lower divertor; see Figure 1.

4 Impact of a non-constant neutral diffusion on neutral transport and plasma equilibrium

Simulations are performed here with a constant gas puff of $1\times 10^{20}$ particles/s. The solution obtained with a self-consistently determined neutral diffusion $D_{n_{\text{n}}}$ (Eq. 2) is compared with the solution obtained with a constant neutral diffusion equal to $1000{\text{m}}^2/\text{s}$, as a typical value used in previous version of the code.

The self-consistently determined $D_{n_{\text{n}}}$ is first plotted in Figure 5. The results show that $D_{n_{\text{n}}}$ varies a great deal in the poloidal cross section. Its values are much higher than the constant value of 1,000 ${\text{m}}^2$/s everywhere except near the separatrix in the lower divertor region. As a consequence, we can expect a large impact on the transport of the neutrals and, hence, on the source’s distribution for the plasma with respect to solutions at constant diffusion $D_{n_{\text{n}}}$.

Figure 5

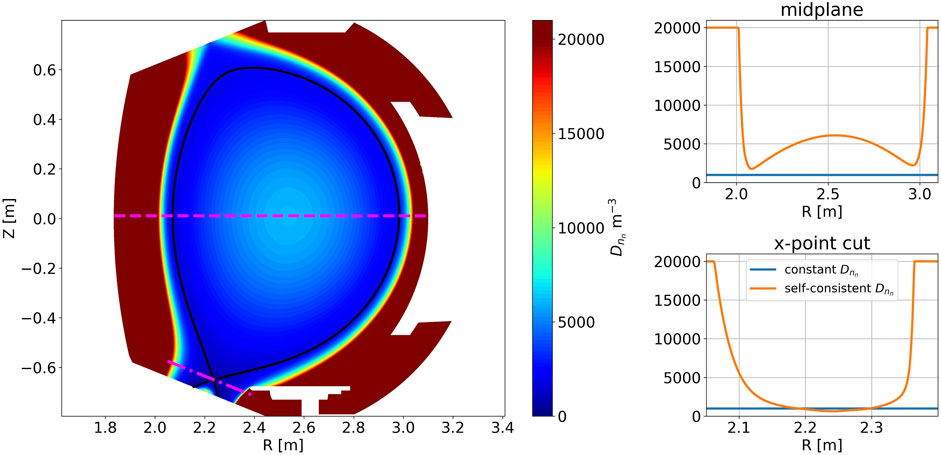
Figure 5. 2D poloidal map of the non-constant neutral diffusion $D_{n_{\text{n}}}$, as defined by Eq. 2 (left). Profiles correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line).

This is supported by the estimations of the mean free paths of neutrals ${\lambda }_{\text{neut}}$ from Eq. 3. The results are plotted in Figure 6. The main differences between the two solutions lie in the far SOL, where in the solution with a non-constant, $D_{n_{\text{n}}}{\lambda }_{\text{neut}}$ is about one order larger than in the solution with constant diffusion and of the order of 1 m and larger. This means that neutrals can easily penetrate from the walls into the core, crossing the separatrix. This seems coherent with what is observed in WEST discharges and, more generally, metallic wall devices [37], where, after short transients, wall-recycling tends to be the dominant contribution to plasma fueling.

Figure 6

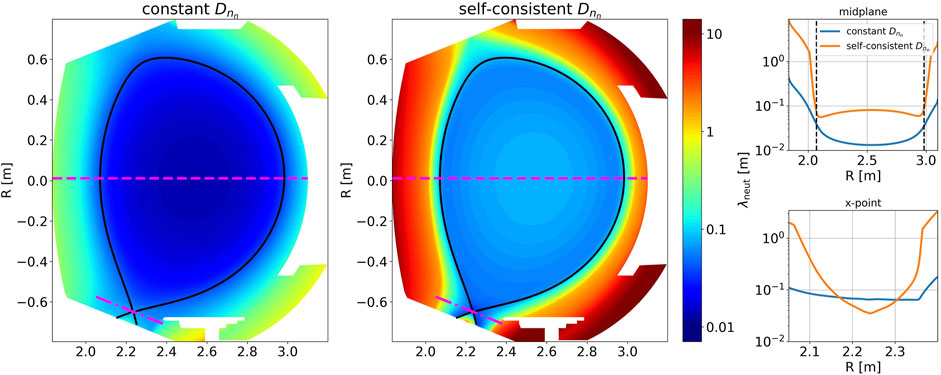
Figure 6. 2D poloidal map of the neutral mean free path as defined from $D_{n_{\text{n}}}$ by Eq. 3 for a simulation with constant $(1000{\text{m}}^2/\text{s})$ (left) and non-constant (middle) $D_{n_{\text{n}}}$. Profiles correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line).

At the same time, with a non-constant $D_{n_{\text{n}}}$, ${\lambda }_{\text{neut}}$ is lower around the X-point and along the divertor legs. This better describes the propagation of neutrals through the dense and rather hot plasma at the divertor.

As expected, these changes in the transport of neutrals impact their distribution in the whole cross section, as shown by the 2D poloidal map of neutral density $n_{\text{n}}$ in Figure 7 (middle row). A non-constant $D_{n_{\text{n}}}$ results in a more uniform distribution of neutrals in the far SOL and slightly lower penetration through the divertor.

Figure 7

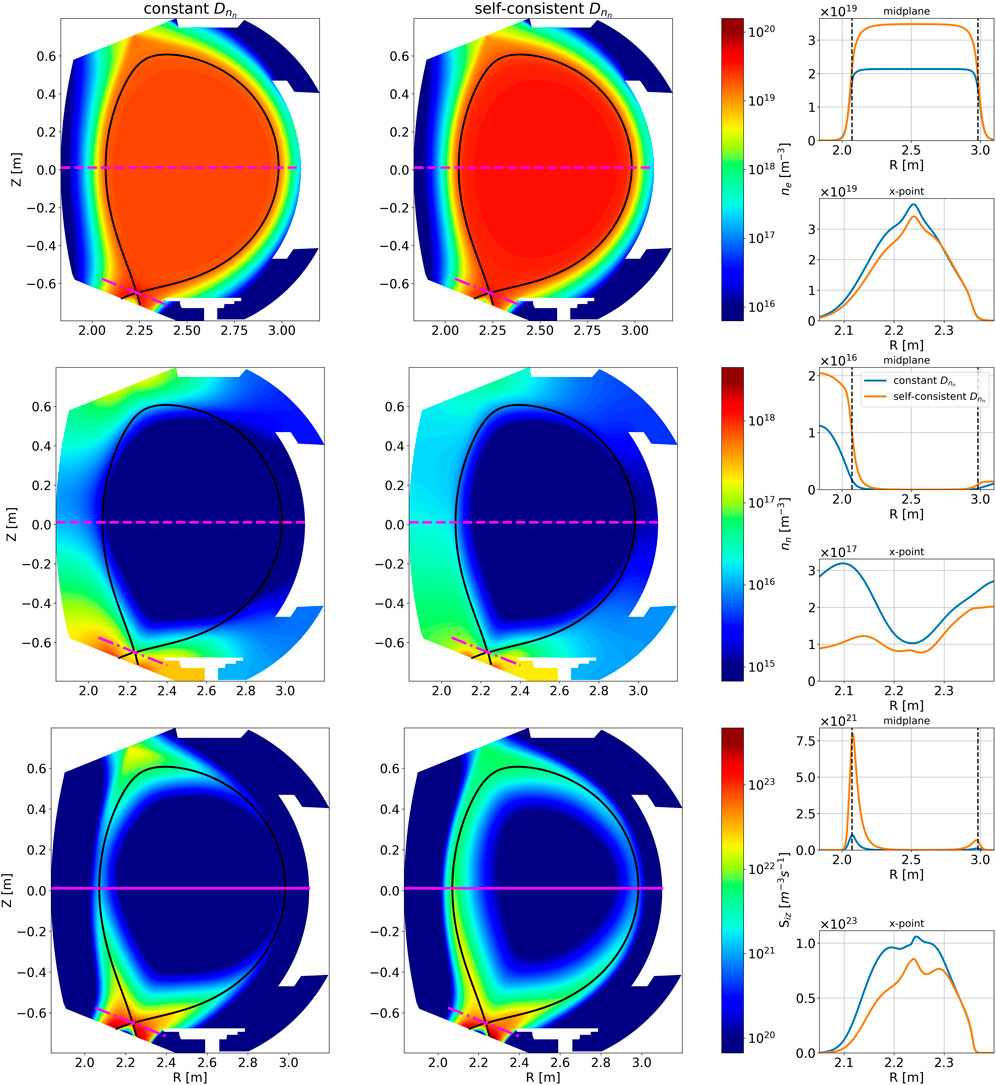
Figure 7. Comparison of solutions with constant ($1000{\text{m}}^2/\text{s}$) (left) and non-constant (Eq. 2) (right) $D_{n_{\text{n}}}$: (top line) plasma density $n_e$, (middle line) neutral density $n_0$, (bottom line) ionization source $S_{iz}$. Profiles for cases with constant $D_{n_{\text{n}}}$ (blue curves) and self-consistent $D_{n_{\text{n}}}$ (orange curves) correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line). WEST∼shot∼\#∼54487.

This is qualitatively similar to what can be observed using a more sophisticated kinetic approach in the Monte Carlo solver EIRENE [38], as shown, for example, in recent SOLEDGE3X-EIRENE simulations (Figure 10 in [39]).

As mentioned above, the higher propagation of neutrals from the walls into the core with the non-constant $D_{n_{\text{n}}}$ model leads to an increase in the core plasma density (Figure 7 (top row)) as well as a more pronounced source of ionization along the entire separatrix (Figure 7 (lower row)). In addition, in the lower divertor, near the targets, the plasma is so dense that $D_{n_{\text{n}}}$ predicted by Eq. 2 is less than 1,000 ${\text{m}}^2$/s, which means that neutrals cannot propagate as far as predicted by the previous simple model with a constant $D_{n_{\text{n}}}$.

Therefore, with non-constant $D_{n_{\text{n}}}$, the neutral density $n_{\text{n}}$ is lower immediately above the X-point and around the divertor targets. Therefore, power and energy losses due to charge-exchange processes are lower, and we can observe an enlargement of the zones at higher temperatures and slightly higher Mach numbers around the divertor, as shown by the comparison between the left and center columns in Figure 8.

Figure 8

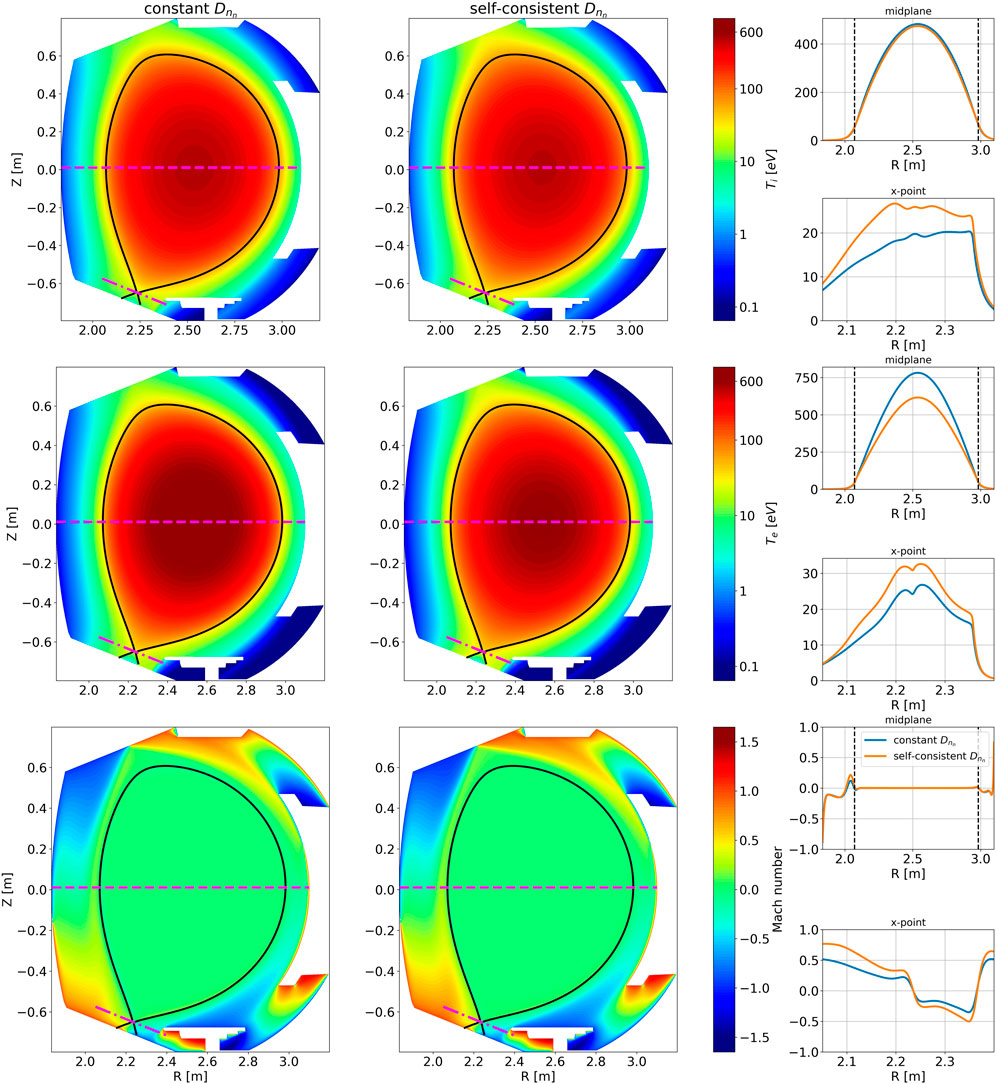
Figure 8. Comparison of solutions with constant ($1000{\text{m}}^2/\text{s}$) (left) and non-constant (Eq. 2) (right) $D_{n_{\text{n}}}$: (top line) ion temperature $T_{\text{i}}$, (middle line) electron temperature $T_{\text{e}}$, (bottom line) Mach number $M$. Profiles for cases with constant $D_{n_{\text{n}}}$ (blue curves) and self-consistent $D_{n_{\text{n}}}$ (orange curves) correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line). WEST∼shot∼\#∼54487.

In summary, this new modeling of neutral transport with self-consistent diffusion removes $D_{n_{\text{n}}}$ as a free parameter and allows neutral transport to be modeled in a more sophisticated physics-based way, which is a beneficial step towards predictive modeling.

5 Gas puff scan

In this section, we describe a gas puff scan investigation, which has been conducted in order to cover all major plasma regimes [36], that is, sheath-limited, high-recycling, and detached. The gas puff rates are varied from $3\times 10^{19}$ to $3.25\times 10^{20}$ particles per second, while the other parameters are kept fixed. These values are in the range of the experimental ones during the WEST shot #54487 [25].

It must be noted that these values of puff rates are at least two orders of magnitude lower than the recycled neutral flux from the wall. Moreover, the change of puff modifies the magnitude of the heat source because the plasma current profile remains the same, while the plasma resistivity has been calculated self-consistently (Supplementary Appendix Equation S7). The increase of the Ohmic heating power with puff rate reaches about 50% of the initial value, varying between 1 MW and 1.5 MW.

We also should underline that this pure puff scan only exists in numerical simulations because changes in the plasma regime will inevitably lead to the modification of the cross-field transport of plasma. Moreover, in real experiments, it is known that transport is not constant across the poloidal cross section; it is usually enhanced at the LFS by interchange instability [40]. Although the work on implementing the self-consistent turbulent model to cover these phenomena is ongoing, it lies beyond the scope of the paper. On top of that, such “isolation” of the pure puff scan effect is an interesting feature, allowing a separate impact on plasma equilibrium due to different drivers.

5.1 Impact of the gas puff on the plasma equilibrium

The evolution of plasma and neutral quantities with gas puff rates is shown in Figures 9, 10. These simulations are representative of sheath-limited, high-recycling, and detached plasma regimes.

Figure 9

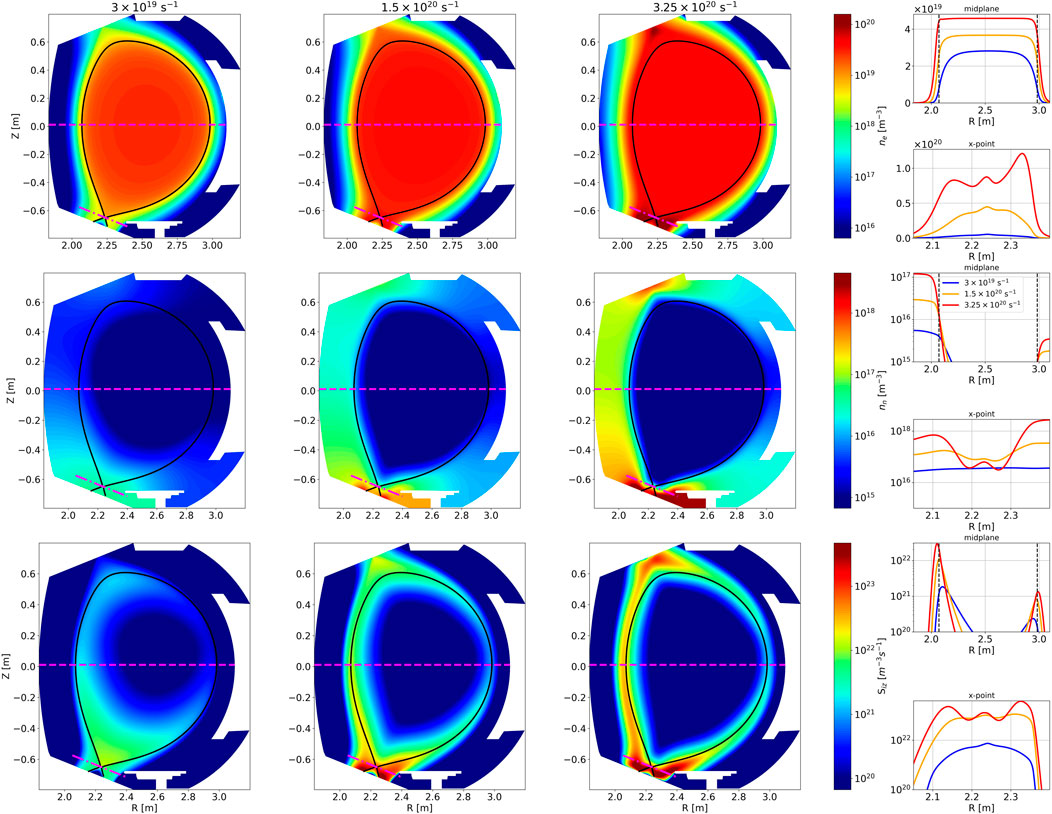
Figure 9. Evolution of plasma equilibrium with gas puff rates ($3\times 10^{19}$, $1.5\times 10^{20}$, $3.25\times 10^{20}$ particles per second): (top line) plasma density $n_{\text{e}}$, (middle line) neutral density $n_{\text{n}}$, (bottom line) ionization source $S_{\text{iz}}$. These solutions are representative of sheath-limited, conduction-limited and detached plasma regimes. Profiles for puff rates of $3\times 10^{19}$ (blue curves), $1.5\times 10^{20}$ (orange curves) and $3.25\times 10^{20}$ (red curves) particles/s correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line). WEST shot \#54487.

Figure 10

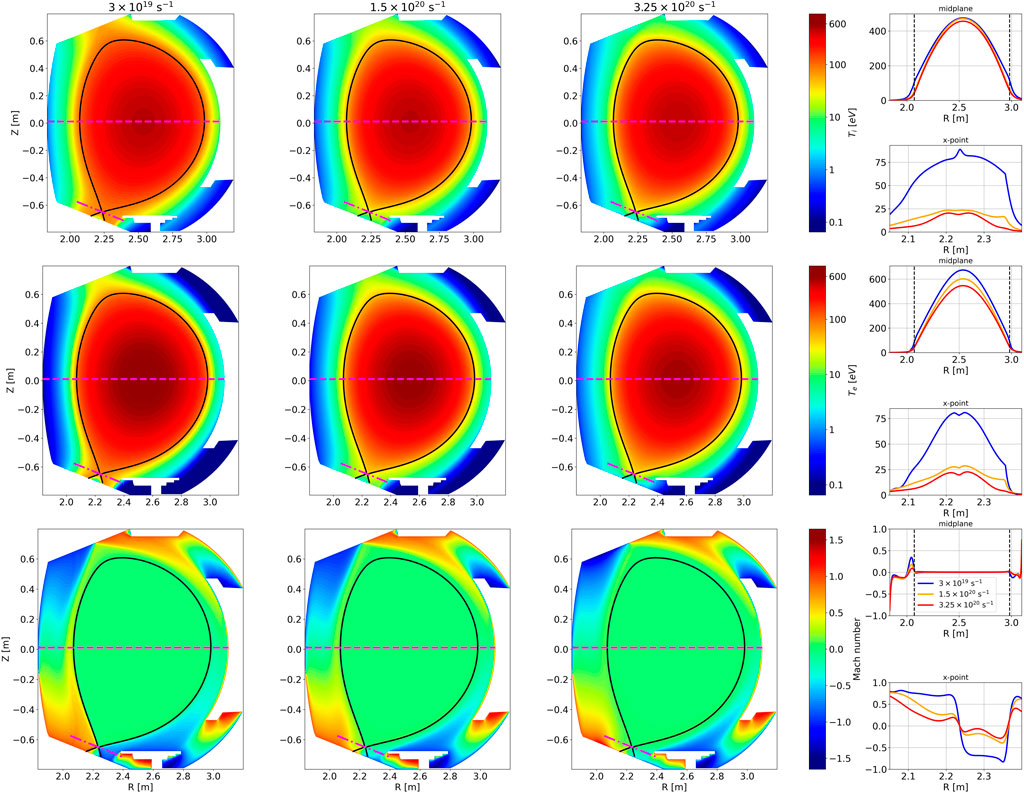
Figure 10. Evolution of plasma equilibrium with gas puff rates ($3\times 10^{19}$, $1.5\times 10^{20}$, $3.25\times 10^{20}$ particles/s per second): (top line) ion temperature $T_{\text{i}}$, (middle line) electron temperature $T_{\text{e}}$, and (bottom line) Mach number $M$ These solutions are representative of sheath-limited, conduction-limited and detached plasma regimes. Profiles for puff rates of $3\times 10^9$ (blue curves), $1.5\times 10^{20}$ (orange curves) and $3.25\times 10^{20}$ (red curves) particles/s correspond to the cuts at midplane (dashed line) and through the X-point (dash-dotted line). WEST∼shot∼\#∼54487.

5.1.1 Plasma density distribution

As expected, the increase in puff rate leads to the global increase of particle content of the plasma (Figure 9 (top row)). Moreover, the density distribution in the poloidal cross section is modified: the larger the puff, the higher the density of the plasma in the SOL, and the greater its propagation towards the wall. The most significant change can be observed in the divertor region. This is particularly evident on the density profiles at the midplane and through the X-point: while the core density increases by less than two times, the density in the vicinity of the X-point rises by more than an order of magnitude.

5.1.2 Neutral distribution

The changes observed on the plasma density profile are caused by changes in the distribution of the ionization source (Figure 9, bottom row). Indeed, at the lowest puff rate, the neutrals are mainly ionized inside the core, whereas as the puff rate increases, the ionization region becomes increasingly narrow around the separatrix and also expands into the SOL. Note that at the highest puff rate, the ionization front is no longer located at the lower divertor target but has moved slightly upstream, which may be one of the features of detachment. The effects described above are also reflected in the neutral density distribution (Figure 9 (middle row)): at the lowest puff rate ($3\times 10^{19}$ particles/s), a non-negligible amount of neutrals is located inside the confined region immediately above the X-point, while at the highest puff rates ($3.25\times 10^{20}$ particles/s), the neutrals are almost all moved into the SOL.

5.1.3 Temperature distribution

Important qualitative changes are also observed in the temperature distribution (Figure 10 (top and middle rows)). As the density of the core increases with the puff, $T_{\text{e}}$ decreases in the confined region while $T_{\text{i}}$ stays almost unchanged due to the higher collisionality, and, therefore, equipartition. Note also that the region where $T_{\text{e}}$ is highest widens in the far SOL, while $T_{\text{i}}$ decreases slightly there. For the highest puff rate, the temperature at the targets drops below 1 eV, and as for the ionization source $S_{\text{iz}}$, it is slightly detached. Moreover, the temperature values change significantly between the midplane and the divertor.

5.1.4 Mach number distribution

The Mach number is only slightly affected globally by the increase in puff rates except in the vicinity of the X-point into the SOL (Figure 10 (bottom row)). Indeed, profiles at midplane remain almost unchanged, while changes are more significant through the X-point. The Mach number is high for the lowest puff plasma, meaning that a significant part of energy flux is driven by convection. It drops below 0.5 in absolute value for the highest puff case and only reaches 1 at the boundary, according to the Bohm boundary conditions.

All these features suggest that the simulation at the lowest puff corresponds to a sheath-limited regime, characterized by high temperatures in the lower divertor region (peak values of approximately 70 eV) and almost no temperature change between the midplane and the targets, while the simulation at the highest puff corresponds to a detached regime, characterized by low temperatures at the divertor target (peak values of approximately 1 eV) and a significant change between the midplane and the targets. Section 5.2 will focus on the lower divertor target, and detailed comparisons between core, separatrix, and target peak values will be made in Section 5.4.

5.1.5 Neutrals mean free path distribution

The evolution with gas puff is plotted in Figure 11 (top row). For the lowest density case, the mfp of the neutrals does not fall lower than 10 cm in the whole plasma domain and not lower than $\approx$50 cm in the lower divertor region in particular. This explains well the concentration of $S_{\text{iz}}$ above the X-point for this lowest puff case (Figure 9 (bottom of the first column)). For the highest puff rate, ${\lambda }_{\text{neut}}$ falls to a few cm in the lower divertor and above the baffle, which is lower than the distance to the confined plasma in these regions. Consequently, the ionization source is mostly located in the non-confined region, close to the targets of the lower divertor (Figure 9 (bottom of the third column)). As for the SOL near the LFS antenna and high-field side (HFS) limiter, even though the mfp at the vicinity of the separatrix decreases to $\approx$3–4 cm, deeper into the SOL, it stays high and even increases with the increased gas puff. This latter effect can explain the change of $S_{\text{iz}}$ with puff rate. Lower mfp at the separatrix leads to the shift of the peak value of the ionization source outside of the LCFS (Figure 9), lower row, and midplane slice); however, the total source increases because the neutrals escape the wall region more easily.

Figure 11

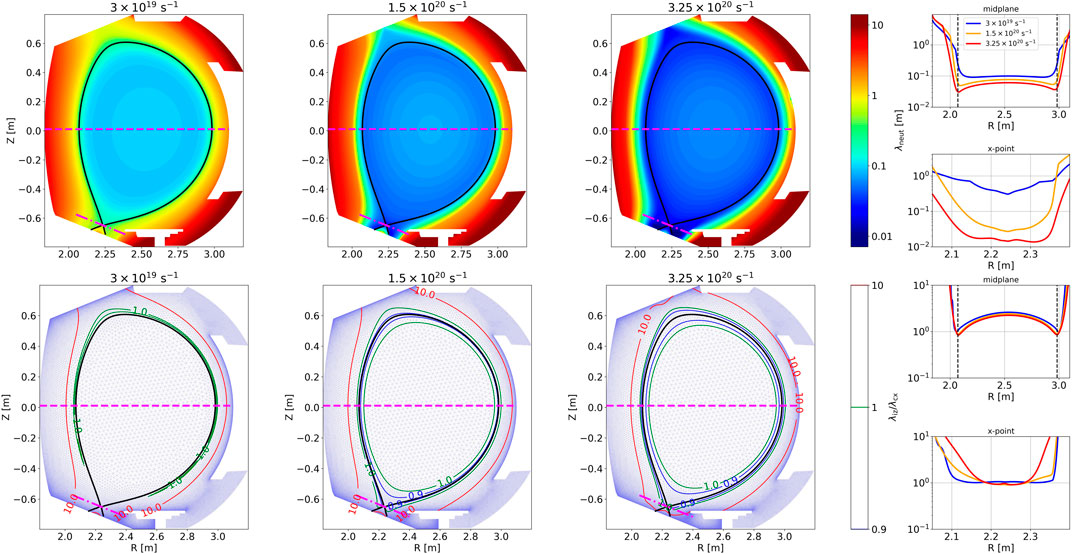
Figure 11. Top line: 2D poloidal map of neutral mean free path as defined by equation Eq. 2 for a simulation with constant low (left) average (middle) and high (right) puff rates. Bottom line: contour plot of the ratio ${\lambda }_{\text{iz}}/{\lambda }_{\text{cx}}$ for the simulations with different puff rates. One can see that in the most part of the domain, except for the vicinity of the separatrix, charge-exchange prevails over ionization. Rightmost column of the plots introduces a midplane cut of 2D plots (magenta dashed line) and x-point cut (dash-dotted line) for puff rates of $3\times 10^{19}$ (blue curves), $1.5\times 10^{20}$ (orange curves) and $3.25\times 10^{20}$ (red curves) particles/s.

The bottom row of Figure 11 demonstrates that in most parts of the computational domain, the ionization mfp is larger than the charge-exchange mfp. This is only slightly violated in the vicinity of the LCFS when expanding this region for higher puff-rate simulations. However, one can see that ${\lambda }_{\text{iz}}<{\lambda }_{\text{cx}}$ in the part of the domain where neutral density (Figure 9, middle row) becomes quite small. Therefore, we may state that in most of the domain, charge-exchange reactions dominate over ionization reactions, confirming the applicability of the neutral model.

5.2 Plasma quantities at the divertor targets

The evolution of plasma quantities at the divertor targets as a function of gas puff rates ($3\times 10^{19}$, $1.5\times 10^{20}$, $3\times 10^{20}$, and $3.25\times 10^{20}$ particles/s) is investigated here. In addition, estimations of the sputtered tungsten fluxes are provided at the baffle (subscript “B” on the figures), lower divertor (LD), and upper divertor (UD) (Figure 1). Compared to the previous section, we also consider the simulation immediately before the particle flux rollover to emphasize the onset of the detachment.

5.2.1 Impact on density and temperatures

The profiles in Figure 12 (top row) show that the solutions evolve from a highly attached plasma with temperatures $T_{\text{i,e}}$ up to 80 eV to a detached plasma with temperatures $T_{\text{i,e}}$ decreasing to approximately 1 eV at the LD as the gas puff rates are increased. At this highest fueling rate, the high density and low temperature correspond to a higher recombination rate (Figure 2), which may lead to further energy losses. This is perhaps why the simulation becomes unstable even for higher puff rates: the solution must be sought on a qualitatively different branch, corresponding to detachment.

Figure 12

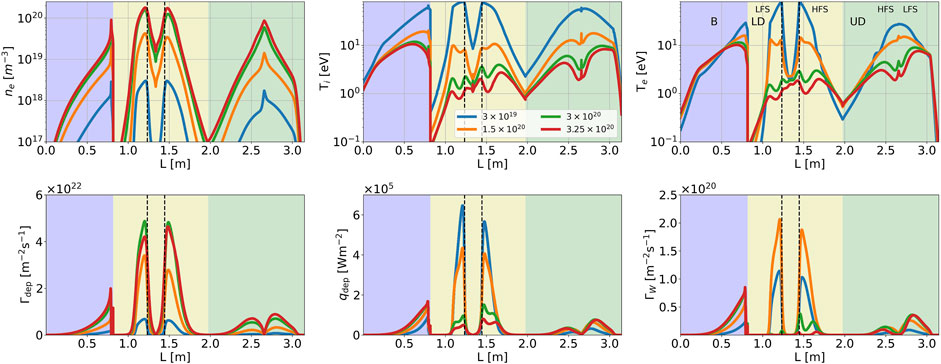
Figure 12. Comparisons of plasma quantity profiles along the tokamak wall for four values of the gas puff rates: $3\times 10^{19}$ particles/s, $1.5\times 10^{20}$ particles/s, $3\times 10^{20}$particles/s, and $3.25\times 10^{20}$ particles/s. Top row from left to right: electron density, $n_{\text{e}}$, and ion $T_{\text{i}}$ and electron $T_{\text{e}}$ temperatures. Bottom row from left to right: particle flux deposited onto the targets ${\mathrm{\Gamma }}_{\text{dep}}$, heat flux $q_{\text{dep}}$, and estimated sputtered tungsten flux ${\mathrm{\Gamma }}_{\text{W}}$ (Eq. 16). B, baffle; LD, lower divertor; UD, upper divertor. The locations of strike points for LD are shown with dashed lines.

5.2.2 Impact on heat flux

The heat flux at the targets (shown in Figure 12, bottom center) begins to decrease when the puff is increased from $3\times 10^{19}$ to $1.5\times 10^{20}$ particles/s but it maintains almost the same shape with a slight asymmetry between the inner and the outer legs and a maximum reached on the former. Note that the heat flux is estimated here, taking into account the tangent angle between the magnetic field and the normal to the surface. However, between $3\times 10^{20}$ and $3.25\times 10^{20}$ particles/s (that correspond to the highest puff rates), the heat flux at the LD targets is not only drastically reduced, but also, the maximum is also now reached on the outer leg. We can also mention the change in the shape of the heat flux profile, even with fixed perpendicular transport coefficients. One can expect even more complex heat flux variations if the restriction is released by employing a more detailed transport model. At the same time, the heat flux increases at the baffle and upper divertor with the gas puff rate to reach, at the highest gas puff rate, a magnitude equivalent to the magnitude at the LD targets, which is, of course, undesirable for WEST operation. The location of the baffle, therefore, seems unfavorable in WEST and places it is facing the hot plasma, which could probably lead to high heating and erosion of this plasma-facing component.

5.2.3 Impact on particle flux

Figure 12 (bottom left) shows the particle flux at the targets monotonously increases with the puff rate up to $3\times 10^{20}$ particles/s. The distribution between the inner and the outer divertor legs also changes with puff rate: the fluxes are nearly equal at the lowest puff rate and become asymmetric when increasing the puff rate before coming back symmetric at the highest puff rates considered here at $3.25\times 10^{20}$ particles/s. At this highest puff rate, the most remarkable change is certainly the drastic reduction of the particle flux at the LD targets while the puff rate has been in only slightly increased from $3\times 10^{20}$ to $3.25\times 10^{20}$ particles/s.

As predicted from theory and demonstrated in the experiments [36], one would expect a faster detachment onset at the inner leg of the divertor. However, due to the proximity of the baffle from the X-point and the LCFS, there are more neutrals near the outer leg (Figure 9, middle row), which leads to more power and momentum losses due to charge exchange, with a corresponding reduction of target temperatures (Figure 12 top row: center ${\mathrm{T}}_{\mathrm{i}}$ and right ${\mathrm{T}}_{\mathrm{e}}$). All these features mean that conditions favorable to detachment in the outer leg of the LD can be achieved more quickly. One can also see that for the simulations at the highest puff rate, the temperatures at the targets reach values approximately or lower than 1 eV, leading to a further increase of recombination energy losses, with volumetric ones being more and more important [36] (Figure 2).

5.3 Impact on the estimated flux of sputtered tungsten

Modeling the material erosion of PFCs depending on plasma conditions is a long-term effort that remains very challenging in fluid transport codes, but it is crucial to target realistic predictions on plasma evolution and fusion performances. A reasonably accurate modeling of this phenomenon can be provided by a dedicated code such as ERO2.0 [41], which can be coupled with SOLEDGE-HDG as proposed in [42]. However, this approach remains computationally expensive, and when only the overall behavior of the wall depending on plasma conditions is of interest, analytical expressions for sputtering such as that proposed in [36] and based on the impact energy of the plasma provide a valuable first guess, as was already shown in [25]. It is written as follows:

$Y\left(E_0\right)=Q{S}_n\left(E_0/E_{\text{TF}}\right)g\left(E_{th}/E_0\right),(13)$

$S_n\left(\epsilon \right)=\frac{3.441\sqrt{\epsilon }\text{ln}\left(\epsilon +2.718\right)}{1+6.355\sqrt{\epsilon }+\epsilon \left(6.882\sqrt{\epsilon }-1.708\right)},(14)$

$g\left(\delta \right)=\left(1-{\delta }^{2/3}\right){\left(1-\delta \right)}^2,(15)$

with $E_0$ being the impact energy obtained by the ions in the sheath, estimated as [43] $E_0=(2+m_Z/m_{\text{D}})k_{\text{b}}{T}_{\text{i}}+3Z{k}_{\text{b}}{T}_{\text{e}}$, where $Z$ is the charge of an ion. The term $m_Z/m_{\text{D}}$ is responsible for the energy gained by impurities in the pre-sheath due to friction. Although this term is rigorously valid only in high-collisionality regimes, it is included here to consider the worst-case estimate. $Q$ is a yield factor, $E_{th}$ is a threshold energy estimated from a simple momentum transfer, and $E_{\text{TF}}$ is a binding energy of the material (Thomas–Fermy energy). These last three parameters are fixed for a given impact and target particles. The PFCs are assumed to be made of tungsten. Taking deuterium as an impact ion would lead to an underestimation of the sputtering due to its low mass. The common approach is to use a proxy light impurity. Following our previous work in [42], we will use oxygen as such an impurity with a concentration of 3%. As a worst-case estimate and for simplicity, $Z=8$ is assumed for all ions at the sheath. For the oxygen-impacting tungsten target, the parameters of the model are respectively equal to $Q$ = 2.2, $E_{th}$ = 40 eV, and $E_{\text{TF}}$ = 91,979 eV [44].

Because the sputtering yield is estimated by Eqs 13–15, the flux of tungsten sputtered ${\mathrm{\Gamma }}_{\text{W}}$ is written as:

${\mathrm{\Gamma }}_{\text{W}}=c_{\text{O}}{\mathrm{\Gamma }}_{\text{dep}}Y,(16)$

where ${\mathrm{\Gamma }}_{\text{dep}}$ is the plasma flux deposited on the wall, and $c_{\text{O}}$ = 3% is the concentration of oxygen.

Its evolution with the gas puff rate is shown along the tokamak wall in Figure 12 (bottom row, right column). Despite the increase in plasma flux on the lower divertor (LD) targets, the reduction of the temperatures is more significant and leads to a reduction in tungsten sputtering yields. Indeed, sputtering on the LD targets becomes low for a puff rate of $3\times 10^{20}$ particles/s and almost negligible when the puff rate is increased slightly to $3.25\times 10^{20}$ particles/s. At the same time, the sputtering on the upper divertor (UD) and the baffle increases. This reduction in erosion is also indicative of a high-recycling and detached plasma on the LD targets, which, according to the simulation, can only be achieved by increasing the main ion fueling. Let us remember that these estimations are probably overestimated, as the oxygen concentration is assumed to be fairly high, and the part of the pre-sheath acceleration due to friction is included in Eq. 13. As a consequence, the estimates of the sputtering fluxes are about an order of magnitude larger than those obtained in [25, 42]. Therefore, the quantitative estimations described here should be considered with caution. In addition, because the work employs fluid-averaged plasma quantities, any correlation between plasma variables is neglected here, which possibly can lead to the change of both the shape and the peak values of the estimated sputtered tungsten flux.

The coherence observed in the current results suggests that this rough modeling of erosion, which is dependent on the plasma temperature, one of the most driving parameters in this phenomenon, can nevertheless be used to describe the overall qualitative behavior of the wall in relation to the gas puff.

5.4 Further discussion

The results presented in this paper showed the evolution of plasma quantities as a function of the gas puff rate. These findings can be further discussed to bring new information on some challenging questions related to the tokamak operation.

$•$ We first examine the current results within the same framework proposed by [36] using the 2-point model (2PM) to study density regimes. The plasma density $n_{\text{e}}$, the ion $T_{\text{i}}$ and electron $T_{\text{e}}$ temperatures, and the total dynamic plasma pressure $p=n{k}_{\text{b}}(T_{\text{i}}+T_{\text{e}})+m_{\text{i}}n{u}^2$ are the variables of interest. Figure 13 shows the evolution of their peak values with the gas puff at three locations in the tokamak cross section: the lower divertor outer target, the outer midplane separatrix, and the magnetic axis.

Figure 13

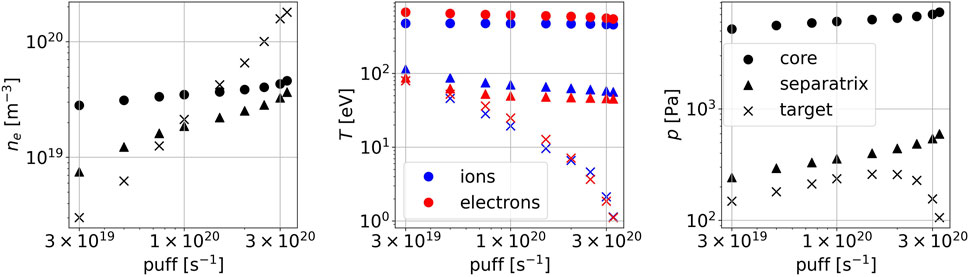
Figure 13. Evolution as a function of puff rate of the density (left), ion (blue) and electron (red) temperatures (middle), total dynamic plasma pressure (right) at three locations in the tokamak cross-section: the magnetic axis (full circles), the outer midplane separatrix (full triangles), and at the target (peak value over the target, crosses).

Considered hereinafter, peak values at the outer targets serve as a valuable proxy for the discussion of the plasma behavior with the change of the puff rate, reasonably reducing the amount of data shown in the figures. We also highlight that if a more detailed perpendicular transport model is included, these peak values (as well as the shape of the profile) can be significantly altered [45]. However, the global trends should be conserved with probably modified exact values of puff rate, corresponding to different regimes.

The temperature evolution at these three locations clearly shows the transition from the sheath-limited to the high-recycling regimes, the latter being characterized by the onset of a significant temperature gradient between the outer midplane and the LD targets. This transition is evaluated here for a gas puff between 5 $\times 10^{19}$ and 7.5 $\times 10^{19}$ particles/s.

The transition from the high-recycling regime to a detached plasma is best shown by the evolution of the plasma pressure (Figure 13, right). For puff rates below 1–2 $\times 10^{20}$ particles/s, there is almost no increase in the pressure drop in the SOL, even though the temperature drop increases significantly. The onset of detachment can be determined between 2 $\times 10^{20}$and 2.5 $\times 10^{20}$ particles/s, where the target pressure moves further and further away from the upstream value and even drops lower than in the case of the lowest puff rate. This is consistent with the observation made in Section 5.1 that the ionization front moves away from the target for the highest puff simulation. According to [46], another characteristic of detachment is when $T<10$ eV, which also corresponds to the simulation with puff rates of about 2 $\times 10^{20}$ particles/s. Note that in these simulations, there is no target density $n_{\text{t}}$ rollover, which is useful, but it is not a mandatory feature of detachment.

Figure 13 also shows the gap between the upstream plasma density (at the separatrix) and in the core (at the magnetic axis), although the latter shows the same tendency to increase with gas puff. However, the density value at the separatrix increases more rapidly than at the magnetic axis, the two becoming comparable at the highest puff rate. In the 2PM analysis of the experiments, when the target and upstream density values are compared, the core or the average $\overline{n_{\text{e}}}$ density values are preferred to those at the separatrix, as they are simpler to evaluate experimentally. Given the significant difference in behavior between the target values and the upstream density values observed in our results, the choice of upstream density (between separatrix, core, and average) will have only a little impact.

It is remarkable that $n_{\text{t}}$ rises faster than linearly as the puff rate is increased. At the same time, current results show that the core density increases much more slowly with the gas puff, which means that fueling the plasma with only gas valves located in the far SOL is a challenging task. This will be even more difficult for ITER and is the subject of recent studies [47, 48].

$•$ The current results also allow us to study the evolution of the distribution of heat channels between ions and electrons by following the $T_{\text{i}}/T_{\text{e}}$ ratio. Because most of the plasma heating is produced by the Ohmic source located in the confined region and acting only on the electrons, $T_{\text{i}}$ is systematically lower than $T_{\text{e}}$ on the magnetic axis. However, from the separatrix $T_{\text{i}}>T_{\text{e}}$, which agrees well with experiments described in the literature [49, 50]. This can be primarily explained by the lower parallel thermal conductivity of the ions, which results in a lower energy transfer from upstream to the targets. Second, the ionization of neutrals is also a source of energy (Supplementary Appendix Equation S6), which is located close to the separatrix, as shown in Section 5.1. The situation is more complicated at the targets, where results do not show any clear trend for ${(T_{\text{i}}/T_{\text{e}})}_{\text{t}}$. In addition to conductivity, all the loss terms, such as recombination, radiation, and charge exchange, come into play and can lead to different power losses in the electron and ion channels for different plasma conditions. In order to better understand this interplay, a deeper investigation of the processes in SOL is foreseen. Collisionality increases for the highest puff rates, and for all three plasma regions considered, $T_{\text{i}}$ tends to equal $T_{\text{e}}$; that is, $T_{\text{i}}/T_{\text{e}}=1$.

$•$ The estimation of the parallel fluxes of particle ${\mathrm{\Gamma }}_{\Vert ,\text{t}}$ and heat $q_{\Vert ,\text{t}}$ at the targets is of major importance for future reactors, as shown in Figure 14. As we have already mentioned, increasing the puff rate causes a particle flow rollover, which is favorable for the divertor erosion problem. A more complex behavior is observed for the heat fluxes. From Figure 14B, one can see that $q_{\Vert ,\text{e}}$ decreases by more than two orders of magnitude, while $q_{\Vert ,\text{i}}$ decreases only by one order of magnitude. This difference in behavior lies in the lower conductivity of ions, leading to the fact that for all simulations, the convective channel is dominant in $q_{\Vert ,\text{i}}$. At the same time, for high target temperature at the lowest puff rate, the $T^{5/2}$ term in parallel heat conductivity almost completely defines the total $q_{\Vert ,\text{e}}$. Therefore, the convective part in $q_{\Vert }\propto T^{3/2}$ (due to the supersonic boundary condition) reduces less with the temperature decrease. Therefore, its contribution is dominant for puff rates larger than 2 $\times 10^{19}$particles/s. Furthermore, taking into account the inertia of ions, it becomes clear why the ion channel begins to dominate over the electron channel, whose inertia is negligible.

$•$ The knowledge of the particle source distribution in the tokamak cross section is useful for the fueling problem. The tokamak cross section has been divided into six characteristic regions, shown in Figure 15B: the confined core region, the high-field side (HFS) and low-field side (LFS) scrape-off layers (SOL), the upper (UD) and lower (LD) divertors, and the baffle. The separation between the core and the SOL plasma has been made along the separatrix, but because the mesh used is not aligned with the magnetic field, the boundary between the regions is not smooth.

Figure 14

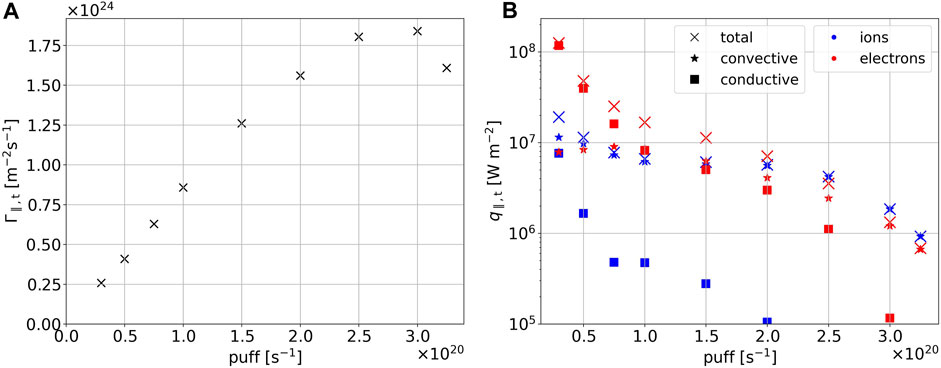
Figure 14. Peak target values for the parallel flux of particle (A) and ion and electron heat (B) predicted by the simulations as the function of the gas puff rate. Additionally, convective (stars) and conductive (squares) contributions to the heat fluxes are shown. WEST lower divertor, outer target.

Figure 15

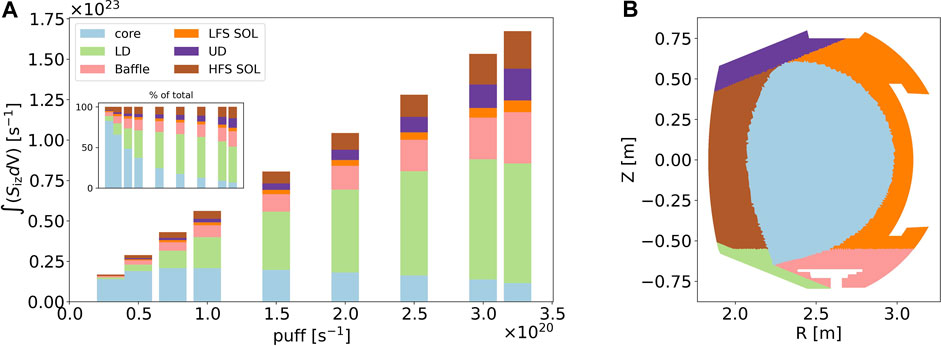
Figure 15. Distribution of the total particle sources in different plasma regions (A). The inset shows the relative part of each region in percentages. Map of the plasma regions (B).

The separation between the other regions is made to take into account the features of the ionization sources observed in the 2D profiles of $S_{\text{iz}}$ (Figure 9). For each simulation, the ionization source $S_{\text{iz}}$ is integrated separately in each region, and the results are shown in Figure 15A as a function of the puff rate. The results show that for puff rates below 5 $\times 10^{19}$ particles/s, the ionization source produced in the core regions is dominant. However, for puff rates from 7.5 $\times 10^{19}$ particles/s, the latter decreases not only relatively (in percent) but also in absolute value. At the highest puff rate, it even falls to a value smaller than the one evaluated at the lowest puff rate. This trend is in agreement with the decrease of the neutral mean free path previously observed in the divertor, baffle, and near-SOL region, as shown in Figure 11. The higher the puff rate, the greater the source in each of the unconfined regions. As expected, the LD region (green) becomes the dominant source of particles from $10^{20}$ particles/s. At 2.5 $\times 10^{20}$ particles/s, the source in the LD region saturates, and the baffle, LD, and HFS SOL contribution become all comparable. This can be explained by the significant decrease in the neutral mean free path in these regions. At the same time, the LFS SOL impact stays negligible because the equilibrium considered in this work is narrow, and neutrals may easily penetrate directly to the core before ionization. Here, we should note again that the fluid-averaged approach can hide some important interactions between plasma and neutral species, which are well described in [18, 21, 22]. This, in turn, may lead to redistribution of sources throughout the domain and should be a part of further investigation.

6 Conclusion and perspectives

This paper investigates the impact of the gas puff magnitude on the mean quantities in a WEST plasma (discharge #54487). The numerical simulations have been performed using the advanced 2D transport code SOLEDGE-HDG based on an original high-order finite-elements method that makes the spatial discretization magnetic equilibrium free. This feature allows accurate discretizing of the tokamak wall and provides a very accurate discretization of the singularities as the X-point or the center of the poloidal section.

In the present work, the fluid neutral transport model has been updated with a self-consistent diffusion that depends on the atomic rates estimated using splines from well-referenced databases and background plasma quantities. This diffusion coefficient is further interpreted by the mean free path of neutrals in the plasma, offering valuable insights into the neutral source distributions depending on the simulation parameters. Additionally, we have presented an investigation into the quality of the magnetic equilibrium reconstruction from experimental data essential for the refined SOLEDGE-HDG meshes.

The main findings of the paper can be summarized as follows.

$•$ The use of an advanced neutral fluid model with a non-constant diffusion significantly improves the accuracy of the results compared with our former simulations carried out with constant diffusion. Constant $D_{n_{\text{n}}}=1000{\text{m}}^2/\text{s}$ of our former simulations is underestimated, except in the divertor region. The new model predicts a stronger transport of neutrals from the tokamak wall with reduced penetration through the divertor region. This leads to an increase in the density of the central plasma and a change in the distribution of ionization sources, which is now more pronounced all along the separatrix. The predicted neutral profile is now qualitatively closer to that obtained with Monte Carlo solvers, such as EIRENE, which represents a significant improvement in the simulation.

$•$ The scan of the gas puff allows the plasma regime to change from sheath-limited to high recycling and then to detached as the puff increases. The second is demonstrated by the appearance of a temperature gradient in the SOL, and the third by the drop in pressure from upstream to the targets due to momentum losses.

- The sheath-limited regime (gas puff rates $3\times 10^{19}$ and $5\times 10^{19}$ particles/s) is associated with low plasma density in both the core and the divertor, a high temperature in the SOL with an almost zero gradient from upstream to the targets, and a high Mach number in the lower divertor. Almost all ionization sources are located in the confined region, with recycled neutrals easily passing through the divertor into the core.

- In the high-recycling regime (gas puff rate between $7.5\times 10^{19}$ and $2\times 10^{20}$ particles/s), the density in the divertor increases significantly, and a temperature gradient is established in the SOL while the Mach number decreased. The ionization source shifts to the separatrix and the lower divertor legs, with many fewer neutrals reaching the core.

- The detached regime (gas puff rate from $2.5\times 10^{20}$ to $3.25\times 10^{20}$ particles/s) is characterized by an ionization source moving upstream of the targets and by a drop in temperature $T$ to approximately 1 eV in front of the divertor. The plasma density significantly increases in the divertor while the number of neutrals in the core becomes negligible.

$•$ As the puff rate increases from $3\times 10^{19}$ particles/s to more than $1\times 10^{20}$ particles/s, the propagation of neutrals from the divertor, the baffle, and through the LCFS becomes increasingly difficult. However, the neutral source coming from the wall is not negligible because of the high mean free path in the LFS and the HFS SOL, even for the highest puff.

$•$ The plasma quantities at the lower and upper divertor, as well as on the baffle, evolve with the gas puff. Hot attached plasmas correspond to the sheath-limited regime, whereas for the detached regime, both $T_{\text{i}}$ and $T_{\text{e}}$ fall below 1 eV at the lower divertor targets. The rollover of density is not observed, while the rollover of particle flux onto both targets of the LD is demonstrated. A drastic reduction of deposited heat flux with the redistribution has been shown for the LD. At the same time, the UD and baffle were still exposed at a level comparable with the LD.

$•$ In a first attempt to address the erosion problem on the PFCs, a rough model based on the impact energy is used to estimate the sputtering flux of tungsten. In the detached regime, the reduction in target temperatures at the lower divertor limits sputtering, which is beneficial for the operation. However, current simulations show that at the same time, the baffle and the upper divertor are highly eroded in WEST.

$•$ The current results also investigate the equipartition of temperature $T_{\text{i}}/T_{\text{e}}$, and how it evolves with the puff rate in various regions of plasma. In the core region, where Ohmic heating is applied to the electrons, the ion temperature is always lower than the electron temperature. The situation inverses changes in the SOL, where $T_{\text{i}}>T_{\text{e}}$ in correspondence with higher parallel conductivity of electrons and ionization sources, transferring energy to ions. No clear trend is shown at the divertor plates. This is probably caused by a cumbersome interplay of various sources and sinks acting in this region and requires a deeper investigation.

$•$ The distribution of the particle ionization source also changes with the puff rate. As the puffing rate increases, the source gradually diminishes in the core while increasing in the SOL, especially at the lower divertor. However, for the highest puff rates, it seems to saturate in the LD, and the sources of ionization at the baffle, the upper divertor, and SOL become comparable in the HFS. This shows the importance of PFCs as a source of particles in WEST, which remain a dominant source in this configuration.

This new modeling in SOLEDGE-HDG opens many perspectives in realistic tokamak configurations. Further work will be devoted to a deeper investigation of the detached regime conditions when varying not only the gas puff as here but also the heating sources. In particular, a focus will be made on the X-point radiator regime with deep divertor detachment induced by impurity seeding, which allows radiation concentration in a small region at the X-point. Indeed, this regime, observed in several machines, needs to be better characterized so that it can be optimized to control heat exhaust in optimized divertor scenarios. This new study will be facilitated by the new set of synthetic diagnostics recently developed by the team [51], which will enable more rigorous comparisons with experiments.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

IK: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing–original draft, and writing–review and editing. Md’A: conceptualization, data curation, investigation, methodology, software, and writing–review and editing. AG: investigation, project administration, resources, supervision, and writing–review and editing. ES: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, writing–original draft, and writing–review and editing. FS: software and writing–review and editing. HB: methodology, software, and writing–review and editing. GC: resources and writing–review and editing. PG: formal analysis, investigation, and writing–review and editing. PT: software and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200 — EUROfusion). This work has been supported by the French National Research Agency grant SISTEM (ANR-19-CE46-0005-03).

Acknowledgments

The authors would like to thank Clarisse Bourdelle for the fruitful discussions and for sharing her experimental insights. They also would like to thank David Moiraf for providing the experimental equilibrium profiles for the discussed WEST discharge.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1407534/full#supplementary-material

References

1. Ikeda K. Progress in the ITER physics basis. Nucl Fusion (2007) 47:E01. doi:10.1088/0029-5515/47/6/e01

CrossRef Full Text | Google Scholar

2. Bigot B. ITER construction and manufacturing progress toward first plasma. Fusion Eng Des (2019) 146:124–9. doi:10.1016/j.fusengdes.2018.11.052

CrossRef Full Text | Google Scholar

3. ITER-JCT. Status of ITER. Plasma Phys Controlled Fusion (1995) 37:A19–35. doi:10.1088/0741-3335/37/11A/002

CrossRef Full Text | Google Scholar

4. Loarte A, Monk R, Martín-Solís J, Campbell D, Chankin A, Clement S, et al. Plasma detachment in JET mark i divertor experiments. Nucl Fusion (1998) 38:331–71. doi:10.1088/0029-5515/38/3/303

CrossRef Full Text | Google Scholar

5. Kallenbach A, Dux R, Mertens V, Gruber O, Haas G, Kaufmann M, et al. H mode discharges with feedback controlled radiative boundary in the asdex upgrade tokamak. Nucl Fusion (1995) 35:1231–46. doi:10.1088/0029-5515/35/10/I07

CrossRef Full Text | Google Scholar

6. Petrie T, Hill D, Allen S, Brooks N, Buchenauer D, Cuthbertson J, et al. Radiative divertor experiments in DIII-D with d2 injection. Nucl Fusion (1997) 37:321–38. doi:10.1088/0029-5515/37/3/I03

CrossRef Full Text | Google Scholar

7. Ghendrih P, Grosman A, Capes H. Theoretical and experimental investigations of stochastic boundaries in tokamaks. Plasma Phys Controlled Fusion (1996) 38:1653–724. doi:10.1088/0741-3335/38/10/002

CrossRef Full Text | Google Scholar

8. Schwander F, Serre E, Bufferand H, Ciraolo G, Ghendrih P. Global fluid simulations of edge plasma turbulence in tokamaks: a review. Comput Fluids (2024) 270:106141. doi:10.1016/j.compfluid.2023.106141

CrossRef Full Text | Google Scholar

9. Simonini R, Corrigan G, Radford G, Spence J, Taroni A. Models and numerics in the multi-fluid 2-D edge plasma code EDGE2D/U. Contrib Plasma Phys (1994) 34:368–73. doi:10.1002/ctpp.2150340242

CrossRef Full Text | Google Scholar

10. Reiter D, May C, Coster D, Schneider R. Time dependent neutral gas transport in tokamak edge plasmas. J Nucl Mater (1995) 220:987–92. doi:10.1016/0022-3115(94)00648-2

CrossRef Full Text | Google Scholar

11. Frerichs H, Bonnin X, Feng Y, Loarte A, Pitts R, Reiter D, et al. Stabilization of EMC3-EIRENE for detachment conditions and comparison to SOLPS-ITER. Nucl Mater Energ (2019) 18:62–6. doi:10.1016/j.nme.2018.11.022

CrossRef Full Text | Google Scholar

12. Bufferand H, Bensiali B, Bucalossi J, Ciraolo G, Genesio P, Ghendrih P, et al. Near wall plasma simulation using penalization technique with the transport code SolEdge2D-Eirene. J Nucl Mater (2013) 438:S445–8. doi:10.1016/j.jnucmat.2013.01.090

CrossRef Full Text | Google Scholar

13. Wiesen S, Reiter D, Kotov V, Baelmans M, Dekeyser W, Kukushkin A, et al. The new SOLPS-ITER code package. J Nucl Mater (2015) 463:480–4. doi:10.1016/j.jnucmat.2014.10.012

CrossRef Full Text | Google Scholar

14. Rognlien T, Brown P, Campbell R, Kaiser T, Knoll D, McHugh P, et al. 2-D fluid transport simulations of gaseous/radiative divertors. Contrib plasma Phys (1994) 34:362–7. doi:10.1002/ctpp.2150340241

CrossRef Full Text | Google Scholar

15. Stotler D, Skinner C, Budny R, Ramsey A, Ruzic D, Turkot JR. Modeling of neutral hydrogen velocities in the tokamak fusion test reactor. Phys Plasmas (1996) 3:4084–94. doi:10.1063/1.871540

CrossRef Full Text | Google Scholar

16. Garcia OE, Pitts R, Horacek J, Nielsen A, Fundamenski W, Graves J, et al. Turbulent transport in the TCV SOL. J Nucl Mater (2007) 363:575–80. doi:10.1016/j.jnucmat.2006.12.063

CrossRef Full Text | Google Scholar

17. Coroado A, Ricci P. Numerical simulations of gas puff imaging using a multi-component model of the neutral–plasma interaction in the tokamak boundary. Phys Plasmas (2022) 29. doi:10.1063/5.0077336

CrossRef Full Text | Google Scholar

18. Thrysøe A, Madsen J, Naulin V, Rasmussen JJ. Influence of molecular dissociation on blob-induced atom density perturbations. Nucl Fusion (2018) 58:096005. doi:10.1088/1741-4326/aac8a4

CrossRef Full Text | Google Scholar

19. Krasheninnikov S, Kukushkin A. Physics of ultimate detachment of a tokamak divertor plasma. J Plasma Phys (2017) 83:155830501. doi:10.1017/s0022377817000654

CrossRef Full Text | Google Scholar

20. Thrysøe AS, Tophøj LE, Naulin V, Rasmussen JJ, Madsen J, Nielsen AH. The influence of blobs on neutral particles in the scrape-off layer. Plasma Phys Controlled Fusion (2016) 58:044010. doi:10.1088/0741-3335/58/4/044010

CrossRef Full Text | Google Scholar

21. Kvist K, Thrysøe AS, Haugbølle T, Nielsen AH. A direct Monte Carlo approach for the modeling of neutrals at the plasma edge and its self-consistent coupling with the 2d fluid plasma edge turbulence model hesel. Phys Plasmas (2024) 31. doi:10.1063/5.0188594

CrossRef Full Text | Google Scholar

22. Thrysøe AS, Løiten M, Madsen J, Naulin V, Nielsen A, Rasmussen JJ. Plasma particle sources due to interactions with neutrals in a turbulent scrape-off layer of a toroidally confined plasma. Phys Plasmas (2018) 25. doi:10.1063/1.5019662

CrossRef Full Text | Google Scholar

23. Bufferand H, Bucalossi J, Ciraolo G, Falchetto G, Gallo A, Ghendrih P, et al. Progress in edge plasma turbulence modelling—hierarchy of models from 2D transport application to 3D fluid simulations in realistic tokamak geometry. Nucl Fusion (2021) 61:116052. doi:10.1088/1741-4326/ac2873

CrossRef Full Text | Google Scholar

24. Zholobenko W, Body T, Manz P, Stegmeir A, Zhu B, Griener M, et al. Electric field and turbulence in global braginskii simulations across the asdex upgrade edge and scrape-off layer. Plasma Phys Controlled Fusion (2021) 63:034001. doi:10.1088/1361-6587/abd97e

CrossRef Full Text | Google Scholar

25. d’Abusco MS, Giorgiani G, Artaud JF, Bufferand H, Ciraolo G, Ghendrih P, et al. Core-edge 2D fluid modeling of full tokamak discharge with varying magnetic equilibrium: from WEST start-up to ramp-down. Nucl Fusion (2022) 62:086002. doi:10.1088/1741-4326/ac47ad

CrossRef Full Text | Google Scholar

26. Bourdelle C, Artaud J, Basiuk V, Bécoulet M, Brémond S, Bucalossi J, et al. WEST physics basis. Nucl Fusion (2015) 55:063017. doi:10.1088/0029-5515/55/6/063017

CrossRef Full Text | Google Scholar

27. Horsten N, Samaey G, Baelmans M. Development and assessment of 2D fluid neutral models that include atomic databases and a microscopic reflection model. Nucl Fusion (2017) 57:116043. doi:10.1088/1741-4326/aa8009

CrossRef Full Text | Google Scholar

28. Borodin DV, Schluck F, Wiesen S, Harting D, Boerner P, Brezinsek S, et al. Fluid, kinetic and hybrid approaches for neutral and trace ion edge transport modelling in fusion devices. Nucl Fusion (2022) 62:086051. doi:10.1088/1741-4326/ac3fe8

CrossRef Full Text | Google Scholar

29. Van Uytven W, Dekeyser W, Blommaert M, Carli S, Baelmans M. Assessment of advanced fluid neutral models for the neutral atoms in the plasma edge and application in ITER geometry. Nucl Fusion (2022) 62:086023. doi:10.1088/1741-4326/ac72b4

CrossRef Full Text | Google Scholar

30. Huba J, Book D. NRL plasma formulary. NRL publication. Naval Research Laboratory (1998).

Google Scholar

31. Summers H. The adas user manual (2004). Available from: http://www.adas.ac.uk/.

Google Scholar

32. Reiter D, et al. The data file AMJUEL: additional atomic and molecular data for EIRENE. Forschungszentrum Juelich GmbH (2000) 52425.

Google Scholar

33. Giorgiani G, Bufferand H, Ciraolo G, Ghendrih P, Schwander F, Serre E, et al. A hybrid discontinuous Galerkin method for tokamak edge plasma simulations in global realistic geometry. J Comput Phys (2018) 374:515–32. doi:10.1016/j.jcp.2018.07.028

CrossRef Full Text | Google Scholar

34. Wesson J, Campbell DJ. Tokamaks, 149. Oxford University Press (2011).

Google Scholar

35. Kudashev I, Glasser AM, d’Abusco MS, Serre E. Impact of variable perpendicular transport coefficients in WEST simulations using SolEdge-HDG. IEEE Trans Plasma Sci (2024) 1–6. doi:10.1109/tps.2024.3384031

CrossRef Full Text | Google Scholar

36. Stangeby PC, et al. The plasma boundary of magnetic fusion devices. Inst Phys Pub. Philadelphia, Pa (2000) 224. doi:10.1201/9780367801489

CrossRef Full Text | Google Scholar

37. Horvath L, Lomanowski B, Karhunen J, Maslov M, Schneider P, Simpson J, et al. Pedestal particle balance studies in JET-ILW h-mode plasmas. Plasma Phys Controlled Fusion (2023) 65:044003. doi:10.1088/1361-6587/acbb23

CrossRef Full Text | Google Scholar

38. Reiter D, Baelmans M, Boerner P. The EIRENE and B2-EIRENE codes. Fusion Sci Technol (2005) 47:172–86. doi:10.13182/fst47-172

CrossRef Full Text | Google Scholar

39. Yang H, Ciraolo G, Bucalossi J, Bufferand H, Fedorczak N, Tamain P, et al. Numerical modelling of the impact of leakage under divertor baffle in WEST. Nucl Mater Energ (2022) 33:101302. doi:10.1016/j.nme.2022.101302

CrossRef Full Text | Google Scholar

40. Ghendrih P, Dif-Pradalier G, Panico O, Sarazin Y, Bufferand H, Ciraolo G, et al. Role of avalanche transport in competing drift wave and interchange turbulence. J Phys Conf Ser (IOP Publishing) (2022) 2397:012018. doi:10.1088/1742-6596/2397/1/012018

CrossRef Full Text | Google Scholar

41. Romazanov J, Borodin D, Kirschner A, Brezinsek S, Silburn S, Huber A, et al. First ERO2. 0 modeling of be erosion and non-local transport in JET ITER-like wall. Phys Scr (2017) 2017:014018. doi:10.1088/1402-4896/aa89ca

CrossRef Full Text | Google Scholar

42. Di GS, Gallo A, Fedorczak N, Yang H, Ciraolo G, Romazanov J, et al. Modelling of tungsten contamination and screening in WEST plasma discharges. Nucl Fusion (2021) 61:106019. doi:10.1088/1741-4326/ac2026

CrossRef Full Text | Google Scholar

43. Stangeby P. Interpretation of Langmuir, heat-flux, deposition, trapping and gridded energy analyser probe data for impure plasmas. J Phys D: Appl Phys (1987) 20:1472–8. doi:10.1088/0022-3727/20/11/017

CrossRef Full Text | Google Scholar

44. Eckstein W, Bohdansky J, Roth J. Physical sputtering. Nucl Fusion (1991) 1:51.

Google Scholar

45. Myra J, D’Ippolito D, Russell D. Turbulent transport regimes and the scrape-off layer heat flux width. Phys Plasmas (2015) 22. doi:10.1063/1.4919255

CrossRef Full Text | Google Scholar

46. Stangeby P. Basic physical processes and reduced models for plasma detachment. Plasma Phys Controlled Fusion (2018) 60:044022. doi:10.1088/1361-6587/aaacf6

CrossRef Full Text | Google Scholar

47. Kaveeva E, Makarov S, Senichenkov I, Rozhansky V, Veselova I, Bonnin X, et al. SOLPS-ITER modeling of deuterium throughput impact on the ITER SOL plasma. Nucl Mater Energ (2023) 35:101424. doi:10.1016/j.nme.2023.101424

CrossRef Full Text | Google Scholar

48. Park JS, Bonnin X, Pitts R, Lore J. Impact of gas injection location and divertor surface material on ITER fusion power operation phase divertor performance assessed with SOLPS-ITER. Nucl Fusion (2024) 64:036002. doi:10.1088/1741-4326/ad1d11

CrossRef Full Text | Google Scholar

49. Brunner D, LaBombard B, Churchill R, Hughes J, Lipschultz B, Ochoukov R, et al. An assessment of ion temperature measurements in the boundary of the Alcator C-Mod tokamak and implications for ion fluid heat flux limiters. Plasma Phys Controlled Fusion (2013) 55:095010. doi:10.1088/0741-3335/55/9/095010

CrossRef Full Text | Google Scholar

50. Tamain P, Kočan M, Gunn J, Kirk A, Pascal JY, Price M. Ion energy measurements in the scrape-off layer of MAST using a retarding field analyzer. J Nucl Mater (2011) 415:S1139–42. doi:10.1016/j.jnucmat.2010.11.078

CrossRef Full Text | Google Scholar

51. Kudashev I, Medvedeva A, Scotto d’Abusco M, Fedorszak N, Di Genova S, Neverov V, et al. Development of a set of synthetic diagnostics for the confrontation between 2D transport simulations and WEST tokamak experimental data. Appl Sci (2022) 12:9807. doi:10.3390/app12199807

CrossRef Full Text | Google Scholar