Low-frequency weak electric field measurement based on Rydberg atoms using cavity-enhanced three photon system

Introduction: Rydberg atoms are ideal for measuring electric fields due to their unique physical properties. However, low-frequency electric fields below MHz can be challenging due to the accumulation of ionized free electrons on the atomic vapor cell’s surface, acting as a shield.

Method: This paper proposes a Cavity-enhanced three-photon system (CETPS) measurement scheme, which uses a long-wavelength laser to excite the Rydberg state, reducing atomic ionization and enhancing detection spectrum resolution. A theoretical model is proposed to explain the quantum coherence effect of the light field, measured electric field, and the atomic system.

Result: The results show that the proposed scheme significantly increases the electromagnetically induced transparency (EIT) spectral peak and narrows the spectral width, resulting in the maximum slope increasing by more than an order of magnitude.

Discussion: The paper also discusses the impact of the Rabi frequency of the two laser fields and the coupling coefficient of the optical cavity on the transmission spectrum amplitude and linewidth, along with the optimal configuration of these parameters in the CEPTS scheme.

1 Introduction

Rydberg atoms possess large interstate transition dipole moments (∼n²) and polarizabilities (∼n⁷), making them highly responsive to external electric fields [1, 2]. As a result, they are suitable for electric field measurements. The rich energy level structure of Rydberg atoms allows for theoretical measurement of electric fields in the DC ∼ THz frequency range through manipulation of quantum states [3–6]. In fact, in quantum measurement systems utilizing Schrodinger cat states, a single Rydberg atom with significant angular momentum can surpass the standard quantum limit in terms of measurement sensitivity [7]. However, the measurement of low-frequency electric fields below MHz poses significant challenges. There are two main problems: 1) The conventional two-photon three-level measurement scheme exhibits a significant shielding effect on the low-frequency electric field [8–10]. This is because the laser causes the atoms in the vapor cell to undergo photoionization, Penning ionization, etc [11, 12]. As a result, free electrons are pulled and accumulated on the surface of the vapor cell by the low-frequency electric field, effectively shielding the external electric field. This effect is particularly pronounced at frequencies as low as kHz, where the external electric field is completely shielded and cannot affect the atoms. 2) The resonance frequency of MHz is far from the energy level of the Rydberg atom, meaning that it will not excite the atomic energy level transition. Instead, it only causes the fine structure energy level to degenerate and form the Stark shift. When a weak field is applied, the disturbance to the energy level is minimal, resulting in a small macroscopic detection spectrum displacement that is difficult to measure [13, 14]. The commonly used two-photon three-level scheme unable to measure low-frequency weak electric field below kHz. A new measurement scheme needs to be proposed to address the shielding issue, and further study to improve the spectral resolution and detection sensitivity.

One possible solution to the shielding problem is to place an electrode plate inside the vapor cell [15–19] and apply a voltage to generate an electric field. However, this method is only suitable for laboratory research and is not practical for measuring electric fields in practical application scenarios. An alternative approach proposed by [13] is a three-photon excitation scheme, which uses two long-wavelength lasers (780 nm and 1,529 nm) instead of a short-wavelength laser (480 nm) for three-level excitations. Experiments have shown that using longer-wavelength lasers can effectively reduce atomic ionization, thereby minimizing the shielding effect caused by charge accumulation. The remaining shielding can be addressed by calibrating the shielding coefficient [20]. The three-photon + heterodyne measurement scheme described in [13] requires an intrinsic signal to generate a beat signal, making it more suitable for radio communication and over-the-horizon radar applications.

To address the issue of non-resonant micro-displacement identification, it is crucial to enhance the quality and precision of the detection spectrum. The phenomenon of electromagnetically induced transparency (EIT) arises from the nonlinear quantum interference effect when multiple laser fields are coupled to the atomic energy level [21–23]. By detecting the EIT spectrum, the atomic state can be accurately determined [24–26]. To further improve the detection sensitivity, an optical resonant cavity can be incorporated into the measurement device, increasing the cyclic power of the laser wave at a specific frequency and extending the interaction length through multiple oscillations, thereby enhancing the transmission spectral resolution [27–31]. This coupled atomic cavity system has been extensively studied in cavity quantum electrodynamics (cavity-QED) [32]. However, its application in measuring low-frequency electric fields has not yet been explored.

In summary, this paper proposes a scheme combining three-photon system and cavity-enhanced EIT (collectively known as Cavity-enhanced three-photon system, CETPS) to achieve high-sensitivity low-frequency electric field measurement. In the second section, the structure of CETPS is described. By solving the Liouville equation of the three-photon excitation system, the cavity-adding effect is defined as the coupling coefficient to correct the susceptibility of the probe laser. Additionally, the transfer function of CEPTS is constructed, and the mathematical relationship between the electric field strength to be measured and the frequency shift of the transmission spectrum is derived.

The transfer function of CEPTS not only characterizes the performance of the entire measurement system, but also reflects the relevant characteristics of the EIT effect and the Stark effect. Therefore, the third section analyzes the performance of the proposed measurement scheme based on the transmission spectrum. Firstly, the transmission spectra generated by two-photon, conventional three-photon and CEPTS measurement systems are compared. It is confirmed that the proposed CEPTS scheme can improve the spectral peak and narrow the half-height width, thereby increasing the measurement sensitivity. Secondly, this paper explains the principle and law of the peak center frequency shift, half-height width, and optical peak distortion (known as the “horn” peak) in the transmission spectrum with the increase of the measured field strength, as shown in simulations and experiments. This is achieved through theoretical modeling of the total response of the periodic electric field by CETPS, which guides the feature extraction of the detection spectrum and the accurate measurement of the electric field. Finally, this paper analyzes the influence of the three-photon Rabi frequency and the optical cavity coupling coefficient on the EIT spectral amplitude and linewidth, and discusses the optimal configuration of the parameters manually regulated in the CEPTS scheme.

2 Theoretical model

We consider an ensemble of a single-mode cavity containing N four-level ⁸⁷Rb atoms with the level structure depicted in Figure 1A, where level $\left|1\right.〉$, $\left|2\right.〉$ and $\left|3\right.〉$ are long-lived ground state 5S_1/2, intermediate states 5P_3/2 and 4D_3/2 respectively, level $\left|4\right.〉$ is highly excited Rydberg state nP_1/2. Three laser beams enter the optical cavity, which is made up of CM1, CM2, and CM3, as depicted in Figure 1B. The cavity mode generated by the 780 nm probe field couples the atomic $\left|1〉\right.$ → $\left|2〉\right.$ transition with a detuning of Δ_p, the coupling constant ${\mathrm{g}=\mu }_{12}\sqrt{{\omega }_p/2\hslash {\epsilon }_{0}V}$. Here, μ₁₂ is the atomic transition dipole moment, ω_p is the probe laser frequency, V is the cavity mode volume, ℏ is the reduced Planck constant, and ε₀ is the vacuum dielectric constant. The 1,529 nm dressed field (Rabi frequency Ω_d) on the $\left|2〉\right.$ → $\left|3〉\right.$ transition with a detuning of Δ_d. The 703 nm coupling field (Rabi frequency Ω_c) on the $\left|3〉\right.$ → $\left|4〉\right.$ transition with a detuning of Δ_c. The dressed laser and the coupled laser overlap in the atomic vapor cell through a polarization beam splitter (PBS) and propagate the probe laser back. The laser emitted from the cavity is detected by a photodiode detector (PD). A low-frequency field E(t) is applied to the atomic vapor cell through two parallel electrode plates.

Figure 1

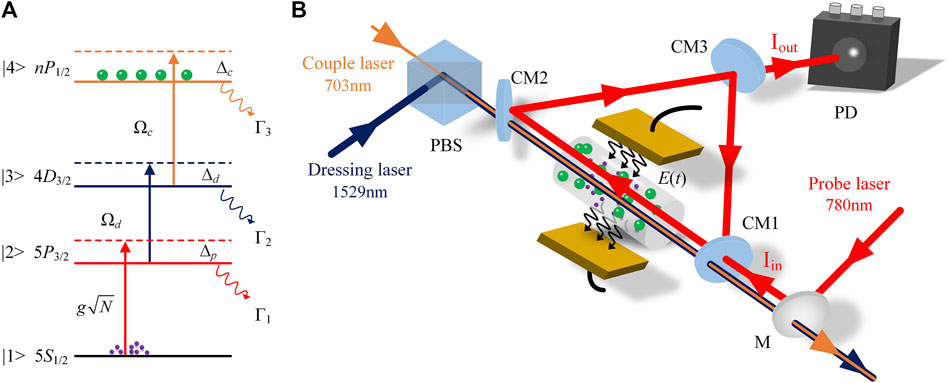
Figure 1. (A) Schematic energy-level diagram for four-level ladder-type system of the ⁸⁵Rb atoms, the state configuration as: 5S_1/2(F = 3)→5P_3/2(F' = 4)→4D_3/2→nP_1/2. Γ_i is the spontaneous decay rate of level |i>. (B) Optical cavity coupling scheme in three-photon system. The 780-nm probe laser counter propagates with the 703-nm couple beam, The 1,529-nm dressing laser propagates in the same direction as the 703-nm beam, applying low-frequency field E_s(t) through electrode plate. CM, cavity mirror; M, mirror; PD, photodiode detector; PBS, polarization beam splitter.

The interaction Hamiltonian for the CETPS in the rotating-wave approximation and in the rotating frame is given by:

$H_{\text{af}}=-\hslash {\sum }_j^N\left(g{\widehat{a}}_p{\widehat{\sigma }}_{21}^{\left(j\right)}+\frac{{\mathrm{\Omega }}_d}{2}{\widehat{\sigma }}_{32}^{\left(j\right)}+\frac{{\mathrm{\Omega }}_c}{2}{\widehat{\sigma }}_{43}^{\left(j\right)}\right)+\mathrm{H}.\mathrm{c}.,(1)$

where ${\widehat{a}}_p$ is the annihilation operator of the probe field mode in the Heisenberg picture and in the rotating frame, with the convention [${\widehat{a}}_p$, ${\widehat{a}}_p^{ϯ}$] = 1, ${\widehat{\sigma }}_{uv}^{\left(j\right)}=\left|u\right.〉〈\left.v\right|$ (u, v = 1,2,3,4) is the atomic operator associated with the jth atom, N is the number of atoms in the cavity mode.

For the expected value $〈\widehat{o}〉$ of the operator $\widehat{o}$ in the atom-cavity system, it can be obtained by solving the Heisenberg equation of motion $\dot{o}=\left(1/\mathrm{i}\hslash \right)〈\left[\widehat{o},H\right]〉$ of the operator $\widehat{o}$, where the total Hamiltonian H = H_af + H_atom + H_field is the sum of the interaction Hamiltonian Eq. 1 and of the atomic and field Hamiltonians Eq. 2:

$\begin{array}{l}{H}_{\text{atom}}=\hslash {\sum }_j^N\left[{\Delta }_p{\widehat{\sigma }}_{22}^{\left(j\right)}+\left({\Delta }_p+{\Delta }_d\right){\widehat{\sigma }}_{33}^{\left(j\right)}+\left({\Delta }_p+{\Delta }_d+{\Delta }_c\right){\widehat{\sigma }}_{44}^{\left(j\right)}\right]+\mathrm{H}.\mathrm{c}.,\\ H_{\text{field}}=\hslash {\Delta }_{cav}{\widehat{a}}_p^{†}{\widehat{a}}_p,\end{array}(2)$

where Δ_cav = ω_cav-ω₁₂ is the cavity detuning between the transition frequency ω₁₂ and the cavity resonance frequencies considered ω_cav.

Considering the spontaneous emission Γ_i of each level $\left|i〉\right.$ (i = 1,2,3,4), the Lindblad operator $\widehat{L}=\sqrt{{\mathrm{\gamma }}_{uv}}\left|u\right.〉〈\left.v\right|$ is introduced to describe this dissipation process, where γ_uv = (Γ_u + Γ_u)/2 represents the spontaneous decay rate between energy levels $\left|u\right.〉$ and $〈\left.v\right|$, one obtains the following set of the atomic equations of motion Eqs 3–5 and coupled field equation of motion Eq. 6 [33]:

${\dot{\widehat{\sigma }}}_{12}^{\left(j\right)}=-\left({\gamma }_{12}-i{\Delta }_p\right){\widehat{\sigma }}_{12}^{\left(j\right)}+ig{\widehat{a}}_p^{\ast }\left({\widehat{\sigma }}_{11}^{\left(j\right)}-{\widehat{\sigma }}_{22}^{\left(j\right)}\right)+i\frac{{\mathrm{\Omega }}_d}{2}{\widehat{\sigma }}_{13}^{\left(j\right)},(3)$

${\dot{\widehat{\sigma }}}_{13}^{\left(j\right)}=-\left[{\gamma }_{13}-i\left({\Delta }_p+{\Delta }_d\right)\right]{\widehat{\sigma }}_{13}^{\left(j\right)}+i\frac{{\mathrm{\Omega }}_d^{\ast }}{2}{\widehat{\sigma }}_{12}^{\left(j\right)}+i\frac{{\mathrm{\Omega }}_c}{2}{\widehat{\sigma }}_{14}^{\left(j\right)}-ig{\widehat{a}}_p^{\ast }{\widehat{\sigma }}_{23}^{\left(j\right)},(4)$

${\dot{\widehat{\sigma }}}_{14}^{\left(j\right)}=-\left[{\gamma }_{14}-i\left({\Delta }_p+{\Delta }_d+{\Delta }_c\right)\right]{\widehat{\sigma }}_{14}^{\left(j\right)}+i\frac{{\mathrm{\Omega }}_c^{\ast }}{2}{\widehat{\sigma }}_{13}^{\left(j\right)}-ig{\widehat{a}}_p^{\ast }{\widehat{\sigma }}_{24}^{\left(j\right)},(5)$

${\dot{\widehat{a}}}_p=-\left(\frac{{\kappa }_1+{\kappa }_2}{2}-i{\Delta }_{cav}\right){\widehat{a}}_p+i{\displaystyle \sum _j^N}g{\widehat{\sigma }}_{12}^{\left(j\right)}+\sqrt{{\kappa }_1}{\widehat{a}}_p^{in},(6)$

where κ_1,2 are the two cavity fields decay rate corresponding to round-trip absorption losses, and κ = κ₁ = κ₂ for a symmetric cavity.

Below we focus on the situation in which all the atoms are in level $\left|1〉\right.$ initially and the probe field is much weaker than the dressed and coupling fields, so that the equation of motion of ${\widehat{\sigma }}_{ii}^{\left(j\right)}$ is not needed to perform a first-order expansion in the probe field, and the interpretive expression of ${\widehat{\sigma }}_{12}^{\left(j\right)}$ can be obtained. In addition, the population of the intermediate state is almost negligible, which means ${\widehat{\sigma }}_{22}^{\left(j\right)}$ ≃0 and ${\widehat{\sigma }}_{11}^{\left(j\right)}$ ≃1. Substituting ${\widehat{\sigma }}_{12}^{\left(j\right)}$ into Eq. 6 and transforming the equation using $\widehat{a}=\widehat{a}\left({\omega }_p\right)e^{i{∆}_{p}t}$, we get the steady-state solution for the intracavity field [30]:

${\dot{\widehat{a}}}_p\left({\omega }_p\right)=\frac{\sqrt{\kappa }{\widehat{a}}_p^{in}\left({\omega }_p\right)}{\kappa -i\Delta -i\frac{{\omega }_{p}l}{2L}\chi },(7)$

where Δ = Δ_p-Δ_cav is the relative frequency, χ is the atomic susceptibility introduced, l is the length of the vapor cell, L is the total cavity length.

If we assume that each atom is independent (${\widehat{\sigma }}_{12}^{\left(j\right)}={\widehat{\sigma }}_{12}$), that is, ${\displaystyle {\sum }_j^N}{\widehat{\sigma }}_{12}^{\left(j\right)}={N\widehat{\sigma }}_{12}$, the χ is given by:

$\chi =i\frac{2g^{2}NL}{{\omega }_{p}l}{\left[{\gamma }_{12}-i{\Delta }_p+\frac{{\mathrm{\Omega }}_d^2/4}{{\gamma }_{13}-i\left({\Delta }_p+{\Delta }_d\right)+\frac{{\mathrm{\Omega }}_c^2/4}{{\gamma }_{14}-i\left({\Delta }_p+{\Delta }_d+{\Delta }_c\right)}}\right]}^{-1},(8)$

In subsequent simulation calculations, the values of the spontaneous decay rates are taken from [34, 35] as Γ₁ = 0, Γ₂ = 2π × 6.07 MHz, Γ₃ = 2π × 0.66 MHz, Γ₄ = 2π × 10 kHz.

To obtain the Doppler averaged absorption we rewrite the susceptibility of the atom in Eq. 8 into the combination of the real part and the imaginary part, χ = χ′+iχ″, and average χ′ and χ″ of the atomic velocity distribution that is found in a vapor cell at room temperature, T_room≈298 K. the atomic medium of moving atoms room temperature is considered to follow the classical Maxwell-Boltzmann velocity distribution function given by Eq. 9:

$f\left(v\right)=\sqrt{\frac{m}{2\pi K_{B}T}}\exp \left(-\frac{m{v}^2}{2K_{B}T}\right),(9)$

where m is the mass of the atom, K_B is the Boltzmann constant, v is the velocity of atom. Since the Doppler effect is caused by contributions from different velocity groups of atoms, the observation frequencies of the three laser beams (probe, dressed and coupling beams) will be different for different atomic velocity groups. The frequency detuning of Δ_p, Δ_d and Δ_c needs to be replaced by the corresponding Doppler shift terms Δ_p→Δ_p + k_pv, Δ_d→Δ_d - k_dv and Δ_c→Δ_c - k_cv, where k_p, k_d and k_c represents the wave vector associated with the probe, dressed and coupling field, and “+” represents the same propagation direction as the probe field (corresponding to Figure 1B). Finally, Eq. 8 is modified by the following:

$\begin{array}{l}\text{Im}\left[{\chi }_D\right]={\int }_{-\infty }^{+\infty }{\chi }^{\prime }f\left(v\right)dv,\\ \text{Re}\left[{\chi }_D\right]={\int }_{-\infty }^{+\infty }{\chi }^{″}f\left(v\right)dv,\end{array}(10)$

where the subscript D on χ presents a Doppler averaged value.

The cavity transmission function S(ω_p) for the probe field in CETPS system can be derived from Eq. 7 and ${\left|{\widehat{a}}_p^{out}\left.\left({\omega }_p\right)\right|\right.}^2=\kappa {\left|{\widehat{a}}_p\left.\left({\omega }_p\right)\right|\right.}^2$:

$S\left({\omega }_p\right)=\frac{{\left|{\widehat{a}}_p^{out}\right|}^2}{{\left|{\widehat{a}}_p^{in}\right|}^2}=\frac{{\kappa }^2}{{\left|\kappa -i\left(\Delta +\frac{{\omega }_{p}l}{2L}\chi \right)\right|}^2},(11)$

In Figure 1B, the probe laser is input from CM1 into the optical cavity with intensity I_in, is reflected back and forth multiple times by the three cavity mirrors CM1, CM2, and CM3 and circulates in the cavity, and is finally output from CM3 with intensity I_out. The cavity output field amplitudes from all round trips are summed, the corresponding transmission of the CETPS has the following form [36]:

$S\left({\omega }_p\right)=\frac{I_{out}}{I_{in}}=\frac{T^2}{{\left(1-R\tau \right)}^2+4R\tau {\sin }^2\left[\left(\mathit{\Phi }\left({\omega }_p\right)\right]\right.},(12)$

where T and R are the cavity transmissivity and reflectivity of the input cavity mirror CM1 and the output cavity mirror CM3 respectively. T is related to the round-trip time through the cavity mirror and κ, T = 2Lκ/c, c is the speed of light, and T²+ R² = 1. Φ(ω_p) is the intracavity round-trip phase shift, and

$\mathit{\Phi }\left({\omega }_p\right)=\frac{L}{c}\left(\Delta +\frac{{\omega }_{p}l}{2L}{\chi }^{\prime }\right),(13)$

Furthermore, the absorption coefficient τ of the intracavity medium is defined:

$\tau =\mathit{exp}\left[-\frac{{\omega }_{p}l}{c}{\chi }^{″}\right],(14)$

It can be seen that under the condition of high reflectivity (R ≈ 1) and small round-trip phase shift, the expansion of both absorption and sinusoidal terms in Eq. 12 has the same form as Eq. 11. We use Eq. 12 to analyze our data.

A more detailed analysis of the transmission spectrum S(ω_p) in CETPS is necessary to fully understand the effects of an external low-frequency electric field. According to the Stark theory, an external field causes a frequency shift in the spectral signal of S(ω_p). Within a certain range of field strength, the frequency shift Δ_stark depends on the field strength amplitude and the atom’s Rydberg state [17, 37], that is,

${\Delta }_{stark}=-\frac{1}{2}\alpha E^2,(15)$

Where E represents the electric field strength, α represents the polarizability of the atom in a Rydberg state.

When the sine law of the measured electric field changes, meaning that the electric field is represented by the equation E_s(t) = A·sin(2πft), the frequency shift of the spectrum will be observed to change periodically with the field strength between 0∼αA²/2, and the change frequency is equal to 2 times the frequency of the electric field. The response of the spectrum to the electric field E_act (t_i) at different moments is expressed as Δ_stark (t_i). This oscillation phenomenon, caused by the accumulation of time, is described by the response of the spectral signal at N moments in one cycle, and the relationship between the spectrum and the low frequency electric field is obtained:

$S_{stark}\left(\Delta \right)=f{\displaystyle \sum _{i=1}^N}S\left[\Delta -{\Delta }_{stark}\left(t_i\right)\right]=f{\int }_0^{1/f}S\left[\Delta -{\Delta }_{stark}\left(t\right)\right]dt,(16)$

The three-photon excitation scheme does not fully address the issue of shielding. The electric field that actually enters the vapor cell is E_act(t) = ηE_s(t), where η is determined by the frequency of the sinusoidal electric field. This is explained in Ref. [20]:

$\eta \left(f\right)=\frac{0.6f}{\sqrt{f^2+{1.31}^2}}+\frac{0.4f}{\sqrt{f^2+{8.96}^2}},(17)$

The combinatorics Eqs 10, 13, 14, 16 obtain Eq. 18:

$S_{stark}\left(\Delta \right)={\int }_0^{1/f}\frac{T^2}{1+R^2{\tau }^2\left({\Delta }_{de}\right)-2R\tau \left[{\Delta }_{de}\right]\cos \left[{\omega }_{p}l{\chi }^{\prime }\left({\Delta }_{de}\right)/2c\right]}dt,(18)$

where the detuning ${\Delta }_{de}=\Delta -{\Delta }_{stark}\left(t\right)$, and ${\Delta }_{stark}\left(t\right)$ = 1/2αE²_act(t) is obtained by Eqs 15, 17.

3 Result analysis

3.1 Analysis of spectral resolution in various measurement schemes

In this section, we examine the impact of the Rabi frequency of the coupled field on the transmission spectrum in the CETPS measurement scheme. This will be compared to the results obtained from conventional two-photon and three-photon measurement schemes.

In the absence of any external field and with the probe field and dressed field set to zero detuning (Δ_p = Δ_d = Δ_θ = 0), Set the probe field and coupling field Rabi frequency to Ω_p/2π = 10 MHz and Ω_d/2π = 25 MHz for the two-photon and three-photon systems respectively, and set the coupling coefficient to g$\sqrt{N}$ = 30 MHz for CETPS. The Rabi frequency for the coupling field Ω_c/2π, can be adjusted within the range of 1∼5 MHz. The transmission spectrum of the probe laser is simulated with varying detuning of the coupling laser, Δ_c, as shown in Figure 2. Where (a)∼(c) represent the results of two-photon, conventional three-photon, and CETPS measurement systems, respectively.

Figure 2

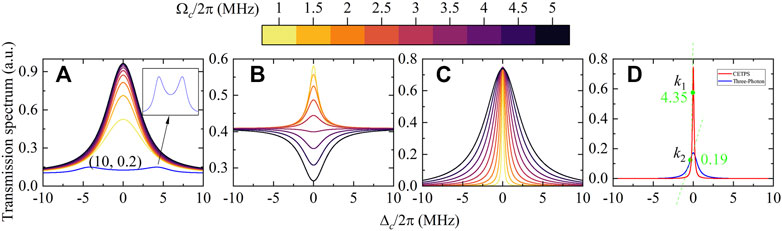
Figure 2. Transmission spectrum plotted as a function of Δ_c/2π for (A) two-photon, (B) three-photon, (C) CETPS, and (D) comparison. The different traces represent different Ω_c/2π (MHz), as labeled in the legend. The parameters used in the calculation are: in the two-photon system, Ω_p/2π = 10 MHz, the atomic density N = 4 × 10⁹cm⁻³, μ₁₂ = 1.9ea₀, the illustration shows the configuration of (Ω_p, Ω_c)/2π = (10,0.1) MHz, Then add Ω_d/2π = 25 MHz [34] to form a three-photon system and CETPS are formed by adding $\mathrm{g}\sqrt{N}=30\text{MHz}$, l = 5 cm, L = 50 cm, r = 0.96 and T² + R² = 1.

In Figure 2A, the EIT peak of the two-photon system increases as Ω_c/2π increase, with a typical spectral linewidth of approximately 3.5 MHz.

In the three-photon scheme shown in Figure 2B, as Ω_c increases, EIT is converted to electromagnetically induced absorption (EIA). This is due to a new nonlinear effect caused by the addition of the strong dressed field. When Ω_c is small (1–3 MHz), there is a destructive interference between the atom and the laser field, resulting in most of the atoms being in the dark state. This inhibits the absorption of photons and produces EIT. However, as Ω_c (3.5–5 MHz) increases, the atomic coherence changes from destructive interference to long interference, leading to enhanced absorption and the production of EIA.

When Ω_c ≪ Ω_p, the EIA phenomenon can also be observed in the two-photon experimental system. This is because the strong detection field’s saturation effect reduces the induced transparency, resulting in EIA [38, 39]. In the two-photon system, we further decrease Ω_c/2π and set the parameters (Ω_p, Ω_c)/2π= (10, 0.1) MHz to simulate the interaction between the strong probe field and the weak coupling field. As shown in Figure 2A (blue curve), the spectrum shifts from a transmission peak to an absorption peak, with the appearance of an AT double peak and an absorption peak between them, indicating the presence of EIA. It is important to note that the numerical solution of the spectral function accurately simulates the formation of EIA or the transition from EIT to EIA when analyzing the optical response of the system under the influence of a strong probe field and coupling field.

Adding an optical cavity to the three-photon system to form the CETPS transmission spectrum as shown in Figure 2C, set the far detuning point as the relative zero point, and set the coupling coefficient g $\sqrt{N}$ = 30 MHz, the intracavity dark-state polariton generated by the strong collective coupling coherence between the probe field and the cavity mode causes the atomic absorption at the resonance to be strongly suppressed. The dispersion near the central peak at the resonance is steep, and the slope of dispersion is approximately inversely proportional to the frequency-locking coefficient ζ∼∂χ′/∂ω_p. The slope of dispersion increases with the increase of ζ, and the EIT transmission window will become narrower. Therefore, by using $\sqrt{N}$ enhancement to the coupling, further reducing the cavity mode volume, or some combination of the two, a strong coupling regime with collective Rydberg interaction can be achieved, and the linewidth of the Rydberg EIT spectrum can be greatly by increasing the degree of narrowing, the spectral amplitude can also be further improved.

The curve corresponding to Ω_c/2π = 1 MHz is plotted in Figure 2D, with the relative zero-point set at a position far from the resonance. In comparison to the transmission spectrum of the three-photon system, the signal amplitude in CETPS is enhanced by more than 4 times, and the maximum slope is increased by more than one order of magnitude. This improvement is also significant when compared to the amplitude and slope of the cavity-enhanced two-photon spectrum observed in previous experiments [40, 41]. This enhancement is crucial for accurately measuring weak electric field.

3.2 Analysis of horn peaks and extraction of features under the influence of an electric field

Research has demonstrated that using either a two-photon or three-photon measurement scheme, as the electric field intensity increases, the transmission spectrum shows a gradual increase in pulse width, a decrease in peak intensity, and a distortion of the peak shape (known as “horn” peak) from a narrow, single peak. This can be seen in Figures 3A, B, which display the spectra obtained from CETPS simulation and two-photon (using a built-in electrode plate) measurement, respectively. The Rydberg state selected was 53S_1/2 (the corresponding atomic polarizability α = 79.98 MHz·cm²/V²), with an electric field frequency of 3 kHz and an intensity range of 0–50 V/m.

Figure 3

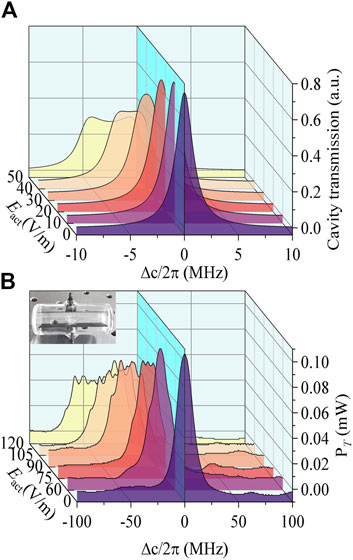
Figure 3. Comparison of theory and experiment. (A) Theoretical model of CETPS: ($\mathrm{g}\sqrt{N}$, Ω_d, Ω_c)/2π = (30, 25,1) MHz, the other parameters are shown in this figure, field intensity frequency 3 kHz, amplitude range 0–50 V/m. (B) Experiment of two-photon scheme, the illustration is a vapor cell with a length of 5 cm and a diameter of 2 cm, and the parallel plates spacing d = 0.6 cm.

Comparing Figures 3A, B, it is evident that the results obtained from the two measurement schemes demonstrate an increase in frequency shift with an increase in field strength. Additionally, the distortion of the spectrum also increases gradually. However, upon comparison, it can be observed that the spectral distortion obtained from the two-photon measurement scheme embedded in the inner plate is more severe. As the field strength increases, the peak of the peak splits into multiple smaller peaks, posing a challenge for accurately extracting the frequency shift of the peak position. In contrast, the peak obtained from the proposed CETPS scheme is narrower and only splits into two peaks at the top.

The mathematical model presented in the second part of this paper can be used to explain the formation and characteristics of double peaks. The results are depicted in Figure 4, where the amplitude of the sinusoidal electric field is A = 50 V/m and the frequency are f = 3 kHz. The electric field is segmented in the time domain, and the characteristics of CETPS spectrum change caused by electric field at different times are obtained. In Figure 4A, the transmission spectrum is displayed as a function of time (vertical axis) and detuning (horizontal axis), and the color bar represents the amplitude of the transmission spectrum. Figure 4B shows the stark frequency shift Δ_stark corresponding to the sinusoidal electric field at different times. The longitudinal axis represents time, and the transverse axis represents Δ_stark obtained by the field strength at a specified time after being calibrated by the shielding coefficient. Additionally, the total response of CETPS to the changing electric field accumulated in a period is also plotted. The horizontal axis is the coupling detuning Δ_c/2π, and the vertical axis is the transmission of the signal after experiencing the periodic changing electric field, as shown in Figure 4C. The “horn” peak is the result of sinusoidal signal sampling near the extreme value. The linear “distortion” position caused by this low-frequency field corresponds to the maximum offset caused by the field intensity amplitude. Accurately modeling and reproducing these linear “distortions” can provide an intuitive low-frequency weak field measurement diagnostic scheme for the experiment.

Figure 4

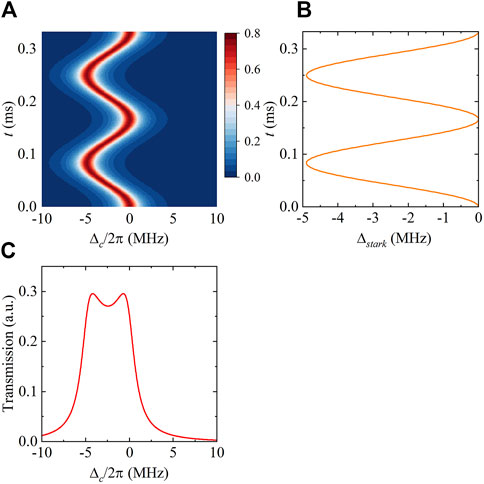
Figure 4. CETPS curve characteristics under electric field action of f = 3 kHz, A = 50 V/m. (A) Transmission at different times, (B) Δ_stark caused by electric field, (C) total response of CETPS to the accumulated changing electric field in a period.

3.3 Effects of Ω_d, Ω_c and g$\sqrt{\mathit{N}}$ in the CETPS

CETPS provides a way to reduce the shielding effect in low-frequency field measurements, resulting in enhanced sensitivity and narrower linewidth. However, the intricate interactions among three-photons and optical cavity present a significant challenge. Variations in Rabi frequencies and cavity-atom coupling coefficients can have a significant influence on the transmission spectrum.

In Figure 5, we analyze the response of CETPS to various configurations of dressed, coupling Rabi frequency and atom-cavity coupling coefficient in order to determine the optimal working region. For a series of coupling coefficients $\mathrm{g}\sqrt{N}$ (the four groups of $\mathrm{g}\sqrt{N}$ set are 5, 10, 30, and 50 MHz respectively), the relationship between signal amplitude, line width, and the two variables Ω_d, Ω_c is plotted in two-dimensional heat map. The variables are within the ranges of (0, 5), and (10, 50). Signal amplitude and linewidth are determined from the transmission intensity and full width at half maximum of the cavity transmission spectrum, respectively.

Figure 5

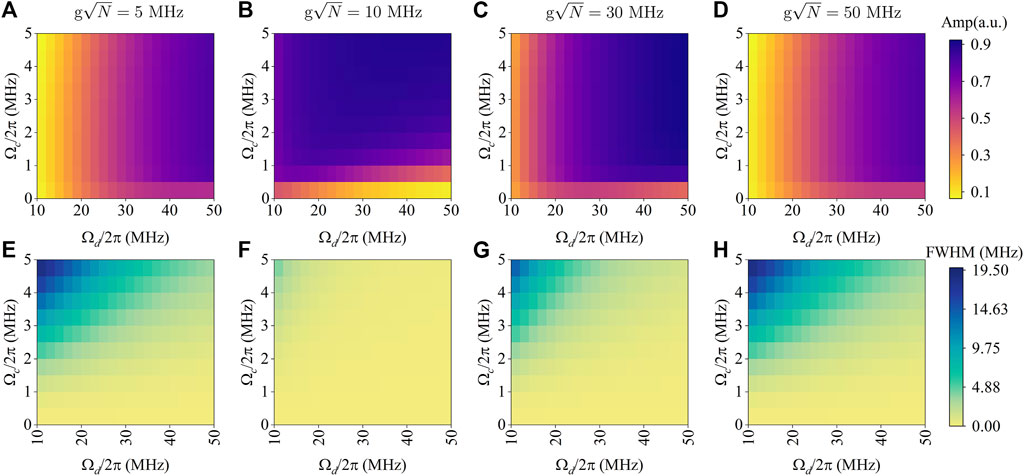
Figure 5. Two-dimensional heat map to study the influence of different intensities $\mathrm{g}\sqrt{N}$, Ω_d, Ω_c on the spectral amplitude and line width of the CETPS spectrum. (A,E), (B,F), (C,G), (D,H) correspond to the coupling coefficients of 5 MHz, 10 MHz, 30 MHz, and 50 MHz respectively. Color bars represent spectral amplitude and linewidth.

In Figures 5A–D, with the slow increase of $\mathrm{g}\sqrt{N}$, the amplitude of the transmission spectrum goes through the process of decreasing from small to large, the maximum amplitude appears near $\mathrm{g}\sqrt{N}$ ≈12.5 MHz (not shown in the picture). When the $\mathrm{g}\sqrt{N}$ is constant, the amplitude of the transmission spectrum increases with the increase of Ω_d. However, when the value of Ω² _c is close to 4γ₁₂γ₁₄, Ω_c≈0.49 MHz, the amplitude undergoes a sharp change process, which is because the strong coherence causes the population to be pumped into the dark state composed of the ground state and the Rydberg state.

In Figures 5E–H, the transmission spectrum linewidth also shows a similar change process of first decreasing and then increasing as $\mathrm{g}\sqrt{N}$ increases, and the linewidth increases with the increase of Ω_d and Ω_c, which is a result of power broadening of the resonance. However, when Ω_d is small, the effect of Ω_c on the line width is not obvious.

The analysis above indicates that coordinating multiple parameters is necessary for transmitting signals to maintain maximum amplitude and minimal linewidth to achieve optimal sensitivity and obtain the best working area of CETPS. Our simulation results show that when Ω_d and Ω_c change within the set parameter range, the maximum value of the transmission spectrum amplitude always appears in the range of $\mathrm{g}\sqrt{N}$ = (10–20) MHz. Although the amplitude can reach 0.95a.u., at this time the line width is larger (>1 MHz). Therefore, in order to obtain a smaller line width, it is necessary to set a larger Ω_d and a smaller Ω_c to reduce the impact of power broadening. It should be noted that Ω_d is limited by the output power of the laser in the experiment, which generally does not exceed 2π × 67 MHz [34]. These findings will serve as a valuable reference for optimizing our future experiment designs.

4 Conclusion

Using the electromagnetically induced transparency effect of Rydberg atoms to measure low-frequency weak fields has always been a challenge. In this paper, an approach has been proposed by combining optical cavity with three photons to prepare Rydberg atoms. This approach not only reduces the shielding effect caused by low-frequency electric fields but also improves the resolution of EIT spectrum. It allows for quantum precision measurement of low-frequency weak fields. To prove this, we established a theoretical model of CETPS under the action of low-frequency weak fields. In this model, the continuous electric field in a period is considered as a combination of N discrete electric fields: ${\displaystyle {\sum }_{i=1}^N}{E}_s\left(t_i\right)$, and obtained the expression S_Stark(Δ) of the spectral signal of the system. Further analysis of the transmission spectrum of the system revealed that the conventional three-photon system experiences a transition process from EIT to EIA as Ω_c changes. However, the strong collective coupling coherence of the atom-cavity coupled system increases the signal amplitude by more than 4 times and the maximum slope by more than one order of magnitude. Our analysis model can improve the measurement sensitivity of low-frequency weak fields by more than one order of magnitude. It accurately reproduces the spectral variation under the action of low-frequency electric fields in the experiment. The spectral frequency broadening and the “horn” peak are the response results of the transmission signal accumulated in a period of the electric field. It provides an intuitive diagnosis scheme for the spectral line distortion that may be caused by the low-frequency weak field in the experiment. Furthermore, we analyzed the influence of the Rabi frequency of the two laser fields and the atomic-cavity coupling coefficient on the transmission peak in the cavity to determine the optimal operating region of CETPS. We plan to conduct further experimental research on CETPS’s measurement of low-frequency weak fields in the near future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

DX: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. ZS: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. LC: Investigation, Writing–original draft. SY: Conceptualization, Investigation, Writing–original draft. LX: Writing–original draft, Writing–review and editing. HZ: Conceptualization, Investigation, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yuan J, Yang W, Jing M, Zhang H, Jiao Y, Li W, et al. Quantum sensing of microwave electric fields based on Rydberg atoms. Rep Prog Phys (2023) 86:106001. doi:10.1088/1361-6633/acf22f

CrossRef Full Text | Google Scholar

2. Adams CS, Pritchard JD, Shaffer JP. Rydberg atom quantum technologies. J Phys B-Atomic Mol Opt Phys (2020) 53:012002. doi:10.1088/1361-6455/ab52ef

CrossRef Full Text | Google Scholar

3. Sedlacek JA, Schwettmann A, Kuebler H, Loew R, Pfau T, Shaffer JP. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances. Nat Phys (2012) 8:819–24. doi:10.1038/nphys2423

CrossRef Full Text | Google Scholar

4. Gordon JA, Simons MT, Haddab AH, Holloway CL. Weak electric-field detection with sub-1 Hz resolution at radio frequencies using a Rydberg atom-based mixer. Aip Adv (2019) 9:045030. doi:10.1063/1.5095633

CrossRef Full Text | Google Scholar

5. Jing M, Hu Y, Ma J, Zhang H, Zhang L, Xiao L, et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat Phys (2020). 16:911–5. doi:10.1038/s41567-020-0918-5

CrossRef Full Text | Google Scholar

6. Liu Z-K, Zhang L-H, Liu B, Zhang Z-Y, Guo G-C, Ding D-S, et al. Deep learning enhanced Rydberg multifrequency microwave recognition. Nat Commun (2022) 13:1997. doi:10.1038/s41467-022-29686-7

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Facon A, Dietsche E-K, Grosso D, Haroche S, Raimond J-M, Brune M, et al. A sensitive electrometer based on a Rydberg atom in a Schrodinger-cat state. Nature (2016) 535:262–5. doi:10.1038/nature18327

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Mohapatra AK, Jackson TR, Adams CS. Coherent optical detection of highly excited rydberg states using electromagnetically induced transparency. Phys Rev Lett (2007) 98:113003. doi:10.1103/PhysRevLett.98.113003

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Holloway CL, Gordon JA, Jefferts S, Schwarzkopf A, Anderson DA, Miller SA, et al. Broadband rydberg atom-based electric-field probe for SI-traceable, self-calibrated measurements. Ieee Trans Antennas Propagation (2014) 62:6169–82. doi:10.1109/tap.2014.2360208

CrossRef Full Text | Google Scholar

10. Ma L, Paradis E, Raithel G. DC electric fields in electrode-free glass vapor cell by photoillumination. Opt Express (2020) 28:3676–85. doi:10.1364/oe.380748

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Abo Zalam A, Bruvelis M, Miculis K, Beterov II, Bezuglov NN, Ekers A, et al. Strong enhancement of Penning ionisation in cold Rydberg gases II: tom and Jerry pairs for alkali-metal atoms. J Phys B-Atomic Mol Opt Phys (2021) 54:065201. doi:10.1088/1361-6455/abd9fe

CrossRef Full Text | Google Scholar

12. Beterov II, Tretyakov DB, Ryabtsev II, Entin VM, Ekers A, Bezuglov NN. Ionization of Rydberg atoms by blackbody radiation. New J Phys (2009) 11:013052. doi:10.1088/1367-2630/11/1/013052

CrossRef Full Text | Google Scholar

13. Liu B, Zhang L-H, Liu Z-K, Zhang Z-Y, Zhu Z-H, Gao W, et al. Highly sensitive measurement of a megahertz rf electric field with a rydberg-atom sensor. Phys Rev Appl (2022) 18:014045. doi:10.1103/PhysRevApplied.18.014045

CrossRef Full Text | Google Scholar

14. Rotunno AP, Berweger S, Prajapati N, Simons MT, Artusio-Glimpse AB, Holloway CL, et al. Detection of 3-300 MHz electric fields using Floquet sideband gaps by "Rabi matching" dressed Rydberg atoms. J Appl Phys (2023) 134:134501. doi:10.1063/5.0162101

CrossRef Full Text | Google Scholar

15. Li L, Jiao Y, Hu J, Li H, Shi M, Zhao J, et al. Super low-frequency electric field measurement based on Rydberg atoms. Opt Express (2023) 31:29228–34. doi:10.1364/oe.499244

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Holloway CL, Prajapati N, Sherman JA, Ruefenacht A, Artusio-Glimpse AB, Simons MT, et al. Electromagnetically induced transparency based Rydberg-atom sensor for traceable voltage measurements. Avs Quan Sci (2022) 4:034401. doi:10.1116/5.0097746

CrossRef Full Text | Google Scholar

17. Anderson DA, Paradis EG, Raithel G. A vapor-cell atomic sensor for radio-frequency field detection using a polarization-selective field enhancement resonator. Appl Phys Lett (2018) 113:073501. doi:10.1063/1.5038550

CrossRef Full Text | Google Scholar

18. Ma L, Viray MA, Anderson DA, Raithel G. Measurement of dc and ac electric fields inside an atomic vapor cell with wall-integrated electrodes. Phys Rev Appl (2022) 18:024001. doi:10.1103/PhysRevApplied.18.024001

CrossRef Full Text | Google Scholar

19. Jau Y-Y, Carter T. Vapor-cell-based atomic electrometry for detection frequencies below 1 kHz. Phys Rev Appl (2020) 13:054034. doi:10.1103/PhysRevApplied.13.054034

CrossRef Full Text | Google Scholar

20. Lim MJ, Cervantes M, Brady C, McPoyle S, Simmermon J. Kilohertz-range electric field calibration in an alkali vapor cell using time-averaged Stark shifts. Appl Phys Lett (2023) 123:051106. doi:10.1063/5.0153752

CrossRef Full Text | Google Scholar

21. Hazra R, Hossain MM. Theoretical study of coherent optical phenomena in a three lasers driven four-level ladder-type system involving a Rydberg state. Laser Phys (2022) 32:065207. doi:10.1088/1555-6611/ac641d

CrossRef Full Text | Google Scholar

22. Laskar R, Hossain MM, Saha JK. The analysis of coherent phenomena for both linear and non-linear interactions in a four-level ladder (Ξ)-type configuration using density matrix formalism in dressed state representation. Physica Scripta (2021) 96:035108. doi:10.1088/1402-4896/abdbf3

CrossRef Full Text | Google Scholar

23. Oyun Y, Cakir O, Sevincli S. Electromagnetically induced transparency and absorption cross-over with a four-level Rydberg system. J Phys B-Atomic Mol Opt Phys (2022) 55:145502. doi:10.1088/1361-6455/ac7096

CrossRef Full Text | Google Scholar

24. Carr C, Tanasittikosol M, Sargsyan A, Sarkisyan D, Adams CS, Weatherill KJ. Three-photon electromagnetically induced transparency using Rydberg states. Opt Lett (2012) 37:3858–60. doi:10.1364/ol.37.003858

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Prajapati N, Bhusal N, Rotunno AP, Berweger S, Simons MT, Artusio-Glimpse AB, et al. Sensitivity comparison of two-photon vs three-photon Rydberg electrometry. J Appl Phys (2023) 134:023101. doi:10.1063/5.0147827

CrossRef Full Text | Google Scholar

26. Bai J, Jiao Y, He Y, Song R, Zhao J, Jia S. Autler-Townes splitting of three-photon excitation of cesium cold Rydberg gases. Opt Express (2022) 30:16748–57. doi:10.1364/oe.457344

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Agarwal GS. Spectroscopy of strongly coupled atom-cavity systems: a topical review. J Mod Opt (1998) 45:449–70. doi:10.1080/09500349808231908

CrossRef Full Text | Google Scholar

28. Wu H, Gea-Banacloche J, Xiao M. Observation of intracavity electromagnetically induced transparency and polariton resonances in a Doppler-broadened medium. Phys Rev Lett (2008) 100:173602. doi:10.1103/PhysRevLett.100.173602

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang Y, Jia Z, Yu Y, Chen B, Peng Y. Rydberg-atom-based measurements of microwave electric fields with cavity quantum electrodynamics. J Opt Soc America B-Optical Phys (2023) 40:2604–11. doi:10.1364/josab.496540

CrossRef Full Text | Google Scholar

30. Sheng J, Chao Y, Kumar S, Fan H, Sedlacek J, Shaffer JP. Intracavity Rydberg-atom electromagnetically induced transparency using a high-finesse optical cavity. Phys Rev A (2017) 96:033813. doi:10.1103/PhysRevA.96.033813

CrossRef Full Text | Google Scholar

31. Li S, Yuan J, Wang L, Xiao L, Jia S. Enhanced microwave electric field measurement with cavity-assisted rydberg electromagnetically induced transparency. Front Phys (2022) 10:846687. doi:10.3389/fphy.2022.846687

CrossRef Full Text | Google Scholar

32. Tanji-Suzuki H, Chen W, Landig R, Simon J, Vuletic V. Vacuum-induced transparency. Science (2011) 333:1266–9. doi:10.1126/science.1208066

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Walls DF, Milburn GJ. Quantum optics. In: DF Walls, and GJ Milburn, editors. Springer Berlin Heidelberg. Berlin, Heidelberg: Quantum Optics (2008).

Google Scholar

34. Thaicharoen N, Moore KR, Anderson DA, Powel RC, Peterson E, Raithel G. Electromagnetically induced transparency, absorption, and microwave-field sensing in a Rb vapor cell with a three-color all-infrared laser system. Phys Rev A (2019) 100:063427. doi:10.1103/PhysRevA.100.063427

CrossRef Full Text | Google Scholar

35. Steck DA. Rubidium 85 D line data. Available from: http://steck.us/alkalidata (last revised September 10, 2023).

Google Scholar

36. Sheng J, Wu H, Mumba M, Gea-Banacloche J, Xiao M. Understanding cavity resonances with intracavity dispersion properties. Phys Rev A (2011) 83:023829. doi:10.1103/PhysRevA.83.023829

CrossRef Full Text | Google Scholar

37. Bai J, Bai S, Han X, Jiao Y, Zhao J, Jia S. Precise measurements of polarizabilities of cesium nS Rydberg states in an ultra-cold atomic ensemble. New J Phys (2020) 22:093032. doi:10.1088/1367-2630/abaf30

CrossRef Full Text | Google Scholar

38. Wielandy S, Gaeta AL. Investigation of electromagnetically induced transparency in the strong probe regime. Phys Rev A (1998) 58:2500–5. doi:10.1103/PhysRevA.58.2500

CrossRef Full Text | Google Scholar

39. Krmpot AJ, Mijailovic MM, Panic BM, Lukic DV, Kovacevic AG, Pantelic DV, et al. Sub-Doppler absorption narrowing in atomic vapor at two intense laser fields. Opt Express (2005) 13:1448–56. doi:10.1364/opex.13.001448

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wang Q, Wang Z, Liu Y, Guan S, He J, Zou C-L, et al. Cavity-enhanced optical bistability of Rydberg atoms. Opt Lett (2023) 48:2865–8. doi:10.1364/ol.486914

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sheng J, Xiao M. Amplification of the intracavity dark-state field by a four-wave mixing process. Laser Phys Lett (2013) 10:055402. doi:10.1088/1612-2011/10/5/055402

CrossRef Full Text | Google Scholar