High-gain lithium niobate brillouin laser with tunable phonon frequency of 1∼31 GHz

Stimulated Brillouin scattering (SBS) is a significant nonlinear optical phenomenon utilized across various fields. Its applications span optical sensing, microwave photonics, and all-optical signal processing. In the current information-driven era, the laser industry is imposing increasingly stringent demands on laser technologies, thus propelling integrable on-chip SBS devices into a pivotal research trajectory. Simultaneously, the quest for materials manifesting heightened SBS effects has emerged as a primary focal point in optical fiber transmission endeavors. Lithium niobate (LN) stands out as a promising nonlinear optical material endowed with numerous exemplary attributes. These encompass a high refractive index, fostering potent photon-phonon interactions, low loss characteristics, and high integration potential. Consequently, employing LN as a material for Brillouin lasers promises to enhance certain aspects of laser performance and enable more comprehensive research into Brillouin lasers. In this paper, a micro-ring waveguide structure with LN as the main material is constructed, and the forward gain of stimulated Brillouin scattering, the distribution of electric field in multiple modes and the maximum tunable range are further analyzed. The simulation results exhibit that the tunable forward SBS effect can be achieved in the LN optical waveguides, the maximum forward Brillouin gain can reach $1.34W^{-1}{m}^{-1}$. Additionally, the tunable phonon frequency can range from 1 GHz to 31 GHz, effectively doubling that of silicon ring waveguides and thus extending the range of phonon tunability. Therefore, the LN micro-ring waveguide structure provides a new reference direction for the construction of a new tunable laser and a new idea for the generation of lasers to find a Brillouin medium with high SBS effect.

1 Introduction

The stimulated Brillouin scattering (SBS) effect is a third-order nonlinear effect, which is produced by the interaction of photons and phonons in a medium. It can be described as the nonlinear interaction of pump light and Stokes light through sound waves [1]. Scattering in silicon-based waveguides is mainly categorized into three types, namely, Rayleigh, Raman, and Brillouin scattering, and the phenomenon of nonlinear coupling is more pronounced in Brillouin scattering compared to the first two types of scattering. The SBS effect has a wide range of applications in optical sensing, microwave photonics, all-optical signal processing and other fields, and integrable on-chip SBS devices have also become a research hotspot. Scientists have begun to study the SBS effect of devices, so far, Whispering Gallery Resonator (WGR for short) devices and planar direct waveguide devices are the most common used to achieve forward stimulated Brillouin scattering (short for FSBS) microstructure devices. However, although WGR devices can produce strong Brillouin nonlinearity, it is difficult to integrate with silicon [2, 3]. The most common of planar straight waveguides is chalcogenide waveguides [4, 5], and their main disadvantage is the complexity of the fabrication process, so it is necessary to find new semiconductor materials to build new integrated optoelectronic devices at this stage.

Silicon stands out as an ideal fabrication platform for FSBS devices in the contemporary landscape. Due to the high hardness of silicon, it is difficult for sound waves to be guided in the SOI (silicon on insulation) waveguide, so the interaction between phonons and photons is suppressed, which in turn affects the SBS effect. To amplify the nonlinear effect within waveguide structures and achieve efficient FSBS outcomes within compact waveguide setups, novel configurations such as suspended waveguides, ring structures, and disc structures are being proposed. Among them, the ring waveguide obtains a higher forward Brillouin scattering gain and is more conducive to on-chip integration than the suspended waveguide structure, but the phonon tunable range of the silicon ring structure is smaller. Therefore, based on the structure of silicon ring waveguide, this paper proposes to replace silicon material with LN to further study the structure of ring waveguide. Micro-ring resonators [6] are one of the most common structures in the field of integrated optoelectronics, and the process of fabricating micro-ring resonators is simple and conducive to on-chip integration. At the same time, the use of micro-ring resonator in the experimental process can more easily control the transmission direction and path of light, which makes the operation simple, and the fault tolerance rate is high. So far, great results have been achieved in the research of silicon ring waveguides, which are widely used in optical filters [7–9], optical switches [10–12], and optical modulators [13–16].

In recent years, LN is a new semiconductor material, has attracted more and more attention, and researchers have studied it more and more deeply. LN has been the main material for nonlinear optics and has many excellent properties, such as a wide low-loss transparent window [17], high second-order nonlinearity [18]and broadband optical transmission. In 2020, Stanford University first reported an acousto-optic modulator based on thin-film LN (TFLN for short) acoustic surface waveguides [19], which reduces the processing difficulty of acoustic suspension structures. Then, based on the superior properties of LN, a LN on insulator (LNOI) platform was fabricated, which provided stronger light confinement, thereby improving the optical signal processing ability and enhancing the interaction between light and matter. LNOI has been used to build many photonic devices, including ultra-high-efficiency inverters [20, 21], high-Q micro resonators [22], and photonic crystal microcavities [23]. With the successful LNOI films on wafer-level insulating substrates and breakthroughs in micro-nano processing technology, the LNOI platform has shown significant advantages in large-scale high-speed optoelectronic device integration. Advances in microfabrication technology provide photonic integration with the potential for continued expansion of device diversity and integration scale.

In this paper, we construct a micro-ring waveguide structure with LN as the main material to further enhance the FSBS effect. First, by changing the waveguide width, the waveguide width to achieve the maximum Brillouin gain is found. Then, at the optimal waveguide width, the electric field distribution of the pump light, the maximum phonon tunable range, and the comparison of the results between different modes are further analyzed. The tunable range of 1–31 GHz, which is larger than that of the silicon ring waveguide structure, provides a new reference direction for the future research on tunable lasers. The LN waveguide is scattered forward towards Brillouin, coupling the light field in different optical spatial modes, which improves the integration of the on-chip Brillouin laser. At the same time, it also provides a new idea for finding a new Brillouin medium that can not only improve the SBS effect, but also have a large communication capacity.

2 Theory model

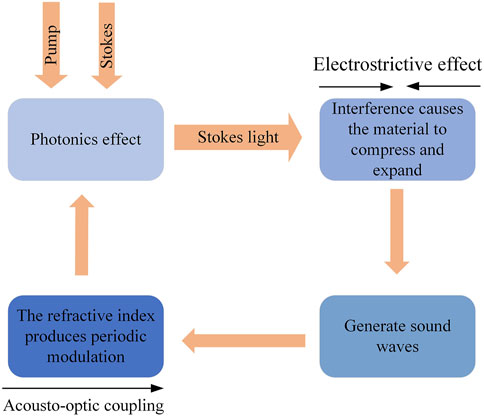
Brillouin scattering manifests as a nonlinear effect stemming from the interaction among pump light, Stokes light, and acoustic waves, as depicted in Figure 1. Simultaneously introducing pump and Stokes light into the medium generates a beat frequency signal, thereby initiating excitation of acoustic waves within the medium. Concurrently, the photo-elastic effect induced by the refractive index of the waveguide engenders periodic modulation. According to the direction of pump light and Stokes light can be divided into forward and backward Brillouin scattering, when the two directions are the same it is forward Brillouin scattering, and when the opposite is backward Brillouin scattering.

Figure 1

Figure 1. FSBS effect in the waveguide.

In 2012, Peter T. Rakich et al. theoretically demonstrated that the structural dimensions in nano-sized waveguides can also have a great effect on the intensity of the SBS, and the maximum value of the FSBS gain coefficient simulation results reaches $2.3\times {10}^4{W}^{-1}{m}^{-1}$, which is times larger than that of the conventional SiO₂ fiber [24]. In 2015, Raphaël Van Laer et al. designed a partially suspended Si nanowire waveguide, and the FSBS gain coefficient of the Si nanowire waveguide measured in the experiments reached $3218W^{-1}{m}^{-1}$ [24]. The effect of the FSBS is significant in the miniature waveguide structure, so in this paper, we focus on investigating the FSBS of the LN ring waveguide structure effect.

In the Brillouin scattering process, under the condition of simultaneous conservation of momentum and energy, ignoring other nonlinear effects in the waveguide, the SBS coupled wave equations are obtained by solving the Maxwell’s equations satisfied by light during transmission and the Venastokes equations satisfied by electrostriction-induced sound waves [25]:

$\frac{{\partial }^2\stackrel{\sim }{E_p}}{\partial z^2}-\frac{n^2}{c^2}\frac{\partial \stackrel{\sim }{E_p}}{\partial t^2}=\frac{4\pi }{c^2}\frac{{\partial }^2{p}_{NL}}{\partial t^2}(1)$

$\frac{{\partial }^2\stackrel{\sim }{E_s}}{\partial z^2}-\frac{n^2}{c^2}\frac{\partial \stackrel{\sim }{E_p}}{\partial t^2}=\frac{4\pi }{c^2}\frac{{\partial }^2{p}_{NL}}{\partial t^2}(2)$

$\frac{{\partial }^2\stackrel{\sim }{\rho }}{\partial z^2}-\mathrm{\Gamma }{\nabla }^2\left(\frac{{\partial }^2\stackrel{\sim }{\rho }}{\partial z^2}\right)-V_A^2{\nabla }^2\stackrel{\sim }{\rho }=\nabla \cdot L(3)$

where p is pump light; s is Stokes wave; $\stackrel{\sim }{E}$ is the electric field vector; $\stackrel{\sim }{\rho }$ is the wave density of the medium; $p_{NL}$ is nonlinear polarization; $\mathrm{\Gamma }$ is the extinction coefficient of sound wave; ${\nabla }^2$ is the Laplace operator; $L=\nabla p_{SL}=\nabla \left(-\frac{\gamma }{8\pi }<\left(E_p{E}_s^{*}\right)>\right)$ is the intrinsic noise term used to describe the thermal excitation of the sound wave, where represents the electrostriction coefficient.

In the coupling process, the pump light will excite a variety of modes of light and transmission. When SBS is generated, N modes of pump light correspond to N modes of Stokes light, so according to the coupling Eqs 1-3, the expressions for pump light, Stokes wave and sound wave are respectively [25]:

$E_p\left(z,t\right)=\frac{1}{2}\left\{{\displaystyle \sum _y}\stackrel{\sim }{E_{p,x}}\left(z\right)e^{\left(i{\omega }_{p,x}t-i{\beta }_{p,x}z\right)}+c.c.\right\}(4)$

$E_s\left(z,t\right)=\frac{1}{2}\left\{{\displaystyle \sum _y}\stackrel{\sim }{E_{s,y}}\left(z\right)e^{\left(i{\omega }_{s,y}t-i{\beta }_{s,y}z\right)}+c.c.\right\}(5)$

$\rho \left(z,t\right)=\frac{1}{2}\left\{{\displaystyle \sum _x}{\displaystyle \sum _y}\stackrel{\sim }{{\rho }_{x,y}}\left(z\right)e^{\left(i2\pi V_{Bxy}t-i{\beta }_{xy}z\right)}+c.c.\right\}(6)$

where $E_{p,x}\left(z,t\right)、E_{s,y}\left(z,t\right)、\rho \left(z,t\right)$ respectively are the amplitudes of pump light, Stokes wave and sound wave; ${\rho }_0$ is the average medium density; ${\omega }_{p,x},{\omega }_{s,y}$ are the frequencies of pump light and Stokes wave respectively; ${\beta }_{p,x},{\beta }_{s,y},{\beta }_{xy}$ are the propagation constants of pump light, Stokes wave and sound wave, respectively; c. c. is complex conjugate. Eqs. 4–6 are substituted into the SBS coupled wave equation, and the distribution of Brillouin scattering spectra of each mode can be obtained.

Upon the incidence of pump light into the waveguide, upon satisfying the phase condition of Brillouin scattering, interaction between the light wave and the sound wave ensues, giving rise to the Brillouin gain spectrum (BGS). During the scattering process, numerous distinct modes emerge, subsequently enabling the calculation and analysis of stimulated Brillouin scattering gain across various modes. $B_m^a$ refers to the overlap of the mode field distribution of the acousto-optic mode on the cross-section of the optical fiber, which can be expressed as:

$B_m^a={\left[\frac{<E_n^2\left(r\right)>}{<u_m\left(r\right)E_n^2\left(r\right)>}\right]}^2<u_m^2\left(r\right)>(7)$

In Eq. 7, $E_n\left(r\right)$ is the distribution of the Nth optical mode along the radius, and the formula is:

$<E_n\left(r\right)>=2\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}}{E}_n\left(r\right)rdr(8)$

In Eq. 7, $u_m\left(r\right)$ is the distribution of the mth acoustic mode along the radius, the formula is:

$<u_m\left(r\right)>=2\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}}{u}_m\left(r\right)rdr(9)$

By substituting Eqs 8 and 9 into Eq. 7, the overlap of the mode field distribution of the optical mode on the cross-section of the fiber can be obtained. Considering the superposition of optical modes, the calculation formula of BFS is as follows:

$V_B=\left(\frac{n_{eff}^p+n_{eff}^s}{\lambda }\right)V_1(10)$

Eq. 10 calculates the frequency deviation between the pumped light and the scattered light, i.e., the frequency of the acoustic wave. When employing LN as a waveguide material, it is crucial to consider the impact of mechanical deformation, primarily due to its substantial refractive index. Mechanical deformation encompasses two key phenomena: the photoelastic effect (PE) and moving boundary scattering (MB). Given the large refractive index of the LN utilized in this experiment, there’s an increase in the Brillouin gain due to the enhanced Brillouin gain coefficient. Moreover, considering that the experiment employs nanometer-level waveguides, the boundary effect becomes more pronounced. Therefore, it is imperative to consider the influence of both the photoelastic effect (PE) and moving boundary scattering (MB) when calculating the Brillouin gain. The peak of Brillouin gain is:

$g_B=\frac{2{\omega }_p}{\rho B_m^a{\mathrm{\Omega }}_m^2}{\left|\int f_{PE}dB+\int f_{MB}dl\right|}^2(11)$

where ${\mathrm{\Omega }}_m$ is the angular frequency of the acoustic mode; $f_{PE}$ is the force of PE on the medium; $f_{MB}$ is the force of MB on the medium.

3 Simulation results

Based on the derivation of the correlation formula for forward Brillouin scattering, a ring-type waveguide structure using LN is proposed, as depicted in Figure 2. Figure 2A illustrates the schematic diagram of the LN ring waveguide, comprising an insulator single crystal base and a LN ring situated above it. Figure 2B presents the design of the annular waveguide structure, while Figure 2C showcases the photoacoustic interaction model within the annular cavity. During the installation process, light is entirely reflected within the annular waveguide cavity.

Figure 2

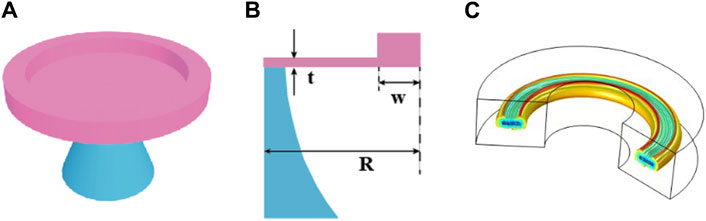
Figure 2. (A) Schematic diagram of LN ring waveguide (the top ring part is LN material). (B) Design diagram of the ring cavity and its parameters: t = 250nm, w = 100 nm-2,000 nm, LN radius corresponds to R = 500 nm. (C) A model of photo-acoustic interaction in an annular cavity.

In the experiment, the basic information of LN is first set. The density of LN is $4659kg/m^3$ , and the sound velocity is $6570m\cdot s^{-1}$. There is a big gap between the propagation speed of sound in LN and air. Its photonics tensors are $p_{11}=-0.026$, $p_{12}=0.07$, $p_{44}=-0.71$, refractive index $n=2.237$, and Poisson’s ratio 0.25 [26].

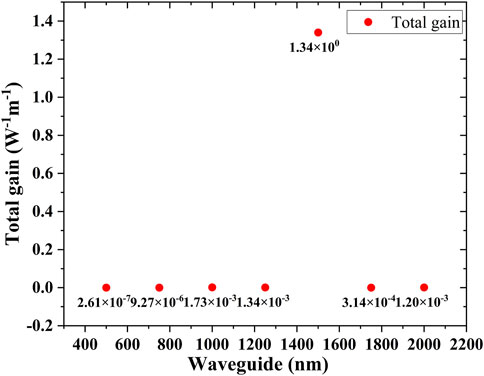
The total gain exhibits a relationship across waveguide widths ranging from 500nm to 2,000 nm, as depicted in Figure 3, where the total gain distribution is most dense and large at 1,500 nm, resulting in a Brillouin gain of $1.34W^{-1}{m}^{-1}$. The reason for this phenomenon is due to the combined effect of the electro strictive force and radiation pressure. At less than 1,500 nm, the role of the moving boundary effect decreases, and the photo elastic effect increases with the increase of the waveguide structure. At the same time, the gain value generated by the electro strictive force is larger than that generated by the radiation pressure, which leads to an increase in the total gain. And when the waveguide width is larger than 1,500 nm, the decrease of the moving boundary effect increases and exceeds the increase value of the photo elastic effect, which leads to the decrease of the total gain. In the subsequent experimental analysis of the LN ring waveguide, the phonon tunable range is chosen to be discussed based on a waveguide width of 1,500 nm.

Figure 3

Figure 3. Total gain at different waveguide widths.

The electric and magnetic field distributions generated by the pump light when the waveguide width is 1,500 nm are shown in Figure 4A and Figure 4B, respectively, which show a high degree of symmetry in both the electric and magnetic fields of the pump light. And the arrows in Figure 4A indicate the direction of the electric field. In this experiment, the finite element method is used to analyze the waveguide length, which is divided into infinitesimal elements to analyze the change of the photoacoustic coupling rate in the waveguide structure. Finite element simulations are used to obtain the nonlinear Brillouin optical-acoustic coupling efficiency versus frequency curves for ring waveguides with different widths, where the ring waveguides generate multiple Brillouin resonances. As shown in Figure 4C, the frequency resonances are realized with the variation of the suspended waveguide dimensions. The red dashed star line in Figure 4C represents the acoustic frequency dispersion curves calculated satisfying the multi-order modes of Fabry-Perot, which are a function of the width of the ridged waveguide for each mode order m. The redder color indicates a large opto-mechanical coupling, and the dark blue color indicates zero opto-mechanical coupling. In Figure 4C, the spatial contours of the main photo elastic and motion boundary components of the radial respirator-like mechanical pattern in the entire ridged waveguide structure are also shown.

Figure 4

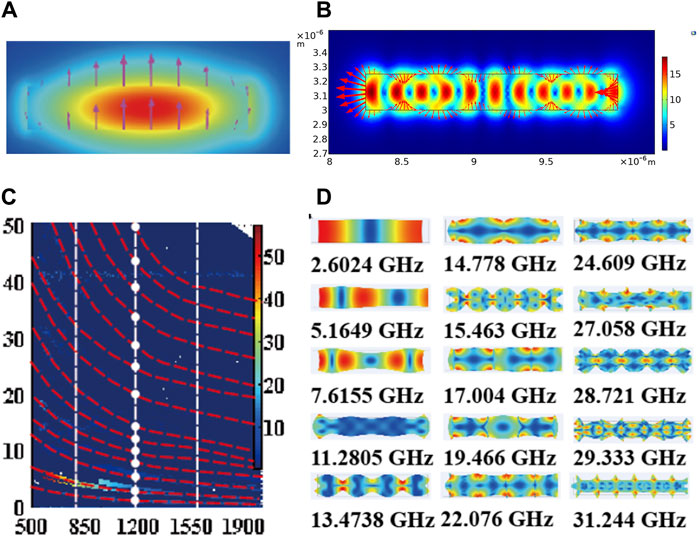
Figure 4. Based on the waveguide width of 1,500 nm: (A) Electric field distribution of pumped light. (B) Magnetic field distribution of pumped light. (C) Finite element simulation of the optical-acoustic coupling rate with cross-section width in an annular cavity structure, the red dashed line is the frequency calculated from Fabry-Perot’s multi-order modes. (D) Mode distributions of phonons with different eigenfrequencies.

Figure 4D shows the phonon vibration patterns of the acoustic modes at different frequencies, and the phonon vibration patterns all show a high degree of symmetry. Both the ring waveguide structure and the suspended waveguide structure have good spatial symmetry in the center. And the generated phonon frequencies have a very strong correlation with the Brillouin frequency shift. The change of the waveguide structure affects the phase matching conditions as well as the Brillouin resonance, which in turn affects the excited phonons. When the waveguide structure is turned into a completely spatially symmetric structure, not only does it solve the problem of chaotic phonon frequency generation, but it also improves the tunable range of phonon frequency. The waveguide structure is further optimized to ensure that it produces high Brillouin gain with good spatial symmetry, so that high frequency phonons can be excited.

The curves of nonlinear Brillouin photoacoustic coupling efficiency with frequency for ring waveguides of different widths are obtained by finite element simulation. The relationship between tunable phonon frequency, waveguide width and gain are plotted as shown in Figure 5. The gain is calculated according to Eq. 11. In the range of waveguide width w = 600–1,200 nm, the curves of resonant Brillouin resonators generated by multiple toroidal waveguides are plotted separately. By calculating the eigenfrequency and forward Brillouin scattering gain of each Brillouin active phonon mode, each trace satisfying the eigenfrequency is obtained. As shown in Figure 5, tunability to almost any frequency within 2.6–31 GHz is achieved within the allowable range of variation of the cavity dimensions. Since the acousto-optic coupling efficiency is proportional to the Brillouin gain, the total gain also decreases as the mode order is increased. As can be seen from the figure, the Brillouin gain is maximum when the mode is of first order, i.e., the acousto-optic coupling efficiency reaches its maximum value. And in the mode with large acousto-optic coupling efficiency, its phonon vibration pattern has good spatial symmetry and is well confined in the waveguide structure. This is since that the optical and acoustic fields are confined in the waveguide structure over a large area, which results in a significant overlap between the optical force density and the elastic displacement field. This greatly improves the acousto-optic coupling efficiency and increases the Brillouin gain.

Figure 5

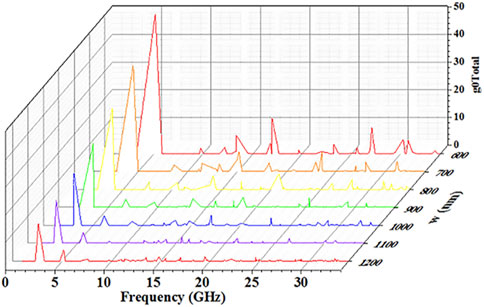
Figure 5. The relationship between the total gain of the Brillouin-suspended laser and the frequency change with the waveguide width.

The probe used in the sweep has a nonlinear induction sideband etched into it. This allows clear signals to be observed that show a nonlinear Brillouin response. During the experiment, a radio frequency (short for RF) filter was used to detect the outlier of the high frequency probe signal. And the resulting RF power is integrated to obtain the spectrum in Figure 5. The g0total in Figure 5 is the same as in the Theory model above, meaning the total gain of forward Brillouin scattering. The quantitative analysis of the Brillouin nonlinearity reveals the Fano-like line shape produced by each Brillouin resonance, from which the magnitude of the Brillouin nonlinearity coefficient can be obtained. In the first-order mode, the acousto-optic coupling efficiency is maximized. Moreover, the acousto-optic coupling efficiency is proportional to the Brillouin gain, while the phonon mode diagram has good spatial symmetry in the mode with large acousto-optic coupling efficiency. In addition, we used a high-resolution RF spectrum analyzer (SA) to resolve the Stokes and inverse Stokes signal spectra while obtaining the data. This asymmetric line shape is caused by coherent interference between the Brillouin and the electronic Kerr nonlinearity of the waveguide. And the electronic Kerr nonlinearity intervenes at the Stokes and anti-Stokes frequencies due to the cross-phase modulation between the pump beam and the probe beam in the waveguide core.

With LN as the main material ring waveguide structure, the forward SBS nonlinear magnetization is measured to be more than 1,000 times stronger than any previous waveguide system. This novel waveguide geometry enables independent control of the phonon modes and the opto-mechanical drive, resulting in customizable Brillouin coupling over a very wide bandwidth. Simultaneous coupling to many transverse phonon modes produces relatively flat Brillouin gain over the entire 1–31 GHz frequency range. We have shown that due to coherent interference from the Kerr and Brillouin effects, structural tuning of 1–31 GHz phonon resonances with high quality factors produces tailorable nonlinear optical magnetization.

The conclusions obtained from the simulation experiments are completely idealized, and the conclusions obtained may be different if the external influences on the actual preparation of LN waveguides are considered. In the actual preparation of LN waveguides, the following aspects are mainly considered. First, because LN is a hard and chemically inert material, it is difficult to, etch LN. The etching method we chose was Inductively Coupled Plasma (ICP) etching, which uses physical ion bombardment and chemical reaction to etch materials. Second, the LN refractive index has a significant temperature dependence, which allows the phase matching to be thermally modulated, resulting in heat generation. We can use air cooling or water cooling with copper tube embedded outside the resonator cavity to dissipate and cool the working material of the laser. Or by designing an integrated external heat dissipation system, i.e., setting heat dissipation fins on the outer side wall of the laser cavity. This not only makes the temperature of the working substance decrease rapidly, but also improves the electro-optical conversion efficiency, and improves the stability and power of the laser output. At the same time, when preparing the waveguide, we do not choose to use ultrasonic vibration to clean the waveguide structure to prevent damage to the waveguide structure. Deionized water is generally used to slowly rinse the waveguide structure, and then leave it to air dry at room temperature. This further ensures the efficiency of the acousto-optic coupling and the accuracy of the SBS measurement in practice.

Furthermore, the phonons emitted by this hybrid photon-phonon system are highly controllable. It can be realized in the form of coherent information transfer through traveling wave processes, thus complementing the latest cavity optomechanical systems. Simulation results show that the tunable FSBS effect is realized in a LN ring waveguide with a maximum FSBS gain of $1.34W^{-1}{m}^{-1}$, and the tunable phonon frequency from 1–31 GHz is realized (about twice that of a silicon ring waveguide) is achieved. Tunable lasers have seen considerable development in recent years and have very bright application prospects. It can be expected that the performance of tunable lasers in fiber optic communication light sources will be further improved, and the market share will gradually increase. Therefore, the novel ring waveguide structure constructed in this experiment will provide a new reference direction for subsequent research.

4 Conclusion

In this paper, we introduce a novel waveguide structure built upon a micro-ring configuration utilizing LN as the primary material. The primary objective of this design is to induce a more pronounced SBS effect. As a new dielectric material, LN has a broad research prospect in the field of optics. The use of LN as a material for tunable lasers mainly utilizes its excellent properties such as better electro-optic effect, photo elastic effect and acousto-optic effect. Simulation results show that the LN micro-ring waveguide structure has a large phonon tunable range, which can realize a more stable Brillouin gain in the range of 1–31 GHz. At the same time, it also has a large forward Brillouin gain, with a maximum forward Brillouin gain of $1.34W^{-1}{m}^{-1}$. This result provides a new direction for the construction of a new tunable brillouin laser and adapts to the need for integrated on-chip SBS devices. Meanwhile, LN as the main material of the laser can reduce the waveguide loss and provides a reference value for the Brillouin effect in optical fiber transmission.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HL: Conceptualization, Investigation, Validation, Visualization, Writing–original draft, Writing–review and editing. YY: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft. KL: Formal Analysis, Project administration, Writing–review and editing. HY: Resources, Supervision, Writing–review and editing. DW: Formal Analysis, Supervision, Writing–review and editing. YW: Data curation, Funding acquisition, Software, Writing–review and editing. ZL: Methodology, Resources, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (No. 62005074, No. 62004059, No. 61927815, and No. 62075056), Natural Science Foundation of Hebei Province (No. F2021202002).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Damzen MJ, Vlad V, Mocofanescu A, et al. Stimulated Brillouin scattering: fundamentals and applications. Boca Raton: CRC Press (2003). p. 95–8. doi:10.1201/9781420033465

CrossRef Full Text | Google Scholar

2. Kim J, Kuzyk MC, Han K, Wang H, Bahl G. Non-reciprocal Brillouin scattering induced transparency. Nat Phys (2015) 11:275–80. doi:10.1038/nphys3236

CrossRef Full Text | Google Scholar

3. Tomes M, Carmon T. Photonic micro-electromechanical systems vibrating at X-band (11-GHz) rates. Phys Rev Lett (2009) 102:113601. doi:10.1103/PhysRevLett.102.113601

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pant R, Poulton CG, Choi D-Y, Mcfarlane H, Hile S, et al. On-chip stimulated Brillouin scattering. Opt Express (2011) 19:8285–90. doi:10.1364/OE.19.008285

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Merklein M, Kabakova IV, Büttner TF, Choi DY, Luther-Davies B, Madden SJ, et al. Enhancing and inhibiting stimulated Brillouin scattering in photonic integrated circuits. Nat Commun (2015) 6:6396. doi:10.1038/ncomms7396

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bogaerts W, De Heyn P, Van Vaerenbergh T, De Vos K, Kumar Selvaraja S, Claes T, et al. Silicon microring resonators. Laser Photon Rev. (2012) 6:47–73. doi:10.1002/lpor.201100017

CrossRef Full Text | Google Scholar

7. Xiao S, Khan MH, Shen H, Qi M. A highly compact third-order silicon microring add-drop filter with a very large free spectral range, a flat passband, and a low delay dispersion. Opt Express (2007) 15:14765–71. doi:10.1364/OE.15.014765

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nawrocka MS, Liu T, Wang X, Panepucci RR. Tunable silicon microring resonator with wide free spectral range. Appl Phys Lett (2006) 89:071110–3. doi:10.1063/1.2337162

CrossRef Full Text | Google Scholar

9. Little BE, Chu ST, Haus HA, Foresi J, Laine JP. Microring resonator channel dropping filters. J Lightwave Technol IEEE Eplore (1997) 15:998–1005. doi:10.1109/50.588673

CrossRef Full Text | Google Scholar

10. Emelett SJ, Soref R. Design and simulation of silicon microring optical routing switches. J Lightwave Technol J Lightwave Technol (2005) 23:1800–7. doi:10.1109/jlt.2005.844494

CrossRef Full Text | Google Scholar

11. Van V, Ibrahim TA, Ritter K, Absil P, Johnson F, Grover R, et al. All-optical nonlinear switching in GaAs-AlGaAs microring resonators. IEEE Photon Technol Lett (2002) 14:74–6. doi:10.1109/68.974166

CrossRef Full Text | Google Scholar

12. Ibrahim TA, Cao W, Kim Y, Li J, Goldhar J, et al. All-optical switching in a laterally coupled microring resonator by carrier injection. IEEE Photon Technol Lett (2003) 15:36–8. doi:10.1109/LPT.2002.805877

CrossRef Full Text | Google Scholar

13. Dong P, Shafiiha R, Liao S, Liang H, Feng NN, Feng D, et al. Wavelength-tunable silicon microring modulator. Opt Express (2010) 18:10941–6. doi:10.1364/OE.18.010941

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xu H, Yu J, Xiong K, Hu Y, Li Z, et al. 25 Gbit/s silicon microring modulator based on misalignment tolerant interleaved PN junctions. Opt Express (2012) 20:2507–15. doi:10.1364/OE.20.002507

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Manipatruni S, Preston K, Chen L, Lipson M. Ultra-low voltage, ultra-small mode volume silicon microring modulator. Opt Express (2010) 18:18235–42. doi:10.1364/OE.18.018235

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rosenberg JC, Green WM, Assefa S, Gill DM, Barwicz T, Yang M, et al. A 25 Gbps silicon microring modulator based on an interleaved junction. Opt Express (2012) 20:26411–23. doi:10.1364/OE.20.026411

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yang KY, Oh DY, Lee SH, Yang Q-F, Yi X, Shen B, et al. Bridging ultrahigh-Q devices and photonic circuits. Nat Photon (2018) 12:297–302. doi:10.1038/s41566-018-0132-5

CrossRef Full Text | Google Scholar

18. Schmidt MK, Poulton CG, Mashanovich GZ, Reed GT, Eggleton BJ, Steel MJ. Suspended mid-infrared waveguides for stimulated brillouin scattering. Opt Express (2019) 17:4976–89. doi:10.1364/OE.27.004976

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sarabalis CJ, McKenna TP, Patel RN, Safavi-Naeini AH. Acousto-optics in lithium niobate-on-sapphire. In: Conference on lasers and electro-optics (CLEO) (2020). doi:10.1364/CLEO_QELS.2020.FTh3C.5

CrossRef Full Text | Google Scholar

20. Nikogosyan DN. Nonlinear optical crystals: a complete survey. New York: Springer-Verlag (2005). p. 70–4. doi:10.1007/b138685

CrossRef Full Text | Google Scholar

21. Sarabalis CJ, McKenna TP, Patel RN, Safavi-Naeini AH. Acousto-optics in lithium niobate-on-sapphire. In: CLEO: QELS_fundamental science 2020Washington DC United States (2020).

CrossRef Full Text | Google Scholar

22. Zhao L, Yongqian L, Zhiniu X. Theoretical calculation of Brillouin scattering spectrum and SBS threshold in multimode fiber. Infrared Laser Eng (2015) 44:93.

Google Scholar

23. Rodrigues CC, Zurita RO, Alegre TP, Wiederhecker GS. Stimulated Brillouin scattering by surface acoustic waves in lithium niobate waveguides. J Opt Soc America B (2023) 40:D56–D63. doi:10.1364/JOSAB.482656

CrossRef Full Text | Google Scholar

24. Rakich PT, Reinke C, Camacho R, Davids P, Wang Z. Giant enhancement of stimulated brillouin scattering in the subwavelength limit. Phys Rev X (2012) 2:011008–22. doi:10.1103/PhysRevX.2.011008

CrossRef Full Text | Google Scholar

25. Van Laer R, Kuyken B, Van Thourhout D, Baets R. Interaction between light and highly confined hypersound in a silicon photonic nanowire. Nat Photon (2015) 9:199–203. doi:10.1038/nphoton.2015.11

CrossRef Full Text | Google Scholar

26. Kippenberg TJ, Kalkman J, Polman A, Vahala K. Demonstration of an erbium-doped microdisk laser on a silicon chip. Phys Rev A (2006) 74:1–2. doi:10.1109/CLEO.2006.4627615

CrossRef Full Text | Google Scholar