Analysis of regional carbon productivity differences and influencing factors—based on new green decomposition model

This paper introduces a new green decomposition model of carbon productivity that aims to further analyze the regional differences in carbon productivity and its interaction with regional industrial performance. We combine desired outputs and undesired outputs orientation, and multiple factor inputs to derive a new green decomposition theorem, establish a new green decomposition model of carbon productivity, and obtain nine effects of regional carbon productivity differences. Empirical analysis is conducted using input-output data from 29 provinces and 15 industries in China, comparing the differences in carbon productivity from both the provincial and industry perspectives and exploring the mechanism of action. This paper provides theoretical basis and empirical evidence for regional carbon productivity enhancement and economic and industrial optimization from the perspective of multi-factor inputs, as well as policy insights for regional low-carbon transition development.

1 Introduction

Since 2006, China has become the largest carbon-emitting country in the world. According to data released by the International Energy Agency (IEA), China’s carbon dioxide emissions in 2021 were approximately 1.014 billion tons, accounting for around 27% of total global emissions, and its carbon dioxide emissions in 2022 are expected to remain at a similar level to those of 2021. China is faced with the dual constraints of economic growth and environmental protection [1], with underlying contradictions such as insufficient innovation capability, worsening environmental pollution, and regional development disparities [2]. Therefore, China has adopted carbon-emission reduction-oriented environmental policies, with a key focus on achieving the proper balance between environmental pollution and industrial performance [3–5]. Clearly, the adoption of carbon-emission reduction-oriented environmental policies requires a more comprehensive understanding of the interaction between carbon productivity and industrial performance, as well as a more in-depth search for the driving factors of carbon productivity.

However, traditional carbon productivity decomposition models often ignore undesirable outputs, making it difficult to efficiently measure production technology efficiency that includes undesirable outputs [6,7]. Additionally, these models overlook the diversity and complexity of factor inputs in the economic production process [8, 9], especially the critical role that knowledge inputs play in regional carbon productivity disparities [10, 11]. This limits our ability to thoroughly understand the interaction between regional carbon productivity and industrial performance, as well as to develop location-specific policies based on the driving factors and impact of carbon productivity. Against the backdrop of environmental policies aimed at reducing carbon emissions, how do the diversity and complexity of factor inputs and the duality of desirable and undesirable outputs affect regional carbon productivity disparities, and what impact do they have on regional industrial performance?

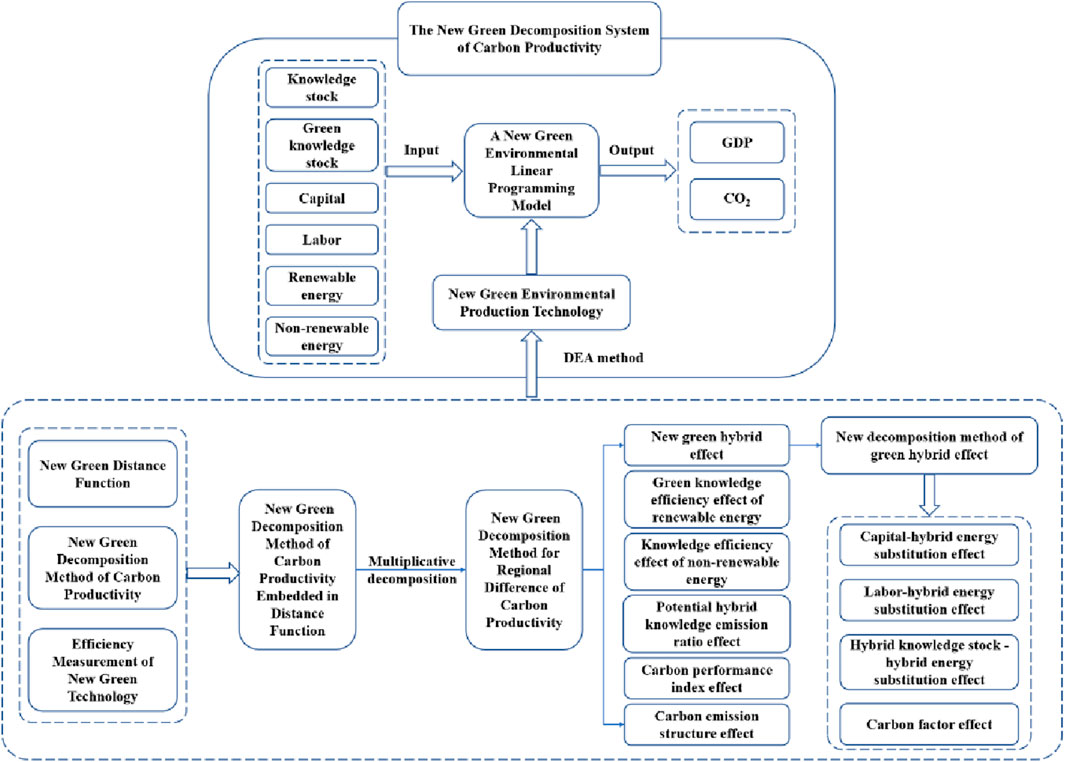
This paper addresses the aforementioned issues by constructing a new green decomposition model of carbon productivity. First, we refine energy input factors into renewable and non-renewable energy inputs, and draws from [2] and [12] to introduce knowledge stock and green knowledge stock inputs, defining a new green environmental production technology. Using data envelopment analysis (DEA) method, we establish a new linear programming model for green environmental production technology with constant returns to scale. Second, based on the traditional output-oriented Shephard distance function, we define a more practical new green Shephard distance function for desirable and undesirable outputs and their corresponding new green Farrell technical efficiency measures. Third, according to the definition of carbon productivity and input factors under the drive of green development, we define a new green decomposition theorem for carbon productivity and a new green decomposition theorem for carbon productivity embedded in distance function. By obtaining the decomposition equation for carbon productivity and constructing a new green decomposition model of carbon productivity, we have decomposed the regional differences of carbon productivity into 9 influencing factors: the green knowledge efficiency effect of renewable energy inputs, knowledge efficiency effect of non-renewable energy inputs, potential hybrid knowledge emission ratio effect, carbon performance index effect, carbon emissions structure effect, capital-hybrid energy substitution effect, labor-hybrid energy substitution effect, hybrid knowledge stock-hybrid energy substitution effect, and carbon factor effect. According to the definition of carbon productivity and input factors under green development drive, we define the new green decomposition theorem for carbon productivity and the embedded distance function green decomposition theorem for carbon productivity, obtaining the decomposition formula for carbon productivity. The new green decomposition model for carbon productivity is constructed, and the regional differences in carbon productivity are decomposed into 9 effects: green knowledge efficiency effect of renewable energy (HEEE), knowledge efficiency effect of non-renewable energy (GEFE), potential hybrid knowledge emission ratio effect (PHGCRE), carbon performance index effect (CPIE), carbon emission structure effect (CESE), capital - hybrid energy substitution effect (KEFSE), labor - hybrid energy substitution effect (LEFSE), hybrid knowledge stock - hybrid energy substitution effect (HGEFSE), carbon factor effect (CFE). The empirical part of this paper selects input and output data from 15 industries in 29 provinces, municipalities, and autonomous regions in China in 2019. By using the new green decomposition model of carbon productivity and the expressions of each effect, we compare the differences in carbon productivity and explore the influencing factors behind the differences, enriching the research content at both the regional and industry levels. The research framework for the new green decomposition system of carbon productivity is shown in Figure 1.

Figure 1

Figure 1. Framework for the new green decomposition system of carbon productivity.

The rest of this paper is described as follows; Section 2 provides a literature review on the research progress of carbon productivity methods and compares this paper with previous research; Section 3 constructs a new green decomposition model of carbon productivity, decomposing the differences in regional carbon productivity into 9 influencing factors; Section 4 presents an empirical analysis of the model, comparing and analyzing the differences and influential factors of carbon productivity from single and double dimensions; Section 5 is conclusion; Section 6 is policy recommendations.

2 Literature review

The concept of carbon productivity first appeared in the study by [13], which refers to the economic benefits generated by unit carbon emissions. In 2008, the report released by [14] elaborated on the significance of carbon productivity, indicating that any technology that successfully mitigates climate change must achieve two objectives: firstly, to stabilize greenhouse gas emissions, and secondly, to maintain high-quality and healthy economic development. Carbon productivity effectively combines both goals. Nowadays, carbon productivity has become one of the important indicators that measure the development of a low-carbon economy, attracting attention from policymakers and researchers in various countries and regions worldwide.

2.1 Research methods for carbon productivity

Regarding the research methods of carbon productivity, scholars and experts have done a lot of research. The main methods include Stochastic Frontier Analysis (SFA) [15] and Data Envelopment Analysis (DEA) [16]. The most important feature of SFA is that it considers the effect of stochastic factors on output, while it enables the study of panel data across time periods, resulting in more realistic research outcomes [17–19]. DEA methods are widely used in efficiency measurement research. [20] used a nonparametric approach to measure technical efficiency with constant returns to scale and proposed the environmental DEA technique. However, the traditional DEA model does not account for undesirable outputs, making it challenging to effectively measure the efficiency of production technology that includes them [7, 21]. Currently, there are three primary methods for dealing with undesirable outputs in efficiency analysis models. The first treats them as input variables for research, but this contradicts actual production processes [22, 23]. The second constructs a variable that is negatively correlated with undesirable output, and then performs calculations within the traditional efficiency analysis model [24], but this method is limited to variable returns to scale cases. The third approach involves using environmental production technology to measure technical efficiency and incorporating undesirable outputs in the actual production process [25], rather than merely representing it through mathematical functions in abstract terms [5]. In addition to the above two traditional analysis methods, [26] have proposed a new approach to measuring carbon productivity in the generalized input-output model, which aims to construct more reasonable carbon productivity indicators. Thus, a theoretical framework for multiple research methods on carbon productivity has been preliminarily established.

2.2 Analysis methods for influencing factors of carbon productivity

The analysis of factors influencing carbon productivity usually uses econometric modeling and factor decomposition methods. Econometric models effectively combine economic theory and statistical methods to quantitatively analyze the research object [27, 28]. The factor decomposition methods are more widely used because they can decompose the variation of the research object into the changes of multiple influencing factors. By comparing and analyzing the contribution rates of various influencing factors to the changes of the research object, it can offer more comprehensive insights. Based on the decomposition principle, factor decomposition methods mainly include Structural Decomposition Analysis (SDA) and Index Decomposition Analysis (IDA) methods [8, 29]. Compared to the SDA method, the IDA method is more widely applied at a cross-time and cross-regional level. The IDA method mainly includes Laspeyres index decomposition method and Divisia index decomposition method. The latter consists of Logarithmic Mean Divisia Index (LMDI) method and Arithmetic Mean Divisia Index (AMDI) method. LMDI is capable of handling residual and zero value problems better [30]. LMDI can be divided into LMDI-1 and LMDI-2, which use different weighting formulas. LMDI-1 is simpler, and thus, more widely applied in energy and environmental research [31]. In 1998, [32] introduced a fully decomposable LMDI method. In 2018, [9] used the LMDI method to decompose carbon emissions into six influencing factors and analyzed the top 23 countries in renewable energy use. [33] compared the contributions of different technology-driving factors related to CO₂ emission growth, using the LMDI method based on energy allocation analysis for different time periods. The diversity of methods for analyzing the factors affecting carbon productivity provides a reference basis and analysis tool for the green decomposition of carbon productivity in this paper.

2.3 Research methods for regional differences in carbon productivity

The comparative research on regional differences of carbon productivity mainly involves two methods: the Theil index and decomposition analysis [34, 35]. The Theil index indicates the level of regional economic disparity, with a larger value indicating greater disparity. [36] effectively combined the decomposition analysis method and environmental production technology, proposing a new Production Decomposition Analysis (PDA) method using Shephard distance function and environmental DEA technology in production theory. [37] quantified the impact of carbon performance index, potential carbon factors, and industrial structure on regional differences in carbon emission intensity using a spatial PDA model based on the production theory framework. [38] used the spatial PDA method and data from various industrial sectors in Chinese provinces to study the regional differences in industrial carbon productivity as well as the driving factors at the provincial and sectoral levels. At the carbon trading and regional carbon productivity level, carbon trading can promote technological progress, factor accumulation, scale allocation and energy substitution effects [39]. [40] provided an in-depth explanation of energy saving and emission reduction in China’s energy system in terms of carbon trading and new energy development mechanism, driving mechanism, evolutionary behavior and policy synergy. This provides us with reference for studying a green decomposition system for multiple sectors and regions.

Carbon productivity is a hot topic in the current field of energy and economic research. Scholars and experts mostly analyze the differences in carbon productivity by using existing methods, exploring the impact of different driving factors on carbon productivity. However, there is less research on the driving factors of carbon productivity that take into account the knowledge stock input needed in the production process and the green knowledge stock input, and most studies neglect the critical role of undesirable outputs, as well as the inherent interaction between regions and industries. This paper investigates multiple types of input factors in the economic production process, considering both desirable and undesirable outputs. It constructs a new green decomposition system of carbon productivity and obtains the results of carbon productivity decomposition in both single-dimensional and dual-dimensional dimensions. The comparative analysis of carbon productivity differences at the regional and industry levels from the perspective of inherent interaction provides targeted policy recommendations for low-carbon development in regions and industries.

3 New green decomposition model of carbon productivity

3.1 New green environmental production technology

Suppose there are N regions R_j (j = 1, … ,N) in the economic system, each of which contains M industries (i = 1, … ,M). Following the MR model in the spatial decomposition strategy, we take the average of all the regions under evaluation to obtain the reference region R_u as a benchmark for comparison. Therefore, our study includes a total of N+1 regions.

In economic production activities, a certain type and amount of production factors can generate economic benefits, or the desirable outputs (referring to GDP added value). However, at the same time, it can also produce some waste and pollutants, or the undesirable outputs (referring to CO₂ emissions). Based on the environmental production technology proposed by [20], this paper endogenizes the production factor input in economic production process in accordance with the requirements of green development [2, 41]. Building on the original energy input, energy input is divided into renewable energy input and non-renewable energy input, where the stock of knowledge input and green knowledge stock input are introduced. Definition 1 is given as follows: The set of new green environmental production technologies.

Definition 1. The set of new green environmental production technologies for industry i in economic production activities is:

$T_i=\left\{\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right):\text{input}\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right),\text{output}\left(Y_i,C_i\right)\right\}(1)$

Where, K_i represents the capital input for industry i, L_i represents the labor input for industry i, E_i represents the renewable energy input for industry i, F_i represents the non-renewable energy input for industry i, and the product of E_i and F_i represents the hybrid energy input for industry i. H_i represents the green knowledge stock input for industry i, G_i represents the knowledge stock input for industry i, and the product of H_i and G_i represents the hybrid knowledge stock input for industry i. Y_i represents the desirable outputs for industry i, referring to the industry added value, while C_i represents the undesirable outputs for industry i, referring to the amount of CO₂ emissions.

According to [42], we present Property 1 of the set of new green environmental production technologies.

Property 1. states that the set of new green environmental production technologies exhibits the following properties:

(1) The production technology demonstrates output neutrality;

(2) The set of new green environmental production technologies is a bounded and closed set;

(3) The input factors have free disposability;

(4) The desirable outputs have free disposability;

(5) The undesirable outputs have weak disposability;

(6) The desirable and undesirable outputs exhibit zero jointness.

Note 1: Explanation of the 6 properties in Property 1:

(1) In the economic production process, the production technology exhibits output neutrality, which means that when the inputs are not all zero, the output can be zero, that is, $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,\right.$ $0,0)\in T_i$, indicating the decision-making unit may not engage in production activities;

(2) In Eq. 1, for any input vector $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$, the subscript i represents the industry, of which there are only finitely many. A finite quantity of inputs can only produce a finite quantity of outputs. Therefore, the set of new green environmental production technologies in production theory is a closed and bounded set;

(3) Each input factor in the production process has free disposability. The free disposability of capital input is expressed as: if $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$ and $K_i\le {K_i}^{\prime }$, then $\left({K_i}^{\prime },L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$. The free disposability of labor input is expressed as: if $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$ and $L_i\le {L_i}^{\prime }$, then $\left(K_i,{L_i}^{\prime },E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$. Similar expressions can be derived for disposal of other input factors;

(4) The desirable outputs have free disposability, which means that if $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$ and ${Y_i}^{\prime }\le Y_i$, then $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,{Y_i}_i^{\prime },C_i\right)\in T_i$;

(5) The undesirable outputs exhibit weak disposability, which means that if $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$ and $0\le \theta \le 1$, then $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,\theta Y_i,\theta C_i\right)\in T_i$. This implies that undesirable outputs cannot be reduced separately during the production process and can only be reduced proportionally with desirable outputs;

(6) The “zero jointness” of the desirable and undesirable outputs indicates that when $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$, if there exists C_i = 0, then Y_i = 0. This means that obtaining desirable outputs during the production process will necessarily generate undesirable outputs, and only by completely terminating the entire production process can undesirable outputs be eliminated. The “zero jointness” is also known as by-productivity, which refers to the feature in the production process where undesirable outputs are considered as a by-product of desirable outputs, and C and Y will be produced simultaneously.

The new green environmental production technology can be modeled and described through an output set. Definition 2 is provided as follows: the output set of new green environmental production technology.

Definition 2. In economic production activities, the output set of new green environmental production technology for a given industry is defined as:

$P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)=\left\{\left(Y_i,C_i\right):\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i\right\}(2)$

Where $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$ represents the input factor combination in industry i, (Y_i,C_i) represents the output factor combination in industry i, and T_i represents the set of new green environmental production technologies in industry i as defined in Definition 1.

Based on the properties of the set of new green environmental production technologies, we present Property 2 of the output set of new green environmental production technologies:

Property 2. The output set of new green environmental production technologies satisfies the following properties:

(1) $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)\in T_i$ if and only if $\left(Y_i,C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$;

(2) Production technologies exhibit output neutrality;

(3) The output set of new green environmental production technologies is a bounded closed set;

(4) Input factors have free disposability;

(5) Desirable outputs have free disposability;

(6) Undesirable outputs have weak disposability;

(7) Desirable outputs and undesirable outputs exhibit “zero association".

Note 2: Explanation of the 7 properties in Property 2:

(1) When an input-output factor combination $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)$ belongs to the set of new green environmental production technologies T_i, that is, given the input vector $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$, the output set of the new green environmental production technologies $P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$ as defined in Definition 2 is composed of all the feasible output vectors (Y_i,C_i). The converse also holds true.

(2) The output neutrality of production technologies is demonstrated by the fact that for any input vector $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$, then $\left\{0,0,0,0\right\}\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$.

(3) In Eq. 2, for any given input vector $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$, the subscript i denotes industry, which is of a finite number. A finite number of inputs can only generate a finite number of outputs, ensuring the closure of the output vector. Clearly, the output set of new green environmental production technologies in the production theory is a closed bounded set.

(4) Each input factor in the production process has free disposability. The free disposability of capital input is manifested by the fact that if $K_i\le {K_i}^{\prime }$, then $P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)\subseteq P_i\left({K_i}^{\prime },L_i,E_i\cdot F_i,H_i\cdot G_i\right)$. The free disposability of labor input is manifested by the fact that if $L_i\le {L_i}^{\prime }$, then $P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)\subseteq P_i\left({K_i}^{\prime },{L_i}^{\prime },E_i\cdot F_i,H_i\cdot G_i\right)$. Similarly, the free disposability of other input factors can be derived.

(5) The free disposability of undesirable outputs is manifested by the fact that if $\left(Y_i,C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$ and ${Y_i}^{\prime }\le Y_i$, then $\left({Y_i}^{\prime },C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$.

(6) The weak disposability of undesirable outputs is manifested by the fact that if $\left(Y_i,C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$ and $0\le \theta \le 1$, then $\left(\theta Y_i,\theta C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$.

(7) The “zero association” of desirable and undesirable outputs is manifested by the fact that when $\left(Y_i,C_i\right)\in P_i\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i\right)$ and C_i = 0, we must have Y_i = 0.

Based on Definition 2 and Property 2, we have drawn Figure 2 to represent the output set of new green environmental production technologies.

Note 3: Explanation on Figure 2:

(1) In Figure 2, the horizontal axis represents non-desirable output, and the vertical axis represents desirable output. The slope from the origin O to any point in the production set represents the ratio of desirable output Y to non-desirable output C, which indicates the carbon productivity of the corresponding output combination.

(2) For example, assuming that A, B, and C are three different decision-making units that use the same amount of input factors to produce different output factor combinations (C, Y), which are (10,30), (30,50), and (50,40), respectively. They are represented by the three vertices A, B, and C in the Figure 2, and the region OABCD represents the production set. Based on the specific values of output factor combinations from A, B, and C, we can obtain the carbon productivities of the three decision-making units P_A = Y_A/C_A = 30/10 = 3, P_B = Y_B/C_B = 50/30 = 5/3, and P_C = Y_C/C_C = 40/50 = 4/5, respectively. Clearly, P_A > P_B > P_C, and the slopes of the three lines OA, OB, and OC decrease in turn in Figure 2.

(3) According to the sixth property of Property 2, any output factor combination (Y, C) in the production set, (θY, θC) after the reduction according to the same ratio θ still belongs to the output set.

(4) According to the seventh property of Property 2, the only intersection of the horizontal and vertical axes with the production set is at the origin O, which indicates that non-desirable output C and desirable output Y are “zero correlated” and can only equal 0 at the same time. Non-desirable output C is the by-product of desirable output Y.

New green environmental production technologies effectively combine six inputs with two outputs. We will now use DEA method to construct a new green environmental linear programming model based on Definition 1 under the assumption of constant returns to scale.

Figure 2

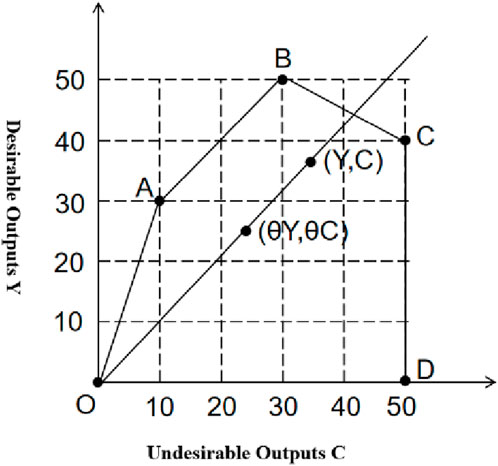
Figure 2. Graphical representation of the output set of new green environmental production technologies.

Model 1. A new green environmental linear programming model for industry i in economic production activities under the assumption of constant returns to scale.

$\begin{array}{l}{T}_i=\{\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right):\\ {\displaystyle \sum _j}{\lambda }_j{K}_{ij}\le K_i,\\ {\displaystyle \sum _j}{\lambda }_j{L}_{ij}\le L_i,\\ {\displaystyle \sum _j}{\lambda }_j\left(E_{ij}\cdot F_{ij}\right)\le \left(E_i\cdot F_i\right),\\ {\displaystyle \sum _j}{\lambda }_j\left(H_{ij}\cdot G_{ij}\right)\le \left(H_i\cdot G_i\right),\\ {\displaystyle \sum _j}{\lambda }_j{Y}_{ij}\ge Y_i,\\ {\displaystyle \sum _j}{\lambda }_j{C}_{ij}=C_i,\\ {\lambda }_j\ge 0,j=1,2,\cdots ,N+1\},\end{array}(3)$

Where, in Eq. 3, $\left(K_i,L_i,E_i\cdot F_i,H_i\cdot G_i,Y_i,C_i\right)$ is the input-output vector for industry i, $\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ is the input-output vector for industry i in region j, and λ_j represents the intensity variable.

Note 4: Explanation of the constraints in Model 1:

(1) Inequalities are used to constrain each input in the production process. The right-hand side of the constraint represents the actual input used by the producer, while the left-hand side represents the input used by a theoretically efficient producer at the optimal production frontier. The inequality indicates that the input used by a theoretically efficient producer must be less than or equal to the input used by the actual producer, which reflects property 1 (3), that input factors are freely disposable. In this paper, constraints on the input of knowledge stock and green knowledge stock are added to the new green environmental linear programming model to further determine the feasible range. The product of renewable energy input and non-renewable energy input is treated as an input factor, and the product of knowledge stock input and green knowledge stock input is treated as an input factor for ease of calculation in subsequent steps.

(2) Inequalities are used to constrain the desirable outputs Y, where the right-hand side of the constraint represents the actual desirable outputs received by the producer, and the left-hand side represents the desirable outputs that a theoretically efficient producer would receive at the optimal production frontier. The inequality indicates that the desirable outputs received by a theoretically efficient producer must be greater than or equal to the actual desirable outputs received by the producer, which reflects Property 1 (4), that desirable outputs are freely disposable.

(3) Equalities are used to constrain the undesirable outputs, which reflects Property 1 (5), that undesirable outputs have weak disposability. The desirable outputs and undesirable outputs can only be reduced proportionally.

(4) λ_j represents the intensity variable, which indicates the weight assigned to each observation when constructing the production possibility boundary. λ_j in Model 1 is unconstrained and hence the new green environmental linear programming model is constructed under the assumption of constant returns to scale.

3.2 New green distance function and technical efficiency measurement

Drawing on the research of [37], a new definition is presented for the Shephard distance function for undesirable outputs orientation, incorporating input factors under the framework of green development and in accordance with Definition 1, based on the traditional output-oriented Shephard distance function.

Definition 3. The new green Shephard distance function for undesirable outputs orientation is defined as:

$\begin{array}{l}{D}_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\\ =\sup \left\{{\beta }_{io}:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\frac{C_{ij}}{{\beta }_{io}}\right)\in T_i\right\},\end{array}(4)$

Where, in Eq. 4, the subscript O indicates the study area.

Property 3. The new green Shephard distance function for undesirable outputs orientation, as defined in Definition 3, has the following properties:

(1) $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\ge 1\iff \left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\in T_i$;

(2) $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=1\iff \left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ at the production technical frontier;

(3) $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ possesses first-degree homogeneity with respect to undesirable outputs: when α is a positive scalar, $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\alpha \cdot C_{ij}\right)=$ $\alpha D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$.

Proof:

(1) When a combination of input-output factors $\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ belongs to the set of new green production technology T_i for undesirable outputs orientation, the new green Shephard distance function is used to measure the technical efficiency of each decision-making unit in terms of carbon emissions, as represented by $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=C_{io}/C_{io}^{*}$, which is the ratio of actual observed undesirable outputs to potential ideal undesirable outputs. Clearly, the actual observed undesirable outputs are greater than or equal to the potential ideal undesirable outputs. Therefore, $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\ge 1$, the opposite is also true;

(2) When a combination of input-output factors $\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ lies on the production technology frontier, the actual observed undesirable outputs are exactly equal to the potential ideal undesirable outputs, that is, $C_{io}=C_{io}^{*}$. Therefore, $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=C_{io}/C_{io}^{*}=1$, and the opposite is also true;

(3) According to the formula of the new green Shephard distance function for undesirable outputs orientation:

$\begin{array}{l}{D}_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\alpha \cdot C_{ij}\right)\\ =\mathit{sup}\left\{{\beta }_{ij}:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\frac{\alpha \cdot C_{ij}}{{\beta }_{ij}}\right)\in T_i\right\}\\ =\mathit{sup}\left\{\alpha \cdot \frac{{\beta }_{ij}}{\alpha }:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\frac{\alpha \cdot C_{ij}}{{\beta }_{ij}}\right)\in T_i\right\}\\ =\mathit{sup}\left\{\alpha \cdot \frac{{\beta }_{ij}}{\alpha }:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\frac{C_{ij}}{{\beta }_{ij}/\alpha }\right)\in T_i\right\}\end{array}$

Based on Definition 3 and Model 1, the definition of the new green Farrell technical efficiency measure for undesirable outputs orientation is presented in this paper.

Definition 4. The new green Farrell undesirable outputs measure of production technical efficiency in Eq. 5 is defined as:

$\begin{array}{l}{\left(D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\right)}^{-1}=\mathit{min}{\beta }_{io},\\ s.t.\left\{\begin{array}{l}{\displaystyle \sum _j}{\lambda }_j{K}_{ij}\le K_{io},\\ {\displaystyle \sum _j}{\lambda }_j{L}_{ij}\le L_{io},\\ {\displaystyle \sum _j}{\lambda }_j\left(E_{ij}\cdot F_{ij}\right)\le \left(E_{io}\cdot F_{io}\right),\\ {\displaystyle \sum _j}{\lambda }_j\left(H_{ij}\cdot G_{ij}\right)\le \left(H_{io}\cdot G_{io}\right),\\ {\displaystyle \sum _j}{\lambda }_j{Y}_{ij}\ge Y_{io},\\ {\displaystyle \sum _j}{\lambda }_j{C}_{ij}={\beta }_{io}{C}_{io},\\ {\lambda }_j\ge 0,j=1,2,\cdots ,N+1\}.\end{array}\right.\end{array}(5)$

Note 5: The new green Farrell undesirable outputs measure used to measure production technical efficiency represents the proportion that needs to shrink to the minimum possible value of undesirable outputs, while keeping the desirable outputs constant, given a constant input factor. According to the meaning of the new green Shephard distance function for undesirable outputs orientation, the new green Farrell undesirable outputs measure of production technical efficiency is the reciprocal of the distance function defined in Definition 3, that is, $D_{io}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\ge 1$. Therefore, β_io is no greater than 1. When β_io = 1, that is, the new green Shephard distance function for undesirable outputs orientation is 1, the new green Farrell undesirable outputs measure of production technical efficiency is 1, and the system is in the optimal production state.

Definition 5. The new green Shephard distance function for desirable outputs orientation is in Eq. 6:

$\begin{array}{l}{D}_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\\ =\inf \left\{{\theta }_{io}:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},\frac{Y_{ij}}{{\theta }_{io}},C_{ij}\right)\in T_i\right\},\end{array}(6)$

Property 4. The new green Shephard distance function for desirable outputs orientation defined in Definition 5 has the following properties:

(1) $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\le 1\iff \left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\in T_i$;

(2) $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=1\iff \left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ at the production technical frontier;

(3) $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ is positively homogeneous of degree +1 with respect to desirable outputs: when α is a positive scalar, $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},\alpha \cdot C_{ij}\right)=\alpha D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$.

Proof:

(1) When a set of input-output factor combinations $\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ belongs to the new green environmental production technology set T_i, the new green Shephard distance function for desirable outputs orientation is used to measure the technical efficiency of each decision unit in producing desirable outputs, represented as $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=Y_{io}/Y^{*}$, the ratio of observed desirable outputs to potential ideal desirable outputs. Obviously, observed desirable outputs are less than or equal to potential ideal desirable outputs, therefore $D_{io}^Y(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},$ $C_{ij})\le 1$ and vice versa.

(2) When a set of input-output factor combinations $\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$ is at the production technical frontier, the observed desirable outputs are exactly equal to the potential ideal desirable outputs, $Y_{io}=Y_{io}^{*}$. Therefore, $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=Y_{io}/Y_{io}^{*}=1$ and vice versa.

(3) According to the formula for the new green Shephard distance function for desirable outputs orientation:

$\begin{array}{l}{D}_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\\ =\inf \left\{{\theta }_{ij}:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},\frac{\alpha \cdot Y_{ij}}{{\theta }_{ij}},C_{ij}\right)\in T_i\right\}\\ =\inf \left\{\alpha \cdot \frac{{\theta }_{ij}}{\alpha }:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},\frac{Y_{ij}}{{\theta }_{ij}/\alpha },C_{ij}\right)\in T_i\right\}\\ =\alpha \cdot \inf \left\{\frac{{\theta }_{ij}}{\alpha }:\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},\frac{Y_{ij}}{{\theta }_{ij}/\alpha },C_{ij}\right)\in T_i\right\}\\ =\alpha \cdot D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right).\end{array}$

According to Definition 5 and Model 1, we present Definition 6: new green Farrell technical efficiency measure for desirable outputs orientation.

Definition 6. The new green Farrell measure of production technical efficiency for desirable outputs orientation is in Eq. 7 defined as follows:

$\begin{array}{l}{\left(D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\right)}^{-1}=\max {\theta }_{io},\\ s.t.\left\{\begin{array}{l}{\displaystyle \sum _j}{\lambda }_j{K}_{ij}\le K_{io},\\ {\displaystyle \sum _j}{\lambda }_j{L}_{ij}\le L_{io},\\ {\displaystyle \sum _j}{\lambda }_j\left(E_{ij}\cdot F_{ij}\right)\le \left(E_{io}\cdot F_{io}\right),\\ {\displaystyle \sum _j}{\lambda }_j\left(H_{ij}\cdot G_{ij}\right)\le \left(H_{io}\cdot G_{io}\right),\\ {\displaystyle \sum _j}{\lambda }_j{Y}_{ij}\ge {\theta }_{io}{Y}_{io},\\ {\displaystyle \sum _j}{\lambda }_j{C}_{ij}=C_{io},\\ {\lambda }_j\ge 0,j=1,2,\cdots ,N+1.\end{array}\right.\end{array}(7)$

Note 6 The new green Farrell measure for desirable outputs orientation used to measure production technical efficiency represents the expansion ratio required to achieve the maximum possible value of desirable outputs, under the condition that undesirable outputs remain constant and given input factors remain unchanged. Based on the definition of the new green Shephard distance function for desirable outputs orientation, it can be seen that the new green Farrell measure of production technical efficiency for desirable outputs orientation is the reciprocal of the distance function defined in Definition 5, $D_{io}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\le 1$. Therefore, θ_io is not less than 1, and when θ_io = 1, the new green Shephard distance function for desirable outputs orientation is 1, the new green Farrell measure of production technical efficiency for desirable outputs orientation is also 1, which represents the optimal production state.

3.3 The new green carbon productivity decomposition theorem

According to [13] definition of carbon productivity and considering the input factors in the context of green development, this paper derives a new green decomposition theorem for carbon productivity in the context of green development.

Theorem 1. (New Green Decomposition Theorem for Carbon Productivity): The carbon productivity in region j can be decomposed into new green components as follows:

$P_j={\displaystyle \sum _{i=1}^M}EF{E}_{ij}\cdot HE{E}_{ij}\cdot GE{F}_{ij}\cdot HGC{R}_{ij}\cdot CE{S}_{ij},(8)$

Where, in Eq. 8 $EF{E}_{ij}=\frac{Y_{ij}}{E_{ij}\cdot F_{ij}}$ represents the hybrid energy utilization efficiency of industry i in region j, which is defined as GDP added value by unit of hybrid energy input; $HE{E}_{ij}=E_{ij}/H_{ij}$ represents the green knowledge efficiency of renewable energy input, which is defined as the consumption of renewable energy per unit of green knowledge stock input; $GE{F}_{ij}=F_{ij}/G_{ij}$ represents the knowledge efficiency of non-renewable energy input, which is defined as the consumption of non-renewable energy per unit of knowledge stock input; $HGC{R}_{ij}=H_{ij}\cdot G_{ij}/C_{ij}$ represents the hybrid knowledge emission ratio, which is defined as the consumption of hybrid knowledge stock per unit of carbon emission spatial resources; $CE{S}_{ij}=C_{ij}/C_j$ represents the carbon emission structure, which is defined as the proportion of carbon emissions from industry i in region j to the total carbon emissions from all industries in region j.

Proof: Carbon productivity in region j is equal to the ratio of the added value of GDP in region j to CO₂ emissions, and the added value of GDP in region j is written in the form of the sum of the added value of GDP in each industry in region j. Proof of Theorem 1 in Eq. 9:

$\begin{array}{l}{P}_j=\frac{Y_j}{C_j}={\displaystyle \sum _{i=1}^M}\frac{Y_{ij}}{C_j}\\ ={\displaystyle \sum _{i=1}^M}\frac{Y_{ij}}{E_{ij}\cdot F_{ij}}\cdot \frac{E_{ij}\cdot F_{ij}}{H_{ij}\cdot G_{ij}}\cdot \frac{H_{ij}\cdot G_{ij}}{C_{ij}}\cdot \frac{C_{ij}}{C_j}\\ ={\displaystyle \sum _{i=1}^M}\frac{Y_{ij}}{E_{ij}\cdot F_{ij}}\cdot \frac{E_{ij}}{H_{ij}}\cdot \frac{F_{ij}}{G_{ij}}\cdot \frac{H_{ij}\cdot G_{ij}}{C_{ij}}\cdot \frac{C_{ij}}{C_j}\\ ={\displaystyle \sum _{i=1}^M}EF{E}_{ij}\cdot HE{E}_{ij}\cdot GE{F}_{ij}\cdot HGC{R}_{ij}\cdot CE{S}_{ij}.\end{array}(9)$

Note 7: Theorem 1 decomposes carbon productivity of any region into the above-mentioned five indicators by using a new green decomposition approach. This paper further introduces three decomposed indicators, namely, green knowledge efficiency of renewable energy input, knowledge efficiency of non-renewable energy input, and hybrid knowledge emission ratio, into the green-decomposed results of carbon productivity. The mechanism for the driving factors of carbon productivity is analyzed from two perspectives, that is, input-output ratio and input-input ratio.

Based on Theorem 1, Definitions 3 and Definitions 5, a new green decomposition theorem of carbon productivity with a Shepherd distance function directed to both desirable outputs and undesirable outputs is derived.

Theorem 2. (New green-decomposition theorem of carbon productivity with embedded distance function) Carbon productivity of region j can be decomposed into a new green-decomposition with an embedded distance function in Eq. 10 as follows:

$P_j={\displaystyle \sum _{i=1}^M}MI{X}_{ij}·HE{E}_{ij}·GE{F}_{ij}·PHGC{R}_{ij}·CP{I}_{ij}·CE{S}_{ij},(10)$

Where, $MI{X}_{ij}=\frac{Y_{ij}/\left(E_{ij}\cdot F_{ij}\right)}{D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}$ represents the new green hybrid indicator of industry i in region j; $PHGC{R}_{ij}=\left(H_{ij}\cdot G_{ij}\right)D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)/C_{ij}$ represents the potential hybrid knowledge emission ratio of industry i in region j; $CP{I}_{ij}=\frac{D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}{D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}$ represents the carbon efficiency index of industry i in region j; while the meanings of HEF_ij, GEF_ij and CES_ij remain the same as in Theorem 1.

Proof: Theorem 2 is proved by embedding the new green Shepherd distance function directed to both desirable outputs and undesirable outputs on the basis of the proof of Theorem 1 in Eq. 11.

$\begin{array}{l}{P}_j={\displaystyle \sum _{i=1}^M}\frac{Y_{ij}}{E_{ij}\cdot F_{ij}}\cdot \frac{E_{ij}}{H_{ij}}\cdot \frac{F_{ij}}{G_{ij}}\cdot \frac{H_{ij}\cdot G_{ij}}{C_{ij}}\cdot \frac{C_{ij}}{C_j}\\ ={\displaystyle \sum _{i=1}^M}\frac{Y_{ij}/D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}{E_{ij}\cdot F_{ij}}\cdot \frac{E_{ij}}{H_{ij}}\cdot \frac{F_{ij}}{G_{ij}}\\ \cdot \frac{H_{ij}\cdot G_{ij}}{C_{ij}/D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}\cdot \frac{D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}{D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}\cdot \frac{C_{ij}}{C_j}\\ ={\displaystyle \sum _{i=1}^M}MI{X}_{ij}·HE{E}_{ij}·GE{F}_{ij}·PHGC{R}_{ij}·CP{I}_{ij}·CE{S}_{ij}.\end{array}(11)$

Note 8: Theorem 2 further decomposes carbon productivity of any region into the above-mentioned six indicators by embedding a new green Shepherd distance function directed to both desirable outputs and undesirable outputs on the basis of Theorem 1. This enables a more in-depth study of the driving factors of carbon productivity from the perspectives of both actual observed state and potential ideal state. The following are explanations for the three newly added indicators among the six decomposed indicators: new green hybrid indicator, potential hybrid knowledge emission ratio, and carbon efficiency index.

(1) In the new green hybrid indicator, the numerator is changed from Y_ij in the original hybrid energy utilization efficiency indicator to $Y_{ij}/D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$, which means that desirable outputs are expanded to potential ideal state under the corresponding undesirable outputs-directed new green Shepherd distance function. The denominator remains the hybrid energy input, so the whole fraction represents the potential hybrid energy utilization efficiency, indicating the potential level of hybrid energy utilization efficiency when the technical performance of desirable outputs reaches the ideal state.

According to [43] study, the new green Shephard distance function with outputs oriented desirable outputs have homogeneous of degree +1, that is, $D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},\alpha \cdot Y_{ij},C_{ij}\right)=\alpha \cdot D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$, and with inputs oriented desirable outputs have homogeneous of degree −1, that is, $D_{ij}^Y\left(\beta \cdot K_{ij},\beta \cdot L_{ij},\beta \cdot E_{ij}\cdot F_{ij},\beta \cdot H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)={\beta }^{-1}\cdot D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)$, where α and β are positive scalars. Hence, the new green hybrid index can be formulated as:

$\begin{array}{l}\frac{Y_{ij}/D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}{E_{ij}\cdot F_{ij}}\\ ={\left[\frac{1}{Y_{ij}}\cdot {\left(\frac{1}{E_{ij}\cdot F_{ij}}\right)}^{-1}\cdot D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)\right]}^{-1}\\ ={\left[\frac{1}{Y_{ij}}\cdot D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},Y_{ij},c_{ij}\right)\right]}^{-1}\\ ={\left(D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)\right)}^{-1},\end{array}$

Where, $k_{ij}=\frac{K_{ij}}{E_{ij}\cdot F_{ij}}$ represents the capital - hybrid energy ratio (KEF); $l_{ij}=\frac{L_{ij}}{E_{ij}\cdot F_{ij}}$ represents the labor - hybrid energy ratio (LEF); $h_{ij}\cdot g_{ij}=\frac{H_{ij}\cdot G_{ij}}{E_{ij}\cdot F_{ij}}$ represents the green knowledge stock input ratio (HGEF), and $c_{ij}=\frac{C_{ij}}{E_{ij}\cdot F_{ij}}$ represents the carbon factor (CF), which denotes the carbon conversion rate of the hybrid energy input. The calculation process highlights the superiority of representing the hybrid energy input as a product of renewable energy input E and non-renewable energy input F and that of representing the hybrid knowledge stock input as a product of green knowledge stock input H and total knowledge stock input G.

(2) In the potential hybrid knowledge emission ratio, the denominator has been changed from C_ij, which was the hybrid knowledge emission ratio for the original index, to $\frac{C_{ij}}{D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}$, which represents the undesirable outputs based on the corresponding undesirable outputs-oriented new green Shephard distance function. This indicates a reduction of the potential output to an ideal state of undesirable outputs. The numerator remains as the hybrid knowledge stock input. The entire fraction represents the potential level of hybrid knowledge emission ratio when the undesirable outputs technical efficiency reaches its ideal state.

(3) The carbon performance index is expressed as the ratio of the new green Shephard distance function oriented towards desirable outputs and the one oriented towards undesirable outputs. According to the meanings of the two distance functions, $D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=Y_{ij}/Y_{ij}^{*}$ and $D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)=C_{ij}/C_{ij}^{*}$. By substituting these values into the expression for the carbon performance index, we obtain $CP{I}_{ij}=\frac{D_{ij}^Y\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}{D_{ij}^C\left(K_{ij},L_{ij},E_{ij}\cdot F_{ij},H_{ij}\cdot G_{ij},Y_{ij},C_{ij}\right)}=\frac{Y_{ij}/Y_{ij}^{*}}{C_{ij}/C_{ij}^{*}}=\frac{Y_{ij}/C_{ij}}{Y_{ij}^{*}/C_{ij}^{*}}=\frac{P_{ij}}{P_{ij}^{*}}$, which represents the ratio of the actual observed carbon productivity to the potential ideal state carbon productivity. The potential ideal state of carbon productivity is greater than or equal to the actual observed carbon productivity. Therefore, the range of the carbon performance index CPI is between 0 and 1, where CPI approaching 1 indicates higher carbon productivity, which means that the actual observed carbon productivity is closer to the potential ideal state carbon productivity. When CPI equals 1, it represents the potential ideal state. This is the optimal level of carbon emission performance.

Based on Theorem 2 and Note 8(1), the decomposition of carbon productivity in the j region can be obtained as:

$P_j={\displaystyle \sum _{i=1}^M}{\left(D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)\right)}^{-1}\cdot HE{E}_{ij}\cdot GE{F}_{ij}\cdot PHGC{R}_{ij}\cdot CP{I}_{ij}\cdot CE{S}_{ij}(12)$

The decomposition results of carbon productivity in the j region have included three indicators: the green knowledge efficiency of renewable energy input, the knowledge efficiency of non-renewable energy input, and the potential hybrid knowledge emission ratio. This paper explores the influential factors of carbon productivity from the perspectives of input quantity and potential ideal states. To compare the differences of carbon productivity among different regions, two methods can be used: additive decomposition and multiplicative decomposition. In this paper, we adopt the multiplicative decomposition method to derive a new green decomposition theorem for regional differences in carbon productivity.

Theorem 3. (A new green decomposition theorem for regional differences of carbon productivity) The carbon productivity ratio between any given region j and a reference region can be decomposed into a new green decomposition as follows:

$\frac{P_j}{P_u}=A_{MIX}^{j,u}\cdot A_{HEE}^{j,u}\cdot A_{GEF}^{j,u}\cdot A_{PHGCR}^{j,u}\cdot A_{CPI}^{j,u}\cdot A_{CES}^{j,u},(13)$

Where, $A_{MIX}^{j,u}$ represents the new green hybrid effect (MIX), which includes four types of differences: the capital-hybrid energy ratio, labor - hybrid energy ratio, hybrid knowledge stock - hybrid energy ratio, and carbon factor, between the two regions. $A_{HEE}^{j,u}$ represents the green knowledge efficiency effect of renewable energy input (HEEE); $A_{GEF}^{j,u}$ represents the knowledge efficiency effect of non-renewable energy input (GEFE); $A_{PHGCRE}^{j,u}$ represents the potential hybrid - knowledge emission ratio effect (PHGCRE); $A_{CPI}^{j,u}$ represents the carbon performance index effect (CPIE); and $A_{CES}^{j,u}$ represents the carbon emission structure effect (CESE).

Proof: According to Eq. 12, dividing the carbon productivity decomposition equation in Eq. 14 of two regions yields:

$\begin{array}{l}\frac{P_j}{P_u}=\frac{{\sum }_{i=1}^M{\left(D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)\right)}^{-1}\cdot HE{E}_{ij}\cdot GE{F}_{ij}\cdot PHGC{R}_{ij}\cdot CP{I}_{ij}\cdot CE{S}_{ij}}{{\sum }_{i=1}^M{\left(D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)\right)}^{-1}\cdot HE{E}_{iu}\cdot GE{F}_{iu}\cdot PHGC{R}_{iu}\cdot CP{I}_{iu}\cdot CE{S}_{iu}}\\ =A_{MIX}^{j,u}\cdot A_{HEE}^{j,u}\cdot A_{GEF}^{j,u}\cdot A_{PHGCR}^{j,u}\cdot A_{CPI}^{j,u}\cdot A_{CES}^{j,u}.\end{array}(14)$

Note 9: Theorem 3 uses the new green decomposition to analyze the regional differences in carbon productivity, decomposing the ratio of carbon productivity between two regions into six effects, which correspond to the six decomposition indicators in Eq. 12 of carbon productivity. Furthermore, we have added the green knowledge efficiency effect of renewable energy inputs, the knowledge efficiency effect of non-renewable energy inputs, and the potential hybrid - knowledge emission ratio effect to investigate the influencing factors of regional differences in carbon productivity from a new perspective. In this paper, carbon productivity is represented as the ratio of industry added value and CO₂ emissions, thus, it is an intensity variable. We use a multiplication decomposition method to study the differences in carbon productivity between regions. Based on the research of [31], we select the LMDI-1 decomposition weight formula to obtain the six effects in Eqs 15–20 in Theorem 3.

$A_{MIX}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right),(15)$

$A_{HEE}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{HE{E}_{ij}}{HE{E}_{iu}}\right),(16)$

$A_{GEF}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{GE{F}_{ij}}{GE{F}_{iu}}\right),(17)$

$A_{PHGCR}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{PHGC{R}_{ij}}{PHGC{R}_{iu}}\right),(18)$

$A_{CPI}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{CP{I}_{ij}}{CP{I}_{iu}}\right),(19)$

$A_{CES}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{CE{S}_{ij}}{CE{S}_{iu}}\right),(20)$

Where, $w_i^{j,u}=\frac{L\left(Y_{ij}/C_{ij},Y_{iu}/C_{iu}\right)}{L\left(P_j,P_u\right)}$ represents the weight function, and $L\left(a,b\right)=\left\{\begin{array}{l}\frac{a-b}{\ln a-\ln b},a\ne b\\ a,a=b\end{array}\right.$ represents the logarithmic averaging function.

Regarding the new green hybrid effect, $A_{MIX}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right)$, there are some parts that can be further decomposed. By separating the four indicators of the capital-hybrid energy ratio, labor-hybrid energy ratio, hybrid knowledge stock-hybrid energy ratio, and carbon factor between the two regions, we derived a decomposition theorem for the new green hybrid effect.

Theorem 4. (New green hybrid effect decomposition theorem): The new green hybrid effect can be decomposed into the following components:

$A_{MIX}^{j,u}=A_{KEF}^{j,u}\cdot A_{LEF}^{j,u}\cdot A_{HGEF}^{j,u}\cdot A_{CF}^{j,u},(21)$

Where, $A_{KEF}^{j,u}$ represents the capital-hybrid energy substitution effect (KEFSE), $A_{LEF}^{j,u}$ represents the labor-hybrid energy substitution effect (LEFSE), $A_{HGEF}^{j,u}$ represents the hybrid knowledge stock-hybrid energy substitution effect (HGEFSE), and $A_{CF}^{j,u}$ represents the carbon factor effect (CFE).

Proof: Referring to the “one-factor-at-a-time” principle of the Laspeyres-linked approach in [43] study, we keep all other factors constant and change only one factor at a time to analyze its driving effect during the research period. For the logarithmic part, $\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{iu}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}$, of the new green hybrid effect, we use this method by sequentially changing k, l, h·g, and c in the distance function ratio in different orders, where h·g is treated as a whole for changes. According to permutation and combination, there are $A^4=4!=24$ decomposition forms in total.

We sequentially alter the values of k, l, h·g, and c in sequence in the equation, and the results of the decomposition are as follows:

$\begin{array}{l}\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\\ =\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}\cdot \frac{D_i^Y\left(k_{ij},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{ij},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}\\ \cdot \frac{D_i^Y\left(k_{ij},l_{ij},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{iu}\right)}\cdot \frac{D_i^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}.\end{array}(22)$

The four terms on the right-hand side of Eq. 22 respectively reflect the influences of KEF, LEF, HGEF, and CF, and similarly, we can obtain 23 other decomposition results. [44] proposed using a geometric mean with equal weights to obtain a complete decomposition of the distance function ratio for all possible decompositions, but the large number of factors can make the calculation process cumbersome. [45] introduced the polar coordinate method, which approximates the complete decomposition by averaging a group of mirrored decomposition possibilities and captures the influences of each factor from the opposite direction. Drawing on the research of [37], we utilize the polar coordinate method in this paper. The decomposition results of the mirrored sequence c, h·g, l, and k in Eq. 22 are presented in Eq. 23 as follow:

$\begin{array}{l}\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\\ =\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{ij}\right)}\cdot \frac{D_i^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{ij}\right)}{D_i^Y\left(k_{iu},l_i,1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\\ \cdot \frac{D_i^Y\left(k_{iu},l_{iu},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}{D_i^Y\left(k_{iu},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\cdot \frac{D_i^Y\left(k_{iu},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}.\end{array}(23)$

The four terms on the right-hand side of Eq. 22 respectively reflect the influences of CF, HGEF, LEF, and KEF. By averaging the group of mirrored decomposition possibilities, we obtain the final decomposition of the distance function ratio as follows:

$\begin{array}{l}\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\\ ={\left[\frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}\cdot \frac{D_i^Y\left(k_{iu},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right]}^{\frac{1}{2}}\\ \cdot {\left[\frac{D_i^Y\left(k_{ij},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{ij},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}\cdot \frac{D_i^Y\left(k_{iu},l_{iu},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}{D_i^Y\left(k_{iu},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right]}^{\frac{1}{2}}\\ \cdot {\left[\frac{D_i^Y\left(k_{ij},l_{ij},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{iu}\right)}\cdot \frac{D_i^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{ij}\right)}{D_i^Y\left(k_{iu},l_{iu},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right]}^{\frac{1}{2}}\\ \cdot {\left[\frac{D_i^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\cdot \frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_i^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{ij}\right)}\right]}^{\frac{1}{2}}\\ =KE{F}_i^{j,u}\cdot LE{F}_i^{j,u}\cdot HGE{F}_i^{j,u}\cdot C{F}_i^{j,u}.\end{array}(24)$

Substituting Eq. 24 into Eq. 15 yields Eq. 25:

$\begin{array}{l}{A}_{MIX}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \frac{D_{iu}^Y\left(k_{iu},l_{iu},1,h_{iu}\cdot g_{iu},1,c_{iu}\right)}{D_{ij}^Y\left(k_{ij},l_{ij},1,h_{ij}\cdot g_{ij},1,c_{ij}\right)}\right)\\ =\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln \left(KE{F}_i^{j,u}\cdot LE{F}_i^{j,u}\cdot HGE{F}_i^{j,u}\cdot C{F}_i^{j,u}\right)\right)\\ =\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln KE{F}_i^{j,u}\right)\cdot \exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln LE{F}_i^{j,u}\right)\\ \cdot \exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln HGE{F}_i^{j,u}\right)\cdot \exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln C{F}_i^{j,u}\right)\\ =A_{KEF}^{j,u}\cdot A_{LEF}^{j,u}\cdot A_{HGEF}^{j,u}\cdot A_{CF}^{j,u}.\end{array}(25)$

Note 10: Theorem 4 decomposes the new green hybrid effect into four effects. In this paper, we adopt a hybrid energy input of the product of renewable energy input and non-renewable energy input, which adds the mutual substitution effect between hybrid knowledge stock input and hybrid energy input. We consider using knowledge stock input to replace energy input in the production process, which optimizes the input factor ratio from a new perspective.

According to Theorem 3 and Theorem 4, substituting Eq. 21 into Eq. 13 yields the decomposition formula for carbon productivity regional differences:

$\frac{P_j}{P_u}=A_{KEF}^{j,u}\cdot A_{LEF}^{j,u}\cdot A_{HGEF}^{j,u}\cdot A_{CF}^{j,u}\cdot A_{HEE}^{j,u}\cdot A_{GEF}^{j,u}\cdot A_{PHGCR}^{j,u}\cdot A_{CPI}^{j,u}\cdot A_{CES}^{j,u}(26)$

We decompose the carbon productivity ratio between region j and reference region u into the above 9 effects. If the decomposition value of any effect is greater than 1, it indicates that the effect has enlarged the differences in carbon productivity between region j and reference region u; otherwise, it has reduced the differences.

4 Empirical analysis

4.1 Data sources and description

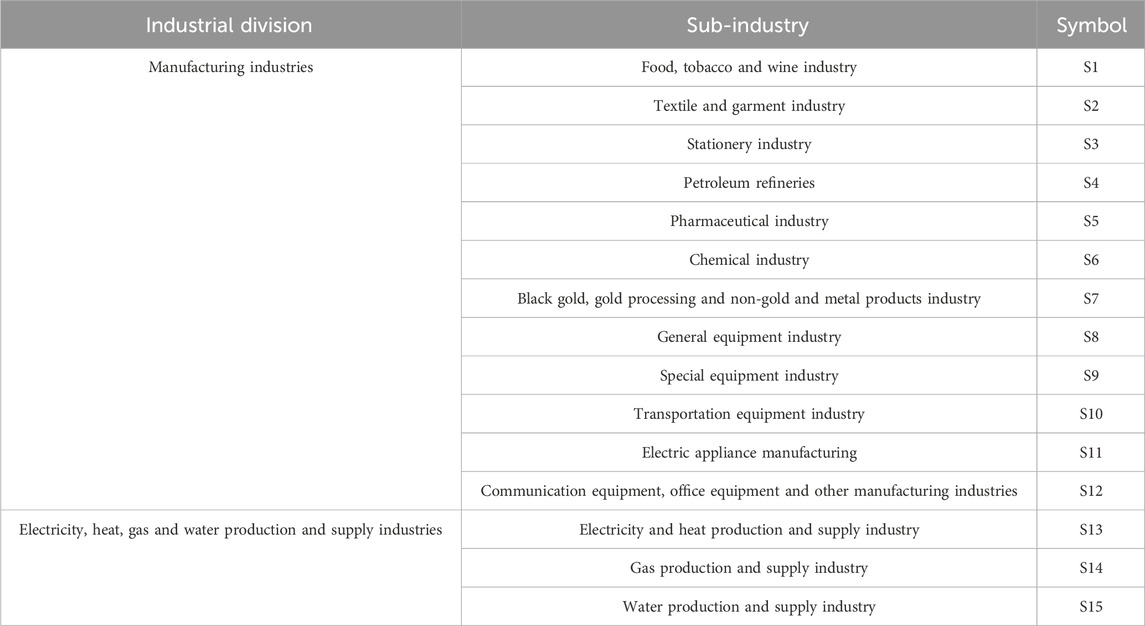
Sample data were selected for the provinces and cities of China in 2019, excluding Hong Kong, Macao, Taiwan, Xinjiang, and Tibet due to missing data. The study objects were divided according to China’s seven major geographical regions (see Table A1), and the reference region was obtained by taking the average of the 29 provinces and autonomous regions, representing the average level of socio-economic activities. Based on China’s national economic industry classification, 38 sub-industries in manufacturing and electricity, heat, gas, and water production and supply were classified and summarized into 15 industries (see Table 1).

Table 1

Table 1. Industry division.

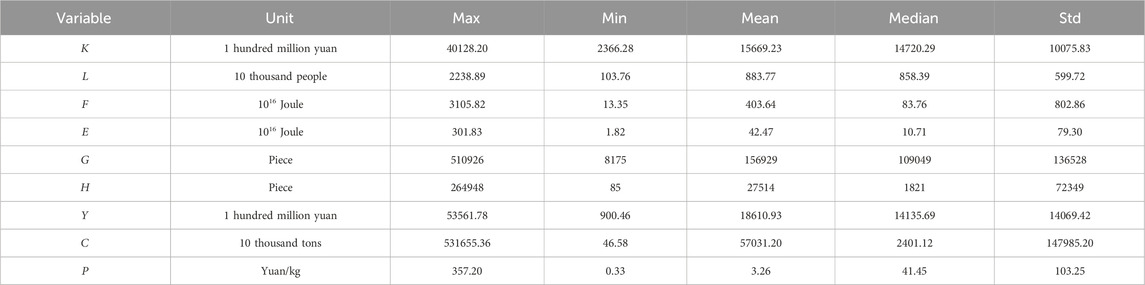
The new green decomposition model of carbon productivity involves a total of 9 variables, namely, capital input K, labor input L, renewable energy input E, non-renewable energy input F, knowledge stock input G, green knowledge stock input H, industrial added value Y, carbon dioxide emissions C, and carbon productivity P. This paper collected and compiled 6 input and 2 output data for 15 industries in 29 provinces in 2019. The capital input was obtained from fixed asset investment data from the “China Investment Statistical Yearbook” in billions of yuan. The labor input was obtained from employment population data from the “China Population and Employment Statistical Yearbook” in ten thousand people. The non-renewable energy input used non-renewable energy heat generation data from the CEADs China carbon accounting database. Referring to relevant research by [46], the usage of different types of energy in provincial energy inventories was converted into unified standard coal based on the conversion factors in the “China Energy Statistical Yearbook” for each type of energy, then converted into heat value, with units in joules of 10^16. Renewable energy input used renewable energy heat generation data from the National Energy Administration and “China Energy Statistical Yearbook”, converted to heat value based on the conversion of each province’s renewable energy power consumption to unified standard coal, with units in joules of 10^16. The knowledge stock input used ordinary patent data from the State Intellectual Property Office and provincial statistical yearbooks, with units in pieces. The green knowledge stock input used green patent data from provincial green patent panel data, with units in pieces. The desirable outputs are used u industrial added value data from the National Bureau of Statistics, “China Industrial Statistical Yearbook”, and provincial statistical yearbooks in billions of yuan. The undesirable outputs are used carbon dioxide emissions data [46] from the CEADs China carbon accounting database’s provincial emission inventory, with units in ten thousand tons. Carbon productivity was calculated based on the P=Y/C formula with units in yuan/kg. A few missing data were obtained using interpolation.

Table 2 summarizes the input and output data for the 29 provinces studied in this paper. There are significant differences between provinces. Table 3 summarizes the input and output data for the 15 industries studied in this paper. There are also significant differences between different industries. Looking at the mean column of Table 2 and Table 3, the mean column data in Table 2 is the input-output data of the reference region, and the mean column in Table 3 is the average data of the 15 industries. The mean carbon productivity of all provinces is the same as the mean carbon productivity of all industries (3.26 yuan/kg), because the mean carbon productivity is not the mean of carbon productivity, but the ratio of industrial added value means to carbon dioxide emissions mean, which matches the provincial and industrial data.

Table 2

Table 2. Descriptive statistics of input-output data of 29 provinces in China.

Table 3

Table 3. Descriptive statistics of input-output data of 15 industries in China.

Table 4 summarizes the input and output data for various industries in the reference region. The carbon productivity of the overall industry is not the sum of carbon productivity of each industry, but rather the ratio of the overall industry GDP added value to the overall industry carbon dioxide emissions. The overall industry carbon productivity for the reference region, located in the bottom right corner of the table, is 3.26 yuan/kg, which further confirms the consistency between provincial and industrial data.

Table 4

Table 4. Input-output related data of reference region.

4.2 One-dimensional comparative analysis

4.2.1 Comparative analysis at provincial level

From a provincial perspective, Figure 3 depicts the carbon dioxide emissions and carbon productivity for the 29 provinces and the reference region studied in this paper. As shown in Figure 3A, the top 3 provinces with the highest carbon dioxide emissions are Hebei (808.20 million tons), Shandong (806.06 million tons), and Inner Mongolia (732.32 million tons), while the top 3 provinces with the lowest carbon dioxide emissions are Hainan (30.70 million tons), Qinghai (33.52 million tons), and Beijing (35.15 million tons). The carbon dioxide emissions for the reference region (294.99 million tons) are marked in red and ranked 11th among the 29 provinces. As shown in Figure 3B, the top 3 provinces with the highest carbon productivity are Beijing (11.81 yuan/kg), Guangdong (8.24 yuan/kg), and Shanghai (8.19 yuan/kg), while the top 3 provinces with the lowest carbon productivity are Ningxia (0.49 yuan/kg), Inner Mongolia (0.58 yuan/kg), and Shanxi (0.63 yuan/kg). The carbon productivity for the reference region (3.26 yuan/kg) is marked in red and ranked 15th among the 29 provinces. By combining Figure 3, it can be found that the provincial ranking of carbon dioxide emissions and carbon productivity varies significantly due to the inter-provincial differences in industrial added value.

Figure 3

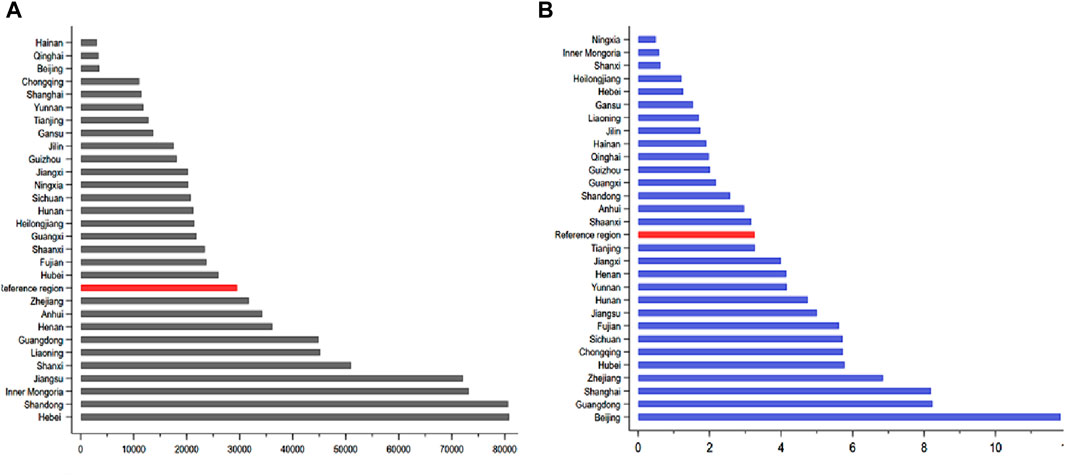
Figure 3. Carbon emissions and carbon productivity of 29 provinces and reference regions in 2019. (A) CO2 emissions (10⁴ tons), (B) Carbon productivity (CNY/Kg).

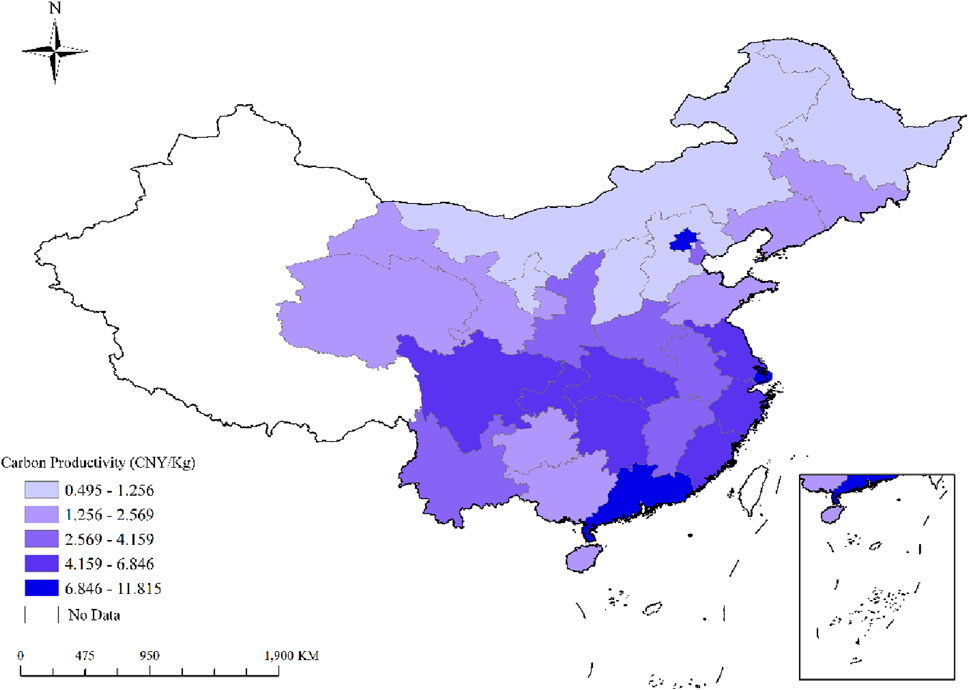
Figure 4 shows the spatial distribution of provincial-level carbon productivity in China, with different shades of color indicating the numerical value of carbon productivity for each province. The white color in the map represents provinces that have not been counted due to data deficiency. From the map, it can be clearly seen that the level of carbon productivity in China is generally higher in the southeast coastal provinces, followed by central provinces, and lower in the southwest and northwest regions. Looking at China’s seven major geographical regions, for the North China region, Beijing has the highest carbon productivity in the country, while Tianjin’s carbon productivity is close to the reference region and therefore at the average level. The carbon productivity of the other provinces in the region is relatively low, especially Shanxi and Inner Mongolia. The overall level of carbon productivity in the three provinces in the Northeast region is poor, all lower than the reference region. In the East China region, except for Anhui and Shandong which are below the average level, the carbon productivity of the other provinces is relatively high, especially Shanghai, Jiangsu, and Zhejiang, which are among the top provinces in the country. The carbon productivity of all three provinces in the Central China region is higher than the average level. In the South China region, Guangdong has a high level of carbon productivity, while Guangxi and Hainan have lower levels than the average. In the southwest region, except for Guizhou, the carbon productivity of the other three provinces is higher than the average level. In the northwest region, the overall level of carbon productivity in the four provinces is relatively low, all lower than the average level.

Figure 4

Figure 4. Spatial distribution of China’s carbon productivity in 2019.

Using the new green decomposition model of carbon productivity, which takes into account carbon emissions, we can apply Theorem 3 and Theorem 4 to compare the carbon productivity of 29 provinces with that of the reference regions. Eq. 26 can be used to decompose the regional differences in carbon productivity:

$\frac{P_j}{P_u}=A_{KEF}^{j,u}\cdot A_{LEF}^{j,u}\cdot A_{HGEF}^{j,u}\cdot A_{CF}^{j,u}\cdot A_{HEE}^{j,u}\cdot A_{GEF}^{j,u}\cdot A_{PHGCR}^{j,u}\cdot A_{CPI}^{j,u}\cdot A_{CES}^{j,u},$

By applying the calculation formula for each specific effect, taking the capital-hybrid energy substitution effect KEF as an example, we obtain:

$A_{KEF}^{ij,iu}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln KE{F}_i^{j,u}\right),$

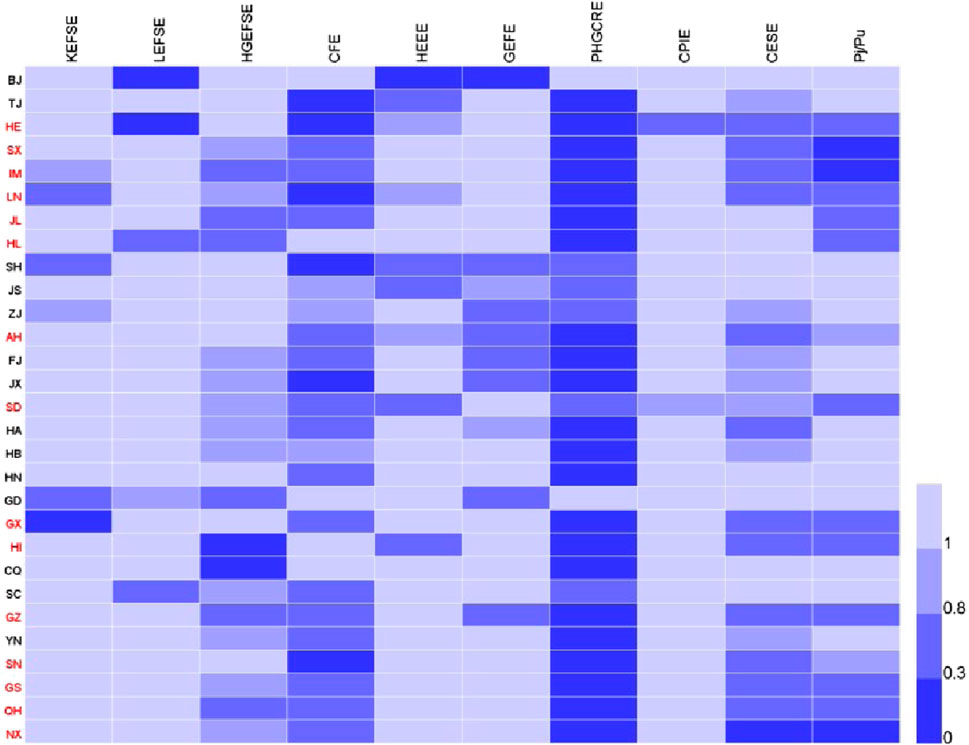
The remaining 8 types of effects can be obtained similarly. By taking j from 1 to 29, we can obtain the effect decomposition results of carbon productivity differences between each province and the reference region, and present them as a heat map. Figure 5 shows the ratio of industry-wide carbon productivity of 29 provinces in this paper to that of the reference region, as well as the effect decomposition results.

Figure 5

Figure 5. Decomposition results of provincial carbon productivity differences.

The y-axis of Figure 5 represents the 29 provinces, and the first nine columns of the x-axis represent the results of the nine decomposition effects. The values of each decomposition effect are represented using different shades of color, with lighter colors indicating larger values of the specific decomposition effect. The lightest color indicates that the decomposition effect is greater than 1, which means it has a positive impact on carbon productivity. On the other hand, darker colors indicate a smaller value of the specific decomposition effect, which has a negative impact on carbon productivity. The last column shows the ratio of the industry-wide carbon productivity of each province to that of the reference region. Provinces whose industry-wide carbon productivity is lower than the reference region are marked in red on the y-axis, indicating that they have significant potential for improvement.

From the first nine columns, we can see that the KEFSE, LEFSE, and CPIE have a positive influence on carbon productivity for the majority of provinces, indicating that these provinces have a reasonable input factor structure and carbon emission performance levels. In contrast, the HGEFSE has a negative impact on the carbon productivity of most provinces, except for the 10 provinces of Beijing, Tianjin, Hebei, Shanghai, Jiangsu, Zhejiang, Anhui, Hunan, Guangxi, and Shaanxi. Therefore, when it comes to improving the carbon productivity of these 19 provinces, the HGEFSE has greater potential compared with the KEFSE, LEFSE, and CPIE. It is a driving factor that requires special attention to improve carbon productivity by increasing the substitution of hybrid knowledge stock for hybrid energy in input factors. The CFE and PHGCRE have negative impacts on carbon productivity of most provinces, indicating the need to optimize energy consumption structure and improve the potential ideal hybrid knowledge emission ratio level in future development. The HEEE and GEFE also have different promotion and inhibition effects on carbon productivity for different provinces. These two effects are important factors that promote further improvement of carbon productivity for provinces with a higher level of carbon productivity. By increasing scientific research investment, promoting technological innovation, encouraging patent research and development, and actively developing green low-carbon technologies, carbon productivity can be enhanced to a higher level. The CESE is another important factor that leads to significant differences in carbon productivity among provinces. Except for the provinces of Beijing, Jilin, Heilongjiang, Shanghai, Jiangsu, Hunan, Guangdong, Chongqing, and Sichuan, there is no significant improvement in the carbon productivity of the remaining 20 provinces, indicating that there is great potential to improve the level of carbon productivity by improving industrial sector structure. The KEFSE and LEFSE are the main driving forces for the development of carbon productivity in most provinces, while the substitution of hybrid knowledge stock for hybrid energy and the potential ideal hybrid knowledge emission ratio still needs to be improved. In particular, the HEEE and GEFE are key factors for further improving carbon productivity in economically developed provinces.

4.2.2 Industry-level comparative analysis

From an industry-level perspective, Figure 6 shows the carbon emissions and carbon productivity of the 15 industries studied in this paper, as well as the overall industry.

Figure 6

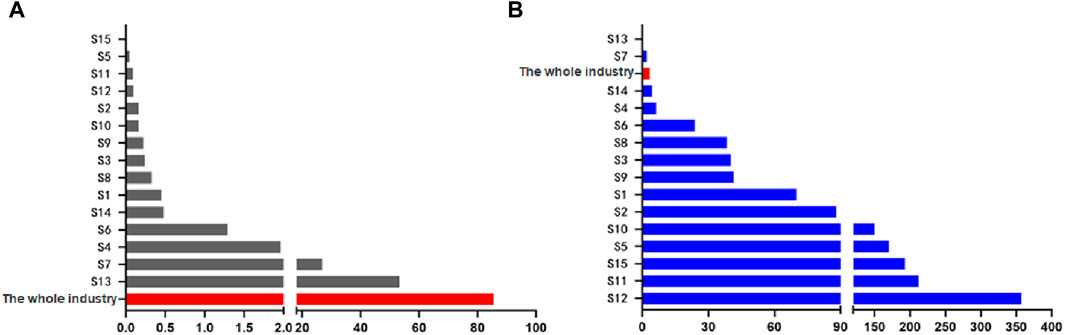
Figure 6. Carbon emissions and carbon productivity of 15 industries and overall industry in 2019. (A) CO₂ emissions (10⁸ tons), (B) Carbon productivity (CNY/Kg).

From Figure 6A, we can see that the top three industries with the highest carbon emissions are the power and heat production and supply industry (S13) with 5.317 billion tons, followed by the black gold, non-ferrous metal, and metal products industry (S7) with 2.685 billion tons, and the petroleum processing industry (S4) with 0.196 billion tons. All of these industries are high-energy consumption industries. The three industries with the lowest carbon emissions are the water production and supply industry (S15) with 0.0047 billion tons, followed by the medical industry (S5) with 0.0441 billion tons, and the electrical equipment manufacturing industry (S11) with 0.0898 billion tons. The industry-wide carbon emissions of all industries combined (85.55 billion tons) are marked in red. From Figure 6B, we can see that the top three industries with the highest carbon productivity are the communication equipment, office equipment, and other manufacturing industry (S12) with 357.20 yuan/kg, followed by the electrical equipment manufacturing industry (S11) with 212.31 yuan/kg, and the water production and supply industry (S15) with 193.30 yuan/kg. The three industries with the lowest carbon productivity are the power and heat production and supply industry (S13) with 0.33 yuan/kg, followed by the black gold, non-ferrous metal, and metal products industry (S7) with 1.99 yuan/kg, and the gas production and supply industry (S14) with 4.47 yuan/kg. The industry-wide carbon productivity (3.26 yuan/kg) is marked in red, which is obtained by comparing the industry-wide GDP added value with the industry-wide carbon emissions. This once again confirms the consistency between provincial data and industry data. By combining Figure 6, we can conclude that high-energy consumption industries tend to have higher carbon emissions but lower carbon productivity. Conversely, industries with lower carbon emissions tend to have higher carbon productivity. For example, the power and heat production and supply industry (S13) have the highest carbon emissions and lowest carbon productivity. While the power industry has been committed to reducing energy consumption, its high reliance on fossil fuels results in high carbon emissions, leaving significant challenges to improve carbon productivity.

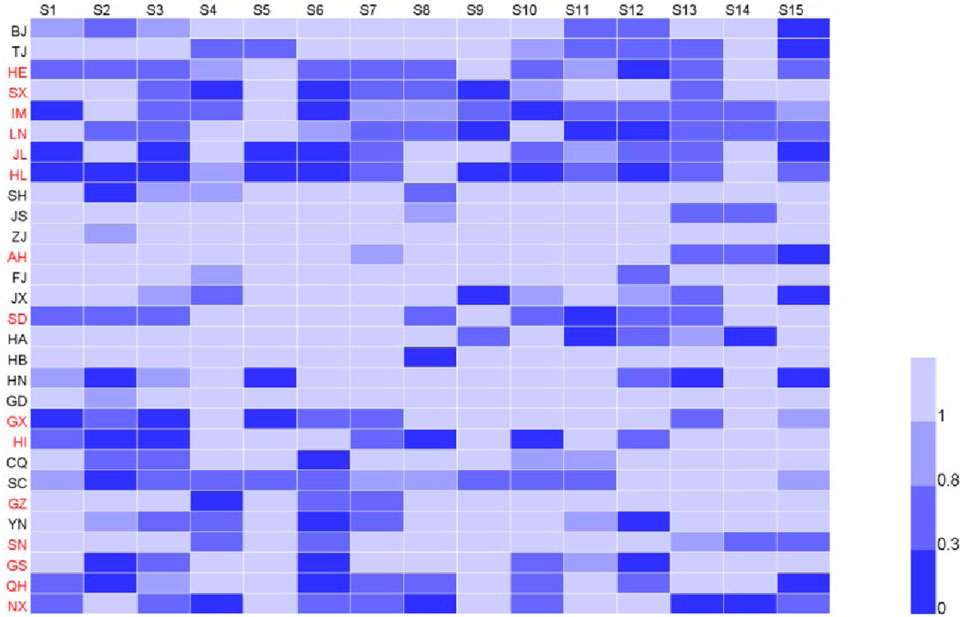
We divide the carbon productivity of each industry in the 29 provinces by the carbon productivity of the corresponding industry in the reference region (P_ij/P_iu). By taking j from 1 to 29 and i from 1 to 15, we obtain the industry decomposition results of the differences in carbon productivity between each province and the reference region and present them in a heat map. Figure 7 depicts the ratio of carbon productivity between the 29 provinces and the reference region, as well as the industry decomposition results. The vertical axis represents the 29 provinces, while the horizontal axis represents the 15 industries. Observing the vertical aspect of Figure 7, we can see that the industries with lower carbon productivity than the reference region are mainly concentrated in 15 provinces, namely, Hebei, Shanxi, Inner Mongolia, Liaoning, Jilin, Heilongjiang, Anhui, Shandong, Guangxi, Hainan, Guizhou, Shaanxi, Gansu, Qinghai, and Ningxia. We mark these 15 provinces in red on the vertical axis. Combining this with the provinces marked in red on the vertical axis in Figure 4, we find that the provinces with overall lower carbon productivity and specific industries with lower carbon productivity than the reference region are completely consistent. Therefore, we identify these 15 provinces as potential areas for improving carbon productivity. Compared to provinces with higher carbon productivity, these provinces are of greater concern and worthy of further study.

Figure 7

Figure 7. Industrial decomposition results of provincial carbon productivity differences.

4.3 Dual dimensional comparative analysis

Based on the comparative analysis of single-dimension province and single-dimension industry, and the comprehensive effect decomposition results and industry decomposition results of each province, we found that there are 15 provinces with carbon productivity levels lower than the reference region. These provinces are Hebei, Shanxi, Inner Mongolia, Liaoning, Jilin, Heilongjiang, Anhui, Shandong, Guangxi, Hainan, Guizhou, Shaanxi, Gansu, Qinghai, and Ningxia. The 8 weak industries that cause the carbon productivity of these 15 provinces to be lower than the average level are: food, tobacco and liquor industry (S1), culture and education supplies industry (S3), chemical industry (S6), black and non-ferrous metal smelting and processing industry (S7), transportation equipment industry (S10), communication equipment, office equipment and other manufacturing industry (S12), electric power, heat production and supply industry (S13), and water production and supply industry (S15).

By combining the differences and influencing factors of carbon productivity at the regional and industry levels, and considering the industry heterogeneity within regions, we obtained the effect decomposition of specific industry-level carbon productivity differences in different regions. In this paper, we conducted an effect decomposition of the carbon productivity differences of these 15 key provinces and 8 key industries from the two dimensions of province and industry, and investigated the factors influencing the differences. Using the new green decomposition model of carbon productivity and applying the decomposition Eq. 26 for regional differences, we obtained the decomposition formula for the carbon productivity differences with provincial and industrial subscripts.

$\frac{P_{ij}}{P_{iu}}=A_{KEF}^{ij,iu}\cdot A_{LEF}^{ij,iu}\cdot A_{HGEF}^{ij,iu}\cdot A_{CF}^{ij,iu}\cdot A_{HEE}^{ij,iu}\cdot A_{GEF}^{ij,iu}\cdot A_{PHGCR}^{ij,iu}\cdot A_{CPI}^{ij,iu}\cdot A_{CES}^{ij,iu},$

This refers to the decomposition effect of the carbon productivity difference between the j region industry and the reference region industry, which is the product of the decomposition effects of the carbon productivity difference between each industry in the j region and the reference region. This paper uses the capital-hybrid energy substitution effect KEF as an example.

$A_{KEF}^{j,u}=\exp \left({\displaystyle \sum _{i=1}^M}{w}_i^{j,u}\ln KE{F}_i^{j,u}\right)=\underset{i=1}{\overset{M}{\mathrm{\Pi }}}\exp \left(w_i^{j,u}\ln KE{F}_i^{j,u}\right)=\underset{i=1}{\overset{M}{\mathrm{\Pi }}}{A}_{KEF}^{ij,iu},$

Furthermore, we obtain the capital-hybrid energy substitution effect KEF of the carbon productivity difference between the i industry in the j region and the i industry in the reference region:

$A_{KEF}^{ij,iu}=\exp \left(w_i^{j,u}\ln KE{F}_i^{j,u}\right),$

The remaining eight effects are obtained similarly. Taking j from 1 to 15 and i from 1 to 8, we obtain the decomposition results of the effects of carbon productivity differences between each province and industry and the reference region industry, which can be presented in heat maps. Figure 8 contains 15 heat maps, each describing the decomposition results of the effects on eight key industries of the relative carbon productivity laggard provinces. Overall, the KEFSE and LEFSE have higher decomposition results in most provinces and industries, indicating a positive role in promoting the development of carbon productivity. In contrast, the PHGCRE has lower decomposition results in most provinces and industries, indicating a negative impact on carbon productivity and significant potential for improvement. This is consistent with the provincial decomposition results presented in Figure 5. The PHGCRE indicates, that is, the consumption of hybrid knowledge resources per unit of carbon emission space, at the point when undesirable outputs reach the ideal state, corresponding to measures aimed at increasing hybrid knowledge stock input and reducing carbon emissions.

Figure 8

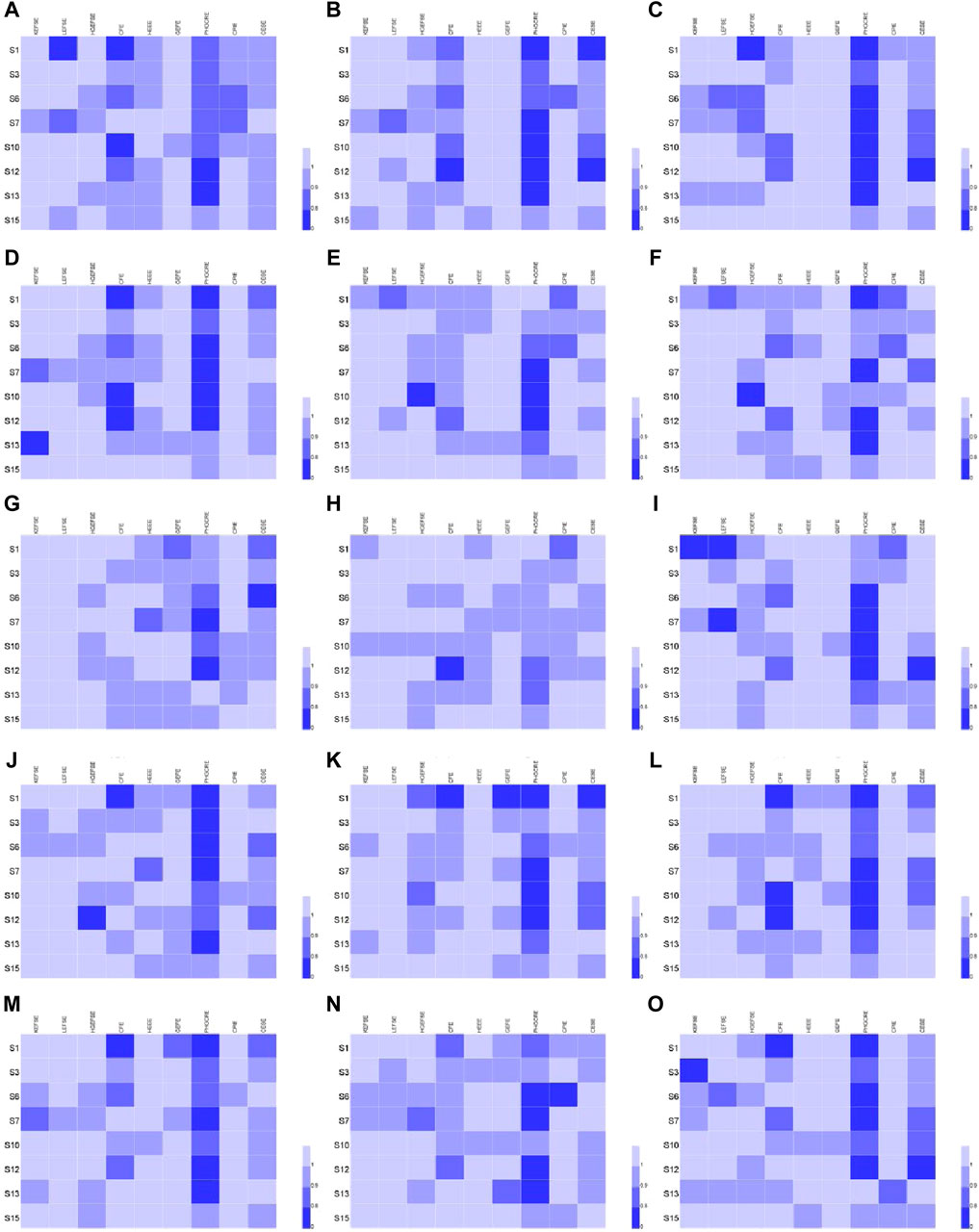
Figure 8. Decomposition results of carbon productivity differences in 8 key industries in 15 key provinces. (A) Hebei, (B) Shanxi, (C) Inner Mongolia, (D) Liaoning, (E) Jilin, (F) Heilongjiang, (G) Anhui, (H) Shandong, (I) Guangxi, (J) Hainan, (K) Guizhou, (L) Shaanxi, (M) Gansu, (N) Qinghai, (O) Ningxia.

Figure 8A shows the decomposition results of the effects on eight key industries in Hebei province. It can be observed that there are significant variations in the decomposition results of various effects across different industries. Overall, the HGEFSE and GEFE have a positive impact on the development of carbon productivity in most industries. On the other hand, the CFE, HEEE, CPIE, and CESE have a negative impact on carbon productivity in most industries. Thus, it is important to focus on increasing the decomposition values of these effects. As an industrial province, Hebei’s economic development has long relied on heavy industry. From the figure, it can be observed that the chemical industry (S6) needs to improve the HGEFSE, CFE, HEEE, CPIE, and CESE.

Figure 8B, C show the decomposition results of the effects on eight key industries in Shanxi and Inner Mongolia, respectively. The results in these two regions are similar. From the figures, it can be observed that the HEEE, GEFE, and CPIE have a positive impact on carbon productivity in most industries. On the other hand, the HGEFSE, CFE, and CESE still have significant potential for improvement. As an economically underdeveloped region, the carbon productivity of many industries in Shanxi province is below the average level. For example, the LEFSE, CFE, and CESE have a negative impact on carbon productivity in the manufacturing industry of communication equipment, office equipment, and other industries (S12). Although Inner Mongolia is also an economically underdeveloped region, it has abundant natural resources that can be reasonably developed and utilized to reduce carbon emissions and improve carbon productivity.

Figure 8D–F show the decomposition results of the effects on eight key industries in the three provinces of Northeast China. Among them, the HGEFSE, GEFE, and CPIE in Liaoning have a positive impact on carbon productivity in most industries. On the other hand, the CFE, HEEE, and CESE have great potential for improvement. The decomposition results of Jilin and Heilongjiang are relatively similar. The HEEE, GEFE, and CESE have a positive impact on carbon productivity in most industries; however, the HGEFSE and CFE need to be improved. For example, the black and non-ferrous metal, and metal products industry (S7) in Liaoning needs to adopt policies such as capital replacement of hybrid energy, labor replacement of hybrid energy, and hybrid knowledge stock replacement of hybrid energy, increase scientific and technological inputs, and encourage the research and application of green patents. The transportation equipment industry (S10) in Jilin needs to vigorously promote the replacement of hybrid knowledge stock for hybrid energy, regulate the structure of production factors, improve technical efficiency, and the potential emission ratio of hybrid knowledge. The chemical industry (S6) in Heilongjiang needs to raise the level of technology and carbon emission efficiency, advocate the development and application of green patents, and vigorously develop high-tech emerging industries.

Figure 8G shows the decomposition results of the effects on eight key industries in Anhui province. The HGEFSE and CPIE have a positive impact on carbon productivity in most industries (S1, S3, S6, S7, S13, S15), while the HEEE, GEFE, and CESE have great potential for improvement. Anhui province is a relatively backward province in the Yangtze River Economic Zone, with great potential for economic development. For instance, the black and non-ferrous metal, and metal products industry (S7) should focus on increasing scientific and technological inputs, promoting the development and application of patents, especially green patents, improving technical efficiency, balancing industrial structure, and applying green and clean energy and low-carbon technologies in the production process to effectively improve the level of carbon productivity.

Figure 8H shows the decomposition results of the effects on eight key industries in Shandong province. The GEFE and CESE have a positive impact on carbon productivity in most industries, while there is still room for improvement for HEEE and CPIE. Shandong province is an important energy base in China, with abundant coal and oil resources. However, this advantage also leads to an imbalanced energy consumption structure, with a high proportion of fossil energy consumption and resulting in large amounts of carbon emissions and low levels of carbon productivity. Therefore, Shandong province urgently needs to improve its energy consumption structure, reduce the use of traditional fossil fuels, and vigorously develop clean energy sources such as wind, solar, and hydropower to reduce carbon emissions.

Figure 8I shows the decomposition results of the effects on eight key industries in Guangxi province. The HEEE, GEFE, and CPIE have a positive impact on carbon productivity in most industries, while there is still room for improvement for HGEFSE and CFE. Guangxi province is relatively backward in the southern region of China, and for specific industries such as the food, tobacco, and liquor industry (S1), which is mainly focused on the sugar industry, it is necessary to focus on improving the capital substitution of hybrid energy, labor substitution of hybrid energy, and hybrid knowledge stock substitution of hybrid energy. Adjusting the proportions of various production factors inputs, further improving technical efficiency, and carbon performance levels, increasing the economic benefits of the industry, and thus further enhancing the level of carbon productivity.

Figure 8J shows the decomposition results of the effects on eight key industries in Hainan province. The CPIE has a positive impact on carbon productivity in most industries, while there is still room for improvement for HEEE and CESE. Hainan has a favorable geographical location, rich forestry and marine resources, and a strong ability to absorb and store carbon dioxide. Hainan has diverse energy structure and enormous potential for developing renewable energy sources such as solar and hydropower generation. Additionally, Hainan has abundant geothermal and tidal energy resources, which should be fully utilized to balance the energy consumption structure, reduce carbon emissions, and promote the absorption and storage of carbon emissions. By combining both carbon sources and carbon sinks, Hainan can lower carbon dioxide concentration in the atmosphere and enhance its carbon productivity.

Figure 8K shows the decomposition results of the effects on eight key industries in Guizhou province. The HEEE and CPIE have a positive impact on carbon productivity in most industries, while there is still room for improvement for HGEFSE, CFE, GEFE and CESE. Guizhou province is relatively underdeveloped in the southwestern region of China, and the carbon productivity levels of most industries need to be improved. For example, in the electric and thermal power generation and supply industry (S13), which is a key area for transmitting electricity from western to eastern China, there is a need to increase capital substitution of hybrid energy and hybrid knowledge stock substitution of hybrid energy, and optimize the input structure of production factors while improving the potential emission rate of hybrid knowledge. By doing so, carbon productivity can be enhanced comprehensively. Another key industry in Guizhou is the food, tobacco, and liquor industry (S1), for which there is a need to increase hybrid knowledge stock substitution of hybrid energy, adjust the energy consumption structure, encourage the development of green patents, reduce carbon emissions, improve economic efficiency, and gradually enhance the level of carbon productivity.

Figure 8L–O show the decomposition results of the effects on eight key industries in four northwestern provinces of China. The results in Shaanxi, Gansu, Qinghai, and Ningxia are quite similar, the HEEE, GEFE, and CPIE have a positive impact on carbon productivity in most industries, while the CFE and CESE still have room for improvement. These northwestern provinces have sparse populations, arid climates, and lack of water resources, while possessing abundant desert and wind-blown sand resources. Therefore, it is necessary to increase scientific and technological investment and make use of existing natural resources to vigorously develop solar power stations and ecological photovoltaic power stations. At the same time, renewable energy sources such as wind power and biogas should be reasonably developed and utilized as new forms of clean energy in order to jointly reduce CO₂ emissions and enhance the level of carbon productivity.

5 Conclusion

This paper explores the input elements in the economic production process under the driving force of green development, where energy input is refined into renewable energy input and non-renewable energy input, and knowledge stock input and green knowledge stock input are introduced. By using the data envelopment analysis (DEA) method and combining traditional environmental production technology with green input elements, a new linear programming model with a constant return to scale is constructed. Based on the traditional output-oriented Shephard distance function, a new green Shephard distance function and corresponding green Farrell technical efficiency measures for desirable outputs orientation and undesirable outputs orientation are also constructed. In addition, a series of new green decomposition methods are derived based on the definition of carbon productivity, and a new green decomposition model of carbon productivity is established. The carbon productivity differences between two regions are decomposed into nine effect types, resulting in the formation of a new green decomposition system of carbon productivity. Using input-output data from 15 industries in 29 Chinese provinces in 2019, this paper investigates the regional differences in carbon productivity and the factors that influence these differences from both a single-dimensional and a two-dimensional perspective.

(1) Conclusion of single-dimensional provincial level comparison analysis: Out of the 29 provinces studied in this paper, 14 provinces have higher carbon productivity than the reference region, mainly including Beijing, Tianjin, most of Eastern China, Central China, and parts of Southwest China, while the remaining 15 provinces have lower carbon productivity than the reference region, mainly including some parts of North China, Northeast China, South China and Northwest China. The regions with relatively backward carbon productivity mostly have rich natural resources, but poor resource utilization efficiency and over-reliance on heavy industry, especially industrial sectors that have been transferred from the eastern regions to the western regions. Therefore, it is necessary to optimize the industrial structure in these regions to gradually improve their carbon productivity.

(2) Conclusion of single-dimensional industry level comparison analysis: Among the 15 industries studied in this paper, high-energy-consuming industries such as the electric power generation and supply industry (S13), the processing of black and non-ferrous metals and other minerals industry (S7), and the petroleum processing industry (S4) have high levels of CO₂ emissions and relatively low carbon productivity. In contrast, industries with low levels of CO₂ emissions such as the water production and supply industry (S15), the pharmaceutical industry (S5), and the electrical machinery manufacturing industry (S11) have relatively higher levels of carbon productivity. Most high-energy-consuming industries use fossil energy sources, which leads to excessive CO₂ emissions and low carbon productivity levels. Therefore, new energy sources need to be continuously developed and utilized, and the proportion of traditional fossil energy use needs to be reduced at its core to minimize carbon emissions, enhance energy utilization efficiency, and improve carbon productivity.

(3) Conclusion of two-dimensional comparison analysis: Among the eight key industries and 15 provinces studied in this paper, the decomposition results for the capital - hybrid energy substitution effect (KEFSE) and labor - hybrid energy substitution effect (LEFSE) are high. This indicates that capital and labor substitution are the main driving forces behind the development of carbon productivity in these 15 key provinces. However, the decomposition results for the potential hybrid knowledge emission ratio effect (PHGCRE) are comparatively low, indicating that there is significant room for improvement in the potential level of hybrid knowledge emission rate under ideal conditions in these 15 key provinces.

6 Policy suggestions

China is the country with the highest carbon dioxide emissions in the world. To achieve low-carbon development, we must simultaneously meet the requirements of increasing industrial added value and reducing carbon emissions, so as to fundamentally and effectively improve carbon productivity. Firstly, based on the input and output data of 15 industries in 29 provinces and the new green decomposition model of carbon productivity, the influencing factors of regional carbon productivity differences are quantitatively studied. Secondly, through the decomposition of provincial effects and provincial industries, 15 key provinces and 8 key industries that affect the improvement of China’s overall carbon productivity will be identified, and potential areas for the development of carbon productivity will be identified. Based on the decomposition results and the actual situation, the following policy recommendations are given:

(1) At the single-dimension provincial level, the carbon factor effect CFE and the potential hybrid knowledge emission ratio effect PHGCRE have negative effects on the carbon productivity of most provinces. Therefore, priority should be given to improving these two effects, optimizing the energy consumption structure in time, improving the level of hybrid knowledge emission ratio, and implementing differentiated energy policies according to the characteristics of natural resources and industrial structure in different regions. Hybrid knowledge stock - hybrid energy substitution effect HGEFSE has a negative impact on the carbon productivity of the rest of the provinces, except for the positive effect on the carbon productivity of nearly one-third of the provinces. Therefore, it is necessary to continuously improve the substitution of hybrid knowledge stock for hybrid energy and adjust the structure of input factors, so as to improve the overall carbon productivity. The carbon emission structure effect CESE has no significant improvement in the carbon productivity of the remaining 20 provinces, except for its positive effects on the nine provinces of Beijing, Jilin, Heilongjiang, Shanghai, Jiangsu, Hunan, Guangdong, Chongqing and Sichuan. Therefore, we should give priority to the development of low-carbon industries, get rid of the high dependence on energy-intensive industries and heavy industries, learn from provinces with advanced technology and experience in this field, and adjust the industrial structure, so as to gradually improve carbon productivity.

(2) At the single-dimension industry level, stationery industry (S3), communication equipment, office equipment and other manufacturing industries (S12) and power and heat production and supply industry (S13) have negative effects on the carbon productivity of most provinces, and the carbon productivity of these three industries needs to be greatly improved. From the perspective of the seven major regions, North China needs to focus on the development of the stationery industry (S3), petroleum processing industry (S4), transportation equipment industry (S10), electrical equipment manufacturing industry (S11), communication equipment, office equipment and other manufacturing industries (S12), power and heat production and supply industry (S13) and water production and supply industry (S15). Northeast China needs to improve weak industries such as stationery industry (S3), chemical industry (S6), metal products industry (S7), electrical appliance manufacturing industry (S11), communication equipment, office equipment and other manufacturing industry (S12), power and heat production and supply industry (S13) and water production and supply industry (S15). Communication equipment, office equipment and other manufacturing industries (S12) and power and heat production and supply industries (S13) in East and Central China need to be further improved. South China needs to focus on improving the relatively backward industries such as food, tobacco and wine industry (S1), textile and clothing industry (S2), stationery industry (S3) and metal products industry (S7). Southwest China needs to focus on textile and clothing industry (S2), stationery industry (S3), petroleum processing industry (S4), chemical industry (S6), metal products industry (S7) and electrical manufacturing industry (S11). The northwest region needs to vigorously develop the stationery industry (S3), chemical industry (S6), transportation equipment industry (S10) and water production and supply industry (S15).

(3) At the provincial level and industry level, priority should be given to improving the carbon productivity of 8 key industries in 15 key provinces. On the whole, it is necessary to improve potential hybrid knowledge emission ratio effect PHGCRE. The government should strengthen investment in science, technology and education, train high-tech talents, and promote the research, development and application of patents. The government should introduce low-carbon technologies in various industries to reduce carbon emissions, so as to vigorously develop low-carbon industries, balance the structure of low-carbon industries and energy-intensive industries, and achieve balanced development. For the eight key industries, each province should adjust the input proportion of various production factors, optimize the energy structure, and reduce carbon emissions under the condition of ensuring stable and healthy economic development, so as to reduce the gap in carbon productivity between provinces. Provinces with close geographical locations should implement assistance policies to improve carbon productivity.

(4) In terms of specific industries in specific provinces, the chemical industry in Hebei should focus on the development of hybrid knowledge stock to replace hybrid energy, adjust the proportion of energy use, increase investment in scientific and technological research and development, and improve technical efficiency and carbon emission performance. Shanxi Province should focus on the development of labor substitution for hybrid energy in communication equipment, office equipment and other manufacturing industries, reduce the use of fossil energy, and reduce carbon emissions. Inner Mongolia should make full and efficient use of natural resources and improve its ability to absorb and store carbon dioxide. The three northeastern provinces as a whole need to develop advanced production technologies and improve traditional production methods. They should vigorously develop capital to replace hybrid energy, labor to replace hybrid energy and hybrid knowledge stock to replace hybrid energy, adjust the input structure of production factors, and increase the research, development and use of green patents. Anhui should increase scientific and technological investment in black gold, gold processing and non-gold and metal products industries, promote scientific and technological innovation, especially the use of clean energy, to reduce carbon dioxide emissions. Shandong Province should focus on adjusting the energy consumption structure in the province and improve the level of carbon productivity fundamentally. Guangxi Province needs to focus on improving the substitution of capital, labor force and hybrid knowledge stock for hybrid energy, and improve the proportion of production factors input, so as to improve the level of technology and carbon emission performance. Hainan Province should make full use of the advantages of natural resources, actively develop renewable energy, reduce carbon emissions, and absorb carbon dioxide that has been generated. The combination of the two will further improve carbon productivity. Guizhou needs to increase the substitution of capital and hybrid knowledge stock for hybrid energy, optimize the input structure of production factors, and comprehensively improve carbon productivity. The four provinces in northwest China need to focus on developing new energy, such as solar power, wind power, and ecological photovoltaic power, to reduce fossil energy consumption and reduce carbon emissions.

Author contributions

MF: Conceptualization, Methodology, Project administration, Supervision, Writing–original draft. YM: Data curation, Methodology, Investigation, Writing–original draft. LT: Funding acquisition, Methodology, Resources, Supervision, Writing–review and editing. CZ: Data curation, Software, Visualization, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This paper is supported by the National Natural Science Foundation of China (Grant Nos. 51976085 and 72174091), the Major Science and Technology Demonstration Program of Jiangsu Province (Grant No. BE2022612 and BE2022610), the National Key R&D Program of China (Grant No. 2020YFA0608601).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dong F, Yu B, Hadachin T, Dai Y, Wang Y, Zhang S, et al. Drivers of carbon emission intensity change in China. Resour Conservation Recycling (2018) 129:187–201. doi:10.1016/j.resconrec.2017.10.035

CrossRef Full Text | Google Scholar

2. Jin P, Peng C, Song M. Macroeconomic uncertainty, high-level innovation, and urban green development performance in China. China Econ Rev (2019) 55:1–18. doi:10.1016/j.chieco.2019.02.008

CrossRef Full Text | Google Scholar

3. Wang Y, Shen N. Environmental regulation and environmental productivity: the case of China. Renew Sustain Energ Rev (2016) 62:758–66. doi:10.1016/j.rser.2016.05.048

CrossRef Full Text | Google Scholar

4. Jin J, Ma XY, Gao YS. China’s carbon emission productivity and its development tendency from an environmental protection perspective. Nat Environ Pollut Tech (2017) 16(4):1293–301.

Google Scholar

5. Chen YF, Ma LH, Zhu ZT. The environmental-adjusted energy efficiency of China’s construction industry: a three-stage undesirable SBM-DEA model. Environ Sci Pollut Res (2021) 28(41):58442–55. doi:10.1007/s11356-021-14728-2

CrossRef Full Text | Google Scholar

6. Scheel H. Undesirable outputs in efficiency valuations. Eur J Oper Res (2001) 132(2):400–10. doi:10.1016/s0377-2217(00)00160-0

CrossRef Full Text | Google Scholar

7. Sueyoshi T, Yuan Y, Goto M. A literature study for DEA applied to energy and environment. Energ Econ (2017) 62:104–24. doi:10.1016/j.eneco.2016.11.006

CrossRef Full Text | Google Scholar

8. Plank B, Eisenmenger N, Schaffartzik A, Wiedenhofer D. International trade drives global resource use: a structural decomposition analysis of raw material consumption from 1990–2010. Environ Sci Tech (2018) 52(7):4190–8. doi:10.1021/acs.est.7b06133

CrossRef Full Text | Google Scholar

9. Moutinho V, Madaleno M, Inglesi-Lotz R, Dogan E. Factors affecting CO2 emissions in top countries on renewable energies: a LMDI decomposition application. Renew Sustain Energ Rev (2018) 90:605–22. doi:10.1016/j.rser.2018.02.009

CrossRef Full Text | Google Scholar

10. Isaksen A, Trippl M. Innovation in space: the mosaic of regional innovation patterns. Oxford Rev Econ Policy (2017) 33(1):122–40. doi:10.1093/oxrep/grw035

CrossRef Full Text | Google Scholar

11. Crescenzi R, Rodríguez-Pose A. The geography of innovation in China and India. Int J Urban Reg Res (2017) 41(6):1010–27. doi:10.1111/1468-2427.12554

CrossRef Full Text | Google Scholar

12. Wan B, Tian L. Health-education-disaster green low-carbon endogenous economic growth model and its new accompanying effects. J Clean Prod (2022) 359:131923. doi:10.1016/j.jclepro.2022.131923

CrossRef Full Text | Google Scholar

13. Kaya Y, Yokobori K. Environment, energy, and economy: strategies for sustainability. Tokyo: United Nations University Press (1997).

Google Scholar

14. McKinsey Global Institute. The carbon productivity challenge: curbing climate change and sustaining economic growth. New York, NY: McKinsey and Company, McKinsey Global Institute (2008).

Google Scholar

15. Aigner DJ, Lovell CAK, Schmidt P. Formulation and estimation of stochastic frontier production function models. J Econom (1977) 6(1):21–37. doi:10.1016/0304-4076(77)90052-5

CrossRef Full Text | Google Scholar

16. Charnes A, Cooper WW, Rhodes E. Measuring the efficiency of decision making units. Eur J Oper Res (1978) 2(6):429–44. doi:10.1016/0377-2217(78)90138-8

CrossRef Full Text | Google Scholar

17. Kumbhakar SC, Lovell CAK. Stochastic frontier analysis. New York: Cambridge University Press (2003).

Google Scholar

18. Li J, Li P. Analysis on urban production efficiency and its influencing factors in the three provinces of NortheastNortheast China—based on the study of stochastic frontier analysis method with three factors input. Econ Horizon (2018) 35(1):14–21. doi:10.15931/j.cnki.1006-1096.20171129.013

CrossRef Full Text | Google Scholar

19. Fang Y, Ma R. Study on the cultural trade potential and influencing factors of countries along the belt and road based on the stochastic frontier gravity model. World Econ Res (2018) 1:112–21. doi:10.13516/j.cnki.wes.2018.01.009

CrossRef Full Text | Google Scholar

20. Färe R, Grosskopf S. Modeling undesirable factors in efficiency evaluation: comment. Eur J Oper Res (2004) 157(1):242–5. doi:10.1016/s0377-2217(03)00191-7

CrossRef Full Text | Google Scholar

21. Chen S Environmental pollution emissions, regional productivity growth and ecological economic development in China. China Econ Rev (2015) 35:171–82. doi:10.1016/j.chieco.2014.08.005

CrossRef Full Text | Google Scholar

22. Seiford LM, Zhu J. Modeling undesirable factors in efficiency evaluation. Eur J Oper Res (2002) 142(1):16–20. doi:10.1016/s0377-2217(01)00293-4

CrossRef Full Text | Google Scholar

23. Gomes EG, Lins MPE Modelling undesirable outputs with zero sum gains data envelopment analysis models. J Oper Res Soc (2008) 59(5):616–23. doi:10.1057/palgrave.jors.2602384

CrossRef Full Text | Google Scholar

24. Hua Z, Bian Y, Liang L. Eco-efficiency analysis of paper mills along the Huai River: an extended DEA approach. Omega (2007) 35(5):578–87. doi:10.1016/j.omega.2005.11.001

CrossRef Full Text | Google Scholar

25. Chen F, Zhao T, Wang J. The evaluation of energy–environmental efficiency of China’s industrial sector: based on Super-SBM model. Clean Tech Environ Policy (2019) 21(7):1397–414. doi:10.1007/s10098-019-01713-0

CrossRef Full Text | Google Scholar

26. Gurgul H, Lach Ł. Linkages-based indicators of production-source sectoral eco-efficiency with application to Polish data. J Clean Prod (2021) 279:123545. doi:10.1016/j.jclepro.2020.123545

CrossRef Full Text | Google Scholar

27. Pan XF, Pan XY, Ming Y, Zhang J. The effect of regional mitigation of carbon dioxide emission on energy efficiency in China, based on a spatial econometrics approach. Carbon Manage (2018) 9(6):665–76. doi:10.1080/17583004.2018.1537514

CrossRef Full Text | Google Scholar

28. Li SJ, Wang SJ. Examining the effects of socioeconomic development on China’s carbon productivity: a panel data analysis. Sci Total Environ (2019) 659:681–90. doi:10.1016/j.scitotenv.2018.12.409

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang ZG, Su B, Xie R, Long H. China’s aggregate embodied CO2 emission intensity from 2007 to 2012: a multi-region multiplicative structural decomposition analysis. Energ Econ (2020) 85:104568. doi:10.1016/j.eneco.2019.104568

CrossRef Full Text | Google Scholar

30. Ang BW, Choi KH. Decomposition of aggregate energy and gas emission intensities for industry: a refined Divisia index method. Energ J (1997) 18(3):59–73. doi:10.5547/issn0195-6574-ej-vol18-no3-3

CrossRef Full Text | Google Scholar

31. Ang BW LMDI decomposition approach: a guide for implementation. Energy Policy (2015) 86:233–8. doi:10.1016/j.enpol.2015.07.007

CrossRef Full Text | Google Scholar

32. Ang BW, Zhang FQ, Choi KH. Factorizing changes in energy and environmental indicators through decomposition. Energy (1998) 23(6):489–95. doi:10.1016/s0360-5442(98)00016-4

CrossRef Full Text | Google Scholar

33. Chong CH, Tan WX, Ting ZJ, Liu P, Li Z. The driving factors of energy-related CO2 emission growth in Malaysia: the LMDI decomposition method based on energy allocation analysis. Renew Sustain Energ Rev (2019) 115:109356. doi:10.1016/j.rser.2019.109356

CrossRef Full Text | Google Scholar

34. Zhang C, Cai WH, Yu TS, Hu SJ, Liu HY, He P. Regional economic growth and carbon productivity: an analysis based on convergence and decoupling index. China Ind Econ (2013) 5:18–30. doi:10.1186/1999-3110-54-18

CrossRef Full Text | Google Scholar

35. Cheng Y, Sun YX, Wang XY. Study on the influence and countermeasures of global technological innovation on carbon productivity. China Popul Resour Environ (2019) 29(9):30–40. doi:10.12062/cpre.20190625

CrossRef Full Text | Google Scholar

36. Zhou P, Ang BW. Decomposition of aggregate CO2 emissions: a production-theoretical approach. Energ Econ (2008) 30(3):1054–67. doi:10.1016/j.eneco.2007.10.005

CrossRef Full Text | Google Scholar

37. Wang H, Zhou P. Multi-country comparisons of CO2 emission intensity: the production-theoretical decomposition analysis approach. Energ Econ (2018) 74:310–20. doi:10.1016/j.eneco.2018.05.038

CrossRef Full Text | Google Scholar

38. Yang H, Lu ZN, Shi XP, Mensah IA, Luo Y, Chen W. Multi-region and multi-sector comparisons and analysis of industrial carbon productivity in China. J Clean Prod (2021) 279:123623. doi:10.1016/j.jclepro.2020.123623

CrossRef Full Text | Google Scholar

39. Liu B, Ding CJ, Hu J, Su Y, Qin C. Carbon trading and regional carbon productivity. J Clean Prod (2023) 420:138395. doi:10.1016/j.jclepro.2023.138395

CrossRef Full Text | Google Scholar

40. Fang GC. The path optimization and policy synergy of new energy development under carbon trading-driving. Beijing, China: China Financial and Economic Publishing House (2023).

Google Scholar

41. Wan B, Tian L, Zhang W, Zhang G. Environmental effects of behavior growth under green development. Environ Develop Sustainability (2022) 25:10821–55. doi:10.1007/s10668-022-02508-y

CrossRef Full Text | Google Scholar

42. Färe R, Grosskopf S, Noh DW, Weber W. Characteristics of a polluting technology: theory and practice. J Econom (2005) 126(2):469–92. doi:10.1016/j.jeconom.2004.05.010

CrossRef Full Text | Google Scholar

43. Wang C. Sources of energy productivity growth and its distribution dynamics in China. Resource Energ Econ (2011) 33(1):279–92. doi:10.1016/j.reseneeco.2010.06.005

CrossRef Full Text | Google Scholar

44. Zhang XP, Zhang J, Tan QL. Decomposing the change of CO2 emissions: a joint production theoretical approach. Energy policy (2013) 58:329–36. doi:10.1016/j.enpol.2013.03.034

CrossRef Full Text | Google Scholar

45. Dietzenbacher E, Hoen AR, Los B. Labor productivity in Western Europe 1975–1985: an intercountry, interindustry analysis. J Reg Sci (2000) 40(3):425–52. doi:10.1111/0022-4146.00182

CrossRef Full Text | Google Scholar

46. Guan YR, Shan YL, Huang Q, Chen H, Wang D, Hubacek K. Assessment to China’s recent emission pattern shifts. Earth’s Future (2021) 9(11):e2021EF002241. doi:10.1029/2021ef002241

CrossRef Full Text | Google Scholar

Appendix A

TABLE A1

TABLE A1. Seven geographical divisions and symbols of China.