- School of Mathematics, North University of China, Taiyuan, China
In this paper, we investigate a Leslie-type predator–prey model that incorporates prey harvesting and group defense, leading to a modified functional response. Our analysis focuses on the existence and stability of the system’s equilibria, which are essential for the coexistence of predator and prey populations and the maintenance of ecological balance. We identify the maximum sustainable yield, a critical factor for achieving this balance. Through a thorough examination of positive equilibrium stability, we determine the conditions and initial values that promote the survival of both species. We delve into the system’s dynamics by analyzing saddle-node and Hopf bifurcations, which are crucial for understanding the system transitions between various states. To evaluate the stability of the Hopf bifurcation, we calculate the first Lyapunov exponent and offer a quantitative assessment of the system’s stability. Furthermore, we explore the Bogdanov–Takens (BT) bifurcation, a co-dimension 2 scenario, by employing a universal unfolding technique near the cusp point. This method simplifies the complex dynamics and reveals the conditions that trigger such bifurcations. To substantiate our theoretical findings, we conduct numerical simulations, which serve as a practical validation of the model predictions. These simulations not only confirm the theoretical results but also showcase the potential of the model for predicting real-world ecological scenarios. This in-depth analysis contributes to a nuanced understanding of the dynamics within predator–prey interactions and advances the field of ecological modeling.
1 Introduction
Since the pioneering work of Lotka and Volterra, who introduced a pair of differential equations to describe predator–prey dynamics, predator–prey models have attracted considerable interest from both mathematicians and biologists due to their widespread applicability [1]. Predominantly, predator–prey models have been developed around two main scenarios: (i) the growth function of the predator is directly proportional to its predation function, capturing the functional response of predators to prey availability, and (ii) the growth function of the predator is decoupled from its predation function, suggesting a more intricate relationship between the predator and prey.
Moreover, the growth term of the predator in these models is often portrayed as a function that depends not only on prey density but also on the predator-to-prey ratio, adding another dimension of complexity to the interactions. Among these diverse models, the Leslie-type model has emerged as a particularly influential paradigm. Its sophisticated treatment of predator–prey interactions has solidified its role as a fundamental framework in ecological studies, aiding in the comprehension of the delicate equilibrium within ecosystems.
[2] proposed a Leslie-type model to describe the relationship between predators and their prey:
where x and y denote the population densities of the prey and predators, respectively. In the absence of predators, the growth of prey populations is commonly modeled using a logistic growth function, characterized by an intrinsic growth rate r and an environmental carrying capacity K. This model assumes that population growth is limited by the availability of resources as the population size approaches the carrying capacity. The functional response, represented by f(x), describes how the rate of prey consumption by predators varies with the density of the prey population. In contrast, the growth rate of the predator is a Leslie-type growth function expressed as
Recently, [9, 10] proposed a novel functional response model that replaces the traditional prey density with the square root of prey density in the context of the Holling type II functional response. This innovation is particularly pertinent for prey species that exhibit herding behavior, where only peripheral individuals engage with predators. This revised functional response more accurately reflects how the protective effects of group living affect the rate at which predators encounter and consume the prey. Combining their functional response functions, we propose the following Leslie-type model:
where α presents the search efficiency of the predator for the prey and Th denotes the average handing time for each prey.
Before going into details, by substituting
into model Eq. 1 and dropping the bars, we obtain
Over the past three decades, a considerable amount of research has been devoted to understanding the effects of harvesting on the dynamics of predator–prey systems and its implications for the management of renewable resources. [11] explored a predator–prey model that includes Michaelis–Menten-type predator harvesting. In a similar vein, [12] discussed a modified Leslie–Gower model incorporating Michaelis–Menten-type prey harvesting. [13] investigated a model where both predator and prey populations exhibit logistic growth and are subject to nonlinear harvesting. The impact of proportional harvesting on the dynamic behavior of predator–prey models was examined by [14, 15]. [16] provided a detailed bifurcation analysis for a model with Holling-type II functional response and a constant harvesting rate. [17] also studied a model with constant prey harvesting. [18, 19] studied the dynamic behaviors of the predator–prey systems with a Holling- and Leslie-type or Leslie–Gower model with constant-yield prey harvesting, revealing a diverse array of bifurcations. [20] and [21] discussed ratio-dependent predator–prey systems with constant harvesting for both prey and predators, respectively. [22] investigated a system where the prey population forms herds as a defense against predators, and both species are exposed to a constant harvesting rate.
Inspired by these studies, we introduce the impact of a constant harvesting rate for the prey into Eq. 2 and obtain the following results:
where h represents the rate of prey harvesting.
It should be noted that system Eq. 2 is a Leslie-type predator–prey model that incorporates prey group defense mechanisms. Furthermore, system Eq. 3 extends this framework by accounting for the constant harvesting of the prey within system Eq. 2. To date, the dynamic behaviors of both systems Eq. 2 and Eq. 3 remain unexplored. Given the significance of biological resources as a sustainable source for human utilization and considering the rapid industrialization and population growth that have led to an inevitable increase in the utilization of various biological assets, it is imperative to investigate the impact of harvesting behavior on the population of both the predator and prey, particularly when prey group defense is involved, for the sake of maintaining ecological balance. In this paper, we study the dynamic behaviors of these two systems. Through rigorous mathematical analysis, we find that the population of the prey will be sustained without the effect of prey harvesting. However, due to the emergence of prey harvesting, system Eq. 3 exhibits complex dynamic behaviors and undergoes saddle-node, Hopf, and Bogdanov–Takens (BT) bifurcations. System Eq. 3 has bi-stable behavior due to saddle-node bifurcation, and whether the prey becomes extinct or not depends on the prey harvesting intensity. Specifically, we determine the maximum sustainable yield as
The structure of this paper is shown in Figure 1. Section 2 discusses the existence and stability of the equilibria for system Eq. 2. Section 3 delves into the investigation of the equilibria for system Eq. 3, providing both analytical insights and corroborating numerical results. Section 4 focuses on the bifurcation analysis of system Eq. 3, examining both saddle-node and Hopf bifurcations. Additionally, this section explores the Bogdanov–Takens bifurcation within the same system. Concluding remarks are given in Section 5, summarizing the key findings and implications of the study.
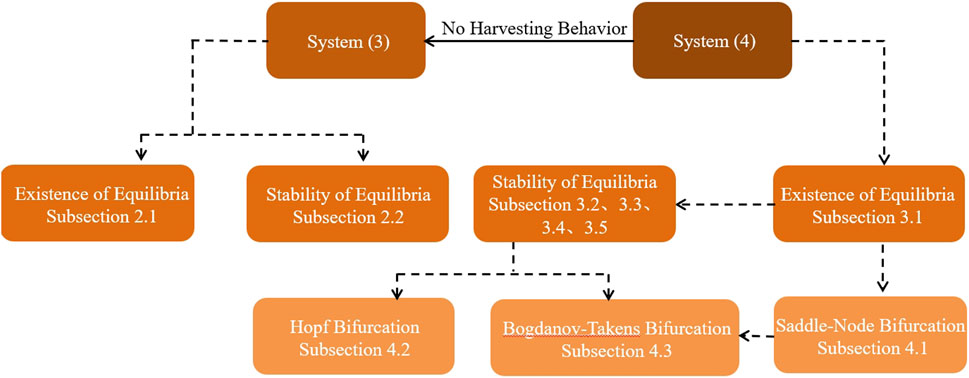
Figure 1. Flowchart of studies of the prey–predator system focusing on the harvesting setting in this paper.
2 Equilibria of system (3)
2.1 Existence of equilibria
To determine the equilibria of system Eq. 2, we analyze the prey and predator nullclines, which are given by the following equations:
From these nullclines, it is evident that system Eq. 2 has a unique boundary equilibrium at
By substituting
Theorem 2.1. System Eq. 2 possesses a unique boundary equilibrium
2.2 Stability of equilibria
Theorem 2.2. For all positive parameters, system Eq. 2 has a boundary equilibrium
Proof. The Jacobian matrix of system Eq. 2 evaluated at
It is obvious that the matrix
The Jacobian matrix of system Eq. 2 evaluated at
According to g(z0) = 0, we can obtain
Hence, when b > b0,
3 Equilibria of system (4)
3.1 Existence of equilibria
This section conducts a qualitative analysis of model Eq. 3. With the biological context in mind, we focus on examining the dynamics of system Eq. 3 within the closed first quadrant, denoted as
In order to obtain the equilibria of system Eq. 3, we first study the roots of the following equations:
Regarding the count of boundary equilibria for system Eq. 3, we derived the subsequent theorem.
Theorem 3.1. (i) When
(ii) When
Proof. When h exceeds
We next explore the existence of boundary equilibria under the condition that
It is straightforward to determine that when
Note that
Regarding the positive equilibria of system Eq. 3, we have the following theorem.
Theorem 3.2. (i) When
(ii) When
where
Proof. When y ≠ 0, then
where
Through algebraic analysis, we find that the equation h1(z) = 0 has a unique positive root, denoted as z1. When g1(z1) < 0, which corresponds to
3.2 Stability of equilibrium E0
Theorem 3.3. When
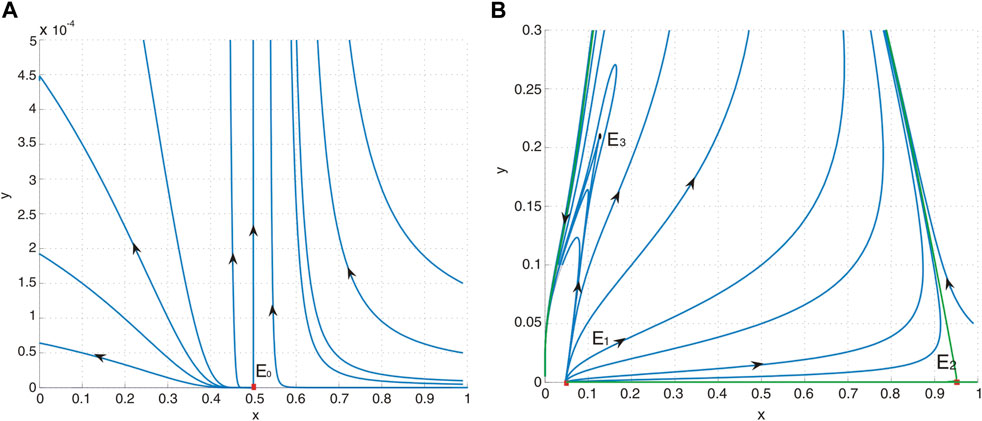
Figure 2. (A) Phase portrait of system (4) with a = 0.4, b = 0.5, d = 0.6, and
Proof. The Jacobian matrix J(E0) of system Eq. 3 evaluated at E0 is
Given that Det[J(E0)] = 0, we can conclude that the equilibrium
where P1(X, Y) and Q1(X, Y) are smooth functions of at least the third order with respect to (X, Y).
Then, making the transformation
and introducing a new time variable τ = bt, for which we retain t to denote τ for notational simplicity, we obtain
where P2(x, y) and Q2(x, y) are smooth functions of at least the third order with respect to (x, y) and
According to Theorem 7.1 from Chapter 2 in [23], the equilibrium E0 is classified as a saddle-node. This implies that the vicinity of E0 is bifurcated by two separatrices that approach E0 from above and below. One region forms a parabolic sector, while the other comprises two hyperbolic sectors. Additionally, the parabolic sector is situated in the right half-plane, and E0 acts as a repelling saddle-node.
3.3 Stability of equilibria E1 and E2
Theorem 3.4. When
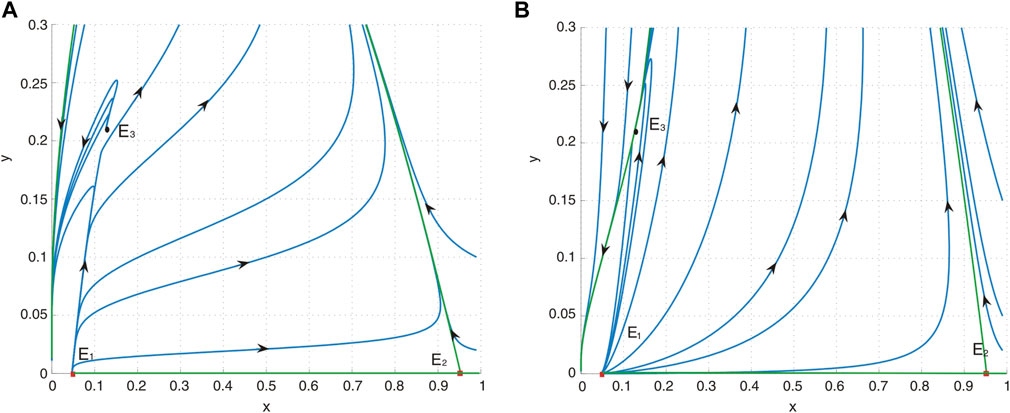
Figure 3. (A) Phase portrait of system (4) with a = 0.4, b = 0.2, d = 0.6, and h = 0.04485055324. E1 is an unstable node, E2 is a saddle, and E3 is a repelling saddle node. (B) Phase portrait of system (4) with a = 0.4, b = 1.2, d = 0.6, and h = 0.04485055324. E1 is an unstable node, E2 is a saddle, and E3 is an attracting saddle node.
Proof. The Jacobian matrix J(E1) of system Eq. 3 evaluated at E1 is
We can obtain that the eigenvalues are
The Jacobian matrix J(E2) of system Eq. 3 evaluated at E2 is
It is easy to observe that the eigenvalues are
3.4 Stability of equilibrium E3
Now, we investigate the stability of equilibrium E3. The Jacobian matrix J(E3) of system Eq. 3 evaluated at E3 is
Straightforward computation shows that, due to
where
Since f(z3) = 0, from Theorem 3.2, we can obtain
Substituting g1(z3) in the above equation yields
Theorem 3.5. (i) If
(i-1)
(i-2)
(ii) When
Proof. Since Tr[J(E3)] = a10 + b01, we know that the eigenvalues of J(E3) are λ1 = 0 and λ2 = a10 + b01.
Similar to the proof outlined in Theorem 3.3, we perform a transformation that shifts equilibrium E3 to the origin. We then expand system Eq. 3 in a power series up to the second order around this new origin. This transformation yields a simplified system that
where P11(X, Y) and Q11(X, Y) are smooth functions of at least the third order with respect to (X, Y), and
When a10 + b01 ≠ 0, J(E3) has one zero eigenvalue and a nonzero eigenvalue. To further analyze the stability of this equilibrium, we introduce a transformation that
and introducing a new time variable τ1 = (a10 + b01)t, for which we retain t to denote τ1 for notational simplicity, we obtain
where P21(x, y) and Q21(x, y) are smooth functions of at least the third order with respect to (x, y), and
Straightforward computation shows that
Consequently, as shown by Theorem 7.1 from Chapter 2 in [23], if a10 + b01 ≠ 0, then the equilibrium E3 qualifies as a saddle-node. Moreover, the characteristics of this saddle-node are determined as follows: (i) if a10 + b01 > 0, the parabolic sector is situated in the upper half-plane, and E3 acts as a repelling saddle-node and (ii) conversely, if a10 + b01 < 0, the parabolic sector remains in the upper half-plane, but E3 is an attracting saddle-node.
When a10 + b01 = 0, J(E3) has one zero eigenvalue with two multiple. Then, making the transformation
and introducing a new time variable τ2 = −b01t = bt. For notational simplicity, we retain t to represent τ2, then system Eq. 7 becomes
where P22(x, y) and Q22(x, y) are smooth functions of at least the third order with respect to (x, y) and
To eliminate y2 terms in system Eq. 8, we make the following near identity transformation:
which transforms system Eq. 8 into
where P23(X, Y) and Q23(X, Y) are smooth functions of at least the third order with respect to (X, Y). Therefore, when f20 ≠ 0
3.5 Stability of equilibria E4 and E5
Theorem 3.6. When system Eq. 3 exists with two positive equilibria E4 and E5, E4 is always a hyperbolic saddle. Furthermore, positive equilibrium E5 is a sink when b > b*, a source when b < b*, or a center when b = b*, where
Proof. The Jacobian matrix J(E4) of system Eq. 3 evaluated at E4 is
Straightforward computation shows that, due to
where
Since f(z4) = 0, from Theorem 3.2, we obtain
Substituting g1(z4) by the above equation, then
Similarly, we obtain
since l(z5) > 0 (z5 > z3). Moreover, we can also obtain
Hence, when b > b*, Tr[J(E5)] < 0, the matrix J(E5) has two negative part eigenvalues, and E5 is a sink. When b < b*, then Tr[J(E5)] > 0, the matrix J(E5) has two positive part eigenvalues, and E5 is a source. When b = b*, then Tr[J(E5)] = 0, the matrix J(E5) has a pair of pure imaginary eigenvalues, and E5 is a center.
4 Bifurcation analysis
In this section, we investigate the bifurcations that take place in system Eq. 3.
4.1 Saddle-node bifurcation
According to Theorem 3.1, we provided the conditions for the existence of E1 and E2 based on some restrictions. We obtain that
is a saddle-node bifurcation surface. Consequently, we can deduce that on the surface SN1, system Eq. 3 possesses a unique equilibrium E0, which is a saddle-node. As the parameters traverse this surface, the quantity of boundary equilibria undergoes a transition from zero to two. Biologically, this bifurcation corresponds to a critical threshold where the maximum sustainable yield (MSY) is at
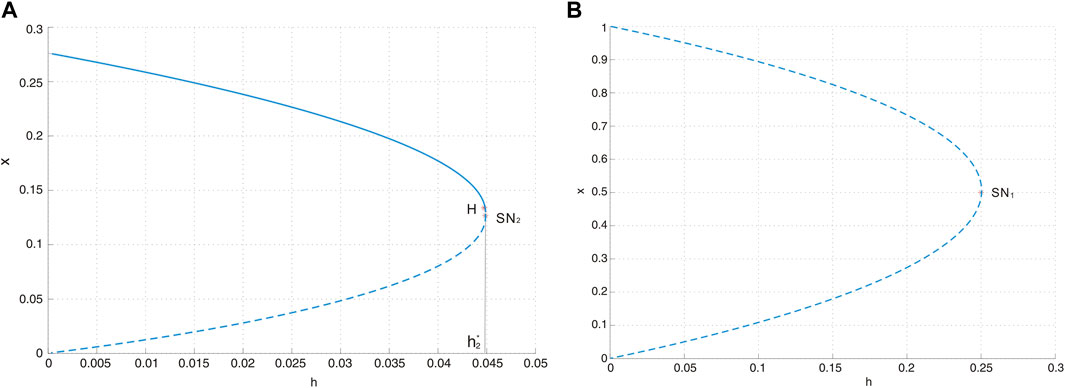
Figure 4. (A) Saddle-node bifurcation diagram SN2 with a = 0.4, d = 0.6, and b = 0.5, where H represents the Hopf bifurcation point. The solid curve represents the stable equilibrium, and the dotted curve stands for the unstable equilibrium. (B) Saddle-node bifurcation diagram SN1 with a = 0.4, d = 0.6, and b = 0.5.
Similar to the above discussion, we obtain
according to Theorem 3.2, is another saddle-node bifurcation surface. When the parameters transition from one side of the surface to the other, the number of positive equilibria in system Eq. 3 changes from zero to two. The saddle-node bifurcation is illustrated in Figure 4A.
4.2 Hopf bifurcation
From Theorem 3.6, we know that the positive equilibrium E5 is a center-type nonhyperbolic equilibrium when b = b* and
Therefore, the stability of the positive equilibrium E5 undergoes a change as the parameters traverse the specific critical surface
To determine the direction of the Hopf bifurcation, we calculate the first Lyapunov number l1 at the equilibrium E5 = (x5, y5). Initially, we shift the equilibrium to the origin using the transformation
where
In accordance with the formula for the first Lyapunov number l1 presented in [24] [p.353], we proceed with the computation
where
and
Consequently, if l1 < 0 (which corresponds to M < 0), then E5 undergoes a supercritical Hopf bifurcation, leading to the emergence of a stable limit cycle in a small neighborhood of E5 as the parameters across the surface H1. Conversely, if l1 > 0 (or M > 0), a subcritical Hopf bifurcation occurs, resulting in an unstable limit cycle appearing in the vicinity of E5 as the parameters across the surface H1.
Given the complexity of l1, which does not readily reveal information about its sign, we turn to a numerical example for further clarification.
Fixing a = 0.4, d = 0.6, and h = 0.04, we obtain b* = 0.3960214438 and M = 0.537259605 and then l1 > 0, which implies that an unstable limit cycle is created around E5 = (0.1742665424, 00.2904442373). For b = 0.41 > b*, we obtain M = 0.652746120 and then l1 > 0, which implies that an unstable limit cycle is created around E5, where E5 is asymptotically stable (see Figure 5B). When b = 0.425, a collision occurs between the periodic orbit and saddle E4, resulting in the formation of a homoclinic orbit. Since M = 0.791862704, then l1 > 0, which means that periodic orbits remain unstable, as shown in Figure 5A.
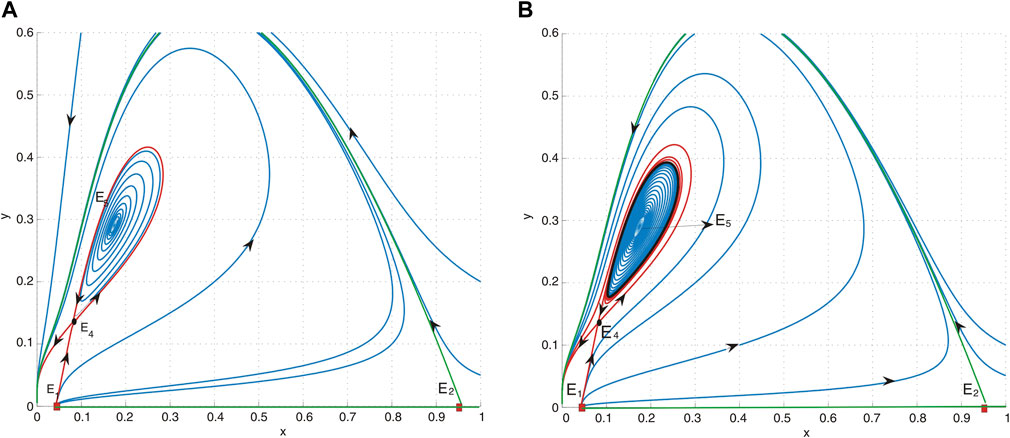
Figure 5. (A) Phase portrait of system (4) with a = 0.4, b = 0.425, d = 0.6, and h = 0.04. E1 is an unstable node, E2 is a saddle, E4 is a saddle, and E5 is a sink. It indicates that the periodic orbit undergoes a collision with the saddle E4. (B) Phase portrait of system (4) with a = 0.4, b = 0.41, d = 0.6, and h = 0.04. E1 is an unstable node, E2 is a saddle, E4 is a saddle, and E5 is a sink. An unstable limit cycle, depicted as a black curve, surrounds the equilibrium point E5.
4.3 Bogdanov–Takens bifurcation
As presented in Theorem 3.5, the positive equilibrium E3 is identified as a cusp of co-dimension 2. This classification holds under certain conditions where a10 + b01 = 0,
Theorem 4.1. When h and d are selected as bifurcation parameters, system Eq. 3 is poised to experience a Bogdanov–Takens bifurcation in a neighborhood of E3 as (h, d) varies near (hBT, dBT) for a10 + b01 = 0,
Proof. To obtain the expressions for the saddle-node, Hopf, and homoclinic bifurcation curves, we derive a normal form for the Bogdanov–Takens bifurcation. This derivation uses the techniques outlined by [11, 18, 25].
Let us examine a perturbation of the parameters h and d centered around their BT bifurcation values. We represent this perturbation as h = hBT + u and d = dBT + v, where u and v are small deviations from the critical values hBT and dBT, respectively. Consider
We begin by translating the equilibrium point E3 = (x3, y3) to the origin using the transformations X = x − x3 and Y = y − y3. Subsequently, we expand system Eq. 9 as a power series centered at the origin. Then, we have
where P1(X, Y) and Q1(X, Y) are smooth functions of at least the third order with respect to (X, Y), whose coefficients depend smoothly on u and v, and where
Let x = X and y = m00 + m10X + m01Y + m11XY + m20X2 + P1(X, Y), then system Eq. 10 can be written as
where Q2(x, y) are smooth functions of at least the third order with respect to (x, y), whose coefficients vary smoothly on u and v, and
By introducing a new variable τ through the relation dt = (1 − l02x)dτ and subsequently rewriting τ back as t, we can recast system Eq. 11 in a new form:
Let X = x and Y = y(1 − l02x), then system Eq. 12 can be written as
where Q3(X, Y) are smooth functions of at least the third order with respect to (X, Y), whose coefficients depend smoothly on u and v, and
Note that d20 is very complex, and we cannot determine the sign of d20 when u and v are small. Hence, we consider two cases: C-1: d20 > 0; C-2: d20 < 0.
C-1: If d20 > 0 for small values of u and v, we perform the following change of variables: x = X,
where Q4(x, y) are smooth of at least the third order with respect to (x, y), whose coefficients depend smoothly on u and v, and
Let
where Q5(X, Y) are smooth of at least the third order with respect to (X, Y), whose coefficients depend smoothly on u and v, and
Suppose d11 ≠ 0, then g11 = h11 ≠ 0. Making the change of variables
where Q6(x, y) are smooth of at least the third order with respect to (x, y), whose coefficients depend smoothly on u and v, and
C-2: If d20 < 0 for small u and v, we perform the following change of variables: x′ = X,
where
Let
where
Suppose d11 ≠ 0,
where
To streamline the analysis, we retain the notation μ1 and μ2 for the transformed parameters
Drawing upon the findings obtained by [24] and as supported by [5, 11, 18, 26], we establish that system Eq. 9 experiences a Bogdanov–Takens bifurcation when the parameters (u, v) are in a small neighborhood of the origin. The local representatisons of the bifurcation curves, derived from the analysis, are as follows (“+” for d20 > 0, “-” for d20 < 0):
(1) The saddle-node bifurcation curve SN = {(u, v): μ1 = 0, μ2 ≠ 0};
(2) The Hopf bifurcation curve
(3) The homoclinic bifurcation curve
Subsequently, we numerically illustrate the locations of the bifurcation curves and the dynamics of the system at the Bogdanov–Takens bifurcation point. This is achieved by selecting specific values for the dimensionless parameters. We choose a = 0.4 and dBT = 0.6, then hBT = 0.04485055333 and b = 0.5193087015. Since d20 = 1729.213892u2 − 1.159964346–9.646351129v − 31.60626034u − 319.1508390uv and d11 = (22.77081918–346.0816837u)v2 + (19.64233118–642.5091021u)v − 284.7831954u − 2.673388394, then d20 < 0 and d11 ≠ 0 for u ∈ (−0.01, 0.01) and v ∈ (−0.1, 0.1), so we compute Eq. 19 and get
(1) The saddle-node bifurcation curve
(2) The Hopf bifurcation curve
(3) The homoclinic bifurcation curve
These bifurcation curves H, HL, and SN divide the small neighborhood of the origin in the parameter plane (u, v) into four regions. The bifurcation diagram of system Eq. 9 is given in Figure 6A, from which we obtain the following observations:
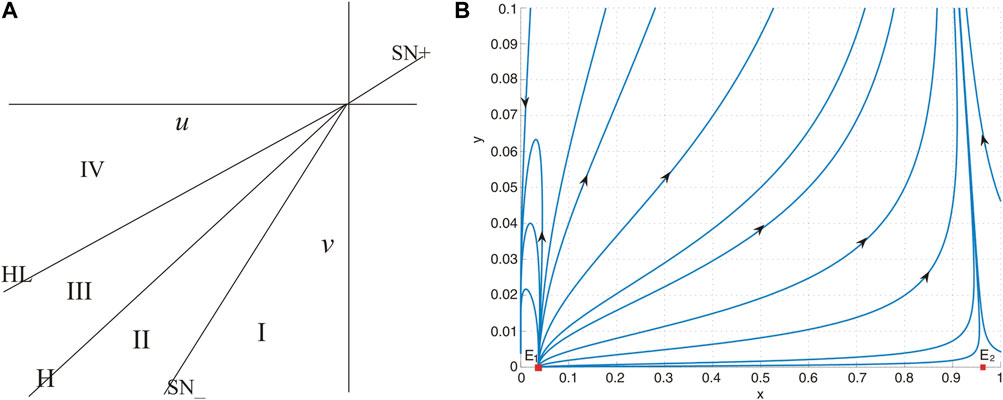
Figure 6. (A) Bifurcation diagram of system (26). (B) No positive equilibrium when (u, v) = (−0.01, − 0.1) lies in region I, and system (26) has two boundary equilibria E1 and E2.
(a) When (u, v) = (0, 0), the unique positive equilibrium is a cusp of co-dimension 2.
(b) When the parameters are situated within region I, the system lacks a positive equilibrium, as shown in Figure 6B. This absence implies that the prey population is inclined toward extinction under nearly all initial conditions.
(c) When the parameters are positioned along the curve SN, the system exhibits a positive equilibrium that is characterized as a saddle node.
(d) In region II, system Eq. 9 possesses two positive equilibria. Specifically, E4 is identified as a saddle, while E5 acts as a source, as shown in Figure 7A.
(e) Upon crossing curve H and entering region III, the system undergoes a subcritical Hopf bifurcation, resulting in the emergence of an unstable limit cycle. This phenomenon is depicted in Figure 7B.
(f) When the parameters are selected along the curve HL, an unstable homoclinic cycle encircles a sink, while the other equilibrium remains a saddle. This configuration is illustrated in Figure 8A.
(g) In region IV, the system is characterized by the presence of a sink and a saddle, as depicted in Figure 8B.
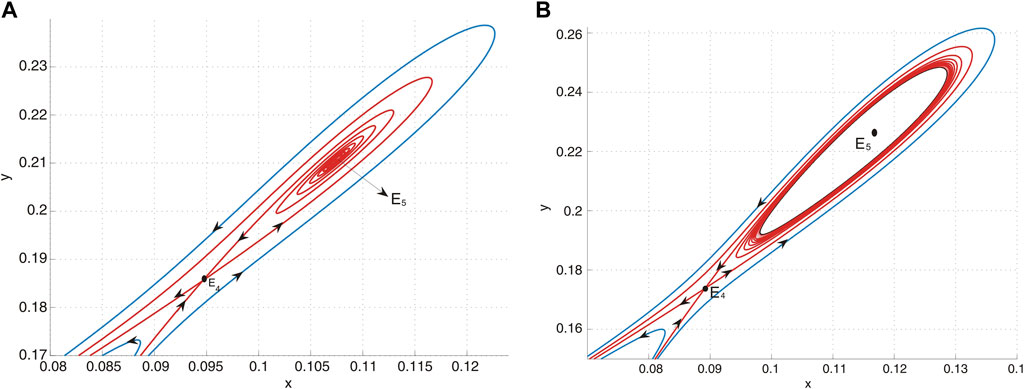
Figure 7. (A) E5 is a source and E4 is a saddle when (u, v) = (−0.01, − 0.09) lies in region II. (B) E5 is a sink and E4 is a saddle when (u, v) = (−0.01, − 0.087) lies in region III, and an unstable limit cycle encloses E5.
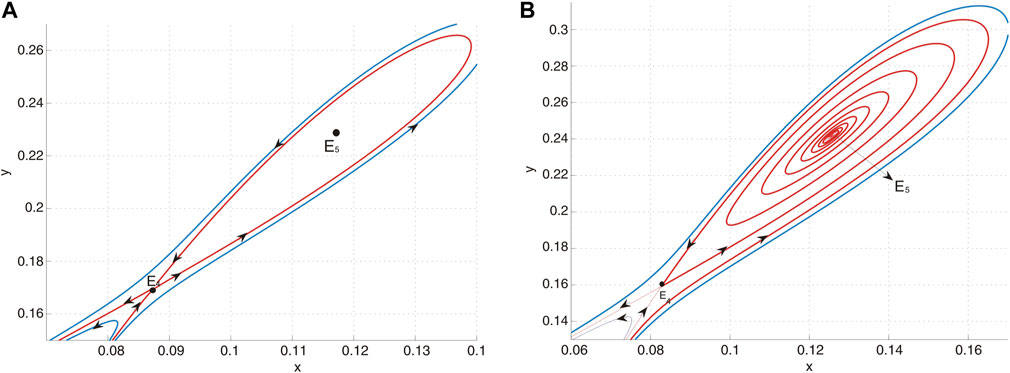
Figure 8. (A) E5 is a sink and E4 is a saddle when (u, v) = (−0.01, − 0.0854) lies on curve HL and an unstable homoclinic orbit encloses E5. (B) E5 is a sink and E4 is a saddle when (u, v) = (−0.01, − 0.08) lies in region IV.
5 Conclusion
In this paper, we explore a Leslie-type predator–prey system incorporating prey harvesting. Initially, we examine system Eq. 2 without prey harvesting, establishing that it possesses a unique boundary equilibrium and a unique positive equilibrium. Theorem 2.2 elucidates the stability of both boundary equilibrium and positive equilibrium. Notably, the boundary equilibrium is consistently unstable, indicating that neither the prey nor the predator will ever become extinct without the influence of prey harvesting.
Furthermore, we study the dynamic behaviors of system Eq. 3 to analyze the effect of prey harvesting on the prey and predator. Hence, we first analyze the existence and stability of equilibria for system Eq. 3 in Section 3. As shown in Theorem 3.1, we identify the maximum sustainable yield as
In Section 4, we chose the constant harvesting rate h as one of the bifurcation parameters to perform the bifurcation analysis of system Eq. 3. We find that system Eq. 3 has complex dynamic behavior and undergoes Hopf bifurcation, Bogdanov–Takens bifurcation of co-dimension 2, and saddle-node bifurcation. Among them, the emergence of saddle-node bifurcation means that system Eq. 3 has bi-stable behavior, and the prey may face extinction or sustain, which depends on the harvesting rate. For the Hopf bifurcation, we calculate the first Lyapunov number to ascertain the direction of the Hopf bifurcation, which indicates whether a stable or unstable limit cycle emerges in the vicinity of the equilibrium E5. By selecting two parameters from system Eq. 3 as bifurcation parameters, we demonstrate that the system undergoes a Bogdanov–Takens bifurcation of co-dimension 2. This conclusion is drawn from our analysis of the universal unfolding near the cusp.
In conclusion, we constructed and provided a detailed dynamic analysis of a Leslie-type predator–prey system that incorporates prey harvesting. Our findings reveal that prey harvesting introduces complex dynamic behaviors into the system, potentially leading to a series of bifurcations. Furthermore, if the harvesting intensity exceeds a critical threshold, the prey may face extinction. These insights offer valuable contributions to the understanding of predator–prey systems and ecological balance. However, it is worth noting that this paper focuses primarily on qualitative analysis and lacks empirical data to support our theoretical findings. Despite this, significant algorithms have been developed to gather and analyze real-world data. We intend to leverage these algorithms to quantitatively assess the impact of harvesting using the methodologies introduced by [27, 28]. Additionally, this study does not consider the removal of both prey and predator species, and human activity can significantly impact ecosystems, as highlighted by [29]. Drawing inspiration from [30–36], our model can be extended to eco-epidemic systems and reaction–diffusion systems. These areas represent promising directions for future research in this field.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
YZ: data curation, methodology, writing–original draft, and writing–review and editing. JL: methodology, writing–original draft, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was supported by the National Natural Science Foundation of China (No. 12201582), Research Project Supported by Shanxi Scholarship Council of China (2022-151), and the Fundamental Research Program of Shanxi Province under grant (No. 202203021212130).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ning L-Y, Luo X-F, Li B-L, Wu Y-P, Sun G-Q, Feng T-C An effective allee effect may induce the survival of low-density predator. Results Phys (2023) 53:106926.
2. May R Stability and complexity in model ecosystems. Princeton: Princeton University Press (1973).
3. Seo G, DeAngelis DL A predator-prey model with a holling type i functional response including a predator mutual interference. J Nonlinear Sci (2011) 21:811–33. doi:10.1007/s00332-011-9101-6
4. Hsu S, Huang T Global stability for a class of predator-prey system. SIAM J Appl Math (1995) 6:763–83.
5. Huang J, Ruan S, Song J Bifurcations in a predator-prey system of leslie type with generalized holling type iii functional response. J Differ Equations (2014) 257:1721–52. doi:10.1016/j.jde.2014.04.024
6. Liu C, Chang L, Huang Y, Wang Z Turing patterns in a predator-prey model on complex networks. Nonlinear Dyn (2020) 99:3313–22. doi:10.1007/s11071-019-05460-1
7. Huang J, Xiao D Analyses of bifurcations and stability in a predator-prey system with holling type-iv functional response. Acta Math Appl Sin Engl Ser (2004) 20:167–78.
8. Li Y, Xiao D Bifurcations of a predator-prey system of holling and lesile types. Chaos Soliton Fract (2007) 34:606–20.
9. Bera S, Maiti A, Samanta G Stochastic analysis of a prey-predator model with herd behaviour of prey. Nonlinear Anal.-Model. (2016) 21:345–61. doi:10.15388/na.2016.3.4
10. Braza A Predator-prey dynamics with square root functional responses. Nonlinear Anal.-Real (2012) 13:1837–43. doi:10.1016/j.nonrwa.2011.12.014
11. Hu D, Cao H Stability and bifurcation analysis in a predator–prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal.-Real (2017) 33:58–82. doi:10.1016/j.nonrwa.2016.05.010
12. Gupta R, Chandra P Bifurcation analysis of modified leslie-gower predator-prey model with michaelis-menten type prey harvesting. J Math Anal Appl (2003) 398:278–95. doi:10.1016/j.jmaa.2012.08.057
13. Das T, Mukherjee R, Chaudhari K Bioeconomic harvesting of a prey-predator fishery. J Biol Dyn (2009) 3:447–62. doi:10.1080/17513750802560346
14. Chakraborty K, Jana S, Kar T Global dynamics and bifurcation in a stage structured prey-predator fishery model with harvesting. Appl Math Comput (2012) 218:9271–90. doi:10.1016/j.amc.2012.03.005
15. Rojas-Palma A, Gonz’alez-Olivares E Optimal harvesting in a predator-prey model with allee effect and sigmoid functional response. Appl Math Model (2012) 36:1864–74. doi:10.1016/j.apm.2011.07.081
16. Xiao D, Ruan S Bogdanov-takens bifurcations in predator-prey systems with constant rate harvesting. Fields Inst Commun (1999) 21:493–506. doi:10.1090/fic/021/41
17. Peng G, Jiang Y, Li C Bifurcations of a holling-type ii predator-prey system with constant rate harvesting. Int J Bifurcat Chaos (2009) 19:2499–514. doi:10.1142/s021812740902427x
18. Huang J, Gong Y, Chen J Multiple bifurcations in a predator-prey system of holling and leslie type with constant-yield prey harvesting. Int J Bifurcat Chaos (2013) 23:1350164. doi:10.1142/s0218127413501642
19. Zhu C, Lan K Phase portraits, hopf-bifurcations and limit cycles of leslie-gower predator-prey systems with harvesting rates. Discrete Contin Dyn Syst Ser B (2010) 14:289–306. doi:10.3934/dcdsb.2010.14.289
20. Xiao D, Jennings LS Bifurcations of a ratio-dependent predator-prey system with constant rate harvesting. SIAM J Appl Math (2005) 65:737–53. doi:10.1137/s0036139903428719
21. Xiao D, Li W, Han M Dynamics in a ratio-dependent predator-prey model with predator harvesting. J Math Anal Appl (2006) 324:14–29. doi:10.1016/j.jmaa.2005.11.048
22. Luo J, Zhao Y Stability and bifurcation analysis in a predator-prey system with constant harvesting and prey group defense. Int J Bifurcat Chaos (2017) 27:1750179. doi:10.1142/s0218127417501796
23. Zhang Z, Ding T, Huang W, Dong Z Qualitative theory of differential equation. Beijing: Science Press (1992).
25. Chen J, Huang J, Ruan S, Wang J Bifurcations of invariant tori in predator-prey models with seasonal prey harvesting. SIAM J Appl Math (2013) 73:1876–905. doi:10.1137/120895858
26. Huang J, Gong Y, Ruan S Bifurcation analysis in a predator-prey model with constant-yield predator harvesting. Discrete Contin Dynam Syst Ser B (2013) 18:2101–21. doi:10.3934/dcdsb.2013.18.2101
27. Li H, Cao H, Feng Y, Li X, Pei J Optimization of graph clustering inspired by dynamic belief systems. IEEE Trans Knowledge Data Eng (2023) 1–14. doi:10.1109/TKDE.2023.3274547
28. Li H, Feng Y, Xia C, Cao J Overlapping graph clustering in attributed networks via generalized cluster potential game. ACM T Knowl Discov D (2023) 18:1–26. doi:10.1145/3597436
29. Hou L-F, Sun G-Q, Perc M The impact of heterogeneous human activity on vegetation patterns in arid environments. Communical Nonlinear SCI (2023) 126:107461. doi:10.1016/j.cnsns.2023.107461
30. Fu S, Luo J, Zhao Y Stability and bifurcations analysis in an ecoepidemic system with prey group defense and two infectious routes. Math Comput Simulat (2023) 205:581–99.
31. Gao S, Chang L, Perc M, Wang Z Turing patterns in simplicial complexes. Phys Rev E (2023) 107:014216. doi:10.1103/physreve.107.014216
32. Wang C, Chang L, Liu H Spatial patterns of a predator-prey system of leslie type with time delay. PLoS One (2016) 11:e0150503. doi:10.1371/journal.pone.0150503
33. Liang J, Sun G-Q Effect of nonlocal delay with strong kernel on vegetation pattern. J Appl Anal Comput (2024) 14:473–505. doi:10.11948/20230290
34. Yang J, Gong M, Sun G-Q Asymptotical profiles of an age-structured foot-and-mouth disease with nonlocal diffusion on a spatially heterogeneous environment. J Differ Equations (2023) 377:71–112. doi:10.1016/j.jde.2023.09.001
35. Liu S-M, Bai Z, Sun G-Q Global dynamics of a reaction-diffusion brucellosis model with spatiotemporal heterogeneity and nonlocal delay. Nonlinearity (2023) 36:5699–730. doi:10.1088/1361-6544/acf6a5
Keywords: saddle-node bifurcation, Hopf bifurcation, prey harvesting, Bogdanov–Takens bifurcation, predation
Citation: Zhang Y and Luo J (2024) Bifurcation analysis of a Leslie-type predator–prey system with prey harvesting and group defense. Front. Phys. 12:1392446. doi: 10.3389/fphy.2024.1392446
Received: 27 February 2024; Accepted: 19 April 2024;
Published: 19 June 2024.
Edited by:
Hui-Jia Li, Beijing University of Posts and Telecommunications (BUPT), ChinaCopyright © 2024 Zhang and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianfeng Luo, amlhbmZlbmdsdW9AbnVjLmVkdS5jbg==
 Yongxin Zhang
Yongxin Zhang Jianfeng Luo*
Jianfeng Luo*