
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 26 August 2024
Sec. Biophysics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1387271
This article is part of the Research TopicQuantum-based Effects on Cell PhysiologyView all 7 articles
Background: Superradiance is the phenomenon of many identical quantum systems absorbing and/or emitting photons collectively at a higher rate than any one system can individually. This phenomenon has been studied analytically in idealized distributions of electronic two-level systems (TLSs), each with a ground and excited state, as well as numerically in realistic photosynthetic nanotubes and cytoskeletal architectures.
Methods: Superradiant effects are studied here in idealized toy model systems and realistic biological mega-networks of tryptophan (Trp) molecules, which are strongly fluorescent amino acids found in many proteins. Each Trp molecule acts as a chromophore absorbing in the ultraviolet spectrum and can be treated approximately as a TLS, with its
Results: We obtained the energies and enhancement rates for realistic microtubules, actin filament bundles, and amyloid fibrils of differing lengths, and we use these values to calculate the quantum yield, which is the ratio of the number of photons emitted to the number of photons absorbed. We find that all three of these structures exhibit highly superradiant states near the low-energy portion of the spectrum, which enhances the magnitude and robustness of the quantum yield to static disorder and thermal noise.
Conclusion: The high quantum yield and stable superradiant states in these biological architectures may play a photoprotective role in vivo, downconverting energetic ultraviolet photons—absorbed from those emitted by reactive free radical species—to longer, safer wavelengths and thereby mitigating biochemical stress and photophysical damage. Contrary to conventional assumptions that quantum effects cannot survive in large biosystems at high temperatures, our results suggest that macropolymeric collectives of TLSs in microtubules, actin filaments, and amyloid fibrils exhibit increasingly observable and robust effects with increasing length, up to the micron scale, due to quantum coherent interactions in the single-photon limit. Superradiant enhancement and high quantum yield exhibited in neuroprotein polymers could thus play a crucial role in information processing in the brain, the development of neurodegenerative diseases such as Alzheimer’s and related dementias, and a wide array of other pathologies characterized by anomalous protein aggregates.
Superradiance is a quantum coherent phenomenon first explored in detail by Robert Dicke [1] in 1954. Superradiance arises from the interaction of a collective of quantum systems with the external electromagnetic field. Thus, the theoretical formalism that describes superradiance is given frequently in the language of open quantum systems. In collectives of quantum systems with discrete energy levels, collective superradiant states are characterized by the collective decay rate
Superradiant effects in the ultraviolet region of the electromagnetic spectrum have been studied for biosystems [2–4] and emerge largely due to collective light-matter interactions involving tryptophan (Trp), which is a strongly fluorescent amino acid found in many proteins. It has many notable photophysical properties, such as its strong ultraviolet absorption, significant absorption-emission Stokes shift, and large transition dipole moment. Trp can be modeled as a two-level system (TLS), which has a ground and an excited state. The TLS approximation for Trp can be derived from the pioneering experiments of Patrik Callis’s group [5, 6], where it has been proven to be an extraordinarily good approximation in several theoretical, computational, and experimental studies [2–4, 7]. Its validity is further supported by experimental quantum yield values obtained in [3] that match closely with theoretical predictions based on this approximation. Other amino acids such as tyrosine, phenylalanine, and cysteine also absorb in the ultraviolet, but much more weakly than Trp. The fact that Trp networks absorb in the ultraviolet means that the excitation wavelengths are frequently shorter than the characteristic length scales of the biological scaffolds in which such networks lie
Coherent quantum phenomena arising from organized networks of chromophores in protein scaffolds have been shown to play a role in the efficiency of photosynthetic complexes [8–12] and of other light-harvesting structures (see [2, 13–16] and references therein). More recently, superradiance arising from single photon-excited superposition states has been experimentally confirmed in solvated microtubules at the micron scale and theoretically predicted in centrioles1 and neuronal axons [3]. In this work, we study the role of superradiance in a wider class of neuroprotein polymers, including cytoskeletal filaments and pathological aggregates, thereby demonstrating the generalizability of our prior experimental results and theoretical predictions for a novel group of chromophore architectures with significant implications for a host of neurodegenerative and other complex diseases.
The cytoskeleton is a dynamic structure in eukaryotic cells that provides structural support and acts as a transport mechanism for molecules inside the cell. It has three main components: microtubules, actin filaments, and intermediate filaments. In this work, we specifically focus on microtubules and actin filaments.
Microtubules (pictured in the leftmost structure of Figure 1), spiral-cylindrical structures made of tubulin dimers, play a role in cell communication and mitosis. They are a dynamic part of the cytoskeleton, being able to quickly grow and shrink via polymerization or depolymerization, respectively. Microtubules also make up the internal structure of external appendages such as flagella and cilia, which are important for locomotion and movement. Intra-cell communication is also facilitated by microtubules, as well as the whole cytoskeleton in general. Microtubules are a primary constituent of axons in the brain. They have been shown to play an important role in transport along axonal processes in neurons [24], so disruption of microtubule transport processes in neurons has been linked to several neurodegenerative diseases.
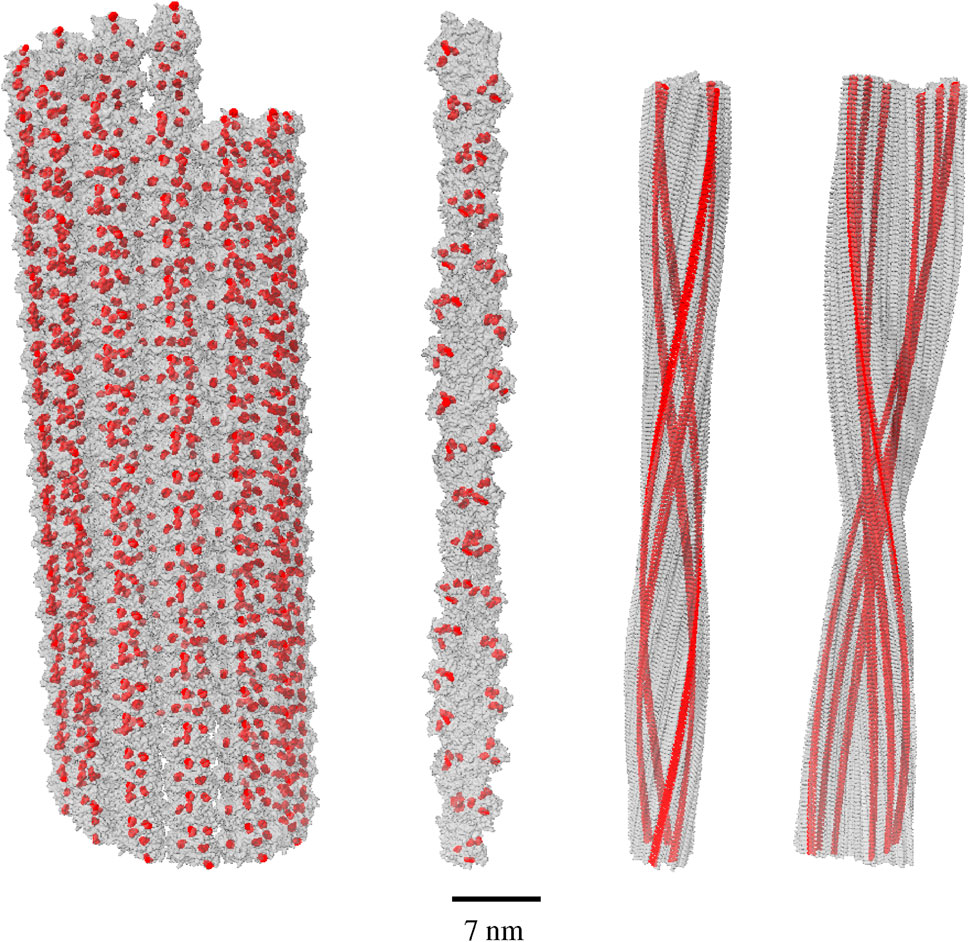
Figure 1. Tryptophan (Trp) network geometries in model biological structures. From left to right, the structures are the following: an 80-nm microtubule (built from tubulin dimer PDB entry 1JFF), a 90-nm actin filament (built from actin subunit PDB entry 6BNO), an 86.4-nm human amyloid fibril (built from amyloid subunit PDB entry 6MST), and an 86.4-nm mouse amyloid fibril (built from amyloid subunit PDB entry 6DSO). The Trp molecules are colored in red and have been enlarged for ease of viewing, within each gray protein lattice. Scale bar is valid for the entire figure.
Actin filaments (pictured in the second from left structure in Figure 1) are strandlike structures that play an important role in the cytoskeleton. Within the context of the cytoskeleton, they are known as microfilaments, reflecting their small diameter generally less than one-third that of microtubules (see Figure 1 for comparison). Actin filaments can bundle together to form hexagonal arrangements [25], which we also analyze in this work. They provide contractile and protrusive forces to stabilize the cytoskeleton and assist with the mobility of the cell. Like microtubules, they assist in transport from outside the cell to the inside. Actin also plays a role in the contractile apparatus of muscle cells, in the form of so-called thin filaments, and helps to maintain the structure of dendritic spines, tiny protrusions from dendrites that form functional contacts with neighboring axons of other neurons in the brain. Dendritic spines play a significant role in plasticity and processing of memory. Therefore, the role of actin has been investigated in synaptic failure in neurodegenerative diseases such as Alzheimer’s [26].
Amyloid fibrils (pictured in the rightmost and second from right structures of Figure 1) are helical aggregates of amyloid proteins. Amyloids, the building blocks of amyloid fibrils, are a class of self-assembling proteins that fold in a
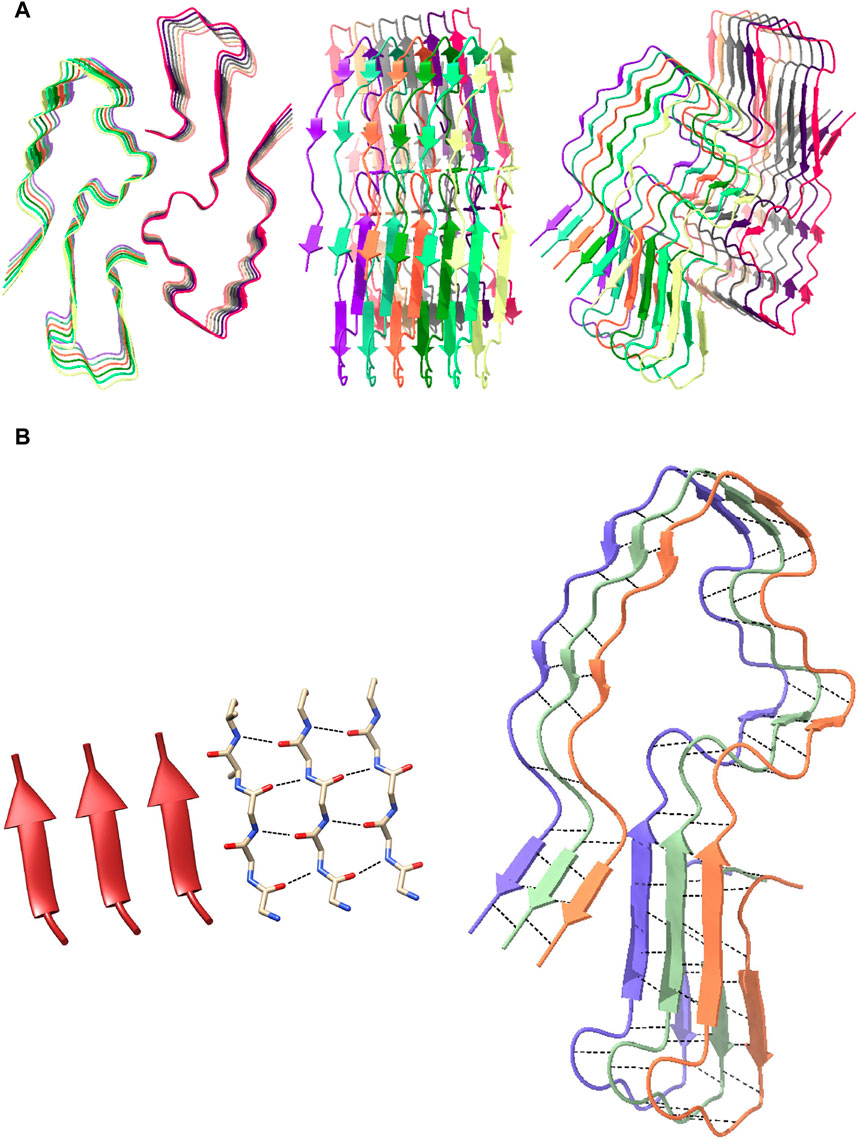
Figure 2. Structure of a single human amyloid subunit and its distinctive parallel β-sheet structure. (A) The structure of a human amyloid subunit (PDB entry 6MST) in cartoon/ribbon from a top-down view (left), side-on view (middle), and angled view (right). (B) Visual of parallel β-sheet structure of the human amyloid subunit. The left image is the structure of a parallel beta sheet, both in ribbon form and molecular form, with black dashed lines indicating hydrogen bonds. The right image is three chains from a human amyloid subunit, again with the hydrogen bonds shown with black dashed lines, showing the similarity with the left image.
Another indicator of Alzheimer’s disease is the formation of neurofibrillary tangles, abnormal aggregates of the tau protein. The tau protein aids in structural support of microtubules in the brain [37], which start to disintegrate in Alzheimer’s disease. The tau proteins undergo hyperphosphorylation and thus dissociate from microtubules, which causes tau to transition from an unfolded state to a folded state capable of aggregating into threadlike structures inside neurons, called tangles [38]. Tangles block transport and inhibit communication between neurons. The population density of tangles is strongly linked to the severity of cognitive decline in Alzheimer’s disease [38, 39].
First, we present a preliminary analysis of some toy models, in order to gain physical intuition and insight on how transition dipole vector orientations affect the photophysical properties of prototypical biological structures with cylindrical symmetry. We consider two idealized architectures of molecules based on the ones studied in [40]. Each molecule has the photophysical parameters of tryptophan (Trp; excitation wavelength of 280 nm and decay rate of
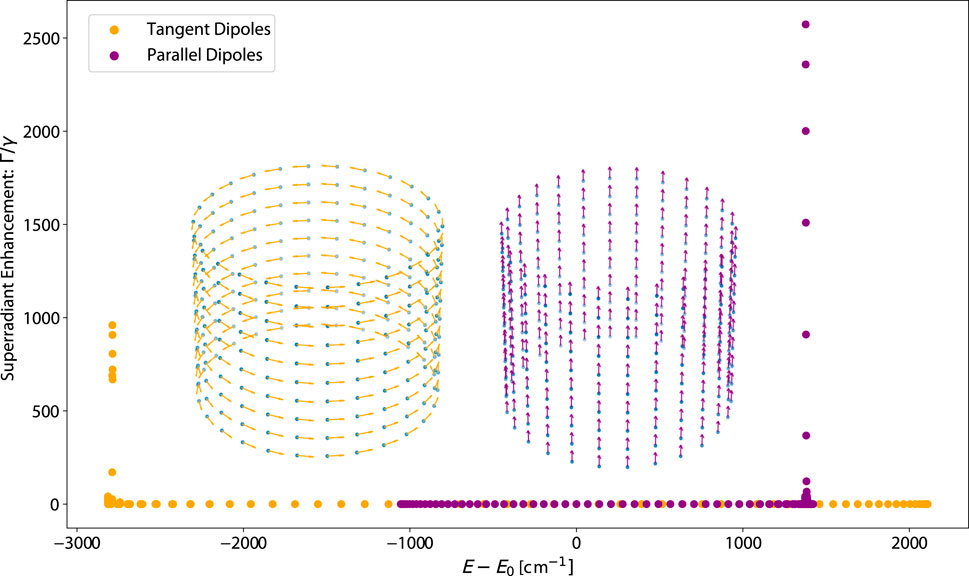
Figure 3. Plot of the eigenvalue spectrum (superradiant enhancement rate vs. energy) of idealized ring structures, with the transition dipole vectors of each cylinder plotted inset in their corresponding colors. Each transition dipole has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of
Figure 3 shows the eigenspectrum of the TD and PD arrangements of an idealized ring structure with
The spectrum having this unique property is significant because it influences the quantum yield (QY), defined as the ratio of the number of photons emitted to the number of photons absorbed, as well as its thermal average (
To show how the Trp packing density affects the superradiance and thermally averaged quantum yield, we present the eigenspectra and quantum yields of our toy models, varying the number of TLSs per ring or the number of rings per unit length. These results are shown in Figure 4, 5, respectively. Figure 4A shows the eigenvalue spectrum of both PD and TD structures, with increasing number of TLSs per ring. If the energy shifts of the most superradiant states are positive, the shifts become more positive, and if the energy shifts of the most superradiant states are negative, they become more negative. In both the PD and TD structures, the maximum superradiance increases with the number of TLSs. However, the QY as displayed in Figure 4B decreases for the PD structure and increases for the TD structure. We can understand this by looking at Figure 4C, which plots the numerator
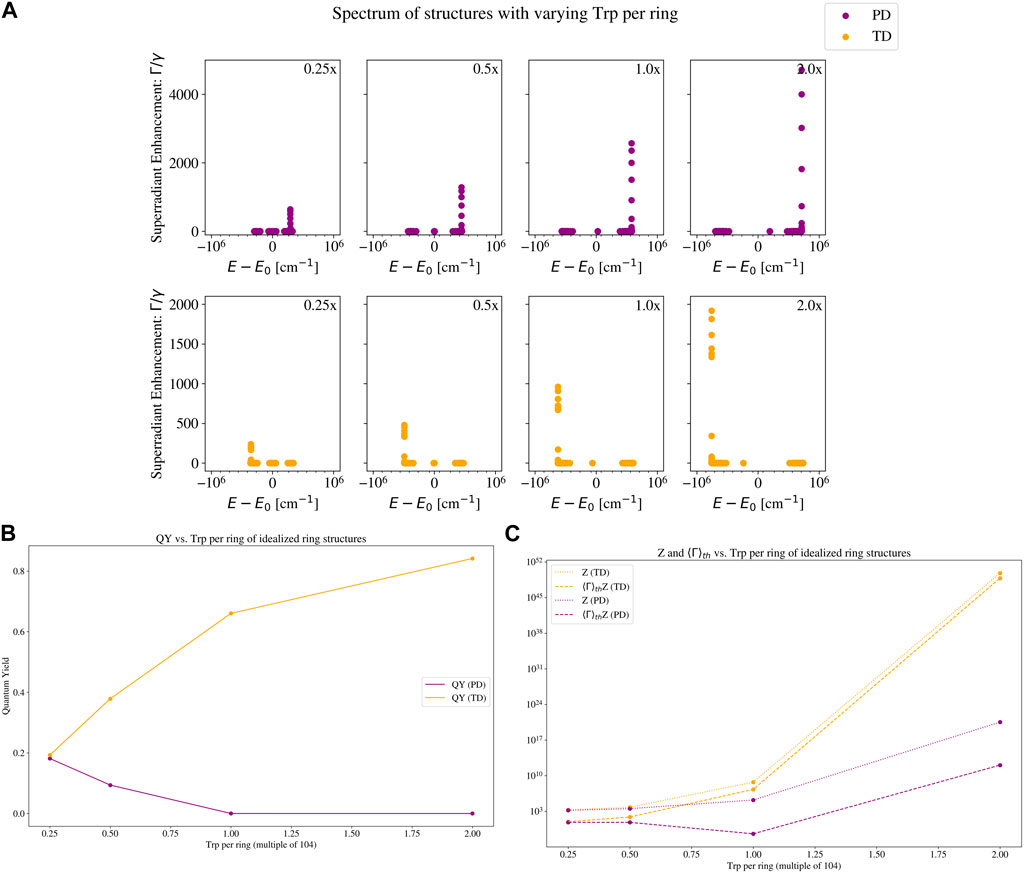
Figure 4. Eigenvalue spectrum and quantum yield plots of a set of idealized ring structures with varying number of two-level systems (TLSs) per ring. The two structures are the ones with a parallel-dipole (PD; purple color) arrangement, and a tangent-dipole (TD; orange color) arrangement. See Section 2.3 for a description of these models, and the insets in Figure 3 for a visual picture of each. Each TLS has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of
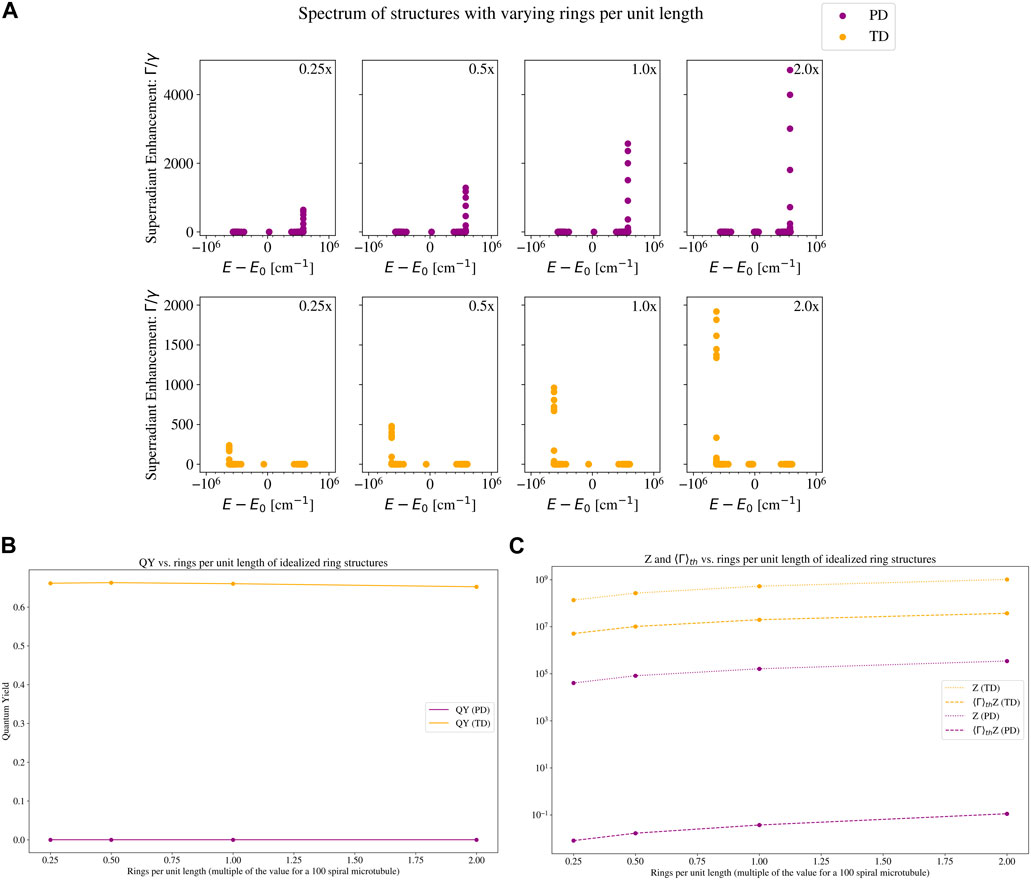
Figure 5. Eigenvalue spectrum and quantum yield plots of a set of idealized ring structures with varying number of rings per unit length. The two structures are the ones with a parallel-dipole (PD; purple color) arrangement, and a tangent-dipole (TD; orange color) arrangement. See Section 2.3 for a description of these models, and the insets in Figure 3 for a visual picture of each. Each TLS has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of
Figure 5 shows the eigenspectra and quantum yields of our toy models, varying the number of rings per unit length. In Figure 5A, we can see that the maximum superradiance increases by an order of magnitude, but the energy shift of the maximally superradiant states remains almost constant. The QY on the other hand, displayed in Figure 5B, is almost unchanged for the PD structure, and slightly decreases for the TD structure. At first glance, this may seem surprising based on the spectra, especially for the TD case. To understand this, compare the leftmost (0.25x the microtubule value) and rightmost (2.0x the microtubule value) subplots of the TD structure in Figure 5A. There are only 7 states in the rightmost subplot that have a higher superradiance than the maximum superradiance in the leftmost subplot. In the thermal average (which is relevant for the QY plotted in Figure 5B), these 7 states are negligible compared to the partition function, which normalizes the thermal average (see Eq. 16). The partition function of the 2.0x TD structure is an order of magnitude larger than the partition function of the 0.25x TD structure. Since the 0.25x TD structure has fewer TLSs (and a smaller partition function), each state has more weight in the thermal average. Thus, the states with the highest superradiance in the 0.25x TD structure enhance the QY more than the states with highest superradiance in the 2.0x TD structure. This is why the QY of the 0.25x TD structure is slightly higher than the QY of the 2.0x TD structure.
We can see how the partition function affects the thermally averaged decay rate (and in turn, the QY) in Figure 5C. The bright superradiant states at the low-energy portion of the spectrum increase the numerator of Eq. 15, but the denominator (partition function) increases more due to the additional number of TLSs, and the net effect is a slight QY decrease. This further demonstrates that neither a high maximum collective decay rate nor a high packing density is sufficient on its own to elicit a high QY.
This analysis is different from the analysis done in [40] in significant ways. Our analysis uses the parameters for the Trp chromophore, which has an absorption peak at
We present the eigensolutions of the effective Hamiltonian given in Eq. 1 for microtubules, actin filaments, and amyloid fibrils of varying lengths. For details on the geometry of these structures, see the Methods in Section 6. For a visual image, see Figure 1. For the transition dipole orientations, see Figure 6. We also consider the thermal average of the quantum yield (see Section 6: Methods for further details), its dependence on system size, and its robustness to static disorder. The effective Hamiltonian is non-Hermitian, and can be written as the sum of a Hermitian part and a non-Hermitian part
where
where

Figure 6. Transition dipole vector geometries of tryptophan (Trp) in the realistic biological structures considered in this paper. The blue dots represent the Trp molecules. The relative size of structures with respect to one another is not to scale. For illustrative purposes, the size of vectors has been enlarged for viewing. (A) Angled longitudinal view of microtubule (built from tubulin dimer PDB entry 1JFF; length 45 nm, radius 22.4 nm). (B) Cross-sectional view of the microtubule. (C) Angled longitudinal view of actin filament (built from actin subunit PDB entry 6BNO; length 112.5 nm, radius ∼6 nm). (D) Cross-sectional view of the actin filament. (E) Angled longitudinal view of human amyloid fibril (built from amyloid subunit PDB entry 6MST; length 20.2 nm, radius ∼4.5 nm). (F) Cross-sectional view of human amyloid fibril. (G) Angled longitudinal view of mouse amyloid fibril (built from amyloid subunit PDB entry 6DSO; length 20.2 nm, radius ∼5 nm). (H) Cross-sectional view of mouse amyloid fibril.
We study single microtubules of varying length constructed as spiral-cylindrical collectives of tubulin dimers (PDB entry 1JFF). One tubulin dimer contains 8 tryptophan (Trp) molecules, and one spiral of the microtubule contains 13 tubulin dimers (so one spiral contains
Shown in Figure 7 is the thermal average of the quantum yield (QY) as a function of the length of the microtubule, reported as the number of Trp molecules. Each color represents a differing static disorder strength, with red being the smallest
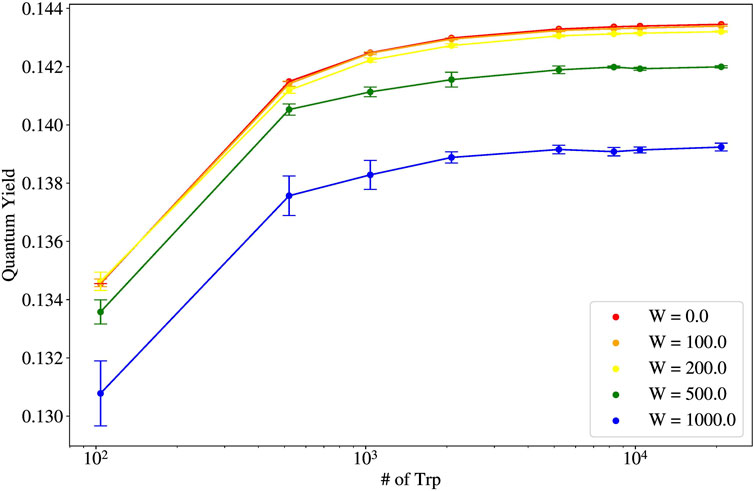
Figure 7. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for single microtubules (pictured in the leftmost structure in Figure 1).
The robustness of the quantum yield for microtubules (and their bundled architectures) is explainable from the shape of the spectrum of eigenvalues of the non-Hermitian Hamiltonian Eq. 1. The spectrum of single microtubules has been studied in [2]. Specifically, in Figure 2C of [2], the spectrum of a 100-spiral microtubule (10,400 Trp molecules) is shown. It can be seen that the most superradiant states lie in the low-energy portion of the spectrum. Examining Eq. 15, if a large
In the case of microtubules, the dependence of the thermal average of the quantum yield on system size also highlights that collective light-matter interactions can enhance quantum effects beyond the length scales normally associated with quantum behavior. Let us define
We also study the effects of mechanical/vibrational degrees of freedom on the superradiant states of microtubules (see Supplementary Figures S1, S2 in the Supplementary Material), within the Born-Oppenheimer approximation. As seen in these figures, the superradiance is dynamically altered by nuclear geometry and changes when microtubules are mechanically deformed in different ways. Purely longitudinal modes (only deforming along the microtubule main axis) have higher superradiance than modes with purely twisting motions around the microtubule main axis, which have higher superradiance than bending motions off the microtubule main axis. Mode 15 has purely longitudinal stretching/contracting motions, which still preserve a
The vibrational modes studied have a mechanical frequency in the low gigahertz range [45], corresponding to a timescale on the order of nanoseconds. As a microtubule oscillates mechanically, any superradiant states supported by the given atomic/nuclear configuration can vary from their enhancement factors reported in both the left and right columns of Supplementary Figures S1, S2, to enhancement factors one or two orders of magnitude higher near the amplitude node of each vibration (see middle panels), where the structure is closest to a “straight” longitudinal configuration. From Table 1, we can see that the lifetimes for the superradiant states of microtubules and of many other structures are on the order of picoseconds. Thus, the photophysical effect of superradiance is operating on a timescale at least three orders of magnitude faster than the mechanical motion of the microtubule, which can be considered more or less static in this ultrafast regime. However, even though our predictions have all been calculated within the Born-Oppenheimer approximation, it is clear from Tables 1, 2 that the most subradiant states—and even a few of the superradiant states—supported by these neuroprotein architectures are extremely long-lived, suggesting potential influence and interaction across electronic and nuclear degrees of freedom in these structures.
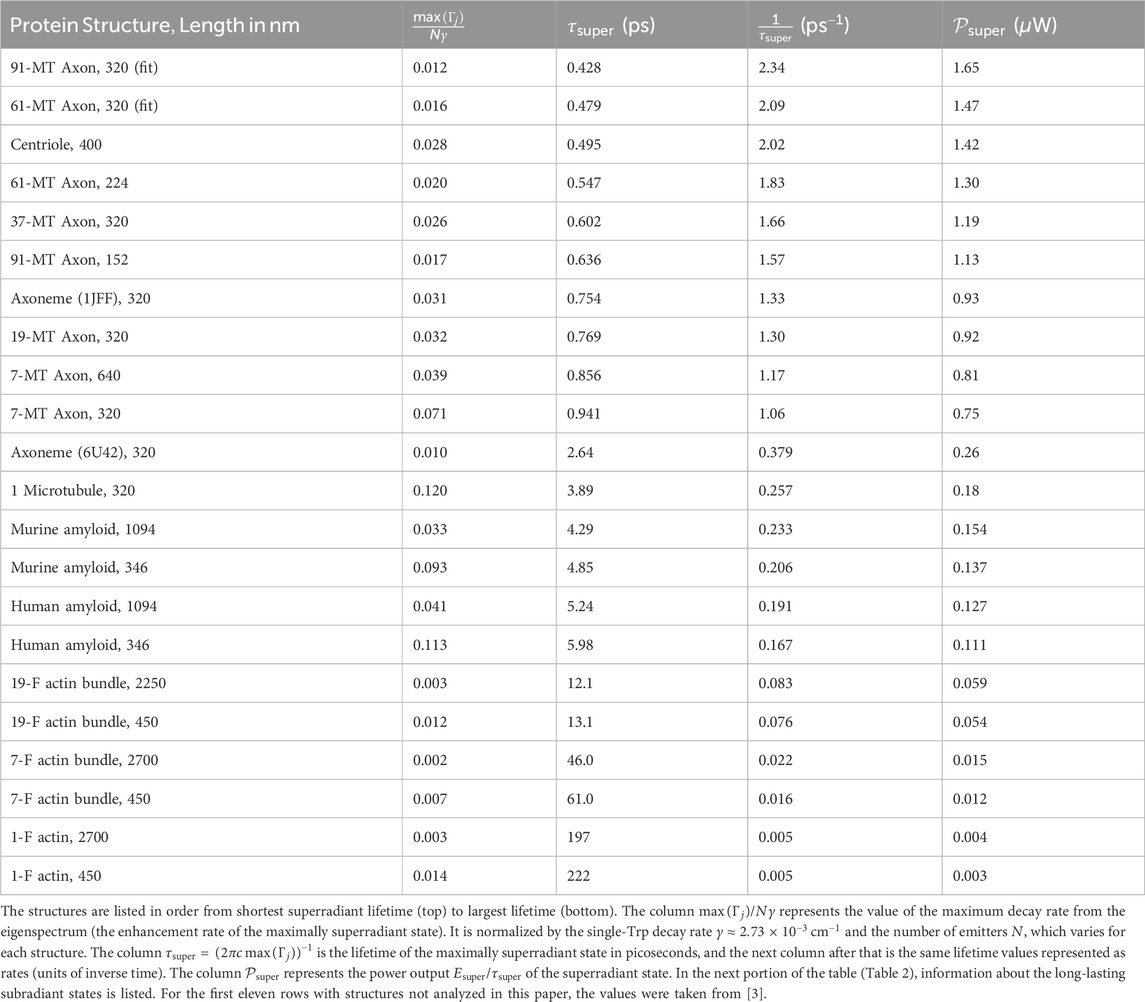
Table 1. Values for the maximum superradiant decay rates calculated by diagonalizing the non-Hermitian Hamiltonian in Eq. 1 for the tryptophan (Trp) network in each protein structure.
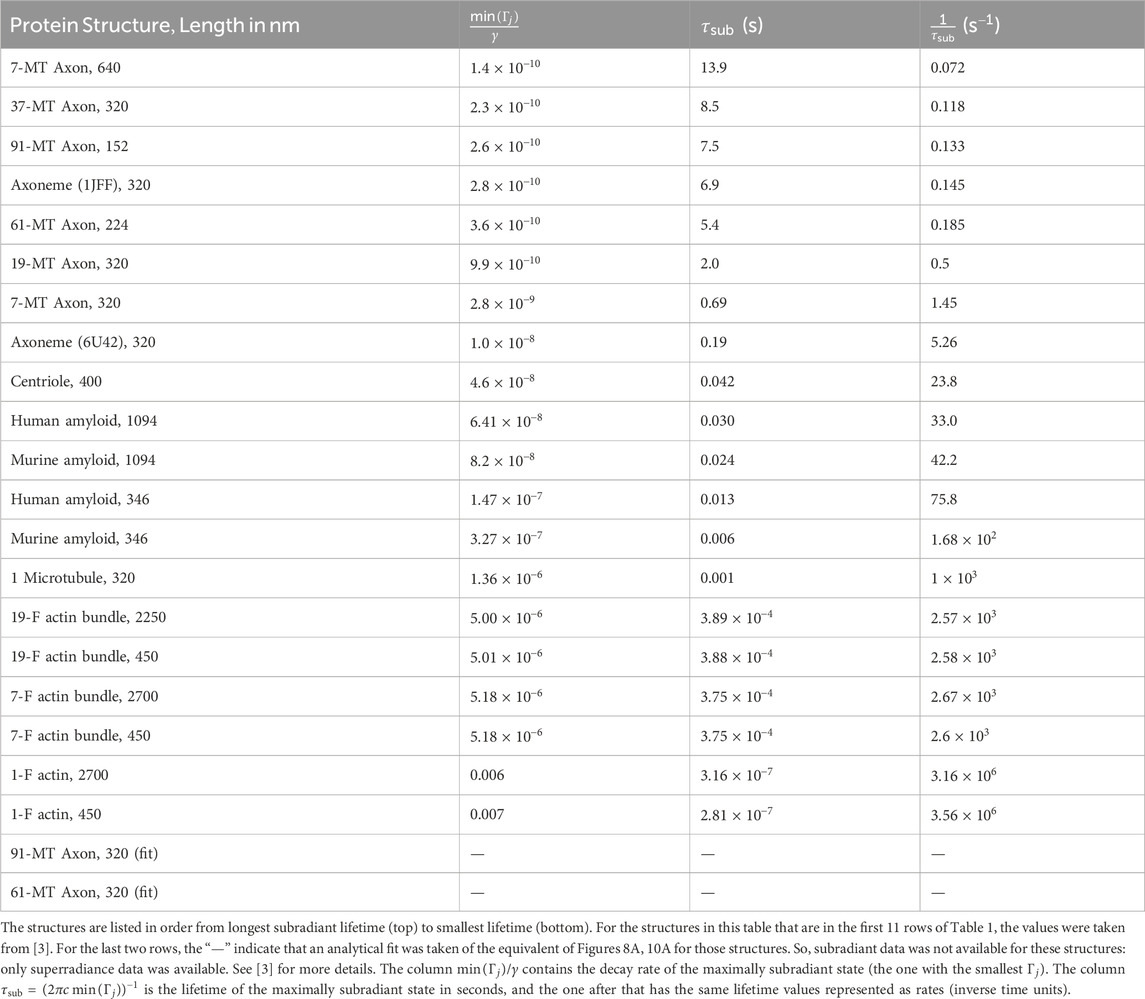
Table 2. Values for the minimum subradiant decay rates calculated by diagonalizing the non-Hermitian Hamiltonian in Eq. 1 for the tryptophan (Trp) network in each protein structure.
In many of the middle columns of Supplementary Figures S1, S2, we can see high exciton probabilities near the ends of the structures, despite the mode being symmetric. This could be a biological manifestation of topological edge states, which have been previously studied in paradigmatic non-Hermitian systems [46, 48].
We study two different types of actin collectives: actin filaments and actin bundles. An actin filament is made from a concatenation of bare actin subunits (PDB entry 6BNO), each of which is a homo-octamer (protein consisting of eight identical chains) about 22.5 nm long. We then study two sizes of actin bundles corresponding to the smallest hexagonal configurations: 7-filament bundles, and 19-filament bundles (a top-down view of both of these are pictured in the inset of Figure 8A). One bare actin subunit contains 32 Trp molecules. So, for example, a 19-filament bundle comprised of single-subunit actin filaments contains
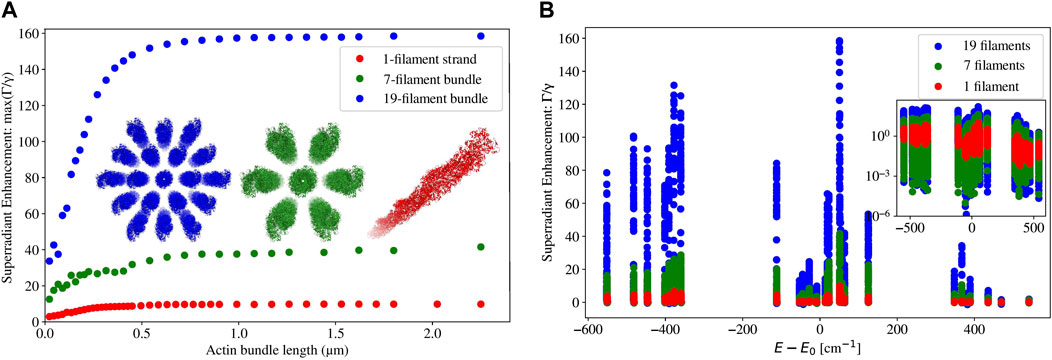
Figure 8. (A) Plot of the maximum superradiance
Figure 8A shows the enhancement rate of the maximally superradiant state against the length of an actin filament or of a bundle of actin filaments. Similarly to the case of microtubules, the maximum superradiant enhancement rate increases with length at first, and then eventually saturates when the length approaches or exceeds the excitation wavelength. This feature is most pronounced in the 19-filament actin bundles. In the single filament and the 7-filament bundle, saturation of the maximum enhancement rate starts to occur when the length of the actin structure is around the length scale of excitation (280 nm). However, in the 19-filament bundle, saturation occurs at about twice that length. This is an interesting difference between microtubules/microtubule bundles [2, 3], which saturate in their maximum superradiant enhancement (in the single-photon limit) at about three or more times the excitation wavelength, and actin filaments/bundles.
In Figure 8B, we can see that the maximally superradiant states of 2.25
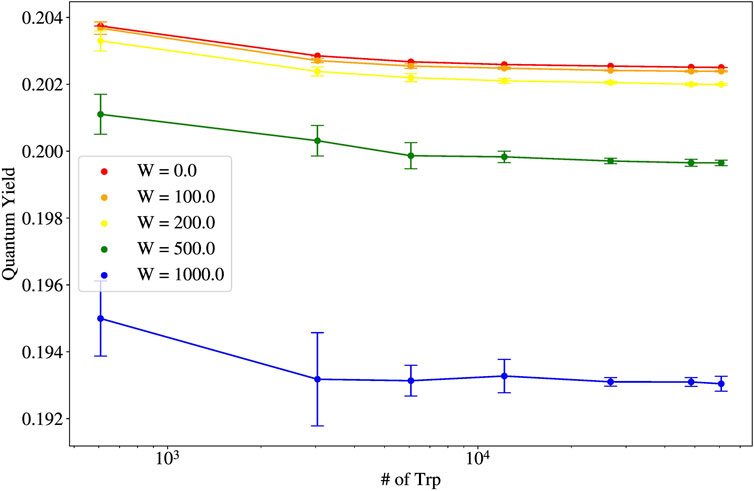
Figure 9. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for 19-filament bundles of actin (one actin filament is pictured in the second from the left structure in Figure 1, and a 19-filament bundle is pictured inset in blue in Figure 8A).
Comparing Figure 8 to the analogous spectrum for microtubules (see Figure 2 of [2]), and by examining the entries of Table 1, we see that microtubules have brighter superradiant states than those for all actin structures. However, 19-filament actin bundles still have higher predicted QY values (see Figure 9) than those for microtubules (see Figure 7). We can understand this by revisiting Eq. 15. Each decay rate
These results show that although the absolute values of the QYs for 19-filament actin bundles are larger than that of single microtubules, these QYs for actin bundles decrease with system size after even a single twist (608 Trp). However, 19-filament actin bundles are comparable to microtubules in their QY robustness to static disorder. Although such actin bundles do exhibit observable and important superradiant effects via the QY, our results imply that their role in cytoskeletal dynamics may be restricted, more so than microtubules, to their conventional mechanical roles rather than having significant photophysical enhancements at long length scales. Experiments in vitro to detect superradiant QY enhancements (from Trp in solution) in actin bundles would be warranted, as has been demonstrated with microtubules [3].
Figure 10 presents the same data as in Figure 8, but for single amyloid fibrils in human and in mouse. We will refer to the length of an amyloid fibril by its absolute length (in
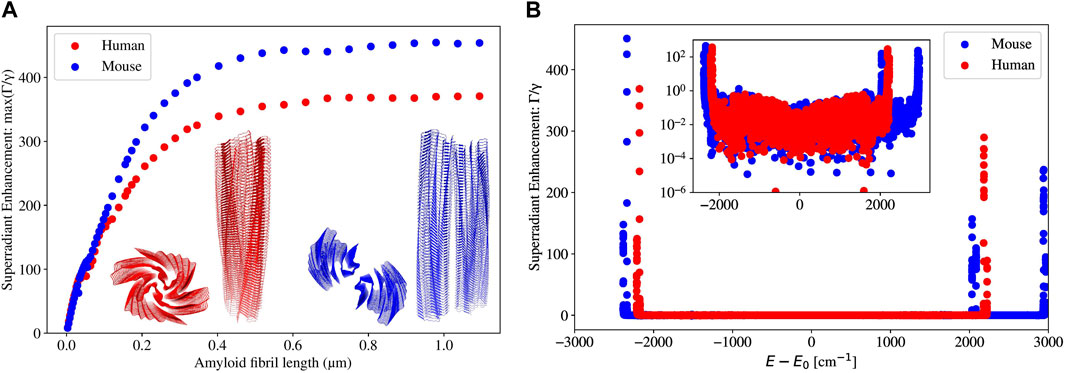
Figure 10. (A) Plot of the maximum superradiance
In Figure 10A, it can be seen that for both human and mouse amyloid fibrils, the maximum superradiant enhancement
In Figure 10B, we can see that superradiant states emerge at very specific bands in both the low- and high-energy portions of the spectrum, and at all other energies, the superradiant enhancement rate is very close to 0. For the human amyloid fibril (built from PDB file 6MST), the superradiant states are only present near the smallest and largest energies, and every other state is subradiant (
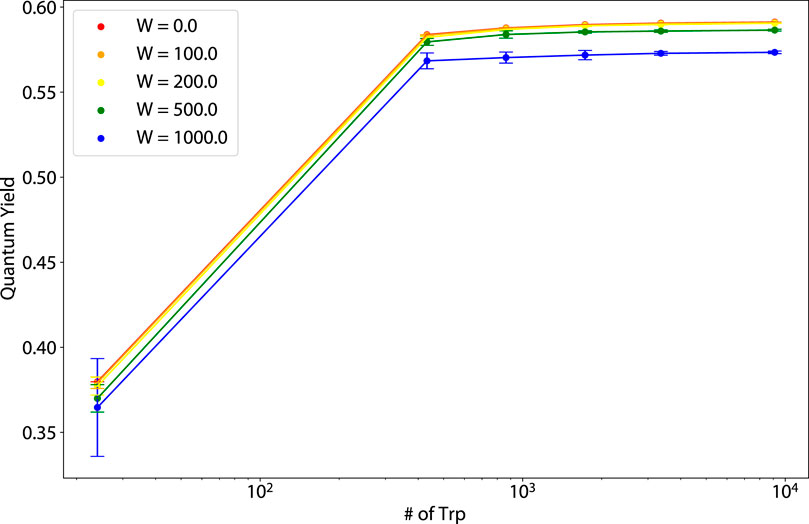
Figure 11. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for human amyloid fibrils (pictured in the second from the right structure of Figure 1).
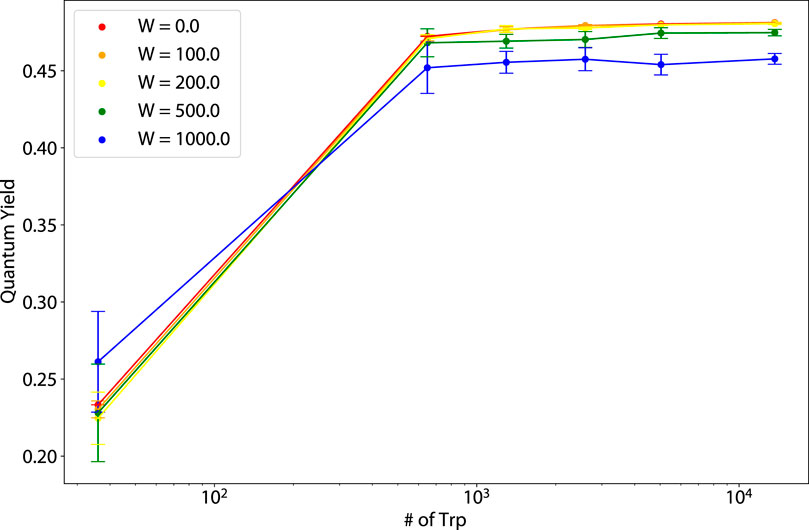
Figure 12. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for murine amyloid fibrils (pictured in the rightmost structure of Figure 1).
For the dependence of the amyloid fibril QY on static disorder, for 864 nm structures,
It should be noted that for both amyloid fibrils, some inter-Trp distances are as small as
Due to the close Trp-Trp spacings in amyloid fibrils, we would expect the Trp-Trp couplings to be very high, and indeed they are. The average Trp-Trp coupling strength for a 100-subunit human (mouse) amyloid fibril, which has a length of 288 nm, is
We create plots of the energy gap
where
In Figure 13,
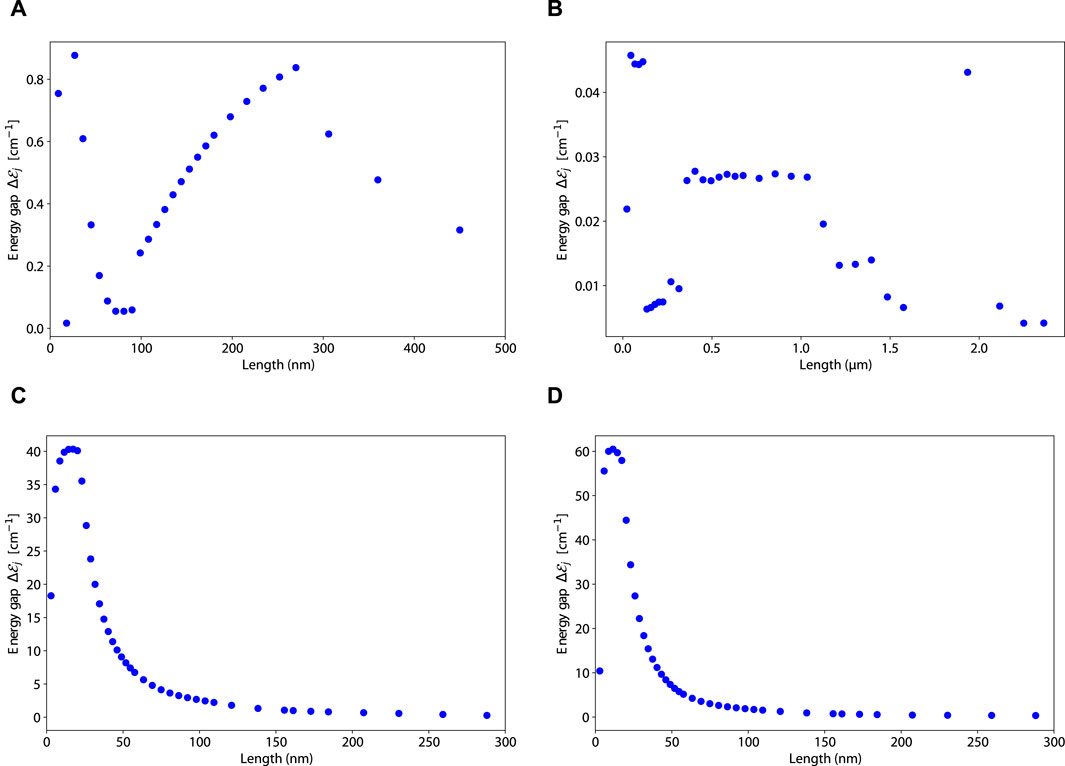
Figure 13. Plots of the energy gap
The energy gap behavior of 19-filament actin bundles (panel (B) from Figure 13) is vastly different from all the other structures. It has a sporadic behavior that does not trend upward with increasing system size. The maximum energy gap for 19-filament actin bundles is at
We also implement static disorder in the single-Trp decay rate
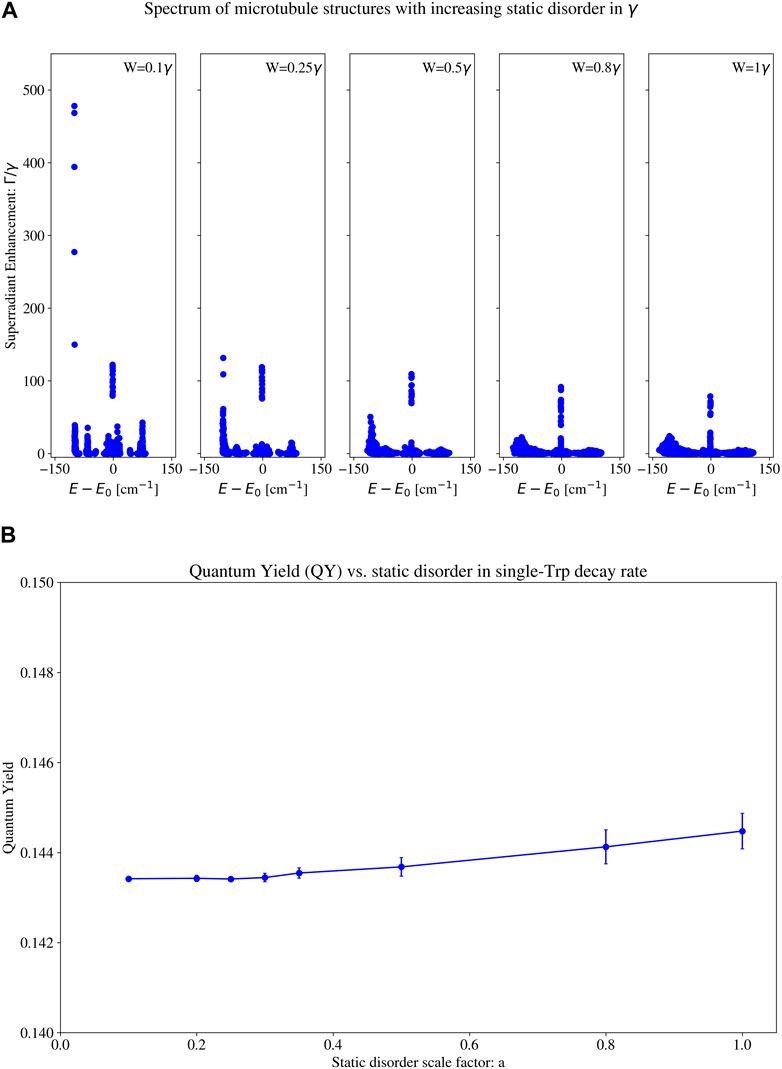
Figure 14. (A) Eigenspectra and (B) thermally averaged quantum yield (QY) with increasing static disorder in the single-tryptophan (Trp) decay rate for a 100 spiral microtubule (pictured in the leftmost structure in Figure 1). Each subplot in (A) contains the eigenvalues of the Hamiltonian for a different static disorder strength. The static disorder in the single-Trp decay rate is implemented as follows (see Section 6.3.2 (specifically, Eqs 18, 19 and surrounding text) for a more detailed description): each on-site
We discuss here the implications of our findings of high quantum yield and robustness for microtubules, actin bundles, and amyloid fibrils. In Alzheimer’s disease and related dementias, the prevailing theory is that amyloid plaque formation is a direct cause of the onset of the disease [39]. Based on our results we propose an alternative hypothesis to these previous observations on amyloid. By definition, if the QY of a structure was 1, then every photon that it absorbed would be re-emitted into the environment. We have predicted here that the QY of even small human amyloid fibrils
It is important to emphasize that the QY increases we predict here do not have any classical interpretation. If an analogous classical system, such as a classical antenna, could be used to describe these biosystems, it would not include the transition dipole moment of tryptophan (Trp), which is a genuinely quantum (electronic) transition. Even if such a classical collective effect were operative, large numbers of photons (e.g., in a Glauber coherent state) constituting a semi-classical light source would be required to excite such an antenna. In the single-photon regime, only a quantum mechanical interpretation is possible.
Tables 1, 2 show the decay rate values of the most superradiant and most subradiant states, along with other key observables associated with these diverse neuroprotein architectures. One trend we can see in Table 1—and according to which it is organized—is that the maximum superradiance of the axon bundles is the highest
After the microtubule-based structures, amyloid fibrils in both humans and mice have the next largest superradiant power outputs
We also see in Tables 1, 2 the general trend of highly subradiant long-lived states correlated with highly superradiant short-lived states. (
The mechanism that makes superradiance possible is the delocalization of the excitation across many chromophores. The delocalization of a superradiant state in microtubules has been shown and visualized in Figure 4 of Ref. [2]. It has also been shown that in supramolecular dye [60] and photosynthetic nanotubes [13], superradiant states are delocalized across many chromophores. This delocalization is a clear sign of quantum coherence in the site basis. Although the study of a specific coherence measure is beyond the scope of this work, we do study the energy gap in the complex plane (Figure 13), which has been associated with cooperative robustness and supertransfer processes [2, 39], indicating quantum coherence. We have also studied coherence indirectly through cooperative robustness in Figure 5 of Ref. [3]. A detailed study of the off-diagonal elements of the density matrix and their dynamics is planned for future work.
An upper bound for the scaling of the decay rate of the maximally superradiant state in the single-excitation limit is
An important and subtle point to consider is the individual addressability of states (as either superradiant or subradiant states), versus the thermal average of the ensemble. In physical environments which are in thermal equilibrium, the thermal average should be used. In these cases, the behavior of the superradiant states dominates the thermal average, while the effect of subradiant states is negligible in the Gibbs ensemble. However, in environments which are not in thermal equilibrium, such as the interior of microtubules, the thermal average does not strictly apply, so subradiant states which are weighted negligibly in the Gibbs ensemble may take on a more pronounced importance.
Significantly, the structures we study in this work contain other aromatic amino acids, such as tyrosine and cysteine, but their transition dipole moments are much smaller than that of Trp at its peak excitation wavelength. Incorporating other amino acids into the network at close range to Trp would in principle change the non-radiative decay rates, especially as ultrafast electron-transfer effects emerge on the sub-picosecond timescale, competing with superradiance and potentially degrading the quantum yield. However, it is known that photoexcited tyrosine resonantly transfers its excitation energy to Trp on ultrafast timescales [61], enhancing the transition dipole strength of Trp rather than quenching it, and thus would increase the superradiant effect.2
It is of particular note that electron transfers from photoexcited Trp to peptide carbonyl groups occur on the 100 ps timescale, but electron transfers from photoexcited Trp to sulfur-containing residues within van der Waals (vdW) contact (∼5–6 Å) occur on the 10 ps timescale [55]. In a tubulin dimer, only
In addition to other aromatic amino acids, there are other objects that may enhance superradiant emission even further. For example, in the
Due to the incredibly high QY of amyloid fibrils and its potential for photoprotection, rather than being a cause of pathological conditions, amyloid fibrils could be a response to them, and to the highly oxidative environments that characterize them. Therapies that target amyloid in the brain for elimination could therefore exacerbate such diseases rather than ameliorating them.
There are at least 37 known proteins that form pathological amyloids [35]. We have found that the amyloids 6MST and 6DSO, which are associated with systemic AA amyloiosis [68], exhibit extremely robust QY. Since amyloids are a geometric class of protein architectures characterized by helical superstructures made of
Furthermore, the formation of structures called cofilin-actin rods from pools of actin and the cofilin protein have also been studied [69–71], with recent suggestions of potentially quantum behavior being disrupted in Alzheimer’s pathogenesis [71]. Cofilin-actin rods do have a helical structure: every subunit that is added to the rod comes with an approximate
As the microtubule results in the Supplementary Material and in Section 3.1 attest, the morphology and mechanical deformations of protein structures are crucial to understanding the modulation of superradiant effects. For example, amyloid fibrils are known to aggregate into macroscopic structures called amyloid plaques, together with glial and neuritic debris [72]. They are found in the grey matter of the brain in the areas associated with memory and cognition. Amyloid plaques can form spherically symmetric aggregates of amyloid fibrils with very dense cores [73]. Plaques have also been observed to form symmetric superarchitectures such as bundles, as well as mesh-like and star-like geometries [74]. Given these observations, amyloid plaques may exhibit even higher, more robust superradiance and quantum yield values than those of single fibrils, which would strengthen the argument of amyloid’s photoprotective role and of the mitigating effect of plaque formation in neurodegenerative pathology.
Our predictions of robust, observable increases in the QY for Trp networks in large protein polymeric architectures has implications for many other diseases outside the neurodegenerative context. For example, sickle-cell anemia results from a
Our results pose opportunities for a paradigm shift in the theory of neuronal information processing and signaling. The role of microtubules in information processing in the brain has been studied extensively [24, 76–79]. Also, classical energy scalings cannot account for the sub-neuronal information processing capacity of the brain [80], given its extremely low input power of around 20 W. There must be another physical mechanism that enables the human brain to achieve the computational efficiency that it does, at orders of magnitude lower power consumptions than high-performance hardware systems. A tantalizing possibility is that extended protein architectures, such as those described here and elsewhere [2, 3], including axons in the brain, may form a highly interconnected, ultrafast quantum-optical network that gives rise to incredibly efficient transfer and processing of information. This mechanism would be much faster than chemical Hodgkin-Huxley-type transport based on neuronal sodium-potassium gradients firing at the millisecond timescale, which is currently used as a standard paradigm in neuroscience.
We analyze the interaction of the electromagnetic field with networks of tryptophan (Trp) chromophores. Geometrical information on these networks and the orientations of the Trp transition dipoles are extracted from realistic simulations of three types of neuroprotein architectural elements: microtubules, actin filaments/bundles, and amyloid fibrils. The Trp chromophores are modeled as two-level systems and exhibit superradiant behavior as a collective when coherently superposed in the single-excitation limit. We see this by diagonalizing the non-Hermitian Hamiltonian used to describe the collective light-matter interaction of such a weakly photoexcited system. All three structures were found to exhibit bright superradiant states due to symmetry and long-range couplings, which support robustness of the quantum yield as a figure of merit with increasing static disorder even up to five times room-temperature energy. In the case of microtubules and amyloid fibrils, the brightest superradiant states are clustered near the lowest-energy portion of their spectra, and these photophysical properties result in a large quantum yield that counterintuitively increases with system size and has been experimentally confirmed for microtubules [3].
Our results display the observable and important consequences that quantum coherent effects have on neuroprotein architectures. These analyses could strengthen our understanding of the etiology of neurodegenerative and other complex diseases, which are frequently characterized by anomalous protein polymers. Furthermore, our investigations of superradiance and subradiance in these neuroproteins are revealing an ultrafast mechanism that our brains may use to process information, which is paired with an extremely long-lived mechanism for coordinating biological function. This work contributes significantly to our understanding of how quantum biology can speed up, enhance, and optimize behavior in the “wetware” environments of living systems. Acknowledging the wide body of research that has been conducted on ultraweak and metabolic photon emissions in the cell, we have incorporated the interaction of neuroprotein Trp lattices with the electromagnetic field via the equations of quantum optics, giving us a totally different lens with which to view biology. Such a paradigm shift can greatly enhance our understanding of nature, to visualize biological architectures as chromophore lattices synchronized by long-range interactions, and imbued with unique and specific photophysical properties that are enhanced by collective light-matter interactions governed by the equations of quantum optics. Such a shift reflects a return to understanding, in the (paraphrased) words of Richard Feynman and with the ancients, how external light from the fiery sun causes trees and plants to grow from the carboniferous air; and in parallel symbiosis how oxygen-metabolizing organisms may have evolved their protein architectures to exploit “internal” photonic emissions for information processing and to mitigate potentially damaging wavelengths in the cell.
Future work will include performing experiments in order to verify the quantum yield predictions that we have made here. Analogous to prior work [3], where the increased quantum yield in microtubules from tubulin dimers in solution was unambiguously associated with the increased radiative rate due to superradiance, we now have a clear path and approach to experimental validation of collective quantum optical behavior in a wide class of protein polymeric aggregates in solution. We hope that this work will stimulate further experimental efforts in this regard.
In this work we model tryptophan (Trp), a strongly fluorescent amino acid in the ultraviolet (UV) band, as a two-level system [5] with transition energy
where.
where
The dynamics of the system is governed by the Schrödinger equation with the non-Hermitian Hamiltonian
This means that the evolution of the state vector is not unitary, representing a leakage of probability into the envirnonment. Utilizing a non-Hermitian Hamiltonian with the Schrödinger equation is completely equivalent to using a Lindblad master-equation approach, in which the environment is modeled by a set of Lindblad operators (not necessarily Hermitian). This means that all the same approximations that go into the Lindblad equation (Born-Markov approximation, rotating wave approximation, weak interaction with environment, etc.) apply to our model. The non-Hermiticity of the Hamiltonian also means that there are two sets of eigenvectors: the right and left eigenvectors, which are given by
Since the Hamiltonian is symmetric, the left and right eigenvectors are transposes of each other.
The quantum yield (QY) is a dimensionless number from 0 to 1 that is defined to be the ratio of the number of photons emitted to the number of photons absorbed. Equivalently, it can be written as
where
Since biological structures exist in a warm and wet environment, we take the thermal average of our quantities. Firstly, the partition function
where
This allows us to calculate the thermal average of the QY
We take
In addition to taking the thermal average of the QY, we also consider the effects of random fluctuations in the site energies, i.e., static disorder, on our model Hamiltonian. We do this by modifying the
where
We then diagonalize the Hamiltonian with the new
Note that we do not study the dynamics of our systems, and thus do not consider dynamical instabilities in this work. However, the structures we study are stable for extraordinarily long times (up to years) in mammalian neurons and eukaryotic cells that are not undergoing mitosis. We also obtain all of our results in the steady-state (thermal equilibrium), so dynamical instabilities are not as significant as the static disorder that we take into account.
We also implement static disorder in the single-Trp decay rate
where
Note that by Eq. 19,
We model three sets of biological structures in this paper: microtubules, actin filaments, and amyloid fibrils. Python scripts that implement all the following procedures and generate all PDB files for structures of a given length can be found in this GitHub repository link in the Data Availability Statement.
We construct models of microtubules of varying length from the tubulin dimer stored in the Protein Data Bank (PDB) entry 1JFF [86] as per the methods given in Appendix A of [2] and Section S3 in [3]. We briefly summarize the procedure here.
Many identical 1JFF tubulin dimers are laid next to one another to form a left-handed helical microtubule structure with a diameter of 22.4 nm. The initial orientation of one tubulin dimer is such that the
After creating a microtubule, the positions and transition dipole moments of the eight Trp residues in each tubulin dimer are extracted. The position of a Trp molecule is given by the midpoint of the positions of the CD2 and CE2 carbon atoms in it. The transition dipole moment of a Trp molecule is taken as the well-known1
We construct models of actin filaments of varying length from the PDB entry 6BNO as per the description of the structure given in [87]. The procedure to generate actin filaments of a specified length is summarized below.
Many identical 6BNO bare actin subunits are laid next to one another to form a right-handed helical filament. Let the logitudinal direction of the filament be defined as the x-axis. Then, the following operations are applied
We also take many actin filaments constructed in this way, and pack them together in concentric hexagons, forming actin bundles. This creates bundles containing
We construct models of human (mouse) amyloid fibrils of varying length from the PDB entries 6MST (6DSO), respectively, as per the descriptions of the structures given in [68]. The procedure to generate amyloid fibrils of a specified length is summarized below. For both human and mouse amyloid, each subunit is characterized by a six-strand
Many identical 6MST (6DSO) amyloid subunits are laid next to one another to form a right (left)-handed helical fibril. Before applying the necessary operations, we find that a preliminary translation is required for each 6MST (6DSO) subunit: -14.0474 (−14.1715) nm in the x-direction, −14.0376 (−14.1595) nm in the y-direction, and −14.0039 (−11.8823) nm in the z-direction. This moves the center of mass of the amyloid subunit to the origin, so that subsequent rotations are performed along the axis parallel to the would-be fibril direction that passes through the center of mass. Let this axis be defined as the x-axis. Then, the following operations are applied
For all systems, we utilized Python’s eig() function from the NumPy library to calculate the eigensolutions for the non-Hermitian symmetric Hamiltonian matrices. The eig() function, according to the NumPy documentation (https://numpy.org/doc/stable/reference/generated/numpy.linalg.eig.html) is implemented using the standard _geev LAPACK Fortran routines which calculate eigensolutions for general complex square matrices. In our case, the specific routine of interest is zgeev. The zgeev routine could handle even the largest Hamiltonian matrices we have studied in this work and in our previous work [3], of dimension
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. The GitLab repository which contains all the code used by the authors can be found at this link: https://gitlab.com/superradiance/superradiance_in_tryptophan_architectures.
HP: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. NB: Data curation, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. PK: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Visualization, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in parts by the Alfred P. Sloan Foundation, Guy Foundation (United Kingdom), and Chaikin-Wile Foundation.
This research used resources of the Argonne Leadership Computing Facility, a U.S. Department of Energy (DOE) Office of Science user facility at Argonne National Laboratory supported by the U.S. DOE Office of Science-Advanced Scientific Computing Research Program, under Contract No. DE-AC02-06CH11357. The authors thank the Howard University RCMI program for supporting publication charges to make this article open access. Portions of the manuscript were drafted and discussed during PK’s 2023 residency as a Fellow of the Kavli Institute for Theoretical Physics (KITP), which was supported in part by grant NSF PHY-1748958 to KITP.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer AH declared a past co-authorship with the author(s) PK to the handling editor.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1387271/full#supplementary-material
1Centrioles are cylindrically symmetric organelles formed from nine triplets of microtubules exhibiting a pinwheel-like structure (see [17] for more specifics on their geometry). They are highly conserved in most eukaryotic cells, but notably absent in yeast and higher plants, among others [17]. Centrioles play an important role in forming the spindle complex in cell division, where they help ensure that the correct number of chromosomes are present in each daughter cell after replication [18, 19]. They have also been shown, in several studies by Guenter Albrecht-Buehler [20–23], to aid orientation of the cell to an external light stimulus.
2The number of Trp-Tyr pairs within van der Waals contact (∼
1. Dicke RH. Coherence in spontaneous radiation processes. Phys Rev (1954) 93:99–110. doi:10.1103/PhysRev.93.99
2. Celardo GL, Angeli M, Craddock TJA, Kurian P. On the existence of superradiant excitonic states in microtubules. New J Phys (2019) 21:023005. doi:10.1088/1367-2630/aaf839
3. Babcock NS, Montes-Cabrera G, Oberhofer KE, Chergui M, Celardo GL, Kurian P. Ultraviolet superradiance from mega-networks of tryptophan in biological architectures. J Phys Chem B (2024) 128:4035–46. doi:10.1021/acs.jpcb.3c07936
4. Kurian P, Obisesan T, Craddock TJ. Oxidative species-induced excitonic transport in tubulin aromatic networks: potential implications for neurodegenerative disease. J Photochem Photobiol B: Biol (2017) 175:109–24. doi:10.1016/j.jphotobiol.2017.08.033
5. Callis PR. [7] 1La and 1Lb transitions of tryptophan: applications of theory and experimental observations to fluorescence of proteins. Fluorescence Spectroscopy (Academic Press). Methods Enzymol (1997) 278:113–50. doi:10.1016/S0076-6879(97)78009-1
6. Vivian JT, Callis PR. Mechanisms of tryptophan fluorescence shifts in proteins. Biophysical J (2001) 80:2093–109. doi:10.1016/s0006-3495(01)76183-8
7. Schenkl S, van Mourik F, van der Zwan G, Haacke S, Chergui M. Probing the ultrafast charge translocation of photoexcited retinal in bacteriorhodopsin. Science (2005) 309:917–20. doi:10.1126/science.1111482
8. Engel GS, Calhoun TR, Read EL, Ahn TK, Mančal T, Cheng YC, et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature (2007) 446:782–6. doi:10.1038/nature05678
9. Panitchayangkoon G, Hayes D, Fransted KA, Caram JR, Harel E, Wen J, et al. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc Natl Acad Sci USA (2010) 107:12766–70. doi:10.1073/pnas.1005484107
10. Collini E, Wong CY, Wilk KE, Curmi PM, Brumer P, Scholes GD. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature (2010) 463:644–7. doi:10.1038/nature08811
11. Strümpfer J, Sener M, Schulten K. How quantum coherence assists photosynthetic light-harvesting. J Phys Chem Lett (2012) 3:536–42. doi:10.1021/jz201459c
12. Jang SJ, Mennucci B. Delocalized excitons in natural light-harvesting complexes. Rev Mod Phys (2018) 90:035003. doi:10.1103/RevModPhys.90.035003
13. Doria S, Sinclair TS, Klein ND, Bennett DI, Chuang C, Freyria FS, et al. Photochemical control of exciton superradiance in light-harvesting Nanotubes. ACS Nano (2018) 12:4556–64. doi:10.1021/acsnano.8b00911
14. Mattiotti F, Kuno M, Borgonovi F, Jankó B, Celardo GL. Thermal decoherence of superradiance in lead halide perovskite nanocrystal superlattices. Nano Lett (2020) 20:7382–8. doi:10.1021/acs.nanolett.0c02784
15. Mattiotti F, Sarovar M, Giusteri GG, Borgonovi F, Celardo GL. Efficient light harvesting and photon sensing via engineered cooperative effects. New J Phys (2022) 24:013027. doi:10.1088/1367-2630/ac4127
16. Werren N, Brown W, Gauger EM. Light harvesting enhanced by quantum ratchet states. PRX Energy (2023) 2:013002. doi:10.1103/prxenergy.2.013002
17. Winey M, O’Toole E. Centriole structure. Philos Trans R Soc B: Biol Sci (2014) 369:20130457. doi:10.1098/rstb.2013.0457
18. Fırat-Karalar EN, Stearns T. The centriole duplication cycle. Philos Trans R Soc B: Biol Sci (2014) 369:20130460. doi:10.1098/rstb.2013.0460
19. Rodrigues-Martins A, Riparbelli M, Callaini G, Glover DM, Bettencourt-Dias M. From centriole biogenesis to cellular function: centrioles are essential for cell division at critical developmental stages. Cell Cycle (2008) 7:11–6. doi:10.4161/cc.7.1.5226
20. Albrecht-Buehler G. Rudimentary form of cellular “vision”. Proc Natl Acad Sci USA (1992) 89:8288–92. doi:10.1073/pnas.89.17.8288
21. Albrecht-Buehler G. Cellular infrared detector appears to be contained in the centrosome. Cell Motil Cytoskeleton (1994) 27:262–71. doi:10.1002/cm.970270307
22. Albrecht-Buehler G. Autofluorescence of live purple bacteria in the near infrared. Exp Cell Res (1997) 236:43–50. doi:10.1006/excr.1996.3688
23. Albrecht-Buehler G. Phagokinetic tracks of 3T3 cells: parallels between the orientation of track segments and of cellular structures which contain actin or tubulin. Cell (1977) 12:333–9. doi:10.1016/0092-8674(77)90109-x
24. Ahmad FJ, He Y, Myers KA, Hasaka TP, Francis F, Black MM, et al. Effects of dynactin disruption and dynein depletion on axonal microtubules. Traffic (2006) 7:524–37. doi:10.1111/j.1600-0854.2006.00403.x
25. Matsudaira P, Mandelkow E, Renner W, Hesterberg LK, Weber K. Role of fimbrin and villin in determining the interfilament distances of actin bundles. Nature (1983) 301:209–14. doi:10.1038/301209a0
26. Pelucchi S, Stringhi R, Marcello E. Dendritic spines in Alzheimer’s disease: how the actin cytoskeleton contributes to synaptic failure. Int J Mol Sci (2020) 21:908. doi:10.3390/ijms21030908
27. Pauling L, Corey RB, Branson HR. The structure of proteins: two hydrogen-bonded helical configurations of the polypeptide chain. Proc Natl Acad Sci USA (1951) 37:205–11. doi:10.1073/pnas.37.4.205
28. Eves BJ, Doutch JJ, Terry AE, Yin H, Moulin M, Haertlein M, et al. Elongation rate and average length of amyloid fibrils in solution using isotope-labelled small-angle neutron scattering. RSC Chem Biol (2021) 2:1232–8. doi:10.1039/d1cb00001b
29. Toyama BH, Weissman JS. Amyloid structure: conformational diversity and consequences. Annu Rev Biochem (2011) 80:557–85. doi:10.1146/annurev-biochem-090908-120656
30. Segers-Nolten I, van Raaij M, Subramaniam V. “Biophysical analysis of amyloid formation,” in Comprehensive Biomaterials. Elsevier (2011). p. 347–59. doi:10.1016/b978-0-08-055294-1.00086-6
31. Findeis MA, Musso GM, Arico-Muendel CC, Benjamin HW, Hundal AM, Lee JJ, et al. Modified-peptide inhibitors of amyloid β-peptide polymerization. Biochemistry (1999) 38:6791–800. doi:10.1021/bi982824n
32. Akter R, Cao P, Noor H, Ridgway Z, Tu LH, Wang H, et al. Islet amyloid polypeptide: structure, function, and pathophysiology. J Diabetes Res (2016) 2016:1–18. doi:10.1155/2016/2798269
33. Kyle RA. Amyloidosis: a convoluted story. Br J Haematol (2001) 114:529–38. doi:10.1046/j.1365-2141.2001.02999.x
34. Nielsen L, Khurana R, Coats A, Frokjaer S, Brange J, Vyas S, et al. Effect of environmental factors on the kinetics of insulin fibril formation: elucidation of the molecular mechanism. Biochemistry (2001) 40:6036–46. PMID: 11352739. doi:10.1021/bi002555c
35. Chiti F, Dobson CM. Protein misfolding, amyloid formation, and human disease: a summary of progress over the last decade. Annu Rev Biochem (2017) 86:27–68. doi:10.1146/annurev-biochem-061516-045115
36. Nelson R, Eisenberg D. Recent atomic models of amyloid fibril structure. Curr Opin Struct Biol (2006) 16:260–5. doi:10.1016/j.sbi.2006.03.007
37. Brion JP, Hanger DP, Bruce MT, Couck AM, Flament-Durand J, Anderton BH. Tau in Alzheimer neurofibrillary tangles. N- and C-terminal regions are differentially associated with paired helical filaments and the location of a putative abnormal phosphorylation site. Biochem J (1991) 273:127–33. doi:10.1042/bj2730127
38. Binder LI, Guillozet-Bongaarts AL, Garcia-Sierra F, Berry RW. Tau, tangles, and Alzheimer’s disease. Biochim Biophys Acta (Bba) - Mol Basis Dis (2005) 1739:216–23. doi:10.1016/j.bbadis.2004.08.014
39. Ow S, Dunstan DE. A brief overview of amyloids and Alzheimer’s disease. Protein Sci (2014) 23:1315–31. doi:10.1002/pro.2524
40. Gullì M, Valzelli A, Mattiotti F, Angeli M, Borgonovi F, Celardo GL. Macroscopic coherence as an emergent property in molecular nanotubes. New J Phys (2019) 21:013019. doi:10.1088/1367-2630/aaf01a
41. Moiseyev N. Non-hermitian quantum mechanics. Cambridge University Press (2011). doi:10.1017/cbo9780511976186
42. Breuer HP, Petruccione F. The theory of open quantum systems. Oxford University Press (2007). doi:10.1093/acprof:oso/9780199213900.001.0001
43. Manzano D. A short introduction to the Lindblad master equation. AIP Adv (2020) 10:025106. doi:10.1063/1.5115323
44. Lindblad G. On the generators of quantum dynamical semigroups. Commun Math Phys (1976) 48:119–30. doi:10.1007/BF01608499
45. Havelka D, Deriu MA, Cifra M, Kučera O. Deformation pattern in vibrating microtubule: structural mechanics study based on an atomistic approach. Scientific Rep (2017) 7:4227. doi:10.1038/s41598-017-04272-w
46. Yao S, Wang Z. Edge states and topological invariants of non-hermitian systems. Phys Rev Lett (2018) 121:086803. doi:10.1103/physrevlett.121.086803
47. Song F, Yao S, Wang Z. Non-hermitian topological invariants in real space. Phys Rev Lett (2019) 123:246801. doi:10.1103/physrevlett.123.246801
48. Bauer B, Sharma R, Chergui M, Oppermann M. Exciton decay mechanism in DNA single strands: back-electron transfer and ultrafast base motions. Chem Sci (2022) 13:5230–42. doi:10.1039/d1sc06450a
49. Renaud N, Berlin YA, Lewis FD, Ratner MA. Between superexchange and hopping: an intermediate charge-transfer mechanism in poly(A)-Poly(T) DNA hairpins. J Am Chem Soc (2013) 135:3953–63. doi:10.1021/ja3113998
50. Bittner ER. Lattice theory of ultrafast excitonic and charge-transfer dynamics in DNA. J Chem Phys (2006) 125:094909. doi:10.1063/1.2335452
51. Spata VA, Matsika S. Role of excitonic coupling and charge-transfer states in the absorption and CD spectra of adenine-based oligonucleotides investigated through QM/MM simulations. J Phys Chem A (2014) 118:12021–30. doi:10.1021/jp507520c
52. Jong KH, Azar YT, Grisanti L, Stephens AD, Jones STE, Credgington D, et al. Low energy optical excitations as an indicator of structural changes initiated at the termini of amyloid proteins. Phys Chem Chem Phys (2019) 21:23931–42. doi:10.1039/c9cp04648h
53. Oakley MT, Hirst JD. Charge-transfer transitions in protein circular dichroism calculations. J Am Chem Soc (2006) 128:12414–5. doi:10.1021/ja0644125
54. Andrea Rozzi C, Maria Falke S, Spallanzani N, Rubio A, Molinari E, Brida D, et al. Quantum coherence controls the charge separation in a prototypical artificial light-harvesting system. Nat Commun (2013) 4:1602. doi:10.1038/ncomms2603
55. Qiu W, Li T, Zhang L, Yang Y, Kao YT, Wang L, et al. Ultrafast quenching of tryptophan fluorescence in proteins: interresidue and intrahelical electron transfer. Chem Phys (2008) 350:154–64. doi:10.1016/j.chemphys.2008.01.061
56. Kao YT, Guo X, Yang Y, Liu Z, Hassanali A, Song QH, et al. Ultrafast dynamics of nonequilibrium electron transfer in photoinduced redox cycle: solvent mediation and conformation flexibility. J Phys Chem B (2012) 116:9130–40. doi:10.1021/jp304518f
57. Asenjo-Garcia A, Moreno-Cardoner M, Albrecht A, Kimble HJ, Chang DE. Exponential improvement in photon storage fidelities using subradiance and “selective radiance” in atomic arrays. Phys Rev X (2017) 7:031024. doi:10.1103/physrevx.7.031024
58. Gutiérrez-Jáuregui R, Asenjo-Garcia A. Directional transport along an atomic chain. Phys Rev A (2022) 105:043703. doi:10.1103/physreva.105.043703
59. Jen HH. Phase-imprinted multiphoton subradiant states. Phys Rev A (2017) 96:023814. doi:10.1103/physreva.96.023814
60. Eisele DM, Cone CW, Bloemsma EA, Vlaming SM, van der Kwaak CGF, Silbey RJ, et al. Utilizing redox-chemistry to elucidate the nature of exciton transitions in supramolecular dye nanotubes. Nat Chem (2012) 4:655–62. doi:10.1038/nchem.1380
61. Li H, Jiang G, Jia M, Cao S, Zhang S, Chen J, et al. Ultrafast Förster resonance energy transfer between tyrosine and tryptophan: potential contributions to protein–water dynamics measurements. Phys Chem Chem Phys (2022) 24:18055–66. doi:10.1039/d2cp02139k
62. Gregory WE, Sharma B, Hu L, Raghavendra AJ, Podila R. Interfacial charge transfer with exfoliated graphene inhibits fibril formation in lysozyme amyloid. Biointerphases (2020) 15(3):031010. doi:10.1116/6.0000019
63. Cha W, Heo C, Lee S, Yun SJ, Cho BW, Ha T, et al. Probing interfacial charge transfer between amyloid-β and graphene during amyloid fibrillization using Raman Spectroscopy. ACS Nano (2023) 17(5):4834–4842. doi:10.1021/acsnano.2c11428
64. Grisanti L, Pinotsi D, Gebauer R, Kaminski Schierle GS, Hassanali AA. A computational study on how structure influences the optical properties in model crystal structures of amyloid fibrils. Phys Chem Chem Phys (2017) 19:4030–40. doi:10.1039/c6cp07564a
65. Stephens AD, Qaisrani MN, Ruggiero MT, Díaz Mirón G, Morzan UN, González Lebrero MC, et al. Short hydrogen bonds enhance nonaromatic protein-related fluorescence. Proc Natl Acad Sci USA (2021) 118:e2020389118. doi:10.1073/pnas.2020389118
66. Grisanti L, Sapunar M, Hassanali A, Došlić N. Toward understanding optical properties of amyloids: a reaction path and nonadiabatic dynamics study. J Am Chem Soc (2020) 142:18042–9. doi:10.1021/jacs.0c07134
67. Mirón GD, Semelak JA, Grisanti L, Rodriguez A, Conti I, Stella M, et al. The carbonyl-lock mechanism underlying non-aromatic fluorescence in biological matter. Nat Commun (2023) 14:7325. doi:10.1038/s41467-023-42874-3
68. Liberta F, Loerch S, Rennegarbe M, Schierhorn A, Westermark P, Westermark GT, et al. Cryo-EM fibril structures from systemic AA amyloidosis reveal the species complementarity of pathological amyloids. Nat Commun (2019) 10:1104–10. doi:10.1038/s41467-019-09033-z
69. Jang DH, Han JH, Lee SH, Lee YS, Park H, Lee SH, et al. Cofilin expression induces cofilin-actin rod formation and disrupts synaptic structure and function in Aplysia synapses. Proc Natl Acad Sci USA (2005) 102:16072–7. doi:10.1073/pnas.0507675102
70. Bamburg JR, Bernstein BW. Actin dynamics and cofilin-actin rods in Alzheimer disease. Cytoskeleton (2016) 73:477–97. doi:10.1002/cm.21282
71. Nichols TW, Berman MH, Tuszynski JA. Is Alzheimer’s disease a manifestation of brain quantum decoherence resulting from mitochondrial and microtubular deterioration? J Multiscale Neurosci (2023) 2 (1):141–158. doi:10.56280/1564010613
72. Bazan NG, Halabi A, Ertel M, Petasis NA. Chapter 34 - Neuroinflammation. In: ST Brady, GJ Siegel, RW Albers, and DL Price, editors. Basic neurochemistry. 8th ed. New York: Academic Press (2012). p. 610–20. doi:10.1016/B978-0-12-374947-5.00034-1
73. Merz PA, Wisniewski HM, Somerville RA, Bobin SA, Masters CL, Iqbal K. Ultrastructural morphology of amyloid fibrils from neuritic and amyloid plaques. Acta Neuropathologica (1983) 60:113–24. doi:10.1007/bf00685355
74. Han S, Kollmer M, Markx D, Claus S, Walther P, Fändrich M. Amyloid plaque structure and cell surface interactions of β-amyloid fibrils revealed by electron tomography. Scientific Rep (2017) 7:43577. doi:10.1038/srep43577
75. Mu XQ, Makowski L, Magdoff-Fairchild B. Analysis of the stability of hemoglobin S double strands. Biophysical J (1998) 74:655–68. doi:10.1016/s0006-3495(98)77825-7
76. Henry ER, Cellmer T, Dunkelberger EB, Metaferia B, Hofrichter J, Li Q, et al. Allosteric control of hemoglobin S fiber formation by oxygen and its relation to the pathophysiology of sickle cell disease. Proc Natl Acad Sci (2020) 117:15018–27. doi:10.1073/pnas.1922004117
77. Craddock TJ, Tuszynski JA, Hameroff S. Cytoskeletal signaling: is memory encoded in microtubule lattices by CaMKII phosphorylation? PLoS Comput Biol (2012) 8:e1002421. doi:10.1371/journal.pcbi.1002421
78. Craddock TJA, Friesen D, Mane J, Hameroff S, Tuszynski JA. The feasibility of coherent energy transfer in microtubules. J R Soc Interf (2014) 11:20140677. doi:10.1098/rsif.2014.0677
79. Craddock TJ, Kurian P, Tuszynski JA, Hameroff SR. Quantum processes in neurophotonics and the origin of the brain’s spatiotemporal hierarchy. In: RR Alfano, and L Shi, editors. Neurophotonics and biomedical spectroscopy. Elsevier (2019). p. 189–213. Nanophotonics. doi:10.1016/B978-0-323-48067-3.00009-3
81. Grad J, Hernandez G, Mukamel S. Radiative decay and energy transfer in molecular aggregates: the role of intermolecular dephasing. Phys Rev A (1988) 37:3835–46. doi:10.1103/PhysRevA.37.3835
82. Spano FC, Mukamel S. Superradiance in molecular aggregates. J Chem Phys (1989) 91:3835–3846. doi:10.1063/1.457174
83. Bienaimé T, Bachelard R, Piovella N, Kaiser R. Cooperativity in light scattering by cold atoms. Fortschritte der Physik (2013) 61:377–92. doi:10.1002/prop.201200089
84. Giusteri GG, Mattiotti F, Celardo GL. Non-Hermitian Hamiltonian approach to quantum transport in disordered networks with sinks: validity and effectiveness. Phys Rev B (2015) 91:094301. doi:10.1103/PhysRevB.91.094301
85. Akkermans E, Gero A, Kaiser R. Photon localization and Dicke superradiance in atomic gases. Phys Rev Lett (2008) 101:103602. doi:10.1103/PhysRevLett.101.103602
86. Löwe J, Li H, Downing K, Nogales E. Refined structure of αβ-tubulin at 3.5 Å resolution. J Mol Biol (2001) 313:1045–57. doi:10.1006/jmbi.2001.5077
Keywords: superradiance, Alzheimer’s, dementia, neuroprotection, quantum optics, neurodegeneration, ultraviolet, tryptophan
Citation: Patwa H, Babcock NS and Kurian P (2024) Quantum-enhanced photoprotection in neuroprotein architectures emerges from collective light-matter interactions. Front. Phys. 12:1387271. doi: 10.3389/fphy.2024.1387271
Received: 17 February 2024; Accepted: 18 June 2024;
Published: 26 August 2024.
Edited by:
Youngchan Kim, University of Surrey, United KingdomReviewed by:
Daniel Kattnig, University of Exeter, United KingdomCopyright © 2024 Patwa, Babcock and Kurian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Philip Kurian, cGt1cmlhbkBob3dhcmQuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.