Magnetohydrodynamics simulation of magnetic reconnection process based on the laser-driven Helmholtz capacitor-coil targets

Magnetic reconnection is an important rapid energy release mechanism in astrophysics. Magnetic energy can be effectively converted into plasma kinetic energy, thermal energy, and radiation energy. This study is based on the magnetohydrodynamics simulation method and utilizes the FLASH code to investigate the laser-driven magnetic reconnection physical process of the Helmholtz capacitor-coil target. The simulation model incorporates the laser driving effect, and the external magnetic field consistent with the Helmholtz capacitor-coil target is written in. This approach achieves a magnetic reconnection process that is more consistent with the experiment. By changing the resistivity, subtle differences in energy conversion during the evolution of magnetic reconnection are observed. Under conditions of low resistivity, there is a more pronounced increase in the thermal energy of ions compared to other energy components. In simulations with high resistivity, the increase in electrons thermal energy is more prominent. The simulation gives the evolution trajectory of magnetic reconnection, which is in good agreement with the experimental results. This has important reference value for experimental research on the low-β magnetic reconnection.

1 Introduction

Magnetic reconnection is an important process in astrophysics [1]. The rapid increase of plasma energy can be achieved through the dissipation of magnetic energy. This phenomenon finds extensive application in elucidating solar flares, coronal mass ejections, geomagnetic storms, and other solar-terrestrial space phenomena [2–4]. Extensive magnetic reconnection data has been acquired through observations by the Magnetospheric Multiscale spacecraft [5–7]. Magnetic reconnection has also been used to explain the high-energy-density astrophysical systems, such as gamma-ray bursts [8, 9], black hole accretion disks [10, 11], and pulsar [12]. Magnetic reconnection increases electron heat energy in the inertial confinement fusion experiment and destroys the uniformity of fusion materials, which has always been an important issue [13, 14]. In recent years, laboratory research on magnetic reconnection has made a lot of progress, complementing astronomical observational research. High-power laser devices reproduced the loop-top X-ray source [15], affirming the pivotal role of magnetic reconnection in solar-terrestrial space phenomena. In the magnetic reconnection experiment (MRX), the length of the current sheet was given as a few ion skin depth [16] and the experiments indicated that magnetic reconnection mechanisms were divided into forced magnetic reconnection and pulled magnetic reconnection [17]. In the experiment of Pei et al. [18], it was the first time to use the Helmholtz capacitor-coil target to reproduce the low-β magnetic reconnection process on a traditional laser device. This kind of target was used to further study the particle acceleration by the magnetic reconnection in many experiments. Shu et al. [19] pointed that the ion acoustic and electron acoustic bursts can lead to electron heating and bulk acceleration. Abraham et al. [20] reported the out-of-plane reconnection electric field had the direct capability to accelerate electrons.

The capacitor-coil target can effectively generate strong magnetic fields in laser-driven experiments. It consists of two parallel upper and lower target disks that connected by a coil. Featuring an upper target disk with a laser injection hole, the lasers are precisely focused onto the lower target disk through this aperture. The lower target disk is ablated by the laser and generates a substantial population of electrons. Due to their light mass, these electrons can reach the upper target disk faster than the ions, leading to a potential difference between the upper and lower target disks. The potential difference drives the electrons back to the lower target disk along the connecting coil, initiating a current and inducing the magnetic field. The intensity of the induced magnetic field will gradually increase with the laser injection process, reaching the strongest at the end of the laser pulse [21]. In 1986, Daido et al. [22] employed a B-dot probe to measure the magnetic field of the capacitive-coil target. The laser power was approximately 1.3 × ${10}^{14}$ W ${\text{cm}}^{-2}$, and the experiment confirmed that the magnetic field intensity up to 60T. This result has been confirmed many times in subsequent studies [23, 24], and Proton deflectometry can obtain two-dimensional magnetic field structure [25–27]. In 2013, Fujioka et al. [28] repeated this experiment on the high-power laser GEKKO-XII and employed the Faraday effect to measure the magnetic field. The obtained magnetic field intensity could reach approximately 1.5 kT. The presence of a smaller reverse magnetic field area between the double coils of the Helmholtz capacitive-coil target was attributed to the consistent direction of the current. This configuration aligns with the typical topological features was observed in magnetic reconnection. Yuan et al. [29] used the Helmholtz capacitive-coil target to produce a parallel reverse magnetic field structure, exhibiting a strength of approximately 38.5T. They successfully replicated the magnetic reconnection process on the XG-III laser. However, among the many current experiments, the systematic and comprehensive magnetohydrodynamic simulation for these experiments are scarce. Recently, Xu et al. [30] used magnetohydrodynamic simulation to confirm that the accumulated of the experimental plasma comes from magnetic reconnection.

In recent years, there are many simulation methods of magnetic reconnection. Egedal et al. [31] obtain the important role of parallel electric field in particle acceleration by using kinetic simulation method. Fox et al. [32] used PIC simulation and found that the fermi acceleration process plays an important part in reconnection acceleration. These simulations revolve around the magnetic reconnection process, and we want to simulate the whole experimental process. PIC simulation can introduce laser parameters, but the computing power is limited to the picosecond level. In order to introduce lasers in nanosecond level, we will utilize the FLASH radiation magnetohydrodynamic code to simulate the magnetic reconnection experiment on three-dimension. The energy conversion of magnetic reconnection is very complex, and the whole process is mixed with many factors such as the electric field, waves, and turbulence. The most fundamental reason is the issue of resistivity. The magnetic diffusion term introduced by resistivity is the key to whether magnetic reconnection can occur. Observational data indicate the existence of anomalous resistivity in astronomical environments [33–35], but the origin of the anomalous resistivity still require extensive research. Different resistivity values were applied in the simulation to confirm the impact of resistivity on the occurrence rate of magnetic reconnection and the energy distribution following magnetic energy conversion. The structure of this paper is delineated as follows. Section 2 introduces the simulation setup, Section 3 displays and analyzes the simulation results, and Section 4 provides the conclusion.

2 The simulation setup

This investigation uses the FLASH simulation code to simulate and study the laser-driven Helmholtz capacitor-coil target magnetic reconnection experiment. FLASH, a radiation magnetohydrodynamics simulation code, was developed by the University of Chicago [36]. It possesses the capability to track the motion patterns of plasma by solving the magnetohydrodynamics equations. The dimensionless magnetohydrodynamics equations are as Eqs 1–6:

$\frac{\partial \rho }{\partial t}+\nabla ·\left(\mathrm{\rho }\overrightarrow{v}\right)=0,(1)$

$\frac{\partial \rho \overrightarrow{v}}{\partial t}+\nabla \left(\rho \overrightarrow{v}\overrightarrow{v}-\overrightarrow{B}\overrightarrow{B}\right)+\nabla p_{*}=0,(2)$

$\frac{\partial \rho E}{\partial t}+\nabla ·\left(\overrightarrow{v}\left(\rho E+p_{*}\right)-\overrightarrow{B}\left(\overrightarrow{v}·\overrightarrow{B}\right)\right)=\nabla ·(\overrightarrow{B}\times \left(\eta \nabla \times \overrightarrow{B}\right),(3)$

$\frac{\partial \overrightarrow{B}}{\partial t}+\nabla ·\left(\overrightarrow{v}\overrightarrow{B}-\overrightarrow{B}\overrightarrow{v}\right)=-\nabla \times \left(\eta \nabla \times \overrightarrow{B}\right),(4)$

Where,

$p_{*}=P+\frac{B^2}{2},(5)$

$\mathrm{E}=\frac{1}{2}{v}^2+ϵ+\frac{B^2}{2\rho }.(6)$

In the expression, ρ represents the density, $\overrightarrow{v}$ represents the velocity, p represents the thermal pressure, T represents the temperature, $\overrightarrow{B}$ represents the magnetic field strength, E represents the total specific energy, ϵ represents the specific internal energy, and $\eta$ represents the resistivity. The FLASH code is a single-fluid simulation, therefore the capacity to replicate the coil current generation process and the naturally induced magnetic field structure. In our simulation, we wrote a magnetic field module to realize the simulation study of magnetic reconnection. The initial structure of the written magnetic field is consistent with the Radia static magnetic field simulation [37], ensuring the correctness.

The FLASH code contains the laser Energy deposition unit, which allow adding the laser parameters to the simulation. Compared with the general hydrodynamics simulation, it can better reproduce the real situation in the experiment. The FLASH code contains magnetic field modules such as Biermann magnetic field and Hall magnetic field. The special magnetic field structure can be written as the initial condition in the Simulation_initBlock.F90 file. However, the magnetic field written in this way cannot be reused or adjusted in the subsequent plasma evolution process. The magnetic field intensity generated by the target will increase with the injection of the laser and reach the maximum strength at the end of the laser. Consequently, it is imperative to ensure that the simulated magnetic field intensity at the conclusion of the laser pulse is indeed at its maximum value. We add an additional code module to write the magnetic field within the main program file hy_uhd_unsplit.F90 of FLASH. To avoid the writing of an external magnetic field from interfering with other modules of the main program, the magnetic field is added following the writing method of the Biermann magnetic field module that treated as a source item. The magnetic field is written using the magnetic vector potential method, defined as $\overrightarrow{B}$ = ∇×A, which satisfies ∇∙$\overrightarrow{B}$ = 0. This method effectively maintains the divergence of the simulated grid magnetic field at zero, ensuring the accuracy of the magnetohydrodynamics simulations.

The target parameters and laser parameters in the simulation are established based on the experiment of Yuan et al. [29]. The simulation is written in a cartesian coordinate system. The simulation range in the x, y, and z directions is (−2200, 2200) × (−1500, 5500) × (−500, 500) μm. The number of simulation grids is 160 × 256 × 64. The outflow boundary conditions are employed. The magnetic field is introduced into the simulation at approximately 1.0 ns. The magnetic field intensity added inside the coil area ranges from ∼50T, and the maximum value is slightly higher than the experimental measurement value of 38.5T. In order to avoid the influence of boundary effects in the simulation, the coil target structure is simplified. Only the lower target disk and coil area are retained, while the upper target disk is removed (as shown in Figure 1A). For stability purposes, the magnetic field is split and the magnetic field of the semi-circular arc coil is written. After the magnetic field is initialized, it undergoes free evolution with the plasma. The accuracy of the written magnetic field is ensured by comparing the written magnetic field structure with the Radia simulation results (as shown in Figure 2). The laser energy is set at 130J, the pulse width is 1.0 ns, and the focal spot radius is 200 μm, which are basically consistent with the experimental parameters. The laser radiation position is set to (0, 1900, −300) μm, which is about 300 μm from the boundary of the lower target disk.

Figure 1

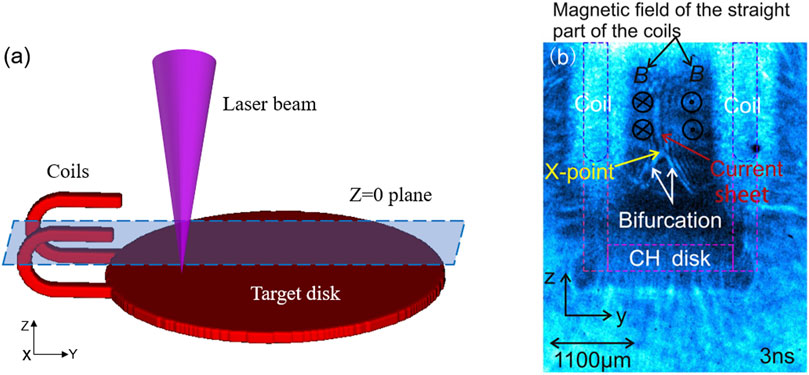
Figure 1. (A) The diagram of the FLASH simulation setup; (B) The shadow image collected in the laboratory from Yuan et al. [29].

Figure 2

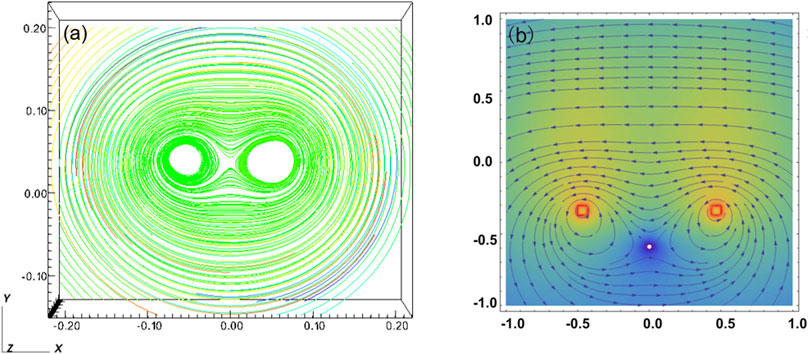
Figure 2. (A) The coils magnetic force lines that was written at the end time of the laser in the FLASH simulation, (B) The structure of the coils magnetic force lines from the Radia simulation.

The FLASH code contains the Spitzer highZ resistivity module that designed for reasonably calculate the resistivity value of each grid. However, this work wanted to study the conversion of magnetic energy under different resistivities, so we chose to use constant resistivity for calculations.

3 Simulation results

Figures 3A–D show the electron number density results in the case of low resistivity (η = 0.716 ${\text{cm}}^2{\mathrm{s}}^{-1}$, data was taken from z = 0 plane marked by the blue frame line in Figure 1A). The white circle in Figure 3 denotes the position of the target disk. The high-density region within the circle corresponds to the plasma generated by the target disk after laser irradiation. Two high-density areas outside the white circle represent the vertex position of the two coils. At 1.0 ns, the laser pulse ends and the magnetic field completes writing. The plasma begins to be constrained by the magnetic field to move around the coils (as shown in Figure 3B). Magnetic reconnection occurs at approximately 2.6 ns (∼46.8 ${\tau }_A$). Magnetic reconnection is still ongoing at the end of the simulation. Note that the 4.0 ns in the simulation corresponds to the 3.0 ns after the laser ended in Yuan et al.‘s experiment [29]. The simulated electron number density results exhibit concordance with the experimental shadow imaging results (as shown in Figures 1B, 3D). The current sheet size obtained from the simulation results can estimate the reconnection rate of magnetic reconnection, which is approximately 0.04 ± 0.05 at 4.0 ns (∼72.0 ${\tau }_A$). In the simulation, the opening angle of the magnetic reconnection outflow region is approximately 55° ± 5°, which is basically consistent with the experimental result of 60° ± 5°. The simulation shows that the electron number density in the magnetic reconnection region is less than ${10}^{19}{\text{cm}}^{-3}$, and the magnetic reconnection process cannot be observed in the range above ${10}^{19}{\text{cm}}^{-3}$. The electron temperature in the magnetic reconnection region is approximately ${2.56\times 10}^6\mathrm{K}$. The simulation parameters are consistent with the experimental data. The plasma β value in the simulation is lower than the predicted 0.016 from the experiment, that is approximately 0.007. This indicates that the magnetic reconnection process dominated by magnetic pressure.

Figure 3

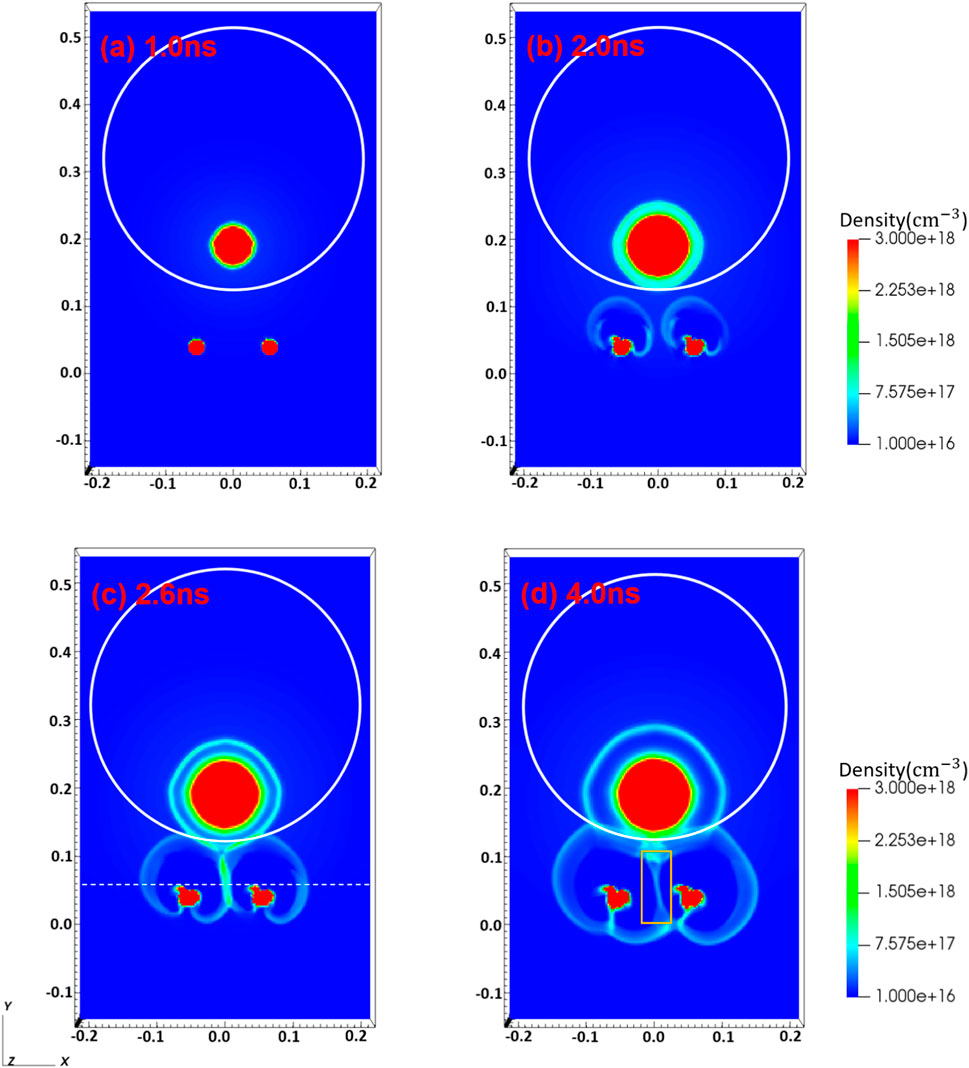
Figure 3. The results of electron number density under the condition of low resistivity in FLASH simulation at (A) 1.0 ns, (B) 2.0 ns, (C) 2.6 ns and (D) 4.0 ns, taking the x-y plane section view of z = 0.0. The two red spots at y = 0.03 indicate the position of the top of the coil, and the white frame line indicates the position of the target plate. The coordinate unit is centimeters.

Figure 4 illustrates the evolution of magnetic field. In the simulation, from the start of magnetic reconnection at 2.6 ns (∼46.8 ${\tau }_A$) to the end of the simulation at 4.0 ns (∼72.0 ${\tau }_A$), the changes in magnetic field topology continue to occur. The position of the x point of magnetic reconnection is shifted in the x direction, and the shape of the magnetic field lines in the magnetic reconnection area is tilted at 3.7 ns (∼66.7 ${\tau }_A$). To exam the two instances of magnetic field topology changes (2.6 ns and 3.7 ns), the electron number density and magnetic field (y-direction component) changes along the x direction are shown in Figure 5. The magnetic field shows obvious positive and negative alternation at the x point. Plasma accumulates in the current sheet area, and the width of the magnetic reconnection current sheet at 2.6 ns is slightly larger than that at 3.7 ns, approximately 2.8 times.

Figure 4

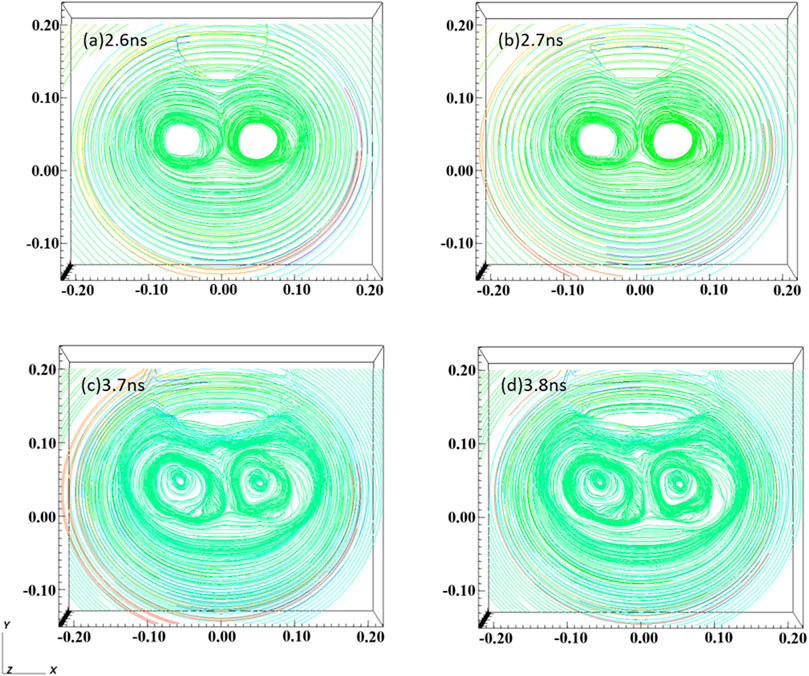
Figure 4. The structure of the magnetic lines of force of the coils before [(A) 2.6 ns and (B) 2.7 ns] and after [(C) 3.7 ns and (D) 3.8 ns] the moment of magnetic reconnection. The coordinate unit is centimeters.

Figure 5

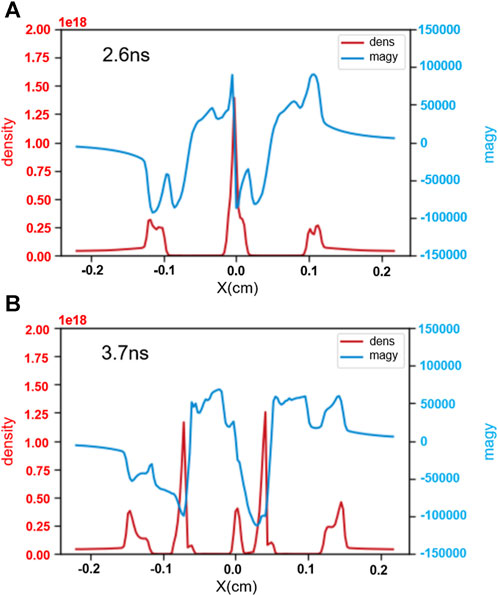
Figure 5. The distribution of the y-component of the magnetic field strength and the electron number density at (A) 2.6 ns and (B) 3.7 ns along the x-direction.

Figures 6A–C depict the simulated electron number density results with high resistivity (η = 71.6 ${\text{cm}}^2{\mathrm{s}}^{-1}$). The magnetic reconnection occurs (as shown in Figure 6B) and gradually characterized by a long current sheet (as shown in Figure 6C). The moment of magnetic reconnection initiation under high resistivity is basically the same as that under low resistivity. The magnetic energy begins to dissipate rapidly from ∼2.5 ns (∼45.0 ${\tau }_A$), as shown in Figure 7B. The estimated reconnection rate is approximately 0.10 ± 0.03, that is higher than the reconnection rate at 4.0 ns in the low resistivity simulation.

Figure 6

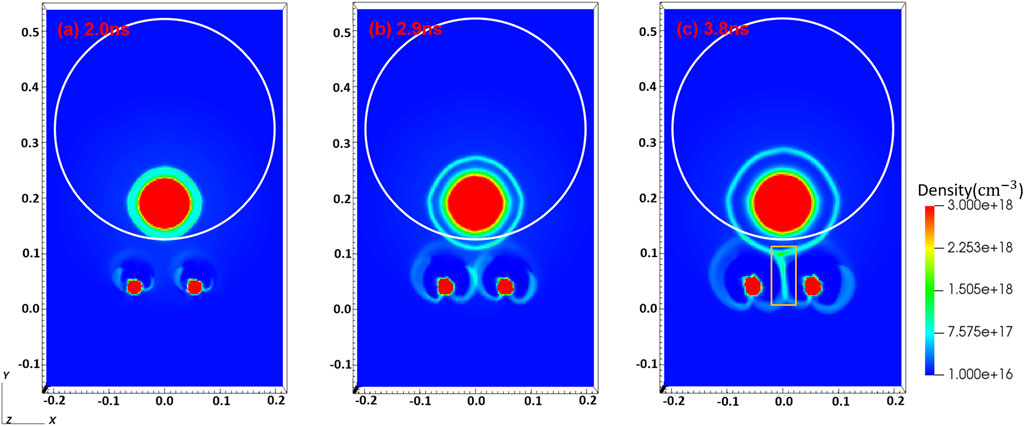
Figure 6. Electron number density simulation results at (A) 2.0 ns, (B) 2.9 ns and (C) 3.8 ns at high resistivity situation. The coordinate unit is centimeters.

Figure 7

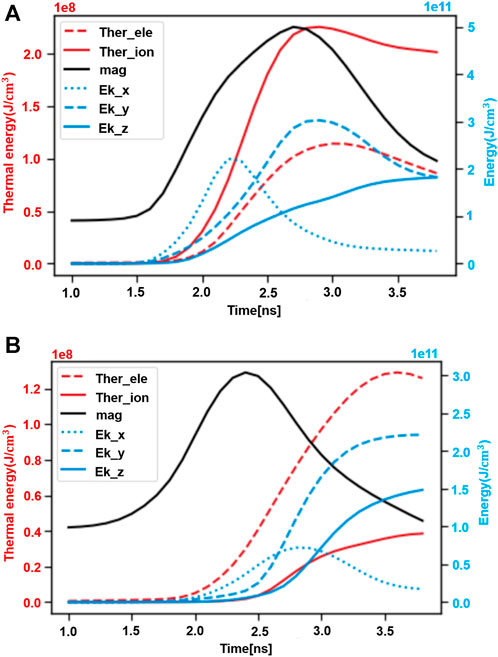
Figure 7. Comparison of trends of magnetic, kinetic, and thermal energy in the case of (A) low resistivity and (B) high Resistivity.

The variations in magnetic energy, kinetic energy and thermal energy within the magnetic reconnection region in low resistivity simulation are shown in Figure 7A (statistics the orange square area of Figure 3D). It can be seen that the magnetic energy is significantly dissipated after about 2.6 ns, which confirms the occurrence of magnetic reconnection. And the thermal energy and kinetic energy of the plasma increase significantly. In Figure 7, the red solid line represents the change of ion thermal energy, and the red dotted line represents the change of electron thermal energy. The increase in ion thermal energy is higher than that of electrons, $∆{Ener}_{ion}/∆{Ener}_{ele}\sim 2.5$. The blue dotted line, dotted line, and solid line represent the plasma kinetic energy in the x, y, and z directions respectively. The increase in plasma kinetic energy is mainly observed in the y and z directions. The y direction corresponds to the outflow direction of magnetic reconnection, and the z direction corresponds to the out-of-plane direction of magnetic reconnection. The increase of the kinetic energy in the two directions is roughly equivalent. In addition, at the end of the simulation, the plasma kinetic energy in the y and z direction is basically at the same intensity as the electron thermal energy. It can be seen from the energy changes that the dissipation of magnetic energy in magnetic reconnection can be effectively converted into thermal energy and kinetic energy of the plasma. In the case of high resistivity, the energy distribution is different from the low resistivity case, as shown in Figure 7B. The thermal energy and kinetic energy of the plasma are still effectively increased. The electron thermal energy exhibits a stronger increase compared to the ion thermal energy, which is different with the result in the low resistivity case, with $∆{Ener}_{ele}/∆{Ener}_{ion}\sim 3.1$. In our simulation, ohmic heating dominates the energy distribution. In the case of high resistivity, the electrons obtain more thermal energy than ions. The increase of kinetic energy in the outflow direction is more severe than that of kinetic energy in the out-plane direction.

Additionally, opposite magnetic field structures in the straight-wire region can also cause magnetic reconnection. The experiments of Pei et al. [18] mainly focused on discussing the magnetic reconnection process within the magnetic field of the straight-wire region. They observed plasma accumulated of magnetic reconnection in the x-y plane (corresponding to the y-z plane in the simulation, as shown in Figures 8A–C). The outflow direction of magnetic reconnection in the straight-line region is mainly in the z direction perpendicular to the x-y plane. The dark region between the two bright lines in Figure 8A corresponds to the high-density plasma outflow generated by magnetic reconnection. Only the straight-wire magnetic field was added to the simulation, and the simulation results were compared with the simulation results of adding the semi-circular arc coil magnetic field. The same current value was set in the two simulations. The evolution of the electron number density simulation results in the x-y plane with only the partial magnetic field of the straight wire added is shown in Figure 9. The plasma is bound by the magnetic field to move around the straight wire, and reconnection begins at 2.5 ns and continues to 4.0 ns (as shown in Figure 9). At the location where the coil magnetic field was added, an obvious high-density plasma accumulation area also appears inside the coil (as shown in Figure 8B). The plasma is the outflow in the y direction generated by the magnetic reconnection of the coil magnetic field. The accumulation of magnetic reconnection outflows in the two different regions inside the coil is in good agreement with the experimental results of Pei et al. [18]. It can be seen that the magnetic reconnection of straight wires and half-arc coils overlap significantly, so experimental research on magnetic reconnection needs to be more cautious. Besides, we find that the laser power intensity has great influence on the experiment, but the target material and coil geometry parameters have little influence on the experiment.

Figure 8

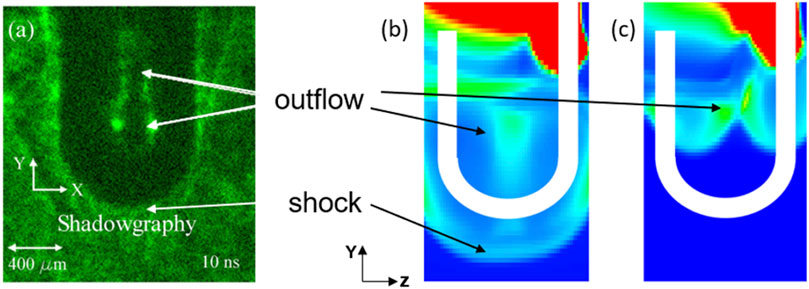
Figure 8. (A) Shadow imaging data collected from Pei et al.’s experiment [18], (B) Electron number density results in the y-z plane at x = 0 for the simulation with a coil magnetic field, (C) Simulation with a straight wire magnetic field at x = 0 The electron number density result of the y-z plane.

Figure 9

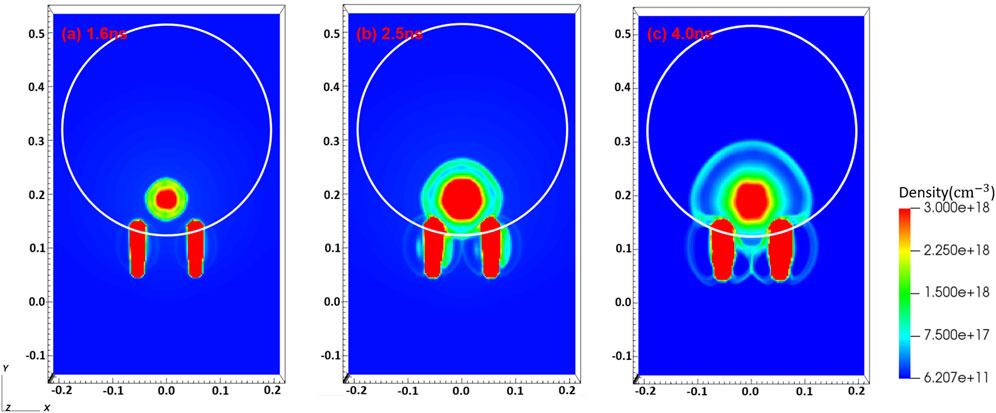
Figure 9. The electron number density at (A) 1.6 ns, (B) 2.5 ns, and (C) 4.0 ns by adding a straight wire magnetic field, intercepting the x-y plane of z = 0.035, which is beneficial to observing the plasma moving around the coil. The coordinate unit is centimeters.

4 Results and discussion

The magnetic reconnection experiments of using Helmholtz capacitor-coil targets are simulated and investigated through the FLASH radiation magnetohydrodynamics simulation code. The simulation replicates the evolution process of magnetic reconnection and is in good agreement with the experimental results of Yuan et al. [29]. Different from previous steady-state models [38] (the Harris layer model), We have not artificially interfered with the plasma properties and magnetic field in the simulation, and can obtain more realistic information on the development of magnetic reconnection. In the simulation, the magnetic energy is effectively converted into the thermal energy and kinetic energy of the plasma. The main reason for the increase in kinetic energy is the electric field of the magnetic reconnection, so it increases significantly in both the outflow direction and the out-of-plane direction. In the case of low resistivity (η = 0.716 ${cm}^2{s}^{-1}$), the thermal energy of ions increases more significantly compared to other energy components. The kinetic energy in the magnetic reconnection outflow direction increases significantly. Ohmic heating dominates the energy conversion, in the high resistivity (η = 71.6 ${cm}^2{s}^{-1}$) simulation, so the increase in electron thermal energy is more prominent. Similar to low-resistivity case, the kinetic energy in the magnetic reconnection outflow direction and the out-plane direction increases significantly. The distribution of plasma energy is discrete compared to the low-resistivity situation. And the reconnection rate increases significantly.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CX: Writing–original draft. YP: Writing–review and editing. XZ: Writing–review and editing. WA: Writing–review and editing. JZ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This Project supported by the National Program on Key Basic Research Project (Grant No. 2022YFA1603203), the National Natural Science Foundation of China (Grant Nos 12325305, 12175018, 12135001, and 1207503), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA25030700). The software used in this work was developed in part by the DOE NNSA- and DOE Office of Science supported Flash Center for Computational Science at the University of Chicago and the University of Rochester.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yamada M, Kulsrud R, Ji H Magnetic reconnection. Rev Mod Phys (2010) 82(1):603–64. doi:10.1103/revmodphys.82.603

CrossRef Full Text | Google Scholar

2. Masuda S, Kosugi T, Hara H, Tsuneta S, Ogawara Y. The solar optical telescope for the hinode mission: an overview. Nature (1994) 371(6497):495–7. doi:10.1038/371495a0

CrossRef Full Text | Google Scholar

3. Bhattacharjee A Impulsive magnetic reconnection in the earth's magnetotail and the solar coronaAnnu Rev Astron Astrophys (2004) 42:365–84. doi:10.1146/annurev.astro.42.053102.134039

CrossRef Full Text | Google Scholar

4. Gosling JT Magnetic reconnection in the solar wind. Space Sci Rev (2012) 172:187–200. doi:10.1007/s11214-011-9747-2

CrossRef Full Text | Google Scholar

5. Ergun RE, Goodrich KA, Wilder FD, Holmes JC, Stawarz JE, Eriksson S, et al. Magnetospheric Multiscale satellites observations of parallel electric fields associated with magnetic reconnection. Phys Rev Lett (2016) 116(23):235102. doi:10.1103/physrevlett.116.235102

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Burch JL, Torbert RB, Phan TD, Chen LJ, Moore TE, Ergun RE, et al. Electron-scale measurements of magnetic reconnection in space. Science (2016) 352(6290):aaf2939. doi:10.1126/science.aaf2939

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Stawarz JE, Eastwood JP, Phan TD, Gingell IL, Pyakurel PS, Shay MA, et al. Turbulence-driven magnetic reconnection and the magnetic correlation length: observations from Magnetospheric Multiscale in Earth's magnetosheath. Phys Plasmas (2022) 29(1). doi:10.1063/5.0071106

CrossRef Full Text | Google Scholar

8. Zhang B, Yan H THE INTERNAL-COLLISION-INDUCED MAGNETIC RECONNECTION AND TURBULENCE (ICMART) MODEL OF GAMMA-RAY BURSTS. Astrophysical J (2010) 726(2):90. doi:10.1088/0004-637x/726/2/90

CrossRef Full Text | Google Scholar

9. Schoeffler KM, Grismayer T, Uzdensky D, Fonseca RA, Silva LO Bright gamma-ray flares powered by magnetic reconnection in QED-strength magnetic fields. Astrophysical J (2019) 870(1):49. doi:10.3847/1538-4357/aaf1b9

CrossRef Full Text | Google Scholar

10. Singh CB, Dal Pino EDG, Kadowaki LHS Astrophysical J Lett (2015) 799(2):L20. doi:10.1088/2041-8205/799/2/l20

CrossRef Full Text

11. Ripperda B, Bacchini F, Philippov AA Magnetic reconnection and hot spot formation in black hole accretion disks. Astrophysical J (2020) 900(2):100. doi:10.3847/1538-4357/ababab

CrossRef Full Text | Google Scholar

12. Contopoulos I. The role of reconnection in the pulsar magnetosphere. Astron Astrophysics (2007) 466(1):301–7. doi:10.1051/0004-6361:20065973

CrossRef Full Text | Google Scholar

13. Joglekar AS, Thomas AGR, Fox W, Bhattacharjee A. Magnetic reconnection in plasma under inertial confinement fusion conditions driven by heat flux effects in ohm’s law. Phys Rev Lett (2014) 112(10):105004. doi:10.1103/physrevlett.112.105004

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hohenberger M, Chang PY, Fiksel G, Knauer JP, Betti R, Marshall FJ, et al. Inertial confinement fusion implosions with imposed magnetic field compression using the OMEGA Laser. Phys Plasmas (2012) 19(5). doi:10.1063/1.3696032

CrossRef Full Text | Google Scholar

15. Zhong J, Li Y, Wang X, Wang J, Dong Q, Xiao C, et al. Modelling loop-top X-ray source and reconnection outflows in solar flares with intense lasers. Nat Phys (2010) 6(12):984–7. doi:10.1038/nphys1790

CrossRef Full Text | Google Scholar

16. Yamada M, Yoo J, Jara-Almonte J, Ji H, Kulsrud RM, Myers CE. Conversion of magnetic energy in the magnetic reconnection layer of a laboratory plasma. Nat Commun (2014) 5:4774. doi:10.1038/ncomms5774

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yamada M, Ji H, Hsu S, Carter T, Kulsrud R, Bretz N, et al. Study of driven magnetic reconnection in a laboratory plasma. Phys Plasmas (1997) 4(5):1936–44. doi:10.1063/1.872336

CrossRef Full Text | Google Scholar

18. Pei XX, Zhong JY, Sakawa Y, Zhang Z, Zhang K, Wei HG, et al. Magnetic reconnection driven by Gekko XII lasers with a Helmholtz capacitor-coil target. Phys Plasmas (2016) 23:032125. doi:10.1063/1.4944928

CrossRef Full Text | Google Scholar

19. Zhang S, Chien A, Gao L, Ji H, Eric GB, et al. Ion and electron acoustic bursts during anti-parallel magnetic reconnection driven by lasers. Nat Phys (2023) 19:909–16. doi:10.1038/s41567-023-01972-1

CrossRef Full Text | Google Scholar

20. Chien A, Gao L, Zhang S, Ji H, Eric GB, William D, et al. (2023). Non-thermal electron acceleration from magnetically driven reconnection in a laboratory plasma Nat Phys 19:254–62. doi:10.1038/s41567-022-01839-x

CrossRef Full Text | Google Scholar

21. Fiksel G, Fox W, Gao L, Ji H A simple model for estimating a magnetic field in laser-driven coils. Appl Phys Lett (2016) 109:134103. doi:10.1063/1.4963763

CrossRef Full Text | Google Scholar

22. Daido H, Miki F, Mima K, Fujita M, Sawai K, Fujita H, et al. Generation of a strong magnetic field by an intenseCO2laser pulse. Phys Rev Lett (1986) 56(8):846–9. doi:10.1103/physrevlett.56.846

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Courtois C, Ash AD, Chambers DM, Grundy RAD, Woolsey NC Creation of a uniform high magnetic-field strength environment for laser-driven experiments. J Appl Phys (2005) 98:054913. doi:10.1063/1.2035896

CrossRef Full Text | Google Scholar

24. Fujioka S, Zhang Z, Yamamoto N, Ohira S, Fujii Y, Ishihara K, et al. High-energy-density plasmas generation on GEKKO-LFEX laser facility for fast-ignition laser fusion studies and laboratory astrophysics. Plasma Phys Controlled Fusion (2012) 54(12):124042. doi:10.1088/0741-3335/54/12/124042

CrossRef Full Text | Google Scholar

25. Gao L, Ji H, Fiksel G, Fox W, Evans M, Alfonso N Ultrafast proton radiography of the magnetic fields generated by a laser-driven coil current. Phys Plasmas (2016) 23:043106. doi:10.1063/1.4945643

CrossRef Full Text | Google Scholar

26. Bradford P, Read MP, Ehret M, Antonelli L, Khan M, Booth N, et al. Proton deflectometry of a capacitor coil target along two axes High Power Laser Sci Eng, 8 (2020). p. e11. doi:10.1017/hpl.2020.9

CrossRef Full Text | Google Scholar

27. Wang W, Shan L, Zhang F, Yuan Z, Liu D, Tian C, et al. Pulsed magnetic fields of over 100 T produced by relativistic intensity laser pulse irradiating no-hole capacitor-coil target. Phys Plasmas (2023) 30(7). doi:10.1063/5.0120697

CrossRef Full Text | Google Scholar

28. Fujioka S, Zhang Z, Ishihara K, Shigemori K, Hironaka Y, Johzaki T, et al. Scientific Rep (2013) 3(1):1–7. doi:10.1038/srep01170

CrossRef Full Text

29. Yuan X, Zhong J, Zhang Z, Zhou W, Teng J, Li Y, et al. Low-βmagnetic reconnection driven by the intense lasers with a double-turn capacitor-coil. Plasma Phys Controlled Fusion (2018) 60(6):065009. doi:10.1088/1361-6587/aabaa9

CrossRef Full Text | Google Scholar

30. Shan-Shan X, Zhi-Xing M, Jia-Yong Z, Jun LIN. Chin Astron Astrophysics (2021) 45(2):131–46. doi:10.1016/j.chinastron.2021.05.001

CrossRef Full Text

31. Egedal J, Daughton W, Le A, et al. Large-scale electron acceleration by parallel electric fields during magnetic reconnection. Nat Phys (2012) 8(4):321–4. doi:10.1038/nphys2249

CrossRef Full Text | Google Scholar

32. Fox W, Park J, Deng W, Fiksel G, Spitkovsky A, Bhattacharjee A. Astrophysical particle acceleration mechanisms in colliding magnetized laser-produced plasmas. Phys Plasmas (2017) 24:092901. doi:10.1063/1.4993204

CrossRef Full Text | Google Scholar

33. Eastwood JP, Phan TD, Bale SD, Tjulin A Observations of turbulence generated by magnetic reconnection. Phys Rev Lett (2009) 102(3):035001. doi:10.1103/physrevlett.102.035001

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Torbert RB, Burch JL, Giles BL, Gershman D, Pollock CJ, Dorelli J, et al. Estimates of terms in Ohm’s law during an encounter with an electron diffusion region. Geophys Res Lett (2016) 43(12):5918–25. doi:10.1002/2016GL069553

CrossRef Full Text | Google Scholar

35. Graham DB, Khotyaintsev YV, André M, Vaivads A, Divin A, Drake JF, et al. Direct observations of anomalous resistivity and diffusion in collisionless plasma. Nat Commun (2022) 13(1):2954. doi:10.1038/s41467-022-30561-8

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lee D New high-order methods using Gaussian processes for computational fluid dynamics simulations. J Comput Phys (2013) 243:269–92. doi:10.1088/1742-6596/837/1/012018

CrossRef Full Text | Google Scholar

37. Elleaume P, Chubar O, Chavanne J. Computing 3D magnetic field from insertion devices. Accel Conf (2008) 3:3509–11. doi:10.1109/PAC.1997.753258

CrossRef Full Text | Google Scholar

38. Potter MA, Browning PK, Gordovskyy M Forced magnetic reconnection and plasmoid coalescence: I. Magnetohydrodynamic simulations. Astron Astrophysics (2019) 623:A15. doi:10.1051/0004-6361/201833565

CrossRef Full Text | Google Scholar