Cross-modal retrieval based on multi-dimensional feature fusion hashing

Along with the continuous breakthrough and popularization of information network technology, multi-modal data, including texts, images, videos, and audio, is growing rapidly. We can retrieve different modal data to meet our needs, so cross-modal retrieval has important theoretical significance and application value. In addition, because the data of different modalities can be mutually retrieved by mapping them to a unified Hamming space, hash codes have been extensively used in the cross-modal retrieval field. However, existing cross-modal hashing models generate hash codes based on single-dimension data features, ignoring the semantic correlation between data features in different dimensions. Therefore, an innovative cross-modal retrieval method using Multi-Dimensional Feature Fusion Hashing (MDFFH) is proposed. To better get the image’s multi-dimensional semantic features, a convolutional neural network, and Vision Transformer are combined to construct an image multi-dimensional fusion module. Similarly, we apply the multi-dimensional text fusion module to the text modality to obtain the text’s multi-dimensional semantic features. These two modules can effectively integrate the semantic features of data in different dimensions through feature fusion, making the generated hash code more representative and semantic. Extensive experiments and corresponding analysis results on two datasets indicate that MDFFH’s performance outdoes other baseline models.

1 Introduction

The swift growth of multimedia data has brought a lot of demand for cross-modal retrieval. With the growing scale of data on the Internet, data types are becoming more and more diversified, including text, images, videos, audio, etc. The data modality that users are interested in is no longer single, and the user retrieval shows a development trend from single modality to cross modalities. Data has different modalities and these expression forms are different, while the semantics behind them may be related to each other and good use of different modal data can facilitate our lives to a certain extent. For instance, when you visit the Great Wall of China, you can retrieve the corresponding text and video introduction through the photos of the Great Wall. The information supplement helps you to quickly familiarize yourself with scenic spots for the first time. Besides the field of daily life, cross-modal retrieval has important applications in many domains such as medicine [1], finance [2], and information security [3]. Therefore, it is an interesting and challenging problem to construct an effective cross-modal retrieval system.

Since the data distributions and feature representations of different modal data are different, they cannot be compared directly. Representation learning can effectively deal with this problem. In such methods, the aim is to learn a function that can transform different modalities into a common feature space [4, 5], where we can compare them directly. Due to the quick expansion of the data scale and the decline of data retrieval efficiency, the hashing codes are applied to cross-modal retrieval tasks [6–8]. This type of method maps high-dimensional features to the Hamming space by transforming data into hash binary codes and uses XOR of hash binary codes to calculate the Hamming distance. Hash binary codes with small Hamming distance have similar original data, and vice versa.

Through many scholars’ research and efforts, cross-modal hashing retrieval has achieved many successes. Specifically, based on artificial features representing the original data, many models [9–14] are proposed, known as traditional cross-modal hashing models. Due to the limitations of handmade features, the retrieval efficiency of such models is hard to further breakthrough. Because of the good performance in feature learning, deep learning has been applied in cross-modal hashing retrieval. For example, deep neural networks can automatically capture the data features and hash functions in Refs. [15–20].

However, existing deep cross-modal hash models usually only pay attention to the single-dimensional semantic features of data and do not fully consider the information complementation between specific features presented by data in different dimensions. Besides, the multi-dimensional fusion of semantic information is more conducive to capturing the semantic correlation of different modal data, thus helping to narrow the semantic gap. So, effective fusing of multi-dimensional semantic features of different modal data is very important in improving cross-modal retrieval. Because of Transformer’s excellent performance in the computer vision field in recent years, we try to use it to better learn the images’ semantic features in different dimensions. Similarly, we construct a text multi-dimensional fusion module in the text network, which learns the text multi-dimensional semantic features. Based on these, we propose a novel method for cross-modal retrieval, which is called Multi-Dimensional Feature Fusion Hashing (MDFFH). Our method has these three characteristics.

• MDFFH constructs multi-dimensional fusion modules in image networks and text networks to learn multi-dimensional semantic features of data, which can effectively complement the semantic features of data in specific dimensions. It is better in semantic relevance, obtained hash codes are more semantic as well.

• Vision Transformer is integrated with a convolutional neural network to form an image multi-dimensional fusion module in MDFFH so the image’s local and global information can be well fused.

• Feature extraction and hash function generation are well integrated into a deep learning framework in MDFFH. Comparative experiments and corresponding analyses on two datasets show that MDFFH is superior to other baseline models.

This paper mainly includes five sections. The related work is introduced in Section 2, MDFFH is given in Section 3, and the experiments and comparative analysis are demonstrated in Section 4. Finally, the conclusion is in Section 5.

2 Related work

Representative cross-modal hashing models: There are two categories in Cross-modal hashing models. If supervised information (such as data tags) needs to be used during model training, this type of model is called an unsupervised model; the other type needs to use supervision information during model training, which is called a supervision model. According to the way they learn features, cross-modal hashing retrieval models are divided into two categories, namely, hand-crafted models and deep network models. Data labels are not used to guide hash codes’ learning in Unsupervised models during model training. For instance, the subspace shared by different modal data is learned and then the correlation between similar different modal data is maximized in Canonical Correlation Analysis (CCA) [21]. Implicit factors of different modal data are learned and unified hash codes are generated based on matrix decomposition in Collective Matrix Factorization Hashing (CMFH) [22]. In latent semantic sparse hashing (LSSH), sparse coding and matrix decomposition are used to capture important structures in images and potential semantics in texts, respectively [23]. Semantic topics and semantic concepts for images and texts are learned and discrete characteristics of different modal data are maintained in Semantic topic multi-modal hashing (STMH) [25]. Cross-Modal Self-Taught Hashing (CMSTH) [24] applies semantic information to detect multimodal topics, and then uses robust matrix decomposition to convert these different modal data into hash codes that are suitable for quantization. Spectral Multimodal Hashing (SMH) [26] uses spectrum analysis of correlation matrices of multi-modal data, learning parameters from the distribution of multi-modal data to get hash codes. On the contrary, supervised models use available data labels to learn more accurate hash features, which is better than unsupervised models in performance. Semantic correlation maximization (SCM) [27] applies nonnegative matrix decomposition and the nearest neighbor preservation algorithm to preserve semantic consistency within modalities and between modalities. Semantic Preserving Hashing (SePH) [28] transforms the semantic matrix into a probability distribution, makes it as close as possible by minimizing the Kullback-Leibler (KL) divergence, and then applies logical regression to learn the hash function of each modal data [29]. Hash functions and binary codes can be learned simultaneously by the data’s similarity matrix with discrete constraints in Enhanced Discrete Multi-modal Hashing (EDMH) [30].

However, the above unsupervised and supervised models all belong to hand-crafted models, which are unable to get the feature relevance between different modal data very well. With the continuous improvement of feature learning, deep neural networks are extensively applied in the cross-modal retrieval field. A deep neural network is introduced into feature learning in Deep Cross-Modal Hashing (DCMH) [31], so the unified model includes feature learning and the generation of hash codes. In Pairwise Relationship Deep Hashing (PRDH) [32], the similarity degree between different modal data is preserved in hash codes while taking into account the similarity between the same modal data. A high-level semantic similarity matrix of continuous values is constructed to guide the learning of hash codes in Deep Multi-level Semantic Hashing (DMSH) [33], which captures the degree of similarity between different modal data. To generate more representative image features, Mask Cross-Modal Hashing (MCMH) [34] effectively combines convolution features with mask features extracted by the Mask R-CNN. Self-supervised adversarial Hashing (SSAH) [35] introduces adversarial loss through the construction of a label network to shorten the distance between image and text distribution, which brings a better retrieval effect. Using cosine distance and Euclidean distance, the same measurement index can accurately reflect the similarity between different modal data in Deep Semantic Cross-Modal Hashing Based on Graph Similarity of Modal-Specific (DCMHGMS) [36]. The distance between similar data can be reduced by constructing ranking alignment loss to unearth the semantic structure between different modal data in Deep Rank Cross-modal Hashing (DRCH) [37, 38]. Semantic weight factors are constructed to guide the optimization of the loss function and obtain better retrieval performance in Multiple Deep neural networks with Multiple labels for Cross-modal Hashing (MDMCH) [39]. A label network is constructed to jointly guide the feature learning of different modal data and innovates discrete optimization strategies to learn hash codes in Deep Discrete Cross-modal Hashing (DDCH) [40]. To increase the correlation between hash codes, Deep Cross-Modal Hashing with Hashing Functions and Unified Hash Codes Jointly Learning (DCHUC) [41] has constructed a new unified joint hash code framework. To improve the accuracy of hash codes in comparative learning, Unsupervised Contrastive Cross-Modal Hashing (UCCH) [42] proposes a momentum optimizer to make the generated hash codes more accurate.

Transformer: The excellent performance of the Transformer is attributed to the exertion of the attention mechanism, and it is widely used in the field of Natural Language Processing (NLP) [43]. It can assign attention weight according to the input data, to determine which part of the data needs attention. On this basis, limited information processing resources are allocated to important parts and so the performance of the model is improved. Google Deep Mind [44] applied it to the computer vision field for the first time and achieved good performance by combining it with Recurrent Neural Network (RNN). Bahdanau et al. [45] prove the effectiveness of attention mechanisms in the NLP. In [46], Google has successfully constructed the Transformer network structure based on the attention mechanism. Due to the limited feature subspace, it is hard to enhance the performance of this ordinary attention mechanism. The multi-head attention mechanism is more likely to capture features from multiple dimensions by dividing attention operations. Inspired by this important achievement, many researchers tried to introduce Transformer structure into computer vision tasks and achieved good results. In 2020, the Vision Transformer (ViT) proposed by Dosovitskiy et al. [47] performed well in many image classification tasks, because it can capture contextual dependencies at different positions in an image. It is simple and effective, with strong scalability. The larger the amount of data, the better the performance of the ViT. When there is enough data for pre-training, the performance of the ViT is even better than that of the convolutional neural network model, which fully proves that ViT can extract excellent features from images.

3 Proposed method

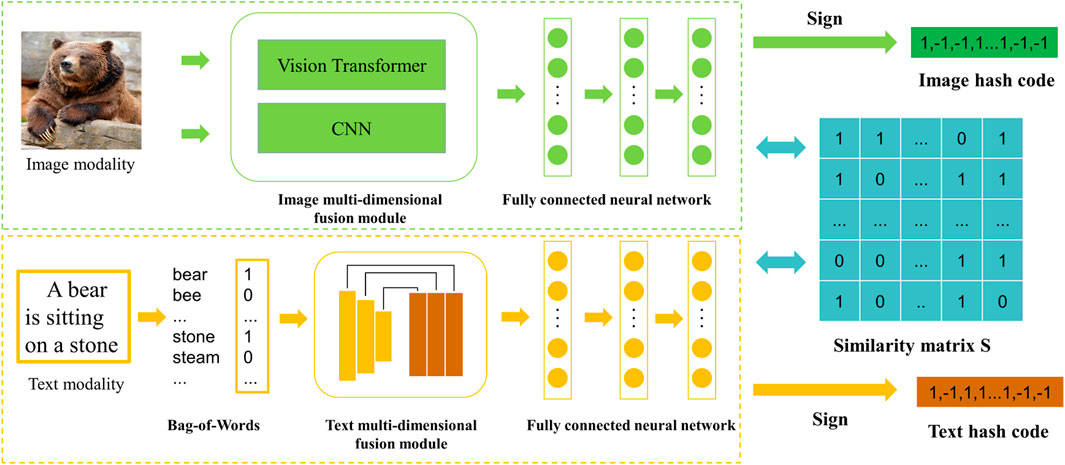
The innovative networks of this paper will be introduced in this section, and the structural framework of MDFFH is shown in Figure 1. To facilitate comparison with other models, images and texts are selected in our model. Our model can be extended to other modalities easily.

Figure 1

Figure 1. The structural framework of MDFFH.

3.1 Notations and problem definitions

Throughout this paper, vectors are denoted by lowercase bold letters (e.g., $\mathbf{z}$), matrices are represented by uppercase bold letters (e.g., $\mathbf{Z}$), and the transposition of the matrix $\mathbf{Z}$ is expressed as ${\mathit{Z}}^{\mathrm{T}}$. For the matrix $\mathbf{Z}$, the ith row, the jth column, the element located in ith row and jth column and the Frobenius norm are denoted by ${\mathit{Z}}_{i\mathrm{*}}$, ${\mathit{Z}}_{\mathrm{*}j}$, $Z_{ij}$ and ${‖\mathbf{Z}‖}_{\text{F}}$, respetively. The sign function represented by $sign\left(x\right)$ is that the value is −1 when x is less than 0, otherwise, the value is 1.

Assume that $O={\left\{O_n\right\}}_{n=1}^N$ denotes the image-text pair dataset, each sample $o_n=(x_n,y_n,l_n)$ includes three parts: one part $x_n\in R^{D_x}$ represents an image feature vector, another part $y\in R^{D_y}$ denotes a text feature vector, and the last part $l_n\in R^C$ denotes the corresponding category labels, where $D_x$, $D_y$ and $C$ are the dimensions of these two modal data’s feature and the number of the category labels respectively. $\mathit{S}\in {\left\{\mathrm{0,1}\right\}}^{N\times N}$ is the matrix to measure the similarity degree between different modalities, called the similarity matrix. $S_{ij}=0$ means that $x_i$ and $y_j$ are not similar to each other and $S_{ij}=1$ denotes that these two data have at least one same category label. The input data is transformed into the corresponding hash codes and the similarity degree between different hash codes is obtained by calculating their Hamming distance in our model. The more similar the hash codes, the smaller the Hamming distance; the greater the difference between hash codes, the greater the Hamming distance. The formula for calculating Hamming distance is

$d\left(c_i,c_j\right)=\frac{1}{2}\left(k-⟨c_i,c_j⟩\right),(1)$

In Eq. 1, $c_i$ and $c_j$ are the hash codes for the vector $x_i$ and $y_j$, $⟨c_i,c_j⟩$ represents their inner product and k is the length of hash codes.

MDFFH aims to obtain two hash functions through training, one is $f\left(x_i;{\theta }_x\right)$ for images, and the other is $g\left(y_j;{\theta }_y\right)$ for texts while maintaining the similarity degree of the original data. Here, ${\theta }_x$ and ${\theta }_x$ denote parameters in the different networks. These hash functions can convert the data into hash codes with unified dimensions for comparison.

3.2 Network architecture

The specific details of the networks in our model are as follows.

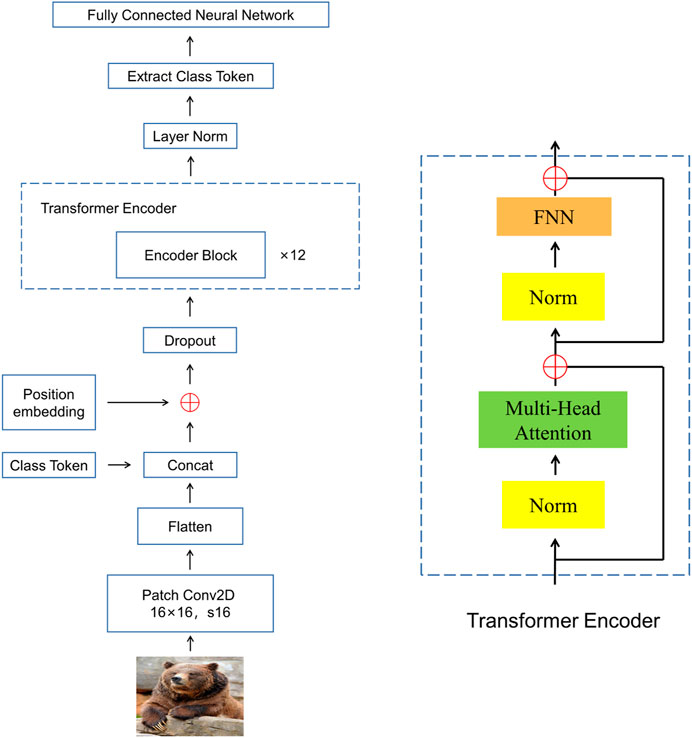
Image network: Image network is mainly composed of an image multi-dimensional fusion module and a fully connected neural network. Specifically, the multi-dimensional image fusion module includes a Vision Transformer network and a convolutional neural network. In the Vision Transformer network, the ViT-B/16 model is chosen as the basic framework and fine-tuned on this basis. We replace the last MLP Head used for the image classification in the ViT-B/16 model with a single-layer completely connected network with 4,096 neurons where the size of each image patch is 16 × 16. The transformer Encoder has 12 Encoder Blocks, which are shown in Figure 2. At the same time, the first six layers of CNN-F [48] are selected as the model of a convolution neural network. In addition, these two networks are pre-rained on ImageNet [49] to obtain initialization parameters. Finally, the output results of these two networks are fused into the multi-dimensional semantic features learned by the image fusion module by vector concatenation. The fully connected neural network has three layers, in which the number of neurons is 8,192, 4,096, and the hash code length in turn.

Figure 2

Figure 2. Detailed introduction of Vision Transformer.

Text network: Bag-of-Words (BoW) is usually used to convert text into vectors, but the sparsity of vectors makes it impossible to fully capture the text’s semantic information. Inspired by [28], we adopt a text multi-dimensional fusion module to solve this problem. The text multi-dimensional fusion module extracts the text semantic features in different dimensions through five average pool layers (the scales are 1a, 2a, 3a, 6a, and 10a, where “a” represents the parameter), and uses 1 × 1 convolution layer to integrate multiple features. At the end of this network, there is a three-layer completely connected network to extract the text’s hash codes and the numbers of neurons in every layer are 4,096, 4,096, and the hash code length.

3.3 Hash code learning

The performance of the cross-modal hashing model depends on whether generated hash codes can effectively reflect the similarity degree between different modalities. Generally speaking, the Hamming distance of hash codes generated by similar original data should be small, and vice versa. To ensure that MDFFH can achieve excellent retrieval performance, we have established an objective function composed of two terms: semantic similarity loss and hashing code quantization loss. We apply ${\mathit{P}}_{*i}=f(x_i;{\theta }_x)$ to denote the learned feature from the image network, where ${\theta }_x$ presents the network parameters. Let ${\mathit{Q}}_{*i}=g(y_i;{\theta }_y)$ denote the learned feature from the text network, where ${\theta }_y$ refers to the network parameters.

To minimize the semantic gap, we transform different modal data to the same common semantic space to measure similarity. Here, the formula of the likelihood function can be written as follows:

$\mathit{p}\left(S_{ij}|{\mathit{P}}_{*i},{\mathit{Q}}_{*j}\right)=\left\{\begin{array}{cc}\sigma \left({\mathrm{\Phi }}_{\mathrm{i}\mathrm{j}}\right),\hfill & S_{ij}=1\hfill \\ 1-\sigma \left({\mathrm{\Phi }}_{\mathrm{i}\mathrm{j}}\right),\hfill & S_{ij}=0\hfill \end{array}\right.(2)$

In Eq. 2, ${\mathrm{\Phi }}_{ij}=\frac{1}{2}{\mathit{P}}_{*i}^T{\mathit{Q}}_{*j}$ and $\sigma ({\mathrm{\Phi }}_{ij})=\frac{1}{1+e^{-{\mathrm{\Phi }}_{ij}}}$. When $S_{ij}=1$, the inner product of ${\mathit{P}}_{\mathrm{*}i}$ and ${\mathit{Q}}_{\mathrm{*}j}$ will be bigger, which is equivalent to that the two data are more similar. On the contrary, the more dissimilar the two data are when $S_{ij}=0$.

The maximization of the likelihood function is equal to the maximization of the negative log-likelihood function. To facilitate the training of MDFFH, the above formula can be converted into the following formula:

$J_{\mathit{similarity}}=-{\displaystyle \sum _{i,j=1}^N}\left(S_{ij}{\mathrm{\Phi }}_{ij}-\log \left(1+e^{{\mathrm{\Phi }}_{ij}}\right)\right),(3)$

where ${\mathrm{\Phi }}_{ij}=\frac{1}{2}{\mathit{P}}_{*i}^T{\mathit{Q}}_{*j}$.

Since the output of the continuous variables from the network is converted into hash binary codes through symbolic functions, there is a certain quantization loss. Therefore, we set the quantization loss term of hash binary codes to reduce this error:

$J_{\mathit{quantization}}={‖{\mathit{H}}^x-\mathit{P}‖}_F^2+{‖{\mathit{H}}^y-\mathit{Q}‖}_F^2,(4)$

where ${\mathit{H}}^x=sign\left(\mathit{P}\right)$ and ${\mathit{H}}^y=sign\left(\mathit{Q}\right)$.

From Equations 3, 4, we can get the objective function for optimizing MDFFH as follows:

$\begin{array}{cc}\hfill \underset{H,{\theta }_x,{\theta }_y}{\min }J& =J_{\mathit{similarity}}+\eta J_{\mathit{quantization}}\hfill \\ \hfill & =-{\displaystyle \sum _{i,j=1}^N}\left(S_{ij}{\mathrm{\Phi }}_{ij}-\log \left(1+e^{{\mathrm{\Phi }}_{ij}}\right)\right)\hfill \\ \hfill & +\eta \left({‖{\mathit{H}}^x-\mathit{P}‖}_F^2+{‖{\mathit{H}}^y-\mathit{V}‖}_F^2\right),\hfill \end{array}(5)$

In Eq. 5, $\eta$ denotes the hyper-parameter of the hash code quantization loss. Inspired by Jiang et al. [31], we set $\mathit{H}={\mathit{H}}^x={\mathit{H}}^y$ during model training.

3.4 Optimization

Given the discreteness of hash codes, we apply an alternating learning strategy to optimize MDFFH: at one time, only one parameter is optimized while the rest of the parameters are unchanged. In the optimization process, the model parameters are updated by the back-propagation with stochastic gradient descent (SGD). The optimization steps are shown in Algorithm 1. Generally, it includes three steps:

1. Optimize ${\theta }_x$ with ${\theta }_y$ and $H$ fixed.

Select any image data $x_i$, and obtain the partial derivative of our objective function as following in Eq. 6:

$\frac{\partial J}{\partial {\mathit{P}}_{*i}}=\frac{1}{2}{\displaystyle \sum _{j=1}^N}\left(\sigma \left({\mathrm{\Phi }}_{ij}\right){\mathit{Q}}_{*j}-S_{ij}{\mathit{Q}}_{*j}\right)+2\eta \left({\mathit{P}}_{*i}-{\mathit{H}}_{*i}\right).(6)$

Then through the chain derivation rule, we can get $\frac{\partial J}{\partial {\theta }_x}$ from $\frac{\partial J}{\partial {\mathit{P}}_{*i}}$ and optimize ${\theta }_x$ according to BP.

2. Optimize ${\theta }_y$ with ${\theta }_x$ and $H$ fixed.

Select any data $y_i$, and obtain the derivative of the objective function as following in Eq. 7:

$\frac{\partial J}{\partial {\mathit{Q}}_{*j}}=\frac{1}{2}{\displaystyle \sum _{i=1}^N}\left(\sigma \left({\mathrm{\Phi }}_{ij}\right){\mathit{P}}_{*i}-S_{ij}{\mathit{P}}_{*i}\right)+2\eta \left({\mathit{Q}}_{*j}-{\mathit{H}}_{*j}\right).(7)$

Then through the chain derivation rule, we can get $\frac{\partial J}{\partial {\theta }_y}$ from $\frac{\partial J}{\partial {\mathit{Q}}_{*j}}$ and optimize ${\theta }_y$ according to BP.

3. Optimize hash codes $\mathit{H}$.

The objective function can be converted into the formula as follows:

$\begin{array}{c}\underset{H}{\max }tr\left({\mathit{H}}^T\left(\eta \left(\mathit{P}+\mathit{Q}\right)\right)\right)=tr\left({\mathit{H}}^T\mathit{R}\right)={\displaystyle \sum _{i,j}}{H}_{ij}{R}_{ij},\hfill \\ s.t.\mathit{H}\in {\left\{-1,+1\right\}}^{k\times N}\hfill \end{array}(8)$

In Eq. 8 $\mathit{R}=\eta (\mathit{P}+\mathit{Q})$. At last, the hash code matrix H is updated according to the feature matrixes of images and text as following in Eq. 9:

$H=sign\left(\eta \left(\mathit{P}+\mathit{Q}\right)\right).(9)$

3.5 Out-of-sample extension

The hash codes of the data not used for training are generated by the hash functions learned by MDFFH. For example, given the query image $x_q$, we can get its hash codes by the hash function as following in Eq. 10:

$h_q^x=sign\left(f\left(x_q;{\theta }_x\right)\right)(10)$

Similarly for text data $y_q$, we can get its hash codes by the hash function as following in Eq. 11:

$h_q^y=sign\left(g\left(y_q;{\theta }_y\right)\right)(11)$

4 Experiments

Based on two commonly used data sets, namely, MIRFLICKR-25K [50] and NUS-WIDE [51], we conduct a large number of experiments comparing the results with some representative baselines to verify the validity of our model. It is noted that our model can be easily applied to other similar datasets.

4.1 Datasets

MIRFLICKR-25K [50]: There are 25,000 images from the Flickr website in this dataset, and every image has text descriptions and labels, thus forming data pairs. During the experiment, we only retain 20,015 data pairs, because there are too few text descriptions for some data pairs. For each text description, the Bag-of-Word model is applied to convert it into 1386-dimensional vector form, and the corresponding label is transformed into 24-dimensional vector form. 2000 data pairs are randomly selected for querying and the rest for retrieval. For model training, we select 10,000 data pairs from retrieval.

NUS-WIDE [51]: There are 269,648 data pairs in this dataset, and each includes images, text descriptions, and data labels. There is a total of 81 categories of original data labels in this dataset. We selected 21 of the most common data labels as the experimental dataset and finally retained 195,834 data pairs after processing. Text descriptions and data labels in each data pair are converted into 1,000 and 21-dimensional vector forms through the Bag-of-Word model. The partition of different sets for model training in this dataset is consistent with the MIRFLICKR-25 dataset.

4.2 Evaluation and baselines

Evaluation: For cross-modal retrieval, researchers usually study two typical tasks: retrieving text with images and retrieving images with text.

To evaluate MDFFH’s performance, we select the two most commonly used evaluation criteria, namely, the Precision-Recall (PR) Curve and Mean Average Precision (MAP) [52]. The average accuracy (AP) of any query data is calculated as follows:

$AP=\frac{1}{K}{\displaystyle \sum _{s=1}^M}U\left(s\right)V\left(s\right),(12)$

where $K$ and $M$ are the numbers of retrieved relevant data and the retrieval set, $U\left(s\right)$ denotes the proportion of the first $s$ retrieved data related to the query data, and $V\left(s\right)$ shows whether the retrieved sth data is related to the query data, which can be judged by the category label. If two data are related, $V\left(s\right)=1$, otherwise, $V\left(s\right)=0$. The MAP value can be calculated by averaging the APs of all query data and is positively correlated with model performance.

In addition, the PR curve is another indicator for evaluating the model performance. The performance can be directly judged by drawing a PR curve of this model: if the area under this curve is larger, the model performance is better. Moreover, the corresponding recall and precision can be obtained by altering the Hamming radius and drawing the PR curve.

Baselines: We compare our MDFFH with nine representative models, which are CCA, CMFH, SCM, STMH, SePH, DCMH, DDCH, DCHUC, and UCCH. The first four models belong to hand-crafted models and the rest are deep network models.

4.3 Implementation details

We use PyTorch, which is a deep-learning framework based on dynamic tensors, to implement our MDFFH on the NVIDIA RTX 3090 server and the iteration number is set to 300. In the iteration, the learning rate gradually decreases from 0.03 initialized to 10^–6. The hyper-parameter $\eta$ is set to 1, and the detailed parameter analysis is in the section Parameter Analysis. For each model result, experiments have been run five times and the average value is obtained as a representative.

4.4 Performance

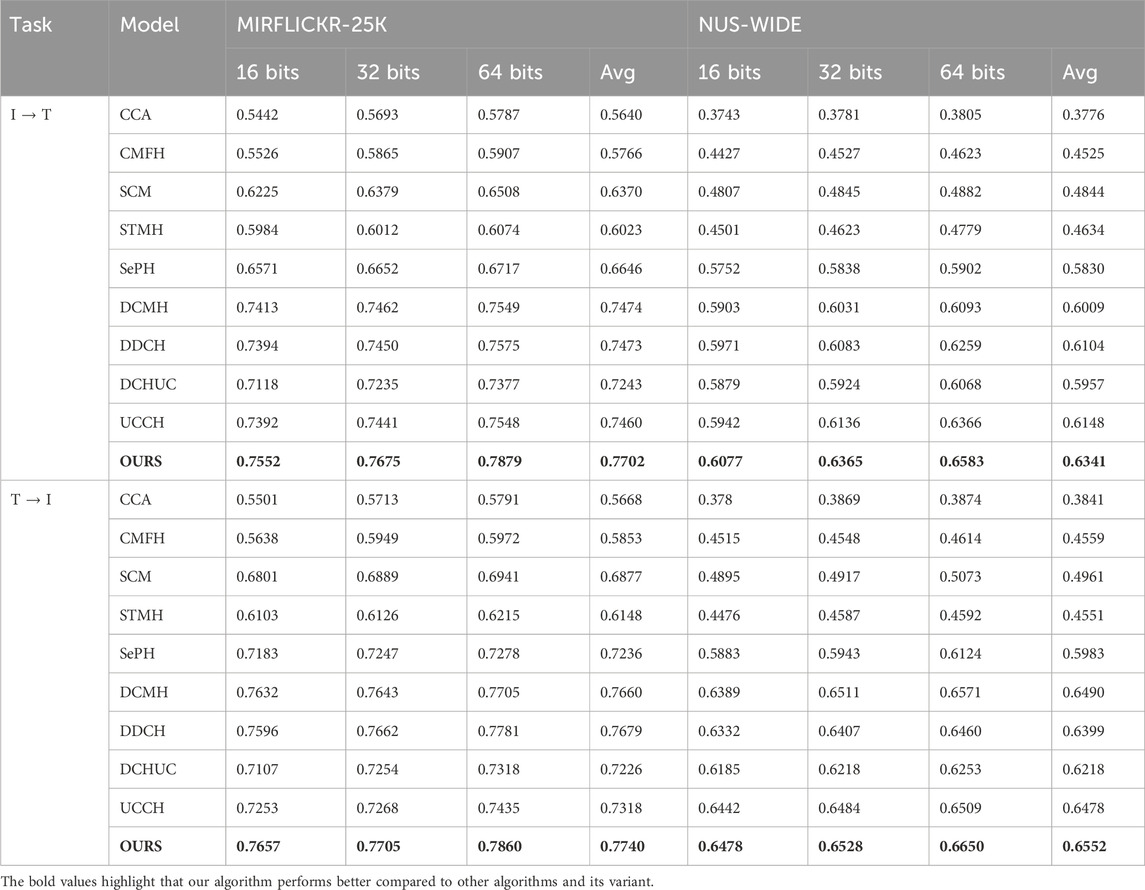
The MAP scores of MDFFH and nine baseline models based on two general datasets are shown in Table 1, where “I → T” represents from image to retrieve text and “T → I” represents from text to retrieve images. We can find that for hash codes with different lengths, our model is superior to baseline models. For example, when we select the MIRFLICKR-25K dataset, compared with DCMH which is the most representative deep cross-modal hashing model, MDFFH on “I → T” tasks increased by 3.05% on average, and its MAP score on text retrieval image tasks increased by 1.04% on average. On the NUS-WIDE dataset, compared with DCMH, MDFFH’s MAP score on image retrieval text tasks increased by 5.52% on average, and its MAP score on text retrieval image tasks increased by 0.95% on average. In particular, compared with these five hand-crafted baseline models, MDFFH has been greatly improved. This proves that better performance can be achieved by integrating feature learning and the generation of hash codes into a unified end-to-end network. At the same time, MDFFH has a better performance compared with DCMH and DDCH. The reason is that DCMH and DDCH generate hash codes only using single-dimensional semantic features, ignoring the information complementation between multi-dimensional semantic features, which has certain limitations. On the contrary, MDFFH applies the image multi-dimensional fusion module and the text multi-dimensional fusion module to get the multi-dimensional semantic features of different modal data, which can mine richer semantic associations and establish more accurate modal relationships, thus helping to narrow the modal gap to greatly improve the retrieval accuracy.

Table 1

Table 1. MAP scores of different models.

When the hash code length is set to 16 bits, the PR curves of MDFFH and baseline models under MIRFLICKR-25K and NUS-WIDE datasets are demonstrated in Figure 3. For PR curves of different models, which curve has a larger area represents better performance. From this figure, it is clear that the performance of MDFFH outperforms other baselines, which is consistent with the application of MAP as a performance evaluation index.

Figure 3

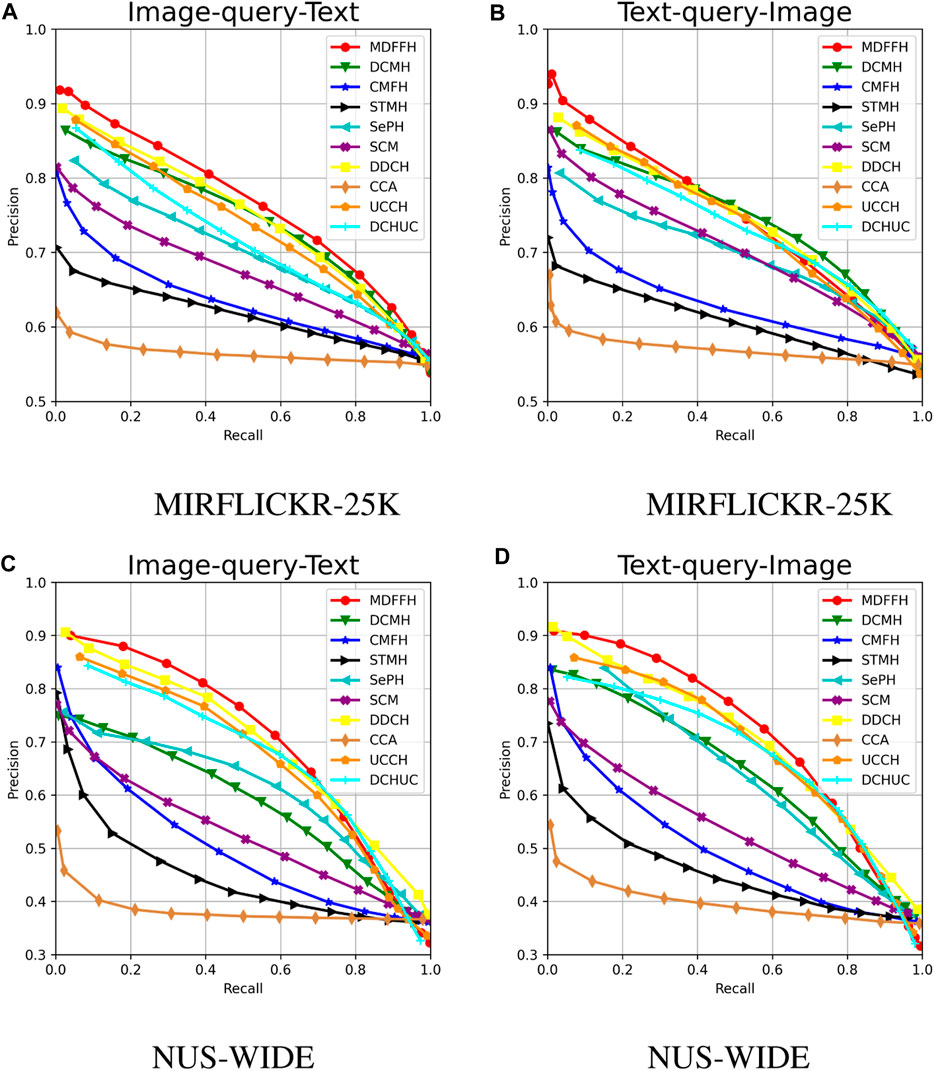
Figure 3. The PR curves with code length 16. (A) MIRFLICKR-25K. (B) MIRFLICKR-25K. (C) NUS-WIDE. (D) NUS-WIDE.

4.5 Parameter analysis

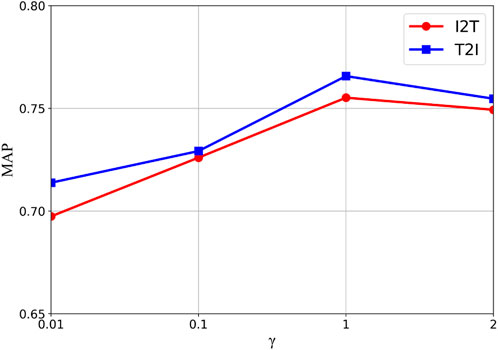
The influence of hyper-parameter values in the model based on the MIRFLICKR-25K dataset is studied in this section. The hash code length is uniformly 16 bits and the experimental results are shown in Figure 4. The MAP scores of two cross-modal retrieval tasks change with the hyper-parameter. During the manual adjustment of the hyper-parameter, the range of values is 0.01, 0.1, 1, and 2. The experimental results demonstrate the MDFFH performance can reach the best under the setting of $\gamma =1$. The initial values of other network parameters are randomly generated and then determined through network learning.

Figure 4

Figure 4. The sensitivity analysis of the hyper-parameter.

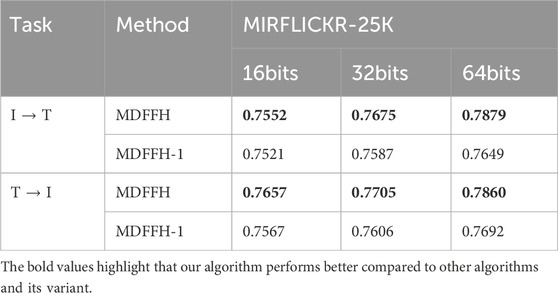
4.6 Ablation study

We have designed one variant and carried out experiments to verify whether the innovative module in MDFFH improves the overall performance. MDFFH-1 is a variant of MOFFH without a Vision Transformer. The variant aims to check the important influence of the innovative image multi-dimensional fusion module on our model’s retrieval performance. Table 2 shows the comparative results. From this table, it is clear that MDFFH’s performance is better than MDFFH-1’s performance on the MIRFLICKR-25K dataset because of the effective role of the image multi-dimensional fusion module. The image multi-dimensional fusion module effectively combines the global image information concerned by the Vision Transformer with the local image information concerned by the convolutional neural network to generate more representative multi-dimensional semantic features. This can more effectively get the semantic similarity between different data to learn more accurate hash mapping functions, and so improve our model performance.

Table 2

Table 2. The MAP scores of MDFFH and its variant.

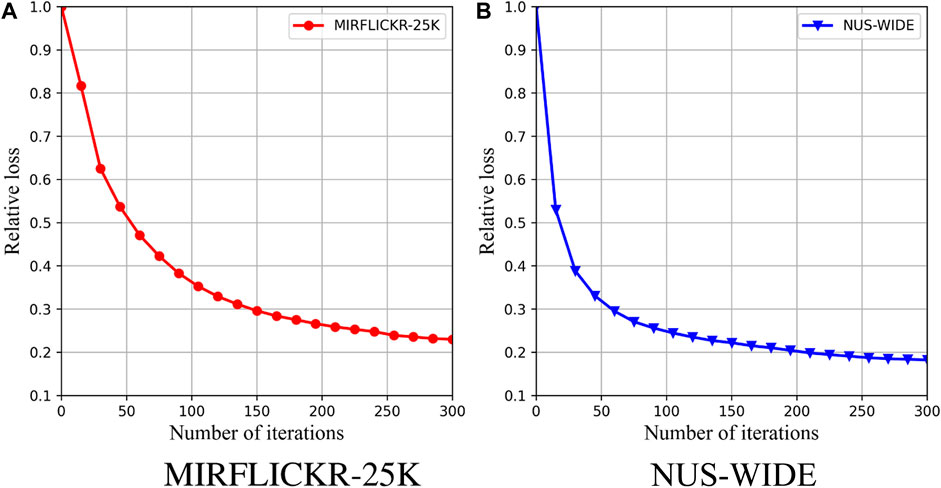
4.7 Convergence analysis

For analyzing MDFFH’s convergence, experiments are conducted on MIRFLICKR-25K and NUS-WIDE datasets. During the experiment, the hash code length is 16 bits and the relative loss is used as an evaluation criterion. The relative loss of the ith iteration is the ratio of the loss function value of the ith iteration divided by the loss function value of the first iteration and the experimental results are shown in Figure 5. With the number of iterations increasing, the relative loss value decreases rapidly and becomes stable, which means our optimization algorithm is effective.

Figure 5

Figure 5. The convergence curve of MDFFH. (A) MIRFLICKR-25K. (B) NUS-WIDE.

5 Conclusion

A new cross-modal hashing model named MDFFH is proposed from the perspective of multi-dimensional semantic features. The image multi-dimensional fusion module constructed effectively combines the convolutional neural network and Vision Transformer and can generate multi-dimensional semantic features of images with richer semantic information. Similarly, we apply the text multi-dimensional fusion module to generate more representative text multi-dimensional semantic features, which provides a basis for mining richer semantic associations and building more accurate modal relationships, thus making the generated hash code more semantic. Experimental analysis of two general datasets can verify that our MDFFH model improves the performance of cross-modal retrieval. In future work, we will attempt to investigate its applications in the field of multimodal generation, multimodal question answering, and health and medical big data retrieval.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DR: Conceptualization, Data curation, Formal Analysis, Investigation, Resources, Supervision, Writing–review and editing. WX: Writing–original draft and Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author WX was employed by the company Industrial and Commercial Bank of China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Li Q, Li L, Li Y. Developing ChatGPT for biology and medicine: a complete review of biomedical question answering. Biophys Rep (2024) 9:1–20. doi:10.52601/bpr.2024.240004

CrossRef Full Text | Google Scholar

2. Mandal RC, Kler R, Tiwari A, Keshta I, Abonazel MR, Tageldin EM, et al. Enhancing stock price prediction with deep cross-modal information fusion network. Fluctuation Noise Lett (2024) 23(02). doi:10.1142/s0219477524400170

CrossRef Full Text | Google Scholar

3. Ma Y, Yu C, Yan M, Sangaiah AK, Wu Y. Dark-side avoidance of mobile applications with data biases elimination in socio-cyber world. IEEE Trans Comput Soc Syst (2023) 1–10. doi:10.1109/TCSS.2023.3264696

CrossRef Full Text | Google Scholar

4. Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via hashing (2000).

Google Scholar

5. Luo K, Zhang C, Li H, Jia X, Chen C. Adaptive marginalized semantic hashing for unpaired cross-modal retrieval. IEEE Trans Multimedia (2022) 25:9082–95. doi:10.1109/tmm.2023.3245400

CrossRef Full Text | Google Scholar

6. Kebaili A, Lapuyade-Lahorgue J, Su R. Deep learning approaches for data augmentation in medical imaging: a review. J Imaging (2023) 9(4):81. doi:10.3390/jimaging9040081

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang J, Shen HT, Song J, Ji J. Hashing for similarity search: a survey (2019). arXiv preprint 2019, arXiv:1408.2927.

Google Scholar

8. Su MY, Gu GH, Ren XL, Fu H, Zhao Y. Semi-supervised knowledge distillation for cross-modal hashing. IEEE Trans Multimedia (2023) 25:662–75. doi:10.1109/TMM.2021.3129623

CrossRef Full Text | Google Scholar

9. Long J, Sun L, Hua L, Yang Z. Discrete semantics-guided asymmetric hashing for large-scale multimedia retrieval. Appl Sci (2021) 11:8769. doi:10.3390/app11188769

CrossRef Full Text | Google Scholar

10. Yao D, Li ZX, Li B, Zhang CL, Ma HF. Similarity graph-correlation reconstruction network for unsupervised cross-modal hashing. Expert Syst Appl (2023) 237:121516. doi:10.1016/j.eswa.2023.121516

CrossRef Full Text | Google Scholar

11. Lu X, Zhang HX, Sun JD, Wang ZH, Guo PL, Wan WB. Discriminative correlation hashing for supervised cross-modal retrieval. In: Signal processing: image communication (2018).

CrossRef Full Text | Google Scholar

12. Shen F, Shen C, Liu W, Shen HT. Supervised discrete hashing. In: Proceedings of the 2015 IEEE conference on computer vision and pattern recognition. Boston, MA, USA: CVPR (2015).

CrossRef Full Text | Google Scholar

13. Song J, Yang Y, Huang Z, Yang Y, Shen HT. Inter-media hashing for large-scale retrieval from heterogeneous data sources. In: Proceedings of the ACM SIGMOD (2013). p. 785–96.

CrossRef Full Text | Google Scholar

14. Hong L, Ji R, Wu Y, Huang F, Zhang B. Cross-modality binary code learning via fusion similarity hashing. In: Proceedings of the 2017 IEEE conference on computer vision and pattern recognition. Honolulu, HI, USA: CVPR (2017).

Google Scholar

15. Ren D, Xu W, Wang Z, Sun Q. Deep label feature fusion hashing for cross-modal retrieval. IEEE Access (2022) 10:100276–85. doi:10.1109/access.2022.3208147

CrossRef Full Text | Google Scholar

16. Zou X, Wang X, Bakker EM, Wu S. Multi-label semantics preserving based deep cross-modal hashing. Signal Processing: Image Communicationbr (2021) 93:116131. doi:10.1016/j.image.2020.116131

CrossRef Full Text | Google Scholar

17. Qiang H, Wan Y, Liu Z, Xiang L, Meng X. Discriminative deep asymmetric supervised hashing for cross-modal retrieval. Knowledge-Based Syst (2020) 204:106188. doi:10.1016/j.knosys.2020.106188

CrossRef Full Text | Google Scholar

18. Jin M, Zhang HX, Zhu L, Sun JD, Liu L. Coarse-to-fine dual-level attention for video-text cross-modal retrieval. Knowledge-Based Syst (2022) 242:108354. doi:10.1016/j.knosys.2022.108354

CrossRef Full Text | Google Scholar

19. Wang Z, Wang M, He P, Xu J, Lu G. Unsupervised cross-modal retrieval based on deep convolutional neural networks. In: 2022 4th international conference on advances in computer technology, information science and communications (CTISC) (2022).

CrossRef Full Text | Google Scholar

20. Wang T, Zhu L, Cheng ZY, Li JJ, Gao Z. Unsupervised deep cross-modal hashing with virtual label regression. Neurocomputing (2020) 386:84–96. doi:10.1016/j.neucom.2019.12.058

CrossRef Full Text | Google Scholar

21. Hotelling H. Relations between two sets of variates. Breakthroughs Stat (1992) 162–90.

CrossRef Full Text | Google Scholar

22. Ding G, Guo Y, Zhou J. Collective matrix factorization hashing for multimodal data. In: Proceedings of the 2014 IEEE conference on computer vision and pattern recognition. Columbus, OH, USA: CVPR (2014).

CrossRef Full Text | Google Scholar

23. Zhou J, Ding G, Guo Y. Latent semantic sparse hashing for cross-modal similarity search. In: Proceedings of the ACM SIGIR (2014). p. 415–24.

CrossRef Full Text | Google Scholar

24. Xie L, Zhu L, Yan P. Cross-Modal Self-Taught Hashing for large-scale image retrieval. In: Signal processing. 124. The Official Publication of the European Association for Signal Processing (2016).

CrossRef Full Text | Google Scholar

25. Wang D, Gao X, Wang X, He L. Semantic topic multimodal hashing for cross-media retrieval. In: Proceedings of the 2015 international joint conference on artificial intelligence. Buenos Aires Argentina: IJCAI (2015).

Google Scholar

26. Zhen Y, Gao Y, Yeung D, Zha H, Li X. Spectral multimodal hashing and its application to multimedia retrieval. IEEE Trans Cybernetics (2016) 46:27–38. doi:10.1109/tcyb.2015.2392052

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang D, Li W. Large-scale supervised multimodal hashing with semantic correlation maximization. In: Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence. Québec City, Québec Canada: AAAI (2014).

CrossRef Full Text | Google Scholar

28. Lin Z, Ding G, Hu M, Wang J. Semantics-preserving hashing for cross-view retrieval. In: Proceedings of the 2015 IEEE conference on computer vision and pattern recognition. Boston, MA, USA: CVPR (2015).

CrossRef Full Text | Google Scholar

29. Qi XJ, Zeng XH, Wang SM, Xie YC, Xu LM. Cross-modal variable-length hashing based on hierarchy. Intell Data Anal (2021) 25(3):669–85. doi:10.3233/IDA-205162

CrossRef Full Text | Google Scholar

30. Chen Y, Zhang H, Tian Z, Wang D, Li X. Enhanced discrete multi-modal hashing: more constraints yet less time to learn. IEEE Trans Knowledge Data Eng (2022) 34:1177–90. doi:10.1109/tkde.2020.2995195

CrossRef Full Text | Google Scholar

31. Jiang Q, Li W. Deep cross-modal hashing. In: Proceedings of the 2017 IEEE conference on computer vision and pattern recognition. Honolulu, HI, USA: CVPR (2017).

CrossRef Full Text | Google Scholar

32. Yang E, Deng C, Liu W, Liu X, Tao D, Gao X. Pairwise relationship guided deep hashing for cross-modal retrieval. In: Proceedings of the 2017 association for the advancement of artificial intelligence. San Francisco, California, USA: AAAI (2017).

CrossRef Full Text | Google Scholar

33. Ji Z, Yao W, Wei W, Song H, Pi H. Deep multi-level semantic hashing for cross-modal retrieval. IEEE Access (2019) 7:23667–74. doi:10.1109/access.2019.2899536

CrossRef Full Text | Google Scholar

34. Lin Q, Cao W, He Z, He Z. Mask cross-modal hashing networks. IEEE Trans Multimedia (2020) 14:550–8. doi:10.1109/tmm.2020.2984081

CrossRef Full Text | Google Scholar

35. Li C, Deng C, Li N, Liu W, Gao X, Tao D. Self-supervised adversarial hashing networks for cross-modal retrieval. In: Proceedings of the 2018 IEEE conference on computer vision and pattern recognition. Salt Lake City, UT, USA: CVPR (2018).

CrossRef Full Text | Google Scholar

36. Li J. Deep semantic cross-modal hashing based on graph similarity of modal-specific. IEEE Access (2021) 9:96064–75. doi:10.1109/access.2021.3093357

CrossRef Full Text | Google Scholar

37. Liu X, Zeng H, Shi Y, Zhu J, Ma K. Deep Rank cross-modal hashing with semantic consistent for image-text retrieval. In: IEEE international conference on acoustics, speech and signal processing (2022). p. 4828–32.

CrossRef Full Text | Google Scholar

38. Zhu X, Cai L, Zou Z, Zhu L. Deep multi-semantic fusion-based cross-modal hashing. Mathematics (2022) 10:430–20. doi:10.3390/math10030430

CrossRef Full Text | Google Scholar

39. Xie Y, Zeng X, Wang T, Xu L, Wang D. Multiple deep neural networks with multiple labels for cross-modal hashing retrieval. Eng Appl Artif Intelligence (2022) 114:105090. doi:10.1016/j.engappai.2022.105090

CrossRef Full Text | Google Scholar

40. Yu E, Ma J, Sun J, Chang X, Zhang H, Hauptmann AG. Deep discrete cross-modal hashing with multiple supervision. Neurocomputing (2022) 486:215–24. doi:10.1016/j.neucom.2021.11.035

CrossRef Full Text | Google Scholar

41. Tu R, Mao X, Ma B, Hu Y, Yan T, Huang H, et al. Deep cross-modal hashing with hashing functions and unified hash codes jointly learning. IEEE Trans Knowledge Data Eng (2022) 34:560–72. doi:10.1109/tkde.2020.2987312

CrossRef Full Text | Google Scholar

42. Hu P, Zhu H, Lin J, Peng D, Zhao Y, Peng X. Unsupervised contrastive cross-modal hashing, IEEE Trans Pattern Anal Mach Intell (2023) 45:3877–89. doi:10.1109/TPAMI.2022.3177356

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Tay Y, Dehghani M, Bahri D, Metzler D. Efficient transformers: a survey (2009). arXiv: 2009.06732.

Google Scholar

44. Mnih V, Heess N, Graves A, Kavukcuoglu K. Recurrent models of visual attention. Adv Neural Inf Process Syst (2014) 27:2204–12. doi:10.48550/arXiv.1406.6247

CrossRef Full Text | Google Scholar

45. Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate (2014). arXiv preprint 2014, arXiv: 1409.0473.

Google Scholar

46. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A, et al. Attention is all you need (2014). arXiv preprint 2017, arXiv: 1706.03762.

Google Scholar

47. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, et al. An image is worth 16x16 words: transformers for image recognition at scale (2020). arXiv preprint 2020, arXiv: 2010.11929v2.

Google Scholar

48. Chatfield K, Simonyan K, Vedaldi A, Zisserman A. Return of the devil in the details: delving deep into convolutional nets (2014). arXiv preprint 2014, arXiv: 1405.3531.

Google Scholar

49. Russakovsky O, Deng J, Su H, Krause J, Satheesh S, Ma S, et al. ImageNet large scale visual recognition challenge. Int J Comput Vis (2015) 115:211–52. doi:10.1007/s11263-015-0816-y

CrossRef Full Text | Google Scholar

50. Huiskes MJ, Lew MS. The MIR Flickr retrieval evaluation. In: Proceedings of the 1st ACM international conference on Multimedia information retrieval (2008). p. 39–43.

CrossRef Full Text | Google Scholar

51. Chua T, Tang J, Hong R, Li H, Luo Z, Zheng Y. NUS-WIDE: a real-world web image database from the National University of Singapore. In: Proceedings of the ACM international conference on image and video retrieval (2009). p. 1–9.

Google Scholar

52. Liu W, Mu C, Kumar S, Chang S. Discrete graph hashing. Adv Neural Inf Process Syst (2014) 4:3419–27.

Google Scholar