Globally optimal interferometry with lossy twin Fock probes

Parity or quadratic spin (e.g., $J_z^2$) readouts of a Mach–Zehnder (MZ) interferometer probed with a twin Fock (TF) input state allow saturating the optimal sensitivity attainable among all mode-separable states with a fixed total number of particles but only when the interferometer phase θ is near zero. When more general Dicke state probes are used, the parity readout saturates the quantum Fisher information (QFI) at θ = 0, whereas better-than-standard quantum limit performance of the $J_z^2$ readout is restricted to an $o(\sqrt{N})$ occupation imbalance. We show that a method of moments readout of two quadratic spin observables $J_z^2$ and $J_{+}^2+J_{-}^2$ is globally optimal for Dicke state probes; i.e., the error saturates the QFI for all θ. In the lossy setting, we derive the time-inhomogeneous Markov process describing the effect of particle loss on TF states, showing that the method of moments readout of four at-most-quadratic spin observables is sufficient for globally optimal estimation of θ when two or more particles are lost. The analysis culminates in a numerical calculation of the QFI matrix for distributed MZ interferometry on the four-mode state $|\frac{N}{4},\frac{N}{4},\frac{N}{4},\frac{N}{4}\rangle$ and its lossy counterparts, showing that an advantage for the estimation of any linear function of the local MZ phases θ₁ and θ₂ (compared to independent probing of the MZ phases by two copies of $|\frac{N}{4},\frac{N}{4}\rangle$) appears when more than one particle is lost.

1 Introduction

In the context of optical interferometry with non-classical states of light, the optical twin Fock (TF) state was introduced as a candidate probe state that minimizes phase fluctuations between the arms of an interferometer [1]. The operating principle of the interferometer is that although the input TF state has maximal phase uncertainty prior to entering a Mach–Zehnder (MZ) interferometer, its phase variance after the first beamsplitter is lower by a factor of O(I⁻¹) compared to a probe state consisting of single-mode lasers of the same total intensity I per measurement interval (lowering the optical standard quantum limit sensitivity of O(I⁻¹) to optical Heisenberg limit sensitivity O(I⁻²)). For present-day laser-based gravitational wave detectors, suppression of phase and amplitude fluctuations across the operating spectrum motivates the use of novel non-classical electromagnetic field probe states. In the LIGO interferometer, for example, phase fluctuations in the quantum electromagnetic field give rise to the photonic shot noise that constitutes the primary limitation to sensitivity in the high-frequency domain. Fluctuations in the amplitude quadrature give rise to the radiation pressure noise that constitutes the primary limitation to sensitivity in the low-frequency domain [2, 3]. Therefore, preparation of a probe field with frequency-dependent quadrature squeezing enables globally improved noise spectral densities [4, 3]. However, even at fixed wavelength, state-of-the-art optical TF states with O(1) photons are produced only probabilistically [5] and not with intensities large enough to be relevant for application in LIGO.

On the other hand, matter–wave interferometry with ensembles of phase-coherent atoms provides an alternative framework for gravitational wave detection [6, 7]. Analogous to the optical TF state, a TF state of massive bosons produced by strong repulsion of atoms in a double-well optical trap could potentially improve the sensitivity of such matter–wave interferometers beyond the atomic standard quantum limit (1/N scaling of the optimal estimator variance, where N is the number of atoms). While traditional atom interferometers apply optimal Bragg-splitting schemes to non-entangled states such as a Bose–Einstein condensate to produce an optimal non-entangled probe state [8, 9], the input TF state exhibits particle entanglement [10] and remains entangled throughout the MZ interferometer sequence. As far as experimental atom interferometry is concerned, the sensitivity boost provided by TF states can allow smaller MZ loops to be used in the interferometry sequence. TF states of neutral atoms in an optical dipole trap have been prepared with O(10⁴) atoms [11].

This work focuses on the parameter estimation setting defined using an MZ interferometer [12], which applies the operation $e^{i\frac{\pi }{2}{J}_x}{e}^{-i\theta J_z}{e}^{-i\frac{\pi }{2}{J}_x}=e^{-i\theta J_y}$ to the probe state ρ, which is generally a mixed state. From the parametrized state ${\rho }_{\theta }≔e^{-i\theta J_y}\rho e^{i\theta J_y}$, the estimate $\tilde{\theta }$ of the parameter θ is calculated, and it satisfies the one-shot quantum Cramér–Rao inequality.

${\left.{\left(\mathrm{\Delta }\tilde{\theta }\right)}^2\right|}_{\theta }\ge \frac{1}{{\mathcal{F}}_{\theta }},(1)$

where ${\mathcal{F}}_{\theta }$ is the quantum Fisher information (QFI) based on the symmetric logarithmic derivative [13]. The relevant expressions for the QFI depend on whether the probe state ρ is pure or mixed, and we refer to [14] and the references therein for explicit formulas. A globally optimal quantum sensing protocol produces an estimator $\tilde{\theta }$ that saturates (Eq. 1) at all parameter values θ.

In the remainder of this section, we review relevant background on quantum sensing aspects of twin Fock states. In Section 2, we move on to considering the possibility of saturating the inequality (Eq. 1) when applying practical readout schemes to pure, but imperfectly prepared, twin Fock states. We generalize the method of moments error of a single readout observable to a generalized signal-to-noise ratio that quantifies correlated errors of a list of non-commuting observables. Observables are identified for which the generalized signal-to-noise ratio globally saturates the QFI (i.e., saturates the QFI for all θ). Sections 3 and 4, respectively, identify lists of observables associated with a generalized signal-to-noise ratio which globally saturates the QFI for the case of lossy twin Fock probe states and for instances of lossy, spatially extended twin Fock probe states. The spatially extended twin Fock states probe multiple spatially separated interferometric phase shifts, which define a multiparameter sensing setting relevant to, for example, spatially resolved gravimetry and magnetometry. Section 5 summarizes the results and discusses directions for future research.

We now define the TF state and provide background on their known properties related to quantum metrology. The TF state of N bosonic atoms distributed between two orthogonal single-particle modes |0⟩ and |1⟩ is the zero J_z weight vector in a spin-N/2 representation of SU(2). It is the $n=\frac{N}{2}$ case of the more general N-particle Dicke state often written as follows:

$|N-n,n\rangle ≔\frac{1}{\sqrt{\left(\genfrac{}{}{0ex}{}{N}{m}\right)}}{\displaystyle \sum _{\text{Ham}\left(x\right)=n}}{|x_1\rangle }_1\otimes \cdots \otimes {|x_N\rangle }_N,(2)$

where x = x₁…x_N ∈ {0,1}^N is a binary string identified with a computational basis element of N qubits and Ham(x) is its Hamming weight. The notation in the left-hand side owes to the Schwinger boson form of the J_z operator: 2J_z = a^†a − b^†b so that $J_z|N-n,n\rangle =(\frac{N}{2}-n)|N-n,n\rangle$. The state (Eq. 2) is mode-separable because the first-quantized state is actually entangled: if the particles themselves are bipartitioned in any way (i.e., if the N qubits are bipartitioned in any way in Eq. 2) and one of the partitions is traced over, the resulting state is impure.

Our model of the MZ interferometer is the standard one: a two-mode, mode-separable bosonic state |ψ⟩ is parametrized by a phase according to the following equation:

$|\psi \rangle \mapsto |\psi \left(\theta \right)\rangle =e^{i\frac{\pi }{2}{J}_x}{e}^{-i\theta J_z}{e}^{-i\frac{\pi }{2}{J}_x}=e^{-i\theta J_y}|\psi \rangle .(3)$

Eq. 3 is an example of the shift model of parameter estimation [13]. The TF state possesses the following optimality property for sensing the phase difference in the arms of the MZ interferometer: it has the largest QFI on the unitary path generated by J_y over all mode-separable probe states with a fixed total number of particles N = a^†a + b^†b, where N is even [15]. The operator J_y generates the phase difference dynamics of the MZ interferometer.

As pointed out by Lang and Caves, mode-separable states (or product states in the setting of optical MZ interferometry) are the only sensible input states to consider in single-parameter MZ interferometry. The whole purpose of the first beamsplitter is to generate the quantum coherence required for the phase difference sensing task. If one has access to mode-entangled states at the input of the MZ interferometer, an optimal input state is a Greenberger–Horne–Zeilinger (GHZ) state (recall that for N atoms, the GHZ states are a class of states defined as an equal amplitude superposition of the highest and lowest eigenvectors of a total spin operator $\vec{n}\cdot \vec{J}$ in the spin-N/2 representation of $\mathfrak{s}\mathfrak{u}(2)$, where $\vec{n}\in {\mathbb{R}}^3$). On the other hand, in the setting of multiparameter estimation of an SU(2) element, the TF state has a similar basic optimality property as the GHZ state in single-parameter MZ interferometry. The parametrized unitary dynamics $U(\theta )=e^{-i{\theta }_1{J}_x-i{\theta }_2{J}_y}$ and task of minimizing the sum of the mean squared errors of estimates of θ₁ and θ₂ are considered. This total error is bounded below by $\text{tr}({\mathcal{F}}^{-1})$, where $\mathcal{F}$ is the QFI matrix [16]. This quantity, in turn, is lower bounded by $\frac{1}{\text{Var}{J}_x+\text{Var}{J}_y}$, with equality achieved on pure states with a reflection symmetry about J_x or J_y. The minimal value is obtained when 1) the variances are equal, 2) the state is centered in the spherical phase space (i.e., ⟨J_x⟩ = ⟨J_y⟩ = ⟨J_z⟩ = 0), and 3) $⟨J_z^2⟩=0$, all three of which are satisfied by the TF state, with the last condition being unique to the TF state [17]. Fujiwara’s condition for achievability of the QFI bound is also satisfied [18], so there is an estimator that obtains this noise value. Indeed, the method of moments estimation of $\vec{\theta }$ by readout of the non-linear observables $O_j|\frac{N}{2},\frac{N}{2}\rangle \langle \frac{N}{2},\frac{N}{2}|O_j$, with O₁ = J_x and O₂ = J_y, allows saturating the QFI matrix for $\vec{\theta }\to (\mathrm{0,0})$ [19]. Saturation of the QFI matrix can also be obtained using four operators which are at most quadratic in the spin operators [20].

Recent work has shown that Dicke states |N − m, m⟩ can be prepared with $O(m\log \frac{N}{m})$-depth quantum circuits that allow two-qubit operations between any qubit registers [21]. Analog schemes for generating approximate TF states of a system of double-well bosons include the implementation of the two-axis countertwisting Hamiltonian [22] and quantum alternating operator ansatz circuits that approximately convert a tensor product state to the TF state for large N [23]. Experimentally, small twin Fock states have also been generated in internal states of spinor Bose–Einstein condensates [24] and in photons in orthogonal polarization modes [25]. Optimal method of moments readouts for specific single-parameter estimation problems, including MZ interferometry, with probe states consisting of coherent states and spin-squeezed states of spin-1 Bose–Einstein condensates have been analyzed in [26, 27, 28, 29].

2 Pure imperfect TF probes

Unlike other entangled probe states of two-mode bosons such as one-axis-twisted states [30], the physical origin of the sensitivity of TF states for interferometry is not spin-squeezing [31]. Rather, it is the property of low uncertainty in the difference of phase (near a phase difference of zero or π) appearing between the paths of the MZ interferometer after the TF state undergoes the first beamsplitting [32]. In fact, the Dicke state amplitudes of the π/2-rotated TF state are greatest on the |N, 0⟩ and |0, N⟩ states, similar to an approximate GHZ state. Although a GHZ state in the arms of the MZ interferometer allows obtaining the minimal uncertainty of an estimator of the MZ phase, the input state required to generate such a configuration is simply a rotated GHZ state, which is clearly not any easier to generate. By contrast, in the case of ultracold atoms, the TF state can be prepared as the ground state of N atoms in a double-well optical trap [33, 34], which makes it practically advantageous compared to a GHZ probe. Furthermore, loss of a single particle from a GHZ state renders it useless for interferometry beyond O(N) scaling of the QFI [i.e., standard quantum limit (SQL) scaling]. Photon-loss-robust optical states for MZ interferometry were explored as GHZ alternatives in [35].

In this section, we consider the case of pure, but imperfectly prepared, twin Fock states. Such states coincide with sequences of Dicke states of the form $|\frac{N}{2}\pm m,\frac{N}{2}\mp m\rangle$ for m scaling as o(N). The QFI $\mathcal{F}$ for MZ interferometry using an arbitrary Dicke state (for even N) $|\frac{N}{2}+m,\frac{N}{2}-m\rangle$ is given by [36]

$\mathcal{F}\left(m\right)=4\text{Var}{J}_y=\frac{N^2}{2}-2m^2+N,(4)$

which is independent of θ. The particle number dependence in Eq. 4 indicates the possibility of Heisenberg scaling, i.e., O(N²), but not the Heisenberg limit N², which is only achievable by a GHZ probe state. In fact, this value of the QFI is attained for any spin generator $\vec{n}\cdot \vec{J}$ with $\vec{n}$ a unit vector in the xy-plane [37]. It should be noted that when $m=\pm \frac{N}{2}$, this expression for the QFI also covers the SQL value N. It can be concluded that Dicke states exhibit asymptotic Heisenberg scaling for interferometry if the magnitude of the J_z component scales as λN with λ < 1/2.

To locally saturate the QFI, we first review two practical measurement schemes that have appeared in the literature. A Bayesian estimation scheme locally achieving the same scaling as the QFI was discussed in [1, 38]. However, a single-mode parity measurement (we will use ${(-1)}^{b^{†}b}$ as the single-mode parity operator) exhibits the same scaling while having practical advantages [39, 40, 41, 32]. A simple calculation using the small-angle asymptotics of Wigner’s little-d function allows showing that with the parity signal

$g\left(\theta \right)≔{⟨{\left(-1\right)}^{b^{†}b}⟩}_{e^{-i\theta J_y}|\frac{N}{2}+m,\frac{N}{2}-m\rangle },(5)$

the method of moments error ${(\mathrm{\Delta }\tilde{\theta })}^2$ for extracting an estimate $\tilde{\theta }$ of θ is given as follows:

${\left(\mathrm{\Delta }\tilde{\theta }\right)}^2{|}_{\theta =0}={\left.\frac{1-g{\left(\theta \right)}^2}{g^{\prime }{\left(\theta \right)}^2}\right|}_{\theta =0}={\left(\frac{N^2}{2}-2m^2+N\right)}^{-1},(6)$

where we recall the formula for the method of moments error

${\left(\mathrm{\Delta }\tilde{\theta }\right)}^2=\frac{{\text{Var}}_{|\psi \left(\theta \right)\rangle }A}{{\left(\frac{d{⟨A⟩}_{|\psi \left(\theta \right)\rangle }}{d\theta }\right)}^2}(7)$

of a phase estimator $\tilde{\theta }$ obtained from the measurement of observable A. The reciprocal QFI $1/\mathcal{F}$ is a lower bound to Eq. 7 for all θ. Equation 6 implies that at θ = 0, the method of moments error of $\tilde{\theta }$ obtained from the parity signal Eq. 5 saturates the reciprocal QFI for the MZ interferometer, regardless of which Dicke state is taken as input. The error of the method of moments estimator $\tilde{\theta }$ at arbitrary angles is shown in Figure 1 for N = 64, m = 0, 4, 8, 16, in which it is observed that the ideal TF state has a revival of saturating the QFI near θ = π/2. The method of moments error for a parity observable also saturates the QFI for the GHZ state [42] but globally over all possible phases [32]. From the plots, we conclude that for small θ, the effect of the interferometer is to change the expected parity of the computational basis support of the rotated Dicke state.

Figure 1

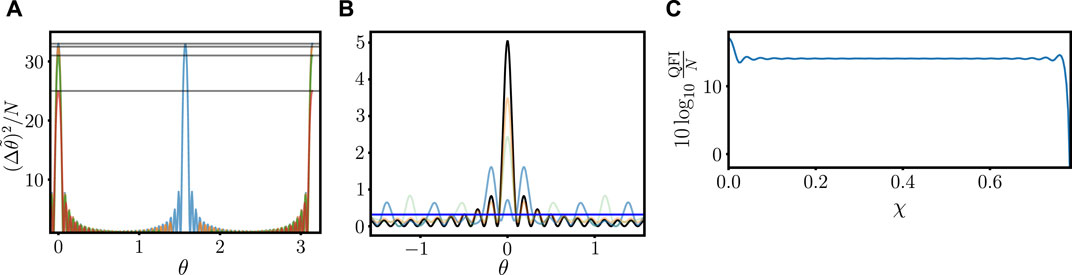
Figure 1. (A) Error of the method of moments estimator $\tilde{\theta }$ of MZ angle θ with parity readout and with a pure Dicke state probe (N =64; blue m =0; orange m =4; green m =8; and red m =16). Black horizontal lines are the QFI. (B) One-shot posterior probability density for the interferometric phase θ with the bosonic phase-diffused probe state (Eq. 14) (N =40; χ =0(black),0.20,0.39,0.59, π/4(dark blue)). Phase diffusion reduces the central peak visibility. (C) QFI for Eq. 14 exhibits greater than O(N) scaling, except for a small domain of χ around π/4.

It should be noted that a parity measurement requires single-particle resolution at a detector. For high-intensity optical systems or a high-occupation two-mode bosonic system, such an idealistic measurement is not always feasible. By contrast, it would be desirable to use low moments of a measurement of a total spin operator to extract a high-precision estimator. It has been shown that for a TF state input, the method of moments error for an estimator obtained from the measurement of $J_z^2$ saturates the QFI at θ = 0 [43]. However, unlike the parity measurement, the $J_z^2$ measurement does not saturate the Dicke state QFI for arbitrary m, and it remains to consider the question of how robust the Heisenberg scaling of this estimation strategy is when a Dicke state is prepared. Theorem 1 is given as follows.

Theorem 1. Let $\mathcal{F}(m)$ be the QFI for an MZ interferometer with input Dicke state $|\frac{N}{2}+m,\frac{N}{2}-m\rangle$, and let $\mathrm{\Delta }\tilde{\theta }$ be the method of moments error (Eq. 7) for a $J_z^2$ measurement. Then,

${\displaystyle \underset{N\to \infty }{\lim }}\frac{{\left(\mathrm{\Delta }\tilde{\theta }\right)}^{-2}{|}_{\theta =0}}{\mathcal{F}\left(m\right)}=\frac{1}{4m^2+1}.(8)$

If m scales with N as $m=o(\sqrt{N})$, then ${\lim }_{N\to \infty }N{(\mathrm{\Delta }\tilde{\theta })}^2{|}_{\theta =0}=0$.

Proof: We use the moments of J_z in Supplemental Section 1 to find that at θ = 0, the method of moments error ${(\mathrm{\Delta }\tilde{\theta })}^2{|}_{\theta =0}$ is given by the following expression:

${\left(\mathrm{\Delta }\tilde{\theta }\right)}^{-2}{|}_{\theta =0}=\frac{{\displaystyle \sum _{u=0}^1}{\left(1+{\left(-1\right)}^{u}2m\right)}^2\left(\frac{N}{2}+{\left(-1\right)}^{u}m+1\right)\left(\frac{N}{2}-{\left(-1\right)}^{u}m\right)}{4{\left(\frac{N^2}{4}-3m^2+\frac{N}{2}\right)}^2}.(9)$

The ratio of the reciprocal of Eq. 9 to the QFI is given by the following equation:

$\frac{{\left(\mathrm{\Delta }\tilde{\theta }\right)}^{-2}{|}_{\theta =0}}{\mathcal{F}\left(m\right)}=\frac{{\left(1-\frac{2m^2}{\frac{N^2}{4}-m^2+\frac{N}{2}}\right)}^2}{4m^2+1},(10)$

which satisfies Eq. 8. The last statement in the theorem follows from taking m to satisfy the scaling assumption in the statement and noting that Eq. 10 implies that $\frac{1}{N}{(\mathrm{\Delta }\tilde{\theta })}^{-2}\sim \frac{1}{N(4m^2+1)}{\left(\frac{N^2}{2}-2m^2+N\right)}^2$ QED.

It should be noted that ${\lim }_{N\to \infty }N{(\mathrm{\Delta }\tilde{\theta })}^2{|}_{\theta =0}=0$ if and only if the reciprocal of the method of moments error is asymptotically greater than the SQL value N for the QFI by more than a constant factor. We conclude that the $J_z^2$ measurement is useful for better-than-SQL interferometry with Dicke states of the form $|\frac{N}{2}+o(\sqrt{N}),\frac{N}{2}-o(\sqrt{N})\rangle$. Although a $J_z^2$ readout does not give a method of moments estimator that saturates the QFI, the correlation of this signal with the parity signal can be used to broaden the domain of θ where QFI saturation occurs, as shown in Figure 1A (although global saturation still does not occur). Specifically, taking $\vec{O}=(O_1,\dots ,O_K)$ to be a row vector of K observables, the inequality [19]

$\begin{array}{c}\hfill \frac{d{⟨\vec{O}⟩}_{{\rho }_{\theta }}}{d\theta }{\text{Cov}}_{{\rho }_{\theta }}{\left(\vec{O}\right)}^{-1}\frac{d{⟨\vec{O}⟩}_{{\rho }_{\theta }}^{⊺}}{d\theta }\le \mathcal{F}\left({\rho }_{\theta }\right)\\ \hfill {\text{Cov}}_{{\rho }_{\theta }}\left(\vec{O}\right)≔{⟨\left(\vec{O}-{⟨\vec{O}⟩}_{{\rho }_{\theta }}\right)◦\left({\vec{O}}^{⊺}-{⟨{\vec{O}}^{⊺}⟩}_{{\rho }_{\theta }}\right)⟩}_{{\rho }_{\theta }}\end{array}(11)$

holds for general parameterized states ρ_θ, and K = 2 with $O_1={(-1)}^{b^{†}b}$ and $O_2=J_z^2$ can be considered. In Eq. 11, the symbol ◦ is the Jordan product of matrices $X◦Y≔\frac{1}{2}XY+\frac{1}{2}YX$. The inequality (Eq. 11) generalizes the relationship between the signal-to-noise ratio in Eq. 7 and the QFI; therefore, the left-hand side of Eq. 11 can be considered a generalized signal-to-noise ratio. By considering more quadratic spin observables in Eq. 11, it is possible to dispense with the parity readout and globally saturate (Eq. 11) for all θ. Taking $O_1=J_z^2$ and $O_2=\frac{1}{2}(J_{+}^2+J_{-}^2)$ if m = 0, and taking $O_1=J_z^2$, $O_2=\frac{1}{2}(J_{+}^2+J_{-}^2)$, and O₃ = J_x if m ≥ 1, minimal operator lists can be obtained, for which Eq. 11 is globally satisfied. A similar conclusion is also obtained in the lossy TF setting in Section 3. Instead of providing individual proofs of these statements, we provide the full details for the QFI saturation in the case of gradiometry with doubled TF probes (Section 4; Supplemental Section 3). The method of proof for the simpler statements of global saturation in this section and in Section 3 follows straightforwardly.

It is worth noting that the N-particle one-axis-twisted probe state [30]

$|{\psi }_{\text{OAT}}\left(t\right)\rangle ≔e^{-it{J}_z^2}|{+\rangle }^{\otimes N}(12)$

at oversqueezed interaction times t = O(N^−α), with 0 < α < 1/2, has asymptotic QFI equal to $\frac{N(N+1)}{2}$ for MZ interferometry, which is asymptotically equal to that of the TF probe state of the same particle number [44]. However, a twist-untwist protocol [45, 46] (which is obtained from Eq. 12 by applying the inverse one-axis twisting $e^{+it{J}_z^2}$ after the MZ interferometer) combined with a total spin readout only saturates the QFI near θ = 0, and the same is true for a parity and $J_z^2$ readout without the untwist operation. However, we are not aware of a quadratic spin readout that globally saturates the QFI for a one-axis-twisted probe state in this interaction time domain.

Last, we note that a measurement in the J_y phase basis

$|\tilde{k}\rangle ≔\frac{1}{\sqrt{N+1}}{\displaystyle \sum _{n=0}^N}{e}^{\frac{2\pi ink}{N+1}}{e}^{i\frac{\pi }{2}{J}_x}|N-n,n\rangle ,k=0,\dots ,N(13)$

(eigenvectors of $e^{i\frac{\pi }{2}{J}_x}C{e}^{-i\frac{\pi }{2}{J}_x}$, where C is the cyclic shift C|N − n, n⟩ = |N − n − 1, n + 1⟩ with addition modulo N + 1) contains sufficient information to form a globally optimal estimator of θ. This can be shown by the numerical computation of the classical Fisher information with respect to the measurement of the complete orthonormal basis (Eq. 13) and verifying that it saturates the black horizontal lines in Figure 1A for all θ.

3 Phase-diffused and lossy TF probes

Interatomic interactions during the interferometric sequence lead to the phenomenon of bosonic phase diffusion [47, 48, 49]. Unlike optical phase diffusion, which is modeled by applying random unitary optical rotations to a continuous-variable probe state [50, 51], bosonic phase diffusion is a unitary error which reduces the phase coherence in the arms of the interferometer. In a modern context, the fact that one-axis twisting can reduce the performance of atom interferometry may seem surprising given that the one-axis-twisted split Bose–Einstein condensate $e^{-i\chi J_z^2}{e}^{-i\frac{\pi }{2}{J}_y}|N,0\rangle$ exhibits Heisenberg scaling as a probe for the MZ interferometric phase (i.e., J_y rotation) for O(N^−1/2) ≲ χ ≲ o(1), transitioning to Heisenberg limit scaling at χ ∼ O(1) [44]. To demonstrate the effect of bosonic phase diffusion on interferometric sensitivity, we use a well-known Bayesian parameter estimation method [1, 52, 53] and the phase-diffused probe state

$|{\psi }_N\left(\chi \right)\rangle ≔e^{-i\chi J_z^2}{e}^{-i\frac{\pi }{2}{J}_y}|\frac{N}{2},\frac{N}{2}\rangle .(14)$

Applying the MZ interferometer to Eq. 14 and using the fidelity with $e^{-i\frac{\pi }{2}{J}_y}|\frac{N}{2},\frac{N}{2}\rangle$ to define a signal, one obtains the posterior probability densities in Figure 1 for various χ (a uniform prior for the phase θ is taken on [−π/2, π/2]). At χ = π/4, sensitivity to the MZ phase disappears because the probe state is equal to $e^{i\frac{\pi }{2}{J}_x}|\frac{N}{2},\frac{N}{2}\rangle$, which is the 0 eigenvector of J_y. Because of the robustness of the Heisenberg scaling of the TF state to strong bosonic phase diffusion, consistent with a more detailed analysis of the effect of phase diffusion on the sensitivity of the local density readout for MZ interferometry with number-squeezed bosons in a double-well trap [34], we do not further consider its effect on the probe states.

We now analyze the QFI after loss of K atoms from the TF state, with the aim of identifying an asymptotic scaling of K with N that allows better-than-SQL scaling to persist. Analyses of mixtures of Dicke states with an uncertain total number of particles appear in [38] and with uncertain spin projection in [54]. The performance of the $J_z^2$ measurement when the TF state is well formed but the total number of particles of the TF state has a non-sharp distribution was analyzed in [11]. We represent the quantum channel describing partial trace over K particles as ${\mathcal{E}}_K$. Starting with a Dicke state |N − m, m⟩, the quantum state subsequent to loss of K < N − m atoms can be computed from the following time-inhomogeneous Markov process (for proof, see Supplemental Section 2).

$p_{k+1}=Q_k{p}_k,k=0,\dots ,K-1,(15)$

where p₀ = (0,…,0,1)^⊺ is a vector of length m + 1, Q_k is a sequence of (m + 1) × (m + 1) bidiagonal, bistochastic matrix defined by non-zero elements

$\begin{array}{ll}\hfill {\left(Q_k\right)}_{i,i+1}& =\frac{i}{n_k}\hfill \\ \hfill {\left(Q_k\right)}_{i,i}& =1-\frac{\left(i-1\right)}{n_k}\hfill \end{array}(16)$

for i = 1, …, m, and n_k = N − k is the particle number after the loss of k particles, k = 0, …, K. The dynamics occurs on the space of probability distributions on the discrete set {0, …, m} due to the fact that loss of an atom cannot increase the Hamming weight that defines a Dicke state. To apply Eq. 15 to the TF state, we take m = N/2 and numerically compute p_K and note that the final state of N − K particles ${\rho }_{N,K}≔{\mathcal{E}}_K\left(|\frac{N}{2},\frac{N}{2}\rangle \langle \frac{N}{2},\frac{N}{2}|\right)$ is a statistical mixture of Dicke states given by the following expression:

${\rho }_{N,K}≔{\displaystyle \sum _{i=1}^{N/2+1}}{\left(p_K\right)}_i{P}_{i-1}^{\frac{N-K}{2}},(17)$

where $P_{\ell }^J$ is the projection to the Dicke state |2J − ℓ, ℓ⟩. The probe state for MZ interferometry is then obtained from Eq. 17 by taking ${\rho }_{N,K}(\theta )≔e^{-i\theta J_y}{\rho }_{N,K}{e}^{i\theta J_y}$. It should be noted that the spin projection is invariant under the particle loss, i.e., ${⟨J_z⟩}_{{\rho }_{N,K}}=0$. The QFI $\mathcal{F}({\rho }_{N,K})$ for this probe state can be computed from the spectral formula [55], using the state $(1-ϵ){\rho }_{N,K}(\theta )+\frac{ϵ}{N-K+1}{\mathbb{I}}_{N-K+1}$ for an infinitesimal ϵ, due to the fact that ρ_N,K(θ) is not generally full rank. The decrease in the QFI with respect to the increase in K is shown in Figure 2. The loss of one particle decreases the QFI by a factor of 2 asymptotically, with the exact value given by ${\left(\frac{N}{2}\right)}^2-1$, which is proven in Supplemental Section 2. This behavior can be contrasted with the optimal pure state probe (viz., the GHZ state), which exhibits SQL scaling if even one particle is lost. In this work, we assume that the loss K is known. To describe an experiment, it would be appropriate to consider a convex mixture of ${\mathcal{E}}_K$ channels to describe the probabilistic loss of particles.

Figure 2

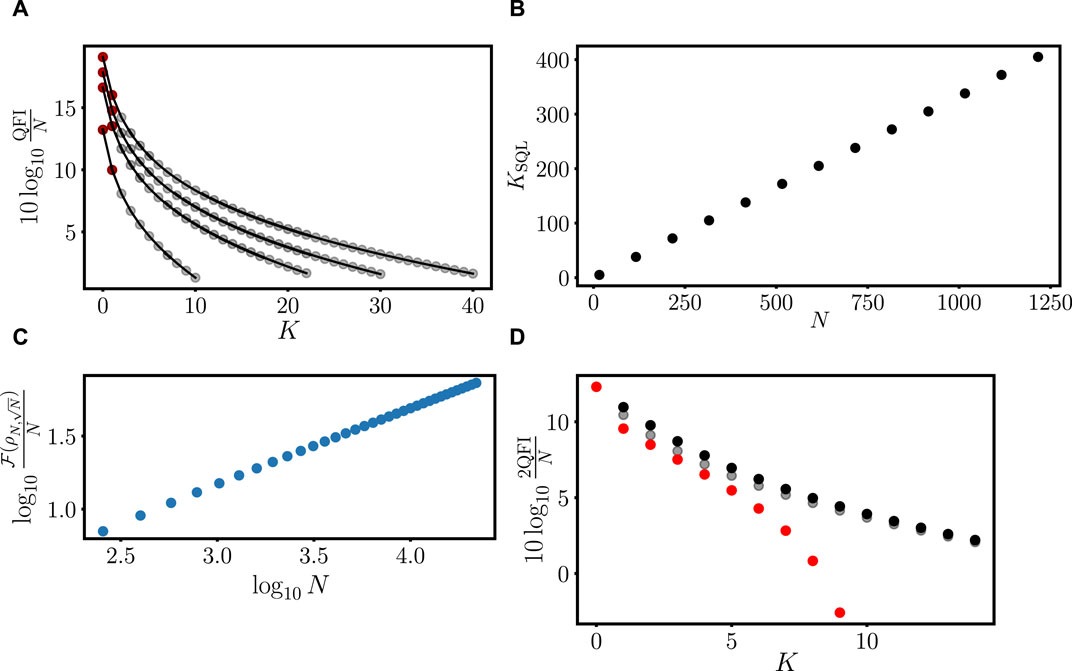
Figure 2. (A) QFI after the application of ${\mathcal{E}}_K$ for $K=0,\dots ,\lfloor \frac{N}{4}\rfloor$ with N =40 (bottom curve), 90, 120, and 160 (top curve). K =0 analytical value $\frac{N^2}{2}+N$ and K =1 analytical value (N/2)²−1 are shown as red dots. (B) Maximal loss tolerance of SQL scaling of the QFI for N =16,…,1216 in steps of 100. (C) $\mathcal{F}({\rho }_{N,\sqrt{N}})$ scaling as O(N^1.52) for large N. (D) Black dots: (1,1) element of the QFI matrix after loss of K =0,1,…,14 particles from the probe state (Eq. 24) with N =64; gray dots: method of moments error for local J_x, $J_z^2$, $\frac{1}{2}(J_{+}^2+h.c.)$, and $\frac{1}{2}(J_{+}{J}_z+h.c.)$ readouts; and red dots: QFI after the application of ${\mathcal{E}}_K$ to the TF state with N =32. The K =0 values coincide at 10 log₁₀17.

Unlike the case for the noiseless TF probe in Section 2, it is not possible to saturate the QFI $\mathcal{F}({\rho }_{N,K})$ for general loss values K using state-agnostic readouts such as parity or $J_z^2$. For a fixed loss value K, the optimal readout depends on the spectrum of the noisy state, i.e., on the ${(p_K)}_m$, through the symmetric logarithmic derivative [13]. It can be expected that the method of moments error for the parity readout saturates $\mathcal{F}({\rho }_{N,K})$ near θ = 0 since this state is a statistical mixture of Dicke states which, if any of these is used as a probe state, allows saturating $\mathcal{F}(m)$, as shown in Figure 1A. However, applying the particle loss channel ${\mathcal{E}}_K$ results in a state with a low-parity signal in the interferometer. For instance, applying ${\mathcal{E}}_1$ to the TF state gives an equally weighted statistical mixture of Dicke states with different parities, and after applying the MZ interferometer for small θ, the state still has equal weights in the even and odd parity sectors. Taking into account the $J_z^2$ readout and its correlation with the parity readout via Eq. 11 to get a smaller error, saturation of the QFI does not occur for any θ domain for loss values K > 1. In fact, by comparing the QFI $\mathcal{F}({\rho }_{N,K})$ to the classical Fisher information $F_K(\theta )={\sum }_{\ell =0}^{N/2}{q}_{\theta }{(\ell )}^{-1}{\left(\frac{d{q}_{\theta }(\ell )}{d\theta }\right)}^2$, where

$q_{\theta }\left(\ell \right)=⟨N-K-\ell ,\ell |{\rho }_{N,K}\left(\theta \right)|N-K-\ell ,\ell ⟩(18)$

is the probability of observing ℓ particles in the second mode, it can be found that a particle number-resolving measurement does not provide enough information to construct an estimator of θ with error saturating the inverse QFI for K > 1. Similar to [54], we find that the greatest sensitivity is obtained away from θ = 0, even for a combined $J_z^2$ and parity readout. Instead of a measurement in the basis of J_z eigenvectors as in Eq. 18, the classical Fisher information of a measurement in the J_y phase basis (Eq. 13) can also be considered. However, the classical Fisher information of this measurement is found not to saturate $\mathcal{F}({\rho }_{N,K})$ for K > 0 but rather has a periodic structure, which causes the greatest sensitivity to occur at a set of equally spaced points in (−π, π].

These results indicate that neither a measurement in the occupation number basis nor a measurement in the J_y phase state basis produces enough information to saturate the QFI for a lossy twin Fock probe. However, we verified numerically that there indeed exists a minimal list $\vec{O}$ of observables such that the method of moment error (left-hand side of Eq. 11) saturates the QFI $\mathcal{F}({\rho }_{N,K})$ for all K and globally for all θ. Specifically, for loss values K = 0, 1, the list

$\vec{O}=\{J_z^2,\frac{1}{2}{J}_{+}^2+h.c.\}(19)$

is sufficient, and for $K=2,\dots ,\frac{N}{2}$, appending the linear spin observable J_x and the quadratic spin observable $\frac{1}{2}{J}_z{J}_{+}+h.c\text{to the list}\vec{O}$, forming

$\vec{O}=\{J_x,J_z^2,\frac{1}{2}{J}_{+}^2+h.c.,\frac{1}{2}{J}_z{J}_{+}+h.c.\},(20)$

is sufficient. Remarkably, a phase observable with eigenvectors in Eq. 13 or the non-linear parity observable ${(-1)}^{b^{†}b}$ are not necessary for globally optimal interferometry with lossy TF states.

From the discussion in Section 2, we recall that a sequence of corrupted (but pure) TF states $|\frac{N}{2}+\lambda N,\frac{N}{2}-\lambda N\rangle$ with λ < 1/2 maintain Heisenberg scaling of the QFI. To understand the tolerance of the lossy probe state ρ_N,K, we found for each total particle number value N, the greatest loss K = K_SQL(N) such that the $\mathcal{F}({\rho }_{N,K_{\text{SQL}}(N)})>N$. Such a loss value is interpreted as the maximal number of particles that may be lost while maintaining better-than-SQL value for the QFI. Figure 2B indicates that K_SQL(N) scales linearly with N, and curve fitting to an affine function suggests that 1/3 of the particles can be lost while maintaining better-than-SQL scaling. It is also of interest to identify exponents 0 < α < 1 and β > 1 for which $\mathcal{F}({\rho }_{N,N^{\alpha }})=O(N^{\beta })$. These exponents characterize the amount of loss (as a function of the total particle number) that can be tolerated while maintaining a QFI scaling as N^β. For β = 2, i.e., Heisenberg scaling, we were not able to identify the existence of an α. However, the loss exponent α = 1/2 allows QFI scaling of N^β with β ≈ 3/2, as shown in Figure 2C.

4 Gradiometry with doubled TF and states

Advantages of using pure, spatially split spin-squeezed atomic ensembles for magnetic gradiometry (estimation of the difference θ₁ − θ₂) beyond SQL were outlined in [20]. Generally, when using atom interferometers for distributed sensing (i.e., sensing a field at many different spatial points), there are two classes of quantum sensing strategies that can be used, which are straightforward generalizations of their single-parameter sensing counterparts [42]. The parallel strategies use identical copies of a probe state or a single global entangled state as a probe which addresses the various points of interest. The probe state is locally parametrized by phases corresponding to the local field values, with the parametrization usually modeled by a tensor product of parametrized quantum channels. By contrast, the sequential strategies expose an initial probe state (which may be entangled with an ancilla register) to the points of interest in temporal succession. The preference of strategy depends on the cost of probe state preparation and the dwell time of the transient that must be sensed. It has been shown that in the parallel generalization of the MZ interferometry protocol which uses general linear optical unitaries in lieu of the $e^{\pm i\frac{\pi }{2}{J}_x}$ two-mode beamsplitters, twin Fock states asymptotically allow saturating the optimal performance (over all mode-separable input states of a fixed total particle number) for estimation of a linear function of phases [56]. Often in distributed sensing, only a single linear function $\vec{w}\cdot \vec{\theta }$ of the parameters is of interest [57], with the normalization $\Vert \vec{w}{\Vert }_2=1$ sometimes chosen so that the largest possible QFI for estimating a linear function coincides with the largest eigenvalue of the QFI matrix.

One possible sequential strategy to estimate $({\theta }_1-{\theta }_2)/\sqrt{2}$ using a TF or Dicke state probe is to π shift the phase of the second MZ interferometer addressing the θ₂ parameter. This results in a full protocol described by the operation

$e^{-i\frac{\pi }{2}{J}_x}{e}^{-i{\theta }_2{J}_z}{e}^{i\frac{\pi }{2}{J}_x}{e}^{i\frac{\pi }{2}{J}_x}{e}^{-i{\theta }_1{J}_z}{e}^{-i\frac{\pi }{2}{J}_x}=e^{-i\left({\theta }_1-{\theta }_2\right)J_y}.(21)$

However, it should be noted that for any global rotation $e^{-i\phi \vec{n}\cdot \vec{J}}$, with $\vec{n}\in {\mathbb{R}}^3$ being a unit vector and $\vec{J}=(J_x,J_y,J_z)$ the vector of spin operators, the following channel commutativity relation holds on the quantum states of N two-mode bosons:

${\mathcal{E}}_K◦e^{-i\phi \vec{n}\cdot \vec{J}}=e^{-i\phi \vec{n}\cdot \vec{J}}◦{\mathcal{E}}_K,(22)$

where the spin operators act in a spin-N/2 representation on the left-hand side and a spin-$\frac{N-K}{2}$ representation on the right-hand side. Therefore, an analysis of this sequential protocol Eq. 21 can be carried out (even with imperfect probes or particle loss) using the methods of Sections 2, 3.

Instead, we consider two parallel strategies in which globally entangled states are used to estimate linear functions of the phases θ_j, j = 1, 2. The first parallel strategy is especially relevant when the initial TF state is a single atomic cloud with N/2 occupation in each of two internal modes, for example, atomic nuclear spin states. The initial TF cloud is then spatially split (we assume perfect splitting) to give the TF probe state in the superposition of spatial modes.

$|{\psi }_{\text{split}}\rangle ≔{\left(\frac{a_1^{†}+a_2^{†}}{\sqrt{2}}\right)}^{N/2}{\left(\frac{b_1^{†}+b_2^{†}}{\sqrt{2}}\right)}^{N/2}|\mathrm{0,0,0,0}\rangle .(23)$

It should be noted that the original internal modes a and b of the TF state have been spatially split to spatial modes a₁ and a₂ and b₁ and b₂, respectively. The local phase shifts are imprinted on |ψ_split⟩ by the operation $U_{\text{MZ}}(\theta )=e^{-\frac{{\theta }_1}{2}(a_1^{†}{b}_1-h.c.)-\frac{{\theta }_2}{2}(a_2^{†}{b}_2-h.c.)}$. This strategy appears especially relevant for magnetic gradiometry with atomic ensembles. However, we find that every entry of the inverse of the QFI matrix scales as N⁻¹. The multiparameter quantum Cramér–Rao bound then implies that an estimator of any linear function of θ₁ and θ₂ has an error scaling at least as N⁻¹, i.e., scaling as SQL. No improvement can be obtained by losing particles, so we cease further exploration of probe state |ψ_split⟩.

The second parallel strategy uses the same local phase shift operation U_MZ(θ) but uses as probe the doubled TF state

$|{\psi }_{\text{doubled}}\rangle ≔a_1^{†\frac{N}{4}}{b}_1^{†\frac{N}{4}}{a}_2^{†\frac{N}{4}}{b}_2^{†\frac{N}{4}}|\mathrm{0,0,0,0}\rangle (24)$

in which two spin modes and two spatial modes are occupied symmetrically. The state (Eq. 24) can also be considered as two copies of bosonic-independent and identically distributed (b.i.i.d.) TF states [58] which, mathematically, correspond to taking the Young product of two copies of the symmetric subspace of ${({\mathbb{C}}^2)}^{\otimes N}$. It should be noted that both (Eqs. 23, 24) are in the symmetric subspace of ${({\mathbb{C}}^4)}^{\otimes N}$ and are, therefore, valid bosonic states of N atoms. For independent MZ interferometers acting on the a_j, b_j mode pairs, the 2 × 2 QFI matrix for Eq. 24 is diagonal with equal (1,1) and (2,2) matrix elements given by $\frac{N^2+4N}{8}$, independent of $\vec{\theta }$ [the probe state (Eq. 23) does not have a diagonal QFI matrix]. Therefore, an optimal estimator of any linear function $\vec{w}\cdot \vec{\theta }$, $\Vert \vec{w}{\Vert }_2=1$ exhibits Heisenberg scaling, and we will, therefore, quantify the performance of a probe state for gradiometry by the (1,1) entry of the QFI matrix. Using Eq. 11, we show analytically that, for example, the (j, j) element of the QFI matrix is globally saturated using the method of moments estimation of the local quadratic spin observables $O_1=J_z^{(a_j,b_j)2}$ and $O_2=\frac{1}{2}(J_{+}^{(a_j,b_j)2}+h.c.)$. The covariance matrix and derivatives are shown in Supplemental Section S3, along with verification that the final expression indeed simplifies to $\frac{N}{8}(N+4)$ regardless of θ₁.

The property of the QFI matrix being a scalar multiple of the identity holds also for the probe state obtained by losing K particles from Eq. 24. This fact follows because taking the trace over K particles produces a statistical mixture of four-mode Dicke states, and the 1 ↔ 2 label symmetry of the state is preserved. It should be noted that atom loss from Eq. 24 is not a strictly local process to the MZ interferometers and cannot be described by, for example, applying the loss channels ${\mathcal{E}}_K$ to the mode pairs a₁, b₁ and a₂, b₂ independently. Furthermore, although the dimension of the symmetric subspace of ${({\mathbb{C}}^4)}^{\otimes N}$ scales as N³, if one considers losing at least K atoms from the doubled TF state with $K\ge \frac{N}{4}$, one must keep track of at least $e^{O(\sqrt{N})}$ weights for an exact description of the state, according to the Hardy–Ramanujan asymptotic for the number of partitions of a large natural number. We briefly describe the channel describing particle loss from a Dicke state with more than two modes in Supplemental Section S2.

The black dots of Figure 2D show the gain over the SQL $\frac{N}{2}$ for the estimation of the first MZ phase θ₁ (with N = 64). The SQL is taken as $\frac{N}{2}$ because at most N/2 particles address each of the MZ interferometers when loss is applied to the probe state (Eq. 24). The red dots show the gain over SQL for the probe state ${\mathcal{E}}_K\left(|\frac{N}{4},\frac{N}{4}\rangle \langle \frac{N}{4},\frac{N}{4}|\right)$ using the same analysis as in Section 3. It is clear that for small loss values, the four-mode state exhibits roughly 1.4 dB gain in the attainable precision of local interferometry compared to a single lossy TF state with the same local energy and loss. The result indicates a different phenomenon from the known distributed sensing results in the multimode optical setting with pure probe states [56] or massive boson setting with pure probe states [59]. In the absence of loss, the optimal strategy for the estimation of a linear function of the MZ phases θ₁ and θ₂ using the probe state (Eq. 24) does not outperform the use of two independent TF states $|\frac{N}{4},\frac{N}{4}\rangle$ to separately probe the MZ interferometers, which indeed indicates that the probe state (Eq. 24) is a suboptimal four mode, N particle probe state (one could apply a linear optical operation to, e.g., $|\frac{N}{2},\frac{N}{2},\mathrm{0,0}\rangle$, to obtain a better probe state) [56]. However, when at least one particle is lost, the distributed entanglement of the lossy version of Eq. 24 allows greater attainable precision than independent copies of the lossy TF probe state.

5 Discussion

We analyzed the method of moments readouts for the TF state and its images under a particle loss channel or unitary phase-diffusion channel. The traditional parity measurement, which saturates the QFI for MZ interferometry near θ = 0 for all Dicke states, can be dispensed with if one can measure both quadratic spin observables $J_z^2$ and $\frac{1}{2}(J_{+}^2+h.c.)$. Although one-shot measurement of both these observables is impossible because they do not commute, allocation of shots to one or the other observable allows extracting an estimator with error asymptotically given by the left-hand side (Eq. 11), according to the central limit theorem. When particle loss is taken into account, we identified minimal lists of observables that give the method of moments error that globally saturates the QFI for any loss value. The observables are again at most quadratic in the spin operators. The fact that better-than-SQL scaling is obtained even when $O(\sqrt{N})$ particles are lost from the TF state indicates the loss robustness of the TF probe state for practical MZ interferometry. To analyze a formal gradiometry protocol, we considered the application of particle loss to the doubled twin Fock state $|{\psi }_{\text{doubled}}\rangle =|\frac{N}{4},\frac{N}{4},\frac{N}{4},\frac{N}{4}\rangle$, which can probe two MZ interferometers describing, for example, distributed sensing of spatially separated external field values. Although the noiseless doubled TF state does not allow estimating θ₁ (chosen without loss of generality) with lower error than is achievable by probing the MZ interferometer with TF states of N/2 particles, the lossy doubled TF state exhibits an advantage over the lossy TF state. This result suggests that an extended bosonic insulating state is, in a practical lossy setting, a more useful resource for distributed quantum sensing than a tensor product of states of a fixed particle number. The advantage can be attributed to the indistinguishability of the particles in the bosonic insulator, giving a fully symmetrized state which causes the loss to be distributed over all occupied modes. Extending this distributed sensing result to include other noise sources, for example, thermal [60], would establish this noisy advantage in experimentally realistic settings such as those realized in recent demonstrations of entanglement between spatially separated atom ensembles [24].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

TV: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. CR: conceptualization, funding acquisition, resources, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge support from the Laboratory Directed Research and Development (LDRD) Program at Los Alamos National Laboratory (LANL). Los Alamos National Laboratory is managed by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under Contract No. 89233218CNA000001.

Acknowledgments

The authors thank Katarzyna Krzyzanowska, Sivaprasad Omanakuttan, and Jonathan Gross for helpful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1369786/full#supplementary-material

References

1. Holland MJ, Burnett K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys Rev Lett (1993) 71:1355–8. doi:10.1103/PhysRevLett.71.1355

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Caves CM. Quantum-mechanical noise in an interferometer. Phys Rev D (1981) 23:1693–708. doi:10.1103/PhysRevD.23.1693

CrossRef Full Text | Google Scholar

3. Ganapathy D, Jia W, Nakano M, Xu V, Aritomi N, Cullen T, et al. Broadband quantum enhancement of the LIGO detectors with frequency-dependent squeezing. Phys Rev X (2023) 13:041021. doi:10.1103/PhysRevX.13.041021

CrossRef Full Text | Google Scholar

4. McCuller L, Whittle C, Ganapathy D, Komori K, Tse M, Fernandez-Galiana A, et al. Frequency-dependent squeezing for advanced LIGO. Phys Rev Lett (2020) 124:171102. doi:10.1103/PhysRevLett.124.171102

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cooper M, Wright LJ, Söller C, Smith BJ. Experimental generation of multi-photon Fock states. Opt Express (2013) 21:5309–17. doi:10.1364/OE.21.005309

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dimopoulos S, Graham PW, Hogan JM, Kasevich MA, Rajendran S. Atomic gravitational wave interferometric sensor. Phys Rev D (2008) 78:122002. doi:10.1103/PhysRevD.78.122002

CrossRef Full Text | Google Scholar

7. Abe M, Adamson P, Borcean M, Bortoletto D, Bridges K, Carman SP, et al. Matter-wave atomic gradiometer interferometric sensor (MAGIS-100). Quan Sci Technol (2021) 6:044003. doi:10.1088/2058-9565/abf719

CrossRef Full Text | Google Scholar

8. Kasevich M, Chu S. Atomic interferometry using stimulated Raman transitions. Phys Rev Lett (1991) 67:181–4. doi:10.1103/PhysRevLett.67.181

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wu S, Wang YJ, Diot Q, Prentiss M. Splitting matter waves using an optimized standing-wave light-pulse sequence. Phys Rev A (2005) 71:043602. doi:10.1103/PhysRevA.71.043602

CrossRef Full Text | Google Scholar

10. Wiseman HM, Vaccaro JA. Entanglement of indistinguishable particles shared between two parties. Phys Rev Lett (2003) 91:097902. doi:10.1103/PhysRevLett.91.097902

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lücke B, Scherer M, Kruse J, Pezzé L, Deuretzbacher F, Hyllus P, et al. Twin matter waves for interferometry beyond the classical limit. Science (2011) 334:773–6. doi:10.1126/science.1208798

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Yurke B, McCall SL, Klauder JR. SU(2) and SU(1,1) interferometers. Phys Rev A (1986) 33:4033–54. doi:10.1103/PhysRevA.33.4033

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Holevo A. Probabilistic and statistical aspects of quantum theory. Amsterdam: North-Holland (1982).

Google Scholar

14. Yu S. Quantum Fisher information as the convex roof of variance. arXiv preprint arXiv:1302.5311 (2013).

Google Scholar

15. Lang MD, Caves CM. Optimal quantum-enhanced interferometry. Phys Rev A (2014) 90:025802. doi:10.1103/PhysRevA.90.025802

CrossRef Full Text | Google Scholar

16. Duivenvoorden K, Terhal BM, Weigand D. Single-mode displacement sensor. Phys Rev A (2017) 95:012305. doi:10.1103/PhysRevA.95.012305

CrossRef Full Text | Google Scholar

17. Vaneph C, Tufarelli T, Genoni MG. Quantum estimation of a two-phase spin rotation. Quan Measurements Quan Metrology 1 (2013) 12–20. doi:10.2478/qmetro-2013-0003

CrossRef Full Text | Google Scholar

18. Fujiwara A. Estimation of SU(2) operation and dense coding: an information geometric approach. Phys Rev A (2001) 65:012316. doi:10.1103/PhysRevA.65.012316

CrossRef Full Text | Google Scholar

19. Gessner M, Smerzi A, Pezzè L. Multiparameter squeezing for optimal quantum enhancements in sensor networks. Nat Commun (2020) 11:3817. doi:10.1038/s41467-020-17471-3

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Fadel M, Yadin B, Mao Y, Byrnes T, Gessner M. Multiparameter quantum metrology and mode entanglement with spatially split nonclassical spin ensembles. New J Phys (2023) 25:073006. doi:10.1088/1367-2630/ace1a0

CrossRef Full Text | Google Scholar

21. Bärtschi A, Eidenbenz S. Short-depth circuits for Dicke state preparation. IEEE Int Conf Quan Comput Eng (Qce) (2022) 87–96. doi:10.1109/QCE53715.2022.00027

CrossRef Full Text | Google Scholar

22. Kajtoch D, Witkowska E. Quantum dynamics generated by the two-axis countertwisting Hamiltonian. Phys Rev A (2015) 92:013623. doi:10.1103/PhysRevA.92.013623

CrossRef Full Text | Google Scholar

23. Jiang Z, Rieffel EG, Wang Z. Near-optimal quantum circuit for Grover’s unstructured search using a transverse field. Phys Rev A (2017) 95:062317. doi:10.1103/PhysRevA.95.062317

CrossRef Full Text | Google Scholar

24. Lange K, Peise J, Lücke B, Kruse I, Vitagliano G, Apellaniz I, et al. Entanglement between two spatially separated atomic modes. Science (2018) 360:416–8. doi:10.1126/science.aao2035

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Hyllus P, Pezzé L, et al. Useful multiparticle entanglement and sub-shot-noise sensitivity in experimental phase estimation. Phys Rev Lett (2011) 107:080504. doi:10.1103/PhysRevLett.107.080504

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhou L, Kong J, Lan Z, Zhang W. Dynamical quantum phase transitions in a spinor Bose-Einstein condensate and criticality enhanced quantum sensing. Phys Rev Res (2023) 5:013087. doi:10.1103/PhysRevResearch.5.013087

CrossRef Full Text | Google Scholar

27. Niezgoda A, Kajtoch D, Dziekańska J, Witkowska E. Optimal quantum interferometry robust to detection noise using spin-1 atomic condensates. New J Phys (2019) 21:093037. doi:10.1088/1367-2630/ab4099

CrossRef Full Text | Google Scholar

28. Guan Q, Biedermann GW, Schwettmann A, Lewis-Swan RJ. Tailored generation of quantum states in an entangled spinor interferometer to overcome detection noise. Phys Rev A (2021) 104:042415. doi:10.1103/PhysRevA.104.042415

CrossRef Full Text | Google Scholar

29. Mao TW, Liu Q, Li XW, Cao JH, Chen F, Xu WX, et al. Quantum-enhanced sensing by echoing spin-nematic squeezing in atomic Bose-Einstein condensate. Nat Phys (2023) 19:1585–90. doi:10.1038/s41567-023-02168-3

CrossRef Full Text | Google Scholar

30. Kitagawa M, Ueda M. Squeezed spin states. Phys Rev A (1993) 47:5138–43. doi:10.1103/PhysRevA.47.5138

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Lücke B, Peise J, Vitagliano G, Arlt J, Santos L, Tóth G, et al. Detecting multiparticle entanglement of Dicke states. Phys Rev Lett (2014) 112:155304. doi:10.1103/PhysRevLett.112.155304

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Campos RA, Gerry CC, Benmoussa A. Optical interferometry at the Heisenberg limit with twin Fock states and parity measurements. Phys Rev A (2003) 68:023810. doi:10.1103/PhysRevA.68.023810

CrossRef Full Text | Google Scholar

33. Gietka K, Chwedeńczuk J. Atom interferometer in a double-well potential. Phys Rev A (2014) 90:063601. doi:10.1103/PhysRevA.90.063601

CrossRef Full Text | Google Scholar

34. Grond J, Hohenester U, Mazets I, Schmiedmayer J. Atom interferometry with trapped Bose–Einstein condensates: impact of atom–atom interactions. New J Phys (2010) 12:065036. doi:10.1088/1367-2630/12/6/065036

CrossRef Full Text | Google Scholar

35. Dorner U, Demkowicz-Dobrzanski R, Smith BJ, Lundeen JS, Wasilewski W, Banaszek K, et al. Optimal quantum phase estimation. Phys Rev Lett (2009) 102:040403. doi:10.1103/PhysRevLett.102.040403

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Pezzè L, Smerzi A, Oberthaler MK, Schmied R, Treutlein P. Quantum metrology with nonclassical states of atomic ensembles. Rev Mod Phys (2018) 90:035005. doi:10.1103/RevModPhys.90.035005

CrossRef Full Text | Google Scholar

37. Hyllus P, Gühne O, Smerzi A. Not all pure entangled states are useful for sub-shot-noise interferometry. Phys Rev A (2010) 82:012337. doi:10.1103/PhysRevA.82.012337

CrossRef Full Text | Google Scholar

38. Meiser D, Holland MJ. Robustness of Heisenberg-limited interferometry with balanced Fock states. New J Phys (2009) 11:033002. doi:10.1088/1367-2630/11/3/033002

CrossRef Full Text | Google Scholar

39. Bollinger JJ, Itano WM, Wineland DJ, Heinzen DJ. Optimal frequency measurements with maximally correlated states. Phys Rev A (1996) 54:R4649–52. doi:10.1103/PhysRevA.54.R4649

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gerry CC. Heisenberg-limit interferometry with four-wave mixers operating in a nonlinear regime. Phys Rev A (2000) 61:043811. doi:10.1103/PhysRevA.61.043811

CrossRef Full Text | Google Scholar

41. Gerry CC, Campos RA, Benmoussa A. Comment on “Interferometric detection of optical phase shifts at the Heisenberg limit”. Phys Rev Lett (2004) 92:209301. doi:10.1103/PhysRevLett.92.209301

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Giovannetti V, Lloyd S, Maccone L. Quantum metrology. Phys Rev Lett (2006) 96:010401. doi:10.1103/PhysRevLett.96.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kim T, Pfister O, Holland MJ, Noh J, Hall JL. Influence of decorrelation on Heisenberg-limited interferometry with quantum correlated photons. Phys Rev A (1998) 57:4004–13. doi:10.1103/PhysRevA.57.4004

CrossRef Full Text | Google Scholar

44. Volkoff TJ, Martin MJ. Saturating the one-axis twisting quantum Cramér-Rao bound with a total spin readout. J Phys Commun (2024) 8:015004. doi:10.1088/2399-6528/ad1dc8

CrossRef Full Text | Google Scholar

45. Davis E, Bentsen G, Schleier-Smith M. Approaching the Heisenberg limit without single-particle detection. Phys Rev Lett (2016) 116:053601. doi:10.1103/PhysRevLett.116.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Volkoff TJ, Martin MJ. Asymptotic optimality of twist-untwist protocols for Heisenberg scaling in atom-based sensing. Phys Rev Res (2022) 4:013236. doi:10.1103/PhysRevResearch.4.013236

CrossRef Full Text | Google Scholar

47. Javanainen J, Wilkens M. Phase and phase diffusion of a split Bose-Einstein condensate. Phys Rev Lett (1997) 78:4675–8. doi:10.1103/PhysRevLett.78.4675

CrossRef Full Text | Google Scholar

48. Sanders BC, Milburn GJ. Optimal quantum measurements for phase estimation. Phys Rev Lett (1995) 75:2944–7. doi:10.1103/PhysRevLett.75.2944

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Jo GB, Shin Y, Will S, Pasquini TA, Saba M, Ketterle W, et al. Long phase coherence time and number squeezing of two Bose-Einstein condensates on an atom chip. Phys Rev Lett (2007) 98:030407. doi:10.1103/PhysRevLett.98.030407

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Vidrighin MD, Donati G, Genoni MG, Jin XM, Kolthammer WS, Kim MS, et al. Joint estimation of phase and phase diffusion for quantum metrology. Nat Commun (2014) 5:3532. doi:10.1038/ncomms4532

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Genoni MG, Olivares S, Paris MGA. Optical phase estimation in the presence of phase diffusion. Phys Rev Lett (2011) 106:153603. doi:10.1103/PhysRevLett.106.153603

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Pezzé L, Smerzi A. Phase sensitivity of a Mach-Zehnder interferometer. Phys Rev A (2006) 73:011801. doi:10.1103/PhysRevA.73.011801

CrossRef Full Text | Google Scholar

53. Uys H, Meystre P. Quantum states for Heisenberg-limited interferometry. Phys Rev A (2007) 76:013804. doi:10.1103/PhysRevA.76.013804

CrossRef Full Text | Google Scholar

54. Apellaniz I, Lücke B, Peise J, Klempt C, Tóth G. Detecting metrologically useful entanglement in the vicinity of Dicke states. New J Phys (2015) 17:083027. doi:10.1088/1367-2630/17/8/083027

CrossRef Full Text | Google Scholar

55. Braunstein SL, Caves CM. Statistical distance and the geometry of quantum states. Phys Rev Lett (1994) 72:3439–43. doi:10.1103/PhysRevLett.72.3439

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ge W, Jacobs K, Eldredge Z, Gorshkov AV, Foss-Feig M. Distributed quantum metrology with linear networks and separable inputs. Phys Rev Lett (2018) 121:043604. doi:10.1103/PhysRevLett.121.043604

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Proctor TJ, Knott PA, Dunningham JA. Multiparameter estimation in networked quantum sensors. Phys Rev Lett (2018) 120:080501. doi:10.1103/PhysRevLett.120.080501

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Volkoff TJ. Distillation of maximally correlated bosonic matter from many-body quantum coherence. Quantum (2020) 4:330. doi:10.22331/q-2020-09-24-330

CrossRef Full Text | Google Scholar

59. Gessner M, Pezzè L, Smerzi A. Sensitivity bounds for multiparameter quantum metrology. Phys Rev Lett (2018) 121:130503. doi:10.1103/PhysRevLett.121.130503

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Volkoff TJ, Sarovar M. Optimality of Gaussian receivers for practical Gaussian distributed sensing. Phys Rev A (2018) 98:032325. doi:10.1103/PhysRevA.98.032325

CrossRef Full Text | Google Scholar