Dynamics analysis and optimal control study of uncertain information dissemination model triggered after major emergencies

In order to effectively prevent and combat online public opinion crises triggered by major emergencies, this paper explores the dissemination mechanism of uncertain information on online social platforms. According to the decision-making behavior of netizens after receiving uncertain information, they are divided into eight categories. Considering that there will be a portion of netizens who clarify uncertain information after receiving it, this paper proposes a SEFTFbTbMR model of uncertain information clarification behavior. The propagation dynamics equations of the model are given based on the theory of differential equations, the basic regeneration number R₀ of the model is calculated, and the existence and stability of the equilibrium point of the model are analyzed. The theoretical analysis of the model is validated using numerical simulation software, and sensitivity analysis is performed on the parameters related to R₀. In order to reduce the influence caused by uncertain information, the optimal control strategy of the model is proposed using the Hamiltonian function. It is found that the dissemination of uncertain information among netizens can be suppressed by strengthening the regulation of social platforms, improving netizens’ awareness of identifying the authenticity of information, and encouraging netizens to participate in the clarification of uncertain information. The results of this work can provide a theoretical basis for future research on the uncertain information dissemination mechanism triggered by major emergencies. In addition, the results can also provide methodological support for the relevant government departments to reduce the adverse effects caused by uncertain information in the future.

1 Introduction

Digital new media platforms are essentially unbounded, interactive, and anonymous, which brings a significant degree of convenience to users but also introduces certain hidden dangers. When a major emergency occurs, various network clusters form to discuss the event. Although the internet users within these clusters are eager to obtain relevant information about the event, its uncertainty and urgency often mean that the relevant departments are unable to announce details to the public in the early stages of the response. Thus, during this information window, some internet users use digital new media to disseminate uncertain information, which may cause unnecessary panic among uninformed internet users, possibly leading to social disquiet and unrest. Thus, to reduce the secondary effects caused by the dissemination of uncertain information after major emergencies, it is critical to construct a model of dissemination of uncertain information and analyze the mechanisms whereby such information is transmitted.

This paper develops an epidemic propagation dynamics model and uses optimal control theory to analyze the delivery mechanism of uncertain information dissemination among internet users. First, based on different decision-making behaviors, netizens are categorized into eight groups: unknowns S, thinkers E, uncertain information publishers F, clarifiers of uncertain information T, internet users who believe uncertain information Fb, internet users who only believe true information Tb, internet users who do not believe any online information M, and information immunizers R. We then construct the SEFTFbTbMR uncertain information dissemination model. Second, the model is solved to find the basic regeneration number R₀ of the system, and the equilibrium points P₀ and P* that exist without and with uncertain information dissemination, respectively, are calculated. The stability of points P₀ and P* is then analyzed, and numerical simulations are conducted using Matlab 2017b to verify the theoretical derivations. Finally, to control the scale of uncertain information dissemination and increase the proportion of thinkers and clarifiers of uncertain information, an optimal control model is established based on the SEFTFbTbMR uncertain information dissemination model.

The main contributions of the research reported in this paper are as follows: 1) Considering that there will be some netizens who will exhibit behaviors such as clarifying or re-disseminating the uncertain information after receiving it, this paper divides the netizens into eight categories according to decision-making behavior in the process of uncertain information dissemination. 2) During the construction of the model, we consider not only the dissemination of uncertain information but also the dissemination of true information that clarifies the uncertain information. 3) In order to reduce the influence caused by uncertain information, the Hamiltonian function is utilized to propose the optimal control strategy of the model. The research in this paper provides a theoretical basis for dealing with the uncertain information dissemination mechanism triggered by major emergencies, and the related conclusions provide methodological support for reducing the adverse effects of uncertain information.

2 Related work

Since the outbreak of COVID-19, various studies have examined major emergencies from different perspectives. Tan [1], Yao [2], Gao [3], and Zhang [4] conducted studies from the perspective of emergency management after the occurrence of a major emergency. Other scholars have investigated the impact of major emergencies, such as Ukwuoma [5], Benifa [6], Asif [7], and Fazmiya [8], who analyzed the physical effects of major emergencies on humans from a medical perspective, using COVID-19 as an example. Mo et al. [9] argued that major emergencies have both an emotional as impact as well as a huge economic impact. Cheng et al. [10] found that secondary disasters of major emergencies can have an impact on international oil prices. Yang et al. [11] concluded that major emergencies can seriously affect the public’s emotions and cause a certain amount of panic. Similarly, De las Heras-Pedrosa et al. [12] argued that major emergencies can also have serious psychological effects on the public. Atehortua et al. [13] reported that the occurrence of major emergencies is followed by large amounts of uncertain information emerging on social networks, leading to the spread of panic. Jalan et al. [14] argued that, after a major emergency, the uncertain information disseminated across new media can cause more panic in the public than traditional media reports. Zhang et al. [15] found that the subsequent control of major emergencies can be hampered by the dissemination of uncertain information after the occurrence of a major emergency.

In the study of uncertain information, it is critical to examine the various actors in the process of information dissemination. Crokidakis [16], Zhao [17], and Yin [18] studied the crucial role of social media in the dissemination of uncertain information. Allington et al. [19] argued that social media platforms are the main disseminators of uncertain information, and Centola [20] showed that netizens tend to believe information when it is received from several different sources. Zhang et al. [21] used the behaviors of online media, internet users, and the government in response to the Chinese COVID-19 Shuanghuanglian incident as an example to examine the dissemination of information. Choi [22] argued that although opinion leaders play a driving role in the dissemination of information, they are not typically its creators. Studies have examined the mechanisms whereby uncertain information is disseminated, including that of Li et al. [23], who examined the information dissemination process under major emergencies, and that of Li et al. [24], who investigated the propagation of uncertain information following an incident. Wei [25] analyzed the propagation process of uncertain information using the theory of heat conduction in physics. Litou et al. [26] studied how to increase the rate of information dissemination at the lowest cost. Wang et al. [27] argued that a higher-status initial disseminator could achieve a faster rate of dissemination, whereas Hong et al. [28] showed that centralizing the release of truthful information effectively reduces the dissemination rate of uncertain information among netizens.

The Susceptible Infected Recovered (SIR) model [29] was first introduced in 1927 by Kermack and McKendrick to study the transmission mechanism of epidemics in populations using a kinetic approach. Their mathematical model underwent further enhancement in 1932 [30] and 1933 [31]. Subsequently, researchers have continued to develop and extend this model to account for the dynamics of infectious diseases, and have progressively merged it with disciplines such as mathematics, sociology, complexity science, cybernetics, and computer science [32–34]. The epidemic transmission model has been extensively utilized in studying cross-disciplinary information transmission owing to the similarity of the transmission pattern of information with that of epidemics [35]. [36] developed the M-SDI model, which uses public comments to assess the credibility of online information; in a subsequent study, they introduced the SRFI model [37], which uses numbers of reads and retweets to measure uncertainty in online content. Rui et al. [38] proposed the SPIR model based on discrete-time dynamics. Trpevski et al. [39] developed an uncertain information dissemination model with two different acceptance probabilities based on the SIS model. Zan [40] constructed the DSIR and C-DSIR models by considering the simultaneous existence of multiple uncertain pieces of information in the real world.

Based on the above-mentioned studies, we find that most scholars often assume that only uncertain information is disseminated among netizens in the process of researching the dissemination mechanism of uncertain information, and the decision-making behavior of netizens after receiving uncertain information is relatively simple. However, in reality, due to the characteristics of digital media technology, Internet users can not only receive uncertain information but also real information that clarifies uncertain information. Moreover, with the continuous improvement of their own quality, some netizens, when faced with uncertain information, will make a judgment by investigating and collecting evidence or thinking for moment, thus spontaneously clarifying the uncertain information and ultimately choosing to publish real information. Considering the above realities, this paper divides netizens into eight categories according to different decision-making behaviors in the process of uncertain information dissemination. When constructing the model, we consider not only the dissemination of uncertain information but also the dissemination of truthful information that clarifies the uncertain information.

3 The model

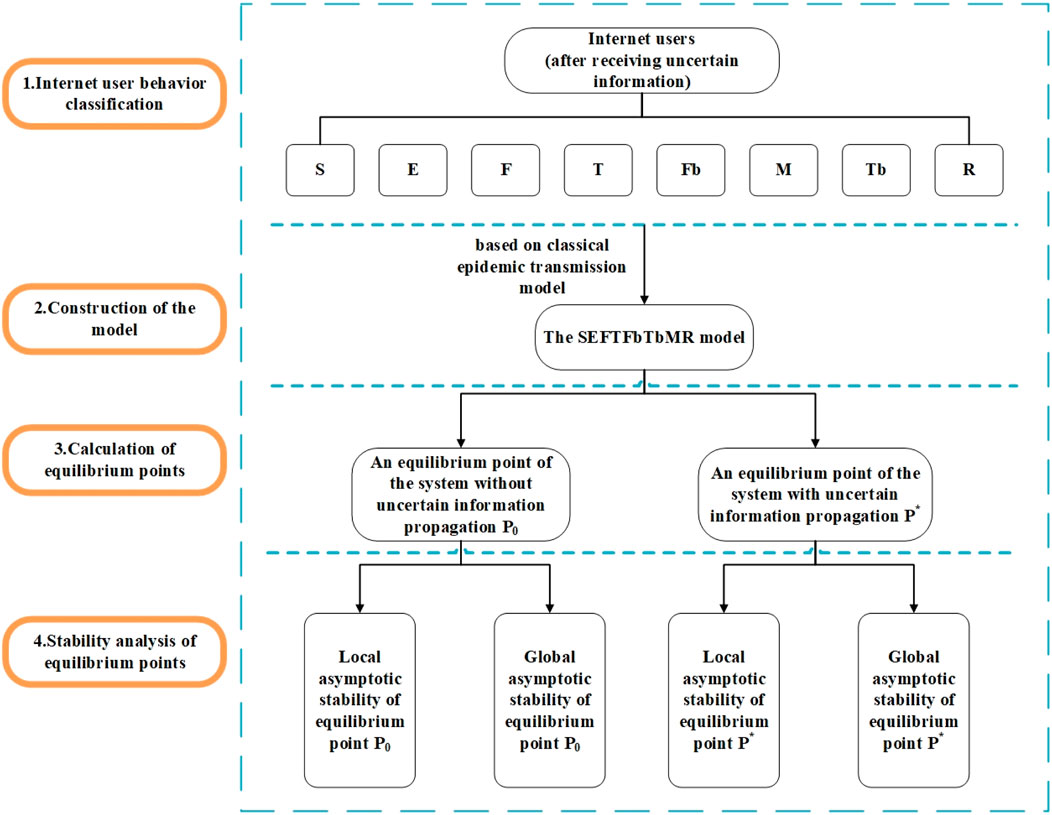
The workflow of the current study in this paper is shown in Figure 1 below, which consists of four main steps: 1) Internet user behavior classification. 2) Construction of the model. 3) Calculation of equilibrium points. 4) Stability analysis of equilibrium points.

FIGURE1

FIGURE1. Organizational diagram of the current study.

The model construction and derivation process in this paper follows the literature [41]. The specific steps are as follows: First, we construct the SEFTFbTbMR model based on the classical infectious disease model. To find the equilibrium point of the model, we calculate the basic regeneration number of the system, R0, using the next-generation matrix method [42]. We then judge the local asymptotic stability and global asymptotic stability of the equilibrium point using the Routh-Hurwitz criterion [43] and Liapunov’s second method [44], respectively. Finally, we conduct numerical simulations of the model.

3.1 Construction of the uncertain information dissemination model

The classical epidemic transmission dynamics model mentioned in the literature [29] is given below:

$\left\{\begin{array}{l}\frac{dS}{dt}=-\beta SI\\ \frac{dI}{dt}=\beta SI-\gamma I\\ \frac{dR}{dt}=\gamma I\end{array}\right.,(1)$

where S refers to susceptible, I refers to infected, R refers to recovered, β is the rate of infection, and γ is the rate of recovery.

In this paper, on the basis of the classical epidemic disease dissemination dynamics model given as Eq. 1, the Internet users in the digital new media platform are divided into eight categories according to their behavior after receiving uncertain information as follows:

(1) The unknowns S are ordinary internet users who have not received uncertain information;

(2) The thinkers E are internet users who, after receiving uncertain information, think about the veracity of this information before acting (i.e., neutral actors);

(3) The uncertain information publishers F are Internet users who, after receiving uncertain information, choose to disseminate the uncertain information;

(4) The clarifiers of uncertain information T are Internet users who, after receiving uncertain information, choose to investigate, obtain evidence, and release true information;

(5) The internet users who believe in uncertain information, Fb;

(6) The internet users who only believe in truthful information, Tb;

(7) The internet users who do not believe any information, M;

(8) The information immunizers R are Internet users who are not interested in either uncertain or true information.

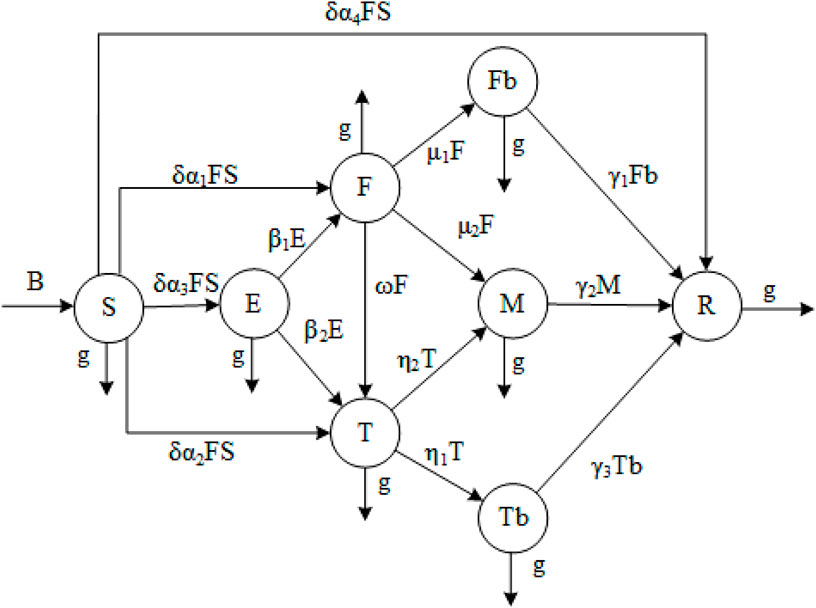
Combining the above eight categories of Internet users with different decision-making behaviors, this paper amends the classical infectious disease SIR model given as Eq. 1 to construct an uncertain information dissemination model, which is defined as the SEFTFbTbMR model. The propagation rules of the SEFTFbTbMR model are as follows:

(I) At moment t, the total number of netizens in the network is N(t), comprising the eight groups identified above, that is,

$S\left(t\right)+E\left(t\right)+F\left(t\right)+T\left(t\right)+Fb\left(t\right)+Tb\left(t\right)+M\left(t\right)+R\left(t\right)=N\left(t\right).(2)$

(II) B individuals enter the system per unit time. These individuals are ordinary internet users who have not received uncertain information (i.e., the transfer rate of unknown internet users in the system is B). Individuals in the eight groups exit the system at the same removal rate g.

(III) The propagation rate of uncertain information is δ. When S makes contact with F and receives some item of uncertain information, one of the following four choices is made: S chooses to propagate the uncertain information immediately, thus becoming a new member of population F; S chooses to clarify the uncertain information immediately, thus becoming a new member of population T; S chooses to think appropriately before acting, thus becoming a new member of population E; or S does not take any interest in the uncertain information and chooses to withdraw from the discussion, thus becoming a new member of population R. The proportions of transformations into F, T, E, and R are α₁, α₂, α₃, and α₄, respectively; where ${\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4=1$.

(IV) Members of population E are converted to population F with probability β₁ and to population T with probability β₂. Members of population F are converted to population T with probability ω after learning the true information. As the uncertain information and the true information in the system come into contact, members of population F will be converted to population Fb with probability μ₁ and to population M with probability μ₂. Members of T will be converted to population Tb with probability η₁ and to population M with probability η₂. As the information is time-sensitive, populations Fb, M, and Tb convert to population R with probabilities γ₁, γ₂, and γ₃, respectively.

Based on the above propagation rules, the dynamics for the SEFTFbTbMR model can be written as follows:

$\left\{\begin{array}{l}\frac{dS}{dt}=B-\delta FS-gS\\ \frac{dE}{dt}={\alpha }_3\delta FS-{\beta }_{1}E-{\beta }_{2}E-gE\\ \frac{dF}{dt}={\alpha }_1\delta FS+{\beta }_{1}E-\omega F-{\mu }_{1}F-{\mu }_{2}F-gF\\ \frac{dT}{dt}={\alpha }_2\delta FS+{\beta }_{2}E+\omega F-{\eta }_{1}T-{\eta }_{2}T-gT\\ \frac{dFb}{dt}={\mu }_{1}F-{\gamma }_{1}Fb-gFb\\ \frac{dM}{dt}={\mu }_{2}F+{\eta }_{2}T-{\gamma }_{2}M-gM\\ \frac{dTb}{dt}={\eta }_{1}T-{\gamma }_{3}Tb-gTb\\ \frac{dR}{dt}={\gamma }_{1}Fb+{\gamma }_{2}M+{\gamma }_{3}Tb+{\alpha }_4\delta FS-gR\end{array}\right..(3)$

The flow chart of the propagation dynamics equations for the SEFTFbTbMR model is shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the propagation dynamics equations for the SEFTFbTbMR model.

Based on Equations 2, 3, we obtain

$\frac{dN\left(t\right)}{dt}=B-gN\left(t\right).(4)$

When $N_0=N\left(0\right)$, Eq. 4 yields $N\left(t\right)=\left(N_0-\frac{B}{g}\right)e^{-gt}+\frac{B}{g}$, namely, $\underset{t\to \infty }{\lim }N\left(t\right)=\frac{B}{g}$. Thus, we can judge the positive invariant set of system (3) to be

$\mathrm{\Omega }=\left\{\begin{array}{l}S,E,F,T,Fb,M,Tb,R\in {\mathbb{R}}_8^{+}:\\ 0\le S+E+F+T+Fb+M+Tb+R\le \frac{B}{g}\end{array}\right\}.(5)$

3.2 Calculation of equilibrium points

Summing up the equilibrium equations in system (3), it can be concluded that there exists an equilibrium point of the system without uncertain information propagation, which is defined as

$P_0=\left(\frac{B}{g},0,0,0,0,0,0,0\right).(6)$

Based on the fundamental regeneration number in propagation dynamics [42], we define the total number of times a member of population F transforms a member of population S into a new member of population F during the average propagation period as the fundamental regeneration number of uncertain information propagation, denoted as R₀. The R₀ of the system can be calculated by the next-generation matrix method. Letting $X={\left(F,E,T,Fb,M,Tb,R,S\right)}^{\mathrm{{\rm T}}}$, system (3) can be rewritten as

$\frac{dX}{dt}=\mathcal{F}\left(X\right)-\mathcal{V}\left(X\right),(7)$

where

$\mathcal{F}\left(X\right)={\left(\begin{array}{cccccccc}{\alpha }_1\delta FS,& {\alpha }_3\delta FS,& 0,& 0,& 0,& 0,& 0,& 0\end{array}\right)}^{\mathrm{{\rm T}}},(8)$

$\mathcal{V}\left(X\right)=\left(\begin{array}{c}-{\beta }_{1}E+\omega F+{\mu }_{1}F+{\mu }_{2}F+gF\\ {\beta }_{1}E+{\beta }_{2}E+gE\\ -{\alpha }_2\delta FS-{\beta }_{2}E-\omega F+{\eta }_{1}T+{\eta }_{2}T+gT\\ -{\mu }_{1}F+{\gamma }_{1}Fb+gFb\\ -{\mu }_{2}F-{\eta }_{2}T+{\gamma }_{2}M+gM\\ -{\eta }_{1}T+{\gamma }_{3}Tb+gTb\\ -{\gamma }_{1}Fb-{\gamma }_{2}M-{\gamma }_{3}Tb-{\alpha }_4\delta FS+gR\\ -B+{\alpha }_1\delta FS+{\alpha }_2\delta FS+{\alpha }_3\delta FS+{\alpha }_4\delta FS+gS\end{array}\right).(9)$

The Jacobian matrix for Equations 8, 9 at equilibrium point (6) is calculated as follows:

$D\mathcal{F}\left(X\right)=\left[\begin{array}{cc}F& 0\\ 0& 0\end{array}\right],(10)$

$D\mathcal{V}\left(X\right)=\left[\begin{array}{cc}V& 0\\ V_1& V_2\end{array}\right],(11)$

where

$F=\left[\begin{array}{cc}{\alpha }_1\delta \frac{B}{g}& 0\\ {\alpha }_3\delta \frac{B}{g}& 0\end{array}\right],(12)$

$V=\left[\begin{array}{cc}\omega +{\mu }_1+{\mu }_2+g& -{\beta }_1\\ 0& {\beta }_1+{\beta }_2+g\end{array}\right].(13)$

According to the literature [45], the R₀ of system (3) is equivalent to the spectral radius of the matrix FV⁻¹:

$\begin{array}{l}{R}_0=\rho \left(F{V}^{-1}\right)\\ =\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}\end{array}.(14)$

From the definition of R₀, there exists an equilibrium point of the system with uncertain information propagation when $R_0>1$, which can be expressed as

$P^{*}=\left(S^{*},E^{*},F^{*},T^{*},F{b}^{*},M^{*},T{b}^{*},R^{*}\right).(15)$

Equilibrium point (15) should satisfy

$\left\{\begin{array}{l}B-{\alpha }_1\delta F^{*}{S}^{*}-{\alpha }_2\delta F^{*}{S}^{*}-{\alpha }_3\delta F^{*}{S}^{*}-{\alpha }_4\delta F^{*}{S}^{*}-g{S}^{*}=0\\ {\alpha }_3\delta F^{*}{S}^{*}-{\beta }_1{E}^{*}-{\beta }_2{E}^{*}-g{E}^{*}=0\\ {\alpha }_1\delta F^{*}{S}^{*}+{\beta }_1{E}^{*}-\omega F^{*}-{\mu }_1{F}^{*}-{\mu }_2{F}^{*}-g{F}^{*}=0\\ {\alpha }_2\delta F^{*}{S}^{*}+{\beta }_2{E}^{*}+\omega F^{*}-{\eta }_1{T}^{*}-{\eta }_2{T}^{*}-g{T}^{*}=0\\ {\mu }_1{F}^{*}-{\gamma }_{1}F{b}^{*}-gF{b}^{*}=0\\ {\mu }_2{F}^{*}+{\eta }_2{T}^{*}-{\gamma }_2{M}^{*}-g{M}^{*}=0\\ {\eta }_1{T}^{*}-{\gamma }_{3}T{b}^{*}-gT{b}^{*}=0\\ {\gamma }_{1}F{b}^{*}+{\gamma }_2{M}^{*}+{\gamma }_{3}T{b}^{*}+{\alpha }_4\delta F^{*}{S}^{*}-g{R}^{*}=0\end{array}\right..(16)$

A specific expression for equilibrium point (15) in terms of R₀ can be obtained by performing calculations on system (16):

$S^{*}=\frac{\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}{\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}=\frac{B}{g{R}_0},(17)$

$E^{*}=\frac{\delta {\alpha }_3{F}^{*}{S}^{*}}{{\beta }_1+{\beta }_2+g}=\frac{{\alpha }_{3}B\left(R_0-1\right)}{\left({\beta }_1+{\beta }_2+g\right)R_0},(18)$

$F^{*}=\frac{B-g{S}^{*}}{\delta S^{*}}=\frac{g\left(R_0-1\right)}{\delta },(19)$

$\begin{array}{l}{T}^{*}=\frac{{\beta }_2{E}^{*}+{\alpha }_2\delta F^{*}{S}^{*}+\omega F^{*}}{g+{\eta }_1+{\eta }_2}\\ =\frac{\left(R_0-1\right)}{g+{\eta }_1+{\eta }_2}\left[\frac{{\beta }_2{\alpha }_{3}B}{\left({\beta }_1+{\beta }_2+g\right)R_0}+\frac{{\alpha }_{2}B}{g{R}_0}+\frac{g\omega }{\delta }\right]\end{array},(20)$

$F{b}^{*}=\frac{{\mu }_1{F}^{*}}{{\gamma }_1+g}=\frac{g{\mu }_1\left(R_0-1\right)}{\delta \left({\gamma }_1+g\right)}(21)$

$\begin{array}{l}{M}^{*}=\frac{{\mu }_2{F}^{*}+{\eta }_2{T}^{*}}{{\gamma }_2+g}\\ =\frac{\left(R_0-1\right)}{{\gamma }_2+g}\left\{\frac{g{\mu }_2}{\delta }+\frac{{\eta }_2}{g+{\eta }_1+{\eta }_2}\left[\frac{{\beta }_2{\alpha }_{3}B}{\left({\beta }_1+{\beta }_2+g\right)R_0}+\frac{{\alpha }_{2}B}{g{R}_0}+\frac{g\omega }{\delta }\right]\right\}\end{array},(22)$

$\begin{array}{l}T{b}^{*}=\frac{{\eta }_1{T}^{*}}{{\gamma }_3+g}\\ =\frac{{\eta }_1\left(R_0-1\right)}{\left(g+{\eta }_1+{\eta }_2\right)\left({\gamma }_3+g\right)}\left[\frac{{\beta }_2{\alpha }_{3}B}{\left({\beta }_1+{\beta }_2+g\right)R_0}+\frac{{\alpha }_{2}B}{R_0}+\frac{g\omega }{\delta }\right]\end{array},(23)$

$\begin{array}{l}{R}^{*}=\frac{{\gamma }_{1}F{b}^{*}+{\gamma }_2{M}^{*}+{\gamma }_{3}T{b}^{*}+{\alpha }_4\delta F^{*}{S}^{*}}{g}\\ =\frac{{\gamma }_1{\mu }_1\left(R_0-1\right)}{\delta \left({\gamma }_1+g\right)}+\frac{B{\alpha }_3\left(R_0-1\right)}{g{R}_0}\\ +\frac{{\gamma }_2\left(R_0-1\right)}{g\left({\gamma }_2+g\right)}\left\{\frac{g{\mu }_2}{\delta }+\frac{{\eta }_2}{g+{\eta }_1+{\eta }_2}\left[\frac{{\beta }_2{\alpha }_{3}B}{\left({\beta }_1+{\beta }_2+g\right)R_0}+\frac{{\alpha }_{2}B}{g{R}_0}+\frac{g\omega }{\delta }\right]\right\}\\ +\frac{{\eta }_1{\gamma }_3\left(R_0-1\right)}{g\left(g+{\eta }_1+{\eta }_2\right)\left({\gamma }_3+g\right)}\left[\frac{{\beta }_2{\alpha }_{3}B}{\left({\beta }_1+{\beta }_2+g\right)R_0}+\frac{{\alpha }_{2}B}{R_0}+\frac{g\omega }{\delta }\right]\end{array}.(24)$

3.3 Stability analysis of equilibrium points

Theorem 1. When $R_0<1,{\beta }_1+{\beta }_2+2g+{\mu }_1+{\mu }_2+\omega >\frac{\delta {\alpha }_{1}B}{g}$, equilibrium point P₀ is locally asymptotically stable in the feasible domain Ω.

Proof:. The Jacobian matrix J(P₀) of system (3) at equilibrium point P₀ is

$J\left(P_0\right)=\left[\begin{array}{cccccccc}-g& 0& -\frac{\delta B}{g}& 0& 0& 0& 0& 0\\ 0& -{\beta }_1-{\beta }_2-g& \frac{{\alpha }_3\delta B}{g}& 0& 0& 0& 0& 0\\ 0& {\beta }_1& \frac{{\alpha }_1\delta B}{g}-{\mu }_1-{\mu }_2-\omega -g& 0& 0& 0& 0& 0\\ 0& {\beta }_2& \frac{{\alpha }_2\delta B}{g}+\omega & -g-{\eta }_1-{\eta }_2& 0& 0& 0& 0\\ 0& 0& {\mu }_1& 0& -g-{\gamma }_1& 0& 0& 0\\ 0& 0& {\mu }_2& {\eta }_2& 0& -g-{\gamma }_2& 0& 0\\ 0& 0& 0& {\eta }_1& 0& 0& -g-{\gamma }_3& 0\\ 0& 0& \frac{{\alpha }_4\delta B}{g}& 0& {\gamma }_1& {\gamma }_2& {\gamma }_3& -g\end{array}\right].(25)$

Let the eigenvalues of matrix (25) be $N_i\left(i=1,2,3,\dots ,8\right)$. From matrix (25), six of the eigenvalues are negative:

$N_1=-g<0,N_2=-g-{\eta }_1-{\eta }_2<0,N_3=-g-{\gamma }_1<0,N_4=-g-{\gamma }_2<0,N_5=-g-{\gamma }_3<0,N_6=-g<0$

The remaining two eigenvalues are also eigenvalues of matrix A₁, which is

$A_1=\left[\begin{array}{cc}-{\beta }_1-{\beta }_2-g& \frac{{\alpha }_3\delta B}{g}\\ {\beta }_1& \frac{{\alpha }_1\delta B}{g}-{\mu }_1-{\mu }_2-\omega -g\end{array}\right].(26)$

The eigenvalues of A₁ satisfy the following quadratic equation:

${\lambda }^2+c_1\lambda +c_2=0,(27)$

where

$c_1={\beta }_1+{\beta }_2+2g+{\mu }_1+{\mu }_2+\omega -\frac{\delta {\alpha }_{1}B}{g},(28)$

$\begin{array}{l}{c}_2=-\delta {\alpha }_{1}B-\frac{\delta B{\alpha }_1{\beta }_1}{g}-\frac{\delta B{\alpha }_3{\beta }_1}{g}-\frac{\delta B{\alpha }_1{\beta }_2}{g}+{\beta }_{1}g+{\beta }_{2}g+g^2+{\beta }_1{\mu }_1\\ +{\beta }_2{\mu }_1+g{\mu }_1+{\beta }_1{\mu }_2+{\beta }_2{\mu }_2+g{\mu }_2+{\beta }_1\omega +{\beta }_2\omega +g\omega \\ =-\delta {\alpha }_{1}B-\frac{\delta B{\alpha }_1{\beta }_1}{g}-\frac{\delta B{\alpha }_3{\beta }_1}{g}-\frac{\delta B{\alpha }_1{\beta }_2}{g}\\ +\left({\beta }_1+{\beta }_2+g\right)\left({\mu }_1+{\mu }_2+g+\omega \right).\end{array}(29)$

From ${\beta }_1+{\beta }_2+2g+{\mu }_1+{\mu }_2+\omega >\frac{\delta {\alpha }_{1}B}{g}$, it can be seen that $c_1>0$. From $R_0=\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}<1$, we have $\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)-\delta {\alpha }_{1}B-\frac{\delta B{\alpha }_1{\beta }_1}{g}-\frac{\delta B{\alpha }_3{\beta }_1}{g}-\frac{\delta B{\alpha }_1{\beta }_2}{g}>0$. Therefore, $c_2>0$.

Based on the Routh–Hurwitz criterion [43], it can be concluded that the locally asymptotically stable equilibrium point P₀ lies within the feasible domain Ω when $R_0<1,{\beta }_1+{\beta }_2+2g+{\mu }_1+{\mu }_2+\omega >\frac{\delta {\alpha }_{1}B}{g}$, which proves Theorem 1.

Theorem 2. When $R_0<1,\delta B\le g^2$, the equilibrium point P₀ is globally asymptotically stable in the feasible domain Ω.

Proof:. We construct the Lyapunov function around the equilibrium point P₀ as follows:

$L_{P_0}\left(t\right)=E\left(t\right)+F\left(t\right)+T\left(t\right)+Fb\left(t\right)+Tb\left(t\right)+M\left(t\right)+R\left(t\right).(30)$

Based on system (3), the derivative of the Lyapunov function (30) at equilibrium point P₀ is

$\begin{array}{l}{L_{P_0}}^{\prime }\left(t\right)=E^{\prime }\left(t\right)+F^{\prime }\left(t\right)+T^{\prime }\left(t\right)+F{b}^{\prime }\left(t\right)+T{b}^{\prime }\left(t\right)+M^{\prime }\left(t\right)+R^{\prime }\left(t\right)\\ ={\alpha }_3\delta FS-{\beta }_{1}E-{\beta }_{2}E-gE+{\alpha }_1\delta FS+{\beta }_{1}E-\omega F-{\mu }_{1}F-{\mu }_{2}F-gF\\ +{\alpha }_2\delta FS+{\beta }_{2}E+\omega F-{\eta }_{1}T-{\eta }_{2}T-gT+{\mu }_{1}F-{\gamma }_{1}Fb-gFb\\ +{\mu }_{2}F+{\eta }_{2}T-{\gamma }_{2}M-gM+{\eta }_{1}T-{\gamma }_{3}Tb-gTb\\ +{\gamma }_{1}Fb+{\gamma }_{2}M+{\gamma }_{3}Tb+{\alpha }_4\delta FS-gR\\ =\left(\delta S-g\right)F-g\left(E+T+Fb+Tb+M+R\right)\end{array}.(31)$

From Eq. 5, we know that $S\le \frac{B}{g}$, and because $\delta B\le g^2$, it follows that

${L_{P_0}}^{\prime }\left(t\right)\le \left(\frac{\delta B}{g}-g\right)F-g\left(E+T+Fb+Tb+M+R\right)\le 0.(32)$

Based on Equations 31, 32, it can be concluded that ${L_{P_0}}^{\prime }\left(t\right)=0$ is only true if $F=E=T=Fb=Tb=M=R=0$. For system (3), the only solution on Ω that satisfies ${L_{P_0}}^{\prime }\left(t\right)=0$ is P₀. Based on the LaSalle invariance principle [46], it can be demonstrated that the globally asymptotically stable equilibrium point P₀ exists in the feasible domain Ω when $R_0<1,\delta B\le g^2$ is true, which proves Theorem 2.

Theorem 3. When $R_0>1,\frac{{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2\right)}{{\alpha }_1}<{\mu }_1+{\mu }_2+\omega$, the uncertain information propagation equilibrium point P^* is locally asymptotically stable in the feasible domain Ω.

Proof:. The Jacobian matrix J(P^*) of system (3) at equilibrium point P^* with uncertain information propagation is

$J\left(P^{*}\right)=\left[\begin{array}{cccccccc}-g-\delta F^{*}& 0& -\delta S^{*}& 0& 0& 0& 0& 0\\ {\alpha }_3\delta F^{*}& -{\beta }_1-{\beta }_2-g& {\alpha }_3\delta S^{*}& 0& 0& 0& 0& 0\\ {\alpha }_1\delta F^{*}& {\beta }_1& {\alpha }_1\delta S^{*}-{\mu }_1-{\mu }_2-\omega -g& 0& 0& 0& 0& 0\\ {\alpha }_2\delta F^{*}& {\beta }_2& {\alpha }_2\delta S^{*}+\omega & -g-{\eta }_1-{\eta }_2& 0& 0& 0& 0\\ 0& 0& {\mu }_1& 0& -g-{\gamma }_1& 0& 0& 0\\ 0& 0& {\mu }_2& {\eta }_2& 0& -g-{\gamma }_2& 0& 0\\ 0& 0& 0& {\eta }_1& 0& 0& -g-{\gamma }_3& 0\\ {\alpha }_4\delta F^{*}& 0& {\alpha }_4\delta S^{*}& 0& {\gamma }_1& {\gamma }_2& {\gamma }_3& -g\end{array}\right].(33)$

We denote the eigenvalues of matrix (33) as $H_i\left(i=1,2,3,\dots ,8\right)$. It is apparent from matrix (33) that five of the eigenvalues are negative:

$H_1=-g<0,H_2=-g-{\eta }_1-{\eta }_2<0,H_3=-g-{\gamma }_1<0,H_4=-g-{\gamma }_2<0,H_5=-g-{\gamma }_3<0$

The remaining three eigenvalues are also eigenvalues of matrix A₂, which is

$A_2=\left[\begin{array}{ccc}-g-\delta F^{*}& 0& -\delta S^{*}\\ {\alpha }_3\delta F^{*}& -{\beta }_1-{\beta }_2-g& {\alpha }_3\delta S^{*}\\ {\alpha }_1\delta F^{*}& {\beta }_1& {\alpha }_1\delta S^{*}-{\mu }_1-{\mu }_2-\omega -g\end{array}\right].(34)$

Converting the elements of matrix A₂ to an expression containing R₀(14) yields matrix A^*:

$A^{*}=\left[\begin{array}{lll}-g{R}_0& 0& -\frac{\delta B}{g{R}_0}\\ {\alpha }_{3}g\left(R_0-1\right)& -{\beta }_1-{\beta }_2-g& \frac{{\alpha }_3\delta B}{g{R}_0}\\ {\alpha }_{1}g\left(R_0-1\right)& {\beta }_1& \frac{{\alpha }_1\delta B}{g{R}_0}-{\mu }_1-{\mu }_2-\omega -g\end{array}\right].(35)$

For ease of writing and derivation later, we let the elements of matrix (35) be

$\begin{array}{l}{K}_1=g{R}_0,K_2=\frac{\delta B}{g{R}_0},K_3=-{\alpha }_{3}g\left(R_0-1\right),K_4={\beta }_1+{\beta }_2+g,K_5\\ =-\frac{{\alpha }_3\delta B}{g{R}_0}\\ K_6=-{\alpha }_{1}g\left(R_0-1\right),K_7=-{\beta }_1,\\ K_8=-\left(\frac{{\alpha }_1\delta B}{g{R}_0}-{\mu }_1-{\mu }_2-\omega -g\right)=\frac{{\alpha }_3{\beta }_1\left({\mu }_1+{\mu }_2+\omega +g\right)}{{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)}\end{array}$

Because $R_0>1$, we have that $K_1>0,K_2>0,K_4>0,K_8>0,K_3<0,K_5<0,K_6<0,K_7<0$.

Writing matrix A^* as

$A^{*}=\left[\begin{array}{ccc}-K_1& 0& -K_2\\ -K_3& -K_4& -K_5\\ -K_6& -K_7& -K_8\end{array}\right],(36)$

the eigenvalues satisfy the following one-dimensional cubic equation:

${\lambda }^3+h_1{\lambda }^2+h_2\lambda +h_3=0,(37)$

where

$h_1=K_1+K_4+K_8>0,(38)$

$h_2=K_1{K}_4-K_2{K}_6-K_5{K}_7+K_1{K}_8+K_4{K}_8,(39)$

$\begin{array}{l}{h}_3=-K_2{K}_4{K}_6+K_2{K}_3{K}_7-K_1{K}_5{K}_7+K_1{K}_4{K}_8\\ =K_1\left(K_4{K}_8-K_5{K}_7\right)+K_2\left(K_3{K}_7-K_4{K}_6\right)\end{array}.(40)$

First, to determine the positive and negative solutions of Eq. 39, recall that $K_6<0$. Then, $K_1{K}_4-K_2{K}_6+K_1{K}_8>0$, and

$\begin{array}{l}{K}_4{K}_8-K_5{K}_7=-\left({\beta }_1+{\beta }_2+g\right)\left(\frac{{\alpha }_1\delta B}{g{R}_0}-{\mu }_1-{\mu }_2-\omega -g\right)-\frac{{\alpha }_3\delta B{\beta }_1}{g{R}_0}\\ =\frac{-{\alpha }_1\delta B\left({\beta }_1+{\beta }_2+g\right)+\left({\beta }_1+{\beta }_2+g\right)\left({\mu }_1+{\mu }_2+\omega +g\right)g{R}_0-{\alpha }_3\delta B{\beta }_1}{g{R}_0}\\ =\frac{\left({\beta }_1+{\beta }_2+g\right)\left({\mu }_1+{\mu }_2+\omega +g\right)g{R}_0-\left[{\alpha }_3\delta B{\beta }_1+{\alpha }_1\delta B\left({\beta }_1+{\beta }_2+g\right)\right]}{g{R}_0}\\ =\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]-\left[{\alpha }_3\delta B{\beta }_1+{\alpha }_1\delta B\left({\beta }_1+{\beta }_2+g\right)\right]}{g{R}_0}\\ =\frac{\left(B\delta -B\delta \right)\left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g{R}_0}\\ =0\end{array}.(41)$

Therefore, $h_2>0$.

Second, to determine the positive and negative solutions of Eq. 40, if $K_3<0,K_6<0,K_7<0$, then $K_2\left(K_3{K}_7-K_4{K}_6\right)>0$. Thus, based on Eq. 41, we have that $h_3>0$.

From Equations 38–40, the values of h₁h₂ and h₁h₂-h₃ are respectively

$\begin{array}{l}{h}_1{h}_2={K_1}^2{K}_4+K_1{K_4}^2-K_1{K}_2{K}_6-K_2{K}_4{K}_6-K_1{K}_5{K}_7-K_4{K}_5{K}_7\\ +{K_1}^2{K}_8\\ +3K_1{K}_4{K}_8+{K_4}^2{K}_8-K_2{K}_6{K}_8-K_5{K}_7{K}_8+K_1{K_8}^2+K_4{K_8}^2,\end{array}(42)$

$\begin{array}{l}{h}_1{h}_2-h_3={K_1}^2{K}_4+K_1{K_4}^2-K_1{K}_2{K}_6-K_4{K}_5{K}_7+{K_1}^2{K}_8\\ +2K_1{K}_4{K}_8+{K_4}^2{K}_8-K_2{K}_6{K}_8-K_5{K}_7{K}_8+K_1{K_8}^2+K_4{K_8}^2\\ -K_2{K}_3{K}_7\\ ={K_1}^2\left(K_4+K_8\right)+\left(K_4+K_8\right)\left(K_4{K}_8-K_5{K}_7\right)-K_2\left(K_3{K}_7+K_6{K}_8\right)\\ +K_1\left({K_4}^2-K_2{K}_6+2K_4{K}_8+{K_8}^2\right)\end{array}.(43)$

Finally, to determine the positive solutions of Eq. 43, recall that $K_6<0$ and $K_4{K}_8-K_5{K}_7=0$. Therefore, the following must hold:

${K_1}^2\left(K_4+K_8\right)+\left(K_4+K_8\right)\left(K_4{K}_8-K_5{K}_7\right)+K_1\left({K_4}^2-K_2{K}_6+2K_4{K}_8+{K_8}^2\right)>0$

The calculation of $K_3{K}_7+K_6{K}_8$ is simplified as follows:

$\begin{array}{l}{K}_3{K}_7+K_6{K}_8={\alpha }_{3}g\left(R_0-1\right){\beta }_1+{\alpha }_{1}g\left(R_0-1\right)\left(\frac{{\alpha }_1\delta B}{g{R}_0}-{\mu }_1-{\mu }_2-\omega -g\right)\\ =g\left(R_0-1\right)\left[{\alpha }_3{\beta }_1+\frac{{{\alpha }_1}^{2}B\delta }{g{R}_0}-{\alpha }_1\left(g+{\mu }_1+{\mu }_2+\omega \right)\right]\\ =g\left(R_0-1\right)\frac{{\alpha }_3{\beta }_1\left[{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2-{\mu }_1-{\mu }_2-\omega \right)\right]}{{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)}.\end{array}(44)$

Because $R_0>1,\frac{{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2\right)}{{\alpha }_1}<{\mu }_1+{\mu }_2+\omega$, we have that $K_3{K}_7+K_6{K}_8<0$. Because $K_2>0$, we have that $-K_2\left(K_3{K}_7+K_6{K}_8\right)>0$, and it follows that $h_1{h}_2-h_3>0$.

Based on the Routh–Hurwitz criterion [43], it can be concluded that the locally asymptotically stable uncertain information propagation equilibrium point P^* lies within the feasible domain Ω when $R_0>1,\frac{{\alpha }_3{\beta }_1+{\alpha }_1\left({\beta }_1+{\beta }_2\right)}{{\alpha }_1}<{\mu }_1+{\mu }_2+\omega$, which proves Theorem 3.

Theorem 4. When $R_0>1$, the uncertain information propagation equilibrium point P^* is globally asymptotically stable in the feasible domain Ω.

Proof:. We construct the Lyapunov function around the equilibrium point P^* as follows:

$L_{P^{*}}\left(t\right)={\left\{\begin{array}{l}\left[S\left(t\right)-S^{*}\right]+\left[E\left(t\right)-E^{*}\right]+\left[F\left(t\right)-F^{*}\right]+\left[T\left(t\right)-T^{*}\right]\\ +\left[Fb\left(t\right)-F{b}^{*}\right]+\left[Tb\left(t\right)-T{b}^{*}\right]+\left[M\left(t\right)-M^{*}\right]+\left[R\left(t\right)-R^{*}\right]\end{array}\right\}}^2.(45)$

Based on system (3), the derivative of the Lyapunov function (45) at the equilibrium point P^* is

$\begin{array}{l}{L_{P^{*}}}^{\prime }\left(t\right)=2\left\{\begin{array}{l}\left[S\left(t\right)-S^{*}\right]+\left[E\left(t\right)-E^{*}\right]+\left[F\left(t\right)-F^{*}\right]+\left[T\left(t\right)-T^{*}\right]\\ +\left[Fb\left(t\right)-F{b}^{*}\right]+\left[Tb\left(t\right)-T{b}^{*}\right]+\left[M\left(t\right)-M^{*}\right]+\left[R\left(t\right)-R^{*}\right]\end{array}\right\}\\ \left[S^{\prime }\left(t\right)+E^{\prime }\left(t\right)+F^{\prime }\left(t\right)+T^{\prime }\left(t\right)+F{b}^{\prime }\left(t\right)+T{b}^{\prime }\left(t\right)+M^{\prime }\left(t\right)+R^{\prime }\left(t\right)\right]\\ =2\left\{\begin{array}{l}\left[S\left(t\right)-S^{*}\right]+\left[E\left(t\right)-E^{*}\right]+\left[F\left(t\right)-F^{*}\right]+\left[T\left(t\right)-T^{*}\right]\\ +\left[Fb\left(t\right)-F{b}^{*}\right]+\left[Tb\left(t\right)-T{b}^{*}\right]+\left[M\left(t\right)-M^{*}\right]+\left[R\left(t\right)-R^{*}\right]\end{array}\right\}\\ \left[B-g\left(S+E+F+T+Fb+Tb+M+R\right)\right].\end{array}(46)$

From point P^* in Eq. 15, it follows that $B-g\left(S^{*}+E^{*}+F^{*}+T^{*}+F{b}^{*}+T{b}^{*}+M^{*}+R^{*}\right)=0$, namely, $B=g\left(S^{*}+E^{*}+F^{*}+T^{*}+F{b}^{*}+T{b}^{*}+M^{*}+R^{*}\right)$.

Therefore, Eq. 46 can be expressed as

$\begin{array}{l}{L_{P^{*}}}^{\prime }\left(t\right)=2\left\{\begin{array}{l}\left[S\left(t\right)-S^{*}\right]+\left[E\left(t\right)-E^{*}\right]+\left[F\left(t\right)-F^{*}\right]\\ +\left[T\left(t\right)-T^{*}\right]+\left[Fb\left(t\right)-F{b}^{*}\right]+\left[Tb\left(t\right)-T{b}^{*}\right]\\ +\left[M\left(t\right)-M^{*}\right]+\left[R\left(t\right)-R^{*}\right]\end{array}\right\}\\ \left[g\left(S^{*}+E^{*}+F^{*}+T^{*}+F{b}^{*}+T{b}^{*}+M^{*}+R^{*}\right)-g\left(\begin{array}{l}S+E+F+T\\ +Fb+Tb+M+R\end{array}\right)\right]\\ =-2g{\left\{\begin{array}{l}\left[S\left(t\right)-S^{*}\right]+\left[E\left(t\right)-E^{*}\right]+\left[F\left(t\right)-F^{*}\right]+\left[T\left(t\right)-T^{*}\right]\\ +\left[Fb\left(t\right)-F{b}^{*}\right]+\left[Tb\left(t\right)-T{b}^{*}\right]+\left[M\left(t\right)-M^{*}\right]\\ +\left[R\left(t\right)-R^{*}\right]\end{array}\right\}}^2\\ \le 0\end{array}(47)$

From Eq. 47, it can be concluded that ${L_{P^{*}}}^{\prime }\left(t\right)=0$ only if $S\left(t\right)=S^{*},E\left(t\right)=E^{*},F\left(t\right)=F^{*},T\left(t\right)=T^{*},Fb\left(t\right)=F{b}^{*},Tb\left(t\right)=T{b}^{*},M\left(t\right)=M^{*},R\left(t\right)=R^{*}$ all hold. From system (3), the only solution on Ω that satisfies ${L_{P^{*}}}^{\prime }\left(t\right)=0$ is P^*. Based on the LaSalle invariance principle [46], it can be demonstrated that the globally asymptotically stable equilibrium point P^* of uncertain information propagation exists in the feasible domain Ω when $R_0>1$ holds, which proves Theorem 4.

3.4 Numerical simulation analysis of equilibrium point stability

To verify the theoretical derivations, we now assign values to the parameters and perform numerical simulations using Matlab2017b. As these parameters cannot be obtained directly in practical cases, we use reasonable values within the context of the situation. The relevant parameters are assigned based on the following scenarios:

Scenario 1: To verify the local and global asymptotic stability of equilibrium point P₀ in the feasible domain Ω for $R_0<1$, the parameters are assigned as follows:

$\left\{\begin{array}{l}B=1,g=0.2,{\alpha }_1=0.2,{\alpha }_2=0.2,{\alpha }_3=0.5,{\alpha }_4=0.1,{\beta }_1=0.2,\\ {\beta }_2=0.3,{\mu }_1=0.4,{\mu }_2=0.3,{\eta }_1=0.3,{\eta }_2=0.3,\omega =0.6,\\ {\gamma }_1=0.5,{\gamma }_2=0.5,{\gamma }_3=0.5,\delta =0.02\end{array}\right..(48)$

Based on the parameters in (48), we have that $R_0=0.0229<1$, which satisfies the basic assumptions of Theorems 1 and 2. To further explore whether the initial values of the various Internet user populations in the system impact the final stability of the equilibrium point P₀, we maintain the values in (48) and conduct numerical simulations with different initial values. Figure 3 shows the evolution of equilibrium point P₀ over time when $R_0<1$.

FIGURE 3

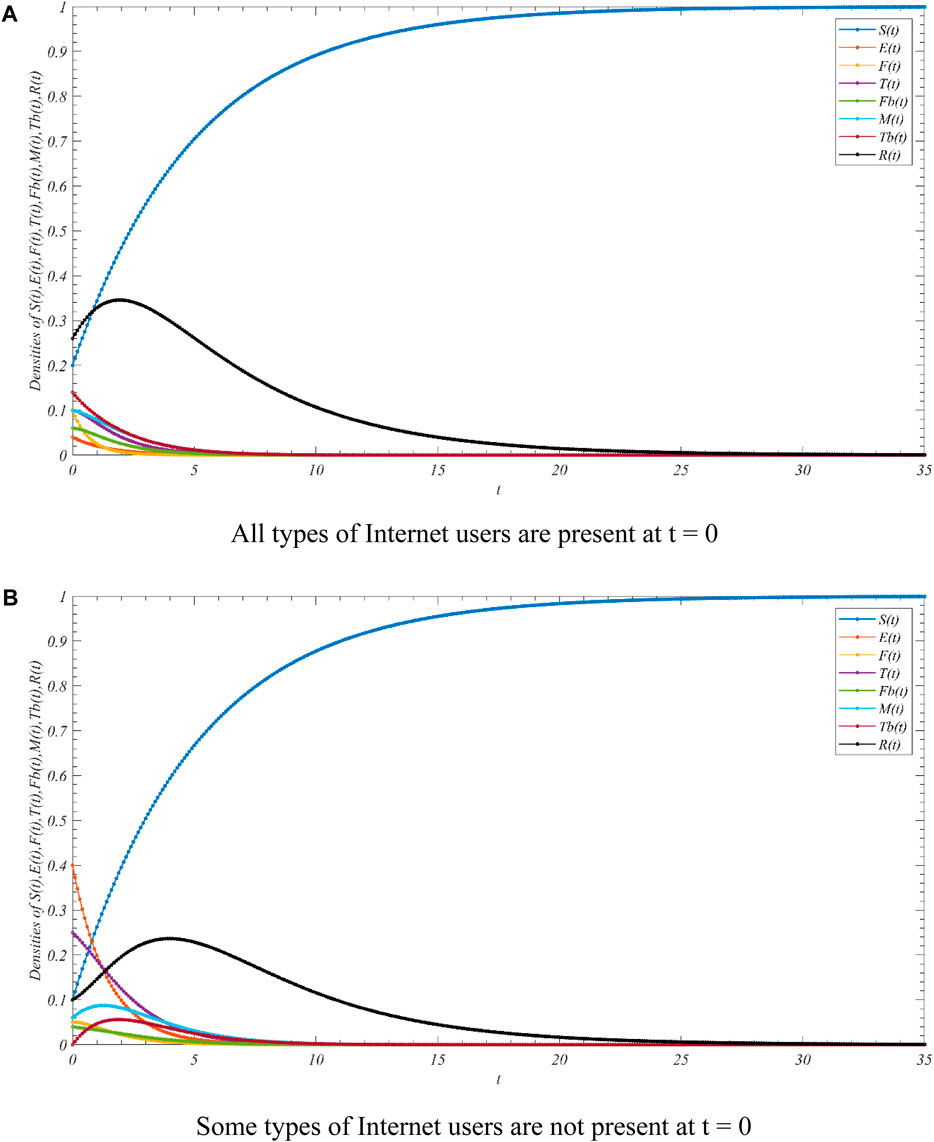
FIGURE 3. Evolution of Internet user populations when R₀ < 1. (A) all types of Internet users are present at t = 0. (B) some types of Internet users are not present at t = 0.

From Figure 3, it is evident that, regardless of the initial proportions of the Internet population, every Internet user eventually becomes an unknown entity. Thus, equilibrium point P₀ is asymptotically stable within the feasible domain Ω when $R_0<1$, which is consistent with the theory.

Based on Scenario 1, we can know that in the real world, when a major emergencies occurs in a certain place, as long as R₀ < 1, the uncertain information in the online social platform will be gradually forgotten by the netizens over time. In this case, the relevant government departments do not need to make additional interventions, and the uncertain information does not affect the stability of society.

Scenario 2: To verify the local and global asymptotic stability of equilibrium point P^* in the feasible domain Ω for $R_0>1$, the parameters are assigned as follows:

$\left\{\begin{array}{l}B=1,g=0.2,{\alpha }_1=0.4,{\alpha }_2=0.15,{\alpha }_3=0.4,{\alpha }_4=0.05,{\beta }_1=0.2,\\ {\beta }_2=0.2,{\mu }_1=0.2,{\mu }_2=0.2,{\eta }_1=0.3,{\eta }_2=0.3,\omega =0.3,{\gamma }_1=0.5,\\ {\gamma }_2=0.5,{\gamma }_3=0.5,\delta =0.5\end{array}\right..(49)$

Based on the parameter values in (49), we have that $R_0=1.4815>1$, which satisfies the basic assumptions of Theorems 3 and 4. To further explore whether the initial values of the various Internet user populations impact the final stability of equilibrium point P^*, we maintain the values in (49) and conduct numerical simulations with different initial values. Figure 4 shows the evolution of the equilibrium point P^* when $R_0>1$.

FIGURE 4

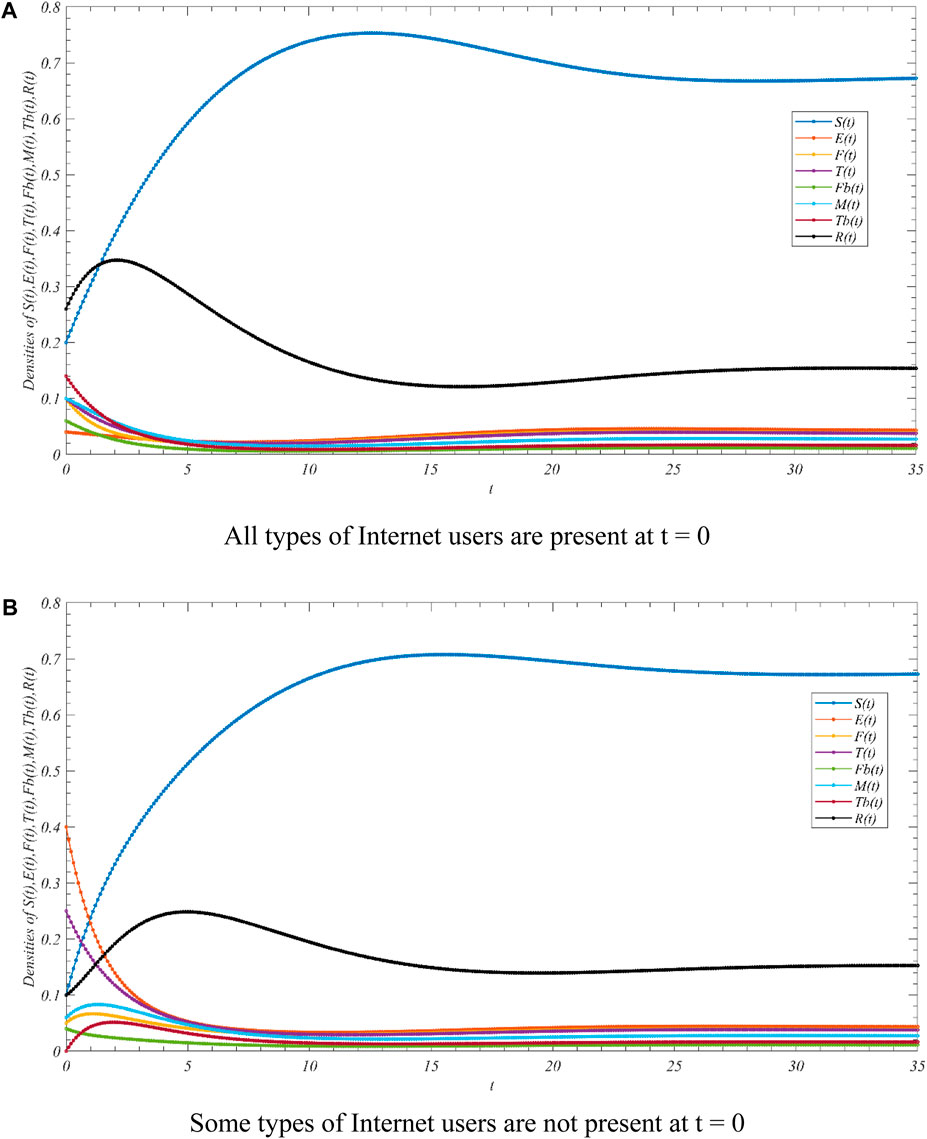
FIGURE 4. Evolution of Internet user populations when $R_0>1$. (A) all types of Internet users are present at t = 0. (B) some types of Internet users are not present at t = 0.

From Figure 4, it is evident that, regardless of the initial populations of each state in the system, all users eventually become an unknown entity. Thus, the uncertain information propagation equilibrium point P^* is asymptotically stable within the feasible domain Ω when $R_0>1$, which is consistent with the theory.

Based on Scenario 2, we can know that in the real world, when a major emergencies occur in a certain place, when $R_0>1$, the uncertain information in the online social platform will keep spreading among netizens over time. In this case, if the relevant government departments do not intervene, it will lead to the continuous spread of panic among netizens, which will eventually affect the stability of society.

4 Optimal control model

Based on the SEFTFbTbMR uncertain information dissemination model, it is recommended that netizens be encouraged to clarify uncertain information as much as possible, or to think and judge uncertain information instead of posting random remarks; this action will reduce the impact of uncertain information. Therefore, the number of thinkers and clarifiers of uncertain information should be increased. Thus, we now examine the effect of modifying the model’s proportionality constants α₂, α₃, β₂, and ω into control variable functions α₂(t), α₃(t), β₂(t), and ω(t), respectively.

The objective function is defined as follows:

$J\left({\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right)={\int }_0^{t_f}\left[\begin{array}{l}E\left(t\right)+T\left(t\right)-\frac{{\psi }_1}{2}{{\alpha }_2}^2\left(t\right)-\frac{{\psi }_2}{2}{{\alpha }_3}^2\left(t\right)-\frac{{\psi }_3}{2}{{\beta }_2}^2\left(t\right)\\ -\frac{{\psi }_4}{2}{\omega }^2\left(t\right)\end{array}\right]dt,(50)$

where t_f is the end moment, and ψ₁, ψ₂, ψ₃, and ψ₄ are the weight coefficients of each function.

We seek to satisfy the following system constraints:

$\left\{\begin{array}{l}\frac{dS}{dt}=B-gS-{\alpha }_1\delta FS-{\alpha }_2\left(t\right)\delta FS-{\alpha }_3\left(t\right)\delta FS-{\alpha }_4\delta FS\\ \frac{dE}{dt}={\alpha }_3\left(t\right)\delta FS-{\beta }_{1}E-{\beta }_2\left(t\right)E-gE\\ \frac{dF}{dt}={\alpha }_1\delta FS+{\beta }_{1}E-\omega \left(t\right)F-{\mu }_{1}F-{\mu }_{2}F-gF\\ \frac{dT}{dt}={\alpha }_2\left(t\right)\delta FS+{\beta }_2\left(t\right)E+\omega \left(t\right)F-{\eta }_{1}T-{\eta }_{2}T-gT\\ \frac{dFb}{dt}={\mu }_{1}F-{\gamma }_{1}Fb-gFb\\ \frac{dM}{dt}={\mu }_{2}F+{\eta }_{2}T-{\gamma }_{2}M-gM\\ \frac{dTb}{dt}={\eta }_{1}T-{\gamma }_{3}Tb-gTb\\ \frac{dR}{dt}={\gamma }_{1}Fb+{\gamma }_{2}M+{\gamma }_{3}Tb+{\alpha }_4\delta FS-gR\end{array}\right..(51)$

The initial conditions necessary to satisfy system (60) are

$\begin{array}{l}S\left(0\right)=S_0,E\left(0\right)=E_0,F\left(0\right)=F_0,T\left(0\right)=T_0,\\ Fb\left(0\right)=F{b}_0,M\left(0\right)=M_0,Tb\left(0\right)=T{b}_0,R\left(0\right)=R_0\end{array},(52)$

where

${\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\beta }_2\left(t\right),\omega \left(t\right)\in U\triangleq \left\{\begin{array}{l}\left({\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right)|\left({\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\beta }_2\left(t\right),\omega \left(t\right)\right)\\ measurable,\\ 0\le {\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\beta }_2\left(t\right),\omega \left(t\right)\le 1,\forall t\in \left[0,t_f\right]\end{array}\right\}.(53)$

Theorem 5. There exists an optimal control tuple $\left({{\alpha }_2}^{*},{{\alpha }_3}^{*},{{\beta }_2}^{*},{\omega }^{*}\right)\in U$ such that

$J\left({{\alpha }_2}^{*},{{\alpha }_3}^{*},{{\beta }_2}^{*},{\omega }^{*}\right)=\max \left\{J\left({\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right):\left({\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right)\in U\right\}.(54)$

Proof:. Set $X\left(t\right)={\left(S\left(t\right),E\left(t\right),F\left(t\right),T\left(t\right),Fb\left(t\right),Tb\left(t\right),M\left(t\right),R\left(t\right)\right)}^T$ and

$\begin{array}{l}L\left(t,X\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\beta }_2\left(t\right),\omega \left(t\right)\right)=E\left(t\right)+T\left(t\right)-\frac{{\psi }_1}{2}{{\alpha }_2}^2\left(t\right)\\ -\frac{{\psi }_2}{2}{{\alpha }_3}^2\left(t\right)-\frac{{\psi }_3}{2}{{\beta }_2}^2\left(t\right)-\frac{{\psi }_4}{2}{\omega }^2\left(t\right)\end{array}$

The existence of optimal control tuples is contingent upon fulfilling the following criteria:

1. The set of control variables and corresponding state variables must constitute a nonempty set.

2. The control set U must be closed and convex.

3. The right-hand side of (60) should take the form of a linear system comprising state variables and control variables.

4. The product of the target generalization must be convex on U.

5. There is a constant $k_1>0,k_2>0,l>0$ such that the product of the intended generalized function satisfies

$-L\left(t,X\left(t\right),{\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right)\ge k_1{\left({\left|{\alpha }_2\right|}^2+{\left|{\alpha }_3\right|}^2+{\left|{\beta }_2\right|}^2+{\left|\omega \right|}^2\right)}^{\frac{l}{2}}-k_2.(55)$

As conditions 1–3 are straightforward, only conditions 4 and 5 are proved.

First, it is easy to obtain inequalities based on system (51):

$\begin{array}{l}{S}^{\prime }\le B,E^{\prime }\le {\alpha }_3\left(t\right)\delta FS,F^{\prime }\le {\alpha }_1\delta FS+{\beta }_{1}E,T^{\prime }\le {\alpha }_2\left(t\right)\delta FS+{\beta }_2\left(t\right)E\\ +\omega \left(t\right)F,F{b}^{\prime }\le {\mu }_{1}F,M^{\prime }\le {\mu }_{2}F+{\eta }_{2}T,T{b}^{\prime }\le {\eta }_{1}T,R^{\prime }\le {\gamma }_{1}Fb+{\gamma }_{2}M\\ +{\gamma }_{3}Tb+{\alpha }_4\delta FS.\end{array}.(56)$

Therefore, condition 4 holds.

Second, for any $t\ge 0$, there exists a positive constant Z satisfying $\left|X\left(t\right)\right|\le Z$. Hence,

$\begin{array}{l}-L\left(t,X\left(t\right),{\alpha }_2,{\alpha }_3,{\beta }_2,\omega \right)=\frac{{\psi }_1}{2}{{\alpha }_2}^2\left(t\right)+\frac{{\psi }_2}{2}{{\alpha }_3}^2\left(t\right)+\frac{{\psi }_3}{2}{{\beta }_2}^2\left(t\right)\\ +\frac{{\psi }_4}{2}{\omega }^2\left(t\right)-E\left(t\right)-T\left(t\right)\\ \ge k_1{\left({\left|{\alpha }_2\right|}^2+{\left|{\alpha }_3\right|}^2+{\left|{\beta }_2\right|}^2+{\left|\omega \right|}^2\right)}^{\frac{l}{2}}-2Z.\end{array}(57)$

Setting $k_1=\min \left\{\frac{{\psi }_1}{2},\frac{{\psi }_2}{2},\frac{{\psi }_3}{2},\frac{{\psi }_4}{2}\right\},k_2=2Z,l=2$, condition 5 then holds.

At this point, all optimal control tuples have been successfully verified, proving Theorem 5.

Theorem 6. For the optimal control tuple $\left({{\alpha }_2}^{*},{{\alpha }_3}^{*},{{\beta }_2}^{*},{\omega }^{*}\right)\in U$ for system (51), there is an associated variable ${\rho }_i\left(i=1,2,...,8\right)$ such that

$\left\{\begin{array}{l}\begin{array}{l}\frac{d{\rho }_1}{dt}=\left({\rho }_1+{\rho }_4\right){\alpha }_2\left(t\right)\delta F+{\rho }_1{\alpha }_4\delta F+{\rho }_3{\alpha }_1\delta F+\left({\rho }_{1}F+{\rho }_{2}S\right){\alpha }_3\left(t\right)\delta \\ +{\rho }_8{\alpha }_4\delta F+{\rho }_{1}g+{\rho }_1{\alpha }_1\delta F\end{array}\\ \frac{d{\rho }_2}{dt}=1+\left({\rho }_2-{\rho }_4\right){\beta }_2\left(t\right)+{\rho }_2\left({\beta }_1+g\right)-{\rho }_3{\beta }_1\\ \begin{array}{l}\frac{d{\rho }_3}{dt}=\left({\rho }_1-{\rho }_4\right){\alpha }_2\left(t\right)\delta S-{\rho }_5{\mu }_1+{\rho }_8{\alpha }_4\delta S+\left({\rho }_1-{\rho }_2\right){\alpha }_3\left(t\right)\delta S\\ +{\rho }_1\left[-{\alpha }_1\delta S+{\alpha }_4\delta S\right]\\ +\left({\rho }_3-{\rho }_4\right)\omega \left(t\right)-{\rho }_6{\mu }_2+{\rho }_3\left[-{\alpha }_1\delta S+{\mu }_1+{\mu }_2+g\right]\end{array}\\ \frac{d{\rho }_4}{dt}=1-{\rho }_7{\eta }_1-{\rho }_6{\eta }_2+{\rho }_4\left({\eta }_1+{\eta }_2+g\right)\\ \frac{d{\rho }_5}{dt}={\rho }_5\left({\gamma }_1+g\right)-{\rho }_8{\gamma }_1\\ \frac{d{\rho }_6}{dt}={\rho }_6\left({\gamma }_2+g\right)-{\rho }_8{\gamma }_2\\ \frac{d{\rho }_7}{dt}={\rho }_7\left({\gamma }_3+g\right)-{\rho }_8{\gamma }_3\\ \frac{d{\rho }_8}{dt}={\rho }_{8}g,\end{array}\right.(58)$

with the following boundary conditions:

${\rho }_1\left(t_f\right)={\rho }_2\left(t_f\right)={\rho }_3\left(t_f\right)={\rho }_4\left(t_f\right)={\rho }_5\left(t_f\right)={\rho }_6\left(t_f\right)={\rho }_7\left(t_f\right)={\rho }_8\left(t_f\right)=0.(59)$

Furthermore, the optimal control tuple $\left({{\alpha }_2}^{*},{{\alpha }_3}^{*},{{\beta }_2}^{*},{\omega }^{*}\right)\in U$ for the state system can be obtained from the following equation:

$\left\{\begin{array}{c}{\alpha }_2^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}\\ {\alpha }_3^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\}\\ {\beta }_2^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_2-{\rho }_4\right)E}{{\psi }_3}\right\}\right\}\\ {\omega }^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_3-{\rho }_4\right)F}{{\psi }_4}\right\}\right\}.\end{array}\right.(60)$

Proof:. To derive the necessary expressions for the optimal control system and control tuple, we define a Hamiltonian function with a penalty term, with the following expression serving as a guideline:

$\begin{array}{l}H=-L\left(t,X\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\beta }_2\left(t\right),\omega \left(t\right)\right)\\ +{\rho }_1\left[B-gS-{\alpha }_1\delta FS-{\alpha }_2\left(t\right)\delta FS-{\alpha }_3\left(t\right)\delta FS-{\alpha }_4\delta FS\right]\\ +{\rho }_7\left[{\eta }_{1}T-{\gamma }_{3}Tb-gTb\right]\\ +{\rho }_2\left[{\alpha }_3\left(t\right)\delta FS-{\beta }_{1}E-{\beta }_2\left(t\right)E-gE\right]+{\rho }_6\left[{\mu }_{2}F+{\eta }_{2}T-{\gamma }_{2}M-gM\right]\\ +{\rho }_3\left[{\alpha }_1\delta FS+{\beta }_{1}E-\omega \left(t\right)F-{\mu }_{1}F-{\mu }_{2}F-gF\right]+{\rho }_5\left[{\mu }_{1}F-{\gamma }_{1}Fb-gFb\right]\\ +{\rho }_4\left[{\alpha }_2\left(t\right)\delta FS+{\beta }_2\left(t\right)E+\omega \left(t\right)F-{\eta }_{1}T-{\eta }_{2}T-gT\right]\\ +{\rho }_8\left[{\gamma }_{1}Fb+{\gamma }_{2}M+{\gamma }_{3}Tb+{\alpha }_4\delta FS-gR\right]\\ -{\lambda }_{11}{\alpha }_2\left(t\right)-{\lambda }_{12}\left(1-{\alpha }_2\left(t\right)\right)-{\lambda }_{21}{\alpha }_3\left(t\right)-{\lambda }_{22}\left(1-{\alpha }_3\left(t\right)\right)\\ -{\lambda }_{31}{\beta }_2\left(t\right)-{\lambda }_{32}\left(1-{\beta }_2\left(t\right)\right)\\ -{\lambda }_{41}\omega \left(t\right)-{\lambda }_{42}\left(1-\omega \left(t\right)\right)\end{array},(61)$

where the penalty term ${\lambda }_{ij}\left(t\right)\ge 0$ satisfies ${\lambda }_{11}\left(t\right){\alpha }_2\left(t\right)={\lambda }_{12}\left(t\right)\left(1-{\alpha }_2\left(t\right)\right)=0$ at the optimal control point for ${\alpha }_2^{*}$, ${\lambda }_{21}\left(t\right){\alpha }_3\left(t\right)={\lambda }_{22}\left(t\right)\left(1-{\alpha }_3\left(t\right)\right)=0$ at the optimal control point for ${\alpha }_3^{*}$, ${\lambda }_{31}\left(t\right){\beta }_2\left(t\right)={\lambda }_{32}\left(t\right)\left(1-{\beta }_2\left(t\right)\right)=0$ at the optimal control point for ${\beta }_2^{*}$, and ${\lambda }_{41}\left(t\right)\omega \left(t\right)={\lambda }_{42}\left(t\right)\left(1-\omega \left(t\right)\right)=0$ at the optimal control point for ${\omega }^{*}$.

Based on Pontryagin’s maximum principle [47], the concomitant system can be expressed as follows:

$\begin{array}{l}\frac{d{\rho }_1}{dt}=-\frac{\partial H}{\partial S},\frac{d{\rho }_2}{dt}=-\frac{\partial H}{\partial E},\frac{d{\rho }_3}{dt}=-\frac{\partial H}{\partial F},\frac{d{\rho }_4}{dt}=-\frac{\partial H}{\partial T},\\ \frac{d{\rho }_5}{dt}=-\frac{\partial H}{\partial Fb},\frac{d{\rho }_6}{dt}=-\frac{\partial H}{\partial M},\frac{d{\rho }_7}{dt}=-\frac{\partial H}{\partial Tb},\frac{d{\rho }_8}{dt}=-\frac{\partial H}{\partial R}.\end{array}(62)$

The boundary conditions of this system are

${\rho }_1\left(t_f\right)={\rho }_2\left(t_f\right)={\rho }_3\left(t_f\right)={\rho }_4\left(t_f\right)={\rho }_5\left(t_f\right)={\rho }_6\left(t_f\right)={\rho }_7\left(t_f\right)={\rho }_8\left(t_f\right)=0.(63)$

The optimality conditions in terms of ${\alpha }_2^{*}$ are

$\frac{\partial H}{\partial {\alpha }_2^{*}}={\psi }_1{\alpha }_2\left(t\right)-{\rho }_1\delta FS+{\rho }_4\delta FS-{\lambda }_{11}+{\lambda }_{12}=0.(64)$

Thus, the optimal control equation can be written as

${\alpha }_2^{*}=\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}+{\lambda }_{11}-{\lambda }_{12}.(65)$

To obtain the final optimal control equation without λ₁₁ or λ₁₂, the following three cases are discussed separately.

1. For $\left\{t\left|0<\right.{\alpha }_2^{*}\left(t\right)<1\right\}$, ${\lambda }_{11}\left(t\right)={\lambda }_{12}\left(t\right)=0$, the optimal control equation can be expressed as follows:

${\alpha }_2^{*}=\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}.(66)$

2. For $\left\{t|{\alpha }_2^{*}\left(t\right)=1\right\}$, ${\lambda }_{11}\left(t\right)=0$, the optimal control equation can be expressed as follows:

$1={\alpha }_2^{*}=\frac{\left({\rho }_1-{\rho }_4\right)\delta FS-{\lambda }_{12}}{{\psi }_1}.(67)$

Because ${\lambda }_{12}\left(t\right)\ge 0$, we have that $\frac{\left({\rho }_1-{\rho }_4\right)\delta FS-{\lambda }_{12}}{{\psi }_1}\ge 1$.

3. For $\left\{t|{\alpha }_2^{*}\left(t\right)=0\right\}$, ${\lambda }_{12}\left(t\right)=0$, the optimal control equation can be expressed as follows:

$0={\alpha }_2^{*}=\frac{\left({\rho }_1-{\rho }_4\right)\delta FS+{\lambda }_{11}}{{\psi }_1}.(68)$

Based on these three cases, the final optimal control equation for ${\alpha }_2^{*}\left(t\right)$ can be written as

${\alpha }_2^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}.(69)$

Similarly, the final optimal control equation for ${\alpha }_3^{*}\left(t\right)$ is

${\alpha }_3^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\},(70)$

and that for ${\beta }_2^{*}\left(t\right)$ is

${\beta }_2^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_2-{\rho }_4\right)E}{{\psi }_3}\right\}\right\}.(71)$

Finally, the optimal control equation for ${\omega }^{*}\left(t\right)$ can be written as

${\omega }^{*}\left(t\right)=\min \left\{1,\max \left\{0,\frac{\left({\rho }_3-{\rho }_4\right)F}{{\psi }_4}\right\}\right\}.(72)$

We have now obtained system (51), which includes the initial conditions (52), and the accompanying system (58), which includes the boundary conditions. The optimal control system can now be expressed as follows:

$\left\{\begin{array}{l}\begin{array}{l}\frac{dS}{dt}=B-gS-{\alpha }_1\delta FS-\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}\left(t\right)\delta FS\\ -\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\}\left(t\right)\delta FS-{\alpha }_4\delta FS\end{array}\\ \begin{array}{l}\frac{dE}{dt}=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\}\left(t\right)\delta FS-{\beta }_{1}E\\ -\min \left\{1,\max \left\{0,\frac{\left({\rho }_2-{\rho }_4\right)E}{{\psi }_3}\right\}\right\}\left(t\right)E-gE\end{array}\\ \frac{dF}{dt}={\alpha }_1\delta FS+{\beta }_{1}E-\min \left\{1,\max \left\{0,\frac{\left({\rho }_3-{\rho }_4\right)F}{{\psi }_4}\right\}\right\}\left(t\right)F-{\mu }_{1}F-{\mu }_{2}F-gF\\ \begin{array}{l}\frac{dT}{dt}=\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}\left(t\right)\delta FS\\ +\min \left\{1,\max \left\{0,\frac{\left({\rho }_2-{\rho }_4\right)E}{{\psi }_3}\right\}\right\}\left(t\right)E\\ +\min \left\{1,\max \left\{0,\frac{\left({\rho }_3-{\rho }_4\right)F}{{\psi }_4}\right\}\right\}\left(t\right)F-{\eta }_{1}T-{\eta }_{2}T-gT\end{array}\\ \frac{dFb}{dt}={\mu }_{1}F-{\gamma }_{1}Fb-gFb\\ \frac{dM}{dt}={\mu }_{2}F+{\eta }_{2}T-{\gamma }_{2}M-gM\\ \frac{dTb}{dt}={\eta }_{1}T-{\gamma }_{3}Tb-gTb\\ \begin{array}{l}\frac{dR}{dt}={\gamma }_{1}Fb+{\gamma }_{2}M+{\gamma }_{3}Tb+{\alpha }_4\delta FS-gR\\ \frac{d{\rho }_1}{dt}=\left({\rho }_1+{\rho }_4\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}\left(t\right)\delta F+{\rho }_1{\alpha }_4\delta F+{\rho }_3{\alpha }_1\delta F\\ +\left({\rho }_{1}F+{\rho }_{2}S\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\}\left(t\right)\delta +{\rho }_8{\alpha }_4\delta F+{\rho }_{1}g+{\rho }_1{\alpha }_1\delta F\\ \frac{d{\rho }_2}{dt}=1+\left({\rho }_2-{\rho }_4\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_2-{\rho }_4\right)E}{{\psi }_3}\right\}\right\}\left(t\right)+{\rho }_2\left({\beta }_1+g\right)-{\rho }_3{\beta }_1\\ \frac{d{\rho }_3}{dt}=\left({\rho }_1-{\rho }_4\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_4\right)\delta FS}{{\psi }_1}\right\}\right\}\left(t\right)\delta S-{\rho }_5{\mu }_1+{\rho }_8{\alpha }_4\delta S\\ +\left({\rho }_1-{\rho }_2\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_1-{\rho }_2\right)\delta FS}{{\psi }_2}\right\}\right\}\left(t\right)\delta S+{\rho }_1\left[-{\alpha }_1\delta S+{\alpha }_4\delta S\right]\\ +\left({\rho }_3-{\rho }_4\right)\min \left\{1,\max \left\{0,\frac{\left({\rho }_3-{\rho }_4\right)F}{{\psi }_4}\right\}\right\}\left(t\right)-{\rho }_6{\mu }_2+{\rho }_3\left[-{\alpha }_1\delta S+{\mu }_1+{\mu }_2+g\right]\\ \frac{d{\rho }_4}{dt}=1-{\rho }_7{\eta }_1-{\rho }_6{\eta }_2+{\rho }_4\left({\eta }_1+{\eta }_2+g\right)\\ \frac{d{\rho }_5}{dt}={\rho }_5\left({\gamma }_1+g\right)-{\rho }_8{\gamma }_1\\ \frac{d{\rho }_6}{dt}={\rho }_6\left({\gamma }_2+g\right)-{\rho }_8{\gamma }_2\\ \frac{d{\rho }_7}{dt}={\rho }_7\left({\gamma }_3+g\right)-{\rho }_8{\gamma }_3\\ \frac{d{\rho }_8}{dt}={\rho }_{8}g\end{array}\end{array}\right.,(73)$

where

$\begin{array}{l}S\left(0\right)=S_0,E\left(0\right)=E_0,F\left(0\right)=F_0,T\left(0\right)=T_0,Fb\left(0\right)=F{b}_0,\\ M\left(0\right)=M_0,Tb\left(0\right)=T{b}_0,R\left(0\right)=R_0\\ {\rho }_1\left(t_f\right)={\rho }_2\left(t_f\right)={\rho }_3\left(t_f\right)={\rho }_4\left(t_f\right)={\rho }_5\left(t_f\right)={\rho }_6\left(t_f\right)\\ ={\rho }_7\left(t_f\right)={\rho }_8\left(t_f\right)=0.\end{array}(74)$

This completes the proof of Theorem 6.

5 Discussion

This paper investigates the dissemination mechanism of uncertain information triggered by major emergencies on online social platforms. Based on the construction of the SEFTFbTbMR model of uncertain information clarification behavior, the optimal control strategy of the model is proposed using the Hamiltonian function. It is known from the analysis of the model that the size of the basic regeneration number plays a crucial role in predicting whether uncertain information can eventually die out. When the basic regeneration number is < 1, uncertain information can die out automatically over time. When the basic regeneration number is > 1, uncertain information will always exist on the online social platform, which can significantly disrupt society.

During major emergencies, due to limited resources for public opinion control, uncertain information may spread unchecked on online social platforms. This can lead to some netizens unintentionally or intentionally becoming disseminators of such information. Currently, government departments are responsible for investigating and managing major emergencies. However, it may not be possible for them to effectively control and remove all sources of uncertain information within a short period of time. The value of this study lies in its ability to provide theoretical support for relevant government departments to reduce the adverse effects caused by the propagation of uncertain information in the future. The experimental results of this article help to deepen our understanding of the propagation mechanism of uncertain information among Internet users and further enrich the related theories and methods of uncertain information propagation research.

5.1 Sensitivity analysis of the basic regeneration number R₀

The experimental results of this paper show that the value of the basic regeneration number determines whether uncertain information can be disseminated in the online social platform. The basic regeneration number R₀ is jointly composed of different parameters in the model. Therefore, this section focuses on the influence of related parameters on the basic regeneration number.

To analyze the influence of parameter value changes on the basic regeneration number R₀, we obtained the first-order partial derivatives for each parameter in R₀. A positive sign in the partial derivative function indicates a positive influence of the parameter on R₀. If the sign of the partial derivative function is negative, it indicates that the parameter has a negative impact on the basic reproduction number R₀.

$\frac{\partial R_0}{\partial B}=\frac{\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}>0(75)$

$\frac{\partial R_0}{\partial \delta }=\frac{B\left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}>0(76)$

$\frac{\partial R_0}{\partial {\alpha }_1}=\frac{B\delta }{g\left(g+{\mu }_1+{\mu }_2+\omega \right)}>0(77)$

$\frac{\partial R_0}{\partial {\alpha }_3}=\frac{B\delta {\beta }_1}{g\left({\beta }_1+{\beta }_2+g\right)\left(g+{\mu }_1+{\mu }_2+\omega \right)}>0(78)$

$\frac{\partial R_0}{\partial {\beta }_1}=\frac{B\delta {\alpha }_3\left({\beta }_2+g\right)}{g{\left({\beta }_1+{\beta }_2+g\right)}^2\left(g+{\mu }_1+{\mu }_2+\omega \right)}>0(79)$

$\frac{\partial R_0}{\partial {\beta }_2}=-\frac{B\delta {\alpha }_3{\beta }_1}{g{\left({\beta }_1+{\beta }_2+g\right)}^2\left(g+{\mu }_1+{\mu }_2+\omega \right)}<0(80)$

$\frac{\partial R_0}{\partial g}=-\frac{B\delta \left\{\begin{array}{l}{\alpha }_1{\left({\beta }_1+{\beta }_2+g\right)}^2\left(2g+{\mu }_1+{\mu }_2+\omega \right)\\ +{\alpha }_3{\beta }_1[\left({\beta }_1+{\beta }_2\right)\left(2g+{\mu }_1+{\mu }_2+\omega \right)\\ +g\left(3g+2{\mu }_1+2{\mu }_2+2\omega \right)]\end{array}\right\}}{g^2{\left({\beta }_1+{\beta }_2+g\right)}^2{\left(g+{\mu }_1+{\mu }_2+\omega \right)}^2}<0(81)$

$\frac{\partial R_0}{\partial {\mu }_1}=-\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right){\left(g+{\mu }_1+{\mu }_2+\omega \right)}^2}<0(82)$

$\frac{\partial R_0}{\partial {\mu }_2}=-\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right){\left(g+{\mu }_1+{\mu }_2+\omega \right)}^2}<0(83)$

$\frac{\partial R_0}{\partial \omega }=-\frac{B\delta \left[{\alpha }_1\left({\beta }_1+{\beta }_2+g\right)+{\alpha }_3{\beta }_1\right]}{g\left({\beta }_1+{\beta }_2+g\right){\left(g+{\mu }_1+{\mu }_2+\omega \right)}^2}<0(84)$

To visualize the impact of various parameter values on R₀, we used Matlab 2017b numerical simulation software. Based on the assignment result (49), we kept the remaining parameters constant and varied the value range of B from 1 to 5, δ from 0.1 to 1, and the rest of the parameters from 0 to 1. We conducted numerical simulations in groups of two by two to determine the effects of different parameter values on R₀.

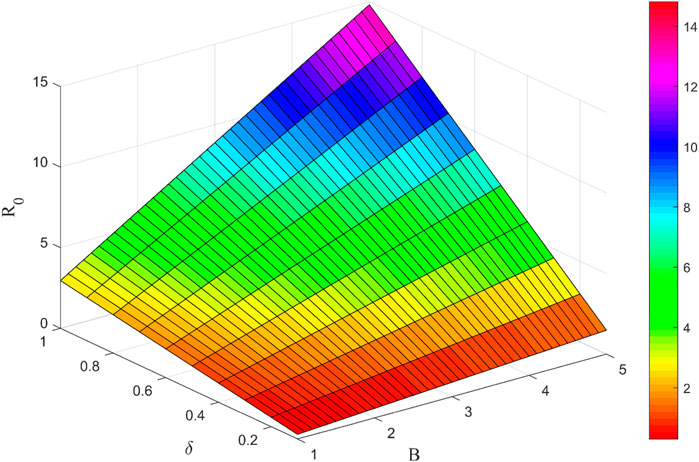
Figure 5 shows that the basic regeneration number R₀ increases as parameters B and δ increase. 1) The larger the number of new Internet users in the social platform per unit of time, the more conducive to the spread of uncertain information. The larger the base of Internet users, the greater the number of individuals who may be concerned about uncertain information, and the more likely it is that such information will become widely known. 2) The speed at which uncertain information spreads affects its propagation. In other words, the more Internet users on a social platform who come into contact with the publisher of uncertain information, the more likely it is to spread. Thus, the spread of uncertain information can be curbed by limiting the speech flow of certain netizens on social media platforms or blocking specific keywords.

FIGURE 5

FIGURE 5. Effect of variations in δ and B on R₀.

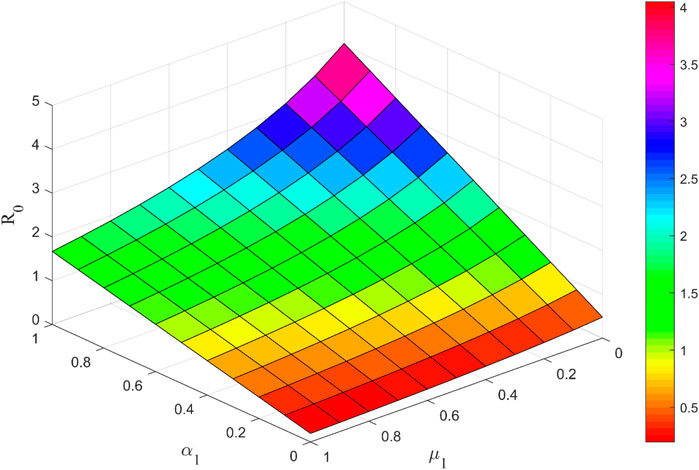
Figure 6 shows that the basic regeneration number R₀ increases with parameter α₁ and decreases with parameter μ₁. 1) When unknown people receive uncertain information, they promote the spread of uncertain information in social platforms if they choose to believe in the content of the uncertain information and spontaneously spread it. 2) Publishers of uncertain information who receive true information on social platforms and choose not to publish their own statements, regardless of whether they believe in the true information or not, inhibit the spread of uncertain information on social platforms.

FIGURE 6

FIGURE 6. Effect of variations in α₁ and μ₁ on R₀.

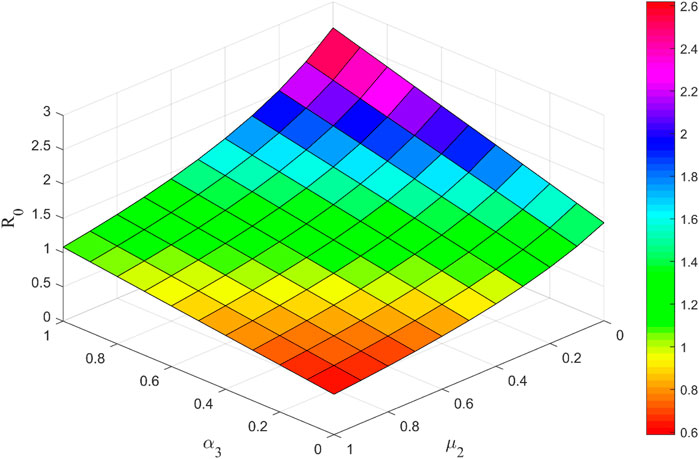
Figure 7 shows that the basic regeneration number R₀ increases with parameter α₃ and decreases with parameter μ₂. 1) When the unknown person receives the uncertain information, if he does not spread the uncertain information, but keeps a wait-and-see attitude, it will promote the spread of uncertain information in the social platform. 2) If an uncertain information publisher receives real information on a social platform, they may choose not to publish their own speech, regardless of whether they believe the real information or not. This can help inhibit the spread of uncertain information on the platform.

FIGURE 7

FIGURE 7. Effect of variations in α₃ and μ₂ on R₀.

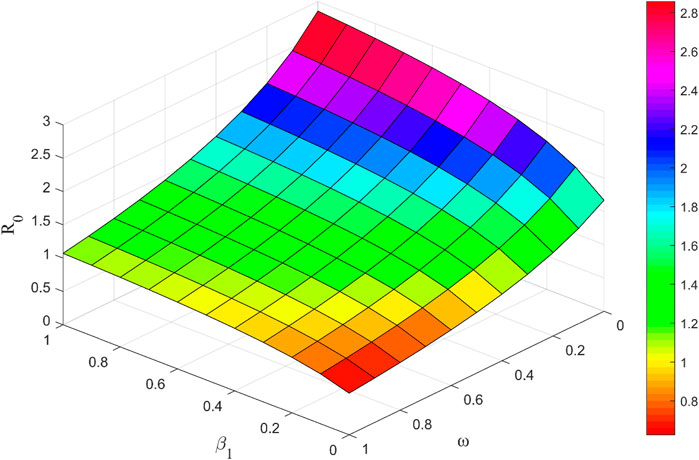
Figure 8 shows that the basic regeneration number R₀ increases with an increase in parameter β₁ and decreases with an increase in parameter ω. 1) The dissemination of uncertain information in social platforms is facilitated when the thinker still chooses to believe in the content of the uncertain information and disseminates it after forensically examining and thinking about the uncertain information. 2) The spread of uncertain information on social media is hindered when the person who originally shared the uncertain information realizes that it is false after receiving accurate information and decides to clarify it.

FIGURE 8

FIGURE 8. Effect of variations in β₁ and ω on R₀.

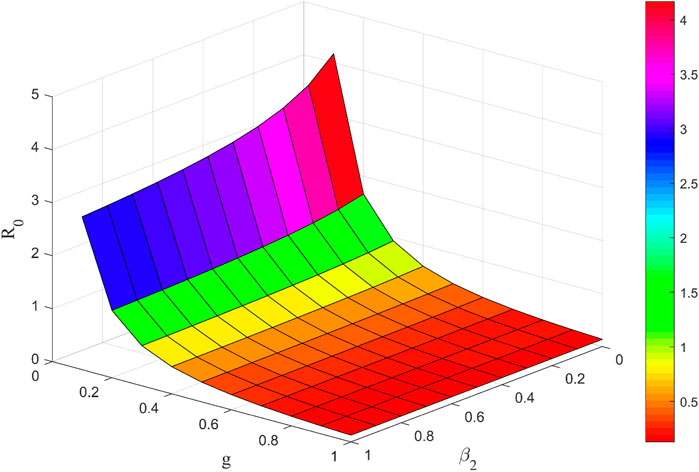
According to Figure 9, the basic regeneration number R₀ decreases as parameters g and β₂ increase. 1) The higher the number of netizens exiting in the social platform per unit time, the more conducive to suppressing the spread of uncertain information. 2) The spread of uncertain information on social media can be reduced when individuals recognize that the information is false and take the time to clarify it after gathering evidence and carefully considering the information.

FIGURE 9

FIGURE 9. Effect of variations in g and β₂ on R₀.

5.2 Comparison with existing research on uncertain information dissemination

This section compares the research in this paper with existing research on uncertain information dissemination. In their study of uncertain information dissemination [21], only distinguish between the decision-making behavior of online media and that of Internet users. However, they fail to consider that different Internet users may exhibit various decision-making behaviors when faced with uncertain information. Some may even adopt the same decision-making behaviors as online media [24, 43]. Only considered two decision-making behaviors of Internet users: dissemination or thinking. However, in reality, some Internet users choose to clarify uncertain information when faced with it, while others maintain their behavior after contacting other Internet users. In a previous study [46], observed this effect but did not consider that some netizens may not immediately change their minds after interacting with others, but rather become more thoughtful.

Compared to the studies conducted by the aforementioned scholars on uncertain information dissemination, this paper considers not only the fact that Internet users exhibit multiple decision-making behaviors when faced with uncertain information, but also that some of them choose to clarify such information. Additionally, it acknowledges that Internet users are influenced not only by uncertain information, but also by real information. This paper categorizes Internet users into eight groups based on their decision-making behaviors during uncertain information dissemination. The model considers both the dissemination of uncertain information and the dissemination of real information that clarifies uncertain information, making it highly innovative.

5.3 Limitations and future prospects

The research presented in this paper has the following limitations. First, in constructing the uncertain information dissemination model, the impact of time lags on uncertain information dissemination was not considered. In reality, information dissemination has a certain degree of lag, and Internet users receive uncertain information at inconsistent times. Therefore, in future research, we will add a time lag to our model. Second, this paper does not differentiate the communication ability of Internet users, whereas, in reality, the information released by opinion leaders is more likely to be trusted by ordinary Internet users. Therefore, in the future, we will combine complex networks with the uncertain information dissemination model to study the propagation mechanism based on different network structures. Finally, this study only used Matlab for the numerical simulations, without any real data. Therefore, in future research, we will integrate real data where possible and simulate real cases.

6 Conclusion

This paper has described the SEFTFbTbMR uncertain information dissemination model, which is based on the classical SIR epidemic dynamics model. The next-generation matrix method was used to calculate the basic regeneration number and equilibrium points of the model, and the local stability and global stability of the equilibrium points were theoretically analyzed according to the Routh–Hurwitz criterion and the Lyapunov function, respectively. The accuracy of the theoretical derivation was verified through numerical simulations, and the sensitivity of the basic regeneration number to various parameters was analyzed. Finally, to reduce the influence of uncertain information, optimal control theory was applied to the model, and a strategy was proposed. This will further enrich the relevant theories and methods for the propagation of uncertain information. The main results of this study are as follows:

(1) Strengthen the supervision of social platforms to block the dissemination of uncertain information (i.e., reduce the value of δ in the model, and increase the values of μ₁ and μ₂). When major emergencies occur, social platforms can use their own authority to supervise related information so as to reduce the emergence of uncertain information at the source. After uncertain information has emerged, the flow of some published remarks should be limited on the platform, or certain keywords should be blocked to reduce the dissemination rate. This suppresses the dissemination of uncertain information.

(2) Improve the ability of internet users to determine the authenticity of information, improve the reward and punishment mechanism, and encourage users to participate in the clarification of uncertain information (i.e., increase the values of ω and β₂ in the model and reduce the values of β₁, α₁, and α₃). Following a major emergency, the relevant governmental departments should release the real information related to the events in a timely manner and provide materials to support Internet users in carrying out independent investigations. The government should also seek to punish Internet users who release uncertain information to reduce its spread. Internet users who publish true information should be rewarded so as to encourage expression of users’ own opinions and greater participation in clarifying uncertain information.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

BL: Writing–original draft, Writing–review and editing. HL: Supervision, Writing–review and editing. QS: Writing–review and editing. RL: Writing–review and editing. HY: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was supported by the Project of Liaoning Provincial Federation Social Science Circles of China (No. L20BGL047) and the Liaoning Provincial Social Science Planning Fund (No. L18AJY001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tan KY, Liu WH, Xu F. Optimization model and algorithm of logistics vehicle routing problem under major emergency. Mathematics (2023) 11(5):1274. doi:10.3390/math11051274

CrossRef Full Text | Google Scholar

2. Yao J, Jin Y, Tang X, Wu J, Hou S, Liu X, et al. Development of intelligent response to public health emergencies. Strateg Study CAE (2021) 23(5):34–40. doi:10.15302/j-sscae-2021.05.005

CrossRef Full Text | Google Scholar

3. Gao Y, Fan YX, Wang J, Duan Z. Evaluation of governmental safety regulatory functions in preventing major accidents in China. Saf Sci (2019) 120:299–311. doi:10.1016/j.ssci.2019.07.002

CrossRef Full Text | Google Scholar

4. Zhang X, Zhou M. Emergency management planning for major epidemic disease prevention and control. J Saf Sci Tech (2020) 16(6):37–42.

Google Scholar

5. Ukwuoma CC, Qin ZG, Heyat MBB, Akhtar F, Smahi A, Jackson JK, et al. Automated lung-related pneumonia and COVID-19 detection based on novel feature extraction framework and vision transformer approaches using chest X-ray images. Bioengineering-basel (2022) 9(11):709. doi:10.3390/bioengineering9110709

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Benifa JVB, Chola C, Muaad AY, Hayat MAB, Bin Heyat MB, Mehrotra R, et al. FMDNet: an efficient system for face mask detection based on lightweight model during COVID-19 pandemic in public areas. Sensors (2023) 23(13):6090. doi:10.3390/s23136090

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Asif S, Zhao M, Tang FX, Zhu Y. A deep learning-based framework for detecting COVID-19 patients using chest X-rays. Multimedia Syst (2022) 28(4):1495–513. doi:10.1007/s00530-022-00917-7

CrossRef Full Text | Google Scholar

8. Fazmiya MJA, Sultana A, Rahman K. Current insights on bioactive molecules, antioxidant, anti-inflammatory, and other pharmacological activities of cinnamomum camphora linn. Oxidative Med Cell Longevity (2022) 2022:9354555.

CrossRef Full Text | Google Scholar

9. Mo TC, Xie C, Li KL, Ouyang Y, Zeng Z. Transmission effect of extreme risks in China?s financial sectors at major emergencies: empirical study based on the GPD-CAViaR and TVP-SV- VAR approach. Electron Res Archive (2022) 30(12):4657–73. doi:10.3934/era.2022236

CrossRef Full Text | Google Scholar

10. Cheng A, Chen TH, Jiang GG, Han X. Can major public health emergencies affect changes in international oil prices?. Int J Environ Res Public Health (2021) 18(24):12955. doi:10.3390/ijerph182412955

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang G, Wang ZD, Chen L. Investigating the public sentiment in major public emergencies through the complex networks method: a case study of COVID-19 epidemic. Front Public Health (2022) 10:847161. doi:10.3389/fpubh.2022.847161

PubMed Abstract | CrossRef Full Text | Google Scholar

12. De Las Heras-Pedrosa C, SáNCHEZ-NúñEZ P, PeláEZ JI. Sentiment analysis and emotion understanding during the COVID-19 pandemic in Spain and its impact on digital ecosystems. Int J Environ Res Public Health (2020) 17(15):5542. doi:10.3390/ijerph17155542

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Atehortua NA, Patino S. COVID-19, a tale of two pandemics: novel coronavirus and fake news messaging. Health Promot Int (2021) 36(2):524–34. doi:10.1093/heapro/daaa140

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Jalan M, Riehm K, Agarwal S, Gibson D, Labrique A, Thrul J. Burden of mental distress in the US associated with trust in media for COVID-19 information. Health Promot Int (2022) 37(6):daac162. doi:10.1093/heapro/daac162

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang H, Zhou H, Li J. Research on the situational awareness of a major emergency under incomplete information. J China Soc Scientific Tech Inf (2021) 40(9):903–13.

Google Scholar

16. Crokidakis N. Effects of mass media on opinion spreading in the Sznajd sociophysics model. Physica a-Statistical Mech Its Appl (2012) 391(4):1729–34. doi:10.1016/j.physa.2011.11.038

CrossRef Full Text | Google Scholar

17. Zhao LJ, Wang Q, Cheng JJ, Zhang D, Ma T, Chen Y, et al. The impact of authorities' media and rumor dissemination on the evolution of emergency. Physica a-Statistical Mech Its Appl (2012) 391(15):3978–87. doi:10.1016/j.physa.2012.02.004

CrossRef Full Text | Google Scholar

18. Yin FL, Shao XY, Wu JH. Nearcasting forwarding behaviors and information propagation in Chinese Sina-Microblog. Math Biosciences Eng (2019) 16(5):5380–94. doi:10.3934/mbe.2019268

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Allington D, Duffy B, Wessely S, Dhavan N, Rubin J. Health-protective behaviour, social media usage and conspiracy belief during the COVID-19 public health emergency. Psychol Med (2021) 51(10):1763–9. doi:10.1017/s003329172000224x

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Centola D. The spread of behavior in an online social network experiment. Science (2010) 329(5996):1194–7. doi:10.1126/science.1185231

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang X, Zhou Y, Zhou FL, Pratap S. Internet public opinion dissemination mechanism of COVID-19: evidence from the Shuanghuanglian event. Data Tech Appl (2022) 56(2):283–302. doi:10.1108/dta-11-2020-0275

CrossRef Full Text | Google Scholar

22. Choi S. The two-step flow of communication in twitter-based public forums. Soc Sci Comp Rev (2015) 33(6):696–711. doi:10.1177/0894439314556599

CrossRef Full Text | Google Scholar

23. Li SY, Liu ZX, Li YL. Temporal and spatial evolution of online public sentiment on emergencies. Inf Process Manag (2020) 57(2):102177. doi:10.1016/j.ipm.2019.102177

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Li L, Wan YJ, Plewczynski D, Zhi M. Simulation model on network public opinion communication model of major public health emergency and management system design. Scientific Programming (2022) 2022:1–16. doi:10.1155/2022/5902445

CrossRef Full Text | Google Scholar

25. Wei Y. Network public opinion propagation control model of major emergencies based on heat conduction theory. Wireless Commun Mobile Comput (2022) 2022:1476231.

CrossRef Full Text | Google Scholar

26. Litou I, Boutsis I, Kalogeraki V. Efficient techniques for time-constrained information dissemination using location-based social networks. Inf Syst (2017) 64:321–49. doi:10.1016/j.is.2015.12.002

CrossRef Full Text | Google Scholar

27. Wang J, Yu H, Wang X. Dissemination and control model of public opinion in online social networks based on users' relative weight. Syst Engineering-Theory Pract (2019) 39(6):1565–79.

Google Scholar

28. Hong W, Li Q, Wu L. Food safety internet public opinion transmission simulation and management countermeasures considering information authenticity. Syst Engineering-Theory Pract (2017) 37(12):3253–69.

Google Scholar

29. Kermack WO, Mckendrick AG. Contributions to the mathematical theory of epidemics—I. Bull Math Biol (1991) 53(1-2):33–55. doi:10.1007/bf02464423

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kermack WO, Mckendrick AG. Contributions to the mathematical theory of epidemics—II. The problem of endemicity. Bull Math Biol (1991) 53(1-2):57–87. doi:10.1007/bf02464424

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kermack WO, Mckendrick AG. Contributions to the mathematical theory of epidemics—III. Further studies of the problem of endemicity. Bull Math Biol (1991) 53(1-2):89–118. doi:10.1007/bf02464425

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Duan W, Fan ZC, Zhang P, Guo G, Qiu X. Mathematical and computational approaches to epidemic modeling: a comprehensive review. Front Comp Sci (2015) 9(5):806–26. doi:10.1007/s11704-014-3369-2

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Chowell G, Sattenspiel L, Bansal S, Viboud C. Mathematical models to characterize early epidemic growth: a review. Phys Life Rev (2016) 18:66–97. doi:10.1016/j.plrev.2016.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li MY, Muldowney JS. Global stability for the SEIR model in epidemiology. Math biosciences (1995) 125(2):155–64. doi:10.1016/0025-5564(95)92756-5

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Haihong E, Hu YX, Peng HP. Theme and sentiment analysis model of public opinion dissemination based on generative adversarial network. Chaos Solitons and Fractals (2019) 121:160–7.

CrossRef Full Text | Google Scholar

36. Yin FL, Lv JH, Zhang XJ, Xia X, Wu J. COVID-19 information propagation dynamics in the Chinese Sina-microblog. Math Biosciences Eng (2020) 17(3):2676–92. doi:10.3934/mbe.2020146

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yin FL, Pang HY, Xia XY. COVID-19 information contact and participation analysis and dynamic prediction in the Chinese Sina-microblog. Physica a-Statistical Mech Its Appl (2021) 570:125788. doi:10.1016/j.physa.2021.125788

CrossRef Full Text | Google Scholar

38. Rui XB, Meng FR, Wang ZX, Yuan G, Du C. SPIR: the potential spreaders involved SIR model for information diffusion in social networks. Physica a-Statistical Mech Its Appl (2018) 506:254–69. doi:10.1016/j.physa.2018.04.062

CrossRef Full Text | Google Scholar

39. Trpevski D, Tang WKS, Kocarev L. Model for rumor spreading over networks. Phys Rev E (2010) 81(5):056102. doi:10.1103/physreve.81.056102

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zan YL. DSIR double-rumors spreading model in complex networks. Chaos Solitons and Fractals (2018) 110:191–202. doi:10.1016/j.chaos.2018.03.021

CrossRef Full Text | Google Scholar

41. Tian Y, Ding XJ. Rumor spreading model with considering debunking behavior in emergencies. Appl Math Comput (2019) 363:124599. doi:10.1016/j.amc.2019.124599

CrossRef Full Text | Google Scholar

42. Diekmann O, Heesterbeek JA, Metz JA. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J Math Biol (1990) 28(4):365–82. doi:10.1007/bf00178324

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kang SD, Hou XL, Hu YH, Liu H. Dynamical analysis and optimal control of the developed information transmission model. Plos One (2022) 17(5):e0268326. doi:10.1371/journal.pone.0268326

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Hu YH, Pan QH, Hou WB, He M. Rumor spreading model considering the proportion of wisemen in the crowd. Physica a-Statistical Mech Its Appl (2018) 505:1084–94. doi:10.1016/j.physa.2018.04.056

CrossRef Full Text | Google Scholar

45. Lv R, Li H, Sun Q. Panic spreading model with different emotions under emergency. Mathematics (2021) 9(24):3190. doi:10.3390/math9243190

CrossRef Full Text | Google Scholar

46. Kang SD, Hou XL, Hu YH, Liu H. Dynamic analysis and optimal control considering cross transmission and variation of information. Scientific Rep (2022) 12(1):18104. doi:10.1038/s41598-022-21774-4

CrossRef Full Text | Google Scholar

47. He ZB, Cai ZP, Yu JG, Wang X, Sun Y, Li Y. Cost-efficient strategies for restraining rumor spreading in mobile social networks. Ieee Trans Vehicular Tech (2017) 66(3):2789–800. doi:10.1109/tvt.2016.2585591

CrossRef Full Text | Google Scholar