
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 12 June 2024
Sec. Soft Matter Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1347934
This article is part of the Research TopicRheology and Complex Fluids in Biomedical ApplicationsView all 7 articles
Cell spheroids are a widely used model to investigate cell-cell and cell-matrix interactions in a 3D microenvironment in vitro. Most research on cell spheroids has been focused on their response to various stimuli under static conditions. Recently, the effect of flow on cell spheroids has been investigated in the context of tumor invasion in interstitial space. In particular, microfluidic perfusion of cell spheroids embedded in a collagen matrix has been shown to modulate cell-cell adhesion and to represent a possible mechanism promoting tumor invasion by interstitial flow. However, studies on the effects of well-defined flow fields on cell spheroids are lacking in the literature. Here, we apply simple shear flow to cell spheroids in a parallel plate apparatus while observing their morphology by optical microscopy. By using image analysis techniques, we show that cell spheroids rotate under flow as rigid prolate ellipsoids. As time goes on, cells from the outer layer detach from the sheared cell spheroids and are carried away by the flow. Hence, the size of cell spheroids declines with time at a rate increasing with the external shear stress, which can be used to estimate cell-cell adhesion. The technique proposed in this work allows one to correlate flow-induced effects with microscopy imaging of cell spheroids in a well-established shear flow field, thus providing a method to obtain quantitative results which are relevant in the general field of mechanobiology.
Cell spheroids are a widely used model to investigate cell-cell and cell-matrix interactions in a 3D microenvironment in vitro. Due to their structural and functional similarities with in vivo tumors [1–6], spheroids have emerged as a valuable tool for cancer research and drug testing in vitro. One of the main advantages of cell spheroids is that they can be prepared by well-established culture protocols, such as the hanging drop method, micro-molding and rotary cell culture systems, which exploit cell aggregation in the absence of adhesive surfaces [7–11]. The initial cell aggregates grow as a sigmoidal function of time, with an initial exponential phase, an intermediate linear growth, and a tendency to reach a plateau at later times [12]. While growing, the cell spheroids undergo a change in their internal microstructure, since at some point diffusion limitation of nutrients, such as oxygen and glucose, and of metabolic waste tends to inhibit cell proliferation inside the spheroid. Therefore, an inner necrotic core develops in the central region of cell spheroids in addition to an outer proliferating and an intermediate non-proliferating layer [13–15]. This complex, heterogeneous microstructure poses several challenges to the study of cell spheroids in response to external factors, such as chemical and mechanical stimuli. The deformability of these structures [16] has been investigated through various techniques, including isotropic compression by osmotic pressure [17, 18], atomic force microscopy (AFM) [19, 20], and micro-indentation. The experimental results have been interpreted in terms of an equivalent surface tension, reflecting the attractive interactions between cells which hold the spheroid together.
While most of the research on cell spheroids has been focused on static conditions, the effect of flow has recently been investigated in the context of tumor invasion in interstitial space. In particular, microfluidic perfusion of cell spheroids embedded in a collagen matrix has been shown to modulate cell-cell adhesion and to represent a possible mechanism promoting tumor invasion by interstitial flow [21]. However, studies on the effects of well-defined flow fields on cell spheroids, which can provide a quantitative characterization of their response to mechanical stimuli, are lacking in the literature.
Here, we apply a simple shear flow to cell spheroids in a parallel plate apparatus while observing their morphology by optical microscopy. By using image analysis techniques, in this Brief Research Report we provide the first characterization of the flow behavior of cell spheroids in a simple shear velocity field.
The cell spheroids are obtained from NIH/3T3 (ATCC Cat# CRL-1658, RRID: CVCL_0594) mouse fibroblasts cultured in Dulbecco’s Modified Eagle’s Medium (DMEM) supplemented with 10% (v/v) Fetal Bovine Serum (FBS), 1% (v/v) antibiotics (50 units/mL penicillin and 50 mg mL−1 streptomycin) and 1% (v/v) L-glutamine. Cells harvested from monolayer cultures were seeded in a multiwall plate pre-coated with non-adhesive agarose at a concentration of 8∙103 cells/well and covered with the cell growth medium. The multiwell plate was then incubated under typical cell culture conditions at 37°C for 5 days to obtain compact spheroids. The culture protocol is schematically illustrated in Figure 1A.
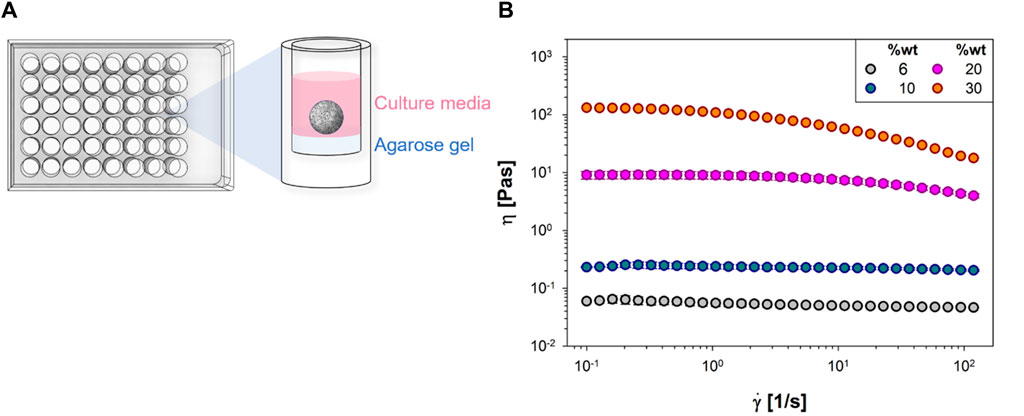
Figure 1. (A) The culture protocol of NIH/3T3 mouse fibroblast spheroids in multiwell plates; (B) Viscosity, η, vs. shear rate,
The so obtained cell spheroids were then transferred in an aqueous solution of polyvinylpyrrolidone (PVP, from Sigma Aldrich, with number average molecular weight Mn 360 kDa, CAS Number 9003-39-8), with concentrations in the range 20–27%wt. The addition of PVP enables to change the viscosity η of the cell spheroids suspending medium and thus to modulate the applied shear stress
The PVP solutions with cell spheroids were loaded in a parallel plate apparatus which has been described in detail elsewhere [22] and is schematically shown in Figure 2A.
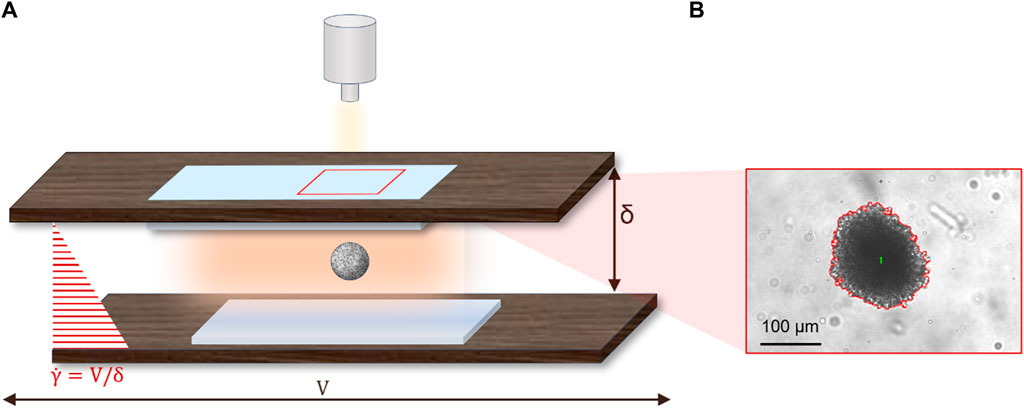
Figure 2. (A) Schematics of the parallel plates used to apply simple shear flow to cell spheroids; (B) Typical image of a cell spheroid in bright field microscopy with a red outline of the boundary as obtained from threshold segmentation.
Briefly, the apparatus is made of two rectangular glass plates inserted in windows cut on two rigid mounts. Parallelism between the two plates is adjusted by a set of micrometric rotary and tilting stages (the residual error is around 20 μm over a length of 10 cm). Shear flow is obtained by translating one of the plates (specifically, the bottom plate) with respect to the other by a computer-controlled motorized translating stage with micrometric precision. The microscope itself is mounted on a motorized translating stage that is used to keep the flowing spheroid within the field of view during motion. The microscope is equipped with a video camera (Hamamatsu, ORCA-spark Digital CMOS camera C11440-36U) for image acquisition during flow. The shear rate
Quantitative analysis of spheroid shape is performed by using standard image analysis routines (Image-Pro Plus) based on threshold segmentation to identify the spheroid contour from the surrounding background. A typical example of the image analysis outcome is presented in Figure 2B, where the red line is the spheroid contour. The geometrical features measured by image analysis include the area and the axes of the cell spheroid, which are assessed utilizing the “Count and Measure Objects” function available in the software.
In the range of shear stress investigated, σ ∈ [20–670] Pa—selected based on published outcomes [23] and to ensure the osmotic pressure of PVP on spheroids is negligible—the cell spheroids exhibited minimal, if any, deformation under shear flow [24]. Instead, they underwent three-dimensional rotational and translational motions which are illustrated in the sequence of images in Figure 3A, which refers to a shear rate of about 1 s−1 and a cell spheroid with a radius of 170 μm.
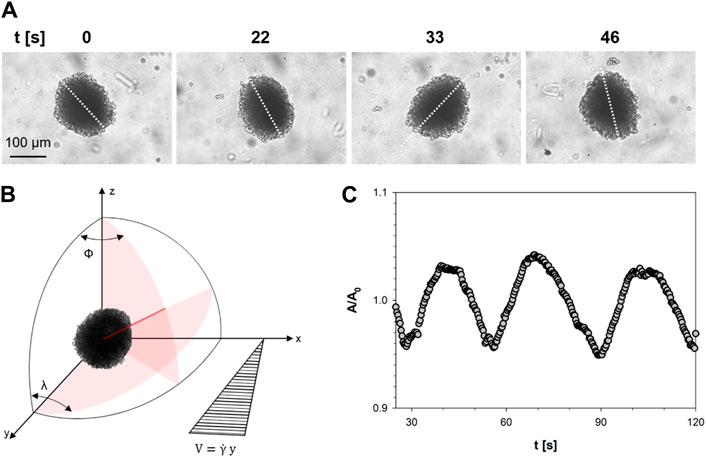
Figure 3. (A) Time-lapse images of a cellular spheroid subjected to shear flow at indicated time points. The white dotted line represents the spheroid’s axis; (B) Reference system used to describe the motion of a cell spheroid; (C) Normalized projected area data of the cellular spheroid plotted as a function of time.
The sequence is part of a video which is available as Supplementary Video S1. The images in Figure 3 show that the cell spheroid rotates in the plane of observation, which is perpendicular to the velocity gradient, while spinning around its long axis. This combined motion is shown by the apparent change of the projected area during flow. The spinning around the long axis reveals that the shape of a cell spheroid can be described with a good approximation by a prolate ellipsoid with a long axis and an essentially circular section perpendicular to it in the equatorial plane. The observed rotations are characteristic of rigid particles in a shear flow field, which have been theoretically studied for ellipsoidal particles by Jeffery under the assumptions of no sedimentation, negligible inertia, rigid particles and no slip at the solid-liquid interface [25] and are schematically represented in Figure 3B. In the latter, ϕ is the angle of rotation around the polar axis Z, which is perpendicular to the shear plane X-Y. The motion of the cell spheroid in Figure 3A is the projection of the long axis in the X-Z plane of observation, which describes the angle λ in the same plane. The predictions of Jeffery have been confirmed later on by experimental results on cylindrical particles in a paper by Trevelyan and Mason [26], from which Figure 1B has been adapted. Further evidence of the rotary motion of the cell spheroids comes from the analysis of the time evolution of its shape. In Figure 3C the projected area of the cell spheroid A, normalized with respect to the initial area A0, is plotted as a function of time for the cell spheroid of Figure 3A. The data of the normalized area fluctuates around an average value with a 4% amplitude oscillation and a period T of approximately 24 s. Such value of the period of the projected area corresponds to twice the value of the period of rotation of the particle around the polar axis Z [26] and is in good agreement with the predictions of the Jeffery’s analysis in the case of a spherical particles
The A/A0 data in Figure 3C seem to exhibit a declining trend in the 3 min time frame of the diagram. Results from a time frame of 25 min from the same experiment as Figure 3C are plotted in Figure 4A, where the decreasing trend of A/A0 is more evident. A similar trend has been found for all the cell spheroids investigated in this work.
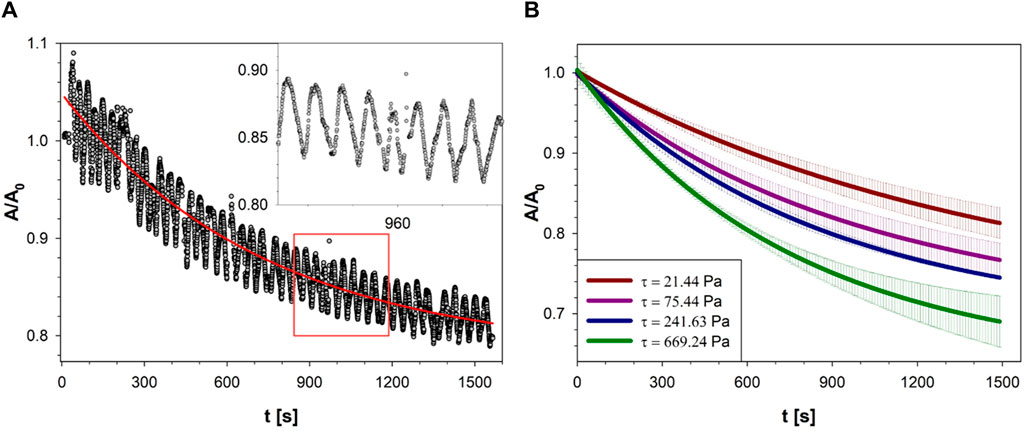
Figure 4. (A) The normalized projected area of the cell spheroid of Figure 3A as a function of time, at
A careful examination of the images taken during shear flow shows indeed that cells from the outer layer tend to detach from the cell spheroid and are taken away by the suspending medium. This phenomenon presents some analogy with the dissociation of cells from spheroids undergoing perfusion, which has been attributed to flow-induced downregulation of cell-cell adhesion by reduced expression and altered localization of E-cadherin [21]. It can be speculated that a similar mechanism is at play in our experiments and that cells detachment from the spheroid is due to downregulation of cell-cell adhesion, although more work is needed to check this hypothesis. While losing cells from the edge and reducing their size, the cell spheroids keep rotating as a rigid particle with almost the same period, as shown by the oscillations in the inset of Figure 4A. To facilitate interpretation, raw data from each spheroid were smoothed to yield an averaged curve, represented by the continuous red line in Figure 4A.
The effect of the applied shear stress was studied by changing the shear rate and/or the viscosity of the suspending solutions. The results are presented in Figure 4B, where the normalized area is plotted as a function of the shear stress. For the sake of clarity, only the average curves are shown in Figure 4B as red lines with the gray regions representing the standard deviation evaluated at least on 5 spheroids. At any given time, the data exhibits a continuous decrease of A/A0 with shear stress from 21 to 699 Pa. This finding is in line with the interpretation of the normalized area reduction with time as a result of flow-induced erosion of the surface.
In this Brief Research Report, we show for the first time the flow behaviour of cell spheroids in a viscous fluid under simple shear flow. The experiments were run in a parallel plate apparatus while observing their morphology by optical microscopy. The results provide strong evidence that cell spheroids rotate as rigid particles under the action of shear flow, with a period in close agreement with the predictions of Jeffery’s theory of ellipsoidal particles. A similar flow behavior has been observed for vesicles and red blood cells under shear flow [29, 30]. In addition, a progressive detachment of cells from the outer spheroids layer was observed in all the experiments. As a consequence, the size of the cell spheroids decreased as a function of time in a shear stress-dependent fashion. No apparent change of T as a consequence of cell spheroid size reduction was found, likely due to the fact that the period is rather insensitive to the aspect ratio in the range investigated in this study. The good agreement with the theoretical values of T was rather robust also taking into account other effects, which were outside the assumptions of Jeffery’s theory. One of such effects is the irregular, rough surface of the cell spheroids, which did not affect the rotation period, in line with the previous results from the literature on particle flocs. Another effect is the influence of the confining walls since the ratio between cell spheroid diameter and gap size was around 0.8. However, the agreement of the experimental values of T with the ones predicted for unbounded flow suggest that wall effects are rather limited. This finding is in agreement with previous results from the literature on rods under shear flow, where little effect of wall proximity on the rotation period was found both in experiments [31] and numerical simulations [32].
However, like any scientific endeavor, there are two main limitations to consider. Firstly, there is the lack of control over temperature in our experimental setup, which affects the maximum experimental time, in order to mitigate any potential temperature-related effects. Secondly, there are spatial constraints within our apparatus, particularly regarding sustaining high shear rates for extended periods without interrupting the course of the experiment and reversing the direction.
Nevertheless, the results of our work are relevant in the general field of mechanotransduction, which is addressed to study the mechanisms used by cells to convert mechanical stimuli in a biological response. As an example, future directions of this study include a biological analysis of the cell response under the applied shear stress to investigate the molecular drivers of cell detachment. Furthermore, the analysis of the shear flow of cell spheroids in the context of Jeffery’s theory is also relevant for the application of the latter theory to active biological matter, such as micro swimmers, which has recently experienced a revival of interest [33]. The study of the motion of cell spheroids in shear flow can also be extended by using different cell lines and by exploring wider ranges of shear rate, but all these activities are outside the scope of this Brief Research Report and can be the subject of future work.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethical approval was not required for the studies on animals in accordance with the local legislation and institutional requirements because only commercially available established cell lines were used.
RF: Data curation, Formal Analysis, Investigation, Validation, Visualization, Writing–original draft. JD: Formal Analysis, Writing–original draft. SC: Conceptualization, Investigation, Methodology, Supervision, Writing–review and editing. SG: Conceptualization, Investigation, Methodology, Visualization, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1347934/full#supplementary-material
1. Nyga A, Cheema U, Loizidou M 3D tumour models: novel in vitro approaches to cancer studies. J Cel Commun signaling (2011) 5:239–48. doi:10.1007/s12079-011-0132-4
2. Yamada KM, Cukierman E Modeling tissue morphogenesis and cancer in 3D. Cell (2007) 130:601–10. doi:10.1016/j.cell.2007.08.006
3. Hoarau-Véchot J, Rafii A, Touboul C, Pasquier J Halfway between 2D and animal models: are 3D cultures the ideal tool to study cancer-microenvironment interactions? Int J Mol Sci (2018) 19:181. doi:10.3390/ijms19010181
4. Edgerton ME, Chuang Y-L, Macklin P, Yang W, Bearer EL, Cristini V A novel, patient-specific mathematical pathology approach for assessment of surgical volume: application to ductal carcinoma in situ of the breast. Anal Cell Pathol (2011) 34:247–63. doi:10.1155/2011/803816
5. Cristini V, Koay E, Wang Z An introduction to physical oncology: how mechanistic mathematical modeling can improve cancer therapy outcomes. CRC Press (2017).
6. Frieboes HB, Chaplain MAJ, Thompson AM, Bearer EL, Lowengrub JS, Cristini V Physical oncology: a bench-to-bedside quantitative and predictive approach. Cancer Res (2011) 71:298–302. doi:10.1158/0008-5472.can-10-2676
7. Lin RZ, Chang HY Recent advances in three-dimensional multicellular spheroid culture for biomedical research. Biotechnol J Healthc Nutr Tech (2008) 3:1172–84. doi:10.1002/biot.200700228
8. Carlsson J, Nederman T Tumour spheroid technology in cancer therapy research. Eur J Cancer Clin Oncol (1989) 25:1127–33. doi:10.1016/0277-5379(89)90404-5
9. Drasdo D, Höhme S A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol (2005) 2:133–47. doi:10.1088/1478-3975/2/3/001
10. Frick C, Dettinger P, Renkawitz J, Jauch A, Berger CT, Recher M, et al. Nano-scale microfluidics to study 3D chemotaxis at the single cell level. PloS one (2018) 13:e0198330. doi:10.1371/journal.pone.0198330
11. Kapałczyńska M, Kolenda T, Przybyła W, Zajączkowska M, Teresiak A, Filas V, et al. 2D and 3D cell cultures–a comparison of different types of cancer cell cultures. Arch Med Sci AMS (2018) 14:910–9. doi:10.5114/aoms.2016.63743
12. Byrne HM Dissecting cancer through mathematics: from the cell to the animal model. Nat Rev Cancer (2010) 10:221–30. doi:10.1038/nrc2808
13. Greenspan HP Models for the growth of a solid tumor by diffusion. Stud Appl Math (1972) 51:317–40. doi:10.1002/sapm1972514317
14. Frieboes HB, Zheng X, Sun C-H, Tromberg B, Gatenby R, Cristini V An integrated computational/experimental model of tumor invasion. Cancer Res (2006) 66:1597–604. doi:10.1158/0008-5472.can-05-3166
15. Mehta G, Hsiao AY, Ingram M, Luker GD, Takayama S Opportunities and challenges for use of tumor spheroids as models to test drug delivery and efficacy. J controlled release (2012) 164:192–204. doi:10.1016/j.jconrel.2012.04.045
16. Ferraro R, Caserta S, Guido S A low-cost, user-friendly rheo-optical compression assay to measure mechanical properties of cell spheroids in standard cell culture plates. Adv Mater Tech (2024) 9:2301890. doi:10.1002/admt.202301890
17. Dolega ME, Delarue M, Ingremeau F, Prost J, Delon A, Cappello G Cell-like pressure sensors reveal increase of mechanical stress towards the core of multicellular spheroids under compression. Nat Commun (2017) 8:14056–9. doi:10.1038/ncomms14056
18. Dolega ME, Monnier S, Brunel B, Joanny J-F, Recho P, Cappello G Extracellular matrix in multicellular aggregates acts as a pressure sensor controlling cell proliferation and motility. Elife (2021) 10:e63258. doi:10.7554/elife.63258
19. Emad A, Heinz WF, Antonik MD, D’Costa NP, Nageswaran S, Schoenenberger C-A, et al. Relative microelastic mapping of living cells by atomic force microscopy. Biophysical J (1998) 74:1564–78. doi:10.1016/S0006-3495(98)77868-3
20. Giannetti A, Revilloud J, Verdier C Mechanical properties of 3D tumor spheroids measured by AFM. Comp Methods Biomech Biomed Eng (2020) 23:S125–7. doi:10.1080/10255842.2020.1816297
21. Huang YL, Ma Y, Wu C, Shiau C, Segall JE, Wu M Tumor spheroids under perfusion within a 3D microfluidic platform reveal critical roles of cell-cell adhesion in tumor invasion. Scientific Rep (2020) 10:9648–11. doi:10.1038/s41598-020-66528-2
22. Guido S, Villone M Three-dimensional shape of a drop under simple shear flow. J rheology (1998) 42:395–415. doi:10.1122/1.550942
23. Shemesh J, Jalilian I, Shi A, Yeoh GH, Tate MLK, Warkiani ME Flow-induced stress on adherent cells in microfluidic devices. Lab A Chip (2015) 15:4114–27. doi:10.1039/c5lc00633c
24. Delarue M, Montel F, Vignjevic D, Prost J, Joanny J-F, Cappello G Compressive stress inhibits proliferation in tumor spheroids through a volume limitation. Biophysical J (2014) 107:1821–8. doi:10.1016/j.bpj.2014.08.031
25. Jeffery GB The motion of ellipsoidal particles immersed in a viscous fluid. Proc R Soc Lond Ser A, Containing Pap a Math Phys character (1922) 102:161–79. doi:10.1098/rspa.1922.0078
26. Trevelyan BJ, Mason SG Particle motions in sheared suspensions. I Rotations. J Colloid Sci (1951) 6:354–67. doi:10.1016/0095-8522(51)90005-0
27. Blaser S Flocs in shear and strain flows. J Colloid Interf Sci (2000) 225:273–84. doi:10.1006/jcis.1999.6671
28. Masoud H, Stone HA, Shelley MJ On the rotation of porous ellipsoids in simple shear flows. J Fluid Mech (2013) 733:R6. doi:10.1017/jfm.2013.476
29. Pommella A, Caserta S, Guida V, Guido S Shear-induced deformation of surfactant multilamellar vesicles. Phys Rev Lett (2012) 108:138301. doi:10.1103/PhysRevLett.108.138301
30. D'Apolito R, Taraballi F, Minardi S, Liu X, Caserta S, Cevenini A, et al. Microfluidic interactions between red blood cells and drug carriers by image analysis techniques. Med Eng Phys (2016) 38:17–23. doi:10.1016/j.medengphy.2015.10.005
31. Stover CA, Koch DL, Cohen C Observations of fibre orientation in simple shear flow of semi-dilute suspensions. J Fluid Mech (1992) 238:277–96. doi:10.1017/s002211209200171x
32. Ingber MS, Mondy LA A numerical study of three-dimensional Jeffery orbits in shear flow. J Rheology (1994) 38:1829–43. doi:10.1122/1.550604
Keywords: cell spheroids, shear flow, Jeffery’s orbits, rheo-optics, flow-induced morphology
Citation: Ferraro R, Di Franco J, Caserta S and Guido S (2024) The morphology of cell spheroids in simple shear flow. Front. Phys. 12:1347934. doi: 10.3389/fphy.2024.1347934
Received: 01 December 2023; Accepted: 27 May 2024;
Published: 12 June 2024.
Edited by:
Andrew Lyon, Chapman University, United StatesReviewed by:
Raj Kumar Manna, Northeastern University, United StatesCopyright © 2024 Ferraro, Di Franco, Caserta and Guido. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sergio Caserta, c2Nhc2VydGFAdW5pbmEuaXQ=
†Present address: Jasmin Di Franco, Faculty of Physics, University of Vienna, Boltzmanngasse, Wien, Austria
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.