Maximum correntropy unscented filter based on unbiased minimum-variance estimation for a class of nonlinear systems

Introduction: The unscented Kalman filter based on unbiased minimum-variance (UKF-UMV) estimation is usually used to handle the state estimation problem of nonlinear systems with an unknown input. When the nonlinear system is disturbed by non-Gaussian noise, the performance of UKF-UMV will seriously deteriorate.

Methods: A maximum correntropy unscented filter based on the unbiased minimum variance (MCUF-UMV) estimation method is proposed on the basis of the UKF-UMV without the need for estimation of an unknown input and uses the maximum correntropy criterion (MCC) and fixed-point iterative algorithm for state estimation.

Results: When the measurement noise of the nonlinear system is non-Gaussian noise, the algorithm performs well.

Discussion: Our proposed algorithm also does not require estimation of an unknown input, and there is no prior knowledge available about the unknown input or any prior assumptions. The unknown input can be any signal. Finally, a simulation example is used to demonstrate the effectiveness and reliability of the algorithm.

1 Introduction

The state estimation problem of systems with unknown input is very common in practical applications, such as target tracking and automatic control [1–6]. There have been many studies on state estimation for linear discrete-time systems with unknown input, and the methods for state estimation are mainly summarized into the following three categories: the first method is the augmented state Kalman filter (ASKF), in which the unknown input is considered a part of the state and then estimated; that is, both the state and the unknown input are estimated simultaneously [7]. This method assumes the unknown input as a random process with known statistical characteristics, but in reality, the dynamic disturbance is unknown, so its performance usually does not achieve the desired effect. The second method is the modified Kalman filter (MKF) using the Bayesian method when the input variable of the state equation is not fully observed [8]. The third method is to use unbiased minimum-variance (UMV) state estimation when information on unknown input is not available [9–11]. Compared with ASKF and MKF, which rely on all or part of the knowledge of the unknown input, the UMV filter does not require any prior knowledge or assumption about the unknown input, and the unknown input can be any signal, making it more practical.

Recently, a large number of research studies have emerged on nonlinear systems with an unknown input. [12–14] proposes an unscented Kalman filter-based unbiased minimum-variance (UKF-UMV) estimation, which uses the UMV state estimation framework to develop a new nonlinear filter to handle the unknown input. [15] proposes a robust unscented unbiased minimum-variance (RU-UMV) estimator for nonlinear systems with unknown input, which can effectively handle innovation and observe outliers. [16] proposes a robust unscented M-estimation-based filter (RUMF) for state estimation of nonlinear systems of actual vehicles with unknown input. The proposed algorithm is robust to non-Gaussian process noise and innovation in different maneuvering scenarios. However, this algorithm adopts a complex 7-degree-of-freedom vehicle dynamics model, which is very time-consuming, and considers non-Gaussian process noise, without considering non-Gaussian measurement noise.

Correntropy is a measure of local similarity defined in kernel space. The maximum correntropy criterion (MCC) has been successfully applied in many fields of signal processing and machine learning in recent years to cope with non-Gaussian measurement noise in the system, especially heavy-tailed measurement noise. [17–21] proposes a maximum correntropy Kalman filter (MCKF), which uses the robust MCC as the optimality criterion instead of the minimum mean square error (MMSE) criterion. [22] derives a multi-kernel maximum correntropy Kalman filter (MKMCKF) to deal with the interference of multivariate non-Gaussian noise for the systems with an unknown input. This algorithm makes the assumption that d_k+1 = d_k when estimating the unknown input, which can indeed be applied in most cases, such as when the unknown input is represented by continuous signal sin or cos cycles, the error is relatively small. However, if the unknown input is discontinuous, such as a pulse square wave function, this simple assumption will reduce the accuracy in a certain sense and become inaccurate. In order to improve the robustness of the unscented Kalman filter (UKF) to impulse noise, [23] proposes a maximum correntropy unscented filter (MCUF) for nonlinear systems, but does not consider nonlinear systems with unknown input.

Based on the analysis of the above research studies, we propose a maximum correntropy unscented filter based on the unbiased minimum-variance (MCUF-UMV) estimation algorithm. When the nonlinear system with unknown input is disturbed by non-Gaussian measurement noise, especially pulse measurement noise, the performance of the algorithm is good. The contributions of this paper are summarized as follows:

1. The MCUF-UMV algorithm is proposed. First, the prior estimate of the state and prior error covariance matrix are obtained through unscented transformation (UT), and then the nonlinear system and measurement equation are transformed into a quasi-linear regression form using statistical linearization technology. A state augmented model is built, and the MCC and fixed-point iterative algorithm are used to estimate the state.

2. Different from [22], we do not use the simple assumption d_k+1 = d_k. Based on the UKF-UMV form in [14], which does not require unknown input estimation, the MCC is used to estimate the state. There is no need for any prior knowledge or assumptions about the unknown input, and the unknown input can be any signal.

3. We show that for non-Gaussian noise interference, MCUF-UMV is significantly superior to the existing filter in simulation.

The remainder of the paper is structured as follows: section 2 presents preliminary preparation and gives the nonlinear system model and problem statement. Section 3 presents the derivation and equations summary of the MCUF-UMV algorithm. Section 4 demonstrates the excellent performance of the MCUF-UMV algorithm through an illustrative example. Section 5 presents the conclusion.

2 Preliminary and problem statement

2.1 Maximum correntropy criterion

The correntropy representing the similarity measure is as follows:

$V\left(X,Y\right)=E\left[\psi \left(X,Y\right)\right]=\int \psi \left(x,y\right)\mathrm{d}{F}_{XY}\left(x,y\right),$

where $X,Y\in \mathbb{R}$ are two random variables, F_XY is the joint probability distribution function, and $\psi (x,y)=G_{\sigma }(e)=exp(-\frac{e^2}{2{\sigma }^2})$ is the shift-invariant Mercer kernel. e = x − y, and σ is the kernel bandwidth. In most practical cases, the correntropy of the Gaussian kernel can be approximated through the sampling estimator:

$\widehat{V}\left(X,Y\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{G}_{\sigma }\left(e\left(i\right)\right),$

where e(i) = x(i) − y(i) and ${\{x(i),y(i)\}}_{i=1}^N$ is the N samples extracted from F_XY. Using Taylor series to expand the Gaussian kernel

$V\left(X,Y\right)={\displaystyle \sum _{n=0}^{\infty }}\frac{{\left(-1\right)}^n}{2^n{\sigma }^{2n}n!}E\left[{\left(X-Y\right)}^{2n}\right],$

the correntropy is the weighted sum of all even moments of the error variable X − Y.

2.2 System model

The following system model can be used to describe nonlinear discrete-time systems with unknown input:

$x_{k+1}=f\left(x_k,u_{k+1}\right)+G_k{d}_k+q_k,(1)$

$z_k=h\left(x_k,u_k\right)+r_k,(2)$

where $x_k\in {\mathbb{R}}^n$, $u_k\in {\mathbb{R}}^l$, $d_k\in {\mathbb{R}}^p$, and $z_k\in {\mathbb{R}}^m$ are, respectively, the state vector, known input vector, unknown input vector, and measurement vector at time k; f(⋅) and h(⋅) are nonlinear functions; G_k is a known matrix; the process noise q_k is assumed to be zero mean white noise and the process noise q_k and the measurement noise r_k are uncorrelated. The covariance matrices of process noise and measurement noise are Q_k and R_k, respectively. In fact, we do not have any prior knowledge about unknown input d_k available, nor do we make a prior assumption that unknown input d_k can be any signal. Our research is based on this fact.

Problem statement: Based on systems 1, 2, this paper first uses UT to obtain the prior estimate of the state and prior error covariance matrix, then uses the statistical linearization technique to transform the nonlinear system and measurement equation into the quasi-linear regression form, and finally uses the MCC and fixed-point iterative algorithm for state estimation, which can effectively solve the interference of non-Gaussian measurement noise on nonlinear systems with unknown input.

3 MCUF-UMV algorithm derivation

3.1 Statistical linear regression

First, the one-step prediction is calculated. Given the mean ${\widehat{x}}_{k-1\mid k-1}$ and covariance $P_{k-1\mid k-1}^{xx}$, 2n + 1 sigma points ${\chi }_{k-1\mid k-1}^i$ and corresponding weight values w can be obtained through UT, which gives the formula ${\chi }_{k-1\mid k-1}^i$

${\chi }_{k-1\mid k-1}^i=\left\{\begin{array}{cc}{\widehat{x}}_{k-1\mid k-1},\hfill & i=0\hfill \\ {\widehat{x}}_{k-1\mid k-1}+{\left(\sqrt{\left(n+\lambda \right)P_{k-1\mid k-1}^{xx}}\right)}_i,\hfill & i=1,\dots ,n\hfill \\ {\widehat{x}}_{k-1\mid k-1}-{\left(\sqrt{\left(n+\lambda \right)P_{k-1\mid k-1}^{xx}}\right)}_{i-n},\hfill & i=n+1,\dots ,2n\hfill \end{array}\right.,$

where n refers to the dimension of the state and ${(\sqrt{P})}_i$ represents the i-th column of the matrix root. The corresponding weights of these sampling points are calculated as follows:

$\left\{\begin{array}{c}{w}_m^0=\frac{\lambda }{\left(n+\lambda \right)},\hfill \\ w_c^0=\frac{\lambda }{\left(n+\lambda \right)}+\left(1-{\alpha }^2+\beta \right),\hfill \\ w_m^i=w_c^i=\frac{1}{2\left(n+\lambda \right)},i=1,\dots ,2n\hfill \end{array}\right.,$

where the subscript m represents the mean, c represents the covariance, and the superscript represents the i-th sampling point. The parameter λ = α²(n + κ) − n is a scaling parameter. The selection of α controls the distribution state of the sampling points, and κ is the parameter to be selected, whose value should generally ensure that the matrix $(n+\lambda )P_{k-1\mid k-1}^{xx}$ is a positive semi-definite matrix. The selected parameter β is a non-negative weight coefficient that can merge the motion errors of higher-order terms in the equation. Using nonlinear process function f(⋅) transformation for each sigma point, we obtain

${\chi }_{k\mid k-1}^i=f\left({\chi }_{k-1\mid k-1}^i,u_k\right),$

The predicted mean and covariance matrix of the state are

${\widehat{x}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_m^i{\chi }_{k\mid k-1}^i,$

$P_{k\mid k-1}^{xx}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left({\chi }_{k\mid k-1}^i-{\widehat{x}}_{k\mid k-1}\right){\left({\chi }_{k\mid k-1}^i-{\widehat{x}}_{k\mid k-1}\right)}^T+Q_{k-1}.$

New sigma points are generated based on one-step prediction

${\chi }_{k\mid k-1}^{*i}=\left\{\begin{array}{cc}{\widehat{x}}_{k\mid k-1},\hfill & i=0\hfill \\ {\widehat{x}}_{k\mid k-1}+{\left(\sqrt{\left(n+\lambda \right)P_{k\mid k-1}^{xx}}\right)}_i,\hfill & i=1,\dots ,n\hfill \\ {\widehat{x}}_{k\mid k-1}-{\left(\sqrt{\left(n+\lambda \right)P_{k\mid k-1}^{xx}}\right)}_{i-n},\hfill & i=n+1,\dots ,2n\hfill \end{array}\right.,$

using nonlinear measurement function h(⋅) transform for newly generated sigma points

$Z_{k\mid k-1}^i=h\left({\chi }_{k\mid k-1}^{*i},u_k\right).$

and the prediction of the measurement vector is

${\widehat{z}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_m^i{Z}_{k\mid k-1}^i.$

The innovation and cross covariance matrices are

$P_{k\mid k-1}^{zz}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right){\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right)}^T+R_k$

$P_{k\mid k-1}^{xz}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left({\chi }_{k\mid k-1}^{*i}-{\widehat{x}}_{k\mid k-1}\right){\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right)}^T.$

Before introducing the proposed algorithm, we transform the nonlinear measurement equation into the linear form using the statistical linearization technique as follows:

$z_k=H_k\left(x_k-{\widehat{x}}_{k\mid k-1}\right)+{\widehat{z}}_{k\mid k-1}+{\theta }_k,(3)$

where H_k is the measurement slope matrix.

$H_k={\left(P_{k\mid k-1}^{xz}\right)}^T{\left(P_{k\mid k-1}^{xx}\right)}^{-1}.$

The covariance of θ_k is

$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_k=& P_{k\mid k-1}^{zz}-{\left(P_{k\mid k-1}^{xz}\right)}^T{\left(P_{k\mid k-1}^{xx}\right)}^{-1}{P}_{k\mid k-1}^{xz}\hfill & \hfill \\ \hfill =& P_{k\mid k-1}^{zz}-H_k{P}_{k\mid k-1}^{xx}{H}_k^T.\hfill & \hfill \end{array}$

3.2 Existing UKF-UMV without unknown input estimation

The MCUF-UMV algorithm we derived in Section 3.3 is based on the UKF-UMV in [14] that does not require estimation of unknown input. Therefore, this section provides an introduction and summary of UKF-UMV without unknown input estimation. According to Eq. 3, the innovation Δz_k is represented as

$\mathrm{\Delta }{z}_k=z_k-{\widehat{z}}_{k\mid k-1}=H_k\left(x_k-{\widehat{x}}_{k\mid k-1}\right)+{\theta }_k.(4)$

According to Eqs 1, 4

$\mathrm{\Delta }{z}_k=H_k{G}_{k-1}{d}_{k-1}+{\eta }_k,$

where

${\zeta }_k=f\left(x_{k-1},u_k\right)-{\widehat{x}}_{k\mid k-1}+q_{k-1},$

${\eta }_k=H_k{\zeta }_k+{\theta }_k,$

and

$E\left[{\zeta }_k{\zeta }_k^T\right]=P_{k\mid k-1}^{xx},$

${\tilde{R}}_k=E\left[{\eta }_k{\eta }_k^T\right]=H_k{P}_{k\mid k-1}^{xx}{H}_k^T+{\mathrm{\Phi }}_k=P_{k\mid k-1}^{zz}.$

The existing UKF-UMV without unknown input estimation is summarized as follows:

$K_k=P_{k\mid k-1}^{xx}{H}_k^T{\tilde{R}}_k^{-1}=P_{k\mid k-1}^{xz}{\left(P_{k\mid k-1}^{zz}\right)}^{-1},$

$M_k={\left(G_k^T{H}_k^T{\tilde{R}}_k^{-1}{H}_k{G}_k\right)}^{-1}{G}_k^T{H}_k^T{\tilde{R}}_k^{-1},$

$L_k=K_k+\left(I-K_k{H}_k\right)G_k{M}_k,$

${\widehat{x}}_{k\mid k}={\widehat{x}}_{k\mid k-1}+L_k\left(z_k-{\widehat{z}}_{k\mid k-1}\right),$

$P_{k\mid k}^{xx}=\left(I-L_k{H}_k\right)P_{k\mid k-1}^{xx}{\left(I-L_k{H}_k\right)}^T+L_k{\mathrm{\Phi }}_k{L}_k^T.$

3.3 State estimation

From the nonlinear model described above, the augmented model is given as follows:

$\left[\begin{array}{c}\hfill {\widehat{x}}_{k\mid k-1}\hfill \\ \hfill z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill I\hfill \\ \hfill H_k\hfill \end{array}\right]x_k+v_k,(5)$

where I is the dimension of the n × n identity matrix and v_k can be expressed as

$v_k=\left[\begin{array}{c}\hfill -\left(x_k-{\widehat{x}}_{k\mid k-1}\right)\hfill \\ \hfill {\theta }_k\hfill \end{array}\right],$

with

$\begin{array}{ccc}\hfill E\left[v_k{v}_k^T\right]& =\hfill & \left[\begin{array}{cc}\hfill P_{k\mid k-1}^{xx}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Phi }}_k\hfill \end{array}\right]\hfill \\ \hfill & =\hfill & \left[\begin{array}{cc}\hfill B_{k\mid k-1}^p{B}_{k\mid k-1}^{pT}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_k^{\mathrm{\Phi }}{B}_k^{\mathrm{\Phi }T}\hfill \end{array}\right]\hfill \\ \hfill & =\hfill & B_k{B}_k^T,\hfill \end{array}$

where $B_{k\mid k-1}^p,B_k^{\mathrm{\Phi }}$ and B_k is obtained by using Cholesky decomposition. Then, multiplying both sides of Eq. 5 by $B_k^{-1}$, the following formula is obtained:

$D_k=W_k{x}_k+e_k,$

where

$\begin{array}{ll}\hfill & D_k=B_k^{-1}\left[\begin{array}{c}\hfill {\widehat{x}}_{k\mid k-1}\hfill \\ \hfill z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\hfill \end{array}\right],\hfill \\ \hfill & W_k=B_k^{-1}\left[\begin{array}{c}\hfill I\hfill \\ \hfill H_k\hfill \end{array}\right],e_k=B_k^{-1}{v}_k.\hfill \end{array}$

Then, the cost function based on the MCC can be obtained as follows:

$J_L\left(x_k\right)=\frac{1}{L}{\displaystyle \sum _{i=1}^L}{G}_{\sigma }\left(D_k^i-W_k^i{x}_k\right),$

where the dimension of D_k is expressed in L and L = n + m.$D_k^i$ is the ith element of D_k, $W_k^i$ is the ith row of W_k, and σ is the kernel bandwidth of correntropy. Then, the optimal estimate of x_k is

${\widehat{x}}_k=arg{\max }_{x_k}\frac{1}{L}{\displaystyle \sum _{i=1}^L}{G}_{\sigma }\left(e_k^i\right),$

where $e_k^i$ is the ith element of e_k:

$e_k^i=D_k^i-W_k^i{x}_k.$

Let

$\frac{\partial J_L\left(x_k\right)}{\partial x_k}=0,$

The optimal solution is given as

$x_k={\left({\displaystyle \sum _{i=1}^L}\left[G_{\sigma }\left(e_k^i\right)W_k^{iT}{W}_k^i\right]\right)}^{-1}\times \left({\displaystyle \sum _{i=1}^L}\left[G_{\sigma }\left(e_k^i\right)W_k^{iT}{D}_k^i\right]\right).$

It can be seen that the optimal solution is a fixed-point x_k equation, which can also be rewritten as

$x_k={\left(W_k^T{C}_k{W}_k\right)}^{-1}{W}_k^T{C}_k{D}_k,(6)$

where

$C_k=\left[\begin{array}{cc}\hfill C_k^x\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill C_k^z\hfill \end{array}\right],$

with

$\begin{array}{ll}\hfill & C_k^x=diag\left(G_{\sigma }\left(e_k^1\right),\dots ,G_{\sigma }\left(e_k^n\right)\right),\hfill \\ \hfill & C_k^z=diag\left(G_{\sigma }\left(e_k^{n+1}\right),\dots ,G_{\sigma }\left(e_k^{n+m}\right)\right).\hfill \end{array}$

Eq. 6 can be further expressed as follows:

$x_k={\widehat{x}}_{k\mid k-1}+{\tilde{K}}_k\left(z_k-{\widehat{z}}_{k\mid k-1}\right),(7)$

where

${\tilde{K}}_k={\tilde{P}}_{k\mid k-1}^{xx}{H}_k^T{\left(H_k{\tilde{P}}_{k\mid k-1}^{xx}{H}_k^T+{\tilde{\mathrm{\Phi }}}_k\right)}^{-1},$

${\tilde{P}}_{k\mid k-1}^{xx}=B_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT},$

${\tilde{\mathrm{\Phi }}}_k=B_k^{\mathrm{\Phi }}{\left(C_k^z\right)}^{-1}{B}_k^{\mathrm{\Phi }T}.$

The detailed derivation process of Eq. 7 is in the Appendix.

3.4 Summary of MCUF-UMV equations

This section presents the summary of the MCUF-UMV algorithm. Given the mean ${\widehat{x}}_{k-1\mid k-1}$ and covariance $P_{k-1\mid k-1}^{xx}$, when 2n + 1 sigma points ${\chi }_{k-1\mid k-1}^i$ and the corresponding weights $w_m^i$, $w_c^i$ are obtained through UT, and ${\chi }_{k\mid k-1}^i$ is obtained through nonlinear process function f(⋅).

1. Time update

$\begin{array}{ll}\hfill & {\widehat{x}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_m^i{\chi }_{k\mid k-1}^i,\hfill \\ \hfill & P_{k\mid k-1}^{xx}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left({\chi }_{k\mid k-1}^i-{\widehat{x}}_{k\mid k-1}\right){\left({\chi }_{k\mid k-1}^i-{\widehat{x}}_{k\mid k-1}\right)}^T+Q_{k-1}.\hfill \end{array}$

Based on ${\widehat{x}}_{k\mid k-1}$ and covariance $P_{k\mid k-1}^{xx}$, new sigma points ${\chi }_{k\mid k-1}^{*i}$ are obtained by UT, and then $Z_{k\mid k-1}^i$ is obtained by the nonlinear measurement function h(⋅). Then

$\begin{array}{ll}\hfill & {\widehat{z}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_m^i{Z}_{k\mid k-1}^i,\hfill \\ \hfill & P_{k\mid k-1}^{zz}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right){\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right)}^T+R_k,\hfill \\ \hfill & P_{k\mid k-1}^{xz}={\displaystyle \sum _{i=0}^{2n}}{w}_c^i\left({\chi }_{k\mid k-1}^{*i}-{\widehat{x}}_{k\mid k-1}\right){\left(Z_{k\mid k-1}^i-{\widehat{z}}_{k\mid k-1}\right)}^T.\hfill \end{array}$

2. Measurement update

Given a suitable kernel bandwidth σ and small constant ϵ for state estimation, let t = 1 and ${\widehat{x}}_{(k\mid k)0}={\widehat{x}}_{k\mid k-1}$, where ${\widehat{x}}_{(k\mid k)t}$ represents the state estimation during fixed-point iteration t.

$\begin{array}{ll}\hfill & e_k^i=D_k^i-W_k^i{\widehat{x}}_{\left(k\mid k\right)t-1},\hfill \\ \hfill & C_k^x=diag\left(G_{\sigma }\left(e_k^1\right),\dots ,G_{\sigma }\left(e_k^n\right)\right),\hfill \\ \hfill & C_k^z=diag\left(G_{\sigma }\left(e_k^{n+1}\right),\dots ,G_{\sigma }\left(e_k^{n+m}\right)\right),\hfill \\ \hfill & {\tilde{P}}_{k\mid k-1}^{xx}=B_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT},\hfill \\ \hfill & {\tilde{\mathrm{\Phi }}}_k=B_k^{\mathrm{\Phi }}{\left(C_k^z\right)}^{-1}{B}_k^{\mathrm{\Phi }T},\hfill \\ \hfill & H_k={\left(P_{k\mid k-1}^{xz}\right)}^T{\left(P_{k\mid k-1}^{xx}\right)}^{-1},\hfill \\ \hfill & {\tilde{K}}_k={\tilde{P}}_{k\mid k-1}^{xx}{H}_k^T{\left(H_k{\tilde{P}}_{k\mid k-1}^{xx}{H}_k^T+{\tilde{\mathrm{\Phi }}}_k\right)}^{-1},\hfill \\ \hfill & {\widehat{x}}_{\left(k\mid k\right)t}={\widehat{x}}_{k\mid k-1}+{\tilde{K}}_k\left(z_k-{\widehat{z}}_{k\mid k-1}\right).\hfill \end{array}$

The following inequality is given as

${\displaystyle \frac{\Vert {\widehat{x}}_{\left(k\mid k\right)t}-{\widehat{x}}_{\left(k\mid k\right)t-1}\Vert }{\Vert {\widehat{x}}_{\left(k\mid k\right)t-1}\Vert }}\le ϵ,$

where ${\widehat{x}}_{k\mid k}={\widehat{x}}_{(k\mid k)t}$. If the above inequality is true, continue to the next step; otherwise, return to iterative steps in the measurement update again.

Finally, the covariance $P_{k\mid k}^{xx}$ of the state measurement update error is obtained:

$P_{k\mid k}^{xx}=\left(I-{\tilde{K}}_k{H}_k\right)P_{k\mid k-1}^{xx}{\left(I-{\tilde{K}}_k{H}_k\right)}^T+{\tilde{K}}_k{\mathrm{\Phi }}_k{\tilde{K}}_k^T.$

4 Illustrative example

In this section, an example of uniformly accelerating linear motion target tracking in [24] with minor modification is used to demonstrate the effectiveness and reliability of the MCUF-UMV algorithm by comparing its performance with that of UKF-UMV in nonlinear systems with unknown input. We only use mixed Gaussian noise as an example to illustrate the performance of the algorithm in the presence of non-Gaussian measurement noise interference. In this example, by manually switching between mixed Gaussian noise and Gaussian noise, we demonstrate the performance of the algorithm under mixed Gaussian noise and Gaussian noise interference, respectively.

4.1 Mixed Gaussian noise

Consider a particle M moving in the two-dimensional plane, whose position, velocity, and acceleration at a certain moment k can be represented by the vector $x_k={[{\bar{x}}_k,{\bar{y}}_k,{\dot{\stackrel{̄}{x}}}_k,{\dot{\stackrel{̄}{y}}}_k,{\ddot{\stackrel{̄}{x}}}_k,{\ddot{\stackrel{̄}{y}}}_k]}^T$. Assuming that M undergoes approximately uniformly accelerated linear motion in the x-axis direction and also approximately uniformly accelerated linear motion in the y-axis direction, the equation of motion for this particle in Cartesian coordinates is

$x_{k+1}=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill T\hfill & \hfill 0\hfill & \hfill \frac{T^2}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill T\hfill & \hfill 0\hfill & \hfill \frac{T^2}{2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill T\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill T\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]x_k+\left[\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \\ \hfill 0.4\hfill \\ \hfill -0.2\hfill \\ \hfill 0.5\hfill \\ \hfill -0.5\hfill \end{array}\right]d_k+q_k,$

where d_k is the unknown input, simulated with d_k = 0.1cos(0.2k). q_k is the process noise. Assuming that the radar with the coordinate position $({\bar{x}}_0,{\bar{y}}_0)$ tracks particle M, the distance l_k between the radar and particle M and the angle ϕ_k of particle M relative to the radar can be obtained. In actual measurements, the radar has noise r_k. In a coordinate system centered on the radar, the measurement equation is

$z_k=h\left(x_k\right)+r_k=\left[\begin{array}{c}\hfill l_k+r_k^l\hfill \\ \hfill {\varphi }_k+r_k^{\varphi }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \sqrt{{\left({\bar{x}}_k-{\bar{x}}_0\right)}^2+{\left({\bar{y}}_k-{\bar{y}}_0\right)}^2}+r_k^l\hfill \\ \hfill arctan\left(\frac{{\bar{y}}_k-{\bar{y}}_0}{{\bar{x}}_k-{\bar{x}}_0}\right)+r_k^{\varphi }\hfill \end{array}\right],$

where $r_k^l$ is the measurement noise regarding the distance l_k between the radar and particle M and $r_k^{\varphi }$ is the measurement noise regarding the angle ϕ_k between the radar and particle M relative to the radar. In the Cartesian coordinate system, the state equation of the model is linear, while the measurement equation is nonlinear. In the simulation, the covariance matrix Q_k of system noise q_k and the measurement noise r_k, which are mixed Gaussian noise, are as follows:

$Q_k=diag\left\{\mathrm{1,1,0}.1^2,0.1^2,0.01^2,0.01^2\right\},$

$r_k\backsim 0.9N\left(\mathrm{0,0.01}\right)+0.1N\left(\mathrm{0,100}\right).$

Initial state x₀ = [1000,5000,10,50,2,−4]^T. Measurement number N = 50 and sampling time T = 0.5s.

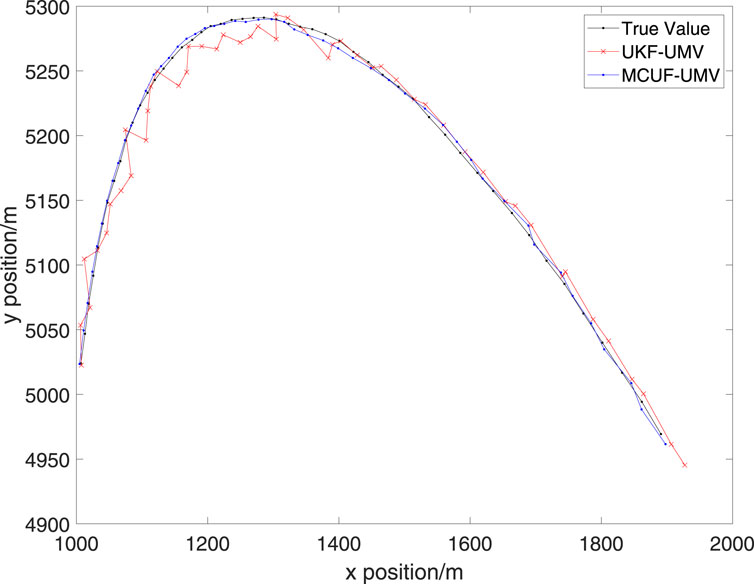
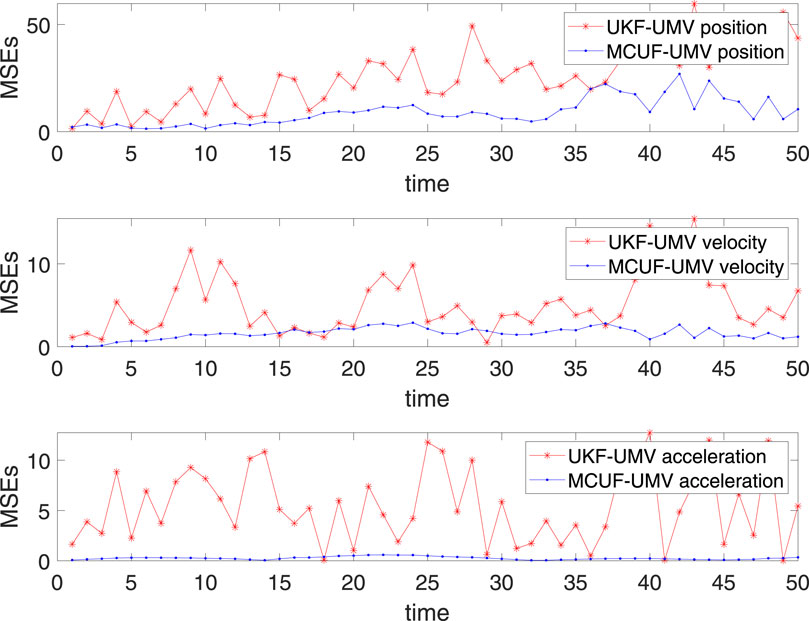
The generated motion trajectory diagram is shown in Figure 1, and the tracking position, velocity, and acceleration mean square errors (MSEs) are shown in Figure 2. Table 1 shows the comparison of MSEs of two algorithms from ten independent experiments. From the experimental results, it can be seen that the MCUF-UMV algorithm performs significantly better under mixed Gaussian noise interference.

Figure 1

Figure 1. Motion trajectory map.

Figure 2

Figure 2. Tracking error chart with mixed Gaussian noise.

Table 1

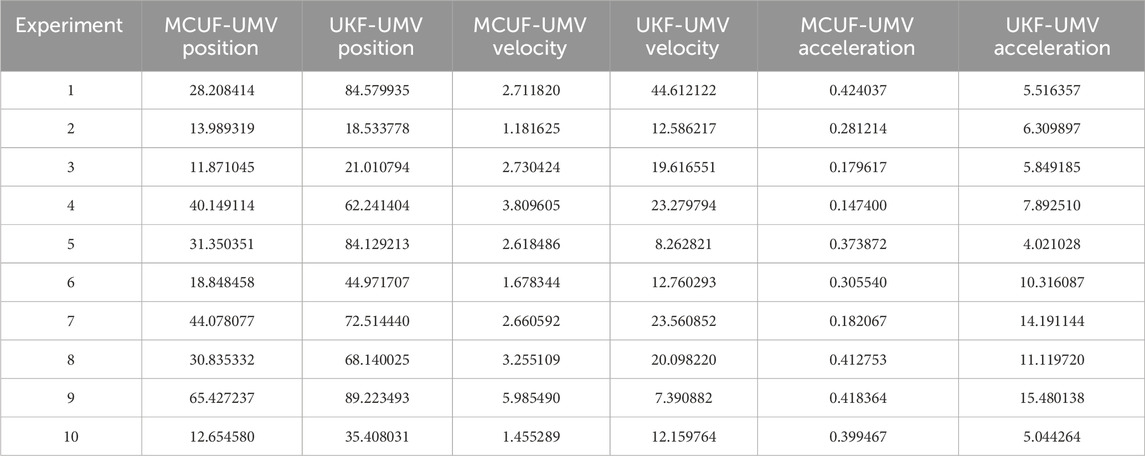
Table 1. MSEs of 10 independent experiments of position, velocity, and acceleration in mixed Gaussian noise.

4.2 Gaussian noise

Using the same model as given in Section 4.1, the measurement noise r_k is replaced with Gaussian noise, and its covariance matrix R_k is represented as follows:

$R_k=diag\left\{10^2,0.001^2\right\}.$

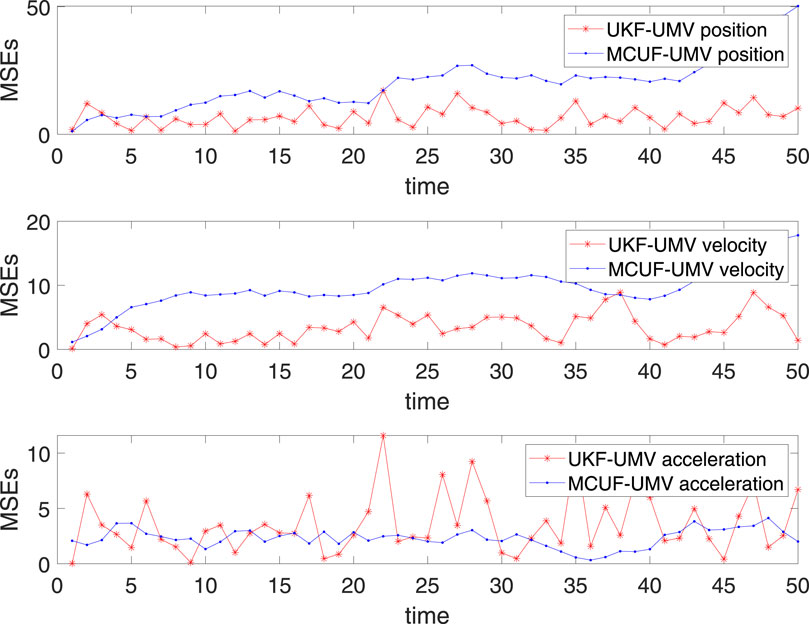
To ensure that the entire system model is in the Gaussian environment, the unknown input is set to a random number. The tracking position, velocity, and acceleration MSEs are shown in Figure 3. Table 2 shows the comparison of the MSEs of two algorithms from ten independent experiments. From the data, it can be seen that when the measurement noise is Gaussian noise, the performance of MCUF-UMV is not as good as compared to that of UKF-UMV.

Figure 3

Figure 3. Tracking error chart with Gaussian noise.

Table 2

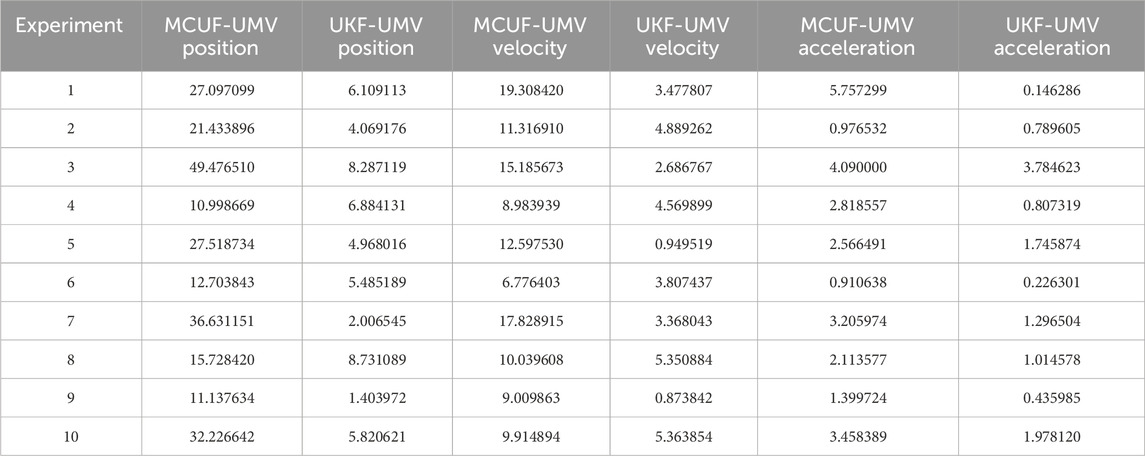
Table 2. MSEs of 10 independent experiments of position, velocity, and acceleration in Gaussian noise.

5 Conclusion

We have proposed the MCUF-UMV algorithm for the nonlinear discrete-time system with the unknown input when the system is disturbed by non-Gaussian noise, especially heavy-tailed impulse noise. First, the prior estimation and prior error covariance of the state are obtained by UT. By using statistical linearization techniques, nonlinear system and measurement equation are transformed into quasi-linear regression forms. Based on the UKF-UMV form that does not require unknown input estimation, the MCC and fixed-point iterative algorithm are used to estimate the state. We do not have any prior knowledge or assumptions about the unknown input, and the unknown input can be any signal. Finally, a simulation experiment has been conducted to demonstrate the effectiveness and reliability of the MCUF-UMV algorithm under non-Gaussian noise interference. In future work, we will further apply this algorithm to specific practical applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YZ: conceptualization, data curation, formal analysis, methodology, software, and writing–original draft. BN: writing–review and editing. XS: resources, supervision, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China (61873152 and 61876101).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

NOTATION: Throughout the entire paper, “superscript “−1” and” superscript “T” represent the inverse and transpose of matrices, respectively. “E” represents the mathematical expectation factor. “I” represents the identity matrix. “${\mathbb{R}}^n$” represents the n-dimensional Euclidean space.

References

1. Nikoukhah R. Innovations generation in the presence of unknown inputs: application to robust failure detection. Automatica (1994) 30:1851–67. doi:10.1016/0005-1098(94)90047-7

CrossRef Full Text | Google Scholar

2. Li Z, Liu X, Ren W, Xie L. Distributed tracking control for linear multiagent systems with a leader of bounded unknown input. IEEE Trans Automatic Control (2013) 58:518–23. doi:10.1109/TAC.2012.2208295

CrossRef Full Text | Google Scholar

3. Song X, Zheng WX. Linear estimation for discrete-time periodic systems with unknown measurement input and missing measurements. ISA Trans (2019) 95:164–72. doi:10.1016/j.isatra.2018.11.013

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wei F, Chen G, Wang W. Finite-time synchronization of memristor neural networks via interval matrix method. Neural Networks (2020) 127:7–18. doi:10.1016/j.neunet.2020.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Mortensen K, Flyvbjerg H, Pedersen J. Confined brownian motion tracked with motion blur: estimating diffusion coefficient and size of confining space. Front Phys (2021) 8. doi:10.3389/fphy.2020.583202

CrossRef Full Text | Google Scholar

6. Chen B, Dang L, Zheng N, Principe JC. Kalman filtering under information theoretic criteria (2023). p. 89–126. doi:10.1007/978-3-031-33764-2_4

CrossRef Full Text | Google Scholar

7. Ding B, Zhang T, Fang H. Infinity augmented state kalman filter and its application in unknown input and state estimation. J Franklin Inst (2023) 360:11916–31. doi:10.1016/j.jfranklin.2023.08.034

CrossRef Full Text | Google Scholar

8. Li B. State estimation with partially observed inputs: a unified kalman filtering approach. Automatica (2013) 49:816–20. doi:10.1016/j.automatica.2012.12.007

CrossRef Full Text | Google Scholar

9. Kitanidis PK. Unbiased minimum-variance linear state estimation. Automatica (1987) 23:775–8. doi:10.1016/0005-1098(87)90037-9

CrossRef Full Text | Google Scholar

10. Darouach M, Zasadzinski M. Unbiased minimum variance estimation for systems with unknown exogenous inputs. Automatica (1997) 33:717–9. doi:10.1016/S0005-1098(96)00217-8

CrossRef Full Text | Google Scholar

11. Gillijns S, De Moor B. Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica (2007) 43:111–6. doi:10.1016/j.automatica.2006.08.002

CrossRef Full Text | Google Scholar

12. Khan M, Khan S, Chu Y. New estimates for the jensen gap using s-convexity with applications. Front Phys (2020) 8. doi:10.3389/fphy.2020.00313

CrossRef Full Text | Google Scholar

13. Qiao J, Lu Z, Lin B, Song J, Xiao Z, Wang Z, et al. A survey of gnss interference monitoring technologies. Front Phys (2023) 11. doi:10.3389/fphy.2023.1133316

CrossRef Full Text | Google Scholar

14. Zheng Z, Zhao J, Mili L, Liu Z, Wang S. Unscented kalman filter-based unbiased minimum-variance estimation for nonlinear systems with unknown inputs. IEEE Signal Process. Lett (2019) 26:1162–6. doi:10.1109/LSP.2019.2922620

CrossRef Full Text | Google Scholar

15. Zheng Z, Zhao J, Mili L, Liu Z. Robust unscented unbiased minimum-variance estimator for nonlinear system dynamic state estimation with unknown inputs. IEEE Signal Process. Lett (2020) 27:376–80. doi:10.1109/LSP.2020.2973116

CrossRef Full Text | Google Scholar

16. Xue Z, Cheng S, Li L, Zhong Z, Mu H. A robust unscented m-estimation-based filter for vehicle state estimation with unknown input. IEEE Trans Vehicular Tech (2022) 71:6119–30. doi:10.1109/TVT.2022.3163207

CrossRef Full Text | Google Scholar

17. Ehrich J, Sivak DA. Energy and information flows in autonomous systems. Front Phys (2023) 11. doi:10.3389/fphy.2023.1108357

CrossRef Full Text | Google Scholar

18. Song H, Ding D, Dong H, Yi X. Distributed filtering based on cauchy-kernel-based maximum correntropy subject to randomly occurring cyber-attacks. Automatica (2022) 135:110004. doi:10.1016/j.automatica.2021.110004

CrossRef Full Text | Google Scholar

19. Fu X, Song X. Distributed maximum correntropy kalman filter with state equality constraints in a sensor network with packet drops. Signal Process. (2023) 213:109218. doi:10.1016/j.sigpro.2023.109218

CrossRef Full Text | Google Scholar

20. Zhang M, Zheng WX, Song X, Yuan H. Two efficient kalman filter algorithms for measurement packet dropping systems under maximum correntropy criterion. Syst Control Lett (2023) 175:105515. doi:10.1016/j.sysconle.2023.105515

CrossRef Full Text | Google Scholar

21. Chen B, Liu X, Zhao H, Principe JC. Maximum correntropy kalman filter. Automatica (2017) 76:70–7. doi:10.1016/j.automatica.2016.10.004

CrossRef Full Text | Google Scholar

22. Li S, Shi D, Zou W, Shi L. Multi-kernel maximum correntropy kalman filter. IEEE Control Syst Lett (2022) 6:1490–5. doi:10.1109/LCSYS.2021.3114137

CrossRef Full Text | Google Scholar

23. Liu X, Chen B, Xu B, Wu Z, Honeine P. Maximum correntropy unscented filter. Int J Syst Sci (2017) 48:1607–15. doi:10.1080/00207721.2016.1277407

CrossRef Full Text | Google Scholar

24. Huang X, Wang Y. Kalman filter principle and application: matlab simulation. Beijing: Electronic Industry Press (2015).

Google Scholar

Appendix A

$W_k=B_k^{-1}\left[\begin{array}{c}\hfill I\hfill \\ \hfill H_k\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill B_{k\mid k-1}^{p-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_k^{\mathrm{\Phi }-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill I\hfill \\ \hfill H_k\hfill \end{array}\right]=\left[\begin{array}{c}\hfill B_{k\mid k-1}^{p-1}\hfill \\ \hfill B_k^{\mathrm{\Phi }-1}{H}_k\hfill \end{array}\right],(\mathrm{A.1})$

$C_k=\left[\begin{array}{cc}\hfill C_k^x\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill C_k^z\hfill \end{array}\right],(\mathrm{A.2})$

$\begin{array}{ccc}\hfill D_k& =\hfill & B_k^{-1}\left[\begin{array}{c}\hfill {\widehat{x}}_{k\mid k-1}\hfill \\ \hfill z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill B_{k\mid k-1}^{p-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_k^{\mathrm{\Phi }-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\widehat{x}}_{k\mid k-1}\hfill \\ \hfill z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\hfill \end{array}\right]\hfill \\ \hfill & =\hfill & \left[\begin{array}{c}\hfill B_{k\mid k-1}^{p-1}{\widehat{x}}_{k\mid k-1}\hfill \\ \hfill B_k^{\mathrm{\Phi }-1}\left(z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\right)\hfill \end{array}\right].\hfill \end{array}(\mathrm{A.3})$

By (A.1) and (A.2), we have

$W_k^T{C}_k{W}_k={\left(B_{k\mid k-1}^{p-1}\right)}^T{C}_k^x{B}_{k\mid k-1}^{p-1}+H_k^T{\left(B_k^{\mathrm{\Phi }-1}\right)}^T{C}_k^z{B}_k^{\mathrm{\Phi }-1}{H}_k.(\mathrm{A.4})$

Next, the matrix inverse lemma was used to obtain:

$\begin{array}{ccc}\hfill {\left(W_k^T{C}_k{W}_k\right)}^{-1}& =\hfill & B_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT}-B_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT}{H}_k^T\hfill \\ \hfill & \hfill & {\left(H_k{B}_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT}{H}_k^T+B_k^{\mathrm{\Phi }}{\left(C_k^z\right)}^{-1}{B}_k^{\mathrm{\Phi }T}\right)}^{-1}{H}_k{B}_{k\mid k-1}^p{\left(C_k^x\right)}^{-1}{B}_{k\mid k-1}^{pT},\hfill \end{array}(\mathrm{A.5})$

and by (A.1)–(A.3), we have

$W_k^T{C}_k{D}_k={\left(B_{k\mid k-1}^{p-1}\right)}^T{C}_k^x{B}_{k\mid k-1}^{p-1}+H_k^T{\left(B_k^{\mathrm{\Phi }-1}\right)}^T{C}_k^z{B}_k^{\mathrm{\Phi }-1}\left(z_k-{\widehat{z}}_{k\mid k-1}+H_k{\widehat{x}}_{k\mid k-1}\right).(\mathrm{A.6})$

Combining (A.5) and (A.6), we have Eq. 7.