- 1School of Physics and Astronomy, University of Southampton, Southampton, United Kingdom
- 2Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
- 3Université de Lyon, Université Claude Bernard Lyon 1, Villeurbanne, France
- 4Department of Physics, University of Johannesburg, Johannesburg, South Africa
- 5Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden
We introduce a new class of renormalizable models for dark matter with a minimal particle content, consisting of a dark SU(2)D gauge sector connected to the standard model through a vector-like fermion mediator, not requiring a Higgs portal, in which a massive vector boson is the dark matter candidate. These models are labeled fermion portal vector dark matter (FPVDM). Multiple realizations are possible, depending on the properties of the vector-like partner and scalar potential. One example is discussed in detail. Fermion portal vector dark matter models have a large number of applications in collider and non-collider experiments, with their phenomenology depending on the mediator sector.
The nature of DM, whose existence has been established beyond any reasonable doubt by several independent cosmological observations, is one of the greatest puzzles of contemporary particle physics. Models with a vector DM, especially in the non-abelian case, are the least explored but well-motivated, as the gauge principle offers guidance and constraints limiting the possible theoretical constructions (see, e.g., [1–26], for a discussion of non-abelian DM in different setups, in particular using non-renormalizable kinetic mixing terms or Higgs portal scenarios). In this article, we develop a new minimal framework that extends the gauge sector of the standard model (SM) by a new non-abelian gauge group for which no renormalizable kinetic mixing terms are allowed1 and under which all SM particles are singlets. The full model structure, Lagrangian, and particle content are presented in the following sections, along with the main results and immediate prospects for experimental testing, while more technical details can be found in [27].
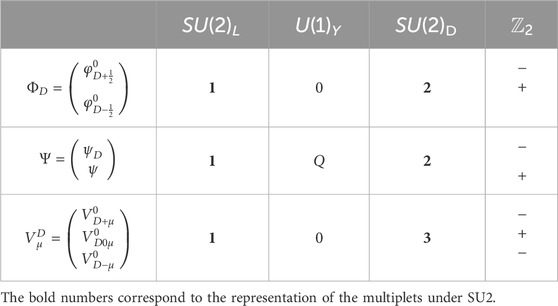
The simplest non-abelian group is SU(2), which in the following will be labeled SU(2)D as it connects the SM to the dark sector. The gauge bosons associated with SU(2)D are labeled as
where gD is the SU(2)D coupling constant and T3D is the D-isospin.
The fields responsible for breaking the gauge symmetries are two scalar doublets:
where the first is breaking SU(2)L × U(1)Y, while the second is breaking SU(2)D via their respective vacuum expectation values (VEVs) v and vD.
The scalar potential for ΦH and ΦD reads
which was introduced in [2] and ensures that the gauge bosons of SU(2)D are degenerate and stable because of the custodial symmetry of the scalar Lagrangian. Although the operator
where
Without this symmetry, such a term would be compulsory since the scalar doublet, ΦD, is in the pseudo-real representation. The symmetry-breaking pattern is
The lightest
Upon diagonalization, the mass eigenvalues read
with the mixing angle
In the fermion sector, the component with T3D = +1/2 gets only a VL mass; therefore,
The mass eigenvalues are
where
The Yukawa couplings and mixings can be expressed in terms of the masses of the physical fermions. The new fermion sector is completely decoupled in the limit
The masses of the SM gauge bosons are not altered by the presence of ΦD. The gauge bosons of SU(2)D are all degenerate in mass at the tree level:
In the following, we assume that new VL fermions interact only with one flavor of the SM. Six independent input parameters are thus necessary to describe the new physics sector of the model, namely, gD,
Let us now discuss a specific realization of the model, assuming only one VL partner interacting exclusively with the SM top quark and no mixing between h and H, i.e., θS = 0. This choice significantly simplifies the Lagrangian: the Higgs sector of the SM is not affected by the new physics at the tree level, and the potential of ΦD has the very same structure as the Higgs potential. A mixing between h and H is induced only by fermionic loops and will be neglected in the following. Therefore, in this case, the model is described by the following five parameters: gD,
The hierarchy between the masses in the fermion sector is
In our study, we tested this realization of the model against multiple observables from cosmology, DM direct, and indirect detection (DD and ID) experiments and LHC searches. For this purpose, the Lagrangian has been implemented in LanHEP [33] and FeynRules [34], while model files have been generated in CalcHEP [35], UFO [36], as well as FeynArts [37] formats and are available on the HEPMDB [38]. This implementation has been used in micrOMEGAs v5.2.7 [39] for the evaluation of various DM observables and for extracting the respective limits. The model implementation in UFO format has been used in MG5_aMC [40] for the determination of the LHC constraints. Collider simulations have been performed at LO using the NNPDF3.0 LO set [41] through the LHAPDF6 library [42] (LHA index 262400). A simplified version of the model has been implemented to calculate cross-sections at one loop in MG5_aMC and FormCalc9.8 [43].
The amount of relic density is determined by the interplay of annihilation and co-annihilation processes, a subset of which is shown in Figure 1A. ID constraints are associated with DM annihilation rates at CMB time, excluding regions of parameter space where the injection into SM-plasma in the early universe is too large to be consistent with CMB data. Both the relic density and ID processes are tested against PLANCK data [44]. DD processes arise from diagrams such as those shown in Figure 1B and are tested against limits from XENON 1T [45].
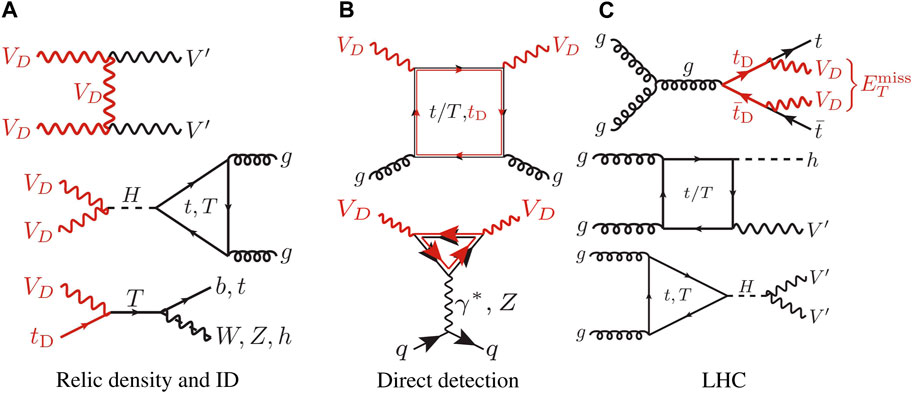
Figure 1. Representative diagrams for (A) t-channel and resonant contributions to DM annihilation and DM-mediator co-annihilation processes; (B) DD processes; (C) production processes at the LHC:
The LHC bound has been obtained via testing of tD pair production with subsequent decay into VD and top quarks against CMS searches for top squark pair production decaying into DM [46]. The relevant limit from
We also estimated the relevance of V′ pair production and associate production of V′ with the Higgs boson, occurring at LO via fermion loops. Representative topologies for the tested processes are shown in Figure 1C.
The complementarity of cosmological and collider constraints has been studied by performing a comprehensive scan over the parameter space (excluding the fixed parameter sin θS = 0) projected onto the
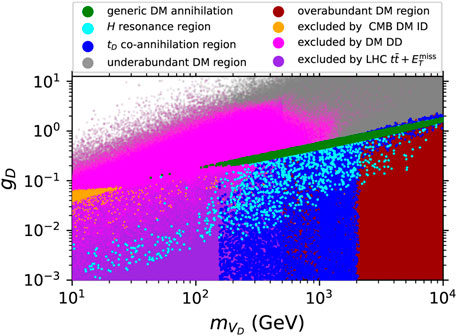
Figure 2. Excluded and allowed region of the parameter space of the model from the full five-dimensional scan (sin θS = 0) of the parameter space projected into a
The generic DM annihilation determines a lower limit on gD as a function of
To assess the relative role of the different constraints, we identify representative benchmarks characterized by different gauge couplings, gD = 0.05 and gD = 0.5, and fixed values for the masses, mT = 1,600 GeV and mH = 1,000 GeV. For these points, gauge coupling is small enough to allow a perturbative treatment in a region of parameter space, which can be tested by both collider and cosmological observables.
We show in Figure 3 the exclusion regions in the
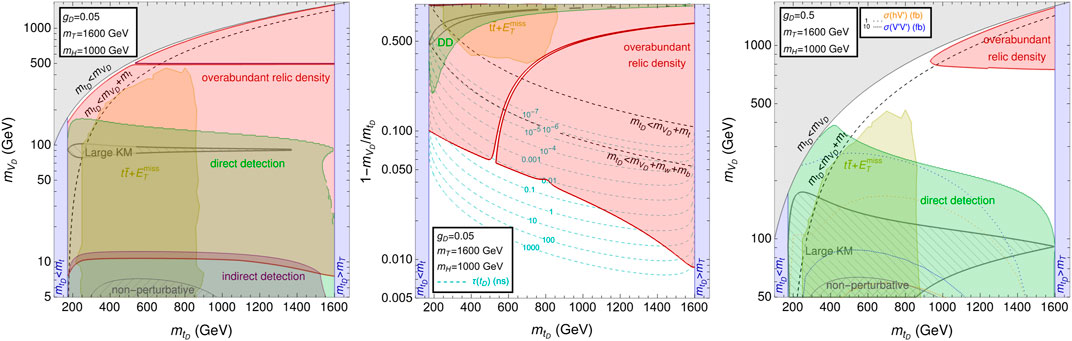
Figure 3. Combination of constraints from LHC, relic density, DD, and ID for the benchmark points in the
The predicted relic density is consistent with PLANCK results only in specific regions: for gD = 0.05 (left and central panels of Figure 3), most of the parameter space predicts an over-abundant relic density, except for an area where the mass difference between tD and DM is less than
The LHC bound is almost independent of the mass of tD until its mass difference with the DM reaches the top-quark threshold: in that region,
The FPVDM scenario introduced in this paper connects a vectorial DM candidate from a non-abelian SU(2)D gauge group to the fermionic sector of the SM without the necessity of a Higgs portal at the tree level, and the mechanism is realized in the most economical way, with a minimal set of new parameters and new particles. Even the simplest realization of FPVDM, involving interactions of the dark sector with only one SM fermion, has great potential to explain DM phenomena and has several important implications for collider and non-collider DM searches. Minimal FPVDM realizations involving other SM fermions can be used to explain outstandingly observed anomalies. For example, if the VL fermion interacts with the leptonic sector of the SM, new contributions might explain (g − 2)μ [49] and, at the same time, provide novel physics cases for future e+e− colliders [50–53]. Non-minimal realizations, including mixing in the scalar sector, further VL partners, or additional interactions of the same VL representation, would open up a vast range of possibilities for future studies, both phenomenological and experimental, and would allow one to explore the complementarity between collider and non-collider observables in multiple scenarios.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AB: writing–original draft and investigation. LP: writing–original draft and investigation. AD: writing–original draft and investigation. SM: writing–original draft and investigation. DR: writing–original draft and investigation. NT: investigation and writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. AB and SM acknowledge support from the STFC Consolidated Grant ST/L000296/1 and are partially financed through the NExT Institute. AB also acknowledges support from Soton-FAPESP and Leverhulme Trust RPG-2022-057 grants. LP’s work is supported by the Knut and Alice Wallenberg Foundation under the SHIFT project (grant KAW 2017.0100). AD is grateful to the LABEX Lyon Institute of Origins (ANR-10-LABX-0066) for its financial support within the program “Investissements d’Avenir”. AD acknowledges partial support from the National Research Foundation in South Africa. NT is supported by the scholarship from the Development and Promotion of Science and Technology Talents Project (DPST).
Acknowledgments
All authors acknowledge the use of the IRIDIS High-Performance Computing Facility and associated support services at the University of Southampton in completing this work.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Contributions to gauge kinetic mixing may arise at the loop level, depending on the structure of the Higgs sector, but they correspond to suppressed higher operator terms.
2VL portals have also been explored in [29, 30], but for scalar DM candidates, and in [26, 31] for vector dark matter, but with either the simplifying assumptions of setting the new Yukawa coupling to zero [31] or with a much larger, hence non-minimal, particle content [26].
3tD decay can only occur through the tD → VDt(*) process, as it is
References
1. (2012). A Multi-TeV Linear Collider Based on CLIC Technology: CLIC Conceptual Design Report, SLAC-R-985, SLAC National Accelerator Lab, Menlo Park, CA, United States, doi:10.5170/CERN-2012-007
2. Aaltonen T., et al. High-precision measurement of the W boson mass with the CDF II detector. Science (2022) 376:170–176. doi:10.1126/science.abk1781
3. Abada A., et al. FCC-ee: the lepton collider: future circular collider conceptual design report volume 2. Eur. Phys. J. ST (2019) 228:261–623. doi:10.1140/epjst/e2019-900045-4
4. Abe T., Fujiwara M., Hisano J., Matsushita K., A model of electroweakly interacting non-abelian vector dark matter. JHEP (2020) 07:136. doi:10.1007/JHEP07(2020)136
5. Abi B., et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. (2021) 126:141801. doi:10.1103/PhysRevLett.126.141801
6. Aghanim N., et al. Planck 2018 results. VI. cosmological parameters. Astron. Astrophys. (2020) 641:A6. doi:10.1051/0004-6361/201833910
7. Alloul A., Christensen N. D., Degrande C., Duhr C., Fuks B., FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput. Phys. Commun. (2014) 185:2250–2300. doi:10.1016/j.cpc.2014.04.012
8. Alwall J., Frederix R., Frixione S., Hirschi V., Maltoni F., Mattelaer O., et al. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP (2014) 07:079. doi:10.1007/JHEP07(2014)079
9. An F., et al. Precision higgs physics at the CEPC. Chin. Phys. C (2019) 43:043002. doi:10.1088/1674-1137/43/4/043002
10. Aprile E., et al. Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. (2018) 121:111302. doi:10.1103/PhysRevLett.121.111302
11. Arcadi G., Djouadi A., Kado M., The Higgs-portal for vector dark matter and the effective field theory approach: A reappraisal. Phys. Lett. B (2020) 805:135427. doi:10.1016/j.physletb.2020.135427
12. ATLAS Collaboration. Search for pair-production of vector-like quarks in pp collision events at $\sqrt{s}=13$˜TeV with at least one leptonically-decaying Z˜boson and a third-generation quark with the ATLAS detector (2021). https://arxiv.org/abs/2210.15413.
13. Babu K. S., Jana S., Thapa A., Vector boson dark matter from trinification. JHEP (2022) 02:051. doi:10.1007/JHEP02(2022)051
14. Baek S., Ko P., Park W.-I., Senaha E., Higgs portal vector dark matter : revisited. JHEP (2013) 05:036. doi:10.1007/JHEP05(2013)036
15. Baek S., Ko P., Wu P., Heavy quark-philic scalar dark matter with a vector-like fermion portal. JCAP (2018) 07:008. doi:10.1088/1475-7516/2018/07/008
16. Baer H., et al. The international linear collider technical design report - volume 2: physics (2013). https://arxiv.org/abs/1306.6352.
17. Ball R. D., et al. Parton distributions for the LHC Run II. JHEP 04 (2015) 040. doi:10.1007/JHEP04(2015)040
18. Baouche N., Ahriche A., Faisel G., Nasri S., Phenomenology of the hidden SU(2) vector dark matter model. Phys. Rev. D (2021) 104:075022. doi:10.1103/PhysRevD.104.075022
19. Barman B., Bhattacharya S., Patra S. K., Chakrabortty J., Non-abelian vector boson dark matter, its unified route and signatures at the LHC. JCAP (2017) 12:021. doi:10.1088/1475-7516/2017/12/021
20. Barman B., Bhattacharya S., Zakeri M., Multipartite dark matter in SU(2)N extension of Standard Model and signatures at the LHC. JCAP (2018) 09:023. doi:10.1088/1475-7516/2018/09/023
21. Barman B., Bhattacharya S., Zakeri M., Non-abelian vector boson as fimp dark matter. JCAP (2020) 02:029. doi:10.1088/1475-7516/2020/02/029
22. Belanger G., Mjallal A., Pukhov A., Recasting direct detection limits within micrOMEGAs and implication for non-standard Dark Matter scenarios. Eur. Phys. J. C (2021) 81:239. doi:10.1140/epjc/s10052-021-09012-z
23. Belyaev A., Christensen N. D., Pukhov A., CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput. Phys. Commun. (2013) 184:1729–1769. doi:10.1016/j.cpc.2013.01.014
24. Belyaev A., Deandrea A., Moretti S., Panizzi L., Thongyoi N., A fermionic portal to vector dark matter from a new gauge sector. Phys. Rev. D (2022) 108.
25. Bhattacharya S., Diaz-Cruz J., Ma E., Wegman D., Dark vector-gauge-boson model. Phys. Rev. D (2012) 85:055008. doi:10.1103/PhysRevD.85.055008
26. Bondarenko M., Belyaev A., Blandford J., Basso L., Boos E., Bunichev V., et al. High Energy Physics Model Database: Towards decoding of the underlying theory (within Les Houches 2011: Physics at TeV Colliders New Physics Working Group Report) (2012). https://hepmdb.soton.ac.uk/index.php?mod=user&act=reference.
27. Buckley A., Ferrando J., Lloyd S., Nordström K., Page B., Rüfenacht M., et al. LHAPDF6: parton density access in the LHC precision era. Eur. Phys. J. C (2015) 75:132. doi:10.1140/epjc/s10052-015-3318-8
28. Buttazzo D., Di Luzio L., Ghorbani P., Gross C., Landini G., Strumia A., et al. Scalar gauge dynamics and Dark Matter. JHEP (2020) 01:130. doi:10.1007/JHEP01(2020)130
29. Chen F., Cline J. M., Frey A. R., Nonabelian dark matter: Models and constraints. Phys. Rev. D (2009) 80:083516. doi:10.1103/PhysRevD.80.083516
30. Chowdhury T. A., Saad S., Non-Abelian vector dark matter and lepton g-2. JCAP (2021) 10:014. doi:10.1088/1475-7516/2021/10/014
31. CMS. Search for pair production of vector-like quarks in leptonic final states in proton-proton collisions at $\sqrt{s}$ = 13 TeV (2022). https://arxiv.org/abs/2209.07327.
32. Colucci S., Fuks B., Giacchino F., Lopez Honorez L., Tytgat M. H. G., Vandecasteele J., Top-philic Vector-Like Portal to Scalar Dark Matter. Phys. Rev. D (2018) 98:035002. doi:10.1103/PhysRevD.98.035002
33. Degrande C., Duhr C., Fuks B., Grellscheid D., Mattelaer O., Reiter T., UFO - the universal feynrules output. Comput. Phys. Commun. (2012) 183:1201–1214. doi:10.1016/j.cpc.2012.01.022
34. Diaz-Cruz J., Ma E., Neutral SU(2) Gauge Extension of the Standard Model and a Vector-Boson Dark-Matter Candidate. Phys. Lett. B (2011) 695:264–267. doi:10.1016/j.physletb.2010.11.039
35. DiFranzo A., Fox P. J., Tait T. M. P., Vector dark matter through a radiative higgs portal. JHEP (2016) 04:135. doi:10.1007/JHEP04(2016)135
36. Farzan Y., Akbarieh A. R., VDM: a model for vector dark matter. JCAP (2012) 10:026. doi:10.1088/1475-7516/2012/10/026
37. Fraser S., Ma E., Zakeri M., SU(2)N model of vector dark matter with a leptonic connection. Int. J. Mod. Phys. A (2015) 30:1550018. doi:10.1142/S0217751X15500189
38. Gross C., Karamitsos S., Landini G., Strumia A., Gravitational vector dark matter. JHEP (2021) 03:174. doi:10.1007/JHEP03(2021)174
39. Gross C., Lebedev O., Mambrini Y., Non-abelian gauge fields as dark matter. JHEP (2015) 08:158. doi:10.1007/JHEP08(2015)158
40. Hahn T., Generating feynman diagrams and amplitudes with FeynArts 3. Comput. Phys. Commun. (2001) 140:418–431. doi:10.1016/S0010-4655(01)00290-9
41. Hahn T., Paßehr S., Schappacher C., FormCalc 9 and extensions. PoS LL2016 (2016) 068. doi:10.1088/1742-6596/762/1/012065
43. Hisano J., Ibarra A., Nagai R., Direct detection of vector dark matter through electromagnetic multipoles. JCAP (2020) 10:015. doi:10.1088/1475-7516/2020/10/015
44. Hu Z., Cai C., Tang Y.-L., Yu Z.-H., Zhang H.-H., Vector dark matter from split SU(2) gauge bosons. JHEP (2021) 07:089. doi:10.1007/JHEP07(2021)089
45. Huang W.-C., Ishida H., Lu C.-T., Tsai Y.-L. S., Yuan T.-C., Signals of new gauge bosons in gauged two higgs doublet model. Eur. Phys. J. C (2018) 78:613. doi:10.1140/epjc/s10052-018-6067-7
46. Huang W.-C., Tsai Y.-L. S., Yuan T.-C., G2HDM : gauged two higgs doublet model. JHEP (2016) 04:019. doi:10.1007/JHEP04(2016)019
47. Hubisz J., Meade P., Phenomenology of the littlest Higgs with T-parity. Phys. Rev. D (2005) 71:035016. doi:10.1103/PhysRevD.71.035016
48. Ko P., Park W.-I., Tang Y., Higgs portal vector dark matter for GeV scale γ-ray excess from galactic center. JCAP (2014) 09:013. doi:10.1088/1475-7516/2014/09/013
49. Ko P., Tang Y., Residual non-abelian dark matter and dark radiation. Phys. Lett. B (2017) 768:12–17. doi:10.1016/j.physletb.2017.02.033
50. Koorambas E., Vector gauge boson dark matter for the SU(N) gauge group model. Int. J. Theor. Phys. (2013) 52:4374–4388. doi:10.1007/s10773-013-1756-3
51. Lebedev O., Lee H. M., Mambrini Y., Vector higgs-portal dark matter and the invisible Higgs. Phys. Lett. B (2012) 707:570–576. doi:10.1016/j.physletb.2012.01.029
52. Semenov A., Lanhep—a package for the automatic generation of feynman rules in field theory. version 3.0. Computer Physics Communications (2009) 180:431–454. doi:10.1016/j.cpc.2008.10.012
Keywords: dark matter, large Hadron collider, vector-like fermions, dark gauge group, relic density, direct dark matter detection
Citation: Belyaev A, Deandrea A, Moretti S, Panizzi L, Ross DA and Thongyoi N (2024) A fermionic portal to a non-abelian dark sector. Front. Phys. 12:1339886. doi: 10.3389/fphy.2024.1339886
Received: 17 November 2023; Accepted: 25 March 2024;
Published: 13 May 2024.
Edited by:
Roman Pasechnik, Lund University, SwedenReviewed by:
Urjit Yajnik, Indian Institute of Technology Bombay, IndiaGiorgio Arcadi, University of Messina, Italy
Copyright © 2024 Belyaev, Deandrea, Moretti, Panizzi, Ross and Thongyoi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefano Moretti, cy5tb3JldHRpQHNvdG9uLmFjLnVr
 Alexander Belyaev
Alexander Belyaev Aldo Deandrea3,4
Aldo Deandrea3,4 Stefano Moretti
Stefano Moretti Luca Panizzi
Luca Panizzi Nakorn Thongyoi
Nakorn Thongyoi