Interplanetary shock induced intensification of electron cyclotron harmonic waves in the Earth’s inner magnetosphere

Electron cyclotron harmonic (ECH) waves are electrostatic emissions frequently observed in the Earth’s magnetosphere. By precipitating magnetospheric hot electrons into the ionosphere, ECH waves play a critical role in the formation of diffuse aurora. Previous research has extensively investigated the strong dependence of ECH waves on the geomagnetic activities. In this study, we present the first report of the prompt response of ECH waves to an interplanetary shock on the basis of WIND and Van Allen Probes observations. Our observations and analyses demonstrate that the interplanetary shock compression can increase $>$0.1 keV hot electron fluxes in the dayside inner magnetosphere, consequently leading to the prompt intensification of ECH waves by promoting the wave instability. These findings expand our comprehension of the impacts of solar wind disturbances on magnetospheric plasma waves and offer fresh insights into solar wind-magnetosphere-ionosphere coupling.

1 Introduction

Electron cyclotron harmonic (ECH) waves are electrostatic emissions [1] that typically appear in thermal plasmas in the Earth’s magnetosphere [2–6]. They are usually observed as harmonic wave bands at frequencies between multiples of electron gyrofrequency (f_ce) [7–9]. Through cyclotron resonance, ECH waves are able to efficiently precipitate keV electrons from the magnetosphere to the ionosphere, contributing to the formation of diffuse aurora [10–16]. Therefore, a comprehensive understanding of the spatiotemporal distribution of ECH waves is required to forecast space weather [17–22].

The generation of ECH waves is proposed to be associated with Bernstein-mode instability driven by hot electron loss cone distributions [23,24]. These emissions with quasi-perpendicular wave vectors are confined near their source regions [24]. While extensive event and statistical studies have focused on the strong dependence of ECH waves on geomagnetic activities [3,25–27], none have directly established a link between ECH waves and solar wind disturbances. Interplanetary shocks, a subset of solar wind discontinuities frequently observed during active days [28–31], are highly geoeffective [32–35]. Numerous works have reported the immediate impacts of interplanetary shocks on magnetospheric plasma waves, including ultra low frequency waves, whistler-mode waves, magnetosonic waves, and EMIC waves [36–44]. Thus, the questions that naturally arise are whether and how an interplanetary shock can abruptly influence magnetospheric ECH waves.

In this study, using observations from the WIND [45] and Van Allen Probes missions [46], we present a representative ECH wave event during an interplanetary shock. The observations and analyses show that a shock compression can increase $>$0.1 keV hot electron fluxes in the Earth’s dayside inner magnetosphere, thus leading to the prompt intensification of ECH waves by promoting the wave instability.

2 Observation

Here we utilize the combined observations of WIND and Van Allen Probes to monitor the prompt response of ECH wave to an interplanetary shock. The Wind satellite operated in a halo orbit near the L1 Lagrange point. The Solar Wind Experiment (SWE) [47], the Magnetic Fields Investigation (MFI) [48], and the Three-Dimensional Plasma and Energetic Particle Investigation (3DP) [49] onboard WIND measured the solar wind parameters. The Van Allen Probes mission, comprising two identical probes (termed as RBSP-A and RBSP-B), orbited near the equator with perigees of approximately 0.1 R_E and apogees of approximately 6 R_E [46]. In this work, we mainly used the High Frequency Receiver (HFR) of the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) instrument [50] to observe ECH waves. The HFR provided electric spectral intensities in the frequency range of 10–400 kHz in survey mode. Note the Waveform Frequency Receiver (WFR) of EMFISIS can provide electric spectral intensities at frequencies ranging from 10 Hz to 12 kHz. However, the WFR electric spectral data had been contaminated seriously above 5 kHz during the event in this work, and did not allow the clear observation of ECH waves. Following the method in Kurth et al. [51], we can derive the background plasma density N_e from the upper hybrid resonance frequency. The fluxgate magnetometer (MAG) of EMFISIS and the Electric Field and Waves (EFW) [52] instrument captured the background electromagnetic field. The Helium Oxygen Proton Electron (HOPE) Mass Spectrometer [53] of the Energetic particle, Composition and the Thermal (ECT) plasma suite [54] provided the electron flux data from several eV to $\sim 50$ keV. The geomagnetic indices were obtained from the OMNI database.

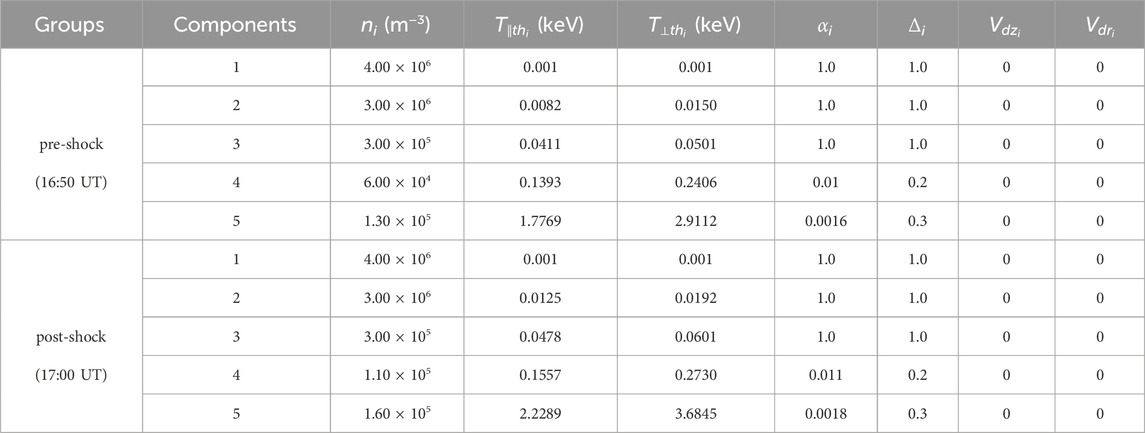
Figures 1A–G plot the solar wind parameters observed by WIND from 07 June 2014 to 11 June 2014. At 16:12 UT on 07 June 2014, a fast forward interplanetary shock was monitored, marked by abrupt increases in magnetic field strength, velocity, density, temperature, and dynamic pressure. According to the list by Chi et al. [55], there was an interplanetary coronal mass ejection (ICME) between approximately 19:00 UT on 08 June 2014 and 10:00 UT on 10 June 2014. This ICME exhibited typical features, including a declining velocity profile, low proton temperature, and bidirectional streaming of suprathermal electrons [56,57]. In a statistical sense, ICMEs ^c1might be the major driver of shocks ^c2during solar maximum, but shocks exist during solar minimum even if few ICMEs are present [58]. The large time lapse between the shock and the ICME front makes it uncertain to determine their relations. Whether this shock was driven by the ICME or a fast solar wind stream requires detailed studies in future and beyond the scope of this work. Approximately 41 min after its arrival in WIND data, the interplanetary shock with a drastic increase in solar wind dynamic pressure from 1 nPa to 6 nPa, compressed the Earth’s magnetosphere. This compression caused an increase of SYM-H index from −5 nT to 23 nT. Figure 1H shows the response of inner magnetospheric ECH waves to the interplanetary shock as observed by RBSP-A on 07 June 2014. Around the shock arrival, RBSP-A operated in the northern hemisphere (MLAT$\sim 15°$) of dayside magnetosphere (L$\sim 6$, MLT$\sim 9$ hr) under relatively quiet conditions (SYM-H$>$-10 nT and AE$<$350 nT). Before the shock arrival, RBSP-A received faint and intermittent ECH wave signals (P_E < 1 × 10⁻¹⁰ mV²m⁻²Hz⁻¹) appearing as harmonic bands below the upper hybrid resonance frequency f_UHR. Note the WFR observations were too noisy to identify ECH waves below 10 kHz. As marked by the vertical dashed lines (16:53 UT), the shock compression caused a sudden and significant intensification of ECH wave power, increasing by approximately one order of magnitude to P_E ∼ 1 × 10⁻⁹ mV²m⁻²Hz⁻¹. Compared with the ECH waves typically confined in the near equatorial region, this ECH wave event was observed at relatively higher latitudes (MLAT$\sim 15°$) with a weak intensity. This is consistent with the statistical characteristics of ECH waves showed in previous studies [25,59,60]. It should also be mentioned that this ECH wave intensification was not a manifestation of the spatial variation of waves but a temporal behavior. During the inbound pass before the shock arrival, RBSP-A only observed weak or no ECH waves in larger L-shells with comparable MLT (as shown in Figure 1H). The inward movement of these weak ECH waves triggered by shock compression could not explain the wave intensification. Thus, the ECH wave intensification should be related to variations in plasma environment triggered by the shock compression, which will be further investigated in the following section.

FIGURE 1

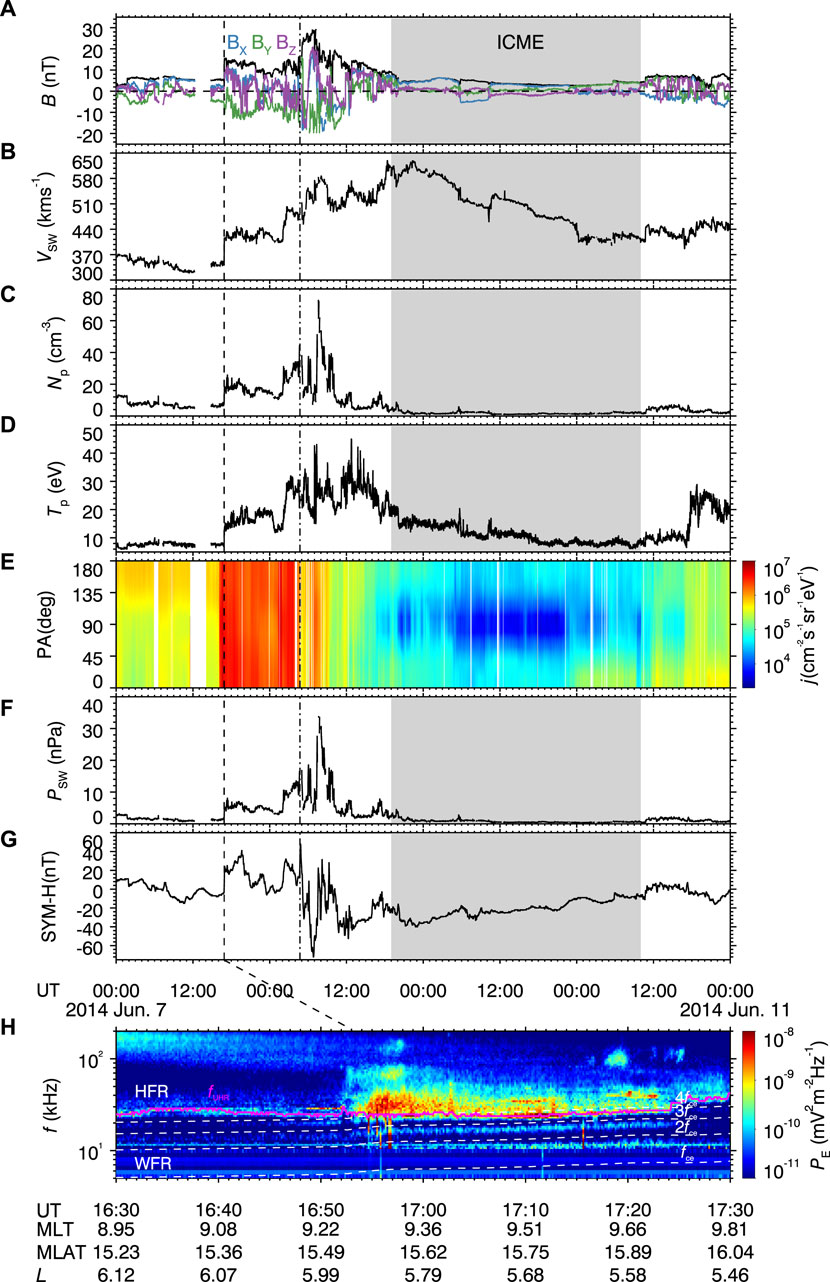
FIGURE 1. Overview of the ECH wave event on 07 June 2014: (A) Magnetic field magnitude B_t and components (B_X, B_Y, B_Z) in the geocentric solar magnetospheric (GSM) coordinate. (B) Bulk velocity V_sw. (C) Proton density N_p. (D) Proton temperature T_p. (E) suprathermal electron flux j. (F) Solar wind dynamic pressure P_sw. (G) Geomagnetic SYM-H index. (H) Zoom-in figure of Wave electric power spectra P_E with overplotted electron gyrofrequency (f_ce) harmonics and upper hybrid resonance frequency (f_UHR). The solar wind measurements by Wind satellite at $\sim 1.26\times 10^6$ km from Earth have been shifted 41 min according to the SYM-H measurements. The shadowed areas mark an ICME. The vertical dashed lines in each panel mark the arrival of interplanetary shock.

3 Physical explanations

Figure 2 presents the temporal evolutions of background electromagnetic fields and plasmas measured by RBSP-A during the event. Corresponding to the shock compression at 16:53 UT (marked by the vertical dashed line in Figure 2), the background magnetic field intensity increased from 200 nT to 223 nT. In contrast, the background plasma density N_e in the low-density plasma trough remained consistently below 10 cm⁻³ (which is dominant by the cold plasma) with no systematic variations after the shock. The interplanetary shock also induced ultralow-frequency waves with impulsive electric field amplitudes of 5 mV/m, subsequently resulting in a significant acceleration of hot electron fluxes above 0.1 keV. It is noteworthy that the similar responses of magnetospheric electron fluxes ranging from low energy to relativistic energy to interplanetary shocks have been reported by numerous studies [37,61–65]. However, the modulation of hot electron fluxes by the ULF wave can not be clearly observed in Figures 2D–F. Possible explanations for this could be the following: 1) rapid relaxation by magnetospheric plasma waves (ECH waves and chorus); 2) the comparable cadence (∼21 s) of HOPE instrument to ULF wave period (∼1–2 min). As reported by previous theoretical studies [23,24], the enhancement of hot electron fluxes could promote the wave instability by providing more free energy, and then lead to the wave intensification.

FIGURE 2

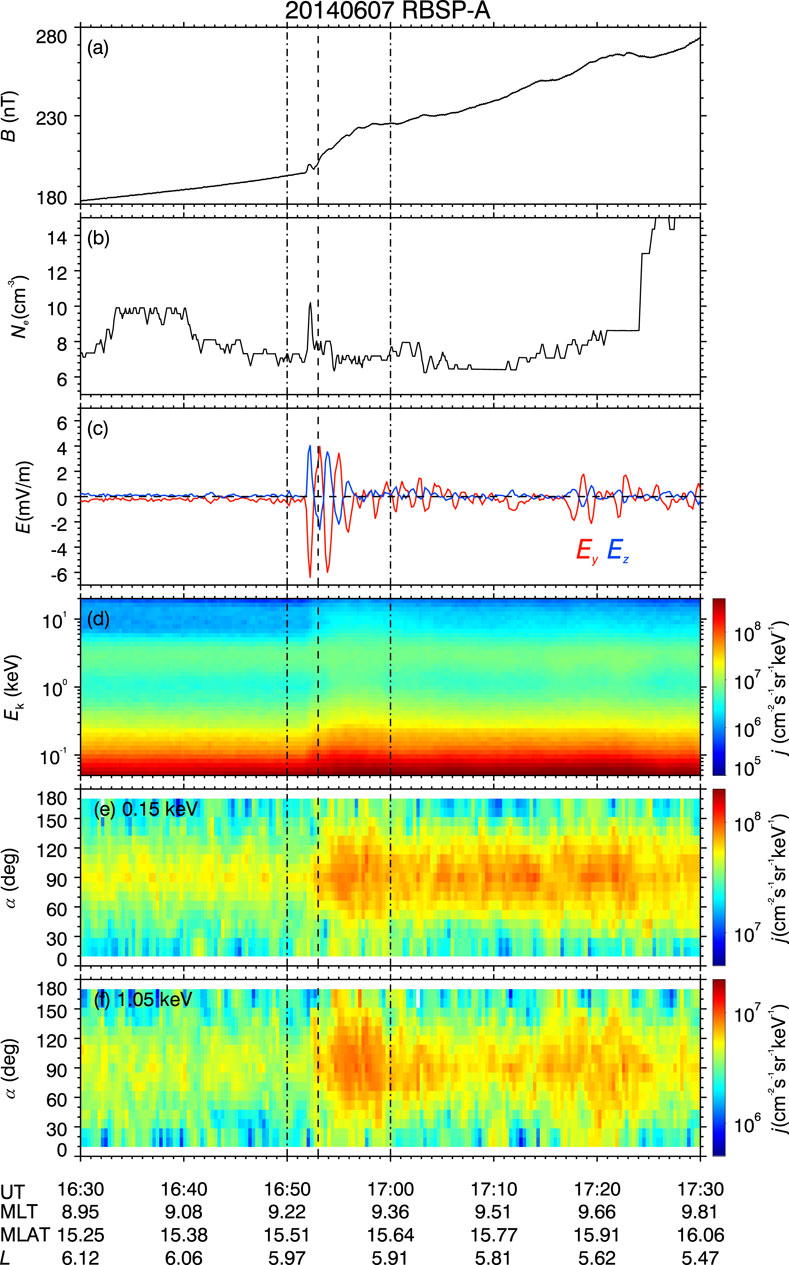
FIGURE 2. Temporal evolution of background fields and plasmas of 07 June 2014 event: (A) background magnetic field strength B. (B) Background plasma density N_e. (C) Electric field components in the modified geocentric solar ecliptic (mGSE) coordinate system. (D) electron spin-averaged differential flux j. (E,F) differential electron fluxes j at specific energies. The vertical dashed line mark the arrival of interplanetary shock, and the vertical dash-dotted lines mark the pre-shock and post-shock moments for the growth rate calculation.

To further determine the influence of shock compression on the generation of ECH waves, we use the BO code [66] to calculate the linear dispersion relations and wave growth rates. The inputs of the code include the background magnetic field intensity and electron phase space density F. The observed electron PSD is fitted by a total of N bi-Maxwellian components.

$F\left(v_{\perp },v_{\Vert }\right)={\displaystyle \sum _{i=1}^N}{F}_i,(1)$

$\begin{array}{ccc}\hfill & \hfill & F_i=\frac{n_i}{{\pi }^{3/2}{V}_{\Vert t{h}_i}{V}_{\perp t{h}_i}^2}\exp \left[-\frac{{\left(v_{\Vert }-V_{d{z}_i}\right)}^2}{V_{\Vert t{h}_i}^2}\right]\hfill \\ \hfill & \hfill & \times \left\{\frac{r_{a_i}}{A_{a_i}}\exp \left[-\frac{{\left(v_{\perp }-V_{d{r}_i}\right)}^2}{V_{\perp t{h}_i}^2}\right]+\frac{r_{b_i}}{{\alpha }_i{A}_{b_i}}\exp \left[-\frac{{\left(v_{\perp }-V_{d{r}_i}\right)}^2}{{\alpha }_i{V}_{\perp t{h}_i}^2}\right]\right\},\hfill \end{array}(2)$

where $r_{a_i}=\frac{1-{\alpha }_i{\mathrm{\Delta }}_i}{1-{\alpha }_i},r_{b_i}=\frac{-{\alpha }_i+{\alpha }_i{\mathrm{\Delta }}_i}{1-{\alpha }_i}$. For the ith plasma component, n_i is the density; $V_{\Vert t{h}_i}$, $V_{\perp t{h}_i}$, $V_{d{z}_i}$, and $V_{d{r}_i}$ are the parallel thermal velocity, perpendicular thermal velocity, parallel drift velocity, and perpendicular ring beam velocity; expressions $A_{a_i}=A_{b_i}=1$ when $V_{d{r}_i}=0$; α_i and Δ_i characterize the size and the depth of the loss cone. According to previous numerical studies [24,67,68], we set the background cold electrons as the 1 eV component for calculation. Note the sum of each component density n_i is equal to the background plasma density N_e.

As the ECH wave powers (Figure 1H) and background plasma conditions (Figure 2) exhibited systematic variations following the interplanetary shock, we selected two specific times for analyses (marked by the vertical dash-dotted lines in Figure 2): 1) pre-shock moment at 16:50 UT; 2) post-shock moment at 17:00 UT. The satellite data provide direct measurements of background magnetic field intensity and plasma density for the growth rate calculation. However, because of the instrumentation constraints and data quality, electron flux data from HOPE are unavailable in small pitch angles $(<18°)$ during this event. Theoretically, the local loss cone angle α_loss of bounced electrons can be determined by the following expression [69]:

$\sin {{\alpha }_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}^2=\frac{B_0}{B_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}(3)$

where B₀ and B_loss are the magnetic field intensities at the satellite position and low altitude mirror point where electrons get lost. Here we assume the mirror point locates at 100 km height. Because of the absence of measurements for B_loss, we rely on geomagnetic models to derive the ratio $\frac{B_0}{B_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}$. Figure 3 shows comparisons between different Tsyganenko geomagnetic models [70–72] around the interplanetary shock. Since the satellite was located in the inner magnetosphere, the field line configurations of the Tsyganenko models closely resemble those of the dipole field. Different with the situation in larger L-shells, there was no off-equatorial magnetic field minimum on the field lines of this event, which has been suggested to explain the latitudinal extension of ECH waves. However, even in the inner magnetosphere (5 < L < 6.6) usually with the absence of off-equatorial magnetic field minimums, ECH waves can extend to MLAT$>15°$ with decreasing amplitudes according to MMS observations (as shown in Figure 3 of Lou et al. [59]). Further understanding of the high-latitude ECH waves requires detailed investigations in the future. Comparing with the T96 and T01 models, the magnetic field strengths derived from TS04 model align more closely with the observation values after the shock compression. Therefore, we use TS04 geomagnetic model [72] to estimate the loss cone size. Based on Eq. 3, the modeled loss cone angles α_loss are 3.49° and 3.68° at the pre-shock and post-shock moments. These approximations suggest that the interplanetary shock may not trigger significant changes in the electron loss cone through adiabatic processes during this event. Taking into account the estimated loss cone sizes, Figure 4 plots the modeled and observed electron phase space densities at the pre-shock and post-shock moments. To reduce the intense fluctuations of electron flux data (as shown in Figures 2E, F), we smoothed the data over 8 adjacent time points (∼168 s) and symmetrized the data with respect to the 90° pitch angle. The detailed fitting parameters of bi-Maxwellian components are given in Table 1. Generally speaking, the modeled electron phase space densities are in reasonable agreement with the observations.

FIGURE 3

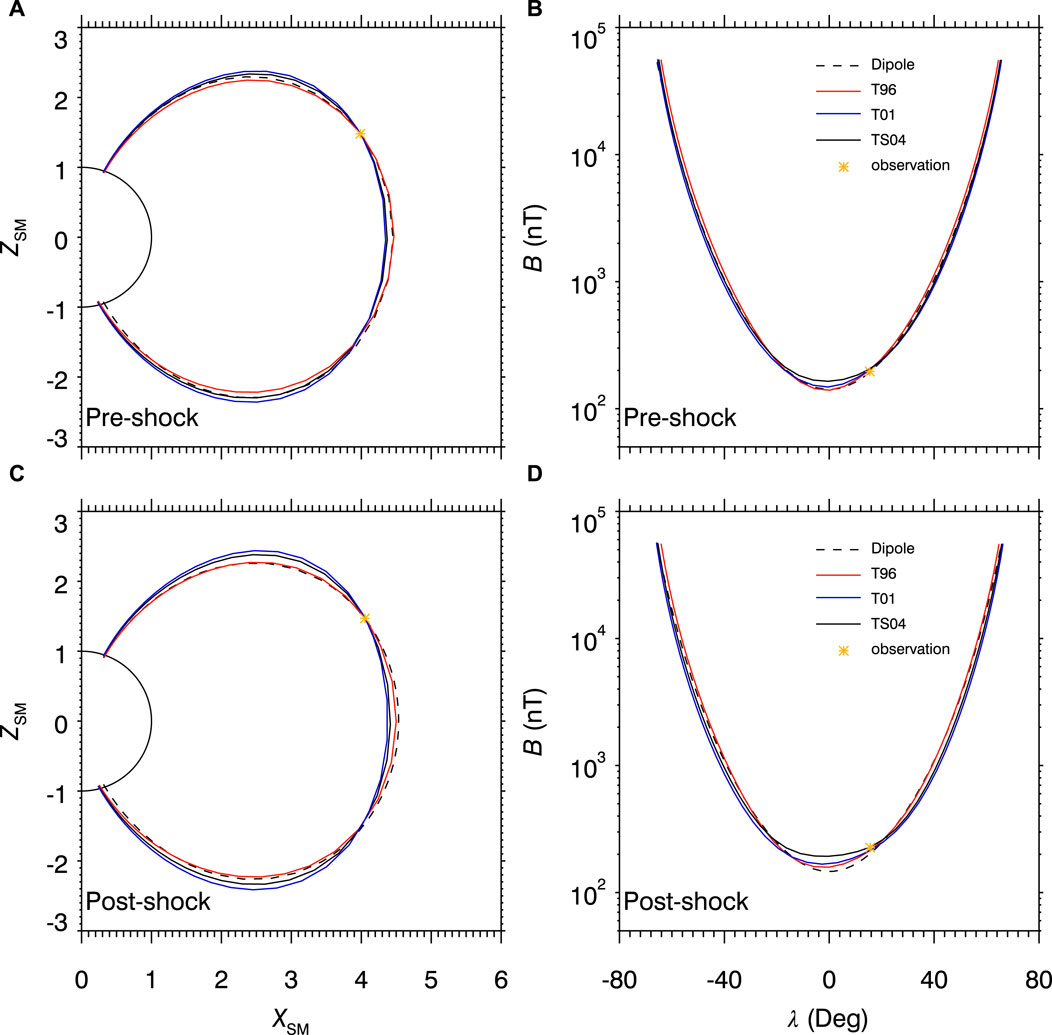
FIGURE 3. Comparison between different geomagnetic models at the pre-shock and post-shock moments on 07 June 2014: (A,C) Modeled magnetic field configurations in the SM X-Z plane along the field lines traced from the RBSP-A location and (B,D) corresponding field intensities as a function of magnetic latitude for dipole (black dashed lines), T96 (red solid lines), T01 (blue solid lines), and TS04 (black solid lines) geomagnetic models. The orange asterisks represent the locations of RBSP-A and observed magnetic field intensities at specific moments.

FIGURE 4

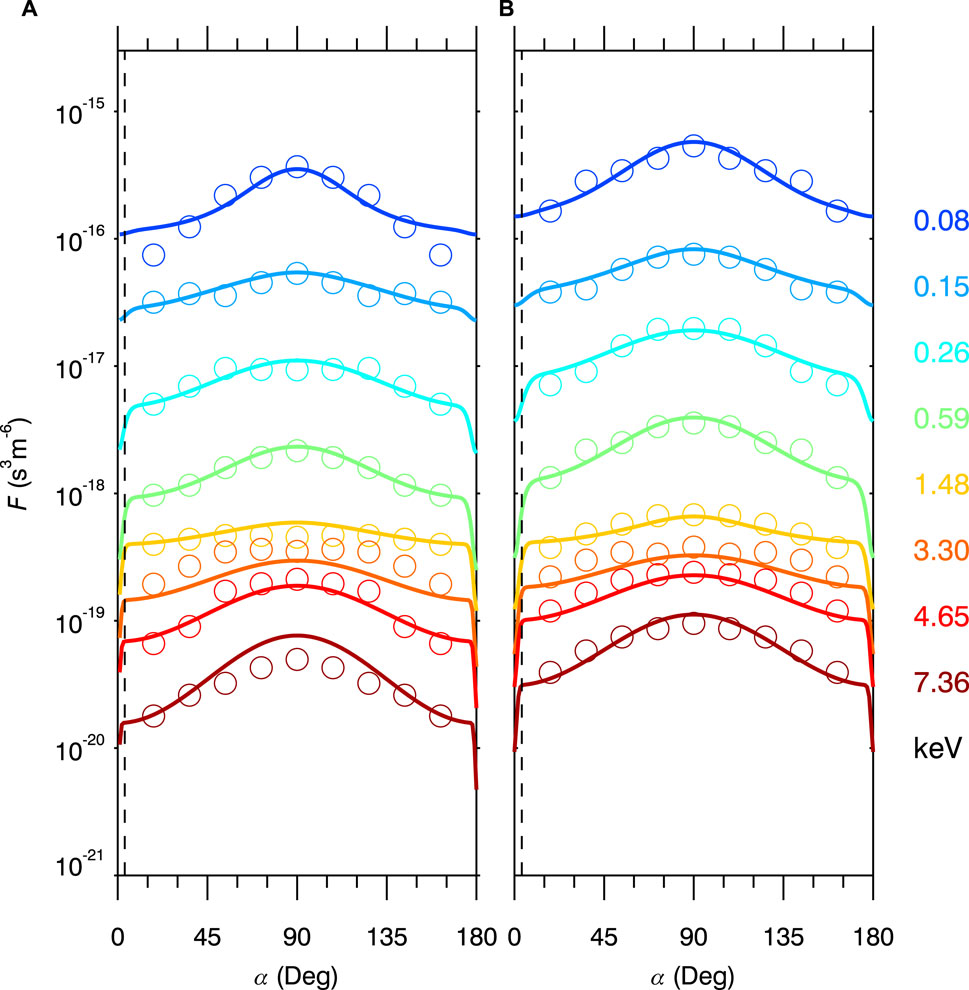
FIGURE 4. Electron phase space densities in pitch angle-energy space at pre-shock (A) and post-shock (B) moments on 07 June 2014. The solid lines and circles represent modeled and observed electron phase space densities, and the black vertical dashed lines represent the modeled loss cone angles.

TABLE 1

TABLE 1. The fitting parameters of electron phase space densities for the 07 June 2014 event.

Figures 5A, D illustrate the ECH wave linear growth rates calculated by the BO code within 87° < θ < 90° at the pre-shock and post-shock moments. Based on the observations (Figure 1H), we focus on the first three harmonic bands below the upper hybrid resonance frequency. It is evident that the modeled growth rates roughly share the similar frequency distributions with the observed ECH wave intensities, indicating the electron phase space density fittings reasonably reflect the real conditions. In comparison to the pre-shock moment, the modeled growth rates at the post-shock moment increase by approximately threefold, qualitatively explaining the intensification of ECH waves after the interplanetary shock. Figures 5B, E show the wave frequency ω/Ω_e as a function of normalized wave vector kρ_e at θ = 89° (ω is the wave angular frequency, Ω_e is the electron angular gyrofrequency, and ρ_e is the gyroradius). These dispersion relations enable the calculation of the wave minimum resonant energy E_min, which can be determined as follows.

$E_{\text{min}}=\frac{1}{2}{m}_{\text{e}}{v}_{\Vert }^2,(4)$

$v_{\Vert }=\frac{\omega -n{\mathrm{\Omega }}_{\text{e}}}{k_{\Vert }},(5)$

here v‖ is the electron parallel velocity, k‖ = k cos θ is the wave parallel vector, n is the resonance order, and m_e is the electron rest mass. Based on Figures 5B, C, E, F show the minimum resonant energy E_min of different harmonic bands (each with a specific resonance order) as a function of wave frequency ω/Ω_e at θ = 89°. Combined with the wave growth rates shown in Figures 5A, D, the corresponding E_min for the frequencies with positive growth rates predominantly falls within the range of 0.1 keV–1 keV. These calculations indicate the ECH wave intensification is highly associated with the shock-induced enhancement of $>$0.1 keV hot electrons, which enlarges the free energy for ECH wave excitation.

FIGURE 5

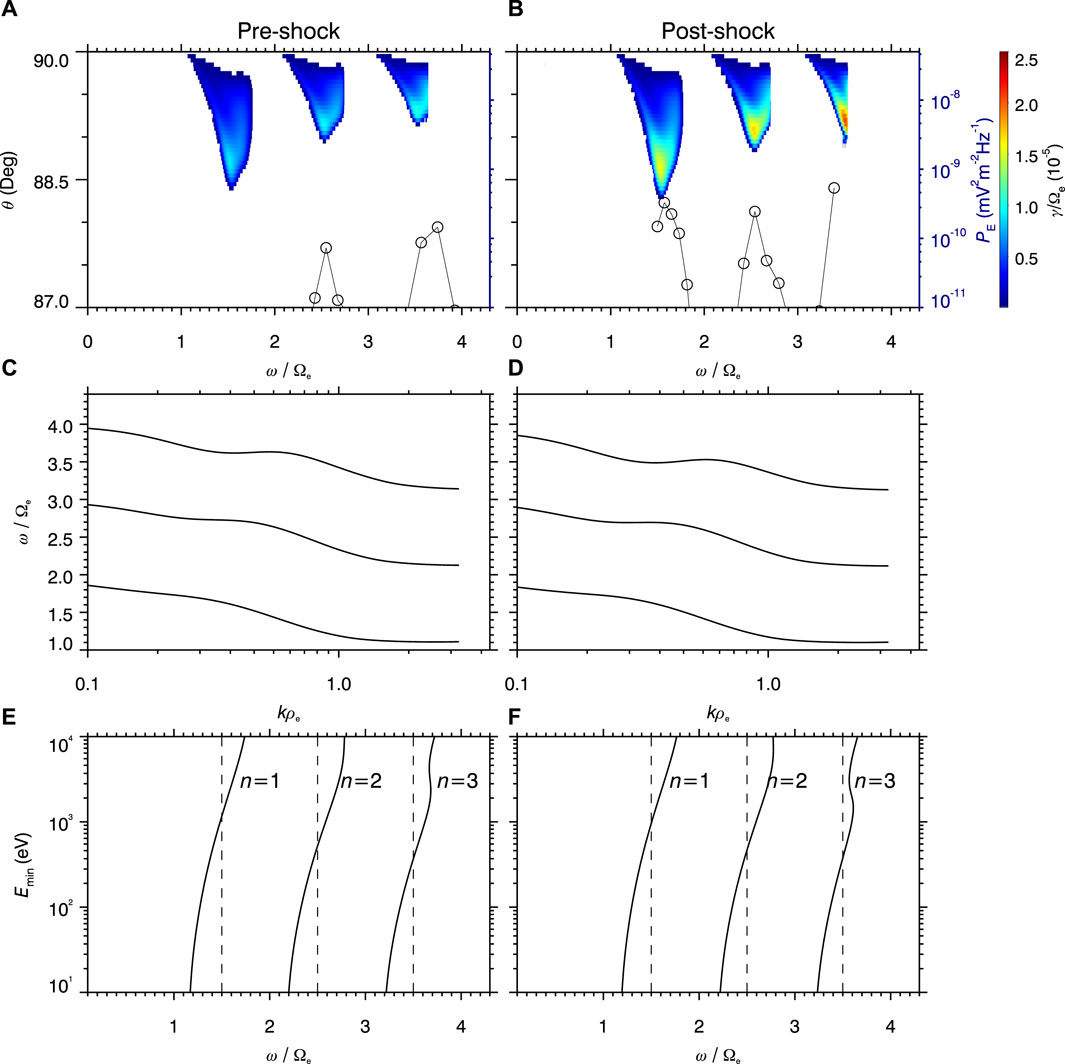
FIGURE 5. ECH wave growth rates, dispersion relations, and minimum resonant energy of first three harmonic bands at pre-shock and post-shock moments. (A,D) linear wave growth rates γ/Ω_e as a function of frequency ω/Ω_e and wave normal angle θ with overplotted electric power intensity P_E of ECH waves from HFR data; (B,E) wave frequency ω/Ω_e as a function of normalized wave vector kρ_e (ρ_e is the gyroradius) at θ = 89°; (C,F) minimum resonant energy E_min of different harmonic bands (with specific resonance order) as a function of wave frequency ω/Ω_e at θ = 89°.

4 Discussion and conclusion

In contrast to previous studies focusing on the dependence of ECH waves on geomagnetic activities [3,25,26,59], here we present the first report of the prompt response of ECH waves to an interplanetary shock based on the WIND and Van Allen Probes observations. A fast forward interplanetary shock with a drastic increase in solar wind dynamic pressure (from 1 nPa to 6 nPa) compressed the Earth’s magnetosphere, causing the prompt intensification of dayside inner magnetospheric ECH waves. The observations and analyses suggest that the shock-induced enhancement of $>$0.1 keV hot electron enlarges the free energy for the ECH wave excitation, consequently leading to the intensification of ECH waves by promoting the wave instability. Another intriguing phenomenon is the impact of a solar wind disturbance on ECH waves on 08 June 2014. As marked by the vertical dash-dotted line in Figures 1A–G, there were increases in solar wind magnetic field and dynamic pressure at ∼04:44 UT on 08 June 2014. Different with the event on 07 June 2014, this structure was not an interplanetary shock. Figure 6 shows ECH wave observations measured by the twin Van Allen Probes satellites on 08 June 2014. Corresponding to the arrival of the solar wind disturbance (marked by the vertical dash-dotted line in Figure 6), RBSP-A near the perigee was unable to receive ECH wave signals, while RBSP-B in the dayside magnetosphere (L ∼ 5.8) observed the prompt intensification of ECH waves. In addition to the prompt impacts, the solar wind compressions in magnetosheath on 07 and 08 June 2014 could increase the dayside reconnection rate and lead to the strong convection in the magnetosphere [73]. Probably because of the associated hot electron injections and plasmasphere erosions, both satellites observed the enhanced occurrences of ECH waves on 08 June 2014. A comprehensive understanding of the dependence of ECH waves on solar winds requires further investigation in the future.

FIGURE 6

FIGURE 6. Wave electric power spectra P_E observed by (A) RBSP-A and (B) RBSP-B on 08 June 2014. The vertical dash-dotted line in (A,B) marks the same moment as the dash-dotted line in Figures 1A–G.

In this work, we employ the BO code to compute the linear wave dispersion relation and growth rate of ECH waves. The calculations are based on the hot electron flux data measured by HOPE. However, as shown in Figure 4, the electron flux data exhibit irregular fluctuations over pitch angles and are notably absent within the loss cone, and the bi-Maxwellian fittings of electron fluxes are unable to capture all the subtle changes. Because of these data and technical limitations, the BO modeling here only provides a qualitative understanding of the observed wave evolutions following the interplanetary shock. In the future, detailed numerical studies are required to evaluate the results obtained in this work.

The prompt responses of magnetospheric waves to solar wind disturbances have attracted increasing interests. Recent works have reported the immediate effects of solar wind disturbances on chorus, hiss, magnetosonic waves, and electromagnetic ion cyclotron waves [36–44,74]. Owing to the important roles of these plasma waves in magnetosphere dynamics, solar wind disturbances could lead to non-negligible changes in space weather by affecting the spatiotemporal distribution of plasma waves. For instance, the ECH wave intensification event reported in this work might contribute to the formation of shock diffuse aurora, attributed to ECH waves’ capacity to scatter keV electrons [75]. Our present findings, in conjunction with previous research, have brought new insights into the solar wind-magnetosphere-ionosphere coupling and highlighted the dependence of magnetospheric waves on the solar wind disturbances.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

YX: Data curation, Formal Analysis, Visualization, Writing–review and editing. NL: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Visualization, Writing–original draft. ZS: Funding acquisition, Project administration, Writing–review and editing. SY: Writing–review and editing. ZH: Writing–review and editing. JY: Writing–review and editing. KL: Writing–review and editing. ZC: Writing–review and editing. JC: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China grants 42004140, 42130204, 42188101, and 42274198, the Strategic Priority Research Program of Chinese Academy of Sciences grant XDB 41000000, and the Key Research Program of the Chinese Academy of Sciences grant ZDRE-KT-2021-3.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shaw RR, Gurnett DA. Electrostatic noise bands associated with the electron gyrofrequency and plasma frequency in the outer magnetosphere. J Geophys Res (1975) 80:4259–71. doi:10.1029/JA080i031p04259

CrossRef Full Text | Google Scholar

2. Roeder JL, Koons HC. A survey of electron cyclotron waves in the magnetosphere and the diffuse auroral electron precipitation. J Geophys Res (1989) 94:2529–41. doi:10.1029/JA094iA03p02529

CrossRef Full Text | Google Scholar

3. Meredith NP, Horne RB, Thorne RM, Anderson RR. Survey of upper band chorus and ECH waves: implications for the diffuse aurora. J Geophys Res (Space Physics) (2009) 114:A07218. doi:10.1029/2009JA014230

CrossRef Full Text | Google Scholar

4. Ni B, Thorne R, Liang J, Angelopoulos V, Cully C, Li W, et al. Global distribution of electrostatic electron cyclotron harmonic waves observed on THEMIS. Geophys Res Lett (2011) 38:L17105. doi:10.1029/2011GL048793

CrossRef Full Text | Google Scholar

5. Liu X, Chen L, Engel MA, Jordanova VK. Global simulation of electron cyclotron harmonic wave instability in a storm-time magnetosphere. Geophys Res Lett (2020) 47:e86368. doi:10.1029/2019GL086368

CrossRef Full Text | Google Scholar

6. Gao Z, Zuo P, Feng X, Wang Y, Jiang C, Wei F. Evidence of nonlinear interactions between magnetospheric electron cyclotron harmonic waves. Geophys Res Lett (2020) 47:e88452. doi:10.1029/2020GL088452

CrossRef Full Text | Google Scholar

7. Kennel CF, Scarf FL, Fredricks RW, McGehee JH, Coroniti FV. VLF electric field observations in the magnetosphere. J Geophys Res (1970) 75:6136–52. doi:10.1029/JA075i031p06136

CrossRef Full Text | Google Scholar

8. Fredricks RW, Scarf FL. Recent studies of magnetospheric electric field emissions above the electron gyrofrequency. J Geophys Res (1973) 78:310–4. doi:10.1029/JA078i001p00310

CrossRef Full Text | Google Scholar

9. Gurnett DA, Anderson RR, Tsurutani BT, Smith EJ, Paschmann G, Haerendel G, et al. Plasma wave turbulence at the magnetopause: observations from ISEE 1 and 2. J Geophys Res (1979) 84:7043–58. doi:10.1029/JA084iA12p07043

CrossRef Full Text | Google Scholar

10. Lyons LR. Electron diffusion driven by magnetospheric electrostatic waves. J Geophys Res (1974) 79:575–80. doi:10.1029/JA079i004p00575

CrossRef Full Text | Google Scholar

11. Horne RB, Thorne RM. Electron pitch angle diffusion by electrostatic electron cyclotron harmonic waves: the origin of pancake distributions. J Geophys Res (2000) 105:5391–402. doi:10.1029/1999JA900447

CrossRef Full Text | Google Scholar

12. Horne RB, Thorne RM, Meredith NP, Anderson RR. Diffuse auroral electron scattering by electron cyclotron harmonic and whistler mode waves during an isolated substorm. J Geophys Res (2003) 108:1290. doi:10.1029/2002JA009736

CrossRef Full Text | Google Scholar

13. Ni B, Thorne RM, Horne RB, Meredith NP, Shprits YY, Chen L, et al. Resonant scattering of plasma sheet electrons leading to diffuse auroral precipitation: 1. Evaluation for electrostatic electron cyclotron harmonic waves. J Geophys Res (2011) 116:A04218. doi:10.1029/2010JA016232

CrossRef Full Text | Google Scholar

14. Tao X, Thorne RM, Li W, Ni B, Meredith NP, Horne RB. Evolution of electron pitch angle distributions following injection from the plasma sheet. J Geophys Res (2011) 116:A04229. doi:10.1029/2010ja016245

CrossRef Full Text | Google Scholar

15. Zhang X, Angelopoulos V, Ni B, Thorne RM, Horne RB. Quasi-steady, marginally unstable electron cyclotron harmonic wave amplitudes. J Geophys Res (Space Physics) (2013) 118:3165–72. doi:10.1002/jgra.50319

CrossRef Full Text | Google Scholar

16. Yang Q, Liu S, Yang H, Zhang S, Tang J, Xiao F, et al. Efficient scattering loss of energetic electrons by enhanced higher-band ECH waves observed by van allen probes. Geophys Res Lett (2023) 50:e2023GL103927. doi:10.1029/2023GL103927

CrossRef Full Text | Google Scholar

17. Shprits YY, Subbotin D, Ni B. Evolution of electron fluxes in the outer radiation belt computed with the VERB code. J Geophys Res (2009) 114:A11209. doi:10.1029/2008JA013784

CrossRef Full Text | Google Scholar

18. Su Z, Xiao F, Zheng H, Wang S. STEERB: a three-dimensional code for storm-time evolution of electron radiation belt. J Geophys Res (2010) 115:A09208. doi:10.1029/2009JA015210

CrossRef Full Text | Google Scholar

19. Su Z, Xiao F, Zheng H, Wang S. CRRES observation and STEERB simulation of the 9 October 1990 electron radiation belt dropout event. Geophys Res Lett (2011) 38:L06106. doi:10.1029/2011GL046873

CrossRef Full Text | Google Scholar

20. Tu W, Cunningham GS, Chen Y, Henderson MG, Camporeale E, Reeves GD. Modeling radiation belt electron dynamics during GEM challenge intervals with the DREAM3D diffusion model. J Geophys Res (2013) 118:6197–211. doi:10.1002/jgra.50560

CrossRef Full Text | Google Scholar

21. Glauert SA, Horne RB, Meredith NP. Three-dimensional electron radiation belt simulations using the BAS Radiation Belt Model with new diffusion models for chorus, plasmaspheric hiss, and lightning-generated whistlers. J Geophys Res (2014) 119:268–89. doi:10.1002/2013JA019281

CrossRef Full Text | Google Scholar

22. Ni B, Thorne RM, Zhang X, Bortnik J, Pu Z, Xie L, et al. Origins of the Earth’s diffuse auroral precipitation. Space Sci Rev (2016) 200:205–59. doi:10.1007/s11214-016-0234-7

CrossRef Full Text | Google Scholar

23. Ashour-Abdalla M, Kennel C. Nonconvective and convective electron cyclotron harmonic instabilities. J Geophys Res (1978) 83:1531–43. doi:10.1029/JA083iA04p01531

CrossRef Full Text | Google Scholar

24. Horne RB. Path-integrated growth of electrostatic waves: the generation of terrestrial myriametric radiation. J Geophys Res (1989) 94:8895–909. doi:10.1029/JA094iA07p08895

CrossRef Full Text | Google Scholar

25. Ni B, Gu X, Fu S, Xiang Z, Lou Y. A statistical survey of electrostatic electron cyclotron harmonic waves based on THEMIS FFF wave data. J Geophys Res (Space Physics) (2017) 122:3342–53. doi:10.1002/2016JA023433

CrossRef Full Text | Google Scholar

26. Liu X, Chen L, Xia Z. The relation between electron cyclotron harmonic waves and plasmapause: case and statistical studies. Geophys Res Lett (2020) 47:e2020GL087365. doi:10.1029/2020GL087365

CrossRef Full Text | Google Scholar

27. Liu S, Chen Y, Yang Q, Yang H, Xiao F, Wang B, et al. Statistical study on spatial distribution of frequency-chirping ech elements by van allen probes. Geophys Res Lett (2023) 50:e2023GL106371. doi:10.1029/2023GL106371

CrossRef Full Text | Google Scholar

28. Colburn DS, Sonett CP. Discontinuities in the solar wind. Space Sci Rev (1966) 5:439–506. doi:10.1007/BF00240575

CrossRef Full Text | Google Scholar

29. Hudson PD. Discontinuities in an anisotropic plasma and their identification in the solar wind. Planet Space Sci (1970) 18:1611–22. doi:10.1016/0032-0633(70)90036-X

CrossRef Full Text | Google Scholar

30. Greco A, Perri S, Servidio S, Yordanova E, Veltri P. The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophys J Lett (2016) 823:L39. doi:10.3847/2041-8205/823/2/L39

CrossRef Full Text | Google Scholar

31. Artemyev AV, Angelopoulos V, Vasko IY, Runov A, Avanov LA, Giles BL, et al. On the kinetic nature of solar wind discontinuities. Geophys Res Lett (2019) 46:1185–94. doi:10.1029/2018GL079906

CrossRef Full Text | Google Scholar

32. Russell CT, Ginskey M, Petrinec SM. Sudden impulses at low-latitude stations: steady state response for northward interplanetary magnetic field. J Geophys Res (1994) 99:253–61. doi:10.1029/93JA02288

CrossRef Full Text | Google Scholar

33. Borodkova NL, Zastenker GN, Sibeck DG. A case and statistical study of transient magnetic field events at geosynchronous orbit and their solar wind origin. J Geophys Res (1995) 100:5643–56. doi:10.1029/94JA03144

CrossRef Full Text | Google Scholar

34. Lyon JG. The solar wind-magnetosphere-ionosphere system. Science (2000) 288:1987–91. doi:10.1126/science.288.5473.1987

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zuo P, Feng X, Xie Y, Wang Y, Li H, Xu X. Automatic detection algorithm of dynamic pressure pulses in the solar wind. Astrophysical J (2015) 803:94. doi:10.1088/0004-637X/803/2/94

CrossRef Full Text | Google Scholar

36. Fu HS, Cao JB, Mozer FS, Lu HY, Yang B. Chorus intensification in response to interplanetary shock. J Geophys Res (2012) 117:A01203. doi:10.1029/2011JA016913

CrossRef Full Text | Google Scholar

37. Su Z, Zhu H, Xiao F, Zheng H, Wang Y, Shen C, et al. Disappearance of plasmaspheric hiss following interplanetary shock. Geophys Res Lett (2015) 42:3129–40. doi:10.1002/2015GL063906

CrossRef Full Text | Google Scholar

38. Liu N, Su Z, Gao Z, Reeves GD, Zheng H, Wang Y, et al. Shock-induced disappearance and subsequent recovery of plasmaspheric hiss: coordinated observations of RBSP, THEMIS, and POES satellites. J Geophys Res (Space Physics) (2017) 122:10. doi:10.1002/2017JA024470

CrossRef Full Text | Google Scholar

39. Liu N, Su Z, Zheng H, Wang Y, Wang S. Prompt disappearance and emergence of radiation belt magnetosonic waves induced by solar wind dynamic pressure variations. Geophys Res Lett (2018) 45:585–94. doi:10.1002/2017GL076382

CrossRef Full Text | Google Scholar

40. Zhou C, Li W, Thorne RM, Bortnik J, Ma Q, An X, et al. Excitation of dayside chorus waves due to magnetic field line compression in response to interplanetary shocks. J Geophys Res (Space Physics) (2015) 120:8327–38. doi:10.1002/2015JA021530

CrossRef Full Text | Google Scholar

41. Yue C, Chen L, Bortnik J, Ma Q, Thorne RM, Angelopoulos V, et al. The characteristic response of whistler mode waves to interplanetary shocks. J Geophys Res (Space Physics) (2017) 122(10). 047057. doi:10.1002/2017JA024574

CrossRef Full Text | Google Scholar

42. Fu H, Yue C, Ma Q, Kang N, Bortnik J, Zong Q-g., et al. Frequency-dependent responses of plasmaspheric hiss to the impact of an interplanetary shock. Geophys Res Lett (2021) 48:e2021GL094810. doi:10.1029/2021GL094810

CrossRef Full Text | Google Scholar

43. Jin Y, Liu N, Su Z, Zheng H, Wang Y, Wang S. Immediate impact of solar wind dynamic pressure pulses on whistler-mode chorus waves in the inner magnetosphere. Geophys Res Lett (2022) 49:e2022GL097941. doi:10.1029/2022GL097941

CrossRef Full Text | Google Scholar

44. Liu N, Su Z. Prompt responses of magnetospheric whistler-mode waves to solar wind dynamic pressure pulses. Front Astron Space Sci (2023) 10. doi:10.3389/fspas.2023.1193600

CrossRef Full Text | Google Scholar

45. Ogilvie K, Desch M. The wind spacecraft and its early scientific results. Adv Space Res (1997) 20:559–68. doi:10.1016/s0273-1177(97)00439-0

CrossRef Full Text | Google Scholar

46. Mauk BH, Fox NJ, Kanekal SG, Kessel RL, Sibeck DG, Ukhorskiy A. Science objectives and rationale for the radiation belt storm probes mission. Space Sci Rev (2013) 179:3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

47. Ogilvie KW, Chornay DJ, Fritzenreiter RJ, Hunsaker F, Keller J, Lobell J, et al. SWE, A comprehensive plasma instrument for the wind spacecraft. Space Sci Rev (1995) 71:55–77. doi:10.1007/BF00751326

CrossRef Full Text | Google Scholar

48. Lepping RP, Acũna MH, Burlaga LF, Farrell WM, Slavin JA, Schatten KH, et al. The wind magnetic field investigation. Space Sci Rev (1995) 71:207–29. doi:10.1007/BF00751330

CrossRef Full Text | Google Scholar

49. Lin RP, Anderson KA, Ashford S, Carlson C, Curtis D, Ergun R, et al. A three-dimensional plasma and energetic particle investigation for the wind spacecraft. Space Sci Rev (1995) 71:125–53. doi:10.1007/BF00751328

CrossRef Full Text | Google Scholar

50. Kletzing CA, Kurth WS, Acuna M, MacDowall RJ, Torbert RB, Averkamp T, et al. The electric and magnetic field instrument suite and integrated science (EMFISIS) on RBSP. Space Sci Rev (2013) 179:127–81. doi:10.1007/s11214-013-9993-6

CrossRef Full Text | Google Scholar

51. Kurth WS, Pascuale SD, Faden JB, Kletzing CA, Hospodarsky GB, Thaller S, et al. Electron densities inferred from plasma wave spectra obtained by the waves instrument on van allen probes. J Geophys Res (2014) 120:904–14. doi:10.1002/2014JA020857

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Wygant J, Bonnell J, Goetz K, Ergun R, Mozer F, Bale S, et al. The electric field and waves instruments on the radiation belt storm probes mission. Space Sci Rev (2013) 179:183–220. doi:10.1007/s11214-013-0013-7

CrossRef Full Text | Google Scholar

53. Funsten HO, Skoug RM, Guthrie AA, MacDonald EA, Baldonado JR, Harper RW, et al. Helium, oxygen, proton, and electron (HOPE) mass spectrometer for the radiation belt storm probes mission. Space Sci Rev (2013) 179:423–84. doi:10.1007/s11214-013-9968-7

CrossRef Full Text | Google Scholar

54. Spence HE, Reeves GD, Baker DN, Blake JB, Bolton M, Bourdarie S, et al. Science goals and overview of the energetic particle, composition, and thermal plasma (ECT) suite on NASA’s Radiation Belt Storm Probes (RBSP) mission. Space Sci Rev (2013) 179:311–36. doi:10.1007/s11214-013-0007-5

CrossRef Full Text | Google Scholar

55. Chi Y, Shen C, Wang Y, Xu M, Ye P, Wang S. Statistical study of the interplanetary coronal mass ejections from 1995 to 2015. Solar Phys (2016) 291:2419–39. doi:10.1007/s11207-016-0971-5

CrossRef Full Text | Google Scholar

56. Zurbuchen TH, Richardson IG. In-situ solar wind and magnetic field signatures of interplanetary coronal mass ejections. Space Sci Rev (2006) 123:31–43. doi:10.1007/s11214-006-9010-4

CrossRef Full Text | Google Scholar

57. Wu C-C, Lepping RP. Statistical comparison of magnetic clouds with interplanetary coronal mass ejections for solar cycle 23. Solar Phys (2011) 269:141–53. doi:10.1007/s11207-010-9684-3

CrossRef Full Text | Google Scholar

58. Kilpua EKJ, Lumme E, Andreeova K, Isavnin A, Koskinen HEJ. Properties and drivers of fast interplanetary shocks near the orbit of the Earth (1995-2013). J Geophys Res (Space Physics) (2015) 120:4112–25. doi:10.1002/2015JA021138

CrossRef Full Text | Google Scholar

59. Lou Y, Gu X, Summers D, Ni B, Liu K, Fu S, et al. Statistical distributions of dayside ECH waves observed by MMS. Geophys Res Lett (2018) 45(12):738. 730–12. doi:10.1029/2018GL080125

CrossRef Full Text | Google Scholar

60. Yu J, Wang J, Chen Z, Ren A, Liu X, Liu N, et al. Statistical evidence for off-equatorial minimum-B-pocket as a source region of electron cyclotron harmonic waves in the dayside outer magnetosphere. Geophys Res Lett (2023) 50:e2022GL102583. doi:10.1029/2022GL102583

CrossRef Full Text | Google Scholar

61. Zong Q, Zhou X, Wang YF, Li X, Song P, Baker DN, et al. Energetic electron response to ULF waves induced by interplanetary shocks in the outer radiation belt. J Geophys Res (2009) 114:A10204. doi:10.1029/2009JA014393

CrossRef Full Text | Google Scholar

62. Foster JC, Wygant JR, Hudson MK, Boyd AJ, Baker DN, Erickson PJ, et al. Shock-induced prompt relativistic electron acceleration in the inner magnetosphere. J Geophys Res Accepted (2015) 120:1661–74. doi:10.1002/2014JA020642

CrossRef Full Text | Google Scholar

63. Ren J, Zong QG, Miyoshi Y, Zhou XZ, Wang YF, Rankin R, et al. Low-energy (<200 eV) electron acceleration by ULF waves in the plasmaspheric boundary layer: van allen probes observation. J Geophys Res (Space Physics) (2017) 122:9969–82. doi:10.1002/2017JA024316

CrossRef Full Text | Google Scholar

64. Ren J, Zong QG, Zhou XZ, Spence HE, Funsten HO, Wygant JR, et al. Cold plasmaspheric electrons affected by ULF waves in the inner magnetosphere: a van allen probes statistical study. J Geophys Res (Space Physics) (2019) 124:7954–65. doi:10.1029/2019JA027009

CrossRef Full Text | Google Scholar

65. Ma X, Tian AM, Shi QQ, Bai SC, Yao ST, Shen XC, et al. Electron pitch angle distributions in compressional Pc5 waves by THEMIS-A observations. Geophys Res Lett (2021) 48:e95730. doi:10.1029/2021GL095730

CrossRef Full Text | Google Scholar

66. Xie H, Xiao Y. PDRK: a general kinetic dispersion relation solver for magnetized plasma. Plasma Sci Tech (2016) 18:97–107. doi:10.1088/1009-0630/18/2/01

CrossRef Full Text | Google Scholar

67. Zhou Q, Xiao F, Yang C, Liu S, He Y, Baker DN, et al. Generation of lower and upper bands of electrostatic electron cyclotron harmonic waves in the Van Allen radiation belts. Geophys Res Lett (2017) 44:5251–8. doi:10.1002/2017GL073051

CrossRef Full Text | Google Scholar

68. Lou Y, Cao X, Ni B, Tu W, Gu X, Fu S, et al. Diffuse auroral electron scattering by electrostatic electron cyclotron harmonic waves in the dayside magnetosphere. Geophys Res Lett (2021) 48:e92208. doi:10.1029/2020GL092208

CrossRef Full Text | Google Scholar

69. Roederer JG, Zhang H. Dynamics of magnetically trapped particles. Berlin: Springer (2016).

Google Scholar

70. Tsyganenko NA, Stern DP. Modeling the global magnetic field of the large-scale Birkeland current systems. J Geophys Res (1996) 101:27187–98. doi:10.1029/96JA02735

CrossRef Full Text | Google Scholar

71. Tsyganenko NA. A model of the near magnetosphere with a dawn-dusk asymmetry 1. mathematical structure. J Geophys Res Space Phys (2002) 107. SMP 12–1–SMP 12–15. doi:10.1029/2001JA000219

CrossRef Full Text | Google Scholar

72. Tsyganenko NA, Sitnov MI. Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. J Geophys Res (2005) 110:A03208. doi:10.1029/2004JA010798

CrossRef Full Text | Google Scholar

73. Boudouridis A, Lyons LR, Zesta E, Ruohoniemi JM. Dayside reconnection enhancement resulting from a solar wind dynamic pressure increase. J Geophys Res (Space Physics) (2007) 112:A06201. doi:10.1029/2006JA012141

CrossRef Full Text | Google Scholar

74. Liu N, Su Z, Gao Z, Zheng H, Wang Y, Wang S. Can solar wind decompressive discontinuities suppress magnetospheric electromagnetic ion cyclotron waves associated with fresh proton injections? Geophys Res Lett (2020) 47:e90296. doi:10.1029/2020GL090296

CrossRef Full Text | Google Scholar

75. Zhou XY, Strangeway RJ, Anderson PC, Sibeck DG, Tsurutani BT, Haerendel G, et al. Shock aurora: FAST and DMSP observations. J Geophys Res (Space Physics) (2003) 108:8019. doi:10.1029/2002JA009701

CrossRef Full Text | Google Scholar