Simulation of a synchronized methodology for MR-based electromechanical property imaging during transcranial electrical stimulation

Introduction: Recent investigations into the biomechanics of the brain have unveiled alteration in tissue stiffness triggered by external stimuli. For instance, visual stimulation effects can be measured in elasticity images of the cortex generated by functional magnetic resonance elastography (MRE). Such a mechanical characterization method combined with non-invasive brain stimulation (NIBS), a technique that seeks to selectively modulate particular parts of the brain using weak electrical currents, has the potential to influence research on various neurological disorders. In this in silico study, we aimed to elucidate individual and interdependent aspects related to a synchronized biomechanical imaging and non-invasive brain stimulation methodology. Magnetic resonance electrical impedance tomography (MREIT) was incorporated to the pipeline, providing a promising way of evaluating NIBS-induced electrical current patterns in the brain while leveraging MRE and transcranial alternating current stimulation (tACS) experimental settings.

Methods: A mouse head model was assembled using open-access atlases to include five anatomical structures: skin/subcutaneous tissue, skull, cerebrospinal fluid (CSF), brain white and grey matters. MRE, tACS, and MREIT experiments were simulated using Comsol Multiphysics with Matlab Livelink. Synthetic MRE and MREIT data were processed using the subzone non-linear inversion and harmonic Bz algorithm, respectively, to reconstruct images of the distributed complex shear modulus and electrical conductivity.

Results and Discussion: Lorentz body forces arising from simultaneous MRE and tACS elicited elastic waves of negligible amplitude compared with the extrinsic actuation levels reported in the literature, which allowed accurate reconstructions of the complex shear modulus. Qualitative electrical conductivity maps retrieved by MREIT accurately delineated anatomical regions of the brain model and could be used to recover reasonably accurate distributions of tACS-induced currents. This multi-physics approach has potential for translation to human brain imaging, and may provide more possibilities for the characterization of brain function together than in isolation.

1 Introduction

Application of non-invasive brain stimulation (NIBS) in neuroscience research has drawn significant attention for investigating psychiatric and neurological disorders, as well as the neuronal mechanisms underlying behavior and cognition. NIBS modulates specific cerebral regions by inducing electric fields within the brain. These fields are generated either through magnetic coils in the case of transcranial magnetic stimulation, or via direct placement of electrodes on the scalp. Since the inception of NIBS, significant research has focused on the intricate interplay between brain function and behavior. As such, various experimental strategies have been devised to investigate individual responses to electrical stimulation and evaluate the physiological impact of brain stimulation sites on vision [1], audition [2], motor function [3–5], somatosensation [6], language [7, 8], attention [9, 10], memory [11, 12], reasoning [13, 14], decision making [15–17], and social behavior [18–20], as reviewed by Polania et al. [4]. In addition to modulating brain function, recent research indicates that non-invasive brain stimulation may also have implications for treating neurological disorders. Notably, alterations in cognitive functions observed in individuals with Alzheimer’s disease subsequent to a non-invasive brain stimulation session lend credence to the hypothesis that neuroplasticity can be modulated as a strategy for symptom reduction [21–25]. Likewise, NIBS was observed to enhance motor functions in cases of Parkinson’s disease, for which no cure currently exists [26–30]. The effectiveness of NIBS treatments on depressive disorders has also been investigated. Despite encouraging results, evidence of beneficial impacts remains sparse and more research is needed [31, 32].

Transcranial magnetic stimulation (TMS) and transcranial electrical stimulation (TES) are the main techniques used to modulate cerebral activity [4]. TMS is based on remote electromagnetic induction of weak electric current loops in the conductive brain tissue using a distant coil supplied with short electric pulses. The temporal profile of the stimulation can be shaped by applying a single or multiple pulses at adjustable repetition rates. Due to the focused nature of the induced electric field, TMS tends to provide more localized stimulations than TES, but has a lower penetration depth, which restricts the stimulation site to shallow cortical regions. In comparison with TMS, TES delivers weak electrical currents through electrodes directly placed on the scalp. The temporal profile of the electrical stimulation determines the TES variant: transcranial direct current stimulation (tDCS), transcranial alternating current stimulation (tACS), and transcranial random noise stimulation (tRNS). In all cases, electrode design and positioning govern the size and location of the stimulated area [33], which is often confined to the cortex as the electric field disperses in deeper tissues. Transcranial temporal interference electrical stimulation (tTIS) is a recent technology that seeks to overcome this limitation by applying two alternating currents oscillating at nearly identical frequencies resulting in constructive and destructive electric field interferences. The interference pattern has a narrow spatial support allowing the recruitment of interior neurons while preventing stimulation of the surrounding area. This method has been demonstrated in mice [34] and further evaluated by simulating electric field distributions in numerical models of the human brain derived from Magnetic Resonance Imaging (MRI) [35]. Applications to hippocampal activity modulation in humans are currently investigated [36]. Finally, transcranial focused ultrasounds have been presented as an emerging technique that complements TES and TMS by its higher spatial resolution and ability to target the deep brain [37].

Overall, published NIBS guidelines underline the importance of combining neuroimaging and computational modelling to optimize NIBS protocols, achieve finer stimulation spatial selectivity, and interpret results [4]. However, the subject-specific electrical conductivity distribution needed to evaluate the stimulation current patterns in the brain is challenging to measure. Magnetic resonance electrical impedance tomography (MREIT) aims at providing such estimates of the ohmic conductivity through the analysis of the magnetic flux density induced in the imaged tissue as an electric flux passes [38–41]. While electric property characterization and computational modelling do not supersede physiological validation, they are seen as tools that may help better understand the brain’s response to NIBS and identify areas that might have been unintentionally activated in the process.

In addition to NIBS, changes in the biomechanics of the brain provide insights into local functional activity [42]. Such measurements are performed with magnetic resonance elastography (MRE) [43], which images non-invasively dynamic tissue deformations in organs [44]. The motion fields used to reconstruct the mechanical model parameters, often the shear modulus, can be induced intrinsically by the cardiac pressure pulse [45, 46] or extrinsically using mechanical surface actuators [47]. Extrinsic MRE (exMRE) offers the possibility of studying the brain’s dynamic response across a range of mechanical actuation frequencies, which helps stabilize numerically the elastography inversion [48] or investigate viscoelastic dispersive effects [49]. For instance, 50-Hz exMRE was used to establish a standard-space atlas of the viscoelastic properties of the human brain [50]. On the lower end of the actuation frequency spectrum, intrinsic MRE operates at the physiological rate of heart pulsation and eliminates the need for external actuators [51]. The tissue mechanical response at such low frequencies, around 1 Hz, is better described by poroelastic models, where the fluid and solid components of the biological medium are represented by separate phases [45, 52, 53]. Intrinsic MRE notably demonstrated sensitivity to stiffness variations in distinct regions of the visual cortex during visual stimulation [42], establishing a proxy to study in physiological operating conditions the biomechanical response of brain tissue to neuronal activity. In similar functional MRE studies, contrasts observed in images of biomechanical features correlated with specific tasks (motor or cognitive) participants were requested to perform in the protocol. For instance, memory performance was related to tissue biomechanics (shear stiffness [54]) and damping ratio [55–57] in the subfields of the hippocampus). Likewise, motor function performances correlated with damping ratio variations in the hippocampus for aerobic exercise tasks [57] and with global brain shear stiffness variations for dynamic balance related tasks [58]. Recently, functional MRE of the mouse brain was used to capture the neuronal activity triggered by fast electrical hind limb stimulation, suggesting rapid changes in brain elasticity [59].

Intrinsic neuronal currents arising from natural neuronal activity manifest a Lorentz force upon exposure to the magnetic field of the magnetic resonance (MR) system. This observation led researchers to develop Lorentz effect imaging (LEI) for visualizing brain activity [60]. The fundamental assumption is that the small distance moved by electrically-active tissue, driven by the Lorentz force, results in a phase shift in the MR signal that can be used for precise localization of neuronal activity. Initial results of brain activity detection using LEI presented by Truong et al. [61–63] were further analyzed by Roth et al. [64–66], who suggested that the size of the Lorentz force-induced displacements would be order of magnitudes too weak to be detected by MRI.

Overall, the growing number of research endeavours aimed at illuminating brain function using MRE and non-invasive brain stimulation has examined biomechanical and bioelectrical properties distinctly. In this study, we anticipate that the individual facets of NIBS, ohmic conductivity, and viscoelasticity mapping hold promise to merge into a valuable multi-physics MR-based tool for neurological disorder characterization. Using simulations in a numerical model of a mouse head, we review and elucidate the underlying principles of the methodology.

2 Methods

2.1 Mouse head model

A well-established pipeline was used to design our numerical simulations. This pipeline involves developing a geometry from anatomical image segmentation and assigning physical properties to the corresponding segments [67–70]. A mouse head model was constructed from open-access CT and MRI mouse scans and consisted of five anatomical structures: skin/subcutaneous tissue, skull, cerebrospinal fluid (CSF), brain white and grey matters. Head contours were segmented from the Digimouse atlas [71], the skull from a surgical atlas [72], and white and grey matter domains from a brain template [73]. Individual segments were then registered to the Digimouse coordinate system and the CSF was represented by the space between the brain and the skull. Handling of mouse scans and domain registration were performed using the medical image processing application ITK-SNAP [74] and exported in NiFTI format to Matlab (Matlab R2019b, The Mathworks, Massachusetts, United States) for a segment-based definition of material physical properties (see Sections 2.2, 2.4 for details). The final mouse head model had a resolution of 120 μm³ and is shown in Figure 1A.

Figure 1

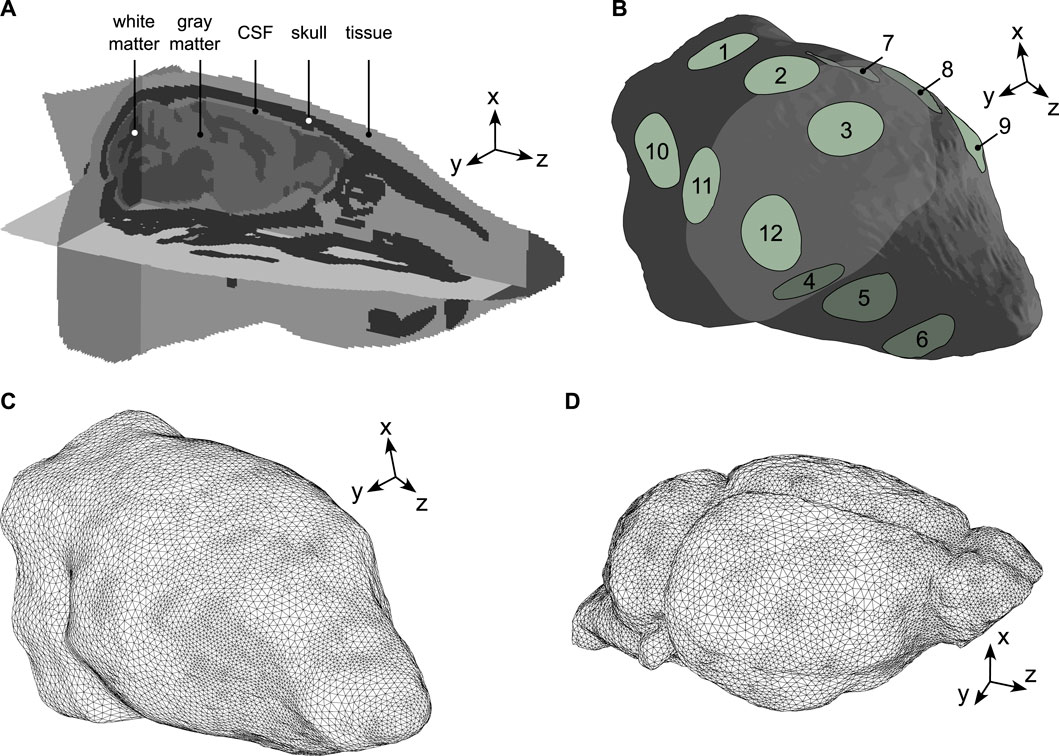
Figure 1. Mouse head geometry and meshes. (A) The model was made of five structural domains: skin/subcutaneous tissue, skull, CSF, brain white and grey matters. The z-axis was modelled along the direction of the MR scanner’s magnetic field (foot-head direction), the x and y-axes were parallel to the antero-posterior and left-right directions, respectively. (B) External view of the mouse head domain where surface electrodes were modelled by 12 2-mm radius circles organized into groups. Group 1: (1,2,3), group 2: (7,8,9), group 3: (4,5,6), group 4: (10,11,12). (C) External view of the mouse head mesh used to simulate electric current propagation (MREIT and tACS). (D) External view of the mouse brain mesh used to simulate the propagation of mechanical elastic waves (MRE).

2.2 MREIT

Typical brain MREIT pipelines induce a direct low-amplitude electric current density in the head, $\mathbf{J}\left(\mathbf{r}\right)$, and images the resulting magnetic flux density’s z component, $B_z\left(\mathbf{r}\right)$. The internal current density is generated by delivering an external current to the scalp through surface electrodes operated by a waveform generator synchronized with the MRI pulse sequence. Four electrodes are usually used and placed to ensure a suitable current coverage as well as generate at least two linearly independent current distributions in the imaged domain. The Biot-Savart law relates the tomographic direct current density in the imaged slices to the induced magnetic flux density’s z component:

$B_z\left(\mathbf{r}\right)=\frac{{\mu }_0}{4\pi }\underset{\mathrm{\Omega }}{\int }\frac{J_x\left({\mathbf{r}}^{\prime }\right)\left(y-y^{\prime }\right)-J_y\left({\mathbf{r}}^{\prime }\right)\left(x-x^{\prime }\right)}{{\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|}^3}d{\mathbf{r}}^{\prime },(1)$

where μ₀ is the magnetic permeability of the free space, which is assumed to be the same as that of the material. The volume integral in Eq. 1 can be expressed as a convolution in the physical space [38, 75]:

$B_z\left(\mathbf{r}\right)={\mu }_0\left(G_y\ast J_x-G_x\ast J_y\right)\left(\mathbf{r}\right),(2)$

where $G_x=\frac{1}{4\pi }\frac{x}{{\left|\mathbf{r}\right|}^3}$ and $G_y=\frac{1}{4\pi }\frac{y}{{\left|\mathbf{r}\right|}^3}$ are scalar arrays, and r is the vector position, which has its origin at the origin of the coordinate system. The convolution in Eq. 2 turns into a product in the k-space:

$B_z\left(\mathbf{r}\right)={\mu }_0{\mathcal{F}}^{-1}\left\{\mathcal{F}\left\{G_y\right\}\cdot \mathcal{F}\left\{J_x\right\}-\mathcal{F}\left\{G_x\right\}\cdot \mathcal{F}\left\{J_y\right\}\right\}\left(\mathbf{r}\right),(3)$

where $\mathcal{F}$ denotes the Fourier transform. The k-space formulation allows a faster evaluation of $B_z\left(\mathbf{r}\right)$  from current densities than the evaluation of the volume integral. The current density distribution is given by the Ohm’s law:

$\mathbf{J}=\sigma \mathbf{E}=-\sigma \nabla V,(4)$

where σ is the electric conductivity and V is the electric potential, which is a solution to following boundary value problem:

$\left\{\begin{array}{ccc}\nabla \cdot \left(\sigma \nabla V\right)=0\hfill & \hfill \hfill & \text{in\hspace{0.17em}}\mathrm{\Omega },\hfill \\ I={\int }_{{\epsilon }^{+}}\sigma \frac{\partial V}{\partial \mathbf{n}}ds=-{\int }_{{\epsilon }^{-}}\sigma \frac{\partial V}{\partial \mathbf{n}}ds,\hfill & \hfill \nabla V\times \mathbf{n}=0\hfill & \text{on\hspace{0.17em}}{\epsilon }^{+}\bigcup {\epsilon }^{-},\hfill \\ \sigma \frac{\partial V}{\partial \mathbf{n}}=0\hfill & \hfill \hfill & \text{on\hspace{0.17em}}\partial \mathrm{\Omega }\backslash \overline{{\epsilon }^{+}\bigcup {\epsilon }^{-}},\hfill \end{array}\right.(5)$

where ∂Ω represents the surface bounding the computational domain Ω, ɛ⁺ and ɛ⁻ represent the load and grounded electrodes, and n is the unit vector normal to ∂Ω.

Current densities in MREIT experiments were simulated in the whole mouse head by solving the forward problem described by Eqs 4, 5 using the electric current module of Comsol Multiphysics with Matlab Livelink (Comsol Inc. Stockholm, Sweden). The induced magnetic flux density was computed with Matlab via Eq. 3. The computational domain was defined in Comsol by lofting the mouse head transverse (x,y) contours along the z-axis. Internal domains were modelled by distributing material properties across the geometry. Electric conductivity values were set to 0.465 S.m^-1 in the skin, 0.01 S.m^-1 in the skull, 1.654 S.m^-1 in the CSF, 0.126 S.m^-1 in the white matter, and 0.275 S.m^-1 in the gray matter [76]. Relative permittivity and permeability were defined globally and set to a homogeneous value of 1 across the entire domain. Then, a set of 12 2-mm radius circular surface electrodes was designed using Comsol’s Computer Aided Design (CAD) tools. Electrodes were organized into four groups of three units evenly spaced along the z-axis on opposing sides of the mouse scalp, and placed to cover to whole brain region. An external view of the mouse head domain with the electrodes is shown in Figure 1B. The computational mesh, shown in Figure 1C, contained 1,283,014 tetrahedral elements with minimum and maximum target sizes of 2.4 × 10⁻⁴ m and 5.0 × 10⁻⁴ m, respectively. Current and magnetic flux densities were computed for six MREIT numerical experiments, where different combinations of electrode groups were used. Each experiment involved one electrode group for current delivery (1 mA in total) and one grounded electrode group. The six combinations were (group 1, group 3), (group 2, group 4), (group 4, group 1), (group 3, group 4), (group 2, group 3), and (group 2, group 1), where the first group of each couple indicates the loading electrodes and the second group the grounded electrodes.

The inverse problem of MREIT was solved using the iterative harmonic B_z method [77, 78]. This technique is based on the observations that B_z is sensitive to conductivity contrasts in directions perpendicular to the tomographic current densities and insensitive in parallel directions. For direct currents, the magnetic flux density, the conductivity of the medium, and the electric potential are related through [79]:

${\nabla }^2\mathbf{B}={\mu }_0\nabla \sigma \times \nabla V.(6)$

The z component of Eq. 6 is then given by:

${\nabla }^2{B}_z={\mu }_0\left(\frac{\partial \sigma }{\partial x}\frac{\partial V}{\partial y}-\frac{\partial \sigma }{\partial y}\frac{\partial V}{\partial x}\right).(7)$

Considering the six MREIT experiments, Eq. 7 can be expressed in matrix form as:

$\underset{\mathbf{U}}{\underbrace{\left[\begin{array}{cc}\hfill \frac{\partial V_1}{\partial y}\hfill & \hfill -\frac{\partial V_1}{\partial x}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial V_6}{\partial y}\hfill & \hfill -\frac{\partial V_6}{\partial x}\hfill \end{array}\right]}}\underset{\mathbf{s}}{\underbrace{\left\{\begin{array}{c}\hfill \frac{\partial \sigma }{\partial x}\hfill \\ \hfill \frac{\partial \sigma }{\partial y}\hfill \end{array}\right\}}}=\frac{1}{{\mu }_0}\underset{\mathbf{b}}{\underbrace{\left\{\begin{array}{c}\hfill {\nabla }^2{B}_{z,1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\nabla }^2{B}_{z,6}\hfill \end{array}\right\}}}.(8)$

The following iterative reconstruction procedure is defined from Eq. 8:

${\mathbf{U}}_k{\mathbf{s}}_{k+1}=\mathbf{b},(9)$

which allows evaluating the x and y components of the conductivity gradient. The actual conductivity distribution is finally recovered from its gradient in Eq. 9 through the following Poisson’s equation [77]:

$\left\{\begin{array}{cccc}{\tilde{\nabla }}^2{\sigma }_{k+1}\hfill & =\hfill & \tilde{\nabla }\cdot {\mathbf{s}}_{k+1}\hfill & \text{in\hspace{0.17em}}{\mathrm{\Omega }}_t,\hfill \\ {\sigma }_{k+1}\hfill & =\hfill & {\sigma }_e\hfill & \text{on\hspace{0.17em}}\partial {\mathrm{\Omega }}_t,\hfill \end{array}\right.(10)$

where $\tilde{\nabla }$ indicates 2D in-plane derivatives in the slice Ω_t and σ_e represents the conductivity on the external boundary of the domain. The harmonic B_z method uses an initial conductivity distribution σ₀ to start the reconstruction procedure and evaluate the matrix termed U in Eq. 8. A homogeneous distribution σ₀ = σ_e = 0.465 S.m^-1 was used and corresponded to the conductivity on the head domain boundary indicated in Eq. 10, which was assumed to be experimentally measurable. The inversion was conducted over ten iterations. For meshing, size constraints were imposed to enforce refinement in specific regions. Target sizes were set to 2.4 × 10⁻⁴ m for elements in the vicinity of expected material discontinuities, based on simulated B_z data, and to 1.0 × 10⁻³ m for elements away from material discontinuities, where low B_z variations were observed. The mesh contained 940,023 tetrahedral elements.

2.3 tACS

For tACS simulations, the same mouse head model as in the MREIT forward model was used. Two numerical experiments were conducted using two two-electrode combinations. This time, electrodes were used in isolation rather than in groups and the combinations were (electrode 2, electrode 11) and (electrode 11, electrode 5), where the first member of each electrode pair indicates the loading electrode and the second member the grounded electrode. Electrode 2 was placed above the cortex, electrode 11 was facing the caudate putamen, and electrode 5 was on the neck, opposing electrode 11. Electrode combinations were chosen with the aim of generating Lorentz body forces (BF) of maximum amplitude. This was achieved by selecting loading and grounded electrodes with the same z coordinate, thus resulting in current densities with main directions lying in (x, y) planes and producing Lorentz BF, f_L, with main directions perpendicular to both the current density, J, and the MR scanner’s magnetic flux density, B₀, according to:

${\mathbf{f}}_L=\mathbf{J}\times {\mathbf{B}}_0.(11)$

The alternating current frequency was set to 900 Hz. In practice, tACS has been operated across a range of frequencies from less than 1 Hz to a few kilohertz [80–82]. Here, the specific value of 900 Hz was chosen to match a typical actuation frequency in mouse brain MRE experiments [83], which allowed evaluating the impact of tACS induced motion, through Lorentz BF, on the MRE reconstruction procedure. Electric conductivities were the same as in the MREIT simulations and were assumed frequency independent in the investigated frequency range [84].

2.4 MRE

In MRE, the mechanical properties of soft solids are reconstructed from the analysis of mechanical elastic waves induced in the imaged tissue and tracked with MRI [85]. The elastic waves are low frequency (up to about 100 Hz in humans and to about 1.5 kHz in mice) and are induced by external actuators or are naturally present in the body from heart pulsations. Assuming that soft brain tissues are heterogeneous, viscoelastic, nearly incompressible, and isotropic materials, the response of the tissue undergoing a harmonic actuation at an angular frequency ω is described by the following boundary value problem with displacement variables:

$\left\{\begin{array}{cc}\nabla \cdot \left(\mu \nabla \mathbf{u}\right)+\nabla \left(\mu \nabla \cdot \mathbf{u}-p\right)+{\mathbf{f}}_b=-\rho {\omega }^2\mathbf{u}\hfill & \text{in\hspace{0.17em}}\mathrm{\Omega },\hfill \\ Ktr\left(\mathit{\epsilon }\right)=-p\hfill & \text{in\hspace{0.17em}}\mathrm{\Omega },\hfill \\ \mathbf{u}={\mathbf{u}}_e\hfill & \text{on\hspace{0.17em}}{\mathrm{\Gamma }}_u,\hfill \\ \mathbf{n}\cdot {\mathit{\sigma }}_e={\mathbf{f}}_e\hfill & \text{on\hspace{0.17em}}{\mathrm{\Gamma }}_{\sigma },\hfill \end{array}\right.(12)$

where μ is the complex shear modulus (Pa), $\mathbf{u}={\left[u,v,w\right]}^T$ is the complex displacement vector (m), p is the pressure field (Pa), f_b is the body force density (N.m^-3), ρ is the mass density (kg.m^-3), ω is the actuation angular frequency (rad.s^-1), Ω is the brain domain, K is the bulk modulus (Pa), ɛ is the strain tensor, u₀ is the displacement vector on the domain’s boundary Γ_u, n is the unit vector normal to the surface boundary Γ_σ, σ_e is the stress tensor, and f_e is the traction force vector. In standard MRE experiments, the scanned tissue is usually free of body forces and the corresponding f_b term in Eq. 12 is neglected in the formulation of the inverse problem of elastography. When MRE and tACS are conducted simultaneously, Lorentz BF develop in the brain, as described by Eq. 11, and the assumption of a negligible source term must be evaluated.

The solid mechanics module of Comsol Multiphysics was used to conduct the MRE simulations in the brain domain of the head model detailed in Section 2.1. First, a stereolitography-format (STL) brain mesh was generated with Matlab using the iso2mesh toolbox [86, 87] and imported in Comsol to create the geometry object. Then, internal domains were modelled by distributing the mechanical properties across the brain geometry. Shear modulus values were set to 5397 + i1836 Pa in the white matter and 4997 + i1426 Pa in the grey matter domains [83]. A homogeneous density and incompressible bulk modulus were defined and set to 1,000 kg .m^-3 and 2.2 × 10⁹ Pa [88], respectively. A heterogeneous mesh was generated with mesh size gradients to resolve the material discontinuities. A target size of 2.2 × 10⁻⁴ m at material boundaries and an overall maximum size of 3.0 × 10⁻⁴ m were imposed. An external view of the final mesh, containing 400,888 tetrahedral elements, is shown in Figure 1D. In a first numerical experiment, a displacement field was simulated in the brain from the application of Dirichlet boundary conditions (BC) (5.0 × 10⁻⁶ m displacements along the x-axis) to mimic a typical mouse brain MRE experiment, free of body forces [89]. In a second numerical experiment, Lorentz BF-induced displacement fields were simulated using the tACS current distributions described in Section 2.3 and a magnetic flux density of 11.7 T oriented along the z-axis of the scanner. Such a high field value was used to depict a situation in which Lorentz body force effects are maximised. The Lorentz BF distributions corresponding to the two two-electrode configurations of Section 2.3 were computed according to Eq. 11 with $\left|\left|{\mathbf{B}}_0\right|\right|=11.7$ T. In Eq. 12, this translates to f_b = f_L. In both experiments, the actuation frequency (through prescribed displacements or Lorentz forces) was 900 Hz [83].

The inverse problem of elastography was addressed using a specialized non-linear inversion (NLI) technique [90, 91]. NLI identifies mechanical property distributions, the shear modulus in the present work, that is a best-fit of the measured displacements u_m through Eq. 12, with f_b = 0. Finite element solutions of this equation, u_c, are computed using sets of shear modulus distributions, successively enhanced with property updates across 100 global iterations in order to minimize the mismatch between u_c and u_m through the following objective function:

$\mathrm{\Phi }=\frac{1}{2}{\left({\mathbf{u}}_c\left(\mathbf{\theta }\right)-{\mathbf{u}}_m\right)}^H\left({\mathbf{u}}_c\left(\mathbf{\theta }\right)-{\mathbf{u}}_m\right),(13)$

where θ is the vector containing the inferred mechanical properties and H is the complex-conjugate transpose. The most likely approximation of the true shear modulus is the distribution that minimizes the objective function (Eq. 13). The particularity of this NLI formulation is the decomposition of the total imaged domain into overlapping subzones processed individually and in parallel. Thus, the inverse problem consisting in identifying relevant property updates is solved at the subzone level, which mitigates the computational cost associated to the 3D problem. In this numerical study, the measured displacements u_m were the displacements simulated with Comsol in the mouse head model. In the inverse problem, the solution to the boundary value system in Eq. 12 (with f_b = 0) was computed on a 27-node hexahedral finite-element mesh. Displacement and property meshes had the same resolution of 120 μm³. Subzones had an isotropic size of 2.1 mm with a 20% overlap. Property updates in each subzone were computed using the conjugate gradient method (CG) and a global property distribution in the total domain was generated by assembling the subzones at the end of each global iteration. Gaussian smoothing with a kernel size of 84 μm was applied to the property distribution at the subzone assembly step in order to stabilize the reconstruction process. The initial shear modulus distribution used to start the reconstruction process was set to 6000 + i2000 Pa. This initial modulus was chosen to lie outside the range of viscoelasticity values used in the mechanical model of the brain.

Three displacement data types were processed with NLI. First, the body force free displacement field resulting from prescribed displacements on boundaries and mimicking standard exMRE. Second, the superposition of the Lorentz BF induced displacements and the body force free displacements, mimicking simultaneous exMRE and tACS experiments. Third, Lorentz BF induced displacements alone, mimicking a tACS experiment.

3 Results

Two MR-assisted tACS sessions were considered, representing the successive use of two distinct electrode sets (configurations 1 and 2). The corresponding distributions of the tACS-induced Lorentz body forces, simulated by solving Eqs 5 and 11 in the two two-electrode configurations, are displayed in Figure 2.

Figure 2

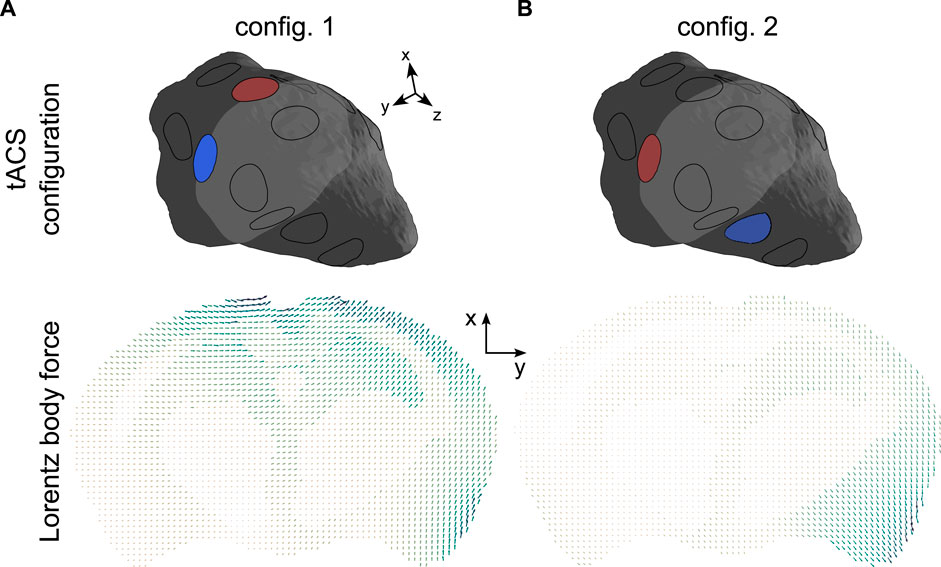
Figure 2. Lorentz BF distributions in a representative slice of the brain corresponding to the two two-electrode tACS configurations ((2, 11) and (11, 5)). The arrows’ lengths are proportional to the amplitude of the body force. In each panel, the minimum and maximum force strengths were respectively: (A) 12.2 N.m^-3and 146.7 N m^-3. (B) 9.8 N.m^-3and 112.9 N.m^-3.

When MRE and tACS are performed simultaneously, the Lorentz BF shown in Figure 2 induce motions that superimpose with the displacement generated by the surface actuators and contribute to the total field encoded by the MR system’s gradients. The real part of the finite element displacement fields, solution to Eq. 12 in the exMRE, simultaneous exMRE and tACS, as well as tACS only experiments, are presented in Figure 3.

Figure 3

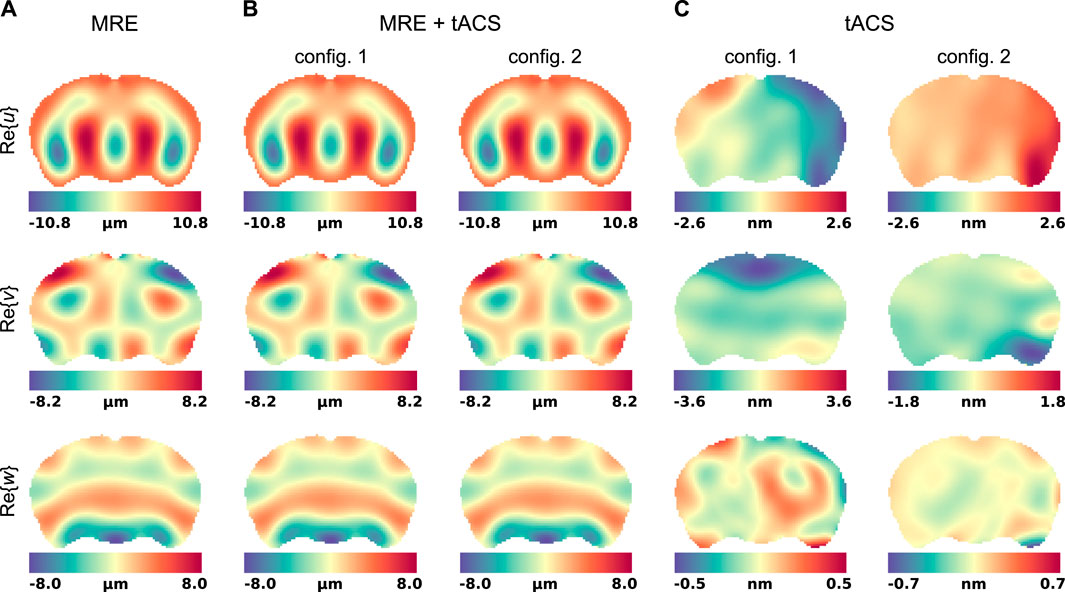
Figure 3. Motion fields in a representative slice of the mouse brain model. Displacements were evaluated in three experiment mimicking situations: (A) standard exMRE, (B) simultaneous exMRE and tACS using two electrode configurations ((2,11) and (11,5)), and (C) tACS only using the same two electrode configurations.

The five displacement fields considered in Figure 3 were used to reconstruct viscoleasticity images of the brain with the subzone NLI algorithm. Figure 4 shows the corresponding storage and loss moduli, μ_r and μ_i, respectively, that form the viscoelastic complex shear modulus μ = μ_r + iμ_i in the MRE and MRE + tACS experiments, as well as the relative property differences observed between the two settings.

Figure 4

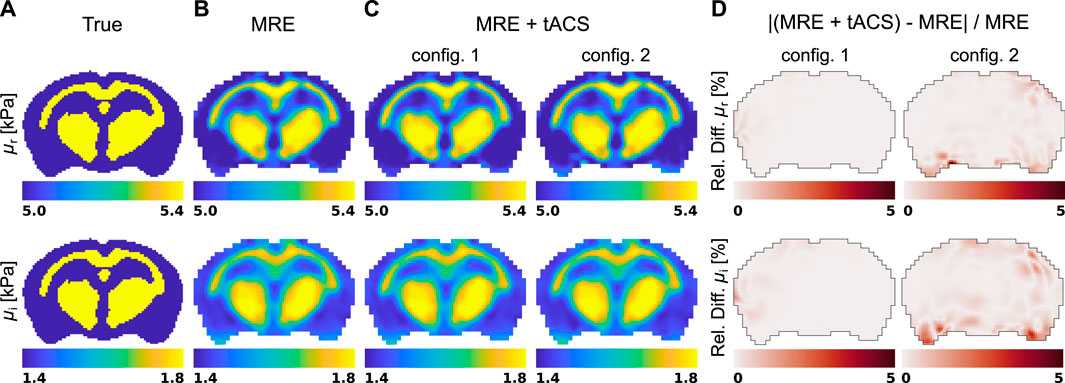
Figure 4. Shear modulus reconstructions in a representative slice of the brain model obtained with the subzone NLI method applied in the two experiment mimicking situations: (A) true distribution, (B) standard exMRE (displacements from Dirichlet BC only), (C) simultaneous exMRE and tACS (displacements from Dirichlet BC and body forces), and (D) the relative property difference between the MRE and MRE + tACS settings.

MR electrical impedance tomography was introduced in the simulation pipeline to reconstruct the electrical conductivity distribution, $\sigma \left(x,y,z\right)$, from images of the magnetic flux density, $B_z\left(x,y,z\right)$, induced by weak direct currents applied to the mouse scalp. Images of B_z corresponding to the six MREIT series were computed using the k-space formulation of the Biot-Savart law, given by Eq. 3, and are shown in Figure 5, along with the corresponding electrode configurations.

Figure 5

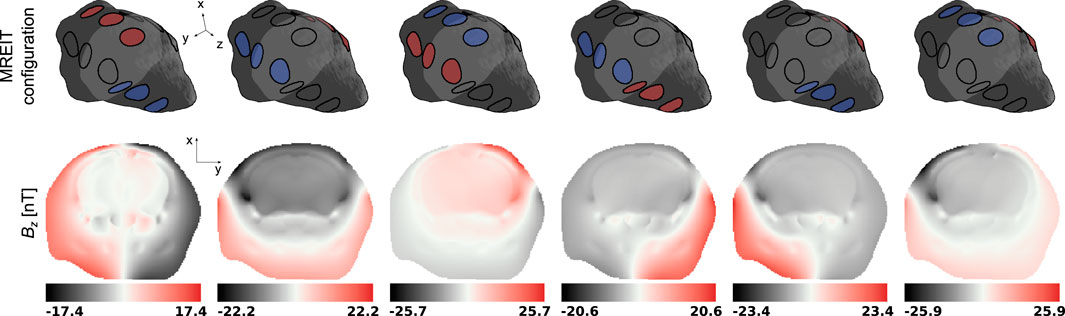
Figure 5. Magnetic flux density B_z in a representative slice of the mouse head model for the 6 electrode group configurations in the MREIT numerical experiment. The representative slice is represented in light gray in the mouse head diagrams.

Then, the six B_z distributions and electric fields evaluated at each iteration of the harmonic B_z algorithm were combined into a global system of equations, Eq. 7, where the electric conductivity was the unknown to be solved for. The true and reconstructed conductivity distributions are shown in a representative slice in Figure 6.

Figure 6

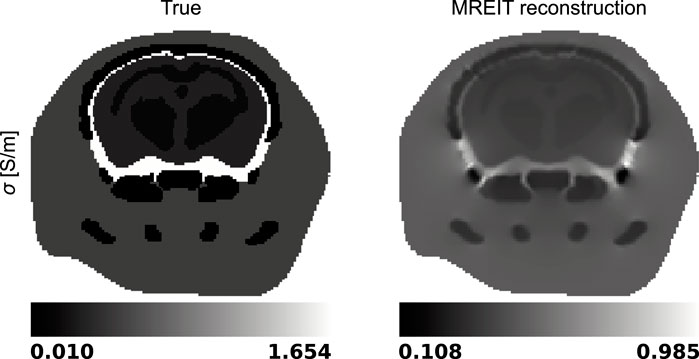
Figure 6. True and reconstructed electric conductivity distributions in a representative slice of the mouse head model.

Finally, the three components of the electric current densities corresponding to the two electrode configurations and evaluated using the true and reconstructed conductivity distributions are presented in Figure 7. The last row of each panel indicates the relative reconstruction error.

Figure 7

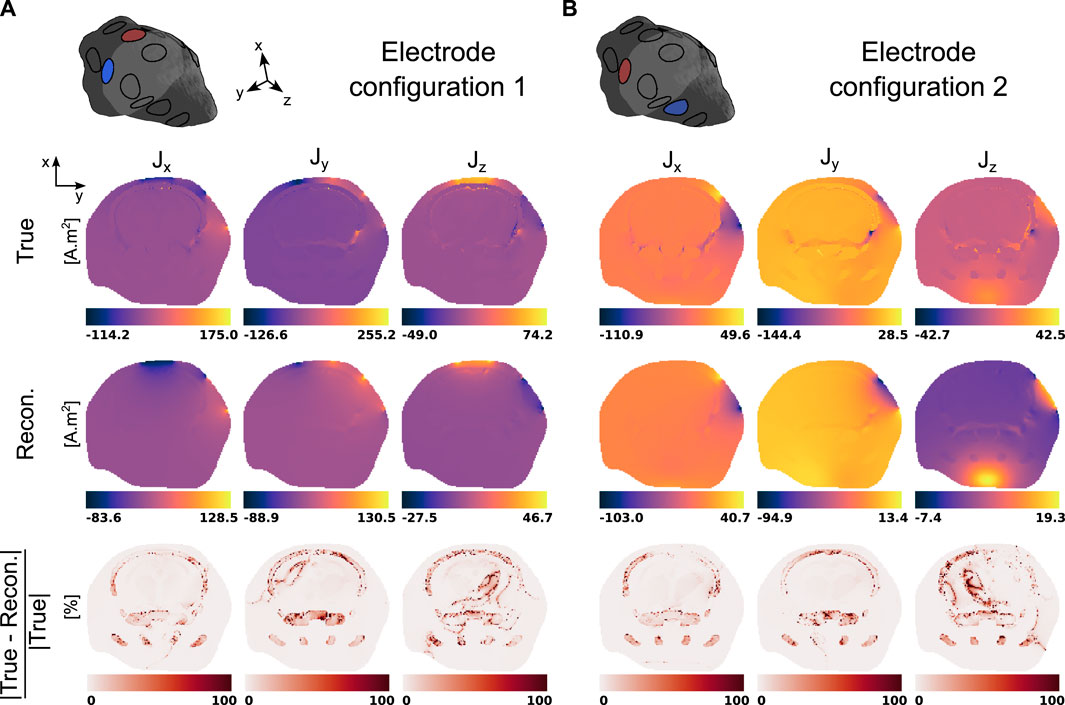
Figure 7. True and reconstructed electric current densities in a representative slice of the mouse head model for the two two-electrode configurations. (A) Electrode configuration 1 (2, 11). (B) Electrode configuration 2 (11, 5).

4 Discussion

We detailed a methodology incorporating NIBS, MRE, and MREIT that shows potential in neuroscience to advance the study of complex cerebral electromechanical interactions [59, 92]. MRE non-invasively probes the biomechanics of the brain, which is an undisputed biomarker of tissue health [93–96], and a proxy for brain activity characterization according to recent research [42, 54, 59]. NIBS has historically attempted to reduce symptoms linked to neurological disorders [97, 98], and has increasingly used head conductivity models to map resulting electrical current patterns [99], which MREIT has the potential to provide [38, 100]. This work reviewed each technique and simulated the pipeline as we envision it in an experimental settings.

The amplitudes and relative orientations of the NIBS currents and the magnetic field of the MR system govern the size of the Lorentz BF shown in Figure 2. In our simulations, a typical current intensity of 1 mA was used, in agreement with a previous TES study [34]. The unusual choice of 11.7 T for modelling the MR’s magnetic flux density was made with the aim of investigating the effects of maximised Lorentz BF on the elastography pipeline. This high field scenario is challenging experimentally (MRE [101, 102], MREIT [103, 104]) and presents limited benefits for our methodology compared with more accessible lower field systems used for human (1.5, 3, 7 T) and small animal imaging (7 T). The absence of Lorentz BF-induced effects in the elastography reconstructions at 11.7 T suggests that MRE and NIBS imaging may be performed in humans at lower field strengths, as will be discussed below.

The displacements generated in an MRE acquisition are represented in Figure 3 and show the respective responses of the brain model to surface actuation and Lorentz BF. Although the interior patterns of displacements induced by pure Dirichlet BC also depend on the biomechanics of the material, care was taken to model realistic conditions (displacement field [59, 105, 106] and viscoelasticity values [83]). Figure 3 showed that pure Dirichlet BC-induced motions dominate the Lorentz BF contribution, which consistently reproduces the order of magnitude predicted by Roth et al. (5–13-nm motion amplitude) [64, 66]. Under such conditions, the NLI method applied to displacement fields dominated by Dirichlet BCs (Dirichlet BC and Dirichlet BC + Lorentz forces) achieved quantitative reconstructions for both storage and loss moduli, as shown in Figures 4A, B, although the storage modulus dominated the loss modulus in all the anatomical domains, similarly to [107]. In these images, the blurred contours at material interfaces occurred because of the intrinsic limitation of elastography reconstructions when the size of the domain to identify is smaller than half of the induced wavelength [108]. From detection and reconstruction perspectives, these results suggest that exMRE and tACS may be performed simultaneously. In intrinsic MRE, the relatively large motion amplitudes due to the cardiac pressure pulse [109] indicate that combined MRE + tACS imaging would also be possible using intrinsic activation [51], although care would need to be taken regarding the tissue’s response rate to electrical stimulation relative to the cardiac frequency and MR motion encoding periods. Resolving the Lorentz BF-induced motion would be an elegant approach to MRE + tACS, however the low amplitude of the displacements shown in Figure 3C would likely be obscured from detection within tACS safety limits using current MR systems and sequences, especially at more available 1.5 T, 3 T, and 7 T systems, where weaker magnetic fields produce weaker Lorentz BF. In addition, the NLI reconstructions based on Lorentz BF-induced motions were unsuccessful due to the data-model mismatch arising from the presence of unaccounted body forces (f_b = 0 in Eq. 12).

MREIT originally used the harmonic B_z algorithm to reconstruct electrical conductivity distributions. This approach has demonstrated a good ability to differentiate structures with impedance contrasts in the presence of data with high signal-to-noise ratios. Figures 5, 6 confirmed this observation and showed recovered distributions of the electric conductivity consistent with the material structure. However, the harmonic B_z method failed to achieve quantitative conductivity estimates, which has also been observed in other published works [110, 111]. The potential of electrical conductivity as a biomarker of pathological tissues has been investigated [112–116], but thus far, MREIT has mostly developed into a tool used for studying the brain’s response to electrical stimulation using modelling. The difficulty in accurately measuring the weak signals generated by MREIT currents explains the limited application of conductivity mapping using MR, although improvements in pulse sequence design have recently been reported [41]. Figure 7 illustrates a typical objective of MREIT consisting in evaluating current density distributions in the imaged brain using the reconstructed electrical conductivity. Higher error levels in the current density reconstructions are found at the interface and within segments of lower conductivity, which reflects the limitations of the harmonic B_z algorithm in such regions. The additional errors visible in J_z images, the z component of the current density, are likely due to the tomographic nature of the reconstruction process.

In practice, NIBS, MRE, and MREIT may be performed through repeated scans within a single imaging session using an all-in-one experimental settings. The acoustic waves in MRE are usually transmitted through a vibrating device placed below or in front of the mouse [105, 106], and electric currents are administered using adjustable scalp electrodes. A challenge in exMRE + tACS experiments may arise from the stability of the setup during acquisitions. Electrical wires as well as head electrodes are experiencing oscillating Lorentz forces and should thus be firmly attached to a fixed head holder. The tACS currents were assumed to have a negligible effect on the MRE acquisition as MRE sequences often involve bipolar scans where the displacement field is sampled twice with opposite MEG polarities, thus canceling out persistent electric current related phase artifacts [117]. Finally, the eddy currents resulting from the oscillation of the conductive brain tissue in a magnetic field are second order effects and were not considered in this work.

5 Limitations

Our study incorporates simplifications and limitations, which warrant further discussion and contextualization. First, five main anatomical domains were integrated in the model to keep the simulation reasonably convenient to manipulate. Although a more detailed representation of structural constituents would better approximate real tissues and further challenge the reconstruction aspects, the proposed model was sufficiently detailed to tackle the study’s specific inquiries. Then, electrodes were modelled as simple disks on the surface of the mouse head to which a normal current density was applied. Whereas this setting does not physically model a metal electrode in contact with skin tissues, it does approximate the MREIT experimental condition where recessed electrodes are used in order to avoid radio-frequency shielding issues related to metal objects placed nearby the imaged field of view. Finally, the same frequency was used for both the tACS current and the exMRE actuation. This characteristic was not crucial in our simulations since the contribution of the tACS-induced motion to the total displacement field were negligible. In ultimate experimental investigations aimed at segregating these contributions, it is worth noting that our simulated settings would be similar to a mono-frequency actuation with a full-waveform encoding scheme where the frequency of the MEG is specifically chosen to match that of the actuation, leading to the acquisition of both Lorentz BF and external actuator induced displacements at 900 Hz. If the mechanical actuator and the tACS system were operating at different frequencies, each motion contribution may be investigated separately by selecting the MEG frequency accordingly.

6 Conclusion

Numerical simulations of MR elastography and MR electrical impedance tomography in the context of MR-assisted transcranial electrical stimulation of the mouse brain were presented. Results suggest that simultaneous tACS and exMRE would be experimentally viable. Optimization of NIBS necessitates precise evaluation of the tACS current flow patterns and subject-dependent electrical conductivity models, which the added MREIT session provides although improvements in the reconstruction method are needed. The benefits of multi-physics (and multi-modality) imaging approaches have been addressed previously in the context of breast cancer, where MRE, electrical impedance tomography, microwave-imaging, and near-infrared spectroscopy were seen as complementary to each other within a global diagnostic and computational framework [118]. The unification of electrical stimulation along with the monitoring of mechanical and electrical brain responses may provide greater neuronal activity mapping and brain function characterization possibilities together than in isolation.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Author contributions

GF: Conceptualization, Formal Analysis, Methodology, Software, Validation, Writing–original draft. EV: Software, Supervision, Writing–review and editing. GG: Conceptualization, Writing–review and editing. GC: Funding acquisition, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was partially funded by the Natural Sciences and Engineering Research Council of Canada (#2022-03729 and Discovery #06660).

Conflict of interest

GG was employed by Philips Healthcare Canada.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Silvanto J, Cowey A, Lavie N, Walsh V. Striate cortex (v1) activity gates awareness of motion. Nat Neurosci (2005) 8:143–4. doi:10.1038/nn1379

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Plewnia C, Reimold M, Najib A, Brehm B, Reischl G, Plontke SK, et al. Dose-dependent attenuation of auditory phantom perception (tinnitus) by pet-guided repetitive transcranial magnetic stimulation. Hum Brain Mapp (2007) 28:238–46. doi:10.1002/hbm.20270

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Muellbacher W, Ziemann U, Wissel J, Dang N, Kofler M, Facchini S, et al. Early consolidation in human primary motor cortex. Nature (2002) 415:640–4. doi:10.1038/nature712

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Polania R, Nitsche MA, Ruff CC. Studying and modifying brain function with non-invasive brain stimulation. Nat Neurosci (2018) 21:174–87. doi:10.1038/s41593-017-0054-4

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Reis J, Schambra HM, Cohen LG, Buch ER, Fritsch B, Zarahn E, et al. Noninvasive cortical stimulation enhances motor skill acquisition over multiple days through an effect on consolidation. Proc Natl Acad Sci (2009) 106:1590–5. doi:10.1073/pnas.0805413106

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bolognini N, Rossetti A, Maravita A, Miniussi C. Seeing touch in the somatosensory cortex: atms study of the visual perception of touch. Hum Brain Mapp (2011) 32:2104–14. doi:10.1002/hbm.21172

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Tarapore PE, Findlay AM, Honma SM, Mizuiri D, Houde JF, Berger MS, et al. Language mapping with navigated repetitive tms: proof of technique and validation. Neuroimage (2013) 82:260–72. doi:10.1016/j.neuroimage.2013.05.018

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Holland R, Leff AP, Josephs O, Galea JM, Desikan M, Price CJ, et al. Speech facilitation by left inferior frontal cortex stimulation. Curr Biol (2011) 21:1403–7. doi:10.1016/j.cub.2011.07.021

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sparing R, Thimm M, Hesse MD, Kuest J, Karbe H, Fink GR. Bidirectional alterations of interhemispheric parietal balance by non-invasive cortical stimulation. Brain (2009) 132:3011–20. doi:10.1093/brain/awp154

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ashbridge E, Walsh V, Cowey A. Temporal aspects of visual search studied by transcranial magnetic stimulation. Neuropsychologia (1997) 35:1121–31. doi:10.1016/s0028-3932(97)00003-1

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Oliveri M, Turriziani P, Carlesimo GA, Koch G, Tomaiuolo F, Panella M, et al. Parieto-frontal interactions in visual-object and visual-spatial working memory: evidence from transcranial magnetic stimulation. Cereb Cortex (2001) 11:606–18. doi:10.1093/cercor/11.7.606

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang JX, Rogers LM, Gross EZ, Ryals AJ, Dokucu ME, Brandstatt KL, et al. Targeted enhancement of cortical-hippocampal brain networks and associative memory. Science (2014) 345:1054–7. doi:10.1126/science.1252900

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kadosh RC, Soskic S, Iuculano T, Kanai R, Walsh V. Modulating neuronal activity produces specific and long-lasting changes in numerical competence. Curr Biol (2010) 20:2016–20. doi:10.1016/j.cub.2010.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Santarnecchi E, Polizzotto N, Godone M, Giovannelli F, Feurra M, Matzen L, et al. Frequency-dependent enhancement of fluid intelligence induced by transcranial oscillatory potentials. Curr Biol (2013) 23:1449–53. doi:10.1016/j.cub.2013.06.022

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Philiastides MG, Auksztulewicz R, Heekeren HR, Blankenburg F. Causal role of dorsolateral prefrontal cortex in human perceptual decision making. Curr Biol (2011) 21:980–3. doi:10.1016/j.cub.2011.04.034

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Beharelle AR, Polania R, Hare TA, Ruff CC. Transcranial stimulation over frontopolar cortex elucidates the choice attributes and neural mechanisms used to resolve exploration-exploitation trade-offs. J Neurosci (2015) 35:14544–56. doi:10.1523/JNEUROSCI.2322-15.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Marechal MA, Cohn A, Ugazio G, Ruff CC. Increasing honesty in humans with noninvasive brain stimulation. Proc Natl Acad Sci (2017) 114:4360–4. doi:10.1073/pnas.1614912114

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Strang S, Gross J, Schuhmann T, Riedl A, Weber B, Sack AT. Be nice if you have to - the neurobiological roots of strategic fairness. Soc Cogn Affective Neurosci (2015) 10:790–6. doi:10.1093/scan/nsu114

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ruff CC, Ugazio G, Fehr E. Changing social norm compliance with noninvasive brain stimulation. Science (2013) 342:482–4. doi:10.1126/science.1241399

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Knoch D, Pascual-Leone A, Meyer K, Treyer V, Fehr E. Diminishing reciprocal fairness by disrupting the right prefrontal cortex. Science (2006) 314:829–32. doi:10.1126/science.1129156

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Buss SS, Fried PJ, Pascual-Leone A. Therapeutic noninvasive brain stimulation in alzheimer’s disease and related dementias. Curr Opin Neurol (2019) 32:292–304. doi:10.1097/wco.0000000000000669

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gonsalvez I, Baror R, Fried P, Santarnecchi E, Pascual-Leone A. Therapeutic noninvasive brain stimulation in alzheimer’s disease. Curr Alzheimer Res (2017) 14:362–76. doi:10.2174/1567205013666160930113907

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Menardi A, Rossi S, Koch G, Hampel H, Vergallo A, Nitsche MA, et al. Toward noninvasive brain stimulation 2.0 in alzheimer’s disease. Ageing Res Rev (2022) 75:101555. doi:10.1016/j.arr.2021.101555

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Brechet L, Yu WT, Biagi MC, Ruffini G, Gagnon M, Manor B, et al. Patient-tailored, home-based non-invasive brain stimulation for memory deficits in dementia due to alzheimer’s disease. Front Neurol (2021) 12:598135. doi:10.3389/fneur.2021.598135

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hsu WY, Ku YX, Zanto TP, Gazzaley A. Effects of noninvasive brain stimulation on cognitive function in healthy aging and alzheimer’s disease: a systematic review and meta-analysis. Neurobiol Aging (2015) 36:2348–59. doi:10.1016/j.neurobiolaging.2015.04.016

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Madrid J, Benninger DH. Non-invasive brain stimulation for Parkinson’s disease: clinical evidence, latest concepts and future goals: a systematic review. J Neurosci Methods (2021) 347:108957. doi:10.1016/j.jneumeth.2020.108957

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Rektorova I, Anderkova L. Noninvasive brain stimulation and implications for nonmotor symptoms in Parkinson’s disease. Int Rev Neurobiol (2017) 134:1091–110. doi:10.1016/bs.irn.2017.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zheng HB, Liu B, Shen J, Xie F, Ji QM, Zhu XY. Non-invasive brain stimulation for treating psychiatric symptoms in Parkinson’s disease: a systematic review and meta-analysis. J Clin Neurosci (2022) 106:83–90. doi:10.1016/j.jocn.2022.10.013

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ni R, Yuan Y, Yang L, Meng QJ, Zhu Y, Zhong YY, et al. Novel non-invasive transcranial electrical stimulation for Parkinson’s disease. Front Aging Neurosci (2022) 14:880897. doi:10.3389/fnagi.2022.880897

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Cosentino G, Todisco M, Blandini F. Noninvasive neuromodulation in Parkinson's disease: neuroplasticity implication and therapeutic perspectives. Handb Clin Neurol (2022) 184:185–98. doi:10.1016/B978-0-12-819410-2.00010-2

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pacheco F, Guiomar R, Brunoni AR, Buhagiar R, Evagorou O, Roca-Lecumberri A, et al. Efficacy of non-invasive brain stimulation in decreasing depression symptoms during the peripartum period: a systematic review. J Psychiatr Res (2021) 140:443–60. doi:10.1016/j.jpsychires.2021.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bucur M, Papagno C. A systematic review of noninvasive brain stimulation for post-stroke depression. J Affective Disord (2018) 238:69–78. doi:10.1016/j.jad.2018.05.026

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Datta A, Bansal V, Diaz J, Patel J, Reato D, Bikson M. Gyri-precise head model of transcranial direct current stimulation: improved spatial focality using a ring electrode versus conventional rectangular pad. Brain Stimulation (2009) 2:201–7.e1. doi:10.1016/j.brs.2009.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Grossman N, Bono D, Dedic N, Kodandaramaiah SB, Rudenko A, Suk HJ, et al. Noninvasive deep brain stimulation via temporally interfering electric fields. Cell (2017) 169:1029–41.e16. doi:10.1016/j.cell.2017.05.024

PubMed Abstract | CrossRef Full Text | Google Scholar

35. von Conta J, Kasten FH, Curcic-Blake B, Aleman A, Thielscher A, Herrmann CS. Interindividual variability of electric fields during transcranial temporal interference stimulation (ttis). Scientific Rep (2021) 11:20357. doi:10.1038/s41598-021-99749-0

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Violante I, Alania K, Cassarà A, Neufeld E, Acerbo E, Williamson A, et al. Non-invasive temporal interference electrical stimulation of the human hippocampus. Brain Stimulation (2023) 16:408. doi:10.1016/j.brs.2023.01.833

CrossRef Full Text | Google Scholar

37. di Biase L, Falato E, Di Lazzaro V. Transcranial focused ultrasound (tfus) and transcranial unfocused ultrasound (tus) neuromodulation: from theoretical principles to stimulation practices. Front Neurol (2019) 10:549. doi:10.3389/fneur.2019.00549

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Sajib SZK, Sadleir R. Magnetic resonance electrical impedance tomography. Cham: Springer International Publishing (2022). p. 157–83.

CrossRef Full Text | Google Scholar

39. Eroglu HH, Puonti O, Goksu C, Gregersen F, Siebner HR, Hanson LG, et al. On the reconstruction of magnetic resonance current density images of the human brain: pitfalls and perspectives. Neuroimage (2021) 243:118517. doi:10.1016/j.neuroimage.2021.118517

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Goksu C, Hanson LG, Siebner HR, Ehses P, Scheffler K, Thielscher A. Human in-vivo brain magnetic resonance current density imaging (mrcdi). Neuroimage (2018) 171:26–39. doi:10.1016/j.neuroimage.2017.12.075

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Goksu C, Scheffler K, Ehses P, Hanson LG, Thielscher A. Sensitivity analysis of magnetic field measurements for magnetic resonance electrical impedance tomography (mreit). Magn Reson Med (2018) 79:748–60. doi:10.1002/mrm.26727

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Forouhandehpour R, Bernier M, Gilbert G, Butler R, Whittingstall K, Van Houten E. Cerebral stiffness changes during visual stimulation: differential physiological mechanisms characterized by opposing mechanical effects. Neuroimage: Rep (2021) 1:100014. doi:10.1016/j.ynirp.2021.100014

CrossRef Full Text | Google Scholar

43. Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science (1995) 269:1854–7. doi:10.1126/science.7569924

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sack I, Beierbach B, Wuerfel J, Klatt D, Hamhaber U, Papazoglou S, et al. The impact of aging and gender on brain viscoelasticity. Neuroimage (2009) 46:652–7. doi:10.1016/j.neuroimage.2009.02.040

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Weaver JB, Pattison AJ, McGarry MD, Perreard IM, Swienckowski JG, Eskey CJ, et al. Brain mechanical property measurement using mre with intrinsic activation. Phys Med Biol (2012) 57:7275–87. doi:10.1088/0031-9155/57/22/7275

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Zorgani A, Souchon R, Dinh AH, Chapelon JY, Ménager JM, Lounis S, et al. Brain palpation from physiological vibrations using mri. Proc Natl Acad Sci (2015) 112:12917–21. doi:10.1073/pnas.1509895112

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Clayton EH, Genin GM, Bayly PV. Transmission, attenuation and reflection of shear waves in the human brain. J R Soc Interf (2012) 9:2899–910. doi:10.1098/rsif.2012.0325

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tzschätzsch H, Guo J, Dittmann F, Hirsch S, Barnhill E, Jöhrens K, et al. Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves. Med Image Anal (2016) 30:1–10. doi:10.1016/j.media.2016.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Testu J, McGarry MDJ, Dittmann F, Weaver JB, Paulsen KD, Sack I, et al. Viscoelastic power law parameters of in vivo human brain estimated by mr elastography. J Mech Behav Biomed Mater (2017) 74:333–41. doi:10.1016/j.jmbbm.2017.06.027

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Hiscox LV, McGarry MDJ, Schwarb H, Van Houten EEW, Pohlig RT, Roberts N, et al. Standard-space atlas of the viscoelastic properties of the human brain. Hum Brain Mapp (2020) 41:5282–300. doi:10.1002/hbm.25192

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Ingeberg MB, Van Houten E, Zwanenburg JJM. Estimating the viscoelastic properties of the human brain at 7 t mri using intrinsic mre and nonlinear inversion. Hum Brain Mapp (2023) 6575–91. doi:10.1002/hbm.26524

CrossRef Full Text | Google Scholar

52. McGarry MDJ, Johnson CL, Sutton BP, Georgiadis JG, Van Houten EEW, Pattison AJ, et al. Suitability of poroelastic and viscoelastic mechanical models for high and low frequency mr elastography. Med Phys (2015) 42:947–57. doi:10.1118/1.4905048

PubMed Abstract | CrossRef Full Text | Google Scholar

53. McGarry M, Van Houten E, Solamen L, Gordon-Wylie S, Weaver J, Paulsen K. Uniqueness of poroelastic and viscoelastic nonlinear inversion mr elastography at low frequencies. Phys Med Biol (2019) 64:075006. doi:10.1088/1361-6560/ab0a7d

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Delgorio PL, Hiscox LV, Daugherty AM, Sanjana F, McIlvain G, Pohlig RT, et al. Structure-function dissociations of human hippocampal subfield stiffness and memory performance. J Neurosci (2022) 42:7957–68. doi:10.1523/jneurosci.0592-22.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Daugherty AM, Schwarb HD, McGarry MDJ, Johnson CL, Cohen NJ. Magnetic resonance elastography of human hippocampal subfields: Ca3-dentate gyrus viscoelasticity predicts relational memory accuracy. J Cogn Neurosci (2020) 32:1704–13. doi:10.1162/jocn_a_01574

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Hiscox LV, Johnson CL, McGarry MDJ, Schwarb H, van Beek EJR, Roberts N, et al. Hippocampal viscoelasticity and episodic memory performance in healthy older adults examined with magnetic resonance elastography. Brain Imaging Behav (2020) 14:175–85. doi:10.1007/s11682-018-9988-8

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Schwarb H, Johnson CL, Daugherty AM, Hillman CH, Kramer AF, Cohen NJ, et al. Aerobic fitness, hippocampal viscoelasticity, and relational memory performance. Neuroimage (2017) 153:179–88. doi:10.1016/j.neuroimage.2017.03.061

PubMed Abstract | CrossRef Full Text | Google Scholar

58. McIlvain G, Tracy JB, Chaze CA, Petersen DA, Villermaux GM, Wright HG, et al. Brain stiffness relates to dynamic balance reactions in children with cerebral palsy. J Child Neurol (2020) 35:463–71. doi:10.1177/0883073820909274

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Patz S, Fovargue D, Schregel K, Nazari N, Palotai M, Barbone PE, et al. Imaging localized neuronal activity at fast time scales through biomechanics. Sci Adv (2019) 5:eaav3816. doi:10.1126/sciadv.aav3816

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Song AW, Takahashi AM. Lorentz effect imaging. Magn Reson Imaging (2001) 19:763–7. doi:10.1016/s0730-725x(01)00406-4

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Truong TK, Avram A, Song AW. Lorentz effect imaging of ionic currents in solution. J Magn Reson (2008) 191:93–9. doi:10.1016/j.jmr.2007.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Truong TK, Song AW. Finding neuroelectric activity under magnetic-field oscillations (NAMO) with magnetic resonance imaging in vivo. Proc Natl Acad Sci (2006) 103:12598–601. doi:10.1073/pnas.0605486103

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Truong TK, Wilbur JL, Song AW. Synchronized detection of minute electrical currents with mri using lorentz effect imaging. J Magn Reson (2006) 179:85–91. doi:10.1016/j.jmr.2005.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Roth BJ, Basser PJ. Mechanical model of neural tissue displacement during lorentz effect imaging. Magn Reson Med (2009) 61:59–64. doi:10.1002/mrm.21772

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Roth BJ. The role of magnetic forces in biology and medicine. Exp Biol Med (2011) 236:132–7. doi:10.1258/ebm.2010.010236

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Roth BJ, Luterek A, Puwal S. The movement of a nerve in a magnetic field: application to mri lorentz effect imaging. Med Biol Eng Comput (2014) 52:491–8. doi:10.1007/s11517-014-1153-y

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Barnhill E, Hollis L, Sack I, Braun J, Hoskins PR, Pankaj P, et al. Nonlinear multiscale regularisation in mr elastography: towards fine feature mapping. Med Image Anal (2017) 35:133–45. doi:10.1016/j.media.2016.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Barnhill E, Davies PJ, Ariyurek C, Fehlner A, Braun J, Sack I. Heterogeneous multifrequency direct inversion (hmdi) for magnetic resonance elastography with application to a clinical brain exam. Med Image Anal (2018) 46:180–8. doi:10.1016/j.media.2018.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Barnhill E, Nikolova M, Ariyurek C, Dittmann F, Braun J, Sack I. Fast robust dejitter and interslice discontinuity removal in mri phase acquisitions: application to magnetic resonance elastography. IEEE Trans Med Imaging (2019) 38:1578–87. doi:10.1109/tmi.2019.2893369

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Li Y, Okamoto R, Badachhape A, Wu C, Bayly P, Daphalapurkar N. Simulation of harmonic shear waves in the human brain and comparison with measurements from magnetic resonance elastography. J Mech Behav Biomed Mater (2021) 118:104449. doi:10.1016/j.jmbbm.2021.104449

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digimouse: a 3d whole body mouse atlas from ct and cryosection data. Phys Med Biol (2007) 52:577–87. doi:10.1088/0031-9155/52/3/003

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Chan E, Kovacevic N, Ho SKY, Henkelman RM, Henderson JT. Development of a high resolution three-dimensional surgical atlas of the murine head for strains 129S1/SvImJ and C57Bl/6J using magnetic resonance imaging and micro-computed tomography. Neuroscience (2007) 144:604–15. doi:10.1016/j.neuroscience.2006.08.080

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Hikishima K, Komaki Y, Seki F, Ohnishi Y, Okano HJ, Okano H. In vivo microscopic voxel-based morphometry with a brain template to characterize strain-specific structures in the mouse brain. Scientific Rep (2017) 7:85. doi:10.1038/s41598-017-00148-1

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, et al. User-guided 3d active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage (2006) 31:1116–28. doi:10.1016/j.neuroimage.2006.01.015

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Yazdanian H, Saturnino GB, Thielscher A, Knudsen K. Fast evaluation of the biot-savart integral using fft for electrical conductivity imaging. J Comput Phys (2020) 411:109408. doi:10.1016/j.jcp.2020.109408

CrossRef Full Text | Google Scholar

76. Alekseichuk I, Mantell K, Shirinpour S, Opitz A. Comparative modeling of transcranial magnetic and electric stimulation in mouse, monkey, and human. Neuroimage (2019) 194:136–48. doi:10.1016/j.neuroimage.2019.03.044

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Sajib SZK, Katoch N, Kim HJ, Kwon OI, Woo EJ. Software toolbox for low-frequency conductivity and current density imaging using mri. IEEE Trans Biomed Eng (2017) 64:2505–14. doi:10.1109/TBME.2017.2732502

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Suk Hoon O, Byung Il L, Eung Je W, Soo Yeol L, Min Hyoung C, Ohin K, et al. Conductivity and current density image reconstruction using harmonicB_zalgorithm in magnetic resonance electrical impedance tomography. Phys Med Biol (2003) 48:3101–16. doi:10.1088/0031-9155/48/19/001

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Scott GC, Joy MLG, Armstrong RL, Henkelman RM. Measurement of nonuniform current-density by magnetic-resonance. IEEE Trans Med Imaging (1991) 10:362–74. doi:10.1109/42.97586

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Chaieb L, Antal A, Paulus W. Transcranial alternating current stimulation in the low khz range increases motor cortex excitability. Restorative Neurol Neurosci (2011) 29:167–75. doi:10.3233/rnn-2011-0589

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Antal A, Paulus W. Transcranial alternating current stimulation (tacs). Front Hum Neurosci (2013) 7:317. doi:10.3389/fnhum.2013.00317

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Neudorfer C, Chow CT, Boutet A, Loh A, Germann J, Elias GJB, et al. Kilohertz-frequency stimulation of the nervous system: a review of underlying mechanisms. Brain Stimulation (2021) 14:513–30. doi:10.1016/j.brs.2021.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Hain EG, Klein C, Munder T, Braun J, Riek K, Mueller S, et al. Dopaminergic neurodegeneration in the mouse is associated with decrease of viscoelasticity of substantia nigra tissue. Plos One (2016) 11:e0161179. doi:10.1371/journal.pone.0161179

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol (1996) 41:2251–69. doi:10.1088/0031-9155/41/11/002

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Hirsch S, Braun J, Sack I. Motion encoding and mre sequences. Hoboken, New Jersey, USA: Wiley online books (2017). p. 41–59.

Google Scholar

86. Fang Q, Boas DA. Ieee. Tetrahedral mesh generation from volumetric binary and gray-scale images. In: 2009 IEEE International Symposium on Biomedical Imaging: From Nano To Macro; June, 2009; Boston, MA, USA (2009). p. 1142–5.

Google Scholar

87. Tran AP, Yan S, Fang Q. Improving model-based functional near-infrared spectroscopy analysis using mesh-based anatomical and light-transport models. Neurophotonics (2020) 7:1. 015008–015008. doi:10.1117/1.nph.7.1.015008

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med Biol (1998) 24:1419–35. doi:10.1016/s0301-5629(98)00110-0

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Klein C, Hain EG, Braun J, Riek K, Mueller S, Steiner B, et al. Enhanced adult neurogenesis increases brain stiffness: in vivo magnetic resonance elastography in a mouse model of dopamine depletion. Plos One (2014) 9:e92582. doi:10.1371/journal.pone.0092582

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Van Houten EEW, Paulsen KD, Miga MI, Kennedy FE, Weaver JB. An overlapping subzone technique for mr-based elastic property reconstruction. Magn Reson Med (1999) 42:779–86. doi:10.1002/(sici)1522-2594(199910)42:4<779::aid-mrm21>3.3.co;2-q

PubMed Abstract | CrossRef Full Text | Google Scholar

91. McGarry MDJ, Van Houten EEW, Johnson CL, Georgiadis JG, Sutton BP, Weaver JB, et al. Multiresolution mr elastography using nonlinear inversion. Med Phys (2012) 39:6388–96. doi:10.1118/1.4754649

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Tyler WJ. The mechanobiology of brain function. Nat Rev Neurosci (2012) 13:867–78. doi:10.1038/nrn3383

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Milbocker KA, Williams LT, Caban-Rivera DA, Smith IF, Kurtz S, McGarry MDJ, et al. Magnetic resonance elastography captures a transient benefit of exercise intervention on forebrain stiffness in a rat model of fetal alcohol spectrum disorders. Alcohol: Clin Exp Res (2024) 48:466–77. doi:10.1111/acer.15265

CrossRef Full Text | Google Scholar

94. Huesmann GR, Schwarb H, Smith DR, Pohlig RT, Anderson AT, McGarry MDJ, et al. Hippocampal stiffness in mesial temporal lobe epilepsy measured with mr elastography: preliminary comparison with healthy participants. Neuroimage: Clin (2020) 27:102313. doi:10.1016/j.nicl.2020.102313

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Schregel K, Nazari N, Nowicki MO, Palotai M, Lawler SE, Sinkus R, et al. Characterization of glioblastoma in an orthotopic mouse model with magnetic resonance elastography. Nmr Biomed (2018) 31:e3840. doi:10.1002/nbm.3840

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Fehlner A, Behrens JR, Streitberger KJ, Papazoglou S, Braun J, Bellmann-Strobl J, et al. Higher-resolution mr elastography reveals early mechanical signatures of neuroinflammation in patients with clinically isolated syndrome. J Magn Reson Imaging (2016) 44:51–8. doi:10.1002/jmri.25129

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Acerbo E, Jegou A, Luff C, Dzialecka P, Botzanowski B, Missey F, et al. Focal non-invasive deep-brain stimulation with temporal interference for the suppression of epileptic biomarkers. Front Neurosci (2022) 16:945221. doi:10.3389/fnins.2022.945221

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Nitsche MA, Paulus W. Noninvasive brain stimulation protocols in the treatment of epilepsy: current state and perspectives. Neurotherapeutics (2009) 6:244–50. doi:10.1016/j.nurt.2009.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Saturnino GB, Puonti O, Nielsen JD, Antonenko D, Madsen KH, Thielscher A. Simnibs 2.1: a comprehensive pipeline for individualized electric field modelling for transcranial brain stimulation, In: Brain and human body modeling: computational human modeling at EMBC 2018. Cham: Springer (2019). p. 3–25.

CrossRef Full Text | Google Scholar

100. Neuling T, Wagner S, Wolters C, Zaehle T, Herrmann C. Finite-element model predicts current density distribution for clinical applications of tdcs and tacs. Front Psychiatry (2012) 3:83. doi:10.3389/fpsyt.2012.00083

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Atay SM, Kroenke CD, Sabet A, Bayly PV. Measurement of the dynamic shear modulus of mouse brain tissue in vivo by magnetic resonance elastography. ASME J Biomechanical Eng (2008) 130:021013. doi:10.1115/1.2899575

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Othman SF, Xu HH, Royston TJ, Magin RL. Microscopic magnetic resonance elastography (mu mre). Magn Reson Med (2005) 54:605–15. doi:10.1002/mrm.20584

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Sadleir R, Grant S, Zhang SU, Oh SH, Lee BI, Woo EJ. High field mreit: setup and tissue phantom imaging at 11 t. Physiol Meas (2006) 27:S261–70. doi:10.1088/0967-3334/27/5/s22

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Sadleir RJ, Grant SC, Woo EJ. Can high-field mreit be used to directly detect neural activity? theoretical considerations. Neuroimage (2010) 52:205–16. doi:10.1016/j.neuroimage.2010.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Clayton EH, Garbow JR, Bayly PV. Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by mr elastography. Phys Med Biol (2011) 56:2391–406. doi:10.1088/0031-9155/56/8/005

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Riek K, Millward JM, Hamann I, Mueller S, Pfueller CF, Paul F, et al. Magnetic resonance elastography reveals altered brain viscoelasticity in experimental autoimmune encephalomyelitis. Neuroimage: Clin (2012) 1:81–90. doi:10.1016/j.nicl.2012.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

107. McGarry M, Johnson CL, Sutton BP, Van Houten EEW, Georgiadis JG, Weaver JB, et al. Including spatial information in nonlinear inversion mr elastography using soft prior regularization. IEEE Trans Med Imaging (2013) 32:1901–9. doi:10.1109/tmi.2013.2268978

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Van Houten E, Geymonat G, Krasucki F, Wattrisse B. General guidelines for the performance of viscoelastic property identification in elastography: a monte-carlo analysis from a closed-form solution. Int J Numer Methods Biomed Eng (2023) 39:e3741. doi:10.1002/cnm.3741

CrossRef Full Text | Google Scholar

109. Soellinger M, Rutz AK, Kozerke S, Boesiger P. 3d cine displacement-encoded mri of pulsatile brain motion. Magn Reson Med (2009) 61:153–62. doi:10.1002/mrm.21802

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Meng ZJ, Sajib SZK, Chauhan M, Sadleir RJ, Kim HJ, Kwon OI, et al. Numerical simulations of mreit conductivity imaging for brain tumor detection. Comput Math Methods Med (2013) 2013:1–10. doi:10.1155/2013/704829

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Seo JK, Woo EJ. Magnetic resonance electrical impedance tomography (mreit). Siam Rev (2011) 53:40–68. doi:10.1137/080742932

CrossRef Full Text | Google Scholar

112. Surowiec AJ, Stuchly SS, Barr JR, Swarup A. Dielectric-properties of breast-carcinoma and the surrounding tissues. IEEE Trans Biomed Eng (1988) 35:257–63. doi:10.1109/10.1374

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Jossinet J. Variability of impedivity in normal and pathological breast tissue. Med Biol Eng Comput (1996) 34:346–50. doi:10.1007/bf02520002

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Jossinet J. The impedivity of freshly excised human breast tissue. Physiol Meas (1998) 19:61–75. doi:10.1088/0967-3334/19/1/006

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Haemmerich D, Staelin ST, Tsai JZ, Tungjitkusolmun S, Mahvi DM, Webster JG. In vivo electrical conductivity of hepatic tumours. Physiol Meas (2003) 24:251–60. doi:10.1088/0967-3334/24/2/302

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Zou Y, Guo Z. A review of electrical impedance techniques for breast cancer detection. Med Eng Phys (2003) 25:79–90. doi:10.1016/s1350-4533(02)00194-7

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Flé G, Gilbert G, Grasland-Mongrain P, Cloutier G. Lorentz force induced shear waves for magnetic resonance elastography applications. Scientific Rep (2021) 11:12785. doi:10.1038/s41598-021-91895-9

CrossRef Full Text | Google Scholar

118. Poplack S, Wells W, Paulsen K. Four alternative breast imaging modalities. In: Chap. Four alternative breast imaging modalities. Boston, MA: Springer (2005). p. 1–24.

Google Scholar