Revolutionizing physics: a comprehensive survey of machine learning applications

In the context of the 21st century and the fourth industrial revolution, the substantial proliferation of data has established it as a valuable resource, fostering enhanced computational capabilities across scientific disciplines, including physics. The integration of Machine Learning stands as a prominent solution to unravel the intricacies inherent to scientific data. While diverse machine learning algorithms find utility in various branches of physics, there exists a need for a systematic framework for the application of Machine Learning to the field. This review offers a comprehensive exploration of the fundamental principles and algorithms of Machine Learning, with a focus on their implementation within distinct domains of physics. The review delves into the contemporary trends of Machine Learning application in condensed matter physics, biophysics, astrophysics, material science, and addresses emerging challenges. The potential for Machine Learning to revolutionize the comprehension of intricate physical phenomena is underscored. Nevertheless, persisting challenges in the form of more efficient and precise algorithm development are acknowledged within this review.

1 Introduction

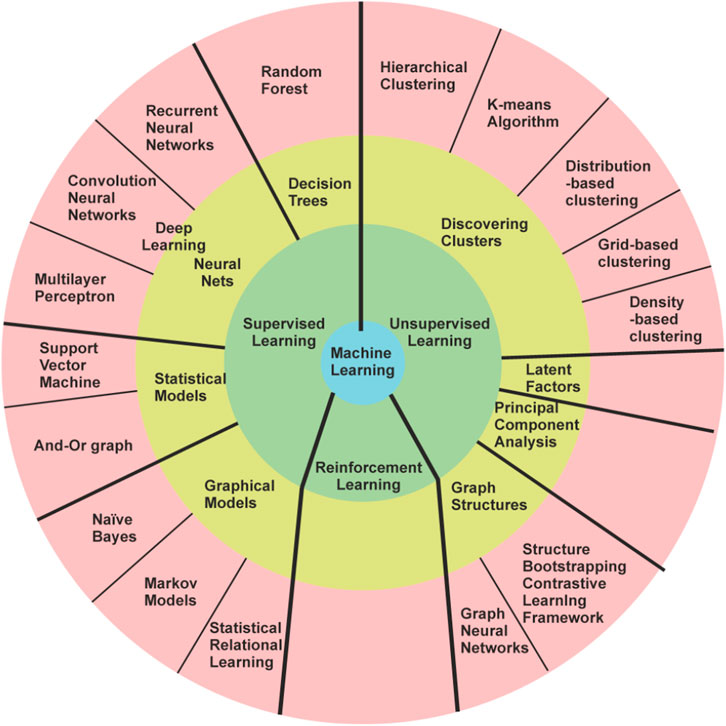
The evolution of programming languages within the context of machine learning techniques is marked by significant milestones. Notably, Alan Turing’s publication of “Computing Machinery and Intelligence” introduced the Turing test, laying the groundwork for AI exploration through human-computer textual interaction [1]. Moreover, the pioneering work of Marvin Minsky and Dean Edmonds in developing Stochastic Neural Analog Reinforcement Calculator (SNARC), the first artificial neural network (ANN) employing 3,000 vacuum tubes to simulate a 40-neuron network, stands as a seminal moment in machine learning history. Additionally, the coining of the term ‘artificial intelligence’ by John McCarthy, Marvin Minsky, Nathaniel Rochester, and Claude Shannon, among other pivotal events, played a foundational role in the emergence of AI. Newell and Simon’s 1956 creation, the Logic Theorist [2] marked a pivotal achievement as it operated as a computer program capable of proving theorems in symbolic logic from Principia Mathematica. This groundbreaking program simulated human problem-solving abilities and significantly influenced the burgeoning field of information-processing psychology, shaping the foundational principles still integral to cognitive psychology and human factors studies today. Frank Rosenblatt’s development of the perceptron, an early form of an artificial neural network (ANN) [3–5], revolutionized machine learning by introducing a model capable of learning from input data and adjusting its parameters to make predictions. Although limited in solving only linearly separable problems, the perceptron laid the foundation for modern neural networks, inspiring subsequent advancements in the field of artificial intelligence and pattern recognition [6]. Oliver Selfridge’s 1959 paper, “Pandemonium: A Paradigm for Learning,” [7] introduced a revolutionary model in machine learning, presenting a framework of interconnected ‘demons’ responsible for cognitive tasks like pattern recognition. This hierarchical model emphasized the collaboration of simpler components to achieve complex cognitive functions, influencing the evolution of neural networks and significantly impacting the fields of artificial intelligence and cognitive psychology. These milestones collectively define the trajectory of programming languages in shaping the landscape of machine learning advancements. In general, ML algorithms are divided into supervised and unsupervised learning [8] as shown in Table 1 and Figures 1 and 2.

TABLE 1

TABLE 1. Difference between supervised and unsupervised learning.

FIGURE 1

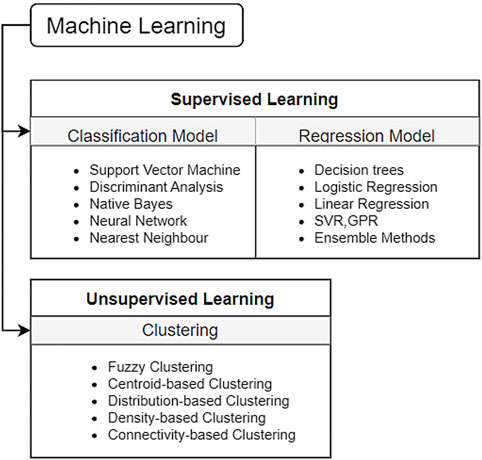
FIGURE 1. Classification of the machine learning algorithm [9].

FIGURE 2

FIGURE 2. Schematic classification of ML.

Apart from Supervised and Unsupervised learning, reinforcement learning [10] is widely used in different aspects of robotics. In reinforcement learning based on the actions of algorithms in the environment, it is given some rewards. Considering the goal of maximizing the rewards, the algorithm learns on its own. Using reinforcement learning makes it easier to design complex, hard-to-hand-engineer frameworks, and rules that are necessary for robots to perform a task. Creating rules becomes complex because the real environments that robots face are not controllable, so a robot trained in a controlled environment with deterministic rules will perform poorly in real-world instances. Through trial-and-error interactions with its surroundings, a robot can independently learn the best behaviour through reinforcement learning (RL) [11]. Further in this section, we will be discussing all these learning processes along with different algorithms in detail.

In Supervised Learning [12], the network is provided with an output for every input pattern. The goal of these algorithms is to map input x to output y. The weights used by the model are updated during the prediction process such that the model produces outputs close to the actual output. As evident from Table 1, supervised learning is utilized for regression and classification-based problems. The goal of regression is to predict one or more target continuous outputs from a given input vector [13]. Similar to regression, classification happens to be one of the most common tasks in ML. Here the discriminant is a function that considers the input and maps it to one of the classes, i.e., discrete outputs [14]. It should be noted that input vectors also can contain continuous and/or discrete parameters. The continuous input data can be easily treated by ML, but discrete data should be encoded or treated by Decision Tree only. There are many predefined models in ML following multiple methodologies e.g., Decision Trees follow the divide and conquer algorithms [15], Naïve Bayes algorithm [16] follows a probabilistic approach, and so on. The simplest model in classification is logistic regression [17] which uses the Gradient Descent approach for parametric estimation. Based on the number of classes i.e., 2 or more, the classifiers are divided into binary and multivariate classifiers. A comparative analysis of Supervised ML Techniques is provided in Table 2. However, it is important to note that there may be several drawbacks of using some methods that although are powerful, fail to account for various case scenarios. One such technique is the Decision Tree. There are several limitations in the use of Decision Trees. One significant limitation of the Decision Tree method is its comparatively low model accuracy when compared to other methods using the same data set [18–20]. The number of samples plays a crucial role in determining the depth of the Decision Tree, which in turn affects the accuracy of its predictions. Furthermore, both the root and each node of the Decision Tree divide the samples in the feature space into two groups using a plane perpendicular to the feature parameter axis, resulting in a rather coarse division. These factors hinder the widespread application of Decision Trees in various domains. Second one is overfitting. Decision Trees can be prone to overfitting, especially if they are very deep. As a result, the model may fit the training data too closely, leading to poor generalization on new data [18]. Third one is sensitivity to noise. Decision Trees can be sensitive to noise in the data, as they aim to create rules that best separate the training examples. Therefore, if the data contains noise or outliers, Decision Trees may create incorrect splits [18–20]. Forth one is inefficiency with large datasets. Building and using Decision Trees can be computationally expensive, especially with large volumes of data. This can limit their practical use in some cases. Last one is multicollinearity issue. Decision Trees may struggle with handling multicollinearity, where features in the data are highly correlated with each other. This can result in incorrect splits and reduced model effectiveness [18–21]. While Naive Bayes presents a viable classification approach, its reliance on assuming distinct and independent features poses limitations in practical scenarios. The algorithm’s inability to generate predictions in the absence of training instances for a particular class results in zero probabilities, rendering it unsuitable for real-life applications where comprehensive training data might not cover all possible scenarios. This issue is commonly referred to as the ‘zero probability/frequency problem’ in the Naive Bayes model [22]. Future research efforts must focus on mitigating this challenge to enhance the algorithm’s applicability in real-world prediction tasks.

TABLE 2

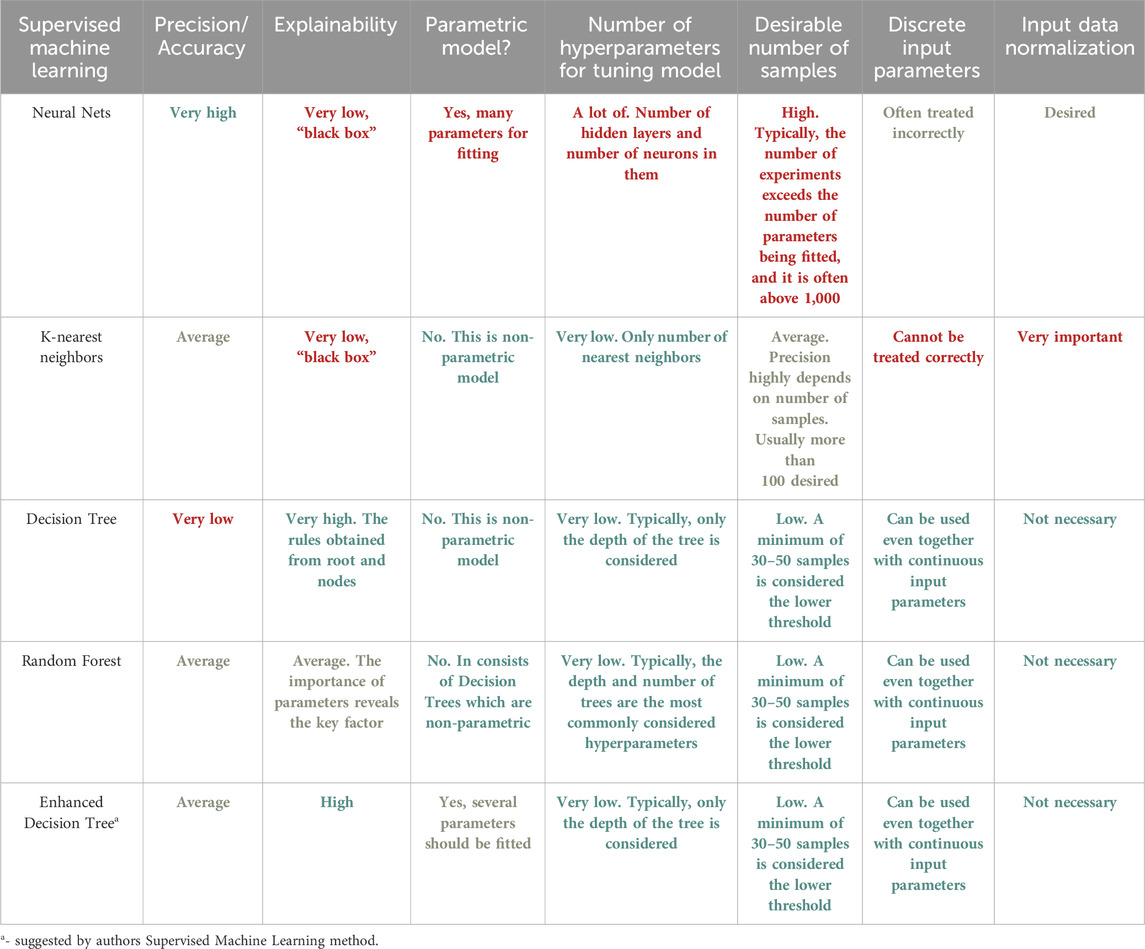
TABLE 2. Comparative analysis of various Supervised Machine Learning Techniques. Green means excellent feature, orange—average feature, red—bad feature.

In unsupervised learning, our available data is solely the input. Here, the aim is to find regularities and (dis)similarities in the input data [23]. This is also called descriptive or knowledge discovery. Unsupervised Learning is widely used in discovering clusters [15], latent factors [24] and graph structures [25]. To build clusters multiple algorithms like K-means [26] and Hierarchical clustering [27] are used. In image analysis, the dimensions of images notably impact the reduction of algorithmic time complexity. To address this, we utilize Principal Component Analysis (PCA) [28], an unsupervised technique that condenses high-dimensional image data into a lower-dimensional space. PCA identifies and captures key variations within the dataset, streamlining subsequent computational tasks like feature extraction and classification by emphasizing crucial image information while reducing computational overhead.

In the realm of physics, the choice between supervised and unsupervised learning techniques hinges on the nature of the available data and the specific objectives of the analysis. In scenarios where labelled datasets are abundant and well-defined, supervised learning proves to be a powerful tool [29]. For instance, in experimental setups where outcomes are known and categorized, such as particle identification in high-energy physics experiments, supervised learning algorithms like convolutional neural networks can efficiently classify and predict outcomes based on training data [29]. On the other hand, unsupervised learning techniques shine in situations where the data lacks clear labels or predetermined classifications. In experimental investigations where patterns or anomalies are sought without prior knowledge, clustering algorithms like k-means or hierarchical clustering can uncover hidden structures within datasets [30,31]. An example could be the analysis of cosmic microwave background radiation maps, where unsupervised techniques can reveal subtle patterns or anomalies that might elude human intuition. Table 2 and Table 3 display a comparisons of supervised and unsupervised techniques.

TABLE 3

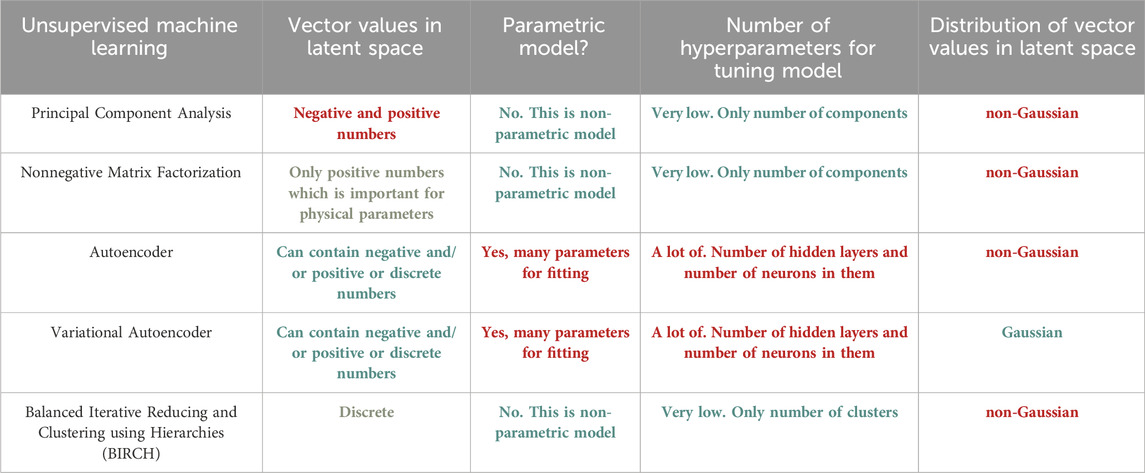
TABLE 3. Comparative analysis of various Unsupervised Machine Learning Techniques. Green means excellent feature, orange—average feature, red—bad feature.

In reinforcement learning, we have a learner who is a decision-making agent that takes actions in an environment and receives a reward for their action in trying to solve a problem. After a set of trial-and-error runs, it learns the best policy to maximize the reward. However, in the modern era, Deep Learning is a widely popular tool. The major reason for preferring Deep Learning over ML is the capability of extracting features automatically [32,33]. However, the major requirement here is to have a lot of data. There exists a diverse array of algorithms within Deep Learning such as Multilayer Perceptron [21], Recurrent Neural Networks [22], and Convolutional Neural Networks [23], Generative Adversarial Networks (GANs), Long Short-Term Memory Networks (LSTMs), Autoencoders, Transformer Networks, Reinforcement Learning models [34–38] such as Deep Q-Networks (DQN), Capsule Networks (CapsNets) and various other architectures designed to address specific tasks, each offering unique capabilities and applications within the realm of Deep Learning [39–41]. Deep Learning has also been attractive in recent days due to better activation functions, better optimization functions, and better regularization techniques.

A Multilayer Perceptron [39,42,43] is a class of feed-forward neural networks that particularly involves one input and output layer and multiple hidden layers. It is a supervised learning technique that has nonlinear activation functions and is trained using a backpropagation algorithm [43]. Similarly, the major advantage of Convolutional Neural Networks [41] is their ability to extract features automatically. This reduces the tasks of extracting features using multiple image processing algorithms. Having enough data for training, this algorithm can be the best option in multiple places including applications like image captioning [44], image classification [45] and object localization [46]. When it comes to time series algorithms, Recurrent Neural Networks (RNN) [47] are widely used. They are special types of NN particularly meant to deal with sequential data. The output of the network acts as feedback to the preceding neuron which allows sharing of parameters. This algorithm along with some modifications can be widely used in multiple applications such as weather forecasting [48], and the prediction of missing data [49]. High Throughput Computation (HTC) involves using distributed computing facilities for tasks requiring high computational power [50] typically provided with clusters and workstations. The tasks on HTC can take a long time varying from a few weeks to a few months. In science, it is widely used in the field of material sciences [51–53].

In spite of ML being a popular tool and finding several application in physics and chemistry, it is not as widespread in these fields as it should be. It seems that the problem is associated with the complexity and diversity of ML methods which have their own hidden disadvantages and specialitied. So actually one can find a big gap between ML and physics because a physicist knows how to collect correct data, but does not know how to treat it correctly and vice versa with ML specialists. We think that in order to make a real ML revolution physicists should use ML as a mandatory tool. The current review is aimed to spread ML in physics by discovering important instruments and highlighting the “underwater rocks” of ML for non-specialists. Additionally the review highlights the problems related to physics (for example: lack of data collection; mixed discrete and real parameters as input data; obtaining the simplest rules from the model) and even some ways of how they can be resolved. The review will hence of interest to ML specialists in order to understand how to improve some methods and write code. The last but not the least problem is that the results of ML models usually cannot be interpreted well even by specialists in ML and this is important to the field of Physics. The current review highlights, for physicists, in the shortest way which methods should be used and why in order to get an interprettable model.

2 History

It is difficult to pinpoint exactly the first-time when ML was used, but looking at its history we can apprehend that it has been recounted with several important events. The entire timeline of the evolution of ML is neatly summarised in these articles [54–56]. The foundation of the Bayes Theorem dates back to 1763 [57] which was further followed by the invention of various statistical techniques like the least square method in 1805 [58] and Markov Chains in 1913 [59]. Walter Pitts, a logician, and cognitive psychologist, and Warren McCulloch, an American neurophysiologist wrote a paper in 1943 related to human cognition in which they quantitatively map out mental processes and decision-making which is considered to be the first neural model invented [60]. Furthermore, Alan Turing’s proposal of the Turing Machine in 1950 [1] was one of the most significant events. This was an artificially intelligent machine that could learn on its own. This discovery piqued the curiosity of many academics, and it played an essential role in the development of the field into what it is today.

The success of ML in recent decades has been boosted by advances in technology and computational capacity. As the area of ML grows in prominence, more scientists and researchers are becoming interested in its applications in a variety of disciplines. As mentioned by Carleo et al. both the disciplines of physics and ML have a similar approach to solving problems but differ in terms of the interpretation of results [61]. In physics, results are gained by scientists applying their knowledge and intuition to solve issues, whereas, in ML, algorithms supply the essential “intelligence” by identifying underlying patterns in data. Consequently, while some advocate for applying ML in physics, others remain skeptical due to a lack of comprehension regarding the acquisition of results. The integration of ML as a tool in physics is a relatively recent concept. The link between statistical mechanics and learning theory began in the mid-1980s, when statistical learning from examples overtook logic and rule-based AI, owing in large part to contributions by statistical physicists. This was a collaborative effort between two key papers, Hopfield’s neural-network model of associative memory [62], which prompted the rich application of notions from spin glass theory to neural-network models, and Valiant’s theory of the learnable [63], which paved the path for rigorous statistical learning in AI.

3 Recent trends in machine learning in physics

The field of Machine Learning is a versatile domain that lies at the frontier of cutting-edge computer science and is allowing us to push the limits of computing to the aid of science. Today, we are surrounded by, generate and record an immense amount of data every second - which has paved the way for advanced AI algorithms to analyse trends by drawing information from data in various fields in science, education, manufacturing, healthcare, telecommunications, marketing, transportation, social networking, and physics [64,65]. Albeit being a very new field, Machine Learning is highly researched, with various new algorithms and strategies arising to tackle different problems and implement solutions to support both theoretical and experimental physics through simulation, trend analysis, and various other models which have helped us deepen our understanding of the universe by big measures [66,67]. Often advances in physics can help accelerate the growth and effectiveness of Machine Learning itself, through research as well as through the investigation of specific domains which directly impact computing technology, for instance, research in quantum computing has significantly helped to accelerate Machine Learning in a world where Moore’s law is approaching its limits [61,68]. While futuristic technologies like quantum computing hold immense promise for revolutionizing computational capabilities, this review primarily focuses on contemporary advancements in machine learning within physics. However, it is important to note that the intersection of quantum computing and machine learning presents a compelling direction for potential future applications in solving complex computational challenges within the realm of physics.

3.1 Automated Machine learning

Many different Machine Learning approaches have been formulated to identify as well as solve problems across various fields. Most problems can be mainly divided into classification analysis, regression analysis, data clustering, association rule learning, feature engineering for dimensionality reduction, as well as deep learning methods [64]. As discussed above, unsupervised learning is a part of ML where the algorithm identifies trends in data by itself, without the need for labels. A recent development in the field of unsupervised learning is Automated Machine learning or AutoML. The goal of AutoML is to provide techniques that construct appropriate Machine Learning models with little to no human involvement [69]. AutoML focuses on automating the construction and training of Machine Learning models which include pre-processing, algorithm selection, and hyperparameter tuning [3]. The problem of hyperparameter tuning has been researched and has led to the development of various techniques such as Feature Engineering, which revolves around automating the selection of the most discriminant features for a particular Machine Learning problem [69,70]. Meta-learning is an AutoML practice consisting of a series of methods that utilize available metadata and those generated from a problem, concerning the types of datasets, algorithms, benchmark numbers, and other statistical figures to help automate the optimization of Machine Learning algorithms as well as model comparison [71]. For example, learning curve prediction allows a machine to predict the performance of Machine Learning models on given problems as well as to compare the performances of chosen models pre-hand [72]. Architecture search is yet another AutoML method that attempts to evaluate the best possible architecture and model that suits a given problem [69,73]. The likelihood function assesses a statistical model’s fit to observed data across various parameter values, while the log-likelihood function simplifies computations by converting products into sums and enhancing numerical stability. These functions are pivotal in optimizing parameters for smoother algorithm convergence and in choosing the most suitable models for the given data [74].

3.2 Explainable AI

Although there has been substantial progress in Machine Learning methods over the past years leading to many algorithms being developed and adopted for solving problems, it has also resulted in cutting-edge Machine Learning algorithms becoming highly complex both syntactically and architecturally. Explainable AI (XAI) is a development in a class of AI that aims at reducing the barrier of complexity and allowing a better human understanding of Machine Learning and AI models in general [75]. Implementing XAI models can lead to a move from “black-box” models toward more transparent Machine Learning models and hence expand our scope for the application of Machine Learning to various other domains [76,77]. In the field of physics, there is a lot of debate regarding the adoption of Machine Learning for computationally intensive tasks and the resolution of new science because of their potential agnostic nature and the “black box” characteristic making the use of such models ‘opaque’ to the understanding [61]. XAI is a frontrunner in resolving the ‘opaqueness’ and revealing the scientific underpinnings left within the workings of a model applied to a research problem, which can also result in the discovery of newer science [78]. Through the use of XAI and interpretable models, we can achieve more clarity with the use and implementation of models on problems, leading to a significant boost in the propagation and development of research, especially in the core sciences.

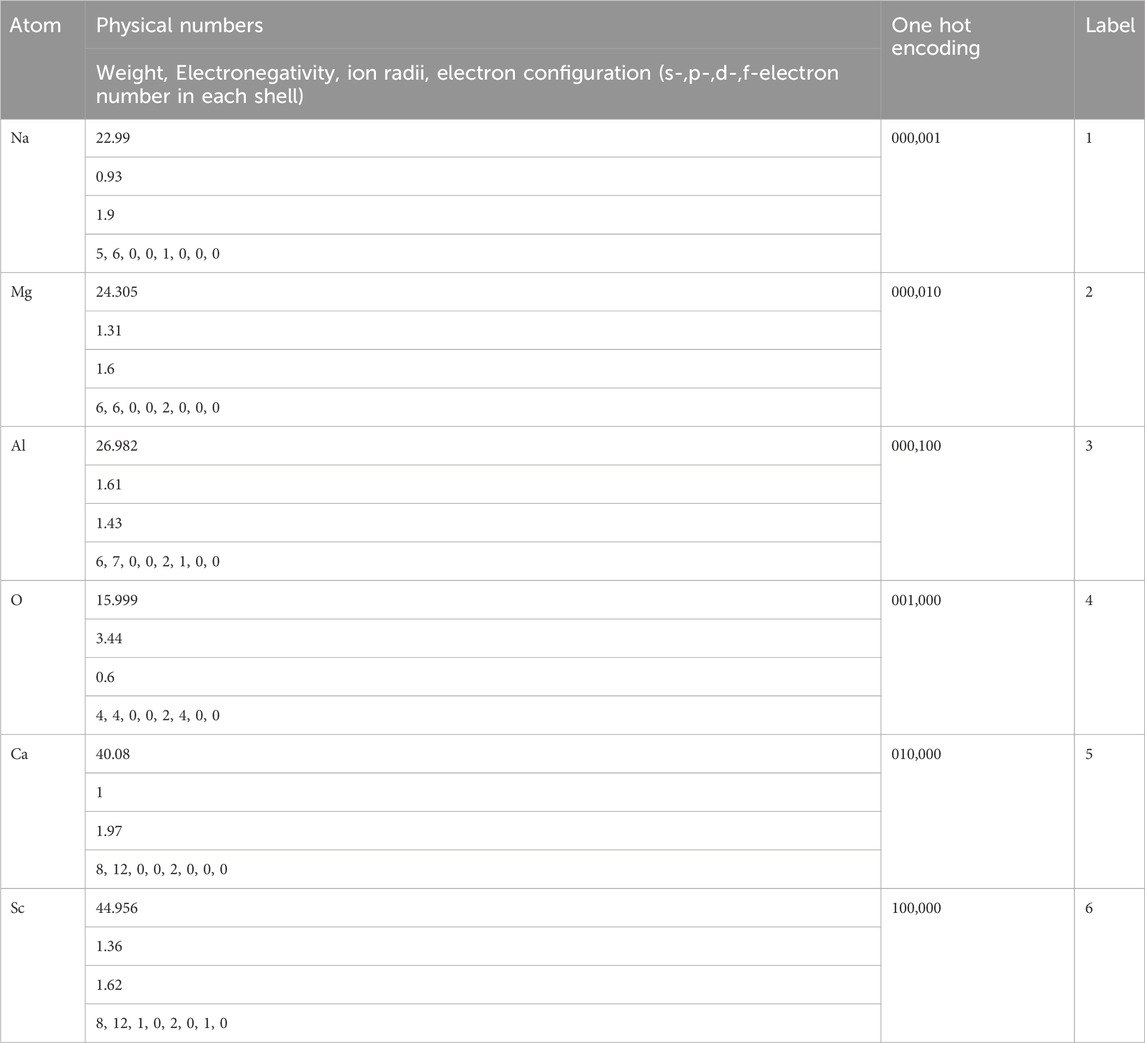
The XAI aims not only to “get the rules”, but also to understand where the model works and where it does not. Investigators cannot trust a model if they do not understand its uses and the cases where it most often does not work. Even 1% of really bad forecasts can reduce the use of the model in medicine, in driving a car, that is, in areas where a person’s life is decided. The XAI should solve mistrust problem and increase the pace of technological development in the ML field. Physics, chemistry and medicine offer devices/materials that can endanger the life of a person or even the whole of humanity. However, on the way, we can find several problems that prevent us from getting the XAI model. One of the problems is that there are numerous numbers of discrete feature parameters in these fields e.g., types of medication, treatment regimens in medicine; types of chemical compositions dissolved in solution in chemistry; atom types in physics, all of them can be hardly presented as numbers. For example, there are several ways to enumerate, Na, Mg, Al, O, Ca, Sc atoms (Table 4).

TABLE 4

TABLE 4. The example of different ways to enumerate atom types.

Using atom weight, electronegativity, ion radii, electron configuration seems to be most specious, but in this case each atom in the chemical formula can combine 11 and more real number parameters, most of them really correlate with others but cannot be diminished easily, and feature parameter vector becomes really large which quench explainability. The « one hot » encoding also leads to a large number of feature parameters. Moreover, further interpretation of ‘1’ and ‘0’ is really hard. The “label” case is invalid at all, because it is not understandable why O ion has greater weight than Na, but lower than Ca. One can see that a lot of ML algorithms cannot be applied with discrete parameters in order to make XAI. At least 1 ML method, named Decision Tree, can work with discrete parameters as is, without transformation to the real numbers. This is the most interpretable ML algorithm with the highest XAI performance. However, it suffers from low prediction accuracy. Ensemble of Decision Trees, named Random Forest, intends to increase accuracy, however, drastically losing explainability. Therefore, the global mathematical aim is to find a method which can still work with discrete parameters as is, and give high accuracy and explainability. Until it is found, the Decision Trees seems to be the most appropriate for some cases.

Further improvement of the Decision Tree model seems to be related to enhancing of data sorting procedure and segregation. Currently, continuous feature data $x_1,x_2\dots ,x_n$ and outputs y are sorted by first feature parameter x₁, and segregated into two datasets with the lowest average MSE (regression task) or lowest average Gini/Entropy values (classification task). After that, the same procedure continues with $x_2,x_3,\dots ,x_n$ feature parameters. The best segregation is chosen and used as a root of the tree. The procedure repeats several times with two appeared segregated data. As a result, the model has a complex segregation surface, which consists of straight planes x₁ = a₁, x₂ = a₂, etc. (Figure 3A). This procedure can be changed by sorting data by a*x₁+b*x₂, c*x₁+d*x₃, or even a*x₁+b*x₂+c*x₃, where $a,b,c,..$—are real numbers. Further segregation should be done like in simple DT. As a result, the model has a simpler segregation surface a*x₁+b*x₂+c*x₃, as it has been presented in Figure 3A. Such Enhanced DT can increase precision/accuracy by using the same number of tree branches in comparison with usual DT, and has the same explainability.

FIGURE 3

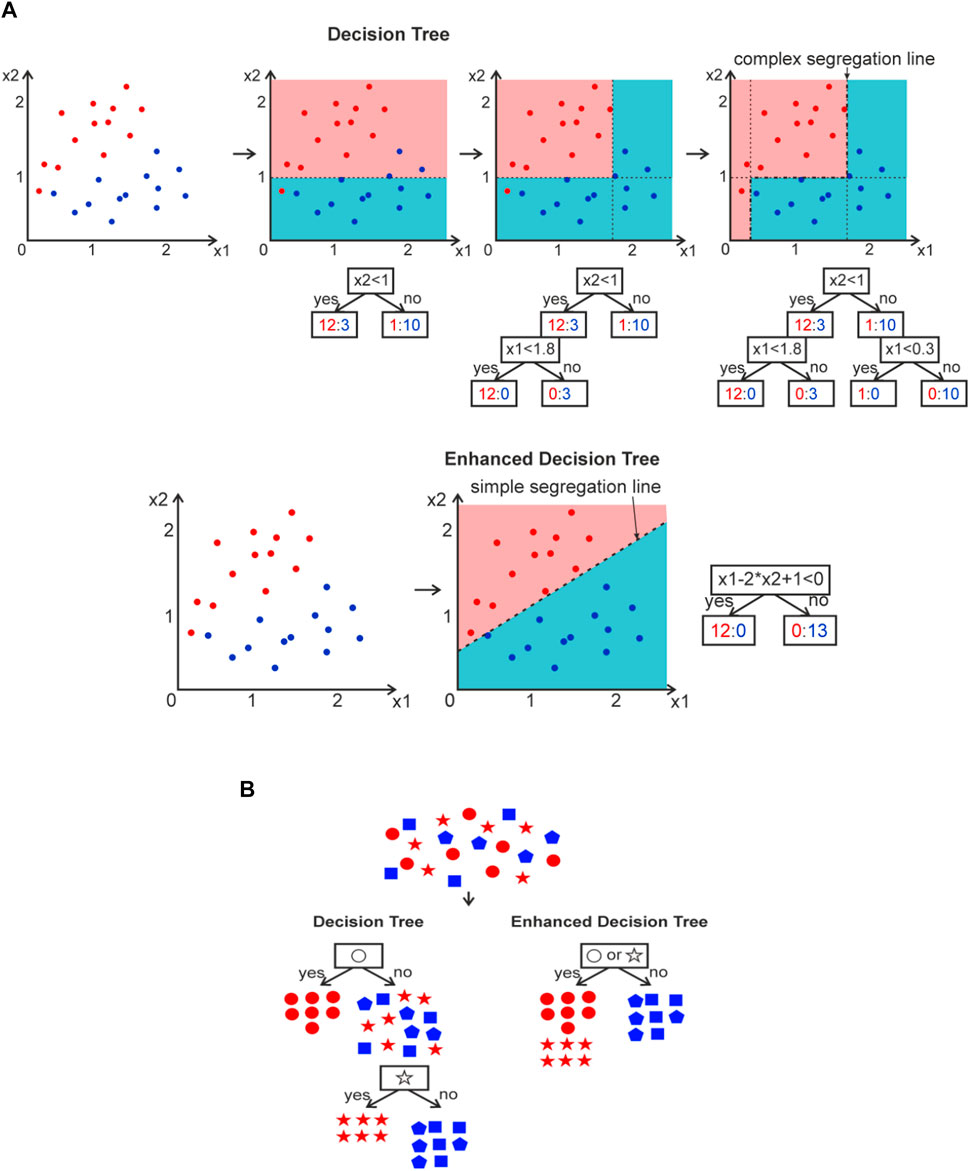
FIGURE 3. (A) Workflow of y = red/blue class segregation with continuous x₁, x₂ feature parameters using DT and Enhanced DT. (B) Workflow of y = red/blue class segregation with discrete x feature parameters (star, circle, square, pentagon) using DT and Enhanced DT.

The same improvement can be done with DT which treats discrete feature parameters $x_1,x_2,\dots ,x_n$. Currently, DT segregates data by only one discrete parameter in x₁, for example, by x₁₁, after that by $x_{12},x_{13},\dots$ and chooses the lowest average MSE (regression task) or lowest average Gini/Entropy values (classification task). The same procedure continues for $x_2,x_3,\dots x_n$ feature parameters and the best segregation is chosen as a root of DT (Figure 3B). The Enhanced DT can segregate data using one, two or more discrete parameters simultaneously (Figure 3B). Further segregation should be done like in simple DT.

It is expected that Enhanced DT can give impulse to XAI model creation in many spheres, including in physics and chemistry where the rules and understanding of model work is preferable.

3.3 Physical-informed machine learning

To date, modelling and predicting the dynamics of multiphysics and multiscale systems have made great strides by numerically solving partial differential equations (PDEs) using finite differences, finite elements, spectral and even meshless methods. However, modelling and predicting the evolution of nonlinear multiscale systems with inhomogeneous cascades-of-scales inevitably faces severe challenges and introduces prohibitive costs and multiple sources of uncertainty [79]. Another problem is physical tasks with missing or noisy boundary conditions, which cannot be solved through traditional approaches. Machine learning methods which use many observable datasets can be used to identify multi-dimensional correlations and manage such problems, but predictions may be physically inconsistent or implausible even for well-fitted purely data-driven models. To fit this problem G.E. Karniadakis with collaborators suggested physics-informed neural networks—neural networks that are trained to solve supervised learning tasks while respecting any given law of physics described by general nonlinear partial differential equations [79,80]. The core idea is to use Physics-informed neural networks (PINN) by constructing a neural network (NN) u(x,t; θ) with θ the set of trainable weights w and biases b. After that, the measurement data {xi, ti, ui } for u and the residual points {xj, tj } for the PDE is specified and the loss L is also specified by summing the weighted losses of the data together with PDE. So that the NN is trained to find the best parameters θ* by minimizing the loss L (Figure 4A). This method was successfully applied to extract edge plasma behaviour for magnetic confinement fusion which is important to reactor performance and operation (Figure 4B).

FIGURE 4

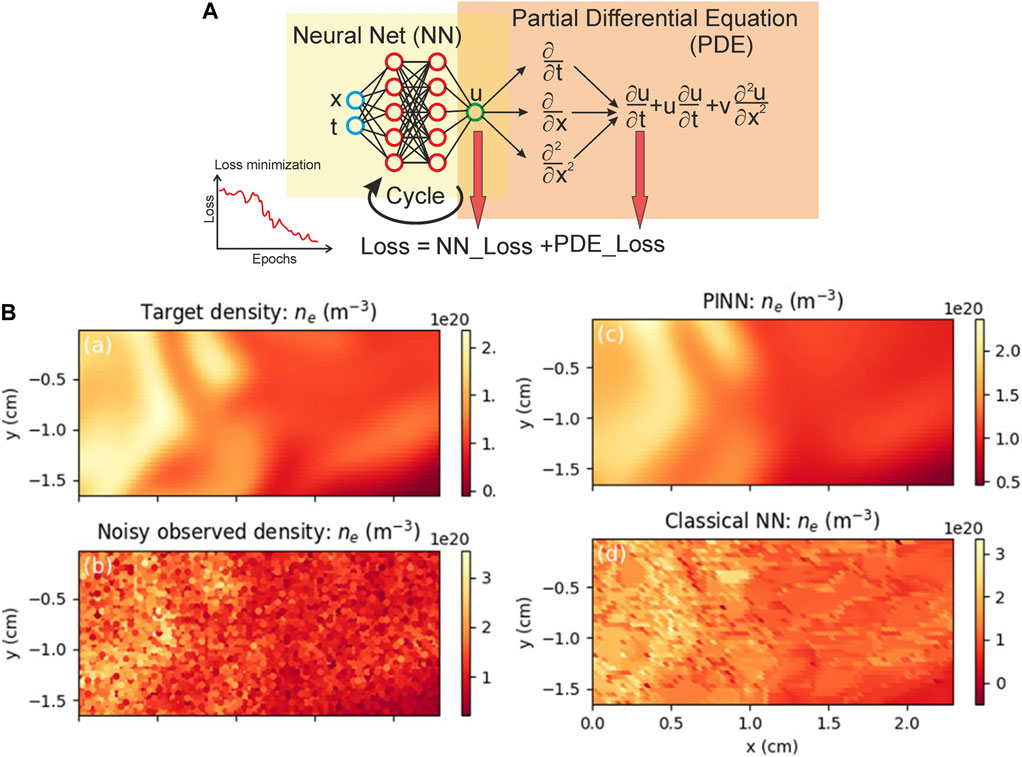
FIGURE 4. (A) Physics-informed neural networks (PINNs) was used to accurately reconstruct the unknown turbulent electric field (middle panel) and underlying electric potential (right panel), directly from partial observations of the plasma’s electron density and temperature from a single test discharge (left panel). The top row shows the reference target solution, while the bottom row depicts the PINN model’s prediction [81]. (B) Principal scheme of Physics-informed neural networks (PINN) [81].

4 Applications of machine learning in physics

4.1 Astronomy and astrophysics

The field of astrophysics is very data-intensive, with huge amounts of computationally worthy data being produced by instruments around the globe. For example, the Gaia Data Release 3 alone (DR3) contains more than 1.812 billion light sources with five to six parameter solutions (Brown et al. 2021). Such an immense amount of data has a lot of potential in store for Machine and Deep Learning applications which may help resolve what is not initially apparent. ML is slowly finding itself commonplace in the field of astronomy for automation of data-filtering and significantly increased workflow.

4.1.1 Gravitational wave detection

The detection of gravitational waves from the GW150914 black-hole merger (BHM) event using the Laser Interferometer Gravitational-wave Observatory (LIGO) [83] made waves in the astrophysics community. This was further followed by the detection of more high-energy events including BHMs with objects nearing 50_☉ and beyond [84,85] Gravitational wave (GW) detections were crucial evidence to validate yet another aspect of Einstein’s General Relativity and this has been made possible by rigorous astrophysics simulations of super heavy objects like black holes [86]. Observing such events also yields massive amounts of data, allowing us to deduce the nature of the event in question as well as the astronomical parameters of the objects involved.

LIGO currently employs the “matched-filtering” algorithm as the primary GW detection method. However, this matched-filtering approach has inconsistent behaviour [87] and may overlook GW signals produced by smaller events, black-hole binaries, and other compact binary interactions, according to various investigations. Several promising methods rooted in deep learning have been able to replicate the result of a matched filtering algorithm. A deep learning-based approach was provided by Gabbard et al. (2017) who used whitened time series data as input of measured gravitational-wave strain, while using data from simulated binary black hole mergers as training and testing data [88]. The training datasets consist of 4 × 10⁵ independent timeseries data, 50% of the data with signal-to-noise and the rest with only noise data. A CNN approach was used and yielded results that are close in accuracy to matched filtering [89]. Later, Yan et al. (2022) proposed MNet-Shallow and MNet-Deep which are Neural-Network equivalents to the matched filtering method, and exceed the previous strategy in terms of computational efficiency in detecting GW from LIGO noise [90,91]. Mnet-Shallow is a shallow neural network approach, while Mnet-deep is a deep learning approach. The L1 strain data from the LIGO O2 run is used as noise data after down sampling and dividing the data into 0.6 s segments.

Other deep-learning methods such as deep-filtering which employ GPU-accelerated CNNs trained on GW signal injections into simulated noise with a high signal-to-noise ratio (>90%) have shown promise in outperforming current methods used to detect GWs [92,93]. This accelerated computational method allows for real-time verification of detection results by conventional matched-filtering methods due to the reduction of waiting time from CPU hours. Deep filtering also shows promise in making automated GW detection faster. Shen et.al. (2017) perform an experiment on gravitational denoising using variational autoencoders (VAEs) [94–98] which introduced the Staired Multi-Timestep Denoising Autoencoder (SMTDAE) based on a sequence-to-sequence bi-directional long-short term memory recurrent neural network (LSTM-RNNs) [37,95,99–102]. It is a model trained on white Gaussian noise capable of removing LIGO input data as well as simulated noise, achieving excellent performance in both scenarios according to the report. Later, Wei and Huerta (2020) also propose a DL-based GW denoising approach by applying WaveNet to noise-contaminated binary black hole merger waveforms [103,104]. The study also finds that CNNs are best suited to remove noise from binary black hole GW events [41,93]. The tuned WaveNet model is used to denoise signals embedded into simulated Gaussian noise as well as raw LIGO noise, obtaining consistent results with denoising binary black hole merger signals with moderate signal-to-noise ratio [105–107]. Recently, Powell et. al. (2023) have applied generative adversarial networks (GANs) to successfully generate artificial noise artefacts into GW merger signals for the purpose of providing test data to studies like those done by Wei and Huerta (2020), as mentioned above [103,108]. The study also investigates an experiment on benchmarking the accuracy of the GANs at simulating real noise and glitches similar to the ones observed at LIGO, KAGRA and VIRGO detectors by classifying them into types of glitches in GW detectors using CNNs, achieving a classification accuracy of over 99% over 22 types of glitches [93,108–110].

4.1.2 Transit event vetting

It is possible to identify the existence of exoplanets through continuous photometry of candidate stars over a large time period to look for periodic dips in observed flux. The captured flux for each particular system after processing can be plotted over time and can be analysed as light curves. Several space and ground-based missions have been deployed to observe a multitude of stars simultaneously. Kepler performed highly sensitive photometry on ∼500,000 stars in Cygnus and Lyra with a very large field-of-view (FOV) of 115 square degrees till it was retired in 2018 [111]. The Kepler Science Processing Pipeline compiled the Threshold Crossing Events (TCEs) identified by Kepler into data releases [112]. However, these data releases demanded human intervention for the removal of false positives. Later, the Transiting Exoplanet Survey Satellite (TESS) made use of four wide-field optical CCD cameras capable of surveying the sky in 600–1,000 nm bandpass [113] with an observing sector of 24 × 24° each, for a total sector of 24 × 96°. TESS proceeded to survey <75% of the night sky and confirmed special candidates named TESS objects of interest (TOIs) which are potential or confirmed exoplanet-harboring systems. TOIs are usually released after passing diagnostic and filtering tests to separate exoplanet candidates from false positives, and further data validation through close inspection by special vetting teams [114]. The TESS Science Office (TSO) has released a list of 2,545 objects which include 120+ confirmed exoplanets, and 757 objects with r_p < R_earth^, [115]. Data from Kepler and later, (TESS) contained false positives stemming from various sources, a large chunk of which was attributed to eclipsing binaries. Manual screening of light curves is hence unreasonable because of the time taken to validate transit events by humans.

Recently, automatic vetting of transit data, also called Auto-Vetting has been experimented with to some degree in the past few years. Many auto-vetting methods have been developed using Machine Learning (ML) and Deep Learning (DL) algorithms. A Random Forest-based model was developed by McCauliff et. al. to classify TCEs into subclasses of either Planet Candidates (PCs) or False Positives (FPs) and achieve an error rate of 5.85% [116]. Robovetter, by Coughlin et al., was the first major algorithm capable of entirely replacing human-aided vetting and producing fully automated catalogues from the Kepler transit data pipeline, and classifying it into either PCs or FPs using several flags to identify the source of each non-transit-like event [117]. A Locality Preserving Projection metric (LPP) defined by Thompson et. al. in 2015 was used by Robovetter for dimensionality reduction and K-nearest neighbours for classification [118].

Later, several projects would bring promising results when dealing with classification on TESS Data Releases, by Osborn et al. in 2019 using a neural network model by Ansdell et al. and produced 97% precision and 92% accuracy on simulations created by the Lilith model [119]. Further, a transfer learning approach through a model pre-trained on Kepler DR24 data was utilized by Stefano et al. on TESS ExoFOP data producing significant results [120]. Agnes et. al (2022) proposed the models ExoSGAN and ExoACGAN in their study which utilizes semi-supervised and auxiliary classifier GANs to train a discriminator model by generating artificial exoplanet transit event data against which the discriminator model could be trained. The ExoACGAN model produced an accuracy of 99.8% with an F-score of 97.6%, with only 8 out of 5,050 non-exoplanet stars being misclassified as exoplanet systems [109,121,122].

4.2 Fluid systems and dynamics

It is known from the theory of fluid systems that the transport of conserved quantities or evolution of observed phenomena can be simplified by a small number of coherent structures or several dynamic processes [123]. This possibility motivates scientists to extract these essential mechanisms from measurements. Several statistical tools, such as variance analysis, conditional averaging, principal component analysis or proper orthogonal decomposition (POD) (Figure 5) [123,124] were used to describe complex fluid behaviour.

FIGURE 5

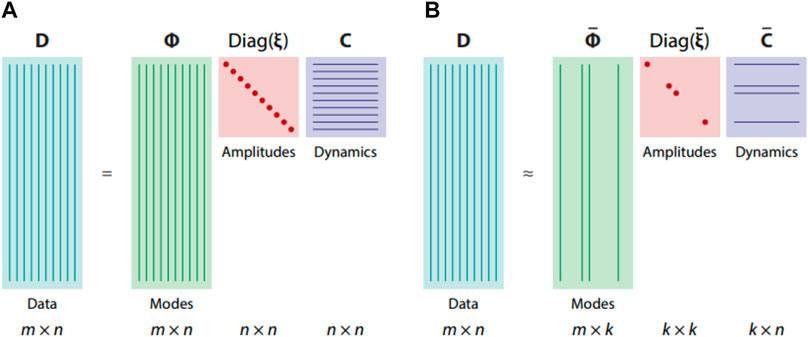
FIGURE 5. Example of application data matrix D factorization into modes Φ, amplitudes diag(ξ), and dynamics C, applying (A) spectral analysis and (B) model reduction [123].

4.2.1 Dynamic mode decomposition in fluid systems

There are other data-driven approaches that are actively developing for fluid systems at present and complement the main methods based on model building. For example, the dimensionality reduction technique for sequential data streams, known as dynamic mode decomposition (DMD) can extract spectral information (Figure 6) from observed data sequences and emphasize various extensions and generalizations [123]. DMD is a factorization and dimensionality reduction technique for data sequences, i.e., Unsupervised ML method, which was first introduced by Schmid as a numerical procedure for extracting dynamical features from flow data [125].

FIGURE 6

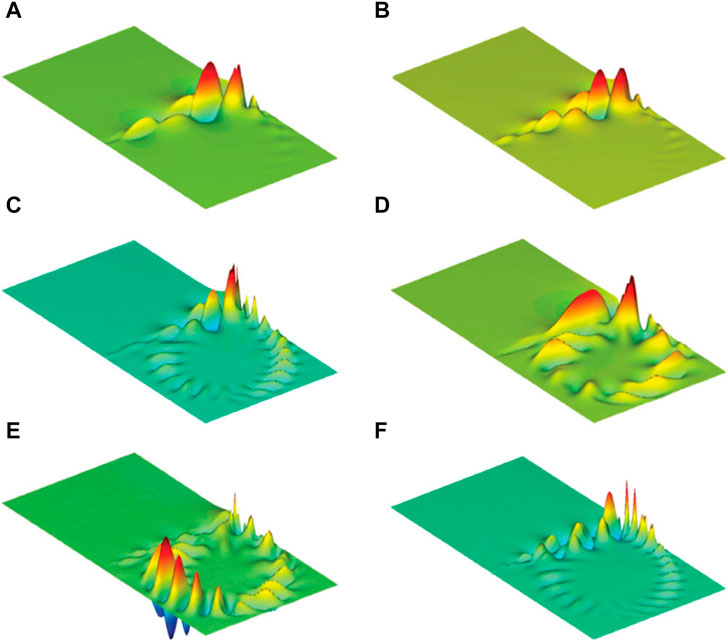
FIGURE 6. Example of application DMD to extract representative dynamic modes. (A) Most unstable dynamic mode, (B–D) dynamic mode from the unstable branch, (E, F) dynamic modes from the stable branch [125].

There is Extended DMD (EDMD) [123] which is the DMD extension that utilizes a larger set of observable functions to obtain more accurate approximations. The EDMD can be assumed as a higher-order Taylor series expansion near equilibrium points, whereas the standard DMD only captures the linear term. Recently [123] Machine Learning techniques have been used to optimize the methodology. For example, an autoencoder [94,96–98,126] (Figure 7), which solves the problem of EDMD, namely, how to choose a set of nonlinear observables has been used.

FIGURE 7

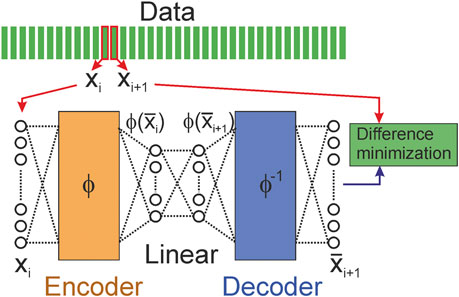
FIGURE 7. Example of autoencoder (the encoder and decoder parts consist of multiple layers of neural nets) which can be used in EDMD [123].

4.2.2 Sparse identification of nonlinear dynamics

One of the urgent tasks of nonlinear dynamic systems is the discovery of governing equations from the data, and advances in sparse regression allows for the extraction of the structure and parameters of a nonlinear dynamical system from data [127]. The smallest number of terms can be extracted which can describe the dynamics without losing important information, which correlates with the well-known Occam’s razor approach. S.L. Brunton together with K. Champion suggested and demonstrated how deep neural networks together with sparse identification of nonlinear dynamics (SINDy) can be used to solve this complex task [127,128] (Figure 8A). The main idea is to use the SINDy autoencoder method [94,96–98,126] for the simultaneous discovery of coordinates and parsimonious dynamics (Figure 8B). It discovers intrinsic coordinates z from high-dimensional input data x and a SINDy model captures the dynamics of these intrinsic coordinates. The active terms in the dynamics are identified by the nonzero elements in Ξ, which are learned as part of the Neural Net training. The time derivatives of z are calculated using the derivatives of x and the gradient of the encoder ϕ [127]. The detailed scheme to use this method for a Lorentz system is demonstrated in (Figure 8C) and several discovered equations obtained in such a way from the data are demonstrated as well.

FIGURE 8

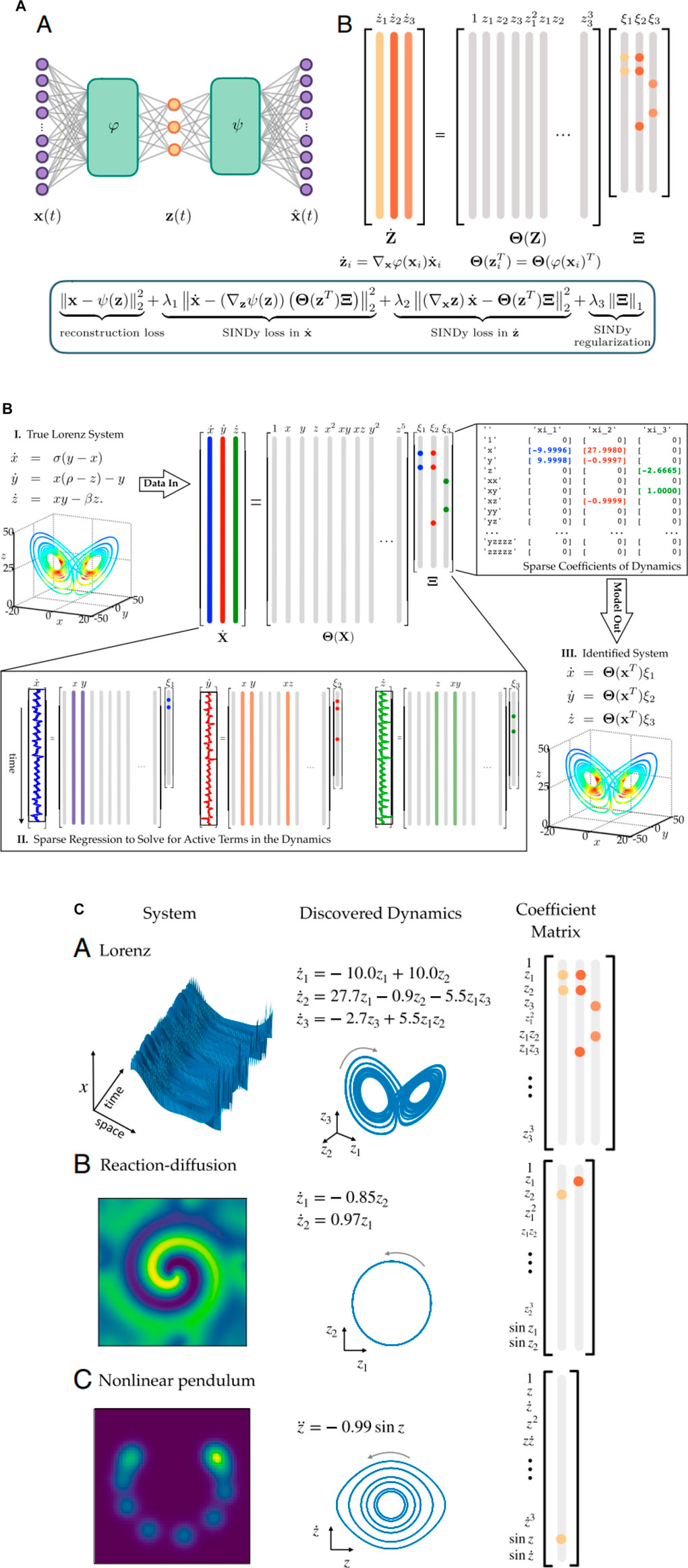
FIGURE 8. (A) Example of autoencoder architecture: the encoder ϕ(x) which maps the input data to the intrinsic coordinates z, and decoder ψ(z) which reconstructs x from the intrinsic coordinates, both consist of multiple layers of neural nets [128]. (B) Schematic of the SINDy algorithm, demonstrated on the Lorenz equations [127]. Several discovered models as the examples. (A–C) Equations, SINDy coefficients Ξ, and attractors for Lorenz (A), reaction–diffusion (B), and nonlinear pendulum (C) systems [128].

4.3 Nuclear and particle physics

After the completion of the standard model with the discovery of the Higgs Boson [129], the field of high-energy physics is entering a new phase and is being led by well-funded and large-scale experiments like the Large Hadron Collider (LHC). These experiments output large amounts of data which have sown seeds of potential in ML methods to probe observations yet unexplained by the standard model.

4.3.1 Nuclear mass prediction

The application of ML in the nuclear physics domain certainly is not new. Gazula et al (1992) worked towards applying artificial neural networks to predict nuclear mass excesses and nuclear stability and analyse neutron separation energies through a feedforward neural network (Figure 9) [130]. Further, feedforward neural nets were trained to learn atomic masses. Nuclear spins and parities and generate highly accurate predictions for test nuclei [131]. With progress in ML algorithms, new strategies were adopted to study nuclear spins and parities, as well as beta-decays. Clark and Li et. al. (2006) reported a study that applied SVMs that worked on atomic and mass numbers of several elements and was able to predict nuclear masses, and beta-decay lifetimes as well as deduce the spins/parities of nuclear ground states [132].

FIGURE 9

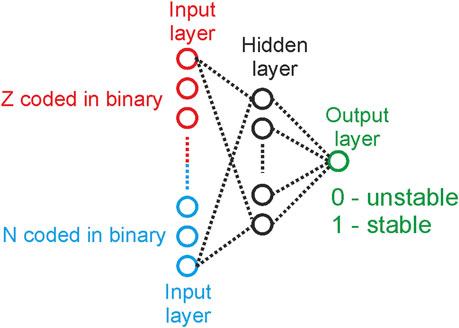
FIGURE 9. Neural Network that us taught to distinguish between stable and unstable nuclides (A). Deviation M_exp–M_calc of learned values of atomic masses Q17 from their experimental values [130].

More recently, Carnini et. al. (2020) brought major improvements in nuclear mass prediction models by using the decision tree algorithm to enhance the accuracy of the liquid drop mass model and the Duflo-Zuker mass model. They commented that even simple algorithms like decision-trees show promise in improving the description of nuclear masses [133]. Later Kernel Regression (KR) model and Artificial Neural Networks (ANNs) were applied to liquid drop mass models [134,135].

4.3.2 Event selection and classification in high-energy particle collisions

ML is an integral part of modern-day high-energy experiments. ML found great success in automating event selection from a multitude of signals produced in a high-energy collision and distinguishing wanted particle signals from the background. Byron et. al. (2004) utilized boosted decision trees for particle identification (PID) at Fermilab, following which, ML has found a wide range of applications in particle physics and PID [136]. The idea of classifying high-energy subatomic particles, known as Jett Classification, encompasses a wide range of classification problems such as identifying jets from heavy and light quarks, gluons, W, Z and H bosons [137]. Precise and effective data analysis is very important for such events. Baldi et. al. (2014) concluded that deep networks (DNs) with low-level features outperformed shallower networks with a similar HIGGS benchmark [138] and hence investigated a supersymmetric particle search algorithm based on DL to improve upon the PID power of particle detector experiments, noting that the DN can also be used a standalone module inside a larger neural network classifier [139]. The ALICE project at the Large Hadron Collider (LHC) is an integral experiment for PID and utilizes a random forest approach to detect ultrarelativistic particles in heavy-ion collisions across a broad momentum range [140]. RNNs were utilized as the first tools for flavour-tagging, which is the classification of particle jets into either light-flavoured or heavy-flavoured quarks by spatially discriminating them since heavy quarks decay quickly in the order of picoseconds [137,141]. The JETNET package was used in flavour-tagging operations in LEP to classify b and c quarks by E.Boos who used a feedforward model for jet classification [4,142].

Perhaps one of the most important uses of Machine Learning based classification in High Energy Physics is the development of the Toolkit for Multivariate Analysis (TMVA) in the ROOT analysis package, a library developed by the Hoecker et. al. (2009) of the CMS collaboration. This method employs several Machine Learning techniques and most notably the widely used Boosted Decision Tree (BDT) classifier, trained on one million simulated events from reconstructions of the CMS detector [143,144]. The classification categories are split based on the momentum of the dimuon pair and presence of high-invariant mass dijet pairs, looking for vector-boson fusion events. The training sample for the project was split into a 75% training and 25% testing regime. The experiment optimizes for maximum signal strength using multivariate ML and reported a 23% increase in signal sensitivity [136,143–146].

Later, G. Aad and B. Abbott from the ATLAS Collaboration produced updated results on the experiment, utilizing an algorithm called XGBoost, which also inherited the 14 kinematic variables and 12 categories with the intent to optimize signal strength contrast with the background [147,148]. The project achieved 50% higher expected sensitivity than the ATLAS result which can be attributed to the increase in luminosity from the algorithmic refinements and analysis. The study also analyses a search for Higgs decay that analysed jet topologies of two types based on data from CERN (2016)—resolved-jets and merged-jets [145,149]. Gradient boosted BDT is used to enhance the separation between the signal and the background for the resolved jet topology with 4 classification categories and 25 variable inputs during training [146]. There has been a paradigm shift towards DL from BDT as newer studies opt for Deep Neural Network implementations for multivariable classification of particles and jets [150]. Another experiment by the CMS collaboration (2017) to measure quark-antiquark pairs used feedforward Neural Networks comprising of three hidden layers for classification the single lepton channel, and BDTs in the dilepton channel. This experiment provided the first evidence for ttH production resulting from $H\to b\overline{b}$ decay. Carminati et. al. (2020) from CERN document cell and feature trained DNN based multivariable classification of particles compared against BDTs trained only on features [151,152]. Two cases are picked for benchmarking against BDTs, charged pions (π^±) and natural pions (π⁰) occurring in electromagnetic calorimeter environments. A dataset comprising of 4 × 10⁵ training and 10⁵ testing events was selected for the experiment on a DNN made up of 4 hidden layers, each layer with 256 individual neurons. The cell based DNN improved on the accuracy of the BDT based approach with 87.2% accuracy over 83.1% accuracy from BDTs when classifying π⁰ against photons (γ) and 99.4% accuracy over 93.8% accuracy from BDTs when distinguishing π^± against electrons (e). The study reports a signal efficiency of 9.4% over background signal than the BDT approach, a significant improvement.

Another attempt was made by Guest et. al. (2016) using a deep-learning-based solution by utilising a database of training samples for three classes of jets (light-flavour, charm, heavy-flavour quarks), trained on feedforward, Long Short-Term Memory (LSTM) and Outer Recursive Networks (ORNs). The feedforward networks with 9 fully connected layers with a learning rate of 0.01 produced an area-under-curve accuracy (AUC), with larger AUC indicative of better performance - of 0.939. The study found that LSTM models best fit the jet classification problem have a small size of the hidden state representation. The LSTM and ORM produced an AUC of 0.939 and 0.937 respectively [100–102,153]. [153]Recently CNN and image classification methods as a basis to classify particle jets were also experimented upon by several studies because of the inherent similarity of HEP detectors to image pixels, with a few managing to outperform shallow neural networks at jet detection [93,154,155]. It is important to note that experiments at LHC may share scope for Machine Learning based cooperation with other particle detection experiments such as neutrino detectors, and searches for dark matter particles [156].

Keck (2017) proposes FastBDT, a Boosted Decision Tree (BDT) based implementation for multivariate classification in the Belle II experiment at the SuperKEKB collider. In the study, the author benchmarks FastBDT against conventional Stochastic Gradient Boosted Decision Tree implementations and provided similar classification strength with less CPU time [157–159]^. Hong et. al. (2021) propose a BDT based implementation to keep up with high data rates and volumes of the future LHC experiments [137,160,161]. The solution is presented in the form of a software package called FWXMACHINA applied to two classification problems—distinguishing photons vs. electrons and event classification for Higgs Bosons produced by vector boson fusion in contrast to the multijet classification method [129]. The study also offers several optimization strategies to decrease latency at the nanosecond interval that can be implemented to FWXMACHINA in six sequential steps, achieving a latency of 10 ns.

4.3.3 Fast simulation in particle collisions

A simulation is a powerful tool in the physical sciences since it allows physicists to study and observe complex systems that may be difficult or impossible to observe directly as well as visualize and display important findings or theories. Simulations have proven as a reliable way of computationally solving various enigmas in physics since they can be used to test and predict the outcomes of a theory or experiment virtually, quickly and repeatedly. Simulation is essential in the field of particle physics since it allows particle physicists to visualise the interactions of various particles by modelling particle interactions based on acquired data to very high precision. However, this task is computationally very demanding and often requires millions of CPU hours. The GEANT4 simulation toolkit is a staple library to simulate Monte Carlo samples of high-energy particle interactions with visualization tools, with the drawback of a large computational footprint (Rahmat et al.; Agostinelli et al. 2003; Allison et al. 2006; Aad et al. 2008, 2010). The ATLAS experiment in LHC required billions of CPU hours with consuming a significant portion of the computational resources allotted to LHC, with Monte Carlo particle simulations taking up more than 50% of WLCG workload [167–170]. To simulate such large number of events, in the order of 10¹⁷ background interactions requires a lot of computational time [169,171].

To combat the high computational footprint and time taken by Monte Carlo simulations in particle physics, Oliveira and Paginini et.al. (2017) developed Location Aware Generative Adversarial Networks or LAGANs. LAGANs could successfully reconstruct jet images, which are two-dimensional representations of a radiation pattern from the scattering of quarks and gluons at high energy [172,173]. LAGAN utilises two-dimensional convolutional layers with leaky rectified activation to accurately simulate the location-based data from high energy particle jets [174]. Further, Paginini et. al. (2017) extended their knowledge from LAGANs to CaloGAN, a Deep Neural Network (DNN) model utilising GANs to produce electromagnetic calorimeter simulations about 100,000 times faster than the conventional Monte Carlo approach [169,172,175]. CaloGAN converges the implicit probability function f on the hypothetical data generation to ensure a realistic simulation. In an experiment, CaloGAN was used to learn and simulate GEANT4 data distributions of γ, e⁺, and π⁺ using a training dataset consisting of images that represent the pixelwise energy depositions in calorimeter layers [176]. It is also interesting to note that the model penalizes any absolute deviation between nominal and reconstructed energy, i.e., |E₀ - Ê|.

Further research and development activity at CERN as documented by Vallecorsa (2018) and Carminati et. al. (2020) for the GeantV project—the successor of GEANT4 for faster and accessible simulation of particle showers—details on the three-dimensional GAN application on high-energy particle physics to simulate 3-D particle showers. The studies evaluate GeantV 3-D GAN as a proof of concept for utilizing GANs to simulate particles at desired energies [163,172,177,178]. This model utilizes DNNs and CNNs for the purpose of classification, energy regression and fast simulation of particles in high-energy collision environments using Machine Learning, in order to match the load of high data volumes from future projects, like the High Luminosity LHC cycle projected in 2025 [93,150,160]. The discriminator and generator models in the Deep Convolutional GAN consist of multiple 3D convolution layers as well as the use of batch normalization layers to improve performance [179,180]. The size and number of filters optimizing the transverse and longitudinal showers shape generations, allowing it to perform three-dimensional image reconstruction of particle showers. The study also stresses the performance leap in fast simulation of particle showers when GANs are used, by approximately 6 orders of magnitude, with the GAN based approach taking about O(10^–3) ms per event simulation in contrast with conventional approaches which may take several minutes.

Another study by Ghosh (2019) explores various Variational Autoencoder (VAE) [94,96–98,126] as well as GAN methods utilized for fast simulation comparable to full simulation by Geant4 [95,181,182]. The VAE consists of two stacked neural networks made up of four hidden layers that act as encoders and decoders for the VAE. The model is conditioned on the energy of the incident particle which allows it to control the specificity of the energy the particle showers are generated at. The encoder and decoder work in tandem in the algorithm which is based on a latent variable model; the encoder compresses the input into a lower dimensional latent space and the decoder reconstructs a new model from this latent representation by learning the inverse mapping of this data. This allows the decoder to generate new data samples independently of the encoder [182].

Graph Neural Networks (GNNs) are Machine Learning models that utilize learning set elements and their pairwise relations have also provided interesting solutions to problems in HEP [183,184] Qasim et. al. (2019) utilize GNNs for the purpose of calorimeter particle shower reconstruction through two distance weighted graph models—GarNET and GravNET. GravNET utilizes a nearest neighbour approach for neighbours in a latent space, and GarNET uses aggregated nodes which are n number of additional nodes in the graph. These nodes represent and provides an output for the energy of a calorimeter cell that corresponds to a particle [183–185]. Keisler (2020) proposes a loss formulation through the object condensation method. The method offers a simplified approach to particle reconstruction and particle flow simulation applications through a graph reduction—this is done by condensing multiple representative points and properties into a single particle [185,186]. It is interesting to note that the object condensation method may also be applied to overlapping particles or objects with a lack of spatial boundaries [187]. The author compares the performance of the algorithm with a much larger LHC environment, with the algorithm producing less fake particle rates and higher efficiency [184,186]. Hariri et al. (2021) propose a Graph Variational Autoencoder based model that combines the properties of GNNs and VAEs. This model, called GVAE, learns compressed data representations for particle reconstruction in high energy environments. The authors also explore the addition of spatial graph convolutional layers to this model aiming at compressing the graphs into representative nodes. The study also benchmarks GVAE on several GPUs to rank performance scaling [183,184,188].

4.4 Material science

Material Science is a field where research is data-driven, and deals with physical and chemical constants on a scale that most other branches of physics do not. This has led to producing large datasets and endeavours to automate the prediction and resolution of material properties as well as material discovery from known data. Machine learning plays a crucial role in advancing material sciences by revolutionizing the way materials are discovered, designed, and optimized. Traditional methods for exploring new materials were time-consuming and labour-intensive, relying heavily on trial and error [189]. Machine learning, however, has transformed this approach by efficiently analysing vast datasets and identifying complex patterns within them. Through algorithms and predictive modelling, machine learning accelerates the identification of novel materials with desired properties, such as strength, conductivity, or thermal resistance [190]. Additionally, it aids in understanding the relationships between the atomic or molecular structure of materials and their resulting characteristics, enabling scientists to make informed decisions during the materials design process.

HTC in material science represents a transformative approach that leverages advanced computational methods to accelerate the discovery, design, and optimization of materials. HTC is recognized as an emerging area in computational materials design. It combines advanced thermodynamic and electronic-structure methods with intelligent data management and analysis techniques, enhancing the understanding and development of new materials [191]. The integration of HTC with data science technologies has shown significant potential in accelerating the discovery and design of novel materials. The vast amount of data generated from HTC [191,192], alongside density functional theory calculations, is being increasingly used with machine learning techniques. This integration is key to accelerating materials discovery and design, making the process more efficient and data-driven [193]. HTC enables the completion of material screenings in large parameter spaces, which would be impractical with manual methods. This is made possible through the design of effective HTC systems based on first-principles calculations, providing a practical approach to screen materials for desired applications such as magnetic materials [194], biomaterials [195], li = ion batteries [196], catalysis [197], optoelectronics [198], and many others.

4.4.1 Material discovery and prediction of material properties

The use of ML for the synthesis of new materials as well as assessing their properties dates back to the 1960s with the Dendritic Algorithm project (DENDRAL) [199,200]. DENDRAL employed an expert system for organic molecular structure synthesis by employing a constrained generator (CONGEN). Modeling and prediction of chemical/molecular properties of known or unknown compounds through ML may take two routes—the first incorporating the physical laws governing atoms and chemistry with ML, and the other dives directly into the prediction of physical properties and structure of a given material, with the latter being usually more computationally intensive [201]. Advanced techniques such as random sampling and simulated annealing algorithms which employ Monte Carlo simulations [202] as well as genetic models such as those studied by Bush et. al. that was able to successfully predict crystal structures of Li₃RuO₄ [203], Gottwald et. al. (2005) which employed genetic algorithms to calculate zero-temperature phase diagrams to predict candidate solid crystal structures that a given fluid may freeze in. However, the prediction of valid organic or crystal structures was either inefficient or inaccurate mainly due to time and computing constraints. Recent interest and development in ML technologies, as well as the increased abundance of specific data, has sparked several successful studies in this field. ML provides a promising solution to this problem, which was pioneered by Corey and Wipke in 1969 through expert systems [204]. Recent advancements in structure predictions, made by Coley et. al (2017), use a dataset of experimental reaction records consisting of over 15,000 patents to train a network that produces and ranks reactions that would most likely produce a chemical compound by predicting a small set of atoms and bonds in the reaction center and then producing all possible candidates and bond configurations [205]. Ren et. al (2018) study an iterative and high throughput ML based approach aimed at discovering metallic glasses [206,207]. The study uses four different supervised ML models including a retuned model by Ward et. al. (2016) and various models trained on sputtering data, and is benchmarked against Ward’s model [208]. The ML model is trained on 6,789 melt-spinning experiments [209]. The model also discovers a previously unexplored Co-V-Zr ternary which indicates a large region of metallic glasses. K. Schütt et. al (2014) presented an ML to predict electronic state densities at Fermi energy, employing the use of a spin-density dataset to train their model [210]. Later in 2018, Schütt et. al. present SchNet—a deep learning model consisting of continuous filter CNNs (O’Shea and Nash 2015; Schütt et al. 2018). SchNet is a DL implementation, a variation of the Deep Tensor Neural Network (DTNN) architecture—instead of tensor layers, it features continuous filter convolutions with filter generating networks [212–214]. The model can build and learn on atom-wise embeddings and layers of those embeddings and predict material properties through a sum over atom-wise calculation which can be approximated by taking an average of atomic contributions to the material’s properties. SchNet was trained with a learning rate decay of 0.96/10,000 steps, on the QM9 dataset of over 1.31 × 10⁵ organic molecules [215–217]. The algorithm fails to perform when predicting the electronic spatial extent and polarizability of the molecule, but does well in the other 8 properties predicted by the model. Interestingly, SchNet requires only 750 epochs to reach convergence in the study. SchNet is also able to learn and predict the formation energies of materials, achieving an absolute mean error of 0.127 eV/atom when trained on the Materials Project repository [218]. As a final study, the model is used to study the molecular dynamics of C₂₀-fullerene to resolve the basic properties of the molecular system, and achieves an error in nuclear and quantum effects by the scale of 0.5%/nm and high accuracy energy predictions.

Behler et. al (2016) applied kernel regression to successfully predict the electronic properties of metal oxides and elastic (shear and bulk modulus) of 1,173 crystals [219]. Improving on that, de Jong et. al (2016) used an ML model called gradient boosting multivariate local regression framework to predict bulk and shear moduli for inorganic compounds using a catalogue of over 1900 compounds as their database, intending to find super-hard materials. The study yielded a relative error of <10% and a root mean square (RMS) error of 0.075log(GPa) (Figure 10) [200,220]. The utilization of ordinal networks, combined with deep convolutional neural networks (CNN) and complexity-entropy methods, represents an innovative approach in exploring physical and optical properties of liquid crystals. This integrative methodology enables a comprehensive analysis to decode intricate patterns within liquid crystal structures, offering deeper insights into their characteristics and behaviors [221–223].

FIGURE 10

FIGURE 10. Comparison of DFT training data with predictions for e elastic bulk modulus K (A) and shear modulus G (B). Training set consists of 65 unary, 1,091 binary, 776 ternary, and 8 quaternary compounds [220].

Qiao et. al. produced OrbNet, an ML method utilizing a graph neural network (GNN) architecture that takes rules from quantum mechanics into account allowing it to outperform previous models to predict chemical synthesis and electronic-structure energies with very high accuracy and achieving a 33% improvement in prediction accuracy over the second-best method [224,225]. Choudhary et. al. (2020) introduce The Joint Automated Repository for Various Integrated Simulations through Machine Learning (JARVIS-ML) for the purpose of accelerating material discovery [226,227]. This package was used in 2019 to discover materials that can be used to build solar cells. The lack of proper materials to build solar cells is a critical hurdle to solving sustainable and cheap renewable energy problems. This was achieved by using JARVIS-ML to predict materials with high spectroscopic limited maximum efficiency (SLME), finding over 1900 potential materials with an SLME higher than 10% [228]. More recently, Chen et. al. (2021) used random forests on a training dataset of over 10,000 compounds and over 60 attributes to predict elastic properties for the discovery of potential super-hard materials. Further, the study also substantiates its results through evolutionary structure prediction and density functional theory [229].There are several machine learning tools that have emerged from the abundance of vast datasets and the development of like the aforementioned predictive models. PyMatGen [230] stands as a cornerstone tool, playing a pivotal role in advancing research and discovery. Developed in Python [231], PyMatGen offers a comprehensive suite of functionalities tailored for materials analysis, particularly in the realm of crystallography and electronic structure [232,233]. Its application spans from the generation and manipulation of crystal structures to the calculation of electronic and thermodynamic properties. Researchers widely embrace PyMatGen for its robustness in automating repetitive tasks, facilitating high-throughput computations, and enabling the systematic exploration of materials databases [234,235]. PyMatGen is closely linked to other essential technologies and tools in materials informatics, forming a synergistic ecosystem. Integration with databases like the Materials Project [218] and MatCloud [236] provides a vast repository of materials data for exploration. Furthermore, the combination of PyMatGen with machine learning libraries such as scikit-learn [237] or TensorFlow [238] allows for the development of predictive models, enhancing the efficiency of property prediction and materials discovery. Close ties with visualization tools like VESTA [239] enhance the interpretability of complex crystal structures, offering researchers a comprehensive toolkit for materials exploration and design [240].

Matminer [241], a powerful Python library tailored for data mining in materials science, has found widespread utility across various domains within the field. One prominent application is in the extraction and analysis of materials data from diverse sources [242,243]. Researchers employ Matminer to seamlessly retrieve information from databases, research papers, and experimental datasets, streamlining the process of aggregating data for materials informatics. Additionally, Matminer facilitates the pre-processing and featurization of raw data, enabling efficient utilization in machine learning workflows [244]. In the realm of property prediction, Matminer is instrumental in constructing and fine-tuning predictive models, allowing scientists to forecast material behaviors and characteristics. Its versatility extends to applications such as high-throughput screening, where the library aids in the systematic exploration of large materials databases to identify promising candidates for specific applications.

ElemNet has emerged as a transformative tool in various facets of material science research due to its unique ability to automatically learn material properties from elemental compositions using deep learning [245]. In the realm of materials informatics, ElemNet has been instrumental in predicting the stability of crystal structures, offering a departure from traditional machine learning approaches that necessitate manual feature engineering. Researchers leverage ElemNet to analyze vast datasets, such as those from the Open Quantum Materials Database, enabling efficient identification of stable compounds and the exploration of previously uncharted material compositions. Furthermore, ElemNet finds application in the rapid screening of material candidates, facilitating combinatorial investigations across a wide composition space. Its speed and accuracy advantages over conventional ML models make ElemNet particularly valuable in accelerating the materials discovery process. Beyond stability predictions, ElemNet has been adopted for tasks like property optimization, aiding researchers in tailoring materials with specific engineering properties.

DeepChem [246], a powerful open-source deep learning framework, has made significant contributions to material science research across diverse applications. One key application lies in its role in molecular property prediction, where DeepChem’s deep learning models analyze and predict various molecular properties, such as binding affinities, electronic structures, and chemical reactivities. The framework facilitates the development of accurate and efficient models for drug discovery and materials design [247]. DeepChem is also instrumental in the field of cheminformatics, enabling the analysis of chemical datasets, structure-activity relationships, and the identification of novel compounds with specific properties. Furthermore, in materials informatics, DeepChem supports the prediction of material properties based on molecular structures, aiding researchers in the exploration and optimization of materials for various applications, including catalysis, energy storage, and electronic devices. Its flexibility and versatility make DeepChem a valuable tool for researchers seeking to leverage the capabilities of deep learning in unraveling the complexities of materials science.

Citrination, the materials data platform developed by Citrine Informatics, has become an invaluable resource in advancing material science across various domains. Its application spans a wide range of areas, with one of the key contributions being in materials discovery and design [248]. Citrination serves as a centralized hub for materials data, allowing researchers to access and analyze an extensive collection of experimental and computational data. This facilitates the rapid identification of trends, correlations, and patterns, enabling scientists to make informed decisions in materials research. Few other software that harness the power of ML is shown in Table 5.

TABLE 5

TABLE 5. Software applications harnessing machine learning in material science.

4.5 Nanophysics

The last few decades have seen an incline in the use of AI tools in the research of nanotechnology [249]. The scale of nanotechnology is a double-edged sword, where it provides huge technological breakthroughs but the price of developing technology in this domain is limited by its sheer size because of the difficulties encountered in the development, design, and manufacture of such technology. The physical laws at this scale differ from what is relevant in macroscopic situations [249,250].

4.5.1 Design of nanoscale computation systems

The idea of Nanoscale devices or Nanodevices is incredibly valued today because of space constraints on computing devices. As more and more computational power gets packed in a smaller volume day by day, Moore’s law is reaching its very limits for traditional transistors, because of quantum mechanical effects coming into play [68,249]. Nanocomputers are a front-running and promising solution to this problem [251]. There have been several initial attempts at nanocomputer construction [252,253]. Early attempts have been made to apply reinforcement learning by Lawson (2004) to program randomly placed “nano-electric components” with the vision of reducing manufacturing costs for highly detailed small computing devices which use transistors [254]. Optimization techniques for nanoscale circuits have emerged, and a study by Bahar et. al (2003) used Markov Random Fields for circuit framework optimization. Improving on that, Kumawat et. al. (2005) proposed probabilistic modelling approaches for the optimization of nanocircuit designs, which aim on making nanocomputers more reliable and remove defects using Markov Random Fields and Probabilistic Decision Diagrams, with Probabilistic Decision Diagrams having the least time complexity amongst the approaches featured in the study [255]. ML has also seen recent use to design computers that can enable high-throughput calculations as well as solve complex optimization problems [249].

4.5.2 Finding and analysing nanomaterials

Similar to material science, ML models have been used to classify and predict nanomaterial properties. For example, artificial neural networks (ANNs) have been popular in resolving the properties of thin-film nanomaterials because of their nonlinear nature [249]. Xu B. et. al. (2004) used an ANN with a Levenberg Marquadt algorithm as an optimizer to predict Poisson’s Ratio, Young’s modulus, and other elastic properties of a thin film substrate by feeding surface displacement responses into the neural network. Out of the 96 samples used in the study, training data consisted of 80 samples and the remaining 16 samples were used as testing data for the ANN, producing a relative error of 4.0% for Poisson’s ratio, 0.48% for Young’s modulus, and 4.9% for density thickness [256]. Further, ANNs were also used by Jiangong et. al. (2007) used an ANN to calculate dispersion curves of a functionally graded material (FGM) plate. This study, like the previous one, used the Levenberg-Marquardt algorithm to hasten the learning process of the neural network [257]. Aside from thin-film nanomaterials, kinetic models have been constructed for steam in naphtha surrogates in a NiMgAl catalyst using ANNs trained for kinetic model discrimination recently by Natalia et. al. (2022) [258] which derived from a study by Amato F. et. al. The model demonstrated an overall accuracy of 74.9% for the test set data containing 800 samples [5] to evaluate kinetic data (Figure 11).

FIGURE 11

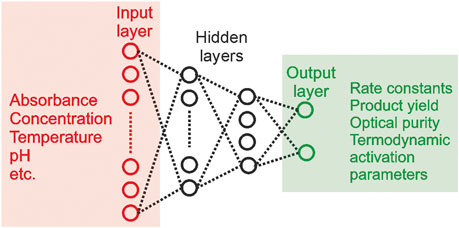
FIGURE 11. Typical Neural Net architecture for application in kinetics [5].

NanoSolveIT [259]is a groundbreaking research project dedicated to advancing safety assessments of engineered nanomaterials (ENMs). By leveraging advanced computational models, the project focuses on predictive toxicology to anticipate and understand potential risks associated with nanomaterials. These computational tools use sophisticated algorithms to simulate various scenarios, incorporating physicochemical properties, exposure conditions, and toxicological outcomes. Notably, NanoSolveIT excels in data integration, consolidating information from diverse sources into a comprehensive database. This integrated approach provides a holistic understanding of nanomaterial behavior.

4.6 Thermodynamics

Thermodynamics is referred to as the science of the relationship between heat, work, temperature, and energy [260]. Thermodynamics, in its broadest sense, is concerned with the transfer of energy from one location to another and from one form to another. Heat can be defined as an interaction distinguishable from work. It involves energy and entropy transfers [261]. In the development of chemical engineering processes, the thermodynamic properties of complex systems are critical. Predicting the thermodynamic parameters of complex systems across a large range and describing the behaviour of ions and molecules in complex systems remains difficult. Because it can explain complicated relationships beyond the capabilities of standard mathematical functions, ML emerges as a powerful tool for resolving this challenge. ML can be applied in three major areas of molecular thermodynamics. In the first area, ML is used to predict the thermodynamic properties of a broad spectrum of systems based on known data. The second area is to integrate ML and molecular simulations to accelerate the discovery of materials. The third area is to develop an ML force field for eliminating the barrier between quantum mechanics and all-atom molecular dynamics simulations. The applications in these three areas illustrate the potential of ML in the molecular thermodynamics of chemical engineering [262].

4.6.1 Machine learning assisted thermodynamical simulations

ML approaches are effective in automatically distinguishing different phases of matter, and they offer a fresh perspective on the study of physical events. On training a restricted Boltzmann machine (RBM) on data constructed using Monte Carlo simulations of spin configurations taken from the Ising Hamiltonian at various temperatures and external magnetic fields, an astute observation was found that the trained RBM’s flow approaches the spin configurations of the maximum feasible specific heat, which mirror the Ising model’s near-criticality area. The trained RBM converges to the critical point of the lattice model’s renormalization group (RG) flow in the exceptional case of the vanishing magnetic field. Instead of linking the recognition technique directly with the RG flow and its fixed points, the findings show that the machine recognizes physical phase transitions by identifying particular attributes of the configuration, such as the maximization of the specific heat, suggesting the importance of using ML methods [263].

In another study, a numerical investigation of entropy generation and heat convection was performed in a hybrid nanofluid (Al₂O₃-Cu-water) flowing around a cylinder embedded in porous media. Results obtained after using an artificial neural network for predictive analysis of the generated data show that when the Reynolds number, permeability parameter, or volume percentage of nanoparticles increases, the heat transmission of the system increases. The functional forms of these dependencies, on the other hand, are complicated. The effect of increasing nanoparticle concentration on entropy generation is found to be nonmonotonic. To establish correlations for the shear stress and Nusselt number, particle swarm optimization is applied to the simulated and forecasted data. This shows how artificial intelligence algorithms can forecast the thermohydraulics and thermodynamics of thermal and solid-state systems [264].

Activity coefficients are an important feature in chemical engineering that may be used to describe chemical and phase equilibria as well as transport processes. They are a measure of the non-ideality of liquid mixtures. Despite the availability of experimental data on thousands of binary combinations, prediction approaches are required to compute the activity coefficients in many relevant mixtures that have yet to be studied. A probabilistic matrix factorization model for predicting the activity coefficients in arbitrary binary mixtures is proposed in this paper which despite the absence of physical descriptors for the components under consideration surpasses the state-of-the-art method, which has been honed over three decades and requires significantly less training (Figure 12) [265].

FIGURE 12

FIGURE 12. A probabilistic matrix factorization model for predicting the activity coefficients in arbitrary binary mixtures [265].

From soap bubbles to suspensions to polymers, many-body systems learn and remember patterns in the forces that push them out of balance. This knowledge could be applied to computing, memory, and engineering. Until now, thermodynamic parameters like work absorption and strain have been used to detect many-body learning. This study [266] goes beyond the macroscopic qualities that were initially specified in equilibrium contexts by using representation learning, a machine-learning model in which information squeezes via a bottleneck, to quantify statistical ML. Quantification of four aspects of many-body systems’ learning by computing bottleneck properties is done: classification ability, memory capacity, discriminating ability, and novelty detection. The method is demonstrated by numerical simulations of a standard spin glass. While offering a unified foundation for many-body learning, the suggested technique appears to be more accurate and precise in detecting and quantifying learning by matter.

The complicated effects of molecule configurations and/or interactions on the thermodynamic properties must generally be taken into account when establishing a reliable equation of state for predominantly non-ideal or multi-component liquid systems. In this aspect, ML has a lot of promise for learning thermodynamic mappings directly from existing data instead of using equations of state. A study presents a generic ML framework for predicting the thermodynamic parameters of pure fluids and their mixtures based on high-efficiency support vector regression. To accurately forecast the thermodynamic parameters of three common pure fluids, the suggested framework consisting of a gaussian kernel is used in conjunction with training data gathered from a high-fidelity database. The mean square errors in the forecasts are extremely low. Furthermore, for ternary mixtures of pure fluids, no loss in prediction accuracy is attained at the cost of a modest increase in the volume of training data provided by state-of-the-art molecular dynamics simulations. The findings show that ML has a lot of potential for creating accurate thermodynamic maps of pure fluids and their mixes. The proposed methodology could pave the stage for the faster study of novel or complicated systems with possibly extraordinary thermodynamic features in the future [267].

4.7 Biophysics

When underlying physical rules are applied in physics, equations can become too difficult to solve. Therefore, approximate practical methods are required. This is where ML comes into play, as it has recently had a considerable impact on the development of approximate approaches for large atomic systems [268]. In biophysics, principles of physics, chemistry, mathematical analysis, and computer modeling are applied to biological systems to understand the structure, dynamics, interactions, and ultimately the function of biological systems at a fundamental level. Biophysics aims to explain the biological function in terms of unique molecular physical features. The structure and behaviour of single biological molecules, as well as the greater architecture into which they organize, are the focus of most research in biophysics. Some of this work entails developing new techniques and devices for observing these dynamic structures in action [269].

Various deep learning (DL) methods have emerged in differential programming as a powerful tools for processing sensory inputs. Bespoke machine learning models, tailored to specific scientific domains, integrate domain-specific knowledge directly into their architecture, by using DL models like convolutional networks and joint visual-textual neural networks fostering innovation in scientific problem-solving through machine learning [270]. Recent studies have showcased the advancements of ML and DL in diverse biomedical applications, including ML-driven real-time simulators for left ventricular mechanics [270–272], predicting abnormalities in Aortic Aneurysm Expansion [271], genomics [273], next-generation sequencing [274], proteomics [275], structure prediction [274], and Super-Resolution 4D Flow MRI [276]. One such tool, 4DFlowNet, a DL-based model, generates noise-free, super-resolution 4D flow phase images from synthetic 4D flow MRI data using Deep Learning and Computational Fluid Dynamics. The tool mimic the actual scans, exhibiting promising accuracy with absolute relative errors of 0.6%–5.8% and 1.1%–3.8% in phantom and normal volunteer data, respectively. There were several other tools which employed ML algorithm and listed in Table 6.

TABLE 6

TABLE 6. Software Applications Harnessing Machine Learning in biophysics.

Apart from various softwares which includes ML techniques to optimize the results, ML has been widely used analyzing in several clinical data. Palumbo et al. [277] compared several ML models to analyze the FTIR spectra to substantiate the utilization of FTIR data in quantifying clinical parameters for diagnosing abnormalities. Similarly, NB, XGB, MLP, LR, KNN, RF, SVM, PLS-DA, and MLPNN (acroyms are at the end) were commonly used ML algorithms to diagnose various disease based on FTIR data [278–280]. The work of Behler and Parrinello led to one of the first applications of ML in biophysics [281–288]. They created Behler-Parrinello networks which aim at learning and predicting potential energy surfaces from QM data and combine all of the relevant physical symmetries and parameter sharing for this problem. ML is being used to solve the problem of molecular simulation. A significant amount of work is done to come up with ML approaches that can accurately reproduce free energy surfaces and global potential energy surface (PES) for small molecules [211,284,288–292] and elemental materials [211,219,281,283,293]. More applications involve the usage of ML in the design of a coarse-grained model of the complex molecular system such as protein, and in Kinetics to learn the embeddings used in equations and in Sampling and Thermodynamics to sample probability distributions using generative learning [95,109,294–296]. Compared to regular ML problems there is an advantage in making decisions and interpreting results when working with molecular problems. This is because researchers know a significant number of physical principles that reduce the possible predictions to meaningful ones.

Another work by M. Sivaramakrishnan et. al (2022) developed a model called EnsembleQS (Figure 13). It was a stacked generalization ensemble model that used the concept of Gradient Boosting Machine (GBM)-based feature selection. It was developed with the aim of effectively identifying quorum sensing (QS) peptides, as a possible therapeutic method for bacterial control has been found as the creation of antibodies against such QS molecules. The superiority of the model was demonstrated when it outperformed finely tuned baseline classifiers On selected GBM features (791D). When the model was further evaluated on an independent dataset of 40 QS peptides, it demonstrated an accuracy of 93.4% with Matthew’s Correlation Coefficient (MCC) and area under the ROC curve (AUC) values of 0.91 and 0.951. These findings imply that EnsembleQS will effectively complement proteomics research and serve as a helpful computational framework for predicting QS peptides [297]. Waibel et al. developed a diffusion-based model DISPR which leverages 2D microscopy images to predict realistic 3D cell shapes, showcasing its utility in solving inverse biomedical problems and enhancing feature-based cell classification [298].

FIGURE 13

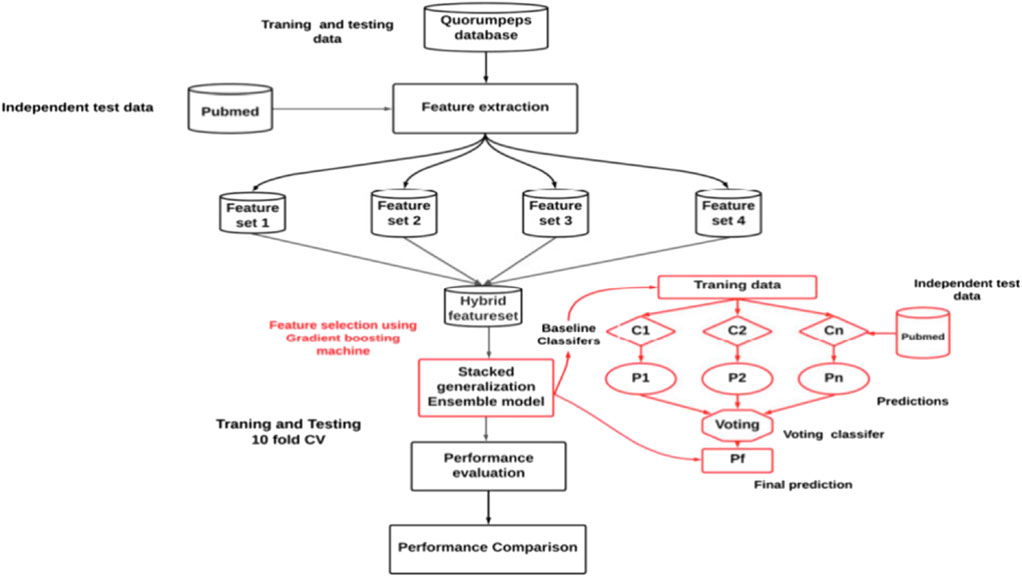
FIGURE 13. EnsembleQS framework for predicting QS peptides [297].

5 Outlook

5.1 Advantages of machine learning in physics

The ability to make predictions is one of the important applications of ML. There are generally two main classes of problems that enable us to choose between a physics-based model and data-driven model.

1) We have no direct theoretical knowledge of the system but we have a lot of experimental data on how it behaves; In such cases given enough examples an ML model should be able to learn the underlying pattern by itself between the information you have about the system (the input variables) and the outcome you would like to predict (the output variables).

2) We have a good understanding of the system and we are also able to describe it mathematically: In these situations using physics-based models are often a good approach but this does not mean ML is useless for such tasks. On the contrary, combining physics with ML to create hybrid models is an exciting area to explore.

3) Hybrid Models are used to reduce computational costs. In some instances, physics-based models can be used to solve a problem but solving the physical equations could become very complicated and time-consuming. Using a hybrid model provides an alternate way in which the intended task could be performed by learning from the underlying data. Even though the training phase for such models takes some amount of time, once the model is trained, making new predictions is significantly straightforward [299].

4) One of the major advantages of using ML in physics is the speed at which results are obtained, for example, a neural network once trained properly, provides the output of a new sample efficiently and accurately. Additionally, ML can discover new patterns in the data by learning themselves and providing useful insights.

In CERN’s Large Hadron Collider (LHC), particles collide every 25 nanoseconds. Processing and analysing these collisions have to be done in an automated and robust way. This is done using ML techniques such as unsupervised learning. Unsupervised learning also allows researchers to see all possible deviations from the hypothesis before concluding. Convolutional Neural Networks perform very well in situations involving the translation of images. For example, consider an image of a cat, if the cat is moved to a different section of the image, it is still a picture of a cat. The generic ML techniques of the past were not able to detect this translation but since advancements in deep learning technology, researchers are now able to automatically incorporate this translational symmetry. This has led to much more robust answers [300]. Physics-Informed Neural Network (PINNs) a scientific ML technique used to solve problems involving Partial Differential Equations (PDEs). PINNs approximate PDE solutions by training a neural network to minimize a loss function. Physics-informed ML can be widely used in personalized medicine in which an individual’s genetic profile is used to guide decisions regarding the prevention, diagnosis, and treatment of disease [301].

5.2 Disadvantages of machine learning in physics

A lot of samples are required to train the model and collecting them in physical settings is expensive. Also, in some cases where enough samples are present, it still might not be enough to prevent catastrophe in high-stakes situations. Self-driving cars make moment-to-moment decisions based on billions of samples. But that still is not enough to eradicate all potential fatalities. As the physics-based models are trained on samples they do not extrapolate well on previously unseen data. This is because neural networks are very good for interpolation, but not good for extrapolation. When a neural network is trained using a collection of samples derived under similar conditions ​​predictions will likely be very good and they can accurately represent high-dimensional functions. But when it is trained using samples that were derived under different conditions, the results can be unpredictable or wrong [79].

We suggest the quality mark (QM) for Supervised ML in order to analyse whether a small number of training datasets is enough for good extrapolation or not. The beneficial is that this QM is general for both classification and regression ML tasks. This QM is involved as QM = AAD/MAE, where AAD is the average absolute deviation of Y_i values (continuous numbers or label numbers for discrete values) from the whole dataset: $\text{\hspace{0.17em}AAD}=\left(1/\mathrm{n}\right){\displaystyle {\sum }_{i=1}^N}\left|Y_i-<Y_i>\right|$, $<Y_i>$ is an average of $<Y_i>=\left(1/\mathrm{n}\right){\displaystyle {\sum }_{i=1}^N}{Y}_i$ , MAE is the mean absolute error: $MAE=\left(1/\mathrm{n}\right){\displaystyle {\sum }_{i=1}^{Ntest}}\left|Y_i-\widehat{Y_i}\right|$, $\widehat{Y_i}$ is predicted values for the test dataset using ML model. The best way to estimate MAE is by using a repeated k-fold cross-validation procedure. Checking QM for several representative datasets from Machine Learning Repository [302] revealed that good values are QM > 1.7, and very good QM > 3. The QM can be used for a small number of training datasets, the data can be accumulated step by step, and if QM reached 1.7-2 value, then it can be concluded the data amount is enough to use/analyze the ML model. Such a strategy excludes excess costs for collecting data, especially in physical/chemical settings. Similar work was recently done with prediction quantum yield for ns² metal halides [303], rare data were collected step by step from the literature and stopped after the QM reached good values. The AAD of quantum yields for all compounds was equal to AAD = 36.6 and MAE after repeated 5-fold cross-validation was equal to MAE = 15+/-5, leading to QM = 2.44 which was a good sign to stop collecting data because ML reached nice quality of prediction. It should be noted that in many cases, ML researchers aim to obtain the best accuracy/MAE and select Neural Networks with the best precision of prediction. However, in physics and chemistry, the explanation is a top priority and the Decision Tree model is preferable, but it has low precision of prediction. Our strategy helps an investigator to withdraw from the race for best accuracy, suggesting reaching just good QM values in the range 1.7-3, concentrating on explanation of results and choosing Decision Trees as a preferable instrument.

In addition, QM metric well works with imbalanced data, when there is an unequal distribution of classes/continuous numbers in the dataset. Let’s consider the dataset with ninety-nine “0” and one “1” classes. If classification ML model always predicts “0” class, the accuracy will be 99%, assuming high precision of prediction. Of course, well-known ROC curve and AUC score can be used to reveal this error in the classification task, however large data amount is preferable. In the case of regression ML model, the MAE will be equal to 1/100 = 0.01 which is a small error, and the model can be wrongly accepted as good. However, according to our scheme, AAD of the whole data equals to AAD = 0.004 and QE = AAD/MAE = 0.004/0.01 = 0.4 which is much smaller than 1. and model cannot be accepted.

We have shown that the biggest problems in application of ML in physics are:

1. Physicists/chemists usually can collect small data which is usually imbalanced, but ML demands a lot of data and all quality metrics (ROC, Accuracy, MAE, etc.) are based on large-scale data. We suggested one new quality mark (QM), which seems to work even with small data and even with imbalanced data, but it should be mathematically explained, tested carefully by AI specialists and/or suggested as a new quality metric for small and imbalanced data.

2. Physicist/chemists usually demand an explanation of the model, but a lot of ML methods are « black box». Moreover, usually feature parameters consists of mixed discrete and/or real values. Only Decision Tree can be accepted as « white box» and can work with mixed discrete/real feature values, and we have at least one instrument which is very good for scientists. But we highlighted that the segregation mechanism based on sorting among only one feature parameter is not good. Such a mechanism sometimes generates a lot of rules and complex segregation lines even for a simple dataset. We suggested Enhanced Decision Tree which includes segregation among all feature parameters at once, which can produce a smaller number of rules with the strongest power (Figure 2). However, this mechanism should be coded and tested, which demands the efforts of AI specialists.

Author contributions

RS: Writing–review and editing. HB: Writing–original draft. AK: Writing–review and editing. AP: Writing–original draft. MM: Writing–original draft, images and tables. RH Writing–original draft. SG: Writing–original draft. PH: Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. RS acknowledges the support of the Russian Science Foundation (Project 22-73-10047). MM acknowledges the support by the Tyumen Oblast Government, as part of the West-Siberian Interregional Science and Education Center’s project No. 89-DON (3).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Turing AM. I.—computing machinery and intelligence. Mind (1950) 59:433–60. doi:10.1093/MIND/LIX.236.433

CrossRef Full Text | Google Scholar

2. Newell A, Simon HA. The logic theory machine a complex information processing system. IRE Trans Inf Theor (1956) 2:61–79. doi:10.1109/TIT.1956.1056797

CrossRef Full Text | Google Scholar

3. Pancioni L, Schwenker F, Trentin E. Artificial neural networks in pattern recognition. In: 8th IAPR TC3 Workshop, ANNPR 2018; September, 2018; Siena, Italy (2018). p. 11081. doi:10.1007/978-3-319-99978-4

CrossRef Full Text | Google Scholar

4. Peterson C, Rögnvaldsson T, Lönnblad L. JETNET 3.0—a versatile artificial neural network package. Comput Phys Commun (1994) 81:185–220. doi:10.1016/0010-4655(94)90120-1

CrossRef Full Text | Google Scholar

5. Amato F, González-Hernández JL, Havel J. Artificial neural networks combined with experimental design: a “soft” approach for chemical kinetics. Talanta (2012) 93:72–8. doi:10.1016/J.TALANTA.2012.01.044

PubMed Abstract | CrossRef Full Text | Google Scholar

6. O’Regan G. History of artificial intelligence. A Brief Hist Comput (2021) 295–319. doi:10.1007/978-3-030-66599-9_22

CrossRef Full Text | Google Scholar

7. Selfridge DOG. Pandemonium: a paradigm for learning. In: Mechanisation of thought processes: proceedings of a symposium held at the national physical laboratory. Cambridge, Massachusetts, United States: MIT Press (2023).

Google Scholar

8. Ayodele TO. Types of machine learning algorithms. New Adv Machine Learn (2010). doi:10.5772/9385

CrossRef Full Text | Google Scholar

9. Kumar I, Singh SP. Shivam. Machine learning in bioinformatics. Bioinformatics Methods Appl (2021) 443–56. doi:10.1016/B978-0-323-89775-4.00020-1

CrossRef Full Text | Google Scholar

10. Van Otterlo M, Wiering M. Reinforcement learning and markov decision processes. Adaptation, Learn Optimization (2012) 12:3–42. doi:10.1007/978-3-642-27645-3_1

CrossRef Full Text | Google Scholar

11. Elguea-Aguinaco Í, Serrano-Muñoz A, Chrysostomou D, Inziarte-Hidalgo I, Bøgh S, Arana-Arexolaleiba N. A review on reinforcement learning for contact-rich robotic manipulation tasks. Robot Comput Integr Manuf (2023) 81:102517. doi:10.1016/J.RCIM.2022.102517

CrossRef Full Text | Google Scholar

12. Cortes C, Vapnik V. Support-vector networks. Mach Learn (1995) 20:273–97. doi:10.1007/bf00994018

CrossRef Full Text | Google Scholar

13. Jongman RHG, Braak CJFter, Tongeren OFRvan. Cambridge, England: Cambridge University Press (1995). doi:10.1017/CBO9780511525575Data analysis in community and landscape ecology

CrossRef Full Text | Google Scholar

14. Cormack RM. A review of classification. J R Stat Soc Ser A (1971) 134:321–53. doi:10.2307/2344237

CrossRef Full Text | Google Scholar

15. Xu D, Tian Y. A comprehensive survey of clustering algorithms. Ann Data Sci (2015) 2(2):165–93. doi:10.1007/S40745-015-0040-1

CrossRef Full Text | Google Scholar

16. Murty MN, Devi VS. Bayes classifier. Berlin, Germany: Springer (2011). p. 86–102. doi:10.1007/978-0-85729-495-1_4

CrossRef Full Text | Google Scholar

17. LaValley MP. Logistic regression. Circulation (2008) 117:2395–9. doi:10.1161/CIRCULATIONAHA.106.682658

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Breiman L, Friedman JH, Olshen RA, Stone CJ.Classification and regression trees New York, NY, USA: Routledge (2017). p. 1–358. doi:10.1201/9781315139470

CrossRef Full Text | Google Scholar

19. Ross Quinlan by J, Kaufmann Publishers M, Salzberg SL. C4.5: programs for machine learning by J. Ross quinlan. Morgan kaufmann publishers, inc. Machine Learn (1994) 16:235–40. doi:10.1007/BF00993309

CrossRef Full Text | Google Scholar

20. Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. Berlin, Germany: Springer (2009). doi:10.1007/978-0-387-84858-7

CrossRef Full Text | Google Scholar

21. Deng H, Runger G, Tuv E. Bias of importance measures for multi-valued attributes and solutions. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); June, 2011; Espoo, Finland (2011). doi:10.1007/978-3-642-21738-8_38

CrossRef Full Text | Google Scholar

22. Webb GI. Naïve Bayes. In: Encyclopedia of machine learning. Berlin, Germany: Springer (2011). p. 713–4. doi:10.1007/978-0-387-30164-8_576

CrossRef Full Text | Google Scholar

23. Barlow HB. Unsupervised learning. Neural Comput (1989) 1:295–311. doi:10.1162/NECO.1989.1.3.295

CrossRef Full Text | Google Scholar

24. Hofmann T. Unsupervised learning by probabilistic latent semantic analysis. Machine Learn (2001) 42:177–96. doi:10.1023/A:1007617005950

CrossRef Full Text | Google Scholar

25. Zhao Z, Liu H. Spectral feature selection for supervised and unsupervised learning. ACM Int Conf Proceeding Ser (2007) 227:1151–7. doi:10.1145/1273496.1273641

CrossRef Full Text | Google Scholar

26. Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm. Pattern Recognit (2003) 36:451–61. doi:10.1016/S0031-3203(02)00060-2

CrossRef Full Text | Google Scholar

27. Johnson SC. Hierarchical clustering schemes. Psychometrika (1967) 32:241–54. doi:10.1007/BF02289588

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Abdi H, Williams LJ. Principal component analysis. Wiley Interdiscip Rev Comput Stat (2010) 2:433–59. doi:10.1002/WICS.101

CrossRef Full Text | Google Scholar

29. Hatfield PW, Gaffney JA, Anderson GJ, Ali S, Antonelli L, Başeğmez du Pree S, et al. The data-driven future of high-energy-density physics. Nature (2021) 593:351–61. doi:10.1038/s41586-021-03382-w

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wu T, Tegmark M. Toward an artificial intelligence physicist for unsupervised learning. Phys Rev E (2019) 100:033311. doi:10.1103/physreve.100.033311

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Andreassen A, Feige I, Frye C, Schwartz MD. JUNIPR: a framework for unsupervised machine learning in particle physics. The Eur Phys J C (2019) 79(79):102–24. doi:10.1140/EPJC/S10052-019-6607-9

CrossRef Full Text | Google Scholar

32. Xin Y, Kong L, Liu Z, Chen Y, Li Y, Zhu H, et al. Machine learning and deep learning methods for cybersecurity. IEEE Access (2018) 6:35365–81. doi:10.1109/ACCESS.2018.2836950

CrossRef Full Text | Google Scholar

33. Ongsulee P. Artificial intelligence, machine learning and deep learning. In: International Conference on ICT and Knowledge Engineering; November, 2018; Bangkok, Thailand (2018). p. 1–6. doi:10.1109/ICTKE.2017.8259629

CrossRef Full Text | Google Scholar

34. Akalin N, Loutfi A, Schmitz A, Distante C. Reinforcement learning approaches in social robotics. Sensors (2021) 21:1292. doi:10.3390/S21041292

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Mitpress. Reinforcement learning (2024). Available at: https://mitpress.mit.edu/9780262039246/reinforcement-learning/(Accessed January 1, 2024).

Google Scholar

36. Landers M, Doryab A. Deep reinforcement learning verification: a survey. ACM Comput Surv (2023) 55:1–31. doi:10.1145/3596444

CrossRef Full Text | Google Scholar

37. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput (1997) 9:1735–80. doi:10.1162/NECO.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. Commun ACM (2020) 63:139–44. doi:10.1145/3422622

CrossRef Full Text | Google Scholar

39. Noriega L. Multilayer perceptron tutorial (2005). https://api.semanticscholar.org/CorpusID:61645526.

Google Scholar

40. Medsker L, Jain LC. Recurrent neural networks. Boca Raton, FL, USA: CRC Press (1999). doi:10.1201/9781420049176

CrossRef Full Text | Google Scholar

41. Albawi S, Mohammed TA, Al-Zawi S. Understanding of a convolutional neural network. In: Proceedings of 2017 International Conference on Engineering and Technology, ICET; January, 2018; Antalya, Turkey (2018). doi:10.1109/ICENGTECHNOL.2017.8308186

CrossRef Full Text | Google Scholar

42. Ramchoun H, Amine M, Idrissi J, Ghanou Y, Ettaouil M. Multilayer perceptron: architecture optimization and training. Int J Interactive Multimedia Artif Intelligence (2016) 4:26. doi:10.9781/IJIMAI.2016.415

CrossRef Full Text | Google Scholar

43. Ruck DW, Rogers SK, Kabrisky M. Feature selection using a multilayer perceptron. J Neural Netw Comput (1990) 2:40–8.

Google Scholar

44. Stefanini M, Cornia M, Baraldi L, Cascianelli S, Fiameni G, Cucchiara R. From show to tell: a survey on deep learning-based image captioning. IEEE Trans Pattern Anal Mach Intell (2021) 45:539–59. doi:10.1109/tpami.2022.3148210

CrossRef Full Text | Google Scholar

45. Gharat S, Dandawate Y. Galaxy classification: a deep learning approach for classifying Sloan Digital Sky Survey images. Mon Not R Astron Soc (2022) 511:5120–4. doi:10.1093/MNRAS/STAC457

CrossRef Full Text | Google Scholar

46. Cabrera-Ponce AA, Martinez-Carranza J. Convolutional neural networks for geo-localisation with a single aerial image. J Real-Time Image Process (2022) 19(19):565–75. doi:10.1007/S11554-022-01207-1

CrossRef Full Text | Google Scholar

47. Connor JT, Martin RD, Atlas LE. Recurrent neural networks and robust time series prediction. IEEE Trans Neural Netw (1994) 5:240–54. doi:10.1109/72.279188

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Salman AG, Kanigoro B, Heryadi Y. Weather forecasting using deep learning techniques. In: 2015 International Conference on Advanced Computer Science and Information Systems; October, 2015; Depok, Indonesia (2016). p. 281–5. doi:10.1109/ICACSIS.2015.7415154

CrossRef Full Text | Google Scholar

49. Che Z, Purushotham S, Cho K, Sontag D, Liu Y. Recurrent neural networks for multivariate time series with missing values. Sci Rep (2018) 8:6085–12. doi:10.1038/s41598-018-24271-9

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Entzeroth M, Flotow H, Condron P. Overview of high-throughput screening. Curr Protoc Pharmacol (2009) 44. doi:10.1002/0471141755.PH0904S44

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Brunin G, Ricci F, Ha VA, Rignanese GM, Hautier G. Transparent conducting materials discovery using high-throughput computing. npj Comput Mater (2019) 5(5):63–13. doi:10.1038/s41524-019-0200-5

CrossRef Full Text | Google Scholar

52. Correa-Baena JP, Hippalgaonkar K, van Duren J, Jaffer S, Chandrasekhar VR, Stevanovic V, et al. Accelerating materials development via automation, machine learning, and high-performance computing. Joule (2018) 2:1410–20. doi:10.1016/j.joule.2018.05.009

CrossRef Full Text | Google Scholar

53. Mounet N, Gibertini M, Schwaller P, Campi D, Merkys A, Marrazzo A, et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat Nanotechnology (2018) 13(13):246–52. doi:10.1038/s41565-017-0035-5

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Marr B. A short history of machine learning -- every manager should read (2024). Available at: https://www.forbes.com/sites/bernardmarr/2016/02/19/a-short-history-of-machine-learning-every-manager-should-read/?sh=75c938e615e7 (Accessed February 1, 2023).

Google Scholar

55. Wang H, Raj B. On the origin of deep learning (2017). Available at: http://arxiv.org/abs/1702.07800 (Accessed February 1, 2023).

Google Scholar

56. Fradkov AL. Early history of machine learning. IFAC-PapersOnLine (2020) 53:1385–90. doi:10.1016/J.IFACOL.2020.12.1888

CrossRef Full Text | Google Scholar

57. Bayes TLII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S. Philos Trans R Soc Lond (1763) 370–418. doi:10.1098/rstl.1763.0053

CrossRef Full Text | Google Scholar

58. Legendre AM. Nouvelles methodes pour la determination des orbites des cometes. chez Firmin Didot, libraire pour lew mathematiques, la marine, l (1806). Available at: https://catalogue.nla.gov.au/Record/866184 (Accessed May 8, 2023).

Google Scholar

59. Hayes B. First links in the Markov chain. Am Sci (2013) 101:92–7. doi:10.1511/2013.101.92

CrossRef Full Text | Google Scholar

60. McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull Math Biophys (1943) 5(5):115–33. doi:10.1007/BF02478259

CrossRef Full Text | Google Scholar

61. Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, et al. Machine learning and the physical sciences. Rev Mod Phys (2019) 91:045002. doi:10.1103/RevModPhys.91.045002

CrossRef Full Text | Google Scholar

62. Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A (1982) 79:2554–8. doi:10.1073/PNAS.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Valiant LG. A theory of the learnable. Commun ACM (1984) 27:1134–42. doi:10.1145/1968.1972

CrossRef Full Text | Google Scholar

64. Sarker IH. Machine learning: algorithms, real-world applications and research directions. SN Comput Sci (2021) 2:160–21. doi:10.1007/s42979-021-00592-x

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Pugliese R, Regondi S, Marini R. Machine learning-based approach: global trends, research directions, and regulatory standpoints. Data Sci Manag (2021) 4:19–29. doi:10.1016/J.DSM.2021.12.002

CrossRef Full Text | Google Scholar

66. Bahri Y, Kadmon J, Pennington J, Schoenholz SS, Sohl-Dickstein J, Ganguli S. Statistical mechanics of deep learning. Annu Rev Condens Matter Phys (2020) 11:501–28. doi:10.1146/annurev-conmatphys-031119-050745

CrossRef Full Text | Google Scholar

67. Denby B. Neural networks and cellular automata in experimental high energy physics. Comput Phys Commun (1988) 49:429–48. doi:10.1016/0010-4655(88)90004-5

CrossRef Full Text | Google Scholar

68. Kinnunen M. Examining the limits of Moore’s law: possible influence of technological convergence on redefining the curriculum in ICT institutions. Thesis for: Bachelor of Engineering (2015).

69. Tuggener L, Amirian M, Rombach K, Lorwald S, Varlet A, Westermann C, et al. Automated machine learning in practice: state of the art and recent results. In: Proceedings - 6th Swiss Conference on Data Science, SDS; June, 2019; Bern, Switzerland (2019). p. 31–6. doi:10.1109/SDS.2019.00-11

CrossRef Full Text | Google Scholar

70. Gaudel R, Sebag M. Feature selection as a one-player game (2010). Available at: https://hal.inria.fr/inria-00484049 (Accessed September 27, 2022).

Google Scholar

71. Pfahringer B, Pfahringer B, Bensusan H, Giraud-Carrier C. Meta-learning by landmarking various learning algorithms. In: Proceedings of the Seventeenth International Conference on Machine Learning; June, 2000; Standord, CA, USA (2000). p. 743–50.

Google Scholar

72. Klein A, Falkner S, Springenberg JT, Hutter F. Learning curve prediction with bayesian neural networks (2022).

Google Scholar

73. Real E, Liang C, So DR, Le QV. AutoML-zero: evolving machine learning algorithms from scratch (2020). Available at: https://proceedings.mlr.press/v119/real20a.html (Accessed January 30, 2023).

Google Scholar

74. Manceur AM, Dutilleul P. Maximum likelihood estimation for the tensor normal distribution: algorithm, minimum sample size, and empirical bias and dispersion. J Comput Appl Math (2013) 239:37–49. doi:10.1016/J.CAM.2012.09.017

CrossRef Full Text | Google Scholar

75. Wells L, Bednarz T. Explainable AI and reinforcement learning—a systematic review of current approaches and trends. Front Artif Intell (2021) 4:550030. doi:10.3389/frai.2021.550030

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Adadi A, Berrada M. Peeking inside the black-box: a survey on explainable artificial intelligence (XAI). IEEE Access (2018) 6:52138–60. doi:10.1109/ACCESS.2018.2870052

CrossRef Full Text | Google Scholar

77. Gunning D, Aha DW. DARPA’s explainable artificial intelligence program. AI Mag (2019) 40:44–58. doi:10.1609/AIMAG.V40I2.2850

CrossRef Full Text | Google Scholar

78. Saeed W, Omlin C. Explainable AI (XAI): a systematic meta-survey of current challenges and future opportunities (2021). https://arxiv.org/abs/2111.06420.

Google Scholar

79. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L. Physics-informed machine learning. Nat Rev Phys (2021) 3(3):422–40. doi:10.1038/s42254-021-00314-5

CrossRef Full Text | Google Scholar

80. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys (2019) 378:686–707. doi:10.1016/J.JCP.2018.10.045

CrossRef Full Text | Google Scholar

81. Mathews A, Francisquez M, Hughes J, Hatch D, Zhu B, Rogers B. Uncovering turbulent plasma dynamics via deep learning from partial observations. Phys Rev E (2020) 104:025205. doi:10.1103/PhysRevE.104.025205

CrossRef Full Text | Google Scholar

82. Collaboration G, Vallenari A, Brown A, Prusti T, de Bruijne J, Arenou F, et al. Gaia data release 3: summary of the content and survey properties. R Gutiérrez-sánchez (2022) 9:A1. doi:10.1051/0004-6361/202243940

CrossRef Full Text | Google Scholar

83. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Observation of gravitational waves from a binary black hole merger. Phys Rev Lett (2016) 116:061102. doi:10.1103/PHYSREVLETT.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys Rev Lett (2016) 116:241103. doi:10.1103/PHYSREVLETT.116.241103

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Observation of a 50-solar-mass binary black hole coalescence at redshift 0.2. Phys Rev Lett (2017) 118. doi:10.1103/PHYSREVLETT.118.221101

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Directly comparing GW150914 with numerical solutions of Einstein’s equations for binary black hole coalescence. Phys Rev D (2016) 94:064035. doi:10.1103/PHYSREVD.94.064035

CrossRef Full Text | Google Scholar

87. Raman A. On signal estimation, detection and interference mitigation in LIGO. In: 2018 IEEE Global Conference on Signal and Information Processing, GlobalSIP 2018 - Proceedings; November, 2019; Anaheim, CA, USA (2019). p. 1086–90. doi:10.1109/GLOBALSIP.2018.8646464

CrossRef Full Text | Google Scholar

88. Gabbard H, Williams M, Hayes F, Messenger C. Matching matched filtering with deep networks for gravitational-wave astronomy. Phys Rev Lett (2017) 120:141103. doi:10.1103/PhysRevLett.120.141103

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Mack W, Habets EAP. Deep filtering: signal extraction and reconstruction using complex time-frequency filters. IEEE Signal Process Lett (2019) 27:61–5. doi:10.1109/LSP.2019.2955818

CrossRef Full Text | Google Scholar

90. Yan J, Avagyan M, Colgan RE, Veske D, Bartos I, Wright J, et al. Generalized approach to matched filtering using neural networks. Phys Rev Journals (2021) 105:043006. doi:10.1103/PHYSREVD.105.043006

CrossRef Full Text | Google Scholar

91. Mehta RM-NET. A convolutional neural network for deep brain structure segmentation. In: 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017); April, 2017; Melbourne, VIC, Australia (2017). doi:10.0/Linux-x86_64

CrossRef Full Text | Google Scholar

92. George D, Huerta EA. Deep Learning for real-time gravitational wave detection and parameter estimation: results with Advanced LIGO data. Phys Lett Section B: Nucl Elem Part High-Energy Phys (2018) 778:64–70. doi:10.1016/J.PHYSLETB.2017.12.053

CrossRef Full Text | Google Scholar

93. O’Shea K, Nash R. An introduction to convolutional neural networks. Int J Res Appl Sci Eng Technol (2015) 10:943–7. doi:10.22214/ijraset.2022.47789

CrossRef Full Text | Google Scholar

94. Hinton GE, Krizhevsky A, Wang SD. Transforming auto-encoders. In: 21st International Conference on Artificial Neural Networks; June, 2011; Espoo, Finland (2011).

Google Scholar

95. Kingma DP, Welling M. Auto-encoding variational Bayes. In: 2nd International Conference on Learning Representations, ICLR 2014 - Conference Track Proceedings; April, 2013; Banff, AB, Canada (2013). doi:10.48550/arxiv.1312.6114

CrossRef Full Text | Google Scholar

96. Doersch C. Tutorial on variational autoencoders (2016). https://arxiv.org/abs/1606.05908.

Google Scholar

97. Vincent P, Larochelle H, Bengio Y, Manzagol P-A. Extracting and composing robust features with denoising autoencoders. In: Proceedings of the 25th international conference on Machine learning, 2008; July, 2008; New York, NY, United States (2008).

CrossRef Full Text | Google Scholar

98. Hinton GE, Zemel RS. Autoencoders, minimum description length and helmholtz free energy. In: Proceedings of the 6th International Conference on Neural Information Processing Systems; November, 1993; Denver Colorado (1993).

Google Scholar

99. Shen H, George D, Huerta EA, Zhao Z. Denoising gravitational waves using deep learning with recurrent denoising autoencoders. In: ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing - Proceedings; May, 2019; Brighton, UK (2019). doi:10.1109/ICASSP.2019.8683061

CrossRef Full Text | Google Scholar

100. Gers FA, Schmidhuber J, Cummins F. Learning to forget: continual prediction with LSTM. Neural Comput (2000) 12:2451–71. doi:10.1162/089976600300015015

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Graves A, Fernández S, Gomez F, Schmidhuber J, Ch J. Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks. In: Proceedings of the 23rd international conference on Machine learning; June, 2015; Pittsburgh Pennsylvania USA (2015).

Google Scholar

102. Sutskever Google I, Vinyals Google O, Le Google QV. Sequence to sequence learning with neural networks. Adv Neural Inf Process Syst (2014) 27.

Google Scholar

103. Wei W, Huerta EA. Gravitational wave denoising of binary black hole mergers with deep learning. Phys Lett B (2020) 800:135081. doi:10.1016/J.PHYSLETB.2019.135081

CrossRef Full Text | Google Scholar

104. Oord Avan den, Dieleman S, Zen H, Simonyan K, Vinyals O, Graves A, et al. WaveNet: a generative model for raw audio (2016). Available at: https://arxiv.org/abs/1609.03499v2 (Accessed April 4, 2023). doi:10.48550/arXiv.1609.03499

CrossRef Full Text | Google Scholar

105. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Observation of a 19 solar-mass binary black hole coalescence. Astrophys J Lett (2017) 851. doi:10.3847/2041-8213/AA9F0C

CrossRef Full Text | Google Scholar

106. Usman SA, Nitz AH, Harry IW, Biwer CM, Brown DA, Cabero M, et al. The PyCBC search for gravitational waves from compact binary coalescence. Class Quan Gravity (2016) 33:215004. doi:10.1088/0264-9381/33/21/215004

CrossRef Full Text | Google Scholar

107. LIGO. LIGO-T1800044-v5: updated Advanced LIGO sensitivity design curve (2023). Available at: https://dcc.ligo.org/LIGO-T1800044/public (Accessed April 4, 2023).

Google Scholar

108. Powell J, Sun L, Gereb K, Lasky PD, Dollmann M. Generating transient noise artefacts in gravitational-wave detector data with generative adversarial networks. Class Quan Gravity (2023) 40:035006. doi:10.1088/1361-6382/ACB038

CrossRef Full Text | Google Scholar

109. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. Adv Neural Inf Process Syst (2014) 27.

Google Scholar

110. Aasi J, Abbott BP, Abbott R, Abbott T, Abernathy MR, Ackley K, et al. Advanced LIGO. Class Quan Gravity (2015) 32:074001. doi:10.1088/0264-9381/32/7/074001

CrossRef Full Text | Google Scholar

111. Borucki WJ, Koch DG. Kepler mission highlights. Proc Int Astronomical Union (2010) 6:34–43. doi:10.1017/S1743921311019909

CrossRef Full Text | Google Scholar

112. Jenkins JM, Twicken JD, McCauliff S, Campbell J, Sanderfer D, Lung D, et al. The TESS science processing operations center. Proc SPIE (2016) 9913. doi:10.1117/12.2233418

CrossRef Full Text | Google Scholar

113. Ricker GR, Winn JN, Vanderspek R, Latham DW, Bakos A, Bean JL, et al. Transiting exoplanet survey satellite (TESS). Proc Space Telescopes Instrumentation 2014: Opt Infrared, Millimeter Wave (2014) 9143:914320–1. doi:10.1117/12.2063489

CrossRef Full Text | Google Scholar

114. Guerrero NM, Seager S, Huang CX, Vanderburg A, Soto AG, Mireles I, et al. The TESS objects of interest catalog from the TESS prime mission. Astrophys J Suppl Ser (2021) 254:39. doi:10.3847/1538-4365/ABEFE1

CrossRef Full Text | Google Scholar

115. Ofman L, Averbuch A, Shliselberg A, Benaun I, Segev D, Rissman A. Automated identification of transiting exoplanet candidates in NASA Transiting Exoplanets Survey Satellite (TESS) data with machine learning methods. New Astron (2022) 91:101693. doi:10.1016/j.newast.2021.101693

CrossRef Full Text | Google Scholar

116. McCauliff SD, Jenkins JM, Catanzarite J, Burke CJ, Coughlin JL, Twicken JD, et al. Automatic classification of kepler planetary transit candidates. Astrophys J (2015) 806:6. doi:10.1088/0004-637X/806/1/6

CrossRef Full Text | Google Scholar

117. Coughlin JL, Coughlin JL, Mullally F, Thompson SE, Rowe JF, Burke CJ, et al. Planetary candidates observed by kepler. VII. The first fully uniform catalog based on the entire 48-month data set (Q1-Q17 DR24). ApJS (2016) 224:12. doi:10.3847/0067-0049/224/1/12

CrossRef Full Text | Google Scholar

118. Thompson SE, Coughlin JL, Hoffman K, Mullally F, Christiansen JL, Burke CJ, et al. Planetary candidates observed by kepler. Viii A Fully Automated Catalog Measured Completeness Reliability Based Data Release (2018) 25. doi:10.17909/T9488N

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Osborn HP, Ansdell M, Ioannou Y, Sasdelli M, Angerhausen D, Caldwell D, et al. Rapid classification of TESS Planet candidates with convolutional neural networks (2019). Available at: https://archive.stsci.edu/tess/bulk_downloads.html (Accessed April 20, 2022).

Google Scholar

120. Fiscale S, Ciaramella A, Inno L, Covone G, Ferone A, Rotundi A, et al. Exploiting kepler’s heritage: a transfer learning approach for identifying exoplanets’ transits in TESS data. Res Notes AAS (2021) 5:91. doi:10.3847/2515-5172/ABF56B

CrossRef Full Text | Google Scholar

121. Agnes CK, Naveed A, Mary A, Chacko MO. ExoSGAN and ExoACGAN: exoplanet detection using adversarial training algorithms (2022). Available at: https://arxiv.org/abs/2207.09665v1 (Accessed April 4, 2023).

Google Scholar

122. Alloghani M, Al-Jumeily D, Mustafina J, Hussain A, Aljaaf AJ. A systematic review on supervised and unsupervised machine learning algorithms for data science. In: Supervised and unsupervised learning for data science. Berlin, Germany: Springer (2020). p. 3–21. doi:10.1007/978-3-030-22475-2_1

CrossRef Full Text | Google Scholar

123. Schmid PJ. Dynamic mode decomposition and its variants. Annurev-Fluid (2022) 54:225–54. doi:10.1146/ANNUREV-FLUID-030121-015835

CrossRef Full Text | Google Scholar

124. Berkooz G, Holmes P, Lumley JL. The proper orthogonal decomposition in the analysis of turbulent flows. Annurev-Fluid (2003) 25:539–75. doi:10.1146/ANNUREV.FL.25.010193.002543

CrossRef Full Text | Google Scholar

125. Schmid PJ. Dynamic mode decomposition of numerical and experimental data. J Fluid Mech (2010) 656:5–28. doi:10.1017/S0022112010001217

CrossRef Full Text | Google Scholar

126. Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature (1986) 323:533–6. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

127. Brunton SL, Proctor JL, Kutz JN, Bialek W. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc Natl Acad Sci U S A (2016) 113:3932–7. doi:10.1073/PNAS.1517384113

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Champion K, Lusch B, Nathan Kutz J, Brunton SL. Data-driven discovery of coordinates and governing equations. Proc Natl Acad Sci U S A (2019) 116:22445–51. doi:10.1073/PNAS.1906995116

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdelalim AA, et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys Lett B (2012) 716:1–29. doi:10.1016/J.PHYSLETB.2012.08.020

CrossRef Full Text | Google Scholar

130. Gazula S, Clark JW, Bohr H. Learning and prediction of nuclear stability by neural networks. Nucl Phys A (1992) 540:1–26. doi:10.1016/0375-9474(92)90191-L

CrossRef Full Text | Google Scholar

131. Gernoth KA, Clark JW, Prater JS, Bohr H. Neural network models of nuclear systematics. Phys Lett B (1993) 300:1–7. doi:10.1016/0370-2693(93)90738-4

CrossRef Full Text | Google Scholar

132. Clark JW, Li H. Application of support vector machines to global prediction of nuclear properties. Int J Mod Phys B (2012) 20:5015–29. doi:10.1142/S0217979206036053

CrossRef Full Text | Google Scholar

133. Shi M, Niu Z-M, Thanh Son D, Stephanov M, Yee - H-U, Carnini M, et al. Trees and forests in nuclear physics. J Phys G: Nucl Part Phys (2020) 47:082001. doi:10.1088/1361-6471/AB92E3

CrossRef Full Text | Google Scholar

134. Wu XH, Guo LH, Zhao PW. Nuclear masses in extended kernel ridge regression with odd-even effects. Phys Lett B (2021) 819:136387. doi:10.1016/J.PHYSLETB.2021.136387

CrossRef Full Text | Google Scholar

135. Lovell AE, Mohan AT, Sprouse TM, Mumpower MR. Nuclear masses learned from a probabilistic neural network (2022). https://arxiv.org/abs/2201.00676.

CrossRef Full Text | Google Scholar

136. Roe BP, Yang H-J, Zhu J, Liu Y, Stancu I, McGregor G. Boosted decision trees as an alternative to artificial neural networks for particle identification. Nucl Instrum Methods Phys Res A (2004) 543:577–84. doi:10.1016/j.nima.2004.12.018

CrossRef Full Text | Google Scholar

137. Guest D, Cranmer K, Whiteson D. Deep learning and its application to LHC physics. Annu Rev Nucl Part Sci (2018) 68:161–81. doi:10.1146/annurev-nucl-101917-021019

CrossRef Full Text | Google Scholar

138. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, et al. TeV. Phys Rev D - Particles, Fields, Gravitation Cosmology (2014) 89:032002. doi:10.1103/PhysRevD.89.032002

CrossRef Full Text | Google Scholar

139. Baldi P, Sadowski P, Whiteson D. Searching for exotic particles in high-energy physics with deep learning. Nat Commun (2014) 5(5):4308–9. doi:10.1038/ncomms5308

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Graczykowski ŁK, Jakubowska M, Rafał K, Μí± DÍ, Kabus M. Using machine learning for particle identification in ALICE (2022). https://arxiv.org/abs/2204.06900.

CrossRef Full Text | Google Scholar

141. ATLAS Collaboration. A search for top squarks with R-parity-violating decays to all-hadronic final states with the ATLAS detector in $\sqrt{s}$ = 8 TeV proton-proton collisions. J High Energ Phys (2016) 2016:1–49. doi:10.1007/JHEP06(2016)067

CrossRef Full Text | Google Scholar

142. Boos EE, Bunichev VE, Dudko Lv., Markina AA. Method of “optimum observables” and implementation of neural networks in physics investigations. Phys At Nuclei (2011) 71(71):388–93. doi:10.1134/S1063778808020191

CrossRef Full Text | Google Scholar

143. CMS Collaboration. Search for the Higgs boson decaying to two muons in proton-proton collisions at $\sqrt{s} =$ 13 TeV. Phys Rev Lett (2018) 122. doi:10.1103/PhysRevLett.122.021801

CrossRef Full Text | Google Scholar

144. Coadou Y. Boosted decision trees. Artif Intelligence High Energ Phys (2022) 9–58. doi:10.1142/9789811234033_0002

CrossRef Full Text | Google Scholar

145. Bourilkov D, Acosta D, Bortignon P, Brinkerhoff A, Carnes A, Gleyzer S, et al. Machine learning techniques in the CMS search for Higgs decays to dimuons. EPJ Web Conf (2019) 214:06002. doi:10.1051/EPJCONF/201921406002

CrossRef Full Text | Google Scholar

146. Saberian M, Delgado P, Raimond Y. Gradient boosted decision tree neural network (2019). Available at: https://arxiv.org/abs/1910.09340v2 (Accessed April 4, 2023).

Google Scholar

147. Chen T, Guestrin C. XGBoost: a scalable tree boosting system. In: Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; August, 2016; San Francisco California USA (2016). p. 785–94. doi:10.1145/2939672.2939785

CrossRef Full Text | Google Scholar

148. Aad G, Abbott B, Abbott DC, Abed Abud A, Abeling K, Abhayasinghe DK, et al. A search for the dimuon decay of the Standard Model Higgs boson with the ATLAS detector. Phys Lett B (2021) 812:135980. doi:10.1016/j.physletb.2020.135980

CrossRef Full Text | Google Scholar

149. Chakraborty A, Dasmahapatra S, Day-Hall HA, Ford BG, Jain S, Moretti S, et al. Revisiting jet clustering algorithms for new Higgs Boson searches in hadronic final states. Eur Phys J C (2022) 82(82):346–14. doi:10.1140/EPJC/S10052-022-10314-Z

CrossRef Full Text | Google Scholar

150. Schmidhuber J. Deep learning in neural networks: an overview. Neural Networks (2015) 61:85–117. doi:10.1016/J.NEUNET.2014.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Search for $$ \mathrm{t}\overline{\mathrm{t}}\mathrm{H} $$ production in the $$ \mathrm{H}\to \mathrm{b}\overline{\mathrm{b}} $$ decay channel with leptonic $$ \mathrm{t}\overline{\mathrm{t}} $$ decays in proton-proton collisions at $$ \sqrt{s}=13 $$ TeV. J High Energ Phys (2019) 2019:26. doi:10.1007/JHEP03(2019)026

CrossRef Full Text | Google Scholar

152. Bebis G, Georgiopoulos M. Feed-forward neural networks. IEEE Potentials (1994) 13:27–31. doi:10.1109/45.329294

CrossRef Full Text | Google Scholar

153. Guest D, Collado J, Baldi P, Hsu S-C, Urban G, Whiteson D. Jet flavor classification in high-energy physics with deep neural networks. Phys Rev D (2016) 94:112002. doi:10.1103/PhysRevD.94.112002

CrossRef Full Text | Google Scholar

154. Almeida LG, Backović M, Cliche M, Lee SJ, Perelstein M. Playing tag with ANN: boosted top identification with pattern recognition. J High Energ Phys (2015) 7:86–21. doi:10.1007/JHEP07(2015)086

CrossRef Full Text | Google Scholar

155. Cogan J, Kagan M, Strauss E, Schwartzman A. Jet-images: computer vision inspired techniques for jet tagging. J High Energ Phys (2014) 2015:118. doi:10.1007/JHEP02(2015)118

CrossRef Full Text | Google Scholar

156. Karagiorgi G, Kasieczka G, Kravitz S, Nachman B, Shih D. Machine learning in the search for new fundamental physics. Nat Rev Phys (2022) 4(4):399–412. doi:10.1038/s42254-022-00455-1

CrossRef Full Text | Google Scholar

157. Friedman JH. Stochastic gradient boosting. Comput Stat Data Anal (2002) 38:367–78. doi:10.1016/S0167-9473(01)00065-2

CrossRef Full Text | Google Scholar

158. Aggarwal L, Banerjee S, Bansal S, Bernlochner F, Bertemes M, Bhardwaj V, et al. Snowmass White Paper: Belle II physics reach and plans for the next decade and beyond. (2022) Available at: https://arxiv.org/abs/2207.06307v2 [Accessed April 4, 2023]

Google Scholar

159. Keck T. FastBDT: a speed-optimized multivariate classification algorithm for the Belle II experiment. Comput Softw Big Sci (2017) 1:2–11. doi:10.1007/s41781-017-0002-8

CrossRef Full Text | Google Scholar

160. Zhang J-Y, Cai X. The high-luminosity upgrade of the LHC: physics and technology challenges for the accelerator and the experiments you may also like upgrade of beam energy measurement system at BEPC-II. J Phys Conf Ser PAPER • OPEN ACCESS (2023). doi:10.1088/1742-6596/706/2/022002

CrossRef Full Text | Google Scholar

161. Hong TM, Carlson BT, Eubanks BR, Racz ST, Roche ST, Stelzer J, et al. Nanosecond machine learning event classification with boosted decision trees in FPGA for high energy physics. J Instrumentation (2021) 16:P08016. doi:10.1088/1748-0221/16/08/P08016

CrossRef Full Text | Google Scholar

162. Rahmat R, Kroeger R, Giammanco A. The fast simulation of the CMS experiment. J Phys Conf Ser OPEN ACCESS (2023) 396:062016. doi:10.1088/1742-6596/396/6/062016

CrossRef Full Text | Google Scholar

163. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. GEANT4 - a simulation toolkit. Nucl Instr Methods A (2003) 506:250–303. doi:10.1016/s0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

164. Allison J, Amako K, Apostolakis J, Araujo H, Dubois PA, Asai M, et al. Geant4 developments and applications. IEEE Trans Nucl Sci (2006) 53:270–8. doi:10.1109/tns.2006.869826

CrossRef Full Text | Google Scholar

165. Aad G, Ackers M, Alberti FA, Aleppo M, Alimonti G, Alonso J, et al. The ATLAS experiment at the CERN large Hadron collider. J Instrum (2008) 3:S08003. doi:10.1088/1748-0221/3/07/p07007

CrossRef Full Text | Google Scholar

166. Aad G, Abbott B, Abdallah J, Abdelalim AA, Abdesselam A, Abdinov O, et al. The ATLAS simulation infrastructure. Eur Phys J C (2010) 70:823–74. doi:10.1140/EPJC/S10052-010-1429-9

CrossRef Full Text | Google Scholar

167. Karavakis E, Andreeva J, Campana S, Gayazov S, Jezequel S, Saiz P, et al. Common accounting system for monitoring the ATLAS distributed computing resources. J Phys Conf Ser (2014) 513:062024. doi:10.1088/1742-6596/513/6/062024

CrossRef Full Text | Google Scholar

168. Novaes S, Wayner D, Kloz D, Bruncko D. Computing RRB (2015). Available at: http://cern.ch/committees/all/welcomeLHCRRB.html (Accessed April 2, 2023).

Google Scholar

169. Paganini M, de Oliveira L, Nachman B. Accelerating science with generative adversarial networks: an application to 3D particle showers in multi-layer calorimeters. Phys Rev Lett (2017) 120:042003. doi:10.1103/PhysRevLett.120.042003

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Carminati F, Khattak G, Loncar V, Ahdida C, Albanese R, Alexandrov A. Generative models for fast simulation. J Phys Conf Ser (2018) 1085:022005. doi:10.1088/1742-6596/1085/2/022005

CrossRef Full Text | Google Scholar

171. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Measurement of the inelastic proton-proton cross section at ffiffi s p = 13 TeV with the ATLAS detector at the LHC. PhysRevLett (2016) 117:182002. doi:10.1103/PhysRevLett.117.182002

CrossRef Full Text | Google Scholar

172. Vallecorsa S. Generative models for fast simulation. J Phys Conf Ser (2018) 1085:022005. doi:10.1088/1742-6596/1085/2/022005

CrossRef Full Text | Google Scholar

173. de Oliveira L, Paganini M, Nachman B. Learning particle physics by example: location-aware generative adversarial networks for physics synthesis. Comput Softw Big Sci (2017) 1:4–24. doi:10.1007/s41781-017-0004-6

CrossRef Full Text | Google Scholar

174. Barnard J, Dawe EN, Dolan MJ, Rajcic N. Parton shower uncertainties in jet substructure analyses with deep neural networks. Phys Rev D (2016) 95:014018. doi:10.1103/PhysRevD.95.014018

CrossRef Full Text | Google Scholar

175. Bang D, Shim H. Improved training of generative adversarial networks using representative features (2018). https://arxiv.org/abs/1801.09195.

Google Scholar

176. Nachman B, de Oliveira L, Paganini M. Electromagnetic calorimeter shower images. Phys Rev Journals (2017) 1. doi:10.17632/PVN3XC3WY5.1

CrossRef Full Text | Google Scholar

177. Amadio G, Ananya , Apostolakis J, Bandieramonte M, Behera S, Bhattacharyya A, et al. GeantV alpha release. J Phys Conf Ser (2018) 1085:032037. doi:10.1088/1742-6596/1085/3/032037

CrossRef Full Text | Google Scholar

178. Belayneh D, Carminati F, Farbin A, Hooberman B, Khattak G, Liu M, et al. Calorimetry with deep learning: particle simulation and reconstruction for collider physics. Eur Phys J C (2020) 80:688–31. doi:10.1140/EPJC/S10052-020-8251-9

CrossRef Full Text | Google Scholar

179. Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. In: 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings; May, 2023; San Juan, Puerto Rico (2015).

Google Scholar

180. Salimans T, Goodfellow I, Zaremba W, Cheung V, Radford A, Chen X, et al. Improved techniques for training GANs. Adv Neural Inf Process Syst (2016) 29.

Google Scholar

181. Rezende DJ, Mohamed S, Wierstra D. Stochastic backpropagation and approximate inference in deep generative models. In: 31st International Conference on Machine Learning, ICML; June, 2014; Beijing China (2014). p. 3057–70. doi:10.48550/arxiv.1401.4082

CrossRef Full Text | Google Scholar

182. Cranmer K, Ghosh A, Louppe G, Salamani D, Gadatsch S, Golling T, et al. Deep generative models for fast photon shower simulation in ATLAS (2022). Available at: http://bayesiandeeplearning.org/2018/papers/24.pdf (Accessed April 2, 2023). doi:10.48550/arXiv.2210.06204

CrossRef Full Text | Google Scholar

183. Hariri A, Dyachkova D, Gleyzer S. Graph variational autoencoder for detector reconstruction and fast simulation in high-energy physics. EPJ Web Conf (2021) 251:03051. doi:10.1051/EPJCONF/202125103051

CrossRef Full Text | Google Scholar

184. Shlomi J, Battaglia P, Vlimant J-R. Graph neural networks in particle physics. Mach Learn Sci Technol (2020) 2:021001. doi:10.1088/2632-2153/ABBF9A

CrossRef Full Text | Google Scholar

185. Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, et al. Graph neural networks: a review of methods and applications. AI Open (2020) 1:57–81. doi:10.1016/J.AIOPEN.2021.01.001

CrossRef Full Text | Google Scholar

186. Kieseler J. Object condensation: one-stage grid-free multi-object reconstruction in physics detectors, graph, and image data. Eur Phys J C (2020) 80:886–12. doi:10.1140/EPJC/S10052-020-08461-2

CrossRef Full Text | Google Scholar

187. Neven D, De Brabandere B, Luc MP, Gool V. Instance segmentation by jointly optimizing spatial embeddings and clustering bandwidth (2019). https://arxiv.org/abs/1906.11109.

CrossRef Full Text | Google Scholar

188. Danel T, Spurek P, Tabor J, Śmieja M, Ł S, Słowik A, et al. Spatial graph convolutional networks. Commun Comp Inf Sci (2019) 1333:668–75. doi:10.1007/978-3-030-63823-8_76

CrossRef Full Text | Google Scholar

189. Ninduwezuor-Ehiobu N, Tula OA, Daraojimba C, Ofonagoro KA, Ogunjobi OA, Gidiagba JO, et al. Tracing the evolution of ai and machine learning applications in advancing materials discovery and production processes. Eng Sci Tech J (2023) 4:66–83. doi:10.51594/ESTJ.V4I3.552

CrossRef Full Text | Google Scholar

190. Juan Y, Dai Y, Yang Y, Zhang J. Accelerating materials discovery using machine learning. J Mater Sci Technol (2021) 79:178–90. doi:10.1016/J.JMST.2020.12.010

CrossRef Full Text | Google Scholar

191. Curtarolo S, Hart GLW, Nardelli MB, Mingo N, Sanvito S, Levy O. The high-throughput highway to computational materials design. Nat Mater (2013) 12(12):191–201. doi:10.1038/nmat3568

PubMed Abstract | CrossRef Full Text | Google Scholar

192. Curtarolo S, Setyawan W, Hart GLW, Jahnatek M, Chepulskii RV, Taylor RH, et al. AFLOW: an automatic framework for high-throughput materials discovery. Comput Mater Sci (2012) 58:218–26. doi:10.1016/J.COMMATSCI.2012.02.005

CrossRef Full Text | Google Scholar

193. Ong SP. Accelerating materials science with high-throughput computations and machine learning. Comput Mater Sci (2019) 161:143–50. doi:10.1016/J.COMMATSCI.2019.01.013

CrossRef Full Text | Google Scholar

194. Chakraborty A, Dixit M, Aurbach D, Major DT. Predicting accurate cathode properties of layered oxide materials using the SCAN meta-GGA density functional. npj Comput Mater (2018) 4(4):60–9. doi:10.1038/s41524-018-0117-4

CrossRef Full Text | Google Scholar

195. Yang L, Pijuan-Galito S, Rho HS, Vasilevich AS, Eren AD, Ge L, et al. High-throughput methods in the discovery and study of biomaterials and materiobiology. Chem Rev (2021) 121:4561–677. doi:10.1021/ACS.CHEMREV.0C00752

PubMed Abstract | CrossRef Full Text | Google Scholar

196. Kirklin S, Meredig B, Wolverton C. High-throughput computational screening of new Li-ion battery anode materials. Adv Energ Mater (2013) 3:252–62. doi:10.1002/AENM.201200593

CrossRef Full Text | Google Scholar

197. Li Z, Wang S, Chin WS, Achenie LE, Xin H. High-throughput screening of bimetallic catalysts enabled by machine learning. J Mater Chem A Mater (2017) 5:24131–8. doi:10.1039/C7TA01812F

CrossRef Full Text | Google Scholar

198. Luo S, Li T, Wang X, Faizan M, Zhang L. High-throughput computational materials screening and discovery of optoelectronic semiconductors. Wiley Interdiscip Rev Comput Mol Sci (2021) 11:e1489. doi:10.1002/WCMS.1489

CrossRef Full Text | Google Scholar

199. Lindsay RK, Buchanan BG, Feigenbaum EA, Lederberg J. DENDRAL: a case study of the first expert system for scientific hypothesis formation. Artif Intell (1993) 61:209–61. doi:10.1016/0004-3702(93)90068-M

CrossRef Full Text | Google Scholar

200. Schmidt J, Marques MRG, Botti S, Marques MAL. Recent advances and applications of machine learning in solid-state materials science. npj Comput Mater (2019) 5(5):83–36. doi:10.1038/s41524-019-0221-0

CrossRef Full Text | Google Scholar

201. Mater AC, Coote ML. Deep learning in chemistry. J Chem Inf Model (2019) 59:2545–59. doi:10.1021/ACS.JCIM.9B00266

PubMed Abstract | CrossRef Full Text | Google Scholar

202. Freeman CM, Catlow CRA. Structure predictions in inorganic solids. J Chem Soc Chem Commun (1992) 89–91. doi:10.1039/C39920000089

CrossRef Full Text | Google Scholar

203. Bush TS, Catlow CRA, Battle PD. Evolutionary programming techniques for predicting inorganic crystal structures. J Mater Chem (1995) 5:1269–72. doi:10.1039/JM9950501269

CrossRef Full Text | Google Scholar

204. Corey EJ, Todd Wipke W. Computer-assisted design of complex organic syntheses. Science (1969) 166:178–92. doi:10.1126/SCIENCE.166.3902.178

PubMed Abstract | CrossRef Full Text | Google Scholar

205. Coley CW, Barzilay R, Jaakkola TS, Green WH, Jensen KF. Prediction of organic reaction outcomes using machine learning. ACS Cent Sci (2017) 3:434–43. doi:10.1021/ACSCENTSCI.7B00064

PubMed Abstract | CrossRef Full Text | Google Scholar

206. Ren F, Ward L, Williams T, Laws KJ, Wolverton C, Hattrick-Simpers J, et al. Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments. Sci Adv (2018) 4. doi:10.1126/SCIADV.AAQ1566

PubMed Abstract | CrossRef Full Text | Google Scholar

207. Patel SK, Swain BK, Patel SK, Swain BK, Behera A, Mohapatra SS, et al. Metallic glasses: a revolution in material science. Metallic Glasses (2020). doi:10.5772/INTECHOPEN.90165

CrossRef Full Text | Google Scholar

208. Ward L, Agrawal A, Choudhary A, Wolverton C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput Mater (2016) 2(2):16028–7. doi:10.1038/npjcompumats.2016.28

CrossRef Full Text | Google Scholar

209. Yoshiyuki KY, Yu J-Z, Jing -Z, Masumoto T, Tsuyoshi) , Tsai AP, et al. Phase diagrams and physical properties of nonequilibrium alloys. Berlin, Germany: Springer (2006).

Google Scholar

210. Schütt KT, Glawe H, Brockherde F, Sanna A, Müller KR, Gross EKU. How to represent crystal structures for machine learning: towards fast prediction of electronic properties. Phys Rev B Condens Matter Mater Phys (2014) 89:205118. doi:10.1103/physrevb.89.205118

CrossRef Full Text | Google Scholar

211. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys (2018) 148:241722. doi:10.1063/1.5019779

PubMed Abstract | CrossRef Full Text | Google Scholar

212. Yu D, Deng L, Seide F. The deep tensor neural network with applications to large vocabulary speech recognition. IEEE Trans Audio Speech Lang Process (2013) 21:388–96. doi:10.1109/TASL.2012.2227738

CrossRef Full Text | Google Scholar

213. Oymak S, Soltanolkotabi M. End-to-end learning of a convolutional neural network via deep tensor decomposition (2018). Available at: https://arxiv.org/abs/1805.06523v1 (Accessed April 5, 2023).

Google Scholar

214. Wang S, Suo S, Ma W-C, Pokrovsky A, Urtasun R. Deep parametric continuous convolutional neural networks (2021). https://arxiv.org/abs/2101.06742.

Google Scholar

215. Blum LC, Reymond JL. 970 Million druglike small molecules for virtual screening in the chemical universe database GDB-13. J Am Chem Soc (2009) 131:8732–3. doi:10.1021/ja902302h

PubMed Abstract | CrossRef Full Text | Google Scholar

216. Ramakrishnan R, Dral PO, Rupp M, Von Lilienfeld OA. Quantum chemistry structures and properties of 134 kilo molecules. Scientific Data (2014) 1(1):140022–7. doi:10.1038/sdata.2014.22

PubMed Abstract | CrossRef Full Text | Google Scholar

217. Reymond JL. The chemical space project. Acc Chem Res (2015) 48:722–30. doi:10.1021/AR500432K

PubMed Abstract | CrossRef Full Text | Google Scholar

218. Jain A, Ong SP, Hautier G, Chen W, Richards WD, Dacek S, et al. Commentary: the Materials Project: a materials genome approach to accelerating materials innovation. APL Mater (2013) 1:011002. doi:10.1063/1.4812323

CrossRef Full Text | Google Scholar

219. Behler J, Parrinello M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys Rev Lett (2007) 98:146401. doi:10.1103/PHYSREVLETT.98.146401

PubMed Abstract | CrossRef Full Text | Google Scholar

220. de Jong M, Chen W, Notestine R, Persson K, Ceder G, Jain A, et al. A statistical learning framework for materials science: application to elastic moduli of k-nary inorganic polycrystalline compounds. Scientific Rep (2016) 6(6):34256–11. doi:10.1038/srep34256

CrossRef Full Text | Google Scholar

221. Pessa AAB, Zola RS, Perc M, Ribeiro HV. Determining liquid crystal properties with ordinal networks and machine learning. Chaos Solitons Fractals (2022) 154:111607. doi:10.1016/J.CHAOS.2021.111607

CrossRef Full Text | Google Scholar

222. Sigaki HYD, Lenzi EK, Zola RS, Perc M, Ribeiro HV. Learning physical properties of liquid crystals with deep convolutional neural networks. Sci Rep (2020) 10:7664. doi:10.1038/s41598-020-63662-9

PubMed Abstract | CrossRef Full Text | Google Scholar

223. Sigaki HYD, De Souza RF, De Souza RT, Zola RS, Ribeiro HV. Estimating physical properties from liquid crystal textures via machine learning and complexity-entropy methods. Phys Rev E (2019) 99:013311. doi:10.1103/PHYSREVE.99.013311

PubMed Abstract | CrossRef Full Text | Google Scholar

224. Qiao Z, Welborn M, Anandkumar A, Manby FR, Miller TF. OrbNet: deep learning for quantum chemistry using symmetry-adapted atomic-orbital features. J Chem Phys (2020) 153:124111. doi:10.1063/5.0021955

PubMed Abstract | CrossRef Full Text | Google Scholar

225. Liu Z, Lin L, Jia Q, Cheng Z, Jiang Y, Guo Y, et al. Chemical space, scaffolds, and halogenated compounds of cmnpd: a comprehensive chemoinformatic analysis. J Chem Inf Model (2021) 61:3323–36. doi:10.1021/acs.jcim.1c00162

PubMed Abstract | CrossRef Full Text | Google Scholar

226. Choudhary K, Garrity KF, Reid ACE, DeCost B, Biacchi AJ, Hight Walker AR, et al. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. npj Comput Mater (2020) 6(6):173–13. doi:10.1038/s41524-020-00440-1

CrossRef Full Text | Google Scholar

227. Choudhary K, et al. usnistgov/jarvis: JARVIS-Tools: an open-source software package for data-driven atomistic materials design (2023). Available at: https://github.com/usnistgov/jarvis (Accessed April 5, 2023).

Google Scholar

228. Choudhary K, Bercx M, Jiang J, Pachter R, Lamoen D, Tavazza F. Accelerated discovery of efficient solar cell materials using quantum and machine-learning methods. Chem Mater (2019) 31:5900–8. doi:10.1021/ACS.CHEMMATER.9B02166

CrossRef Full Text | Google Scholar

229. Chen WC, Schmidt JN, Yan D, Vohra YK, Chen CC. Machine learning and evolutionary prediction of superhard B-C-N compounds. NPJ Comput Mater (2021) 7:114. doi:10.1038/S41524-021-00585-7

CrossRef Full Text | Google Scholar

230. Ong SP, Richards WD, Jain A, Hautier G, Kocher M, Cholia S, et al. Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis. Comput Mater Sci (2013) 68:314–9. doi:10.1016/J.COMMATSCI.2012.10.028

CrossRef Full Text | Google Scholar

231. Van Rossum G, Drake FL. Python 3 reference manual. Scotts Valley, CA, USA: CreateSpace (2009).

Google Scholar

232. Ardiyanti AD, Mustaqim T. Crystal structure modelling of magnetic material on computational study. Proc Int Conf Sci Eng (ICSE-UIN-SUKA 2021) (2021) 211:138–42. doi:10.2991/AER.K.211222.022

CrossRef Full Text | Google Scholar

233. Waroquiers D, George J, Horton M, Schenk S, Persson KA, Rignanese GM, et al. ChemEnv: a fast and robust coordination environment identification tool. Acta Crystallogr B Struct Sci Cryst Eng Mater (2020) 76:683–95. doi:10.1107/s2052520620007994

PubMed Abstract | CrossRef Full Text | Google Scholar

234. Latimer K, Dwaraknath S, Mathew K, Winston D, Persson KA. Evaluation of thermodynamic equations of state across chemistry and structure in the materials project. npj Comput Mater (2018) 4(4):40–7. doi:10.1038/s41524-018-0091-x

CrossRef Full Text | Google Scholar

235. Boland TM, Singh AK. Computational synthesis of 2D materials: a high-throughput approach to materials design. Comput Mater Sci (2022) 207:111238. doi:10.1016/J.COMMATSCI.2022.111238

CrossRef Full Text | Google Scholar

236. Yang X, Wang Z, Zhao X, Song J, Zhang M, Liu H. MatCloud: a high-throughput computational infrastructure for integrated management of materials simulation, data and resources. Comput Mater Sci (2018) 146:319–33. doi:10.1016/J.COMMATSCI.2018.01.039

CrossRef Full Text | Google Scholar

237. Pedregosa Fabianpedregosa F, Michel V, Grisel Oliviergrisel O, Blondel M, Prettenhofer P, Weiss R, et al. Scikit-learn: machine learning in Python gaël varoquaux bertrand thirion vincent dubourg alexandre passos PEDREGOSA, VAROQUAUX, GRAMFORT ET AL. Matthieu perrot. J Machine Learn Res (2011) 12:2825–30.

Google Scholar

238. Singh P, Manure A. Introduction to TensorFlow 2.0. Learn Tensorflow (2020) 20:1–24. doi:10.1007/978-1-4842-5558-2_1

CrossRef Full Text | Google Scholar

239. Momma K, Izumi F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J Appl Crystallogr (2008) 41:653–8. doi:10.1107/S0021889808012016

CrossRef Full Text | Google Scholar

240. Yang W, Dilanga Siriwardane EM, Dong R, Li Y, Hu J. Crystal structure prediction of materials with high symmetry using differential evolution. J Phys Condensed Matter (2021) 33:455902. doi:10.1088/1361-648X/AC1D6C

CrossRef Full Text | Google Scholar

241. Ward L, Dunn A, Faghaninia A, Zimmermann NER, Bajaj S, Wang Q, et al. Matminer: an open source toolkit for materials data mining. Comput Mater Sci (2018) 152:60–9. doi:10.1016/J.COMMATSCI.2018.05.018

CrossRef Full Text | Google Scholar

242. Dunn A, Wang Q, Ganose A, Dopp D, Jain A. Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm. npj Comput Mater (2020) 6:138–10. doi:10.1038/s41524-020-00406-3

CrossRef Full Text | Google Scholar

243. Jiayuan D, Xiaoyu Y, Jiayuan D, Xiaoyu Y. Integration and optimization of material data mining and machine learning tools. Front Data Domputing (2020) 2:105–20. doi:10.11871/JFDC.ISSN.2096-742X.2020.04.009

CrossRef Full Text | Google Scholar

244. Imran QF, Kim DH, Bong SJ, Chi SY, Choi YH. A survey of datasets, preprocessing, modeling mechanisms, and simulation tools based on AI for material analysis and discovery. Materials (2022) 15:1428. doi:10.3390/MA15041428

PubMed Abstract | CrossRef Full Text | Google Scholar

245. Jha D, Ward L, Paul A, Liao W., Choudhary A, Wolverton C, et al. ElemNet: deep learning the chemistry of materials from only elemental composition. Scientific Rep (2018) 8:17593–13. doi:10.1038/s41598-018-35934-y

CrossRef Full Text | Google Scholar

246. Ramsundar B. Molecular machine learning with deepchem (2018). Available at: http://purl.stanford.edu/js264hd4826 (Accessed December 23, 2023).

Google Scholar

247. Altae-Tran H, Ramsundar B, Pappu AS, Pande V. Low data drug discovery with one-shot learning. ACS Cent Sci (2017) 3:283–93. doi:10.1021/ACSCENTSCI.6B00367

PubMed Abstract | CrossRef Full Text | Google Scholar

248. O’Mara J, Meredig B, Michel K. Materials data infrastructure: a case study of the citrination platform to examine data import, storage, and access. JOM (2016) 68:2031–4. doi:10.1007/s11837-016-1984-0

CrossRef Full Text | Google Scholar

249. Sacha GM, Varona P. Artificial intelligence in nanotechnology. Nanotechnology (2013) 24:452002. doi:10.1088/0957-4484/24/45/452002

PubMed Abstract | CrossRef Full Text | Google Scholar

250. Ly DQ, Paramonov L, Davidson C, Ramsden J, Wright H, Holliman N, et al. The Matter Compiler-towards atomically precise engineering and manufacture. Nanotechnol Percept (2011) 7:199–217. doi:10.4024/N13LY11A.NTP.07.03

CrossRef Full Text | Google Scholar

251. Hall JS. Nanocomputers and reversible logic. Nanotechnology (1994) 5:157–67. doi:10.1088/0957-4484/5/3/002

CrossRef Full Text | Google Scholar

252. Tseng GY, Ellenbogen JC. Toward nanocomputers. Science (2001) 294:1293–4. doi:10.1126/SCIENCE.1066920

PubMed Abstract | CrossRef Full Text | Google Scholar

253. Vishal S, Goswami D. Nanocomputing: the future of computing. India: Tata McGraw Hill (2008). p. 174.

Google Scholar

254. Lawson JW, Wolpert DH. Adaptive programming of unconventional nano-architectures. J Comput Theor Nanosci (2006) 3:272–9. doi:10.1166/JCTN.2006.3009

CrossRef Full Text | Google Scholar

255. Kumawat R, Sahula V, Gaur MS. Probabilistic modeling approaches for nanoscale devices. In: Proceedings of IEEE International Conference on Circuit, Power and Computing Technologies, ICCPCT; March, 2013; Nagercoil, India (2013). p. 720–4. doi:10.1109/ICCPCT.2013.6528997

CrossRef Full Text | Google Scholar

256. Xu B, Shen Z, Ni X, Wang J, Guan J, Lu J. Determination of elastic properties of a film-substrate system by using the neural networks. Appl Phys Lett (2004) 85:6161–3. doi:10.1063/1.1841472

CrossRef Full Text | Google Scholar

257. Yu J, Wu B, He C. Determination of material properties of functionally graded plate using the dispersion of guided waves and an artificial neural network. J Test Eval (2008) 36:103–8. doi:10.1520/JTE100587

CrossRef Full Text | Google Scholar

258. Morlanés N, Lezcano G, Yerrayya A, Mazumder J, Castaño P. Improving robustness of kinetic models for steam reforming based on artificial neural networks and ab initio calculations. Chem Eng J (2022) 433:133201. doi:10.1016/J.CEJ.2021.133201

CrossRef Full Text | Google Scholar

259. Afantitis A, Melagraki G, Isigonis P, Tsoumanis A, Varsou DD, Valsami-Jones E, et al. NanoSolveIT Project: driving nanoinformatics research to develop innovative and integrated tools for in silico nanosafety assessment. Comput Struct Biotechnol J (2020) 18:583–602. doi:10.1016/J.CSBJ.2020.02.023

PubMed Abstract | CrossRef Full Text | Google Scholar

260. Drake G. Thermodynamics | laws, definition, & equations | britannica (2022). Available at: https://www.britannica.com/science/thermodynamics (Accessed January 30, 2023).

Google Scholar

261. Beretta GP, Gyftopoulos EP. What is Heat? J Energ Resour Technol Trans ASME (2015) 137:137. doi:10.1115/1.4026382

CrossRef Full Text | Google Scholar

262. Ding J, Xu N, Nguyen MT, Qiao Q, Shi Y, He Y, et al. Machine learning for molecular thermodynamics. Chin J Chem Eng (2021) 31:227–39. doi:10.1016/J.CJCHE.2020.10.044

CrossRef Full Text | Google Scholar

263. Funai SS, Giataganas D. Thermodynamics and feature extraction by machine learning. PhysRevRes (2020) 2:033415. doi:10.1103/PHYSREVRESEARCH.2.033415

CrossRef Full Text | Google Scholar

264. Alizadeh R, Abad JMN, Fattahi A, Mohebbi MR, Doranehgard MH, Li LKB, et al. A machine learning approach to predicting the heat convection and thermodynamics of an external flow of hybrid nanofluid. J Energ Resour Technol Trans ASME (2021) 143:143. doi:10.1115/1.4049454

CrossRef Full Text | Google Scholar

265. Jirasek F, Alves RAS, Damay J, Vandermeulen RA, Bamler R, Bortz M, et al. Machine learning in thermodynamics: prediction of activity coefficients by matrix completion. J Phys Chem Lett (2020) 11:981–5. doi:10.1021/acs.jpclett.9b03657

PubMed Abstract | CrossRef Full Text | Google Scholar

266. Zhong W, Gold JM, Marzen S, England JL, Yunger Halpern N. Machine learning outperforms thermodynamics in measuring how well a many-body system learns a drive. Scientific Rep (2021) 11(11):9333–11. doi:10.1038/s41598-021-88311-7

CrossRef Full Text | Google Scholar

267. Liu Y, Hong W, Cao B. Machine learning for predicting thermodynamic properties of pure fluids and their mixtures. Energy (2019) 188:116091. doi:10.1016/J.ENERGY.2019.116091

CrossRef Full Text | Google Scholar

268. Noé F, Tkatchenko A, Müller K-R, Clementi C. Machine learning for molecular simulation. Annu Rev Phys Chem (2019) 71:361–90. doi:10.1146/annurev-physchem-042018-052331

CrossRef Full Text | Google Scholar

269. Glaser R. Biophysics: an introduction Berlin, Germany: Sringer (2012). doi:10.1007/978-3-642-25212-9/COVER

CrossRef Full Text | Google Scholar

270. AlQuraishi M, Sorger PK. Differentiable biology: using deep learning for biophysics-based and data-driven modeling of molecular mechanisms. Nat Methods (2021) 18:1169–80. doi:10.1038/S41592-021-01283-4

PubMed Abstract | CrossRef Full Text | Google Scholar

271. Jiang Z, Do HN, Choi J, Lee W, Baek S. A deep learning approach to predict abdominal aortic Aneurysm expansion using longitudinal data. Front Phys (2020) 7:501904. doi:10.3389/fphy.2019.00235

CrossRef Full Text | Google Scholar

272. Maso Talou GD, Babarenda Gamage TP, Sagar M, Nash MP. Deep learning over reduced intrinsic domains for efficient mechanics of the left ventricle. Front Phys (2020) 8:508377. doi:10.3389/fphy.2020.00030

CrossRef Full Text | Google Scholar

273. Casas L, Saborido-Rey F. A review of genomics methods and bioinformatics tools for the analysis of close-kin mark-recapture. Front Mar Sci (2023) 10:1113870. doi:10.3389/fmars.2023.1113870

CrossRef Full Text | Google Scholar

274. Kuhlman B, Bradley P. Advances in protein structure prediction and design. Nat Rev Mol Cel Biol (2019) 20(20):681–97. doi:10.1038/s41580-019-0163-x

CrossRef Full Text | Google Scholar

275. Al-Amrani S, Al-Jabri Z, Al-Zaabi A, Alshekaili J, Al-Khabori M. Proteomics: concepts and applications in human medicine. World J Biol Chem (2021) 12:57–69. doi:10.4331/WJBC.V12.I5.57

PubMed Abstract | CrossRef Full Text | Google Scholar

276. Ferdian E, Suinesiaputra A, Dubowitz DJ, Zhao D, Wang A, Cowan B, et al. 4DFlowNet: super-resolution 4D flow MRI using deep learning and computational fluid dynamics. Front Phys (2020) 8:533501. doi:10.3389/fphy.2020.00138

CrossRef Full Text | Google Scholar

277. Palumbo D, Giorni A, Minocchi R, Amendola R, Cestelli Guidi M. Optimization of machine learning techniques for the determination of clinical parameters in dried human serum samples from FTIR spectroscopic data. Vib Spectrosc (2022) 121:103408. doi:10.1016/J.VIBSPEC.2022.103408

CrossRef Full Text | Google Scholar

278. Slattery C, Nguyen K, Shields L, Vega-Carrascal I, Singleton S, Lyng FM, et al. Application of advanced non-linear spectral decomposition and regression methods for spectroscopic analysis of targeted and non-targeted irradiation effects in an in-vitro model. Int J Mol Sci (2022) 23:12986. doi:10.3390/IJMS232112986

PubMed Abstract | CrossRef Full Text | Google Scholar

279. Fadlelmoula A, Catarino SO, Minas G, Carvalho V. A review of machine learning methods recently applied to FTIR spectroscopy data for the analysis of human blood cells. Micromachines (2023) 14:1145. doi:10.3390/MI14061145

PubMed Abstract | CrossRef Full Text | Google Scholar

280. Mwanga EP, Minja EG, Mrimi E, Jiménez MG, Swai JK, Abbasi S, et al. Detection of malaria parasites in dried human blood spots using mid-infrared spectroscopy and logistic regression analysis. Malar J (2019) 18:341–13. doi:10.1186/s12936-019-2982-9

PubMed Abstract | CrossRef Full Text | Google Scholar

281. Bartók AP, Payne MC, Kondor R, Csányi G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys Rev Lett (2010) 104:136403. doi:10.1103/PHYSREVLETT.104.136403

PubMed Abstract | CrossRef Full Text | Google Scholar

282. Rupp M, Tkatchenko A, Müller KR, Von Lilienfeld OA. Fast and accurate modeling of molecular atomization energies with machine learning. Phys Rev Lett (2012) 108:058301. doi:10.1103/physrevlett.108.058301

PubMed Abstract | CrossRef Full Text | Google Scholar

283. Schütt KT, Arbabzadah F, Chmiela S, Müller KR, Tkatchenko A. Quantum-chemical insights from deep tensor neural networks. Nat Commun (2017) 8(8):13890–8. doi:10.1038/ncomms13890

PubMed Abstract | CrossRef Full Text | Google Scholar

284. Smith JS, Isayev O, Roitberg AE. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem Sci (2017) 8:3192–203. doi:10.1039/C6SC05720A

PubMed Abstract | CrossRef Full Text | Google Scholar

285. Smith JS, Nebgen BT, Zubatyuk R, Lubbers N, Devereux C, Barros K, et al. Outsmarting quantum chemistry through transfer learning (2018). https://chemrxiv.org/engage/chemrxiv/article-details/60c7426a702a9b113718a43d.

Google Scholar

286. Brockherde F, Vogt L, Li L, Tuckerman ME, Burke K, Müller KR. Bypassing the Kohn-Sham equations with machine learning. Nat Commun (2017) 8(8):872–10. doi:10.1038/s41467-017-00839-3

PubMed Abstract | CrossRef Full Text | Google Scholar

287. Bereau T, DiStasio RA, Tkatchenko A, Von Lilienfeld OA. Non-covalent interactions across organic and biological subsets of chemical space: physics-based potentials parametrized from machine learning. J Chem Phys (2018) 148:241706. doi:10.1063/1.5009502

PubMed Abstract | CrossRef Full Text | Google Scholar

288. Chmiela S, Sauceda HE, Müller KR, Tkatchenko A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat Commun (2018) 9(9):3887–10. doi:10.1038/s41467-018-06169-2

PubMed Abstract | CrossRef Full Text | Google Scholar

289. Chmiela S, Tkatchenko A, Sauceda HE, Poltavsky I, Schütt KT, Müller KR. Machine learning of accurate energy-conserving molecular force fields. Sci Adv (2017) 3:e1603015. doi:10.1126/SCIADV.1603015

PubMed Abstract | CrossRef Full Text | Google Scholar

290. Dral PO, Owens A, Yurchenko SN, Thiel W. Structure-based sampling and self-correcting machine learning for accurate calculations of potential energy surfaces and vibrational levels. J Chem Phys (2017) 146:244108. doi:10.1063/1.4989536

PubMed Abstract | CrossRef Full Text | Google Scholar

291. Han J, Zhang L, Car R, Weinan E. Deep potential: a general representation of a many-body potential energy surface. Commun Comput Phys (2018) 23:629–39. doi:10.4208/CICP.OA-2017-0213

CrossRef Full Text | Google Scholar

292. Gastegger M, Behler J, Marquetand P. Machine learning molecular dynamics for the simulation of infrared spectra. Chem Sci (2017) 8:6924–35. doi:10.1039/C7SC02267K

PubMed Abstract | CrossRef Full Text | Google Scholar

293. Li Z, Kermode JR, De Vita A. Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces. Phys Rev Lett (2015) 114:096405. doi:10.1103/PHYSREVLETT.114.096405

PubMed Abstract | CrossRef Full Text | Google Scholar

294. Rumelhart DE, Hinton GE, McClelland JL. A general framework for parallel distributed processing. In: Parallel distributed processing: explorations in the microstructure of cognition. Cambridge, MA, USA: MIT Press (2023). p. 45–76.

Google Scholar

295. Smolensky P. Information processing in dynamical systems: foundations of harmony theory. In: Parallel distributed processing: explorations in the microstructure of cognition. Cambridge, MA, USA: MIT Press (2023). p. 194–281.

Google Scholar

296. Dinh L, Krueger D, Bengio Y. NICE: non-linear independent components estimation (2014). https://arxiv.org/abs/1410.8516.

Google Scholar

297. Sivaramakrishnan M, Suresh R, Ponraj K. Predicting quorum sensing peptides using stacked generalization ensemble with gradient boosting based feature selection. J Microbiol (2022) 60(60):756–65. doi:10.1007/S12275-022-2044-9

PubMed Abstract | CrossRef Full Text | Google Scholar

298. Waibel DJE, Röell E, Rieck B, Giryes R, Marr C. A diffusion model predicts 3D shapes from 2D microscopy images (2022). https://arxiv.org/abs/2208.14125.

Google Scholar

299. Flovik V. How do you teach physics to machine learning models? Hybrid analytics: combining the best of two worlds (2018). Available at: https://towardsdatascience.com/how-do-you-combine-machine-learning-and-physics-based-modeling-3a3545d58ab9 (Accessed January 30, 2023).

Google Scholar

300. Mols B. Using AI to drill down in physics | news | communications of the ACM (2021). Available at: https://cacm.acm.org/news/253847-using-ai-to-drill-down-in-physics/fulltext (Accessed January 30, 2023).

Google Scholar

301. Vogenberg FR, Barash CI, Pursel M. Personalized medicine: Part 1: evolution and development into theranostics. Pharm Ther (2010) 35:560–76.

PubMed Abstract | Google Scholar

302. Dua D, Graff C. UCI machine learning repository (2017). Available at: http://archive.ics.uci.edu/ml.

Google Scholar

303. Molokeev MS, Su B, Aleksandrovsky AS, Golovnev NN, Plyaskin ME, Xia Z. Machine learning analysis and discovery of zero-dimensional ns2 metal halides toward enhanced photoluminescence quantum yield. Chem Mater (2022) 34:537–46. doi:10.1021/ACS.CHEMMATER.1C02725

CrossRef Full Text | Google Scholar