The effects of plasma density structure on the propagation of magnetosonic waves: 1-D particle-in-cell simulations

Magnetosonic (MS) waves, i.e., ion Bernstein mode waves, are one of the common plasma waves in the Earth’s magnetosphere, which are important for regulating charged particle dynamics. How MS waves propagate in the magnetosphere is critical to understanding the global distribution of the waves, but it remains unclear. Although previous studies present that MS waves can be reflected by fine-scale density structures, the dissipation of waves by background plasma has long been neglected. In this study, we perform one-dimensional (1-D) particle-in-cell (PIC) simulations to study the propagation of MS waves through density structures, where both absorption and reflection have been included. We find that absorption is as important as reflection when considering the propagation of MS waves through density structures, and both of them are strongly dependent on the shape of density structures. Specifically, the reflectivity of MS waves is positively and negatively correlated with the height and width of density structures, respectively, while the absorptivity of MS waves has a positive correlation with both the height and width of density structures. Our study demonstrates the significance of absorption during the propagation of MS waves, which may help better understand the distribution of MS waves in the Earth’s magnetosphere.

1 Introduction

Magnetosonic (MS) waves, also known as ion Bernstein mode waves, are one of the intense electromagnetic emissions observed in the Earth’s inner magnetosphere [1]. These waves were first detected by the OGO 3 satellite and named “equatorial noise” due to their occurrence within about $\pm 2°$ of the magnetic equator [2–4]. Recent observations made by Cluster and THEMIS satellites [5,6] have shown that MS waves can occur both inside and outside the plasmasphere near the magnetic equator. The waves are excited at harmonics of the proton gyrofrequency [7] and at large (∼$90°$) wave normal angles [8,9] by ring velocity distributions of ring current protons [10,11]. MS waves play a significant role in regulating the dynamics of charged particles in the Earth’s magnetosphere [12–18]. They have been proposed as a candidate for accelerating ∼100 keV electrons up to relativistic energies in the outer radiation belt [14]. Additionally, scattering by MS waves may explain the formation of butterfly distributions of radiation belt electrons [19,18,21–23]. Furthermore, MS waves can effectively energize the background cold protons and electrons [24,25].

Understanding the propagation of MS waves in the Earth’s magnetosphere is crucial in comprehending the global distributions of these waves and their impact on energy transfer among different particle populations. Satellite observations indicate that the occurrence rate of MS waves strongly depends on the magnetic local time (MLT) outside the plasmapause, but remains nearly uniform inside the plasmapause [26]. This coincides with the scenario that MS waves are initially generated outside the plasmasphere in the noon and dusk sectors and then propagate both outward and inward, crossing the plasmapause and migrating globally over MLT [27,28]. Moreover, the occurrence rate and intensity of MS waves outside the plasmapause are higher than inside it [26] and the majority of MS waves inside the plasmapause have lower frequencies than the local proton cyclotron frequency [7,22], making radial propagation the most plausible explanation [5,6,29].

The propagation of MS waves is strongly influenced by the inhomogeneous background plasma density. By performing one-dimensional (1-D) full wave simulations with the finite difference time domain (FDTD) method, Liu et al. [30] have found that MS waves can propagate deep into the plasmasphere with only a small fraction of the MS wave power being reflected by the plasmapause. Instead, the fine-scale density structures near the outer edge of the plasmapause can effectively reflect MS waves. Such fine-scale density structures have been widely observed in the Earth’s magnetosphere [29,30–31]. However, previous simulations have also revealed that MS waves can be significantly damped by the background cold plasma [17,24,34], which was neglected in the study of Liu et al. [30] due to the limitation of their model. Therefore, we utilize the 1-D PIC model to simulate the propagation of MS waves through the fine-scale density structures, where both absorption and reflection have been considered. We have also quantified the reflectivity and absorptivity of MS waves passing through the density structure and investigated their dependences on the shape of the density structure.

2 Simulation model and method

In this study, we employ a 1-D PIC simulation model to investigate the effects of density structures on the propagation of MS waves. The background magnetic field ${\mathit{B}}_{\mathbf{0}}$ is directed along the z-axis, and the wave vector of MS waves is lying in the $\mathrm{x}$-$\mathrm{z}$ plane. Here, the simulation box is along the wave vector (or the propagating direction), which is defined as the r direction. This model includes full three-dimensional electromagnetic fields and velocities but only allows spatial variations in the r direction. The periodic boundary conditions are adopted. The units of time and space are the inverse of the proton gyrofrequency ${\mathrm{\Omega }}_{cp}^{-1}$, and the proton inertial length ${\lambda }_p$, respectively. The plasma system only consists of background protons and electrons which are denoted by subscripts “p” and “e” hereafter. Both protons and electrons satisfy a Maxwellian velocity distribution and have the same temperature $T_p=T_e=1eV$. To reduce computational costs, the mass ratio of proton to electron $m_p/m_e$ is set to 1600, and the ratio of light speed to the Alfven speed $c/V_A$ is set to 20. The simulation domain with a length of $41.89{\lambda }_p$ is divided equally into 30000 grids. The average number of superparticles in each grid is approximately 100 for each species, and the time step is set to $∆t=3.125\times {10}^{-5}{\mathrm{\Omega }}_{cp}^{-1}$.

The angle between the wave vector and the background magnetic field is defined as $\theta$, i.e., the wave normal angle. Here we will consider two categories of MS waves: perpendicular ($\theta =90°$) and quasi-perpendicular waves ($\theta =85°$). For each run, we initially pump the monochromatic MS wave from the left boundary to $r=10{\lambda }_w$ (${\mathrm{\lambda }}_{\mathrm{w}}$ is the wavelength) by assigning fluctuating wave fields on each grid and fluctuating bulk velocity to each particle in the form of $A_i{e}^{ikr}$ ($A_i$ is the related parameter and $\mathrm{k}$ is the wave number, respectively) along the r direction. Based on the dispersion relation of MS waves in a cold plasma, we can obtain the wave fields by the following relations:

$B_{wx}=-\frac{1}{\mathit{tan}\theta }{B}_{wz}(1)$

$B_{wy}=\frac{-i\left(n^2-S\right)P}{Dtan\theta \left(P-n^{2}si{n}^2\theta \right)}{B}_{wz}(2)$

$E_{wy}=\frac{\omega }{k\mathit{sin}\theta }{B}_{wz}(3)$

$E_{wx}=\frac{n^2-S}{iD}{E}_{wy}(4)$

$E_{wz}=\frac{n^{2}si{n}^2\theta -P}{n^2\mathit{sin}\theta \mathit{cos}\theta }{E}_{wx}(5)$

$n=\frac{ck}{\omega }=\frac{RL}{S}(6)$

where P, D, R, L, and S are the Stix parameters [35,36] and $n$ is the refraction index in Eqs 1–6. Besides, the corresponding bulk velocities of protons and electrons are given by Eqs 7–9:

$v_{xj}\left(r,t\right)=\left\{\frac{-i{q}_j}{m_j\omega }\left[\frac{1}{{\left({\mathrm{\Omega }}_{cj}/\omega \right)}^2-1}{E}_{wx}+i\frac{{\mathrm{\Omega }}_{cj}/\omega }{{\left({\mathrm{\Omega }}_{cj}/\omega \right)}^2-1}{E}_{wy}\right]\right\}(7)$

$v_{yj}\left(r,t\right)=\text{Re}\left\{\frac{-i{q}_j}{m_j\omega }\left[-i\frac{{\mathrm{\Omega }}_{cj}/\omega }{{\left({\mathrm{\Omega }}_{cj}/\omega \right)}^2-1}{E}_{wx}+\frac{1}{{\left({\mathrm{\Omega }}_{cj}/\omega \right)}^2-1}{E}_{wy}\right]\right\}(8)$

$v_{zj}\left(r,t\right)=Re\left(\frac{i{q}_j}{m_j\omega }{E}_{wz}\right)(9)$

where q_j, m_j, and Ω_cj denote the charge, mass, and cyclotron frequency of the j-component of plasma (j indicates p or e), respectively. In each run, the $B_{wz}$ is set to $0.02B_0$, and other parameters can be calculated according to the above relations.

For convenience, the density structure is assumed as the sinusoidal variation of density, so the plasma density as a function of r is given by Eq. 10:

$n_p=\left\{\begin{array}{c}{n}_0\left[1+\left(H-1\right)\sin \left(\frac{r-r_0+\frac{∆L}{2}}{∆L}\pi \right)\right],r_0-\frac{∆L}{2}\le r\le r_0+\frac{∆L}{2}\\ n_0,otherwise\end{array}\right.(10)$

where n₀ is the ambient number density (outside the density structure), and H is the height of the density structure which is the ratio of the peak density to the ambient density $n_0$. $r_0$ and $\Delta L$ denote the location and width of the density structure, respectively. The location of the density structure is fixed at $r_0=20.95{\lambda }_p$ in each run.

In the following section, we will present the simulation results of three runs in detail: Run 1 with $\theta =90°$, $H=5$, and $\Delta L=1{\lambda }_w$, Run 2 with $\theta =90°$ and no structure, and Run 3 with $\theta =85°$, $H=5$, and $\Delta L=1{\lambda }_w$. To show how we initialize the simulation model, we present the spatial profiles of (a) plasma density, (b) wave fields, bulk velocities of (c) electrons, and (d) protons at $t=0$ for Run 1 in Figure 1. There is a density structure located at $r_0=20.95{\lambda }_p$ with the width $\Delta L=1.2{\lambda }_p=1{\lambda }_w$ and the height $H=5$ (Figure 1A). The MS waves are launched within the region of $0\le r\le 12{\lambda }_p$ (i.e., $10{\lambda }_w$). For the perpendicular MS wave, there are only one component of fluctuating magnetic fields (δB_z) and two components of fluctuating electric fields (δE_x and δE_y) (Figure 1B). The bulk velocities of protons and electrons are shown in Figures 1C, D, respectively. Although the corresponding fluctuating density is not initialized, the density fluctuation will be self-consistently coupled to the MS wave very quickly in the PIC model

Figure 1

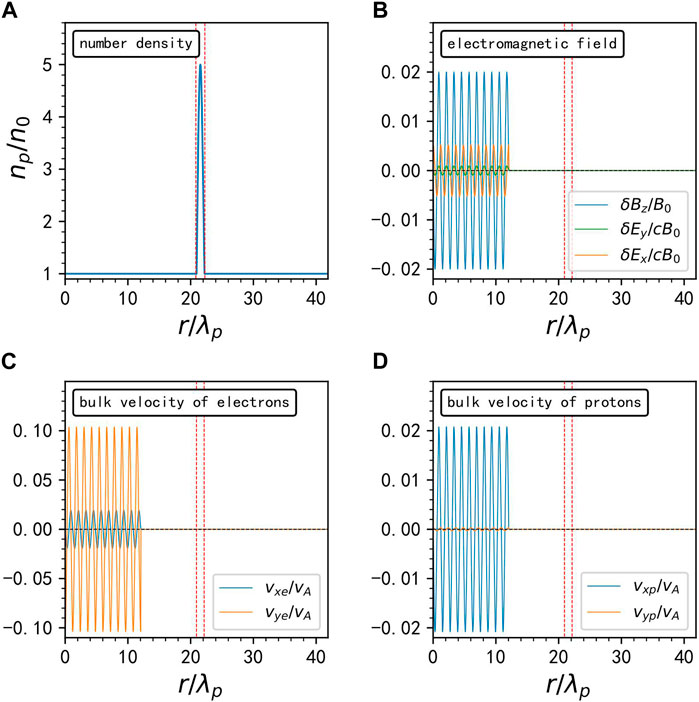
Figure 1. The initialization of the spatial distribution of (A) plasma number density, (B) wave fields $\delta B_z$ (blue line), $\delta E_x$ (orange line), $\delta E_y$ (green line) (C) bulk velocities of electrons $v_{xe}$ (blue line), $v_{ye}$ (orange line) and (D) bulk velocities of protons $v_{xp}$ (blue line), $v_{yp}$ (orange line) at $t{\mathrm{\Omega }}_{cp}=0$ in Run 1. The central vertical red dashed lines denote the position of the density structure.

3 Simulation results

3.1 Perpendicular waves: $\mathit{\theta }=\mathbf{90}°$

Figure 2 displays the propagation of the MS waves in Run 1 with a density structure and in Run 2 without it. Without the density structure, the MS waves propagate along the r direction (x-axis) with a constant speed of $0.96V_A$, which is consistent with the linear dispersion relation (Figures 2C, D). As expected, we can find that the wave amplitude is gradually decreasing during the propagation due to the dissipation caused by background plasma. In Run 1, the MS wave encounters the density structure at about $9{\mathrm{\Omega }}_{cp}^{-1}$, and then there appears the weak backward propagating MS wave emitting from the left boundary of the density structure. Such a wave is just reflected by the density structure. Besides, the phase velocity inside the density structure becomes smaller than that outside the structure due to the enhanced plasma density (Figure 2A). Meanwhile, the wave fields $\delta B_z$ and $\delta E_x$ become larger and smaller inside the density structure (Figures 2A, B), respectively, consistent with the results of Liu et al. [30].

Figure 2

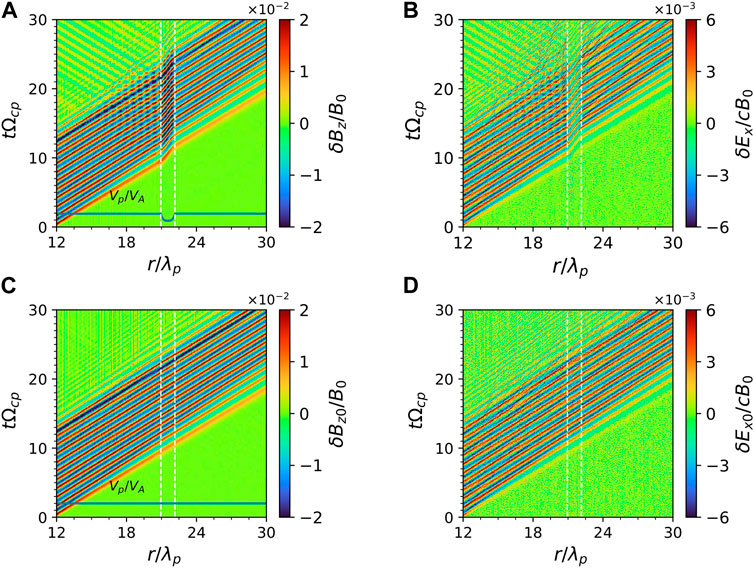
Figure 2. The temporal evolution of wave (A) magnetic field and (B) electric field in Run 1, and wave (C) magnetic field and (D) electric field in Run 2.The blue curves in (A, C) denote the variation of phase velocity along the simulation direction.

Figure 3A shows the time evolution of the energy of MS wave fields (orange line), the kinetic energy of charged particles (green line), and their sum (blue line) for Run 1. First of all, the total energy in our model is well conserved within a 0.06% margin of error. Secondly, it is clearly shown that the wave energy decreases as the particle kinetic energy increases with time, suggesting the wave dissipation takes effect during the propagation. We further display the time evolution of kinetic energies of protons and electrons inside the density structure in Figures 3B, C, respectively, where the vertical dashed lines mark the tie when the wave enters and leaves this structure. For both protons and electrons, their parallel kinetic energy remains nearly unchanged, since the perpendicular MS wave does not have the parallel electric field and cannot energize particles in the parallel direction. The perpendicular kinetic energy of protons $E_{p\perp }$ rapidly increases as the wave enters the density structure mainly due to the pick-up process. After the wave leaves the density structure, the $E_{p\perp }$ rapidly drops, but there is still the obvious net increase of kinetic energy (Figure 3B), which is caused by the perpendicular heating by the MS wave (also see Supplementary Material). However, the net increase of kinetic energy for electrons is not significant (Figure 3C).

Figure 3

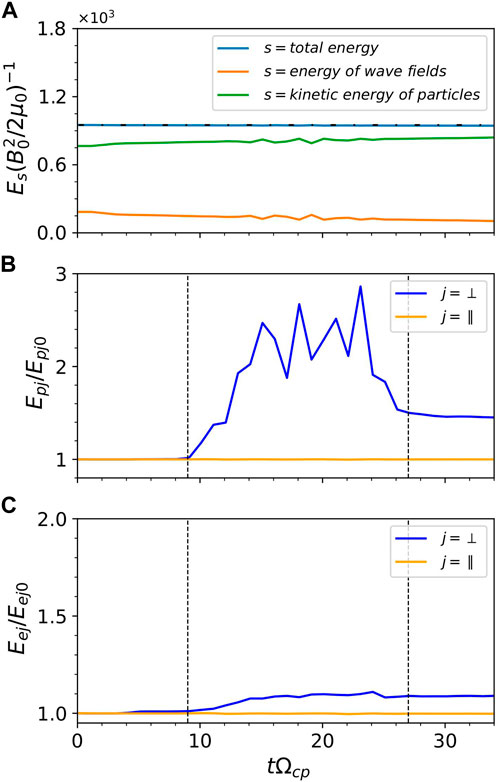
Figure 3. (A) The time evolution of the energy of the electromagnetic fields (green line), the kinetic energy of the particles (orange line), and their sum (blue line), respectively. The horizontal black dash-dotted line denotes the initial value of the total energy. The time evolution of kinetic energy of (B) protons and (C) electrons. Blue lines and orange lines denote the perpendicular direction and parallel direction, respectively. $E_{pj0}$ denotes the kinetic energy of species j at $t{\mathrm{\Omega }}_{cp}=0$. The black dashed lines in (B, C) denote the time of wave arrival and departure of the density structure.

To quantify the effects of the density structure on the propagation of MS waves, we need to calculate the reflectivity $R_M$, absorptivity $A_M$, and transmissivity $T_M$ of MS waves. Here, the $R_M$, $T_M$, $A_M$ are estimated based on the following formulas:

$R_M=\frac{P_r}{P_i}={\left(\frac{{\overline{B}}_{wzr}}{{\overline{B}}_{wzi}}\right)}^2(11)$

$T_M=\frac{P_t}{P_i}={\left(\frac{{\overline{B}}_{wzt}}{{\overline{B}}_{wzi}}\right)}^2(12)$

$A_M=1-R_M-T_M(13)$

where $P_i$, $P_r$, and $P_t$ are the Poynting flux of the incident, reflected, and transmitted waves, respectively, and the corresponding amplitudes are ${\overline{B}}_{wzi}$, ${\overline{B}}_{wzr}$, and ${\overline{B}}_{wzt}$. The waveform of transmitted waves is shown in Figure 4C, which is directly obtained by recording the time series of ${\delta B}_z$ at the right boundary of the density structure. The eight clearest wavelengths are selected by marking the peaks and troughs with red dots, and then the amplitude of transmitted wave ${\overline{B}}_{wzt}$ is given by their average. However, the reflected and incident MS waves cannot be directly obtained, since the incident and reflected waves are mixed at the left boundary in Run 1. Instead, we use the recorded waveform at the left boundary of the density structure in Run 2 to represent the incident wave (Figure 4A), and the amplitude ${\overline{B}}_{wzi}$ is the average of those marked points. Then, the waveform of reflected waves is obtained by subtracting the reflected waveform shown in Figure 4A from the mixed waveform recorded at the left boundary in Run 1, and the amplitude ${\overline{B}}_{wzr}$ is calculated as above. For Run 1, the ${\overline{B}}_{wzi}$, ${\overline{B}}_{wzr}$, and ${\overline{B}}_{wzt}$ are estimated as 0.01783, 0.00392, and 0.01683, so the $R_M$, $A_M$, and $T_M$ are 4.83%, 6.07%, and 89.1% according to Eqs 11–13. It is clearly found that the absorption of MS wave by the density structure is even more significant than the reflection in this case.

Figure 4

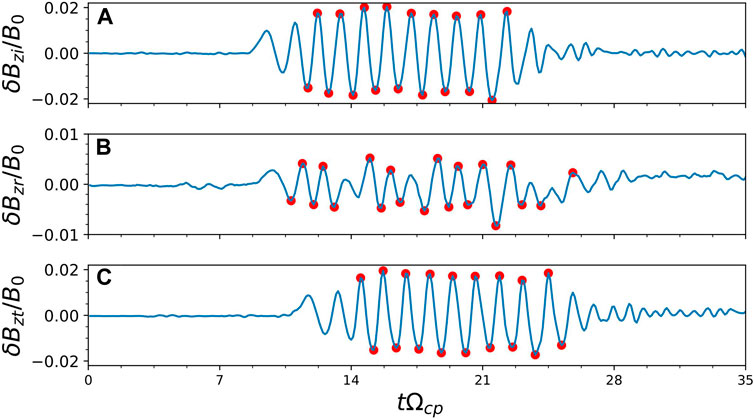
Figure 4. The time evolution of the fluctuating magnetic field of (A) the incident MS wave (δB_zi) and (B) reflected MS wave (δB_zr) at the left boundary (x₁ = 20.94λ_p) of the density structure, and of (C) the transmitted MS wave (δB_zt) at the right boundary (x₂ = 22.15λ_p) of the density structure for the Run 1. Red circles denote the wave peaks used to calculate the wave magnetic amplitude.

Furthermore, we have also studied the effects of the shape of density structure on the reflection and absorption of MS wave by considering the various widths $\Delta L$ and heights $H$. Figure 5 summarizes the simulation results (32 additional runs). First of all, there is a clear trend that both the $R_M$ and $A_M$ are positively correlated with the height of density structure $\mathrm{H}$ (Figures 5A, B). Just as expected, the corresponding transmissivity $T_M$ must be decreasing with the height $H$ (Figure 5C). However, with the increasing $\Delta L$, the $R_M$ decreases while the $A_M$ increases (Figures 5D, E). Their opposite correlation with the width of density structure $\Delta L$ results in the particular dependence of $T_M$ on the $\Delta L$. With the increasing $\Delta L$, the $T_M$ first increases and then decreases, leading to a maximum on a certain value of $\Delta L$ (Figure 5F). Moreover, comparing the $A_M$ with $T_M$, we can find that the absorptivity $A_M$ is comparable to or even larger than the reflectivity $R_M$ in most cases, suggesting the absorption of waves should not be neglected when modeling the propagation of MS wave through the density structure.

Figure 5

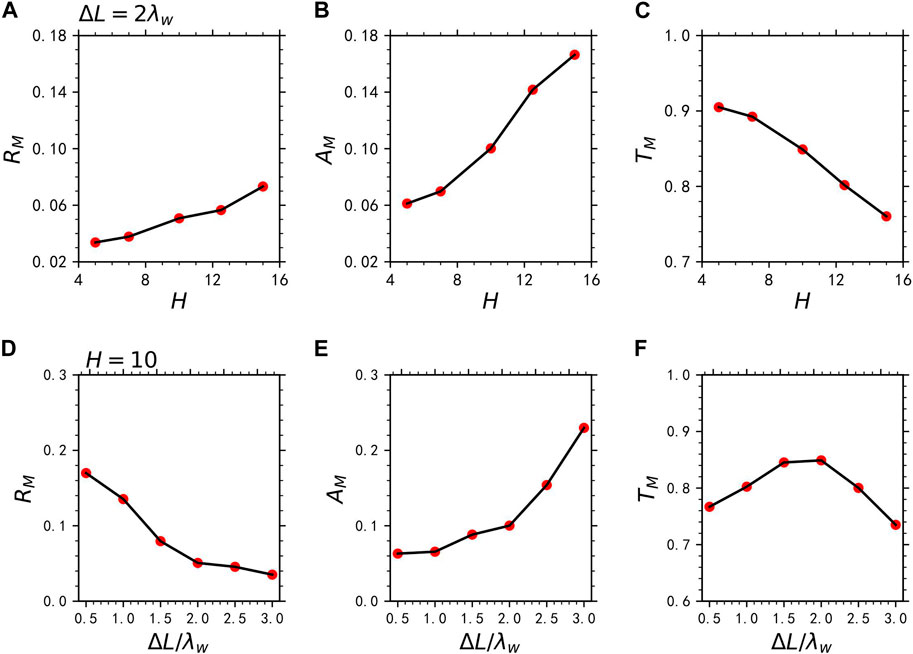
Figure 5. The (A) reflectivity $R_M$, (B) absorptivity $A_M$ and (C) transmissivity $T_M$ as a function of various heights with a constant width $\Delta L=2{\lambda }_w$, and the (D) reflectivity $R_M$, (E) absorptivity $A_M$, and (F) transmissivity $T_M$ as a function of various widths with a constant height $H=10$. Red dots are the simulation runs with different parameters when the pump wave propagates exactly perpendicularly.

3.2 Quasi-perpendicular waves: $\mathit{\theta }=\mathbf{85}°$

Besides the strictly perpendicular waves, we have also studied the propagation of MS waves with $\theta =85°$ through the density structure due to the different interactions with charged particles [24]. Figure 6 shows the spatial-temporal evolution of wave fields for Run 3. Similar to Run1, the reflected wave immediately shows up when the MS wave encounters the left boundary of the density structure at $t\approx 7{\mathrm{\Omega }}_{cp}^{-1}$, and the transmitted waves become weaker after the MS wave leaves the density structure.

Figure 6

Figure 6. Temporal evolution of wave magnetic field (A) $\delta B_z$, electric field (B) $\delta E_x$, (C) $\delta E_y$ in Run 3.

Figure 7A displays the time history of the wave energy and particle kinetic energy for Run 3. The total energy (blue line) is well conserved in this simulation model, and the energy exchange between MS wave and plasma can be easily found. Figures 7B, C present the time evolution of the kinetic energies of protons and electrons inside the density structure, respectively. The perpendicular kinetic energy of protons and electrons inside the structure first increases as the wave enters the density structure and then decreases after the wave leaves, with a weak net increase. However, the parallel kinetic energy of electrons gradually increases when the wave passes through the structure and then remains nearly constant after the wave leaves. This is due to the efficient parallel heating of electrons by quasi-parallel MS waves (Supplementary Figure S2).

Figure 7

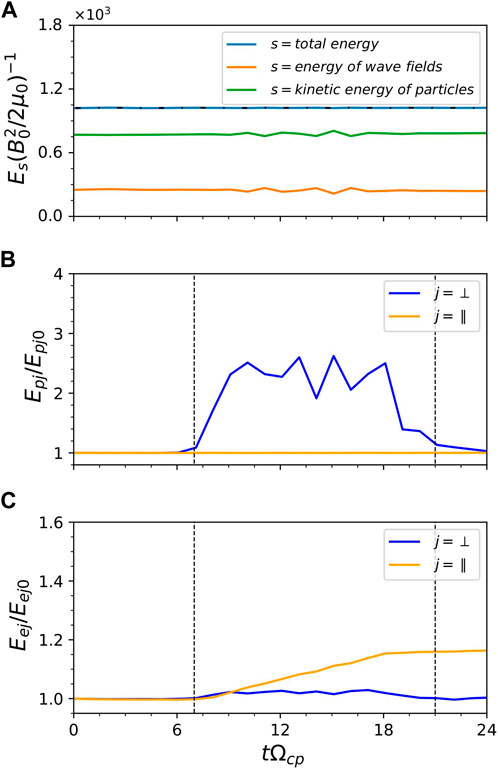
Figure 7. (A) The time evolution of the energy of the electromagnetic fields (green line), the kinetic energy of the particles (orange line), and their sum (blue line), respectively. The horizontal black dash-dotted line denotes the initial value of the total energy. The time evolution of kinetic energy of (B) protons and (C) electrons. Blue lines and orange lines denote the perpendicular direction and parallel direction, respectively. $E_{pj0}$ denotes the kinetic energy of species j at $t{\Omega }_{cp}=0$. The black dashed lines in (B, C) denote the time of wave arrival and departure of the density structure.

We further investigate the effects of the shape of density structure on the reflection and absorption of the MS wave with $\theta =85°$. The calculation method of $R_M$, $A_M$, and $T_M$ is the same as above. The simulation results marked by red dots and solid lines are summarized in Figure 8. Similar to the perpendicular MS wave, the $R_M$ and $A_M$ increase with the increasing $H$, resulting in the decreasing $T_M$. Then, the $A_M$ and the $R_M$ have a positive correlation and an anti-correlation with the $\Delta L$, respectively, leading to a maximum of $T_M$ at a certain $\Delta L$. Although the trends of $A_M$, $R_M$, and $T_M$ with the $H$ and $\Delta L$ are very similar to the perpendicular cases, the reflectivity $R_M$ and the absorptivity $A_M$ of the quasi-perpendicular MS waves are smaller than those of the MS waves with $\theta =90°$, which may imply that the quasi-perpendicular MS waves can propagate further than those perpendicular waves in the magnetosphere.

Figure 8

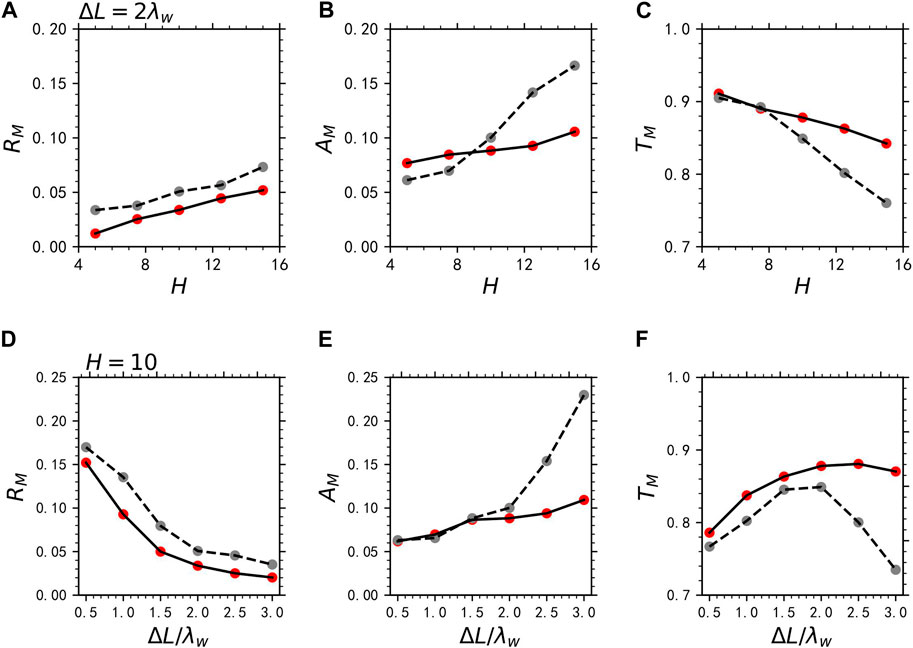
Figure 8. The (A) reflectivity $R_M$, (B) absorptivity $A_M$, and (C) transmissivity $T_M$ as a function of various heights with a constant width $\Delta L=2{\lambda }_w$, and (D) the reflectivity $R_M$, (E) absorptivity $A_M$, and (F) transmissivity $T_M$ as a function of various widths with a constant height $H=10$. Red dots are the simulation runs with different parameters when the pump wave propagates quasi-perpendicularly. The gray dots and black dashed lines denote the result of Figure 5.

4 Conclusion and discussion

The effects of density structures on MS waves are important to understand the distribution and propagation of MS waves in the Earth’s magnetosphere, which are attracting more and more attention. However, previous simulations and theoretical models [30,36] only include the reflection of MS waves caused by the density structure. To include both the absorption and reflection of waves, we utilize a self-consistent model, i.e., PIC model, to study the propagation of MS waves across density structures. We find that both perpendicular and quasi-perpendicular propagating MS waves can be effectively reflected and absorbed by the fine-scale density structure. Generally, the absorption of MS waves is as important as the reflection when MS waves propagate through the density structure, and they are strongly dependent on the shape of the density structure. The reflection of MS waves is positively correlated with the height but is inversely related to the width of a density structure. While the absorption of MS waves is positively correlated with the height and width of a density structure. Our simulation results reveal that the absorption also plays an important role in the propagation of MS waves in the Earth’s magnetosphere, which can help better understand the properties and distribution of MS waves.

To obtain the reliable reflectivity, absorptivity, and transmissivity of the MS waves, we must ensure that the total energy of this system is conserved. As shown in Figures 3A, 7A, it is clear shown that the total energy is well conserved within a margin of error below 0.1%, which is much lower than the energy change (>5%) of charged particles or wave fields. This is true for all simulation runs in this study. Thus, the dependences of reflectivity and absorptivity of MS waves on the shape of density structure as shown in Figures 5, 8 are quite reliable. Since the reflectivity of MS wave is strongly dependent on the density gradient, so the $R_M$ will increase with the increase of the height or the decrease of width, i.e., steep density structure. While, the absorptivity should be positively correlated with the number of particles inside the density structure, so the $A_M$ increases with the increase of the height or width, i.e., large density structure. However, because the corresponding transmissivity $T_M$ relies on the sum of $R_M$ and $A_M$, the dependence of $T_M$ on the shape of density structure is somehow unpredictable.

Data availability statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s. Figure data are available at https://cstr.cn/14804.41.sciencedb.space.00813.00D00D7D.

Author contributions

TS: Writing–original draft. XG: Writing–review and editing. YK: Writing–review and editing. QL: Writing–original draft, Writing–review and editing, Supervision. XW: Writing–original draft, Writing–review and editing, Validation.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. This work was supported by the NSFC grant 41774151, 42104155, B-type Strategic Priority Program of the Chinese Academy of Sciences, Grant No. XDB41000000.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1254024/full#supplementary-material

References

1. Santolík O, Němec F, Gereová K, Macúšová E, de Conchy Y, Cornilleau-Wehrlin N. Systematic analysis of equatorial noise below the lower hybrid frequency. Ann Geophys (2004) 22:2587–95. doi:10.5194/angeo-22-2587-2004

CrossRef Full Text | Google Scholar

2. Russell C, Holzer R, Smith E. OGO 3 observations of ELF noise in the magnetosphere: 1. Spatial extent and frequency of occurrence. J Geophys Res (1969) 74:755–77. doi:10.1029/JA074i003p00755

CrossRef Full Text | Google Scholar

3. Russell CT, Holzer RE, Smith EJ. OGO 3 observations of ELF noise in the magnetosphere 2. The nature of the equatorial noise. J Geophys Res (1970) 75:755–68. doi:10.1029/JA075i004p00755

CrossRef Full Text | Google Scholar

4. Gurnett DA. Plasma wave interactions with energetic ions near the magnetic equator. J Geophys Res (1976) 81:2765–70. doi:10.1029/JA081i016p02765

CrossRef Full Text | Google Scholar

5. Xiao F, Zhou Q, He Y, Yang C, Liu S, Baker DN, et al. Penetration of magnetosonic waves into the plasmasphere observed by the Van Allen Probes. Geophys Res Lett (2015) 42:7287–94. doi:10.1002/2015GL065745

CrossRef Full Text | Google Scholar

6. Ma Q, Li W, Thorne RM, Angelopoulos V. Global distribution of equatorial magnetosonic waves observed by THEMIS. Geophys Res Lett (2013) 40:1895–901. doi:10.1002/grl.50434

CrossRef Full Text | Google Scholar

7. Boardsen SA, Hospodarsky GB, Min K, Averkamp TF, Bounds SR, Kletzing CA, et al. Determining the wave vector direction of equatorial fast magnetosonic waves. Geophys Res Lett (2018) 45(16):7951–9. doi:10.1029/2018GL078695

CrossRef Full Text | Google Scholar

8. Kasahara Y, Kenmochi H, Kimura I. Propagation characteristics of the ELF emissions observed by the satellite Akebono in the magnetic equatorial region. Radio Sci (1994) 29(4):751–67. doi:10.1029/94RS00445

CrossRef Full Text | Google Scholar

9. Ke Y, Chen L, Gao X, Lu Q, Wang X, Chen R, et al. Whistler-mode waves trapped by density irregularities in the earth's magnetosphere. Geophys Res Lett (2021) 48:e2020GL092305. doi:10.1029/2020GL092305

CrossRef Full Text | Google Scholar

10. Meredith N, Horne R, Anderson R. Survey of magnetosonic waves and proton ring distributions in the Earth’s inner magnetosphere. J Geophys Res (2008) 113:A06213. doi:10.1029/2007JA012975

CrossRef Full Text | Google Scholar

11. Min K, Němec F, Liu K, Denton RE, Boardsen SA. Equatorial propagation of the magnetosonic mode across the plasmapause: 2-D PIC simulations. J Geophys Res Space Phys (2019) 124:4424–44. doi:10.1029/2019JA026567

CrossRef Full Text | Google Scholar

12. Bortnik J, Thorne RM. Transit time scattering of energetic electrons due to equatorially confined magnetosonic waves. J Geophys Res (2010) 115:A07213. doi:10.1029/2010JA015283

CrossRef Full Text | Google Scholar

13. Bortnik J, Thorne RM, Ni B, Li J. Analytical approximation of transit time scattering due to magnetosonic waves. Geophys Res Lett (2015) 42:1318–25. doi:10.1002/2014GL062710

CrossRef Full Text | Google Scholar

14. Horne RB, Thorne RM, Glauert SA, Meredith NP, Pokhotelov D, Santolık O. Electron acceleration in the Van Allen radiation belts by fast magnetosonic waves. Geophys Res Lett (2007) 34(17):L17107. doi:10.1029/2007GL030267

CrossRef Full Text | Google Scholar

15. Horne RB, Wheeler GV, Alleyne HSCK. Proton and electron heating by radially propagating fast magnetosonic waves. J Geophys Res (2000) 105(27):27597–610. doi:10.1029/2000JA000018

CrossRef Full Text | Google Scholar

16. Li X, Tao X. Validation and analysis of bounce resonance diffusion coefficients. J Geophys Res Space Phys (2018) 123:104–13. doi:10.1002/2017JA024506

CrossRef Full Text | Google Scholar

17. Chen L, Sun J, Lu Q, Wang X, Gao X, Wang D, et al. Two-dimensional particle-in-cell simulation of magnetosonic wave excitation in a dipole magnetic field. Geophys Res Lett (2018) 45:8712–20. doi:10.1029/2018GL079067

CrossRef Full Text | Google Scholar

18. Li J, Bortnik J, Thorne RM, Li W, Ma Q, Baker DN, et al. Ultrarelativistic electron butterfly distributions created by parallel acceleration due to magnetosonic waves. J Geophys Res Space Phys (2016) 121:3212–22. doi:10.1002/2016JA022370

CrossRef Full Text | Google Scholar

19. Xiao FL, Yang C, Su ZP, Zhou QH, He ZG, He YH, et al. Wave-driven butterfly distribution of Van Allen belt relativistic electrons. Nat Commun (2015) 6(1):8590. doi:10.1038/ncomms9590

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ni BB, Zou ZY, Fu S, Cao X, Gu XD, Xiang Z. Resonant scattering of radiation belt electrons by off-equatorial magnetosonic waves. Geophys Res Lett (2018) 45(3):1228–36. doi:10.1002/2017GL075788

CrossRef Full Text | Google Scholar

21. Yang C, Su Z, Xiao F, Zheng H, Wang Y, Wang S, et al. A positive correlation between energetic electron butterfly distributions and magnetosonic waves in the radiation belt slot region. Geophys Res Lett (2017) 44:3980–90. doi:10.1002/2017GL073116

CrossRef Full Text | Google Scholar

22. Ma QL, Li W, Thorne RM, Bortnik J, Kletzing CA, Kurth WS, et al. Electron scattering by magnetosonic waves in the inner magnetosphere. J Geophys Res Space Phys (2016) 121(1):274–85. doi:10.1002/2015JA021992

CrossRef Full Text | Google Scholar

23. Sun J, Gao X, Lu Q, Chen L, Liu X, Wang X, et al. Spectral properties and associated plasma energization by magnetosonic waves in the Earth’s magnetosphere: particle-in-cell simulations. J Geophys Res Space Phys (2017) 122:5377–90. doi:10.1002/2017JA024027

CrossRef Full Text | Google Scholar

24. Yuan Z, Yu X, Huang S, Qiao Z, Yao F, Funsten HO. Cold ion heating by magnetosonic waves in a density cavity of the plasmasphere. J Geophys Res Space Phys (2018) 123:1242–50. doi:10.1002/2017JA024919

CrossRef Full Text | Google Scholar

25. Zhou Q, Jiang Z, Yang C, He Y, Liu S, Xiao F. Correlated observation on global distributions of magnetosonic waves and proton rings in the radiation belts. J Geophys Res Space Phys (2021) 126:e2020JA028354. doi:10.1029/2020JA028354

CrossRef Full Text | Google Scholar

26. Chen L, Thorne RM. Perpendicular propagation of magnetosonic waves. Geophys Res Lett (2012) 39:L14102. doi:10.1029/2012GL052485

CrossRef Full Text | Google Scholar

27. Xiao F, Zhou Q, He Z, Tang L. Three-dimensional ray tracing of fast magnetosonic waves. J Geophys Res (2012) 117:A06208. doi:10.1029/2012JA017589

CrossRef Full Text | Google Scholar

28. Santolík O, Parrot M, Němec F. Propagation of equatorial noise to low altitudes: decoupling from the magnetosonic mode. Geophys Res Lett (2016) 43:6694–704. doi:10.1002/2016GL069582

CrossRef Full Text | Google Scholar

29. Liu X, Chen L, Yang L, Xia Z, Malaspina DM. One-dimensional full wave simulation of equatorial magnetosonic wave propagation in an inhomogeneous magnetosphere. J Geophys Res Space Phys (2018) 123:587–99. doi:10.1002/2017JA024336

CrossRef Full Text | Google Scholar

30. Mauk BH, Fox NJ, Kanekal SG, Kessel RL, Sibeck DG, Ukhorskiy A. Science objectives and rationale for the radiation belt storm probes mission. Space Sci Rev (2013) 179(1):3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

31. Ma Q, Li W, Chen L, Thorne RM, Angelopoulos V. Magnetosonic wave excitation by ion ring distributions in the Earth’s inner magnetosphere. J Geophys Res Space Phys (2014) 119:844–52. doi:10.1002/2013JA019591

CrossRef Full Text | Google Scholar

32. Boardsen SA, Hospodarsky GB, Kletzing CA, Pfaffff RF, Kurth WS, Wygant JR, et al. Van Allen Probe observations of periodic rising frequencies of the fast magnetosonic mode. Geophys Res Lett (2014) 41:8161–8. doi:10.1002/2014GL062020

CrossRef Full Text | Google Scholar

33. Sun J, Lu Q, Wang X, Liu X, Gao X, Yang H. Modulation of magnetosonic waves by background plasma density in a dipole magnetic field: 2-D PIC simulation. J Geophys Res Space Phys (2021) 126:e2021JA029729. doi:10.1029/2021JA029729

CrossRef Full Text | Google Scholar

34. Stix. Waves in plasmas. College Park, MD: American Institute of Physics (1992).

Google Scholar

35. Streltsov AV, Goyal R. Whistlers in micro ducts. J Geophys Research:SpacePhysics (2021) 126:e2021JA029868. doi:10.1029/2021JA029868

CrossRef Full Text | Google Scholar

36. Yu X, Yuan Z, Ouyang Z, Yao F. Effects of the plasmapause on the radial propagation of fast magnetosonic waves: an analytical approach. J Geophys Res Space Phys (2021) 126:e2020JA028330. doi:10.1029/2020JA028330

CrossRef Full Text | Google Scholar