Biplanar quadrature coil for versatile low-field extremity MRI

Biplanar magnets offer extended flexibility in MRI, particularly appealing due to unmatched accessibility to the patient. At low field strength (<0.2 T), such geometries could be particularly suitable for interventional settings or purpose-built applications such as musculoskeletal imaging. In the proposed work, we present a dual-channel, biplanar coil array for low-field MRI featuring almost fully open access when sited in a biplanar magnet. The proposed detector relies on the assembly of two orthogonal biplanar coils (single transmit channel, two receive channels in quadrature) respectively interfaced with custom inductive couplers. Simulations of the B₁ field in each element were performed before the quadrature coil was built and used at $\sim$ 0.1 T (4.33 MHz). Once assembled, the best performance in our setup was achieved in undermatched conditions in place of conventional 50-$\mathrm{\Omega }$ matching. Phantom images display the extended coverage of the quadrature coil, with similar SNR from each individual biplanar coil. The combined images show an expected SNR gain of $\sqrt{2}$ that confirms good decoupling between the two channels (−36 dB). To the best of our knowledge, the proposed coil represents the first implementation of a biplanar geometry at low field and the first quadrature detection for a biplanar design. The open design and overall good sensitivity of our biplanar design enabled fast and quasi-isotropic 3D imaging with (1.6 × 1.6 × 2.2) mm³ resolution in vivo in human extremities.

1 Introduction

In complement to conventional MRI scanners available in the clinics, open magnet geometries have been proposed that offer better access to the patient [1], improved patient experience, and better claustrophobia tolerance [2]. The sole benefit of improved physical access to the subjects further allowed to diversify the use of MRI in a wide range of applications, including image-guided (IG) proton therapy [3], thermal therapy [4], laser ablation [5], brain surgery [6–8], upright MRI [9, 10], musculoskeletal (MSK) biopsy [11, 12] and other MSK interventions [13] (more examples reviewed in [14, 15]). For most of the applications cited above, the referenced scanners operated at mid-field (i.e., not exceeding 0.5 T) with C-shaped or Helmholtz geometries, as opposed to tunnel-shaped conventional high field systems. In recent years, there has been a renewed interest for low and very-low field MRI systems (<0.2 T) [16] which designs can be adapted to point-of-care imaging. Leveraging smaller and lighter technologies well suited for dedicated, mobile (and eventually portable) MRI [15, 17–28], these initiatives usually also target lower purchase, siting, and maintenance costs [29] that will increase their overall value [16]. Benefitting from reduced main and fringe fields, low-field scanners can further be sited in non-shielded rooms (neither magnetically nor radio frequency) [2] and ferromagnetic tools can be used safely inside the scanner while producing less or no artifacts [8, 14, 30]. Naturally, low-field systems can also feature open biplanar magnets with open, planar gradient coils, hence combining enhanced access to the patient with the above mentioned advantages of lower magnetic fields [8, 12, 14, 23, 31–34]. Yet, the full potential of an open access scanner can only be unleashed if the entire system is open, including radiofrequency coils mandatory for signal detection. Eventually, the latter can be true bottlenecks to an open design as most NMR/MRI coils feature limited access to the imaged sample of interest.

A common option for MR-guided interventional applications that typically require good access to the patient consists of surface transmit/receive coils with a suitable access aperture [1, 5, 12, 35–38]. Among these, flexible surface coils have been used to better match the anatomy, but they require further tuning/matching adjustments once positioned [35, 37]. Phased-array radiofrequency (RF) coils with open access have also been used to improve coverage and signal-to-noise ratio (SNR) for intra-/inter-operative brain MRI [35, 39]. While one would expect higher performance (i.e., coverage, homogeneity) from volume coils, their use is however less common due to the inherent difficulty to maintain an open access. Previously, a four-bar birdcage design with open sides was reported that is compatible with “double-doughnut” magnets [37]. Another interesting alternative was proposed by Roberts et al. [40] who used biplanar coil geometries combining the benefits of a volume coil while providing fully open access. In their work, this design was built and tested at 1.5 and 1.8 T, and to our knowledge has not been further explored neither at high nor low magnetic field. Their B₁ magnetic field orientation, although also compatible with tunnel-shaped magnets, is particularly suitable for biplanar magnets. In such case, the coil planes are parallel to those of the magnet and leave the access completely open for three out of four sides, as opposed to most volume coil geometries [41]. Such an open coil could bring new perspectives for extremity imaging, in particular weight-bearing applications or kinematic studies of joints [42, 43], and be particularly appealing for MR-guided interventions in general [5, 12, 44]. The coil proposed in the presented work is inspired from the latter biplanar design by Roberts et al. [40]. To further increase SNR, a quadrature configuration can be beneficial at low field [45–51], leading to a maximum theoretical SNR improvement factor of $\sqrt{2}$ [47, 49, 50], corresponding to an acceleration factor of 2 in terms of acquisition time. However, quadrature operation also brings additional challenges, and is only possible if the separate coil channels are well decoupled between each other and with respect to the main, static magnetic field B₀.

In this work, we demonstrate the design of an optimized, open-geometry coil array with high potential for future use in image-guided surgery, biomechanics studies, or weight-bearing applications. The coil array is composed of two orthogonal, biplanar coils operating as a single-channel transmit and two-channel receive in quadrature mode at 4.33 MHz (0.1 T). We show that such an optimized coil provides good SNR and filling factor, while maintaining an open access, a rather homogeneous B₁, and a good coverage over a large volume of interest in a compact biplanar magnet.

2 Materials and methods

2.1 Biplanar coils

2.1.1 Simulations

Simulations of the B₁ field of the separate coils and coupler described below were performed using the AC/DC module of COMSOL Multiphysics 5.4 (COMSOL AB, Sweden) on a workstation with Windows 10, 96 GB RAM, 14 CPU cores, and 2 Nvidia GTX 1080 Ti graphics cards (no GPU calculation supported by the software). A “Magnetic Fields” physics definition was used with a lumped port source at the location of the capacitors and coaxial feeding points. The input current amplitude was 1 A and the frequency 4.33 MHz. The results were displayed as magnetic field vector plots and orthogonal sections of the magnetic field magnitude normalized to the value at the center of the coils.

2.1.2 Coil description

The design of the biplanar coil was conditioned by two main constraints. The first was the magnet geometry which restricted space between the two magnet planes defined the maximum coil size that can be inserted in the magnet bore (see MR system description in Section 2.2.1). The second was the desired, expanded field-of-view compatible with body parts that do not fit in conventional, solenoid-like RF detectors like the elbow and ankle.

The proposed coil array is composed of two biplanar coils indicated as A and B (Figure 1). Coil A was operated in transceiver mode, while coil B was used as receive only. The design of the coil planes consisted in five parallel copper (Cu) strips (150 mm × 13 mm) equally spaced by 8.75 mm connected in parallel for coil B, and four parallel Cu strips of identical spacing for coil A. The coil planes were cut from a 350-μm thick copper (Cu) sheet, sufficient for the RF penetration depth at both surfaces at our frequency, estimated as 5 × δ, where δ is the skin depth of about 31 μm given by:

$\mathrm{\delta }=\sqrt{\frac{2}{\mu \omega \sigma }}$

with $\omega$ the angular frequency, $\mu$ the permeability and $\sigma$ the conductivity of the conductor [52]. The two planes were connected in series using a 13-mm wide liaison Cu strip on one side, and a 1.8-mm diameter Cu wire on the opposite side, with an interplane distance of respectively 105 and 115 mm for coil A and B. For coil A, the liaison connections were soldered to the bottom corners of the planes, thereby maintaining the access to the inside completely open (Figure 1A). As opposed to coil B featuring planes with five Cu strips, only four were used on coil A to compensate for the strong B₁ contribution of the interplane connections. This modification ensures that the coil current is not concentrated at the bottom of the coil, and thus better B₁ homogeneity is achieved within the coil volume. For coil B, the interplane connections were placed between the middle strip of each plane (Figure 1B) to allow good decoupling between coils when assembled for quadrature detection.

FIGURE 1

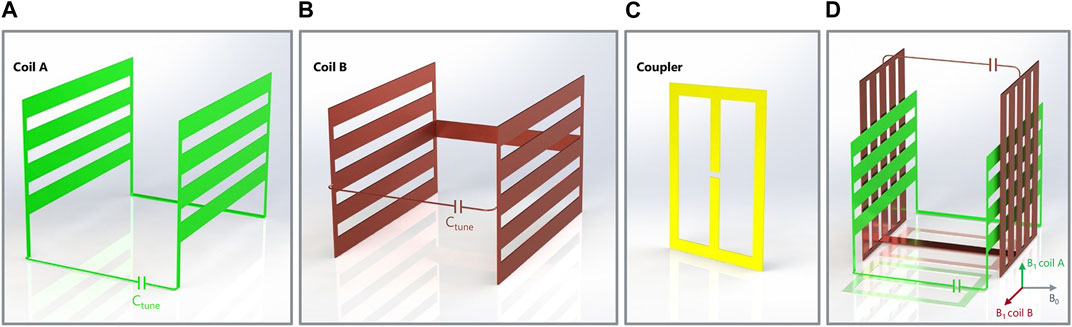
FIGURE 1. Rendered 3D representations of the quadrature coil elements: coil A (A), coil B (B), mirrored-M inductive coupler (C), and the assembled coil composed of coil A and B with their corresponding couplers (in slight transparency) positioned underneath (D). In the final assembly, the coils magnetic fields are orthogonally oriented with respect to one another and B₀ (D).

Coils A and B were tuned at 4.33 MHz using a modified variable capacitor (GME11501, Sprague-Goodman, United States) in parallel with a fixed one, with a total capacitance of 4.83 nF for coil A and 3.86 nF for coil B, for an inductance of 280 nH for coil A and 350 nH for coil B. Both coils were interfaced via inductive coupling, which has two main advantages: first, the coils are intrinsically electrically balanced [53–57], and second, there is no need for large variable matching capacitors for capacitive matching, known to have lower quality factors and to require complex adjustments [56].

2.1.3 Inductive coupling and quadrature decoupling

Two rectangular mirrored-M shape couplers were designed and built from the same 350-μm thick Cu sheet (Figure 1C). Their unique shape was chosen such that they could be both positioned underneath the coil assembly (coil A + B) and maintain open access (Figure 1D). In this coupler design, three strips (two lateral and a middle one, where the feed gap is located) are connected in parallel. The goal of such design is to achieve a preferential directionality of the coupler’s magnetic field perpendicular to the strips and to concentrate the current prevalently near the middle strip. This way, two couplers can be positioned next to each other on the same plane (here, at the bottom of the coil assembly) and only interact with the intended coil A or B, via the local coupling with one of their respective interplane connectors (i.e., connecting Cu wire for coil A, and Cu strip for coil B).

After assembly (with coil B orthogonal to coil A), the coil array was positioned inside the scanner. Tuning, matching and decoupling were adjusted using a Vector Network Analyzer (VNA E5061B-3L4, Keysight Technologies, United States). We intentionally diverged from traditional 50-Ω matching that systematically resulted in higher noise and impeded SNR (cf. Section 2.3.1), and opted for a less conventional configuration as non-50-Ω impedance consistently provided higher SNR in both FID and imaging acquisitions.

After tuning the coils at the same frequency with variable capacitors, decoupling was achieved by adjusting the position of coil A with respect to coil B, shifting the former in the horizontal direction. The resonant peaks and the amount of decoupling were monitored simultaneously via the S-parameters S₁₁, S₂₂ and S₂₁ (both coils connected to the two VNA ports). Additionally, noise acquisitions were performed on each separate channel with the RF transmit off to compute a noise covariance matrix. Quality factors of resonators interfaced using any amount of impedance matching can be measured using the Smith Chart technique described in [58]. In practice, it provides the resonator’s quality factor $Q_0=Q\left(1+\kappa \right)$ by measuring Q as $f_0/∆f_{-3dB}$ with $f_0$ the resonant frequency, $∆f_{-3dB}$ the bandwidth at −3 dB and the coupling factor $\kappa$ estimated from the diameter $d$ of the complex impedance circle on the Smith Chart as $\kappa =d/\left(2-d\right)$. For a 50-Ω matched coil, $\kappa$ = 1, which leads to the $Q_0=2Q$ measurement [59].

2.2 MR experiments

2.2.1 MR system

MRI was performed on a resistive biplanar 0.1-T system (EAR54L, Drusch & Cie, France) designed for extremity imaging [32]. This system has a horizontal B₀ and three out of four sides presenting an open access. The magnet features ∼60-cm diameter planar coils, and an 18-cm interplane gap. Thanks to its resistive technology, B₀ can easily be varied by adjusting the current fed to the magnet coils. The system includes separate shim coils to further improve the static magnetic field homogeneity. The system usually operates without shielding, neither magnetic nor RF (no Faraday cage). For all measurements and experiments reported here though, a 60 × 40 cm² food-grade aluminum sheet (about 0.02 mm thick) was positioned on top of the magnet, that significantly protected from parasitic RF sources in the laboratory environment (the observed decrease in noise magnitude level was typically between a factor of 2 and 3). In general, it is worth mentioning that noise did not exhibit significant variations when the coil was loaded with human body parts to be imaged.

The TX/RX-coil (coil A) was interfaced using a passive transcoupler (NMR Service, Germany), a pulsed RF power amplifier (500-W BT00500-AlphaS, Tomco Technologies, Australia) and a custom low-noise preamplifier built in house [60]. The RX-only coil (coil B) was connected directly to another of our custom, low-noise preamplifiers. The output signals from the preamplifiers were collected by two separate RX channels.

All sequences were implemented on a Cameleon 3 spectrometer (RS²D, France). Flip-angle calibration was performed by acquiring bulk free-induction-decay (FID) signals while varying the duration of the transmit pulse with a rectangular envelope and maintaining its amplitude constant. The calibrated 90° and 180° flip angles were identified from the first maximum and minimum of recorded FID time-integrals, collected with coil B.

2.2.2 Phantom

A custom, homogeneous, high-filling-factor phantom was built to assess the coil sensitivity and SNR. It consisted in a parallelepipedoid shape (10.5 cm × 15 cm × 15 cm, total volume 2362.5 cm³), fabricated from bi-component silicone rubber (Eurosil4 A+B, Schouten SynTec, Netherlands) [61].

2.2.3 MR sequences

Sensitivity, SNR and performance comparison of each channel for the quadrature coil were assessed using the phantom with a spoiled gradient-echo sequence (parameters listed in Table 1). The sequence parameters were only optimized for the field-of-view (FOV) and scan time, not for contrast. The TX pulse parameters used 21 dB attenuation for the biplanar coil A in the quadrature coil, with a hard pulse duration of 120 μs corresponding to a 90° flip-angle.

TABLE 1

TABLE 1. Details of the MR sequences used in phantoms and in vivo. GRE: spoiled gradient-echo, bSSFP: balanced steady-state free precession, DESS: dual-echo steady state, TR: repetition time, TE: echo time, SW: spectral width of the readout points, FA: flip angle, FOV: field-of-view, NA: number of signal averages, T_acq: acquisition time.

The protocol for in vivo acquisitions was approved by the local ethic committee (EKNZ/2022-00348) and imaging was performed after informed consent was obtained. A balanced steady-state free precession (bSSFP) sequence and a double-echo steady-state gradient echo sequence (DESS) were used to acquire in vivo images of the ankle and elbow of healthy volunteers. These sequences where chosen depending on the respective contrast desired in the two body regions. The imaging parameters are summarized in Table 1. All presented 3D acquisitions used the same gaussian undersampling scheme for the two phase-encoding directions to reduce the acquisition time by 50% [62].

2.3 Data processing and analyses

2.3.1 Undermatched vs. matched coil conditions

FID signals were acquired in the phantom using coil A and B separately (before assembling them into the quadrature configuration), both in 50-Ω matched condition and in their respective, preferred undermatched configurations. Matching was varied by adjusting the relative position of a loop coupler with respect to the coil. For each configuration, the coil’s TX flip angle was recalibrated. Four FID signals were then acquired with a flip angle of 90° and a spectral width of 3 kHz for 1,024 acquisition points, with the readout sampling starting 500 µs after the TX pulse. The SNR was estimated from the magnitude of the FID in the time domain, as the ratio between its maximum and the standard deviation of the noise in a selected region. Mean and standard deviation of the four SNR values were calculated for each case.

2.3.2 Multichannel noise equalization

At low frequency, noise in the reception chain is expected to predominantly come from the coil [63] and is assumed uncorrelated. In our case, quadrature reception can thus be achieved by summing up the separate magnitude images of coil A and B [50]. Yet, when our coil assembly was positioned in the magnet, the noise floor of coil B was observed to be slightly higher than coil A, both considering its mean and standard deviation. For this reason, the second channel dataset was scaled down by a constant factor prior to the combination of the two channels to equalize their noise contributions. The scaling factor was estimated from the ratio of noise standard deviations σ_η,1 and σ_η,2 calculated within a rectangular region of interest (ROI) on the magnitude image for each channel (size in voxels: 10 × 10 × number of slices). This scaling was applied before summing up the magnitude images from coil A and B.

2.3.3 Image analysis and processing

For phantom images, a noise standard deviation σ_η was calculated within a rectangular ROI (size in voxels: 10 × 10 × number of slices) on the magnitude images obtained after Fourier transformation of raw data and without any prior filtering or interpolation, for each coil and channel. An SNR map of the whole object was computed by dividing the 3D magnitude images by σ_η and multiplying them by 0.655 to account for Rayleigh noise distribution [64, 65]. Finally, the SNR mean and standard deviation were calculated in a 3D ROI in the center of the object (30 × 30 × 12 voxels, corresponding to 60 × 60 × 52.8 mm³).

For in vivo imaging, the data from each channel was pre-processed separately; first by filtering k-space via custom MATLAB scripts (Mathworks, United States) using a 3D Tukey window (cosine fraction 0.2), then by zerofilling the filtered k-space to double the size of each dataset (hence dividing by two the reconstructed voxel size) in all three directions [66]. Finally, 3D Fourier transform and noise-equalization (as described above) were applied before the resulting magnitude images of the two channels were summed. Since the acquired voxel size was almost isotropic, different orthogonal views could then be extracted from the obtained 3D image dataset.

3 Results

3.1 Simulations: coils and coupler

Simulations of coils A and B are presented in Figure 2. The dominant B₁ component is oriented orthogonally to the YZ plane for coil A, and orthogonally to the XY plane for coil B, as intended. Once assembled in quadrature configuration (Figure 1D), the two coils’ B₁ fields are naturally oriented orthogonally to each other and to B₀. While B₁ appears homogeneous over most of the coil inner volumes, it is strongest at the vicinity of the wiring connecting the coil planes, respectively at the bottom of coil A, and transverse, center section of coil B.

FIGURE 2

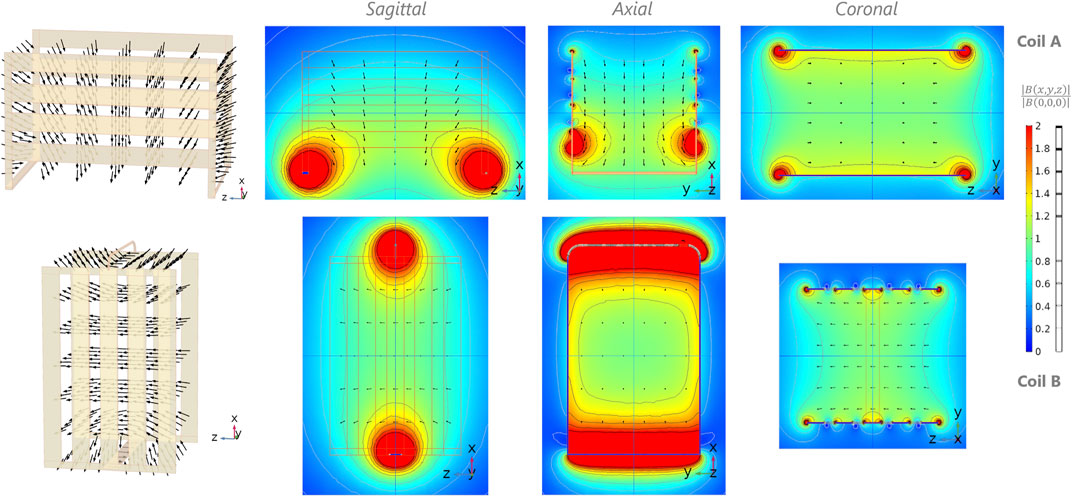
FIGURE 2. Simulations of magnetic field B for coil A (first row) and B (second row) composing the quadrature biplanar coil. First column: magnetic field (vector) distribution inside the rendered 3D view of the coils. Second-fourth column: normalized B field with respect to the center of the coil with corresponding isocontours (grayscale) in steps of 20%, on the three central orthogonal planes (XZ, XY, and YZ respectively). The coil conductor contours are depicted using thin orange lines (columns 2 and 3).

The simulated magnetic field of the inductive couplers is represented in Figure 3. By design, due to the feeding point of the coupler located at the center gap of the middle strip, the latter carries twice as much current as the lateral ones and the magnetic field B is strongest near the center of the coupler. Furthermore, as depicted by the B orientation, such geometry provides a localized and conveniently oriented magnetic field suitable for coupling with the biplanar coil’s interconnections.

FIGURE 3

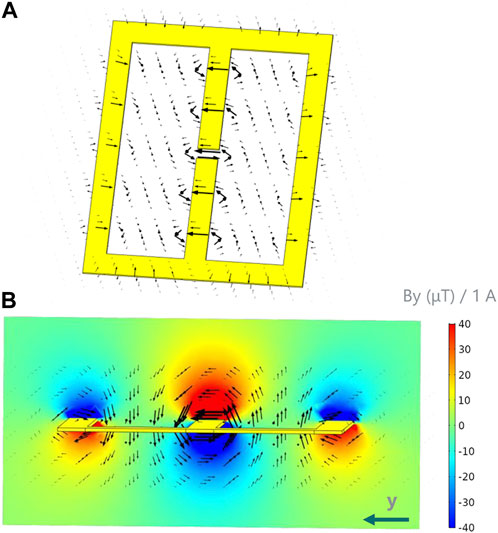
FIGURE 3. Simulation of the total magnetic field B generated by a mirrored-M coupler. (A) Magnetic field (black vectors) distribution around the coupler. The feeding point of the coupler is the gap located at the center of the middle strip. (B) Side view of the magnetic field around the coupler’s conductors, overlayed with By (color, coupler’s central section). Note: By is the dominant component (By >> Bx, Bz) in such region.

3.2 Coil realization

Figure 4 presents the assembled coil array, with the achieved electrical conditions summarized in Figure 5. Noise covariance matrix values were N₁₁: 10.5, N₂₂: 41.5, N₁₂ = N₂₁: 6.4. At our frequency of interest, no interaction between matching and tuning was observed, even while using an untuned coupler. Therefore, only coil tuning capacitors were used, which makes the interfacing simple and easily adjustable. No coil loading effect was observed (no frequency shift, no S₁₁ variation, no impedance change) in any of the coils.

FIGURE 4

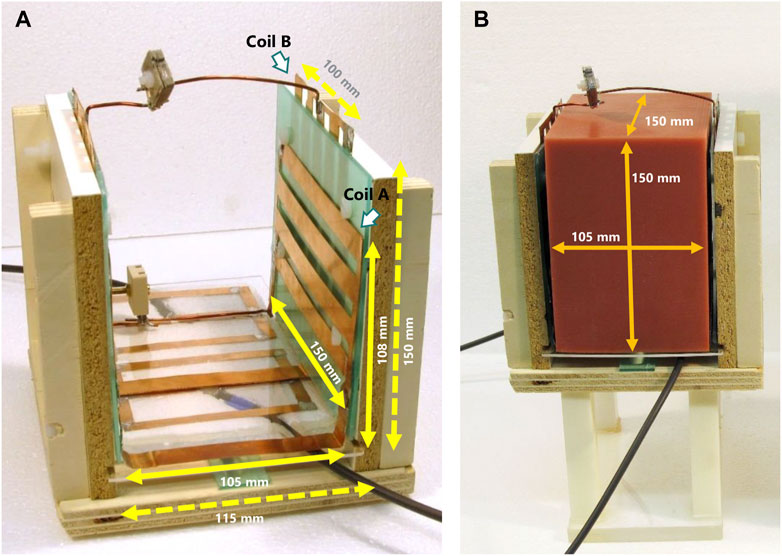
FIGURE 4. (A) Final, assembled quadrature coil. (B) Quadrature coil with the employed silicone phantom.

FIGURE 5

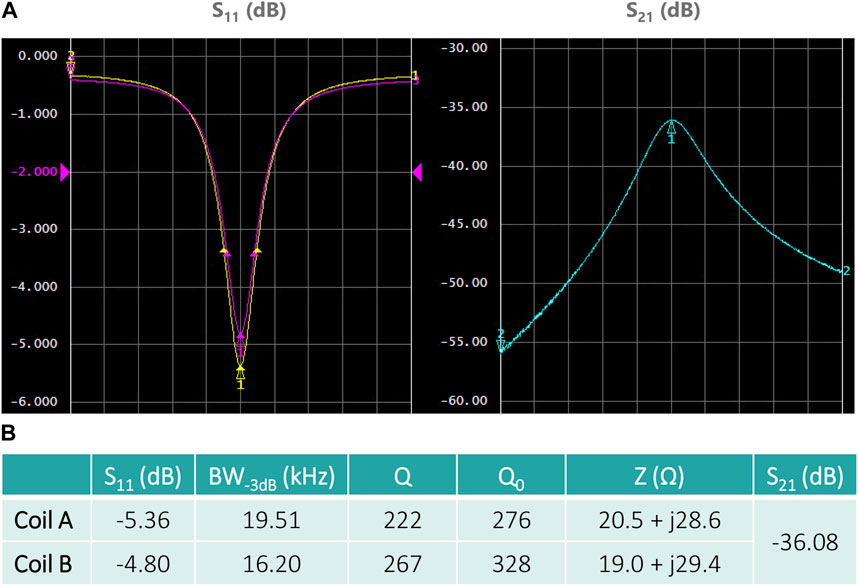
FIGURE 5. Tuning/matching, and decoupling characteristics measured with a VNA. (A) Two channels of the quadrature coil. Left: parameters S₁₁ (yellow curve, coil A) and S₂₂ (magenta curve, coil B); right: parameter S₂₁. The plots are centered at the coil resonant frequency with a span of 200 kHz. (B) The table summarizes the measured quantities, namely, the S-parameters at resonant frequencies, the bandwidth at −3 dB, the quality factors Q and Q₀ and the impedance Z of each channel/coil. No difference was observed between body-loaded and unloaded coil conditions.

3.3 Comparison of undermatched conditions vs. 50-Ω matching

Figure 6 illustrates the coils’ SNR normalized to the 50-Ω case in the 50-Ω matching conditions (S₁₁ coil A: −36.7 dB, coil B: −34.7 dB) and in the undermatched conditions of the quadrature coil operation (S₁₁ coil A: −5.4 dB, coil B: −4.8 dB). With T₂* $\sim$ 4 ms in the acquired phantom, the selected noise region to compute the SNR was consistently picked between t_acq = 100 ms and the end of the acquisition window. An SNR advantage of 40%–45% in the undermatched case is observed for both coils.

FIGURE 6

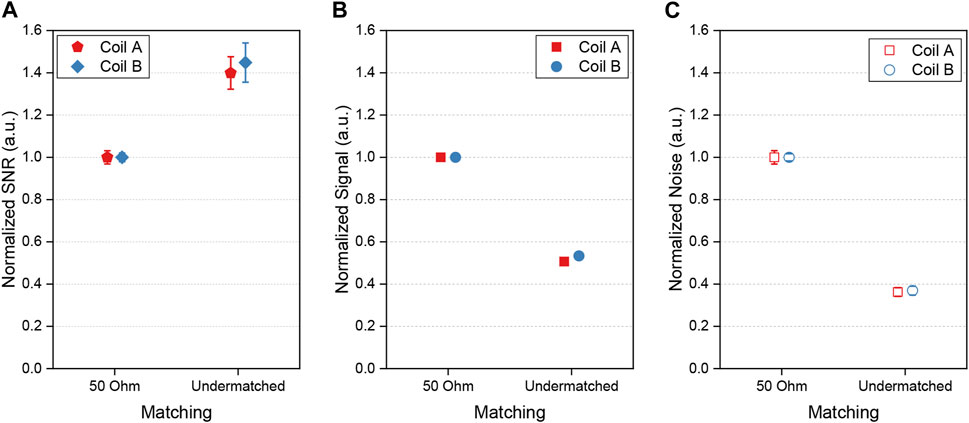
FIGURE 6. Results estimated from FIDs of a phantom using single biplanar coils in various matching conditions: 50-Ω impedance (coil A: S₁₁ −36.7 dB, bandwidth_-3dB 46.6 kHz; coil B: S₁₁ −34.7 dB, bandwidth_-3dB 46.2 kHz), and undermatching (coil A: S₁₁ −5.4 dB, bandwidth_-3dB 18.0 kHz, coil B: S₁₁ −4.8 dB, bandwidth_-3dB 16.1 kHz) conditions. (A) normalized SNR, (B) normalized signal, (C) normalized noise. The error bars in (B) are smaller than the data symbols.

3.4 Phantom results

The fabricated, custom silicone phantom is presented in Figure 4B. Phantom images obtained with the proposed biplanar coil are shown in Figure 7. From the resulting extended field-of-view, we observe distortions at the phantom edges and extremities (axial and coronal views, Figure 7*-ii and 7*-iii) while the sagittal view shows a rounding effect on the top edges (Figure 7C-i). Coil A exhibits higher sensitivity near the coil planes, and along the wiring connecting the coil planes (Figure 7A-i). A ringing effect arises from clipped, high-intensity signal in k-space, corresponding to the location of the liaison wire on the image (Figure 7A-i, bottom right corner of the phantom). Similarly to coil A, coil B exhibits higher sensitivity in the proximity of its liaison Cu conductors at the phantom’s top and bottom, particularly emphasized in the center of the axial slice (Figure 7B-ii).

FIGURE 7

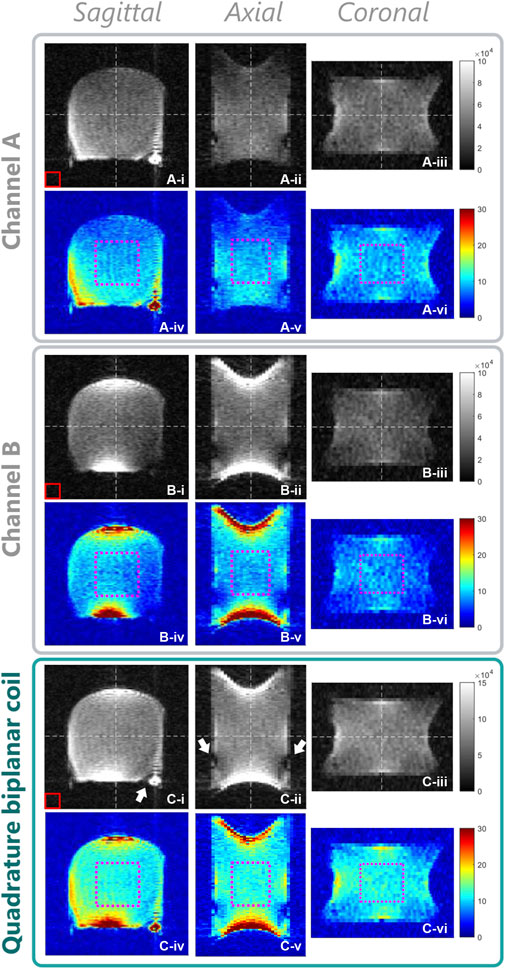
FIGURE 7. Phantom experiments: magnitude images (grayscale) in three orthogonal orientations (white dashed lines) reconstructed from the 3D datasets, and their corresponding SNR maps (color). (A) and (B) sets: data acquired separately with channels A and B; (C) set: combined images (channel A + B) of the phantom after noise equalization. *-i, iv: sagittal view, *-ii, v: axial, *-iii, vi: coronal. Red rectangle: 3D ROI used to calculate the noise standard deviation for the SNR maps; magenta dotted rectangle: 3D SNR_ROI used to calculate the SNR mean and standard deviation values. The bottom of the biplanar quadrature coil is the lower side on the sagittal and axial images.

The combined two-channel images (Figure 7C) expectedly merge the sensitivity profiles of coil A and B in a complementary fashion, resulting in an overall more homogeneous coverage of the imaged phantom. SNR in the central ROI of the combined image is 11.7 ± 1.4; its mean is 1.35 and 1.37 times greater than that of the separate channels, with a lower standard deviation (SNR A: 8.8 ± 1.5, SNR B: 8.5 ± 1.5). A noise equalizing factor between 1.5 and 2.4 was typically obtained for the coil with the higher noise level (coil B) depending on the employed sequence parameters.

3.5 In vivo images

Figure 8 shows selected in vivo images from the 3D datasets obtained with the proposed biplanar quadrature coil that display different contrasts depending on the sequence used. Images of a female ankle were acquired in a dorsiflexed foot position, with the hindfoot resting on the coil’s bottom and forefoot facing upwards. The employed bSSFP sequence exhibits good contrast between the bones and the skin (hypersignal), the muscles (lower signal) and the ligaments (hyposignal). With the foot and ankle in this position (Figure 8A), the coil sensitivity covers well the area of the ankle joints, the tarsal bones and the distal tibia, as well as the proximal metatarsals. Typical bSSFP banding artifacts are visible at the edges of the FOV (cf. tibia, heel and distal metatarsals in Figures 8C, G).

FIGURE 8

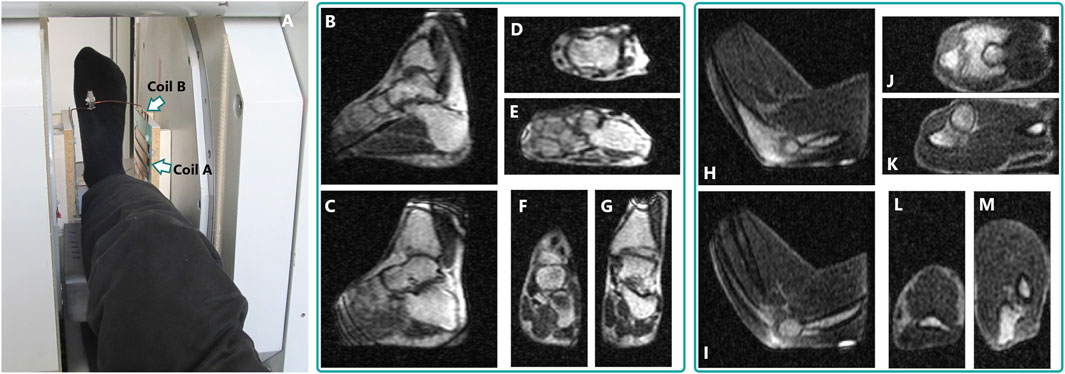
FIGURE 8. (A) Example of a foot positioned inside the quadrature coil, in the 0.1-T magnet. (B–M): Examples of images extracted from a single 3D dataset acquired in vivo with the quadrature biplanar coil: dorsiflexed ankle of a healthy female volunteer [(B–G), bSSFP sequence, 7 min 54 s acquisition time] and flexed elbow of a healthy male volunteer [(H–M), DESS gradient-echo sequence, 9 min 18 s]. On the ankle images, the bottom of the quadrature coil is on the right side of (B,C) and (D,E); on the elbow images, at the bottom of (H,I) and (L,M). The reconstructed voxel size is 0.80 × 0.80 × 1.08 mm³ for both datasets. Animations of both datasets are available as Supplementary Material.

The elbow images were obtained by resting the elbow on the coil’s bottom and flexing the joint (Figures 8H–M). Contrast similar to the bSSFP ankle images is obtained from the first echo of the DESS sequence, with hypersignal from the skin and bones, and overall lower signal in the muscle. In spite of the fewer bones and low muscle signal, main anatomical features of the joint are nevertheless visible. Bright, localized areas at the bottom of the sagittal views (Figures 8H, I) correspond to the location of coil B’s interconnecting copper strip. The signal vanishes around the distal forearm due to B₀ inhomogeneity.

4 Discussion

In this work, we describe a biplanar coil array optimized for a low-field biplanar MRI system operating at 0.1 T. The proposed coil shows good homogeneity over large volumes with an almost completely open design (top connecting wire from coil B remains), and good performance for in vivo imaging. We demonstrated that both a flexed foot and elbow can be easily positioned inside such a coil for imaging (Figure 7).

As confirmed by the simulations and further with imaging, coil A and B achieve a rather homogeneous B₁, which clear directionality facilitates quadrature-mode operations. Phantom images showcase the sensitivity distribution of the two channels of the quadrature coil on a large volume. While the areas with higher B₁ expectedly occur near the main copper conductors, they are sufficiently localized and confined to the edges of the quadrature coil. In the phantom images (Figures 7C-i, C-ii), this effect translates into dark regions with both channels because the excitation flip angle is locally much greater than the nominal one. While the simulations predict a higher sensitivity at the bottom edges of coil A (Figure 2, sagittal/axial views), it is not the case in practice (Figure 7Aiii). This behavior could be ascribed to the B₀ inhomogeneities and gradients nonlinearity. Similar observations for coil B show higher B₁ near the liaison wires (Figure 2, top and bottom of sagittal and axial views). In the simulations, the represented normalized B magnitude values may include the contribution of the component parallel to B₀ that does not participate to the MR detection (y-direction in Figure 2). However, the represented B arrow orientation shows that this component is negligible over most of the inner coil volume except for very localized areas near the conductors.

Particular care was required when designing the connections (copper wire, strips) between the coil planes, for two main reasons. First, these structures represent an important contribution to the B₁ field since they convey the entire current of each plane, and thus disturb the homogeneous magnetic field distribution produced by the planes alone. Second, these connecting structures must not impede physical access, and yet keeping them far from the volume of interest is detrimental when a high filling factor is sought. In addition, and because of the low coil inductance, any slight modification of the wires position will impact the resonance frequency. We chose to compromise by siting them rather close to the coil planes, yet further investigation will be led to improve physical access in future versions.

Severe image distortions arise in phantoms and typical bSSFP bands can be seen in vivo that reflect the magnet inhomogeneity and gradients non-linearity, that now become the overall imaging limiting factor. The proposed coil provides good sensitivity and coverage over large FOVs. SNR of the two-channel coil is greater than the single channels by $\sim \sqrt{2}$ (Figure 7). This result stems from the intrinsic high geometric decoupling obtained with the proposed couplers and coil configuration. Although our S₂₁ measurement is most certainly affected by the low matching of the coils, the value of −36 dB measured seems consistently representative of good decoupling performance, where the $\sim \sqrt{2}$ SNR improvement is achieved. Fine-tuning of the decoupling between coils is done rather simply, by adjusting the coils relative position. In addition, the proposed mirrored-M couplers have two main advantages: 1) their extremely compact arrangement that can be placed underneath the coil; and 2) their rather localized magnetic field, which serves decoupling performance. The choice of inductive coupling made our biplanar coils rather simple to tune and decouple, involving only two variable capacitors. We assume that capacitive matching networks with these coils is possible, however it may entail more complex adjustments and interactions between tuning, matching and decoupling capacitors.

The proposed noise equalization proves to be a simple and reliable method to combine magnitude images from separate channels while avoiding SNR deterioration. In our low-field system, the specific RF noise regime is expected to be coil-dominated (as suggested by the absence of loading effect [67]), which means that the noise levels can be different in decoupled coils. In case of much larger equalizing factors though, the contribution of the second coil might become too small to improve the performance of the two-channel coil. Overall, similar SNR values were observed on the two separate channels (cf. SNR_ROI in Figures 7A, B), indicating that both the noise and signal levels are higher with coil B than coil A. After verifying that our preamplifiers perform identically, we hypothesize this difference may originate from differences in coil geometries and electrical properties, from the presence of our transcoupler, or simply from inter-channel processing differences in our spectrometer (analog/digital conversion, separate gain stages, etc.). The described noise normalization method could be further extended to combine complex images as well, for example, by weighting the phase information by the corresponding magnitude of the channel or using other methods for coil-array phase retrieval developed at higher fields [68] and recently proof-tested at low field [69].

In terms of electrical properties and depending on the biplanar coil volume envisioned, inductance and B₁ can be quite low compared to a solenoid, which may translate in lower sensitivity and the need for higher RF power. On the other hand, a lower inductance can help reducing dielectric losses [70]. The longest current path in a biplanar design can be much shorter compared to the conductor length required for an equivalent-size solenoid coil, with less need for voltage splitting capacitors. In relation to this, the coil resistance is possibly lower, although a theoretical analysis taking into account all resistance contributions, such as the proximity effect between the plane strips, would be required. Overall, optimizing the coil noise along with possible noise cancelling strategies [71, 72] and not only increasing B₁ can yield a great SNR improvement, especially at RF noise regimes of coil-dominance. The relatively shallow S₁₁ and S₂₂ of the two channels should not be considered as a limitation, although they may appear unusual: for our coil and RX chain, the presented electrical conditions perform better than 50-Ω matching conditions due to better noise matching. In fact, as noted elsewhere, one does not need to seek a 50-Ω matching as it is a condition for maximizing power transfer and not necessarily SNR (more important from an RX point-of-view) [59, 73].

In our configuration, only one coil was used as TX and coil A was preferred as its B₁ distribution is more homogeneous than that of coil B. The transceiver role could however be swapped between coils according to the desired application and imaging area. We also foresee that the coil assembly could be successfully tested in full quadrature-TX operation, using a double-transceiver configuration to decrease the transmitted power by a factor close to $\sqrt{2}$ and to improve the excitation homogeneity. The low matching of the biplanar coils does not necessarily lead to lower power efficiency and higher losses in the TX chain (due to the long electrical wavelength) and can even be advantageous at low fields, as described in [74]. However, in the present work, we did not focus on TX aspects, as our goal was to optimize RX performance.

In general, a biplanar geometry is easy to build and potentially allows a wide range of design that can suit different sizes of biplanar magnets even in the quadrature configuration. With a horizontal-B₀ magnet, open access is available from three sides, with the fourth side (bottom) acting as a support plane for the extremities. In narrow magnets, the coil planes can potentially be integrated with those of the magnet. In such case, virtually all the inner magnet volume would become exploitable for MR detection. The quadrature coil could also be used in biplanar magnets with a vertical B₀. In this case though, a different design shall be envisioned to maintain all four sides of the coil open. Cylindrical-shaped magnets with non-axial or axial B₀, such as Halbach or conventional tunnel-bore magnets, could be compatible with the quadrature design or a biplanar single-channel coil, respectively, albeit with potentially worse spatial exploitation of the inner bore and reduced access to the patient.

5 Conclusion

Our biplanar coil array combines the advantage of a volume coil homogeneity with open access and high performance at 0.1 T. Our initial results set the ground for future work including biomechanics studies, image-guided interventions, or weight-bearing applications. While careful optimization of the current path is necessary to maintain the homogeneity in such a coil, this is an interesting geometry where one can even envision more irregular-shaped planes according to the desired application. Although we maintained symmetrical plane shapes for coil A and B to simplify decoupling, asymmetrical designs should be possible if mutual coupling is kept low. Besides, the described original inductive couplers and coil configuration provide high geometrical decoupling between the two channels. Together with our noise equalization method, the proposed coil leads to a high SNR, allowing fast fine-resolution in vivo MR imaging at low magnetic field as well as a broad range of possible applications where open access is needed [69]. To the best of our knowledge, this is the first time that a biplanar coil is designed for operating in a low-field scanner and in quadrature mode.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by EKNZ/2022-00348. The patients/participants provided their written informed consent to participate in this study.

Author contributions

MY, NS, and MS: study design, experimental optimization and data analysis. MY: coil simulations, design and construction, phantom fabrication. MY, PC, NS, and MS: writing and proofreading the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Swiss National Science Foundation (Grant Numbers 170575, 186861, and 198905).

Acknowledgments

The authors warmly thank Prof. Dr. André Constantinesco for sharing his expertise in low-field technologies, as well as for his generosity and strong support especially during the early days of the AMT Center, when the platform was still in the making.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.987197/full#supplementary-material

References

1. Schenck JF, Jolesz FA, Roemer PB, Cline HE, Lorensen WE, Kikinis R, et al. Superconducting open-configuration MR imaging system for image-guided therapy. Radiology (1995) 195:805–14. doi:10.1148/radiology.195.3.7754014

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Shellock FG, Hollister MC. In-office MR imaging. Clin Sports Med (2002) 21:261–87. doi:10.1016/S0278-5919(02)00003-0

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schellhammer SM, Hoffmann AL, Gantz S, Smeets J, Van Der Kraaij E, Quets S, et al. Integrating a low-field open MR scanner with a static proton research beam line: proof of concept. Phys Med Biol (2018) 63:23LT01. doi:10.1088/1361-6560/aaece8

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Abe H, Kurumi Y, Naka S, Shiomi H, Umeda T, Naitoh H, et al. Open-configuration MR-guided microwave thermocoagulation therapy for metastatic liver tumors from breast cancer. Breast Cancer (2005) 12:26–31. doi:10.2325/jbcs.12.26

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sequeiros RB, Hyvönen P, Sequeiros AB, Jyrkinen L, Ojala R, Klemola R, et al. MR imaging-guided laser ablation of osteoid osteomas with use of optical instrument guidance at 0.23 T. Eur Radiol (2003) 13:2309–14. doi:10.1007/s00330-003-1897-5

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Senft C, Franz K, Ulrich CT, Bink A, Szelényi A, Gasser T, et al. Low field intraoperative MRI-guided surgery of gliomas: a single center experience. Clin Neurol Neurosurg (2010) 112:237–43. doi:10.1016/j.clineuro.2009.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Levivier M, Wikler D, De Witte O, Van de Steene A, Balériaux D, Brotchi J. PoleStar N-10 low-field compact intraoperative magnetic resonance imaging system with mobile radiofrequency shielding. Neurosurgery (2003) 53:1001–7. doi:10.1227/01.NEU.0000084167.18475.BA

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hadani M, Spiegelman R, Feldman Z, Berkenstadt H, Ram Z. Novel, compact, intraoperative magnetic resonance imaging-guided system for conventional neurosurgical operating rooms. Neurosurgery (2001) 48:799–809. doi:10.1227/00006123-200104000-00021

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Charest-Morin R, Zhang H, Shewchuk JR, Wilson DR, Phillips AE, Bond M, et al. Dynamic morphometric changes in degenerative lumbar spondylolisthesis: a pilot study of upright magnetic resonance imaging. J Clin Neurosci (2021) 91:152–8. doi:10.1016/j.jocn.2021.06.027

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Pai SA, Zhang H, Street J, Wilson DR, Brown SHM, Oxland TR. Outgoing editor's thoughts - on Sisyphean tasks and the last refuge of scoundrels. JOR Spine (2021) 4:1–2. doi:10.4103/ijc.IJC_56_21

CrossRef Full Text | Google Scholar

11. Li C, Lü Y, Liu M, Fritz J. Magnetic resonance imaging-guided biopsy of musculoskeletal lesions using open low-field systems. Top Magn Reson Imaging (2011) 22:135–41. doi:10.1097/RMR.0b013e3182805f7b

PubMed Abstract | CrossRef Full Text | Google Scholar

12. König CW, Trübenbach J, Böhm P, Fritz J, Duda SH, Pereira PL. Magnetic resonance-guided transcortical biopsy of bone marrow lesions using a magnetic resonance imaging-compatible piezoelectric power drill: preliminary experience. Invest Radiol (2003) 38:159–63. doi:10.1097/01.RLI.0000053670.71386.B9

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Genant JW, Vandevenne JE, Bergman AG, Beaulieu CF, Kee ST, Norbash AM, et al. Interventional musculoskeletal procedures performed by using MR imaging guidance with a vertically open MR unit: assessment of techniques and applicability. Radiology (2002) 223:127–36. doi:10.1148/radiol.2231010900

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Blanco RT, Ojala R, Kariniemi J, Perälä J, Niinimäki J, Tervonen O. Interventional and intraoperative MRI at low field scanner - a review. Eur J Radiol (2005) 56:130–42. doi:10.1016/j.ejrad.2005.03.033

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Masciocchi C, Barile A, Satragno L. Musculoskeletal MRI: dedicated systems. Eur Radiol (2000) 10:250–5. doi:10.1007/s003300050041

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Sarracanie M, Salameh N. Low-field MRI: how low can we go? A fresh view on an old debate. Front Phys (2020) 8:1–14. doi:10.3389/fphy.2020.00172

CrossRef Full Text | Google Scholar

17. Gries P, Constantinesco A, Brunot B, Facello A. MR imaging of hand and wrist with a dedicated 0.1-T low-field imaging system. Magn Reson Imaging (1991) 9:949–53. doi:10.1016/0730-725X(91)90541-S

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Arbogast-Ravier S, Xu F, Choquet P, Brunot B, Constantinesco A. Dedicated low-field MRI: a promising low cost-technique. Med Biol Eng Comput (1995) 33:735–9. doi:10.1007/BF02510797

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ghazinoor S, Crues JV, Crowley C. Low-field musculoskeletal MRI. J Magn Reson Imaging (2007) 25:234–44. doi:10.1002/jmri.20854

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cooley CZ, Stockmann JP, Armstrong BD, Sarracanie M, Lev MH, Rosen MS, et al. Two-dimensional imaging in a lightweight portable MRI scanner without gradient coils. Magn Reson Med (2015) 73:872–83. doi:10.1002/mrm.25147

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lother S, Schiff SJ, Neuberger T, Jakob PM, Fidler F. Design of a mobile, homogeneous, and efficient electromagnet with a large field of view for neonatal low-field MRI. Magn Reson Mater Physics, Biol Med (2016) 29:691–8. doi:10.1007/s10334-016-0525-8

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Obungoloch J, Harper JR, Consevage S, Savukov IM, Neuberger T, Tadigadapa S, et al. Design of a sustainable prepolarizing magnetic resonance imaging system for infant hydrocephalus. Magn Reson Mater Physics, Biol Med (2018) 31:665–76. doi:10.1007/s10334-018-0683-y

PubMed Abstract | CrossRef Full Text | Google Scholar

23. He Y, He W, Tan L, Chen F, Meng F, Feng H, et al. Use of 2.1 MHz MRI scanner for brain imaging and its preliminary results in stroke. J Magn Reson (2020) 319:106829. doi:10.1016/j.jmr.2020.106829

PubMed Abstract | CrossRef Full Text | Google Scholar

24. O’Reilly T, Teeuwisse WM, Gans D, Koolstra K, Webb AG. In vivo 3D brain and extremity MRI at 50 mT using a permanent magnet Halbach array. Magn Reson Med (2021) 85:495–505. doi:10.1002/mrm.28396

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Mazurek MH, Cahn BA, Yuen MM, Prabhat AM, Chavva IR, Shah JT, et al. Portable, bedside, low-field magnetic resonance imaging for evaluation of intracerebral hemorrhage. Nat Commun (2021) 12:5119–1. doi:10.1038/s41467-021-25441-6

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cooley CZ, McDaniel PC, Stockmann JP, Srinivas SA, Cauley SF, Śliwiak M, et al. A portable scanner for magnetic resonance imaging of the brain. Nat Biomed Eng (2021) 5:229–39. doi:10.1038/s41551-020-00641-5

PubMed Abstract | CrossRef Full Text | Google Scholar

27. de Vos B, Parsa J, Abdulrazaq Z, Teeuwisse WM, Van Speybroeck CDE, de Gans DH, et al. Design, characterisation and performance of an improved portable and sustainable low-field MRI system. Front Phys (2021) 9:1–16. doi:10.3389/fphy.2021.701157

CrossRef Full Text | Google Scholar

28. Naval TG, Algarín JM, Guridi RP, Galve F, Gilabert YV, Bosch R, et al. Portable magnetic resonance imaging of patients indoors, outdoors and at home. Sci Rep (2022) 2022:1. doi:10.1038/s41598-022-17472-w

CrossRef Full Text | Google Scholar

29. Wald LL, McDaniel PC, Witzel T, Stockmann JP, Cooley CZ. Low-cost and portable MRI. J Magn Reson Imaging (2020) 52:686–96. doi:10.1002/jmri.26942

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Iturri-Clavero F, Galbarriatu-Gutierrez L, Gonzalez-Uriarte A, Tamayo-Medel G, de Orte K, Martinez-Ruiz A, et al. “Low-field” intraoperative MRI: a new scenario, a new adaptation. Clin Radiol (2016) 71:1193–8. doi:10.1016/j.crad.2016.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sheth KN, Mazurek MH, Yuen MM, Cahn BA, Shah JT, Ward A, et al. Assessment of brain injury using portable, low-field magnetic resonance imaging at the bedside of critically ill patients. JAMA Neurol (2020) 78:41. doi:10.1001/jamaneurol.2020.3263

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Constantinesco A, Choquet P, Cauffet G, Fournier JM, Ravier S, Drillon JM, et al. Low-field dedicated and desktop magnetic resonance imaging systems for agricultural and food applications. Magn Reson Chem (1997) 35:69–75. doi:10.1002/(sici)1097-458x(199712)35:13<s69::aid-omr198>3.0.co;2-5

CrossRef Full Text | Google Scholar

33. Sepponen RE. Low-field MR imaging — development in Finland. Acta Radiol (1996) 37:446–54. doi:10.3109/02841859609177679

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Davies F. Resistive and permanent magnets for whole body MRI. In: encyclopedia of magnetic resonance. Chichester, UK: John Wiley & Sons, Ltd (2023). p. 1–7. doi:10.1002/9780470034590.emrstm0469

CrossRef Full Text | Google Scholar

35. Hushek SG, Martin AJ, Steckner M, Bosak E, Debbins J, Kucharzyk W. MR systems for MRI-guided interventions. J Magn Reson Imaging (2008) 27:253–66. doi:10.1002/jmri.21269

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Honda Y, Hata N. Dynamic imaging of swallowing in a seated position using open-configuration MRI. J Magn Reson Imaging (2007) 26:172–6. doi:10.1002/jmri.20992

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Schirmer T, Geoffroy Y, Koran SJ, Ulrich F. Signa SP/2 - a MRI system for image guided surgery. Med Laser Appl (2002) 17:105–16. doi:10.1078/1615-1615-00053

CrossRef Full Text | Google Scholar

38. Doornbos J, Grimbergen HAA, Booijen PE, te Strake L, Bloem JL, Vielvoye GJ, et al. Application of anatomically shaped surface coils in MRI at 0.5 T. Magn Reson Med (1986) 3:270–81. doi:10.1002/mrm.1910030210

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Merkle EM, Lewin JS, Liebenthal R, Lorenz CH. The interventional MR imaging suite: magnet designs and equipment requirements. Magn Reson Imaging Clin N Am (2005) 13:401–13. doi:10.1016/j.mric.2005.04.014

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Roberts DA, Insko EK, Bolinger L, Leigh JS. Biplanar radiofrequency coil design. J Magn Reson Ser A (1993) 102:34–41. doi:10.1006/jmra.1993.1065

CrossRef Full Text | Google Scholar

41. Mispelter J, Lupu M. Homogeneous resonators for magnetic resonance: a review. Comptes Rendus Chim (2008) 11:340–55. doi:10.1016/j.crci.2007.10.003

CrossRef Full Text | Google Scholar

42. Shellock FG, Stone KR, Crues JV. Development and clinical application of kinematic MRI of the patellofemoral joint using an extremity MR system. Med Sci Sport Exerc (1999) 31:788–91. doi:10.1097/00005768-199906000-00005

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Shellock FG, Powers C. In: FG shellock, and C Powers, editors. Kinematic MRI of the joints. United States: CRC Press (2001). doi:10.1201/b16364

CrossRef Full Text | Google Scholar

44. Koenig CW, Duda SH, Truebenbach J, Schott UG, Maurer F, Claussen CD, et al. MR-guided biopsy of musculoskeletal lesions in a low-field system. J Magn Reson Imaging (2001) 13:761–8. doi:10.1002/jmri.1106

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Tomanek B, Volotovskyy V, Tyson R, Yin D, Sharp J, Blasiak B. A quadrature volume RF coil for vertical B0 field open MRI systems. Concepts Magn Reson B Magn Reson Eng (2016) 46B:118–22. doi:10.1002/cmr.b.21327

CrossRef Full Text | Google Scholar

46. Blasiak B, Volotovskyy V, Tyson R, Sharp J, Tomanek B. An RF breast coil for 0.2 T MRI. Concepts Magn Reson Part B Magn Reson Eng (2016) 46:3–7. doi:10.1002/cmr.b.21316

CrossRef Full Text | Google Scholar

47. Chen C-N, Hoult D, Sank V. Quadrature detection coils—a further √2 improvement in sensitivity. J Magn Reson (1983) 54:324–7. doi:10.1016/0022-2364(83)90057-4

CrossRef Full Text | Google Scholar

48. Koonjoo N, Sheng S, Sappo C, Rosen MS. Optimized quadrature head coil improves SNR at ultra-low field. Proc Intl Soc Mag Reson Med (2020) 2020.

Google Scholar

49. Hoult DI, Chen CN, Sank VJ. Quadrature detection in the laboratory frame. Magn Reson Med (1984) 1:339–53. doi:10.1002/mrm.1910010305

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Redpath TW. Quadrature rf coil pairs. Magn Reson Med (1986) 3:118. doi:10.1002/mrm.1910030115

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Shen S, Kong X, Wu J, He Y, Guo P, Xu Z, et al. An optimized quadrature RF receive coil for very-low-field (50.4 mT) magnetic resonance brain imaging. J Magn Reson (2022) 342:107269. doi:10.1016/j.jmr.2022.107269

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Hoult DI, Lauterbur PC. The sensitivity of the zeugmatographic experiment involving human samples. J Magn Reson (1979) 34:425–33. doi:10.1016/0022-2364(79)90019-2

CrossRef Full Text | Google Scholar

53. Kuhns PL, Lizak MJ, Lee SH, Conradi MS. Inductive coupling and tuning in NMR probes; Applications. J Magn Reson (1988) 78:69–76. doi:10.1016/0022-2364(88)90157-6

CrossRef Full Text | Google Scholar

54. Decorps M, Blondet P, Reutenauer H, Albrand J, Remy C. An inductively coupled, series-tuned NMR probe. J Magn Reson (1985) 65:100–9. doi:10.1016/0022-2364(85)90378-6

CrossRef Full Text | Google Scholar

55. Hoult DI, Tomanek B. Use of mutually inductive coupling in probe design. Concepts Magn Reson Part B Magn Reson Eng (2002) 15:262–85. doi:10.1002/cmr.10047

CrossRef Full Text | Google Scholar

56. Cassidy PJ, Clarke K, Edwards DJ. Determining the tuning and matching requirements of RF coils using electromagnetic simulation and electric circuit analysis. Concepts Magn Reson Part B Magn Reson Eng (2005) 25:27–41. doi:10.1002/cmr.b.20029

CrossRef Full Text | Google Scholar

57. Raad A, Darrasse L. Optimization of NMR receiver bandwidth by inductive coupling. Magn Reson Imaging (1992) 10:55–65. doi:10.1016/0730-725X(92)90373-8

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Kajfez D, Hwan EJ. Q-factor measurement with network analyzer. IEEE Trans Microw Theor Tech (1984) 32:666–70. doi:10.1109/TMTT.1984.1132751

CrossRef Full Text | Google Scholar

59. Miller JB, Suits BH, Garroway AN, Hepp MA. Interplay among recovery time, signal, and noise: series- and parallel-tuned circuits are not always the same. Concepts Magn Reson (2000) 12:125–36. doi:10.1002/(SICI)1099-0534(2000)12:3<125::AID-CMR2>3.0.CO;2-P

CrossRef Full Text | Google Scholar

60. Quirin T, Yushchenko M, Salameh N, Sarracanie M. High-input impedance preamplifiers for multi-channel strategies at low frequency. Annu Meet Eur Soc Magn Reson Med Biol (2020) 33:164–5. Abstract L01.108. doi:10.1007/s10334-020-00876-y

CrossRef Full Text | Google Scholar

61. Yushchenko M, Sarracanie M, Amann M, Sinkus R, Wuerfel J, Salameh N. Elastography validity criteria definition using numerical simulations and MR acquisitions on a low-cost structured phantom. Front Phys (2021) 9:9. doi:10.3389/fphy.2021.620331

CrossRef Full Text | Google Scholar

62. Sarracanie M, Armstrong BD, Stockmann J, Rosen MS. High speed 3D overhauser-enhanced MRI using combined b-SSFP and compressed sensing. Magn Reson Med (2014) 71:735–45. doi:10.1002/mrm.24705

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Darrasse L, Ginefri J-C. Perspectives with cryogenic RF probes in biomedical MRI. Biochimie (2003) 85:915–37. doi:10.1016/j.biochi.2003.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Edelstein WA, Bottomley PA, Pfeifer LM. A signal-to-noise calibration procedure for NMR imaging systems. Med Phys (1984) 11:180–5. doi:10.1118/1.595484

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Gudbjartsson H, Patz S. The rician distribution of noisy mri data. Magn Reson Med (1995) 34:910–4. doi:10.1002/mrm.1910340618

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Netherlands: Elsevier (2004). doi:10.1016/B978-0-12-092861-3.X5000-6

CrossRef Full Text | Google Scholar

67. Gilbert KM, Scholl TJ, Chronik BA. RF coil loading measurements between 1 and 50 MHz to guide field-cycled MRI system design. Concepts Magn Reson Part B Magn Reson Eng (2008) 33B:177–91. doi:10.1002/cmr.b.20118

CrossRef Full Text | Google Scholar

68. Robinson SD, Bredies K, Khabipova D, Dymerska B, Marques JP, Schweser F. An illustrated comparison of processing methods for MR phase imaging and QSM: combining array coil signals and phase unwrapping. NMR Biomed (2017) 30:e3601. doi:10.1002/nbm.3601

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Yushchenko M, Sarracanie M, Salameh N. Fast acquisition of propagating waves in humans with low-field MRI: toward accessible MR elastography. Sci Adv (2022) 8:5739–12. doi:10.1126/sciadv.abo5739

CrossRef Full Text | Google Scholar

70. Doty FD. Probe design and construction. In: eMagRes. Chichester, UK: John Wiley & Sons, Ltd (2009). doi:10.1002/9780470034590.emrstm0414.pub2

CrossRef Full Text | Google Scholar

71. Liu Y, Leong ATL, Zhao Y, Xiao L, Mak HKF, Tsang ACO, et al. A low-cost and shielding-free ultra-low-field brain MRI scanner. Nat Commun (2021) 12:7238–14. doi:10.1038/s41467-021-27317-1

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Srinivas SA, Cauley SF, Stockmann JP, Sappo CR, Vaughn CE, Wald LL, et al. External dynamic InTerference estimation and removal (EDITER) for low field MRI. Magn Reson Med (2022) 87:614–28. doi:10.1002/mrm.28992

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Hoult DI, Richards RE. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J Magn Reson (1976) 24:71–85. doi:10.1016/0022-2364(76)90233-X

CrossRef Full Text | Google Scholar

74. Harper JR, Zárate C, Krauch F, Muhumuza I, Molina J, Obungoloch J, et al. An unmatched radio frequency chain for low-field magnetic resonance imaging. Front Phys (2022) 9:727536. doi:10.3389/fphy.2021.727536

CrossRef Full Text | Google Scholar