- 1Department of Physics, Faculty of Physical Sciences, Modibbo Adama UniversityYola, Adamawa, Nigeria
- 2Department of Pure and Applied Sciences, Taraba State PolytechnicJalingo, Taraba, Nigeria
- 3Department of Physics, Faculty of Science, University of AbujaAbuja, Nigeria
- 4Department of Physics, Faculty of Natural Sciences, University of JosJos, Plateau, Nigeria
In this work, the reparameterized Scarf II oscillator was employed to describe the internal vibration of diatomic systems. Analytical equations for bound state pure vibrational energies and canonical partition function were obtained. The equations were used to derive statistical-mechanical models for the prediction of molar entropy, enthalpy, Gibbs free energy and constant pressure (isobaric) heat capacity of gaseous substances. The obtained model equations were used to generate numerical data on bound state energy eigenvalues and, to investigate the thermodynamic properties of the ground states chloroborane (BCl), bromine fluoride (BrF), and bromine chloride (BrCl) molecules. With the aid of the expression for molar entropy of the system, average absolute deviations obtained for the molecules are 0.1878%, 0.1267%, and 0.0586% from experimental data. The isobaric heat capacity model yields average absolute deviation of 2.1608%, 1.8601%, and 1.9805%. The results obtained are in good agreement with available literature data on gaseous molecule. The work could be applicable in the fields of molecular physics, chemical physics, solid-state physics and chemical engineering.
1 Introduction
Potential energy function (simply known as potential) is a mathematical model used to describe the interaction of a physical system with its environment. One of the problems of this representation is the absence of a universal potential energy function that can model every atomic and molecular interactions. Numerous versions of potential models have been proposed by chemist and physicist to account for observed atomic and molecular phenomena. The list of potential models includes the Morse potential [1], Eckart potential [2], Frost-Musulin potential [3], Rosen-Morse potential [4], Tietz potential [5], Hua potential [6], and Schiöberg potential [7] amongst others.
A potential energy function whose potential parameters are formulated in terms of the spectroscopic constants of a diatomic molecule is referred to as oscillator. The oscillator is a specialized model potential used to describe interactions in diatomic molecules. A diatomic molecule oscillator is required to satisfy the so-called Varshni conditions [8, 9]. The Varshni conditions ensure that the potential parameters of an oscillator are expressed in terms of molecular constants such as equilibrium harmonic vibrational frequency (ωe), rotational-vibrational coupling coefficient (αe), equilibrium dissociation energy (De), anharmonicity constant (ωexe), and equilibrium bond length (re) [10].
The solution of Schrödinger and other wave equations of quantum mechanics can be obtained analytically or by numerical approach. Quite a number of analytical solution methods have been suggested in the literature, the Nikiforov-Uvarov (NU) method, exact and proper quantization rules, supersymmetric quantum mechanics approach (SUSYQM), asymptotic iteration method (AIM), and the recently introduced Nikiforov-Uvarov functional analysis (NUFA) method are some of the methods. Some illustrative examples where the different solution techniques are used to solve the Schrödinger equation can be found in Ref. [11–16] and the references therein. The solution of Schrödinger wave equation has been instrumental in retrieving information regarding the quantum mechanical system of interest. For instance, expectation values, information theoretic, optical, magnetic, electrical, and thermodynamic properties of substances have been investigated through eigen energy levels and eigenfunctions of wave Eqs 17–34.
The need to obtain analytical (or statistical-mechanical) models for the prediction of thermodynamic properties of gaseous substances have recently attracted much attention from the research community. The thermodynamic property of a gaseous molecule can be predicted theoretically with the aid of analytical model equation; it can also be determined by experimental procedures. The statistical-mechanical models are easy to use and are not expensive, only few molecular constants of a diatomic molecule are required to predict the thermal property of the system. In contrast, experimental method is time consuming, usually very expensive and require huge experimental task.
Different oscillator models have been employed to describe the internal vibration of diatomic molecules. Through such representation, canonical partition function is obtained which is then used to derive other useful thermodynamic models for the gaseous substance. Statistical-mechanical models such as Helmholtz free energy (F), mean thermal energy (U), entropy (S), enthalpy (H), Gibbs free energy (G), isobaric heat capacity (Cp), and constant volume heat capacity (CV) have successfully been used to examine thermal properties of substances [35–39].
This paper is concerned with improved versions of hyperbolical-type oscillators. Available three parameter models are the specialized Pöschl-Teller potential [40], improved generalized Pöschl-Teller potential [41], and improved Scarf II potential energy function (ISPEF) [42]. On the other hand, existing four parameter models are the improved Pöschl-Teller potential [43], improved q-deformed Scarf II oscillator [10], and modified hyperbolical-type potential [44]. Analytical expressions for the prediction of molar entropy, enthalpy, Gibbs free energy, and isobaric heat capacity have been obtained with various formulations of the improved hyperbolical-type oscillators [10, 45–48]. However, the reparameterized Scarf oscillator has not been considered in the literature. It is against this background that this research is aimed at obtaining the pure vibrational state energies and some statistical-mechanical models for the reparameterized Scarf oscillator (RSO). The paper is organized as follows. In Section 2, potential parameters are developed for the RSO. Equation for pure vibrational state energy is obtained in Section 3. Statistical-mechanical models are derived in Section 4. Results of numerical computations are discussed in Section 5. A brief conclusion of the work is given in Section 6.
2 Potential parameters of the RSO
In previous study, the Varshni conditions for diatomic molecule potential were used to construct the IqSO. By employing the IqSO, analytical equations for the prediction of molar entropy and Gibbs free energy were derived [10]. However, statistical-mechanical models for the prediction of molar enthalpy and heat capacity have not been reported for the IqSO. In the present work, statistical-mechanical models for the prediction of molar entropy, enthalpy, Gibbs free energy and isobaric heat capacity are obtained using the RSO. The RSO can be obtained by subjecting the ISPEF through the transformation r → r–r0, where r0 is a real constant. Using this transformation on Eq. 1 of Ref. [42], the RSO is proposed via the following equation
where V1, V2, and α are the potential parameters. The potential Eq. 1 is an oscillator if it satisfies the following constraints (Varshni conditions)
where Be = ħ/(4πcμre2), ħ = h/2π, h being the Planck constant, c represents the speed of light, and fj (j = 1, 2, 3, …) is the jth derivative of V (r) at r = re. Substituting Eq. 1 into Eqs 2–4 yields
To obtain the parameter r0, we first note that f2 = 2α2De, and f3 = – 6α3Detanhα (re–r0). Inserting these expressions into Eq. 5 gives
3 Pure vibrational state energy levels for the RSO
In this section, the analytical equation for bound state vibrational energy levels is derived using the Nikiforov-Uvarov (NU) solution approach. To ensure continuity of the concept, a brief outline of the NU method is outlined.
3.1 An overview of the NU solution method
The NU solution approach is one of the most widely used methods of solving a second order differential equation. With the aid of a convenient transformation, the Schrödinger equation can be converted to a hypergeometric-type differential equation of the form [11].
where σ (s),
where
π(s) is a polynomial of degree at most one, it is given by [11].
k is obtained by requiring that the quantity under the square root is a perfect square of a first degree polynomial. λ is deduced via the expression
Successively differentiating Eq. 11 ν times (ν = 0, 1, 2, …) leads to quantum condition given as
energy eigenvalues are obtained by equating the expressions Eqs 14, 15.
3.2 Solution of schrödinger equation with the RSO by NU method
The radial Schrödinger equation in the presence of any potential field V (r) is given as
where ν, and J are the vibrational and rotational quantum numbers, respectively. EνJ is the ro-vibrational energy eigenvalue of the quantum state νJ, RνJ is the corresponding radial wave function. For non-zero values of J, only approximate analytical solutions of Eq. 16 are possible with the RSO. Nevertheless, exact analytical solutions are feasible if J = 0, the solutions are referred to as the pure vibrational state solutions. Thus, substituting Eq. 1 into Eq. 16 and letting J = 0 gives
where Eν0 → Eν, Rν0 → Rν. The substitution s = sinh α(r–r0) transforms Eq. 17 to
where, for compactness the following notations have been used;
Setting the discriminant of the expression under square root to zero gives
Eq. 20 leads to
Thus, k is a two-valued parameter viz: k = k obtained by choosing the negative square root, and k = k+ if the positive square root is chosen. Using Eq. 20 to eliminate γ0 in Eq. 19, with some algebraic simplifications, one obtains
It is evident that for each value of k, π (s) has four possible expressions: π--, π-+, π+-, and π++ obtained from all possible combinations of the ± signs in Eq. 22. The next task is to deduce equations for λ and λν whose results are required to derive vibrational energy levels of the RSO. To satisfy the restriction τ′ (s) < 0 of the NU method, we choose from Eqs 21, 22
with the help of expressions Eqs 12, 23, 24, gives
with the help of relationships Eqs 23–25, and recalling that
By equating expressions Eqs 26, 27, and eliminating γν, γ0, γ1 in the resulting equation, the vibrational energy levels for the RSO is obtained as
The energy spectrum defined by Eq. 28 increases with increasing ν, the upper bound vibrational quantum number, νmax at which the eigen energies ceases to increase is given by
Therefore, ν can assume values 0, 1, 2, …, [νmax]. Here, the notation [νmax] means the largest integer less than νmax for non-integer values of νmax.
4 Some statistical-mechanical models for the RSO
The partition function is the master key connecting the microscopic model of a system with its macroscopic property. Other thermodynamic quantities can easily be expressed in terms of the partition function. Therefore, explicit expression of the partition function of a gas system is vital in this study. Statistical-mechanical models considered in this paper include molar entropy, enthalpy, Gibbs free energy, and isobaric specific heat capacity.
4.1 The canonical partition function
The canonical partition function of a gaseous molecule is composed of the translation (Qtra), vibrational (Qvib), and rotational (Qrot) [49] components. The canonical partition function is given by the product Q (T) = QtraQvibQrot, T being the temperature of the enclosed gas. The vibrational partition function depends on the vibrational energy levels of the diatomic system which in turn depends on the diatomic oscillator used to describe the internal vibration of the gas molecules. The vibrational partition function is given by [50].
where gν is the factor of the degeneration of the spectrum, β = (kBT)−1, kB is the Boltzmann constant. Given a non-degenerate system of gas molecules, gν = 1. Eqs 28–30 leads to
where
for a finite series with an upper bound νmax, the Poisson series formula can be written [51].
Inserting expression Eq. 32 in Eq. 33 gives
by evaluating the definite integral, Eq. 34 yields
where
If the molecules of a diatomic gas are visualized as rigid rotors, neglecting molecular interactions, the translational and rotational partition functions are given as [33, 47].
where σ is assigned the value 1, 2 for heteronuclear and homonuclear diatomic molecules, respectively. Θrot = ħ2/(2μre2kB) is the characteristic temperature, m is the mass of the molecules which make up gas, p is the gas pressure.
4.2 Molar entropy model for the RSO
The molar entropy for the system is evaluated from the expression [48].
where R = NAkB is the molar gas constant, NA is the Avogadro number, V is the volume of gas enclosed. Substituting Q = QtraQvibQrot into the second term in Eq. 39 gives
where, for brevity we have employed the representation
4.3 Molar enthalpy model for the RSO
The molar enthalpy of the system is defined by the equation [48].
with the aid of the substitution Q = QtraQvibQrot, expression Eq. 42 and the relations Eqs 36–38 gives
For the purpose of comparing theoretical results to experimental data, the reduced molar enthalpy is considered, it is given as [46–48].
where H298.15 is the molar enthalpy computed at p = 1 bar, and T = 298.15 K. Therefore, putting Eq. 43 in Eq. 44, we have
4.4 Molar Gibbs free energy model for the RSO
The molar Gibbs free energy of the system can be deduced from the expression [48].
Inserting the equation of canonical partition function in to the first term of Eq. 46, we obtain the molar Gibbs free energy in compact form as
The reduced or scaled Gibbs free energy is often required for comparison with experimental data, it is given as Gred = (G–H′298.15)/T. Inserting Eq. 47 into this equation yields
4.5 Molar specific heat capacity model for the RSO
Molar specific heat capacity at constant pressure can be deduced from the Eq. 33.
Substituting Eq. 43 in Eq. 49 and using expressions Eqs 36–38 to simplify the resulting equation, we obtained
where the parameter Γvib is given by
5 Results and discussion
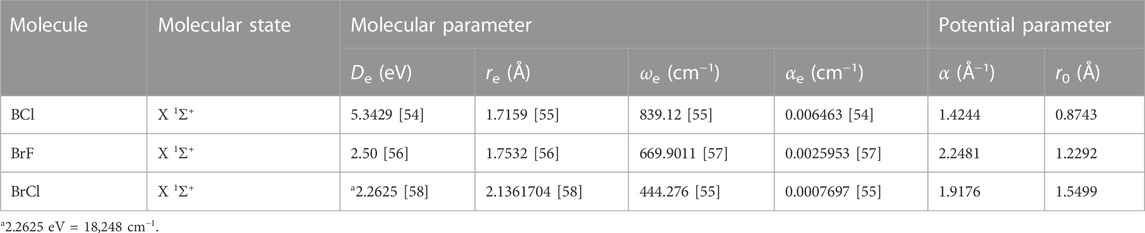
In this section, the analytical equations developed for the reparameterized Scarf II oscillator are analyzed on some selected diatomic molecules. The experimental values of the relevant molecular constants De, re, ωe, αe of the ground state BCl, BrF, and BrCl molecules are taken from Refs. [54–59]. The molecular constants and computed potential parameters of the molecules are shown in Table 1.
With the aid of Eq. 1, potential energy data, V (rmin) = Vmin, and V (rmax) = Vmax are obtained. Due to unavailability of literature data on BrCl molecule, only results for BCl and BrF molecules are obtained. Tables 2, 3 summarizes results of numerical computations, and available literature data on vibrational energies of the molecules. The literature data were those obtained by multireference configuration interaction (MRCI), and Rydberg-Klein-Rees (RKR) method [54, 59].
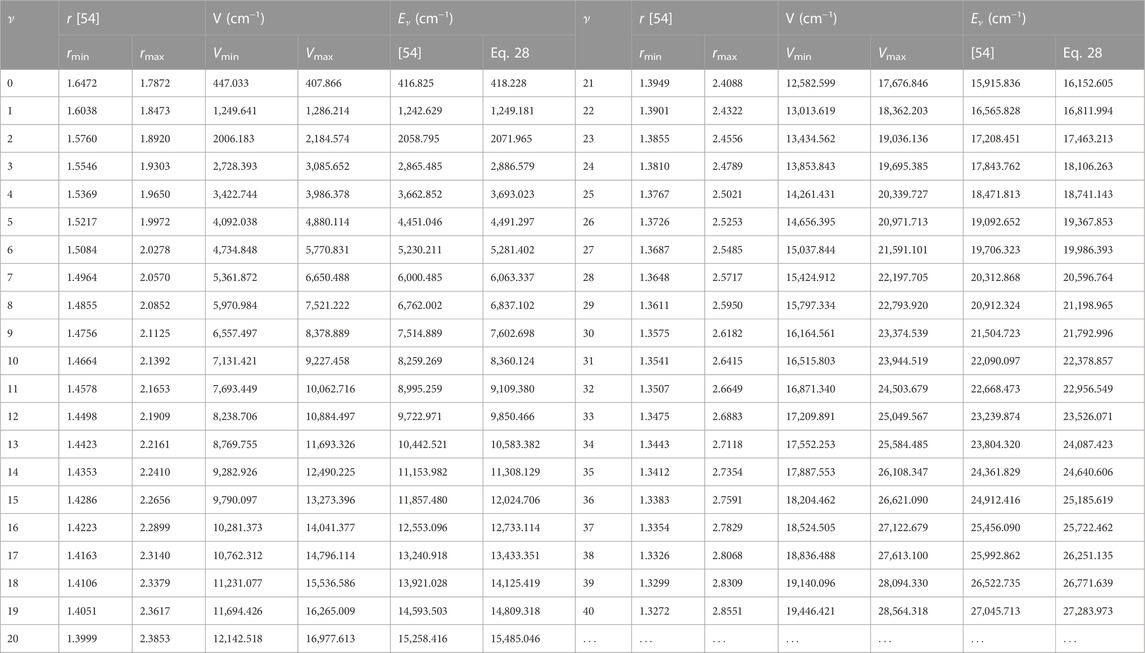
TABLE 2. Potential energies (cm) and bound state pure vibrational state energies (cm−1) as a function of internuclear separation (Å) for the BCl (X 1Σ+) molecule.
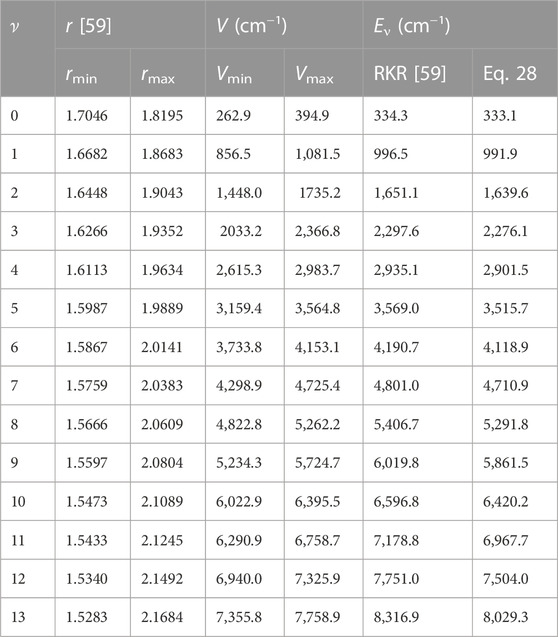
TABLE 3. Potential energies (cm) and bound state pure vibrational state energies (cm−1) as a function of internuclear separation (Å) for the BrF (X 1Σ+) molecule.
Figure 1 shows graphical fitting of the RSO to (A) MRCI data points of BCl molecule, and (B) RKR data points of BrF molecule. The plots reveal that the RSO could model the internuclear potential energy curves of the BCl and BrF molecules. However, graphical plots only give an idea of the agreement between predicted data and experimental results. The average absolute deviation from experimental data (σave) is one of the most widely used goodness-of-fit indicators to evaluate the accuracy of an empirical model. Previously, the average absolute deviation has been used to substantiate the accuracy of proposed model Eqs 38, 41, 43, 48. The average absolute deviation can be written as
where Np is the number of experimental data points, (X, Y, Z) ≡ (V, E, S, H, G, Cp). Average absolute deviations less than 1% shows good agreement between predicted and observed data, the smaller the σave, better the model.
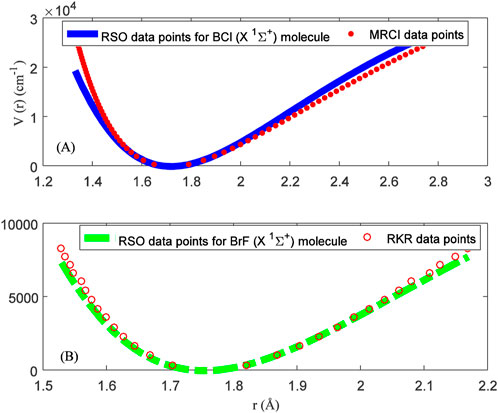
FIGURE 1. Modeling of reparameterized Scarf II oscillator to (A) multireference configuration interaction curve for the BCl (X 1Σ+) molecule. (B) Rydberg-Klein-Rees internuclear potential energy curve for the BrF (X 1Σ+).
Using Eq. 52 and the data in Tables 2, 3, average absolute deviations of 5.3976% and 1.6790% are obtained from the experimental data of the BCl and BrF molecules, respectively. The results show that data predicted by the RSO are relatively high for the BCl molecule. To within 2% error limit of the RKR data, the RSO can approximately reproduced the internuclear potential energy curve of the ground state BrF molecule.
Figure 2 shows the variation of energy levels Eq. 28 of the molecules against vibrational quantum number, ν. The plot reveal that as ν is gradually increased from zero, the energy of the molecules also increases. The upper bound vibrational quantum numbers obtained for the BCl, BrF and BrCl molecules are 102, 60 and 82, respectively. As ν is further increased beyond νmax, the bound state energy of the molecules begins to decrease, leading to degenerate energy levels of the molecules. Eq. 28 is also used to generate numerical data on bound state pure vibrational energies of the molecules. As there are no available literature data on energies of BrCl molecule to allow comparison, only the results for BCl and BrF molecules are displayed in Tables 2, 3. Using Eq. 52 and the energy data in Tables 2, 3, average absolute deviation obtained are 1.1949% for BCl molecule, and 1.8353% for BrF molecule. Thus, it can be seen that the energy values predicted by expression Eq. 28 are in good agreement with existing experimental data on the diatomic molecules.
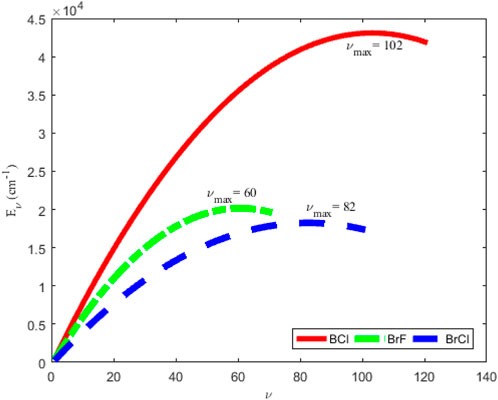
FIGURE 2. Variation of bound state energy eigenvalues versus vibrational quantum number for the ground state BCl, BrF, and BrCl molecules.
To authenticate the applicability of the statistical-mechanical models proposed in this study, Eq. 43 is used to compute the value of H′298.15 at T = 298.15 K, p = 0.1 MPa to yield; 14.502 kJmol−1 for BCl, 13.626 kJmol−1 for BrF and 12.533 kJmol−1 for BrCl molecules. Using these results and the data in Table 1, the expressions for molar entropy Eq. 40, reduced enthalpy Eq. 45, reduced Gibbs free energy Eq. 48, and constant pressure specific heat capacity Eq. 51 are used to obtain numerical data for the diatomic molecules. The computations are carried out at p = 0.1 MPa and temperature in the range 300 K–6,000 K. The results of computations are shown in Tables 4–6. Also included in the tables are literature data on molar entropy (SNIST), reduced molar enthalpy (HNIST), reduced molar Gibbs free energy (GNIST) and constant pressure specific heat capacity (CpNIST). The data are those reported in the National Institute of Standards and Technology (NIST) database [60]. Figures 2–5 represent the temperature variation of the thermal functions.
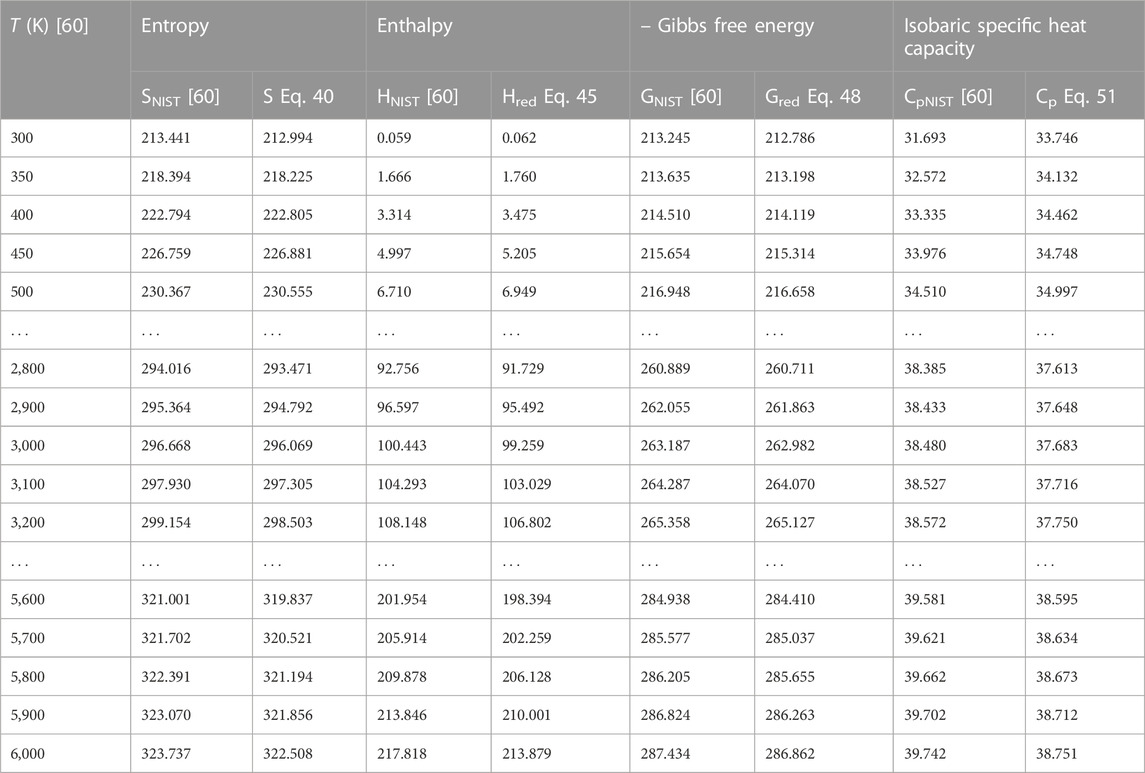
TABLE 4. Computed data on molar entropy (J mol−1 K−1), reduced enthalpy (kJ mol−1), reduced Gibbs free energy, and isobaric specific heat capacity for the BCl (X 1Σ+) molecule. Np = 60.
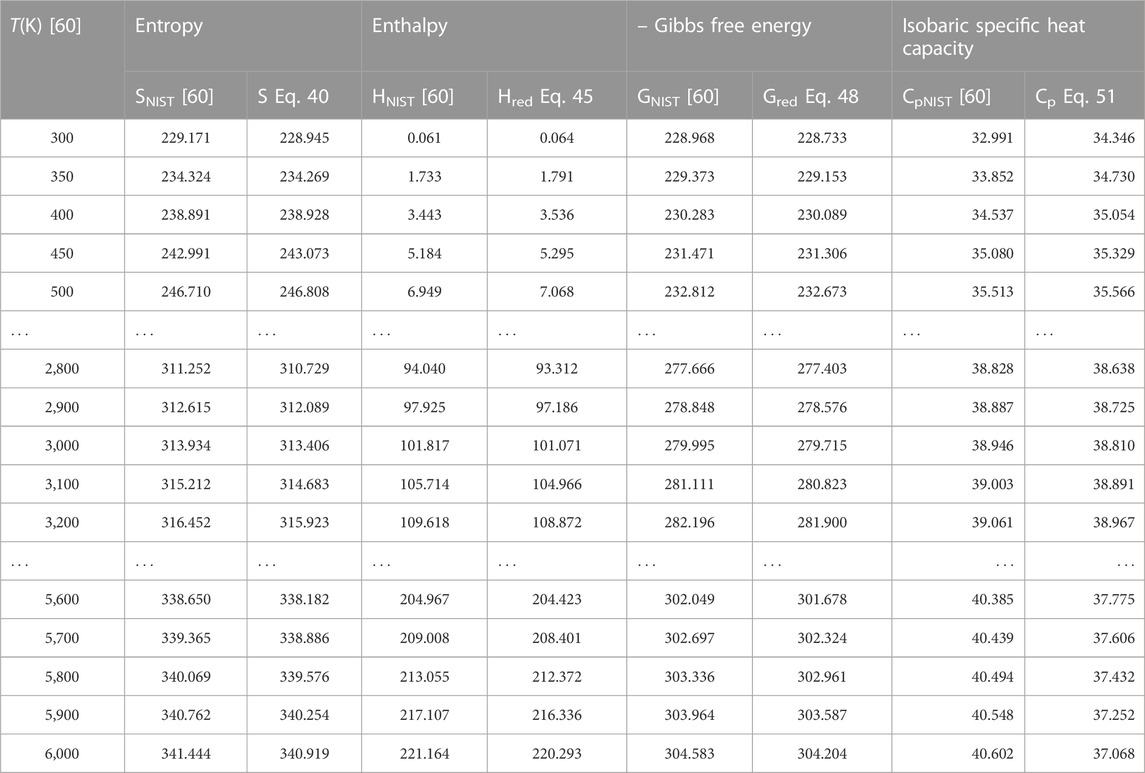
TABLE 5. Computed data on molar entropy (J mol−1 K−1), reduced enthalpy (kJ mol−1), reduced Gibbs free energy, and isobaric specific heat capacity for the BrF (X 1Σ+) molecule. Np = 60.
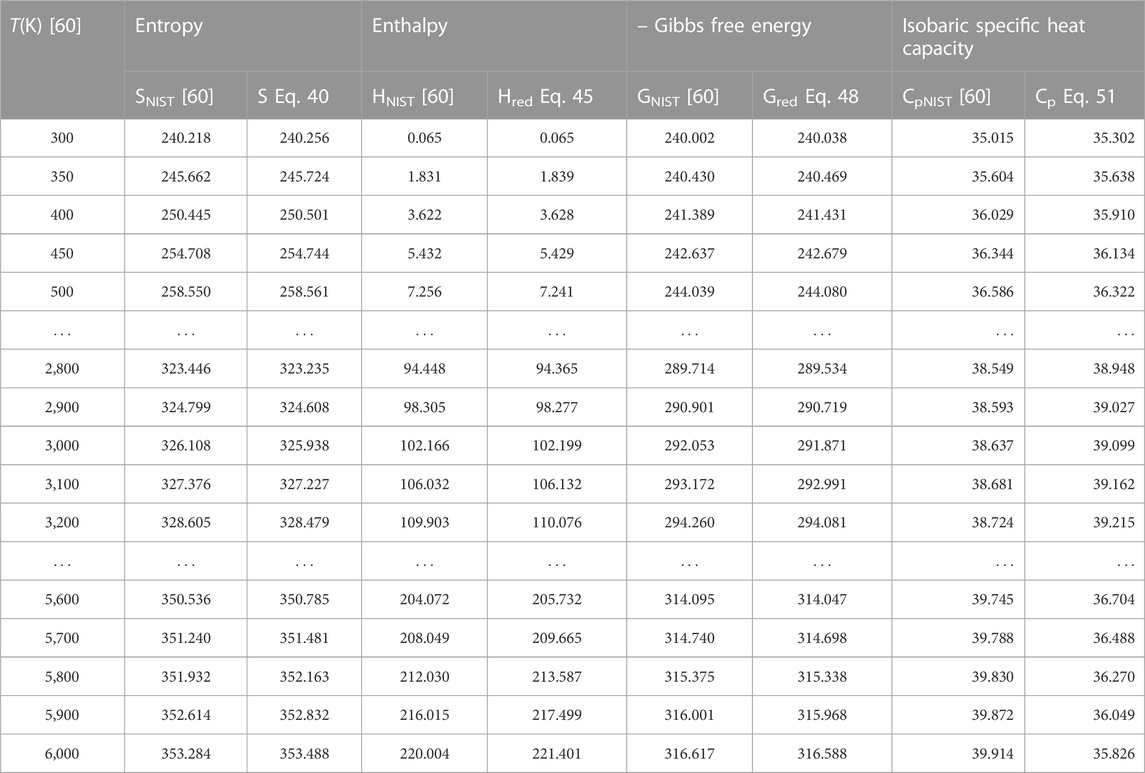
TABLE 6. Computed data on molar entropy (J mol−1 K−1), reduced enthalpy (kJ mol−1), reduced Gibbs free energy, and isobaric specific heat capacity for the BrCl (X 1Σ+) molecule. Np = 60.
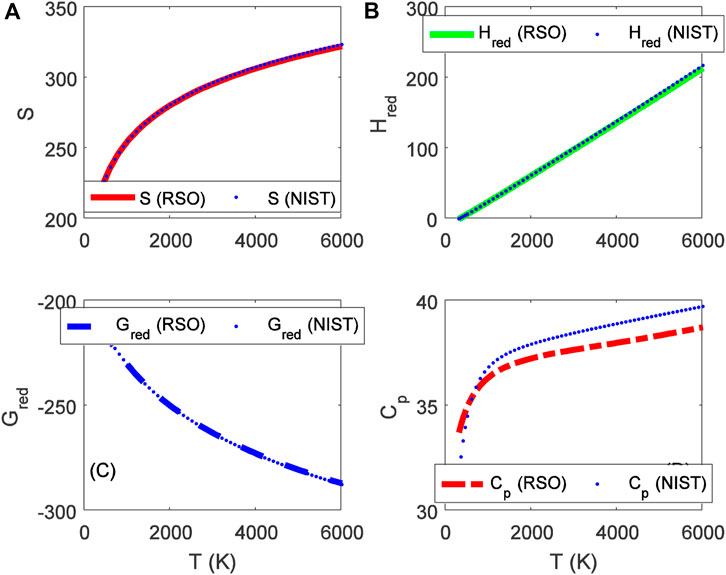
FIGURE 3. Variation of (A) molar entropy (J mol−1 K−1), (B) reduced enthalpy (kJ mol−1), (C) reduced Gibbs free energy (J mol−1 K−1), and (D) isobaric specific heat capacity as a function of temperature for the ground state BCl (X 1Σ+) molecule.
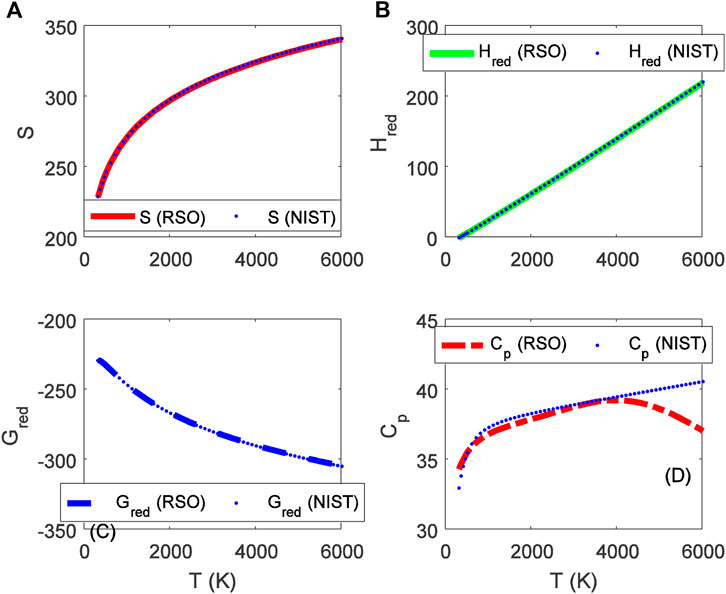
FIGURE 4. Variation of (A) molar entropy (J mol−1 K−1), (B) reduced enthalpy (kJ mol−1), (C) reduced Gibbs free energy (J mol−1 K−1), and (D) isobaric specific heat capacity as a function of temperature for the ground state BrF (X 1Σ+) molecule.
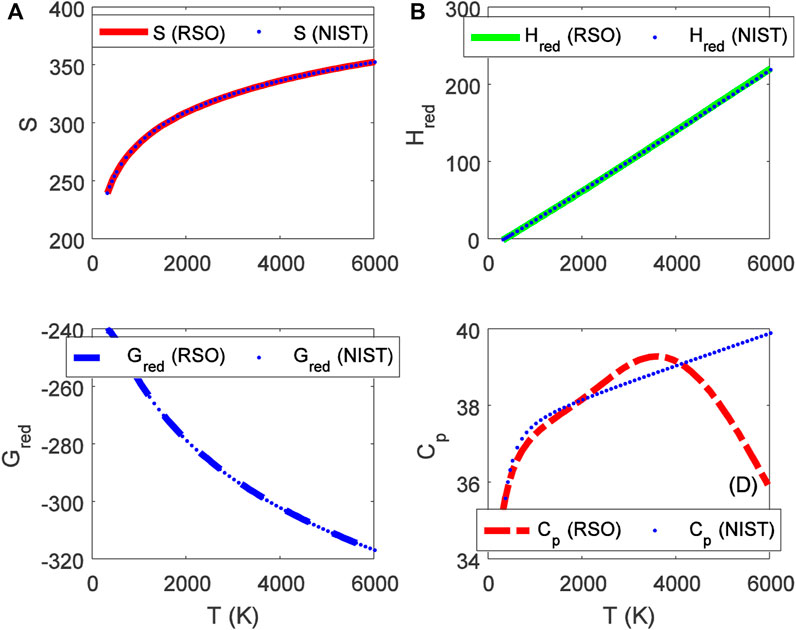
FIGURE 5. Variation of (A) molar entropy (J mol−1 K−1), (B) reduced enthalpy (kJ mol−1), (C) reduced Gibbs free energy (J mol−1 K−1), and (D) isobaric specific heat capacity as a function of temperature for the ground state BrCl (X 1Σ+) molecule.
Choosing X ≡ Z ≡ SNIST to represent experimental data on molar entropy and setting Y ≡ S, average absolute deviations obtained for the BCl, BrF and BrCl molecules are 0.2011%, 0.1224% and 0.5323%, respectively. Thus, it is obvious that within error limit of 1% of the NIST data, entropy equation proposed in this work can accurately predict the experimental data on molar entropy of the diatomic molecules.
To confirm the suitability of expression Eq. 45 to predict molar entropy of the diatomic molecules, we let X ≡ Y ≡ HNIST to denote the experimental data on reduced molar entropy. Choosing Y ≡ Hred. The average absolute deviation deduced for the diatomic molecules are 1.5346% for BCl, 0.688% for BrF and 0.5323% for BrCl molecules. The results reveal that statistical-mechanical model proposed for the RSO can accurately predict the NIST data on molar enthalpy of the examined molecules.
To show the relevance of expression Eq. 51 to model experimental data on molar Gibbs free energy, average absolute deviation is computed for each of the molecules. By appropriately choosing the parameters in Eq. 52 with respect to experimental data, such that X ≡ Y ≡ GNIST, and Z ≡ Gred, average absolute deviations obtained for the BCl, BrF and BrCl diatomic molecules are 0.1033%, 0.0903%, and 0.0367%, respectively. The results show that on a scale of 1% of the NIST data, Gibbs free energy expression proposed by the RSO is a near perfect model to accurately predict experimental results of the examined diatomic molecules.
The analytical expression of constant pressure specific heat capacity is also analyzed for the diatomic molecules. Average absolute deviation deduced for the BCl, BrF, and BrCl molecules are 2.1565%, 1.9731%, and 1.9805%, respectively. The results are in good agreement with NIST data particularly in the low to moderate temperature regions. However, in the high temperature regime, the predicted results are relatively higher than observed data. The discrepancy arises as a result of rigid-rotor approximation of the diatomic molecules and also, the quantum correction terms excluded in the expression of vibrational partition function, which by extension are also excluded in all the statistical-mechanical models of the system.
6 Conclusion
In this paper, conditions to be satisfied by a diatomic molecule potential are used to construct the reparameterized Scarf II oscillator (RSO), suitable for application to diatomic molecules. Using the Nikiforov-Uvarov method to solve the radial Schrödinger equation for the RSO, analytical expression of bound state pure vibrational energy is derived for the system. With the aid of the formula for energy eigenvalues, analytical equations representing canonical partition function and other relevant statistical-mechanical models are obtained, including molar entropy, enthalpy, Gibbs free energy and isobaric specific heat capacity. The obtained equations were used to study thermodynamic properties of three diatomic molecules viz BCl, BrF, and BrCl. Average absolute deviations of 1.5364%, 0.688%, and 0.5323%, respectively are obtained using the expression of reduced molar enthalpy. The equation of reduced Gibbs free energy yields average absolute deviations of 0.1033%, 0.0903%, and 0.0367% for the diatomic molecules. The results are in excellent agreement with existing literature data on the diatomic molecules. The developed statistical-mechanical models could be useful in scientific and engineering researches involving thermochemical processes.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
EE: Conceptualization, methodology, validation, data curation, formal analysis, project administration, supervision, writing–original draft, writing–review and editing. PN: Methodology, formal analysis, validation, data curation, writing–review and editing, formal analysis. GN: Formal analysis, validation, data curation, formal analysis, writing–review and editing. YJ: Methodology, validation, data curation, visualization, supervision, writing–review and editing. MI: Methodology, validation, formal analysis, data curation, visualization, supervision, writing–review and editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Morse PM. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys Rev (1929) 34:57–64. doi:10.1103/PhysRev.34.57
2. Eckart C. The penetration of a potential barrier by electrons. Phys Rev (1930) 35:1303–9. doi:10.1103/PhysRev.35.1303
3. Frost AA, Musulin B. Semi empirical potential energy functions. I. The H2 and H2+ diatomic molecules. J Chem Phys (1954) 22:1017–20. doi:10.1063/1.1740254
4. Rosen N, Morse PM. On the vibrations of polyatomic molecules. Phys Rev (1932) 42:210–7. doi:10.1103/PhysRev.42.210
5. Tietz T. Potential-energy function for diatomic molecules. J Chem Phys (1963) 38:3036–7. doi:10.1063/1.1733648
6. Hua W. Four-parameter exactly solvable potential for diatomic molecules. Phys Rev A (1990) 42:2524–9. doi:10.1103/PhysRevA.42.2524
7. Schiöberg D. The energy eigenvalues of hyperbolical potential functions. Mol Phys (1986) 59:1123–37. doi:10.1080/00268978600102631
8. Yanar H, Aydoğdu O, Saltı M. Modelling of diatomic molecules. Mol Phys (2016) 114:3134–42. doi:10.1080/00268976.2016.1220645
9. Horchani R, Al-Kindi N, Jelassi H. Ro-vibrational energies of caesium molecules with the Tietz-Hua oscillator. Mol Phys (2020) 119:e1812746. doi:10.1080/00268976.2020.1812746
10. Eyube ES, Nyam GG, Notani PP. Improved q-deformed Scarf II oscillator. Phys Scr (2021) 96:125017. doi:10.1088/1402-4896/ac2eff
11. Nikiforov AF, Uvarov VB. Special functions of mathematical physics. Basel: Birkhauser (1988). doi:10.1007/978-1-4757-1595-8
12. Horchani R, Al-Aamri H, Al-Kindi S, Ikot AN, Okorie US, Rampho GJ, et al. Energy spectra and magnetic properties of diatomic molecules in the presence of magnetic and AB fields with the inversely quadratic Yukawa potential. Eur Phys J D (2021) 75:36. doi:10.1140/epjd/s10053-021-00038-2
13. Ma ZQ, Xu BW. Quantum correction in exact quantization rules. EPL (2005) 69:685–91. doi:10.1209/epl/i2004-10418-8
14. Kumar PR, Dong SH. A new quantization rule to the bound state problem in non-relativistic quantum mechanics. Phys Lett A (2021) 417:127700. doi:10.1016/j.physleta.2021.127700
15. Sun GH, Dong Q, Bezetta VB, Dong SH. Exact solutions of an asymmetric double well potential. J Math Chem (2022) 60:605–12. doi:10.1007/s10910-022-01328-9
16. Edet CO, Mahmoud S, Inyang PE, Ali N, Aljunid SA, Endut R, et al. Non-Relativistic treatment of the 2D electron system interacting via varshni–shukla potential using the asymptotic iteration method. Mathematics (2022) 10:2824. doi:10.3390/math10152824
17. Deng M, Jia CS. Prediction of enthalpy for nitrogen gas. Eur Phys J Plus (2018) 133:258. doi:10.1140/epjp/i2018-12090-2
18. Jia CS, Wang CW, Zhang LH, Peng XL, Tang HM, Liu JY, et al. Predictions of entropy for diatomic molecules and gaseous substances. Chem Phys Lett (2018) 692:57–60. doi:10.1016/j.cplett.2017.12.013
19. Jiang R, Jia CS, Wang YQ, Peng XL, Zhang LH. Prediction of enthalpy for the gases CO, HCl, and BF. Chem Phys Lett (2018) 715:186–9. doi:10.1016/j.cplett.2018.11.044
20. Jia CS, Wang CW, Zhang LH, Peng XL, Tang HM, Zeng R. Enthalpy of gaseous phosphorus dimer. Chem Eng Sci (2018) 183:26–9. doi:10.1016/j.ces.2018.03.009
21. Peng XL, Jiang R, Jia CS, Zhang LH, Zhao YL. Gibbs free energy of gaseous phosphorus dimer. Chem Eng Sci (2018) 190:122–5. doi:10.1016/j.ces.2018.06.027
22. Wang J, Jia CS, Li CJ, Peng XL, Zhang LH, Liu JY. Thermodynamic properties for carbon dioxide. ACS Omega (2019) 4:19193–8. doi:10.1021/acsomega.9b02488
23. Jia CS, Zhang LH, Peng XL, Luo JX, Zhao YL, Liu JY, et al. Prediction of entropy and Gibbs free energy for nitrogen. Chem Eng Sci (2019) 202:70–4. doi:10.1016/j.ces.2019.03.033
24. Horchani R, Jelassi H. A four-parameters model for molar entropy calculation of diatomic molecules via shifted Tietz-Wei potential. Chem Phys Lett (2020) 753:137583. doi:10.1016/j.cplett.2020.137583
25. Horchani R, Jelassi H. Accurate and general model to predict molar entropy for diatomic molecules. S Afr J Chem Eng (2020) 33:103–6. doi:10.1016/j.sajce.2020.07.001
26. Jia CS, Li J, Liu YS, Peng XL, Jia X, Zhang LH, et al. Predictions of thermodynamic properties for hydrogen sulfide. J Mol Liq (2020) 315:113751. doi:10.1016/j.molliq.2020.113751
27. Ikot AN, Edet CO, Amadi PO, Okorie US, Rampho GJ, Abdullah HY. Thermodynamic properties of Aharanov–Bohm (AB) and magnetic fields with screened Kratzer potential. Eur Phys J D (2020) 74:159. doi:10.1140/epjd/e2020-10084-9
28. Ikot AN, Okorie US, Osonboye G, Amadi PO, Edet CO, Sithole MJ, et al. Superstatistics of Schrödinger equation with pseudo-harmonic potential in external magnetic and Aharanov-Bohm fields. Heliyon (2020) 6:e03738. doi:10.1016/j.heliyon.2020.e03738
29. Ikot AN, Rampho GJ, Amadi PO, Sithole MJ, Okorie US, Lekala MI. Shannon entropy and Fisher information-theoretic measures for Mobius square potential. Eur Phys J Plus (2020) 135:503. doi:10.1140/epjp/s13360-020-00525-2
30. Horchani R, Al Shafi S, Friha H, Jrlassi H. A straightforward model for molar enthalpy prediction of CsO, CsF, and CsCl molecules via shifted Tietz-Wei potential. Int J Thermophys (2021) 42:84. doi:10.1007/s10765-021-02839-4
31. Wang CW, Wang J, Liu YS, Li J, Peng XL, Jia CS, et al. Prediction of the ideal-gas thermodynamic properties for water. J Mol Liq (2021) 321:114912. doi:10.1016/j.molliq.2020.114912
32. Oluwadare OJ, Oyewumi KJ, Abiola TO. Thermodynamic properties of some diatomic molecules confined by an harmonic oscillating system. Indian J Phys (2022) 96:1921–8. doi:10.1007/s12648-021-02139-5
33. Fan QC, Jian J, Fan XZ, Fu J, Li HD, Ma J, et al. A method for predicting the molar heat capacities of HBr and HCl gases based on the full set of molecular rovibrational energies. Spectrochim Acta A Mol Biomol Spectrosc (2022) 267:120564. doi:10.1016/j.saa.2021.120564
34. Liang DC, Zeng R, Wang CW, Ding QC, Wei LS, Peng XL, et al. Prediction of thermodynamic properties for sulfur dioxide. J Mol Liq (2022) 352:118722. doi:10.1016/j.molliq.2022.118722
35. Khordad R, Ghanbari A. Analytical calculations of thermodynamic functions of lithium dimer using modified Tietz and Badawi-Bessis-Bessis potentials. Comput Theor Chem (2019) 1155:1–8. doi:10.1016/j.comptc.2019.03.019
36. Ghanbari A, Khordad R. Theoretical prediction of thermodynamic properties of N2 and CO using pseudo harmonic and Mie-type potentials. Chem Phys (2020) 534:110732. doi:10.1016/j.chemphys.2020.110732
37. Khordad R, Ghanbari A. Theoretical prediction of thermodynamic functions of TiC: Morse ring-shaped potential. J Low Temp Phys (2020) 199:1198–210. doi:10.1007/s10909-020-02368-8
38. Khordad R, Ghanbari A. Theoretical prediction of thermal properties of K2 diatomic molecule using generalized mobius square potential. Int J Thermophys (2021) 42:115. doi:10.1007/s10765-021-02865-2
39. Khordad R, Edet CO, Ikot AN. Application of Morse potential and improved deformed exponential-type potential (IDEP) model to predict thermodynamics properties of diatomic molecules. Int J Mod Phys C (2022) 33. doi:10.1142/S0129183122501066
40. Tang B, Jia CS. Relativistic spinless rotation-vibrational energies of carbon monoxide. Eur Phys J Plus (2017) 132:375. doi:10.1140/epjp/i2017-11657-7
41. Yanar H, Taş A, Salti M, Aydogdu O. Ro-vibrational energies of CO molecule via improved generalized Pöschl–Teller potential and Pekeris-type approximation. Eur Phys J Plus (2020) 135:292. doi:10.1140/epjp/s13360-020-00297-9
42. Eyube EE, Notani PP, Izam MM. Potential parameters and eigen spectra of improved Scarf II potential energy function for diatomic molecules. Mol Phys (2022) 120:e1979265. doi:10.1080/00268976.2021.1979265
43. Jia CS, Zhang LH, Peng KL. Improved Pöschl-Teller potential energy model for diatomic molecules. Int J Quan Chem. (2017) 117:e25383. doi:10.1002/qua.25383
44. Eyube ES, Notani PP, Dikko AB. Modeling of diatomic molecules with modified hyperbolical-type potential. Eur Phys J Plus (2022) 137:329. doi:10.1140/epjp/s13360-022-02526-9
45. Eyube ES, Bitrus BM, Samaila H, Notani PP. Model entropy equation for gaseous substances. Int J Thermophys (2022) 43:4355. doi:10.1007/s10765-022-02980-8
46. Eyube ES, Notani PP, Samaila H. Analytical prediction of enthalpy and Gibbs free energy of gaseous molecules. Chem Thermodynamics Therm Anal (2022) 6:100060. doi:10.1016/j.ctta.2022.100060
47. Eyube ES, Onate CA, Omugbe E, Nwabueze CM. Theoretical prediction of Gibbs free energy and specific heat capacity of gaseous molecules. Chem Phys (2022) 560:111572. doi:10.1016/j.chemphys.2022.111572
48. Eyube ES. Prediction of thermal properties of phosphorus dimer – the analytical approach. Chem Phys Lett (2022) 801:139702. doi:10.1016/j.cplett.2022.139702
49. Gordillo-Vázquez FJ, Kunc JA. Statistical–mechanical calculations of thermal properties of diatomic gases. J Appl Phys (1998) 84:4693–703. doi:10.1063/1.368712
51. Strekalov ML. An accurate closed-form expression for the partition function of Morse oscillators. Chem Phys Lett (2007) 439:209–12. doi:10.1016/j.cplett.2007.03.052
52. Song XQ, Wang CW, Jia CS. Thermodynamic properties for the sodium dimer. Chem Phys Lett (2017) 673:50–5. doi:10.1016/j.cplett.2017.02.010
53. Jia CS, Wang CW, Zhang LH, Peng XL, Zeng R, You XT. Partition function of improved Tietz oscillators. Chem Phys Lett (2017) 676:150–3. doi:10.1016/j.cplett.2017.03.068
54. Shi DH, Liu H, Zhang XN, Sun JF, Liu YF, Zhu ZL. MRCI investigations on dissociation energy and molecular constants of BCl (X 1Σ+) radical. Int J Quan Chem. (2010) 111:2825–34. doi:10.1002/qua.22699
55. Liu X, Truppe S, Meijer G, Pérez-Ríos J. The diatomic molecular spectroscopy database. J Cheminform (2020) 12:31. doi:10.1186/s13321-020-00433-8
56. Li R, Zhang X, Feng W, Jiang Y, Fei D, Jin M, et al. Ab initio CI calculations on potential energy curves of low-lying states of BrF and its cation including spin–orbit coupling. Comput Theor Chem (2014) 1032:20–6. doi:10.1016/j.comptc.2014.01.016
57. Bürger H, Jacob E, Fähnle M. The fourier transform IR spectra of CIF and BrF. Z Naturforsch (1986) 41a:1015–20. doi:10.1515/zna-1986-0806
58. Beckert M, Wouters ER, Ashfold MNR, Wrede E. High resolution ion imaging study of BrCl photolysis in the wavelength range 330–570 nm. J Chem Phys (2003) 119:9576–89. doi:10.1063/1.1615951
59. Clyne MAA, Curran AH, Coxon JA. Studies of labile molecules with a tunable dye laser: Laser excitation spectrum of BrF (B 3Π (0+) – X 1Σ+). J Mol Spectrosc (1976) 63:43–59. doi:10.1016/0022-2852(67)90133-6
Keywords: schrödinger equation, diatomic molecules, energy eigenvalues, entropy, enthalpy, gibbs free energy, specific heat capacity, statistical-mechanical models
Citation: Eyube ES, Notani PP, Nyam GG, Jabil YY and Izam MM (2023) Pure vibrational state energies and statistical-mechanical models for the reparameterized scarf oscillator. Front. Phys. 11:978347. doi: 10.3389/fphy.2023.978347
Received: 25 June 2022; Accepted: 13 February 2023;
Published: 23 February 2023.
Edited by:
Carlo Gabbanini, CNR INO, ItalyReviewed by:
C. O. Edet, Cross River University of Technology, NigeriaBoumali Abdelmalek, University of Tébessa, Algeria
Copyright © 2023 Eyube, Notani, Nyam, Jabil and Izam. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: E. S. Eyube, ZWR3aW5leXViZXNAbWF1LmVkdS5uZw==
 E. S. Eyube
E. S. Eyube P. P. Notani2
P. P. Notani2