A refractive index sensor based on metal-insulator-metal coupling ring resonator with a stub

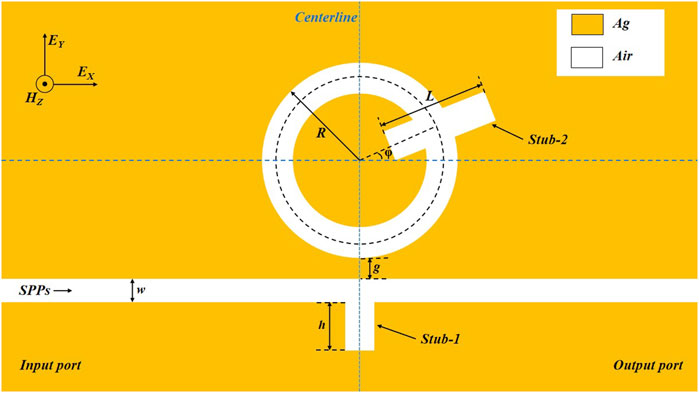
In this work, a refractive index sensor structure is proposed, which consists of the met-al-insulator-metal (MIM) waveguide coupling with ring resonator with a rectangular cavity. Its sensing characteristics are analyzed by the finite element analysis method. SPPs is an electromagnetic wave mode excited by the oscillatory coupling of free electron-photon interactions on the surface region of a metal, whose field strength is maximum at the metal-dielectric partition interface and then decays exponentially to both sides The results show that the sensing characteristics of the ring resonator can be changed by introducing a stub, which can achieve the purpose of enhancing the coupling efficiency of SPPs. The structure has two Fano peaks, and each peak can be individually regulated by changing the size of the sensing structure. Sensitivity is the key performance indicator of the system, which is the shift in resonance wavelength caused by a change in refractive index when the ambient medium is changed. The best sensitivity of this structure can reach 2,300 nm/RIU with a figure of merit (FOM) value of 60 RIU⁻¹. The proposed structure has great potential in nano-sensors.

1 Introduction

Surface plasmon polaritons (SPPs) are generated by electrons under the influence of an external electromagnetic field [1, 2]. Its essence is an electromagnetic wave mode excited by the interaction of free electrons and photons on the metal surface area [3, 4]. The field strength is the largest at the interface of the metal medium. The exponential form decays to both sides. SPPs can break through the optical diffraction limit of traditional optics, thereby realizing the adjustment and transmission of light at sub-wavelengths [5, 6].

Resonant phenomena are the tendencies of a physical system to absorb more energy from the environment when it is near the natural frequency of oscillation (called the resonant frequency) and near the natural wavelength. Unlike the symmetrical Lorentz resonance, Fano resonance is an asymmetric line-shaped scattering resonance phenomenon, which usually occurs during the coupling of the SPPs [7]. Hence, it has a high spatial electromagnetic field confinement ability, and can better identify small frequency shifts [8]. Various SPP based light devices were born, such as refractive index sensors [9–13], slow light devices [14, 15], optical switches [16, 17], biosensors [18–24], etc. Because the resonator structure is also an important factor in generating Fano resonance, rectangular resonators, annular resonators, semi-ring resonators, tie resonators, etc. All exhibit different sensing characteristics due to different structures, such as in [12], who designed a plasmon system coupled with a MIM waveguide and a ring cavity, and its sensitivity can reach 1,600 nm/RIU. It achieves coordinated multiple Fano resonances and similar electromagnetic transparency effects [25]. Chau-Yuan Fong Chou et al. designed a sensor structure of a MIM waveguide coupled with an elliptical resonator with a stub, and by embedding an air path in the MIM waveguide to increase its coupling efficiency, the performance of the sensor was greatly improved [26]. [18] proposed a sensor structure of a MIM waveguide coupled with a rectangular ring resonator with defects. By changing the position, number and other parameters of the defects, it was proved that under certain conditions, the symmetrical resonator structure, the anti-symmetric mode cannot be stimulated. The sensitivity of the improved structure can reach 1,850 nm/RIU [27].

A necessary condition for the creation of Fano resonance is the simultaneous generation of high-level multi-order sub-radiative and super-radiative modes. The subsequent overlapping coupling behavior of these modes is guaranteed. In some structures, there will be a situation where the structure is extremely symmetrical, and the dipole resonance mode and the higher-order resonance mode will be converted in-to orthogonal coupling, and the coupling cannot be overlapped at this time. In this case, it is necessary to modify the degree of symmetry of the structure, that is, to adjust the structural model. Or directly use asymmetric structures to excite bright and dark states to generate Fano resonance waveforms. This is a common approach in designing optical sensor structures, where the microstructure can be altered so that enough light can be confined to the gas sample to increase the interaction between the light and the sample. For example, the photonic crystal fiber based high sensitivity, low confinement loss gas sensor designed by [28] The insertion of circular dot matrix air holes in the core region and hexagonal dot matrix air holes in the cladding region allows more swift waves to pass through the cladding holes and interact with the detected gas, thus increasing the relative sensitivity of the gas sensor. In most of the previous articles, the coupling efficiency was increased by changing the structure and the MIM waveguide. In this paper, we try to embed a simple rectangular cavity (stub-2) into the ring structure to break the symmetry structure, and investigate whether Fano can exhibit different characteristics. In this work, we propose a MIM waveguide structure. This structure includes the MIM bus waveguide with a rectangular cavity (stub-1) and a ring resonator with stub-2. Stub-2 is used to break the symmetric structure to obtain different sensing characteristics. In-depth study of the influence of different parameters on Fano curve, sensitivity S, figure of merit (FOM) and other parameters.

2 Geometry structure and analysis methods

The structure model is built with COMSOL Multiphysics 5.4. We used the FEM to analyze the transmission performance exhibited by the SPPs. Most researchers of MIM plasmonic sensors make the height infinite because the height affects the loss of the waveguide. This phenomenon is due to the inverse relationship between the height and the real and imaginary parts of the effective refractive index. As the height increases, the real and imaginary parts decrease and remain stable for infinite height values. And only under the irradiation of the TM wave mode, the metal-dielectric interface layer will produce SPPs. For the TM mode, the electromagnetic wave propagates forward along the xoy plane, so we can build a two-dimensional model to study SPPs [29]. Above and below of the structure, we set up boundary conditions for a perfectly matched layer that absorbs the waves escaping from the structure (The size of the model is 1,320 nm $\times$ 950 nm, the perfect matching layer size is 1,320 nm $\times$ 200 nm), and set the ultra-fine meshing, which can perfectly divide the structure to ensure the simulation accuracy (the step size of the wavelength is 500 nm, the mesh size is wave-length/100, and the value of degrees of freedom is 12,356). The two-dimension structure is shown in Figure 1. This two-dimension structure is composed of a MIM bus wave-guide with stub-1 coupled to a ring resonator with stub-2 (RRS). The radius of RRS is R. The length of stub-2 is L, and the angle formed by the center of RRS is $\mathrm{\phi }$. The distance between the RRS and MIM waveguide is g. The height of stub-1 is h. When the width w of the MIM waveguide and the annular cavity with a stub-2 is small, the SPPs transported in the upper and lower metal-dielectric interfaces couple and produce two dispersion modes called odd-symmetric and even-symmetric modes. Among them, in the odd-symmetric mode, the SPPs have a large energy loss and a close transmission distance during propagation, while in the even-symmetric mode, the SPPs are transmitted over a long distance with a small energy loss. When the incident wave length is larger than w, only TM0 mode, i.e., even symmetric mode, exists in the MIM waveguide structure. In the MIM waveguide structure, in order to ensure the existence of only one transmission mode, TM0, the width of the dielectric layer is generally set to 50 nm, and its dispersion relation is defined as [30]:

$\mathbf{tanh}\left(\mathit{k}\mathit{\omega }\right)=-\frac{\mathbf{2}\mathit{k}{\mathit{\alpha }}_{\mathit{c}}}{{\mathit{k}}^{\mathbf{2}}+{\mathit{p}}^{\mathbf{2}}{\mathit{\alpha }}_{\mathit{c}}}(1)$

FIGURE 1

FIGURE 1. Two-dimension structure.

In Eq. (1), k represents the wave loss in the waveguide. $\mathit{p}={\mathit{\epsilon }}_{\mathit{i}\mathit{n}}/{\mathit{\epsilon }}_{\mathit{m}}$, ${\alpha }_c={\left[{k_0}^2*\left({\mathrm{\epsilon }}_{\text{in}}-{\mathrm{\epsilon }}_{\mathrm{m}}\right)+\mathrm{k}\right]}^{\frac{1}{2}}$, The ${\epsilon }_{in}$ and ${\epsilon }_m$ are the permittivity of the medium and the metal. The $k_0=2\pi /{\lambda }_0$ is the wave vector in free space.

The mental (orange area) and insulator material (while area) represented silver and air. The silver was chosen as a filler metal because it had a low imaginary part of the relative permittivity in the near-infrared range, resulting in low power consumption. The relative dielectric constant of silver is defined by the Debye-Drude dispersion model [31]:

$\mathit{\epsilon }\left(\mathit{\omega }\right)={\mathit{\epsilon }}_{\mathbf{\infty }}+\frac{{\mathit{\epsilon }}_{\mathit{s}}-{\mathit{\epsilon }}_{\mathbf{\infty }}}{\mathbf{1}+\mathit{i}\mathit{\tau }\mathit{\omega }}+\frac{\mathit{\sigma }}{\mathit{i}\mathit{\omega }{\mathit{\epsilon }}_{\mathbf{0}}}(2)$

In Eq. (2), the relative permittivity of infinite frequencies (${\epsilon }_0$) and the static permittivity ($\left.{\epsilon }_s\right)$ are 3.8344 and −9,530.5, respectively. $\mathrm{\tau }=7.35\times {10}^{-15}s$ is the relaxation time of silver, and $\mathrm{\sigma }=1.1486\times {10}^{7}S/m$ represent the conductivity of silver.

The performance of the sensor can be expressed by sensitivity and FOM, which defined are as follow [32, 33]:

$\mathit{S}=∆\mathit{\lambda }/∆\mathit{n}(3)$

$\mathit{F}\mathit{O}\mathit{M}=\mathit{S}/\mathit{F}\mathit{W}\mathit{H}\mathit{M}(4)$

In Eq. (3), $∆\lambda$ is the amount of drift of resonance tilt, $∆\mathrm{n}$ is the amount of change in refractive index, and in Eq. (4), FWHM is the peak width of half the peak height. (that is, a straight line parallel to the bottom of the peak is drawn through the midpoint of the peak height. distance).

Resonant wavelength expressions:

$\mathit{\lambda }=\frac{\mathbf{2}\mathit{D}\mathit{R}\mathit{e}\left({\mathit{n}}_{\mathit{e}\mathit{f}\mathit{f}}\right)}{\mathit{m}-{\mathit{\phi }}_{\mathit{r}\mathit{e}\mathit{f}/\mathit{\pi }}}(5)$

where D represents the effective side length of the resonant cavity, $Re\left(n_{eff}\right)$ denotes the real part of the effective refractive index, m represents the mode order, and ${\phi }_{ref}$ refers to the phase shift caused by the reflection of the SPPs on the metal wall.

3 Simulation results and analysis

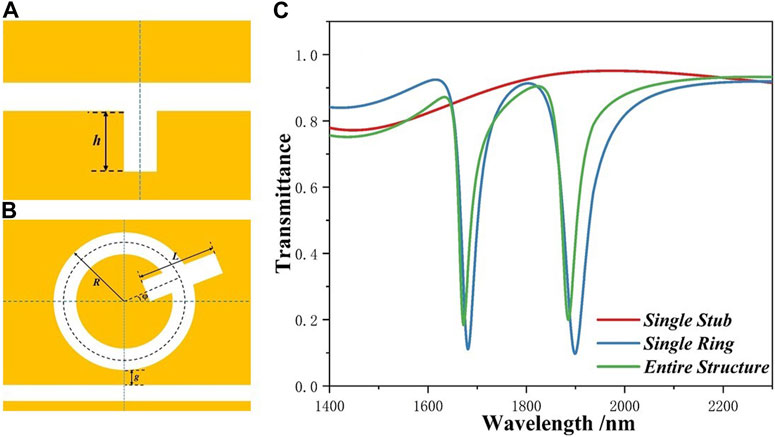
Firstly, we studied the difference between a single stub structure (red line), a single ring structure (blue line), and the entire structure (green line) to understand the cause of Fano resonance, as shown in Figure 2A–C. Its specific parameters are set as following: R = 220 nm, h = 50 nm, L = 200 nm, g = 10 nm, $\mathrm{\phi }=45°$. The transmittance (T) can express by $\mathrm{T}=P_{out}/P_{in}$, where output power Pout and input power Pin are calculated as integral values of energy-flux density [34]. The red line is a curve with a transmittance as high as 0.8, as a wider continuous state, and the blue line exhibits ultra-low transmittance (transmittance less than 0.1), which acts as a narrow discrete state. The Fano curve (green line) is produced under the combined action of the continuous state and the discrete state. The green line shows a very narrow FWHM and low transmittance. Therefore, the entire structure has better system performance.

FIGURE 2

FIGURE 2. (A) Single stub structure; (B) Single ring structure; (C) Transmittance spectrums.

In order to study how the $\mathrm{\phi }$ affects the transmission performance of the system, we set its parameters as: $90°,45°,30°,0°,-30°,-45°$, and its images are shown in Figures 3A (when changing the angles, 45° and 135° are symmetrical about the centerline, so we only take values to the right of the centerline and discuss the results). Regardless of the structure of $90°$, we find that the angle has almost no effect on the inclination position and the transmittance of FR1 ($\lambda$ = 1654 nm), but it has a greater effect on the transmittance of FR2 ($\lambda$ = 1885 nm). The performance is best under the $45°$ structure, and its transmittance value is 0.199. For the $90°$ structure, the inclination angle of FR1 almost disappears, and the inclination position of FR2 increases to 1,905 but the transmittance decreases to 0.128. This is due to the perturbation in the MIM waveguide and the resonator, resulting in an asymmetric Fano curve. At the resonance peak, the incoming electromagnetic wave will be coupled into the resonant cavity, part of it will be reflected, and part of it will be transmitted to the output port. This phenomenon can be seen in Figure 2B ($\lambda$ = 1651 nm) and c ($\lambda$ = 1904 nm). In Figure 3B, when SPPs is transmitted, a coherent enhancement phenomenon (that is, the same color) will occur between the bottom of the RRS and the MIM waveguide, which is due to the fact that the SPPs that are in the state of entering the ORR structure are in the same phase as the SPPs that are escaping, and the interference phenomenon they produce causes the electric field strengths to be superimposed, which enhances their response signals and leads to high transmittance. In Figure 3C, interference will occur between the SPP entering the RRS structure and the escaping SPP, which exhibits the phenomenon of coherent cancellation (that is, different colors), resulting in extremely low transmittance at $\lambda$ = 1904 nm.

FIGURE 3

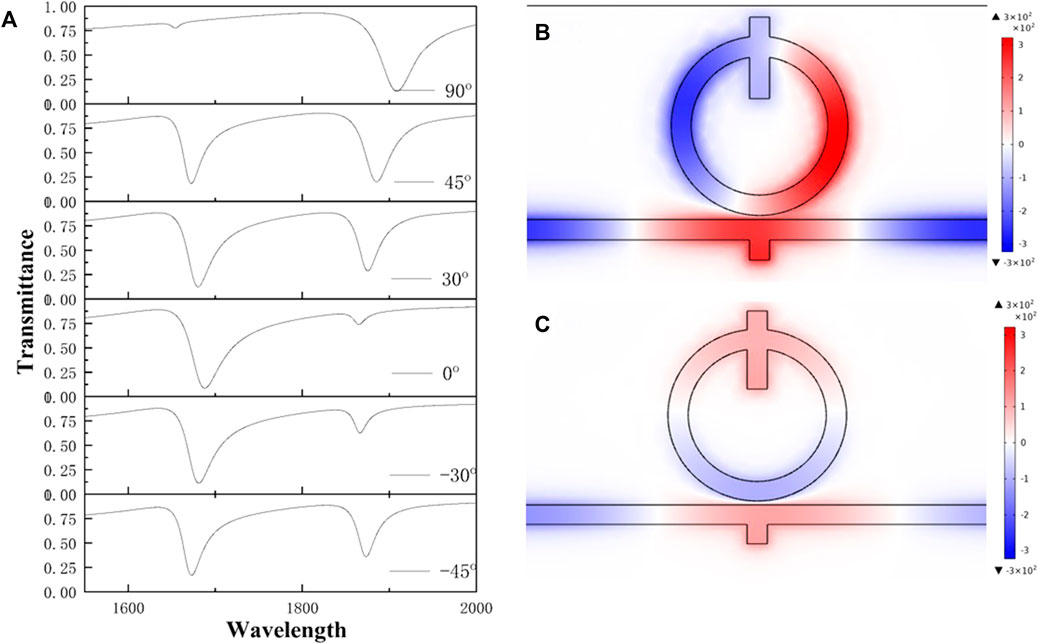
FIGURE 3. (A) Transmittance spectrums at different angles; (B) Magnetic field intensity in the FR1 ($\mathrm{\lambda }$ = 1601 nm) resonance mode in the $90°$ structure; (C) Magnetic field intensity in the FR2 ($\mathrm{\lambda }$ = 1904 nm) resonance mode in the $90°$ structure.

Next, the mode order of the structure is calculated from the magnetic field normalisation diagram. Taking FR1 as an example, when the incident wavelength is 1,601 nm, the effective edge length of the SPPs: ${\lambda }_{spps}$ = $\mathrm{\lambda }$/$Re\left(n_{eff}\right)$ = 1,143.57 and the finite edge length of the structure L = $2\pi \mathrm{R}$ $\approx$ 1,256 nm, then the mode order: m $=$ 2L/${\lambda }_{spps}$ $\approx$ 2.197 $\approx$ 2. The calculation results are the same as the simulation results. The same analysis was performed for FR2. We break the symmetry of the resonator by adding a stub-2. When the magnetic fields on both sides of the stub-2 are in phase, the symmetric modes are stimulated, when the magnetic fields on both sides of the stub-2 are in phase, the antisymmetric modes are stimulated. This means that at different angles, the coupling strength of the resonator to the bus waveguide is also different. Hence, introducing a stub and changing its parameters plays an important role in the transmission characteristics of the designed structure.

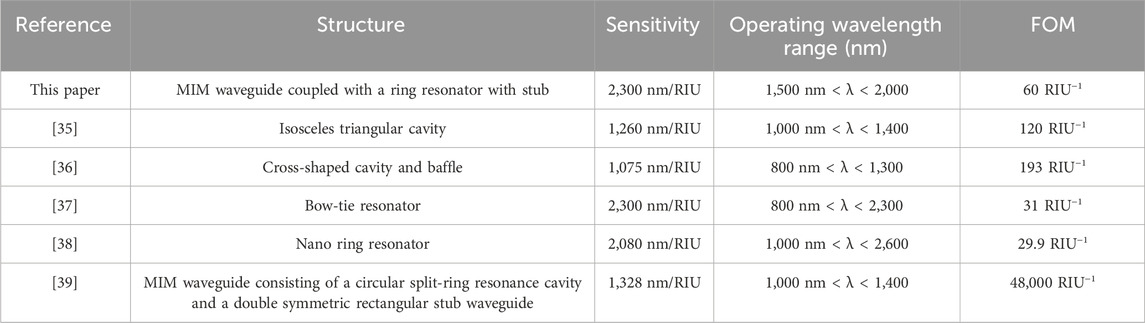
Subsequently, we studied how the R parameter value affects the system performance. The different parameter R settings are as follows: 180 nm, 190 nm, 200 nm, 210 nm, 220 nm. Its spectrums chart and sensitivity image are depicted in Figures 4A, B. With the increase of the outer radius R, the curve has a red shift phenomenon, its dip position has moved from 1,541 nm to 1,885 nm and the sensitivity has enhanced from 1,540 nm/RIU to 2,300 nm/RIU. This result also proves that the RRS acts as a narrow discrete state, and if its outer radius is changed, it will have an effect on the performance of the system. At the same time, we can also use the resonant wavelength formula to explain this phenomenon. When R (that is, the effective wavelength L) increases, the wave-length will increase, so that the position of the dip shifts to the right. When R = 220 nm, the sensitivity reaches 2,300 nm/RIU and has a FOM of 64.24 RIU⁻¹, which is better than the data in Table 1. But this does not mean that the larger R the better, we need to consider the transmittance, FOM, and the required wavelength of the laser.

FIGURE 4

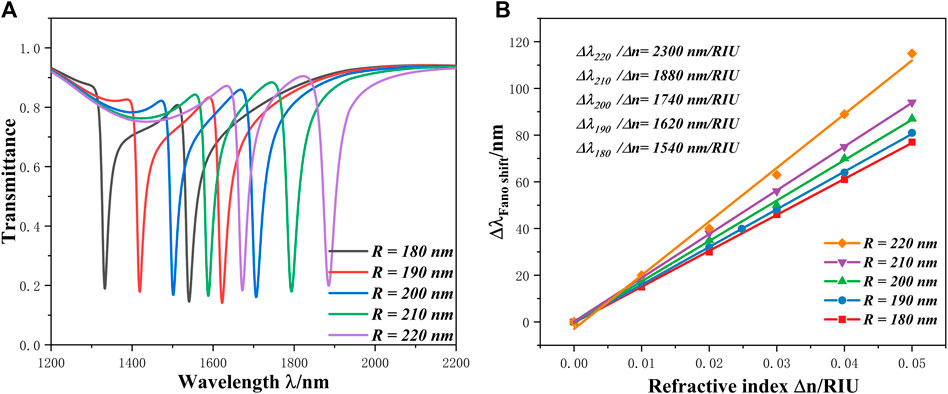
FIGURE 4. (A) Change in transmittance obtained via COMSOL simulations, as radius of the waveguide R is varied from 180 nm to 220 nm with a interval of 10 nm; (B) Sensitivity change images of R from 180 nm to 220 nm with a interval of 10 nm.

TABLE 1

TABLE 1. Comparison of performance of different structures.

Moreover, the influences of the L parameter on system performance were studied, and its parameters are set as follows: L = 150 nm, 175 nm, 200 nm, 225 nm, and 250 nm. From Figure 5A, the change of L will not affect FR1, but for FR2, the curve is red-shifted and the inclination position becomes larger. In order to explore the reasons for this phenomenon, we have drawn their normalized Hz field maps. Observed from Figures 5B, C, a node of FR1 is located on the stub, while the node of FR2 is not on the stub. The number of nodes is also used to reflect the intensity of the normalized Hz field. The more the number, the weaker the intensity. However, there is no normalized Hz field at the stub of FR1, so the influence of L change on it is weak, and whether the two ends of stub-2 are in-phase or out-of-phase will also show different system performance to a certain extent. Hence, we can achieve the separate modulation of FR2 by change L.

FIGURE 5

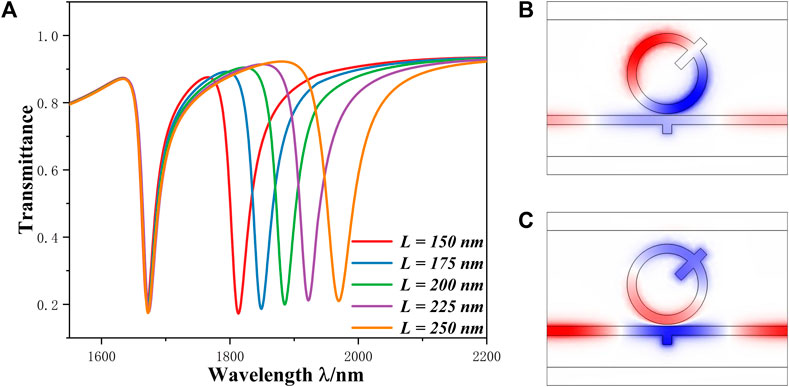
FIGURE 5. (A) Change in transmittance obtained via COMSOL simulations, as length of stub-2 (L) is varied from 150 nm to 220 nm with a interval of 25 nm; (B) Magnetic field intensity in the FR1 ($\mathrm{\lambda }$ = 1601 nm) resonance mode in the $90°$ structure; (C) Magnetic field intensity in the FR2 ($\mathrm{\lambda }$ = 1904 nm) resonance mode in the $90°$ structure.

We changed the parameters of g from 25 nm to 5 nm at intervals of 5 nm to observe the characteristics of the system. From Figure 6A, we can observe that with the change of g, the transmittance minimum of the curve decreases sharply and the curve blue shifts, the resonance wavelength drifts significantly in the range from 5 nm to 15 nm, while there is little movement in the range from 15 nm to 25 nm. The reason for this phenomenon is that as the coupling distance increases, the binding between the waveguide and the resonant cavity becomes weaker and weaker, resulting in a significant weakening of the effective refractive index part of the coupling mode of the resonant cavity, which can be neglected when the coupling distance reaches a certain value. According to Eq. 5, when the coupling distance increases to 15 nm, the wavelength drift corresponding to the wave valley will be smaller as the structural parameters are fixed and the effective refractive index becomes smaller.

FIGURE 6

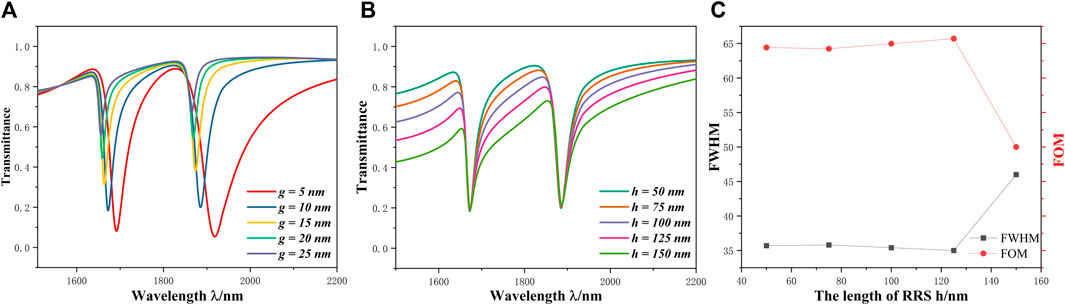
FIGURE 6. (A) Spectrum chart of diverse g from 5 nm to 25 nm with a interval of 5 nm; (B) Transmittance spectrums of different h from 50 nm to 150 nm with a interval of 25 nm; (C) FWHM image.

Subsequently, by changing the h parameter, its transmission spectrums and FWHM diagram are shown in Figures 6B, C. The change of the h parameter has almost no effect on the transmittance minimum and tilt position, but it will change the value of FWHM. When the value of S is constant, the FOM value will also change. It can be seen from Figure 6C when h = 125 nm, the FWHM is the narrowest, and the best performance at this time is: the sensitivity value of 2,300 nm/RIU and the FOM value of 65.71 RIU-1. Compared with the structural properties listed in Table 1, the structure can be excited at a smaller wavelength with higher sensitivity, but the FOM value will be slightly lower.

Finally, the principle of the plasma refractive index sensor is that the resonant tilt angle changes with the change of the refractive index, so when the structural parameters are fixed (i.e., R = 220 nm, h = 125 nm, L = 200 nm, g = 10 nm, $\mathrm{\phi }=45°$) to achieve the best performance, we also drew a graph of refractive index changes, the parameters of which varied from 1.00 to 1.05 with an interval of 0.01. Figure 7 shows that as the refractive index increases, the curve has a red shift. It is worth mentioning that many physical quantities in life are related to the refractive index, so it can be calculated in-directly through the value of the detectable refractive index. We have also calculated the accuracy of the structure sensitivity, with a sensitivity deviation of 19 nm/RIU per 1 nm, provided that the nano-process and etching techniques are satisfied.

FIGURE 7

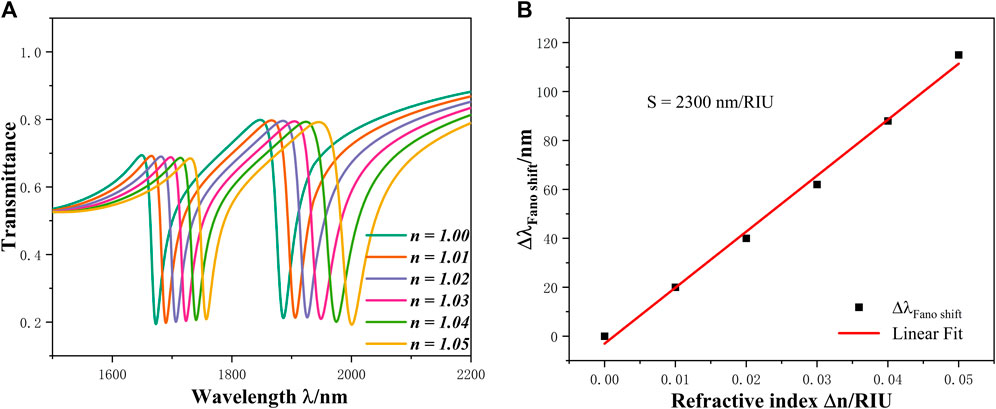
FIGURE 7. (A) Spectrum chart of the refractive index from 1.00 to 1.05; (B) Linear fitting of the sensitivity.

4 Application

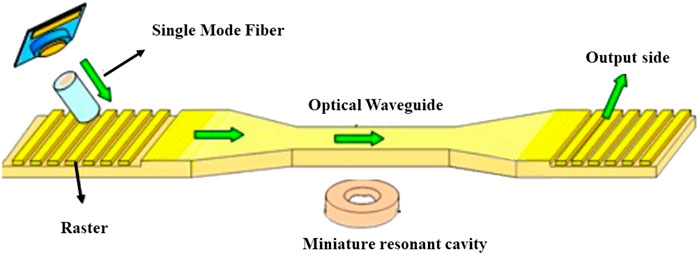
The designed sensor structure is shown in Figure 8 and is mainly composed of a laser, a conical waveguide, an optical waveguide, a high-Q optical microcavity and an array of metal nanoparticles. The optical field is localed in a small cavity mode volume, high Q resonant cavity and transmitted in WGM mode, resulting in a strong abrupt field around the surface of the high Q microcavity, the conical waveguide region and the interaction with the specimen, and the excitation of metal nanoparticles on the surface of the microcavity generating Fano resonance peaks with extremely high sensitivity to the external environment.

FIGURE 8

FIGURE 8. Schematic diagram of the sensing structure.

When the air medium in the resonant cavity is replaced with an ethanol solution it can be used as a temperature sensor, the essence of which is that when the temperature of the surrounding environment changes, the refractive index of the solution in the structure changes as well. Ethanol has a melting point of −114.3$°\mathrm{C}$ and a boiling point of 78$°\mathrm{C}$, so the maximum detection range of the structure is between −114.3$°\mathrm{C}$ and 78$°\mathrm{C}$ when it is chosen as the filling solution. The equation for its refractive index as a function of temperature is:

$\mathit{n}=\mathbf{1.36048}-\mathbf{3.94}\times \mathbf{1}{\mathbf{0}}^{-\mathbf{4}}\left(\mathit{T}-{\mathit{T}}_{\mathbf{0}}\right)(6)$

T in the formula indicates the temperature to be measured, ${\mathrm{T}}_0$ indicates the ambient temperature, which is usually taken as 20. The expression for temperature sensitivity is:

${\mathit{T}}_{\mathit{S}\mathit{E}\mathit{M}}=\frac{∆\mathit{\lambda }}{∆\mathit{T}}(7)$

The T in the equation represents the amount of change in the environment. Taking into account the limits of the detection range of the structure, we set the temperature to be measured to change from −40$°\mathrm{C}$ to 60$°\mathrm{C}$ with an interval of 20$°\mathrm{C}$, and the results obtained are shown in Figure 9A. The images show that as the temperature increases, the resonance curve blueshifts, the trough moves from 2,566 nm to 2,456 nm and the transmittance increases slightly from 0.0344 to 0.0411, the change in transmittance directly affects the performance of the sensor, a lower transmittance means that the coupling strength is greater, the sensor is more sensitive to the change in refractive index, and small changes in the refractive index can be detected, thus improving the sensor sensitivity; at the same time, lower transmittance also means less light reflection loss, which helps to improve the stability of the sensor. Temperature and refractive index show a negative correlation, a phenomenon that is also consistent with Eq. 6. Substituting the values into Eq. 7 can calculate the temperature sensitivity as: 1.5 and its linear fitting curve is shown in Figure 9B.

FIGURE 9

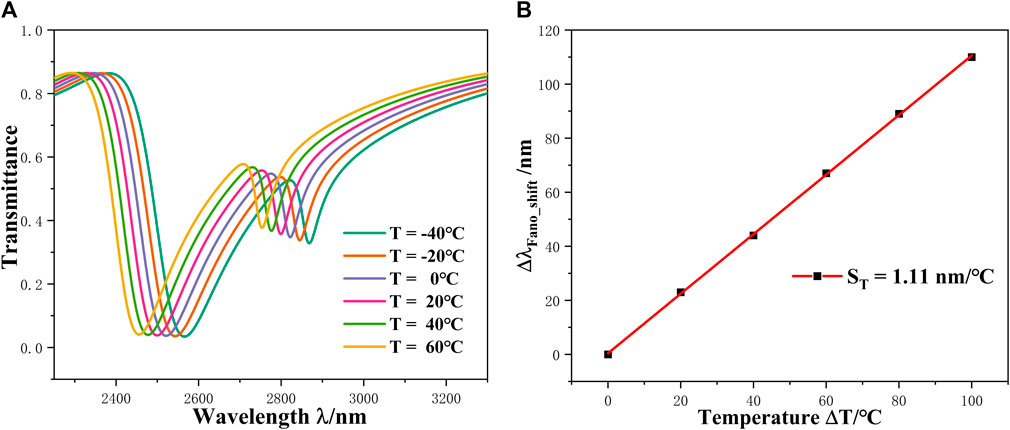
FIGURE 9. (A) Graphs of spectral changes under temperature variations; (B) Temperature sensitivity linear fit.

5 Conclusion

In this study, we present a refractive index nano-sensor based on a MIM waveguide consisting of a MIM bus waveguide with stub-1 and a ring resonator with stub-2. This structure realizes the modulation of the double Fano resonance. This structure realizes the modulation of the double Fano resonance. We analyzed the sensing characteristics using finite element analysis and found that the parameters of Stub-1 mainly affect the values of FWHM and FOM, while the parameters of the ring resonator mainly affect the sensitivity S and wavelength range. Changing the value of L parameter only affects the transmission performance of FR2, so we can realize independent modulation of FR2 by changing the value of L without any effect on the performance of FR1. When R = 220 nm, h = 125 nm, L = 200 nm, g = 10 nm, and $\mathrm{\phi }=45°$, the sensitivity performance of the system can reach 2,300 nm/RIU with a FOM value of 60 RIU⁻¹. Our refractive index sensor provides a better choice for nano-sensors.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SY: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Validation, Writing–review and editing. YC: Conceptualization, Formal Analysis, Visualization, Writing–original draft. JW: Data curation, Writing–original draft. SC: Data curation, Writing–original draft. GL: Validation, Writing–review and editing. BH: Methodology, Validation, Supervision, Writing–review and editing. TW: Software, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work was supported in part by the National Natural Science Foundation of China under Grant Nos 62374148, 62003315, and 61975189, in part by the Zhejiang Provincial Natural Science Foundation of China under Grant No. LD21F050001, the Key Research Project by Department of Water Resources of Zhejiang Province under Grant No. RA2101, the Key Research and Development Project of Zhejiang Province under Grant No. 2021C03019, the Scientific research foundation of Zhejiang University of Water Resources and Electric Power under Grant No. xky2022032, and the Funds for Special Projects of the Central Government in Guidance of Local Science and Technology Development under Grant No. YDZJSX20231A031.

Acknowledgments

The authors are thankful to other colleagues in their laboratory for their understanding and help. They also appreciate the affiliated institution to provide research platform and the sponsor to provide financial support for them.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zheng Z, Luo Y, Yang H, Yi Z, Zhang JG, Song Q, et al. Thermal tuning of terahertzmet-amaterial properties based on phase change material vanadium dioxide. Phys Chem Chem Phys (2022) 2022:8846–53. doi:10.1039/D2CP01070D

CrossRef Full Text | Google Scholar

2. Meng C, Lu F, Zhang W, Wang J, Mao D, Gao F, et al. Selective remote-excitation of gap mode in metallic nanowire-nanoparticle system using chiral surface plasmon polaritons. IEEE Ouantum Electron (2020) 56:1–6. doi:10.1109/jqe.2020.3026491

CrossRef Full Text | Google Scholar

3. Law M, Sirbuly DJ, Johnson JC, Goldberger J, Saykally RJ, Yang P. Nanoribbon waveguides for subwavelength photonics integration. Science (2004) 305:1269–73. doi:10.1126/science.1100999

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kresic l., Kruljac M, Ban T, Aumiler D. Electromagnetically induced transparency with a single frequency comb mode probe. J.Opt Soc.Am B (2019) 36:1758–64. doi:10.1364/josab.36.001758

CrossRef Full Text | Google Scholar

5. Li W, Su Y, Zhai X, Shang X, ia S, Wang L. High-multiple Fano resonances sensor in single dark mode metamaterial waveguide structure. IEEE Photon Technol. Lett. (2018) 30:2068–71. doi:10.1109/lpt.2018.2877192

CrossRef Full Text | Google Scholar

6. Khani S, Danaie M, Rezaei P. Double and triple-wavelength plasmonic demultiplexers based on improved circular nanodiskresonators. Opt Eng (2018) 57:1. doi:10.1117/1.oe.57.10.107102

CrossRef Full Text | Google Scholar

7. Chen J, Li Z, Li J, Gong Q. Compact and high-resolution plasmonic wavelength demultiplexers based on Fano interference. Opt Express (2011) 19:9976–85. doi:10.1364/oe.19.009976

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kong DQ, Isubokawa M. Evaluation of slot-to-slot coupling between dielectric slot waveguides and metal-insulator-metal slot waveguides. Opt Express (2015) 23:19082–91. doi:10.1364/oe.23.019082

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nishiima Y, Rosa L, Juodkazis S. Surface plasmon resonances in periodic and random patterns of gold nano-disks forbroadband light harvesting. Opt Express (2012) 20:11466–77. doi:10.1364/oe.20.011466

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Horvath C, Bachman D, Wu M, Perron D, Van V. Polymer hybrid plasmonic waveguides and microring resonators. IEEE Photon Technol. Lett. (2011) 23:1267–9. doi:10.1109/lpt.2011.2159784

CrossRef Full Text | Google Scholar

11. Chen Y, Xu Y, Cao J. Fano resonance sensing characteristics of MM waveguide coupled square convex ring resonator withmetallic baffle. Results Phs (2019) 14:102420. doi:10.1016/j.rinp.2019.102420

CrossRef Full Text | Google Scholar

12. Wang S, Li Y, Xu 0., Li S. A MM filter based on a side-coupled crossbeam square-ring resonator. Plnsmonics (2016) 11:1291–6. doi:10.1007/s11468-015-0174-1

CrossRef Full Text | Google Scholar

13. Wu XL, Zheng Y, Luo Y, Zhang JG, Yi Z, Wu XW, et al. A four-band and polarizationindependent BDS-based tunable absorber with high refractive index sensitivity. Phys Chem Chem Phys (2021) 23:26864–73. doi:10.1039/d1cp04568g

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zhou C, Huo Y, Guo Y, Niu Q. Tunable multiple Fano resonances and stable plasmonic band-stop filter based on a metal-insulator-metal waveguide. Plasmonics (2021) 3:1735–43. doi:10.1007/s11468-021-01437-2

CrossRef Full Text | Google Scholar

15. Zhang Y, Cui M. Refractive index sensor based on the symmetric MM waveguide structure. J Electron Mater (2019) 48:1005–10. doi:10.1007/s11664-018-6823-3

CrossRef Full Text | Google Scholar

16. Hwang Y, Kim JE, Park HY. Frequency selective metal-insulator-metal splitters for surface plasmons. Opt Commun (2011) 284:4778–81. doi:10.1016/j.optcom.2011.05.069

CrossRef Full Text | Google Scholar

17. Ozbay E. Plasmonics: merging photonics and electronics at nanoscale dimensions. Science (2006) 311:189–93. doi:10.1126/science.1114849

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yi X, Tian J, Yang R. Tunable Fano resonance in plasmonic MDM waveguide with a square type split-ring resonator. Optik (2018) 171:139–48. doi:10.1016/j.ijleo.2018.06.027

CrossRef Full Text | Google Scholar

19. Ren X, Ren K, Cai Y. Tunable compact nanosensor based on Fano resonance in a plasmonic waveguide system. Appl Opt (2017) 56:H1–H9. doi:10.1364/ao.56.0000h1

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hu F, Chen F, Zhang H, Sun L, Yu C. Sensor based on multiple Fano resonances in MIM waveguide resonator system with silver nanorod-defect. Optik (2021) 229:166237. doi:10.1016/j.ijleo.2020.166237

CrossRef Full Text | Google Scholar

21. Sonntag MD, Klingsporn JM, Zrimsek AB, Sharma B, Ruvuna LK, Van Duyne RP. Molecular plasmonics for nanoscale spectroscopy. Chem Soc Rev (2014) 43:1230–47. doi:10.1039/c3cs60187k

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xie Y, Huang Y, Xu W, Zhao W, He C. A plasmonic temperature-sensing structure based on dual laterally side-coupled hexagonal cavities. Sensors (2016) 16:706. doi:10.3390/s16050706

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yang X, Hua E, Su H, Guo J, Yan S. A nanostructure with defect based on Fano resonance for application on refractive index and temperature sensing. Sensors (2020) 20:4125. doi:10.3390/s20154125

PubMed Abstract | CrossRef Full Text | Google Scholar

24. He Y-J, Hung W-C, Lai Z-P. Using finite element and eigenmode expansion methods to investigate the periodic and spectral characteristic of superstructure fiber bragg gratings. Sensors (2016) 16:192. doi:10.3390/s16020192

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ren W, Wang F, Ren G. Mode coupling analysis for a mode selective coupler using the supermode theory. Photonics (2022) 9:63. doi:10.3390/photonics9020063

CrossRef Full Text | Google Scholar

26. Chau YFC, Chou Chao CT, Jumat SZBH, Kooh MRR, Thotagamuge R, Lim CM. Improved refractive index-sensing performance of multimode Fano-resonance-based metal-insulator-metal nanostructures. Nanomaterials (2021) 11:2097. doi:10.3390/nano11082097

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Li S, Wang Y, Jiao R, Duan G, Yu L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt Express (2017) 25:3525–33. doi:10.1364/oe.25.003525

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Mishra GP, Kumar D, Chaudhary VS, Kumar S. Design and sensitivity improvement of microstructured-core photonic crystal fiber based sensor for methane and hydrogen fluoride detection. IEEE Sensors J (2022) 1:1265–72. doi:10.1109/jsen.2021.3131694

CrossRef Full Text | Google Scholar

29. Qiao L, Zhang G, Wang Z, Fan G, Yan Y. Study on the Fano resonance of coupling M-type cavity based on surface plasmon polaritons. Opt Commun (2019) 433:144–9. doi:10.1016/j.optcom.2018.09.055

CrossRef Full Text | Google Scholar

30. Zhu J, Li N. MIM waveguide structure consisting of a semicircu-lar resonant cavity coupled with a key-shaped resonant cavity. Opt Express (2020) 28:19978–87. doi:10.1364/oe.395696

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Xu W, Chen L, Zhu F, Liu J, Sui C, Hong Z. Double Fano resonances in S-shaped plasmonic metasurfaces in terahertz region. Front Phys (2020) 8:256. doi:10.3389/fphy.2020.00256

CrossRef Full Text | Google Scholar

32. Diao J, Han B, Yin J, Li X, Lang T, Hong Z. Analogue of electromagnetically induced transparency in an S-shaped all-dielectric metasurface. IEEE Photon J (2019) 11:1–10. doi:10.1109/jphot.2019.2920433

CrossRef Full Text | Google Scholar

33. Xie Y, Huang Y, Zhao W, Xu W, He C. A novel plasmonic sensor based on metal–insulator–metal waveguide with side-coupled hexagonal cavity. IEEE Photon J (2015) 7:1–12. doi:10.1109/jphot.2015.2419635

CrossRef Full Text | Google Scholar

34. Zhang Y, Kuang Y, Zhang Z, Tang Y, Han J, Wang R, et al. High-sensitivity refractive index sensors based on Fano resonance in the plasmonic system of splitting ring cavity-coupled MIM waveguide with tooth cavity. Appl Phys.A (2019) 125:13. doi:10.1007/s00339-018-2283-0

CrossRef Full Text | Google Scholar

35. Bazgir M, Jalalpour M, Zarrabi FB, Arezoomand AS. Design of an optical switch and sensor based on a MIM coupled waveguide using a DNA composite. J Electron Mater (2020) 49:2173–8. doi:10.1007/s11664-019-07902-3

CrossRef Full Text | Google Scholar

36. Qi YP, Wang LY, Zhang Y, Zhang T, Zhang BH, Deng XY, et al. Multiple Fano resonances in metal-insulator-metal waveguide with umbrella resonator coupled with metal baffle for refractive index sensing. Chin Phys B (2020) 29:067303. doi:10.1088/1674-1056/ab888c

CrossRef Full Text | Google Scholar

37. Butt A, Khonina SN, Kazanskiy NL. Highly sensitive refractive index sensor based on plasmonic bow tie configuration. Photonic Sens (2020) 10:223–32. doi:10.1007/s13320-020-0588-z

CrossRef Full Text | Google Scholar

38. Nejat M, Nozhat N. Multi-band MIM refractive index biosensor based on Ag-air grating with equivalent circuit and T-matrix methods in near-infrared region. Sci Rep (2020) 10:6357–12. doi:10.1038/s41598-020-63459-w

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Xie C, Yang H, Fang Z, Zhao M. Refractive index sensing based on multiple Fano resonances in a split-ring cavity-coupled MIM waveguide. Photonics (2021) 8:472. doi:10.3390/photonics8110472

CrossRef Full Text | Google Scholar