Microscopic theory of current-induced skyrmion transport and its application in disordered spin textures

Introduction: Magnetic skyrmions hold great promise for realizing compact and stable memory devices that can be manipulated at very low energy costs via electronic current densities.

Methods: In this work, we extend a recently introduced method to describe classical skyrmion textures coupled to dynamical itinerant electrons. In this scheme, the electron dynamics is described via nonequilibrium Green’s function (NEGF) within the generalized Kadanoff–Baym ansatz, and the classical spins are treated via the Landau–Lifshitz–Gilbert equation. Here, the framework is extended to open systems by the introduction of a non-interacting approximation to the collision integral of NEGFs. This, in turn, allows us to perform computations of the real-time response of skyrmions to electronic currents in large quantum systems coupled to electronic reservoirs, which exhibit linear scaling in the number of time steps. We use this approach to investigate how electronic spin currents and dilute spin disorder affect skyrmion transport and the skyrmion Hall drift.

Results: Our results show that the skyrmion dynamics is sensitive to a specific form of the spin disorder, such that different disorder configurations lead to qualitatively different skyrmion trajectories for the same applied bias.

Discussion: This sensitivity arises from the local spin dynamics around the magnetic impurities, a feature that is expected not to be well-captured by phenomenological or spin-only descriptions. At the same time, our findings illustrate the potential of engineering microscopic impurity patterns to steer skyrmion trajectories.

1 Introduction

Technological progress often stems from the discovery and exploitation of new materials and forms of energy. While self-evident, this paradigm has recently undergone criticism and revision due to mounting awareness of the negative impact that indiscriminate technological development has on the environment and climate. This is also true for electronics: it has become clear that the production, use, and casual disposal of electronic devices can lead to a sharp increase in energy consumption, waste, and greenhouse effects [1]. Thus, together with a steady increase in the use of high-performance technology, there is a need for novel electronics with reduced dimensionality, large integration, and low energy consumption [2].

Pursuing these two directives on equal footing is the core aim of spintronics [3]: magnetic excitations allow for less energy-intensive ways of storing and processing digital information, and thus devices based on magnetic materials and phenomena offer an attractive alternative to conventional electronics. For a long time, fundamental and applied research in magnetism was largely concerned with macroscopic samples, and primarily with simple magnetic orders, such as ferro- and antiferromagnets. However, more recently, it has been possible to experimentally realize magnetic systems with nontrivial magnetic textures, creating unprecedented possibilities for spintronic applications [4, 5].

A notable example in this respect is provided by magnetic skyrmions [6]. These are topologically nontrivial spin textures stabilized by a competition of exchange, Dzyaloshinskii–Moriya interactions (DMIs), and magnetic anisotropies [7]. With their compact size, topological protection, and non-intensive energy requirements for manipulation, skyrmions are of great potential interest to realize racetrack memories [8–10] and quantum computation devices [11–14]. However, this requires efficient ways of writing, deleting, and manipulating skyrmions on short time scales and with high spatial precision, via electronic spin currents.

Here, we describe a scheme to perform large-scale simulations of the intertwined dynamics of interacting and open spin–electron systems (Figure 1). Our method is an extension of the approach introduced in [15, 16] and amounts to propagating the equation of motion for the electronic spin-dependent single-particle density matrix, together with the Landau–Lifshitz–Gilbert (LLG) equation for the classical spins. The former equation can be derived from the general theory of nonequilibrium Green’s functions using the so-called generalized Kadanoff–Baym ansatz (GKBA) [17–30], and therefore allows to systematically introduce the effects of electron–electron interactions via diagrammatic many-body perturbation theory. In what follows, we apply this scheme to study current-induced skyrmion motion, fully accounting for the dynamics of the itinerant electrons resulting from an applied bias. In agreement with phenomenological theories [31], we find that for a clean sample, skyrmions are pinned below a critical spin current density I₀, after which the velocity is found to be a linear function of the current I − I₀. The situation is found to be qualitatively different in the presence of (dilute) spin disorder, where the skyrmion motion is strongly dependent on the location, size, and form of the disorder configuration (for previous work on the role of disorder, see, e.g., [32]). This provides a clear indication that treatments based on the standard Thiele or LLG equation are not always adequate and that the dynamics of the electrons must be explicitly taken into account.

FIGURE 1

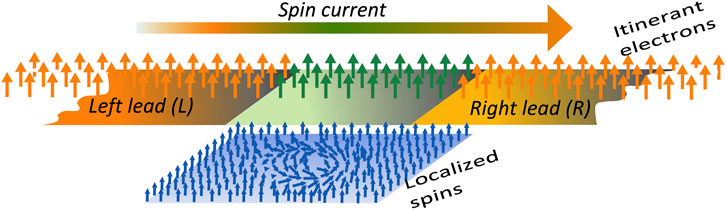
FIGURE 1. Sketch of the composite spin–electron system. A central region consisting of itinerant electrons interacting with localized spins is in contact with two-dimensional leads. By applying a spin-dependent bias in the leads, an electronic current is generated in the central system, giving rise to skyrmion motion.

This paper is structured as follows: Section 2 briefly reviews previous approaches to coupled spin–electron dynamics, and Section 3 introduces the system and Hamiltonian to be considered and discusses the coupling between the itinerant electrons and external reservoirs. The spin and electron equations of motion are presented in Section 4 and Section 5, and Section 6 introduces an approximate wide-band limit (AWBL) as a numerically efficient way to propagate the equations of motion in the presence of large central regions connected to external reservoirs. Section 7 presents some observables used to interrogate the skyrmion content of the spin configuration. In Section 8, we use the AWBL to investigate the skyrmion motion induced by current densities in the itinerant electron system, and in Section 9, we consider skyrmion motion in the presence of magnetic disorder. Finally, in Section 10, we conclude with a discussion of experimental signatures and possible material platforms for which our results are of relevance.

2 Review of previous approaches

Magnetic skyrmions are made up of localized magnetic moments, typically arising from a large Hund’s coupling J favoring a high-spin state of the d- or f-orbitals of the magnetic ion. Therefore, from a microscopic perspective, it is natural to expect that a quantum description of the magnetic structure should be necessary¹. However, since magnetic moments in typical skyrmion materials (consisting of transition metal ions such as Fe, Co, and Mn) are of large magnitude, spin fluctuations are suppressed and a classical approximation usually works well.

In most cases, skyrmion textures are large compared to the underlying lattice constant. More precisely, the ratio of the electronic hopping t to the strength α of the spin–orbit interaction is typically of the order α/t ∼ 0.01–0.1, resulting in a spin spiral wavelength λ ∼ 10–100 nm [9, 34]. However, in certain cases, such as at an interface between metallic thin films and a material with large spin–orbit coupling, the effective Dzyaloshinskii–Moriya interaction can be significantly enhanced and lead to skyrmions with radii on the order of a few nanometers [35]. For skyrmions of large sizes, it is common to take a continuum limit of the microscopic spin Hamiltonian, resulting in a magnetic energy functional that can be minimized with micromagnetic methods. As a result, calculations for lattice skyrmions of realistic size (up to approximately 10 nm in radius in two-dimensional systems) are usually based on an atomistic description of classical spins, with external fields such as electromagnetic radiation or electronic current densities included as non-dynamical variables. For example, the motion of skyrmions in response to an external current density can be described via an effective equation for the skyrmion’s center of mass, the so-called Thiele equation [36], assuming that the form of the skyrmion is rigid. Based on the Thiele equation, electrons enter only via the external current density, taken from a static solution of the macroscopic Maxwell equations. A more detailed description often considered in the literature is to obtain the individual spin dynamics from the LLG equation [31] and to include the effects of electrons and external fields via a generalized force [37, 38]. The LLG equation, with itinerant electrons included implicitly, has provided important insights into skyrmion behavior in a large range of materials, and its use is widespread. Furthermore, other approaches have been introduced, besides the LLG equation, which go beyond the semiclassical Thiele’s description to study the dynamics of skyrmions [39–42].

Indeed, there are many cases where neglecting the explicit dynamics of the electrons severely hinders a more detailed understanding, and possibly even the development of novel physical ideas and technological opportunities in skyrmionics.

The importance of explicitly accounting for itinerant electrons in the description of skyrmion dynamics was originally pointed out in [15], where a small two-dimensional spin texture containing a single skyrmion was made to interact with a nanowire carrying a time-dependent current. Since then, the significance of including electronic degrees of freedom in the description of skyrmion dynamics (as well as more general spin textures) has been addressed in several contexts [16, 37, 38, 43–45]. For example, it was recently demonstrated [16] that explicitly accounting for the dynamics of itinerant electrons can be of crucial importance in capturing the interaction between skyrmions and laser light. In particular, such a treatment shows that photo-generation of skyrmions resulting from laser excitation can occur on much shorter time scales than previously thought.

Similarly, electrons and currents are expected to play a key role in skyrmion transport phenomena, both for clean samples and in the presence of spin disorder. However, investigating such dynamics requires overcoming an additional hurdle on the methodological side, i.e., it is necessary to simultaneously treat large system sizes and extended time scales within an open quantum system framework. In the remainder of this paper, we show how such a framework can be constructed.

3 System and Hamiltonian

We consider a system at zero temperature and of finite size, referred to as the central region C, in contact with two macroscopic reservoirs (see Figure 2). The central region consists of a finite square lattice with N = N_x × N_y sites, and at each lattice site, there is one electronic orbital and one localized spin. The electronic orbitals are populated by spinful itinerant electrons that can tunnel in and out of the reservoirs, also referred to as leads. The leads are coupled only to the electronic degrees of freedom, i.e., there are no localized spins in the reservoirs. Inside the leads, the electrons are assumed to be non-interacting and spin-polarized, with the density set by the chemical potential. Furthermore, in the central region, the electrons are assumed to be non-interacting, although electron–electron interactions are straightforward (but numerically demanding) to include [15]. However, the itinerant electrons of the central region interact with the localized magnetic moments via a local exchange coupling, and the magnetic moments in turn interact among themselves via various magnetic interactions. The Hamiltonian of the composite system is

$H\left(t\right)=H_C\left(t\right)+H_R\left(t\right)+H_{CR},(1)$

where a possible time dependence is explicitly indicated both for the central region and for the reservoirs. This is necessary to initiate the dynamics of the system. We now discuss each contribution to H separately.

FIGURE 2

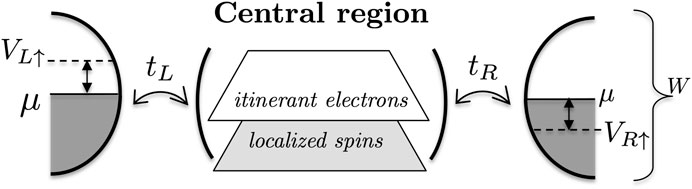
FIGURE 2. Schematic illustration of the transport setup and the relevant parameters of the system–reservoir Hamiltonian. The leads have a common bandwidth W and chemical potential μ and are connected to a central region of 20 × 40 sites comprising both electrons and localized spins via a nearest-neighbor tunneling amplitude t_L/R at the left/right edge. To initiate the skyrmion dynamics, a spin-dependent bias (V_L↑ = −V_R↑ and V_L↓ = V_L↓ = 0) is applied to the leads.

3.1 The central region

The Hamiltonian of the central region is H_C(t) = H_e + H_s + H_s−e, where H_e describes the itinerant electrons, H_s is the localized spins, and H_s−e is the spin–electron coupling. These terms are respectively given by

$H_e={\displaystyle \sum _{⟨ij⟩\sigma {\sigma }^{\prime }}}{c}_{i\sigma }^{†}{\left(-t_{ij}\mathbf{1}+{\mathit{\alpha }}_{ij}\cdot \mathit{\tau }\right)}_{\sigma {\sigma }^{\prime }}{c}_{j{\sigma }^{\prime }}-B{\displaystyle \sum _i}{\widehat{s}}_i^z,(2)$

$H_s=-\frac{1}{2}{\displaystyle \sum _{⟨ij⟩}}{J}_{ij}{\widehat{\mathit{S}}}_i\cdot {\widehat{\mathit{S}}}_j-\frac{1}{2}{\displaystyle \sum _{⟨ij⟩}}{\mathit{D}}_{ij}\cdot \left({\widehat{\mathit{S}}}_i\times {\widehat{\mathit{S}}}_j\right)-B{\displaystyle \sum _i}{\widehat{S}}_i^z-\frac{K}{2}{\displaystyle \sum _i}{\left({\widehat{S}}_i^z\right)}^2,(3)$

$H_{s-e}=-g{\displaystyle \sum _i}{\widehat{\mathit{S}}}_i\cdot {\widehat{\mathit{s}}}_i.(4)$

Here, $c_{i\sigma }^{†}$ creates an itinerant electron at site i with spin projection σ, the hopping amplitude between nearest-neighbor sites i and j (denoted by $⟨ij⟩$) is given by t_ij, α_ij accounts for spin–orbit interactions, and $\mathbf{B}=B\widehat{\mathbf{z}}$ is an external magnetic field along the z-axis. The electronic spin operator at site i is defined by ${\widehat{\mathbf{s}}}_i={\sum }_{\sigma {\sigma }^{\prime }}{c}_{i\sigma }^{†}{\mathit{\tau }}_{\sigma {\sigma }^{\prime }}{c}_{i{\sigma }^{\prime }}$, where τ denotes the vector of Pauli matrices. The parameters J_ij = J_ji and D_ij = −D_ji provide the exchange interaction and DMI [46, 47] between spins ${\widehat{\mathbf{S}}}_i$ and ${\widehat{\mathbf{S}}}_j$, and K quantifies an easy-axis single-ion anisotropy. The itinerant electrons interact with localized spins via a local exchange coupling of strength g. We note that in magnetic thin films, skyrmions are often stabilized by the easy-axis anisotropy [35], and an external magnetic field is not strictly necessary. However, including a Zeeman term in the Hamiltonian provides an additional physical mean to control the equilibrium magnetic state, and in particular to tune the system between a ferromagnetic state and the skyrmion crystal phase.

Depending on the symmetries of the system, the DMI vector D_ij can be of different forms. Assuming that the overall magnitude of the interaction is fixed at |D_ij| = D, the spatial dependence typically takes one of the following two forms:

$\begin{array}{ll}\hfill {\mathit{D}}_{ij}& =D{\mathit{d}}_{ij}\left(\text{Bloch}\right)\hfill \\ \hfill {\mathit{D}}_{ij}& =D{\mathit{d}}_{ij}\times \widehat{\mathit{z}}.\left(\text{Néel}\right).\hfill \end{array}(5)$

Here, d_ij is the vector between lattice sites i and j, and $\widehat{\mathit{z}}$ is a normal vector to the two-dimensional lattice plane. The Néel-type DMI gives rise to Néel-type (hedgehog) skyrmions and is typically generated by the inversion symmetry breaking induced at a surface. Therefore, the Néel-type DMI is most common in single-layer or few-layer substrates since thicker materials tend to restore the bulk inversion symmetry. On the other hand, the Bloch-type DMI that commonly arises in systems with non-centrosymmetric crystal structures gives rise to Bloch-type (spiral) skyrmions. Even so, many bulk materials that support Bloch-type skyrmions can be fabricated as thin-film samples, while still hosting skyrmions [34].

In this work, we limit ourselves to a Bloch-type DMI, while considering for computational simplicity a monolayer geometry for the localized spins. Similarly, we focus on a Rashba-type spin–orbit coupling of the form

${\mathit{\alpha }}_{ij}=i{\alpha }_R{\mathit{d}}_{ij}\times \widehat{\mathit{z}},(6)$

where the parameter α_R sets the overall magnitude of the interaction. This reflects the fact that the forms of the spin–orbit coupling and Dzyaloshinskii–Moriya interaction are intimately related, such that to the lowest order in a strong coupling expansion D_ij ∝α_ij [47]. We note that the Hamiltonian H_C can be generalized further by including both a local on-site potential v_i(t) for the itinerant electrons as well as a complex hopping $t_{ij}{e}^{i{\varphi }_{ij}}$, the phase of which encodes the interaction with an external electromagnetic field [16]. It is similarly straightforward to include a direct coupling between the localized spins and external electromagnetic fields, e.g., via the inverse Faraday effect. For the present work, such terms are not of relevance and are therefore omitted.

3.2 The reservoirs and their coupling to the central region

The leads are taken to be two-dimensional and semi-infinite (see Figure 1) and are described by the Hamiltonian

$H_R\left(t\right)={\displaystyle \sum _{\alpha \sigma }}{H}_{\alpha ,\sigma }^R\left(t\right),(7)$

$H_{\alpha \sigma }^R\left(t\right)=t_{R\alpha }{\displaystyle \sum _{⟨ij⟩\sigma }}{a}_{i\sigma ,\alpha }^{†}{a}_{j\sigma ,\alpha }+{\displaystyle \sum _{i\sigma }}{v}_{\sigma }^{\alpha }\left(t\right)a_{i\sigma ,\alpha }^{†}{a}_{i\sigma ,\alpha }.(8)$

Here, α ∈ {L, R} denotes the left (L) and right (R) lead, σ labels the spin projection, and the parameter t_Rα is the hopping amplitude within lead α. The hopping amplitude is related to the nominal bandwidth by W_α = 4t_Rα, and $v_{\sigma }^{\alpha }(t)$ is a time-dependent bias measured from the chemical potential μ. The leads interact with the central region via the Hamiltonian $H_{CR}={\sum }_{\alpha \sigma }{H}_{\alpha ,\sigma }^{CR}$, where

$H_{L\sigma }^{CR}=t_L{\displaystyle \sum _{i_y=1}^{N_y}}\left[a_{\left(1,i_y\right)\sigma ,L}^{†}{c}_{\left(1,i_y\right)\sigma }+H.c.\right],(9)$

$H_{R\sigma }^{CR}=t_R{\displaystyle \sum _{i_y=1}^{N_y}}\left[a_{\left(1,i_y\right)\sigma ,L}^{†}{c}_{\left(N_x,i_y\right)\sigma }+H.c.\right].(10)$

Here, i_y denotes the y-component of the site index i and runs over the transverse dimension N_y of the system. For the left (right) lead, the values of the x-component i_x run backward (forward) along the x-axis. The geometry of the system–reservoir setup is pictorially illustrated in Figure 1, with semi-infinite and spin-polarized leads coupled to the left and right edges of the central system, supporting a spin-polarized current that interacts with the magnetic texture. Furthermore, a schematic of the parameters relevant to the transport setup and to support charge and spin currents is shown in Figure 2.

4 Spin equations of motion

We now consider the system’s nonequilibrium dynamics, which is initiated by applying a voltage bias to the reservoirs. Since the radius of a typical skyrmion is $\sim 100$ nm [48], a full quantum mechanical description of the spin texture is extremely challenging. A commonly adopted strategy is then to resort to a classical description of the spins, where ${\widehat{\mathbf{S}}}_i\to ⟨{\widehat{\mathbf{S}}}_i⟩\equiv {\mathbf{S}}_i=S{\mathbf{n}}_i$ and |n_i| = 1. This limit is exact for S → ∞ [49, 50] and considered to be a suitable approximation already when S > 1 [35]. Taking the classical limit leads to a semi-classical approximation for the coupled spin and electron subsystems [15, 16], where the quantum electronic Hamiltonian depends parametrically on the classical variables n_i. In this approximation, the system’s time evolution is, therefore, governed by two coupled differential equations, one for the classical spins and one for the quantum mechanical electrons.

To obtain a dynamical equation for the localized spins, we start from the Heisenberg equations of motion for the spin operators and then take the classical limit. The result is a Landau–Lifshitz equation of the form

$\frac{\mathrm{d}{\mathit{n}}_i}{\mathrm{d}t}=-{\mathit{n}}_i\times \left[{\displaystyle \sum _{⟨j⟩}}S\left(J_{ij}{\mathit{n}}_j+{\mathit{D}}_{ij}\times {\mathit{n}}_j\right)+\left(B+SK{n}_{iz}\right)\widehat{\mathbf{z}}+g⟨{\widehat{\mathit{s}}}_i⟩\right],(11)$

where the last term provides the coupling between the classical spins and the instantaneous quantum average of the itinerant electron spins. In the following, we absorb the factors of S into the couplings, i.e., we define SJ_ij → J_ij and similarly for D_ij and K, and for simplicity, we assume J_ij = J. As commonly done in spintronics simulations, we add a small Gilbert damping to the equations of motion to stabilize the dynamics, which amounts to adding an extra term αn_i × (∂n_i/∂t) to Eq. 11. The equations of motion for the itinerant electrons are discussed in detail in the next section.

5 Nonequilibrium Green’s functions

To describe the dynamics of the electrons, we use a nonequilibrium Green’s functions (NEGFs) description within the GKBA. NEGFs are a general and powerful approach to nonequilibrium phenomena [51–55], to describe the real-time dynamics of a system by exactly including external perturbations with an arbitrary temporal dependence. Within this theory, the time-dependent expectation values of any single-particle observable, such as currents, densities and magnetization, can be obtained from the one-particle, two-time Green’s function

$G_{ij}^{\sigma {\sigma }^{\prime }}\left(z,z^{\prime }\right)=-i{⟨{\mathcal{T}}_{\gamma }\left\{c_{i\sigma }^H\left(z\right){\left[c_{j{\sigma }^{\prime }}^H\left(z^{\prime }\right)\right]}^{†}\right\}⟩}_0.(12)$

Here, the brackets ${⟨\cdot ⟩}_0$ denote an ensemble average with respect to the thermal density operator ρ = e^−βH/Z, where β = 1/k_BT is the inverse temperature, H is the equilibrium Hamiltonian, and Z = tr e^−βH is the canonical partition function. In the low-temperature limit β → ∞, the ensemble average reduces to a ground-state expectation value. The operator $c_{i\sigma }^H(z)$ is the annihilation operator of an itinerant electron written in the Heisenberg picture with respect to the full time-dependent Hamiltonian H(z), where z is a complex time argument living on the Keldysh contour [52], and all operators inside the brackets are time-ordered on the contour by the operator ${\mathcal{T}}_{\gamma }$. As mentioned before, the indices i and j run over all lattice sites, while σ and σ′ denote spin projections.

We note that within the semi-classical scheme discussed above, the one-particle Green’s function depends parametrically on the classical spin variables via the spin–electron coupling H_s−e. Therefore, we should write $G_{ij}^{\sigma {\sigma }^{\prime }}(z,z^{\prime })=G_{ij}^{\sigma {\sigma }^{\prime }}(z,z^{\prime };\{{\mathbf{S}}_i\})$, but for notational simplicity, we keep the dependence on S_i implicit in the following. In addition, we suppress the site and spin indexes of Green’s function, with the implicit understanding that all quantities are matrices in the site and spin space and only explicitly indicate the time variables of G(z, z′). The equations of motion for the one-particle Green’s function, the so-called Kadanoff–Baym equations, can be written as [51]

$\left[i\frac{\mathrm{d}}{\mathrm{d}z}-h\left(z\right)\right]G\left(z,z^{\prime }\right)=\delta \left(z,z^{\prime }\right)+{\int }_{\gamma }d\bar{z}\mathrm{\Sigma }\left(z,\bar{z}\right)G\left(\bar{z},z^{\prime }\right).(13)$

Here, h(z) is the time-dependent mean-field Hamiltonian and the self-energy Σ(z, z′) contains all correlation effects beyond the Hartree approximation. A strength of the NEGF formalism is that non-interacting leads can be exactly incorporated in the equation of motion for Green’s function of the central system through the introduction of a so-called embedding self-energy [56]. Denoting the correlation and embedding self-energies by Σ_c and Σ_emb, respectively, the total self-energy can be written as Σ = Σ_c + Σ_emb. We note that in the present case, the electronic Hamiltonian contains no interaction terms, and therefore Σ_c = 0.

In the following, we consider a wide-band limit (WBL) approximation to the embedding self-energy, obtained when the hopping amplitude inside the leads tends to infinity, while the ratio $t_{R\alpha }^2/t_{\alpha }$ remains fixed. In the formal treatment, this approximation is only performed in the extended direction of the leads (the one perpendicular to the system edge). In physical terms, it amounts to the assumption that the density of states of the leads is constant over the bandwidth of the central system. Performing the WBL approximation results in the following expression for the embedding self-energy [20, 30, 57, 58]:

$\begin{array}{ll}\hfill {\mathrm{\Sigma }}_{\text{emb}}^{<}\left(t,t^{\prime }\right)& =i{\displaystyle \sum _{\alpha }}{\mathrm{\Gamma }}_{\alpha }s\left(t\right)s\left(t^{\prime }\right)e^{-i{\int }_t^{t^{\prime }}{V}_{\alpha }\left(\bar{t}\right)d\bar{t}}\int \frac{dϵ}{2\pi }f\left(ϵ-\mu \right)e^{-iϵ\left(t-t^{\prime }\right)}\hfill \\ \hfill {\mathrm{\Sigma }}_{\text{emb}}^R\left(t,t^{\prime }\right)& =-\frac{i}{2}\delta \left(t-t^{\prime }\right)s\left(t\right)s\left(t^{\prime }\right){\displaystyle \sum _{\alpha }}{\mathrm{\Gamma }}_{\alpha },\hfill \end{array}$

where the superscripts denote the so-called lesser $(<)$ and retarded (R) components of the self-energy [54]. Here, s(t) is a smooth function used to equilibrate the central system in the presence of the leads, V_α(t) is the time-dependent bias in lead α, and f(ϵ) is the Fermi–Dirac distribution.

5.1 Generalized Kadanoff–Baym ansatz

Provided that we have full knowledge of the self-energy Σ, the Kadanoff–Baym equations are an exact reformulation of the many-body problem. However, in practice, Σ needs to be approximated, which is commonly done using the diagrammatic many-body perturbation theory. A computational difficulty met with the full Kadanoff–Baym formalism is that the numerical solution of Eq. 13 scales cubically with the number of time steps, which is a consequence of the memory integral (the right-hand side of Eq. 13) accounting for the full history of the dynamic evolution. Calculations with double-time Green’s functions, as in Eq. 12, are highly expensive and scale unfavorably with basis size and simulation time. Since skyrmions typically occur on large lattice distances of 100 nm [9] and move on typical time scales of 1 ps, the simulation of interacting spin–electron systems through a straightforward use of the Kadanoff–Baym equations is prohibitive. A significant improvement in the time-step scaling can be achieved by employing the so-called GKBA [17], where only the time diagonal of Green’s function needs to be time-evolved. This approximation was originally derived for equilibrium systems and in the weak scattering limit but has been found to work well also out of equilibrium [17–30]. Within the NEGF–GKBA and its recent reformulation as a time-linear scheme [25, 26], it is currently possible to simulate the long-time dynamics of electronic systems with a basis size on the order of 100 orbitals [28].

The GKBA for electronic degrees of freedom is achieved by the following factorization [17]:

$G^{<}\left(t,t^{\prime }\right)=i{G}^R\left(t,t^{\prime }\right)G^{<}\left(t^{\prime },t^{\prime }\right)-i{G}^{<}\left(t,t\right)G^A\left(t,t^{\prime }\right),(14)$

where the superscript A denotes the advanced component of Green’s function. Using transformation rules introduced by Langreth [59], we can project Eq. 13 from the Keldysh contour to the physical time axis and obtain a dynamical equation for G^<(t, t′). When taking t′ → t and using the GKBA, the equation for G^<(t, t′) reduces to an equation of motion for the one-particle density matrix ρ(t) = iG^<(t, t) of the form

$\frac{\partial \rho \left(t\right)}{\partial t}+i\left[h\left(t\right)\rho \left(t\right)\right]=-\left[{\int }_{t_0}^t\text{d}\bar{t}{\mathrm{\Sigma }}^{<}\left(t,\bar{t}\right)G^A\left(\bar{t},t\right)+{\int }_{t_0}^t\text{d}\bar{t}{\mathrm{\Sigma }}^R\left(t,\bar{t}\right)\rho \left(\bar{t}\right)G^A\left(\bar{t},t\right)\right]+H.c.(15)$

To close the equation for ρ, we further assume that $G^R(t,t^{\prime })=-i\theta (t-t^{\prime })\mathcal{T}{e}^{-i{\int }_{t^{\prime }}^{t}d\bar{t}[h(\bar{t})+i\mathrm{\Gamma }/2]}$, with the interaction between the leads and the central region adiabatically turned on before the bias is applied. Here, Γ = ∑_αΓ_α accounts for the presence of the leads [20].

6 Approximate wide-band limit

Introducing the GKBA improves the time scaling of the Kadanoff–Baym equations, but solving the equation of motion for ρ still scales quadratically with the number of time steps. Since we are interested in large systems with both fast and slow degrees of freedom, it is useful to make further approximations to reduce the time scaling. To this end, and inspired by other work on open systems [29, 30, 57, 58], we introduce an AWBL based on an approximation to the collision integral (the right-hand side of Eq. 15). As demonstrated below, this prescription offers a good trade-off between computation time and accuracy and allows us to simulate large systems as required to describe skyrmion textures. The proposed AWBL amounts to neglecting the spin–electron coupling in the advanced Green’s function G^A, such that

$G^A\left(t,t^{\prime }\right)=i\theta \left(t^{\prime }-t\right)\bar{\mathcal{T}}{e}^{-i{\int }_{t^{\prime }}^{t}d\bar{t}\left[H_e+H_{s-e}\left(\bar{t}\right)+i\mathrm{\Gamma }/2\right]}\approx i\theta \left(t^{\prime }-t\right)e^{-i\left(t-t^{\prime }\right)\left(H_e+i\mathrm{\Gamma }/2\right)}.(16)$

With this approximation, the advanced Green’s function becomes a function of the time difference, G^A(t, t′) = G^A(t − t′). As a consequence, the entire collision integral becomes a function of t − t′, only a single evaluation needs to be performed at each time step, and the time-step scaling becomes linear (further technical details can be found in Supplementary Material S1). In general, the AWBL is a quite drastic approximation, but, as demonstrated below, it works rather well for the present system. One reason for this is that the spin–electron coupling only constitutes a higher-order correction to the embedding self-energy since the spins do not couple directly to the leads. A second reason is that for most of the time evolution, and in the dominant region of the central system, the spin texture is constant both in time and space.

7 Skyrmion indicators

Before discussing the response of magnetic skyrmions to electronic currents, we define the observables used to determine the presence of a magnetic skyrmion in a classical spin texture. Since the spins live on the unit sphere S² and the central region can be approximately compactified to the torus T² (assuming a ferromagnetic ordering along the edges), a topological charge measuring the winding number of the map S: T²↦S² can be defined. On a lattice, it can be shown that a suitable definition of this topological charge is given by [60]

$Q=\frac{1}{4\pi }{\displaystyle \sum _{\left\{jkl\right\}\in \mathrm{\Delta }}}{\mathrm{\Omega }}_{\mathit{jkl}},(17)$

where the sum is over the triangulated lattice and Δ is the set that contains the indexes for the lattice sites for every triangle in the lattice. The solid angle Ω_jkl is defined by

$\begin{array}{ll}\hfill & \text{exp}\left(i{\mathrm{\Omega }}_{\mathit{jkl}}/2\right)={\rho }_{\mathit{jkl}}^{-1}\left(1+{\mathit{S}}_j\cdot {\mathit{S}}_k+{\mathit{S}}_k\cdot {\mathit{S}}_l+{\mathit{S}}_l\cdot {\mathit{S}}_j+i{\eta }_{\mathit{jkl}}{\mathit{S}}_j\cdot \left({\mathit{S}}_k\times {\mathit{S}}_l\right)\right),\hfill \\ \hfill & {\rho }_{\mathit{jkl}}=\sqrt{2\left(1+{\mathit{S}}_j\cdot {\mathit{S}}_k\right)\left(1+{\mathit{S}}_k\cdot {\mathit{S}}_l\right)\left(1+{\mathit{S}}_l\cdot {\mathit{S}}_j\right)},\hfill \end{array}(18)$

and the function ${\eta }_{\mathit{jkl}}=\mathrm{s}\mathrm{g}\mathrm{n}[({\mathit{S}}_j\cdot \left({\mathit{S}}_k\times {\mathit{S}}_l\right.)]$ ensures that the last term is positive. Geometrically, the topological charge sums up the solid angles spanned by all spin triplets {jkl}, which, when divided by the surface 4π of the unit sphere, gives the integer winding number (for appropriate boundary conditions). The solid angle Ω_jkl serves as an indicator of the extent to which the spins twist. Specifically, within the core of a skyrmion, Ω_jkl has a large magnitude, gradually diminishing radially from the core. The extent of twisting at a specific location can be conceptualized as the skyrmion density at that particular site, with this density being invariably distributed across multiple sites. Furthermore, in the presence of a skyrmion within the system, we define the center of mass as

${\mathit{R}}_{cm}=\frac{1}{M}{\displaystyle \sum _{i_x=2}^{N_x-1}}{\displaystyle \sum _{i_y=2}^{N_y-1}}{\rho }_{i_x,i_y}\left(\begin{array}{c}\hfill i_x\hfill \\ \hfill i_y\hfill \end{array}\right).(19)$

The expressions for M and ${\rho }_{i_x,i_y}$ are respectively given by

$M={\displaystyle \sum _{i_x=2}^{N_x-1}}{\displaystyle \sum _{i_y=2}^{N_y-1}}{\rho }_{i_x,i_y},(20)$

${\rho }_{i_x,i_y}=|{\mathrm{\Omega }}_{\left(i_x,i_y\right),\left(i_x+1,i_y\right),\left(i_x+1,i_y+1\right)}+{\mathrm{\Omega }}_{\left(i_x,i_y\right),\left(i_x,i_y+1\right),\left(i_x+1,i_y+1\right)}|.(21)$

In Eqs 19, 20, the index i_x (i_y) ranges between 2 and N_x − 1 (2 and N_y − 1) rather than, as intuitively expected, between 1 and N_x (1 and N_y). Observations of spin oscillations at the periphery of the central region motivate the exclusion of these edges in the determination of the skyrmion’s center of mass. The rationale behind these oscillations and the specific way we perform the site exclusion are further detailed in Section 8.1.

8 Current-driven skyrmion motion

We now consider the motion of skyrmions generated by a current density in the itinerant electron system, in turn driven by an external bias. However, first, we need to prepare the system in a state featuring a skyrmion, a state that may not necessarily correspond to the ground state of the semi-classical system. This entails the selection of a suitable initial spin configuration, subsequently coupled in a self-consistent manner to the electron system. The interaction with the leads is slowly turned on in the time interval t < τ using the contact function s(t) = sin²(πt/2τ). After time t = τ, a bias is applied, here considered to be of the form

$v_{\alpha }\left(t\right)=\theta \left(t-\tau \right)\left\{\begin{array}{cc}V\hfill & \text{if\hspace{0.17em}}\alpha =L\text{\hspace{0.17em}and\hspace{0.17em}}\sigma =\uparrow \hfill \\ -V\hfill & \text{if\hspace{0.17em}}\alpha =R\text{\hspace{0.17em}and\hspace{0.17em}}\sigma =\uparrow \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right..(22)$

This bias generates a spin current through the central system. In the simulations below, we fix the energy unit by setting the hopping t_ij = t_s = −1 and take ℏ = 1.

8.1 Benchmarks for the approximate wide-band limit and the role of damping

As a primer for our discussion of disorder effects on skyrmion dynamics, we briefly investigate the performance of the AWBL in the absence of disorder. For this purpose, we compare the dynamics obtained within the WBL and AWBL of a small central region denoted by C₁₆, consisting of a 4 × 4 cluster, as illustrated in Figure 3A.

FIGURE 3

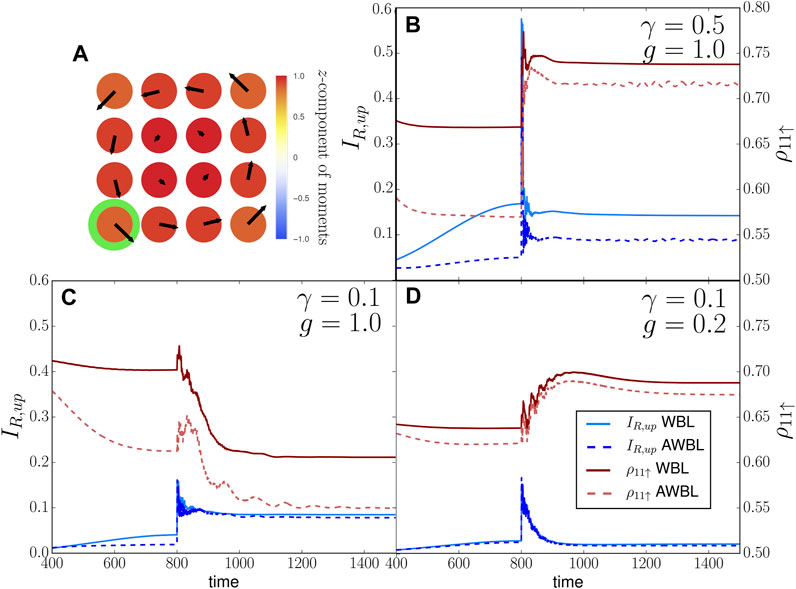
FIGURE 3. Benchmarks for the approximate wide-band limit. (A) Initial relaxed configuration of a 4 × 4 spin texture interacting with a corresponding layer of electrons. (B–D) Spin current I_R,↑ and electronic spin density ρ_11↑ of the lattice site encircled in green in (A), for different values of γ and g, as obtained within the wide-band limit (WBL) and approximate wide-band limit (AWBL). Due to a large value of the spin damping α, the spin texture is approximately the same for all cases and throughout the time evolution. The parameters used are B = 0.05, K = 0.6, α = 3, α_R = 0, J = 0.5, D = 0.4, τ = 800, μ = 0, and V = 3. The color on the spins indicates their z-component, while the arrows show their direction in the xy-plane. The values of g and γ are given in each panel.

We start from the ground state of the isolated region C₁₆ and gradually connect the system to the leads in the time interval t ∈ [0, 800] measured in units of ℏ/t_s. This prepares the stationary initial state of the fully connected system. At time t = 800, a symmetric and spin-polarized bias of the form shown in Eq. 22 is then applied. The subsequent part of the simulation, i.e., for times t > 800, is the one relevant for the skyrmion dynamics to be discussed later. To compare the performance of the WBL and AWBL, we choose as indicators the spin current and the spin-up density at a given site. The representative results are shown in Figures 3B–D and indicate that the agreement between the WBL and AWBL varies noticeably with the strength of the spin–electron coupling g and the lead–device connection γ.

It is useful at this point to make a couple of remarks about the damping term in the spin dynamics. The results given in Figures 3B–D are obtained with a large Gilbert damping of α = 3.0, which results in a spin texture that remains essentially stationary during the time evolution. Therefore, these comparisons mainly concern the regime of electron dynamics in the presence of a static magnetic background. Using the initial spin of Figure 3A in G^A instead of neglecting H_s−e would provide a very good agreement between the AWBL and the WBL. Strictly speaking, one can modify the AWBL to include a fixed spin texture in G^A instead of neglecting it completely and still retain time-linear scaling. However, for the time-dependent disorder simulations discussed later, the spin texture changes significantly in time due to the skyrmion motion. We have verified numerically that, replacing in G^A the exact contribution from the time-evolving texture with a static one (chosen at any time during the time evolution) is no better than using a G^A with zero spin–electron coupling. This is why no spin configuration is included in G^A in Eq. 16 or later on in the dynamics in the presence of spin disorder.

The purpose of using a large α in Figure 3 is to attain a stationary initial state before the bias is applied. In Figure 3, such large damping is maintained throughout the whole time evolution (i.e., during the lead attachment and afterward, when the bias is applied) for consistency and to focus on the electronic behavior. However, for the results obtained later (Section 8.2 and afterward, where we consider skyrmion dynamics in central regions of 20 × 40 sites), the damping is set small (α = 0.1) in order not to influence the system’s intrinsic dynamics but still facilitate the adiabatic preparation of the initial state. In this respect, we have found that, even when evolving the system with no bias, and using very small or no damping after fully connecting the leads, there is a very slow build-up of oscillations in the current and the spin densities. Such oscillations primarily occur in the sites at the edges of the central region (and especially at the sites in contact with the leads). This holds both for the small cluster shown in Figure 3A and for the larger systems studied later and indicates that, when the bias is applied, the system has not yet reached in full the ground state in the presence of the leads due to the very complex energy and fluctuating landscape provided by the interaction of the electrons with the classical spins. However, in the spirit of having a microscopic current inducing the skyrmion motion, it is still meaningful to apply a bias to this configuration and interpret the oscillations as physical in character. At the same time, these oscillations affect in a rather artificial way the estimate of the skyrmion’s center of mass R_cm. Accordingly, in the results presented in the next sections, R_cm is calculated using Eq. 19, i.e., without including the contribution of the peripheral sites of the 20 × 40 region.

Coming back to the results shown in Figures 3B–D, an interesting feature is that the agreement between the AWBL and WBL spin currents, for small γ, is generally better than the agreement between the spin densities. While we do not have a clear explanation for this, we note that this trend is confirmed in additional simulations (not shown), where γ is varied at constant g and vice versa. To summarize, our results suggest that the AWBL produces fairly accurate electronic and spin currents, overall in good agreement with the full WBL. Therefore, it constitutes a microscopic and semi-quantitative method to investigate skyrmion dynamics at low computational cost, appropriate for both transient and steady-state regimes.

8.2 Current-induced motion

Having shown that the AWBL is in good quantitative agreement with the WBL for small systems, we now employ it to describe skyrmion motion in systems beyond the scope of the WBL. These results provide a useful benchmark for the discussion in later sections, where the effect of magnetic impurities on skyrmion motion is analyzed. To obtain the reference results, we consider a central region with 40 × 20 sites and investigate the dynamics in response to an applied bias. These results are henceforth referred to as “base case.” In the base case, as well as in the impurity studies below, a potential of strength V = 2 is applied in the leads, and the coupling between the system and leads is of strength γ = 0.2.

The system starts off with a relaxed skyrmion texture in the center (see Figure 4B) and in response to the bias starts to drift toward the right with a slight additional downward movement (see Figure 4A). As seen from the figure, the velocity in the x-direction is not constant but rather ramps up, then slows down, and finally starts to ramp up again. While the dominant rightward motion is due to the spin current, the downward force is due to the so-called skyrmion Hall effect [9]. Additionally, there are some small-scale oscillations, which are especially visible in the y-direction. These oscillations could be due to the discrete nature of the underlying lattice since the skyrmion has a preferred equilibrium. When it moves between lattice sites, the skyrmion form gets distorted but returns to its original configuration when it arrives at a new site. We finally note that it takes some time for the skyrmion to pick up speed as the current goes through the system, which is a general trend in our simulations. This is indicative of the presence of a finite skyrmion mass, which has been discussed in previous studies [61, 62]. In particular, it was recently proposed that the magnitude of the skyrmion mass is affected by the interactions between localized moments and free electrons [37, 38], consistent with the present findings.

FIGURE 4

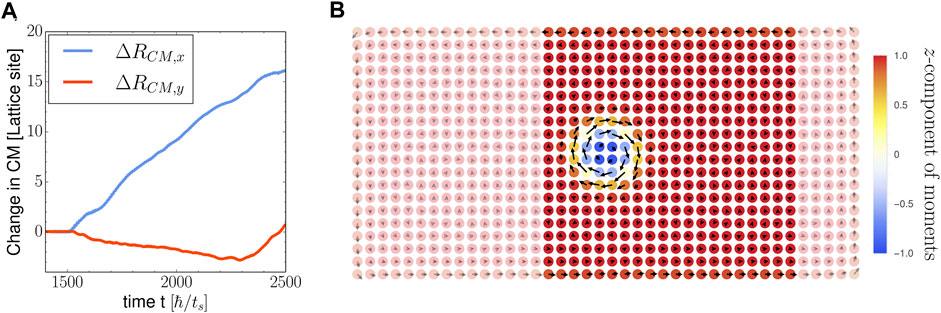
FIGURE 4. Skyrmion motion in response to electronic spin currents. (A) Center of mass motion of the skyrmion and (B) initial spin configuration at t = 200. The highlighted region corresponds to the area shown in Figures 5–7. The parameters used are g = 1, B = 0.05, K = 0.6, α = 0.1, α_R = 0, J = 0.5, D = 0.4 (corresponding to the Bloch-type DMI), γ = 0.2, τ = 1,500, μ = 0, and V = 2. The color of the spins indicates their z-component, while the arrows display their direction in the xy-plane.

9 Disorder effects

Knowing the trajectory of the skyrmion in the base case, we can now investigate the effects of placing impurities in its path. In the panels of Figures 5–7 showing the spin configuration, the positions of the impurities are marked in green. Here, we restrict ourselves to a simple form of impurity, corresponding to a reduction in the symmetric exchange interaction by J → J/2 between the impurity site and its nearest neighbors. Therefore, it is expected that the skyrmion will be hindered by a smaller interaction. This change is effected at t = 1,400 in order not to disturb the system before the bias is applied at t = 1,500.

FIGURE 5

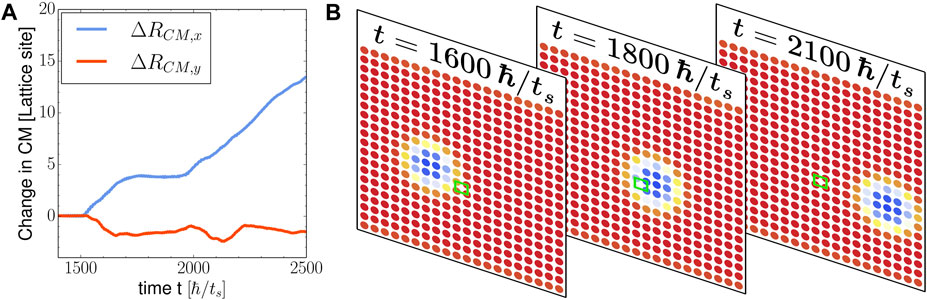
FIGURE 5. Skyrmion motion in the presence of a small impurity on the skyrmion path. (A) Center of mass movement of the skyrmion and (B) some snapshots of the z-component of the spins in the highlighted area in Figure 4. The parameters used are g = 1, B = 0.05, K = 0.6, α = 0.1, α_R = 0, J = 0.5, D = 0.4 (corresponding to the Bloch-type DMI), γ = 0.2, τ = 1,500, μ = 0, and V = 2. The color of the spins indicates their z-component.

FIGURE 6

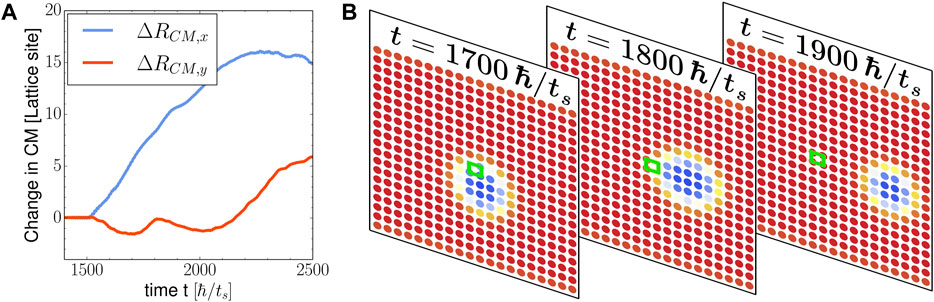
FIGURE 6. Skyrmion motion in the presence of a small impurity near the skyrmion path. (A) Center of mass movement of the skyrmion and (B) some snapshots of the z-component of the spins in the highlighted area of Figure 4. The parameters used are g = 1, B = 0.05, K = 0.6, α = 0.1, α_R = 0, J = 0.5, D = 0.4 (corresponding to the Bloch-type DMI), γ = 0.2, τ = 1,500, μ = 0, and V = 2. The color of the spins indicates their z-component.

FIGURE 7

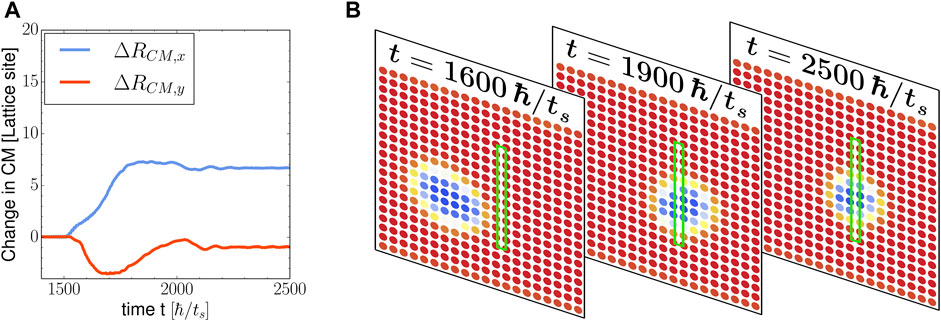
FIGURE 7. Skyrmion motion in the presence of an extended impurity. (A) Center of mass movement of the skyrmion and (B) some snapshots of the z-component of the spins in the highlighted area in Figure 4. The parameters used are g = 1, B = 0.05, K = 0.6, α = 0.1, α_R = 0, J = 0.5, D = 0.4 (corresponding to the Bloch-type DMI), γ = 0.2, τ = 1,500, μ = 0, and V = 2. The color of the spins indicates their z-component.

9.1 Case 1: A small impurity on the skyrmion path

As a typical example of a small magnetic impurity, we consider an impurity cluster consisting of a square of four lattice sites (see Figure 5). One possible realization of this form of disorder is the presence of adsorbate atoms in the center of these four lattice sites. The impurity is placed right in the path of the skyrmion, slightly to the right and below the skyrmion’s initial position.

The center of mass movement of the skyrmion in response to a spin current is shown in Figure 5. In the x-direction, it seems like the skyrmion does not feel the effect of the impurity until it is on top of it since the movement of the center of mass is quite similar to the base case before t ∼ 1,700. However, a careful comparison reveals that it moves slightly slower. In contrast, the skyrmion starts to pick up speed in the y-direction as it approaches the impurity, indicating that the velocity in the x-direction is transferred to a downward motion. After the skyrmion has entered the impurity, it gets pinned and struggles to escape. More specifically, between t = 1,700 and t = 2,000, the skyrmion is stuck to the impurity and can only move around as long as some part of it is still on the impurity. For a few times during the center of mass movement (see Figure 5), there were bumps, which indicate that the skyrmion gathered velocity to try to escape but was pulled back again by the impurity. Finally, at t ∼ 2,000, the skyrmion managed to escape and move past the impurity. The dynamics shown in Figure 5 clearly illustrates the advantage of a microscopic description, where the motion of the skyrmion can be tracked atom by atom. During the dynamics, the shape of the skyrmion changes, and the direction of motion changes several times, effects that are not possible to capture with a Thiele-type description. Furthermore, it is quite reasonable to expect that the observed dynamics is a direct result of the motion of the itinerant electrons, especially at the skyrmion boundary, where the local spin changes must take into account the redistribution of the electronic spin density during the time evolution.

9.2 Case 2: A small impurity near the skyrmion path

Next, we shift the impurity position two lattice sites upward compared to the previous section (Figure 6), such that the impurity is now slightly above the skyrmion’s path. At the beginning of the dynamics, the center of mass movement seems very similar to the previous case, with the velocity along the x-direction slightly reduced compared to the base case and a significant downward movement. However, in the present case, the movement does not force the skyrmion on top of the impurity, and the impurity pinning is avoided. In the center of the mass movement shown in Figure 6, as well as in the snapshots at t = 1,700 and t = 1,800 shown in Figure 6, the skyrmion is seen to move beneath the impurity. It is likely that, if the system was extended further in the y-direction, the skyrmion would continue its motion downward. However, in the present case, the edge of the system prevents this since our simulations suggest that the repulsive force induced by the edges makes the skyrmion recoil upward in the y-direction. This illustrates, on a microscopic level, the importance of considering the track width when designing efficient racetrack memories. If the width of the track is too small, the skyrmion might not be able to get around impurities, while if the width is too large, skyrmions can be deflected by impurities and substantially deviate from their path.

Although the skyrmion’s core, shown in blue in Figure 4, comprises only 4 × 4 spins, a rotation of the xy-components of the spins away from the ferromagnetic background can be observed in an area extending up to 12 × 12 sites. This indicates that the effective skyrmion size is much larger than the central 4 × 4 region, which in turn implies that the skyrmion feels the presence of the edge much earlier that would be expected from only considering its core.

9.3 Case 3: A larger impurity configuration

As an example of dynamics in the presence of a more extended magnetic impurity, Figure 7 shows the center of mass motion of the skyrmion in a system containing a columnar impurity that covers almost the entire lattice in the y-direction. Again, the impurity is only two lattice site thick, but this time with only four sites at the top and the bottom left unperturbed. The characteristic downward bump in the center of mass motion along the y-direction is also observed here, but it is twice as big as in the previous cases. As shown in Figure 7, the velocity in the y-direction is large before the skyrmion is suddenly halted. This detail, together with the observation that at t = 1,900 the skyrmion is slightly smaller, suggests that a small skyrmion could be annihilated even by a small impurity. After t = 1,900, the skyrmion recoils upward, but the collision with the top does not seem as severe as in the case shown in Figure 5. This is likely because the velocity is lower and the skyrmion is already stuck.

The observed motion along the vertical direction is most likely aided by the lower wall. However, the impurity likely also plays an important role since we have observed that it is hard for the skyrmion to escape once it moves on top of the impurity. In addition to the vertical motion, Figure 7 also shows that the skyrmion keeps wiggling along the x-direction while moving. In particular, the snapshot at t = 1,900 strongly indicates that this movement is due to the skyrmion expanding to the right. Subsequently, for times after t ∼ 2,100, the skyrmion shrinks and expands in a quasi-steady state.

9.4 Summary of the results

In summary, the results of Figures 5–7 show that by placing impurities in selected places along a skyrmion’s path, it is possible to engineer the skyrmion’s trajectory and to steer skyrmions in the desired direction in logic devices [12]. At the same time, it is also clear that, in order to accurately engineer the dynamics of the desired skyrmion in the presence of impurities and provide some conceptual guidance for the experimental realization of skyrmion architectures, a microscopic and explicit equal-footing account of the behavior of itinerant electrons and localized spins is of high relevance.

10 Discussion and outlook

In this work, we have presented a recently introduced method to deal with magnetic skyrmions, where a skyrmion magnetic texture made of classical spins is embedded in a background of quantum electrons. We considered the skyrmion dynamics in quantum transport geometry, where a central region of coupled electrons and spins is connected to electron reservoirs. Our treatment is based on a two-component description where the electrons are treated via NEGFs, coupled to classical spins governed by an LLG equation.

To describe the skyrmion motion in large systems, we introduced an approximate approach to include the effect of the electronic reservoir coupled to the central system. This so-called AWBL shows a satisfactory level of agreement with the full WBL approach. Similar to other schemes in the literature, it is a time-linear scaling method and, in addition, has a very advantageous scaling prefactor of great convenience to deal with systems of large size.

This approach was used to investigate the effects of magnetic impurities on the current-induced motion of magnetic skyrmions. Our results show that it is possible to characterize at the atomic level processes such as skyrmion scattering, recoil, drift, and trapping in disordered samples. This is a subject of high relevance since understanding how to tailor the disorder level of a given sample is crucial in order to control skyrmion dynamics.

A natural extension of this work is to take into account the additional correlation effects arising from electron–electron interaction. This would bring the simulation closer to realistic systems, where correlations between the electrons could, e.g., lead to destabilization of a skyrmion or introduce effects competing with the disorder. In a different direction, the results obtained here can be used to benchmark other methods that deal with electron and localized spins. For example, one can imagine validating methods that, still in a spin-only framework, go beyond the standard LLG equation [37, 38].

Finally, we note that the methods presented here open the door for simulations of the intertwined spin–electron dynamics of small but realistic nanoscale systems. This provides a new approach to investigate the ultrafast dynamics of magnetic systems with general noncollinear orders, as initiated by ultrashort laser or current pulses [16, 63]. Apart from its importance for skyrmionic systems, the presented method will, therefore, be of large relevance to describe the coupled dynamics of spins, electrons, and lattice vibrations in spintronic devices and for material engineering, thereby helping facilitate a microscopic understanding of driven magnetic materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

EÖ: conceptualization, formal analysis, investigation, methodology, software, and writing–original draft. EVB: conceptualization, formal analysis, investigation, methodology, software, supervision, and writing–review and editing. CV: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. EV acknowledges funding from the European Union’s Horizon Europe Research and Innovation Program under the Marie Skłodowska-Curie Grant Agreement No 101106809. CV acknowledges funding from the Swedish Research Council (Grant No VR 2022 04486).

Acknowledgments

Discussions with Riku Tuovinen are gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1340288/full#supplementary-material

Footnotes

¹For current work in this direction, see, e.g., [33].

References

1. Cucchiella F, D’Adamo I, Lenny Koh S, Rosa P. Recycling of weees: an economic assessment of present and future e-waste streams. Renew Sust Energ Rev (2015) 51:263–72. doi:10.1016/j.rser.2015.06.010

CrossRef Full Text | Google Scholar

2. Irimia-Vladu M. Green electronics: biodegradable and biocompatible materials and devices for sustainable future. Chem Soc Rev (2014) 43:588–610. doi:10.1039/c3cs60235d

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hirohata A, Yamada K, Nakatani Y, Prejbeanu IL, Dieny B, Pirro P, et al. Review on spintronics: principles and device applications. J Magnetism Magn Mater (2020) 509:166711. doi:10.1016/j.jmmm.2020.166711

CrossRef Full Text | Google Scholar

4. Coronado E. Molecular magnetism: from chemical design to spin control in molecules, materials and devices. Nat Rev Mater (2020) 5:87–104. doi:10.1038/s41578-019-0146-8

CrossRef Full Text | Google Scholar

5. Parkin S, Yang SH. Memory on the racetrack. Nat Nanotechnology (2015) 10:195–8. doi:10.1038/nnano.2015.41

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Göbel B, Mertig I, Tretiakov OA. Beyond skyrmions: review and perspectives of alternative magnetic quasiparticles. Phys Rep (2021) 895:1–28. doi:10.1016/j.physrep.2020.10.001

CrossRef Full Text | Google Scholar

7. Back C, Cros V, Ebert H, Everschor-Sitte K, Fert A, Garst M, et al. The 2020 skyrmionics roadmap. J Phys D: Appl Phys (2020) 53:363001. doi:10.1088/1361-6463/ab8418

CrossRef Full Text | Google Scholar

8. Sampaio J, Cros V, Rohart S, Thiaville A, Fert A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat Nanotechnology (2013) 8:839–44. doi:10.1038/nnano.2013.210

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions. Nat Nanotechnology (2013) 8:899–911. doi:10.1038/nnano.2013.243

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R. Field-dependent size and shape of single magnetic skyrmions. Phys Rev Lett (2015) 114:177203. doi:10.1103/PhysRevLett.114.177203

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang G, Stano P, Klinovaja J, Loss D. Majorana bound states in magnetic skyrmions. Phys Rev B (2016) 93:224505. doi:10.1103/PhysRevB.93.224505

CrossRef Full Text | Google Scholar

12. Chauwin M, Hu X, Garcia-Sanchez F, Betrabet N, Paler A, Moutafis C, et al. Skyrmion logic system for large-scale reversible computation. Phys Rev Appl (2019) 12:064053. doi:10.1103/PhysRevApplied.12.064053

CrossRef Full Text | Google Scholar

13. Rex S, Gornyi IV, Mirlin AD. Majorana bound states in magnetic skyrmions imposed onto a superconductor. Phys Rev B (2019) 100:064504. doi:10.1103/PhysRevB.100.064504

CrossRef Full Text | Google Scholar

14. Psaroudaki C, Panagopoulos C. Skyrmion qubits: a new class of quantum logic elements based on nanoscale magnetization. Phys Rev Lett (2021) 127:067201. doi:10.1103/PhysRevLett.127.067201

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Viñas Boström E, Verdozzi C. Steering magnetic skyrmions with currents: a nonequilibrium green’s functions approach. physica status solidi (b) (2019) 256:1800590. doi:10.1002/pssb.201800590

CrossRef Full Text | Google Scholar

16. Viñas Boström E, Rubio A, Verdozzi C. Microscopic theory of light-induced ultrafast skyrmion excitation in transition metal films. Npj Comput Mater (2022) 8:62. doi:10.1038/s41524-022-00735-5

CrossRef Full Text | Google Scholar

17. Lipavský P, Špička V, Velický B. Generalized kadanoff-baym ansatz for deriving quantum transport equations. Phys Rev B (1986) 34:6933–42. doi:10.1103/PhysRevB.34.6933

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hermanns S, Balzer K, Bonitz M. The non-equilibrium green function approach to inhomogeneous quantum many-body systems using the generalized kadanoff–baym ansatz. Physica Scripta (2012) T151:014036. doi:10.1088/0031-8949/2012/T151/014036

CrossRef Full Text | Google Scholar

19. Hermanns S, Schlünzen N, Bonitz M. Hubbard nanoclusters far from equilibrium. Phys Rev B (2014) 90:125111. doi:10.1103/PhysRevB.90.125111

CrossRef Full Text | Google Scholar

20. Latini S, Perfetto E, Uimonen AM, van Leeuwen R, Stefanucci G. Charge dynamics in molecular junctions: nonequilibrium green’s function approach made fast. Phys Rev B (2014) 89:075306. doi:10.1103/PhysRevB.89.075306

CrossRef Full Text | Google Scholar

21. Boström EV, Mikkelsen A, Verdozzi C, Perfetto E, Stefanucci G. Charge separation in donor–c60 complexes with real-time green functions: the importance of nonlocal correlations. Nano Lett (2018) 18:785–92. doi:10.1021/acs.nanolett.7b03995

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hopjan M, Stefanucci G, Perfetto E, Verdozzi C. Molecular junctions and molecular motors: including coulomb repulsion in electronic friction using nonequilibrium green’s functions. Phys Rev B (2018) 98:041405. doi:10.1103/PhysRevB.98.041405

CrossRef Full Text | Google Scholar

23. Karlsson D, Hopjan M, Verdozzi C. Disorder and interactions in systems out of equilibrium: the exact independent-particle picture from density functional theory. Phys Rev B (2018) 97:125151. doi:10.1103/physrevb.97.125151

CrossRef Full Text | Google Scholar

24. Kalvová A, Velický B, Špička V. Generalized master equation for a molecular bridge improved by vertex correction to the generalized kadanoff-baym ansatz. Europhysics Lett (2018) 121:67002. doi:10.1209/0295-5075/121/67002

CrossRef Full Text | Google Scholar

25. Schlünzen N, Joost JP, Bonitz M. Achieving the scaling limit for nonequilibrium green functions simulations. Phys Rev Lett (2020) 124:076601. doi:10.1103/PhysRevLett.124.076601

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Karlsson D, van Leeuwen R, Pavlyukh Y, Perfetto E, Stefanucci G. Fast green’s function method for ultrafast electron-boson dynamics. Phys Rev Lett (2021) 127:036402. doi:10.1103/PhysRevLett.127.036402

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pavlyukh Y, Perfetto E, Karlsson D, van Leeuwen R, Stefanucci G. Time-linear scaling nonequilibrium green’s function methods for real-time simulations of interacting electrons and bosons. i. formalism. Phys Rev B (2022) 105:125134. doi:10.1103/PhysRevB.105.125134

CrossRef Full Text | Google Scholar

28. Pavlyukh Y, Perfetto E, Karlsson D, van Leeuwen R, Stefanucci G. Time-linear scaling nonequilibrium green’s function method for real-time simulations of interacting electrons and bosons. ii. dynamics of polarons and doublons. Phys Rev B (2022) 105:125135. doi:10.1103/PhysRevB.105.125135

CrossRef Full Text | Google Scholar

29. Balzer K, Schlünzen N, Ohldag H, Joost JP, Bonitz M. Accelerating nonequilibrium green function simulations with embedding self-energies. Phys Rev B (2023) 107:155141. doi:10.1103/physrevb.107.155141

CrossRef Full Text | Google Scholar

30. Tuovinen R, Pavlyukh Y, Perfetto E, Stefanucci G. Time-linear quantum transport simulations with correlated nonequilibrium green’s functions. Phys Rev Lett (2023) 130:246301. doi:10.1103/physrevlett.130.246301

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Iwasaki J, Mochizuki M, Nagaosa N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat Commun (2013) 4:1463. doi:10.1038/ncomms2442

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Stier M, Strobel R, Krause S, Häusler W, Thorwart M. Role of impurity clusters for the current-driven motion of magnetic skyrmions. Phys Rev B (2021) 103:054420. doi:10.1103/PhysRevB.103.054420

CrossRef Full Text | Google Scholar

33. Haller A, Groenendijk S, Habibi A, Michels A, Schmidt TL. Quantum skyrmion lattices in heisenberg ferromagnets. Phys Rev Res (2022) 4:043113. doi:10.1103/PhysRevResearch.4.043113

CrossRef Full Text | Google Scholar

34. Everschor-Sitte K, Masell J, Reeve RM, Kläui M. Perspective: magnetic skyrmions—overview of recent progress in an active research field. J Appl Phys (2018) 124:240901. doi:10.1063/1.5048972

CrossRef Full Text | Google Scholar

35. Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat Phys (2011) 7:713–8. doi:10.1038/nphys2045

CrossRef Full Text | Google Scholar

36. Thiele AA. Steady-state motion of magnetic domains. Phys Rev Lett (1973) 30:230–3. doi:10.1103/PhysRevLett.30.230

CrossRef Full Text | Google Scholar

37. Reyes-Osorio F, Nikolic BK. Anisotropic skyrmion mass induced by surrounding conduction electrons: a Schwinger-Keldysh field theory approach (2023). arXiv.2302. doi:10.48550/arXiv.2302.0422004220

CrossRef Full Text | Google Scholar

38. Reyes-Osorio F, Nikolic BK. Gilbert damping in metallic ferromagnets from Schwinger-Keldysh field theory: nonlocality, nonuniformity, and anisotropy in the presence of spin-orbit coupling (2023). arXiv.2302. doi:10.48550/arXiv.2306.1301304220

CrossRef Full Text | Google Scholar

39. Weißenhofer M, Rózsa L, Nowak U. Skyrmion dynamics at finite temperatures: beyond Thiele’s equation. Phys Rev Lett (2021) 127:047203. doi:10.1103/PhysRevLett.127.047203

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Huang L, Burnell G, Marrows CH. Transient retrograde motion of spin wave driven skyrmions in magnetic nanotracks. Phys Rev B (2023) 107:224418. doi:10.1103/PhysRevB.107.224418

CrossRef Full Text | Google Scholar

41. Baláž P, Zwierzycki M, Cosco F, Carva K, Maldonado P, Oppeneer PM. Theory of superdiffusive spin transport in noncollinear magnetic multilayers. Phys Rev B (2023) 107:174418. doi:10.1103/PhysRevB.107.174418

CrossRef Full Text | Google Scholar

42. Gupta R, Cosco F, Malik RS, Chen X, Saha S, Ghosh A, et al. Element-resolved evidence of superdiffusive spin current arising from ultrafast demagnetization process. Phys Rev B (2023) 108:064427. doi:10.1103/PhysRevB.108.064427

CrossRef Full Text | Google Scholar

43. Ghosh S, Freimuth F, Gomonay O, Blügel S, Mokrousov Y. Driving spin chirality by electron dynamics in laser-excited antiferromagnets. Commun Phys (2022) 5:69. doi:10.1038/s42005-022-00840-3

CrossRef Full Text | Google Scholar

44. Zarzuela R, Sinova J. Effective spin-charge transport theory and spin-transfer physics in frustrated magnets within the slave-boson approach. Phys Rev B (2022) 105:024423. doi:10.1103/PhysRevB.105.024423

CrossRef Full Text | Google Scholar

45. Ghosh S, Blügel S, Mokrousov Y. Ultrafast optical generation of antiferromagnetic meron-antimeron pairs with conservation of topological charge. Phys Rev Res (2023) 5:L022007. doi:10.1103/PhysRevResearch.5.L022007

CrossRef Full Text | Google Scholar

46. Dzyaloshinsky I. A thermodynamic theory of weak ferromagnetism of antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3

CrossRef Full Text | Google Scholar

47. Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/PhysRev.120.91

CrossRef Full Text | Google Scholar

48. Wang XS, Yuan HY, Wang XR. A theory on skyrmion size. Commun Phys (2018) 1:31. doi:10.1038/s42005-018-0029-0

CrossRef Full Text | Google Scholar

49. Lieb EH. The classical limit of quantum spin systems. Commun Math Phys (1973) 31:327–40. doi:10.1007/bf01646493

CrossRef Full Text | Google Scholar

50. Fradkin E. Field theories of condensed matter Physics. Cambridge University Press (2013). doi:10.1017/CBO9781139015509

CrossRef Full Text | Google Scholar

51. Kadanoff LP, Baym G. Quantum statistical mechanics: green’s function methods in equilibrium and nonequilibrium problems. W.A. Benjamin (1962).

Google Scholar

52. Keldysh LV. Diagram technique for nonequilibrium processes. Soviet Phys JETP (1965) 20:1018–26.

Google Scholar

53. Balzer K, Bonitz M. Nonequilibrium Green’s functions approach to inhomogeneous systems. Lecture notes in Physics. Springer Berlin Heidelberg (2012).

Google Scholar

54. Stefanucci G, van Leeuwen R. Nonequilibrium many-body theory of quantum systems: a modern introduction. Cambridge University Press (2013). doi:10.1017/CBO9781139023979

CrossRef Full Text | Google Scholar

55. Hopjan M, Verdozzi C. Probing strongly correlated materials in non-equilibrium: basic concepts and possible future trends in first principle approaches. Berlin, Heidelberg: Springer Berlin Heidelberg (2014). 347–84. doi:10.1007/128_2014_528

CrossRef Full Text | Google Scholar

56. Myöhänen P, Stan A, Stefanucci G, van Leeuwen R. A many-body approach to quantum transport dynamics: initial correlations and memory effects. Europhysics Lett (2008) 84:67001. doi:10.1209/0295-5075/84/67001

CrossRef Full Text | Google Scholar

57. Tuovinen R, Perfetto E, Stefanucci G, van Leeuwen R. Time-dependent landauer-büttiker formula: application to transient dynamics in graphene nanoribbons. Phys Rev B (2014) 89:085131. doi:10.1103/PhysRevB.89.085131

CrossRef Full Text | Google Scholar

58. Ridley M, MacKinnon A, Kantorovich L. Partition-free theory of time-dependent current correlations in nanojunctions in response to an arbitrary time-dependent bias. Phys Rev B (2017) 95:165440. doi:10.1103/PhysRevB.95.165440

CrossRef Full Text | Google Scholar

59. Langreth DC. Linear and nonlinear response theory with applications. In: JT Devreese, and VE van Doren, editors. Linear and nonlinear electron transport in solids. Boston, MA: Springer US (1976). p. 3–32. doi:10.1007/978-1-4757-0875-2_1

CrossRef Full Text | Google Scholar

60. Berg B, Lüscher M. Definition and statistical distributions of a topological number in the lattice o(3) σ-model. Nucl Phys. B (1981) 190:412–24. doi:10.1016/0550-3213(81)90568-X

CrossRef Full Text | Google Scholar

61. Schütte C, Iwasaki J, Rosch A, Nagaosa N. Inertia, diffusion, and dynamics of a driven skyrmion. Phys Rev B (2014) 90:174434. doi:10.1103/PhysRevB.90.174434

CrossRef Full Text | Google Scholar

62. Makhfudz I, Krüger B, Tchernyshyov O. Inertia and chiral edge modes of a skyrmion magnetic bubble. Phys Rev Lett (2012) 109:217201. doi:10.1103/PhysRevLett.109.217201

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Truc B, Sapozhnik AA, Tengdin P, Boström EV, Schönenberger T, Gargiulo S, et al. Light-induced metastable hidden skyrmion phase in the mott insulator cu₂OSeO₃. Adv Mater (2023) 35:e2304197. doi:10.1002/adma.202304197

PubMed Abstract | CrossRef Full Text | Google Scholar