Absence of the impurity-resonance spot at a Bi defect located near the Zn impurity in Bi2Sr2Ca(Cu1-xZnx)2O8+δ

Zn dopants to Cu sites in high-T_c cuprates strongly suppress superconductivity and act as impurities with a strong quasiparticle scattering resonance. Using the scanning tunneling microscope, we investigate the electronic structure in the atomic scale around Zn impurities in Bi₂Sr₂Ca(Cu_1-xZn_x)₂O_8+δ. The intense scattering resonance of the Zn impurity in the CuO₂ layer strongly affects the measured local density of states of the BiO layer on the surface. The pattern of the bound state induced by a Zn impurity consists of a central spot at the Bi atom just above the Zn impurity and eight symmetric spots at the next nearest neighboring (NNN) and the third nearest neighboring (3NN) sites of Bi atoms. When the Bi atom above the NNN Cu atom is missing, the corresponding scattering spot is absent simultaneously. Our results indicate that the measured impurity-induced bound state pattern is strongly influenced by Bi atoms on the surface and therefore supports the “filter” theoretical model of the nonlocal interlayer tunneling effect from the CuO₂ layer to the BiO layer on the surface. Our research provides extra information about the impurity-induced bound state by Zn impurities.

Introduction

High-T_c cuprates have been the focus of investigation in condensed matter physics for decades because of the potential application and underlying mechanism of unconventional high-T_c superconductivity. The parent compound of cuprates is a Mott insulator, and superconductivity is induced by the hole or electron doping [1]. The chemical doping is usually carried out to the ‘charge-reservoir’ layers in cuprates, while the charge carriers are transferred to the conducting and superconducting CuO₂ planes. However, substituting Cu atoms in the CuO₂ plane usually breaks the superconductivity and lowers T_c; meanwhile, the impurity bound state is induced at the substitution site [2–4]. This impurity effect provides critical insights into the underlying physics of high-T_c superconductivity. For instance, according to Anderson’s theorem [5], the non-magnetic impurity does not influence superconductivity in an s-wave superconductor, however, it has a strong pair-breaking effect in a d-wave superconductor with a gap sign change [6–8]. As a result, in a d-wave superconductor, T_c decreases rapidly with the increase in nonmagnetic impurities following the well-known Abrikosov-Gor’kov formula [9, 10]. This formula can apply to other superconductors with a sign-change order parameter like the s± or the p wave. Moreover, impurities in a d-wave superconductor can give rise to the so-called gapless superconductivity [11] and the phase transition to this state is proved to be a Lifshitz type of the 2.5 order [12, 13].

Among the various impurity substitutions into CuO₂ planes, Zn dopants have attracted much experimental and theoretical attention. Experimentally, a dramatic decrease of T_c is observed in Zn-doped cuprates, which is evidence of a d-wave gap if Zn dopants are regarded as non-magnetic impurities [14, 15]. Doping Zn impurities reduces the superfluid density [16, 17] and increases the residual specific heat coefficient [18], which can be explained by the non-superconducting regions induced by Zn dopants with the effective size of the coherence length [16]. The scanning tunneling microscopy/spectroscopy (STM/STS) experiments confirm the local effect of Zn impurities within a few nanometers [3], and the impurity-induced resonance behaves as a strong in-gap peak of density of states (DOS) located at about −2 meV near the Fermi energy. The hole doping level can influence the impurity resonance, and the bound state peak disappears in the underdoped sample with a larger gap [19, 20]. Zn dopants are usually regarded as nonmagnetic impurities. However, the staggered antiferromagnetic spin structure is observed near the Zn dopant [21–25], which may be due to the exposure of the antiferromagnetic background after the superconductivity is killed by the Zn impurities. These fascinating experimental findings demonstrate how Zn impurities locally disturb the surrounding electronic and spin structures. There are also theoretical interpretations to describe the scattering resonance pattern. It is calculated that impurity bound states are located at the four nearest Cu sites to the Zn impurity, and the complex interlayer tunneling effect makes the surface pattern on the BiO layer different from that on the CuO₂ layer [26, 27]. Based on the so-called ‘filter’ model, tunneling from the STM tip into the CuO₂ layer requires tunneling through the insulating BiO surface, effectively filtering the signal [26, 27]. The subsequently developed BdG-Wannier approach [28] further improves the model, and the theoretical result shows excellent agreement with the experiment.

Recently, the charge-reservoir layer has been argued to play an essential role in the unconventional superconductivity in cuprates. For example, the obtained gap feature on the exposed surface of the charge-reservoir layer is different from that on the CuO₂ plane [29, 30]. These experiment results provide another angle of view showing that the charge-reservoir layer may influence the detected local density of states (LDOS) on the surface.

Using STM/STS, we investigate the influence to the impurity-bound-state by Bi vacancies on the surface near the Zn impurity on the CuO₂ plane in Bi₂Sr₂Ca(Cu_1-xZn_x)₂O_8+δ (Zn-Bi2212).A Bi vacancy above the next nearest neighboring Cu atom near the Zn impurity leads to the missing of the corresponding scattering resonance spot at the Bi vacancy. This result indicates that the measured impurity-induced bound state on the surface is significantly affected by the Bi atom in the BiO layer. Our observation provides a crucial clue for understanding the interaction between different layers in cuprates and facilitates the comprehension of the tunneling path in STM experiments.

Material and methods

Bi₂Sr₂Ca(Cu_1-xZn_x)₂O_8+δ single crystals with a nominal doping level of x = 2% were grown by the self-flux method [31]. Stoichiometric proportional powders of Bi₂O₃, SrCO₃, CuO, CaCO₃, and ZnO compounds were used as starting material for growth. The mixed powder was calcined at 860°C for 48 h and ground to fine powder again. To ensure a complete solid-state reaction, the grinding and calcining procedure were repeated three times [32]. The obtained polycrystalline powder is a pure single phase examined by the powder x-ray diffraction. The polycrystalline powder was calcined at 1,020°C for 2 hours; it was cooled to 940°C at a rate of 2°C/h, then 840°C at a rate of 1°C/h, to 500°C at a rate of 1°C/min, and finally it is cooled to the room temperature with the furnace. The superconducting property was characterized by the magnetization measurement, and the transition is sharp, with a T_c of about 86 K. The STM/STS measurements were carried out in a scanning tunneling microscope (USM-1300, Unisoku Co., Ltd.). The Zn-Bi2212 samples were cleaved at room temperature in an ultra-high vacuum with a base pressure of about 2 × 10⁻¹⁰ torr and then transferred into the STM system working at 1.5 K. All the STM/STS measurements used the electrochemically etched chromium tips. The Cr tip was electrochemically etched by 3 mol/L NaOH solution with the immersed end covered by a polytetrafluoroethylene tube with a specific length [33]. The differential conductance is measured using the lock-in method with an AC modulation amplitude of 2 mV and frequency of 987.5 Hz. All the STM/STS data were taken at 1.5 K in this work. The setpoint conditions are V_set = −100 mV and I_set = 100 pA for all measurements of topographies and tunneling spectra.

Results and discussion

Figure 1A shows the crystal structure of the Bi₂Sr₂CaCu₂O_8+δ (Bi2212) unit cell. STM measurement is carried out after cleavage, and the exposed surface is universally the BiO layer because of the weak interaction between adjacent BiO planes. Cu atoms reside directly beneath the Bi atoms based on the crystal structure. When Zn impurities are doped into Bi2212, they replace the Cu atoms, and the situation of the BiO surface with an individual Zn impurity is shown in Figure 1B. To facilitate the discussion, we label the Bi atom positions as Bi0, Bi1, Bi2, and Bi3, representing the Bi atom directly above the Zn impurity, the nearest neighboring (NN) Cu atom, the next nearest neighboring (NNN) Cu atom, and the third nearest neighboring (3NN) Cu atom, respectively. Figure 1C shows the topography of the cleaved surface of Zn-Bi2212, and the atoms are Bi atoms. There are supermodulations on the surface along the diagonal direction. The Cu atoms are supposed to be just below the Bi atoms on the surface, even considering the impact of supermodulation [34]. Due to the supermodulation, the Zn impurity is unclear on the topographic image. Following a previous study [3], the bound-state pattern induced by a Zn impurity can be recognized by the differential conductance mapping at −2 mV, and the result is shown in Figure 1D. Here, the differential conductance is proportional to the LDOS, and the brightest spot corresponds to the strongest in-gap density of states at −2 mV. Compared to a previous study [3], the center of the brightest spot is just above the Zn site. Eight bright spots also surround the Zn impurity symmetrically: four second-brightest spots near the NNN Cu atoms and four third-brightest spots near the 3NN Cu atoms. In contrast, no prominent spot is near the NN Cu atoms. Tunneling spectra are measured at Bi0 sites just above the Zn impurity, and the Bi atoms above the Cu atoms surrounding the Zn impurity; they are displayed in Figure 1E. The spectrum measured far away from the Zn impurity is also shown in the figure, and the superconducting coherence peaks are indicated by arrows at about ±37 meV. The finite zero-bias differential conductance is due to the impurity scattering in the d-wave superconductor [35–37]. On the spectrum measured at the Zn impurity, one can see the significant suppression of the coherence peak. Meanwhile, there is a solid bound state peak at Ω ≈ −1.7 mV, similar to the value from the previous report [3]. It should be noted that Ω slightly changes from −5 to 0 meV for different Zn impurities, and the peak amplitude also changes. This is possibly due to the slight difference in impurity scattering potential or the local superconducting gap [37, 38]. Nevertheless, a relatively small value of Ω compared to the superconducting gap suggests a strong scattering close to the unitary limit [7, 8]. The impurity bound state is weakened at the NNN and the 3NN Cu sites, and the peak is negligible at the NN Cu site. Meanwhile, the recovery of the coherence peak energy and the peak amplitude only correlates to the distance between the site and the Zn impurity.

FIGURE 1

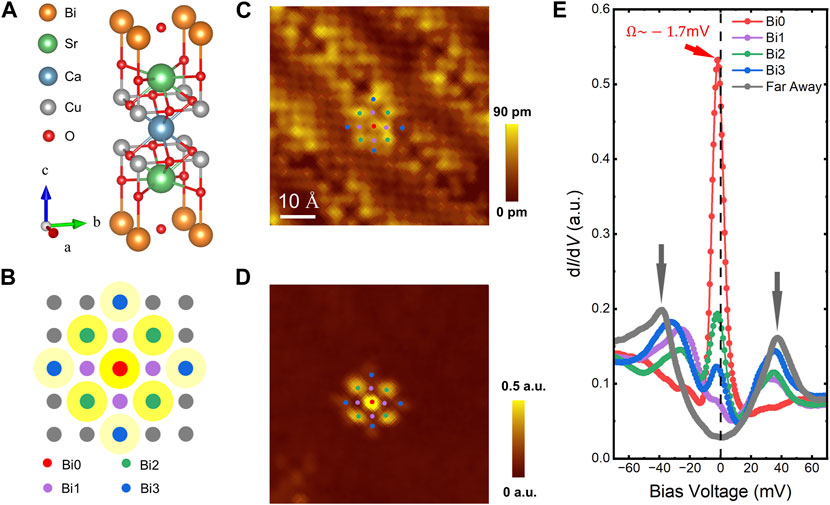
FIGURE 1. (A) Crystal structure of Bi2212 shown in a unit cell. (B) Schematic diagram of the BiO plane with a single Zn impurity (denoted by a red spot). The impurity bound state is also illustrated in the figure as yellow patterns, and different colors plot the neighbored Cu atoms in the central effective area by the Zn. (C) Atomically resolved topographic image near a Zn impurity. (D) Differential conductance mapping recorded at −2 mV in the same field of view of (C). Locations of the Zn impurity and neighbored Cu atoms are shown in (C) and (D) by using some symbols in (B). (E) Several tunneling spectra measured at specific positions. The shown spectra for Bi1, Bi2, and Bi3 sites are the average one of four spectra measured above the four corresponding Bi1, Bi2, and Bi3 sites.

The supermodulation structure in Bi2212 can spontaneously introduce lattice defects, particularly Bi defects, and it is interesting to investigate the influence on the Zn impurity by the missing Bi atoms. One example in the presence of Bi vacancies is shown in Figure 2, and the topography is shown in Figure 2A. Two Bi1 atoms are missing above two NN Cu sites around the Zn impurity, as illustrated in Figure 2D. This feature is more evident in the inverse Fourier transform result to the Bragg peaks and the vectors around ($\pm \frac{\mathrm{\pi }}{a_0}$, $\pm \frac{\mathrm{\pi }}{a_0}$), where $a_0$ is the lattice constant of Zn-Bi2212. The inverse Fourier transform image is shown in Figure 2B. Figure 2C shows the differential conductance mapping measured at −2 mV, similar to the one measured in the typical case of the Zn impurity without Bi vacancies (Figure 1D). We also measure the tunneling spectra at the Zn and Bi1 sites or vacancies above the NN Cu atom. The results are shown in Figure 2E. The spectrum measured at the Zn impurity shows a strong resonance peak at about −2.3 mV. It should be noted that impurity resonance peaks have different energies and amplitudes for different impurities. Therefore, the slight shift of the bound state energy and the decrease of the bound state peak is unlikely due to the B1 vacancies. For spectra measured at the Bi1 sites and Bi1 vacancies just above NN Cu sites, the impurity bound state peaks are weak at these two positions.

FIGURE 2

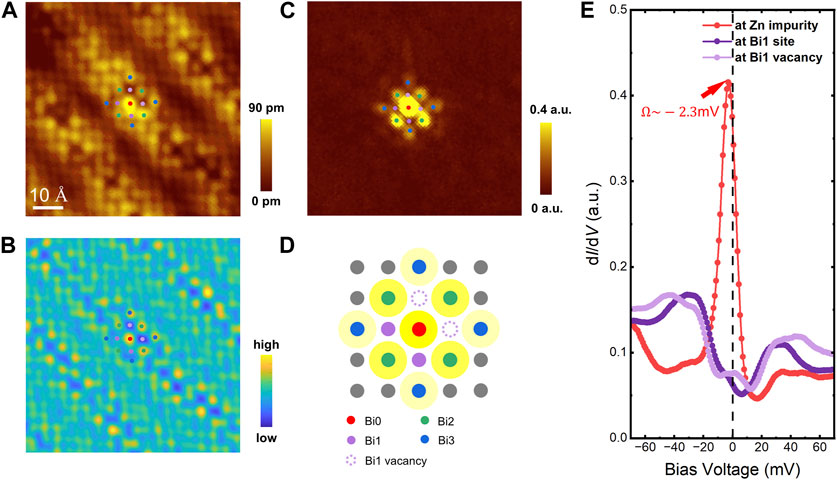
FIGURE 2. (A) Typical topographic image near a Zn impurity with two Bi1 vacancies on the surface. (B) Inverse Fourier transform results in the Bragg peaks and the vectors around ($\pm \frac{\mathrm{\pi }}{a_0}$, $\pm \frac{\mathrm{\pi }}{a_0}$) in the Fourier transform pattern of (A). There are two Bi vacancies near the Zn impurity. (C) Differential conductance mapping measured at −2 mV in the same field of view as (A). (D) Schematic illustration of the Zn impurity with two Bi1 vacancies, just above two NN Cu sites. (E) Tunneling spectra measured at Zn impurity and B1 sites or vacancies. The spectrum for Bi1 sites (or Bi1 vacancies) is the average of two spectra measured above two Bi1 sites (or two Bi1 vacancies).

Although Bi1 vacancies have negligible influence on the bound state pattern on the surface, Bi2 vacancies seem to have a significant impact on the pattern. One example is shown in Figure 3. The Bi2 atom is missing from the topography shown in Figure 3A, while the resonance spot of the bound state pattern is missing simultaneously (Figure 3B). Figure 3D shows tunneling spectra measured at the Zn impurity, the Bi2 site above the NNN Cu atom, and the Bi2 vacancy above the NNN Cu atom. The resonance peak on the spectrum measured at the Bi2 site is similar to that shown in Figure 1E. However, the resonance peak is significantly weakened on the spectrum measure at the Bi2 vacancy. To investigate the electronic property of the Bi2 vacancy, we measure a set of tunneling spectra along an arrowed line in Figure 3A across a Bi2 site, a Zn impurity, and the Bi2 vacancy, and the result is shown in Figure 3F. Meanwhile, the corresponding height profile along the arrowed line is shown in Figure 3E, and the Bi2 vacancy can be observed as a valley. The superconducting gapped feature can be identified on spectra measured at the terminus of the arrowed line, indicating that the impurity scattering from the Zn dopant is localized. Above the Zn impurity, the bound state peak can be seen on the spectra measured at positions within the range with a diameter approximately equaling the size of a Bi atom. The bound state peak with a weakened amplitude can be seen on the spectra near the Bi2 atom. However, the bound state peak is absent on the spectra measured near the Bi2 vacancy. Consequently, one can robustly conclude that the Bi2 vacancy will strongly affect the Zn impurity-induced bound state pattern on the surface and cause the absence of the scattering resonance spot at the Bi vacancy.

FIGURE 3

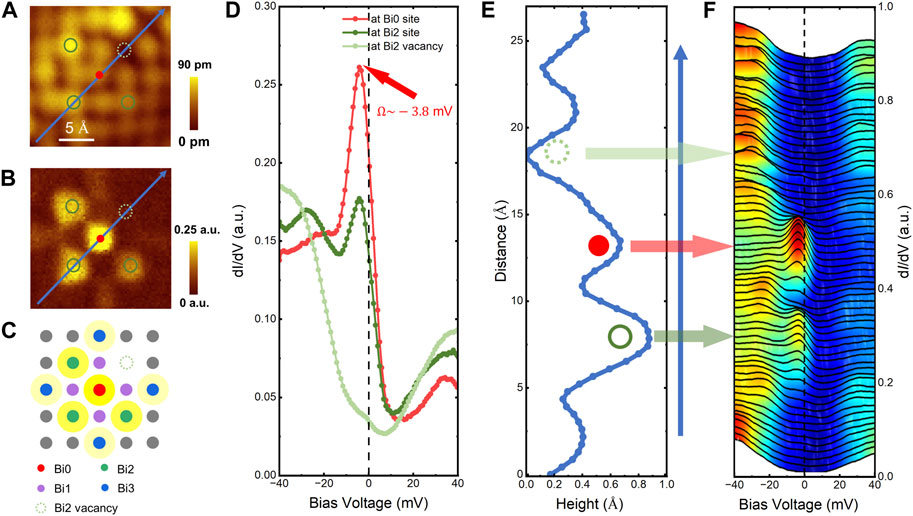
FIGURE 3. (A) Topographic image near a Zn impurity with a Bi2 vacancy on the surface. (B) Differential conductance mapping measured at −2 mV measured in the same area of (A). The resonance spot of the bound state pattern is missing at the B2 vacancy site. (C) Schematic illustration of the Zn impurity with a Bi2 vacancy nearby. (D) Spectra measured at the Zn impurity, Bi2 sites above the NNN Cu atoms, and Bi2 vacancy above the NNN Cu atom. The spectrum of Bi2 sites is the average one of three spectra measured above three NNN Cu sites. The bound state peak behaves differently at the Bi2 vacancy and at Bi2 sites. (E) Height profile along the arrowed line in (A) or (B). (F) A set of tunneling spectra measured along the arrowed line in (A) or (B). The bound state peak is missing from the spectra measured near the Bi2 vacancy.

Here we report the influence on the Zn impurity-induced bound states by the out-of-plane Bi defects on the surface, which has not been reported in previous works [3, 19, 20]. The detailed STM/STS measurement shows that the Bi2 vacancy significantly weakens the bound-state peak and the resonance spot measured at the impurity bound state energy. Besides, a similar phenomenon can also be observed in the case of the Bi3 vacancy, and the corresponding resonance spot also disappears in the presence of the Bi3 vacancy. In contrast, the Bi1 vacancy does not affect the bound state pattern at the bound state energy. However, it should be noted that the impurity bound state peak is negligible at the Bi1 site. Therefore, it is understandable that the Bi1 vacancy does not influence the impurity bound state pattern. Bi atoms are located in the charge-reservoir layer, and the Bi vacancy may induce a slight hole doping. Meanwhile, the Bi vacancy may increase the distance between the apical oxygen and the Cu atom underneath, which may be related to the superconductivity in the CuO₂ layer [39–41] and further modify the impurity bound state. These are the possible ways that the Bi vacancy in the charge-reservoir layer affects the impurity bound state in the CuO₂ layer. However, the resonance peak recorded just above the Zn impurity seems to be not affected by any Bi vacancies. In addition, the Bi1 site is closer to the Zn impurity than the Bi2 site, but the Bi1 vacancy has negligible influence on the impurity-bound-state peak or the bound-state pattern at the peak energy. Therefore, it is unlikely that the Bi vacancies will directly influence the Zn impurity state on the CuO₂ plane.

Based on theoretical calculations [26–28], the impurity bound state pattern behaves differently on the CuO₂ plane and the surface BiO layer because the measured pattern on the surface is affected by the interlayer tunneling matrix elements with the so-called “filter effects”. In this picture, the hybridization of the in-plane $3d_{x^2-y^2}$ orbital of the metal atom (Zn or Cu) with p orbitals of apical O and Bi right above is forbidden by symmetry. Specifically, the strongest impurity bound state is located at four NN Cu atoms from the calculation [26–28], and the result is shown in Figure 4A. Figure 4B shows the tunneling process proposed by the theory, and the tunneling to the Bi atom through 6p_z orbital on the surface is from the in-plane ${3d}_{x^2-y^2}$ orbital of neighboring metal atoms (Zn or Cu) instead of the one right underneath. Additionally, the tunneling is assisted by the p orbital of apical O just below the surface Bi atom [28]. Based on this model, the obtained resonance pattern (Figure 4C) on the surface is very similar to the experimental result (Figure 3B) in the presence of a Bi2 vacancy since the impurity bound state in the CuO₂ plane cannot show up without the Bi2 atom (Figure 4D). Therefore, our experiment strongly supports the theoretical calculation results of the “filter effects” in the interlayer tunneling process.

FIGURE 4

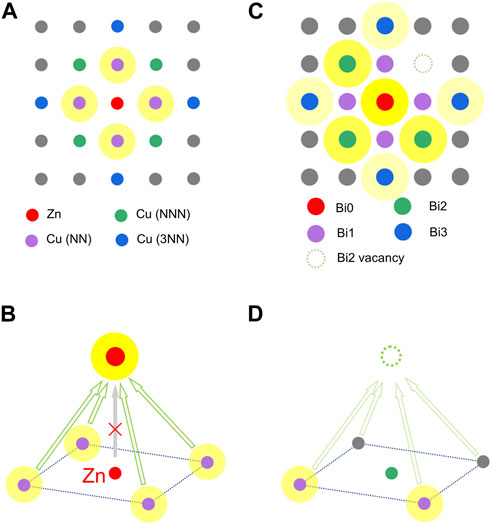
FIGURE 4. (A) Schematic illustration of CuO₂ plane with one Zn impurity. (B) Schematic illustration of the tunneling process when the STM tip is directly above the Bi0 site. (C) Schematic illustration of BiO plane corresponding to the case of one Zn impurity with one Bi2 defect. (D) Schematic illustration of the tunneling process when the STM tip is directly above the Bi2 vacancy. The dotted arrows indicate that the missing Bi atom will lead to the failure of the tunneling from the neighboring Cu-3d_x2-y2 to the surface and then to the STM tip.

Conclusion

In summary, we have carried out the studies on the influence of Bi defects on Zn impurity scattering resonance states in Zn-Bi2212 using STM/STS. Our findings reveal several intriguing characteristics: i) In the case of Bi1 defects, we observed no significant deviations compared to normal resonance states. ii) for the Bi2 defects situation, we detected a notable absence of LDOS at the corresponding Cu sites beneath these Bi defects. These observations collectively indicate that the BiO plane plays a crucial role in the impurity-induced bound state formation from a different perspective. Our research underscores how structural distortions and defects, even outside the CuO₂ plane, significantly impact resonance states we measured through STM/STS. These results shed new light on understanding the interaction between different layers in cuprate and facilitate the comprehension of the tunneling process.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZW: Investigation, Visualization, Formal Analysis, Writing–original draft, Writing–review and editing. SF: Formal Analysis, Writing–original draft. HaL: Validation, Writing–original draft. HuL: Writing–original draft. HY: Investigation, Formal Analysis, Writing–review and editing, Writing–original draft. H-HW: Supervision, Investigation, Writing–review and editing, Project administration, Funding acquisition.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by National Key R&D Program of China (No. 2022YFA1403201), and National Natural Science Foundation of China (Nos. 12061131001 and 11927809).

Acknowledgments

We thank X. Zhu for the efforts in growing the single crystals, and we also acknowledge helpful discussions with S. Wan, X. Zhang and R. Yan.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From quantum matter to high-temperature superconductivity in copper oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Alloul H, Bobroff J, Gabay M, Hirschfeld PJ. Defects in correlated metals and superconductors. Rev Mod Phys (2009) 81:45–108. doi:10.1103/revmodphys.81.45

CrossRef Full Text | Google Scholar

3. Pan SH, Hudson EW, Lang KM, Eisaki H, Uchida S, Davis JC. Imaging the effects of individual zinc impurity atoms on superconductivity in Bi₂Sr₂CaCu₂O_8+δ. Nature (2000) 403:746–50. doi:10.1038/35001534

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hudson EW, Lang KM, Madhavan V, Pan SH, Eisaki H, Uchida S, et al. Interplay of magnetism and high-T_c superconductivity at individual Ni impurity atoms in Bi₂Sr₂CaCu₂O_8+δ. Nature (2001) 411:920–4. doi:10.1038/35082019

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Anderson PW. Theory of dirty superconductors. J Phys Chem Sol (1959) 11:26–30. doi:10.1016/0022-3697(59)90036-8

CrossRef Full Text | Google Scholar

6. Lee PA. Localized states in a d-wave superconductor. Phys Rev Lett (1993) 71:1887–90. doi:10.1103/PhysRevLett.71.1887

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Salkola MI, Balatsky AV, Scalapino DJ. Theory of scanning tunneling microscopy probe of impurity states in a d-wave superconductor. Phys Rev Lett (1996) 77:1841–4. doi:10.1103/PhysRevLett.77.1841

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Balatsky AV, Salkola MI, Rosengren A. Impurity-induced virtual bound states in d-wave superconductors. Phys Rev B (1995) 51:15547–51. doi:10.1103/PhysRevB.51.15547

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Abrikosov AA, Gor'kov LP. Contribution to the throry of superconducting alloys with paramagnetic impurities. Sov Phys JETP (1961) 12:1243–53.

Google Scholar

10. Larkin A, Varlamov A. Theory of fluctuations in superconductors. New York: Oxford University Press (2005). doi:10.1093/acprof:oso/9780198528159.001.0001

CrossRef Full Text | Google Scholar

11. Botelho SS, Sá de Melo CAR. Lifshitz transition in d-wave superconductors. Phys Rev B (2005) 71:134507. doi:10.1103/PhysRevB.71.134507

CrossRef Full Text | Google Scholar

12. Yerin Y, Varlamov AA, Petrillo C. Topological nature of the transition between the gap and the gapless superconducting states. Europhys Lett (2022) 138:16005. doi:10.1209/0295-5075/ac64b9

CrossRef Full Text | Google Scholar

13. Yerin Y, Petrillo C, Varlamov AA. Topological phase transition between the gap and the gapless superconductors. Scipost Phys Core (2022) 5:009. doi:10.21468/SciPostPhysCore.5.1.009

CrossRef Full Text | Google Scholar

14. Fukuzumi Y, Mizuhashi K, Takenaka K, Uchida S. Universal superconductor-insulator transition and T_c depression in Zn-substituted high-T_c cuprates in the underdoped regime. Phys Rev Lett (1996) 76:684–7. doi:10.1103/PhysRevLett.76.684

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bonn DA, Kamal S, Zhang K, Liang R, Baar DJ, Klein E, et al. Comparison of the influence of Ni and Zn impurities on the electromagnetic properties of YB₂Cu₃O_6.95. Phys Rev B (1994) 50:4051–63. doi:10.1103/PhysRevB.50.4051

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nachumi B, Keren A, Kojima K, Larkin M, Luke GM, Merrin J, et al. Muon spin relaxation studies of Zn-substitution effects in high-T_c cuprate superconductors. Phys Rev Lett (1996) 77:5421–4. doi:10.1103/PhysRevLett.77.5421

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bernhard C, Tallon JL, Bucci C, De Renzi R, Guidi G, Williams GVM, et al. Suppression of the superconducting condensate in the high-T_c cuprates by Zn substitution and overdoping: evidence for an unconventional pairing state. Phys Rev Lett (1996) 77:2304–7. doi:10.1103/PhysRevLett.77.2304

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Nakano T, Momono N, Nagata T, Oda M, Ido M. Contrasting Ni- and Zn-substitution effects on magnetic properties and superconductivity in La_2-xSr_xCuO₄. Phys Rev B (1998) 58:5831–8. doi:10.1103/PhysRevB.58.5831

CrossRef Full Text | Google Scholar

19. Machida T, Kato T, Nakamura H, Fujimoto M, Mochiku T, Ooi S, et al. Disappearance of zinc impurity resonance in large-gap regions of Bi₂Sr₂CaCu₂O_8+δ probed by scanning tunneling spectroscopy. Phys Rev B (2010) 82:180507. doi:10.1103/PhysRevB.82.180507

CrossRef Full Text | Google Scholar

20. Machida T, Kato T, Nakamura H, Fujimoto M, Mochiku T, Ooi S, et al. Quantum interference of impurity bound states in Bi₂Sr₂Ca(Cu_1-xZn_x)₂O_8+δ probed by scanning tunneling spectroscopy. Phys Rev B (2011) 84:064501. doi:10.1103/PhysRevB.84.064501

CrossRef Full Text | Google Scholar

21. Mahajan AV, Alloul H, Collin G, Marucco JF. ⁸⁹Y NMR probe of Zn induced local moments in YBa₂(Cu_1-yZn_y)₃O_6+x. Phys Rev Lett (1994) 72:3100–3. doi:10.1103/PhysRevLett.72.3100

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Alloul H, Mendels P, Casalta H, Marucco JF, Arabski J. Correlations between magnetic and superconducting properties of Zn-substituted YBa₂Cu₃O_6+x. Phys Rev Lett (1991) 67:3140–3. doi:10.1103/physrevlett.67.3140

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hirota K. Neutron scattering studies of Zn-doped La_2−xSr_xCuO₄. Physica C (2001) 357-360:61–8. doi:10.1016/S0921-4534(01)00195-2

CrossRef Full Text | Google Scholar

24. Suchaneck A, Hinkov V, Haug D, Schulz L, Bernhard C, Ivanov A, et al. Incommensurate magnetic order and dynamics induced by spinless impurities in YBa₂Cu₃O_6.6. Phys Rev Lett (2010) 105:037207. doi:10.1103/PhysRevLett.105.037207

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kimura H, Hirota K, Matsushita H, Yamada K, Endoh Y, Lee S-H, et al. Neutron-scattering study of static antiferromagnetic correlations in La_2-xSr_xCu_1-yZn_yO₄. Phys Rev B (1999) 59:6517–23. doi:10.1103/PhysRevB.59.6517

CrossRef Full Text | Google Scholar

26. Martin I, Balatsky AV, Zaanen J. Impurity states and interlayer tunneling in high temperature superconductors. Phys Rev Lett (2002) 88:097003. doi:10.1103/PhysRevLett.88.097003

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhu J-X, Lee TK, Ting CS, Hu C-R. Quasiparticle resonant states induced by a unitary impurity in a d-wave superconductor. Phys Rev B (2000) 61:8667–70. doi:10.1103/PhysRevB.61.8667

CrossRef Full Text | Google Scholar

28. Kreisel A, Choubey P, Berlijn T, Ku W, Andersen BM, Hirschfeld PJ. Interpretation of scanning tunneling quasiparticle interference and impurity states in cuprates. Phys Rev Lett (2015) 114:217002. doi:10.1103/PhysRevLett.114.217002

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lv Y-F, Wang W-L, Peng J-P, Ding H, Wang Y, Wang L, et al. Mapping the electronic structure of each ingredient oxide layer of high-T_c cuprate superconductor Bi₂Sr₂CaCu₂O_8+δ. Phys Rev Lett (2015) 115:237002. doi:10.1103/PhysRevLett.115.237002

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Fan J-Q, Yu X-Q, Cheng F-J, Wang H, Wang R, Ma X, et al. Direct observation of nodeless superconductivity and phonon modes in electron-doped copper oxide Sr_1−xNd_xCuO₂. Natl Sci Rev (2022) 9:nwab225. doi:10.1093/nsr/nwab225

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Lovleena BIK, Kholkin AL, Kumar B. Structural changes in ab-plane of Zn doped Bi-2212 HTSC single crystals. Physica C (2007) 451:44–8. doi:10.1016/j.physc.2006.10.003

CrossRef Full Text | Google Scholar

32. Liu S-Y, Zhang W-T, Zhao L, Liu H-Y, Wu Y, Liu G-D, et al. Growth and characterization of high-quality single crystals of Ni- and Zn-doped Bi₂Sr₂Ca(Cu_2−xM_x)O_8+δ (M = Ni or Zn) high-temperature superconductors. Chin Phys Lett (2012) 29:087401. doi:10.1088/0256-307X/29/8/087401

CrossRef Full Text | Google Scholar

33. Huang D, Liu S, Zeljkovic I, Mitchell JF, Hoffman JE. Etching of Cr tips for scanning tunneling microscopy of cleavable oxides. Rev Sci Instrum (2017) 88:023705. doi:10.1063/1.4976567

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Hamidian MH, Firmo IA, Fujita K, Mukhopadhyay S, Orenstein JW, Eisaki H, et al. Picometer registration of zinc impurity states in Bi₂Sr₂CaCu₂O_8+δ for phase determination in intra-unit-cell Fourier transform STM. New J Phys (2012) 14:053017. doi:10.1088/1367-2630/14/5/053017

CrossRef Full Text | Google Scholar

35. Pan SH, O'Neal JP, Badzey RL, Chamon C, Ding H, Engelbrecht JR, et al. Microscopic electronic inhomogeneity in the high-Tc superconductor Bi₂Sr₂CaCu₂O_8+δ. Nature (2001) 413:282–5. doi:10.1038/35095012

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Renner C, Fischer O. Vacuum tunneling spectroscopy and asymmetric density of states of Bi₂Sr₂CaCu₂O_8+δ. Phys Rev B (1995) 51:9208–18. doi:10.1103/PhysRevB.51.9208

PubMed Abstract | CrossRef Full Text | Google Scholar

37. McElroy K, Lee J, Slezak JA, Lee D-H, Eisaki H, Uchida S, et al. Atomic-scale sources and mechanism of nanoscale electronic disorder in Bi₂Sr₂CaCu₂O_8+δ. Science (2005) 309:1048–52. doi:10.1126/science.1113095

PubMed Abstract | CrossRef Full Text | Google Scholar

38. McElroy K, Lee D-H, Hoffman JE, Lang KM, Lee J, Hudson EW, et al. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi₂Sr₂CaCu₂O_8+δ. Phys Rev Lett (2005) 94:197005. doi:10.1103/PhysRevLett.94.197005

PubMed Abstract | CrossRef Full Text | Google Scholar

39. O’Mahony SM, Ren W, Chen W, Chong YX, Liu X, Eisaki H, et al. On the electron pairing mechanism of copper-oxide high temperature superconductivity. Proc Natl Acad Sci USA (2022) 119:e2207449119. doi:10.1073/pnas.2207449119

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zou C, Hao Z, Li H, Li X, Ye S, Yu L, et al. Effect of structural supermodulation on superconductivity in trilayer cuprate Bi₂Sr₂Ca₂Cu₃O_10+δ. Phys Rev Lett (2020) 124:047003. doi:10.1103/PhysRevLett.124.047003

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Slezak JA, Lee J, Wang M, McElroy K, Fujita K, Andersen BM, et al. Imaging the impact on cuprate superconductivity of varying the interatomic distances within individual crystal unit cells. Proc Natl Acad Sci USA (2008) 105:3203–8. doi:10.1073/pnas.0706795105

PubMed Abstract | CrossRef Full Text | Google Scholar