Quantum squeezing induced nonreciprocal enhancement of optomechanical cooling

We theoretically propose how to achieve nonreciprocal enhancement of mechanical cooling in a compound cavity optomechanical system composed of an optomechanical resonator and a χ⁽²⁾-nonlinear resonator. By parametric pumping the χ⁽²⁾-nonlinear resonator unidirectionally with a classical coherent field, quantum squeezing of the resonator mode emerges in one direction but not in the other, resulting in asymmetric optical detuning and a tunable chiral photon interaction between two resonators. As a result, nonreciprocal mechanical cooling is achieved. More importantly, enhanced mechanical cooling deep into the ground-state can be achieved in the selected directions due to the squeezing effect. These results provide an experimentally feasible way to realize nonreciprocal ground-state cooling of mechanical resonator, which may have a wide range of applications in quantum communication and quantum technologies.

1 Introduction

Cavity optomechanical (COM) systems [1], featuring the interaction between light and mechanical vibrations, have emerged as a promising platform for quantum information processing [2], ultra-sensitive sensing [3, 4], and investigating macroscopic quantum phenomena [5–7], etc. However, in order to reveal the various quantum phenomena in the COM devices, such as quantum entanglement [5], nonclassical states generation [6], and mechanical quantum squeezing [7], it is a crucial step to suppress the uncontrollable thermal noise of mechanical vibrations [8, 9]. Up to now, COM-based ground-state cooling of mechanical resonators has been proposed in theory [10–12] and demonstrated in experiments [13–15] by exploiting different cooling mechanisms such as feedback cooling and sideband cooling. Recently, to overcome the resolved sideband limit in the sideband cooling scheme or to realize the synchronous cooling of multiple mechanical modes, several proposals have been made by introducing auxiliary optical or magnon modes [16–18], nonreciprocal coupling [19–21], nonlinearity effect [22, 23], as well as hybrid approaches [24–28].

In parallel, nonreciprocal devices that exhibit different responses when interchanging the ports of input and output have been demonstrated experimentally with a wide range of structures, including optical [29–33], acoustic [34–38], mechanics [39], and optomechanics [40–45]. In a COM system, the optical nonreciprocal effect can be realized based on the momentum difference between forward and backward-moving light beams [40], the phase difference between the optomechanical coupling rates [41–44], or the optomechanically induced transparency and amplification effect [45]. In the past few decades, various schemes have also been proposed to realize on-chip nonreciprocal optical devices, which are generally based on nonlinear or chiral interactions [46–50], non-Hermitian [51, 52], synthetic gauge fields [53, 54], thermal motion of atoms [55–58], and the Sagnac effect in spinning resonators [30, 59–64]. By selectively rotating the resonators and appropriately adjusting their rotation directions [30], the frequency of the optical mode undergoes a Sagac-Fizeau frequency shift, which provides a unique approach for achieving, e.g., a one-way photon blockade [59, 60], a nonreciprocal phonon laser [61], backscattering-immune quantum entanglement [62, 63], and nanoparticle sensing [64]. Very recently, nonreciprocal phononic devices have also been realized by using circulating fluids [34], macroscopic metamaterials [65], and nonlinear media [36, 66]. As a crucial element for engineering the propagation of phonons, nonreciprocal phononic devices have a wide range of applications, including phonon isolation [34], one-way mechanical networks [36, 65], acoustic imaging, and chiral phonon transport or cooling [19, 20, 66]. In particular, nonreciprocal mechanical cooling was theoretically proposed by using the relativistic Sagnac effect in a spinning COM device [67]. However, these schemes are technically challenging in experiments as they require high-speed rotation of the optical resonators while maintaining stable resonator-fiber or resonator-resonator coupling strengths [30]. In addition, the mechanical modes are typically excited in the resonators of micron-scale dimensions, as opposed to the millimeter-sized resonators suitable for rotation. Therefore, in terms of simplifying experimental implementation for nonreciprocal mechanical cooling, seeking an efficient approach that can be free from spinning components is highly desirable.

We note that quantum squeezing has recently been demonstrated to be effective for amplifying the interactions between quantum objects [68, 69], and it has become a versatile tool for solving various challenging tasks. Recently, directional quantum squeezing has been used to realize optical diodes and quasicirculators [70], nonreciprocal photon correlations or blockades [71–73], and nonreciprocal magnon lasers [74], which exhibit superior unique properties and open up a new route for realizing chip-compatible nonreciprocal devices. Inspired by these pioneering works, here we study how to achieve nonreciprocal enhancement of mechanical cooling by the quantum squeezing effect. We find that by unidirectionally pumping the χ⁽²⁾-nonlinear resonator, asymmetric optical detuning and a tunable chiral photon interaction between two resonators can be achieved. As a result, nonreciprocal mechanical cooling is achieved when the device is driven in one direction but not in the other. Moreover, we find that the cooling efficiency is improved; that is, mechanical cooling deep into the ground-state is accessible due to the squeezing effect. Compared to the schemes based on spinning the optical resonators [67], our scheme for achieving nonreciprocal enhancement of optomechanical cooling requires only two-mode matching in one resonator, and therefore could be practical to implement in experiments. As such, we anticipate that our work could serve as a useful tool to explore controlled switching between classical and quantum states, provide a solid foundation to engineer various backscatter-immune quantum effects with diverse nonreciprocal devices, and facilitate a variety of emerging quantum technologies ranging from quantum information processing to quantum sensing.

2 Theoretical model

As shown in Figure 1, we consider a compound COM system consisting of two coupled whispering-gallery-mode (WGM) microtoroid resonators and two nearby optical waveguides. One of the resonators R₁ (with frequency ω₁ and decay rate κ₁) supports a mechanical breathing mode b (with frequency ω_m and effective mass m) and is driven by a signal field of frequency ω_l from port 1 (or port 2) corresponding to the forward-input case (or backward-input case). The other resonator R₂ (with frequency ω₂ and decay rate κ₂) is made of silicon nitride, aluminum nitride, or lithium niobate [75–80], which can generate the common χ⁽²⁾-nonlinearity and support the parametric amplification process [68, 69]. To achieve nonreciprocal enhancement of mechanical cooling, a strong pump field (with frequency ω_p and phase θ_p) is pumped from port 3. In R₂, the pump field generates a squeezing interaction with strength Λ for the counterclockwise (CCW) mode a_2,↺, which is squeezed to a mode a_s,↺ due to the directional phase-matching condition (i.e., the conservation of energy and momentum) [68, 69], but the clockwise (CW) mode a_2,↻ is unsqueezed [70]. For the forward-input case, in a frame rotating at frequency ω_p/2, the total Hamiltonian of this system can be written as (ℏ = 1):

$\begin{array}{cc}\hfill H=& {\mathrm{\Delta }}_1^p{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }+{\mathrm{\Delta }}_2^p{a}_{2,\circlearrowleft }^{†}{a}_{2,\circlearrowleft }+{\omega }_m{b}^{†}b+J_0\left(a_{1,\circlearrowright }^{†}{a}_{2,\circlearrowleft }+a_{2,\circlearrowleft }^{†}{a}_{1,\circlearrowright }\right)\hfill \\ \hfill & +{\mathrm{\Delta }}_c{c}^{†}c+g_d\left(a_{2,\circlearrowleft }^{†2}c+a_{2,\circlearrowleft }^2{c}^{†}\right)-g{x}_0{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }\left(b+b^{†}\right)\hfill \\ \hfill & +i{\epsilon }_l\left(a_{1,\circlearrowright }^{†}{e}^{-i{\mathrm{\Delta }}_{\text{in}}t}-a_{1,\circlearrowright }{e}^{i{\mathrm{\Delta }}_{\text{in}}t}\right)+i{\lambda }_p\left(c^{†}-c\right),\hfill \end{array}(1)$

where ${\mathrm{\Delta }}_{\mathrm{1,2}}^p={\omega }_{\mathrm{1,2}}-{\omega }_p/2$, Δ_in = ω_l − ω_p/2, and Δ_c = ω_c − ω_p. ω_c is the frequency of the second-harmonic modes c in R₂. J₀ denotes the coupling strength between the two WGM resonators. g and g_d are the COM coupling rate in the radiation-pressure process and the nonlinear single-photon coupling strength in the parametric nonlinear process. ${\epsilon }_l=\sqrt{2{\kappa }_1{P}_{\text{in}}/\hslash {\omega }_l}$ is the drive strength with input power P_in. ${\lambda }_p=\sqrt{2{\kappa }_2{P}_p/\hslash {\omega }_p}$ is the pump light with the power P_p. The dynamical equation of c can be solved by the Heisenberg equation

$\dot{c}=-\left(i{\mathrm{\Delta }}_c+{\kappa }_p\right)c+{\lambda }_p-i{g}_d{a}_{2,\circlearrowleft }^2.(2)$

FIGURE 1

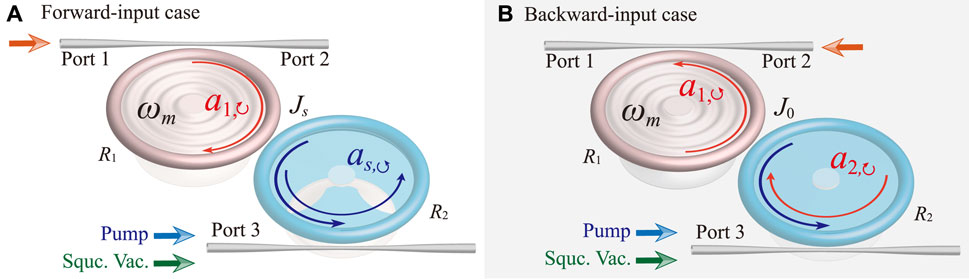
FIGURE 1. Schematic illustration of the COM system composed of two coupled WGM resonators (R₁ and R₂). To achieve a nonreciprocal enhancement of mechanical cooling, the system is pumped from port 3 with a classical coherent field and a broadband squeezed-vacuum-field, where the coherent field causes the CCW mode a_2,↺ to be squeezed a_s,↺, while the squeezed-vacuum field keeps the dissipation of a_s,↺ the same as that in regular mode. (A) For the forward-input case, a CW mode a_1,↻ in R₁ can be stimulated by driving the system from port 1, which is coupled to the squeezed mode a_s,↺ with a coupling rate J_s. (B) For the backward-input case, a CCW mode a_1,↺ in R₁ can be excited by driving the system from port 2, which is coupled to the unsqueezed mode a_2,↻ in R₂ with a coupling rate J₀.

Here, κ_p denotes the external decay rate for the pump field. We consider the strong pump field to excite mode c in R₂ [70]. In this strong pump case, we can omit the terms related to g in Eq. 2 for the purpose of calculating the steady state of mode c c_s = λ_p/(iΔ_c + κ_p). After that, the Hamiltonian of Eq. 1 can be rewritten as

$\begin{array}{cc}\hfill \mathcal{H}& ={\mathrm{\Delta }}_1^p{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }+{\mathrm{\Delta }}_2^p{a}_{2,\circlearrowleft }^{†}{a}_{2,\circlearrowleft }+{\omega }_m{b}^{†}b,\hfill \\ \hfill & +J_0\left(a_{1,\circlearrowright }^{†}{a}_{2,\circlearrowleft }+a_{2,\circlearrowleft }^{†}{a}_{1,\circlearrowright }\right)-g{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }\left(b+b^{†}\right),\hfill \\ \hfill & +i{\epsilon }_l{a}_{1,\circlearrowright }^{†}{e}^{-i{\mathrm{\Delta }}_{\text{in}}t}+\frac{\mathrm{\Lambda }}{2}{a}_{2,\circlearrowleft }^{†2}{e}^{-i{\theta }_p}+\mathrm{h}.\mathrm{c}.,\hfill \end{array}(3)$

where the squeezing strength and phase are

$\mathrm{\Lambda }=2g_d\sqrt{\frac{2{\kappa }_2{P}_p}{\left({\mathrm{\Delta }}_c^2+{\kappa }_p^2\right)\hslash {\omega }_p}},\theta =-\mathrm{A}\mathrm{r}\mathrm{g}\left(c_s\right).(4)$

It is clearly seen that the squeezing strength Λ is dependent on the second-order polarizability of the medium (i.e., g_d) and pump power P_p. Therefore, the squeezing strength Λ can be modulated experimentally by the pump power P_p [75–80]. It is worth noting that the external pump field will cause additional thermalization noise in CCW mode in R₂. According to Refs. [68, 69], by applying a broadband squeezed-vacuum-field (with frequency ω_v and phase θ_v), the additional noise can be suppressed under the condition θ_v − θ_p = ±nπ (n = 1, 3, 5, … ). To transform $\mathcal{H}$ to the squeezing picture, we define the squeezed operator a_s,↺ via the Bogoliubov transformation [68, 69]:

$a_{s,\circlearrowleft }=\cosh \left(r\right)a_{2,\circlearrowleft }+e^{-i{\theta }_p}\sinh \left(r\right)a_{2,\circlearrowleft }^{†},$

where r = (1/4) ln[(1 + β)/(1 − β)] is the squeezing parameter, and $\beta =\mathrm{\Lambda }/{\mathrm{\Delta }}_2^p$ is the pump ratio, which requires β < 1 to avoid system instability. Then, with the rotating wave approximation [68, 69], the Hamiltonian in the frame rotating at a frequency of Δ_in can be changed into

$\begin{array}{cc}\hfill {\mathcal{H}}_{\text{f}}& ={\mathrm{\Delta }}_1{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }+{\mathrm{\Delta }}_s{a}_{s,\circlearrowleft }^{†}{a}_{s,\circlearrowleft }+J_s\left(a_{1,\circlearrowright }^{†}{a}_{s,\circlearrowleft }+a_{s,\circlearrowleft }^{†}{a}_{1,\circlearrowright }\right)\hfill \\ \hfill & +{\omega }_m{b}^{†}b-g{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }\left(b+b^{†}\right)+i{\epsilon }_l\left(a_{1,\circlearrowright }^{†}-a_{1,\circlearrowright }\right),\hfill \end{array}(5)$

where Δ₁ = ω₁ − ω_l, ${\mathrm{\Delta }}_s={\mathrm{\Delta }}_2^{ps}-{\mathrm{\Delta }}_{\text{in}}$,

${\mathrm{\Delta }}_2^{ps}={\mathrm{\Delta }}_2^p\sqrt{1-\beta },J_s=J_0\cosh \left(r\right).$

It is clearly seen that the effective squeezed mode detuning Δ_s and the effective coupling rate J_s are controlled by the pump ratio β, thus causing a nonreciprocal enhancement of mechanical cooling. For the backward-input case (i.e., by driving the system from port 2), a CCW mode a_1,↺ in R₁ can be excited, which is coupled to the unsqueezed mode a_2,↻ in R₂ with a coupling rate of J₀. Therefore, the Hamiltonian of this system reads

$\begin{array}{cc}\hfill {\mathcal{H}}_{\text{b}}=& {\mathrm{\Delta }}_1{a}_{1,\circlearrowleft }^{†}{a}_{1,\circlearrowleft }+{\mathrm{\Delta }}_2{a}_{2,\circlearrowright }^{†}{a}_{2,\circlearrowright }+J_0\left(a_{1,\circlearrowleft }^{†}{a}_{2,\circlearrowright }+a_{2,\circlearrowright }^{†}{a}_{1,\circlearrowleft }\right)\hfill \\ \hfill & +{\omega }_m{b}^{†}b-g{a}_{1,\circlearrowleft }^{†}{a}_{1,\circlearrowleft }\left(b+b^{†}\right)+i{\epsilon }_l\left(a_{1,\circlearrowleft }^{†}-a_{1,\circlearrowleft }\right),\hfill \end{array}(6)$

where Δ₂ = ω₂ − ω_l. Comparing the Hamiltonians ${\mathcal{H}}_{\text{f}}$ and ${\mathcal{H}}_{\text{b}}$, it can be clearly seen that the detuning and coupling strengths between the resonators in these two Hamiltonians are completely different due to the directional squeezing effect.

In the following, we study the role of directional squeezing in achieving nonreciprocal mechanical cooling and enhancing mechanical cooling deep into the ground-state. To see this, we expand every operator as the sum of its steady value and a small fluctuation, i.e., o(t) = o^s + δo, where o(t) denotes one of these quantities a₁(t), a₂(t), and b(t). For the forward-input case, the effective linearized Hamiltonian of the fluctuation operators (hereafter we drop the notation “δ” for all fluctuation operators for the sake of simplicity, like “δa → a”) can be obtained:

$\begin{array}{cc}\hfill H_{\text{eff}}=& {\mathrm{\Delta }}_1^{\prime }{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }+{\mathrm{\Delta }}_s{a}_{s,\circlearrowleft }^{†}{a}_{s,\circlearrowleft }+J_s\left(a_{1,\circlearrowright }^{†}{a}_{s,\circlearrowleft }+a_{s,\circlearrowleft }^{†}{a}_{1,\circlearrowright }\right)\hfill \\ \hfill & +{\omega }_m{b}^{†}b+G\left(a_{1,\circlearrowright }+a_{1,\circlearrowright }^{†}\right)\left(b+b^{†}\right),\hfill \end{array}(7)$

where ${\mathrm{\Delta }}_1^{\prime }={\mathrm{\Delta }}_1+g(b^s+b^{s*})$, and $G=g{a}_{1,\circlearrowright }^s$ is the effective COM coupling rate with the steady-state values

$\begin{array}{cc}\hfill a_{1,\circlearrowright }^s& =\frac{{\epsilon }_l\left({\kappa }_2+i{\mathrm{\Delta }}_s\right)}{\left({\kappa }_1+i{\mathrm{\Delta }}_1^{\prime }\right)\left({\kappa }_2+i{\mathrm{\Delta }}_s\right)+J_s^2},\hfill \\ \hfill a_{s,\circlearrowleft }^s& =\frac{-i{J}_s{a}_{1,\circlearrowright }^s}{i{\mathrm{\Delta }}_s+{\kappa }_2},b^s=\frac{ig|a_{1,\circlearrowright }^s{|}^2}{i{\omega }_m+{\gamma }_m}.\hfill \end{array}(8)$

In our calculations, for the backward-input case, we need to, respectively, replace a_1,↻, a_s,↺, J_s, Δ_s with a_1,↺, a_2,↻, J₀, Δ₂. In the weak coupling regime, the reaction of the mechanical resonator to photon can be neglected [11]. So the fluctuation spectrum $S_{FF}\left(\omega \right)$ of the optomechanical force $F=a_{1,\circlearrowright }+a_{1,\circlearrowright }^{†}$ is totally determined by the optical part in the effective Hamiltonian of Eq. 7:

$H={\mathrm{\Delta }}_1^{\prime }{a}_{1,\circlearrowright }^{†}{a}_{1,\circlearrowright }+{\mathrm{\Delta }}_s{a}_{s,\circlearrowleft }^{†}{a}_{s,\circlearrowleft }+J_s\left(a_{1,\circlearrowright }^{†}{a}_{s,\circlearrowleft }+a_{s,\circlearrowleft }^{†}{a}_{1,\circlearrowright }\right).(9)$

The linearized quantum Langevin equations (QLEs) are given by

$\begin{array}{cc}\hfill {\dot{a}}_{1,\circlearrowright }& =-\left(i{\mathrm{\Delta }}_1^{\prime }+{\kappa }_1\right)a_{1,\circlearrowright }-i{J}_s{a}_{s,\circlearrowleft }+a_{1,\circlearrowright }^{\text{in}},\hfill \\ \hfill {\dot{a}}_{s,\circlearrowleft }& =-\left(i{\mathrm{\Delta }}_s+{\kappa }_2\right)a_{s,\circlearrowleft }-i{J}_s{a}_{1,\circlearrowright }+a_{s,\circlearrowleft }^{\text{in}},\hfill \end{array}(10)$

where $a_{1,\circlearrowright }^{\text{in}}$ and $a_{s,\circlearrowleft }^{\text{in}}$ are the noise operators. In the frequency domain, the linearized QLEs as

$\begin{array}{cc}\hfill -i\omega a_{1,\circlearrowright }\left(\omega \right)& =-\left(i{\mathrm{\Delta }}_1^{\prime }+{\kappa }_1\right)a_{1,\circlearrowright }\left(\omega \right)-i{J}_s{a}_{s,\circlearrowleft }\left(\omega \right)+a_{1,\circlearrowright }^{\text{in}}\left(\omega \right),\hfill \\ \hfill -i\omega a_{s,\circlearrowleft }\left(\omega \right)& =-\left(i{\mathrm{\Delta }}_s+{\kappa }_2\right)a_{s,\circlearrowleft }\left(\omega \right)-i{J}_s{a}_{1,\circlearrowright }\left(\omega \right)+a_{s,\circlearrowleft }^{\text{in}}\left(\omega \right).\hfill \end{array}(11)$

As a result, we obtain

$S_{FF}\left(\omega \right)=\frac{1}{A\left(\omega \right)}+\frac{1}{A^{*}\left(\omega \right)},(12)$

with $A(\omega )={\kappa }_1-i(\omega -{\mathrm{\Delta }}_1^{\prime })+J_s^2/[{\kappa }_2-i(\omega -{\mathrm{\Delta }}_s)]$. Following the methods as given in Ref. [11], we can obtain the rate equations of the mechanical mode as

$\begin{array}{cc}\hfill {\dot{P}}_n& ={\mathrm{\Gamma }}_{n\leftarrow n+1}{P}_{n+1}+{\mathrm{\Gamma }}_{n\leftarrow n-1}{P}_{n-1}-{\mathrm{\Gamma }}_{n-1\leftarrow n}{P}_n-{\mathrm{\Gamma }}_{n+1\leftarrow n}{P}_n\hfill \\ \hfill & +{\gamma }_m\left(n_m+1\right)\left(n+1\right)P_{n+1}+{\gamma }_m{n}_{m}n{P}_{n-1}\hfill \\ \hfill & -{\gamma }_m\left(n_m+1\right)n{P}_n-{\gamma }_m{n}_m\left(n+1\right)P_n,\hfill \end{array}(13)$

Here, γ_m is the mechanical damping rate; P_n is the probability for the mechanical element to be in the Fock state |n⟩; Γ_n−1←n is the transition rate from $\left|n\right.⟩$ to $\left|n-1\right.⟩$ induced by the effective magnomechanical coupling. According to the Fermi’s golden rule [8, 9], the heating and cooling rate are given by

${\mathrm{\Gamma }}_{+}=G^2{S}_{FF}\left(-{\omega }_m\right),{\mathrm{\Gamma }}_{-}=G^2{S}_{FF}\left({\omega }_m\right).$

Hence, we can obtain the final mean phonon number of the mechanical resonator and the quantum limit of cooling, which reads

$n_f=\frac{{\gamma }_m{n}_m+{\mathrm{\Gamma }}_m{n}_c}{{\gamma }_m+{\mathrm{\Gamma }}_m},n_c=\frac{{\mathrm{\Gamma }}_{+}}{{\mathrm{\Gamma }}_{-}-{\mathrm{\Gamma }}_{+}},(14)$

where Γ_m = G²[S_FF(ω_m) − S_FF(−ω_m)] is the net cooling rate, and $n_m={(e^{\hslash {\omega }_m/k_{B}T}-1)}^{-1}$ is the thermal phonon number with the environment temperature T and the Boltzmann constant k_B. We computed Eqs. 12–14 with experimentally feasible parameters to better understand the behavior of the nonreciprocal mechanical cooling [81, 82]. These parameters are λ = 1,550 nm, ω_m = 2π × 23.4 MHz, κ₁/ω_m = 3, κ₂/ω_m = 0.5, m = 5 × 10⁻¹¹ kg, mechanical quality factor Q_m = ω_m/γ_m = 10⁵, g = 2 × 10⁴ Hz, P_in = 1 mW, the initial phonon number n_m = 312 (environment temperature T = 300 mK), and J₀/ω_m = 1, which can be tuned by controlling the air gap between the resonators. For a controllable gap (0.2 μm ∼ 2 μm), J₀ is typically between 5 MHz ∼ 5 GHz [81]. We point out that the compound COM system consisting of two coupled silica microtoroid WGM resonators and a nearby optical fiber has been investigated experimentally [81, 82]. In addition, microring resonators with large χ⁽²⁾-nonlinearity and high-Q have been successfully fabricated in experiments [75–80].

3 Nonreciprocal enhancement of mechanical cooling

As mentioned above, when the directional squeezing effect is not applied, the response of the system to the external driving field is reciprocal. However, by applying a directional quantum squeezing effect, the system exhibits nonreciprocal features when interchanging the ports of input and output. Firstly, we show that for our COM system, this squeezing effect leads to distinct changes in the effective squeezed mode detuning Δ_s and the effective coupling strength J_s. Figure 2A shows the squeezing parameter r (inset figure), the detuning Δ_s, and the enhanced coupling rate J_s as a function of pump ratio β. Increasing the pump ratio β approaches 1, r increases greatly (see inset figure), and the detuning Δ_s decreases to 0 (see blue solid curve in Figure 2A). Furthermore, the effective coupling strength J_s is enhanced exponentially with respect to J₀ with increasing β. This indicates that the presence of a directional quantum squeezing effect results in a shifted detuning of the squeezed mode and enhanced coupling strength.

FIGURE 2

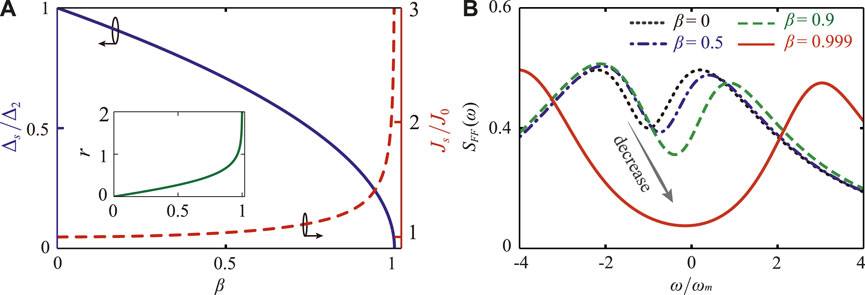
FIGURE 2. (A) The squeezing parameter r (inset figure), the detuning Δ_s, and the enhanced coupling rate J_s as a function of pump ratio β. (B) For the forward-input case, the fluctuation spectrum S_FF(ω) (in arbitrary units) versus the frequency ω for different values of the ratio β. We have selected ${\mathrm{\Delta }}_1^{\prime }/{\omega }_m=-1$, and Δ₂/ω_m =−1. The other parameters can be found in the main text.

In the following, to verify the role of the squeezing effect in influencing the optical fluctuation spectrum, we plot Figure 2B to demonstrate that the optical fluctuation spectrum S_FF(ω) varies with the frequency ω for different values of the ratio β. In our discussion, we focus on unresolved sideband cases, that is, κ₁ > ω_m. For comparisons, in the forward-input case, we first consider the case without a squeezing effect. For β = 0, two narrower peaks appear, with a dip emerging between them due to the interference between the two optical modes (see black dotted curve in Figure 2B) [16, 17]. If the directional quantum squeezing effect is present, increasing the ratio β leads to a more pronounced depth of the dip. The reason for the phenomenon is that the squeezing effect enhances the effective coupling strength J_s [70–74]. This implies that mechanical cooling deep into the ground-state is accessible.

In fact, in the case of a unresolved sideband, the cooling efficiency of mechanical mode is mainly determined by the positive-frequency S_FF(+ω_m) and negative-frequency S_FF(−ω_m) parts of the optical fluctuation spectrum, i.e., the fluctuation spectrum values S_FF(ω = −ω_m) and S_FF(ω = ω_m) determining the heating and cooling processes [11], respectively. Hence, in order to obtain optimal cooling, we should ensure that the optical fluctuation spectrum takes the minimum value at ω = −ω_m and the maximum value at ω = ω_m. As discussed in Ref. [16], in the double-COM system, the two peaks of the optical fluctuation spectrum are caused by the normal optical mode splitting. According to the optimal cooling condition $J_s=\sqrt{2{\omega }_m({\omega }_m-{\mathrm{\Delta }}_1^{\prime })}$ [16], to maximize the transition rate of the cooling process, we choose ${\mathrm{\Delta }}_1^{\prime }/{\omega }_m=-3$ (focus only on the case of ${\omega }_m-{\mathrm{\Delta }}_1^{\prime }>0$), Δ_s/ω_m = −1, β = 0.9, and $J_s/{\omega }_m=2\sqrt{2}$, and thus $J_0/{\omega }_m=\sqrt{2}$. In Figure 3, the optical fluctuation spectrum S_FF(ω) is shown as a function of the frequency ω for different optical decay rates. As shown in Figure 3A, for κ₁/ω_m = 3, S_FF takes the minimum value at ω = −ω_m and the maximum value at ω = ω_m, corresponding to the heating and cooling processes, respectively. Moreover, increasing the optical decay rate of the COM resonator κ₁/ω_m results in suppression of the cooling process but not the heating process (see Figure 3A). Also, it is worth noting that by increasing the optical decay rate of the pure optical resonator κ₂/ω_m, the height of the peak of the cooling process increases while the depth of the valley of the heating process decreases (see Figure 3B). This suggests that in the compound COM system, in order to get nice cooling, it is necessary to control the decay rates of the two resonators while satisfying the optimal cooling conditions.

FIGURE 3

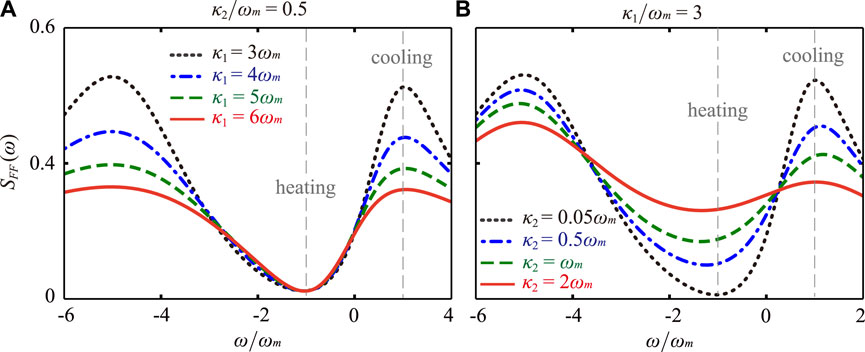
FIGURE 3. For the forward-input case, the fluctuation spectrum $S_{FF}\left(\omega \right)$ (in arbitrary units) as a function of the frequency ω for different optical decay rates of (A) the optomechanical resonator κ₁/ω_m and (B) the pure optical resonator κ₂/ω_m. Here we have chosen ${\mathrm{\Delta }}_1^{\prime }/{\omega }_m=-3$, Δ_s/ω_m = −1, β = 0.9, and $J_0/{\omega }_m=\sqrt{2}$ in (A,B); κ₂/ω_m = 0.5 in (A) and κ₁/ω_m = 3 in (B). The other parameters can be found in the main text.

Below, we will show that nonreciprocal enhancement of mechanical cooling can be achieved by directional squeezing effects. First, we consider that the system is not in the optimal optical coupling condition, i.e., $J_0/{\omega }_m=\sqrt{2}$. As mentioned above, for the forward-input case (input from port 1), the effective coupling strength J_s is enhanced exponentially relative to J₀ with increasing pump ratio β. Accordingly, by increasing β, the system will gradually approach the optimal optical coupling conditions. In Figure 4A, the net cooling rate Γ_m is plotted versus the optical detuning Δ₂ for different input directions, where the blue dotted line denotes the signal field input from port 2. For the backward-input case, it can be seen that the maximum net cooling rate is located around Δ₂/ω_m = −1. However, for the forward-input case, the maximum net cooling rate is not just located around Δ₂/ω_m = −1, and enhancement of the cooling rate can be achievable with increasing pump ratio β. For example, for the forward-input case, Γ_m takes its maximum value at Δ₂/ω_m = −2 (see red solid line in Figure 4A), while for the backward-input case, Γ_m takes its minimum value at Δ₂/ω_m = −2 (see blue dotted line in Figure 4A). The corresponding final mean phonon number, n_f, is plotted in Figure 4B. For the backward-input case, it can be seen that the mechanical resonator can be cooled around Δ₂/ω_m = −1, corresponding to the maximum net cooling rate as shown in Figure 4A. However, for the forward-input case, mechanical cooling deep into the ground-state is accessible with an increase in the pump ratio β. For instance, the mean phonon number n_f is about 0.4 for β = 0.9.

FIGURE 4

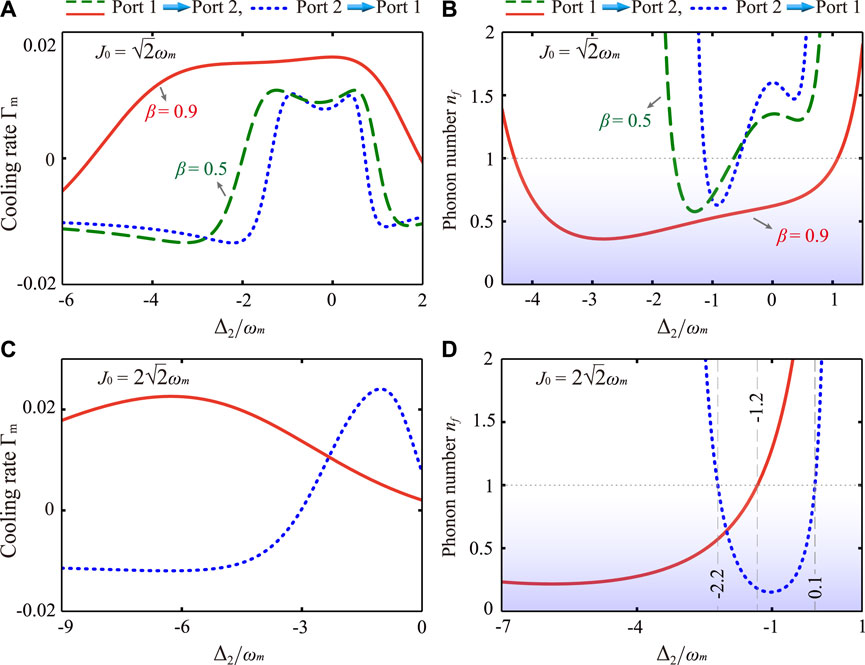
FIGURE 4. For $J_0=\sqrt{2}{\omega }_m$, (A) the net cooling rate Γ_m (in arbitrary units) and (B) the mean phonon number n_f as a function of the optical detuning Δ₂ for different input directions. The green dashed line and red solid line denote the signal field input from the left-hand side (port 1), corresponding to β = 0.5 and β = 0.9, respectively. The blue dotted line denotes the signal field input from the right-hand side (port 2). For $J_0=2\sqrt{2}{\omega }_m$, (C) Γ_m (in arbitrary units) and (D) n_f versus Δ₂ for different input directions. We have selected β =0.9 in (C,D). The other parameters can be found in the main text.

Finally, we consider that the system is in the optimal optical coupling condition, i.e., $J_0/{\omega }_m=2\sqrt{2}$. As shown in Figure 4C, for the backward-input case, Γ_m takes its maximum value at Δ₂/ω_m = −1. Accordingly, one can see that the final mean phonon number n_f can be less than 0.5 (see blue dotted line in Figure 4D). That means the mechanical resonator can be cooled close to its ground-state under optimal cooling conditions. More importantly, for the forward-input case, Γ_m takes its maximum value at Δ₂/ω_m = −6 (see red solid line in Figure 4C). Accordingly, the minimum final mean phonon number is obtained at Δ₂/ω_m = −6 (see red solid line in Figure 4D). That is to say, for a given pump ratio β, when a signal field is driven from the left-hand side (port 1), the mechanical resonator can be cooled down to its ground state; meanwhile, when a signal field is driven from the right-hand side (port 2), it cannot be effectively cooled, and vice versa, i.e., nonreciprocal mechanical cooling is achieved. As shown in Figure 4D, for β = 0.9, there are two nonreciprocal cooling segments on the x-axis, corresponding to Δ₂/ω_m < − 2.2 and −1.2 < Δ₂/ω_m < 0.1. The reason is that the directional quantum squeezing leads to effective squeezed mode detuning and chiral photon hopping between two optical modes.

4 Conclusion

In conclusion, we theoretically investigate the role of directional quantum squeezing in achieving nonreciprocal enhancement of mechanical cooling in a compound cavity optomechanical system consisting of an optomechanical resonator and a χ⁽²⁾-nonlinear resonator. By unidirectionally pumping the χ⁽²⁾-nonlinear resonator, the squeezed effect occurs only in the selected direction, resulting in asymmetric optical detuning a tunable chiral photon interaction between two resonators. As a result, the cooling and heating process depends on the driving direction, making it possible to achieve a nonreciprocal mechanical cooling. Moreover, enhanced mechanical cooling deep into the ground-state can be achievable in the selected direction due to the squeezing effect. These results provide a different route for manipulating COM systems through the directional quantum squeezing effect, and may lead to applications in various quantum acoustic devices.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

T-XL: Conceptualization, Methodology, Writing–original draft, Funding acquisition. L-SC: Writing–review and editing, Formal Analysis, Investigation. W-JZ: Writing–review and editing, Formal Analysis, Investigation. XX: Funding acquisition, Project administration, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the funding from the National Natural Science Foundation of China (NSFC) (12205054 and 12265004), the Jiangxi Provincial Education Office Natural Science Fund Project (GJJ211437), and Ph.D. Research Foundation (BSJJ202122).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

2. Stannigel K, Komar P, Habraken SJM, Bennett SD, Lukin MD, Zoller P, et al. Optomechanical quantum information processing with photons and phonons. Phys Rev Lett (2012) 109:013603. doi:10.1103/PhysRevLett.109.013603

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yang H, Hu ZG, Lei Y, Cao X, Wang M, Sun J, et al. High-sensitivity air-coupled megahertz-frequency ultrasound detection using on-chip microcavities. Phys Rev Appl (2022) 18:034035. doi:10.1103/PhysRevApplied.18.034035

CrossRef Full Text | Google Scholar

4. Hu YW, Xiao YF, Liu YC, Gong Q. Optomechanical sensing with on-chip microcavities. Front Phys (2013) 8:475–90. doi:10.1007/s11467-013-0384-y

CrossRef Full Text | Google Scholar

5. Riedinger R, Wallucks A, Marinković I, Löschnauer C, Aspelmeyer M, Hong S, et al. Remote quantum entanglement between two micromechanical oscillators. Nature (2018) 556:473–7. doi:10.1038/s41586-018-0036-z

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Riedinger R, Hong S, Norte RA, Slater JA, Shang J, Krause AG, et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature (2016) 530:313–6. doi:10.1038/nature16536

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wollman EE, Lei CU, Weinstein AJ, Suh J, Kronwald A, Marquardt F, et al. Quantum squeezing of motion in a mechanical resonator. Science (2015) 349:952–5. doi:10.1126/science.aac5138

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Liu YC, Hu YW, Wong CW, Xiao YF. Review of cavity optomechanical cooling. Chin Phys B (2013) 22:114213. doi:10.1088/1674-1056/22/11/114213

CrossRef Full Text | Google Scholar

9. Wen P, Wang M, Long GL. Ground-state cooling in cavity optomechanical systems. Front Phys (2023) 11:1218010. doi:10.3389/fphy.2023.1218010

CrossRef Full Text | Google Scholar

10. Xia K, Evers J. Ground state cooling of a nanomechanical resonator in the nonresolved regime via quantum interference. Phys Rev Lett (2009) 103:227203. doi:10.1103/PhysRevLett.103.227203

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Marquardt F, Chen JP, Clerk AA, Girvin SM. Quantum theory of cavity-assisted sideband cooling of mechanical motion. Phys Rev Lett (2007) 99:093902. doi:10.1103/PhysRevLett.99.093902

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Gan JH, Liu YC, Lu C, Wang X, Tey MK, You L. Intracavity-squeezed optomechanical cooling. Laser Photon Rev (2019) 13:1900120. doi:10.1002/lpor.201900120

CrossRef Full Text | Google Scholar

13. Teufel JD, Donner T, Li D, Harlow JW, Allman MS, Cicak K, et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature (2011) 475:359–63. doi:10.1038/nature10261

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Clark JB, Lecocq F, Simmonds RW, Aumentado J, Teufel JD. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature (2017) 541:191–5. doi:10.1038/nature20604

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ockeloen-Korppi CF, Gely MF, Damskägg E, Jenkins M, Steele GA, Sillanpää MA. Sideband cooling of nearly degenerate micromechanical oscillators in a multimode optomechanical system. Phys Rev A (2019) 99:023826. doi:10.1103/PhysRevA.99.023826

CrossRef Full Text | Google Scholar

16. Guo Y, Li K, Nie W, Li Y. Electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system. Phys Rev A (2014) 90:053841. doi:10.1103/PhysRevA.90.053841

CrossRef Full Text | Google Scholar

17. Liu YC, Xiao YF, Luan X, Gong Q, Wong CW. Coupled cavities for motional ground-state cooling and strong optomechanical coupling. Phys Rev A (2015) 91:033818. doi:10.1103/PhysRevA.91.033818

CrossRef Full Text | Google Scholar

18. Fan ZY, Qian H, Zuo X, Li J. Ground-state cooling of a massive mechanical oscillator by feedback in cavity magnomechanics (2022). arXiv (2022) 2212.09002 Available at: https://arxiv.org/pdf/2212.09002.pdf (Accessed December, 20 2022).

Google Scholar

19. Lai DG, Huang JF, Yin XL, Hou BP, Li W, Vitali D, et al. Nonreciprocal ground-state cooling of multiple mechanical resonators. Phys Rev A (2020) 102:011502. doi:10.1103/PhysRevA.102.011502

CrossRef Full Text | Google Scholar

20. Xu H, Jiang L, Clerk AA, Harris JGE. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature (2019) 568:65–9. doi:10.1038/s41586-019-1061-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Huang J, Lai DG, Liu C, Huang JF, Nori F, Liao JQ. Multimode optomechanical cooling via general dark-mode control. Phys Rev A (2022) 106:013526. doi:10.1103/PhysRevA.106.013526

CrossRef Full Text | Google Scholar

22. Wen P, Mao X, Wang M, Wang C, Li GQ, Long GL. Simultaneous ground-state cooling of multiple degenerate mechanical modes through the cross-kerr effect. Opt Lett (2022) 47:5529–32. doi:10.1364/OL.473885

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yang Z, Zhao C, Peng R, Chao SL, Yang J, Zhou L. The simultaneous ground-state cooling and synchronization of two mechanical oscillators by driving nonlinear medium. Ann Phys (2022) 534:2100494. doi:10.1002/andp.202100494

CrossRef Full Text | Google Scholar

24. Huang S, Chen A. Cooling of a mechanical oscillator and normal mode splitting in optomechanical systems with coherent feedback. Appl Sci (2019) 9:3402. doi:10.3390/app9163402

CrossRef Full Text | Google Scholar

25. Chen X, Liu YC, Peng P, Zhi Y, Xiao YF. Cooling of macroscopic mechanical resonators in hybrid atom-optomechanical systems. Phys Rev A (2015) 92:033841. doi:10.1103/PhysRevA.92.033841

CrossRef Full Text | Google Scholar

26. Yang ZX, Wang L, Liu YM, Wang DY, Bai CH, Zhang S, et al. Ground state cooling of magnomechanical resonator in $${\cal P}{\cal T}$$-symmetric cavity magnomechanical system at room temperature. Front Phys (2020) 15:52504. doi:10.1007/s11467-020-0996-y

CrossRef Full Text | Google Scholar

27. Li G, Nie W, Li X, Chen A. Dynamics of ground-state cooling and quantum entanglement in a modulated optomechanical system. Phys Rev A (2019) 100:063805. doi:10.1103/PhysRevA.100.063805

CrossRef Full Text | Google Scholar

28. Huang S, Chen A. Improving the cooling of a mechanical oscillator in a dissipative optomechanical system with an optical parametric amplifier. Phys Rev A (2018) 98:063818. doi:10.1103/PhysRevA.98.063818

CrossRef Full Text | Google Scholar

29. Dong CH, Shen Z, Zou CL, Zhang YL, Fu W, Guo GC. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat Commun (2015) 6:6193. doi:10.1038/ncomms7193

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Maayani S, Dahan R, Kligerman Y, Moses E, Hassan AU, Jing H, et al. Flying couplers above spinning resonators generate irreversible refraction. Nature (2018) 558:569–72. doi:10.1038/s41586-018-0245-5

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Dong MX, Xia KY, Zhang WH, Yu YC, Ye YH, Li EZ, et al. All-optical reversible single-photon isolation at room temperature. Sci Adv (2021) 7:eabe8924. doi:10.1126/sciadv.abe8924

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Qie J, Wang C, Yang L. Chirality induced nonreciprocity in a nonlinear optical microresonator. Laser Photon Rev. (2023) 17:2200717. doi:10.1002/lpor.202200717

CrossRef Full Text | Google Scholar

33. Yang Z, Cheng Y, Wang N, Chen Y, Wang S. Nonreciprocal light propagation induced by a subwavelength spinning cylinder. Opt Express (2022) 30:27993–8002. doi:10.1364/OE.462107

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Fleury R, Sounas DL, Sieck CF, Haberman MR, Alù A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science (2014) 343:516–9. doi:10.1126/science.1246957

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang Q, Zhou Z, Liu D, Ding H, Gu M, Li Y. Acoustic topological beam nonreciprocity via the rotational Doppler effect. Sci Adv (2022) 8:eabq4451. doi:10.1126/sciadv.abq4451

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Shao L, Mao W, Maity S, Sinclair N, Hu Y, Yang L, et al. Non-reciprocal transmission of microwave acoustic waves in nonlinear parity–time symmetric resonators. Nat Electron (2020) 3:267–72. doi:10.1038/s41928-020-0414-z

CrossRef Full Text | Google Scholar

37. Tian T, Zhang Y, Zhang L, Wu L, Lin S, Zhou J, et al. Experimental realization of nonreciprocal adiabatic transfer of phonons in a dynamically modulated nanomechanical topological insulator. Phys Rev Lett (2022) 129:215901. doi:10.1103/PhysRevLett.129.215901

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Nomura T, Zhang XX, Takagi R, Karube K, Kikkawa A, Taguchi Y, et al. Nonreciprocal phonon propagation in a metallic chiral magnet. Phys Rev Lett (2023) 130:176301. doi:10.1103/PhysRevLett.130.176301

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang X, Li Z, Wang S, Sano K, Sun Z, Shao Z, et al. Mechanical nonreciprocity in a uniform composite material. Science (2023) 380:192–8. doi:10.1126/science.adf1206

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Manipatruni S, Robinson JT, Lipson M. Optical nonreciprocity in optomechanical structures. Phys Rev Lett (2009) 102:213903. doi:10.1103/PhysRevLett.102.213903

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ruesink F, Mathew JP, Miri MA, Alù A, Verhagen E. Optical circulation in a multimode optomechanical resonator. Nat Commun (2018) 9:1798. doi:10.1038/s41467-018-04202-y

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ruesink F, Miri MA, Alù A, Verhagen E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat Commun (2016) 7:13662. doi:10.1038/ncomms13662

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Shen Z, Zhang YL, Chen Y, Xiao YF, Zou CL, Guo GC, et al. Nonreciprocal frequency conversion and mode routing in a microresonator. Phys Rev Lett (2023) 130:013601. doi:10.1103/PhysRevLett.130.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Bernier NR, Tóth LD, Koottandavida A, Ioannou MA, Malz D, Nunnenkamp A, et al. Nonreciprocal reconfigurable microwave optomechanical circuit. Nat Commun (2017) 8:604. doi:10.1038/s41467-017-00447-1

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Shen Z, Zhang YL, Chen Y, Zou CL, Xiao YF, Zou XB, et al. Experimental realization of optomechanically induced non-reciprocity. Nat Photon (2016) 10:657–61. doi:10.1038/nphoton.2016.161

CrossRef Full Text | Google Scholar

46. Fan L, Wang J, Varghese LT, Shen H, Niu B, Xuan Y, et al. An all-silicon passive optical diode. Science (2012) 335:447–50. doi:10.1126/science.1214383

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Cao QT, Wang H, Dong CH, Jing H, Liu RS, Chen X, et al. Experimental demonstration of spontaneous chirality in a nonlinear microresonator. Phys Rev Lett (2017) 118:033901. doi:10.1103/PhysRevLett.118.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Xia K, Nori F, Xiao M. Cavity-free optical isolators and circulators using a chiral cross-kerr nonlinearity. Phys Rev Lett (2018) 121:203602. doi:10.1103/PhysRevLett.121.203602

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Xia K, Lu G, Lin G, Cheng Y, Niu Y, Gong S, et al. Reversible nonmagnetic single-photon isolation using unbalanced quantum coupling. Phys Rev A (2014) 90:043802. doi:10.1103/PhysRevA.90.043802

CrossRef Full Text | Google Scholar

50. Tang L, Tang J, Wu H, Zhang J, Xiao M, Xia K. Broad-intensity-range optical nonreciprocity based on feedback-induced kerr nonlinearity. Photon Res (2021) 9:1218–25. doi:10.1364/PRJ.413286

CrossRef Full Text | Google Scholar

51. Liu M, Zhao C, Zeng Y, Chen Y, Zhao C, Qiu CW. Evolution and nonreciprocity of loss-induced topological phase singularity pairs. Phys Rev Lett (2021) 127:266101. doi:10.1103/PhysRevLett.127.266101

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Lannebère S, Fernandes DE, Morgado TA, Silveirinha MG. Nonreciprocal and non-hermitian material response inspired by semiconductor transistors. Phys Rev Lett (2022) 128:013902. doi:10.1103/PhysRevLett.128.013902

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Xu XW, Li Y, Li B, Jing H, Chen AX. Nonreciprocity via nonlinearity and synthetic magnetism. Phys Rev Appl (2020) 13:044070. doi:10.1103/PhysRevApplied.13.044070

CrossRef Full Text | Google Scholar

54. Xu XW, Li Y. Optical nonreciprocity and optomechanical circulator in three-mode optomechanical systems. Phys Rev A (2015) 91:053854. doi:10.1103/PhysRevA.91.053854

CrossRef Full Text | Google Scholar

55. Wang DW, Zhou HT, Guo MJ, Zhang JX, Evers J, Zhu SY. Optical diode made from a moving photonic crystal. Phys Rev Lett (2013) 110:093901. doi:10.1103/PhysRevLett.110.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Lu X, Cao W, Yi W, Shen H, Xiao Y. Nonreciprocity and quantum correlations of light transport in hot atoms via reservoir engineering. Phys Rev Lett (2021) 126:223603. doi:10.1103/PhysRevLett.126.223603

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Zhang S, Hu Y, Lin G, Niu Y, Xia K, Gong J, et al. Thermal-motion-induced non-reciprocal quantum optical system. Nat Photon (2018) 12:744–8. doi:10.1038/s41566-018-0269-2

CrossRef Full Text | Google Scholar

58. Liang C, Liu B, Xu AN, Wen X, Lu C, Xia K, et al. Collision-induced broadband optical nonreciprocity. Phys Rev Lett (2020) 125:123901. doi:10.1103/PhysRevLett.125.123901

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Huang R, Miranowicz A, Liao JQ, Nori F, Jing H. Nonreciprocal photon blockade. Phys Rev Lett (2018) 121:153601. doi:10.1103/PhysRevLett.121.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Li B, Huang R, Xu X, Miranowicz A, Jing H. Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photon Res (2019) 7:630–41. doi:10.1364/PRJ.7.000630

CrossRef Full Text | Google Scholar

61. Jiang Y, Maayani S, Carmon T, Nori F, Jing H. Nonreciprocal phonon laser. Phys Rev Appl (2018) 10:064037. doi:10.1103/PhysRevApplied.10.064037

CrossRef Full Text | Google Scholar

62. Jiao YF, Zhang SD, Zhang YL, Miranowicz A, Kuang LM, Jing H. Nonreciprocal optomechanical entanglement against backscattering losses. Phys Rev Lett (2020) 125:143605. doi:10.1103/PhysRevLett.125.143605

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Jiao YF, Liu JX, Li Y, Yang R, Kuang LM, Jing H. Nonreciprocal enhancement of remote entanglement between nonidentical mechanical oscillators. Phys Rev Appl (2022) 18:064008. doi:10.1103/PhysRevApplied.18.064008

CrossRef Full Text | Google Scholar

64. Jing H, Lü H, Özdemir S, Carmon T, Nori F. Nanoparticle sensing with a spinning resonator. Optica (2018) 5:1424–30. doi:10.1364/optica.5.001424

CrossRef Full Text | Google Scholar

65. Li Y, Shen C, Xie Y, Li J, Wang W, Cummer SA, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys Rev Lett (2017) 119:035501. doi:10.1103/PhysRevLett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Kim S, Xu X, Taylor JM, Bahl G. Dynamically induced robust phonon transport and chiral cooling in an optomechanical system. Nat Commun (2017) 8:205. doi:10.1038/s41467-017-00247-7

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Yang J, Zhao C, Yang Z, Peng R, Chao S, Zhou L. Nonreciprocal ground-state cooling of mechanical resonator in a spinning optomechanical system. Front Phys (2022) 17:52507. doi:10.1007/s11467-022-1202-1

CrossRef Full Text | Google Scholar

68. Lü XY, Wu Y, Johansson JR, Jing H, Zhang J, Nori F. Squeezed optomechanics with phase-matched amplification and dissipation. Phys Rev Lett (2015) 114:093602. doi:10.1103/PhysRevLett.114.093602

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Qin W, Miranowicz A, Li PB, Lü XY, You JQ, Nori F. Exponentially enhanced light-matter interaction, cooperativities, and steady-state entanglement using parametric amplification. Phys Rev Lett (2018) 120:093601. doi:10.1103/PhysRevLett.120.093601

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Tang L, Tang J, Chen M, Nori F, Xiao M, Xia K. Quantum squeezing induced optical nonreciprocity. Phys Rev Lett (2022) 128:083604. doi:10.1103/PhysRevLett.128.083604

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Shen CP, Chen JQ, Pan XF, Ren YM, Dong XL, Hei XL, et al. Tunable nonreciprocal photon correlations induced by directional quantum squeezing. Phys Rev A (2023) 108:023716. doi:10.1103/PhysRevA.108.023716

CrossRef Full Text | Google Scholar

72. Wang DY, Yan LL, Su SL, Bai CH, Wang HF, Liang E. Squeezing-induced nonreciprocal photon blockade in an optomechanical microresonator. Opt Express (2023) 31:22343–57. doi:10.1364/OE.493208

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Liu DW, Huang KW, Wu Y, Si LG. Parametric amplification induced giant nonreciprocal unconventional photon blockade in a single microring resonator. Appl Phys Lett (2023) 123:061103. doi:10.1063/5.0158334

CrossRef Full Text | Google Scholar

74. Huang KW, Wu Y, Si LG. Parametric-amplification-induced nonreciprocal magnon laser. Opt Lett (2022) 47:3311–4. doi:10.1364/OL.459917

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Guo X, Zou CL, Jung H, Tang HX. On-chip strong coupling and efficient frequency conversion between telecom and visible optical modes. Phys Rev Lett (2016) 117:123902. doi:10.1103/PhysRevLett.117.123902

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Lin J, Xu Y, Ni J, Wang M, Fang Z, Qiao L, et al. Phase-matched second-harmonic generation in an on-chip LiNbO₃ microresonator. Phys Rev Appl (2016) 6:014002. doi:10.1103/PhysRevApplied.6.014002

CrossRef Full Text | Google Scholar

77. Zhang X, Cao QT, Wang Z, Liu Y, Qiu CW, Yang L, et al. Symmetry-breaking-induced nonlinear optics at a microcavity surface. Nat Photon (2019) 13:21–4. doi:10.1038/s41566-018-0297-y

CrossRef Full Text | Google Scholar

78. Ma Z, Chen JY, Li Z, Tang C, Sua YM, Fan H, et al. Ultrabright quantum photon sources on chip. Phys Rev Lett (2020) 125:263602. doi:10.1103/PhysRevLett.125.263602

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Wang JQ, Yang YH, Li M, Hu XX, Surya JB, Xu XB, et al. Efficient frequency conversion in a degenerate χ⁽²⁾ microresonator. Phys Rev Lett (2021) 126:133601. doi:10.1103/PhysRevLett.126.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Xu Y, Sayem AA, Fan L, Zou CL, Wang S, Cheng R, et al. Bidirectional interconversion of microwave and light with thin-film lithium niobate. Nat Commun (2021) 12:4453. doi:10.1038/s41467-021-24809-y

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Grudinin IS, Lee H, Painter O, Vahala KJ. Phonon laser action in a tunable two-level system. Phys Rev Lett (2010) 104:083901. doi:10.1103/PhysRevLett.104.083901

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Wang G, Zhao M, Qin Y, Yin Z, Jiang X, Xiao M. Demonstration of an ultra-low-threshold phonon laser with coupled microtoroid resonators in vacuum. Photon Res (2017) 5:73–6. doi:10.1364/PRJ.5.000073

CrossRef Full Text | Google Scholar