A generalized isogeometric boundary element method for the uncertain analysis of infinite domain two-dimensional acoustic problems

The key aim of this paper is to provide a new nth generalized order perturbed isogeometric fast multistage technique of boundary elements to compute the propagation of time harmonics in an infinite region. Structural geometry and boundary integral equations are constructed by using non-uniform rational B-splines. The source of system uncertainty is believed to be the incident plane wave number’s unpredictability. The actual field, depending on the input random variables, is simulated using the extended nth-order perturbation method. The field and kernel values for boundary integral formulas are generated via the nth-order generalized series of Taylor expansions using perturbation parameters. The fast multipole method (FMM) is utilized to speed up the process. The effectiveness and correctness of the proposed algorithm are verified by Monte Carlo simulations (MCs) with numerical examples.

1 Introduction

Numerous areas are affected practically by wave propagation in an unlimited domain [1–8]. Although a lot of efforts have been put into modeling this issue, it focuses on deterministic systems. The parameters obtained from laboratory experiments and measurements are essentially random. In order to take into account the influence of these uncertainties on the system response, it is advisable to incorporate some uncertainty analysis techniques into various theoretical and computational methodologies, such as Monte Carlo simulation (MCs) [9–11], the stochastic spectrum methods [12, 13], and the perturbation technique [14–18]. Among them, MCs is the most common and simplest method, but its accuracy is largely based on the quantity of samples, resulting in high-level computational costs [19–21]. Therefore, MCs is often used as a reference solution to validate other probabilistic methods [22–24]. The stochastic spectrum method is more efficient and takes advantage of generality, but it is still difficult to apply to large-scale problems. Perturbation is the most effective method, but it is mainly limited to linear problems.

Because numerical analysis frequently uses the finite element method (FEM), stochastic analysis with FEM is extensively studied. For example, spectral stochastic FEM is investigated by [12]. The stochastic FEM with the perturbation method is presented in [14–17]. Kamiński puts forward the generalized second-order and nth-order stochastic perturbation techniques [25, 26], which provide results with high computational accuracy. A smoothed finite element approach based on generalized perturbation for stochastic analysis is proposed in [22] to effectively maintain accuracy and withstand mesh distortion, especially in irregular mesh.

Despite its versatility, the finite element method is not easy to use when simulating wave scattering in unbounded media. A significant issue arises because the unbounded domain must be truncated into a sizable bounded domain enclosed by an artificial border using the finite element method. In addition, there are specific methods that must be used to estimate the boundary conditions at infinity. In contrast, known alternatively as the method of moments (MOM) in electromagnetic fields [27, 28], the boundary element method (BEM) is preferred for infinite domain problems [29–34]. Boundary element method has advantages such as reduced dimensionality calculation, and boundary element method only discretizes the surface of the structure and naturally satisfies the boundary conditions at infinity. The creation of an asymmetrical, thick coefficient matrix, resulting in higher memory needs and processing complexity, is a common drawback of the boundary element approach. Some fast-solving algorithms are proposed, such as the fast direct solution method [35], adaptive cross approximation method [36], and fast multipole method (FMM) [37]. Another unavoidable disadvantage of the boundary element method is the need to precisely calculate the singular integral. The singularity subtraction technique is successfully utilized to remove the boundary integrals’ singularity [38].

Isogeometric analysis (IGA), first suggested by Hughes and others [39], has developed into a key numerical approach in recent years. In traditional numerical analysis, grids must be constructed using computer-aided design (CAD), which is time-consuming and necessitates a sizable amount of human involvement. The basis functions that have given rise to CAD are used by IGA to solve systems of partial differential equations, such as PHT-splines, which are hierarchy T-meshes over quadratic splines [40], and non-uniform rational B-splines (NURBS) [41, 42]. IGA eliminates the need for gridding while maintaining geometric precision. IGA has been widely employed in numerous domains, including uncertainty analysis, since its beginnings. A nth-order generalized perturbation isometric approach that is a steady-state heat transfer analysis simulation with material uncertainties was created by Rojas et al. [43]. Ding et al. [24] studied the nth-order perturbation method based on IGA to simulate the geometric uncertainty of shell structure. Cao et al. [44] used uncertainty analysis to solve the equi-geometric bi-reciprocal finite element for non-Fourier transient heat transfer problems. Chen et al. [45, 46] proposed an effective deep learning method based on IGA samples for the quantification of multivariable uncertainty issues with the interplay of vibration and sound. IGA was first put forth in relation to finite element methods before being expanded to boundary element method [47]. Boundary units and CAD are compatible since they both employ boundary notation. The boundary element also satisfies the boundary criteria at infinity, making it highly accurate and efficient for modeling the spread of waves across infinite domains, such as the sound [27] and electromagnetic field [48].

The generalized nth-order perturbation based on the isogeometric boundary element method (IGABEM) is proposed to assess the uncertainty of the propagation of time harmonics in an infinite region. The fact that the coefficient matrix in the boundary element system is an asymmetric complete matrix, which raises computing complexity and storage needs, is a characteristic drawback of the boundary element system. Therefore, we avoid directly calculating the coefficient matrix in the equation of boundary integrals of components of the nth order; instead, we apply the fast multipole method suggested in [37] to quicken the computation of multiplication of vectors in matrices. As a result, uncertainty analysis using isogeometric boundary elements is more effective. This increases how well uncertainty analysis works based on isogeometric border elements. Another disadvantage of the boundary element is the existence of singular integrals in the equation, which requires careful calculation. In order to address this issue, the singularity of the boundary integral is generally eliminated using the singular subtraction approach suggested in [38].

The remainder of this paper is organized as follows: a technique of extending nth order perturbation is introduced in Section 2 that employs equations for boundary integrals using random coefficients from the Taylor series. The equal geometric boundary element approach is described in Section 3. Section 4 provides three numerical instances that might be used to verify the suggested uncertainty analysis technique, followed by the conclusions in Section 5.

2 2D acoustic scattering using an isogeometric BEM based on perturbation method

Consider a two-dimensional domain enclosed by a boundary Γ. The symbol Ω represents the limitless domain outside the structural surface. Within Ω, the medium is a uniform ideal fluid. So the sound pressure satisfies the following wave equation:

${\nabla }^{2}P\left(m,t\right)-\frac{1}{c_f^2}\frac{{\partial }^{2}P\left(m,t\right)}{\partial t^2}=0,\forall m\in \mathrm{\Omega },(1)$

where ∇² represents the Laplacian operator, P(m, t) represents the sound pressure at point m in the middle of the sound field at time t, and $c_f^2$ represents the wave velocity. The sound pressure is expressed as

$P\left(m,t\right)=p\left(m\right)e^{-\mathrm{i}\omega \mathrm{t}},(2)$

where p(m) represents the sound pressure value independent of time, $i=\sqrt{-1}$ represents an imaginary number, 2πf represents the circular frequency, and e^−iωt represents the time-dependent terms. Then, the Helmholtz governing differential equation based on the sound pressure is obtained as follows:

${\nabla }^{2}p\left(m\right)+k^{2}p\left(m\right)=0,\forall m\in \mathrm{\Omega },(3)$

where $k=\omega \sqrt{ϵ\mu }$ denotes the wave number of the medium Ω. The boundary integral formula of the scalar Helmholtz formula can be obtained as

$c\left(\mathbf{m}\right)p\left(\mathbf{m};k\right)+{\int }_{\mathrm{\Gamma }}R\left(\mathbf{m},\mathbf{y};k\right)p\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)={\int }_{\mathrm{\Gamma }}G\left(\mathbf{m},\mathbf{y};k\right)q\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)+p_{\text{inc}}\left(\mathbf{m};k\right).(4)$

If the source point is represented by m and the field point is represented by y, the coefficient $c\left(\mathbf{m}\right)$ is determined by the geometric features at point m. $c\left(\mathbf{m}\right)$ equals 1/2 when the boundary is smooth at m. The symbol ∫ in Eq. 4 represents the integral in the sense of Cauchy principal value. It implies that the integral does not include the case where m = y. $q\left(\mathbf{y};k\right)=\frac{\partial p\left(\mathbf{y};k\right)}{\partial n\left(\mathbf{y}\right)}$ represents the acoustic flux, and $p_{\text{inc}}\left(\mathbf{m};k\right)$ is the sound pressure present at location m of the incident wave. The Green functions in media are defined as $G\left(\mathbf{m},\mathbf{y};k\right)$ and are expressed as

$G\left(\mathbf{m},\mathbf{y};k\right)=\frac{\text{i}}{4}{H}_0^{\left(1\right)}\left(k\mathbf{r}\right),(5)$

where H_n⁽¹⁾ is the first kind of the nth-order Hankel function and r = ‖m − y‖ is the Euclidean distance between the source location and the field point. $R\left(\mathbf{m},\mathbf{y};k\right)$, representing the variations of the Green’s functions G(m, y; k) with regard to the standard $n\left(\mathbf{y}\right)$, is given by

$R\left(\mathbf{m},\mathbf{y};k\right)=\frac{\partial G\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{y}\right)}=-\frac{\text{i}k}{4}{H}_1^{\left(1\right)}\left(k\mathbf{r}\right)\frac{\left[\mathbf{r}\right]\cdot \widehat{\mathbf{n}}\left(\mathbf{y}\right)}{\mathbf{r}}.(6)$

It is important to note that the non-uniqueness issue arises when solving outer boundary-value issues using Eq. 4. This issue may be solved using the Burton–Miller formulation [49, 50]; it is derived by combining Eq. 4 with its standard derivation while considering the outside standard at the location specified in Eq. 4. This secondary formulation is written as

$c\left(\mathbf{m}\right)q\left(\mathbf{m};k\right)+{\int }_{\mathrm{\Gamma }}\frac{\partial R\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}p\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)={\int }_{\mathrm{\Gamma }}\frac{\partial G\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}q\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)+\frac{\partial p_{\text{inc}}\left(\mathbf{m};k\right)}{\partial n\left(\mathbf{m}\right)},(7)$

where

$\left\{\begin{array}{c}\frac{\partial G\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}=-\frac{\text{i}k}{4}{H}_1^{\left(1\right)}\left(k\mathbf{r}\right)\frac{\left[\mathbf{r}\right]\cdot \widehat{\mathbf{n}}\left(\mathbf{m}\right)}{\mathbf{r}},\hfill \\ \frac{\partial R\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}=\frac{\text{i}k}{4\mathbf{r}}{H}_1^{\left(1\right)}\left(k\mathbf{r}\right)\left[\widehat{\mathbf{n}}\left(\mathbf{m}\right)\cdot \widehat{\mathbf{n}}\left(\mathbf{y}\right)\right]-\hfill \\ \frac{\text{i}{k}^2}{4}{H}_2^{\left(1\right)}\left(k\mathbf{r}\right)\frac{\left[\mathbf{r}\cdot \widehat{\mathbf{n}}\left(\mathbf{m}\right)\right]\left[\mathbf{r}\cdot \widehat{\mathbf{n}}\left(\mathbf{y}\right)\right]}{{\mathbf{r}}^2}.\hfill \end{array}\right.(8)$

The linear mixture formulas of Eqs 4, 7 are generated as

$\begin{array}{cc}\hfill & c\left(\mathbf{m}\right)\left(p\left(\mathbf{m};k\right)+\alpha q\left(\mathbf{m};k\right)\right)+{\int }_{\mathrm{\Gamma }}\left[R\left(\mathbf{m},\mathbf{y};k\right)+\alpha \frac{\partial R\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}\right]p\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)=\hfill \\ \hfill & {\int }_{\mathrm{\Gamma }}\left[G\left(\mathbf{m},\mathbf{y};k\right)+\alpha \frac{\partial G\left(\mathbf{m},\mathbf{y};k\right)}{\partial n\left(\mathbf{m}\right)}\right]q\left(\mathbf{y};k\right)d\mathrm{\Gamma }\left(\mathbf{y}\right)+q_{\text{inc}}\left(\mathbf{m};k\right),\hfill \end{array}(9)$

where $q_{\text{inc}}\left(\mathbf{m};k\right)=p_{\text{inc}}\left(\mathbf{m};k\right)+\alpha \frac{\partial p_{\text{inc}}\left(\mathbf{m};k\right)}{\partial n\left(\mathbf{m}\right)}$. Its coupling coefficient α = i/k for k⩾1, and α = i for k < 1.

2.1 nth-order generalized perturbation

In this work, the wave number k is used as a random input parameter. Given the unpredictability of this input parameter k, every variable and functions of state are extended using a Taylor series to approximate to their expected values. This is done by expanding the Taylor series around the point k₀, which serves as the expected value of k. The expansion of p, q, G, and R functions with Δk = k − k₀ can be written as

$\left\{\begin{array}{cc}\hfill p\left(k\right)& =p\left(k_0\right)+\epsilon p^{\left(1\right)}\left(k_0\right)\mathrm{\Delta }k+\frac{1}{2}{\epsilon }^2{p}^{\left(2\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^2+\cdots +\frac{1}{n!}{\epsilon }^n{p}^{\left(n\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^n,\hfill \\ \hfill q\left(k\right)& =q\left(k_0\right)+\epsilon q^{\left(1\right)}\left(k_0\right)\mathrm{\Delta }k+\frac{1}{2}{\epsilon }^2{q}^{\left(2\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^2+\cdots +\frac{1}{n!}{\epsilon }^n{q}^{\left(n\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^n,\hfill \\ \hfill G\left(k\right)& =G\left(k_0\right)+\epsilon G^{\left(1\right)}\left(k_0\right)\mathrm{\Delta }k+\frac{1}{2}{\epsilon }^2{G}^{\left(2\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^2+\cdots +\frac{1}{n!}{\epsilon }^n{G}^{\left(n\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^n,\hfill \\ \hfill R\left(k\right)& =R\left(k_0\right)+\epsilon R^{\left(1\right)}\left(k_0\right)\mathrm{\Delta }k+\frac{1}{2}{\epsilon }^2{R}^{\left(2\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^2+\cdots +\frac{1}{n!}{\epsilon }^n{R}^{\left(n\right)}\left(k_0\right){\left[\mathrm{\Delta }k\right]}^n.\hfill \end{array}\right.(10)$

The derivation of the boundary integral in Eq. 9 involves a nth-order expansion, which is written as

$\begin{array}{c}\hfill c\left(\mathbf{m}\right)\left[p^{\left(n\right)}\left(\mathbf{m}\right)+\alpha {\widehat{q}}^{\left(n\right)}\left(\mathbf{m}\right)\right]={\displaystyle \sum _{s=0}^n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill s\hfill \end{array}\right){\int }_{\mathrm{\Gamma }}\left[G^{\left(s\right)}\left(\mathbf{m},\mathbf{y}\right){\widehat{q}}^{\left(n-s\right)}\left(\mathbf{y}\right)-R^{\left(s\right)}\left(\mathbf{m},\mathbf{y}\right)p^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)\\ \hfill +\alpha {\displaystyle \sum _{s=0}^n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill s\hfill \end{array}\right){\int }_{\mathrm{\Gamma }}\left[\frac{\partial G^{\left(s\right)}\left(\mathbf{m},\mathbf{y}\right)}{\partial n\left(\mathbf{m}\right)}{\widehat{q}}^{\left(n-s\right)}\left(\mathbf{y}\right)-\frac{\partial R^{\left(s\right)}\left(\mathbf{m},\mathbf{y}\right)}{\partial n\left(\mathbf{m}\right)}{p}^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)+{\widehat{p}}_{\text{inc}}^{\left(n\right)}\left(\mathbf{m}\right).\end{array}(11)$

To obtain a clear and simple expression corresponding to the sth-order derivative of the kernel function, as given in Eq. 11, we must first compute the product of the Hankel function. The Hankel function exhibits the following recursive feature:

$\frac{\text{d}{H}_n^{\left(1\right)}\left(z\right)}{\text{d}z}=\frac{n}{z}{H}_n^{\left(1\right)}\left(z\right)-H_{n+1}^{\left(1\right)}\left(z\right).(12)$

The Hankel function’s formula corresponding to the sth-order derivatives can be derived by repeatedly differentiating the aforementioned equation with respect to the variable z, as follows:

${\left[H_n^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)}={\displaystyle \sum _{\ell =1}^s}{\left[H_n^{\left(1\right)}\left(z\right)\right]}^{\left(s-\ell \right)}\frac{{\left(-1\right)}^{\ell +1}\left(s-1\right)!}{z^{\ell }\left(s-\ell \right)!}-{\left[H_{n+1}^{\left(1\right)}\left(z\right)\right]}^{\left(s-1\right)}.(13)$

Additionally, the functions $z{H}_1^{(1)}(z)$ and $z^2{H}_2^{(1)}(z)$ that define the kernel’s sth-order derivative are obtained as

$\begin{array}{cc}\hfill & {\left[z{H}_1^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)}=s{\left[H_1^{\left(1\right)}\left(z\right)\right]}^{\left(s-1\right)}+z{\left[H_1^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)},\hfill \\ \hfill & {\left[z^2{H}_2^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)}=\left\{\begin{array}{c}s\left(s-1\right){\left[H_2^{\left(1\right)}\left(z\right)\right]}^{\left(s-2\right)}+2sz{\left[H_2^{\left(1\right)}\left(z\right)\right]}^{\left(s-1\right)}+z^2{\left[H_2^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)},s>1\hfill \\ 2z{\left[H_2^{\left(1\right)}\left(z\right)\right]}^{\left(s-1\right)}+z^2{\left[H_2^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)},s=1.\hfill \end{array}\right.\hfill \end{array}(14)$

Assuming z = k‖m − y‖ and z₀ = k₀‖m − y‖, the kernel operations for the sth-order derivative in Eq. 11 are deduced using Eqs 13, 14.

$\begin{array}{ll}\hfill G^{\left(s\right)}\left(\mathbf{m},\mathbf{y};k_0\right)=& \frac{\text{i}{r}^s}{4}{\left[H_0^{\left(1\right)}\left(z_0\right)\right]}^{\left(s\right)},\hfill \\ \hfill R^{\left(s\right)}\left(\mathbf{m},\mathbf{y};k_0\right)=& -\frac{\text{i}{r}^{\left(s-1\right)}}{4}\frac{\partial r}{\partial n\left(\mathbf{y}\right)}{\left[z_0{H}_1^{\left(1\right)}\left(z_0\right)\right]}^{\left(s\right)},\hfill \\ \hfill \frac{\partial G^{\left(s\right)}\left(\mathbf{m},\mathbf{y};k_0\right)}{\partial n\left(\mathbf{m}\right)}=& -\frac{\text{i}{r}^{\left(s-1\right)}}{4}\frac{\partial r}{\partial n\left(\mathbf{m}\right)}{\left[z_0{H}_1^{\left(1\right)}\left(z_0\right)\right]}^{\left(s\right)},\hfill \\ \hfill \frac{\partial R^{\left(s\right)}\left(\mathbf{m},\mathbf{y};k_0\right)}{\partial n\left(\mathbf{m}\right)}=& \underset{R_1^{\left(s\right)}}{\underbrace{\frac{\text{i}{r}^{\left(s-2\right)}}{4}\left[\widehat{\mathbf{n}}\left(\mathbf{m}\right)\cdot \widehat{\mathbf{n}}\left(\mathbf{y}\right)\right]{\left[z_0{H}_1^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)}}}-\underset{R_2^{\left(s\right)}}{\underbrace{\frac{\text{i}{r}^{\left(s-2\right)}}{4}\frac{\partial r}{\partial n\left(\mathbf{m}\right)}\frac{\partial r}{\partial n\left(\mathbf{y}\right)}{\left[z_0^2{H}_2^{\left(1\right)}\left(z\right)\right]}^{\left(s\right)}}},\hfill \end{array}(15)$

where r = ‖m − y‖, $\frac{\partial r}{\partial n(\mathbf{m})}=\frac{[\mathbf{m}-\mathbf{y}]\cdot \widehat{\mathbf{n}}(\mathbf{m})}{\Vert \mathbf{m}-\mathbf{y}\Vert }$, and $\frac{\partial r}{\partial n(\mathbf{y})}=\frac{[\mathbf{m}-\mathbf{y}]\cdot \widehat{\mathbf{n}}(\mathbf{y})}{\Vert \mathbf{m}-\mathbf{y}\Vert }$.

3 BEM with isogeometric fast multipole

3.1 Irrational B-splines which is not uniform

In isogeometric analysis, geometric and physical fields are approximated using NURBS basis functions. A knot vector, which is a collection of non-decreasing real values, generates a non-uniform rational B-splines (NURBS) curve as follows: Ξ = [ξ₀, ξ₁, … , ξ_n+p+1]with ${\xi }_a\in \mathbb{R}$, where p is the rank of the polynomial, n is the basic function or control point count, and a is the node index. The recursive formulation of the B-spline basis function N_a,p is written as

$N_{a,0}\left(\xi \right)=\left\{\begin{array}{c}1\mathrm{i}\mathrm{f}{\xi }_a\le \xi <{\xi }_{a+1},\hfill \\ 0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.(16)$

and for p = 1, 2, 3, …,

$N_{a,p}\left(\xi \right)=\frac{\xi -{\xi }_a}{{\xi }_{a+p}-{\xi }_a}{N}_{a,p-1}\left(\xi \right)+\frac{{\xi }_{a+p+1}-\xi }{{\xi }_{a+p+1}-{\xi }_{a+1}}{N}_{a+1,p-1}\left(\xi \right).(17)$

The basis functions for B-splines exhibit some advantageous characteristics, including locality, point non-negativeness, linear independence, and simplicity of numerical analysis. NURBS is created using a B-spline and control point weights:

$B_{a,p}\left(\xi \right)=\frac{N_{a,p}\left(\xi \right)w_a}{W\left(\xi \right)},(18)$

with

$W\left(\xi \right)={\displaystyle \sum _{a=0}^n}{w}_a{N}_{a,p}\left(\xi \right),(19)$

where w_a stands for a weight connected to each control point and B_a,p(ξ) stands for NURBS basis functions. Consequently, the NURBS curve point x(ξ) is calculated as

$\mathbf{x}\left(\xi \right)={\displaystyle \sum _{a=0}^n}{B}_{a,p}\left(\xi \right){\mathbf{P}}_a,(20)$

where P_a refers to the ath command point.

3.2 Discretizations

The coefficients of the derivative of the pressure of sound and flux fields on the boundary, as given in Eq. 11, have been interpolated applying NURBS basis functions utilizing the IGA technique, as follows:

$p^{\left(n\right)}\left(\xi \right)={\displaystyle \sum _{a=0}^{n_f}}{B}_{a,p_f}\left(\xi \right)p_a^{\left(n\right)},q^{\left(n\right)}\left(\xi \right)={\displaystyle \sum _{a=0}^{n_f}}{B}_{a,p_f}\left(\xi \right)q_a^{\left(n\right)},(21)$

where n_f indicates the amount of integration points, p_f denotes the order of the polynomial, and $p_a^{(n)}$ and $q_a^{(n)}$ represent the worldwide derivative sound pressure and flow characteristics associated with the ath control point, respectively.

Because the Kronecker delta condition is not satisfied with NURBS basis functions, $p_a^{(n)}$ and $q_a^{(n)}$ do not represent a field and flux within the boundary’s derivative values. As a result, the collocation points must be rebuilt. In this study, the Greville abscissa method is utilized, and collocation points are created in the parameter space, as demonstrated in the following equation:

$\widehat{{\xi }_a}=\frac{{\xi }_{a+1}^f+{\xi }_{a+2}^f+\cdots +{\xi }_{a+p_f}^f}{p_f},a=\mathrm{0,1},\dots ,n_f.(22)$

The discretized versions of isogeometric BEM are obtained by substituting Eq. 21 into Eq. 11.

$\begin{array}{ll}\hfill c\left(\mathbf{x}\left(\widehat{{\xi }_a}\right)\right)& {\displaystyle \sum _{\kappa =0}^{n_f}}{B}_{\kappa }\left(\widehat{{\xi }_a}\right)\left(p_{\kappa }^{\left(n\right)}+\alpha q_{\kappa }^{\left(n\right)}\right)={\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}{\displaystyle \sum _{e=1}^{N_e}}{\displaystyle \sum _{\kappa =0}^{n_f}}\left[{\int }_{{\xi }_e}^{{\xi }_{e+1}}{G}^{\left(s\right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi \right]q_{\kappa }^{\left(n-s\right)}\hfill \\ \hfill & -{\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}{\displaystyle \sum _{e=1}^{N_e}}{\displaystyle \sum _{\kappa =0}^{n_f}}\left[{\int }_{{\xi }_e}^{{\xi }_{e+1}}{R}^{\left(s\right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi \right]p_{\kappa }^{\left(n-s\right)}\hfill \\ \hfill & +\alpha {\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}{\displaystyle \sum _{e=1}^{N_e}}{\displaystyle \sum _{\kappa =0}^{n_f}}\left[{\int }_{{\xi }_e}^{{\xi }_{e+1}}\frac{\partial G^{\left(s\right)}}{\partial n\left(\mathbf{x}\right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi \right]q_{\kappa }^{\left(n-s\right)}\hfill \\ \hfill & -\alpha {\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}{\displaystyle \sum _{e=1}^{N_e}}{\displaystyle \sum _{\kappa =0}^{n_f}}\left[{\int }_{{\xi }_e}^{{\xi }_{e+1}}\frac{\partial R^{\left(s\right)}}{\partial n\left(\mathbf{x}\right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi \right]p_{\kappa }^{\left(n-s\right)}+q_{\text{inc}}^{\left(n\right)}\left(\mathbf{x}\left(\widehat{{\xi }_a}\right)\right),\hfill \end{array}(23)$

where a = 0, 1, … , n_f. The period of time between two non-repeating intersections is represented by the NURBS element [ξ_e, ξ_e+1], N_e indicates the number of NURBS elements, and J(ξ) indicates the Jacobian.

The matrix representation of the discretization of the boundary value integral equations using the nth-order derivative is as follows:

${\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}\left[{\bar{\mathbf{R}}}^{\left(s\right)}{\mathit{p}}^{\left(n-s\right)}-{\bar{\mathbf{G}}}^{\left(s\right)}{\mathit{q}}^{\left(n-s\right)}\right]={\mathit{q}}_{\text{inc}}^{\left(n\right)}.(24)$

By rearranging each term and applying the boundary conditions, the equations can be solved as follows:

$\mathbf{A}\mathbf{x}=\mathbf{B}.(25)$

Taking the incident wave into consideration, x = p⁽ⁿ⁾ is an unknown quantity on the boundary of the matrix. $\mathbf{A}={\bar{\mathbf{R}}}^0$, which is an asymmetrical dense matrix. B is a known vector obtained by the matrix multiplication of vector operations.

$\mathbf{B}={\displaystyle \sum _{s=0}^n}\frac{n!}{s!\left(n-s\right)!}{\bar{\mathbf{G}}}^{\left(s\right)}{\mathit{q}}^{\left(n-s\right)}-{\displaystyle \sum _{s=1}^n}\frac{n!}{s!\left(n-s\right)!}{\bar{\mathbf{R}}}^{\left(s\right)}{\mathit{p}}^{\left(n-s\right)}+{\mathit{q}}_{\text{inc}}^{\left(n\right)}.(26)$

Eq. 25 can be solved with n = 0 to obtain the field vector p⁰ result. Next, the field’s initial derivative value concerning the random number is determined by substituting p⁰ into Eq. 25 with n = 1. By analogy, it is possible to determine the value of a field derivative for any order. Finally, the following two equations can be used to determine the expectation and variance of the field at these border points:

$E\left(u\left(k\right)\right)={\int }_{-\infty }^{+\infty }u\left(k\right)\rho \left(k\right)\mathrm{d}k(27)$

and

$V\left(u\left(k\right)\right)={\int }_{-\infty }^{+\infty }{\left[u\left(k\right)-E\left(u\left(k\right)\right)\right]}^2\rho \left(k\right)\mathrm{d}k.(28)$

Where ρ(k) represents the probability density function, and the field variable of is represented by u of p, q, G or R, and u(k) represents the k-fold density of probability function.

It is crucial to remember that the kernel functions’ derivatives of the boundary integral, as given in Eq. 11, are singular. Singular integrals of this nature require special treatment. Such integrals may be explicitly and directly derived utilizing the Hadamard finite-part integral and Cauchy principal value methods.

The singularity of Eq. 24 is up to the second order. Therefore, a numerical instance of spline order 2 can thus be accepted.

3.3 Accelerating using the fast multipole method

Applying the FMM will accelerate the matrix–vector product of isogeometric finite elements in Eq. 11. The key core of FMM is to form a tree structure and delineate the boundary integrals. The original boundary integral is divided into a near-field part and a far-field part, and the near-field part is generally calculated using conventional BEM, while the far-field part is calculated using accelerated FMM-based BEM. In the stochastic analysis involved in this work, the presence of higher-order derivatives of the Green’s function can make the fast algorithm more complex and difficult to implement. The detailed calculation procedure is as follows:

$G\left(\mathbf{x},\mathbf{y}\right)=\frac{\text{i}}{4}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}{O}_{\tilde{m}}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{x}}\right)I_{-\tilde{m}}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{y}}\right),(29)$

where y_c is the unfolding point around y and the functions $O_{\tilde{m}}$ and $I_{\tilde{m}}$ are defined as

$\begin{array}{cc}\hfill O_{\tilde{m}}\left(\mathbf{z}\right)& ={\text{i}}^{\tilde{m}}{H}_{\tilde{m}}^{\left(1\right)}\left(kr\right)e^{\text{i}\tilde{m}\theta },\hfill \\ \hfill I_{\tilde{m}}\left(\mathbf{z}\right)& ={\left(-\text{i}\right)}^{\tilde{m}}{J}_{\tilde{m}}\left(kr\right)e^{\text{i}\tilde{m}\theta },\hfill \end{array}(30)$

where $J_{\tilde{m}}$ denotes a Bessel function of order $\tilde{m}$ and (r, θ) is the polar coordinate of the vector z. The random input variable is repeatedly used to distinguish Eq. 29 from the following equation.

$G^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right)=\frac{\text{i}}{4}{\displaystyle \sum _{\ell =0}^s}\left[\frac{s!}{\ell !\left(s-\ell \right)!}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}{O}_{\tilde{m}}^{\left(\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{x}}\right)I_{-\tilde{m}}^{\left(s-\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{y}}\right)\right].(31)$

Substituting Eq. 31 into Eq. 11, the integral equation can be expressed as follows:

$\begin{array}{c}{\int }_{{\mathrm{\Gamma }}_{\text{far}}}\left[G^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right){\mathrm{\Phi }}^{\left(n-s\right)}\left(\mathbf{y}\right)-R^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right){\psi }^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)\hfill \\ ={\displaystyle \sum _{\ell =0}^s}\left[\frac{s!}{\ell !\left(s-\ell \right)!}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}{O}_{\tilde{m}}^{\left(\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{x}}\right)M_{\tilde{m},s-\ell }\left({\mathbf{y}}_{\mathbf{c}}\right)\right],\hfill \\ {\int }_{{\mathrm{\Gamma }}_{\text{far}}}\left[\frac{\partial G^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right)}{\partial n\left(\mathbf{x}\right)}{\mathrm{\Phi }}^{\left(n-s\right)}\left(\mathbf{y}\right)-\frac{\partial R^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right)}{\partial n\left(\mathbf{x}\right)}{\psi }^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)\hfill \\ ={\displaystyle \sum _{\ell =0}^s}\left[\frac{s!}{\ell !\left(s-\ell \right)!}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}\frac{\partial O_{\tilde{m}}^{\left(\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{x}}\right)}{\partial n\left(\mathbf{x}\right)}{M}_{\tilde{m},s-\ell }\left({\mathbf{y}}_{\mathbf{c}}\right)\right],\hfill \end{array}(32)$

where Γ_far stands for a subsection of the structural boundary located away from the source point x and $M_{\tilde{m},j-\ell }({\mathbf{y}}_{\mathbf{c}})$ is the multipole moment of (j − ℓ) at the expansion point y_c, which is denoted as follows:

$M_{\tilde{m},s-\ell }\left({\mathbf{y}}_{\mathbf{c}}\right)=\frac{\text{i}}{4}{\int }_{{\mathrm{\Gamma }}_{\text{far}}}\left[I_{-\tilde{m}}^{\left(s-\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{y}}\right){\mathrm{\Phi }}^{\left(n-s\right)}\left(\mathbf{y}\right)-\frac{\partial I_{-\tilde{m}}^{\left(s-\ell \right)}\left(\overrightarrow{{\mathbf{y}}_{\mathbf{c}}\mathbf{y}}\right)}{\partial n\left(\mathbf{y}\right)}{\psi }^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right).(33)$

Substituting Eq. 21 into Eq. 33, the discrete formula for the multipole moment is expressed as follows:

$M_{\tilde{m},s-\ell }\left({\mathbf{y}}_{\mathbf{c}}\right)=\frac{\text{i}}{4}{\displaystyle \sum _{e=1}^{N_e}}{\displaystyle \sum _{\kappa =0}^{n_f}}\left[{\int }_{{\xi }_e}^{{\xi }_{e+1}}{I}_{-\tilde{m}}^{\left(s-\ell \right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi {\mathrm{\Phi }}_{\kappa }^{\left(n-s\right)}-{\int }_{{\xi }_e}^{{\xi }_{e+1}}\frac{\partial I_{-\tilde{m}}^{\left(s-\ell \right)}}{\partial n\left(\mathbf{y}\left(\xi \right)\right)}{B}_{\kappa }\left(\xi \right)J\left(\xi \right)d\xi {\psi }_{\kappa }^{\left(n-s\right)}\right].(34)$

The calculation of the residual coefficients and translations, such as local-to-local, multipole-to-local, and multipole-to-multipole translations, is independent of the geometric representation and approximation of the field variables. So we can refer to [51] to establish the continuum formulation of FMM for BEM, and the far-field integral equation could be written as

$\begin{array}{cc}\hfill & {\int }_{{\mathrm{\Gamma }}_{\text{far}}}\left[G^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right){\mathrm{\Phi }}^{\left(n-s\right)}\left(\mathbf{y}\right)-R^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right){\psi }^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)\hfill \\ \hfill & ={\displaystyle \sum _{\ell =0}^s}\left[\frac{s!}{\ell !\left(s-\ell \right)!}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}{I}_{-\tilde{m}}^{\left(\ell \right)}\left(\overrightarrow{{\mathbf{x}}_{\mathbf{1}}\mathbf{x}}\right)L_{\tilde{m},s-\ell }\left({\mathbf{x}}_{\mathbf{1}}\right)\right],\hfill \\ \hfill & {\int }_{{\mathrm{\Gamma }}_{\text{far}}}\left[\frac{\partial G^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right)}{\partial n\left(\mathbf{x}\right)}{\mathrm{\Phi }}^{\left(n-s\right)}\left(\mathbf{y}\right)-\frac{\partial R^{\left(s\right)}\left(\mathbf{x},\mathbf{y}\right)}{\partial n\left(\mathbf{x}\right)}{\psi }^{\left(n-s\right)}\left(\mathbf{y}\right)\right]d\mathrm{\Gamma }\left(\mathbf{y}\right)\hfill \\ \hfill & ={\displaystyle \sum _{\ell =0}^s}\left[\frac{s!}{\ell !\left(s-\ell \right)!}{\displaystyle \sum _{\tilde{m}=-\infty }^{+\infty }}\frac{\partial I_{-\tilde{m}}^{\left(\ell \right)}\left(\overrightarrow{{\mathbf{x}}_{\mathbf{1}}\mathbf{x}}\right)}{\partial n\left(\mathbf{x}\right)}{L}_{\tilde{m},s-\ell }\left({\mathbf{x}}_{\mathbf{1}}\right)\right],\hfill \end{array}(35)$

where $L_{\tilde{m},s-\ell }({\mathbf{x}}_{\mathbf{1}})$ is the local moment of (s − ℓ) of the unfolding point x₁, as detailed in [51].

It is important to note that the number of terms $\tilde{m}$ used in Eq. 31 should be truncated. An increase in the number of expansion terms usually not only results in higher precision but also consumes more memory and time. The formula $\tilde{M}=kd+c\cdot \log (kd+\pi )$ is provided in [52], where the parameter $\tilde{M}$ is the number of truncations, c is a constant, and d is the size of the cell. When c = 5, there is a good balance between precision and performance, and it will be used in the following calculations [52]. The solution summary of geometric boundary element methods was studied in detail by [53]. The results of the study show that the solution time is improved when a corresponding higher order of convergence is reached in geometric boundary element methods. Therefore, it is the key parameter of the fast multipole isogeometric boundary element method.

4 Scattering by an infinite cylinder

Uncertainty analysis is used in this section using an example of acoustic dispersion from an endless cylinder. The existing direct uncertainty analysis approaches are first used to compare the derivative values with arbitrary ordering, and the global finite difference method (FDM) is established by

${\psi }^{\prime }\left(x\right)=\frac{\psi \left(x+\mathrm{\Delta }x\right)-\psi \left(x\right)}{\mathrm{\Delta }x},(36)$

where Δx represents the minor disruption connected to x.

Several scenarios are taken into consideration in order to research the impact of perturbation Δx on the values of derivatives of field functions of every order, as illustrated in Figure 1. The image contrasts the magnitude of the field function’s sixth-order derivative at various wave numbers k. Even for high-order derivatives, FDM and direct uncertainty analysis are trustworthy methods. The derivative value increases under a particular wave number as the field function’s derivative number increases. Additionally, this behavior can be observed in real-world engineering applications.

FIGURE 1

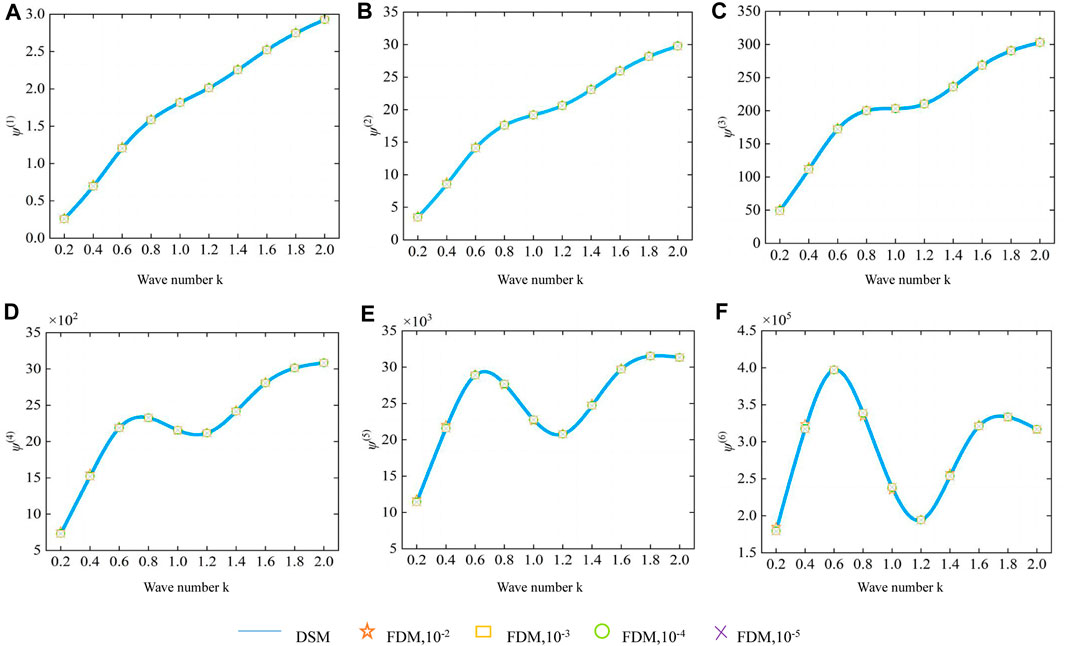
FIGURE 1. Curve of the amplitude of the field function of an infinite cylinder with a wave number k: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

Their relative errors under various Δx values are given to further analyze FDM and the accuracy of the initial uncertainty analysis. The estimated findings are shown in Tables 1, 2, which compare the relative errors ɛ_err of the direct uncertainty analysis method (DSM) and FDM.

${\epsilon }_{\mathit{err}}=\frac{\left|{\psi }_{\left(DSM\right)}-{\psi }_{\left(FDM\right)}\right|}{\left|{\psi }_{\left(FDM\right)}\right|},(37)$

where ψ_(DSM) and ψ_(FDM) indicate the direct calculation approach and the finite difference method of solving the problem, respectively.

TABLE 1

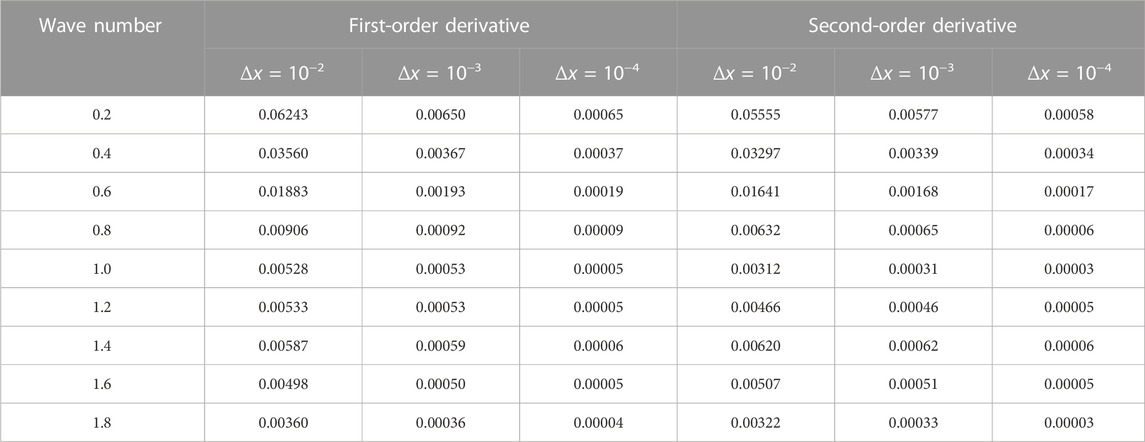
TABLE 1. Relative errors ɛ_err in first- and second-order derivatives of the field function of an infinite cylinder.

TABLE 2

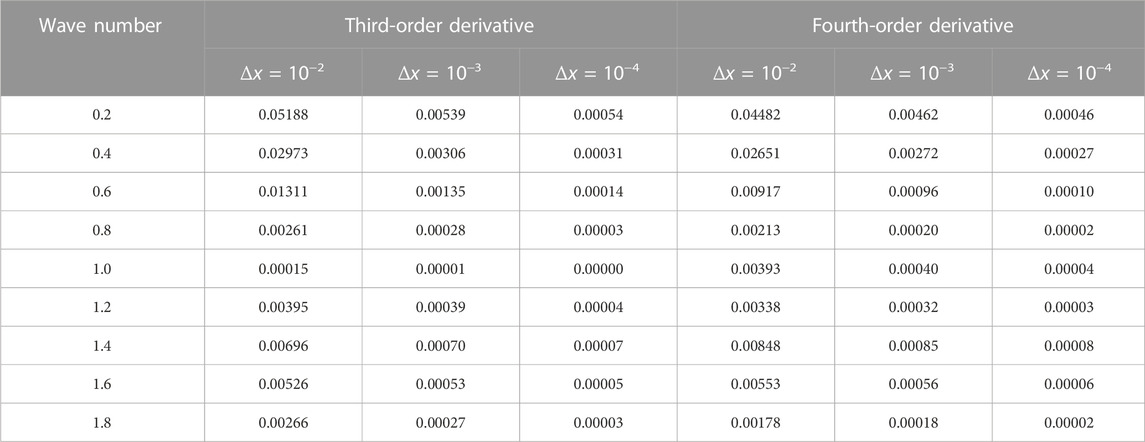
TABLE 2. Relative errors ɛ_err in third- and fourth-order derivatives of the field function of an infinite cylinder.

Tables 1, 2 show that, as the disturbance Δx reduces, the relative inaccuracy gradually diminishes. The relative errors of the various field function derivatives are typically limited to a relatively low number, which confirms the algorithm’s accuracy.

Subsequently, the infinite cylinder’s field function sensitivity distribution, as shown in Figure 2, facilitates a straightforward check of the algorithm’s accuracy at a wave number k = 1. The fact is that the distributions resulting from applying DSM and FDM were substantially consistent, as shown in Figure 2, confirming the accuracy of the algorithm used in this work once more.

FIGURE 2

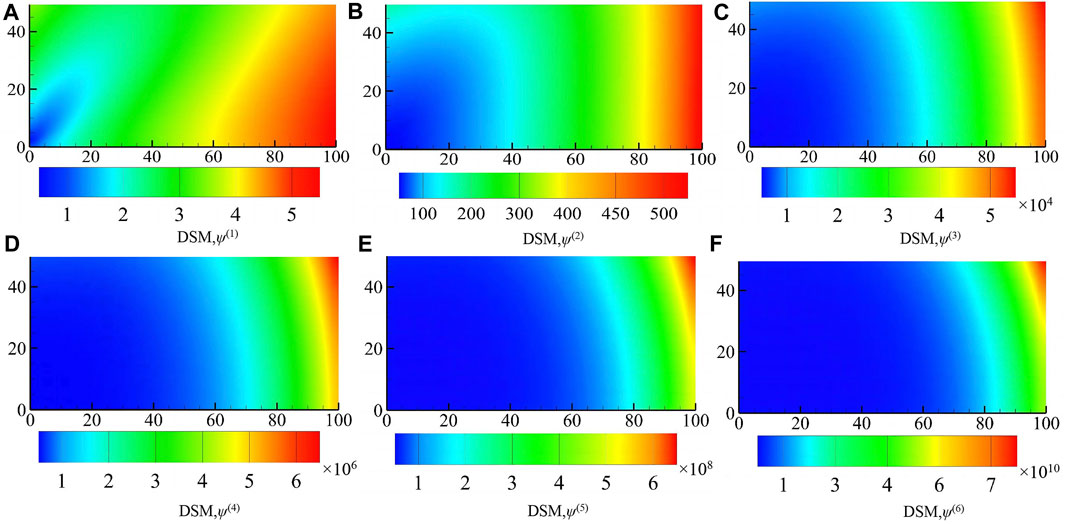
FIGURE 2. Infinite cylindrical field function derivative distribution cloud: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

The uncertainty of an infinite cylinder model is then examined using the perturbation method, where the value of the random variable k is set to be the wave number with a Gaussian distribution. The standard deviation is set in the range of $\sigma \in \left[0.05,0.15\right]$, the corresponding disruption parameter ɛ is 1, and the wave number k’s average value μ is 1. The perturbation method with various order expansion terms is used to compare the first two probability moments of the field function at a position (10,0) with those of MCs. Here, the control group for MCs consists of 500 sample points produced utilizing a random number generator. The responses of 500 sampling points were obtained by repeatedly solving 500 inferior geometric fast multipole BEM equations using the isogeometric fast multipole BEM group. In actuality, this phase is time-consuming.

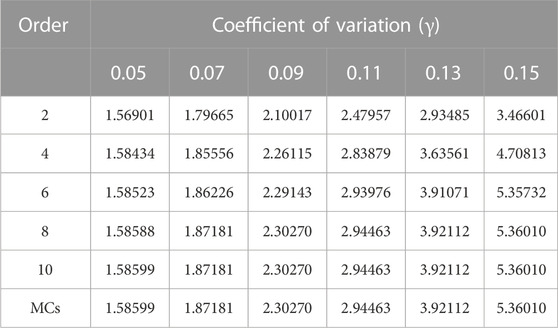
The predicted value of the field function for various γ = σ/μ coefficients of variation is shown in Table 3. The table shows that as the order of expansion increases, the perturbation method’s output approaches that of MCs. The field function’s standard deviation is shown in Figure 3 along with several coefficients of variation. Similar to this, the closer the outcome of the perturbation method is to MCs, the higher the order. We can also discover that this affects the perturbation method’s computational convergence. The Taylor expansion’s restriction causes the convergence to decline as the γ value increases.

TABLE 3

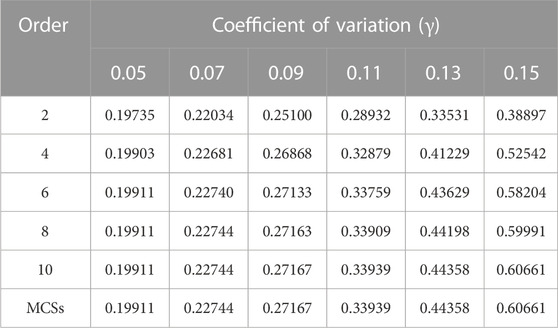
TABLE 3. Expectation of the field function of an infinite cylinder with different coefficients of variation.

FIGURE 3

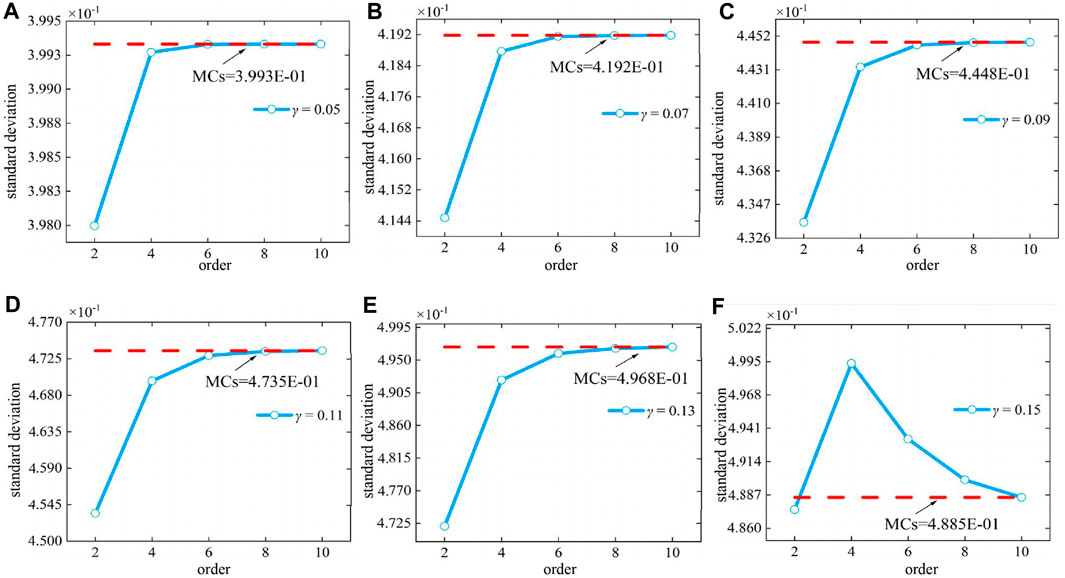
FIGURE 3. Curve of the standard deviation of the field function with derivatives for an infinite cylinder: (A) γ = 0.05, (B) γ = 0.07, (C) γ = 0.09, (D) γ = 0.11, (E) γ = 0.13, and (F) γ = 0.15.

4.1 Sound barrier structure

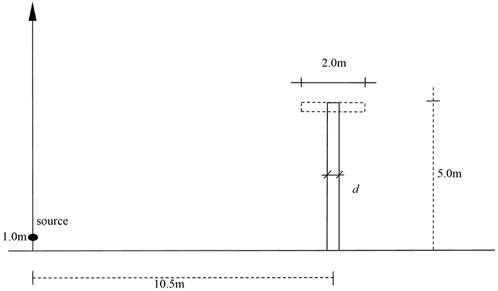
This section presents the noise distribution in the sound shadow area under two simple top shapes. The top shape is an upright rectangle, where the height of the linear sound source from the ground is 1 m, the distance from the sound barrier is 10.5 m, the width of the bottom of the sound barrier is 0.2 m, and the vibration frequency of the sound barrier is 100 Hz, as shown in Figure 4. All surfaces are assumed to be rigid surfaces, so the amount of attenuation of the diffracted sound waves determines the sound barrier’s ability to reduce noise. Due to the total reflection of the ground, this analysis is used to solve a two-dimensional semi-space sound field problem. In the study of the sound barrier structure, the boundary element method only needs to be discretized by a grid instead of discretizing the infinite ground, which shows that the boundary element method has great advantages in calculating the sound field problem in an infinite domain. The vertical sound barrier boundary is discretized into 100 constant boundary units.

FIGURE 4

FIGURE 4. The apical shape is a cross-sectional view of the upright and T-shaped acoustic barriers.

4.1.1 Rectangular model

We regard the input parameter as random—the wave number that adheres to the Gaussian distribution. Figure 5 studies the first, second, and third and fourth, fifth, and sixth variations of the field function with respect to random parameters at the position (10, 0). The derivative amplitude of the field function is calculated using FDM DSM. The steps of FDM are set at Δk = 10⁻²k, Δk = 10⁻³k, Δk = 10⁻⁴k, and Δk = 10⁻⁵k. The results of FDM and the direct uncertainty analysis approach are comparable, as shown in Figure 5.

FIGURE 5

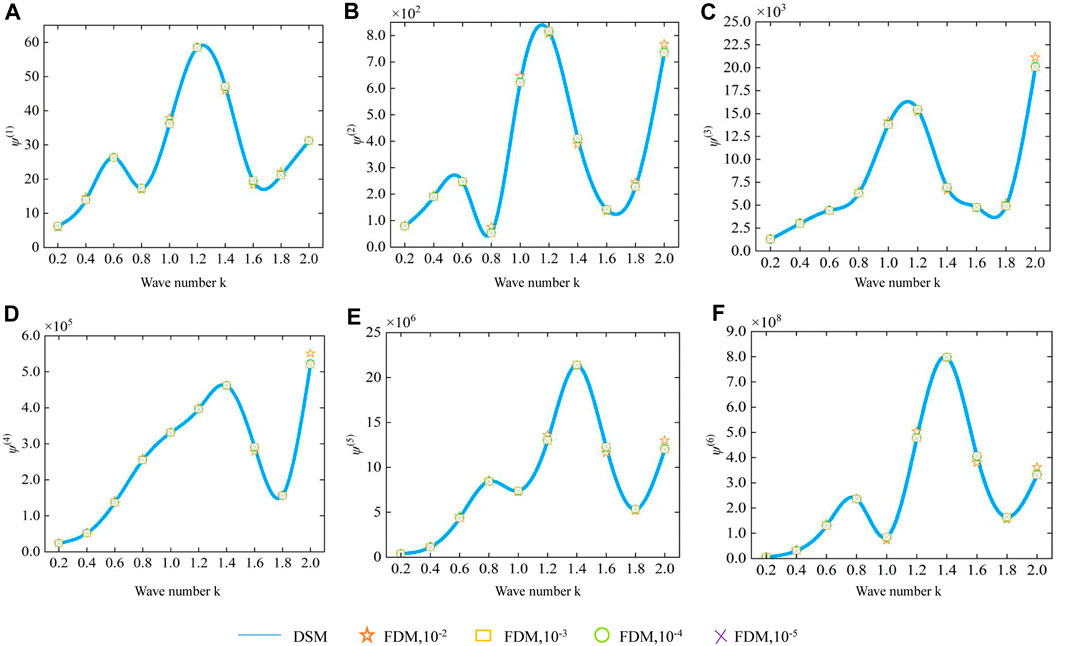
FIGURE 5. Curve plot of the amplitude of the rectangular field function oscillations as a function of the wave number k: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

Their relative errors under various Δx values are given to further investigate the accuracy of FDM and the explicit uncertainty analysis technique. The relative error ɛ_err values of the direct uncertainty analysis approach and FDM are provided in Tables 4, 5. They show that when the disruptions Δx increase, the relative error steadily reduces. The fact that the relative errors of the various field function derivatives are maintained at a relatively low level confirms the algorithm’s accuracy.

TABLE 4

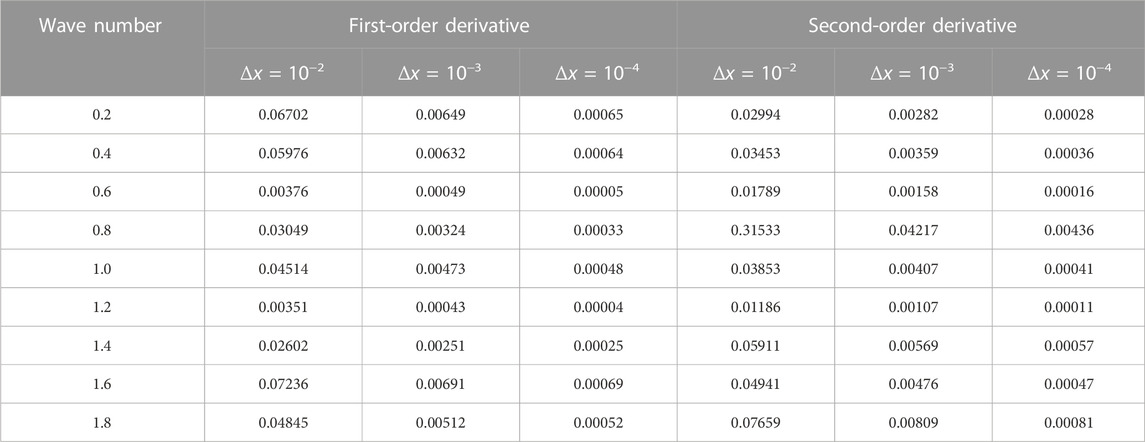
TABLE 4. Relative errors ɛ_err of the first- and second-order derivatives of the rectangular field function.

TABLE 5

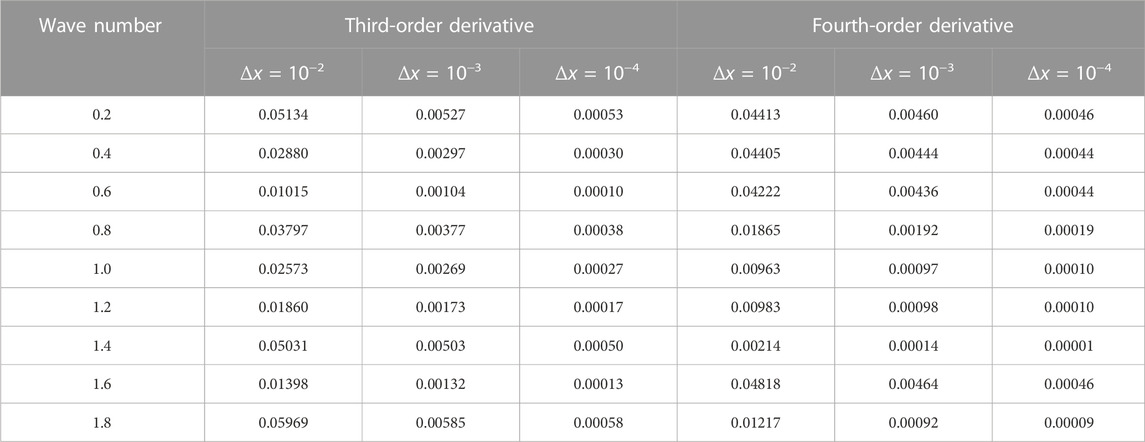
TABLE 5. Relative errors ɛ_err of the third- and fourth-order derivatives of the rectangular field function.

We look at the sensitivity field function’s distribution around the infinite cylinder when the wave number k = 1 to more easily ascertain the algorithm’s accuracy, as shown in Figure 6. It shows that the distribution generated by the direct technique for uncertainty analysis is essentially consistent with that obtained by FDM, further demonstrating the algorithm’s accuracy.

FIGURE 6

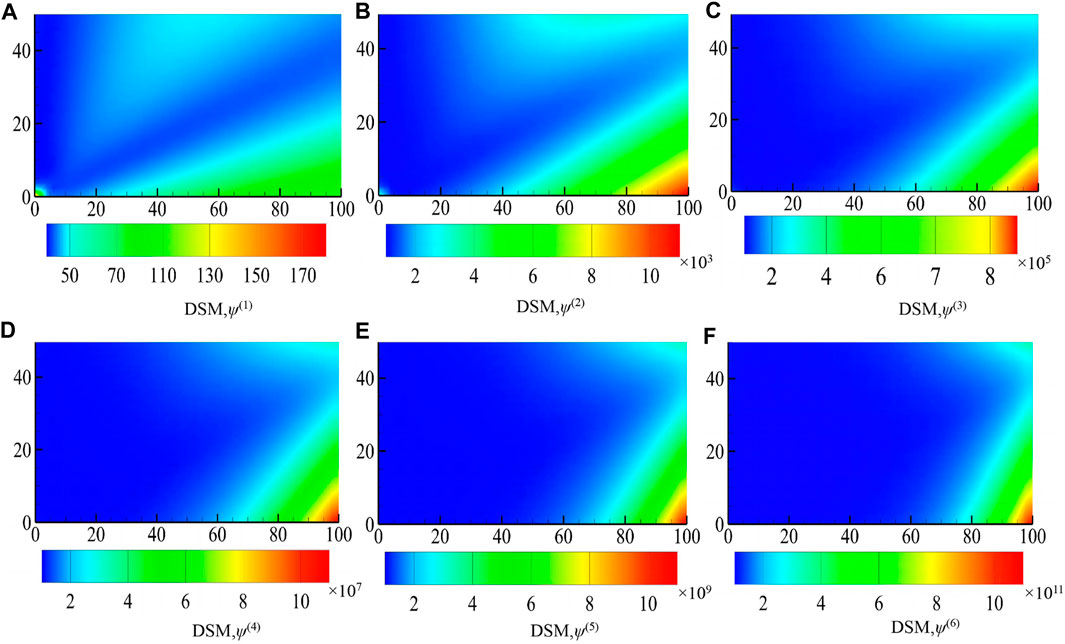
FIGURE 6. Rectangular field function derivative distribution cloud image: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

Then, using a rectangular model with the number of waves k considered to be a Gaussian-distributed random quantity, we analyzed uncertainty using the perturbation method. The relevant interference parameter ɛ is set to 1, the mean value of the number of waves k is set to 1, and the normal deviation is set in the range of $\sigma \in \left[0.05,0.15\right]$. Comparisons are made between the probability moments acquired by MCs and the first two probability moments of the field function at a position (10, 0) generated by the perturbation method with extensions of various orders. The predicted value of the field function for various coefficients of variation γ = σ/μ is shown in Table 6. It shows that as the order of expansion increases, the perturbation method’s results approach those of the MCs. The predicted value and standard deviation of the field function for the extension are displayed in Figure 7.

TABLE 6

TABLE 6. Expectation of the rectangular field function with different coefficients of variation.

FIGURE 7

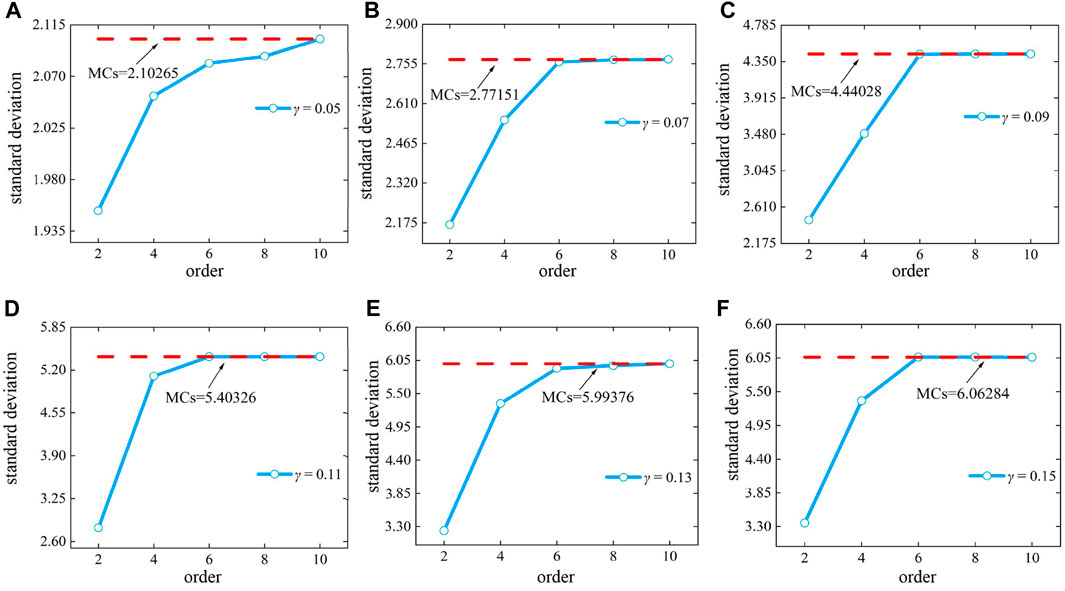
FIGURE 7. Plot of amplitude and standard deviation of the rectangular field function with different derivatives: (A) γ = 0.05, (B) γ = 0.07, (C) γ = 0.09, (D) γ = 0.11, (E) γ = 0.13, and (F) γ = 0.15.

The predicted value and standard deviation of the field function for the extension are displayed in Figure 7. The figure illustrates that, as the expansion term lengthens, the results of the two probability moments calculated using this approach closely approximate to those of MCs. In addition, poor convergence results from an increase in the coefficient of variation γ.

4.1.2 T-shaped model

Similar to the aforementioned rectangular model in this paper, we consider the input parameters to be random parameters and treat the computation of the derivative amplitudes of the treated field functions in the same way. That is, the following figure shows the variation in the first- to sixth-order derivative random parameters of the field function for the position point (10, 0), and the comparison of the results of FDM and the direct deterministic analysis method is shown in Figure 8. Then, the accuracy of FDM and direct uncertainty analysis techniques is further analyzed by their relative errors at different Δx. The relative errors, as shown in Tables 7, 8, indicate a decreasing trend with increasing Δx.

FIGURE 8

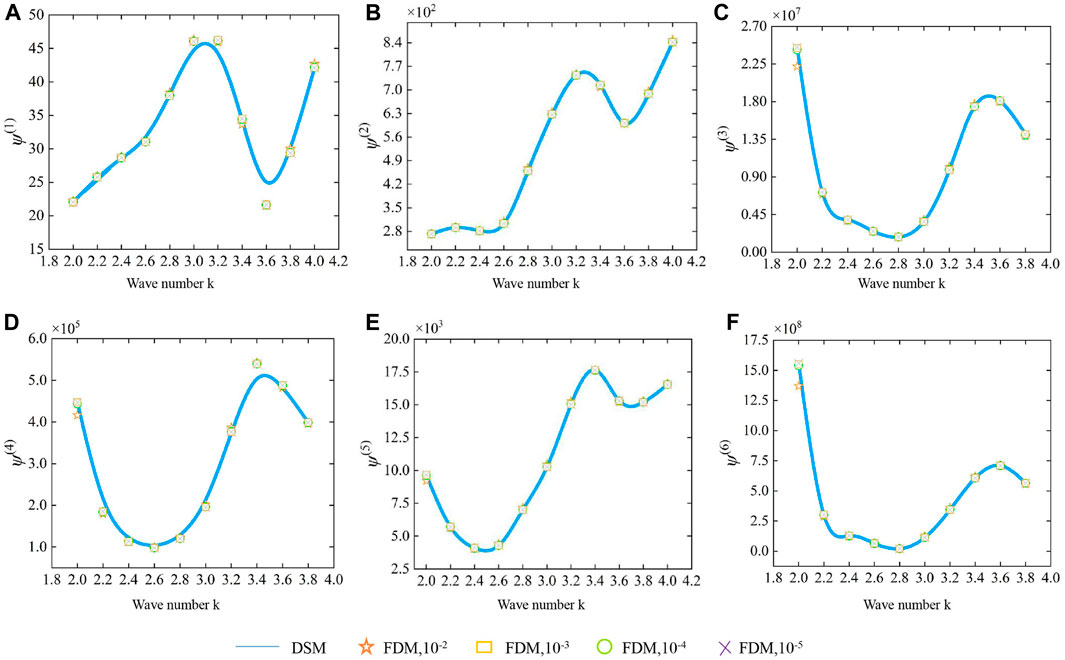
FIGURE 8. Plot of the amplitude of the T-shaped field function as a function of the wave number k: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

TABLE 7

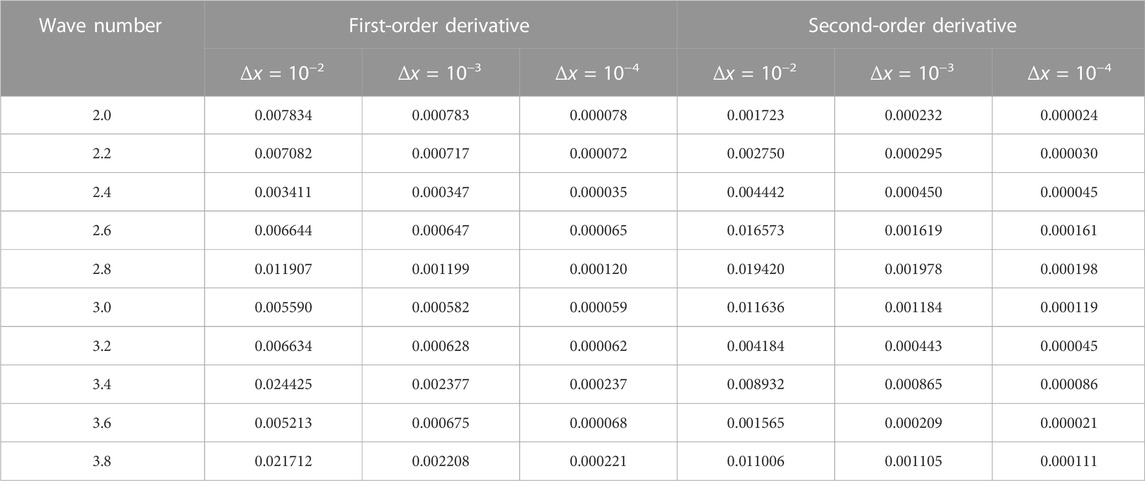
TABLE 7. Relative errors ɛ_err of the third- and fourth-order derivatives of the T-shaped field function.

TABLE 8

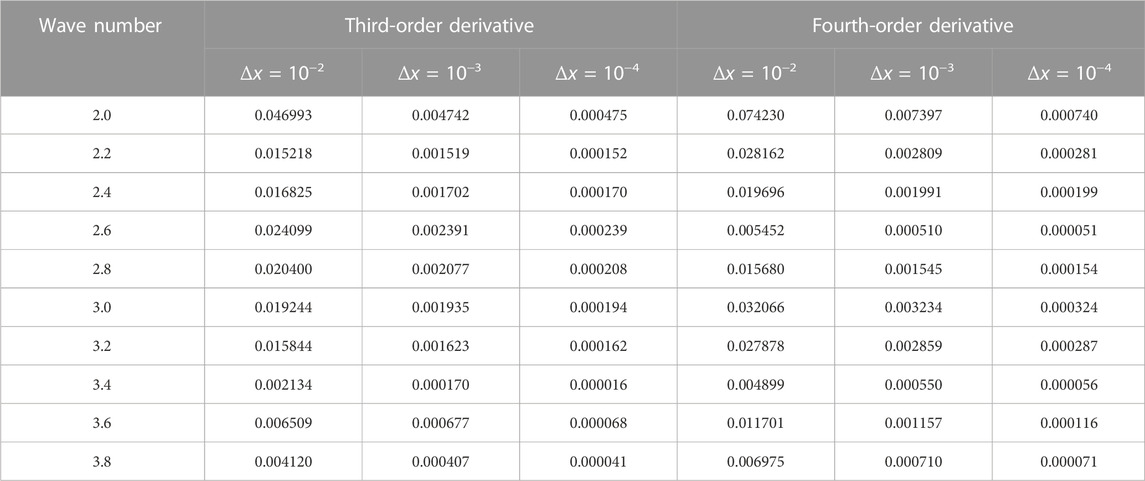
TABLE 8. Relative errors ɛ_err of first- and second-order derivatives of the T-shaped field function.

We also investigate the distribution of the sensitivity field function around the infinite cylinder when the wave number is 1, as shown in Figure 9. This result further demonstrates the accuracy of the algorithm. Using a T-shaped model with a Gaussian-distributed random quantity with a wave number k, the uncertainty is analyzed using the perturbation method, the relevant disturbance parameter ɛ is set to 1, the mean value μ is also set to 1, and the normal deviation is set in the range of $\sigma \in \left[0.05,0.15\right]$. By comparing the probability moments obtained under the perturbation method with those obtained by MCs, the predicted values of the field function under different coefficients of variation γ = σ/μ are shown in Table 9, and the predicted values and standard deviations of the extended field function are shown in Figure 10.

FIGURE 9

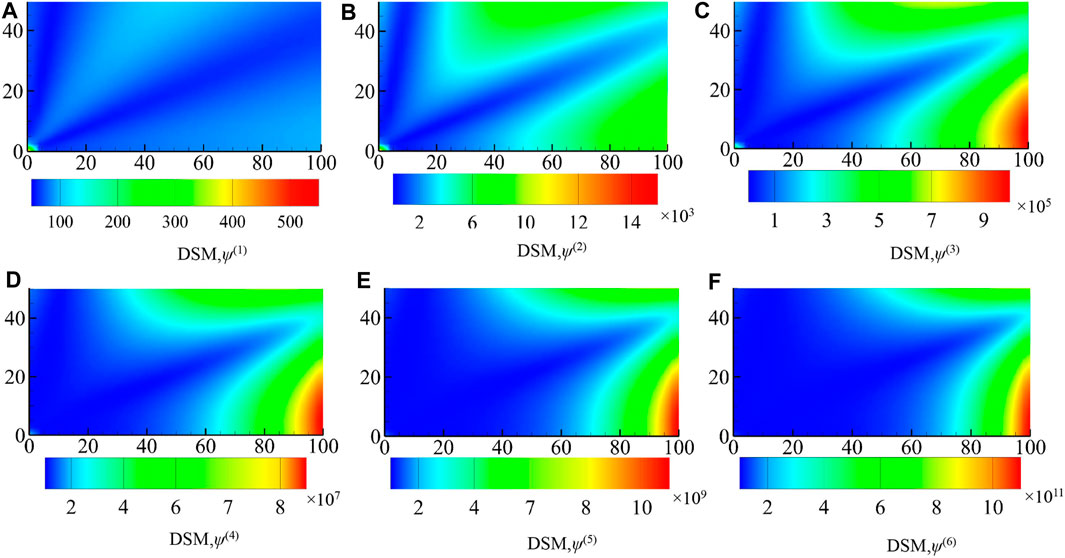
FIGURE 9. Distribution of T-shaped field functions under different derivatives: (A) first-order, (B) second-order, (C) third-order, (D) fourth-order, (E) fifth-order, and (F) sixth-order derivatives.

TABLE 9

TABLE 9. Expectation of the T-shaped field function with different coefficients of variation.

FIGURE 10

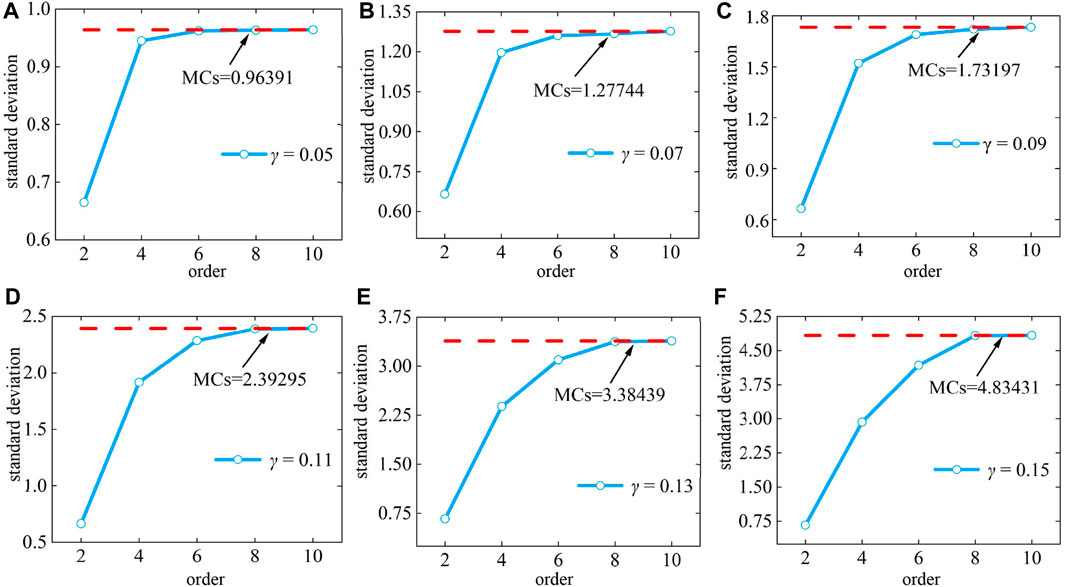
FIGURE 10. The curve where the standard deviation of a T-shaped field function changes with the derivative: (A) γ = 0.05, (B) γ = 0.07, (C) γ = 0.09, (D) γ = 0.11, (E) γ = 0.13, and (F) γ = 0.15.

By analyzing these two numerical examples, Figures 7, 10 illustrate that as the expansion term lengthens, the results of the two probability moments calculated using this approach closely approximate to those of MCs. In addition, poor convergence results from an increase in the coefficient of variation γ.

5 Conclusion

The generalized nth-order perturbation approach is used in this study to analyze the uncertainty around sound wave propagation in an infinite domain. IGABEM enhances the precision and effectiveness of the stochastic perturbation method through the seamless integration of CAD and numerical analysis. Furthermore, it mainly uses NURBS to construct structural geometry and discretize the boundary integral equation. We discover that the isogeometric BEM simulation, which uses an exact geometric representation compared to a traditional Lagrange-based BEM simulation, is often more accurate. The investigation of the immediate uncertainty approach and finite difference method proves accurate for larger derivatives, which confirms the validity of the suggested algorithm. In addition, we compare this method with other derivatives generated by the global finite difference method. Under a specific wave number, the derivative value increases as the field function’s derivative order increases. Additionally, this phenomenon can be utilized in real-world engineering applications. The result of uncertainty qualification shows that with the increase in the extended order term, the predicted value of field functions based on this technique is comparable to the anticipated value of MCSs, demonstrating the accuracy of the suggested methodology. The existing strategy has some drawbacks. When the unpredictability of the input random variable is high, capturing its statistical characteristics adequately can be challenging. While improving computation accuracy by modifying the order of the Taylor expansion, it also increases the cost of the calculation. In the future, we can extend the perturbation method to deal with three-dimensional acoustic scattering problems as well as target objects with more complex geometries, which will not only increase the complexity of the problem but also expand its range of applications. Uncertainty analysis of acoustic scattering problems at different frequencies can also be investigated to gain a more comprehensive understanding of the properties of acoustic wave propagation. This is essential for solving multi-frequency acoustic scattering problems and for practical applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YY: conceptualization, methodology, and writing–review and editing. RH: formal analysis, software, validation, and writing–original draft. XY: project administration, supervision, and writing–original draft. WW: software and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Postgraduate Education Reform and Quality Improvement Project of Henan Province under Grant No. YJS2023JD52 and sponsored by the Laboratory of Aerodynamic Noise Control under Grant No. ANCL20220301. This research was supported by the Youth Backbone Teacher Training Program of Henan Province under Grant No. 2019GGJS232 and sponsored by the Key Scientific Research Project of Henan University under Grant No. 23A560015. This research was supported by the school funds of Guangzhou University under Grant No. 202201020134.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Marburg S. Developments in structural-acoustic optimization for passive noise control. Arch Comput Methods Eng (2002) 9:291–370. doi:10.1007/bf03041465

CrossRef Full Text | Google Scholar

2. Liu Y. On the bem for acoustic wave problems. Eng Anal Boundary Elem (2019) 107:53–62. doi:10.1016/j.enganabound.2019.07.002

CrossRef Full Text | Google Scholar

3. Chen L, Lian H, Liu Z, Chen H, Atroshchenko E, Bordas S. Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Comp Methods Appl Mech Eng (2019) 355:926–51. doi:10.1016/j.cma.2019.06.012

CrossRef Full Text | Google Scholar

4. Chen L, Lu C, Lian H, Liu Z, Zhao W, Li S, et al. Acoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Comp Methods Appl Mech Eng (2020) 362:112806. doi:10.1016/j.cma.2019.112806

CrossRef Full Text | Google Scholar

5. Zhang J, Lin W, Shu X, Zhong Y. A dual interpolation boundary face method for exterior acoustic problems based on the burton–miller formulation. Eng Anal Boundary Elem (2020) 113:219–31. doi:10.1016/j.enganabound.2020.01.005

CrossRef Full Text | Google Scholar

6. Bourlier C, Pinel N, Kubicke G. Method of moments for the scattering from 2d problems: basic concepts and applications (2013).

Google Scholar

7. Li H, Zhao J, Guo X, Cheng Y, Xu Y, Yuan X. Sensitivity analysis of flexoelectric materials surrogate model based on the isogeometric finite element method. Front Phys (2022) 10:1343. doi:10.3389/fphy.2022.1111159

CrossRef Full Text | Google Scholar

8. Qu Y, Pan E, Zhu F, Jin F, Roy A. Modeling thermoelectric effects in piezoelectric semiconductors: new fully coupled mechanisms for mechanically manipulated heat flux and refrigeration. Int J Eng Sci (2023) 182:103775. doi:10.1016/j.ijengsci.2022.103775

CrossRef Full Text | Google Scholar

9. Xu Y, Li H, Chen L, Zhao J, Zhang X. Monte Carlo based isogeometric stochastic finite element method for uncertainty quantization in vibration analysis of piezoelectric materials. Mathematics (2022) 10:1840. doi:10.3390/math10111840

CrossRef Full Text | Google Scholar

10. Shen X, Du C, Jiang S, Zhang P, Chen L. Multivariate uncertainty analysis of fracture problems through model order reduction accelerated sbfem. Appl Math Model (2024) 125:218–40. doi:10.1016/j.apm.2023.08.040

CrossRef Full Text | Google Scholar

11. Shen X, Du C, Jiang S, Sun L, Chen L. Enhancing deep neural networks for multivariate uncertainty analysis of cracked structures by pod-rbf. Theor Appl Fracture Mech (2023) 125:103925. doi:10.1016/j.tafmec.2023.103925

CrossRef Full Text | Google Scholar

12. Ghanem R, Spanos P. Stochastic finite elements: a spectral approach (1991).

Google Scholar

13. Honda R. Stochastic bem with spectral approach in elastostatic and elastodynamic problems with geometrical uncertainty. Eng Anal Bound Elem (2005) 29:415–27. doi:10.1016/j.enganabound.2005.01.007

CrossRef Full Text | Google Scholar

14. Liu W, Belytschko T, Mani A. Random field finite elements. Internat J Numer Methods Engrg (1986) 23:1831–45. doi:10.1002/nme.1620231004

CrossRef Full Text | Google Scholar

15. Chen L, Liu C, Zhao W, Liu L. An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Comp Methods Appl Mech Eng (2018) 336:507–32. doi:10.1016/j.cma.2018.03.025

CrossRef Full Text | Google Scholar

16. Chen L, Cheng R, Li S, Lian H, Zheng C, Bordas S. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic–vibration interaction problems. Comp Methods Appl Mech Eng (2022) 393:114784. doi:10.1016/j.cma.2022.114784

CrossRef Full Text | Google Scholar

17. Kamiński M. Stochastic perturbation approach to engineering structure vibrations by the finite difference method. J Sound Vibration (2001) 251:651–70. doi:10.1006/jsvi.2001.3850

CrossRef Full Text | Google Scholar

18. Kamiński M. On generalized stochastic perturbation-based finite elements. Comm Numer Methods Engrg (2006) 22:23–31. doi:10.1002/CNM.795

CrossRef Full Text | Google Scholar

19. Au S, Beck J. Subset simulation and its application to seismic risk based on dynamic analysis. J ENG Mech (2003) 129:901–17. doi:10.1061/(asce)0733-9399(2003)129:8(901)

CrossRef Full Text | Google Scholar

20. Feng Y, Li C, Owen D. A directed Monte Carlo solution of linear stochastic algebraic system of equations. Finite Elem Anal Des (2010) 46:462–73. doi:10.1016/j.finel.2010.01.004

CrossRef Full Text | Google Scholar

21. Ding C, Tamma K, Lian H, Ding Y, Dodwell T, Bordas S. Uncertainty quantification of spatially uncorrelated loads with a reduced-order stochastic isogeometric method. Comput Mech (2021) 67:1255–71. doi:10.1007/s00466-020-01944-9

CrossRef Full Text | Google Scholar

22. Hu X, Cui X, Feng H, Li G. Stochastic analysis using the generalized perturbation stable node-based smoothed finite element method. Eng Anal Boundary Elem (2010) 70:40–55. doi:10.1016/j.enganabound.2016.06.002

CrossRef Full Text | Google Scholar

23. Ding C, Cui X, Deokar RR, Li G, Cai Y, Tamma KK. Modeling and simulation of steady heat transfer analysis with material uncertainty: generalized n-th order perturbation isogeometric stochastic method. Numer Heat Transfer A Appl (2018) 74:1565–82. doi:10.1080/10407782.2018.1538296

CrossRef Full Text | Google Scholar

24. Ding C, Tamma K, Cui X, Ding Y, Li G, Bordas S. An nth high order perturbation-based stochastic isogeometric method and implementation for quantifying geometric uncertainty in shell structures. Adv Eng Softw (2020) 148:102866. doi:10.1016/j.advengsoft.2020.102866

CrossRef Full Text | Google Scholar

25. Kamiński M. Stochastic second-order perturbation approach to the stress-based finite element method. Int J Sol Structures (2001) 38:3831–52. doi:10.1016/s0020-7683(00)00234-1

CrossRef Full Text | Google Scholar

26. Kamiński M. Generalized perturbation-based stochastic finite element method in elastostatics. Comput Struct (2007) 85:586–94. doi:10.1016/j.compstruc.2006.08.077

CrossRef Full Text | Google Scholar

27. Chen L, Lian H, Natarajan S, Zhao W, Chen X, Bordas SPA. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comp Methods Appl Mech Eng (2022) 395:114997. doi:10.1016/j.cma.2022.114997

CrossRef Full Text | Google Scholar

28. Chen L, Lian H, Liu Z, Gong Y, Zheng CJ, Bordas SPA. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric fem–bem. Eng Anal Boundary Elem (2022) 135:182–95. doi:10.1016/j.enganabound.2021.11.005

CrossRef Full Text | Google Scholar

29. Chen L, Wang Z, Peng X, Yang J, Wu P, Lian H. Modeling pressurized fracture propagation with the isogeometric bem. Geomechanics Geophys Geo-Energy Geo-Resources (2021) 7:51. doi:10.1007/s40948-021-00248-3

CrossRef Full Text | Google Scholar

30. Chen L, Zhang Y, Lian H, Atroshchenko E, Ding C, Bordas S. Seamless integration of computer-aided geometric modeling and acoustic simulation: isogeometric boundary element methods based on catmull-clark subdivision surfaces. Adv Eng Softw (2020) 149:102879. doi:10.1016/j.advengsoft.2020.102879

CrossRef Full Text | Google Scholar

31. Chen L, Li H, Guo Y, Chen P, Atroshchenko E, Lian H. Uncertainty quantification of mechanical property of piezoelectric materials based on isogeometric stochastic fem with generalized n th-order perturbation. Eng Comput (2023) 1–21. doi:10.1007/s00366-023-01788-w

CrossRef Full Text | Google Scholar

32. Chen L, Lu C, Zhao W, Chen H, Zheng C. Subdivision surfaces—boundary element accelerated by fast multipole for the structural acoustic problem. J Theor Comput Acoust (2020) 28:2050011. doi:10.1142/s2591728520500115

CrossRef Full Text | Google Scholar

33. Qu Y, Zhang G, Gao X, Jin F. A new model for thermally induced redistributions of free carriers in centrosymmetric flexoelectric semiconductor beams. Mech Mater (2022) 171:104328. doi:10.1016/j.mechmat.2022.104328

CrossRef Full Text | Google Scholar

34. Qu Y, Jin F, Yang J. Temperature effects on mobile charges in thermopiezoelectric semiconductor plates. Int J Appl Mech (2021) 13:2150037. doi:10.1142/s175882512150037x

CrossRef Full Text | Google Scholar

35. Martinsson P, Rokhlin V. A fast direct solver for scattering problems involving elongated structures. J Comput Phys (2007) 221:288–302. doi:10.1016/j.jcp.2006.06.037

CrossRef Full Text | Google Scholar

36. Bebendorf M, Rjasanow S. Adaptive low-rank approximation of collocation matrices. Computing (2003) 70:1–24. doi:10.1007/s00607-002-1469-6

CrossRef Full Text | Google Scholar

37. Chen L, Wang Z, Lian H, Ma Y, Meng Z, Li P, et al. Reduced order isogeometric boundary element methods for CAD-integrated shape optimization in electromagnetic scattering. Comp Methods Appl Mech Eng (2024) 419:116654. doi:10.1016/j.cma.2023.116654

CrossRef Full Text | Google Scholar

38. Guiggiani M, Casalini P. Direct computation of Cauchy principal value integrals in advanced boundary elements. Int J Numer Methods Eng (1987) 24:1711–20. doi:10.1002/nme.1620240908

CrossRef Full Text | Google Scholar

39. Hughes T, Cottrell J, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comp Methods Appl Mech Eng (2005) 194:4135–95. doi:10.1016/j.cma.2004.10.008

CrossRef Full Text | Google Scholar

40. Qin X, Dong C, Yang H. Isogeometric vibration and buckling analyses of curvilinearly stiffened composite laminates. Appl Math Model (2019) 73:72–94. doi:10.1016/j.apm.2019.03.045

CrossRef Full Text | Google Scholar

41. Dölz J, Kurz S, Schöps S, Wolf F. A numerical comparison of an isogeometric and a parametric higher order raviart–thomas approach to the electric field integral equation. IEEE Trans Antennas Propagation (2020) 68:593–7. doi:10.1109/tap.2019.2935778

CrossRef Full Text | Google Scholar

42. Dölz J, Kurz S, Schöps S, Wolf F. Isogeometric boundary elements in electromagnetism: rigorous analysis, fast methods, and examples. SIAM J Scientific Comput (2019) 41:B983–B1010. doi:10.1137/18m1227251

CrossRef Full Text | Google Scholar

43. Rojas J, Bendaou O, Hami A, Rade D. Stochastic and reliability analysis of fluid-structure interaction problems using finite element models. Multidiscipline Model Mater structures (2010) 6:6–22. doi:10.1108/15736101011055248

CrossRef Full Text | Google Scholar

44. Cao G, Yu B, Chen L, Yao W. Isogeometric dual reciprocity bem for solving non-fourier transient heat transfer problems in fgms with uncertainty analysis. Int J Heat Mass Transfer (2023) 203:123783. doi:10.1016/j.ijheatmasstransfer.2022.123783

CrossRef Full Text | Google Scholar

45. Chen L, Lian H, Xu Y, Li S, Liu Z, Atroshchenko E, et al. Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl Math Model (2023) 114:360–78. doi:10.1016/j.apm.2022.09.030

CrossRef Full Text | Google Scholar

46. Chen L, Zhao J, Lian H, Yu B, Atroshchenko E, Li P. A bem broadband topology optimization strategy based on taylor expansion and soar method—-application to 2d acoustic scattering problems. Int J Numer Methods Engineering/(2023) 124:5151–82. doi:10.1002/nme.7345

CrossRef Full Text | Google Scholar

47. Dölz J, Harbrecht H, Kurz S, Multerer M, Schöps S, Wolf F. Bembel: the fast isogeometric boundary element c++ library for laplace, helmholtz, and electric wave equation. SoftwareX (2020) 11:100476. doi:10.1016/j.softx.2020.100476

CrossRef Full Text | Google Scholar

48. Simpson R, Liu Z, Vázquez R, Evans J. An isogeometric boundary element method for electromagnetic scattering with compatible b-spline discretizations. J Comput Phys (2018) 362:264–89. doi:10.1016/j.jcp.2018.01.025

CrossRef Full Text | Google Scholar

49. Burton A, Miller G. The application of integral equation methods to the numerical solution of some exterior boundary-value problems. Proc R Soc Lond A. Math Phys Sci (1971) 323:201–10. doi:10.1098/rspa.1971.0097

CrossRef Full Text | Google Scholar

50. Marburg S. The burton and miller method: unlocking another mystery of its coupling parameter. J Comput Acoust (2016) 24:1550016. doi:10.1142/s0218396x15500162

CrossRef Full Text | Google Scholar

51. Nishimura N. Fast multipole accelerated boundary integral equation methods. Appl Mech Rev (2002) 55:299–324. doi:10.1115/1.1482087

CrossRef Full Text | Google Scholar

52. Coifman R, Rokhlin V, Wandzura S. The fast multipole method for the wave equation: a pedestrian prescription. Antennas Propag Mag IEEE (1993) 35:7–12. doi:10.1109/74.250128

CrossRef Full Text | Google Scholar

53. Dölz J, Harbrecht H, Kurz S, Schöps S, Wolf F. A fast isogeometric bem for the three dimensional laplace- and helmholtz problems. Comp Methods Appl Mech Eng (2018) 330:83–101. doi:10.1016/j.cma.2017.10.020

CrossRef Full Text | Google Scholar