- 1Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
- 2Department of Mathematics, University College of Umluj, University of Tabuk, Umluj, Saudi Arabia
- 3Department of Physics, Faculty of Sciences, University of Monastir, Monastir, Tunisia
- 4Department of Mathematics, College of Duba, University of Tabuk, Duba, Saudi Arabia
- 5Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
- 6Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
- 7Department of Basic Science, Zagazig Higher Institude of Engineering & Technology, Zagazig, Egypt
- 8Department of Mathematics, College of Science, Taibah University, Al-Madinah Al-Munawarah, Saudi Arabia
The Thomson influence on semiconductors can be studied by investigating the connection between the presence of thermoelectric and magnetic fields and porosity and the photothermal transport mechanism. Elastic waves, voids, magnetic fields, and thermoelectric effects in plasma are investigated. The governing equations were analyzed for a uniformly distributed and isotropic medium under two-dimensional [electronic and elastic (plasmaelastic)] deformations. The charge density is considered solely dependent on the induced electric current over time. The Laplace-Fourier transforms method in two dimensions is employed to obtain solutions for the primary variables. The recombination process results in the application of electro-mechanical loads and thermal effects on the free surface of a porous medium. The Laplace-Fourier transformations inversion operations help obtain comprehensive solutions in this study. The effects of porosity parameters and silicon (Si) on a semiconductor porous material are considered, and the resulting physical field distributions are analyzed and represented graphically.
Introduction
The absorption of light by a substance and its subsequent conversion to heat, resulting in thermal expansion or contraction, is known as the photothermal effect. When elastic qualities like stress or strain alter in response to light or heat, we call that material a photothermal elastic media. The principles of photothermal effects and elasticity can be used to explain the behavior of a photothermal elastic media. Photothermal elastic media have been intensively explored in the realm of photonics, particularly in the construction of tunable photonic devices. Applications where the properties of the photothermal elastic media must be regulated include optical switches, filters, sensors, robotics, aerospace, and biomedical engineering. There are a variety of uses for photothermal elastic media. Materials scientists and engineers, for instance, can use these materials to create structures with malleable mechanical properties. When light is absorbed by a photothermal elastic media, the energy is transformed into heat. The mechanical properties of a material, such as its elasticity parameters Young’s modulus, and Poisson’s ratio, are affected by thermal expansion as a result of temperature changes. Applications involving altered stress or strain are possible. Photothermal stimulation of semiconductor materials has received a lot of attention in recent years due to the potential impact on those materials’ thermo-mechanical properties. Engineering, petroleum, aviation, electronics, and photovoltaics are just a few of the many fields that benefit greatly from semiconductors. Deformations and strains in semiconductors, for example, are thought to be strongly influenced by temperature, according to current physics ideas. This is especially the case when the semiconductor medium is subjected to a wide range of temperatures. Photothermal excitation processes with refined multi-dual phase-lags theory for semiconductor elastic medium are studied by Khamis et al. [1]. Ailawalia et al. [2] produced ramp-type heating in a semiconductor medium under photothermal theory.
The elasticity of a substance is its capacity to stretch and then recover its original form after being stretched or compressed. The vibrations and collisions of particles in the internal medium generate heat, which in turn causes the material to deform. Free electrons and plasma waves are produced when a laser beam is shone on the surface of a semiconductor material. In light of this, investigating how thermal waves, plasma waves, and elastic materials interact is essential. The mechanical, electric, and thermal properties of semiconductor materials change with temperature variations. When a temperature gradient arises in a semiconductor elastic material due to light absorption, it causes an electric potential difference between the endpoints. In such cases, the relationship between heat production and electrical resistance needs to be examined. Hobiny and Abbas [3] described a GL photo-thermal theory on new hyperbolic two-temperature in a semiconductor material. Abbas et al. [4] introduced Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. Alshehri and Lotfy [5] produced memory-dependent derivatives (MDD) for magneto-thermal-plasma semiconductor medium induced by laser pulses with hyperbolic two temperature theory. Lotfy and El-Bary [6] studied magnetic-thermal-elastic waves under the impact of induced laser pulses and hyperbolic two-temperature theory with memory-dependent derivatives (MDD). Magneto-photo-thermo-microstretch semiconductor elastic medium due to the photothermal transport process is discussed by Lotfy and El-Bary [7]. Aldwoah et al. [8] produced a novel magneto-photo-elasto-thermodiffusion electrons-holes model of an excited semiconductor.
Porosity is a material feature that characterizes the presence of internal voids. The ability to absorb or hold liquids or gases is sometimes indicated by this term. Porosity can occur for many reasons depending on the material. Dissolved minerals or the absence of fossils can leave behind voids, which geologists refer to as porosity. In construction materials, porosity can be deliberate, such as in lightweight concrete or aerated blocks, or inadvertent due to poor fabrication procedures or inadequate compaction. Many facets of human existence depend on porosity. The porosity of rock formations is crucial, for instance, in the oil and gas business, for assessing the viability of energy extraction. Porosity is an important material attribute because it influences the material’s physical, chemical, and mechanical properties. Benefits in technology, energy production, building, and healthcare are just some of the areas that could result from a better understanding of and ability to manipulate porosity. Raddadi et al. [9] studied a novel model of a semiconductor porosity medium according to photo-thermoelasticity excitation with initial stress. Bouslimi et al. [10] produced a mathematical model of photothermal and voids in a semiconductor medium in the context of Lord-Shulman theory. Kilany et al. [11] introduced the photothermal and void effect of a semiconductor rotational medium based on Lord–Shulman theory. Bayones et al. [12] discussed a rotational gravitational stress and voids effect on an electromagnetic photothermal semiconductor medium under three models of thermoelasticity. Khalil et al. [13] studied electromagnetic field and initial stress on a photothermal semiconducting void medium under thermoelasticity theories. Jawa et al. [14] produced machine learning and statistical methods for studying voids and photothermal effects of a semiconductor rotational medium with thermal relaxation time.
The creation of heat or cooling at the junction of two different conductive materials caused by an electric current passing through them is referred to as the Thomson effect. Lord Kelvin (then known as William Thomson) made the discovery. The connection can be heated by the Thomson effect or cooled by it. The Thomson effect is strongly linked to the thermalization of semiconducting materials upon their absorption of electromagnetic radiation in the context of electromagnetic photo-thermal media. Electromagnetic radiation (including visible and infrared light) photons can be absorbed by a semiconductor medium to impart energy to the substance. Then, the heat is produced from this source of energy. The Thomson effect in electromagnetic photo-thermal semiconductor mediums involves the formation of heat or cooling at the junction of two conductive materials due to the absorption of electromagnetic radiation in semiconducting materials. Useful in thermoelectric cooling and other related technologies, the phenomena has been observed in nature. Lotfy et al. [15] studied electromagnetic and Thomson effects during the photothermal transport process of a rotator semiconductor medium under hydrostatic initial stress. Mahdy et al. [16] described analytical solutions of time-fractional heat order for a magneto-photothermal semiconductor medium with Thomson effects and initial stress. Alharbi et al. [17] introduced the Thomson effect with hyperbolic two-temperature on magneto-thermo-visco-elasticity. In a photothermal elastic medium, the porosity influences the flow of heat and therefore affects the temperature gradient within the material. As porosity increases, the void spaces act as insulators, hindering the flow of heat through the material. Consequently, this alters the temperature distribution and leads to variations in the Thomson effect. The Thomson effect can cause variations in porosity through electrochemical reactions, thereby modifying the material’s properties. Understanding this relationship is crucial for studying the behavior of photothermal elastic media and designing materials with specific thermal and electrical properties. On the other hand, Zenkour [18, 19] studied the properties of thermal activation during photoexcited semiconductor medium using a refined multi-phase-lag technique. Zenkour [20] investigated the gravitational impact on a refined photothermal half-space material. Zenkour and Abouelregal [21] used a long semiconductor cylinder to study the influence of variable harmonic heat in the context of photoexcited processes.
In the present work, the photothermal theory with the porosity of an electromagnetic semiconductor elastic medium is being utilized to examine the Thomson effect. By employing the photothermal transport process and thermoelasticity equations, the propagation of waves in an external electromagnetic field is described. In this particular model, three effects occur: the first is due to the electromagnetic field, resulting in the appearance of the Thomson effect; the second effect is due to the impact of photo-excitation, leading to the appearance of plasma (carrier density); and finally, the third effect is caused by porosity. To acquire the precise expressions of certain physical quantities distribution in a two-dimensional deformation, the Laplace transform method is employed alongside electro-mechanical, voids, plasma, and thermal loads. The obtained results are then discussed and presented graphically for various scenarios, including the presence or absence of the Peltier coefficient (Thomson parameter), different porosity parameters (with and without porosity), and varying values of the induced magnetic field.
Mathematical model and basic equations
This problem investigates the impact of porosity on a two-dimensional
The medium has magnetic permeability and electric permeability that determine its ability to conduct magnetic and electric fields respectively
Differentiating the above equation for
Substituting from Equation 5 in Equation 1, yields
Using Eqs 7–9, the general form of paraphrasing the heat conductive equation for a semiconductor elastic medium is as follows:
Where, the term
The expression of the equation of continuity for charges in the presence of an electromagnetic field can be stated as follows:
Where
Assume that the charge density
Therefore, the equation of continuity (11) takes the form:
Consider the velocity
Where
Eq. 12 can be rewritten in the following form
Integrating Equation 14 and using series expand, we have
Where
Then the heat Equation 10 takes the form:
The Lorentz force, which arises due to the influence of electromagnetic fields, can be formulated as [24]:
The components of Lorentz force take the form [25]:
In addition, the following are presented: equations that describe the electromagnetic field, the impact of porosity on the system, and the influence of the Thomson effect on the photo-induced process in a semiconductor medium.
The coupling between plasma waves and thermal waves [26–30]:
The porous (voids) equation can be given as [31]:
The constitutive relations for the generalized photo-thermoelastic theory in tensor form can be paraphrased as follows [32]:
In the above equations, the parameter
Mathematical formulations
The modified linear semiconductor thermoelasticity in the presence of carrier density and an initial external magnetic field, without considering internal heat sources, can be expressed as follows:
The dimensionless form can be obtained by using non-dimension variables to represent the main fields.
Eq. 37, when utilized as the key governing equation, paraphrasing leads to the following outcomes:
The main coefficients of the equations (38)-(48) can be obtained in the (Appendix A1). Assume that the normal stress is
Solving the problem.
Laplace transform for function
The formula for the exponential Fourier transforms with parameter
Applying Laplace-Fourier double transform into Equations 38–45, yields:
Where,
The main coefficients of the equation (57) can be obtained in the (Appendix A1). The primary 10th ordinary differential Equation 57 were solved using the factorization technique as follows:
Where
Where,
Boundary conditions
Consider the elastic semiconductor medium is initially in a state of rest at the vertical plane (free surface)
(I) The plasma boundary condition when the Laplace transform is used at the free surface to transport and photo-generate the carrier density diffusion during the recombination processes with speed
Therefore,
(II) At the free surface, the isothermal boundary condition sensitive to thermal shock is defined as:
Therefore,
(III) The mechanical boundary condition: the surface has zero strain at the bounding
So,
(IV) The boundary condition of the change in the volume fraction field at the free surface (
So
(V) Conditions of induced magnetism at the free surface
So,
The quantities
Inversion of the fourier-laplace transforms
To achieve comprehensive solutions of non-dimensional physical field variable distributions in 2D, it is important to reverse the previous main expressions in the physical domain. The numerical inversion technique for Laplace transform, specifically the Riemann-sum approximation method, is utilized to accomplish this [36].
In the Fourier domain, the inverse of any function
In the Laplace domain, any function’s inverse
Using the Fourier series expand for the function
Where the imaginary unit is
Numerical results and discussions
To be used in numerical simulation with the Mathematica program, silicon (Si) is an elastic semiconductor material. Its physical constants are utilized in the computational analysis and investigation of fundamental quantity fields, which have diverse applications in modern industries and plasma physics technologies. The mentioned physical constants for Si material, specifically for the n-type, are as follows [39–43]: are taken in SI units:
During the phase of the numerical approach that was described earlier, the real components of the elastic wave (
Figure 1 presents the relationship between different levels of an externally induced magnetic field and the propagation of photo-thermal-elastic-electric waves over a distance. This was the first category explored in the study. Every computation was checked using a short amount of time,
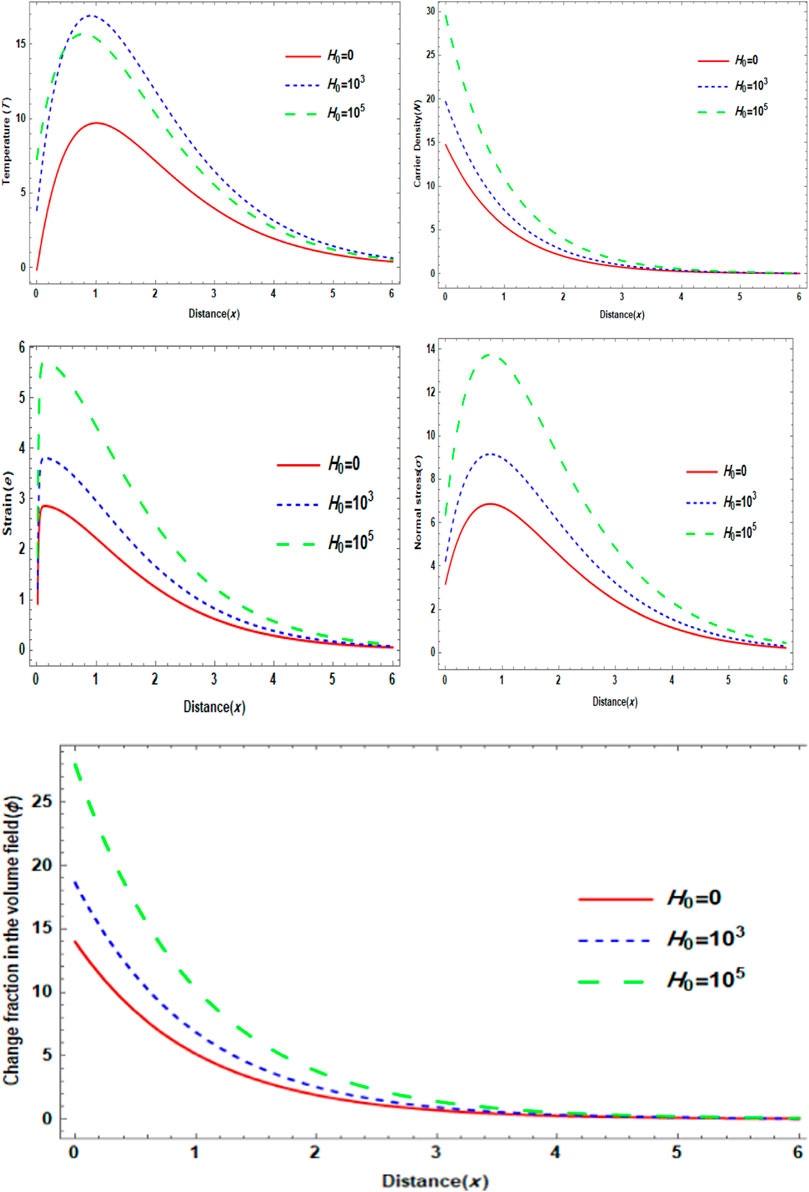
FIGURE 1. Variation of the main physical distributions with respect to the distance for different values of Induced magnetic field.
Figure 2 illustrates how different values of the Peltier coefficient affected the distribution of the physical field in the photo-thermo-elastic model with porosity when time

FIGURE 2. Variation of the main physical distributions against the distance for different values of Peltier coefficient.
Figure 3 presents the impact of different values of porosity parameters (both with and without porosity) on the physical field distribution in the photo-thermo-elastic model when time
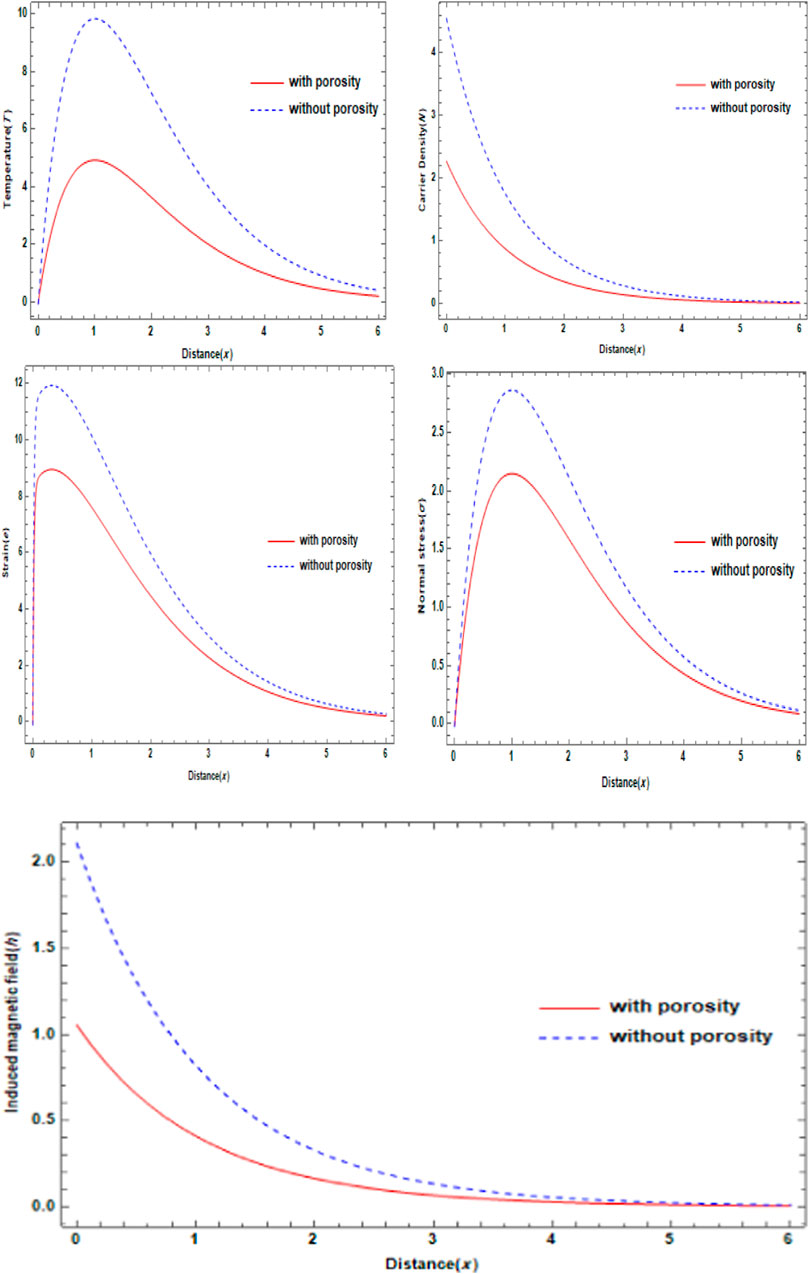
FIGURE 3. Variation of the main physical distributions verses the distance with porosity and without porosity.
Conclusion
In this study, we look into how a magnetic field affects a porous, generalized photo-thermo-elastic solid medium. The impact of the Thomson effect on some physical parameters is also investigated. The findings demonstrate that the magnetic field has a positive effect on all physical fields, with the carrier density displaying a distinct oscillating structure. Figure 1 also illustrates numerical computations showing the variation in field and stress distributions with horizontal distance for various values of the initial uniform magnetic field. The fluctuation of dimensionless physical variables as a function of distance is shown in Figure 2 for a range of Peltier coefficients, porosities, and magnetic fields. Figure 3 similarly illustrates how porosity parameters affect the scatter in these metrics. When a magnetic field and the Peltier coefficient are taken into account, it is clear that the primary fields are enhanced. The principal fields are profoundly impacted by the porosity characteristics. It is shown that the distribution of all physical fields in the photo-thermo-elastic model is greatly impacted by the porosity parameters, the initial magnetic field, and the Peltier coefficient. The results of this study can be used to improve the performance and longevity of electronic devices, energy harvesting systems, sensors, structural health monitoring materials, and infrastructure in a variety of environments, including those with varying magnetic field strengths, air gaps, Peltier coefficient effects, and temperatures.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
WA: Project administration, Resources, Investigation, Writing–original draft. ME: Conceptualization, Methodology, Software, Data curation, Supervision, Formal analysis, Writing–review and editing. HC: New software; Validation; Writing–reviewing and editing. RC: New software; Validation; Writing–reviewing and editing. AE-B: Conceptualization, Methodology, Visualization, Software, Validation, Writing–review and editing. NA: Software, Validation, Supervision, Investigation, Visualization, Writing–review and editing. RT: Resources, Writing–original draft, Writing–review and editing, Software, Supervision, Visualization, Investigation. KL: Conceptualization, Methodology, Software, Data curation, Formal Analysis, Funding acquisition, Resources, Writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R229) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Acknowledgments
Authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R229) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Khamis AK, El-Bary A, Lotfy K, Bakali A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alexandria Eng J (2020) 59(1):1–9. . doi:10.1016/j.aej.2019.11.016
2. Ailawalia P, Kumar A. Ramp type heating in a semiconductor medium under photothermal theory. Silicon (2020) 12(2):347–56. . doi:10.1007/s12633-019-00130-8
3. Hobiny A, Abbas IA, A GL photo-thermal theory upon new hyperbolic two-temperatures in a semiconductor material. Waves in Random and Complex Media (2021) 1–14. . doi:10.1080/17455030.2021.1999534
4. Abbas I, Hobiny A, Marin . Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J Taibah Univ Sci (2020) 14(1):1369–76. . doi:10.1080/16583655.2020.1824465
5. Alshehri HM, Lotfy. K. Memory-Dependent-Derivatives (MDD) for magneto-thermal-plasma semiconductor medium induced by laser pulses with hyperbolic two temperature theory. Alexandria Eng J (2022) 61(3):2396–406. doi:10.1016/j.aej.2021.06.091
6. Lotfy K, El-Bary AA, Magnetic-thermal-elastic waves under the impact of induced laser pulses and hyperbolic two temperature theory with memory-dependent derivatives (MDD). Waves in Random and Complex Media (2022) 1–19. . doi:10.1080/17455030.2021.2025278
7. Lotfy K, El-Bary AA, Magneto-photo-thermo-microstretch semiconductor elastic medium due to photothermal transport process. Silicon (2022) 14(9):4809–21. . doi:10.1007/s12633-021-01205-1
8. Aldwoah KA, Lotfy K, Mhemdi A, El-Bary A. A novel magneto-photo-elasto-thermodiffusion electrons-holes model of excited semiconductor." Case Stud Therm Eng 32 (2022): 101877.doi:10.1016/j.csite.2022.101877
9. Raddadi MH, El-Bary A, Tantawi RS, Anwer N, Lotfy K. A novel model of semiconductor porosity medium according to photo-thermoelasticity excitation with initial stress. Crystals (2022) 12(11):1603. doi:10.3390/cryst12111603
10. Bouslimi J, Omri M, Kilany AA, Abo-Dahab SM, Hatem A. Mathematical model on a photothermal and voids in a semiconductor medium in the context of Lord-Shulman theory. Waves in Random and Complex Media (2021) 1–18. . doi:10.1080/17455030.2021.2010835
11. Kilany AA, Abo-Dahab SM, Abd-Alla AM, Abd-alla AN. Photothermal and void effect of a semiconductor rotational medium based on Lord–Shulman theory. Mech Based Des Structures Machines (2022) 50(7):2555–68. . doi:10.1080/15397734.2020.1780926
12. Bayones FS, Kilany AA, Abouelregal AE, Abo-Dahab SM. A rotational gravitational stressed and voids effect on an electromagnetic photothermal semiconductor medium under three models of thermoelasticity. Mech Based Des Structures Machines (2023) 51(2):1115–41. . doi:10.1080/15397734.2020.1863229
13. Khalil EM, Abo-Dahab SM, Kilany AA, Electromagnetic field and initial stress on a photothermal semiconducting voids medium under thermoelasticity theories. Math Methods Appl Sci (2021) 44(9):7778–98. . doi:10.1002/mma.6942
14. Jawa TM, Elhag AA, Aloafi TA, Sayed-Ahmed N, Bayones FS, Bouslim J. Machine learning and statistical methods for studying voids and photothermal effects of a semiconductor rotational medium with thermal relaxation time. Math Probl Eng (2022) 2022:1–18. doi:10.1155/2022/7205380
15. Lotfy K, El-Bary A, Hassan W, Alharbi A, Almatrafi M. Electromagnetic and Thomson effects during photothermal transport process of a rotator semiconductor medium under hydrostatic initial stress." Results Phys 16 (2020): 102983.doi:10.1016/j.rinp.2020.102983
16. Mahdy AMS, Lotfy K, Ismail E, El-Bary A, Ahmed M, El-Dahdouh A. Analytical solutions of time-fractional heat order for a magneto-photothermal semiconductor medium with Thomson effects and initial stress." Results Phys 18 (2020): 103174.doi:10.1016/j.rinp.2020.103174
17. Alharbi AM, Othman MIA, Atef HM, Thomson effect with hyperbolic two-temperature on magneto-thermo-visco-elasticity. Appl Math Mech (2021) 42(9):1311–26. . doi:10.1007/s10483-021-2763-7
18. Zenkour A, Exact coupled solution for photothermal semiconducting beams using a refined multi-phase-lag theory. Opt Laser Tech (2020) 128:106233. doi:10.1016/j.optlastec.2020.106233
19. Zenkour A, Effect of thermal activation and diffusion on a photothermal semiconducting half-space. J Phys Chem Sol (2019) 132:56–67. doi:10.1016/j.jpcs.2019.04.011
20. Zenkour A, Refined multi-phase-lags theory for photothermal waves of a gravitated semiconducting half-space. Compos Structures (2019) 212:346–64. doi:10.1016/j.compstruct.2019.01.015
21. Zenkour A, Abouelregal A, Effects of variable harmonic heat and photothermal elasticity on an infinitely long solid semiconductor cylinder. J Korean Phys Soc (2021) 79:725–33. doi:10.1007/s40042-021-00146-7
22. Ezzat M, Youssef H, A thermal and thermal stress analysis in thermoelectric solid under the influence of Thomson effect. J Thermoelasticity (2013) 1(2):4–12.
23. Abd-Elaziz S, Hilal M, The influence of Thomson effect and inclined loads in an electro-magneto-thermoelastic solid with voids under green–Naghdi theories. J Ocean Eng Sci (2018) 3(3):253–64. doi:10.1016/j.joes.2018.08.003
24. Mandelis A, Nestoros M, Christofides C, Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt Eng (1997) 36(2):459–68. doi:10.1117/1.601217
25. Yépez-Martínez H, Gómez-Aguilar J, Baleanu D, Beta-derivative and sub-equation method applied to the optical solutions in medium with parabolic law nonlinearity and higher order dispersion. Optics (2018) 155:357–65. doi:10.1016/j.ijleo.2017.10.104
26. Kh L. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci Rep (2019) 9:3319. doi:10.1038/s41598-019-39955-z
27. Rasheed A, Anwar M, Interplay of chemical reacting species in a fractional viscoelastic fluid flow. J Mo.l Liq (2019) 273:576–88. doi:10.1016/j.molliq.2018.10.028
28. Christofides C, Othonos A, Loizidou E. Influence of temperature and modulation frequency on the thermal activation coupling term in laser photothermal theory. J Appl Phys (2002) 92:1280–5. doi:10.1063/1.1484232
29. Hobiny A, Abbas I, A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys (2019) 15:102588. doi:10.1016/j.rinp.2019.102588
30. Liu J, Han M, Wang R, Xu S, Wang X, Photothermal phenomenon: extended ideas for thermo physical properties characterization. J Appl Phys (2022) 131:065107. doi:10.1063/5.0082014
31. Cowin SC, Nunziato JW, Linear theory of elastic materials with voids. J Elasticity (1983) 13:125–47. doi:10.1007/BF00041230
32. Tam AC, Photothermal investigations in solids and fluids. Boston, USA: Academic Press (1989). p. 1–33.
33. Todorovic DM, Plasma, thermal, and elastic waves in semiconductors. Rev Sci Instrum (2003) 74:582–5. doi:10.1063/1.1523133
34. Vasil’ev AN, Sandomirskii VB, Photoacoustic effects in finite semiconductors. Sov Phys Semicond (1984) 18:1095. doi:10.1002/pssb.2221200203
35. Christofides C, Othonos A, Loizidou E, Influence of temperature and modulation frequency on the thermal activation coupling term in laser photothermal theory. J Appl Phys (2002) 92:1280–5. doi:10.1063/1.1484232
36. Honig G, Hirdes U, A method for the numerical inversion of Laplace transforms. Comp App Math (1984) 10(1):113–32. doi:10.1016/0377-0427(84)90075-x
37. Abbas I, Finite element analysis of the thermoelastic interactions in an unbounded body with a cavity. Forsch Ingenieurwes (2007) 71:215–22. doi:10.1007/s10010-007-0060-x
38. Alzahrani F, Hobiny A, Abbas I, Marin M, An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry (2020) 12:848. doi:10.3390/sym12050848
39. Abbas I, Kumar R, 2D deformation in initially stressed thermoelastic half-space with voids. Steel Compos Struct (2016) 20:1103–17. doi:10.12989/scs.2016.20.5.1103
40. Mandelis A, Nestoros M, Christofides C, Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt Eng (1997) 36(2):459–68. doi:10.1117/1.601217
41. Hobiny A, Abbas I, A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech Time-depend Mater (2016) 6:61–72. doi:10.1007/s11043-016-9318-8
42. Abbas I, Hobiny A, Marin M, Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J Taibah Univ Sci (2020) 14:1369–76. doi:10.1080/16583655.2020.1824465
43. Marin M, Hobiny A, Abbas I, The effects of fractional time derivatives in porothermoelastic materials using finite element method. Mathematics (2021) 9:1606. doi:10.3390/math9141606
Nomenclature
Appendix
Equations 38–48 have the primary variables which can be represented as:
Coefficients of Eq. 57:
The main parameters in equations (64-73) can be expressed as:
Keywords: plasmaelastic, semiconductor, Thomson effect, magnetic field, porosity, fourier transform
Citation: Alhejaili W, Elamin MA, Chtioui H, Chteoui R, El-Bary AA, Anwer N, Tantawi RS and Lotfy K (2023) Semiconductor elastic medium with electromagnetic porosity, photothermal excitation, and the Thomson effect. Front. Phys. 11:1309912. doi: 10.3389/fphy.2023.1309912
Received: 08 October 2023; Accepted: 23 November 2023;
Published: 21 December 2023.
Edited by:
Teoman Özer, Istanbul Technical University, TürkiyeReviewed by:
Ibrahim A Abbas, Sohag University, EgyptAshraf M. Zenkour, King Abdulaziz University, Saudi Arabia
Copyright © 2023 Alhejaili, Elamin, Chtioui, Chteoui, El-Bary, Anwer, Tantawi and Lotfy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kh. Lotfy, a2hsb3RmeV8xQHlhaG9vLmNvbQ==
 Weaam Alhejaili
Weaam Alhejaili Mahjoub A. Elamin2
Mahjoub A. Elamin2 Alaa A. El-Bary
Alaa A. El-Bary Kh. Lotfy
Kh. Lotfy