- 1School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, China
- 2Department of Mathematics, University of Management and Technology, Lahore, Pakistan
- 3School of Computer Science and Technology, Zhejiang Normal University, Jinhua, Zhejiang, China
- 4Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, Saudi Arabia
- 5Research Centre, Future University in Egypt, New Cairo, Egypt
The study of hybrid nanoliquids can aid in developing numerous advanced features that facilitate heat transmission, such as pharmaceutical processes, hybrid-powered engines, microelectronics, engine cooling, and domestic refrigerators. In the current study, a mathematical model is designed to elaborate the physical inception of an unsteady second-grade hybrid nanofluid with
1 Introduction
Investigations into non-Newtonian materials have been ongoing since the past century due to their unique characteristics and fascinating rheological properties. These materials are widely used across various industries, including chemical engineering, metal processing, food, and plastics. Non-Newtonian fluids have a range of applications, including biofluids, glassblowing, synthetic fibers, cosmetics, food, pharmaceuticals, shampoo, and metal spinning. These fluids exhibit different behaviors and can be classified as dilatant, shear-thickening, thixotropic, or shear-thinning. Rheologists have identified various fluid models, such as Casson, Maxwell, Burgers, Williamson, Oldroyd-B, third-grade, Jeffrey, micropolar, Sisko, and Sutterby Cross. However, second-grade fluids behave differently under different conditions, which explains the characteristics of shear-thickening, shear-thinning, and Newtonian effects. Second-grade fluids have gained the attention and devotion of intellectuals due to their dynamic properties [1–8]. Stretching a plastic sheet, on the other hand, is not always linear. An exponentially stretched sheet’s heat transport characteristics have a broader range of technical applicability. The heat transfer ratio of the continuously expanded surface increases rapidly with the expansion rate and temperature variations, which regulates the outcome when the copper wire is thinned and diluted. The techniques involved in these methods significantly impact the final product quality due to the effect of stretching kinematics and concurrent heating or cooling. Khan and Sanjayanand [9] analyzed a second-grade fluid’s steady flow and heat conductivity with an exponentially extending surface using the Runge–Kutta fourth-order (RK4) method. Rehman et al. [10] investigated the steady flow of a second-grade fluid over an exponentially stretching sheet using the Keller box and homotopy analysis approaches. Nadeem et al. [11] explored the flow and heat transfer of second-grade (viscoelastic) liquids in thermal radiation. Ramzan and Bilal [12] calculated the mixed convection of a second-grade nanofluid caused by time-dependent MHD, thermal radiation, and diffuse surfaces. Pakdemirli et al. [13] used perturbation analysis to examine the properties of a second-grade fluid. Recently, many researchers have studied second-grade nanofluids over an exponentially stretching surface [14–23].
Professionals like unsteady flow in several engineering organizations since it contributes to better mechanisms over their deeds [24, 25]. Moreover, even in ideal flow conditions, unnecessary destabilizing effects can occur around the system. The behavior of unstable boundary layer (BL) flow is unique compared to steady-state flow because the control equation has additional time-dependent conditions that degrade the structure of BL separation and fluid motion. However, through a healthier consideration of unstable fluid flow presentations in manufacturing dealings, contemporary enterprise techniques that permit improved structure dependability, productivity, and cost saving of multiple dynamical devices are possible [26]. Zaib et al. [27] discussed the computational exploration of a time-dependent flow with heat flux past an exponentially contracting surface.
The spectacle of heat transfer in electromagnetic waves is called thermal radiation. It happens because the two mediums have a significant temperature difference. In manufacturing and physical science, radiative influences are a crucial part. In the polymer manufacturing sectors, where heat-controlling variables influence the ultimate product quality to some extent, thermal radiation impacts are essential in controlling heat transfer. In addition, the radiation effects of missiles, aircraft, solar radiation, gas turbines, liquid metal fluids, spacecraft, nuclear power plants, and MHD accelerators are also prominent. Pantokratoras and Fang [28] were pioneers in examining the effect of nonlinear thermal radiation on Sakiadis flow. Dogonchi and Ganji [29] evaluated the impact of radiant heat on the MHD flow of a water-based nanofluid in a channel that can shrink, stretch, and diverge or converge. Khan et al. [30] studied the radiation flow of hybrid nanofluids through porous surfaces [30]. Many researchers [31–36] are involved in nonlinear thermal radiation.
Recognizing the need for improved thermal conductivity in traditional fluids, a new type of nanofluid called “hybrid nanofluid” is presented to provide highly industrialized heat conductivity. Two or more semiconductor materials are mixed with a base fluid to make a hybrid nanofluid. Different nanomaterials include carbon nanotubes [37], metals, metal oxides, and carbides. Numerous investigators are now interested in hybrid nanofluid due to its significance for the betterment of thermodynamic characteristics in real-world applications [38, 39], as a result of Choi and Eastman’s [40] outstanding findings that gave the unique notion of nanoliquid. Hybrid nanofluids are also used in various applications, including electrical gadget cooling [41], cooling of domestic refrigerators [42], automobile braking fluid, transformers, heat exchangers, and solar water heating [43]. Suresh et al. [44] explored the effects of a hybrid nanofluid
The fuzzy set theory (FST) [54] has proved to be a valuable technique for modeling uncertainties in recent decades, providing models with a more accurate view of reality and allowing them to express themselves with a broader perspective [55–59]. After modeling real-world problems, they convert into partial differential equations (PDEs) or ordinary differential equations (ODEs). Uncertainty issues may arise during the development of a dynamic model. Researchers must deal with inaccurate data, parameters, dynamical variability, and complex relationships. As a result, many scientists use fuzzy models to depict dynamical systems to prevent artificial data accuracy and produce more realistic results. The fuzzy differential equation (FDE) is critical in overcoming these challenges. Initially, Chang and Zadeh [60] proposed the basic idea of fuzzy derivatives. Dubois and Prade [61] proposed the idea of fuzzy numbers (FNs) for solving an FDE. Kaleva [62] introduced the concept of FDEs in a fuzzy environment. Recently, FDEs played a significant role in fluid dynamics, such as the effects of MHD and gravitation on the third-grade fluid through an inclined channel in a fuzzy atmosphere, which were quantitatively explored by Nadeem et al. [63]. They used the triangular fuzzy numbers to analyze ambiguity. The heat transmission of SWCNTs MWCNTS on a third-grade nanofluid along an inclined channel in a fuzzy atmosphere was explored by Siddiqui et al. [64]. For comparison and uncertainty, they used nanoparticle volume fraction as TFN.
A careful review of the previously cited literature reveals several breaks and confines. No preceding studies have examined the unsteady MHD flow of the second-grade hybrid
The motivations for performing this analysis inspire the following research questions:
1) How do the thermal characteristics of nanoparticles vary when nonlinear thermal radiation features are used?
2) How do different developing parameters affect heat transfer and flow rates?
3) How does heat transfer improve in heat source/sink and magnetic force implications?
4) Why is the homotopy analysis method (HAM) preferred over the other methods?
5) Ho\w does the Lorentz force affect the velocity of the second-grade hybrid nanofluid by applying the magnetic field?
2 Mathematical formulation
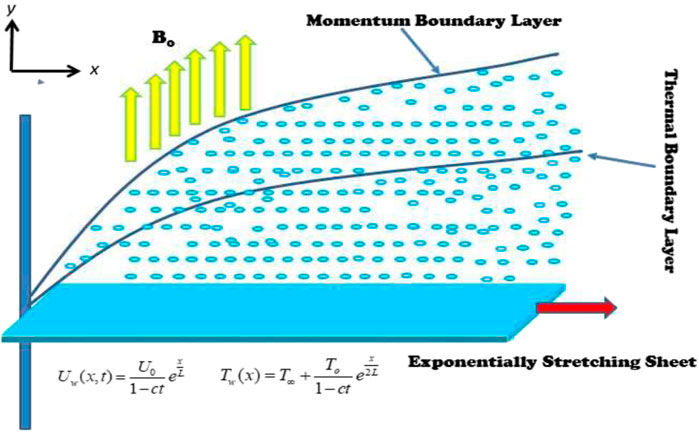
The time-dependent, 2D incompressible, and unsteady flow of the MHD viscoelastic (second-grade) hybrid
When using the BL approximation, the governing equations for continuity, momentum, and heat are established on all of the preceding assumptions [12, 51]:
and the boundary conditions are
where

TABLE 1.
The thermophysical properties of hybrid nanofluids are as follows [51]:
The following similarity transformations are presented in [10] to simplify the governing Eqs 1–3 along with the boundary conditions (4). The stream function
Using Eq. 6, Eqs (2), (3) can be condensed to the following set of nonlinear ODEs in the context of the abovementioned relations [36]:
with the constraints
where the unsteadiness parameter is
The stretching/shrinking parameter is
Using Eq. 6 in Eq. 10 and Eq. (11) yields the following relationship:
where
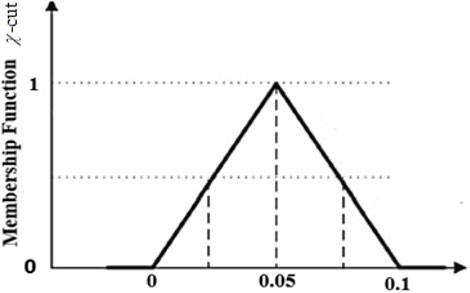
FIGURE 2. Membership function of TFN [54].
2.1 Homotopy analysis method
The HAM is a multifaceted investigative system that solves nonlinear equations with several variables. Based on Eq. 9, the HAM computes consequential Eqs 7, 8. Linear operators and preliminary approximations are mandatory to surprise the process through this technique. Consequently, we used them as
The properties of the operator described above are as follows:
where
where
The boundary conditions become [12]
Equations (7)–(9) convert into nonlinear operators like Eqs 18–21, and then, the series solution becomes
2.2 Fuzzification
Using fuzzy concepts, comparing nanofluid and hybrid nanofluid is also explored in this study. The nonlinear ODEs convert into FDEs, and the nanoparticle volume percentage is taken as a TFN. The governing FDE is converted into a double parametric form. In this case, Eq. 8 can be converted into an interval form using the
Let
The
To handle this scenario, the FDEs are renewed into lower
3 Results and discussion
An unsteady flow analysis was performed on a second-grade hybrid
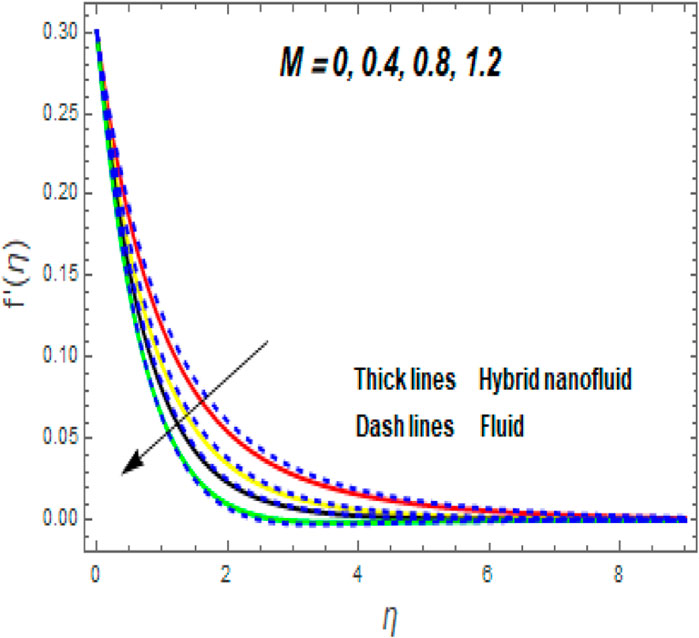
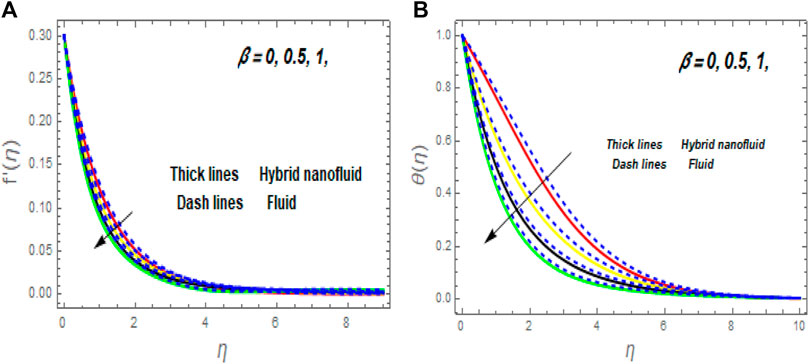
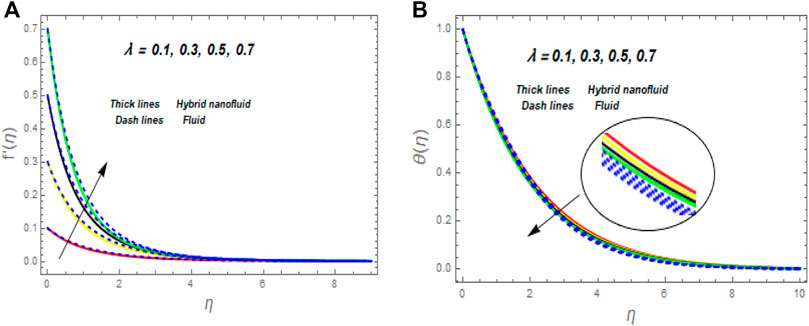
The influence of the magnetic (M) parameter on the velocity field is depicted in Figure 3. For higher values of M, the velocity dropped in both cases. Lorentz pressure is responsible for this phenomenon, which arises from the cooperation of electric and magnetic fields during an electrically conducted fluid flow. So, the fluid velocity in the BL is controlled by the generated Lorentz force. As a result, as M rises, the velocity of the fluid and hybrid nanofluids falls. The interaction of magnetic fields is significant in different technical and industrial applications, such as crude oil extraction, geothermal systems, and groundwater hydrology. The change of the second-grade parameter (
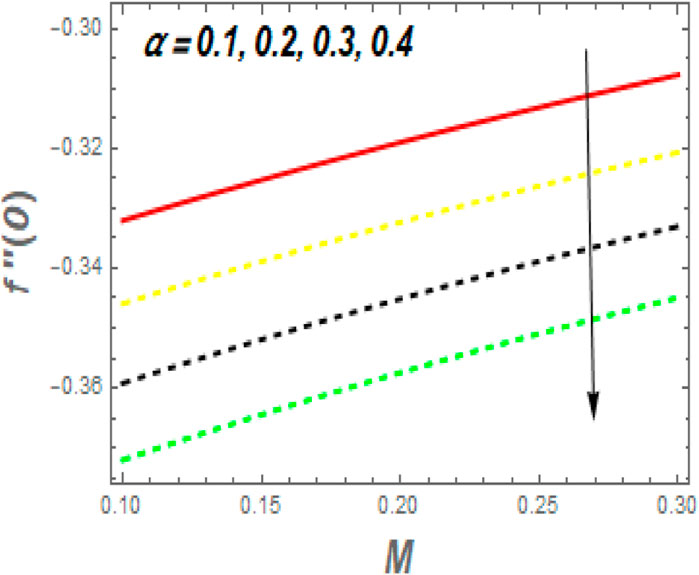
As shown in Figure 12, f ′′(0) increases with M and decreases as
3.1 Fuzzy results and discussion
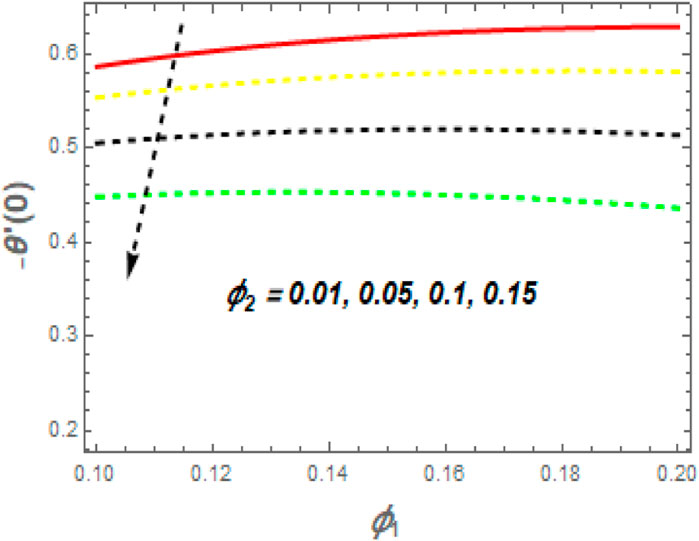
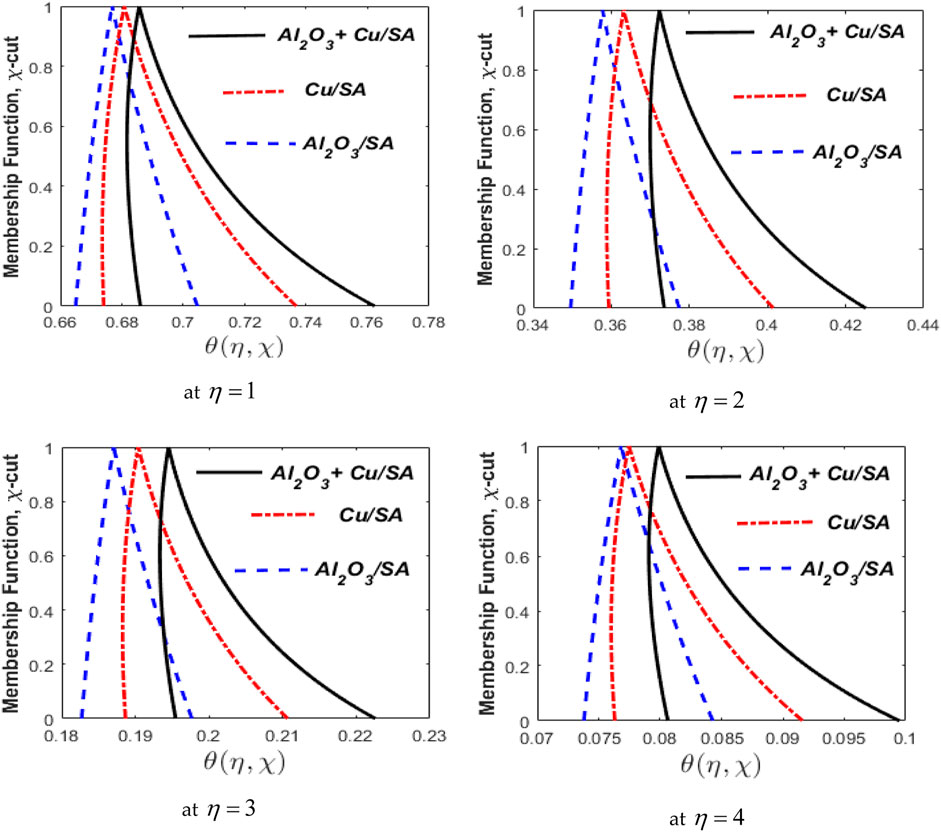
Figure 16 portrays the calculated fuzzy temperature using volume fractions of
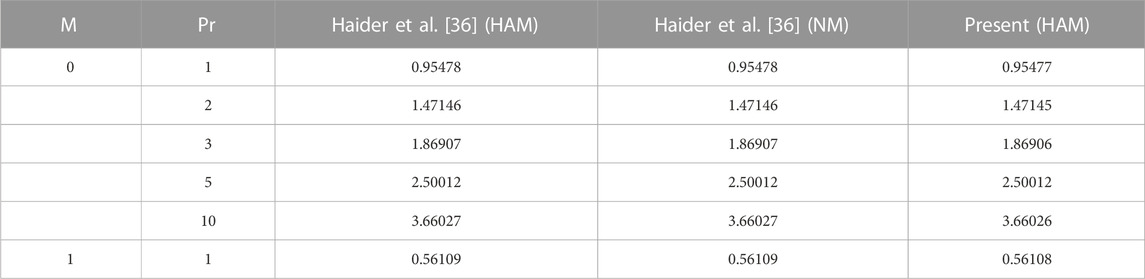
TABLE 3. Comparison of current results of
4 Conclusion
This study analyzed the unsteady MHD second-grade hybrid
• The fluid velocity is dropped with the magnetic parameter, while the fluid velocity is boosted with the second-grade fluid parameter.
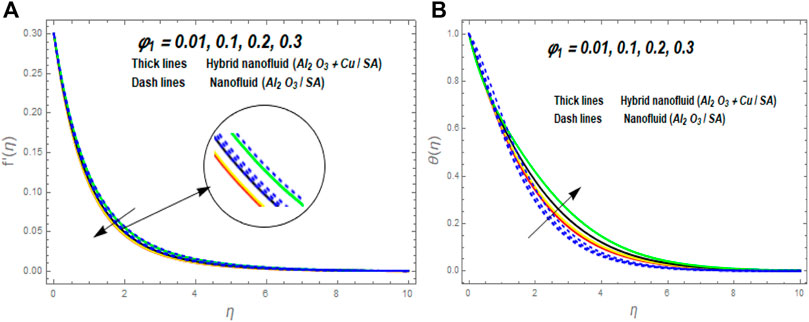
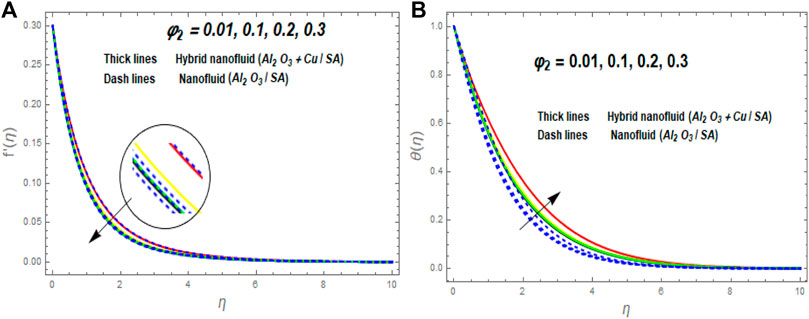
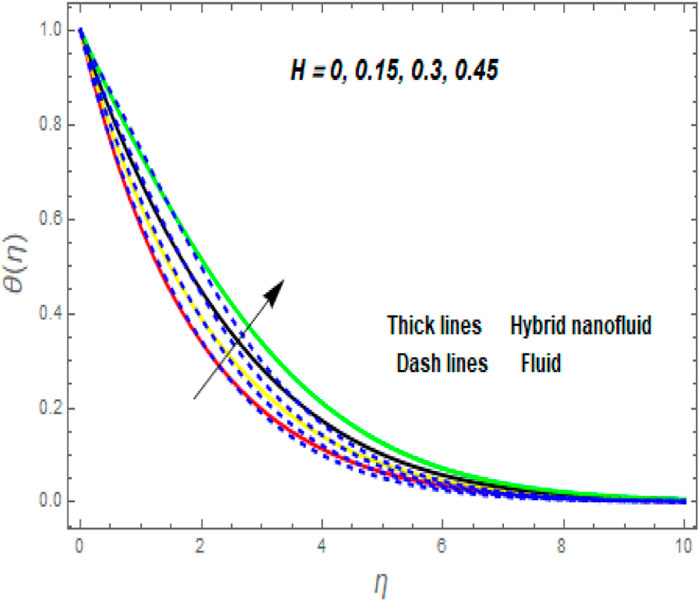
• The fluid temperature increases while the fluid velocity declines with the improvement of
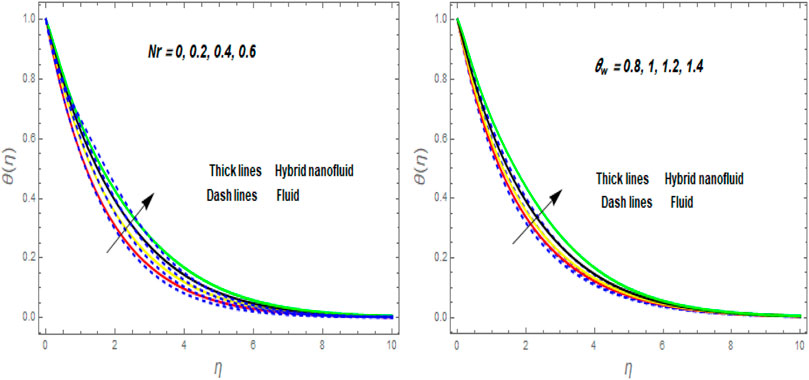
• The fluid temperature boosts against higher values of
• The fluid velocity grows versus the stretching/shirking parameter while the fluid temperature declines.
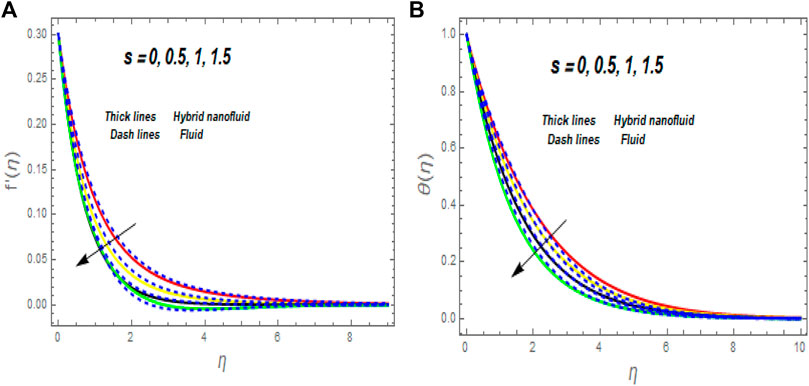
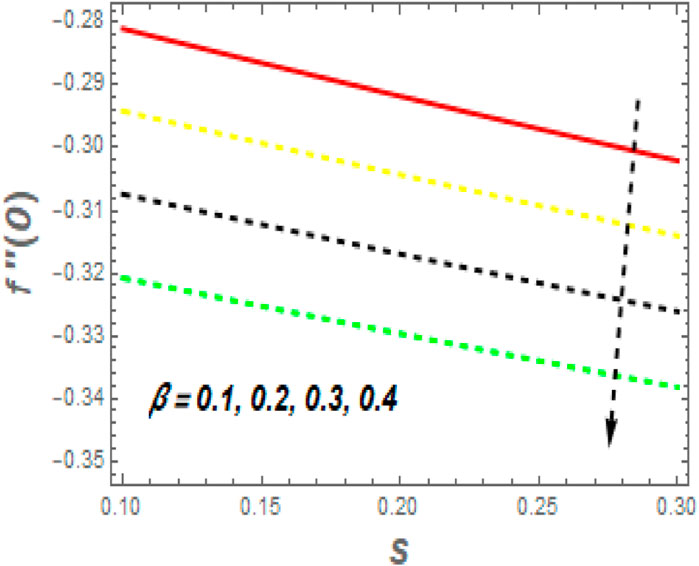
• The skin friction coefficient is reduced with a rise in unsteady and second-grade parameters while growing with magnetic parameters.
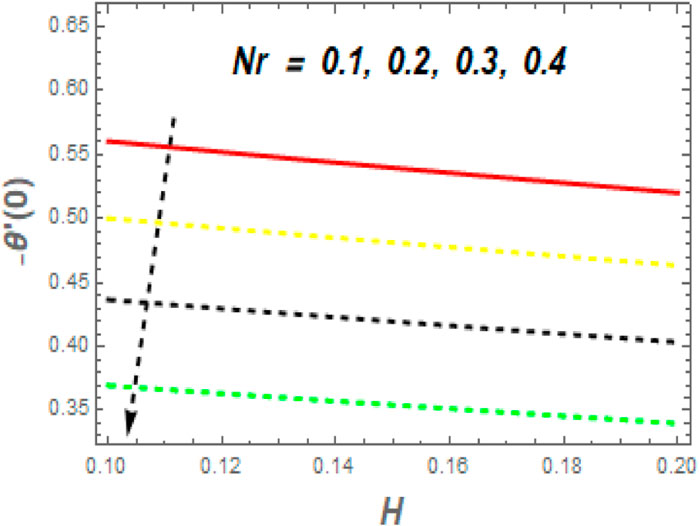
• For higher values of Nr, H,
• The maximum width of the fuzzy fluid temperature of the hybrid nanofluid was observed during a fuzzy analysis using a triangular MF, indicating that the fuzziness level is higher than that of regular nanofluids.
• The
The findings of this study can be used to drive future progress in which the heating system’s heat outcome is analyzed with nanofluids or hybrid nanofluids of various kinds (Maxwell, third-grade, Casson, Carreau, micropolar fluids, etc).
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
RZ, MN: conceptualization, methodology, and writing–original draft. MN, MS: data curation, investigation, resources, software, and writing–original draft. IS: formal analysis, supervision, validation, and writing–original draft. IK, AM: funding acquisition, project administration, resources, visualization, and data curation, writing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. This project was funded by Zhejiang Normal University, Jinhua, Zhejiang, China.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Rajagopal KR. On boundary conditions for fluids of the differential type. In: A Sequira, editor. Navier- Stokes equations and related nonlinear problems. New York: Plenum Press (1995). p. 273. doi:10.1007/978-1-4899-1415-6_22
2. Vejravelu K, Roper T. Flow and heat transfer in a second-grade fluid over a stretching sheet. Int J Non Linear Mech (1999) 34:1031–6. doi:10.1016/S0020-7462(98)00073-0
3. Rajeswari GK, Rathna SL. Flow of a particular class of non-Newtonian visco-elastic and visco-inelastic fluids near a stagnation point. Z Angew Math Phys (1962) 13:43–57. doi:10.1007/BF01600756
4. Garg VK, Rajagopal KR. Flow of a non-Newtonian fluid past a wedge. Acta Mech (1991) 88:113–23. doi:10.1007/BF01170596
5. Bilal S, Mustafa Z, Rehman KU, Malik MM. MHD second grade NanoFluid flow induced by a rotatory cone. J Nanofluids (2019) 8:876–84. doi:10.1166/jon.2019.1627
6. Mushtaq M, Asghar S, Hossain MA. Mixed convection flow of second grade fluid along a vertical stretching flat surface with variable surface temperature. Heat Mass Transf (2007) 43:1049–61. doi:10.1007/s00231-006-0177-8
7. Vieru D, Siddique I, Kamran M. Energetic balance for the flow of a second-grade fluid due to a plate subject to a shear stress. Comput Maths Appl (2008) 56(4):1128–37. doi:10.1016/j.camwa.2008.02.013
8. Mahmood A, Fetecau C, Siddique I. Exact solutions for some unsteady flows of generalized second grade fluids in cylindrical domains. J Prime Res Maths (2008) 4:171–80. Available at: https://jprm.sms.edu.pk/media/pdf/jprm/volume_04/jprm10_4.pdf (Accessed 2008).
9. Khan SK, Sanjayanand E. Viscoelastic boundary layer flow and heat transfer over an exponential stretching sheet. Int J Heat Mass Transf (2005) 48:1534–42. doi:10.1016/j.ijheatmasstransfer.2004.10.032
10. Rehman A, Farooq G, Ahmed I, Naseer M, Zulfiqar M. Boundary-layer stagnation-point flow of second grade fluid over an exponentially stretching sheet. Am J Appl Maths Stat (2015) 3(6):211–9. Available at: http://pubs.sciepub.com/ajams/3/6/1/ (Accessed 2015). doi:10.12691/ajams-3-6-1
11. Nadeem S, Hayat T, Malik MY, Rajput SA. Thermal radiation effects on the flow by an exponentially stretching surface: a series solution. Z Naturforsch (2010) 65a:495–503. doi:10.1515/zna-2010-6-703
12. Ramzan M, Bilal M. Time dependent MHD nano-second grade fluid flow induced by permeable vertical sheet with mixed convection and thermal radiation. PLoS One (2015) 10:e0124929. doi:10.1371/journal.pone.0124929
13. Pakdemirli M, Hayat T, Yurusoy M, Abbasbandy S, Asghar S. Perturbation analysis of a modified second-grade fluid over a porous plate. Nonlinear Anal Real World Appl (2011) 12:1774–85. doi:10.1016/j.nonrwa.2010.11.010
14. Rehman KU, Shatanawi W, Firdous U. A comparative thermal case study on thermophysical aspects in thermally magnetized flow regime with variable thermal conductivity. Case Stud Therm Eng (2022) 44:102839. doi:10.1016/j.csite.2023.102839
15. Nadeem M, Siddique I, Awrejcewicz J, Bilal M. Numerical analysis of a second-grade fuzzy hybrid nanofluid flow and heat transfer over a permeable stretching/shrinking sheet. Scientific Rep (2022) 12(1):1631–17. doi:10.1038/s41598-022-05393-7
16. Rehman KU, Shatanawi W, Çolak AB. Levenberg–marquardt training technique analysis of thermally radiative and chemically reactive stagnation point flow of non-Newtonian fluid with temperature dependent thermal conductivity. Mathematics (2023) 11(3):753. doi:10.3390/math11030753
17. Rehman KU, Shatanawi W, Laraib K. Mutual impact of thermal radiations and temperature dependent thermal conductivity on non-Newtonian multiple flow regimes. Case Stud Therm Eng (2023) 42:102752. doi:10.1016/j.csite.2023.102752
18. Siddique I, Nadeem M, Awrejcewicz J, Pawłowski W. Soret and Dufour effects on unsteady MHD second-grade nanofluid flow across an exponentially stretching surface. Sci Rep (2022) 12:11811. doi:10.1038/s41598-022-16173-8
19. Jawad M, Saeed A, Tassaddiq A, Khan A, Gul T, Kumam P, et al. Insight into the dynamics of second grade hybrid radiative nanofluid flow within the boundary layer subject to Lorentz force. Scientific Rep (2021) 11:4894. doi:10.1038/s41598-021-84144-6
20. Rehman KU, Shatanawi W, Yaseen S. A comparative numerical study of heat and mass transfer individualities in Casson stagnation point fluid flow past a flat and cylindrical surfaces. Mathematics (2023) 11(2):470. doi:10.3390/math11020470
21. Shafiq A, Çolak AB, Sindhu TN. Modeling of Darcy-Forchheimer magnetohydrodynamic Williamson nanofluid flow towards nonlinear radiative stretching surface using artificial neural network. Int J Numer Methods Fluids (2023) 95(9):1502–20. doi:10.1002/fld.5216
22. Shafiq A, Çolak AB, Sindhu TN. Significance of EMHD graphene oxide (GO) water ethylene glycol nanofluid flow in a Darcy–Forchheimer medium by machine learning algorithm. The Eur Phys J Plus (2023) 138(3):213. doi:10.1140/epjp/s13360-023-03798-5
23. Nadeem M, Siddique I, Ali R, Alshammari N, Jamil RN, Hamadneh N, et al. Study of third-grade fluid under the fuzzy environment with Couette and Poiseuille flows. Math Probl Eng (2022) 2022:1–19. doi:10.1155/2022/2458253
24. Smith FT. Steady and unsteady boundary layer separation. Annu Rev Fluid Mech (1986) 18:197–220. 18.010186.001213. doi:10.1146/annurev.fl.18.010186.001213
26. McCroskey WJ. The 1976 freeman scholar lecture: some current research in unsteady fluid dynamics. J Fluids Eng (1977) 99:8–39. doi:10.1115/1.3448570
27. Zaib A, Bhattacharyya K, Shafie S. Unsteady boundary layer flow and heat transfer over an exponentially shrinking sheet with suction in a copper-water nanofluid. J Cent South Univ (2015) 22:4856–63. doi:10.1007/s11771-015-3037-1
28. Pantokratoras A, Fang T. Sakiadis flow with nonlinear Rosseland thermal radiation. Phys Scr (2012) 87(1):015703. doi:10.1088/0031-8949/87/01/015703
29. Dogonchi AS, Ganji DD. Investigation of MHD nanofluid flow and heat transfer in a stretching/shrinking convergent/divergent channel considering thermal radiation. J Mol Liq (2016) 224:592–603. doi:10.1016/j.molliq.2016.05.022
30. Khan U, Zaib A, Sheikholeslami M, Wakif A, Baleanu D. Mixed convective radiative flow through a slender revolution bodies containing molybdenum-disulfide graphene oxide along with generalized hybrid nanoparticles in porous media. Crystals (2020) 10(9):771. doi:10.3390/cryst10090771
31. Shafiq A, Colak AB, Sindhu TN. Construction of neural network based intelligent computing for treatment of Darcy-forchheimer sisko nanofluid flow with rosseland's radiative process. Heat Transfer Res (2023) 54(9):77–98. doi:10.1615/HeatTransRes.2023046617
32. Nadeem M, Siddique I, Bilal M, Anjum K. Numerical study of MHD Prandtl Eyring fuzzy hybrid nanofluid flow over a wedge. Numer Heat Transfer, A: Appl (2023) 1–17. doi:10.1080/10407782.2023.2257379
33. Shahzad F, Jamshed W, Eid MR, Safdar R, Putri Mohamed Isa SS, El Din SM, et al. Thermal cooling efficacy of a solar water pump using Oldroyd-B (aluminum alloy-titanium alloy/engine oil) hybrid nanofluid by applying new version for the model of Buongiorno. Scientific Rep (2022) 12(1):19817. doi:10.1038/s41598-022-24294-3
34. Nadeem M, Siddique I, Riaz Z, Makhdoum BM, Zulqarnain RM, Sallah M. Numerical study of unsteady tangent hyperbolic fuzzy hybrid nanofluid over an exponentially stretching surface. Scientific Rep (2023) 13(1):15551. doi:10.1038/s41598-023-32374-1
35. Bilal M, Tariq H, Urva Y, Siddique I, Shah S, Sajid T, et al. A novel nonlinear diffusion model of magneto-micropolar fluid comprising Joule heating and velocity slip effects. Waves in random and complex media (2022). p. 1–17. doi:10.1080/17455030.2022.2079761
36. Haider S, Saeed Butt A, Li YZ, Imran SM, Ahmad B, Tayyaba A. Study of entropy generation with multi-slip effects in MHD unsteady flow of viscous fluid past an exponentially stretching surface. Symmetry (2020) 12(3):426. doi:10.3390/sym12030426
37. Lee KJ, Yoon SH, Jang J. Carbon nanofibers: a novel nanofiller for nanofluid applications. Small (2007) 3(7):1209–13. doi:10.1002/smll.200700066
38. Shah TR, Ali HM. Applications of hybrid nanofluids in solar energy, practical limitations and challenges: a critical review. Sol Energ (2019) 183:173–203. doi:10.1016/j.solener.2019.03.012
39. Huminic G, Huminic A. Hybrid nanofluids for heat transfer applications – a state-of-the-art review. Int J Heat Mass Transf (2018) 125:82–103. doi:10.1016/j.ijheatmasstransfer.2018.04.059
40. Choi SU, Eastman J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ Fed (1995) 231:99–103. doi:10.1002/smll.200700066
41. Ijam A, Saidur R. Nanofluid as a coolant for electronic devices (cooling of electronic devices). Appl Therm Eng (2012) 32:76–82. doi:10.1016/j.applthermaleng.2011.08.032
42. Saidur R, Kazi SN, Hossain MS, Rahman MM, Mohammed HA. A review on the performance of nanoparticles suspended with refrigerants and lubricating oils in refrigeration systems. Renew Sustain Energ Rev. (2011) 15(1):310–23. doi:10.1016/j.rser.2010.08.018
43. Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf (2007) 50:2002–18. doi:10.1016/j.ijheatmasstransfer.2006.09.034
44. Suresh S, Venkitaraj KP, Selvakumar P, Chandrasekar M. Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Exp Therm Fluid Sci (2012) 38:54–60. doi:10.1016/j.expthermflusci.2011.11.007
45. Momin GG. Experimental investigation of mixed convection with water–Al2O3 & hybrid nanofluid in an inclined tube for laminar flow. Int J Sci Technol Res (2013) 2:195–202. doi:10.1002/smll.200700066
46. Waini I, Ishak A, Pop I. Hybrid nanofluid flow towards a stagnation point on an exponentially stretching/shrinking vertical sheet with buoyancy effects. Int J Numer Methods Heat Fluid Flow (2020) 31:216–35. doi:10.1108/HFF-02-2020-0086
47. Khan MI. Transportation of hybrid nanoparticles in forced convective Darcy- Forchheimer flow by a rotating disk. Int Commun Heat Mass Tran (2021) 122:105177. doi:10.1016/j.icheatmasstransfer.2021.105177
48. Takabi B, Salehi S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv Mech Eng (2014) 6:147059. doi:10.1155/2014/147059
49. Aminuddin NA, Nasir NAAM, Jamshed W, Ishak A, Pop I, Eid MR. Impact of thermal radiation on MHD GO-Fe2O4/EG flow and heat transfer over a moving surface. Symmetry (2023) 15(3):584. doi:10.3390/sym15030584
50. Sajid T, Pasha AA, Jamshed W, Shahzad F, Eid MR, Ibrahim RW, et al. Radiative and porosity effects of trihybrid Casson nanofluids with Bödewadt flow and inconstant heat source by Yamada-Ota and Xue models. Alexandria Eng J (2023) 66:457–73. doi:10.1016/j.aej.2022.11.009
51. Shahzad F, Jamshed W, Eid MR, Ibrahim RW, Aslam F, Isa SSPM, et al. The effect of pressure gradient on MHD flow of a tri-hybrid Newtonian nanofluid in a circular channel. J Magnetism Magn Mater (2023) 568:170320. doi:10.1016/j.jmmm.2022.170320
52. Sajid T, Jamshed W, Eid MR, Altamirano GC, Aslam F, Alanzi AM, et al. Magnetized Cross tetra hybrid nanofluid passed a stenosed artery with nonuniform heat source (sink) and thermal radiation: novel tetra hybrid Tiwari and Das nanofluid model. J Magnetism Magn Mater (2023) 569:170443. doi:10.1016/j.jmmm.2023.170443
53. Nadeem M, Elmoasry A, Siddique I, Jarad F, Zulqarnain RM, Alebraheem J, et al. Study of triangular fuzzy hybrid nanofluids on the natural convection flow and heat transfer between two vertical plates. Comput Intelligence Neurosci (2021) 2021:1–15. doi:10.1155/2021/3678335
55. Zulqarnain RM, Xin XL, Siddique I, Asghar Khan W, Yousif MA. TOPSIS method based on correlation coefficient under pythagorean fuzzy soft environment and its application towards green supply chain management. Sustainability (2021) 13(4):1642. doi:10.3390/su13041642
56. Zulqarnain RM, Siddique I, Ali R, Jarad F, Samad A, Abdeljawad T. Neutrosophic hypersoft matrices with application to solve multiattributive decision-making problems. Complexity (2021) 2021:1–17. Article ID 5589874. doi:10.1155/2021/5589874
57. Siddique I, Nadeem M, Khan I, Jamil RN, Shamseldin MA, Akgül A. Analysis of fuzzified boundary value problems for MHD Couette and Poiseuille flow. Scientific Rep (2022) 12(1):8368–28. doi:10.1038/s41598-022-12110-x
58. Zulqarnain RM, Saddique I, Jarad F, Ali R, Abdeljawad T. Development of TOPSIS technique under pythagorean fuzzy hypersoft environment based on correlation coefficient and its application towards the selection of antivirus mask in COVID-19 pandemic. Complexity (2021) 2021:1–27. Article ID 6634991, 27 pages. doi:10.1155/2021/6634991
59. Siddique I, Zulqarnain RM, Ali R, Jarad F, Iampan A. Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Comput Intelligence Neurosci (2021) 2021:1–19. doi:10.1155/2021/2036506
60. Chang SS, Zadeh LA. On fuzzy mapping and control. In: Fuzzy sets, fuzzy logic, and fuzzy systems: selected papers by lotfi A Zadeh. World Scientific (1996). p. 180–4. doi:10.1155/2021/2036506
61. Dubois D, Prade H. Towards fuzzy differential calculus Part 3: differentiation. Fuzzy Sets Syst (1982) 8(3):613–26. doi:10.1080/00207727808941724
62. Kaleva O. Fuzzy differential equations. Fuzzy Sets Syst (1987) 24(3):301–17. doi:10.1016/0165-0114(87)90029-7
63. Nadeem M, Siddique I, Jarad F, Jamil RN. Numerical study of MHD third-grade fluid flow through an inclined channel with ohmic heating under fuzzy environment. Math Probl Eng (2021) 2021:1–17. doi:10.1155/2021/9137479
64. Siddique I, Zulqarnain RM, Nadeem M, Jarad F. Numerical simulation of MHD Couette flow of a fuzzy nanofluid through an inclined channel with thermal radiation effect. Comput Intelligence Neurosci (2021) 2021:1–16. Article ID 6608684. doi:10.1155/2021/6608684
Nomenclature
Keywords: second-grade fluid, exponential stretching surface, thermal radiation, hybrid nanofluid, triangular fuzzy number (TFN)
Citation: Zulqarnain RM, Nadeem M, Siddique I, Samar M, Khan I and Mohamed A (2023) Numerical study of second-grade fuzzy hybrid nanofluid flow over the exponentially permeable stretching/shrinking surface. Front. Phys. 11:1301453. doi: 10.3389/fphy.2023.1301453
Received: 25 September 2023; Accepted: 17 October 2023;
Published: 09 November 2023.
Edited by:
Felix Sharipov, Federal University of Paraná, BrazilReviewed by:
B. Venkateswarlu, Yeungnam University, Republic of KoreaAndaç Batur Çolak, Istanbul Commerce University, Türkiye
Wasfi Shatanawi, Hashemite University, Jordan
Copyright © 2023 Zulqarnain, Nadeem, Siddique, Samar, Khan and Mohamed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mahvish Samar, bWFodmlzaHNhbWFyQGhvdG1haWwuY29t
 Rana Muhammad Zulqarnain
Rana Muhammad Zulqarnain Muhammad Nadeem2
Muhammad Nadeem2