Ternary combinational logic gate design based on tri-valued memristors

Traditional binary combinational logic circuits are generally obtained by cascading multiple basic logic gate circuits, using more components and complicated wiring. In contrast to the binary logic circuit design in this method, ternary combinational logic circuit implementation is more complicated. In this paper, a ternary circuit design method that does not require cascading basic ternary logic gates is proposed based on a tri-valued memristor, which can directly realize specific logic functions through a series connection of memristors. The ternary encoder, ternary decoder, ternary comparator, and ternary data selector are implemented by this method, and the effectiveness of the circuits is verified by LTspice simulations.

1 Introduction

Traditional digital systems are built on binary numbers, where only two levels are considered, namely, “0” and “1.” However, with the rapid development of modern information technology and the increasing integration of digital systems, interconnection limitations have become one of the main challenges in implementing the binary logic in the nano-scale circuit design [1]. Interconnect lines cause increased latency, noise, and power consumption in the system. In multi-valued logic (MVL), a single signal line carries more information, which can effectively reduce the number of interconnecting lines and solve the interconnection problem in binary digital systems [2]. After the calculation demonstration in [3], it can be seen that when the base is e, the complexity and cost of the multi-valued system are the lowest and 3 is the integer closest to e. Therefore, compared with binary logic, ternary logic has significant advantages. In 1840, the British mathematician and inventor Thomas Fowler first proposed the concept of a ternary computer, but the relevant details have long been lost. Glusker studied and sorted it, and elaborated the relevant concepts of ternary logic and ternary computer in [4] in 2005. Although the same number of binary signals are easier to process than ternary signals, ternary signals can carry more information, which can effectively improve the efficiency of information transmission and storage. Therefore, compared with binary logic, ternary logic has stronger information processing capabilities and can solve some complex and cumbersome problems in binary logic.

Memristor is a nonlinear nano-component with many excellent properties such as stable resistive performance, low power consumption, and compatibility with traditional CMOS technology. In particular, the circuit realized by the memristor can have both operation and storage functions, so a memristor is considered to be a strong competitor to replace traditional silicon chips and continue Moore’s law. Compared with traditional digital logic circuits using CMOS, memristor-based digital logic circuits can effectively reduce the area and power consumption of the circuit [5–9]. At present, there are still few research studies on ternary logic based on the memristor, and most of them need to realize corresponding functions by memristors combined with complementary metal–oxide semiconductor (CMOS). In 2016, Khalid designed a basic ternary logic gate using a circuit structure similar to MRL (hybrid CMOS/memristive logic gate) [10], which reduced the number of components. In 2020, Zhang designed flexible logic circuits based on spintronic memristors and CMOS switches to implement basic unbalanced logic gates with non-volatility, good load capacity, and constant voltage input and output without signal degradation [11]. In the same year, Wang designed ternary AND gates, OR gates, NOT gates, and maximum and minimum circuits by utilizing the compatibility of memristors and CMOS, and achieved an order of magnitude improvement in data density; the switching speed of the memristor is reduced by a factor of about 13 [12]. However, the aforementioned circuits require CMOS devices to work together, which leads to more circuit area and power consumption, as well as more complex operation steps and the amount of running power supply. In addition, some of the ternary logic circuits are designed by the memristor combined with the carbon nanotube field-effect transistor (CNTFET). In 2018, basic ternary logic gates, ternary decoders, 2-bit adders, and standard ternary inverters based on memristors and CNTFETs were proposed [13,14]. In 2019, Soliman proposed a systematic method for constructing a 2-bit ternary function based on the concept of the memristive threshold logic [15]. A 2-bit ternary adder and multiplier are implemented using VTEAM memristors and Stanford CNTFET transistor models. In the same year, Chen fabricated a memristor device based on nano-columnar crystalline ZnO thin films and used it to realize a complete set of ternary logic and a ternary multiplier unit [16]. Nevertheless, the logic variables of these circuits are voltage, and the memristors are only used as a computing unit rather than a storage unit. Therefore, these designs have the problems of signal degradation and loss of power-off information.

Due to the lack of actual ternary components corresponding to ternary logic, the promotion of ternary logic in practical applications is not smooth. Based on the asymmetric piecewise linear memristive mathematical model [17] extended by Chua on the basis of the voltage-controlled odd-symmetric piecewise linear memristive model in 2015, Wang’s team first proposed the concept of the tri-valued memristor in 2019, obtained tri-valued and multi-valued memristor models on this asymmetric piecewise linear memristor model, and realized a new chaotic circuit based on the tri-valued memristor model [12]. In [18], a method for realizing ternary basic logic gates based on tri-valued memristors is proposed. The designed logic gates do not need to use other CMOS devices, and the power consumption of the circuit is lower. As a multi-valued memristor, the tri-valued memristor can exhibit three different resistance states without using any additional devices to represent “0,” “1,” and “2” in ternary logic, and the application of tri-valued memristors to digital logic circuits can further reduce circuit power consumption and the circuit area, which improves the storage density. In addition, a tri-valued memristor provides a non-traditional computing architecture, that is, combines information storage and processing, which create favorable conditions for the realization of ternary logic circuits.

The rest of this paper is as follows: Section 2 explains the process of constructing a voltage-controlled tri-valued memristor, and the threshold characteristics and pinched hysteresis loop of this memristor are analyzed. Section 3 proposes a tri-value circuit design method using the resistance state of the memristor to represent the logic value. This method does not require cascading the basic tri-value logic gates and allows specific logic functions to be implemented directly through series and parallel connections of the memristors. Concretely, the ternary combinational logic gate circuits based on a tri-valued memristor include a ternary encoder, a decoder, a comparator, and a data selector, and the designed circuit is verified by LTspice. Section 4 gives the summary of this paper.

2 A tri-valued memristor built by two common binary memristors

Ternary logic is a multivalued logic with three different logic states. The tri-valued memristor is a crude element which exhibits three different states (resistances) matching “0,” “1,” and “2” in the ternary logic without using any additional devices. In this paper, the resistances of the tri-valued memristor are used as the logic state variables, where R_H, R_M, and R_L are used to represent logics “0,” “1,” and “2”. The voltage threshold tri-valued memristor explained in this paper and its threshold characteristics are introduced as follows.

2.1 Modeling of a tri-valued memristor

In 2021, Wang proposed a voltage threshold tri-valued memristor model that has the characteristics of simple structure and clear principle. The model parameters can be modified according to the actual application requirements [18]. In [19], an implementation method of connecting two tri-valued memristors in series and parallel to obtain a multi-valued memristor was proposed. As a result, a voltage-controlled tri-valued memristor model is obtained in this paper by connecting two voltage-controlled binary memristors in parallel, and the resulting tri-valued memristor model is used to design ternary combinational logic circuits. It is also proved that the tri-valued memristor model in [18] can be realized using the binary memristor through the circuit structure.

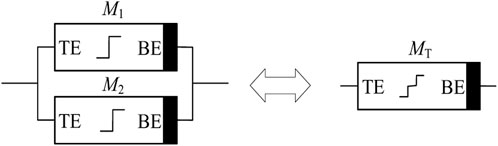
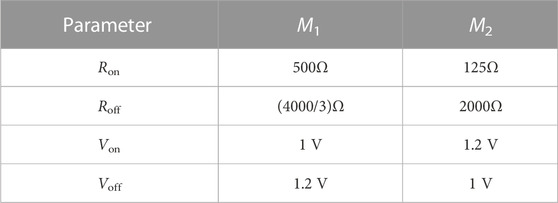
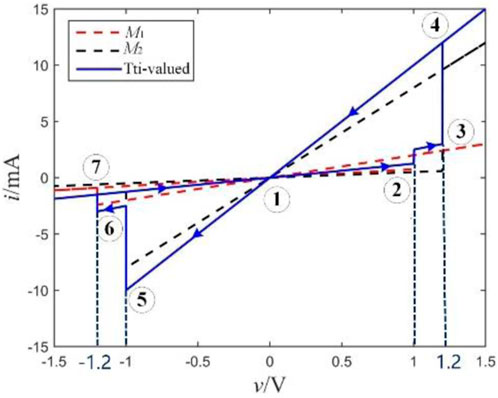
In 2015, Knowm Inc. company designed and produced a voltage threshold binary memristor called the Knowm memristor. In this paper, by modifying the expression of G(v) of the Knowm memristor from G(v) = v/R_on +(1- v)/R_off to G(v) = IF (v < 0.5, 1/R_off, 1/R_on), a better threshold binary memristor model is obtained. Based on this model, we obtained a tri-valued memristor by putting two Knowm memristors in parallel, as shown in Figure 1, with parameters shown in Table 1. The v-i curves of two single memristors (M₁ and M₂) and the tri-valued memristor with three distinct resistance states are shown in Figure 2.

FIGURE 1

FIGURE 1. Constructing a tri-valued memristor in parallel with binary memristors.

TABLE 1

TABLE 1. Parameter values of the two binary memristors.

FIGURE 2

FIGURE 2. v-i curve of the tri-valued, M₁ and M₂ memristors.

2.2 Characteristics of the tri-valued memristor

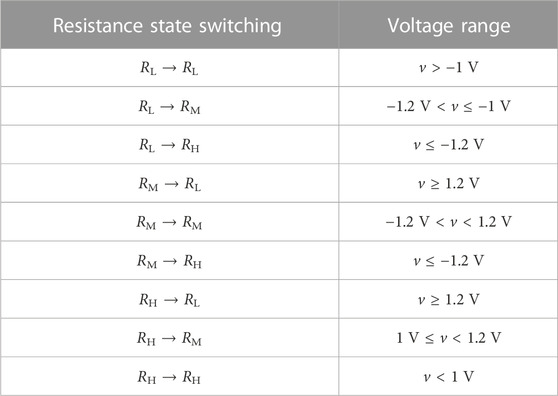
The tri-valued memristor mentioned previously has voltage threshold characteristics, and its two threshold voltages are v_th1 = 1 V and v_th2 = 1.2 V, respectively. R_L, R_M, and R_H correspond to three different resistance states of the model. According to the characteristics of the tri-valued memristor, voltages with different amplitudes (applied to the positive electrode of the memristor) will be used to initialize the memristor and implement the update of the memristor resistance value in the subsequent logic gate design. Specifically, when the voltage v ≥ 1.2 V, the memristor switches from any resistance state to R_L. When 1 V ≤ v < 1.2 V, if the resistance state of the memristor is R_H at this time, it will switch to R_M; otherwise, it will remain unchanged. When -1 V < v < 1 V, the memristor will continue to maintain its original state. When −1.2 V < v ≤ −1 V, if the resistance state of the memristor is R_L at this time, it will switch to R_M; otherwise, it will not change. When v ≤ −1.2 V, the memristor switches from any resistance state to R_H. Table 2 summarizes the voltage range required for the resistance state switching of the tri-valued memristor. The symbol “→” indicates that the resistance state on the left side is switched to that on the right side of the symbol.

TABLE 2

TABLE 2. Voltage range required for resistance state switching.

In order to verify the threshold characteristics of the tri-valued memristor model, the voltage signals v = t and v = -t are applied to the memristor models with initial states of R_H and R_L, respectively, and the LTspice simulation results, as shown in Figure 3, are obtained, which indicate that the resistance switching process of the memristor is consistent with Table 2, proving that the tri-valued memristor built exhibit the threshold characteristics.

FIGURE 3

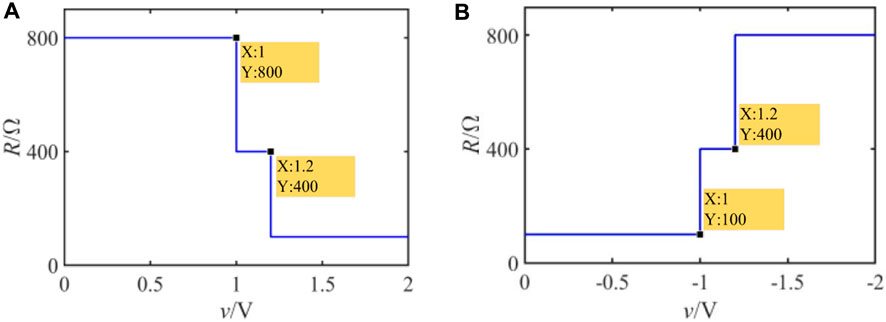
FIGURE 3. Relationship between the input voltage and the resistance of the tri-valued memristor; (A) the initial resistance is R_H, and the input voltage is v = t; (B) the initial resistance value is R_L, and the input voltage is v = -t.

2.3 Analysis of the pinched hysteresis loop of the tri-valued memristor

Figure 2 shows the trajectory of the pinched hysteresis loop obtained by applying the voltage v = 2sin (2πt) to the tri-valued memristor. The starting point of the pinched hysteresis loop, as shown in Figure 2, is ①; at this time, the resistances of M₁ and M₂ are both R_off, so the state of the tri-valued memristor at point ① is the initial state R_H. Before reaching point ②, the voltage value across the memristor will not exceed the threshold voltage 1V, so the state of the memristor will not change. When point ② is reached, since the input voltage exceeds the threshold voltage 1V, it exceeds the threshold voltage V_on of M₁, and the resistance of M₁ is switched to R_on, while the resistance of M₂ remains unchanged. At this time, the resistance of the tri-valued memristor is set to R_M.

At point ③, the voltage across the memristor reaches the threshold voltage of 1.2 V; at this time, the threshold voltages V_on of M₁ and M₂ are exceeded at the same time, and the resistances of M₁ and M₂ are both switched to R_on; the resistance of the tri-valued memristor is set to R_L. On the trajectory before reaching point ④, the voltage continues to increase, but the resistance of the tri-valued memristor will remain at R_L. Along with the applied voltage decrease, from points ④ to ⑤, although the threshold voltage 1 V is crossed at this stage, the state of the memristor will not change because the resistance of the tri-valued memristor is R_L during this period. When point ⑤ is reached, the voltage across the memristor reaches the threshold voltage −1 V, it exceeds the threshold voltage V_off of M₂, and the resistance of M₂ is switched to R_off, while the resistance of M₁ remains unchanged, making the tri-valued memristor set to R_M again. As the input voltage further decreases, reaching point ⑥, the voltage across the memristor exceeds the threshold voltage −1.2 V; at this time, the threshold voltages V_off of M₁ and M₂ are exceeded at the same time, and the resistances of M₁ and M₂ are both switched to R_off, making the tri-valued memristor set to R_H again. Then, the input voltage reaches peak point ⑦ and begins to increase, during which the resistance of the tri-valued memristor will not change until it returns to the initial point ① to start the next cycle.

Overall, the pinched hysteresis loop of the tri-valued memristor model shows the characteristics that the resistance decreases with the increase in the forward voltage, and the resistance increases with the increase in the negative voltage. It is worth noting that the change law of the resistance value of this tri-valued memristor model is consistent with the change law of the resistance value shown by the HP memristor. So this tri-valued memristor model can be used to research on the application of multivalued memristors manufactured in the method of an HP memristor.

3 Ternary combination logic gates design

In this section, a series of ternary combinational logic circuits with memristor resistance as the logic state variable will be proposed. Specifically, it includes a ternary encoder, ternary decoder, ternary comparator, and ternary data selector, and the effectiveness of the designed ternary combinational logic gate will be verified by LTspice simulation.

3.1 Ternary encoder

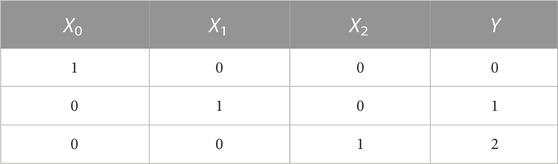
In the traditional binary or multivalued encoder, the circuit structure of the encoder is composed of cascaded basic logic gates, and the circuit structure is relatively complex. In this paper, a ternary encoder circuit based on the tri-valued memristor is proposed, which does not require cascading basic ternary logic gates. The circuit consists of three input memristors, one output memristor, and a corresponding number of voltage-controlled switches, and can realize the function of converting three channels of binary signals into one channel of ternary signals. The truth table of the designed 3-line–1-line ternary encoder is shown in Table 3, where X₀, X₁, and X₂ are input signals, and Y is the output signal.

TABLE 3

TABLE 3. Truth table of the 3-line to 1-line ternary encoder.

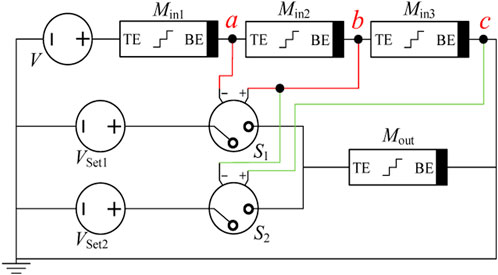
Figure 4 shows the circuit structure of a 3-line to 1-line ternary encoder based on tri-valued memristors. Among them, M_in1, M_in2, and M_in3 are input memristors, M_out is the output memristor, and the initial resistance value of M_out is R_H. The magnitudes of the output voltages of the DC voltage sources V_set1 and V_set2 are 1.1 and 1.3 V, respectively, which are used to complete the operations of setting “1” and setting “2”to M_out. S₁ and S₂ are voltage-controlled switches, which are turned on when the applied control voltages V_ba and V_cb across M_in2 and M_in3 exceed their threshold voltages. After evaluation, the threshold voltages of S₁ and S₂ are set to satisfy that only one of these two switches is turned on or none of the switches is turned on (the output memristor maintains the initial value) under different inputs to realize the encoding function of the ternary encoder.

FIGURE 4

FIGURE 4. 3-line–1-line ternary encoder circuit.

The operation of the encoder is driven by an excitation voltage source V, and its working process can be divided into two stages: the first stage is the initial stage where V outputs initial voltage V_Init, which is used to measure the initial resistance state of each memristor. The second stage is the running stage, and in this stage, V will output running voltage V_Run to complete the encoding operation. The initial voltage V_Init must meet two conditions to complete the operation of measuring the initial state of the memristor: the first condition is to ensure that the voltage division of each input memristor does not exceed the threshold voltages v_th1 and v_th2 of the memristor when V_Init is input. Otherwise, the resistance state of the input memristor will be changed; The second condition is that when V_Init is input, the divided voltages V_ba and V_cb on M_in2 and M_in3 would not exceed the threshold voltages of S₁ and S₂; otherwise, the resistance of the output memristor will change in the initial stage, which will cause the encoding result not correct under the running voltage V_Run. Here, the only demand on V_Run is to ensure that the voltage division of each input memristor does not exceed the threshold voltages v_th1 and v_th2 of the memristor when V_Run works as an input. Based on the aforementioned rules, the initial voltage V_Init and the operating voltage V_Run of the ternary encoder are determined as 1.5 and 1.2 V, respectively. The operation stage of the 3-line–1-line ternary encoder designed in this paper can be divided into the following three situations:

(1) When the input logic is “100,” namely, M_in1 = 400Ω, M_in2 = 800Ω, and M_in3 = 800Ω, according to the input voltage division calculation, V_ba = V_cb = −0.48 V can be obtained. In the circuit, switches S₁ and S₂ need not be turned on at the same time to ensure the output logic “0,” so the threshold voltages of switches S₁ and S₂ must be greater than −0.48 V.

(2) When the input logic is “010,” namely, M_in1 = 800Ω, M_in2 = 400Ω, and M_in3 = 800Ω, V_ba = −0.24V and V_cb = −0.48 V can be produced at this moment based on the input voltage division computation. To assure the output logic “1,” switches S₁ must be switched on and S₂ need to turn off, so the threshold voltage of switches S₁ must be less than −0.24 V and S₂ must be more than −0.48 V.

(3) When the input logic is “001,” namely, M_in1 = 800Ω, M_in2 = 800Ω, and M_in3 = 400Ω, the corresponding output logic should be “2.” In this case, the input voltage yields V_ba = −0.48V and V_cb = −0.24 V, so the switch S₁ need to be turned off and S₂ must be switched on, which force the threshold voltage of switches S₁ must be greater than −0.48 V and S₂ must be less than −0.24 V.

Through the aforementioned analysis, it can be obtained that the range of the threshold voltages of S₁ and S₂ should be between −0.48, and −0.24 V to complete the function of the encoding circuit, so −0.3 V is chosen as the threshold voltages of both S₁ and S₂ at the end.

The ternary encoder circuit is built using LTspice, and the simulation results are shown in Figure 5. It can be observed that when the inputs are “100,” “010,” and “001”, the logic values of the output memristor are “0,” “1,” and “2,” which is consistent with the truth table of the ternary encoder, which proves the rationality of the designed ternary encoder circuit.

FIGURE 5

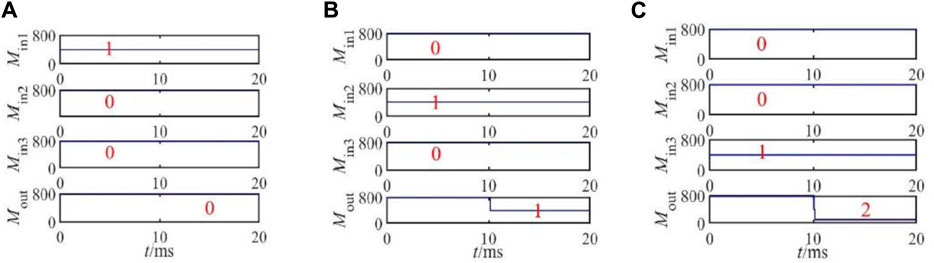
FIGURE 5. LTspice simulation results of the ternary encoder: (A) input as (1,0,0), (B) input as (0,1,0), and (C) input as (0,0,1).

3.2 Ternary decoder

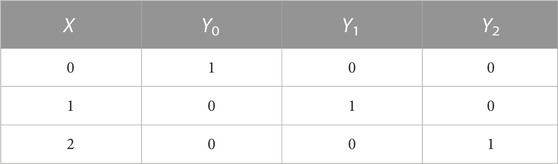
Decoding is the reverse operation of encoding, and the function of the ternary decoder is to convert one ternary signal into three binary signals. Table 4 shows the truth table of the ternary decoder, where X represents the input of the ternary decoder, and Y₀, Y₁, and Y₂ represent the outputs of the ternary decoder. It is worth noting that the valid logic values output by Y₀, Y₁, and Y₂ can be either logic “1” or logic “2” according to actual needs, and in this paper, we take logic “1” as an example to design the ternary decoder.

TABLE 4

TABLE 4. Truth table of the 1-line to 3-line ternary decoder.

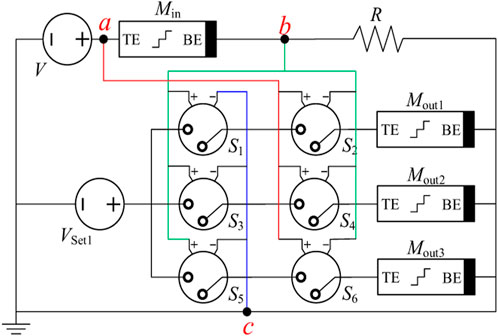
Figure 6 shows the 1-line to 3-line decoder circuit based on tri-valued memristors and voltage-controlled switches. The resistance state of the memristor M_in is used to represent the logic value of the input variable X. The initial resistance values of M_out1, M_out2, and M_out3 are all R_H, which represent the logic values of the output variables Y₀, Y₁, and Y₂, respectively. The voltage source V_set1 outputs 1.1 V to set each of the output memristor as logic “1.” The auxiliary resistor R is a key component in the circuit, and it helps realize more voltage division cases in the circuit. Without this resistor, the negative pole of M_in would be grounded directly so that the voltage source V will be applied directly to M_in. During the resistance state of M_in changing, the divided voltage on it will always be equal to the power voltage V, which means the three input conditions cannot be distinguished, resulting in the inability to complete the decoding function. The value of R needs to be between the high resistance value and the low resistance value of the tri-valued memristor; in this part, R is selected as 400Ω. Similar to the 3–1 encoder circuit, the ternary decoder work in two stages, which are the initial stage with V=V_Init = 0.5 V and running stage V = V_Run = 1.2 V, respectively.

FIGURE 6

FIGURE 6. 1-line to 3-line decoder circuit.

In the decoder design, if only one voltage-controlled switch is connected to each output memristor in the circuit, there is no guarantee that only one branch of each output is selected through. For example, each output memristor is connected to only one voltage-controlled switch, whose control voltage is the voltage across M_in. In Case 1, when M_in = R_L, the switch with the smallest threshold voltage will be turned on. In Case 2, when M_in = R_M, the switch with the minimum and middle threshold voltages will be both turned on. In Case 3, when the resistance value of M_in is the maximum value, that is, M_in = R_H, all three switches will be turned on, which do not guarantee that only one switch is turned on at each case. Therefore, in this design, we connect two voltage-controlled switches to each output memristor to ensure that under different input conditions, only one output memristor is connected to the voltage source V_set1 so that the corresponding output memristor can be set to R_M.

In Figure 6, the control voltage of switches S₁, S₃, and S₅ is the divided voltage V_bc on the resistor R. The control voltages of S₂, S₄, and S₆ are the divided voltage V_ab on the memristor M_in. In the ternary decoder circuit design process, an operating voltage is first selected; then, by analyzing the voltage division under different inputs, the threshold voltage of switches S₁–S₆ is set to meet the command above as 0.3, 0.7, 0.5, 0.5, 0.9, and 0.2 V, respectively.

According to the specific resistance state of M_in, the circuit operation stage of the ternary decoder can be summarized into the following three situations under the threshold voltage of switches S₁–S₆ set previously:

(1) When the input is logic “0,” that is, M_in = 800Ω, at this time, V_bc = 0.4V and V_ab = 0.8V, all of the switches S₁, S₂, S₄, and S₆ are turned on, and S₃ and S₅ are turned off, so only the output memristor M_out1 is set to 400Ω. The other two output memristors remain in their initial status. The logic gate output is “100.”

(2) When the input is logic “1,” M_in = 400Ω. V_bc = V_ab = 0.6 V. Switches S₁, S₃, S₄, and S₆ are all on, S₃ and S₅ are turned off, and only the output memristor M_out2 can be set to 400Ω. So the output of the logic gate is “010.”

(3) When the input is logic “2,” that is, M_in = 100Ω, then V_bc = 0.96V and V_ab = 0.24 V. Switches S₁, S₃, S₅, and S₆ are all on, and S₂ and S₄ are turned off, while the output memristor M_out3 is set to 400Ω; the other memristors will not change, so we obtain the outputs of the logic gate as “001.”

Similarly, the ternary decoder is simulated and verified using SPICE, as shown in Figure 7. When the inputs are “0,” “1,” and “2”, the corresponding outputs are “100,” “010,” and “001,” respectively. The function of converting one ternary signal into three binary signals is realized, which confirms the effectiveness of the designed 1-line–3-line ternary decoder circuit.

FIGURE 7

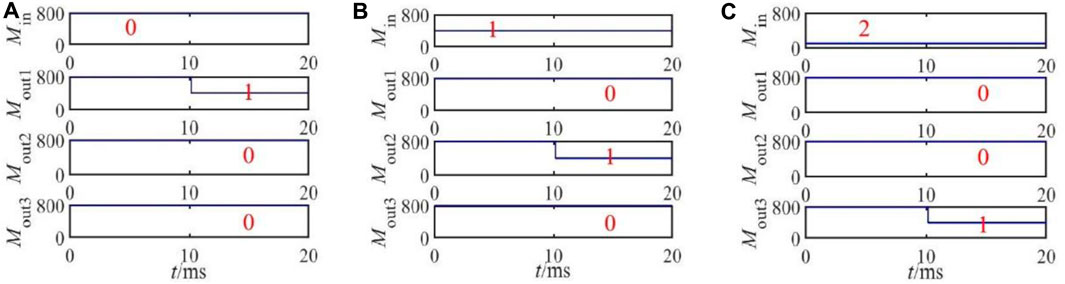
FIGURE 7. LTspice simulation results of the ternary decoder, (A) input “0,” (B) input “1,” and (C) input “2.”

3.3 Ternary comparator

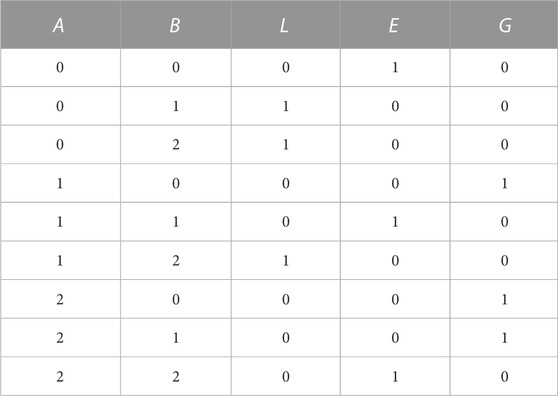
In digital logic circuits, it is often necessary to compare the magnitude of two numbers, and the circuit that completes this logic function is called a numerical comparator. For a one-bit ternary comparator, its input is two ternary numbers, and the output is the result of the comparison of the two numbers. The truth table of the one-bit ternary comparator is shown in Table 5, where A and B are the two input ternary numbers, and L, E, and G represent the three output binary numbers. L, E and G are valid when output logic “1,” representing A < B, A = B, and A > B, respectively.

TABLE 5

TABLE 5. Truth table of the one-bit ternary comparator.

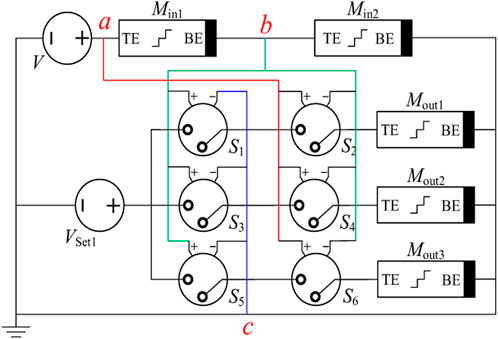
As shown in Figure 8, the one-bit ternary comparator consists of two input memristors, three output memristors, two voltage sources, and six voltage-controlled switches. Input variables A and B are represented by the resistances of M_in1 and M_in2, and the resistances of M_out1, M_out2, and M_out3 are used to represent variables L, E, and G. The initial resistances of M_out1, M_out2, and M_out3 are all R_H. Similar to the decoder circuit, each output memristor in the circuit is connected with two switches to ensure that only one output memristor is connected to the voltage source V_set1 during the operation phase of the circuit. The two output voltages V_Init and V_Run of the voltage source V are 0.5V and 1 V, respectively, and V_set1 outputs 1.1 V for the operation of “1.”

FIGURE 8

FIGURE 8. One-bit ternary comparator circuit.

In Figure 8, the control voltages of switches S₁, S₃, and S₅ are V_bc across M_in2, and V_ab cross M_in1 is used to control S₂, S₄, and S₆. The threshold voltages of S₁–S₆ are 0.1, 0.6, 0.4, 0.4, 0.6, and 0.1 V, respectively. According to the specific logic states of M_in1 and M_in2, the specific operation of the ternary comparator in the running phase can be summarized as follows:

(1) If A < B, there are three cases of input resistances of M_in1 and M_in2, namely, (800Ω, 400Ω), (800Ω, 100Ω), and (400Ω, 100Ω). The divided voltages V_ab and V_bc of M_in1 and M_in2 are (0.67 V, 0.33 V), (0.89 V, 0.11 V), and (0.8 V, 0.2 V). In the aforementioned three cases, all the switches S₁, S₂, S₄, and S₆ are turned on, and S₃ and S₅ are turned off. Therefore, only the output memristor M_out1 is set to 400Ω. The resistance of the other two output memristors remains unchanged, and the ternary comparator output is “100.”

(2) If A = B, the input resistances of M_in1 and M_in2 are the same, that is, (800Ω, 800Ω), (400Ω, 400Ω), and (100Ω, 100Ω). If V_ab = V_bc = 0.5 V, at this time, switches S₁, S₃, S₄, and S₆ are all on, and S₂ and S₅ are turned off. Thus, only M_out2 is set to 400Ω, and the corresponding logic gate output is “010.”

(3) If A > B, there are also three cases of input resistance of M_in1 and M_in2, namely, (400Ω, 800Ω), (100Ω, 800Ω), and (100Ω, 400Ω). V_ab and V_bc are (0.33 V, 0.67 V), (0.11 V, 0.89 V), and (0.2 V, 0.8 V). Switches S₁, S₃, S₅, and S₆ are all on, and S₂ and S₄ are turned off, which corresponds to the output memristor of M_out3, which is set to 400Ω; M_out1 and M_out2 remain R_H. At this point, the output of the logic gate is “001.”

Figure 9 shows the LTspice simulation results of the ternary comparator. When the logic value of M_in1 is less than that of M_in2, M_out1, which is corresponding to the variable “L,” is set to logic “1.” Similarly, when the logic value of M_in1 is equal to that of M_in2, M_out2 corresponding to the variable “E” will output “1.” When the logic value represented by M_in1 is greater than M_in2, the output memristor M_out3, which represents the variable G, outputs the effective resistance value “1.” The simulation results are consistent with the truth table of the ternary comparator, which verifies the effectiveness of the designed one-bit ternary comparator circuit.

FIGURE 9

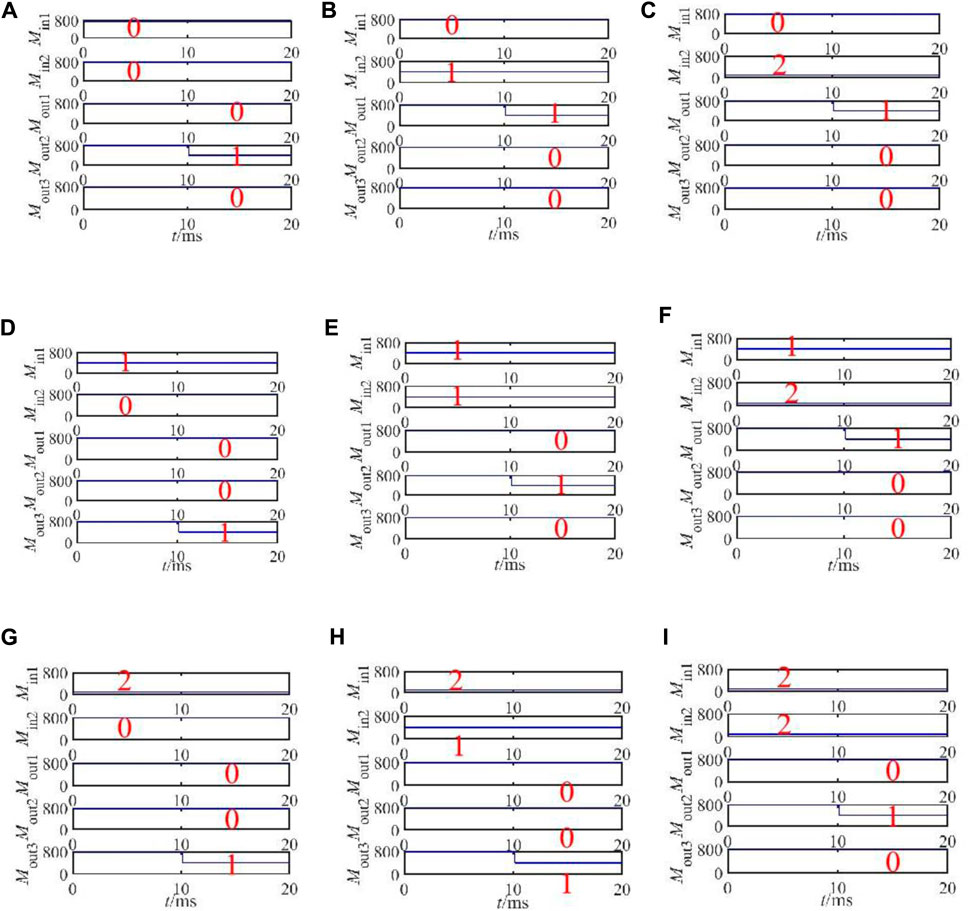
FIGURE 9. LTspice simulation results of the ternary comparator: (A) input as (0, 0), (B) input as (0, 1), (C) input as (0, 2), (D) input as (1, 0), (E) input as (1, 1), (F) input as (1, 2), (G) input as (2, 0), (H) input as (2, 1), and (I) input as (2, 2)

3.4 Ternary data selector

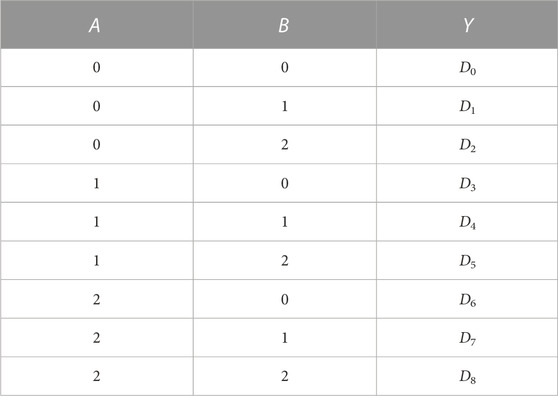
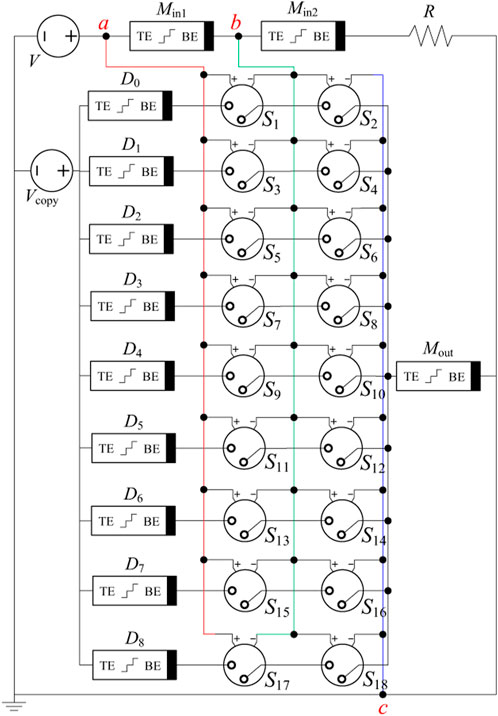
In the process of digital signal transmission, sometimes, it is necessary to select one from a group of data, and then, a logic circuit called data selector or multiplexer is used. The traditional binary data selector can select one data from four data through two address signals, while the ternary data selector based on the tri-valued memristor can select one output from nine data through two address signals. The truth table of the 9-out-of-1 ternary data selector is shown in Table 6, where A and B are two address signals, and Y outputs the data selected by the address signal.

TABLE 6

TABLE 6. Truth table of the 9-to-1 ternary data selector.

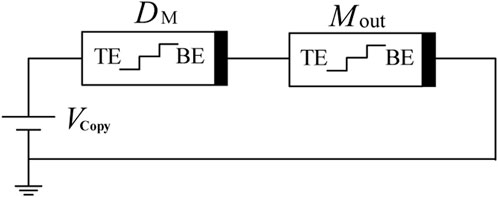
Before designing the ternary data selector circuit, a ternary copy gate needs to be introduced, whose function is to copy the information from the data memristor to the output memristor. The circuit structure is shown in Figure 10, which consists of an operating voltage source V, a data memristor D_M, and an output memristor M_out. Among them, V outputs the operating voltage V_copy, and the initial resistance of M_out is R_H. According to the different input logic, it can be divided into the following three cases:

FIGURE 10

FIGURE 10. Ternary copy circuit.

(1) If D_M = 800Ω and the logic is “0,” the voltage of M_out should be less than 1 V to ensure M_out remain its initial resistance, which demand the divided voltage of M_out meets (800/1600)*V_copy <1V, that is, V_copy<2 V.

(2) If D_M = 400Ω and the logic is “1,” to ensure M_out change from R_H to R_M, the divided voltage of M_out should be between 1 V and 1.2 V, so the divided voltage of M_out should satisfy the condition of ‘1 V< (800/1200)*V_copy<1.2 V’, that is, 1.5 V ≤ V_copy<1.8 V.

(3) If D_M = 100Ω and the logic is “2,” M_out need to change from R_H to R_L, which needs to meet the condition of V_copy≥1.35 V.

Combining the three aforementioned situations, the operating voltage of the ternary copy gate circuit must satisfy 1.5 V ≤ V_copy<1.8 V. So we choose 1.6 V as the operating voltage of the copy gate, and the specific voltage division between the data memristor and the output memristor is shown in Table 7.

TABLE 7

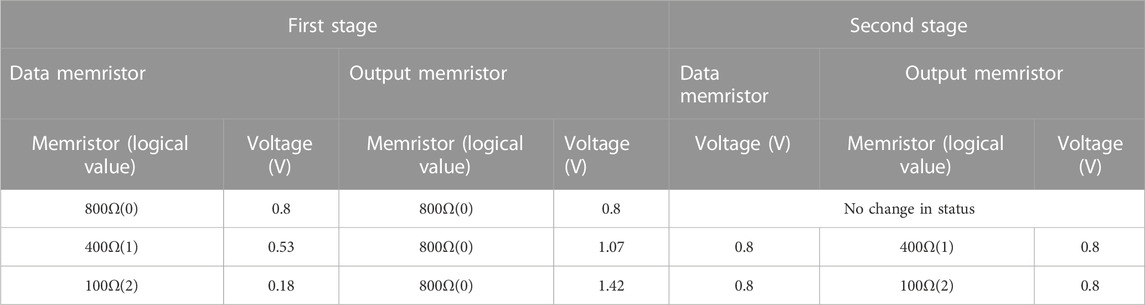
TABLE 7. Specific voltage division of each memristors in the calculation stage of the ternary copy gate.

The circuit structure of the 9-out-of-1 ternary data selector based on tri-valued memristors is shown in Figure 11, where the input memristors M_in1 and M_in2 store two address signals A and B, and the data memristors D₀–D₈ store, respectively, nine channels of known ternary data. M_out outputs the data D_i (i = 0, 1, 2, $\dots$, 8) selected by the address signals, and all of the initial resistance values of M_out are R_H. In this design, D_i forms a ternary copy gate with the output memristor M_out and the voltage source V_copy, and its function is to copy the data on D_i to M_out. Switches S₁–S₁₈ are used to control the access conditions of the memristors D₀–D₈, ensuring that only one data memristor D_i is connected to the circuit during the circuit operation stage. It is worth mentioning that the auxiliary resistor R is also added to the data selector circuit, and its function is to make the circuit have more voltage divider cases. If there is no auxiliary resistor, when the values of M_in1 and M_in2 are same, there will be three different cases (M_in1 = M_in2 = 800Ω, M_in1 = M_in2 = 400Ω, and M_in1 = M_in2 = 100Ω), but the divided voltages on M_in1 and M_in2 in these three cases will always be the same, which will cause the switch groups that work for these cases to be the same. However, with the help of an auxiliary resistor R, the voltage division in these three cases will easily be distinguished, and different switch groups can be turned on according to different cases. To meet this demand, R is calculated as 500Ω, and the other parameters are V_copy = 1.6 V, V_Init = 0.5 V, and V_Run = 1.2 V.

FIGURE 11

FIGURE 11. 9-out-of-1 ternary data selector circuit.

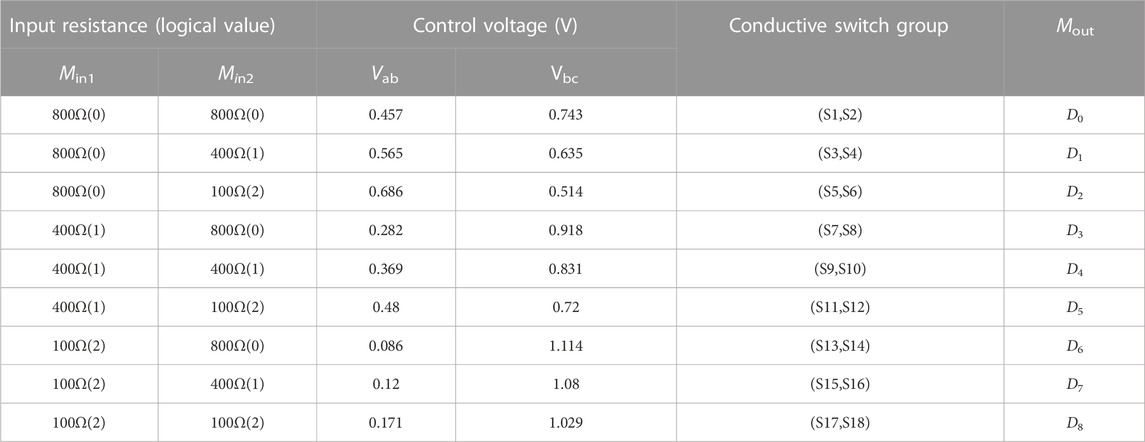
For convenience, switches S₁–S₁₈ are divided into nine groups. Each group is called a switch group, which is expressed as (S₁, S₂) ∼ (S₁₇, S₁₈), and each switch group is turned on only when two switches in the switch group are turned on at the same time. The threshold voltages of S₁–S₁₈ are set to 0.4, 0.73, 0.5, 0.6,0.6, 0.5, 0.2, 0.9, 0.3, 0.8, 0.47, 0.7, 0.05, 1.1, 0.1, 1.05, 0.15, and 1 V. Table 8 lists the situation of conductive switch groups and the output of M_out under different inputs of the 9-out-of-1 ternary data selector. According to the specific logic states of M_in1 and M_in2, the specific operation of the ternary data selector in the running phase can be summarized as follows. In this paper, the input logic “00” and “01” are taken as examples for detailed analysis. The analysis process of other inputs is the same, and the description will not be repeated here.

(1) The input logic is “00,” that is, M_in1 = 800Ω and M_in2 = 800Ω. V_ab = 0.457V and V_bc = 0.743 V can be obtained by voltage division calculation. At this time, only S₁ and S₂ will be closed at the same time among the nine switch groups. Then, memristors D₀ and M_out are connected in series for the copy operation, and the logic gate outputs the data stored in D₀.

(2) The input logic is “01,” that is, M_in1 = 800Ω, M_in2 = 400Ω, V_ab = 0.565V, and V_bc = 0.635 V. Only S₃ and S₄ are turned on at the same time among the nine switch groups. So the memristor pair D₁ and M_out will be connected in series for the copy operation, and the logic gate outputs the data stored in D₁.

TABLE 8

TABLE 8. Conduction of the 9-to-1 ternary data selector under different inputs.

The 9-out-of-1 ternary data selector is simulated using LTspice software, in which the data memristors D₀–D₈ store nine channels of ternary signals, and its resistance value and corresponding logic value are D₀ = 800Ω (“0”), D₁ = 400Ω (“1”), D₂ = 100Ω (“2”), D₃ = 800Ω (“0”), D₄ = 400Ω (“1”), D₅ = 100Ω (“2”), D₆ = 100Ω (“2”), D₇ = 400Ω (“1”), and D₈ = 800Ω (“0”). The simulation results under different combinations of address signals are shown in Figure 12, which shows the data selection results of the 9-out-of-1 ternary data selector. The resistance values of M_in1 and M_in2 are the input address signals, and the resistance value of M_out is the output signal. When the inputs are “00,” “01,” “02,” “10,” “11,” “12,” “20,” “21,” and “22,” the ternary signals stored in D₀, D₁, D₂, D₃, D₄, D₅, D₆, D₇, and D₈ are outputs, which are consistent with the output of the ternary data selector in Table 6, and verify the effectiveness of the designed ternary data selector circuit.

FIGURE 12

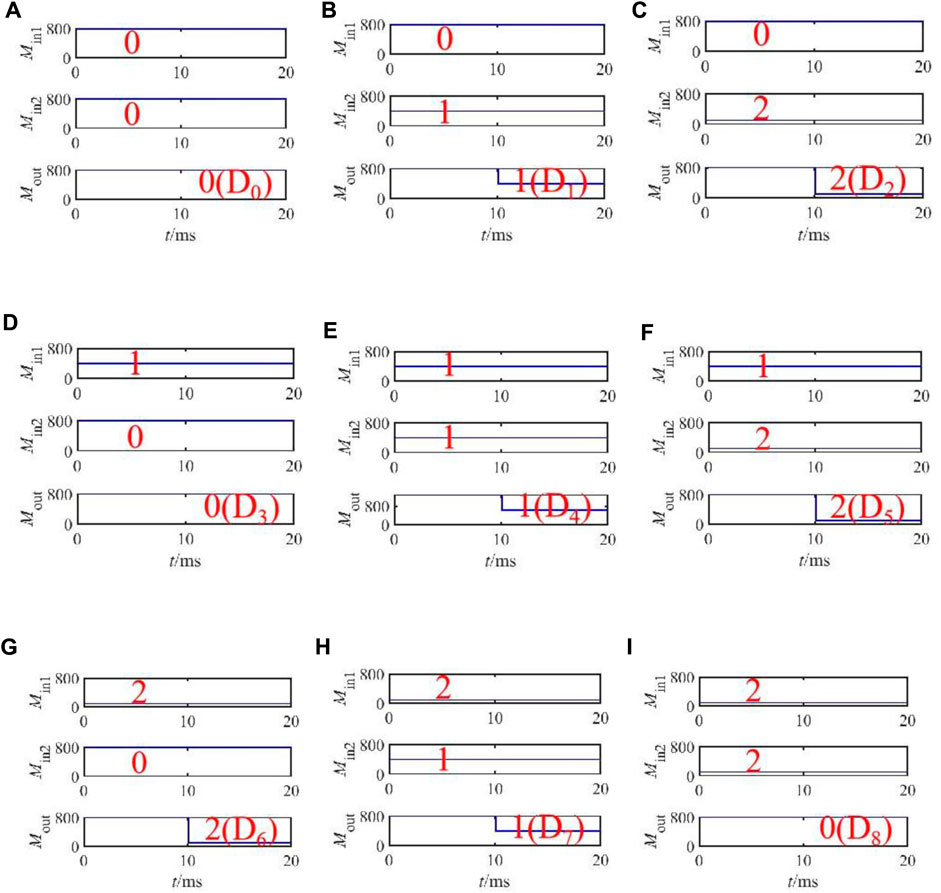
FIGURE 12. LTspice simulation result of the ternary data selector: (A) input as (0, 0), (B) input as (0, 1), (C) input as (0, 2), (D) input as (1, 0), (E) input as (1, 1), (F) input as (1, 2), (G) input as (2, 0), (H) input as (2, 1), and (I) input as (2, 2).

4 Conclusion

This paper presents a design method of the ternary combinational logic gate circuit based on a tri-valued memristor and realizes the ternary encoder, ternary decoder, ternary comparator, and ternary data selector with the resistance of the tri-valued memristor as the logic state variable. First, a voltage threshold tri-valued memristor is introduced, and the threshold characteristics of the tri-valued memristor are analyzed in detail. Second, using the tri-valued memristor, a series of complex combinational logic circuits with the resistance of the memristor as the logic state variable are designed, respectively, and the implementation principle of each gate is analyzed in detail. Finally, the effectiveness of the designed combinational logic gate circuits is verified by LTspice circuit simulation. Compared with the existing binary or ternary combinational logic gate circuits, the ternary combinational logic gate circuit based on the tri-valued memristor proposed in this paper does not need to be realized by cascading basic logic gates and can be realized only by a small number of tri-valued memristors and voltage-controlled switches. In addition, the logic gate designed by this method can not only perform logic operations but also store logic values.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

X-JL: validation, writing–review and editing, methodology, and writing–review and editing. X-YW: writing–review and editing, data curation, conceptualization, funding acquisition, investigation, methodology, project administration, and supervision. PL: writing–review and editing, data curation, and investigation. HI: visualization, and writing–review and editing. Z-QC: visualization, and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant No. 61871429), the Natural Science Foundation of Zhejiang Province, China (Grant No. LY18F010012), and the Project of Ministry of Science and Technology of China (Grant No. D20011).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hamedani SG, Moaiyeri MH. Impacts of process and temperature variations on the crosstalk effects in sub-10 nm multilayer graphene nanoribbon interconnects. IEEE Trans Device Mater Reliability (2019) 19(4):630–41. doi:10.1109/TDMR.2019.2937789

CrossRef Full Text | Google Scholar

2. Khezeli MR, Moaiyeri MH, Jalali A. Analysis of crosstalk effects for multiwalled carbon nanotube bundle interconnects in ternary logic and comparison with Cu interconnects. IEEE Trans Nanotechnology (2016) 16(1):107–17. doi:10.1109/TNANO.2016.2633460

CrossRef Full Text | Google Scholar

3. Hurst . Multiple-valued logic—Its status and its future. IEEE Trans Comput (1984) 100(12):1160–79. doi:10.1109/TC.1984.1676392

CrossRef Full Text | Google Scholar

4. Glusker M, Hogan DM, Vass P. The ternary calculating machine of Thomas Fowler. IEEE Ann Hist Comput (2005) 27(3):4–22. doi:10.1109/MAHC.2005.49

CrossRef Full Text | Google Scholar

5. Talati N, Gupta S, Mane P, Kvatinsky S. Logic design within memristive memories using memristor-aided loGIC (MAGIC). IEEE Trans Nanotechnology (2016) 15(4):635–50. doi:10.1109/TNANO.2016.2570248

CrossRef Full Text | Google Scholar

6. Thangkhiew PL, Datta K. Scalable in-memory mapping of Boolean functions in memristive crossbar array using simulated annealing. J Syst Architecture (2018) 89:49–59. doi:10.1016/j.sysarc.2018.07.002

CrossRef Full Text | Google Scholar

7. Thangkhiew PL, Gharpinde R, Datta K. Efficient mapping of Boolean functions to memristor crossbar using MAGIC NOR gates. IEEE Trans Circuits Syst Regular Pap (2018) 65(8):2466–76. doi:10.1109/TCSI.2018.2792474

CrossRef Full Text | Google Scholar

8. Wald N, Kvatinsky S. Understanding the influence of device, circuit and environmental variations on real processing in memristive memory using Memristor Aided Logic. Microelectronics J (2019) 86:22–33. doi:10.1016/j.mejo.2019.02.013

CrossRef Full Text | Google Scholar

9. Min F, Xue L. Routes toward chaos in a memristor-based Shinriki circuit. Chaos: Interdiscip J Nonlinear Sci (2023) 33(2):023122. doi:10.1063/5.0126900

CrossRef Full Text | Google Scholar

10. Khalid M, Singh J. Memristor based unbalanced ternary logic gates. Analog Integrated Circuits Signal Process. (2016) 87:399–406. doi:10.1007/s10470-016-0733-1

CrossRef Full Text | Google Scholar

11. Zhang H, Zhang Z, Gao M, Luo L, Duan S, Dong Z, et al. Implementation of unbalanced ternary logic gates with the combination of spintronic memristor and CMOS. Electronics (2020) 9(4):542. doi:10.3390/electronics9040542

CrossRef Full Text | Google Scholar

12. Wang XY, Zhou PF, Eshraghian JK, Lin CY, Iu HHC, Chang TC, et al. High-density memristor-CMOS ternary logic family. IEEE Trans Circuits Syst Regular Pap (2020) 68(1):264–74. doi:10.1109/TCSI.2020.3027693

CrossRef Full Text | Google Scholar

13. Soliman NS, Fouda ME, Radwan AG. Memristor-CNTFET based ternary logic gates. Microelectronics J (2018) 72:74–85. doi:10.1016/j.mejo.2017.12.008

CrossRef Full Text | Google Scholar

14. Mohammed MU, Vijjapuram R, Chowdhury MH. “Novel CNTFET and memristor based unbalanced ternary logic gate”, In 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS) (2018). IEEE, 1106–9. doi:10.1109/MWSCAS.2018.8623845

CrossRef Full Text | Google Scholar

15. Soliman N, Fouda ME, Alhurbi AG, Said LA, Madian AH, Radwan AG. Ternary functions design using memristive threshold logic. Ieee Access (2019) 7:48371–81. doi:10.1109/ACCESS.2019.2909500

CrossRef Full Text | Google Scholar

16. Chen QL, Liu G, Tang MH, Chen XH, Zhang YJ, Zheng XJ, et al. A univariate ternary logic and three-valued multiplier implemented in a nano-columnar crystalline zinc oxide memristor. RSC Adv (2019) 9(42):24595–602. doi:10.1039/c9ra04119b

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chua L. Everything you wish to know about memristors but are afraid to ask. Handbook of Memristor Networks (2019) 89–157. doi:10.1007/978-3-319-76375-0_3

CrossRef Full Text | Google Scholar

18. Wang X, Zhang X, Gao M. A novel voltage-controlled tri-valued memristor and its application in chaotic system. Complexity (2020) 2020:1–8. doi:10.1155/2020/6949703

CrossRef Full Text | Google Scholar

19. Li P, Wang X, Zhang X, Eshraghian JK, Lu HHC. Spice modelling of a tri-state memristor and analysis of its series and parallel characteristics. IET Circuits, Devices Syst (2022) 16(1):81–91. doi:10.1049/cds2.12086

CrossRef Full Text | Google Scholar

20. Wang X, Li P, Jin C, Dong Z, Iu HH. General modeling method of threshold-type multivalued memristor and its application in digital logic circuits. Int J Bifurcation Chaos (2021) 31(16):2150248. doi:10.1142/S0218127421502485

CrossRef Full Text | Google Scholar