
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 19 October 2023
Sec. Optics and Photonics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1289062
The polarization state is described by a quantum mechanical two-level system, which is known as special unitary group of degree 2 [SU(2)]. Polarization is attributed to an internal spin degree of freedom inherent to photons, while photons also possess an orbital degree of freedom. A fundamental understanding of the nature of spin and orbital angular momentum of photons is significant to utilize the degrees of freedom for various applications in optical communications, computations, sensing, and laser-patterning. Here, we show that the orbital angular momentum of coherent photons emitted from a laser diode can be incremented using a vortex lens, and the magnitude of orbital angular momentum increases with an increase in the topological charge inside the mode. The superposition state of the left and right vortices is described by the SU(2) state, similar to polarization; however, the radius of the corresponding Poincaré sphere depends on the topological charge. Consequently, we expect a nested SU(2) structure to describe various states with different magnitudes in orbital angular momentum. We have experimentally developed a simple system to realize an arbitrary SU(2) state of orbital angular momentum by controlling both amplitudes and phases of the left and right vortices using a spin degree of freedom, whose interplays were confirmed by expected far-field images of dipoles and quadruples.
Angular momentum is a generator of rotation for a quantum mechanical state, such that spin angular momentum and orbital angular momentum are manipulated upon the application of angular momentum operators [1–4]. It is a fundamental principle supporting the optical selection rule upon the absorption and emission of a photon that the total angular momentum is conserved in a rotationally invariant system [5]. For an electron in an atom, the Schrödinger equation for a wavefunction under spherical symmetric Coulomb potential from a proton was solved analytically by an associated Laguerre function for a radial (r) distribution and a spherical harmonic function
Compared to the development of an electron during the foundation of quantum mechanics, it was surprisingly recent for a photon to recognize that the orbital angular momentum is quantized to be ℓ3 = ℏm, where m
The SU(2) description of the orbital angular momentum state and the corresponding SO(3) Poincaré spheres was already discussed by several researchers [18, 25, 27–35, 45, 46]. After the pioneering work of the Poincaré sphere for the orbital angular momentum using a pair of cylindrical lenses [27], the vectorial nature of the orbital angular momentum together with the spin angular momentum was successfully demonstrated [28–30]. More recently, the multi-dimensional nature of structured light was extensively studied both theoretically and experimentally [18, 32–35, 45, 46]. In particular, amazing local control of trajectories was achieved, and the corresponding SU(2) state with the orbital angular momentum was established [18, 32–35, 45, 46]. Upon understanding these intrinsic features, it was astonishing to classically demonstrate the entangled Greenberger–Horne–Zeilinger (GHZ) state [34]. Here, we focus on the nested Poincaré spheres which are considered theoretically [25, 32]. In particular, we observe that the radius of the Poincaré sphere is increased upon the ladder operation to increase the magnitude of the orbital angular momentum [25]. The larger radius of the Poincaré sphere could be confirmed by the cyclic symmetry of the far-field images of multi-poles, such as a dipole and quadrupole, around the equator of the Poincaré sphere [25, 32].
The purpose of this work is to prove the aforementioned concepts for SU(2) symmetry of the orbital angular momentum of photos in experiments. Due to the increased radius of ℓ0 upon incrementing m, the sphere for m + 1 should be larger than that of m, such that we expected nested Poincaré spheres. We have also developed a many-body field theory to account for the orbital angular momentum in a coherent state. Based on the theory, we have experimentally demonstrated the arbitrary SU(2) operations as a rotator and a phase-shifter for an SU(2) state of the orbital angular momentum.
First, we will briefly discuss the theoretical aspect of coherent photons with spin angular momentum and orbital angular momentum [25, 26, 47]. Here, we consider coherent photons emitted from a conventional laser diode (LD) [9, 10, 40–42]. The rotational symmetry of photons emitted from LD is spontaneously broken down upon lasing, and the spin of a macroscopic number of photons is aligned to a direction with the minimum loss for propagation in a cavity to form a coherent state [26, 48–51]. We assumed a single-mode operation of LD [9, 41, 42] for simplicity. If the beam propagates in vacuum, air, or a fiber with no polarization dependence, the polarization state can be maintained and controlled by various optical components, such as wave-plates, rotators, phase-shifters, and polarizers [9, 10, 40–42]. We have previously demonstrated, both theoretically [48] and experimentally [50], that an arbitrary polarization state can be realized by a combination of half-wave plates (HWPs) and quarter-wave plates (QWPs) using the proposed Poincaré rotator. The idea was to realize a proper rotator using two HWPs, of which one of HWPs is physically rotated, while the other is fixed. This allows converting the well-known pseudo-rotation behavior (a mirror reflection) of a rotated HWP [41, 42] to a proper rotator, which constructs group operations [48, 50]. By introducing QWPs before and after the rotator, we could also realize a phase-shifter, whose phase is determined by the rotation angle [48, 50]. Here, we will establish the construction of a Poincaré rotator for the orbital angular momentum.
We define field operators of
The SU(2) state of the orbital angular momentum for a fixed polarization state is described by a direct product state of |αmσ, α−mσ⟩ = |αmσ⟩|α−mσ⟩, where we have defined the coherent state [11, 26, 52, 53] as follows:
with the complex
We have previously derived the orbital angular momentum operator [26] which is given as follows:
where the
The expectation value of the orbital angular momentum in the coherent state is calculated as follows:
where * means a complex conjugate operation. This formula shows that the Jones vector of
which can be shown as an extended Poincaré sphere [26–31, 54] (Figure 1). The magnitude of the orbital angular momentum, defined by
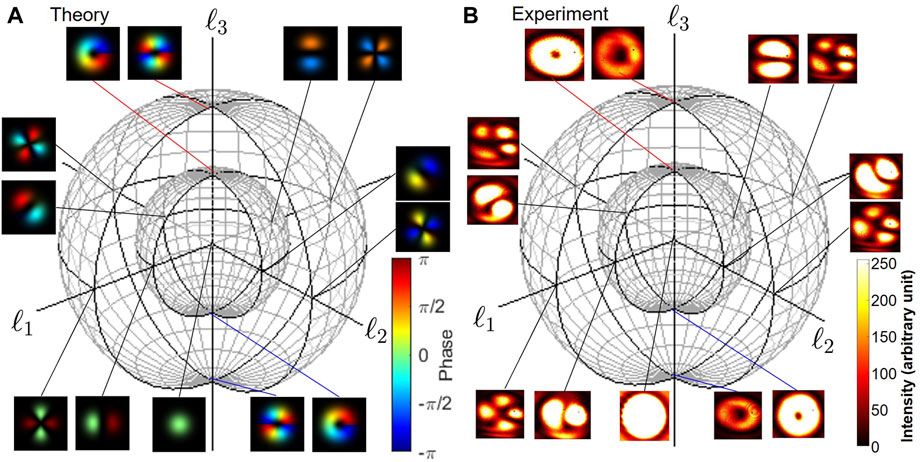
FIGURE 1. Nested Poincaré sphere for the orbital angular momentum per photon (ℓ1, ℓ2, ℓ3). (A) Theoretical calculations of mode profiles are shown. The phase changes are shown by the color profile, while the intensities of modes are represented by brightness. The chirality is defined by the phase change, observed from the detector side, such that the left-twisted state (eimϕ) is located at the north pole and the right-twisted state (e−imϕ) is located at the south pole. The Gaussian beam without topological charge has no orbital angular momentum, and the state is located at the origin. The inner sphere for SU(2) states with a topological charge of 1 has the radius of ℏ, and the outer sphere for SU(2) states with a topological charge of 2 has the radius of 2ℏ. The nested spherical structure will continue to expand as the magnitude of the orbital angular momentum is increased with the step of ℏ. (B) Experimental far-field images, shown by intensity profiles on the spheres. It is impossible to distinguish left and right vortices at north and south poles, but we can recognize dipoles and quadrupoles around the equator, which rotates in the ℓ1–ℓ2 plane, similar to linear polarization.
As shown in Figure 1, a standard Gaussian beam should correspond to the state at the origin since there is no topological charge in the mode profile, and thus, the orbital angular momentum must be zero. This is a remarkable contrast with the Poincaré sphere for the spin angular momentum since we cannot realize a state with a vanishing spin expectation value for coherent photons with the full degree of polarization. As the magnitude of the orbital angular momentum is increased in the unit of ℏ, the radius of ℓ0 is quantized to have integer values, as
Next, we demonstrate that the many-body field operator of
where n is the unit vector (|n| = 1) for the rotational axis and δϕ is the angle of rotation, measured for the anticlock-wise direction (δϕ > 0 for left rotation).
In order to prove the expected rotation for the SU(2) state by the generator of rotation, we apply the operator to obtain
where the SU(2) wavefunction
is transferred by the exponential map [3, 55–57] for the SU(2) operation
Therefore,
As described previously, the many-body operator of the orbital angular momentum works as the generator of rotation for the SU(2) states, and the expectation values of the orbital angular momentum become real numbers
In order to realize an arbitrary SU(2) state for the orbital angular momentum, our experimental challenge is to realize an SU(2) rotational operator [2, 26, 48, 49, 58].
which corresponds to an extension of Euler’s formula for 2 × 2 complex matrices. We have previously realized the SU(2) operator for the spin angular momentum by using the HWPs and QWPs [50]. In order to apply the same technique for the orbital angular momentum, we need HWPs and QWPs for the orbital angular momentum [64], together with beamsplitters [65–69] to separate left- and right-twisted components from the mixed SU(2) state. These optical components for the orbital angular momentum are certainly very important for SU(2) manipulations, but they are not widely available, compared with the polarization components for the spin angular momentum. In our previous scheme [50, 70], if we use the pair of cylindrical lenses (Cyls) [64] as the half-wave phase shifter (HWPS) for the orbital angular momentum, similar to a HWP for polarization, we need to rotate the paired HWPS, while another HWPS must also be employed to realize the genuine rotation rather than the mirror reflection [48, 50, 70]. Moreover, we also need two pairs of QWPs [48, 50, 70], which require mode matching to control Gouy phases at the waist [64], such that it is difficult to manipulate the SU(2) state while keeping the collimation. Therefore, we have considered an alternative approach to maximizing the use of commercially available polarization components, and only one HWPS was used.
The proposed experimental setup is shown in Figure 2. We used a green LD, operated at the wavelength of 532 nm with the output power of

FIGURE 2. Poincaré rotator to realize an arbitrary SU(2) rotation for a beam with the orbital angular momentum. HWP1 was physically rotated to control the relative amplitudes for left and right vortices. Half-wave phase shifter (HWPS) was used to change the chirality of the orbital angular momentum among beams for the paths along mirror 1 (M1) (left vortex at the CMOS camera) and M2 (right vortex). Quarter-wave plates (QWPs) and HWPs after M2 were used to control the phase, and HWP3 was physically rotated to change the phase between left and right vortices. The insets show the orientations of fast axis (FA) and slow axis (SA) in QWPs and HWPs, and the phase profile of the far-field images during the propagation are also shown. LD, laser diode; CL, collimator lens; PH, pin hole; PL, polarizer; HWP, half-wave plate; QWP, quarter-wave plate; FA, fast axis; SA, slow axis; PBS, polarization beamsplitter; NPBC, non-polarization beam combiner; NPBS, non-polarization beamsplitter; M, mirror; PM, polarimeter; CMOS, complementary metal-oxide semiconductor; HWPS, half-wave phase shifter for the vortex; Cyl, cylindrical lens.
We used non-polarization beamsplitter (NPBS1) to convert the input of the left vortex to the right vortex, and the other output (through-port, the beam is not shown) was used for the alignment. Then, the beam passes through HWP1, which was used to rotate the polarization to control the amplitude at the polarization beamsplitter (PBS). The vertically polarized component is reflected toward the HWPS, made of two paired cylindrical lenses (Cyl1 and Cyl2). HWPS works as the
On the other hand, the beam reflected at M2 was phase-shifted at the series of HWPs and QWPs. We have aligned the fast axis (FA) of QWP1 to the antidiagonal (A) direction, which is rotated 45° to the clockwise direction from the horizontal (H) direction [48, 50] (insets of Figure 2). The FA of HWP2 was aligned horizontally, while HWP3 was rotated to control the phase [48, 50]. Then, the FA of QWP2 was aligned to the diagonal (D) direction, which is rotated 45° to the counter-clockwise direction from the H-direction [48, 50]. Consequently, QWP1, HWPs, HWP3, and QWP2 worked as a phase-shifter for H-polarization [48, 50], and we have brought the H-polarized state back to the V-polarized state by HWP4, whose FA was aligned to the D-direction. Then, the beam was reflected at NPBS2, such that the beam became the right vortex at CMOS. The beams from the path from M1 and the path from M2 were combined at NPBS2, and the combined beam became the superposition state between the left and right vortices under V-polarization.
In the aforementioned explanations, the changes of states for both polarization and orbital angular momentum might not be obvious. Therefore, we have included the schematic images of the input state, states during the propagation, and the output state in Figure 1. In order to explain complementary, we describe how the state is changed upon propagation. After passing through VL, the input state is characterized by the left vortex with V-polarization, while the component of the horizontal polarization vanishes. Then, the beam is reflected by NPBS1, which converts the input state to the right vortex with V-polarization upon reflection. Then, the rotated HWP1 works as an amplitude controller, which rotates the polarization state to have a H-polarization component together with a V-polarization component, depending on the rotation angle. Here, it is important to recognize both polarization states are based on the right vortex. Then, the beam is split at PBS, the V-polarization state is reflected to be the left vortex due to the reflection, while the H-polarization state passes through the PBS without changing the right vortex state. For the reflected beam with V-polarization, the beam passes through HWPS, which works to convert the vortex state while maintaining the polarization state. Therefore, after passing through HWPS, the beam becomes the right vortex, which is reflected at M1 to finally become the left vortex with V-polarization. On the other hand, when the beam passes through M2, it is passing through a series of waveplates (QWP1, HWP2, HWP3, QP2, and HWP4) to control the phase. It is a straightforward calculation of Jones matrices, as shown in our previous papers for the polarization state [48, 50]. After passing through theses waveplates, the beam reaches the V-polarization state, while the left vortex is maintained throughout the phase control. Finally, the beam is reflected at NPBS2 to become the right vortex while V-polarization is maintained. Consequently, the input of a left vortex with V-polarization was converted to be a superposition state of the left and right vortices with variable amplitudes and phases while V-polarization was maintained.
First, we used a VL for generating the left vortex with a topological charge of 1, which corresponds to the rotation of states on the inner Poincaré sphere, as shown in Figure 1. We examined the rotator operation for the vortex to see the expected dipoles rotating in far-field images (Figure 3), which correspond to rotate the SU(2) states along the equator of the Poincaré sphere [25, 27, 29, 43, 47]. We set the rotation angle of FA of HWP1 at 22.5° from the H-direction along the clockwise direction, which corresponds to the 90° rotation on the Poincaré sphere for changing V-polarization to D-polarization, since the physical rotation angle of ΔΨ induces the rotation of 4ΔΨ on the Poincaré sphere [9, 10, 40–42, 48, 50]. This allowed splitting the beam with the ratio of 50:50 at PBS, and the extra phase-shift was induced for the path along M2. Consequently, we expect the SU(2) operation.
where n3 = (0, 0, 1) corresponds to the rotation along ℓ3. In fact,
to change ϕ → ϕ + δϕ/2. Here, we must be cautious for the factor of 2 in δϕ = 2ΔΨ against the amount of rotation of HWP3 instead of the previous factor of 4 [9, 10, 40–42, 48, 50] because only H-polarization mode for the path along M2 was affected by the phase-shifter, while the V-polarization mode for the path along M1 was not affected. Therefore, the physical rotation of 180° for HWP3 was required to realize the whole 360° rotation on the Poincaré sphere. The expected rotation of the dipoles in far-field images was observed (Figures 3A–C), and the dipoles rotated in the counter-clockwise direction as we rotated HWP3 to the same direction. Here, it is worth noting that two peak intensities of left and right portions of the dipole, shown in Figure 3B1, were exchanged to be right and left portions of the dipole, shown in Figure 3B19, respectively, after one continuous circulation on the Poincaré sphere. As shown in Figure 3A1, the left and right portions of the dipole have the opposite phase, and the phase difference is π. This can be confirmed by the phase factor of
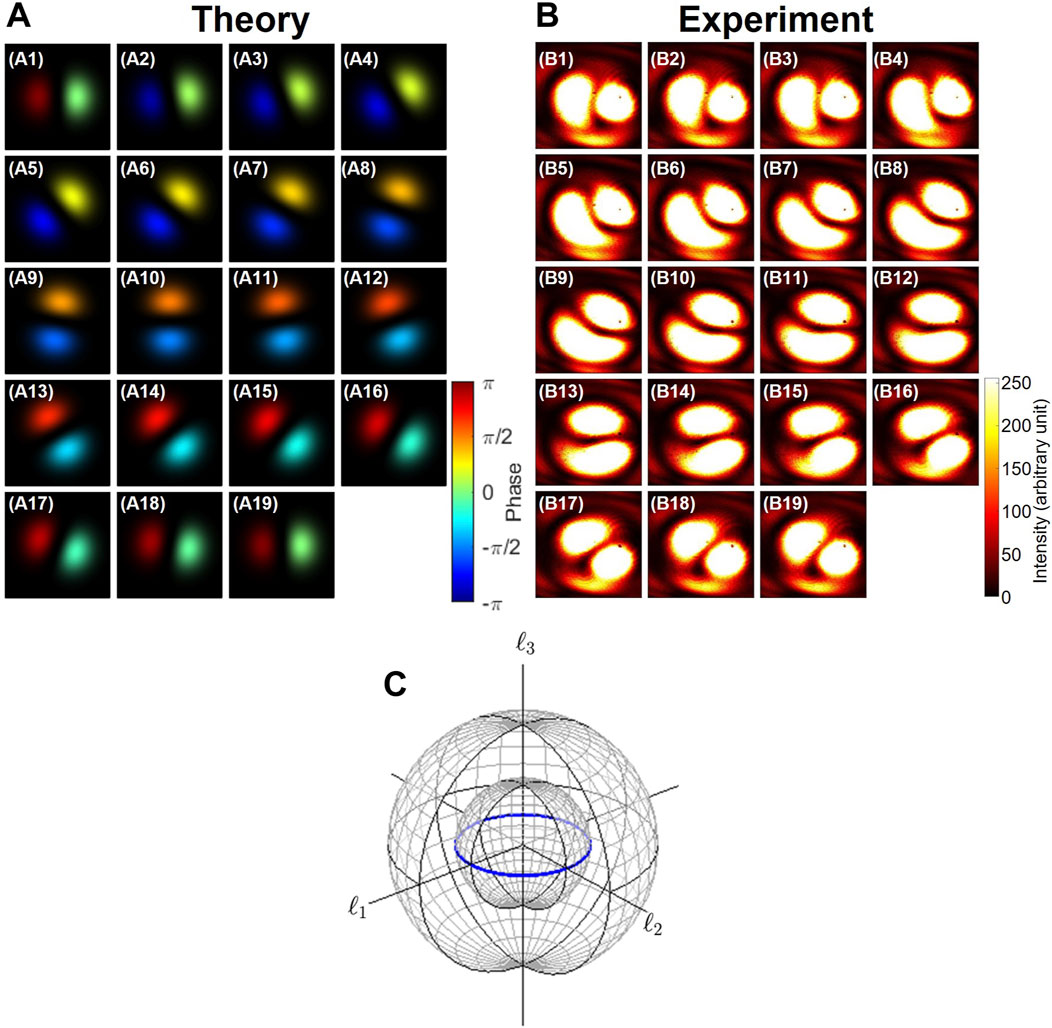
FIGURE 3. Rotator operation for the dipole made of left and right vortices with a topological charge of 1. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the blue curve. (A1–A19) and (B1–B19) Far-field images of the dipole after rotating HWP3 from 0° to 180° at the step of 10°. This rotation corresponds to the counter-clockwise rotation along the equator in the ℓ1–ℓ2 plane with the axis of ℓ3. The dipole was rotated 90° from (B1) the horizontal dipole to (B11) the vertical dipole. Another 90° rotation brings the vertical dipole (B11) back to (B19) the horizontal dipole. The horizontal dipole (B1) was rotated 180° to be (B19) in images, which corresponds to the 360° rotation on the Poincaré sphere.
Next, we confirmed the phase-shifter operation for SU(2) states of the orbital angular momentum (Figures 4A–C). This was achieved simply by rotating HWP1 to change the splitting ratio for left and right vortices, while the rotation angle of HWP3 was adjusted through the images of the dipole to realize the rotation in the ℓ3–ℓ1 plane along the ℓ2 axis. The phase-shifter along n2 = (0, 1, 0) is set the same as a standard rotation matrix in SO(2) [9, 10, 40–42, 48, 50] to obtain
where δθ = 4ΔΨ against the amount of rotation of HWP1 [9, 10, 40–42, 48, 50], since beams in both paths were affected by splitting. The experimental far-field images are shown in Figure 4. We demonstrated that the left vortex was transferred to the right vortex and vice versa through horizontal and vertical dipoles in between during the transformation. This means that we can continuously rotate SU(2) states of the orbital angular momentum simply by mechanical rotations of HWPs, as we previously demonstrated for polarization [50].
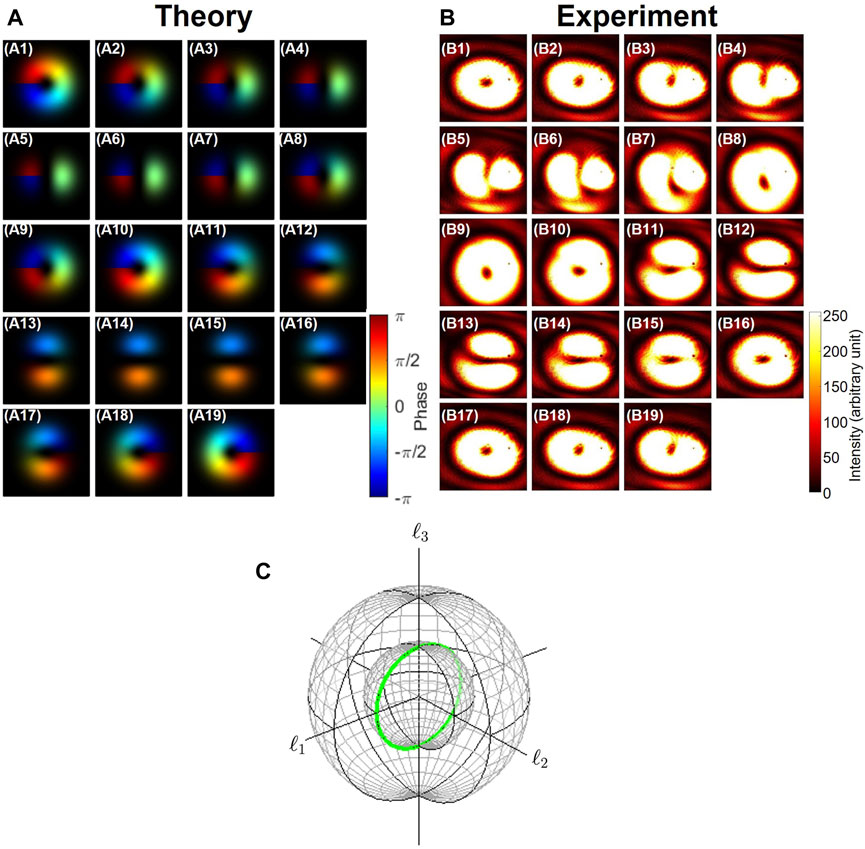
FIGURE 4. Phase-shifter operation to rotate in the ℓ3–ℓ1 plane along the ℓ2 axis. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the green curve. The rotation axis was adjusted by rotating HWP3. (A1–A19) and (B1–B19) Far-field images after rotating HWP1 from 0° to 90° at the step of 5°. The left vortex (B1) was rotated to (B5) the horizontal dipole, (B10) the right vortex, (B14) the vertical dipole, and back to (B19) the left vortex.
We have demonstrated both rotator and phase-shifter operations of SU(2) states of the orbital angular momentum, such that we can realize any state on the Poincaré sphere by combining these operations. As for completeness, we have also demonstrated the phase-shifter operation along the ℓ1 axis in the ℓ3–ℓ1 plane, as shown in Figures 5A–C. The operation principle is exactly the same as that for the rotation along the ℓ2 axis.
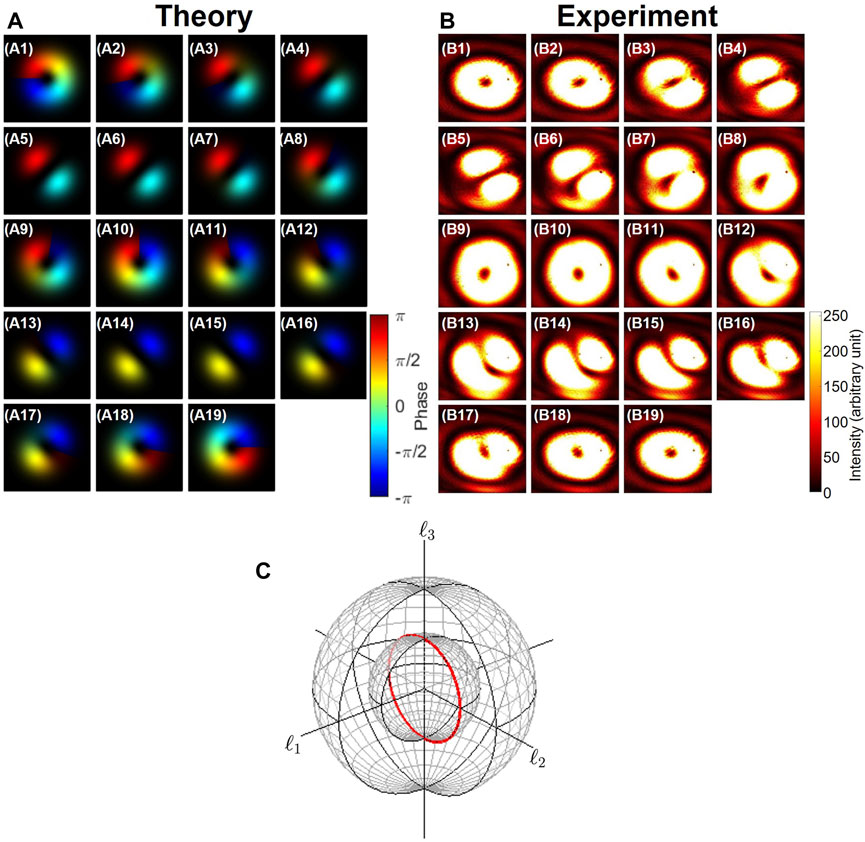
FIGURE 5. Phase-shifter operation for left and right vortices with a topological charge of 1 to rotate in the ℓ3–ℓ2 plane along the ℓ1 axis. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the red curve. (A1–A19) and (B1–B19) Far-field images after rotating HWP1 from 0° to 90° at the step of 5°. The left vortex (B1) was rotated to (B5) the antidiagonal dipole, (B10) the right vortex, (B14) the diagonal dipole, and back to (B19) the left vortex.
In the previous subsection, we have realized an optical dipole, whose symmetry is characterized by a cyclic group of degree 2, C2, which means that we require two steps upon one circulation of the dipole and the rotation of 180° brings the dipole back to the one with the same intensity profile. Then, we proceed to explore an optical quadrupole, whose symmetry is described by C4, which means that the intensity profile of the quadrupole is not changed upon the rotation of 90° due to the 4-fold symmetry. Obviously, this symmetry argument is valid for higher-order topological charge, and if we consider the topological charge of 3, the six-fold symmetric multipole is expected in far-field images with C6 symmetry. In general, for the topological charge of m, we expect 2m-fold symmetric multipole in far-field images, which are symmetric under C2m operations.
Experimentally, we used a VL [6, 20, 27, 29–31, 43, 65, 71–73] for the topological charge of 2, and the rest of the experimental setup was the same as described previously. The rotator operation for the quadrupole is shown in Figures 6A–C. We define the rotational origin of the quadrupole (ϕ = 0) to be the mode profile shown in Figures 6A1, B1 and call it to be horizontal, corresponding to the SU(2) state for (ℓ1, ℓ2, ℓ3) = (2, 0, 0)ℏ (Figure 1). The mode, which is orthogonal to the horizontal mode, is the vertical profile shown in Figures 6A10, B10, corresponding to the state for (ℓ1, ℓ2, ℓ3) = (−2, 0, 0)ℏ. As we can confirm that the dipole rotated in the counter-clockwise direction, we rotated HWP3 in the same direction. We can also observe that the 90° rotation shown in the far-field image was enough to perform one rotation along the equator on the outer shell of the nested Poincaré spheres, as shown in Figure 1. It is also true that the phase difference between horizontal and vertical portions in the quadrupole is π, such that the phase factor of

FIGURE 6. Rotator operation for the quadrupole made of left and right vortices with a topological charge of 2. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the blue curve. (A1–A19) and (B1–B19) Far-field images of the quadrupole after rotating HWP3 from 0°–180° at the step of 10°. This rotation corresponds to the counter-clockwise rotation along the equator in the ℓ1–ℓ2 plane with the axis of ℓ3. The horizontal quadrupole (B1) was rotated to (B5) diagonal, (B10) vertical, (B14) antidiagonal, and back to (B19) horizontal quadrupoles. The horizontal quadrupole of (B1) was rotated 90° to be (B19) in images, which corresponds to the 360° rotation on the Poincaré sphere.
Next, we have examined the phase-shifter operation for vortices with the topological charge of 2 (Figures 7A–C; Figures 8A–C). We could change the rotation axes from the ℓ1 axis to the ℓ2 axis, as shown in Figures 7A–C and Figures 8A–C, respectively, by rotating HWP3, while the amplitudes for the left and right vortices were controlled by rotating HWP1 for both cases to change the splitting at PBS. We confirmed continuous changes in far-field images from the left vortex to the right vortex and vice versa through tilted quadrupoles in between.
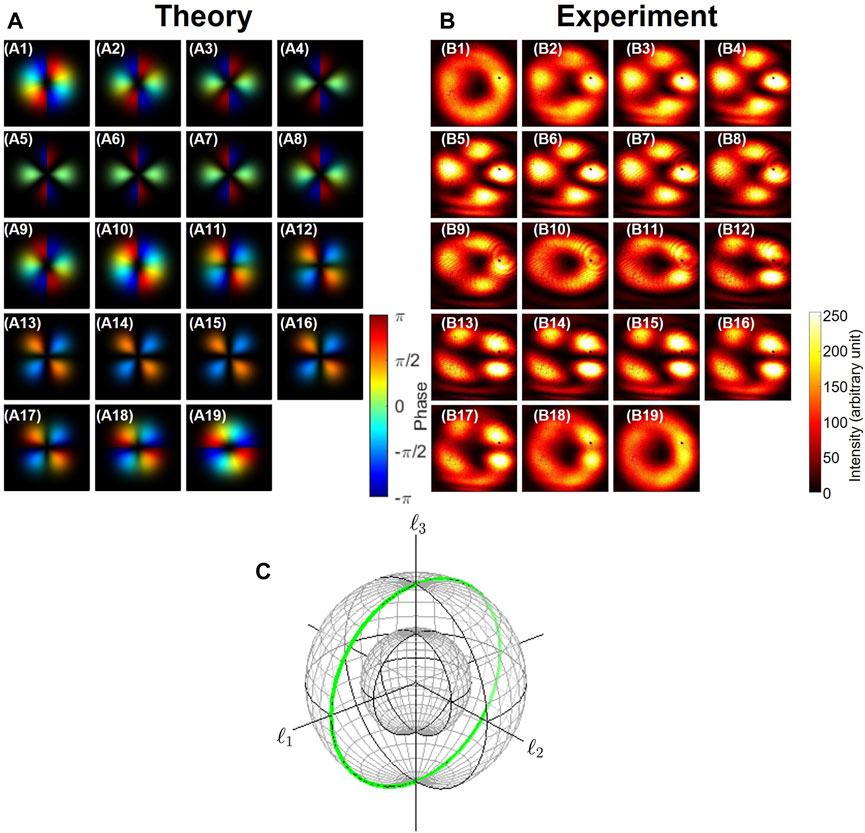
FIGURE 7. Phase-shifter operation to rotate in the ℓ3–ℓ1 plane along the ℓ2 axis. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the green curve. The rotation axis was adjusted by rotating HWP3. (A1–A19) and (B1–B19) Far-field images after rotating HWP1 from 0° to 90° at the step of 5°. The left vortex (B1) was rotated to (B5) the horizontal quadrupole, (B10) the right vortex, (B14) the vertical quadrupole, and back to (B19) the left vortex.
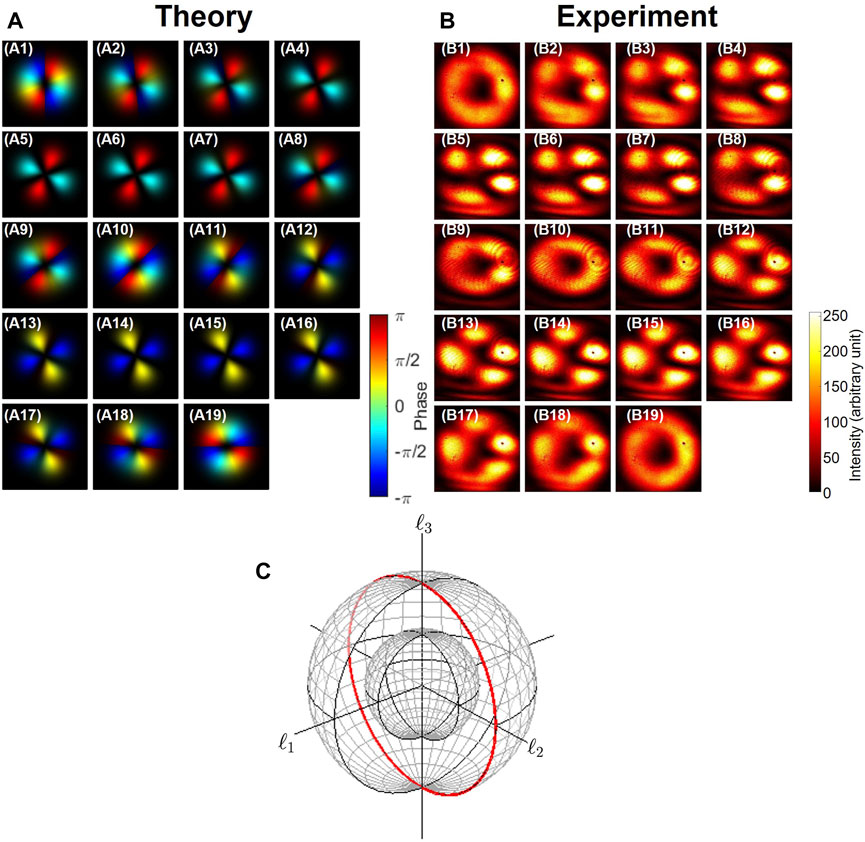
FIGURE 8. Phase-shifter operation for left and right vortices with a topological charge of 2 to rotate in the ℓ3-ℓ2 plane along the ℓ1 axis. (A) Theoretical calculation, (B) experimental results, and (C) corresponding trajectories on the Poincaré sphere, shown by the red curve. (A1–A19) and (B1–B19) Far-field images after rotating HWP1 from 0° to 90° at the step of 5°. The left vortex (B1) was rotated to (B5) the antidiagonal quadrupole, (B10) the right vortex, (B14) the diagonal quadrupole, and back to (B19) the left vortex.
We can realize an arbitrary SU(2) rotation [2, 26, 47–50, 58, 63] by combining the rotator and the phase-shifter to realize
where |Left ⟩ = (1, 0) is the SU(2) state for the left vortex. We have previously demonstrated the SU(2) rotation of the polarization state and proposed the device “Poincaré rotator” since we can realize an arbitrary rotation on the Poincaré sphere [47, 50]. Here, we have demonstrated the operation of the Poincaré rotator for the orbital angular momentum.
We have theoretically shown [25] that the ladder operators of the orbital angular momentum worked properly for the Laguerre–Gaussian modes to increase and decrease the helical component in the orbital angular momentum along the direction of the propagation (ℓ3) in the unit of ℏ. This work was conducted to confirm the theoretical expectations in experiments, while we have also developed a Lie group theory for coherent states to control the SU(2) state of the orbital angular momentum. The proposed Poincaré operator successfully rotates the SU(2) states, which was confirmed by far-field images, and we could observe the expected behaviors as phase-shifters and rotators simply by rotating the waveplates. We found the rotations of dipoles and quadrupoles by changing the phase between the left and right vortices. It is a simple theoretical consequence that the magnitude of the orbital angular momentum is increased upon the application of a vortex lens to increase the topological charge, such that the radius of the Poincaré sphere must be increased, while the standard Gaussian beam without the topological charge has vanished the orbital angular momentum. Therefore, the Poincaré spheres have a nested structure. It is worth noting the fact that the orbital angular momentum is observable and has a dimension of [ℏ] = [J ⋅ s]. The radius of the Poincaré sphere takes integer values in the unit of ℏ, and we can distinguish the spheres for states with different topological charges. Another important aspect was the nature of Bose–Einstein condensation for coherent states of photons emitted from a laser. The coherent states contain a macroscopic number of photons degenerated at the same state due to the Bose–Einstein statistics. Regardless of the macroscopic number of photons involved, we only need to consider two relevant states for the left and right vortices to consider the SU(2) states. We have both theoretically and experimentally proved that the SU(2) states could be controlled simply by manipulating amplitudes and phases for these two states, and the many-body operator for the orbital angular momentum worked properly as a generator of rotation to change the SU(2) states through the exponential mapping of the SU(2) operators. The underlying mathematical principle was the structure of Lie algebra and Lie group [3, 26, 48, 55–57, 63], and the many-body nature of photons did not impede to realize the quantum mechanical superposition state due to the Bose–Einstein statistics. Consequently, we can realize the arbitrary SU(2) states of the orbital angular momentum [6, 20, 27, 29–31, 43, 65, 71–73], similar to the polarization states [2, 9, 10, 26, 28, 29, 36–44, 48, 49, 58]. This is also consistent with the recent theoretical demonstrations that spin angular momentum and orbital angular momentum can be split into two independent observables [24, 26], such that we can safely discuss the expectation values of the orbital angular momentum at least for beams propagating in a waveguide or in vacuum under finite mode fields.
In this work, we have considered a superposition state among left and right vortices with the same topological charge to form the SU(2) states. This is a natural expectation for propagation under chiral symmetry, such as multi-mode or a few-mode fibers [9, 26, 41, 42], where refractive indices could be different for modes with different topological charges but the refractive indices for left and right vortices with the same topological charge are the same. In this case, we can control the phase and amplitudes for the SU(2) states during the propagation. On the other hand, we can also envisage considering a superposition state among beams with different topological charges in vacuum or in air, where the refractive indices are the same for modes with different topological charges. Then, we can consider a superposition state among orthogonal states with a larger number of orthogonal states. We have recently considered the SU(3) states for mixing a Gaussian beam and beams with the left and right vortices with topological charge [63, 70]. For these orthogonal modes, we can assign effective color charge, such that we can employ the theory of quantum chromodynamics (QCD) for elementary particles [3, 4, 55–57, 75–77] to explore photonic QCD [63, 70]. For the SU(3) states, Gell-Mann showed that eight generators of rotation are required to describe quarks. Similarly, we expect eight real values to characterize the SU(3) state, whose expectation values can be described on the hypersphere. We have proposed to call it a Gell-Mann hypersphere, whose rotation can be considered by a rotation in SO(8) [63]. We can extend our experimental system to explore the SU(3) states or even larger Hilbert space using the coherent states of photons.
In the present proof-of-concept (PoC)-level experiments, we admit the observed far-field images are not clear enough to allow quantitative analysis. Our experimental apparatus only has an accuracy of
In this work, we have focused on generations of various superposition states with SU(2) symmetry upon changing amplitudes and phases of coherent-twisted photons. In future, we need to establish the detection scheme, as proposed by several researchers [46]. This is very important since convenient experimental schemes are not completely well established as compared with the polarimetry for polarization states [41, 42]. In the polarimetry, Stokes parameters are easily measured using polarization beamsplitters, HWPs, QWPs, polarizers, and detectors [41, 42]. On the other hand, the corresponding tools are not widely available for the orbital angular momentum states. In the present case, we would like to measure (ℓ0, ℓ1, ℓ2, ℓ3) quantitatively, but to the best of our knowledge, we cannot quantitatively measure these parameters at least using commercially available apparatuses. It is on our agenda for future work to establish a procedure to accurately characterize these parameters.
In conclusion, we have shown that the superposition states of the left and right optical vortices are described by the coherent states with SU(2) symmetry, whose orbital angular momentum is shown on the Poincaré sphere, similar to polarization. The radius of the Poincaré sphere depends on the topological charge, such that the trajectories of states are described on the nested Poincaré spheres with the quantized radius in the unit of ℏ per photon. We have proposed a Poincaré rotator to realize arbitrary rotations of SU(2) states on the Poincaré sphere and successfully demonstrated the operations as rotators and phase-shifters, which will be useful to manipulate quantum states of macroscopically coherent photons.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
SS: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, visualization, writing–original draft, and writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by JSPS KAKENHI (Grant Number JP 18K19958).
The author would like to express his gratitude to Prof I. Tomita for continuous discussions and encouragements.
Author SS was employed by the company Hitachi, Ltd.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
3. Georgi H. Lie algebras in particle Physics: from isospin to unified theories (Frontiers in Physics). Massachusetts): Westview Press (1999).
4. Weinberg S. The quantum theory of fields: foundations, Vol. 1. Cambridge: Cambridge University Press (2005).
5. Tomonaga S. Quantum mechanics: volume I: old quantum theory. Amsterdam: North-Holland Co. (1962).
6. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185
7. v Enk SJ, Nienhuis G. Commutation rules and eigenvalues of spin and orbital angular momentum of radiation fields. J Mod Opt (1994) 41:963–77. doi:10.1080/09500349414550911
8. Barnett SM, Allen L, Cameron RP, Gilson CR, Padgett MJ, Speirits FC, et al. On the natures of the spin and orbital parts of optical angular momentum. J Opt (2016) 18:064004. doi:10.1088/2040-8978/18/6/064004
9. Yariv Y, Yeh P. Photonics: optical electronics in modern communications. Oxford): Oxford University Press (1997).
11. Grynberg G, Aspect A, Fabre C. Introduction to quantum Optics: from the semi-classical approach to quantized light. Cambridge): Cambridge University Press (2010).
12. Bliokh KY, Rodríguez-Fortuño FJ, Nori F. Spin–orbit interactions of light. Nat Photon 9 (2015) 796–808. doi:10.1038/NPHOTON.2015.201
13. Spreeuw BJC. A classical analogy of entanglement. Found Phys (1998) 28:361–74. doi:10.1023/A:1018703709245
14. Forbes A, d Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15:253–62. doi:10.1038/s41566-021-00780-4
15. Nape I, Sephton B, Ornelas P, Moodley C, Forbes A. Quantum structured light in high dimensions. APL Photon (2023) 8:051101. doi:10.1063/5.0138224
16. Ma M, Lian Y, Wang Y, Lu Z. Generation, transmission and application of orbital angular momentum in optical fiber: a review. Front Phys (2021) 9:773505. doi:10.3389/fphy.2021.773505
17. Rosen GFQ, Tamborenea PI, Kuhn T. Interplay between optical vortices and condensed matter. Rev Mod Phys (2022) 94:035003. doi:10.1103/RevModPhys.94.035003
18. Shen Y. Rays, waves, SU(2) symmetry and geometry: toolkits for structured light. J Opt (2021) 23:124004. doi:10.1088/2040-8986/ac3676
19. Shen Y, Rosales-Guzmán C. Nonseparable states of light: from quantum to classical. Laser Photon Rev (2022) 16:2100533. doi:10.1002/lpor.202100533
20. Cisowski C, Götte JB, Franke-Arnold S. Colloquium: geometric phases of light: insights from fiber bundle theory. Rev Mod Phys (2022) 94:031001. doi:10.1103/revmodphys.94.031001
21. Chen XS, Lü XF, Sun WM, Wang F, Goldman T. Spin and orbital angular momentum in gauge theories (II): QCD and nucleon spin structure. Phys Rev Lett (2008) 100:232002. doi:10.1103/PhysRevLett.100.232002
22. Ji X. Comment on Spin and orbital angular momentum in gauge theories: nucleon spin structure and multipole radiation revisited. Phys Rev Lett (2010) 104:039101. doi:10.1103/PhysRevLett.104.039101
23. Leader E, Lorcé C. The angular momentum controversy: what’s it all about and does it matter? Phys Rep (2014) 541:163–248. doi:10.1016/j.physrep.2014.02.010
24. Yang LP, Khosravi F, Jacob Z. Quantum field theory for spin operator of the photon. Phys Rev Res (2022) 4:023165. doi:10.1103/PhysRevResearch.4.023165
25. Saito S. Quantum commutation relationship for photonic orbital angular momentum. Front Phys (2023) 11:1225346. doi:10.3389/fphy.2023.1225346
26. Saito S. Spin and orbital angular momentum of coherent photons in a waveguide. Front Phys (2023) 11:1225360. doi:10.3389/fphy.2023.1225360
27. Padgett MJ, Courtial J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt Lett 24 (1999) 430–2. doi:10.1364/OL.24.000430
28. Holleczek A, Aiello A, Gabriel C, Marquardt C, Leuchs G. Classical and quantum properties of cylindrically polarized states of light. Opt Exp (2011) 19:9714–36. doi:10.1364/OE.19.009714
29. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-order Poincaré sphere, stokes parameters, and the angular momentum of light. Phys Rev Lett 107 (2011) 053601. doi:10.1103/PhysRevLett.107.053601
30. Liu Z, Liu Y, Ke Y, Liu Y, Shu W, Luo H, et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photon Res 5 (2017) 15–21. doi:10.1364/PRJ.5.000015
31. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: new quantum perspectives in high dimensions. Light Sci Appl (2018) 7:17146. doi:10.1038/lsa.2017.146
32. Shen Y, Yang X, Naidoo D, Fu X, Forbes A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica (2020) 7:820–31. doi:10.1364/OPTICA.382994
33. Shen Y, Wang Z, Fu X, Naidoo D, Forbes A. SU(2) Poincaré sphere: a generalized representation for multidimensional structured light. Phys Rev A (2020) 102:031501. doi:10.1103/PhysRevA.102.031501
34. Shen Y, Nape I, Yang X, Fu X, Gong M, Naidoo D, et al. Creation and control of high-dimensional multi-partite classically entangled light. Light Sci Appl (2021) 10:50. doi:10.1038/s41377-021-00493-x
35. He C, Shen Y, Forbes A. Towards higher-dimensional structured light. Light Sci Appl (2022) 11:205. doi:10.1038/s41377-022-00897-3
36. Poincaré JH. Théorie mathématique de la lumière. Tome (1892) 2. Available at: https://gallica.bnf.fr/ark:/12148/bpt6k5462651m (Accessed October 13, 2023).
37. Stokes GG. On the composition and resolution of streams of polarized light from different sources. Trans Cambridge Phil Soc (1851) 9:399–416. doi:10.1017/CBO9780511702266.010
38. Jones RC. A new calculus for the treatment of optical systems i. description and discussion of the calculus. J Opt Soc Am (1941) 31:488–93. doi:10.1364/JOSA.31.000488
39. Fano U. A Stokes-parameter technique for the treatment of polarization in quantum mechanics. Phy Rev (1954) 93:121–3. doi:10.1103/PhysRev.93.121
40. Born M, Wolf E. Principles of Optics. Cambridge): Cambridge University Press (1999). doi:10.1017/9781108769914
41. Gil JJ, Ossikovski R. Polarized light and the mueller matrix approach. London): CRC Press (2016). doi:10.1201/b19711
43. Naidoo D, Roux FS, Dudley A, Litvin I, Piccirillo B, Marrucci L, et al. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat Photon (2016) 10:327–32. doi:10.1038/NPHOTON.2016.37
44. Sotto M, Tomita I, Debnath K, Saito S. Polarization rotation and mode splitting in photonic crystal line-defect waveguides. Front Phys (2018) 6:85. doi:10.3389/fphy.2018.00085
45. Shen Y, Yang X, Gong M. Periodic-trajectory-controlled, coherent-state-phase-switched, and wavelength-tunable SU(2) geometric modes in a frequency-degenerate resonator. Appl Opt (2018) 32:9543–9. doi:10.1364/AO.57.009543
46. Shen Y, Fu X, Gong M. Truncated triangular diffraction lattices and orbital-angular-momentum detection of vortex SU(2) geometric modes. Opt Exp (2018) 26:25545–57. doi:10.1364/OE.26.025545
47. Saito S. Poincaré rotator for vortexed photons. Front Phys (2021) 9:646228. doi:10.3389/fphy.2021.646228
48. Saito S. Spin of photons: nature of polarisation. arXiv (2023) 2303:17112. doi:10.48550/arXiv.2303.17112
49. Saito S. Dirac equation for photons: origin of polarisation. arXiv (2023) 2303:18196. doi:10.48550/arXiv.2303.18196
50. Saito S. SU(2) symmetry of coherent photons and application to Poincaré rotator. Front Phys (2023) 11:1225419. doi:10.3389/fphy.2023.1225419
51. Saito S. Macroscopic single-qubit operation for coherent photons. arXiv (2023) 2304:00013. doi:10.48550/arXiv.2304.00013
53. Parker MA. Physics of optoelectronics. Boca Raton): Taylor and Francis (2005). doi:10.1201/9781420027716
54. Saito S. Topological polarisation states. Front Phys (2023) 11:1225462. doi:10.3389/fphy.2023.1225462
56. Hall BC. Lie groups, Lie algebras, and representations; an elementary introduction. Switzerland): Springer (2003).
59. Gori F, Guattari G, Padovani C. Bessel gauss beams. Opt Commun (1987) 64:491–5. doi:10.1016/0030-4018(87)90276-8
60. Wang W, Zhang G, Ye T, Wu Z, Bai L. Scintillation of the orbital angular momentum of a bessel Gaussian beam and its application on multi-parameter multiplexing. Opt Exp (2023) 31:4507–20. doi:10.1364/OE.478127
61. Durnin J, Jjj M, Eberly JH. Diffraction-free beams. Phys Rev Lett (1987) 58:1499–501. doi:10.1103/physrevlett.58.1499
62. Bandres MA, Gutiérrez-Vega JC. Ince-Gaussian beams. Opt Lett (2004) 29:144–6. doi:10.1364/OL.29.000144
63. Saito S. Photonic quantum chromo-dynamics. Front Phys (2023) 11:1225488. doi:10.3389/fphy.2023.1225488
64. Beijersbergen MW, Allen L, v Veen Helo , Woerdman JP. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt Commun (1993) 96:123–32. doi:10.1016/0030-4018(93)90535-D
65. Golub MA, Shimshi L, Davidson N, Friesem AA. Mode-matched phase diffractive optical element for detecting laser modes with spiral phases. Appl Opt (2007) 46:7823–8. doi:10.1364/AO.46.007823
66. Leach J, Padgett MJ, Barnett SM, Franke-Arnold S, Courtial J. Measuring the orbital angular momentum of a single photon. Phys Rev Lett (2002) 88:257901. doi:10.1103/PhysRevLett.88.257901
67. Schlederer F, Krenn M, Fickler R, Malik M, Zeilinger A. Cyclic transformation of orbital angular momentum modes. New J Phys (2016) 18:043019. doi:10.1088/1367-2630/18/4/043019
68. Huang H, Milione G, Mpj L, Xie G, Ren Y, Cao Y, et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fibre. Sci Rep (2015) 5:14931. doi:10.1038/srep14931
69. Ruffato G, Massari M, Romanato F. Multiplication and division of the orbital angular momentum of light with diffractive transformation optics. Light Sci Appl (2019) 8:113. doi:10.1038/s41377-019-0222-2
70. Saito S. Macroscopic singlet, triplet, and colour-charged states of coherent photons. arXiv (2023) 2304:01216. doi:10.48550/arXiv.2304.01216
71. Andrews DL. Symmetry and quantum features in optical vortices. Symmetry (2021) 13:1368. doi:10.3390/sym.13081368
72. Angelsky OV, Bekshaev AY, Dragan GS, Maksimyak PP, Zenkova CY, Zheng J. Structured light control and diagnostics using optical crystals. Front Phys (2021) 9:715045. doi:10.3389/fphy.2021.715045
73. Agarwal GS. SU(2) structure of the poincaré sphere for light beams with orbital angular momentum. J Opt Soc A A (1999) 16:2914–6. doi:10.1364/JOSAA.16.002914
74. Saito S. Special theory of relativity for a graded index fibre. Front Phys (2023) 11:1225387. doi:10.3389/fphy.2023.1225387
75. Gell-Mann M. The eightfold way: a theory of strong interaction symmetry. Murray Gell-Mann(Caltech) (1961). doi:10.2172/4008239
76. Gell-Mann M. A schematic model of baryons and mesons. Phys Lett (1964) 8:214–5. doi:10.1016/S0031-9163(64)92001-3
77. Ne’eman Y. Derivation of strong interactions from a gauge invariance. Nuc Phys (1961) 26:222–9. doi:10.1016/0029-5582(61)90134-1
Keywords: orbital angular momentum, special unitary group of degree 2, Lie algebra, optical vortex, ladder operator, Laguerre–Gaussian mode, coherent state
Citation: Saito S (2023) Nested SU(2) symmetry of photonic orbital angular momentum. Front. Phys. 11:1289062. doi: 10.3389/fphy.2023.1289062
Received: 05 September 2023; Accepted: 06 October 2023;
Published: 19 October 2023.
Edited by:
Yuxuan Ren, Fudan University, ChinaReviewed by:
Huapeng Ye, South China Normal University, ChinaCopyright © 2023 Saito. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shinichi Saito, c2hpbmljaGkuc2FpdG8ucXRAaGl0YWNoaS5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.