- Department of Physics, University of Helsinki, Helsinki, Finland
We draw insight into the neutron star structure and characteristics from the neutron structure. The eigenvectors of the special unitary group, SU(3), describing baryons, imply that neutron quarks reside on three faces of a tetrahedron. The tetrahedral structure accounts for the neutron magnetic moment and mass. Thus, we reason that neutrons precipitate with aligned magnetic moments into the triakis truncated tetrahedron tessellation under immense gravitational pressure. As the particle’s tetrahedral symmetry does not match the crystal’s rhombic symmetry, the total magnetic moment invariably misaligns with the star’s spinning axis. We infer further from the neutron structure that with increasing gravitational pressure, two neutrons condense into the same tetrahedron. Due to doubling density, the contracting star spins up abruptly but then settles down slowly as the gradients in density smoothen. As down quarks are positioned for pairwise fusions into anti-up quarks in the dineutron, we reason that tetraquark indeed forms as gravitational pressure increases further. The star balances the accompanying loss of mass by spinning down suddenly but recovers as the gradients in density smoothen again. Ultimately, when gravitational pressure increases even more, the anti-up quarks will annihilate with up quarks. As the core becomes ever more structured, such high-energy events fade out, and eventually, only magnetic field-collimated radio-frequency dissipation drives the spin down. The nuclear moments manifest fully in a magnetar, free from floating, hence counteraligning baryonic matter. In conclusion, the neutron structure makes sense of the neutron star density, magnetism, beams at an angle to the spinning axis, and pulsing transients, and paves the way for making sense of reactions in a black hole.
1 Introduction
The idea of deriving macroscopic characteristics from microscopic properties is ingrained in physics. In this vein, the discovery of the neutron laid the foundation for the whole discipline of neutron star astrophysics [1,2]. Ideally, the neutron structure explains neutron star properties and phenomena, most notably steady spinning, oblique bipolar beaming, massive magnetism, and transients. But in practice, reductionist reasoning ultimately fails by facing features that cannot be reduced to the presumed parts.
Undoubtedly, the neutron star is more than neutrons. Nonetheless, we are motivated by the bottom-up approach because once the role of the principal component, the neutron, is played out fully, other elements profile more sharply. However, rather than attempting to exhaust the reductionist line of thought, the study exemplifies how the key characteristics of compact stars can be comprehended from the characteristic constituent. Ultimately, the results elude what happens to neutrons in black holes [3].
We start off with the neutron structure to determine how neutrons pack into an orderly array under extreme gravity, which is similar to how the atom size and shape specify crystal packing. Then, we reason from the neutron structure how increasing gravitational pressure causes changes in the neutron lattice that, in turn, alter inertia, affecting the spinning rate. Specifically, sudden spin-up glitches, more common among young than old pulsars, indicate avalanche gains in density as the neutrons pack even tighter. On the other hand, spin-down glitches disclose reorganization in response to reactions decreasing density.
This view of the compact star as a giant nucleus, n ∼ 1057, of a radius, r ∼ 10 km, evolving through restructuring transients toward a solid stationary state, was presented a long ago [4]. However, it was soon superseded by the superfluid model, but perhaps prematurely. After all, the neutron star superfluid model was not derived from the first principles. Instead, it was adopted from the theory of superfluidity, offering phenomena, most notably vortices, to account for the neutron star cooling and glitches [5–7]. Our critical stance toward superfluid stellar core does not discredit that spin-1/2 particles 3He and 1n obey the same quantum statistics of the Pauli exclusion principle, but still, neutrons precipitating into a lattice under high pressure is not out of the question, as helium-3 crystallization demonstrates.
Although quantum fluctuations do favor fluid, motions do damp down in a dense gravitational field where mass is effectively higher. Likewise, although the Pauli exclusion principle does put spin-1/2 particles antiparallel in a gas, in a dense lattice, the net electromagnetic field can no longer be reconstructed from neutron fields but from those of quarks because the quarks of one neutron are as close to each other as they are to the quarks of a neighboring neutron. Indeed, the delicate balance between repulsion and attraction is a subject of speculation, for example, when cooking up nuclear pasta [8–11]. Moreover, the dense lattice, comprising essentially quarks rather than distinct neutrons, may hold heat better than thought [12–14]. Furthermore, the supernova remnant, cooling rapidly by transforming protons and electrons through the Urca process into precipitating neutrons and escaping neutrinos [15], does not exclude neutrons from ending up in an orderly array deep down in the core. Thus, we fail to recognize any absolute fact that would prevent a massive star from collapsing and condensing into a neutron lattice rather than invariably ending up in a superfluid state.
Accordingly, by reductionist logic, we reason that neutron star massive magnetism amasses from an array of neutron magnetic moments, similar to the magnetism of solids emerging from the exchange interaction between neighboring electron spins [16,17]. In this view, a magnetar presents the purest case of a bare core, which is free from counteracting moments floating on the stellar surface. Then, the back-of-an-enveloped calculation,
As the strong force can stand up against the enormous magnetic field that μn presents on the neutron itself, we extrapolate that only its defeat by gravity leads to the neutron star core collapse and concomitant magnetic field decline. Thus, we take the neutron breakdown as the characteristic of an active black hole [3].
We find it noteworthy that the neutron lattice naturally explains the persistent misalignment between the field axis and the spinning axis. It follows from the symmetry mismatch between the neutron structure and the neutron lattice structure. So, we find no need for the ad hoc idea that there is a crust of perfectly conducting plasma for freezing the flux. Moreover, when maintaining those charged particles in the inner crust embody neutron star magnetism [19,20], it is not obvious to us how electrons would escape the capture already at the surface where protons transform into neutrons in thermonuclear reactions. Expressly, despite absorption edges and cyclotron resonant scattering in X-ray spectra do imply a stellar surface heavier than hydrogen and helium, thermonuclear bursts through the proton–proton chain, in turn, suggest us that charged particles may not last forever on the surfaces of accretion-powered pulsars, let alone in the depths, and certainly not for stars without a companion [21].
Furthermore, it is not crystal clear how the superfluid maintains super-steady spinning and magnetic field-line misalignment over eons. For example, vortices ought to damp down periodic and correlated variations in the pulse shape and the slow-down rate of precessing pulsars [22–24]. It is problematic to reconcile vortex pinning with precession [25]. All in all, we wonder how things add up when vortices are employed for magnetic flux freezing as well as for pinning and unpinning angular momentum transfer between crust and core to account for spin-up and spin-down glitches. Also, the magnetic field strength disparity between magnetars and pulsars presents its own challenge for scenarios amplifying the magnetic field during the post-explosion stellar collapse.
Of course, our questioning as such is not refuting anything. In fact, multi-parameter models are hard to rule out even with multi-messenger astronomy [26]. Still, their explanatory power can be contested and contrasted by accounting as much as possible with as little as possible.
In this sense of reductionist reasoning, we remark that the state of a neutron star rests on the strength of the neutron’s valence quark structure, just as a crystalline state counts on the strength of the atomic valence structure. Explicitly, when gravity outstrips strong force at the critical pressure, pc = ρcc2, corresponding to the critical mass density, ρc, neutrons, in numbers n, making mass, M = ρV, dissolve into light quanta, by mass–energy equivalence. Beyond this breakdown point, T ∼ 1013 K, by the state equation, E = Mc2 = pcV = nkBT, the star is no longer a neutron star but has become an active black hole.
The reductionist reasoning from the well-defined neutron structure onward reproduces the early ideas of the neutron star with a crystalline core and fluid surface. Conversely, the contemporary modeling of the neutron without a well-defined form projects the prevailing images of the neutron star with a superfluid core and solid crust. However, the disparity is more profound than pitting one model against another. Namely, rather than modeling outcomes of high-energy physics experiments with exotic matter, the neutron structure is anchored in the age-old atomism [27]. It posits that all phenomena, irrespective of their complexity, can ultimately be comprehended as the rearrangements of the fundamental universal constituents. Today, this many-body theory is recognized as statistical physics that underlies thermodynamics [28]. Building upon this atomistic axiom, we first develop the neutron structure, then deduce forms of dense packing, and then relate the lattice structures and their changes to the characteristics of neutron stars.
2 Core particles
Toward the end of the 18th century, the existence of atoms was inferred from observing that compounds react in fixed proportions. Similarly, during the 20th century, the presence of quarks became apparent from noticing that particles react in distinct ratios, generally conserving electric charge, lepton number, and baryon number [29,30].
However, quarks, electrons, or other seemingly point-like particles cannot be truly elementary because matter and antimatter annihilate into photons. As a matter of fact, the name for the light quantum, “photon,” was derived from the Greek word “ph
As the basic building block, the photon, propagating at the speed of light, is inherently a relativistic notion. Thus, it is not surprising that the tenet makes sense of astronomical observations and measurements of microscopic constituents, by and large, in agreement with general relativity and quantum mechanics [32–36]. Whereas two photons seem far too few to constitute, for example, an electron and a positron, many more do emerge from these particles of opposite chirality but as pairs where the photons are paired up with opposite phases, hence transparent [3,37,38]. Similarly, detecting all photons from baryon breakdown may be hard, but inferring baryon composition is certainly possible as follows.
Reactions, such as electron capture, balancing the fractional charges of quarks, and electron–positron annihilation yielding at times also quarks, weak bosons, and mesons, imply that elementary particles share common ingredients. Moreover, the electron’s physical properties, most notably charge and magnetic moment, suggest the internal structure, in conflict with the common belief that an electron would be a point-like particle based on experimental evidence. However, the measurements at accessible energies could only have revealed constituents if they were weakly bound, not if they were strongly bound [39].
Thus, Ampère [40], Parson [41], and Compton [42,43] may not be all outdated with the idea that the electron is a closed helical coil to explain its charge and magnetic moment. Also, geometric analyses of solutions to the Dirac equation suggests that motion, known as Zitterbewegung, arises from quanta in circulation along a helical coil in line with the SU(2) symmetry [44–46]. But first, the fine structure constant, α = e2Zo/4πℏ ≈ 1/137.036, details the electron structure by relating the electron action, e2Zo/4π, to the neutrino action, ℏ = h/2π [3,37,47]. Geometrically speaking, the neutrino action is the photon, h, in the form of an elementary loop, ℏ. In turn, the electron action is a string of photons forming a helical torus with n loops.
This understanding of particles as geodesics composed of light quanta aligns with theory [48] and measurements [49]. The particle’s chirality, representing its charge, gives rise to the electric field. In turn, the particle’s helicity induces vortices, that is, the magnetic field around the particle [46,50]. Last, the particle’s geodesic curvature causes surrounding space to curve, that is, the gravitational field around the particle, which is curved space-time in terms of general relativity.
First, we work out the Ampère electron in terms of photons. The length of a torus,
Second, we identify the fractional charge of the down quark to the 1/3-arc of the electron and the fractional charge of the up quark to the 2/3-arc of the positron.
Third, we reason from the SU(3) symmetry that when on three faces of a tetrahedron, three quarks, as toroidal arcs, can only link through gluons, that is, short wavelength photons, into a closed structure. Then, the helical coil continues seamlessly from one quark to the other.
These Ampèrian coils of photons agree well with measurements of charges, magnetic moments, and masses, most notably, of particles comprising the first-generation constituents [3,37,47,51]. Moreover, in place of color charge, the sense circulation distinguishes one quark from the other and hence also one gluon from the other. By the same reasoning, rather than requiring a net neutral color, the circulation by closing onto itself renders the particle stable.
2.1 Neutron
The neutron structure can be visualized as a string of photons comprising three helical quarks that gluons as short wavelets connect from one tetrahedron face to another (Figure 1). This geometry determines the neutron properties.
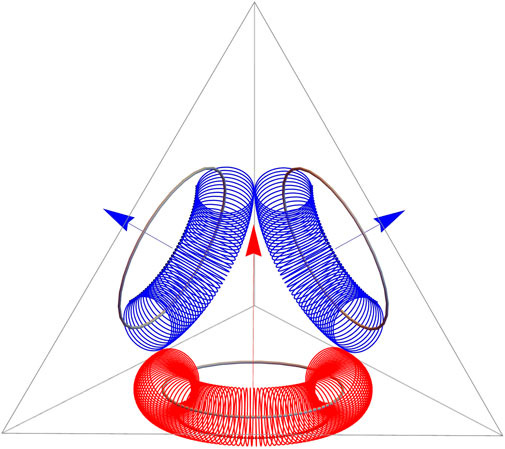
FIGURE 1. Neutron (udd) model as a string of quanta. The up quark (red torus arc) comprising 92 quanta is a 2/3 arc of the full torus, the positron, comprising 138 quanta. Accordingly, each of the two down quarks (blue torus arcs) comprising 46 quanta is a 1/3 arc of the full torus of opposite handedness, the electron. The quarks cannot but coordinate on the faces of a tetrahedron when gluons connect them into a closed circulation. Gluons are short-wavelength photons crossing from the end of one quark to the beginning of another. The neutron is a signed geodesic, that is, a least-action path with a sense of circulation. The total magnetic moment sums up from the up-quark component of circulation (red arrow) and the two down-quark components of circulation (blue arrows) (Illustration by Mathematica).
The neutron charge totals zero with an equal number of right-handed windings, 92, of the up quark and left-handed windings, 46 + 46 = 92, of two down quarks.
Similar to the magnetic moment produced by an electric current flowing along a loop of wire, the neutron magnetic moment, μn = 1/2∫r × ρvdV, integrates the density, ρ, moving with velocity, v, along the closed path, γ, of 187 = 92 + 1 + 46 + 1 + 46 + 1 photons. In the tetrahedral framework, the resultant moment points from the up quark face to the edge between the down quarks.
In line with general relativity, mass measures the curvature. It is proportional to the Euler characteristic, 2πχ = ∫kgdγ, where the geodesic curvature, kg = n ⋅ (γ′ × γ″)/|γ′|3, is the projection of the path, γ, onto the vacuum, that is, the universal surroundings defined by the normal, n, [52,53]. In simpler terms, mn can be computed from the projections of the 184 loop quanta comprising the quarks because the gluons, as straight as the photons in the surrounding vacuum, do not contribute. In that aggregate, the central half of the up quark, from quantum 24 to quantum 68, contributes the most, whereas the side segments contribute very little, only 1/3 electron mass, because the first 1–23 and last 69–92 quanta are pairwise almost antiparallel, that is, apart from the helical pitch [54]. For the same reason, the neutron (udd) and proton (uud) masses are very similar despite their differing quark content.
2.2 Dineutron
The baryon tetrahedron unit cell can accommodate two neutrons in the form of dineutron [55,56], with 2-fold rotational symmetry, C2 (Figure 2). Thus, the dineutron mass density and magnetic density are double those of the neutron. The dineutron magnetic moment points along the edge-to-edge tetrahedron diagonal.
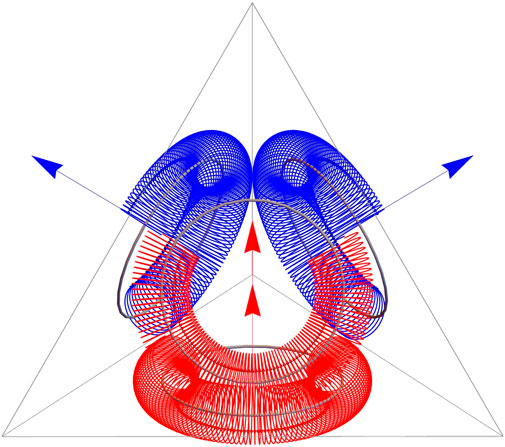
FIGURE 2. Dineutron (udd udd) model as two strings of quanta in the doubly dense C2 configuration. The total magnetic moment along the tetrahedral diagonal sums up from the two up-quark (red torus arcs) components (red arrows) and the four down-quark (blue torus arcs) components (blue arrows) (Illustration by Mathematica).
2.3 Tetraquark
The dineutron (udd udd) structure suggests that the two down quarks on the same face fuse pairwise, 2dd → 2ū + 2 g, into two anti-up quarks, (ū), so that the two gluons (g) excise out, rendering the reaction irreversible (Figure 3). For this to happen, gravity must be already closing in on strong force.
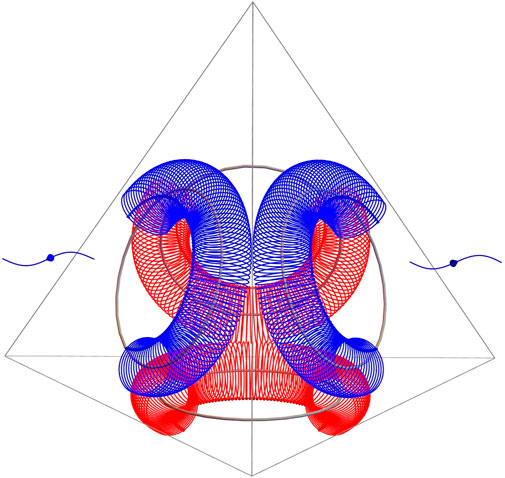
FIGURE 3. Tetraquark (uūuū) model as a string of quanta. Under high pressure, the consecutive down quarks have fused pairwise into anti-up quark, ū (fused blue torus arcs), excising out two gluons (blue wavelets). The two up quarks (red torus arcs) remain intact (Illustration by Mathematica).
To a first approximation, the mass of the tetraquark, mq, is 2/3 of the dineutron mass, 2mn. The geodesic curvature decreases from the dineutron because in the tetraquark, only half of each anti-up quark, just as half of each up quark, contributes to the overall mass, namely, the first 1–23 and last 69–92 loops have minimal impact, only 1/3 of the electron mass, because the loop normals are pairwise antiparallel, apart from the slight tilt due to the helical rise.
Like the dineutron magnetic moment, the tetraquark moment is along the tetrahedron’s edge-to-edge diagonal.
3 Core structures
Neutrons (udd), dineutrons (udd udd), and tetraquarks (uūuū) occupying the same volume but having different masses suggest that these particles, layered by density, form a lattice in the neutron star core. Accordingly, increasing gravitational pressure drives transformations from one neutronic particle into another, causing density changes displayed as transients in the pulsar period.
3.1 Neutron lattice
We take nuclear matter saturation density ρo = mnno ≈ 2.5 ⋅ 1017 kg/m3 as the reference because at ρn = ρo, neutrons are definitely stable. The baryon tetrahedral symmetry with vertices free from arcs of quarks suggests that neutrons pack into the space-filling triakis truncated tetrahedron honeycomb (Figure 4). The minimal lattice block comprises the truncated tetrahedron, that is, the neutron, and a small tetrahedron, that is, space. Two blocks face-to-face make the unit cell.
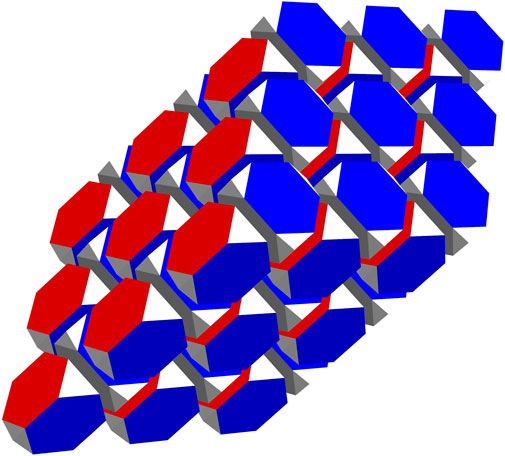
FIGURE 4. Exploded view of triakis truncated tetrahedron honeycomb. Each truncated tetrahedron houses a neutron so that red faces mark up quarks and blue ones down quarks. Regions in white indicate space. In addition to this orderly array, other configurations are also conceivable (Illustration by Mathematica).
Unlike common atomic and molecular crystals, where particle fluctuations are small compared to the distances between them, fluctuations in the neutron lattice are not negligible because the neutron mass is small. Nevertheless, the crystal is stable because the apparent mass is higher in a dense gravitation field, damping down fluctuations.
Moreover, in the bitruncated alternated cubic honeycomb, the electromagnetic field cannot be partitioned among individual neutrons because the quarks of one neutron are as close to each other as they are to the quarks of another adjacent neutron. Therefore, unlike in an ideal Fermi gas of non-interacting fermions, the Pauli exclusion principle does not necessarily apply and align the neutrons antiparallel in the neutron lattice. In any case, the net nuclear moment must be considered because a symmetrical spin configuration is favored over an arbitrary one [16,57,58]. In fact, parallel moments may produce the least vorticity inside the lattice while expelling a huge moment outside.
Importantly, no configuration is without a net magnetic moment because the particle’s tetrahedral symmetry does not align with the crystal’s rhombic symmetry. Consequently, the total magnetic moment misaligns with the neutron star spinning axis, presumably parallel to a normal lattice.
3.2 Dineutron lattice
As gravitational pressure, p = ρc2, approaches ρd = 2ρn, where the dineutron forms, the neutron lattice becomes unstable. The instability manifests as increased irregularities in the spinning, that is, timing noise [59]. Indeed, toggling between neutron and dineutron packing could account for quick switching between discrete states, usually two [60]: the faster on-state corresponding to denser dineutron domains of larger magnetic moment (Figure 5) and the slower off-state corresponding to sparser neutron domains of smaller moment.
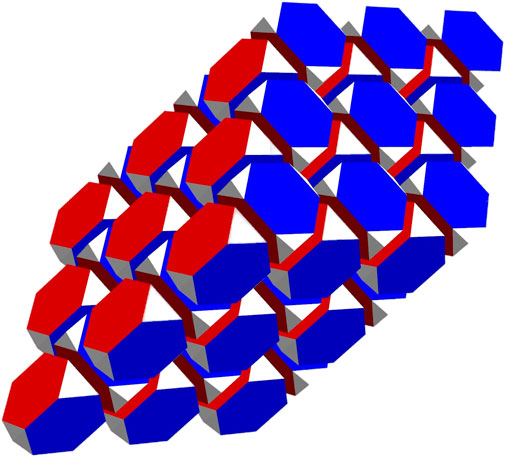
FIGURE 5. Exploded view of triakis truncated tetrahedron honeycomb. Each truncated tetrahedron houses two neutrons. Red faces mark up quarks and blue ones down quarks. Regions in white indicate space (Illustration by Mathematica).
Similarly, the correlation between the timing noise and pulse shape as well as between nulling and mode-switching [61] signals that the magnetic field stems from the core rather than from the crust of postulated plasma. Switching between voluminous neutron and dineutron domains would cause major but recurrent reorientation of the magnetic moment, explaining intermittent pulsars [62].
As the doubling of density catalyzes the dineutron formation, the chain reaction overshoots the point of balance by transforming neutrons for dineutrons faster than the sparser surroundings replenishing them, and as the core contracts, the star spins up suddenly to balance the plummeting matter. It is in the nature of a chain reaction to trigger sharply and shoot above the threshold that may account for minimum glitch size [63]. The immediate disorder displays itself as diminished intensity or even missing pulses. Because motion changes its driving forces, the avalanche is intrinsically non-deterministic, yet the motion follows a power–law pattern [64,65]. Therefore, although glitches occur unpredictably, waiting times follow power law [66–68].
The star settles to spin steadily through subsequent sorting and shuffling of neutrons and dineutrons. This relaxation reestablishing a stationary density gradient proceeds along a power law, in line with attaining balance in the least time [64,65]. Although the size and waiting time distributions of glitches across a range of pulsars are scale-invariant [69], as expected for avalanche processes [70], we emphasize that power laws characterize natural processes universally, not just glitches but, for example, spectra of isolated neutron stars [71]. Hence, we acknowledge that scale-invariance as such does not speak for quakes in a quantum solid over quavers in a superfluid. Eventually, the core crystal is distinguished from the stellar fluid by other arguments [72].
As the neutron star core evolves under immense gravity into a denser and more orderly lattice, spin-up glitches become less frequent and smaller. Consistently, the degree of recovery depends inversely on the characteristic age [59,67]. Glitch after glitch, the magnetic moment grows as the crystallinity grows, boosting magnetic braking. In fact, the spin-down rate increases with glitching in a scale-free manner [73,74]. Eventually, the initial mass is big enough to yield a star entirely free from floating particles. Then nothing shields the magnetism from playing out fully, manifesting as magnetars [75]. Conversely, the magnetic field weakens significantly, for example, due to diamagnetic screening, only when the neutron star acquires material from a companion [76,77]. Also, a bumpy spin-down would point to a solid oblate body in rotation rather than a fluid core [78].
3.3 Tetraquark lattice
Ultimately, gravity rivals strong force. As the energy difference between gluons linking quarks and gluons connecting to the quanta of the surrounding gravitational field narrows, dineutron transformations begin through the pairwise fusion of down quarks into uūuū tetraquarks (Figure 3). To first approximation, the lattice structure remains the same (Figure 5), but density decreases due to tetraquark mass, mq ≈ 2/3 2mn. Thus, the star spins down suddenly. However, inferences about decreasing density may not be quite that straightforward because the high-energy conditions might favor, to some extent, the second-generation massive c and c̄ quarks over the first-generation u and ū.
As the fusion of down quarks is irreversible, as much as the gluons are lost in space, the core is in for rearranging to regain a steady density gradient. The star spins up slowly as tetraquarks settle between the dineutron and neutron domains.
Such an emissive glitch scenario accompanied by major structural changes complies with magnetar radiative changes, short and bright X-ray bursts [75], as well as with pulsars bursting X-rays while shutting off radio emission [79,80]. Core reactions could also make sense of anomalous X-ray pulsars, whose characteristics are not easily explained by accretion from a companion or injection of rotational energy in the pulsar wind/magnetosphere [81].
Subsequent shuffling of tetraquarks, dineutrons, and neutrons in the least time displays a power–law course toward steady spinning [82,83], however, never quite attaining the pre-glitch period. Recovery is incomplete because matter is lost. The star spins down one fusion after another until it becomes a solid, orderly block. When matter has become inert, the field is the sole source of dissipation by magnetic braking.
Although the glitch activity correlates with the change in the spin-down rate for all pulsars, the distribution of glitch activity is bimodal, suggesting that there are two distinct but concurrent mechanisms [74], possibly the neutron–dineutron and dineutron–tetraquark transformations, or eventually breakdown of particles with voluminous consequences. Indeed, the avalanche collapse of neutron lattice into dineutron lattice could surpass the balance point, yielding tetraquark domains, if not flattening particles all the way down to quark matter. Consistently with scale-free thinking [65], the least-structured youngest pulsars, loaded with free energy, are predisposed to take the largest leaps toward stationary states. Conversely, the least-dissipative pulsars, scant with free energy, spin down slowly.
3.4 Breakdown
Eventually, gravity outrivals strong force. When gluons cut loose, the neutronic particles open up and lattice collapses. This scenario resembles nucleons merging and undergoing a transition to quark matter [84–86]. When ending up face-to-face, quarks (u) and anti-quarks (ū) annihilate, just as electrons and positrons annihilate. As the stellar core flattens, gravity gives in most along the spinning axis [3,87,88]. As the magnetic moment is also largely lost, the star jets high-energy photons and particles and antiparticles from its poles—the black hole is active.
The critical pressure of breakdown, corresponding to the critical density, can be worked from the ratio of the electrostatic and gravitational potential,
given in terms of the electron mass, me, charge, e, and vacuum permittivity, ɛo. Inserting the fine structure constant, α ≈ 1/137.036, gives the strong force to gravity ratio, 1/αG ≈ 5.71 ⋅ 1044. Thus, the critical mass density, ρc, corresponding to the breakdown, is 1/αG times higher than the average mass density of the universe, ρM = 1/4πGt2 ≈ 0.6 ⋅ 10–26 kg/m3 [89], that derives from the mass–energy equivalence, Mc2 = GM2/R, between all mass, M, and its gravitational potential [90,91], for the universe of radius, R = ct, and age of t ≈ 13.8 billion years. Thus, matter breaks when the pressure of gravity corresponds to ρc = ρM/αG ≈ 3.3 ⋅ 1018 kg/m3.
As the ratio of strong force to gravity yields an order of magnitude ρc larger than the Tolman–Oppenheimer–Volkov limit or the nuclear saturation density, ρo [92], there should be stars in the range from ρd ≈ 5.0 ⋅ 1017 kg/m3 to ρc ≈ 3.3 ⋅ 1018 kg/m3 that are massive, M, enough to be black, c2 < 4πGρr2 = GM/r, but sparse, ρ, enough not to collapse [93,94]. From this perspective, dormant stellar black holes are, in fact, compact stars with inner shells of neutron, tetraquark, and dineutron lattices.
This overarching conclusion might appear confounding, but in the end, both neutron stars and stellar black holes are explosion remnants of massive stars. Apart from the speed limit of light, the division between them is theoretical—an incommensurate split between physical substance and mathematical singularity.
Consistent with the idea that black holes are stars among stars, gamma rays burst from mergers of stellar black holes and neutron stars [95–97] only when a critical density threshold is surpassed. Fast radio bursts from the black hole and neutron star collisions [98] suggest the same.
4 Discussion
Since the turn of the millennium, ground-based and space-based observatories have yielded a more coherent and comprehensive view of neutron stars in the broader cosmic context. The strength of matter under extreme gravity is now known better after capturing gravitational waves from mergers concurrent with gamma ray bursts as well as through studies of magnetars, including soft gamma ray repeaters and anomalous X-ray pulsars, neutron stars in X-ray binaries, and millisecond pulsars [99,100]. Glitch activity correlating with the changes in the spin-down rate, glitching correlating with timing noise, and glitch size correlating with recurrence time, all in a power–law manner [63,101], and all correlating with the pulsar age, suggest a universal principle—evolution toward a state of balance in the least time. Moreover, glitches preceding or accompanying X-ray and gamma ray bursts or flares suggest changes in the elemental matter rather than in the neutron superfluid vorticity. Also, glitches correlating with changes in the beam profile, eventually due to wobbling or even nulling, point to magnetism originating from a structured core rather than a superconducting crust.
Whereas observations are converging to the neutron star with a crystalline core, theoretical models are dispersing. The superfluid model with vortex pinning and unpinning is extended with parameters for vortex density, motion, and stress buildup to account for the glitch data [102–104]. Global oscillation modes within the star’s crust are introduced to deal with observed X-rays and gamma rays. Moreover, magnetospheric models are developed to explain particle acceleration and coherent radio beams. Also, scenarios for nuclear matter transforming into quark matter are elaborated, for example, including hyperons [105], deconfined quark matter with color superconductivity that just might be tested against masses and radii as well as cooling of neutron stars [86,106,107].
Clearly, neutron star astrophysics has advanced far from the early stages of theorizing neutron stars as gigantic atoms or crystals of neutrons. Whereas such bodies were seen as too homogeneous in their properties to account for the richness of episodes in spinning and emission, the superfluid core and superconducting crust have ever since supplied a wealth of ingredients to make up various phenomena [103,108,109]. In turn, exotic particles produced at accelerators have offered ideas, albeit controversial, about matter under extreme gravity [14,110,111]. Still, when data are scant as they are from neutron stars, effective theories, however fitting models they might be, are too malleable to falsify. Therefore, we took a different approach, to explain as much as possible with as little as possible by deducing the neutron star properties and phenomena from the neutron. Accordingly, our Achilles’ heel, vulnerable to the arrow of falsification, is the premise that everything comprises photons [31,38].
As explained, the neutron star density and magnetism can be understood to result from neutrons condensing with orderly moments into a lattice aligned with the spinning axis but invariably with a misaligned magnetic field. Likewise, spin-down evolution, interrupted by glitches, magnetic field reconfiguration, and outbursts of X-rays and gamma rays, can be understood to manifest further condensing through abrupt chain reactions into dineutron and tetraquark lattices. In essence, the greater the initial mass, the denser the neutron lattice and the stronger the magnetic field.
This comprehension emerging from the neutron structure is sparse with ingredients compared with the superfluid model. Admittedly, the stellar fluid with vortices could account for glitches by pinning and unpinning to the highly conductive crust that, in turn, could account for the magnetic field and its misalignment with the spinning axis by flux freezing. But already at the onset, the low-temperature superfluidity and superconductivity seem rather remote to ascribe to the bodies among the hottest in the universe. Moreover, it is not obvious how superfluid core and superconductive crust display themselves in the spectrum from millisecond pulsars to massive magnetars [112]. A superfluid star would also remain detached from the sequence of stars, whereas the neutron, proton, electron, and neutrino structures explain how nuclear reactions in the main sequence produce neutrons, how neutrons eventually collapse under even stronger pressure, and how quarks annihilate in black holes [3]. In this manner, the comprehensive theory explains not just the neutron star from the neutron but much more by connecting seemingly isolated phenomena [113].
Of course, one may opine that the behavior of neutrons under extreme gravity is as uncertain as the behavior of superfluids [102,114] or the forms of exotic matter emerging from quantum chromodynamics [115,116]. However, as outlined here, when it comes to critical densities, maximum mass, maximum magnetic field, and glitches up or down, they all hinge only on the neutron. When data are limited, as they are from neutron stars, the theory with less is more.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
AA: writing–original draft, review, and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Baade W, Zwicky F. Remarks on super-novae and cosmic rays. Phys Rev (1934) 46:76–7. doi:10.1103/physrev.46.76.2
2. Yakovlev DG, Haensel P, Baym G, Pethick C. Lev Landau and the concept of neutron stars. Physics-Uspekhi (2013) 56:289–95. doi:10.3367/ufne.0183.201303f.0307
3. Lehmonen L, Annila A. Baryon breakdown in black hole. Front Phys (2022) 10:954439. doi:10.3389/fphy.2022.954439
4. Baym G, Pethick C. Neutron stars. Annu Rev Nucl Sci (1975) 25:27–77. doi:10.1146/annurev.ns.25.120175.000331
5. Migdal A. Superfluidity and the moments of inertia of nuclei. Nucl Phys (1959) 13:655–74. doi:10.1016/0029-5582(59)90264-0
6. Ginzburg VL, Kirzhnits DA. Zh. Eksperim. i Theor. Fiz (1964) 47:2006, translated in Sov. Phys. JETP. (1965) 20:1346.
7. Pines D, Shaham J. Microquakes and macroquakes in neutron stars. Nat Phys Sci (1972) 235:43–9. doi:10.1038/physci235043a0
8. Ravenhall D, Pethick C, Wilson J. Structure of matter below nuclear saturation density. Phys Rev Lett (1983) 50:2066–9. doi:10.1103/physrevlett.50.2066
9. Hashimoto M-a., Seki H, Yamada M. Shape of nuclei in the crust of neutron star. Prog Theor Phys (1984) 71:320–6. doi:10.1143/ptp.71.320
10. Pons JA, Viganò D, Rea N. A highly resistive layer within the crust of X-ray pulsars limits their spin periods. Nat Phys (2013) 9:431–4. doi:10.1038/nphys2640
11. Caplan ME, Schneider A, Horowitz CJ. Elasticity of nuclear pasta. Phys Rev Lett (2018) 121:132701. doi:10.1103/physrevlett.121.132701
12. Pines D, Shaham J, Ruderman M. Neutron star structure from pulsar observations. In: C Hansen, and IA Union, editors. Physics of dense matter. D. Reidel Publishing Company (1974). p. 189.
13. Tsuruta S. Cooling of dense stars. In: C Hansen, and IA Union, editors. Physics of dense matter. D. Reidel Publishing Company (1974). p. 209.
14. Page D, Reddy S. Dense matter in compact stars: theoretical developments and observational constraints. Annu Rev Nucl Part Sci (2006) 56:327–74. doi:10.1146/annurev.nucl.56.080805.140600
15. Haensel P. Urca processes in dense matter and neutron star cooling. Space Sci Rev (1995) 74:427–36. doi:10.1007/bf00751429
16. Weis J-J, Levesque D. Ferroelectric phases of dipolar hard spheres. Phys Rev E (1993) 48:3728–40. doi:10.1103/physreve.48.3728
17. Kondratyev V. Statistics of magnetic noise in neutron star crusts. Phys Rev Lett (2002) 88:221101. doi:10.1103/physrevlett.88.221101
18. Horowitz C, Piekarewicz J, Reed B. Insights into nuclear saturation density from parity-violating electron scattering. Phys Rev C (2020) 102:044321. doi:10.1103/physrevc.102.044321
19. Anderson P, Itoh N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature (1975) 256:25–7. doi:10.1038/256025a0
20. Chamel N, Haensel P. Physics of neutron star crusts. Living Rev relativity (2008) 11:10–182. doi:10.12942/lrr-2008-10
21. Van Paradijs J, Taam R, Van den Heuvel E. On the nature of the ’anomalous’ 6-s X-ray pulsars. Astron Astrophysics (1995) 299:L41.
22. Shaham J. Free precession of neutron stars-role of possible vortex pinning. Astrophysical J (1977) 214:251–60. doi:10.1086/155249
23. Sedrakian A, Wasserman I, Cordes JM. Precession of isolated neutron stars. I. effects of imperfect pinning. Astrophysical J (1999) 524:341–60. doi:10.1086/307777
24. Stairs I, Lyne A, Shemar S. Evidence for free precession in a pulsar. Nature (2000) 406:484–6. doi:10.1038/35020010
25. Link B. Precession as a probe of the neutron star interior. Astrophysics Space Sci (2007) 308:435–41. doi:10.1007/s10509-007-9315-0
26. Blaschke D, Cierniak M. Studying the onset of deconfinement with multi-messenger astronomy of neutron stars. Astronomische Nachrichten (2021) 342:227–33. doi:10.1002/asna.202113909
27. Berryman S. Ancient atomism. In: EN Zalta, and U Nodelman, editors. The stanford encyclopedia of philosophy. Winter: Metaphysics Research Lab, Stanford University (2022).
28. Renn J. Einstein’s controversy with drude and the origin of statistical mechanics: A new glimpse from the “love letters”. Archive Hist exact Sci (1997) 51:315–54. doi:10.1007/bf00518232
29. Nambu Y. An empirical mass spectrum of elementary particles. Prog Theor Phys (1952) 7:595–6. doi:10.1143/ptp.7.5.595
30. Primakoff H, Rosen SP. Baryon number and lepton number conservation laws. Annu Rev Nucl Part Sci (1981) 31:145–92. doi:10.1146/annurev.ns.31.120181.001045
32. Tuisku P, Pernu TK, Annila A. In the light of time. Proc R Soc A: Math Phys Eng Sci (2009) 465:1173–98. doi:10.1098/rspa.2008.0494
33. Annila A. Least-time paths of light. Monthly Notices R Astronomical Soc (2011) 416:2944–8. doi:10.1111/j.1365-2966.2011.19242.x
34. Koskela M, Annila A. Least-action perihelion precession. Monthly Notices R Astronomical Soc (2011) 417:1742–6. doi:10.1111/j.1365-2966.2011.19364.x
35. Annila A. Probing mach’s principle. Monthly Notices R Astronomical Soc (2012) 423:1973–7. doi:10.1111/j.1365-2966.2012.21022.x
36. Annila A. Cosmic rays report from the structure of space. Adv Astron (2015) 2015:1–11. doi:10.1155/2015/135025
38. Annila A, Wikström M. Dark matter and dark energy denote the gravitation of the expanding universe. Front Phys (2022) 10:1017. doi:10.3389/fphy.2022.995977
39. Bender D, Derrick M, Fernandez E, Gieraltowski G, Hyman L, Jaeger K, et al. Tests of qed at 29 gev center-of-mass energy. Phys Rev D (1984) 30:515–27. doi:10.1103/PhysRevD.30.515
40. Williams LP. Ampère’s electrodynamic molecular model. Contemp Phys (1962) 4:113–23. doi:10.1080/00107516208201724
41. Parson AL. A magneton theory of the structure of the atom. Smithsonian Miscellaneous Collections (1915) 65:1.
42. Compton AH. Scientific papers of arthur holly Compton: X-ray and other studies. Chicago University Press (1973).
43. Allen HS. The case for a ring electron. Proc Phys Soc Lond (1918) 31:49–68. doi:10.1088/1478-7814/31/1/303
44. Huang K. On the zitterbewegung of the Dirac electron. Am J Phys (1952) 20:479–84. doi:10.1119/1.1933296
45. Barut AO, Bracken AJ. Zitterbewegung and the internal geometry of the electron. Phys Rev D (1981) 23:2454–63. doi:10.1103/PhysRevD.23.2454
46. Hestenes D. The zitterbewegung interpretation of quantum mechanics. Foundations Phys (1990) 20:1213–32. doi:10.1007/BF01889466
47. Annila A, Kolehmainen E. Atomism revisited. Phys Essays (2016) 29:532–41. doi:10.4006/0836-1398-29.4.532
48. Fermi E. Über die magnetischen momente der atomkerne. Z für Physik (1930) 60:320–33. doi:10.1007/BF01339933
49. Mezei F. La nouvelle vague in polarized neutron scattering. Physica B+C (1986) 137:295–308. doi:10.1016/0378-4363(86)90335-9
50. Povh B, Lavelle M, Rith K, Scholz C, Zetsche F. Particles and nuclei: An introduction to the physical concepts. Springer Berlin Heidelberg (2008).
52. Do Carmo M. Differential geometry of curves and surfaces. Englewood Cliffs, NJ, USA: Prentice-Hall, Inc. (1976).
53. Slobodyan Y. Geodesic curvature. Encyclopedia of mathematics. Dordrecht, Netherlands: Springer (2001).
54. Annila A. The meaning of mass. Int J Theor Math Phys (2012) 2:67–78. doi:10.5923/j.ijtmp.20120204.03
56. Spyrou A, Kohley Z, Baumann T, Bazin D, Brown B, Christian G, et al. First observation of ground state dineutron decay: Be 16. Phys Rev Lett (2012) 108:102501. doi:10.1103/physrevlett.108.102501
57. Canuto V, Chitre S. Solid core in neutron stars. Nat Phys Sci (1973) 243:63–5. doi:10.1038/physci243063a0
58. Canuto V, Chitre S. Crystallization of dense neutron matter. Phys Rev D (1974) 9:1587–613. doi:10.1103/physrevd.9.1587
59. Lyne A, Pritchard R, Shemar S. Timing noise and glitches. J Astrophysics Astron (1995) 16:179–90. doi:10.1007/bf02714833
60. Lyne A. Timing noise and the long-term stability of pulsar profiles. Proc Int Astronomical Union (2012) 8:183–8. doi:10.1017/s1743921312023605
61. Lorimer D, Lyne A, McLaughlin M, Kramer M, Pavlov G, Chang C. Radio and X-ray observations of the intermittent pulsar j1832+ 0029. Astrophysical J (2012) 758:141. doi:10.1088/0004-637x/758/2/141
62. Kramer M, Lyne A, O’Brien J, Jordan C, Lorimer D. A periodically active pulsar giving insight into magnetospheric physics. Science (2006) 312:549–51. doi:10.1126/science.1124060
63. Espinoza C, Antonopoulou D, Stappers B, Watts A, Lyne A. Neutron star glitches have a substantial minimum size. Monthly Notices R Astronomical Soc (2014) 440:2755–62. doi:10.1093/mnras/stu395
64. Mäkelä T, Annila A. Natural patterns of energy dispersal. Phys Life Rev (2010) 7:477–98. doi:10.1016/j.plrev.2010.10.001
65. Annila A. Natural thermodynamics. Physica A Stat Mech its Appl (2016) 444:843–52. doi:10.1016/j.physa.2015.10.105
66. Wong T, Backer D, Lyne A. Observations of a series of six recent glitches in the crab pulsar. Astrophysical J (2001) 548:447–59. doi:10.1086/318657
67. Espinoza CM, Lyne AG, Stappers BW, Kramer M. A study of 315 glitches in the rotation of 102 pulsars. Monthly Notices R Astronomical Soc (2011) 414:1679–704. doi:10.1111/j.1365-2966.2011.18503.x
68. Warszawski L, Melatos A. Knock-on processes in superfluid vortex avalanches and pulsar glitch statistics. Monthly Notices R Astronomical Soc (2013) 428:1911–26. doi:10.1093/mnras/sts108
69. Melatos A, Peralta C, Wyithe J. Avalanche dynamics of radio pulsar glitches. Astrophysical J (2008) 672:1103–18. doi:10.1086/523349
70. Jensen HJ. Self-organized criticality: emergent complex behavior in physical and biological systems, 10. Cambridge University Press (1998).
71. Mignani RP. Optical, ultraviolet, and infrared observations of isolated neutron stars. Adv Space Res (2011) 47:1281–93. doi:10.1016/j.asr.2009.12.011
72. Andersson N, Glampedakis K, Ho WC, Espinoza CM. Pulsar glitches: The crust is not enough. Phys Rev Lett (2012) 109:241103. doi:10.1103/physrevlett.109.241103
73. Lyne A, Shemar S, Graham Smith F. Statistical studies of pulsar glitches. Monthly Notices R Astronomical Soc (2000) 315:534–42. doi:10.1046/j.1365-8711.2000.03415.x
74. Fuentes J, Espinoza C, Reisenegger A, Shaw B, Stappers B, Lyne A. The glitch activity of neutron stars. Astron Astrophysics (2017) 608:A131. doi:10.1051/0004-6361/201731519
75. Kaspi VM, Beloborodov AM. Magnetars. Annu Rev Astron Astrophysics (2017) 55:261–301. doi:10.1146/annurev-astro-081915-023329
76. Bhattacharya D. Evolution of neutron star magnetic fields. J Astrophysics Astron (2002) 23:67–72. doi:10.1007/bf02702467
77. Konar S. Magnetic fields of neutron stars. J Astrophysics Astron (2017) 38:47. doi:10.1007/s12036-017-9467-4
78. Melatos A. Bumpy spin-down of anomalous x-ray pulsars: the link with magnetars. Astrophysical J (1999) 519:L77–80. doi:10.1086/312104
79. Archibald R, Burgay M, Lyutikov M, Kaspi V, Esposito P, Israel G, et al. Magnetar-like x-ray bursts suppress pulsar radio emission. Astrophysical J Lett (2017) 849:L20. doi:10.3847/2041-8213/aa9371
80. Lower ME, Younes G, Scholz P, Camilo F, Dunn L, Johnston S, et al. The 2022 high-energy outburst and radio disappearing act of the magnetar 1e 1547.0–5408. Astrophysical J (2023) 945:153. doi:10.3847/1538-4357/acbc7c
81. Turolla R, Zane S, Watts A. Magnetars: the physics behind observations. a review. Rep Prog Phys (2015) 78:116901. doi:10.1088/0034-4885/78/11/116901
82. Woods P, Kaspi V, Thompson C, Gavriil F, Marshall H, Chakrabarty D, et al. Changes in the X-ray emission from the magnetar candidate 1E 2259+ 586 during its 2002 outburst. Astrophysical J (2004) 605:378–99. doi:10.1086/382233
83. Archibald RF, Kaspi V, Ng C-Y, Gourgouliatos K, Tsang D, Scholz P, et al. An anti-glitch in a magnetar. Nature (2013) 497:591–3. doi:10.1038/nature12159
84. Baym G, Pethick C. Physics of neutron stars. Annu Rev Astron Astrophysics (1979) 17:415–43. doi:10.1146/annurev.aa.17.090179.002215
85. Ma F, Xie B. Super-giant glitches and quark stars: Sources of gamma-ray bursts? Astrophysical J (1996) 462:L63. doi:10.1086/310033
86. Annala E, Gorda T, Kurkela A, Nättilä J, Vuorinen A. Evidence for quark-matter cores in massive neutron stars. Nat Phys (2020) 16:907–10. doi:10.1038/s41567-020-0914-9
87. Semenov V, Dyadechkin S, Punsly B. Simulations of jets driven by black hole rotation. Science (2004) 305:978–80. doi:10.1126/science.1100638
88. Bannikova EY, Vakulik VG, Shulga VM. Gravitational potential of a homogeneous circular torus: a new approach. Monthly Notices R Astronomical Soc (2011) 411:557–64. doi:10.1111/j.1365-2966.2010.17700.x
89. Unsöld A, Baschek B. The new cosmos: An introduction to astronomy and astrophysics. New York NY USA: Springer (2001).
90. Dicke RH. Gravitation without a principle of equivalence. Rev Mod Phys (1957) 29:363–76. doi:10.1103/RevModPhys.29.363
91. Feynman R, Morínigo F, Wagner W, Hatfield B. Feynman lectures on gravitation. Reading, Massachusetts: Addison-Wesley (1995).
93. Kalogera V, Baym G. The maximum mass of a neutron star. Astrophysical J (1996) 470:L61–4. doi:10.1086/310296
94. Fryer CL, Kalogera V. Theoretical black hole mass distributions. Astrophysical J (2001) 554:548–60. doi:10.1086/321359
95. Loeb A. Electromagnetic counterparts to black hole mergers detected by ligo. Astrophysical J (2016) 819:L21. doi:10.3847/2041-8205/819/2/l21
96. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Observation of gravitational waves from a binary black hole merger. Phys Rev Lett (2016) 116:061102. doi:10.1103/PhysRevLett.116.061102
97. Abbott R, Abbott TD, Abraham S, Acernese F, Ackley K, Adams A, et al. Observation of gravitational waves from two neutron star–black hole coalescences. Astrophysical J Lett (2021) 915:L5. doi:10.3847/2041-8213/ac082e
98. Lorimer DR, Bailes M, McLaughlin MA, Narkevic DJ, Crawford F. A bright millisecond radio burst of extragalactic origin. Science (2007) 318:777–80. doi:10.1126/science.1147532
99. Enoto T, Kisaka S, Shibata S. Observational diversity of magnetized neutron stars. Rep Prog Phys (2019) 82:106901. doi:10.1088/1361-6633/ab3def
100. Margutti R, Chornock R. First multimessenger observations of a neutron star merger. Annu Rev Astron Astrophysics (2021) 59:155–202. doi:10.1146/annurev-astro-112420-030742
101. Haskell B. Probing neutron star interiors with pulsar glitches. Proc Int Astronomical Union (2017) 13:203–8. doi:10.1017/s1743921317010663
102. Sedrakian A, Clark JW. Superfluidity in nuclear systems and neutron stars. The Eur Phys J A (2019) 55:167–56. doi:10.1140/epja/i2019-12863-6
103. Andersson N. A superfluid perspective on neutron star dynamics. Universe (2021) 7:17. doi:10.3390/universe7010017
104. Antonopoulou D, Haskell B, Espinoza CM. Pulsar glitches: observations and physical interpretation. Rep Prog Phys (2022) 85:126901. doi:10.1088/1361-6633/ac9ced
105. Chatterjee D, Vidaña I. Do hyperons exist in the interior of neutron stars? Eur Phys J A (2016) 52:29–18. doi:10.1140/epja/i2016-16029-x
106. Lugones G, Bombaci I. Deconfinement and color superconductivity in cold neutron stars. Phys Rev D (2005) 72:065021. doi:10.1103/physrevd.72.065021
107. Popov SB, Grigorian H, Blaschke D. Neutron star cooling constraints for color superconductivity in hybrid stars. Phys Rev C (2006) 74:025803. doi:10.1103/PhysRevC.74.025803
108. Pines D, Alpar MA. Superfluidity in neutron stars. Nature (1985) 316:27–32. doi:10.1038/316027a0
109. Haskell B, Sedrakian A. Superfluidity and superconductivity in neutron stars. The Phys Astrophysics Neutron Stars (2018) 401–54. doi:10.1007/978-3-319-97616-7_8
110. Özel F. Soft equations of state for neutron-star matter ruled out by exo 0748-676. Nature (2006) 441:1115–7. doi:10.1038/nature04858
111. Alford M, Blaschke D, Drago A, Klähn T, Pagliara G, Schaffner-Bielich J. Quark matter in compact stars? Nature (2007) 445:E7–E8. doi:10.1038/nature05582
113. Kuhn TS. The essential tension: Selected studies in scientific tradition and change. Chicago: University of Chicago Press (1977).
114. Chamel N. Superfluidity and superconductivity in neutron stars. J Astrophysics Astron (2017) 38:43–14. doi:10.1007/s12036-017-9470-9
115. Kurkela A, Fraga ES, Schaffner-Bielich J, Vuorinen A. Constraining neutron star matter with quantum chromodynamics. Astrophysical J (2014) 789:127. doi:10.1088/0004-637x/789/2/127
Keywords: dineutron, glitch, gluon, magnetic misalignment, neutron magnetic moment, neutron structure, quark, tetraquark
Citation: Annila A (2023) Neutron star characteristics from the neutron structure. Front. Phys. 11:1286802. doi: 10.3389/fphy.2023.1286802
Received: 31 August 2023; Accepted: 22 September 2023;
Published: 12 October 2023.
Edited by:
Sehrish Iftikhar, Lahore College for Women University, PakistanReviewed by:
Muhammad Farasat Shamir, National University of Computer and Emerging Sciences, PakistanAbdul Jawad, COMSATS University Islamabad, Pakistan
Copyright © 2023 Annila. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arto Annila, YXJ0by5hbm5pbGFAaGVsc2lua2kuZmk=
 Arto Annila
Arto Annila