The Feynman chessboard model in 3 + 1 dimensions

The chessboard model was Feynman’s adaptation of his path integral method to a two-dimensional relativistic domain. It is shown that chessboard paths encode information about the contiguous pairs of paths in a spacetime plane, as required by discrete worldlines in Minkowski space. The application of coding by pairs in a four-dimensional spacetime is then restricted by the requirements of the Lorentz transformation, and the implementation of these restrictions provides an extension of the model to 4D, illuminating the relationship between relativity and quantum propagation.

1 Introduction

1.1 History and objective

Feynman’s extension of his path-integral to a relativistic context requires a change in perspective from non-relative to relativistic physics.

In this paper we shall use a textual convention to distinguish between the arenas of Newtonian and Relativistic mechanics by referring to “space-time” and “spacetime” respectively. In space-time, space and time are independent dimensions and there is no relativity of simultaneity. Two events that are simultaneous in one inertial frame in space-time are simultaneous in all inertial frames. The use of the hyphen is a signifier of this assumed complete segregation of time as a universal sequencing parameter.

In relativistic mechanics, signified by “spacetime”, space and time are no longer independent and events that are simultaneous in one inertial frame are not necessarily simultaneous in another. Removing the hyphen from space-time to produce the compound word spacetime provides a textual reminder of Minkowski’s famous declaration:

Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.

Feynman did not publish his chessboard model¹ as a journal article, but it is clear from his Nobel Prize presentation and other work that he was intrigued by the model’s simplicity and anticipated the potential importance of an appropriate extension to a 4D spacetime [1, 2]. Having first established his original path integral approach in the non-relativistic domain, Feynman developed the chessboard model (FCM) with the same visualization of paths, hoping to shed light on the Dirac equation. The model did this remarkably well, providing the correct Dirac propagator from a straightforward procedure that was appealing as a path integral and easily visualized. Unfortunately, how to construct paths in a 4D domain was not evident, particularly in comparison to the non-relativistic case. As a result, the use of the FCM has been limited and the model has attracted relatively little attention compared to its non-relativistic counterpart. However, a sample of different formulations may be found in [3–24].

The goal of this article is to present the FCM in such a way that a direct extension to a 4D spacetime becomes clear. This is carried out through comparison to a simpler stochastic model that allows us to associate the formal analytic continuation (FAC) that has been built into the FCM with the requirements of Minkowski space. Furthermore, on close inspection, we find that the odd signature of Minkowski spacetime by itself produces the Feynman “corner rule” [25] that makes the FCM “quantum mechanical” rather than classical. Using this result, an extension to 4D is relatively straightforward and illuminates the emergence of “quantum” propagation from the requirements of spacetime.

1.2 Description and perspective

The FCM, although invented in the 1940s, first made an appearance in physics pedagogy when it was mentioned as a problem in the text by Feynman and Hibbs [1, see Problem 2.6]. Feynman proposed that the propagator for an electron in a 2D spacetime could be written as:

$K\left(x,t\right)={\displaystyle \sum _R}N\left(R\right){\left(imϵ\right)}^R,(1)$

where ϵ is a small finite step size in time, R is the number of corners in the piecewise-null path from the origin to (x, t), N(R) is the number of paths with R corners, and m is a positive constant representing the particle mass (Figure 1). The fact that path weights are not strictly real places the resulting function outside the domain of probability density functions. Since K has been shown to satisfy the Dirac equation (26), the sum-over-paths is regarded as an element of relativistic quantum mechanics.

FIGURE 1

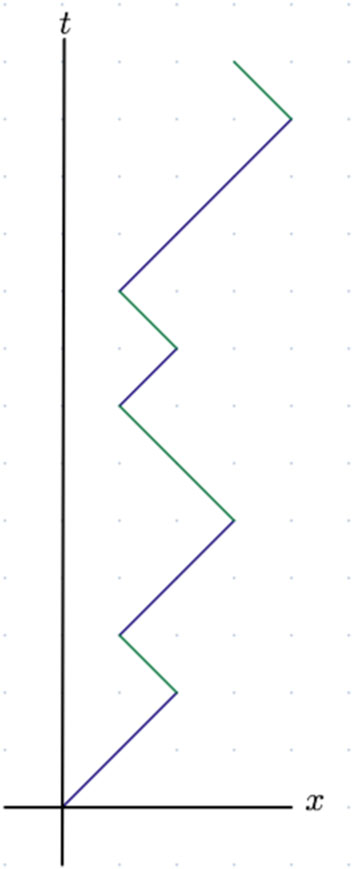
FIGURE 1. A typical path in the Kac/Feynman model. Particles move at speed v = ±1, but occasionally switch directions.

If we remove the unit imaginary from Eq. 1, the result is a model that has a direct interpretation as a random walk model of diffusion that includes an analog of a mean free path [27]. Then, the FCM appears to be a FAC of a probabilistic statistical mechanical model. The FAC involved is simply t → it, which is the same analytic continuation that takes the diffusion equation to Schrödinger’s equation. While this suggestively links the FCM to canonical quantization, t → it also takes spacetime to Minkowski space-time. Since the FCM produces the Dirac equation, which is both relativistically correct and “quantum mechanical,” it appears that the chessboard model has inherited both spacetime and quantum propagation for the price of a single judiciously chosen inclusion of the algebra of complex numbers. This raises a general question as follows:

$\begin{array}{ll}\hfill & \text{Is\hspace{0.17em}the\hspace{0.17em}FAC\hspace{0.17em}we\hspace{0.17em}associate\hspace{0.17em}with\hspace{0.17em}quantum\hspace{0.17em}propagation\hspace{0.17em}a\hspace{0.17em}manife}-\hfill \\ \hfill & \text{station\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}transition\hspace{0.17em}from\hspace{0.17em}space}-\text{time\hspace{0.17em}to\hspace{0.17em}spacetime?}\hfill \end{array}(2)$

The failure of the FCM to extend simply to 4D seems to argue against this. The simplicity of the FCM could just be an artifact of a 2D spacetime. However, the extension to a 4D spacetime has always been primarily guided by Feynman’s original striking vision of the path integral, which arose in the context of the Galilean transformation. What if “paths” in Minkowski space have a different context that, in a sense, projects the “phase” of time dilation onto the Wiener paths of classical physics? In that case, the analog of the path integral in the 4D Minkowski space may appear in a different form to the non-relativistic case. In particular, the idea of a sum over all paths that is part of the non-relativistic formulation may require a re-definition of what constitutes all in the relativistic case.

To resolve this issue, we step back and appeal to classical statistical mechanics. H. A Gersch first made a direct connection between the FCM and statistical mechanics by noting a relation to the one dimensional Ising model [28] and its use of matrix products to calculate partition functions [29]. A significant amount of subsequent work on the FCM has used “transfer matrices” for path counting, and in the following section, we visit their application in a probabilistic context where counting path configurations is central.

The chessboard model in a probabilistic context describes a statistical model of the telegraph equations² due to Mark Kac [27]. We start with a sketch of this model as it has few interpretive problems over and above those of probability theory in general. Its extension to higher dimensions is also not problematic. By comparison, the FCM suffers from the interpretive problems of quantum mechanics and the lingering issue of dimension extension.

We pursue the Kac model far enough to see how matrix products are useful in the visualization and organization of path counting and how this is relatively transparent in a probabilistic setting.

In Section 3, we note that a key feature of paths in the Kac model is that special pairs of paths code for representations of the discrete forms of worldlines in Minkowski space. We then find that the FCM makes an appearance, not as a progenitor of quantum mechanics, but as a consequence of discrete markings on worldlines in Minkowski space. Considering this feature, we refer to the FCM in this context as the Kac–Minkowski model (KMM), from its relationship to the Kac model in spacetime.

The KMM generalizes directly to 4D through its relation with Minkowski space, showing that the free-particle Dirac equation is intimately linked to the general properties of spacetime in a context that appears independent of its role in relativistic quantum mechanics.

The KMM is in actuality the FCM from a different perspective, so its 4D version provides the required extension of the FCM.

2 The Kac model

Looking at the chessboard paths (Figure 1), we imagine an associated discrete Markov process in which a particle moves in space-time with speed v = 1 at each discrete step, while occasionally changing direction with probability mϵ ≪ 1. The transition matrix is

$T_K=\left(\begin{array}{cc}\hfill 1-mϵ\hfill & \hfill mϵ\hfill \\ \hfill mϵ\hfill & \hfill 1-mϵ,\hfill \end{array}\right),(3)$

where the upper state is right-moving and the lower state is left-moving. The rows of the transition matrix sum to 1, as appropriate for a probabilistic model. Figure 2 shows a transition diagram for the process.

FIGURE 2

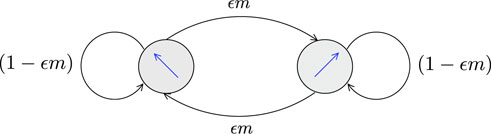
FIGURE 2. A transition diagram for a classical version of the chessboard model, where the arrows denote the two directions along “light cones” in a two-dimensional spacetime.

The transition matrix guides the evolution of the stochastic process at each step, and these steps are independent, so the transition matrix for n steps between states is the n′th power of T_K shown as follows:

$T_K\left(n\right)=T_K^{n}n=\mathrm{1,2},\dots .(4)$

Refining this discrete process to approach a continuous one, we diagonalize the transition matrix, calculate the n’th power, and consider the limit ϵ → 0 with n represented as n = t/ϵ. Transforming back and expressing the result in terms of the approach to equilibrium gives

$T_K\left(t\right)=\frac{1}{2}\left(\left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill 1\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 1\hfill \end{array}\right)\exp \left(-2mt\right)\right),$

$=\frac{1}{2}\left(\left(I_2+{\sigma }_x\right)+\left(I_2-{\sigma }_x\right)\exp \left(-2mt\right)\right),(5)$

where I₂ is the 2 × 2 identity matrix and σ_x is the first Pauli matrix.

The first term $\frac{1}{2}(I_2+{\sigma }_x)$ represents the equilibrium distribution of equal occupancy of the left- and right-moving states. It is to be noted that any valid initial condition is immediately mapped onto the equilibrium state of equal probabilities by this term. The aforementioned model is a very simplified sketch of a model explored by Kac [27] in a remarkable paper that revealed a stochastic process underlying the telegraph equations. The approach taken worked in any number of dimensions in space and revealed a universality that arose because of the statistics generated by an underlying binomial process.

We can see part of this generality if we look at the transition diagram in Figure 2 and reinterpret it as a process. A particle in a given state either persists in that state with probability 1 − mϵ or switches to the other state with probability mϵ. We could write the transition matrix symbolically as

$T_K=\left(pP+qS\right),(6)$

where P stands for ‘persist’ and S stands for ‘switch’. Here, p and q are the probabilistic weights p = 1 − mϵ and q = mϵ = 1 − p, respectively. We can think of persist and switch in terms of directions with respect to the space axis, that is, orientation. Figure 3 illustrates how persist and switch act as operators on column vectors. The sketched path in Figure 1 illustrates a typical path from the Kac model where, if the steps of size ϵ are small, there would be many more “P’s” in path sequences than “S’s.”

FIGURE 3

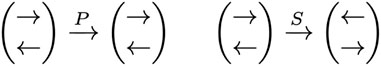
FIGURE 3. Persist and switch in walks for the Kac model. The upper coefficient in the column vector initially refers to right-moving, the lower to left-moving. The switch reverses the orientation of both components. Keeping track of walks acquires the combinatorial factors in expanding powers of the binomial term pP + qS.

In the Kac model, P and S are implemented using 2 × 2 matrices with P₀ = I₂ and S_K = σ_x, each used with appropriate weights, p and q, respectively. If we rewrite Eq. 5 in terms of P and S, we obtain

$T_K\left(t\right)=\frac{1}{2}\left(\left(P+S_K\right)+\left(P-S_K\right)\exp \left(-2mt\right)\right).(7)$

We can “read” this equation directly in terms of the Kac paths. At any step, a path can either maintain its direction (P) or switch direction (S_K). The operator $\frac{1}{2}(P+S_K)$ considers any valid state occupancy and maps it onto the equilibrium state $\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)/2$, so the result is not time dependent. However, the orthogonal operator (P − S)/2 operates on the differences between the state occupancies. It is this difference that changes over time.

To include the spatial distribution of paths, Kac uses a Fourier transform to count persistent steps [27]. In the model, the persistence operator is adjusted to count through a Fourier transform becoming

$P_0=I_2\to P_F=\left(\begin{array}{cc}\hfill e^{-ipϵ}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{ipϵ}\hfill \end{array}\right)=\exp \left[-ipϵ{\sigma }_z\right],(8)$

where the exponential on the right is defined in terms of its Taylor expansion, and P_F approaches the identity matrix as ϵ → 0.³

The binomial term T_K (Eq. 3) with the replacement of the identity matrix with the Fourier kernel becomes, to order ϵ,

$T_K\to \left(1-mϵ\right)\left(\begin{array}{cc}\hfill 1-ipϵ\hfill & \hfill mϵ\hfill \\ \hfill mϵ\hfill & \hfill 1+ipϵ\hfill \end{array}\right)=\left(1-mϵ\right)\left(I_2+ϵ\left(-ip{\sigma }_z+m{\sigma }_x\right)\right).(9)$

We can consider the limit of the aforementioned equation to the power t/ϵ as ϵ → 0 to obtain T_K (p, t), the transition matrix in the Fourier domain. The explicit result is not of immediate interest; however, differentiating the propagator with respect to t gives the following:

$\begin{array}{ll}\hfill \frac{\partial T_K\left(p,t\right)}{\partial t}& =-ip{\sigma }_z{T}_K-m\left(I_2-{\sigma }_x\right)T_K\hfill \\ \hfill & =-ip{\sigma }_z{T}_K-m\left(P-S\right)T_K,\hfill \end{array}(10)$

where we can see the roles of persistence, the switch, and the Fourier transform in the evolution of the propagator.

Kac’s analysis was focused on the paths and the eventual ensemble average behavior. We note two relevant features of his analysis.

1. His model ultimately gave rise to probability density functions that satisfy the following:

$\frac{{\partial }^{2}F}{\partial t^2}=\frac{{\partial }^{2}F}{\partial x^2}-2m\frac{\partial F}{\partial t}.(11)$

This is a version of the “telegraph” equation that, as a model, essentially replaces the diffusion equation with a partial differential equation that recognizes an inner scale or “mean free path” between collisions characterized by the frequency m. By a change of variables to G (x, t) = exp (mt)F (x, t), the equation may be written in the form

$\frac{{\partial }^{2}G}{\partial t^2}=\frac{{\partial }^{2}G}{\partial x^2}-m^{2}G.(12)$

We note that this is a formal analytic continuation (m → im) away from the Klein–Gordon equation.⁴

2. In the Kac model, the mathematical paths are an abstraction of paths that you might expect in a one-dimensional fluid; that is, one would expect the law of inertia to maintain a particle at a fixed speed until it hits another particle, where it reverses its direction but maintains the same speed. In the Kac model, the free time between collisions is a random variable that is ultimately exponential, with inter-collision times being Poisson, so the zig–zag paths being tracked are analogs of “worldlines” that are stochastic in orientation⁵ but not in speed [27]. Under these circumstances, paths of individual particles necessarily have discontinuous velocities. The partial differential equation that results from the model has to acquire its smooth evolution by averaging over the ensembles of particles as does the diffusion equation, a close relative. The averaging process ends up constructing density functions, keeping the model within the domain of probability theory.

3 The Kac-Minkowski model

3.1 Minkowski space

The Kac model assumes that space and time are independent in the sense that transformations between inertial frames do not involve the time coordinate. To adapt the model to Minkowski space, we note relevant restrictions. The first two are standard, and the third is an adaptation of the concept of worldlines that allows the incorporation of mass into the kinematics of special relativity [22, 30, 31].

$\begin{array}{ll}\hfill \left(\text{a}\right)& \text{\hspace{0.17em}The\hspace{0.17em}equivalence\hspace{0.17em}of\hspace{0.17em}inertial\hspace{0.17em}frames.\hspace{0.17em}}\hfill \\ \hfill \left(\text{b}\right)& \text{\hspace{0.17em}The\hspace{0.17em}constancy\hspace{0.17em}of\hspace{0.17em}}c\text{\hspace{0.17em}throughout\hspace{0.17em}all\hspace{0.17em}inertial\hspace{0.17em}frames.}\hfill \\ \hfill \left(\text{c}\right)& \text{\hspace{0.17em}The\hspace{0.17em}‘two\hspace{0.17em}photon’\hspace{0.17em}view\hspace{0.17em}of\hspace{0.17em}worldlines.}\hfill \end{array}(13)$

In relation to the Kac model, the existence of a single characteristic speed is already in place. We simply set the fixed speed of the model to v = c = 1. There is no appeal to inertial frames within the model, but a special reference frame, in which the mean free speed is equal in both directions, is assumed. This choice may always be made by attaching the reference frame to the center of mass of the ensemble of particles, and this is assumed at the outset.

In requirement c), the term “two photon” alludes to an assumed continuity of null lines, the analog of Kac particle paths, through worldline Events⁶. These null lines form the borders of inter-event “causal” areas in Minkowski space. This is mimicked in Figure 4 by coloring the edges as if they were photons that cross at Events but change directions and colors at the intersection of light cones.

FIGURE 4

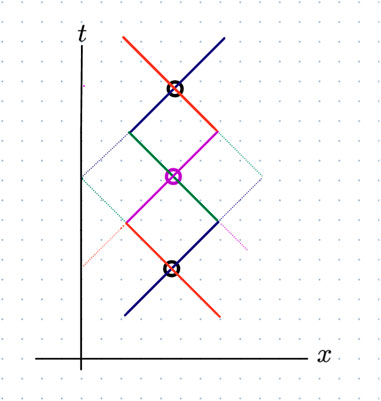
FIGURE 4. In Minkowski space, any event divides spacetime into four regions, two of which are time-like connected to the event. Above, three successive events on a worldline define closed causal regions in which all included points are time-like connected to successive events. Continuity of edges through events divide the events into even and odd, suggesting a minimum of four colors for edges corresponding to two edge directions and two photons. The two “photons” alternate colors with the direction. One alternates between blue and green on direction change, and the other alternates red and purple. The coloring illustrates the “two-photon” picture of causal areas.

Conventional descriptions of spacetime implicitly ignore the discrete aspect of c) and associated inter-event areas, based on the assumption that “events” are just points on worldlines and these are dense. This is sensible in the case where the discussion is about matter in general where, in order to complete the picture traditionally, mass and energy become features of Minkowski space that are brought in through dynamics rather than kinematics.

However, the assumption of smooth worldlines for individual particles automatically eliminates the uncertainty principle and quantum propagation with it. Requirement c), then, ultimately provides the opportunity of identifying mass with a characteristic frequency, instead of externally through dynamics. However, what of the worldline? The question becomes

$\begin{array}{ll}\hfill & \text{If\hspace{0.17em}we\hspace{0.17em}keep\hspace{0.17em}}m\text{\hspace{0.17em}as\hspace{0.17em}a\hspace{0.17em}characteristic\hspace{0.17em}frequency\hspace{0.17em}}\left(\text{or\hspace{0.17em}mean\hspace{0.17em}free\hspace{0.17em}path}\right)\hfill \\ \hfill & \text{associated\hspace{0.17em}with\hspace{0.17em}a\hspace{0.17em}particle,\hspace{0.17em}can\hspace{0.17em}we\hspace{0.17em}find\hspace{0.17em}a\hspace{0.17em}‘natural’\hspace{0.17em}smoothing\hspace{0.17em}}\hfill \\ \hfill & \text{process,\hspace{0.17em}compatible\hspace{0.17em}with\hspace{0.17em}Minkowski\hspace{0.17em}space,\hspace{0.17em}that\hspace{0.17em}provides\hspace{0.17em}a\hspace{0.17em}}\hfill \\ \hfill & \text{substitute\hspace{0.17em}for\hspace{0.17em}the\hspace{0.17em}classical\hspace{0.17em}smooth\hspace{0.17em}worldline?}\hfill \end{array}(14)$

The answer to this question is a qualified “Yes.” Minkowski space has a smooth process, which is consistent with a version of the Kac model that becomes apparent when you consider the causal areas between events. We turn to this feature as it appears in the Kac model.

3.2 Paired paths

To associate the Kac model with Minkowski space, we require a feature of the paths that can mimic the mixed signature of spacetime and the equivalence of inertial frames.

In the Kac model, one feature of every sample path with an even number of switches is that there exists a Fraternal Twin path in the ensemble of paths, as shown in Figure 5. The twin is equally likely in the ensemble and, when paired, partitions the x − t plane into a sequence of areas. We shall call the areas illustrated in the figure Causal Areas for their similarity to spacetime diagrams in Minkowski space. It is to be noted that the fraternal twin path is obtained from the original by interchanging the inter-switch links, in pairs, starting at the origin (compare the left two paths in Figure 5.).

FIGURE 5

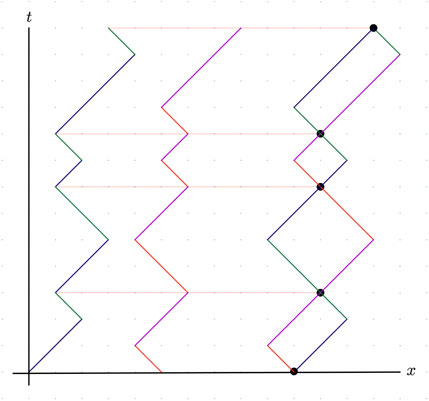
FIGURE 5. The path on the left is a typical path from the Kac model (Figure 1). The next path to the right is the “fraternal twin” that interchanges the order of edges by pairs. Pushing the left path through to the right of the middle path, so they collide at every other corner, gives the pair of paths on the right. Notably, this creates a sequence of “causal areas” that would be associated with the events represented by nodes at the osculation points. The sequence of causal areas forms a causal trail.

Considering Figure 5, we can see that the rightmost portion of the figure shows a sequence of causal areas between the black nodes that we call Events, again for similarity to marked worldlines in Minkowski space. The analog of the worldline is, then, a contiguous sequence of events and causal areas that we call a Causal Trail.

The reason for the suggestive terminology is that if the five black nodes shown in Figure 5 were located on the worldline of a single particle in Minkowski space, then the rectangular areas drawn between them would be part of a spacetime diagram that showed the regions that were time-like connected or “causal” for successive Events. The coloring on the right uses four colors that maintain the continuity of coloring through the Events, but consistently alternate colors at the outside corners. The coloring mimics the two-photon view of (13 c). Notably, we shall use one of the fraternal paths to code for the pairs of paths that describe the causal areas.⁷

It is to be noted that in the Kac model, the switch S did two things simultaneously. At each occurrence, it changed states via σ_x and it flipped a direction indicator (“orientation”) that was 1 for right-moving and −1 for left-moving, when considering the right twin. We can see this, for example, in the time dependence of the ensemble average (Eq. 7) where the departure from equilibrium is represented by I₂ − σ_x. In the Kac ensemble, the operator σ_x switches direction, subtracting particles from one direction state and adding them to the other.

If we are to reproduce the causal areas from, say, the right fraternal twin, we have to distinguish between corners that become Events (black dots shown in Figure 6) and those that remain as kinks. The right-to-left corners that remain as kinks switch both the state and the orientation from +1 to −1, as in the Kac model. The left-to-right corners that become Events switch state, but not orientation. This is because left “corners” (Events) correspond to the crossing of the photon paths, each of which maintains the continuity of direction and orientation. Thus, the corners that code for Events switch state but keep their orientation. So Events maintain the orientation of the paths that enter them. The intersection of lightcones away from Events (kinks) switch orientation. Then, geometrically, the coding for the areas simply modifies the switch from the Kac switch of σ_x to the alternating switch:⁸

$S_M=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill -1\hfill & \hfill 0\hfill \end{array}\right)=i{\sigma }_y.(15)$

FIGURE 6

FIGURE 6. In the Kac model, paths change direction when they change state. At each change of state, implemented by σ_x, the sign of the orientation changes. This is illustrated by the Kac path on the left in which the sign is with respect to the +x direction. The negative sign on the left moving segments represent an orientation of −1. In the paired paths on the right, counting is modified to encode the fraternal twin. This brings in the symmetry of light-cone coordinate pairs and is implemented when counting with the right twin by having both state and orientation change at the right-to-left corners (kinks), as in the Kac model, but left-to-right corners (Events) inherit the sign from the fraternal twin so that the “continuous” paths through the nodes do not change sign. This changes the coding from Kac paths to the two photon paths that cross at Events.

What was a transition matrix that counted paths in a way that could be normalized for a probability density function is now a transfer matrix that counts paired paths with a detailed balance condition (two photon), ensuring that the paths themselves establish a chain of causal areas, the causal trail of a particle. Therefore, Kac paths may be used as a model keeping the path counting statistics the same, but modifying the switch so that the pair-counting codes for the crossing of the two photon paths.

The pairing de-couples the Kac model from space-time and anchors it in spacetime. Qualitatively, we can see this from the change in the switch. The switch is the digital analog of the tick of a clock. The Kac switch completes a cycle with two switches. $S_K^2=1$. The KM switch in space is still the same in that each photon path switches orientation at the outer extent of the causal areas (at kinks). However, the KM switch in time requires a cycle of four because $S_M^2=-1$. This is ultimately because spacetime distinguishes even and odd Events. The result is a change of the assumed signature of space-time in the Kac model to the spacetime signature (1, −1) in the KMM. This will become evident when we observe the result of the continuum limit.

If we use Kac paths to code for fraternal pairs by changing the switch from S_K = σ_x to S = S_M, it is not immediately evident what the normalization should be. However, since paths are now paired and the orientation switch frequency is halved, we might suspect we shall lose the 1 − ϵm prefix in the transition matrix⁹. Since this is an issue of normalization, we check the continuum limit to see if the limit is sensible. Proceeding, our replacement for the (Fourier) persist and switch operators for the pairs is

$T_M\to \left(P_F+mϵS_M\right),$

$=\left(\begin{array}{cc}\hfill 1-ipϵ\hfill & \hfill mϵ\hfill \\ \hfill -mϵ\hfill & \hfill 1+ipϵ\hfill \end{array}\right),$

$=I_2-i\left(p{\sigma }_z-m{\sigma }_y\right)ϵ,(16)$

where we changed the switch and removed the probabilistic normalization factor 1 − ϵm as a prefactor.

Considering the limit of $K_M^{t/ϵ}$ as ϵ → 0 such that t/ϵ is an integer gives, after some simplification, the following:

$K_M\left(p,t\right)=\left(\begin{array}{cc}\hfill \cos \left(\text{E}t\right)-\frac{ip\sin \left(\text{E}t\right)}{\text{E}}\hfill & \hfill \frac{m\sin \left(\text{E}t\right)}{\text{E}}\hfill \\ \hfill -\frac{m\sin \left(\text{E}t\right)}{\text{E}}\hfill & \hfill \cos \left(\text{E}t\right)+\frac{ip\sin \left(\text{E}t\right)}{\text{E}}\hfill \end{array}\right),$

$=\cos \left(\text{E}t\right)I_2-\frac{i\sin \left(\text{E}t\right)}{E}\left(p{\sigma }_z-m{\sigma }_y\right),(17)$

where

$E=\sqrt{m^2+p^2}.(18)$

It can be verified that this satisfies a form of the Dirac equation, namely,

$\frac{\partial K_M}{\partial t}=i\left(m{\sigma }_y-p{\sigma }_z\right)K_M.(19)$

There are a few points to note here. First, K_M cannot be a probability density function since it is not non-negative, even for p = 0. However, our choice of normalization is not totally inadvisable. Notably,

$K_M\left(p,t\right)K_M^{†}\left(p,t\right)=I_2.(20)$

If we think of p and m as characterizing the worldline of our free particle of mass m, the operation $K_M(p,t)K_M^{†}(p,t)$ removes dependence on both m and p. In our attempt to model the worldline of a particle of specific mass, we have the † operation that removes that identification and should return us to a model of matter, not mass. It does this in the sense that the spacetime signature remains, even when we remove the kinematic representation of mass. This provides a type of correspondence principle that allows us to re-identify mass through dynamics to recover traditional special relativity.

Looking at Eq. 17, we can see in its structure the remnants of the Fourier version of persist and the new switch. The identity matrix is the original persist, and this is modified by the Fourier term ipϵσ_z to count configurations along the space axis [6], giving the diagonal term. The switch is the imϵσ_y term, and it is this term that changes the Kac model to count path pairs. Table 1¹⁰ compares the models.

TABLE 1

TABLE 1. Comparison of the Kac and KM models. The Kac model extracts one of either P or S from each term in the n’th power of the binomial sum. The result is a sample path, and the coefficients of P and S implement an ensemble average. In the KMM, the persist term does not need a coefficient to adjust for the switch. This is because the Minkowski binomial term ultimately codes for a rotation and as a result “Persist or Switch,” mutually exclusive in a binary term are not mutually exclusive when combined as an operator. The binomial term can then be considered a “small” deviation from persist and the sum-over paths evaluated as a product of rotations.

We can also see how the algebra of complex numbers is implemented. The “Real” part is the coefficient of “Persist,” the scalar multiplying I₂, cos (Et). The “Imaginary” part is associated with the unit “vector,” $\frac{(p{\sigma }_z-m{\sigma }_y)}{E}$, namely, sin (Et).

The context of the KMM is that we are working in a spacetime plane in which the x and t axes are specified along with the origin. However, by coding for the pairs of paths, we brought in a symmetry that mimics the role of lightcone coordinates. By welding together fraternal twins to mimic bound photons as the edges of causal areas, we arranged a classification of paths that fixes a detailed balance condition maintaining the characteristic speed consistent in both directions and ensuring that the analog of the worldline maintains an appropriate event/causal area structure.

In constructing the propagator, we used the Pauli algebra to implement the switch and the Fourier transform. However, we have not yet encoded the fact that our space axis could point in any direction in a three-dimensional space. The Pauli algebra is not large enough to include this along with the structure it provides in the KMM. We remedy this in the next section.

4 The Extension to include three space dimensions

To adapt the KMM to 4D Minkowski space, we have to be more explicit than the list (13) that guided our formulation of the 2D version mentioned previously. Here is the list repeated, keeping in mind that we are now allowing for three dimensions in space.

$\begin{array}{ll}\hfill \left(a\right)& \text{Free\hspace{0.17em}particles,\hspace{0.17em}passing\hspace{0.17em}through\hspace{0.17em}the\hspace{0.17em}origin\hspace{0.17em}and\hspace{0.17em}the\hspace{0.17em}point\hspace{0.17em}}\mathbf{x}\text{\hspace{0.17em}at\hspace{0.17em}}\hfill \\ \hfill & \text{time\hspace{0.17em}}t\text{,\hspace{0.17em}remain\hspace{0.17em}in\hspace{0.17em}the\hspace{0.17em}spacetime\hspace{0.17em}plane\hspace{0.17em}generated\hspace{0.17em}by\hspace{0.17em}the\hspace{0.17em}}t-\text{axis\hspace{0.17em}}\hfill \\ \hfill & \text{and\hspace{0.17em}the\hspace{0.17em}point\hspace{0.17em}}\left(\mathbf{x},t\right)\text{,\hspace{0.17em}maintaining\hspace{0.17em}the\hspace{0.17em}same\hspace{0.17em}momentum.\hspace{0.17em}}\hfill \\ \hfill \left(b\right)& \text{The\hspace{0.17em}speed\hspace{0.17em}}c\text{\hspace{0.17em}is\hspace{0.17em}the\hspace{0.17em}same\hspace{0.17em}physical\hspace{0.17em}constant\hspace{0.17em}in\hspace{0.17em}all\hspace{0.17em}inertial\hspace{0.17em}frames\hspace{0.17em}}\hfill \\ \hfill & \mathit{\text{and in all directions.}}\hfill \\ \hfill \left(c\right)& \text{The\hspace{0.17em}‘two\hspace{0.17em}photon’\hspace{0.17em}view\hspace{0.17em}of\hspace{0.17em}worldlines\hspace{0.17em}applies}\mathit{\text{in the same}}\hfill \\ \hfill & \mathit{\text{spacetime plane as specified in}}\left(\text{a}\right).\hfill \end{array}(21)$

The second item requires that c be a universal constant, the value of which is irrespective of the direction in space. Item a) was modified to explicitly embed the law of inertia in 4D Minkowski space. The “explicit” part is that if a particle is “free,” then it does not change momentum, thus remaining in a single spacetime plane. In the 2D case, there was only one spacetime plane so there was no need to emphasize this.

Part a) above tells us how c) has to be implemented. We just import paired paths from the 2D case, making sure that the spacetime plane in which we draw paths, is the plane specified in a).

Notably, a) is an enormous simplification that is contrary to the coding expected from paths in Feynman’s non-relativistic formulation. Those paths have vastly more degrees of freedom. Free particles in the non-relativistic formulation are required to deviate randomly from their inertial spacetime plane to maintain consistency with Galilean transformations.¹¹

In short, our list mentioned above tells us that the only thing we have to do to generalize the KMM is to provide the same construction for all spacetime planes available to a particle in 4D. If we think of the chain of causal areas shown in Figure 6 as a spacetime diagram, that diagram pertains only to the spacetime plane established by the argument of the propagator¹². All that is necessary is to label the spacetime diagram appropriately.

In the KMM, each step of length ϵ is considered along a one-dimensional subspace that we have labeled by x. To extend this to 4D, we need two more dimensions. If the spatial argument of the propagator is the point x = (x₁, x₂, x₃), we require the direction as a unit vector which we write as $\widehat{r}=\mathbf{x}/\Vert \mathbf{x}\Vert$. The direction of $\widehat{r}$ is a projection of the one-dimensional subspace that runs through the origin and the point (x₁, x₂, x₃, t), this being the end point of the propagator.

We can formally rewrite the Fourier version of persist as follows:

$P_F\to \exp \left[-ipϵ\widehat{r}{\sigma }_z\right]=\left(\begin{array}{cc}\hfill \mathbf{1}\exp \left[-ip\widehat{r}ϵ\right]\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{1}\exp \left[ip\widehat{r}ϵ\right]\hfill \end{array}\right),(22)$

where 0 and 1 are 2 × 2 matrices.

The switch can be the analog of either iσ_y or iσ_x.¹³ If we choose the latter, we obtain

$S_Q=i\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)\to i\left(\begin{array}{cc}\hfill 0\hfill & \hfill \mathbf{1}\hfill \\ \hfill \mathbf{1}\hfill & \hfill 0\hfill \end{array}\right).(23)$

For convenience, we can now specify $\widehat{r}$ in terms of the Pauli matrices as $\widehat{r}=(x_1{\sigma }_x+x_2{\sigma }_y+x_3{\sigma }_z)/\Vert \mathbf{x}\Vert$.

In order for P_F to work appropriately along the direction $\widehat{r}$, we must have, for example,

$P_F^2=\left(\begin{array}{cc}\hfill \mathbf{1}\exp \left[-i2p\widehat{r}ϵ\right]\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}\exp \left[i2p\widehat{r}ϵ\right]\hfill \end{array}\right).(24)$

This will occur provided our multiplication supports $\exp [\widehat{r}]\exp [\widehat{r}]=\exp [2\widehat{r}]$. This is guaranteed by our representation of $\widehat{r}$ in terms of the Pauli matrices that anti-commute and are orthonormal as vectors. To view our representation, the (1,1) element of P_F becomes

$\left(\begin{array}{cc}\hfill \cos \left(pϵ\right)-iz\sin \left(pϵ\right)\hfill & \hfill \left(-y-ix\right)\sin \left(pϵ\right)\hfill \\ \hfill \left(y-ix\right)\sin \left(pϵ\right)\hfill & \hfill \cos \left(pϵ\right)+iz\sin \left(pϵ\right),\hfill \end{array}\right),(25)$

where for brevity, we write (x, y, z) = (x₁, x₂, x₃)/‖x‖ as a unit vector. The 4 × 4 version of P_F is, then,

$\left(\begin{array}{cccc}\hfill \cos \left(pϵ\right)-iz\sin \left(pϵ\right)\hfill & \hfill \left(-y-ix\right)\sin \left(pϵ\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \left(y-ix\right)\sin \left(pϵ\right)\hfill & \hfill \cos \left(pϵ\right)+iz\sin \left(pϵ\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cos \left(pϵ\right)+iz\sin \left(pϵ\right)\hfill & \hfill \left(y+ix\right)\sin \left(pϵ\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill i\left(x+iy\right)\sin \left(pϵ\right)\hfill & \hfill \cos \left(pϵ\right)-iz\sin \left(pϵ\right).\hfill \end{array}\right).(26)$

For more compact notation, we define

${\alpha }_k={\sigma }_z\otimes {\sigma }_k\text{for}k=\mathrm{1,2,3},(27)$

where ⊗ is the Kronecker product. It may be verified that the α_k anti-commute and square to the identity.

The switch in our chosen matrix representation for $P_{\widehat{r}}$ is

$S_{\widehat{r}}=i{\sigma }_x\otimes I_2=i\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)=i\mathit{\beta }.(28)$

The three α_k and β form an anti-commuting orthonormal set.

The sum of persist and switch is

$\begin{array}{ll}\hfill K_{\widehat{r}}\left(p\widehat{r},ϵ\right)& =P_{\widehat{r}}+S_{\widehat{r}}\hfill \\ \hfill & =\exp \left[\left(-ipϵ\right)\mathit{\alpha }\cdot \widehat{\mathbf{r}}\right]+imϵ\mathit{\beta },\hfill \end{array}(29)$

where we used the abbreviation $\mathit{\alpha }\cdot \widehat{\mathbf{r}}=x{\alpha }_x+y{\alpha }_y+z{\alpha }_z$.

To first order in ϵ, the aforementioned equation may be written suggestively (cf. Eq. 16) as follows:

$\begin{array}{ll}\hfill K_{\widehat{r}}\left(p\widehat{r},ϵ\right)& =P_{\widehat{r}}+S_{\widehat{r}}\hfill \\ \hfill & =I_4+iϵ\left(-p\mathit{\alpha }\cdot \widehat{\mathbf{r}}+m\mathit{\beta }\right),\hfill \end{array}(30)$

and we see the infinitesimal propagator written as a binomial term that codes for a rotation. When we consider powers of $K_{\widehat{r}}$, we will obtain the same binomial coefficients enumerating paths as we did for the 2D KMM and FCM. As in the two-dimensional case, we can raise $K_{\widehat{r}}$ to the power t/ϵ in the limit as ϵ → 0. The result is

$K_{\widehat{r}}\left(p\widehat{r},t\right)=\left(I_4\cos \left(E_{p}t\right)+\frac{i\sin \left(E_{p}t\right)\left(m\mathit{\beta }-p\widehat{r}\right)}{E_p}\right),(31)$

where $E_p=\sqrt{m^2+p^2}$. Differentiating this with respect to t and simplifying leads to the differential equation

$\frac{\partial K_{\widehat{r}}}{\partial t}=i\left(p\mathit{\alpha }.\widehat{r}+m\mathit{\beta }\right)K_{\widehat{r}},(32)$

a form of the Dirac equation. As in the case of Eq. 17, we can identify the encoding of the algebra of complex numbers in Eq. 31. The real part is the coefficient of the identity matrix I₄, cos (E_pt). The imaginary part is sin (E_pt) times the unit vector $\frac{(m\mathit{\beta }-p\widehat{r})}{E_p}$. The appearance of this structure can be traced back to the pairing of paths, and the resulting switch observed in Eq. 15 effectively changing the spacetime signature.

5 Discussion

The purpose of this article was to extend the FCM to 4D in such a way as to preserve the simplicity of the 2D version, while making sure the extension provides a coherent picture of the sum over paths. We noted that factors complicating such an extension were the entangled effects of special relativity and quantization within the concept of paths. The FCM seemed to embed the algebra of complex numbers in such a way that a single analytic continuation sufficed for a transition to both Minkowski space and quantum propagation.

In order to disentangle the transition itself, we stepped back into Kac’s probabilistic model to focus on the role of combinatorial factors and paths in a context where neither interpretation nor space dimensions were troublesome. The reason for this choice was that the Kac model shares the same paths and combinatorial coefficients as the FCM, but in a simpler and more transparent context.

Upon examination, the Kac model provided a key insight in the form of fraternal path pairs. Kac paths in spacetime, when paired with their fraternal twins, produce a structure that mimics spacetime endowed with a worldline analogy consisting of a causal trail. A causal trail is not a path; it is a higher dimensional object linked to paths, the “higher dimension” ultimately requiring a shift from real to complex numbers.

In order to force the Kac model to code for fraternal pairs, the “switch” involved in path counting was changed from σ_x to iσ_y, and the probabilistic normalization removed. This preserved the “counting” of the Kac model, while applying it to the enumeration of spacetime areas rather than just lengths. However, the resulting KMM is simply a version of the FCM with a clear provenance. Maintaining a distinction between the two was a convenience allowing the extension of the KMM through the dictates of Minkowski space. This is to be compared to an appeal as to how a relativistic path integral might be extended, based on an analogy with the non-relativistic version.¹⁴ Interpreting the FCM in terms of the KMM, we see that Feynman’s chessboard paths code for causal trails, rather than just the paths themselves. This physically adds another dimension in that causal areas interpolate between Events on causal trails. The areas themselves induce a complex structure on spacetime because the parallel edges of the areas have opposite orientation and can be smoothly rotated into one another, as shall be shown in future publications.

The extension of the KMM to a 4D Minkowski space was relatively straightforward because its embedding in 4D was restricted by the Lorentz transformation. We neither expect free particles to detect special directions in space nor do we classically expect that free particles passing through the origin deviate from the spacetime hyperplanes in which they start. In this case, the KMM must then apply, regardless of the actual spacetime hyperplane containing the classical free-particle worldline. All that is missing from the KMM is the appropriate labeling of coordinates. The implication for the FCM is that Feynman’s prescription, Eq. 1, needs little alteration. The 4D version would be

$K\left(\mathbf{x},t\right)={\left({\displaystyle \sum _R}N\left(R\right){\left(i\mathit{ϵ}m\right)}^R\right)}_{\mathit{ϵ}=ϵ\widehat{\mathbf{x}}},(33)$

where the subscript $\mathit{ϵ}=ϵ\widehat{\mathbf{x}}$ indicates that the paths in the sum are in the spacetime plane defined by the spatial unit vector $\widehat{\mathbf{x}}$ and the t-axis.

6 Conclusion

In the introduction, the context of the extension of the chessboard model was framed in a central question (2). Minkowski’s original insight of changing the spacetime signature via x₄ = ict, and Schrödinger’s analytic continuation that replaced a (real positive) diffusion constant with $\frac{i\hslash }{2m}$, appears to be united in the FCM as the single “corner rule” that facilitates both spacetime and quantum propagation.

The failure of a simple 4D generalization of the chessboard seemed to indicate that the FCM itself might be an artefact of a 2D spacetime. This would support the commonly held view that the Dirac equation represents a marriage of two distinct entities, quantum propagation and spacetime.

In this article, we have seen that regardless of its status as a quantum mechanical model, from the perspective of spacetime, the FCM arises from spacetime diagrams that allow worldlines to have a fixed inner scale determined by the mass m. Furthermore, this context extends to a 4D spacetime based on the behavior of Lorentz transformation. This is, then, compatible, via the KMM, with a propagator that satisfies the full free-particle Dirac equation.

The simple extension to 4-D argues for a more intimate relationship between special relativity and quantum propagation than usually assumed. It supports the view that quantum propagation is a manifestation of the odd signature of spacetime, making quantum propagation itself an intrinsically relativistic effect that manifests itself at low speeds as “non-relativistic” quantum mechanics.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

GO: writing–original draft and writing–review and editing.

Funding

The author declares that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

This paper is dedicated in memory of J. A. Gualtieri, explorer, mentor, and troubadour of science and life.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1286030/full#supplementary-material

Footnotes

¹First referred to as such by H. A. Gersch, it is also known as the Checkerboard model. We shall refer to it as the FCM.

²There are many formulations and contexts for these equations. They may be written as a pair of first-order coupled partial differential equations or as a single second-order partial differential equation. A useful context for our purposes is for diffusive particles with a fixed mean free speed.

³The Fourier transform here is a generating function that counts steps along the spatial axis. Notably, $P_F^n(ϵ)=P_F(nϵ)$ and in products involving the switch S_K, the effect of the switch is to change the direction of counting.

⁴Cf. the relation between the diffusion equation and Schrödinger’s equation.

⁵Orientation here is the sign of velocity with respect to the chosen space axis.

⁶To distinguish events as just points in spacetime, from successive events on worldlines separated by causal areas, we refer to the latter by capitalizing the E.

⁷Each individual fraternal path contains enough information to reproduce its fraternal twin and the pair itself. A single photon path does not contain enough information to reproduce the other photon path.

⁸An alternative view of the new switch is that it changes the interaction of the fraternal paths from spatial reflection on crossing to transparency on crossing. In terms of geometric algebra, if the Pauli matrix σ_x is the vector that represents space and σ_z represents time, then S_M = iσ_y is the bivector that represents the resulting oriented area σ_z ∧ σ_x.

⁹Supplementary Appendix A1 provides some perspective on this. If instead we keep the original orientation, we still inherit the algebraic structure of the M-switch, but the implicit ensemble average places it underneath an exponential decay.

¹⁰As in Feynman paths vs. Wiener paths, the former code for a “virtual” ensemble of paths is associated with a single “wavefunction,” whereas the Wiener integral codes for a probability density function of an ensemble of actual paths in a fluid.

¹¹For example, in space-time, x and t are independent, but so are y and t and x and y, so in the propagator, the two orthogonal space-time planes are handled separately. In Minkowski space, neither x and t nor y and t are independent. The two spacetime planes cannot be separately handled. This represents a severe restriction on available paths.

¹²This is a feature of Lorentz boosts. They produce time dilation and length contraction only in spacetime planes generated by the boost direction.

¹³Either choice only gives different representations of the same process [7].

¹⁴Indeed, looking at (21 a)’s amendment to Minkowski space, we see in retrospect that the Dirac equation corrects the Schrödinger equation in two ways. The first way is the obvious imposition of c as a maximum speed. The second is the preservation of the inertial direction through all scales. In a way, Schrödinger propagation is a happy collusion between the removal of the finite speed limit and allowing the independence of space and time. In the classical case, it is mirrored by the fact that the telegraph and diffusion equations are connected in a similar fashion.

¹⁵Here, we are choosing $m=\frac{\pi }{2}$, so the switching conveniently occurs at integers

References

1. Feynman RP, Hibbs AR. Quantum mechanics and path integrals. New York: McGraw-Hill, USA, 1965.

Google Scholar

2. Gleick J. Genius. UK: Abacus (1992).

Google Scholar

3. Narlikar J. Path ampltudes for Dirac particles. J Indian Math Soc (1972) 36(9–32).

Google Scholar

4. Gaveau B, Jacobson T, Kac M, Schulman LS. Relativistic extension of the analogy between quantum mechanics and brownian motion. Phys Rev Lett (1984) 53(5):419–22. doi:10.1103/physrevlett.53.419

CrossRef Full Text | Google Scholar

5. Jacobson T, Schulman LS. Quantum stochastics: the passage from a relativistic to a non-relativistic path integral. J Phys A (1984) 17:375–83. doi:10.1088/0305-4470/17/2/023

CrossRef Full Text | Google Scholar

6. Ord GN. A reformulation of the feynman chessboard model. J Stat Phys (1992) 66:647–59. doi:10.1007/bf01060086

CrossRef Full Text | Google Scholar

7. Kauffman LH, Noyes HP. Discrete physics and the Dirac equation. Phys Lett A (1996) 218:139–46. doi:10.1016/0375-9601(96)00436-7

CrossRef Full Text | Google Scholar

8. Ord GN. Classical particles and the Dirac equation with an electromagnetic field. Chaos, Solitons and Fractals (1997) 8(5):727–41. doi:10.1016/s0960-0779(96)00059-8

CrossRef Full Text | Google Scholar

9. Ord GN, Gualtieri JA. Information loss in the continuum limit and Schrödinger’s equation in an electromagnetic field. BioSystems (1998) 46:21–8. doi:10.1016/s0303-2647(97)00077-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Frank D, Tony) Smith . Hyperdiamond feynman checkerboard in 4-dimensional spacetime (1995). quant-ph 9503015.

Google Scholar

11. McKeon DGC, Ord GN. Time reversal in stochastic processes and the Dirac equation. Phys Rev Lett (1992) 69(1):3–4. doi:10.1103/physrevlett.69.3

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ord GN. The Schrödinger and diffusion propagators coexisting on a lattice. J Phys A (1996) 29(5):L123–8. doi:10.1088/0305-4470/29/5/007

CrossRef Full Text | Google Scholar

13. Jacobson T. Spinor chain path integral for the Dirac equation. J Phys A (1984) 17:2433–51. doi:10.1088/0305-4470/17/12/015

CrossRef Full Text | Google Scholar

14. McKeon DGC, Ord GN. On the Dirac equation in 3+1 space. Ann Phys (1993) 222:244–53.

CrossRef Full Text | Google Scholar

15. Rosen G. Feynman path summation for the Dirac equation: an underlying one-dimensional aspect of relativistic particle motion. Phys Rev A (1983) 28(2):1139–40. doi:10.1103/physreva.28.1139

CrossRef Full Text | Google Scholar

16. Kull A, Treumann R. On the path integral of the relativistic electron. Int J Theo Phys (1999) 38:1423–8. doi:10.1023/a:1026637015146

CrossRef Full Text | Google Scholar

17. McKeon DGC, Ord GN. Time reversal and a stochastic model of the Dirac equation in an electromagnetic field. Can J Phys (2004) 82(1):19–27. doi:10.1139/p03-120

CrossRef Full Text | Google Scholar

18. Ord GN, Gualtieri JA. A realistic setting for feynman paths. Chaos, Solitons and Fractals (2002) 14(7):929–35. doi:10.1016/s0960-0779(02)00043-7

CrossRef Full Text | Google Scholar

19. Ord GN, Gualtieri JA. The Feynman propagator from a single path. Phys Rev Lett (2002) 89(25):250403–7. doi:10.1103/physrevlett.89.250403

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Jack Ng Y, van Dam H. A geometrical derivation of the Dirac equation. Phys Lett A (2003) 309(5-6):335–9. doi:10.1016/s0375-9601(03)00210-x

CrossRef Full Text | Google Scholar

21. Ord GN, Gualtieri JA, Mann RB. A discrete, deterministic construction of the phase in Feynman paths. Foundations Phys Lett (2006) 19(5):471–80. doi:10.1007/s10702-006-0905-9

CrossRef Full Text | Google Scholar

22. Ord GN. Statistical mechanics and the ghosts of departed quantities (2019). arXiv:1901.11066 [physics.hist-ph].

Google Scholar

23. Ord GN, Mann RB, Harley E. Zenon harley, qin qin lin, and andrew lauritzen. Numerical experiments in relativistic phase generation through time reversal. Adv Stud Theor Phys (2009) 3(3):99–130.

Google Scholar

24. Ord GN. Spacetime and quantum propagation from digital clocks. In: PRRL Amoroso, and LH Kauffman, editors. The physics of reality: space, time, matter, cosmos. Shanghai: World Scientific (2013). p. 111–8.

CrossRef Full Text | Google Scholar

25. Ord GN. Feynman’s corner rule; quantum propagation from special relativity. Int J Theor Phys (2010) 49:2528–39. doi:10.1007/s10773-010-0445-8

CrossRef Full Text | Google Scholar

26. Gersch HA. Feynman’s relativistic chessboard as an Ising model. Int J Theor Phys (1981) 20:491–501. doi:10.1007/bf00669436

CrossRef Full Text | Google Scholar

27. Kac M. A stochastic model related to the telegrapher’s equation. Rocky Mountain J Maths (1974) 4(3):497–509. doi:10.1216/rmj-1974-4-3-497

CrossRef Full Text | Google Scholar

28. Ising E. Beitrag zur theorie des ferromagnetismus. Z Phys (1925) 31(1):253–8. doi:10.1007/bf02980577

CrossRef Full Text | Google Scholar

29. Kramers HA, Wannier GH. Statistics of the two-dimensional ferromagnet. Part I. Phys Rev (1941) 60:252–62. doi:10.1103/physrev.60.252

CrossRef Full Text | Google Scholar

30. Ord GN. Superposition as a relativistic filter. Int J Theor Phys (2017) 56:2243–56. doi:10.1007/s10773-017-3372-0

CrossRef Full Text | Google Scholar

31. Ord GN. How does spacetime tell an electron how to move? Symmetry (2021) 13(12):2283. doi:10.3390/sym13122283

CrossRef Full Text | Google Scholar