- 1Department of Big Data Management and Application, School of International Economics and Management, Beijing Technology and Business University, Beijing, China
- 2Department of Automation, School of Information Science and Technology, Donghua University, Shanghai, China
- 3School of Electrics and Computer Engineering, Nanfang College, Guangzhou, China
- 4Advanced Data Group, Tencent, Palo Alto, CA, United States
This paper studies the influence of diverse strategy-updating timescales on the evolution of cooperation, defection, and extortion strategies in a double-layer lattice. Individuals can adjust the frequencies with which they updating their strategies adaptively according to their fitness and interlayer information. On the basis of Fermi dynamics, we find that information sharing between the two lattice layers can effectively promote cooperative behavior in a double-layer lattice. In each lattice layer, cooperation–extortion alliances can be formed to defend against invasion by defection. We find that there exists an optimal value of the extortion factor to promote the evolution of cooperation and that the frequency of cooperation in a double-layer lattice is higher than that in a single-layer one.
1 Introduction
The emergence of cooperation is a scientific problem widely studied in both natural and social contexts. The prisoner’s dilemma (PD) game model provides a uniform framework in which this phenomenon can be studied [1]. In the PD game model, a cooperator pays a certain cost (c) to provide benefits (b) to an opponent, while a defector pays nothing, and the corresponding Nash equilibrium is mutual defection. In the traditional PD game model, the payoff of both sides depends on the strategy of the opponent, and the zero-determinant (ZD) strategy ensures that the payoff of both sides is linear [2]. One important subset of the ZD strategy is called the extortion strategy, in which it is unilaterally guaranteed that a player’s own payoff is χ > 1 times that of its opponent. When the extortion strategy meets the defection strategy, both of players gain zero, and the relationship between them is neutral drifting. Hence, defection can invade an extortion population, which means that the evolution of the extortion strategy is unstable within a well-mixed population [3]. Studies have suggested that the extortion strategy can act as a catalyst to promote the emergence of cooperation in small well-mixed populations [4–7]. Therefore, the evolution of cooperation in populations based on the extortion strategy deserves further study [8–11].
Network reciprocity provides a useful mechanism for escaping the dilemma of mutual defection [12–14]. In networked games, each individual is located on a node of the underlying interactive network and competes with those neighbors that are directly connected. In the PD game, in regular spatial networks, cooperators can form tight clusters for defense from invasion by defectors [15–24]. In heterogeneous scale-free networks, cooperators can easily occupy the hubs and establish positive feedback with their cooperative neighbors, thereby ensuring the evolution of cooperation [25–30]. In multilayer networks, the reciprocity between different layers greatly facilitates the emergence of cooperation [31–41].
There are many other mechanisms to facilitate the evolution of cooperation, such as those based on memory [42, 43] and timescales [44, 45]. The process of an evolutionary game usually involves two timescales: an interaction timescale, which describes how many times individuals play the game, and a strategy-updating timescale, which represents the frequency with which strategies are updated [46]. Most previous studies have assumed that these two timescales are identical, with individuals updating strategies immediately after playing a round of games. However, some investigations have considered cases in which the two timescales differ, which leads to a nontrivial evolutionary path of cooperation [8, 10, 47–52].
This paper studies the evolution of cooperation in a double-layer network where interactions occur on a shorter timescale than that on which strategies are updated, i.e., individuals are allowed to hold on to their current strategies and interact in several rounds of the PD game before updating these strategies. In particular, we assume that the strategy-updating timescale of an individual is dependent on both its fitness and its current strategy. In this paper, the strategy-updating timescale of each individual is associated with the performance of its current strategy in the other layer of the network in such a way that the higher the fitness of its strategy in the other layer, the longer is the time interval in which the individual is able to retain its current strategy. Under the reciprocity between the different layers of the network, the individual is reluctant to change its current strategy even if a neighbor with another strategy has a higher fitness. We study a networked evolutionary PD game in a double-layer lattice with the aim of revealing the interaction mechanism in the case of heterogeneous timescales. We first introduce our model and then present our numerical and analytical results in detail. Finally, we present the conclusions of our work.
2 Methods
We consider the PD game staged in a double-layer lattice where each layer is a 100 × 100 square lattice with periodic boundary conditions. The two lattices are not physically connected, while their interdependence is one-to-one, and will be introduced as part of the strategy updating described below. In each layer of the lattice, individuals choose one of three strategies: unconditional cooperation (C), unconditional defection (D), or extortion (Eχ) and interact with their k = 4 von Neumann neighbors. The long-term payoff matrix of the three strategies can be obtained as follows [5]:
 (1)Here, χ > 1 is the extortion factor: the larger the value of χ, the more extortioners exploit their partners. In contrast to the neutral drifting relationship between extortion and defection, a cooperator can obtain a small but positive benefit from its extortionate neighbor and form a snowdrift-like relationship, i.e., the best response to the extortionate neighbor is to choose cooperation. The parameter b determines the benefit factor: the larger the value of b, the more difficult it is for cooperation to emerge. By setting b − c = 1, there are only these two parameters in the payoff matrix.
(1)Here, χ > 1 is the extortion factor: the larger the value of χ, the more extortioners exploit their partners. In contrast to the neutral drifting relationship between extortion and defection, a cooperator can obtain a small but positive benefit from its extortionate neighbor and form a snowdrift-like relationship, i.e., the best response to the extortionate neighbor is to choose cooperation. The parameter b determines the benefit factor: the larger the value of b, the more difficult it is for cooperation to emerge. By setting b − c = 1, there are only these two parameters in the payoff matrix.We assume that strategy updating can only be carried out between neighbors in the same layer of the lattice, rather than between networks in different layers. That is, at each step t, the individual i in the upper layer of the lattice updates its strategy according to the probability
Here fi represents the fitness of individual i, which is calculated according to the payoff matrix. If individual i decides to update its strategy, it will randomly select a neighbor j from the four neighbors in the upper layer of the lattice and learns j’s strategy with probability
Here, Si (Sj) is the current strategy of i (j), and κ represents the rationality of the individual, and generally is set as κ = 0.1 [47]. Individual i′ in the lower layer of the lattice performs the same strategy-updating step. ηi is the strategy-updating timescale factor of the individual i and is calculated by
Here, Γi′ is the set consisting of individual i′ and its neighbors in the other layer of the lattice corresponding to i. It can be seen that the strategy-updating timescale factor η of the individual is closely related to the current strategy of that individual, and it is related to the fitness of the individual and the fitness of the current strategy in the other layer of the lattice. If the current strategy of the individual can obtain a higher fitness in the other layer of the lattice, feedback of interlayer information will make the individual tend to maintain its current strategy and delay the updating of this strategy.
Initially, each individual has an equal chance to choose one behavior from the strategies C, D, and Eχ. In this paper, we perform 20 independent runs in the double-layer lattice to eliminate randomness in the process of updating strategies. Each time, we obtain the frequencies of different strategies for each layer lattice through averaging over the last 10 000 generations after the transient state of 90 000 generations. Below, we presents results and an analysis to reveal how cooperation evolves in the presence of defection and extortion strategies in the double-layer lattice.
3 Results
First, we study the influence of the interlayer information sharing mechanism on the evolution of the three strategies in the double-layer lattice when the extortion factor is relatively small (χ = 1.5). Figure 1 shows the influence of the interlayer information sharing mechanism on the frequencies of the cooperation, defection, and extortion strategies. The trends of the strategy frequencies are the same in both layers, and so here we only present the results for one of them. As can be seen in Figure 1A, in the case of η = 1, i.e., when there is no information sharing between the two layers of the lattice, the strategy-updating timescale factor is only related to the fitness of the individuals. With increasing benefit factor b, the frequency of cooperation rapidly drops to zero, and the frequency of defection rapidly rises to one, while the frequency of the extortion strategy is always zero, and an extortion strategy cannot exist in the network. Interestingly, when the interlayer information sharing mechanism is introduced, the frequency of cooperation is greatly promoted, as is shown in Figure 1B. As b increases, an extortion strategy can emerge in the network. When b is large (b = 2), the cooperation and extortion strategies vanish, and defection dominates the network.
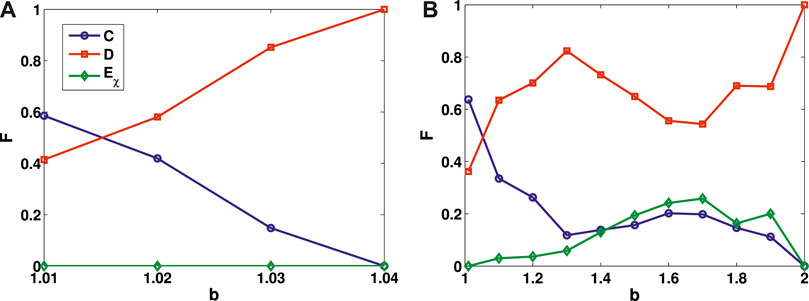
FIGURE 1. Frequencies of cooperation, defection, and extortion strategies as functions of benefit factor b for an extortion factor χ = 1.5. (A) No interlayer information sharing mechanism. (B) Information sharing between the two layers of the lattice.
We then analyze the evolution of the average fitness ⟨f⟩ and strategy frequency F over time without and with an interlayer information sharing mechanism. At first, the three strategies are randomly distributed in the network. Because the values of b and χ are both small (b = 1.1 and χ = 1.5), cooperators have the highest fitness, as shown in Figure 2A. In the absence of an interlayer information sharing mechanism, an individual only adjusts the strategy-updating timescale according to its own fitness. The frequency of cooperation reaches its peak quickly at around t = 20, as shown in Figure 2B. At the same time, the average fitness of cooperators in the network reaches its maximum. Since the value of χ is relatively small at this time, extortioners tend to share payoff with cooperators, and the neighbors who encounter extortion and defection get nothing. Cooperators get a small but positive payoff from extortioners and a positive payoff from their cooperative neighbors. Hence, cooperators can invade extortionate clusters, and the extortion strategy will gradually diminish and eventually die out. When the extortion strategy dies out and cooperation faces defection alone, the average fitness of the cooperators in the network drops sharply to a negative value. Finally, cooperation dies out in the network, while defection takes over the whole network.
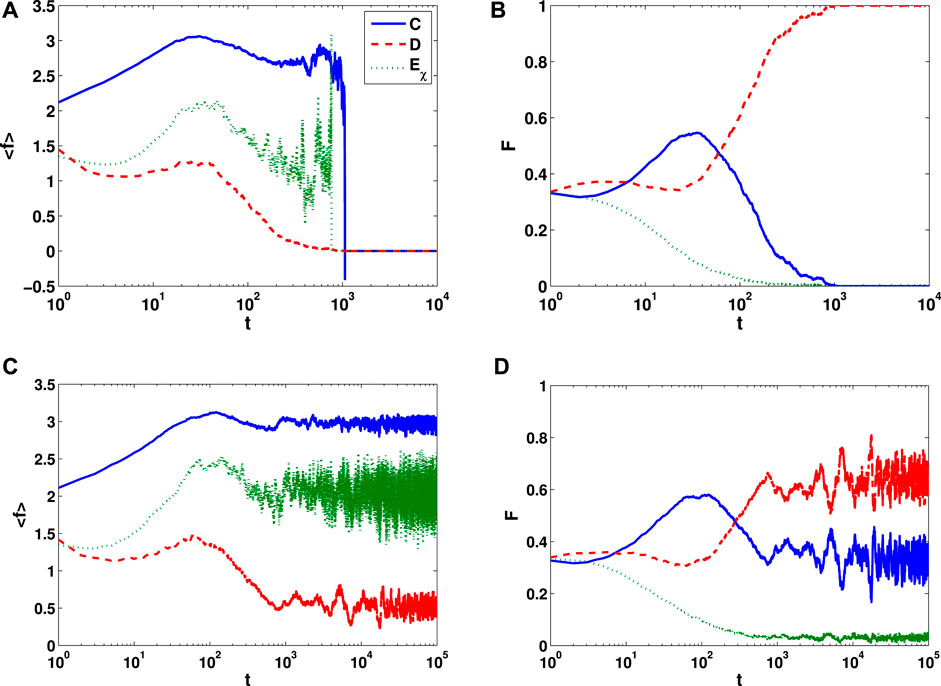
FIGURE 2. Average fitnesses ⟨f⟩ and frequencies F of cooperation, defection, and extortion strategies as functions of the time step t for an extortion factor χ = 1.5 and a benefit factor b = 1.1. (A,B) No interlayer information sharing mechanism. (C,D) Information sharing between the two layers of the lattice.
When the interlayer information sharing mechanism is introduced, the fitness of the current strategy in the other layer of the lattice needs to be taken into account when an individual updates its strategy. With the evolution of the time step, as is shown in Figure 2C, the average fitness of cooperators in the network becomes higher than those of extortioners and defectors. It can be seen from Figure 2D that the frequency of cooperation first increases and then decreases, the frequency of defection first fluctuates slightly and then increases, and the frequency of the extortion strategy gradually decreases. At about t = 800, cooperation and defection wane and wax, and the extortion strategy is less prominent in the network. Since the average fitness of extortion strategies in the network is positive, it can be inferred that the few extortioners that survive are primarily close to cooperators. Finally, cooperation, defection, and extortion strategies coexist in the network.
Next, we observe the evolution of strategies without interlayer information sharing through a set of strategy distribution patterns at different time intervals. Figure 3 describes the distribution of the cooperation, defection, and extortion strategies in the network when t = 1, 20, 100, and 10 000. Blue, red, and green represent the cooperation, defection, and extortion strategies, respectively. Initially, as shown in Figure 3A, the three strategies are randomly mixed in the network. Cooperators with high fitness can persist and spread their cooperative behaviors to their neighbors under regulation of the strategy-updating timescale. As shown in Figure 3B, cooperation has spread to the positions originally belonging to the extortion strategy. Since cooperative pairs in the network are randomly established at this time, and their mutual support is very fragile, cooperation cannot be maintained in the absence of large cooperative clusters. Under the influence of the fast Fermi updating rules and the rationality κ of the individual, cooperation is gradually reduced, as shown in Figure 3C. In the absence of the extortion strategy, it is difficult for cooperation to defend against defection. In the final state, defectors occupy the whole network, as shown in Figure 3D.
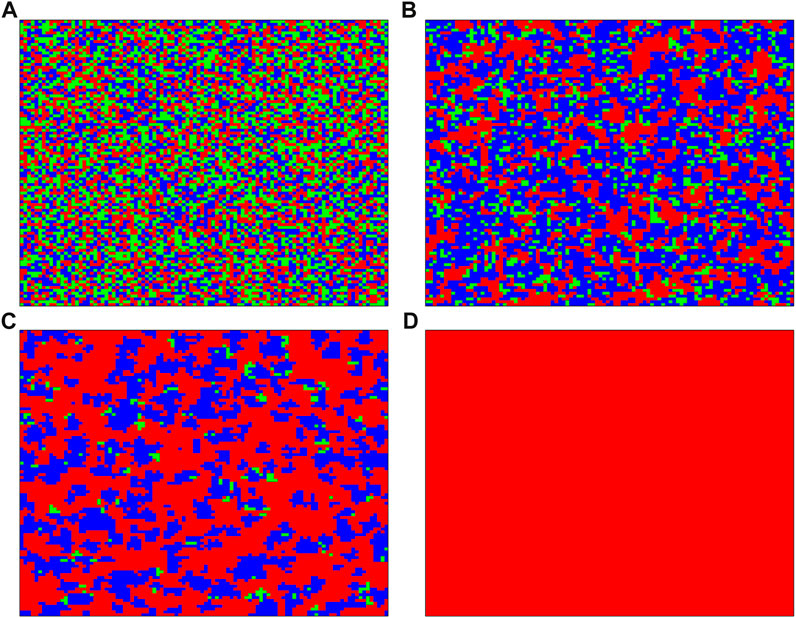
FIGURE 3. Strategy distribution pattern at different time steps without an interlayer information sharing mechanism for b = 1.1 and χ = 1.5. Blue, red, and green represent the cooperation, defection, and extortion strategies, respectively. The time steps are (A) t = 1, (B) t = 20, (C) t = 100, and (D) t = 10 000.
In the same way, we analyze the distribution of strategies that introduce interlayer information sharing mechanism between layers by using the spot map. At the initial time (t = 1), cooperation, defection, and extortion strategies are randomly distributed in the network, as shown in Figure 4A. Because the fitness of cooperation is high, under adjustment of the strategy-updating timescale, cooperators can persist and spread their cooperative behaviors. When t = 100 and t = 200, cooperation gradually invades the extortion strategy, as shown in Figures 4B, C. Owing to the regulation of the information sharing mechanism between layers, a few extortioners can be connected with the cooperators to survive. However, after cooperators with high fitness form an alliance with extortioners, they can effectively resist invasion by defectors. Finally, the three strategies coexist in the network, as shown in Figure 4D.
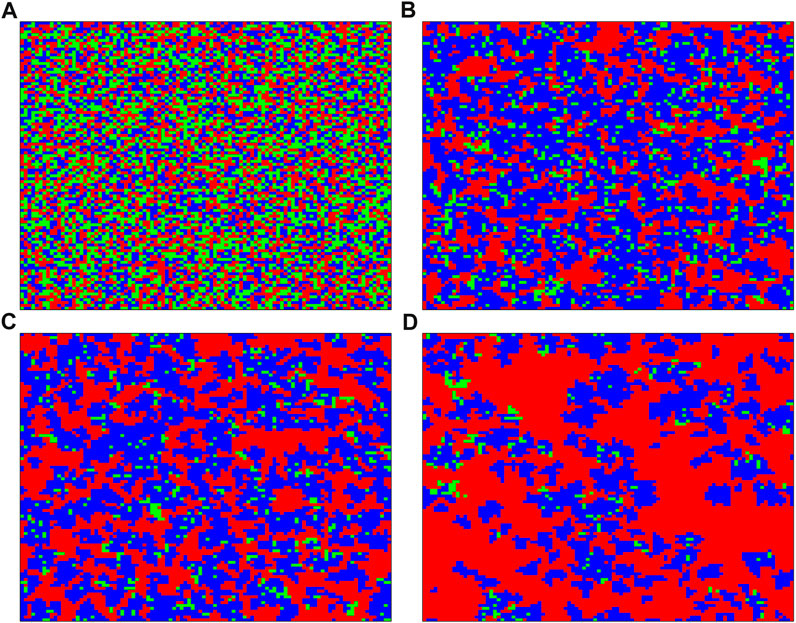
FIGURE 4. Strategy distribution patterns at different time steps with an interlayer information sharing mechanism for b = 1.1 and χ = 1.5. Blue, red, and green represent the cooperation, defection, and extortion strategies, respectively. The time steps are (A) t = 1, (B) t = 100, (C) t = 200, and (D) t = 100 000.
We have analyzed and compared the evolution of strategies without and with an interlayer information sharing mechanism in the case of a relatively small extortion factor. Now, we change it to χ = 5.0 to further study the influence of the extortion strategy on cooperation under adjustment of the interlayer information sharing mechanism. As shown in Figure 5A, in the absence of an information sharing mechanism, a relatively high extortion factor can greatly promote the evolution of cooperation strategies. With increasing benefit factor b, the frequency of cooperation first decreases, then increases, and then decreases, the frequency of extortion strategy keeps increasing, and the frequency of defection first increases and then decreases sharply to zero. When b ≥ 1.2, defection vanishes, and cooperation and extortion strategies coexist in the network. Comparison with Figure 1A shows that when the extortion factor is increased, extortion strategies can emerge in the network and help cooperation evolve. Reference [10] have found that in a single-layer lattice, when individuals adjust the strategy-updating timescale according to fitness under a high extortion factor, a variable strategy-updating timescale can help cooperation reduce the speed of strategy updating after a high fitness has been obtained, thus promoting the formation of a cooperation–extortion strategy alliance in the network. In this way, the frequency of cooperation can be increased. Henceforth in this paper, we will no longer consider evolution without information sharing between layers, but will focus on interlayer information feedback.
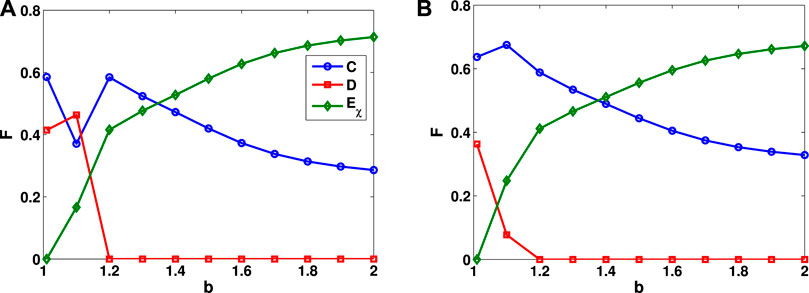
FIGURE 5. Frequencies F of cooperation, defection, and extortion strategies as functions of the benefit factor b for χ = 5.0. (A) No interlayer information sharing mechanism; (B) Information sharing between the two layers of the lattice.
When the interlayer information sharing mechanism is introduced, with increasing benefit factor b, the frequency of cooperation first increases slightly and then decreases, the frequency of the extortion strategy increases continuously, while the frequency of defection decreases to zero, as shown in Figure 5B. When b ≥ 1.2, cooperation and extortion strategies coexist in the network. As can be seen from comparison with Figure 5A, when the interlayer information sharing mechanism is introduced, the frequency of cooperation increases, while the threshold for extinction of defection stays the same. Comparison with Figure 1B shows that with the increased extortion factor, extortion strategies can emerge in the network, and the frequency of cooperation is greatly increased, while defection cannot exist in the network when b ≥ 1.2.
Next we analyze the evolution of the strategies and their pairs with time. The three strategies of cooperation, defection, and extortion can form six different pairs in the network, namely, cooperation–cooperation (C–C), cooperation–defection (C–D), cooperation–extortion (C–Eχ), defection–defection (D–D) pair, defection-extortion (D–Eχ), and extortion–extortion (Eχ–Eχ) pairs. Figures 6A, B show the evolution of the upper layer of the lattice, and Figures 6C, D show the evolution of the lower layer. It can be seen that the frequencies of the strategies and strategy pairs evolve similarly over time in the upper and lower layers of the network. At first, the three strategies are distributed randomly and occupy one-third of the network, as shown in Figures 6A, C. Meanwhile, as shown in Figures 6B, D, C–C, D–D, and Eχ–Eχ pairs each account for one-ninth, and the remaining three strategy pairs C–D, D–Eχ, and D–Eχ each account for two-ninths. Since the values b = 1.3 and χ = 5.0 are both large, cooperation is invaded by the defection and extortion strategies, and therefore the frequency of cooperation decreases, while the frequencies of defection and extortion strategies increase, and those of C–C, C–D and C–Eχ pairs decrease. At around t = 10, the rate of decline of C–C and C–Eχ pairs slows down to give a stable period, while the proportion of C–D pairs is still decreasing, which indicates that some individuals adopting an extortion strategy form a stable cooperation–extortion strategy alliance structure with the remaining cooperators in the network. As time passes, the cooperation–extortion strategy alliance gradually comes to occupy part of the network and begin to spread, and hence the frequency of cooperation begins to rise, while the frequency of defection begins to decline, and the frequencies of C–C and C–Eχ pairs gradually increase. Finally, cooperation and extortion strategies coexist in the lattice, while defection vanishes.
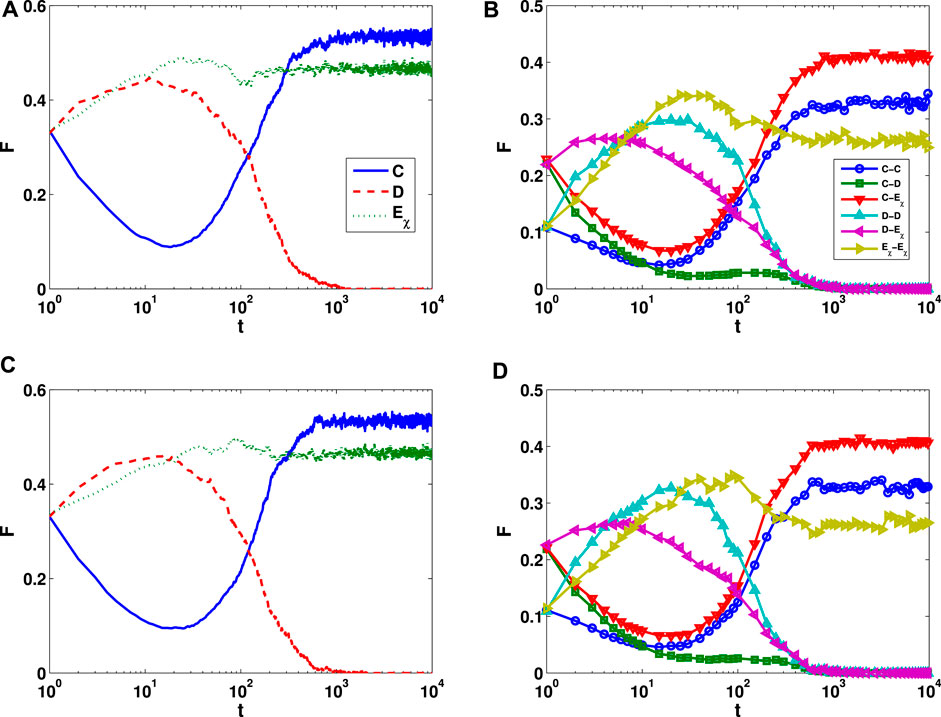
FIGURE 6. Evolution of strategies and strategy pairs in a double-layer lattice for b = 1.3 and χ = 5.0. (A,B) Results in the upper layer of the lattice. (C,D) Results in the lower layer.
Although the trends of the frequencies of strategies and pairs in the two lattice layers are similar, we find that the strategy distribution in the upper and lower layers of the network is asymmetrical. Figure 7 shows the strategy distribution patterns of the upper and lower layers at different time steps. Figures 7A–D show the results for the upper layer and Figures 7E–H those for the lower layer. Initially, the strategies are randomly distributed in the network, as shown in Figures 7A, E. It can be seen from the payoff matrix (1) that in the beginning, the defection and extortion strategies gain more from cooperation, and cooperation is invaded by the defection and extortion strategies. As shown in Figures 7B, F, at around t = 20, the surviving cooperators are mainly associated with extortioners. Once the fitness of a cooperator becomes high, the cooperator slows down its rate of strategy renewal and forms an alliance with an extortioner to spread across the network. At around t = 100, in the cooperation–extortion strategy alliance, the extortion strategy protects cooperation from being invaded by defection, and hence defection cannot get in touch with cooperation and gain benefit from it, while the extortion strategy on the border can resist invasion by defection, because it can gain greater benefit from internal cooperation, as shown in Figures 7C, G. Finally, as shown in Figures 7D, H, extortion and cooperation strategies coexist in the network, while defection can no longer survive in the network.
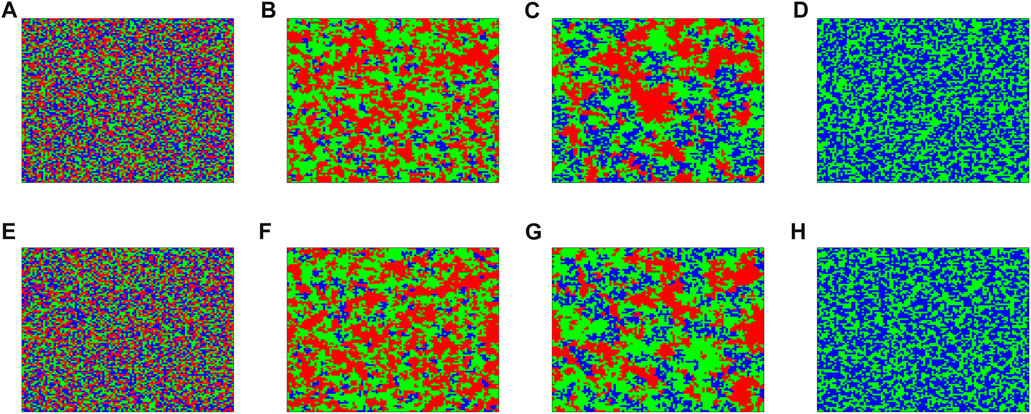
FIGURE 7. Strategy distribution patterns at different times in a double-layer lattice for b = 1.3 and χ = 5.0. (A–D) Results in the upper layer of the lattice. (E–H) Results in the lower layer. The time steps are (A,E) t = 1, (B,F) t = 20, (C,G) t = 100, and (D,H) t = 10 000.
We finally study the effects of the extortion factor χ on the frequencies of cooperation (FC), defection (FD), and extortion
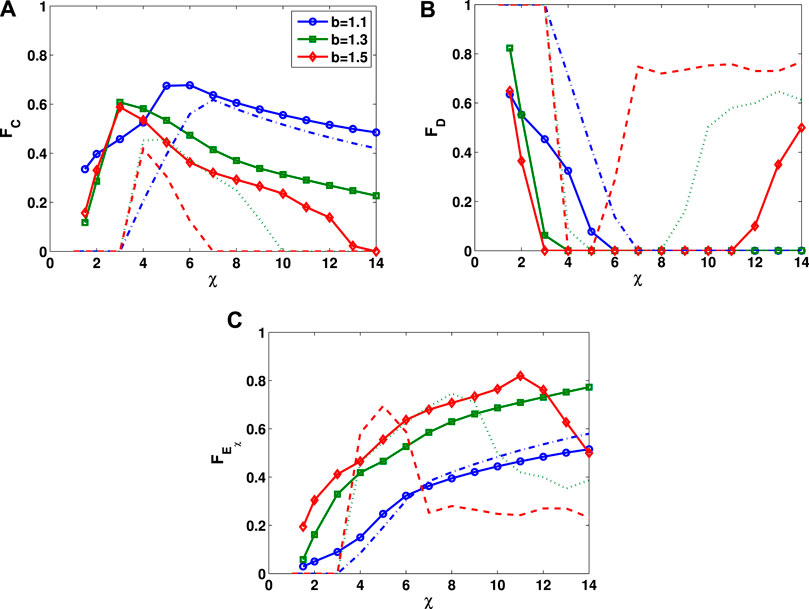
FIGURE 8. Frequencies of (A) cooperation (FC), (B) defection (FD), and (C) extortion
The dashed lines in Figure 8 show the results for a single-layer lattice. We find that no matter whether a lattice is single-layer or double-layer, there exists an optimal extortion factor χ for which cooperation have the highest frequency. However, for the same value of the benefit factor b, the optimal value of χ in a single-layer lattice is higher than that in a double-layer lattice, which means that in a single-layer lattice, a greedy extortion strategy is needed to resist invasion by defection. Meanwhile, we find that when the value of χ is small, in contrast to the defection-dominant network that arises in a single-layer lattice, cooperation, defection, and extortion strategies can coexist in a double-layer lattice. At each value of χ, the frequency of cooperation in a double-layer lattice is higher than that in a single-layer lattice. Therefore, under adjustment of the strategy-updating timescale, a double-layer lattice is more conducive to the emergence of cooperation than a single-layer lattice.
4 Discussion
In this paper, we have studied the effects of extortion strategies on the evolution of cooperation in a double-layer lattice. Individuals can adjust the strategy-updating timescale according to their fitness and the current performance of their strategy in the other layer of the network. Strategy updating occurs only in the same layer lattice, and interlayer information sharing will affect the speed of strategy updating. Our results show that when the extortion factors in the two layers of the lattice are the same, the trend of strategy evolution in the upper and lower layers is similar. When the extortion factors in a double-layer lattice are small, the diversity in the strategy-updating timescale, that is, enabled by the double-layer network structure greatly promotes the level of cooperation compared with what can be achieved in the absence of an interlayer information sharing mechanism. Finally, we find that the extortion factor has a nonmonotonic effect on the emergence of cooperation in the network. An appropriate value for the extortion factor can promote the evolution of cooperation in the network, and a double-layer lattice is more conducive to the evolution of cooperation than a single-layer network.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YM: Data curation, Formal Analysis, Methodology, Writing–original draft. ZR: Data curation, Methodology, Writing–original draft. XX: Writing–original draft. ZH: Writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Program of China (No. 2022YFC3302600), and the Research Foundation for Youth Scholars of Beijing Technology and Business University, and the Project of Science and Technology Commission of Shanghai Municipality, China (22JC1401403), and the Humanities and Social Sciences Fund of Ministry of Education of the People’s Republic of China Grant (No. 21YJCZH028).
Conflict of interest
Author XX was employed by the company Tencent.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Press WH, Dyson FJ. Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proc Natl Acad Sci USA (2012) 109:10409–13. doi:10.1073/pnas.1206569109
3. Adami C, Hintze A. Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nat Commun (2013) 4:2193. doi:10.1038/ncomms3193
4. Hilbe C, Nowak MA, Sigmund K. Evolution of extortion in iterated prisoner’s dilemma games. Proc Natl Acad Sci USA (2013) 110(17):6913–8. doi:10.1073/pnas.1214834110
5. Stewart AJ, Plotkin JB. From extortion to generosity, evolution in the iterated prisoner’s dilemma. Proc Natl Acad Sci USA (2013) 110:15348–53. doi:10.1073/pnas.1306246110
6. Hilbe C, Nowak MA, Traulsen A. Adaptive dynamics of extortion and compliance. PLoS ONE (2013) 8:e77886. doi:10.1371/journal.pone.0077886
7. Stewart AJ, Plotkin JB. Collapse of cooperation in evolving games. Proc Natl Acad Sci USA (2014) 111:17558–63. doi:10.1073/pnas.1408618111
8. Rong ZH, Wu ZX, Hao D, Chen MZQ, Zhou T. Diversity of timescale promotes the maintenance of extortioners in a spatial prisoner’s dilemma game. New J Phys (2015) 17:033032–43. doi:10.1088/1367-2630/17/3/033032
9. Mao YJ, Xu XR, Rong ZH, Wu ZX. The emergence of cooperation–extortion alliance on scale-free networks with normalized payoff. EPL (2018) 122:50005. doi:10.1209/0295-5075/122/50005
10. Xu XR, Rong ZH, Tian ZH, Wu ZX. Timescale diversity facilitates the emergence of cooperation-extortion alliances in networked systems. Neurocomputing (2019) 350:195–201. doi:10.1016/j.neucom.2019.03.057
11. Zhu YY, Xia CY, Wang Z, Chen ZQ. Networked decision-making dynamics based on fair extortionate and generous strategies in iterated public goods games. IEEE Trans Netw Sci Eng (2022) 9(4):2450–62. doi:10.1109/tnse.2022.3164094
12. Szabó G, Fáth G. Evolutionary games on graphs. Phys Rep (2007) 446:97–216. doi:10.1016/j.physrep.2007.04.004
13. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep (2017) 687:1–51. doi:10.1016/j.physrep.2017.05.004
14. Allen B, Lippner G, Chen YT, Fotouhi B, Momeni N, Yau ST, et al. Evolutionary dynamics on any population structure. Nature (2017) 544:227–30. doi:10.1038/nature21723
15. Nowak MA, May R. Evolutionary games and spatial chaos. Nature (1992) 359:826–9. doi:10.1038/359826a0
16. Szabó G, Vukov J, Szolnoki A. Phase diagrams for an evolutionary prisoner’s dilemma game on two-dimensional lattices. Phys Rev E (2005) 72:047107. doi:10.1103/PhysRevE.72.047107
17. Szolnoki A, Perc M. Evolutionary dynamics of cooperation in neutral populations. New J Phys (2018) 20:013031. doi:10.1088/1367-2630/aa9fd2
18. Yang HX, Chen XJ. Promoting cooperation by punishing minority. Appl Math Comput (2018) 316:460–6. doi:10.1016/j.amc.2017.08.049
19. He NR, Chen XJ, Szolnoki A. Central governance based on monitoring and reporting solves the collective-risk social dilemma. Appl Math Comput (2018) 347:334–41. doi:10.1016/j.amc.2018.11.029
20. Huang KK, Chen XF, Yu ZF, Yang CH, Gui WH. Heterogeneous cooperative belief for social dilemma in multi-agent system. Appl Math Comput (2018) 320:572–9. doi:10.1016/j.amc.2017.10.018
21. Shen C, Chu C, Shi L, Perc M, Wang Z. Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner’s dilemma game. R Soc Open Sci (2018) 5:180199. doi:10.1098/rsos.180199
22. Li ZB, Jia DY, Guo H, Geng YN, Shen C, Wang Z, et al. The effect of multigame on cooperation in spatial network. Appl Math Comput (2019) 351:162–7. doi:10.1016/j.amc.2018.12.059
23. Shi L, Shen C, Geng YN, Chu C, Meng HR, Perc M, et al. Winner-weaken–loser-strengthen rule leads to optimally cooperative interdependent networks. Nonlinear Dyn (2019) 96:49–56. doi:10.1007/s11071-019-04772-6
24. Ding H, Zhang GS, Wang SH, Li J, Wang Z. Q-learning boosts the evolution of cooperation in structured population by involving extortion. Physica A (2019) 536:122551. doi:10.1016/j.physa.2019.122551
25. Santos FC, Pacheco JM, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl Acad Sci USA (2006) 103:3490–4. doi:10.1073/pnas.0508201103
26. Gómez-Gardeñes J, Campillo M, Floriá LM, Moreno Y. Dynamical organization of cooperation in complex topologies. Phys Rev Lett (2007) 98:108103. doi:10.1103/physrevlett.98.108103
27. Rong ZH, Li X, Wang XF. Roles of mixing patterns in cooperation on a scale-free networked game. Phys Rev E (2007) 76:027101. doi:10.1103/PhysRevE.76.027101
28. Aleta A, Meloni S, Perc M, Moreno Y. From degree-correlated to payoff-correlated activity for an optimal resolution of social dilemmas. Phys Rev E (2016) 94:062315. doi:10.1103/PhysRevE.94.062315
29. Kleineberg KK. Metric clusters in evolutionary games on scale-free networks. Nat Commun (2017) 8:1888. doi:10.1038/s41467-017-02078-y
30. Xu HD, Tian CZ, Xiao XR, Fan SH. Evolutionary investors’ power-based game on networks. Appl Math Comput (2018) 330:125–33. doi:10.1016/j.amc.2018.02.041
31. Gómez-Garde J, Reinares I, Arenas A, Floría LM. Evolution of cooperation in multiplex networks. Sci Rep (2012) 2:620. doi:10.1038/srep00620
32. Wang Z, Szolnoki A, Perc M. Rewarding evolutionary fitness with links between populations promotes cooperation. J Theor Biol (2014) 349:50–6. doi:10.1016/j.jtbi.2014.01.037
33. Wang Z, Szolnoki A, Perc M. Self-organization towards optimally interdependent networks by means of coevolution. New J Phys (2014) 16:033041. doi:10.1088/1367-2630/16/3/033041
34. Wang BK, Chen XJ, Wang L. Probabilistic interconnection between interdependent networks promotes cooperation in the public goods game. J Stat Mech Theor Exp (2012) 2012:P11017. doi:10.1088/1742-5468/2012/11/P11017
35. Jiang LL, Perc M. Spreading of cooperative behaviour across interdependent groups. Sci Rep (2013) 3:2483. doi:10.1038/srep02483
36. Wang Z, Szolnoki A, Perc M. How much interconnected should networks be for cooperation to thrive? In: A Garas, editor. Interconnected networks. Cham: Springer International Publishing (2016). p. 125–39. doi:10.1007/978-3-319-23947-7-7
37. Wang Z, Szolnoki A, Perc M. Interdependent network reciprocity in evolutionary games. Sci Rep (2013) 3:1183. doi:10.1038/srep01183
38. Szolnoki A, Perc M. Information sharing promotes prosocial behaviour. New J Phys (2013) 15:053010. doi:10.1088/1367-2630/15/5/053010
39. Xia CY, Li XP, Wang Z, Perc M. Doubly effects of information sharing on interdependent network reciprocity. New J Phys (2018) 20:075005. doi:10.1088/1367-2630/aad140
40. Santos MD, Dorogovtsev SN, Mendes JFF. Biased imitation in coupled evolutionary games in interdependent networks. Sci Rep (2014) 4:4436. doi:10.1038/SREP04436
41. Wang Z, Wang L, Perc M. Degree mixing in multilayer networks impedes the evolution of cooperation. Phys Rev E (2014) 89:052813. doi:10.1103/PhysRevE.89.052813
42. Danku Z, Perc M, Szolnoki A. Knowing the past improves cooperation in the future. Sci Rep (2019) 9:262. doi:10.1038/s41598-018-36486-x
43. Ying X, Wang J, Jin X, Wang C, Zhang Z, Wang Z. Temporal–spatial perception adjustment to fitness enhances the cooperation in the spatial prisoner’s dilemma game. Front Phys (2023) 11:1200506. doi:10.3389/fphy.2023.1200506
44. Roca CP, Cuesta JA, Sánchez A. Time scales in evolutionary dynamics. Phys Rev Lett (2006) 97:158701. doi:10.1103/physrevlett.97.158701
45. Han WW, Zhang ZP, Sun JQ, Xia CY. Emergence of cooperation with reputation-updating timescale in spatial public goods game. Phys Lett A (2021) 393:127173. doi:10.1016/j.physleta.2021.127173
46. Ohtsuki H, Nowak MA, Pacheco JM. Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs. Phys Rev Lett (2007) 98:108106. doi:10.1103/PhysRevLett.98.108106
47. Rong ZH, Wu ZX, Chen GR. Coevolution of strategy-selection time scale and cooperation in spatial prisoner’s dilemma game. EPL (2013) 102:68005. doi:10.1209/0295-5075/102/68005
48. Huang CW, Dai QL, Cheng HY, Li HH. Preferential selection based on degree difference in the spatial prisoner’s dilemma games. EPL (2017) 120:18001. doi:10.1209/0295-5075/120/18001
49. Wu ZX, Rong ZH, Holme P. Diversity of reproduction time scale promotes cooperation in spatial prisoner’s dilemma games. Phys Rev E (2009) 80:036106. doi:10.1103/PhysRevE.80.036106
50. Rong ZH, Wu ZX, Wang WX. Emergence of cooperation through coevolving time scale in spatial prisoner’s dilemma. Phys Rev E (2010) 82:026101. doi:10.1103/physreve.82.026101
51. Li ZH. Lifetime and fitness: Life process in spatial prisoner’s dilemma games. Physica A (2011) 390:4244–50. doi:10.1016/j.physa.2011.07.045
Keywords: double-layer network, cooperation, timescale variation, extortion strategy, evolutionary game theory
Citation: Mao Y, Rong Z, Xu X and Han Z (2023) Influence of diverse timescales on the evolution of cooperation in a double-layer lattice. Front. Phys. 11:1272395. doi: 10.3389/fphy.2023.1272395
Received: 04 August 2023; Accepted: 25 September 2023;
Published: 10 October 2023.
Edited by:
Minyu Feng, Southwest University, ChinaReviewed by:
Chengyi Xia, Tiangong University, ChinaXiaojie Chen, University of Electronic Science and Technology of China, China
Copyright © 2023 Mao, Rong, Xu and Han. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhihai Rong, cm9uZ3poaEBnbWFpbC5jb20=
 Yajun Mao
Yajun Mao Zhihai Rong
Zhihai Rong Xiongrui Xu
Xiongrui Xu Zhongming Han
Zhongming Han