Evolution of nanohillocks by fullerene ion-induced localized plasma

Surface nanostructures etch without chemicals; owing to this, their development is a crucial technical process. Surface nanohillocks may be created by irradiating yttrium iron garnet (YIG) with 30-MeV C₆₀ cluster ions. The nanohillock creation mechanism is disputed. In this study, we propose that the formation mechanism is a plasma collective effect of charged particles that depends on localized rogue waves. Rogue waves will explain YIG surface nanohillock creation using a traditional hydrodynamic plasma model. Analytically solving hydrodynamic ion fluid equations and Maxwellian electron distributions yields a non-linear Schrödinger equation. Solving the latter gives us plausible rogue wave domains. Rogue waves concentrate charged ions from the surroundings into a small, confined zone, generating surface nanohillocks. The relevance of different plasma parameters is highlighted in the rogue wave profile.

Introduction

The formation of surface nanostructures is of high importance in today’s nanotechnology applications. In particular, surface nanostructures created by single-ion impact have garnered tremendous interest during the last 2 decades [1, 2]. The motivation for forming nanostructures by single-ion impact is to create a nanostructure in an accurate way without chemical treatment, as in traditional lithographic techniques. The nanostructure formation is mainly located by the energy deposition of the incident ion and the material sensitivity [3]. The incident ion needs to develop accelerator technology to make it possible to produce a MeV cluster ion beam [4]. The criterion to obtain a MeV cluster beam is the ability to produce high energy comparable to, and even higher than, those observed in mono-atomic single highly charged ions. Furthermore, the volume of the impacted region where the kinetic energy is deposited and the smallness of the velocity of the cluster ions could lead to a high electronic energy density that may be enough to create nanostructures [5]. The creation mechanism of the nanostructures is still ambiguous. One of these mechanisms is based on the creation of plasma by highly charged ions. This mechanism suggests that the plasma is generated because of the strong ion-induced agitation in a nanometer-sized area close to the surface. Different theoretical approaches in plasma physics were used to explain the formation mechanisms of the nanostructures, such as plasma expansion and wake field approaches [2, 6].

We suggest another approach based on the plasma collective effect of the charged particles, which depends on the formation of rogue waves. Actually, rogue waves are governed by a strongly compressed, high number density coupled with a high energy content. The rogue wave amplitude is more than two and less than five times higher than the average wave crests. Rogue waves collect the wave energy with amplitudes substantially taller than those present in the initial conditions. Rogue waves have been explored in a variety of systems, ranging from plasma, fluids, discrete lattices, optics, ultracold quantum gases, lasers, and optical fibers [see, e.g., [7–9] and references therein]. Usually, rogue waves are created because the pulses of the system are modulationally unstable. These unstable modes were investigated in different plasma media. For example, Farokhi et al. [10] examined the propagation of nonlinear dust lattice waves in a two-dimensional hexagonal crystal. It is found that evidence is provided of modulational instability and of the occurrence of bright-type envelopes at shorter wavelengths. Shahmansouri et al. [11] examined the excitation of breather structures in degenerate relativistic plasma consisting of non-extensive electrons and cold ions. For this purpose, the multiple-time-scale perturbation technique was used to obtain a nonlinear Schrödinger equation to investigate the modulational instability of the system. Alinejad and Shahmansouri [12] studied the dissipative dust-ion acoustic (DIA) rogue waves in collisional dusty plasma with superthermal electrons. Multiple-time-scale reduction showed that the nonlinear dynamics of low-frequency waves can be reduced to a modified nonlinear Schrödinger (mNLS) equation. This equation captures the main features of modulated waves and shows a criterion for determining the maximum time for the occurrence of modulational instability.

In this context, the use of 30-MeV C₆₀ cluster ions enables the creation of nanohillocks in yttrium iron garnet (YIG) (Y₃Fe₅O₁₂), providing evidence for the nanostructures induced by MeV clusters [13]. Understanding of such nanostructure formation was attained through the plasma expansion approach in various physical situations [14, 15]. On the other hand, the high kinetic energy density deposited by C₆₀ cluster ions into a small localized region leads to strong electronic excitation. Thus, the temperature increases in the impact region, which consequently leads to the creation of nanoplasma. The plasma expansion approach used cannot explain why the ion number density of the plasma accumulates in a very small localized region, i.e., nanohillocks. It explains how the plasma propagates above the surface. Thus, it is of interest to introduce another approach that can elucidate the accumulation of the charged ions in a tiny localized zone, forming nanohillocks.

Although the present experiment was conducted using low-energy ions, we can explain this point below. One of the most important things about the MeV cluster beam is that it can produce high energy per unit volume, at least as high as single highly charged atoms (SHI). The small velocity of the cluster ions and the volume of the region where the kinetic energy is deposited result in a high electronic energy density, which is enough to create nanostructures in various materials, even those where the monatomic SHI failed. Multiplying the coefficients of the non-linear term and dispersion term shows the condition for rogue waves. After an external disruption, the amplitude-modulated envelope becomes unstable. Plasma-charged particle concentrations (rogue waves) can occur in the unstable area. For ion-acoustic waves to develop, their phase velocity must be smaller than the electron thermal speed and larger than the ion thermal speed.

Theoretical model

We suggest a new mechanism for explaining the observed results of surface nanohillocks in YIG using a hydrodynamic fluid model. We consider homogeneous and unmagnetized three-ion plasma, which consists of two positive ions “Y″ and “Fe” (hereafter, we refer to them as i and 1, respectively), one negative ion “O” (we refer to it as 2), and a background of Boltzmann-distributed electrons. Note that in our plasma model for YIG materials, the number density is high. Typical experimental data are used, such as the unperturbed electron number density of 2.91 × 10¹⁹ cm⁻³, the nanohillock height of $\approx 10^{-7}$ cm, and the time of hillock formation occurring in approximately a picosecond [14], to evaluate the electron relaxation time (or electron collision rat), which corresponds to $\approx 10^{-13}$ second [16]. Then, in such a brief time span, electrons have the possibility to thermalize and can be represented by the Boltzmann distribution. Actually, the heavier ion is yttrium. Since all three ions contribute to the system’s inertia, the electrons are responsible for its restoring force. Adopting a one-dimensional (1D) planar geometry, for simplicity, the fluid model equations read

$\frac{\partial n_j}{\partial t}+\frac{\partial }{\partial x}\left(n_j{u}_j\right)=0,(1)$

$m_i{n}_i\left(\frac{\partial u_i}{\partial t}+u_i\frac{\partial u_i}{\partial x}\right)=-q_i{n}_i\frac{\partial \varphi }{\partial x},(2)$

$m_1{n}_1\left(\frac{\partial u_1}{\partial t}+u_1\frac{\partial u_1}{\partial x}\right)=-q_1{n}_1\frac{\partial \varphi }{\partial x},(3)$

$m_2{n}_2\left(\frac{\partial u_2}{\partial t}+u_2\frac{\partial u_2}{\partial x}\right)=+q_2{n}_2\frac{\partial \varphi }{\partial x},(4)$

$\frac{{\partial }^2\varphi }{\partial x^2}=\frac{1}{{ϵ}_0}\left(e{n}_e-q_1{n}_1+q_2{n}_2-q_i{n}_i\right),(5)$

where j = i, 1, 2, |q_i| = z_ie, |q₁| = z₁e, and |q₂| = z₂e, e is the electronic charge, m_j is the mass of the j ion, n_j is the number density of the j ion, u_j is the fluid velocity of the j ion, z_j is the number of charges in the j ion, ϵ₀ is the vacuum permittivity, ϕ is the electrostatic potential, and n_e is the electron number density.

The model equations may be cast in a dimensionless form for simplicity in algebraic manipulation. Adopting appropriate scales, the normalized evolution equations become

$\frac{\partial n_j}{\partial t}+\frac{\partial }{\partial x}\left(n_j{u}_j\right)=0,(6)$

$\frac{\partial u_i}{\partial t}+u_i\frac{\partial u_i}{\partial x}=-\frac{\partial \varphi }{\partial x},(7)$

$\frac{\partial u_1}{\partial t}+u_1\frac{\partial u_1}{\partial x}=-\frac{1}{{\mu }_1}\frac{\partial \varphi }{\partial x},(8)$

$\frac{\partial u_2}{\partial t}+u_2\frac{\partial u_2}{\partial x}=\frac{1}{{\mu }_2}\frac{\partial \varphi }{\partial x},(9)$

$\frac{{\partial }^2\varphi }{\partial x^2}={\delta }_e{n}_e-{\delta }_1{n}_1+{\delta }_2{n}_2-n_i.(10)$

The re-scaled electron number density (n_e) reads

$n_e=e^{\varphi }\approx 1+\varphi +{\varphi }^2/2+{\varphi }^3/6+\cdots .(11)$

We define the quantities μ₁, μ₂, δ₁, δ₂, and δ_e as

${\mu }_1=\frac{m_1{z}_i}{z_1{m}_i},{\mu }_2=\frac{m_2{z}_i}{z_2{m}_i},{\delta }_1=\frac{z_1{n}_{10}}{z_i{n}_{i0}},{\delta }_2=\frac{z_2{n}_{20}}{z_i{n}_{i0}},{\delta }_e=\frac{n_{e0}}{z_i{n}_{i0}},(12)$

where n_i0, n₁₀, n₂₀, and n_e0 are the unperturbed number densities of “Y,” “Fe,” “O” ions, and electrons, respectively.

Time t is normalized by the “Y” positive ion plasma frequency (ω_pi), where ${\omega }_{pi}={(z_i^2{e}^2{n}_{i0}/{ϵ}_0{m}_1)}^{1/2}$. The space x is normalized by the positive ion Debye length (λ_Di), where ${\lambda }_{Di}={\left({ϵ}_0{k}_B{T}_e/z_i{e}^2{n}_{i0}\right)}^{1/2}$. The electrostatic potential ϕ is normalized by k_BT_e/e, where k_B is the Boltzmann constant and T_e is the electron temperature.

Neutrality at equilibrium imposes the following condition:

$1={\delta }_e-{\delta }_1+{\delta }_2.(13)$

Multiscale perturbative analysis

Let S be the state (column) vector (n_i, u_i, n₁, u₁, n₂, u₂, and ϕ)^T, describing the system’s state at a given position x and instant t. We shall consider small deviations from the equilibrium state S⁽⁰⁾ = (1,0,1,0,1,0,0)^T by taking

$\mathbf{S}={\mathbf{S}}^{\left(0\right)}+ϵ{\mathbf{S}}^{\left(1\right)}+{ϵ}^2{\mathbf{S}}^{\left(2\right)}+\cdots ={\mathbf{S}}^{\left(0\right)}+{\displaystyle \sum _{n=1}^{\infty }}{ϵ}^n{\mathbf{S}}^{\left(n\right)},(14)$

where ϵ ≪ 1 is a small (real) parameter. Following the standard multiple-scale technique (see e.g., in Ref. [17] for details), we shall consider a set of stretched space and time variables: T_r = ϵ^rt and X_r = ϵ^rx (for r = 0, 1, 2, 3, … ). Furthermore, the variables are expanded around their equilibrium values as

$\begin{array}{ll}\hfill n_j& =1+ϵn_{j1}+{ϵ}^2{n}_{j2}+{ϵ}^3{n}_{j3}+\cdots ,\hfill \\ \hfill u_j& =ϵu_{j1}+{ϵ}^2{u}_{j2}+{ϵ}^3{u}_{j3}+\cdots ,\hfill \\ \hfill \varphi & =ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+{ϵ}^3{\varphi }_3+\cdots ,\hfill \end{array}(15)$

for j = i, 1, 2.

We will assume that all of the perturbed states

$S^{\left(n\right)}={\displaystyle \sum _{l=-\infty }^{\infty }}{S}_l^{\left(n\right)}\left(X_j,T_j\right)e^{il\left(kx-\omega t\right)}(16)$

depend on the fast scales via the phase θ = kx − ωt only, while the slow scales enter the argument of the l − th harmonic amplitude $S_l^{(n)}$, which is allowed to vary in {X_j, T_j}. The reality condition $S_{-l}^{(n)}=S_l^{(n)*}$ is met by all state variables. According to these considerations, the derivative operators are treated as follows:

$\begin{array}{ll}\hfill {\partial }_t& ={\partial }_0+ϵ{\partial }_1+{ϵ}^2{\partial }_2+{ϵ}^3{\partial }_3+\cdot \cdot ,\hfill \\ \hfill \nabla & ={\nabla }_0+ϵ{\nabla }_1+{ϵ}^2{\nabla }_2+{ϵ}^3{\nabla }_3+\cdots ,\hfill \end{array}(17)$

i.e., defining the operators ∂_j = ∂/∂T_j and ∇_j = ∂/∂X_j. The stretched variables are treated as independent variables. Substituting the above information into the evolution Eqs 6–10, a set of polynomial equations in ϵ is obtained. Since ϵ is a free parameter, the coefficients of ϵ must vanish. Solving at successive orders provides a solution for the state variables, in terms of their harmonic amplitudes.

First order in ϵ: fundamental harmonics and linear dispersion relation. The equations in the first order of ϵ can be expressed in the form of a linear algebraic equation (a Cramer system). In order for non-trivial solutions to exist, a compatibility condition must be satisfied, leading to the dispersion relation (DR):

${\omega }^2=\left(1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}\right)\frac{k^2}{k^2+{\delta }_e},(18)$

where

$\left(\begin{array}{c}\hfill n_{i1}^{\left(1\right)}\hfill \\ \hfill u_{i1}^{\left(1\right)}\hfill \\ \hfill n_{11}^{\left(1\right)}\hfill \\ \hfill u_{11}^{\left(1\right)}\hfill \\ \hfill n_{21}^{\left(1\right)}\hfill \\ \hfill u_{21}^{\left(1\right)}\hfill \\ \hfill {\varphi }_2^{\left(1\right)}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{\mathrm{1,1}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,2}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,3}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,4}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,5}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,5}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{1,7}}^{\left(1\right)}\hfill \end{array}\right){\varphi }_1^{\left(1\right)}=\left(\begin{array}{c}\hfill \frac{k^2}{{\omega }^2}\hfill \\ \hfill \frac{k}{\omega }\hfill \\ \hfill \frac{1}{{\mu }_1}\frac{k^2}{{\omega }^2}\hfill \\ \hfill \frac{1}{{\mu }_1}\frac{k}{\omega }\hfill \\ \hfill -\frac{1}{{\mu }_2}\frac{k^2}{{\omega }^2}\hfill \\ \hfill -\frac{1}{{\mu }_2}\frac{k}{\omega }\hfill \\ \hfill 1\hfill \end{array}\right){\varphi }_1^{\left(1\right)}.(19)$

Second order in ϵ.

For zero harmonic, i.e., l = 0:

${\varphi }_2^{\left(0\right)}=\frac{1}{{\delta }_e}\left({\displaystyle \sum _j}{S}_j{\delta }_j{n}_{j2}^{\left(0\right)}-{\delta }_e|{\varphi }_1^{\left(1\right)}{|}^2\right).(20)$

The second-order corrections to the first harmonic (i.e., l = 1) amplitudes are now obtained as the vector ${\mathbf{S}}_2^{(1)}$, say, given by

$\left(\begin{array}{c}\hfill n_{i2}^{\left(1\right)}\hfill \\ \hfill u_{i2}^{\left(1\right)}\hfill \\ \hfill n_{12}^{\left(1\right)}\hfill \\ \hfill u_{12}^{\left(1\right)}\hfill \\ \hfill n_{22}^{\left(1\right)}\hfill \\ \hfill u_{22}^{\left(1\right)}\hfill \\ \hfill {\varphi }_2^{\left(1\right)}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{\mathrm{2,1}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,2}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,3}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,4}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,5}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,5}}^{\left(1\right)}\hfill \\ \hfill C_{\mathrm{2,7}}^{\left(1\right)}\hfill \end{array}\right){\nabla }_1{\varphi }_1^{\left(1\right)}=\left(\begin{array}{c}\hfill -2i\frac{k}{{\omega }^3}\left(\omega -v_{g}k\right)\hfill \\ \hfill -i\frac{1}{{\omega }^2}\left(\omega -v_{g}k\right)\hfill \\ \hfill -2i\frac{1}{{\mu }_1}\frac{k}{{\omega }^3}\left(\omega -v_{g}k\right)\hfill \\ \hfill -i\frac{1}{{\mu }_1}\frac{1}{{\omega }^2}\left(\omega -v_{g}k\right)\hfill \\ \hfill 2i\frac{1}{{\mu }_2}\frac{k}{{\omega }^3}\left(\omega -v_{g}k\right)\hfill \\ \hfill i\frac{1}{{\mu }_2}\frac{1}{{\omega }^2}\left(\omega -v_{g}k\right)\hfill \\ \hfill 0\hfill \end{array}\right){\nabla }_1{\varphi }_1^{\left(1\right)}.(21)$

The compatibility requirement for the first-harmonic component system of equations imposes the following condition:

${\partial }_1{\varphi }_1^{\left(1\right)}=-v_g{\nabla }_1{\varphi }_1^{\left(1\right)},(22)$

where we have defined the group velocity:

$v_g=\frac{d\omega }{dk}=\left(\frac{{\delta }_e}{1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}}\right)\frac{{\omega }^3}{k^3}.(23)$

Qualitatively speaking, imposing this constraint reflects the physical fact that the dominant harmonic envelope moves at the group velocity at this order, i.e., ${\varphi }_1^{(1)}={\varphi }_1^{(1)}(X_1-v_g{T}_1,X_2,T_2,\dots )$.

In an analogous way, the equations for n = l = 2 for the second-order harmonic amplitudes lead to the vector ${\mathbf{S}}_2^{(2)}$, given by

$\left(\begin{array}{c}\hfill n_{i2}^{\left(2\right)}\hfill \\ \hfill u_{i2}^{\left(2\right)}\hfill \\ \hfill n_{12}^{\left(2\right)}\hfill \\ \hfill u_{12}^{\left(2\right)}\hfill \\ \hfill n_{22}^{\left(2\right)}\hfill \\ \hfill u_{22}^{\left(2\right)}\hfill \\ \hfill {\varphi }_2^{\left(2\right)}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{\mathrm{2,1}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,2}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,3}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,4}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,5}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,6}}^{\left(2\right)}\hfill \\ \hfill C_{\mathrm{2,7}}^{\left(2\right)}\hfill \end{array}\right){\left({\varphi }_1^{\left(1\right)}\right)}^2=\left(\begin{array}{c}\hfill \frac{1}{2}\frac{k^2}{{\omega }^4}\left(3k^2+2A{\omega }^2\right)\hfill \\ \hfill \frac{1}{2}\frac{k}{{\omega }^3}\left(k^2+2A{\omega }^2\right)\hfill \\ \hfill \frac{1}{2}\frac{1}{{\mu }_1^2}\frac{k^2}{{\omega }^4}\left(2A{\mu }_1{\omega }^2+3k^2\right)\hfill \\ \hfill \frac{1}{2}\frac{1}{{\mu }_1^2}\frac{k}{{\omega }^3}\left(2A{\mu }_1{\omega }^2+k^2\right)\hfill \\ \hfill -\frac{1}{2}\frac{1}{{\mu }_2^2}\frac{k^2}{{\omega }^4}\left(2A{\mu }_2{\omega }^2-3k^2\right)\hfill \\ \hfill -\frac{1}{2}\frac{1}{{\mu }_2^2}\frac{k}{{\omega }^3}\left(2A{\mu }_2{\omega }^2-k^2\right)\hfill \\ \hfill A\hfill \end{array}\right){\left({\varphi }_1^{\left(1\right)}\right)}^2,(24)$

where we have defined the quantity:

$A=\frac{3k^4\left(1+\frac{{\delta }_1}{{\mu }_1^2}-\frac{{\delta }_2}{{\mu }_2^2}\right)-{\delta }_e{\omega }^4}{2{\omega }^2\left({\omega }^2\left(4k^2+{\delta }_e\right)-k^2\left(1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}\right)\right)}.(25)$

Third order in ϵ: derivation of a non-linear Schrödinger (NLS) equation. Non-linear self-interaction of the carrier wave also results in the creation of zeroth-order harmonics, which are obtained by the second-order equations, in combination with their third-order counterparts, for l = 0. The “vector” ${\mathbf{S}}_2^{(0)}$ thus obtained reads

$\left(\begin{array}{c}\hfill n_{i2}^{\left(0\right)}\hfill \\ \hfill u_{i2}^{\left(0\right)}\hfill \\ \hfill n_{12}^{\left(0\right)}\hfill \\ \hfill u_{12}^{\left(0\right)}\hfill \\ \hfill n_{22}^{\left(0\right)}\hfill \\ \hfill u_{22}^{\left(0\right)}\hfill \\ \hfill {\varphi }_2^{\left(0\right)}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{\mathrm{2,1}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,2}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,3}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,4}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,5}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,6}}^{\left(0\right)}\hfill \\ \hfill C_{\mathrm{2,7}}^{\left(0\right)}\hfill \end{array}\right)|{\varphi }_1^{\left(1\right)}{|}^2=\left(\begin{array}{c}\hfill \frac{1}{v_g^2{\omega }^3}\left(\left(\omega +2v_{g}k\right)k^2+B{\omega }^3\right)\hfill \\ \hfill \frac{1}{v_g{\omega }^2}\left(k^2+B{\omega }^2\right)\hfill \\ \hfill \frac{1}{{\mu }_1^2}\frac{1}{v_g^2{\omega }^3}\left(B{\mu }_1{\omega }^3+\left(\omega +2v_{g}k\right)k^2\right)\hfill \\ \hfill \frac{1}{{\mu }_1^2}\frac{1}{v_g{\omega }^2}\left(B{\mu }_1{\omega }^2+k^2\right)\hfill \\ \hfill -\frac{1}{{\mu }_2^2}\frac{1}{v_g^2{\omega }^3}\left(B{\mu }_2{\omega }^3-\left(\omega +2v_{g}k\right)k^2\right)\hfill \\ \hfill -\frac{1}{{\mu }_2^2}\frac{1}{v_g{\omega }^2}\left(B{\mu }_2{\omega }^2-k^2\right)\hfill \\ \hfill B\hfill \end{array}\right)|{\varphi }_1^{\left(1\right)}{|}^2,(26)$

where

$B=\frac{k^2\left(\omega +2v_{g}k\right)\left(1+\frac{{\delta }_1}{{\mu }_1^2}-\frac{{\delta }_2}{{\mu }_2^2}\right)-{\delta }_e{v}_g^2{\omega }^3}{{\omega }^3\left({\delta }_e{v}_g^2-\left(1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}\right)\right)}.(27)$

For the first harmonic, i.e., l = 1, in third order (n = 3), an analytical constraint is obtained, bearing the form of a partial differential equation for the electrostatic potential envelope (amplitude), say, ${\varphi }_1^{(1)}=\mathrm{\Psi }$:

$i\frac{\partial \mathrm{\Psi }}{\partial \tau }+P\frac{{\partial }^2\mathrm{\Psi }}{\partial {\zeta }^2}+Q|\mathrm{\Psi }{|}^2\mathrm{\Psi }=0,(28)$

where we have defined the stretched variables $\zeta =ϵ(x-v_{g}t)=X_1-v_g{T}_1=\frac{1}{ϵ}(X_2-v_g{T}_2)$ and τ = ϵ²t = ϵT₁ = T₂. The dispersion coefficient P is related to the curvature of the dispersion curve as P = (d²ω/dk²)/2. The exact form of P in our case reads

$P=-\frac{3}{2}\frac{{\delta }_e}{{\left(1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}\right)}^2}\frac{{\omega }^5}{k^4}.(29)$

The nonlinearity coefficient Q arises due to the carrier wave self-interaction. The exact form of Q reads

$\begin{array}{ll}\hfill Q& =-\frac{{\omega }^3}{2k^2}\frac{1}{\left(1+\frac{{\delta }_1}{{\mu }_1}+\frac{{\delta }_2}{{\mu }_2}\right)}\{-{\delta }_e\left(\left(A+B\right)+\frac{1}{2}\right)+\left(1+\frac{{\delta }_1}{{\mu }_1^3}+\frac{{\delta }_2}{{\mu }_2^3}\right)\left(\frac{5k^6}{2{\omega }^6}+\frac{4k^5}{v_g{\omega }^5}+\frac{k^4}{v_g^2{\omega }^4}\right)\hfill \\ \hfill & +\left(1+\frac{{\delta }_1}{{\mu }_1^2}+\frac{{\delta }_2}{{\mu }_2^2}\right)\left(\frac{3A{k}^4}{{\omega }^4}+\frac{2B{k}^3}{v_g{\omega }^3}+\frac{B{k}^2}{v_g^2{\omega }^2}\right)\}.\hfill \end{array}(30)$

The solution of the NLS Eq. 28 is [18] as follows:

$\mathrm{\Psi }\left(\zeta ,\tau \right)=e^{iQ\tau }\left[1-\frac{4\left(1+2iQ\tau \right)}{1+\frac{2Q}{P}{\zeta }^2+4Q^2{\tau }^2}\right].(31)$

Another solution in the form of breather is obtained by Akhmediev’s breather, and it is given by [19]

$\mathrm{\Psi }\left(\zeta ,\tau \right)=e^{iQ\tau }\frac{cosh\left(Qsin\left(2\varphi \right)\tau -2i\varphi \right)-cos\left(\varphi \right)cos\left(2sin\left(\varphi \right)\sqrt{\frac{Q}{2P}}\zeta \right)}{cosh\left(Qsin\left(2\varphi \right)\tau \right)-cos\left(\varphi \right)cos\left(2sin\left(\varphi \right)\sqrt{\frac{Q}{2P}}\zeta \right)},(32)$

where ϕ is the phase angle.

Results and discussion

The NLS Eq. 28 modulates the amplitude of the electrostatic envelope wave packet Ψ. Thus, the envelope wave packet’s propagation and stability depend on the dispersion coefficient P and the nonlinear coefficient Q. The modulation instability analysis of the NLS Eq. 28 can show how the envelope wave packet propagation stability changes over time [20]. If PQ < 0, the amplitude-modulated envelope remains constant, regardless of external perturbations. However, if PQ > 0, external perturbations make the amplitude-modulated envelope unstable. The unstable region allows accumulation of plasma-charged particles (rogue waves). Studying these regions and their physical characteristics is essential.

Starting with the fact that this is the first perturbation-based attempt to explain the genesis of surface nanohillocks in YIG materials, we used a typical data ratio from an experiment to interpret our qualitative description. In the future, we will use quantitative descriptions to improve models. Figure 1 clearly depicts the positive or negative PQ area. For wave numbers larger than 0.3, the unstable area PQ > 0 dominates, except when positive iron ions are minimal and unstable pulses remain for wave numbers $>0.4$. A stable region cannot have localized charge concentrations or rogue waves. This phenomenon can be explained physically: for small values of δ₁ (specifically, low iron concentration), there is a high likelihood of the presence of rogue waves at high wave numbers. This occurrence may be attributed to the sufficient concentration of charged ions in a specific region. At high values of δ₁ (i.e., iron concentration), the localized concentration of charged ions is high at low wave numbers, which means that enough energy can be concentrated at lower wave numbers to concentrate a considerable amount of charged ions in a localized region. The existence of stable pulses at low values of wave number is undoubtedly due to the fact that the plasma at lower δ₁ (i.e., iron concentration) turns into approximately positive–negative ion plasma, which becomes relatively stable at high wave numbers. When δ₁ increases, the plasma converts to multi-component plasma, which is relatively unstable plasma.

FIGURE 1

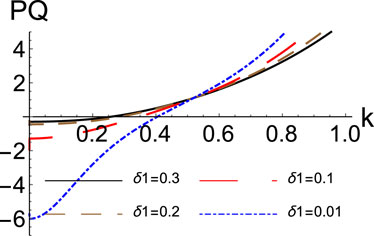
FIGURE 1. The product PQ is plotted versus the carrier wavenumber k, varying δ1, as indicated. Other parameters are δ₂=0.9, μ₁=0.62, and μ₂=0.27.

Figure 2 displays the contour plot and two-dimensional profile of the normalized rogue wave as a function of distance and time. The solution (29) is shown in Figure 2A. Rogue pulses can be intense in a limited, confined region. The rogue pulse is a high peak that concentrates many ions in a tiny area, forming surface nanohillocks. The contour map of the normalized rogue wave as a function of distance and time is shown in Figure 2B. The peak of charged ions correlates with nanohillocks in [14], highlighting the impact of ion-induced modifications on electronic energy deposition by 30-MeV C₆₀ cluster ions in creating energetic plasma. Upon collision, 30-MeV C₆₀ cluster ions deposit high energy and form plasma ions on the surface of the YIG material. Explosions caused by excess energy concentrate charged ions in a concentrated location, creating plasma components outward from the surface. A periodic rogue wave solution (30) is Akhmediev’s breather. Figures 2C,D show the result. Undoubtedly, a periodic pattern can concentrate many ions in periodic confined locations.

FIGURE 2

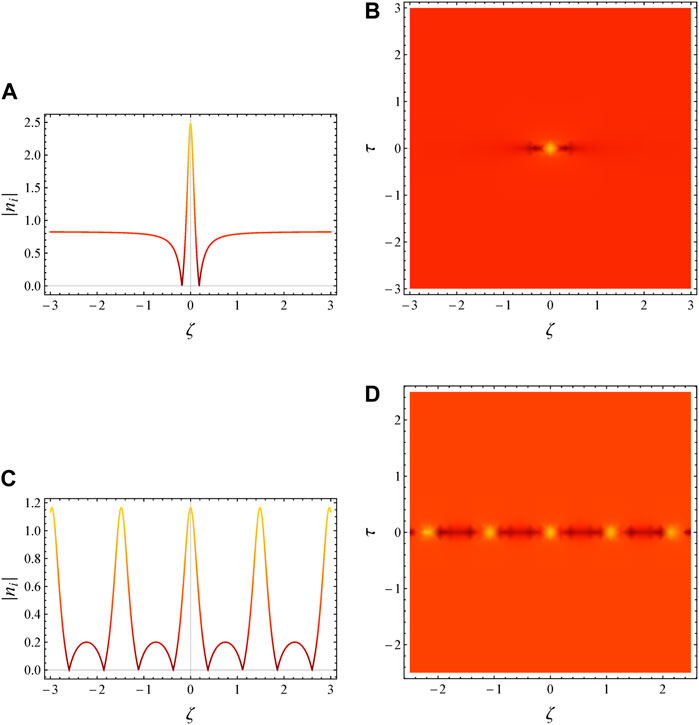
FIGURE 2. (A, B) The Peregrine soliton and (C, D) the Akhmediev breather are depicted for δ₁=0.3, δ₂=0.5, μ₁=0.62, μ₂=0.27, p =−0.559, Q =−10.73, τ =0, and ϕ =10.

Figure 3 displays the two-dimensional rogue wave profile reflecting the fluctuation of δ₁ (iron concentration). Increasing δ₁ decreases the rogue wave profile amplitude. In general, lowering the amplitude causes wave energy to escape from the system and prevents the plasma from concentrating charged ions. In our scenario, increasing δ₁ (iron content) wastes energy through a large number of charged ions. This might lower pulse amplitude and shorten nanohillocks.

FIGURE 3

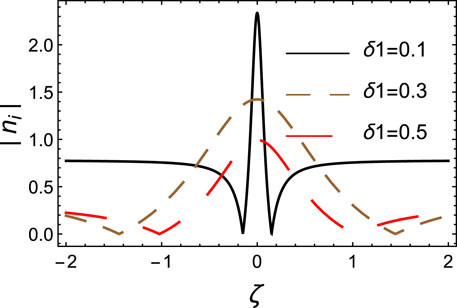
FIGURE 3. The Peregrine soliton is depicted for different values for δ₁. The values of the other parameters are δ₂=0.9, μ₁=0.62, μ₂=0.27, p =−0.558, Q =−9.43, τ =0, and ϕ =10.

The Peregrine soliton (PS) is a type of solitary wave that can occur in dispersive nonlinear systems. It is characterized by its sharp peak and rapid decay, and it is known to be highly localized in both space and time. PS was first discovered in the context of water waves, but it has since been shown to exist in a variety of other systems, including plasma [21]. In the context of plasma physics, PS is a solution of the nonlinear Schrödinger equation (NLSE), which describes the propagation of ion-acoustic waves in a plasma. NLSE is a dispersive equation, which means that the phase velocity of a wave depends on its frequency. This dispersion can cause waves to steepen and eventually break, leading to the formation of rogue waves. PS is a type of rogue wave that is particularly well-suited for study in plasma. This is because PS is a localized wave, which means that it can be isolated from other waves in the system. This isolation allows for a more detailed study of the PS’s properties, such as its stability and its interaction with other waves. PS has been experimentally observed in plasma, and it has also been studied extensively in simulations [22, 23]. These studies have shown that PS is a stable wave that can propagate for long distances without breaking. However, PS is also known to be very sensitive to perturbations, which can cause it to break. PS is a fascinating wave that has many potential applications in plasma physics. For example, it could be used to study the propagation of ion-acoustic waves in plasma, or it could be used to develop new methods for controlling plasma waves [24]. PS is also a potential source of rogue waves in plasma, which could have implications for spacecraft operations and other applications. As for the question of whether PS is a true soliton, there is some debate. Solitons are typically defined as waves that can propagate without distortion for long distances. PS is a localized wave that can propagate for long distances, but it is also known to be sensitive to perturbations, which can cause it to break. This suggests that PS may not be a true soliton in the strictest sense of the word [25].

Summary

Our study introduces a hydrodynamic fluid model to explain the production of surface nanohillocks caused by 30-MeV C₆₀ cluster ions hitting YIG. Our study gives a new technique to describe surface nanohillocks using a plasma collective effect of charged particles and rogue waves. We are continuing studying this region and expect to validate the plasma collective impact of the charged particle generation process. Analytically solving hydrodynamic multi-ion fluid equations with background electrons yields a nonlinear Schrödinger equation. Solving the latter gives us feasible regions for localized ion concentration. When rogue waves in this location concentrate charged ions in a very small region, surface nanohillocks occur. As the density ratio δ₁ increases, the rogue wave amplitude decreases due to energy distribution among charged ions. Thus, nanohillocks shorten.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

RA: writing–review and editing. LE: methodology and writing–review and editing. MA: writing–review and editing. NA: writing–review and editing. WM: conceptualization and writing–review and editing. IE: investigation, methodology, supervision, and writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The study was supported by Princess Nourah Bint Abdulrahman University Researchers supporting project number (PNURSP2024R399), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ritter R, Wilhelm R, Ginzel R, Kowarik G, Heller R, El-Said A, et al. Pit formation on poly (methyl methacrylate) due to ablation induced by individual slow highly charged ion impact. EPL (Europhysics Letters) (2012) 97:13001. doi:10.1209/0295-5075/97/13001

CrossRef Full Text | Google Scholar

2. Moslem WM, El-Said AS, Sabry R, Bahlouli H. Nanostructuring of sapphire by ion-induced plasma. Results Phys (2023) 46:106297. doi:10.1016/j.rinp.2023.106297

CrossRef Full Text | Google Scholar

3. Ochedowski O, Lehtinen O, Kaiser U, Turchanin A, Ban-d’Etat B, Lebius H, et al. Nanostructuring graphene by dense electronic excitation. Nanotechnology (2015) 26:465302. doi:10.1088/0957-4484/26/46/465302

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Jensen J, Dunlop A, Della-Negra S, Toulemonde M. A comparison between tracks created by high energy mono-atomic and cluster ions in y3fe5o12. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1998) 146:412–9. doi:10.1016/s0168-583x(98)00442-x

CrossRef Full Text | Google Scholar

5. Singhal R, Singh F, Tripathi A, Avasthi D. A comparative study of ion-induced damages in c60 and c70 fullerenes. Radiat Effects Defects Sol (2009) 164:38–48. doi:10.1080/10420150802479638

CrossRef Full Text | Google Scholar

6. Moslem WM, El-Said AS, Morsi SA, Sabry R, Yahia ME, El-Labany SK, et al. On the formation of nanostructures by inducing confined plasma expansion. Results Phys (2019) 15:102696. doi:10.1016/j.rinp.2019.102696

CrossRef Full Text | Google Scholar

7. Yahia ME, Tolba RE, El-Bedwehy NA, El-Labany SK, Moslem WM. Rogue waves lead to the instability in gan semiconductors. Scientific Rep (2015) 5:12245. doi:10.1038/srep12245

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yahia ME, Tolba RE, Moslem WM. Super rogue wave catalysis in titan’s ionosphere. Adv Space Res (2021) 67:1412–24. doi:10.1016/j.asr.2020.11.027

CrossRef Full Text | Google Scholar

9. Mouhammadoul BB, Alim AAA, Tiofack C, Mohamadou A, Alrowaily AW, Ismaeel S, et al. On the super positron-acoustic rogue waves in q-nonextensive magnetoplasmas. Phys Fluids (2023) 35:9. doi:10.1063/5.0144915

CrossRef Full Text | Google Scholar

10. Farokhi B, Shahmansouri M, Kourakis I. Modulated transverse off-plane dust-lattice wave packets in hexagonal two-dimensional dusty plasma crystals. Phys Plasmas (2009) 16:11. doi:10.1063/1.3121221

CrossRef Full Text | Google Scholar

11. Shahmansouri M, Alinejad H, Tribeche M. Breather structures in degenerate relativistic non-extensive plasma. J Plasma Phys (2017) 83:905830303. doi:10.1017/s0022377817000332

CrossRef Full Text | Google Scholar

12. Alinejad H, Shahmansouri M. Evolution of dissipative low-frequency rogue waves in superthermal dusty plasmas. IEEE Trans Plasma Sci (2019) 47:4378–84. doi:10.1109/tps.2019.2932504

CrossRef Full Text | Google Scholar

13. El-Said A. Tracks of 30-mev c60 clusters in yttrium iron garnet studied by scanning force microscopy. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2009) 267:953–6. doi:10.1016/j.nimb.2009.02.020

CrossRef Full Text | Google Scholar

14. Moslem WM, El-Said AS, Sabry R, Shalouf A, El-Labany SK, Bahlouli H. Nonlinear phenomenon in nanostructures creation by fast cluster ions. Phys Lett A (2017) 381:102–5. doi:10.1016/j.physleta.2016.10.008

CrossRef Full Text | Google Scholar

15. Morsi SA, Moslem WM, El-Said AS, Bahlouli H. Creation of surface nanometer-scale plasma region by irradiation with slow highly charged ions. Physica Scripta (2020) 95:095602. doi:10.1088/1402-4896/aba865

CrossRef Full Text | Google Scholar

16. Braginskii S. Transport processes in a plasma. Rev plasma Phys (1965) 1:205.

Google Scholar

17. Kourakis I, Shukla PK. Exact theory for localized envelope modulated electrostatic wavepackets in space and dusty plasmas. Nonlinear Process Geophys (2005) 12:407–23. doi:10.5194/npg-12-407-2005

CrossRef Full Text | Google Scholar

18. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J (1983) 25:16–43. doi:10.1017/s0334270000003891

CrossRef Full Text | Google Scholar

19. Akhmediev N, Korneev V. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor Math Phys (1986) 69:1089–93. doi:10.1007/BF01037866

CrossRef Full Text | Google Scholar

20. Alharthi NS, Tolba RE, Moslem WM. Nonlinear propagation of dust-acoustic waves and its modulation instability. Physica Scripta (2023) 98:115236. doi:10.1088/1402-4896/ad007e

CrossRef Full Text | Google Scholar

21. Bailung H, Sharma S, Nakamura Y. Observation of peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Sharma S, Bailung H. Observation of hole peregrine soliton in a multicomponent plasma with critical density of negative ions. J Geophys Res Space Phys (2013) 118:919–24. doi:10.1002/jgra.50111

CrossRef Full Text | Google Scholar

23. Pathak P, Sharma SK, Nakamura Y, Bailung H. Observation of ion acoustic multi-peregrine solitons in multicomponent plasma with negative ions. Phys Lett A (2017) 381:4011–8. doi:10.1016/j.physleta.2017.10.046

CrossRef Full Text | Google Scholar

24. Moslem WM, Shukla PK, Eliasson B. Surface plasma rogue waves. Europhysics Lett (2011) 96:25002. doi:10.1209/0295-5075/96/25002

CrossRef Full Text | Google Scholar

25. Blanco-Redondo A, de Sterke CM, Xu C, Wabnitz S, Turitsyn SK. The bright prospects of optical solitons after 50 years. Nat Photon (2023) 17:937–42. doi:10.1038/s41566-023-01307-9

CrossRef Full Text | Google Scholar