Entanglement witness measurement of time-bin two-qubit states using fiber-based Franson interferometers

Entanglement, that is, quantum correlations that do not have a classical counterpart, is a precondition to establishing communication protocols beyond the existing classical protocols, such as quantum key distribution, that achieves a higher level of security without computational assumptions. In this work, we present a proof of demonstration of detecting various entangled states, prepared by time-bin encoding with photons that are natural resources for long-distance quantum communication. We generate a maximally entangled state in time-bin qubits and verify the state in two ways. We first consider measurements that realize entanglement witnesses for the verification of entanglement. We then perform a quantum state tomography for the full characterization. Experimental resources are also discussed.

1 Introduction

Entanglement signifies quantum correlations existing in multipartite quantum states that cannot be prepared by local quantum operations and classical communication only [1]. It has been identified as a key resource that enables quantum information processing to outperform its counterpart [2]. In particular, entanglement is a precondition for quantum cryptographic protocols [3, 4], that is, the quantum key distribution, that establishes secure communication between two legitimate parties with a higher level of security without relying on computational assumptions [5, 6].

On the one hand, entangled states can be completely verified by quantum state tomography (QST) [7]. Two parties prepare tomographically complete or informationally complete measurements, that is, a set of measurements that can uniquely identify a single state for the given measurement statistics. Instances of tomographically complete states correspond to mutually unbiased bases [8], such as observables X, Y, and Z for qubits, and also symmetric and informationally complete (SIC) states [9]. Once a state is fully characterized, known theoretical methods of detecting entangled states can be applied. For instance, the partial transpose criteria on two-qubit states can find whether a given state is entangled or separable [10, 11].

On the other hand, there are observables that can distinguish entangled states from separable states, known as entanglement witnesses (EWs) [12–14]. An EW presents non-negative expectation values for all separable states whereas negative values for some entangled states. Conversely, positive expectation values of EW do not guarantee that the given states are separable, as some entangled states have positive expectation values. Therefore, a negative expectation value of an EW obtained from an experiment can unambiguously conclude an entangled state. It is worth mentioning that measurements for EWs can be tomographically incomplete [15]. Namely, an EW can find a set of entangled states in a cost-effective manner with a smaller number of measurement operators.

For instance, Bell inequalities such as the Clauser–Horne–Shimony–Holt (CHSH) inequality for a two-input and two-outcome scenario [16, 17] can be derived as EWs. A violation of Bell inequalities finds a set of entangled states with a measurement that is tomographically incomplete: yet, a measurement suffices to detect entangled states. EWs also contain advantages over quantum state tomography in the verification of entanglement for multipartite and high-dimensional quantum systems: while experimental costs for quantum tomography increase exponentially, a few measurements suffice to detect genuine multipartite entangled states.

Extensive experimental efforts have been made to realize and exploit entangled states for practical quantum information applications. For instance, quantum teleportation has been realized with photonic qubits [18], quantum sensing, quantum computing, and quantum communication [19]. Various degrees of freedom of photonic systems have been exploited to prepare entangled states: polarization [20, 21], spatial mode [22, 23], time-bin [24, 25], and path [26, 27].

For practical purposes, in a realistic quantum communication scenario, time-bin qubits harbor distinct advantages when integrated with optical fiber systems. Challenges in optical fibers, including polarization fluctuations and depolarization [28], pose complications for the utilization of polarization-based qubits, while time-bin qubits are not affected. Moreover, while dispersion is a concern when a pulsed laser is transmitted through a long optical fiber, the insertion of dispersion compensation fibers can reduce the pulse-broadening effects [29, 30]. Due to these practical benefits, time-bin qubits have been empirically demonstrated and employed in experiments involving long-distance optical fibers [29, 31, 32].

In this paper, we generate entangled time-bin qubits and demonstrate the detection of entanglement and verification of shared states. We prepare time-bin entangled states using fiber-based Franson interferometers and perform tomographically complete measurements. We collect the measurement outcomes to reconstruct an entangled state that has been designed and also demonstrate that a subset of measurement data can be used to construct an EW for the verification of entanglement. Our results present a proof-of-principle demonstration of an EW for time-bin qubits.

2 Theory and methods

2.1 Entanglement witness

A Hermitian operator $\widehat{W}$ is said to be EW if it has non-negative expectation values for all separable states, ${\rho }_{sep}$, and negative expectation values for some entangled states, ${\rho }_{ent}$ [10, 12, 13, 33, 34]:

$\mathrm{T}\mathrm{r}\left[\widehat{W}{\sigma }_{sep}\right]\ge 0\forall {\sigma }_{sep},\mathrm{T}\mathrm{r}\left[\widehat{W}{\rho }_{ent}\right]<0\exists {\rho }_{ent}.(1)$

Extensive efforts have been made to develop suitable witness operators. In Refs [35, 36], the authors have developed EW operators using two orthogonal local observables. To develop EW operators, let us consider an experimental setup that has been constructed to prepare the state $\left|\mathrm{\Psi }〉\right.$. In practice, the generated state becomes the mixed state ρ, which is in proximity to the state $\left|\mathrm{\Psi }〉\right.$. To test whether the state $\rho$ is entangled or not, the authors in Refs [35, 36] proposed a witness operator in the form

$\widehat{W}=c_{0}I-{\displaystyle \sum _k}{c}_k{S}_k,(2)$

where “$I$” represents the identity operator, the operator $S_k$ stabilizes the state $\left|\mathrm{\Psi }〉\right.$, that is, $S_k\left|\mathrm{\Psi }〉\right.=\left|\mathrm{\Psi }〉\right.$, and $c_k$ is the constant. In this work, two time-bin entangled photons are prepared in one of four two-qubit Bell states, e.g.,

${\left|{\mathrm{\varphi }}^{\pm }〉\right.}_{12}=\frac{{\left|00〉\right.}_{12}\pm {\left|11〉\right.}_{12}}{\sqrt{2}},(3)$

${\left|{\mathrm{\psi }}^{\pm }〉\right.}_{12}=\frac{{\left|01〉\right.}_{12}\pm {\left|10〉\right.}_{12}}{\sqrt{2}},(4)$

where the subscript i corresponds to the ith photon. For the aforementioned Bell states, the stabilizing operators are $S_1=X_1{X}_2$ and $S_2=Z_1{Z}_2$, where $\left\{X_i,Z_i\right\}$ are Pauli operators acting on the ith photon. The corresponding witness operators certifying the Bell states are as follows [35, 36]:

${\widehat{W}}_{\left|{\varphi }^{+}〉\right.}=\frac{1}{4}\mathrm{I}-\frac{1}{4}\left(X_1{X}_2+Z_1{Z}_2\right),(5)$

${\widehat{W}}_{\left|{\varphi }^{-}〉\right.}=\frac{1}{4}\mathrm{I}+\frac{1}{4}\left(X_1{X}_2-Z_1{Z}_2\right),(6)$

${\widehat{W}}_{\left|{\psi }^{+}〉\right.}=\frac{1}{4}\mathrm{I}-\frac{1}{4}\left(X_1{X}_2-Z_1{Z}_2\right),(7)$

${\widehat{W}}_{\left|{\psi }^{-}〉\right.}=\frac{1}{4}\mathrm{I}+\frac{1}{4}\left(X_1{X}_2+Z_1{Z}_2\right).(8)$

The experimentally generated state ${\rho }_{\mathit{exp}}$ is said to be entangled if

$\underset{\left|\mathrm{\Psi }\right.〉\in \{\left|{\varphi }^{\pm }\right.〉,\left|{\psi }^{\pm }\right.〉\}}{\text{min}}\left\{\mathrm{Tr}\left[{\widehat{\text{W}}}_{\left|\mathrm{\Psi }\right.〉}{\rho }_{\text{exp}}\right]\right\}<0.(9)$

In the ideal scenario, $\mathrm{Tr}\left[{\widehat{W}}_{\left|\mathrm{\Psi }〉\right.}\left|\mathrm{\Psi }〉\right.〈\left.\mathrm{\Psi }\right|\right]=-1/4$.

2.2 Experimental setup and method

The experimental setup is shown in Figure 1A. The pump laser is a picosecond pulsed laser operating at a wavelength of 1552.52 nm. The repetition rate, spectrum width, and pulse width are 20 MHz, 0.26 nm, and 13.23 ps, respectively. First, this pump pulse is amplified using an erbium-doped fiber amplifier (EDFA), following which a dense wavelength division multiplexing (DWDM) is utilized to remove the amplified spontaneous emission from EDFA [37]. Then, the amplified pump pulse is temporally divided into two peaks with a 3-ns interval by passing through the pump interferometer. We construct each interferometer with an optical fiber splice and optical delay lines, each with an optical path length difference of 3 ns. Faraday mirrors and the Michelson interferometer are utilized to match the polarization of two peaks [38]. Furthermore, we use a variable optical attenuator (VOA) to correct the optical loss difference due to the path difference between the short and long paths in the interferometer. Afterward, a time-bin entangled photon pair state is generated in the dispersion-shifted fiber (DSF) by spontaneous four-wave mixing (SFWM). Here, to reduce spontaneous Raman scattering, DSF was immersed in liquid nitrogen to lower the temperature [37], and an in-line polarizer (ILP) was used. These are divided into the signal at 1549.32 nm and idler channels at 1555.75 nm through the DEMUX composed of DWDM with a 100 GHz bandwidth.

FIGURE 1

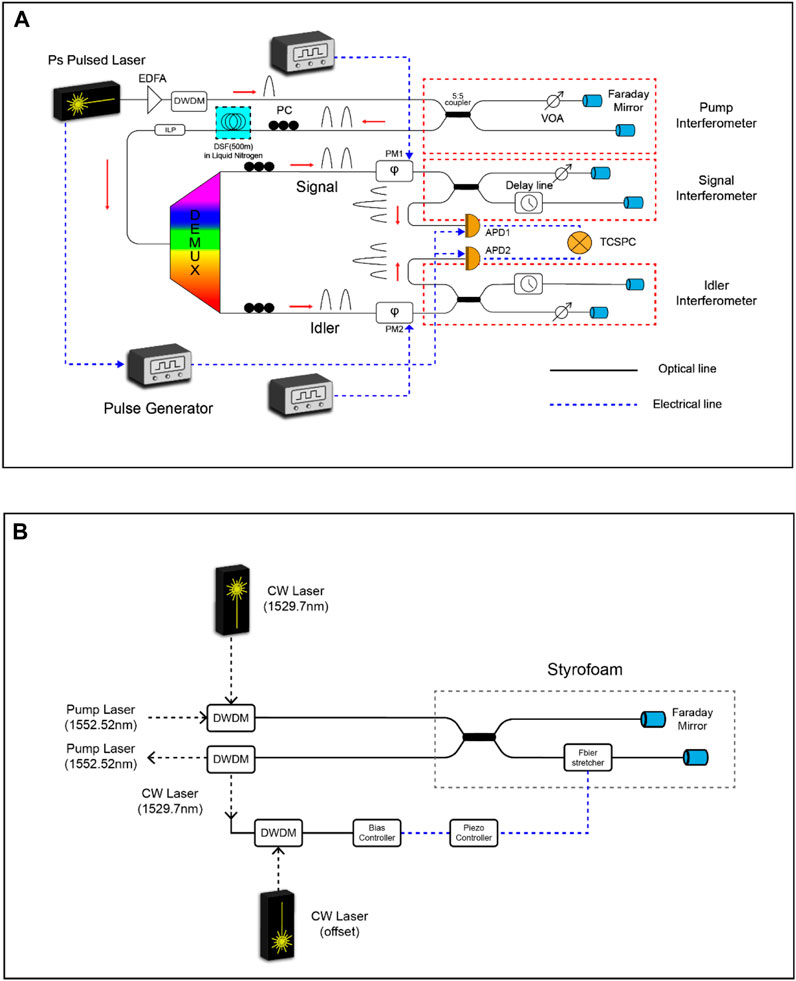
FIGURE 1. (A) Experimental setup: EDFA, erbium-doped fiber amplifier; DWDM, dense wavelength division multiplexing; VOA, variable optical attenuator; PC, polarization controller; DSF, dispersion-shifted fiber; ILP, in-line polarizer; PM, phase modulator; APD, InGaAs avalanche photodiode; TCSPC, time-correlated single-photon counting. (B) Thermal stabilization setup in the fiber interferometer.

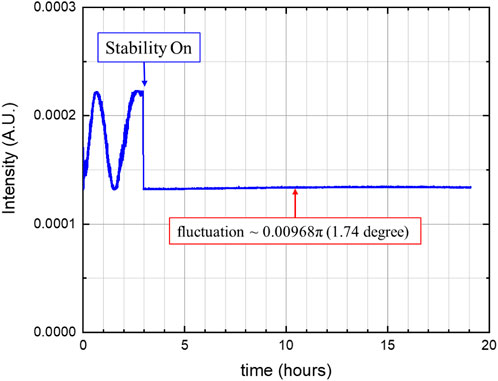
In fiber optics, the phase of the fiber interferometer changes with temperature. Therefore, thermal stabilization is required. The scheme for thermal stabilization is shown in Figure 1B. This stabilization setup is included in the red dotted line in Figure 1A. For feedback, a continuous wave (CW) laser in a range different (1529.7 nm) from the wavelength of the pump was used [39]. Feedback is more stable when the tracking point is minimum. The minimum detector power of the bias controller is −30 dBm, and the minimum optical power of interference used in the CW laser is less than −30 dBm. Therefore, another CW laser for offset is used. Output power before and after stabilization is shown in Figure 2. In addition, we placed the interferometer inside the styrofoam for thermal stabilization.

FIGURE 2

FIGURE 2. Output power before and after stabilization.

Phase modulators (PMs), equipped with a 3-dB bandwidth of 10 GHz, are utilized to alter the phase of the signal and idler photons’ second peak (late peak). We apply rectangular voltage pulses to the PMs using an arbitrary pulse generator. Each voltage pulse possesses a rise time less than the 3-ns interval between the first and second pulses and is applied at the second peak time. Notably, the pulse heights are controlled from one pulse to another, leading to alterations in the phase of the second peak of the signal and idler photons, denoted by ${\phi }_s$ and ${\phi }_i$, respectively. When these time-bin qubits pass through the interferometer, they are temporally separated into three peaks with an interval of 3 ns. Then, the state of the center peak becomes the superposed state as follows:

$\frac{1}{\sqrt{2}}\left(\left|0〉\right.+e^{i({\phi }_p-\phi )}\left|1〉\right.\right),(10)$

where $\phi$ is the phase of the signal or the idler changed by PM. In the interference between the center peak of the signal and the center peak of the idler, the coincidence count rate is given by

$R_c\sim 1+\cos \left({\phi }_s+{\phi }_i-2{\phi }_p\right),(11)$

where ${\phi }_p$ is the phase of the pump changed by the pump’s PM, and in our experiment, ${\phi }_p=0\pi$. In order to know the phase change for voltage applied to PM, we measured the coincidence between the center peaks of the signal and idler by changing the voltage applied to the PM of the signal (idler), while the voltage of the PM of the idler (signal) is fixed. The results are shown in Figure 3. From the fitting curves, we obtain $V_{-1\pi }\left(V_{0\pi }\right)$ and $V_{-\frac{1}{2}\pi }\left(V_{\frac{1}{2}\pi }\right)$ of the signal and idler, respectively. The difference in the voltage values of the signal and idler is due to an error in the PM itself. Finally, we performed projection measurement by using PMs and time-correlated single-photon counting (TCSPC) and adjusting the gate delay of the single-photon detector based on the InGaAs avalanche photodiode (APD). The gate width and quantum efficiency of the two APDs are 1 ns and 20%, respectively. The gate frequency of APDs is synchronized with the repetition rate of the pump pulse laser through the pulse generator.

FIGURE 3

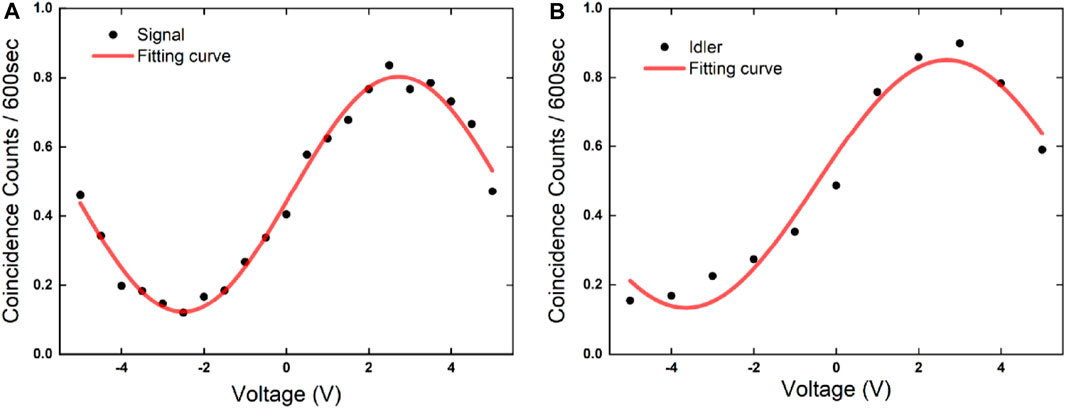
FIGURE 3. Coincidence count for the applied voltage of PM. (A) PM of the signal interferometer at ${\mathrm{V}}_{0\pi }$ of the idler’s PM; (B) PM of the idler interferometer at ${\mathrm{V}}_{-\frac{1}{2}\pi }$ of the signal’s PM.

3 Results

3.1 Quantum state tomography

First, we checked whether the Bell state $\left|{\varphi }^{+}\right.〉$ was properly generated by performing QST [40, 41] before the measurement of EW. In order to proceed with QST, we used $\left|0〉\right.,\left|1〉\right.,\left|R〉\right.,\left|-〉\right.$ for the signal and $\left|0〉\right.,\left|1〉\right.,\left|L〉\right.,\left|+〉\right.$ for the idler, and the coincidence counts for these combinations are shown in Table 1. In addition, since only one detector is connected at the output of each interferometer in our setup, a 50% intrinsic loss occurs in time basis measurement. Therefore, for the project measurement including one-time basis and the project measurement including two-time basis, the coincidence measurement time was doubled and quadrupled, respectively [37]. The coincidence counts were corrected by subtracting the accidental coincidence count, as shown in Table 1. As a result of QST performed using these coincidence counts, the obtained density matrix is given by

${\mathrm{\rho }}_{\mathit{exp}}=\left(\begin{array}{cc}\begin{array}{cc}0.498& -0.0064+i0.0098\\ -0.0064-i0.0098& 0.0139\end{array}& \begin{array}{cc}-0.0158+i0.0048& 0.48-i0.0041\\ 0.0029+i0.0015& -0.0093-i0.0241\end{array}\\ \begin{array}{cc}-0.0158-i0.0048& 0.0029-i0.0015\\ 0.48+i0.0041& -0.0093+i0.0241\end{array}& \begin{array}{cc}0.0013& -0.0181-i0.0073\\ -0.0181+0.0073& 0.486\end{array}\end{array}\right),(12)$

and is shown in Figure 4. The state ${\rho }_{\mathit{exp}}$ has a fidelity of $96.31\%\pm 1.61\%$ with the ideal state $\left|{\varphi }^{+}\right.〉$. The concurrence of the state ${\rho }_{\mathit{exp}}$ is $0.94\pm 0.03$. The aforementioned parameters confirm that the prepared state ${\rho }_{\mathit{exp}}$ is an entangled and Bell state, $\left|{\varphi }^{+}\right.〉.$

TABLE 1

TABLE 1. Coincidence counts of projection measurements for QST.

FIGURE 4

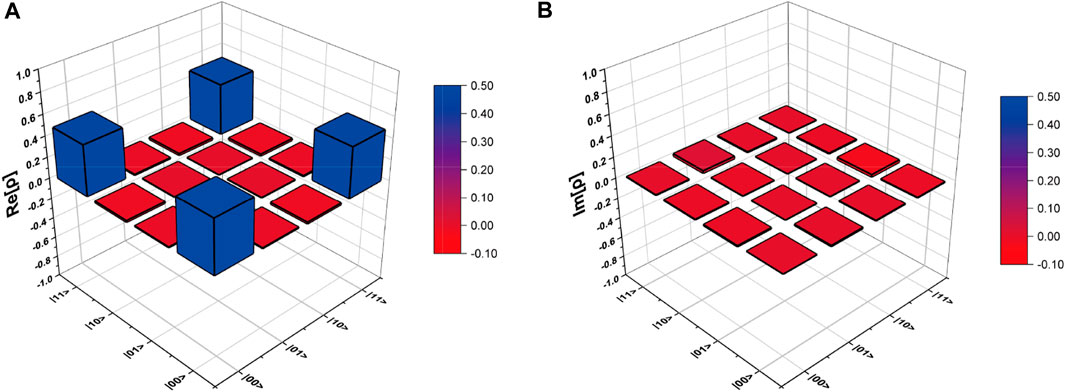
FIGURE 4. Density matrix obtained by QST. (A) Real part of the density matrix. (B) Imaginary part of the density matrix.

3.2 Entanglement witness

3.2.1 Experimental results

Since we generated the $\left|{\varphi }^{+}\right.〉$ state, we need to use the witness of Eq. 5. In addition, the measurement of $Z_1{Z}_2$ and $X_1{X}_2$ can be expressed, respectively, as follows:

$〈Z_1{Z}_2〉={\left|〈00|\varphi 〉\right|}^2-{\left|〈01|\varphi 〉\right|}^2-{\left|〈10|\varphi 〉\right|}^2+{\left|〈11|\varphi 〉\right|}^2,(13)$

$〈X_1{X}_2〉={-4\left|〈-+|\varphi 〉\right|}^2+{2\left|〈-0|\varphi 〉\right|}^2+{2\left|〈-1|\varphi 〉\right|}^2+{2\left|〈1+|\varphi 〉\right|}^2{2\left|〈0+|\varphi 〉\right|}^2-{\left|〈00|\varphi 〉\right|}^2-{\left|〈01|\varphi 〉\right|}^2-{\left|〈10|\varphi 〉\right|}^2-{\left|〈11|\varphi 〉\right|}^2.(14)$

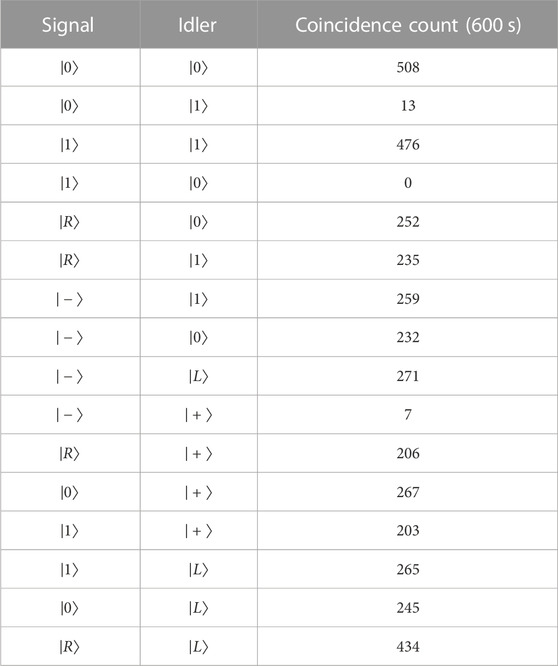
Using coincidence count in Table 2, these can be calculated as follows:

$〈Z_1{Z}_2〉=\frac{N_{00}-N_{01}-N_{10}+N_{11}}{N_{total}}=0.97\pm 0.01,(15)$

$〈X_1{X}_2〉=\frac{{-4N}_{-+}+2N_{-0}+2N_{-1}+2N_{1+}+2N_{0+}-N_{00}-N_{01}-N_{10}-N_{11}}{N_{total}}=0.91\pm 0.09,(16)$

where $N_{ij}$ is the coincidence count of the signal photon in the state $\left|i〉\right.$ and the idler photon in the state $\left|j〉\right.$, and these are provided in Table 2.

TABLE 2

TABLE 2. Coincidence counts of projection measurements for EW.

The result of the witness measurement is given by

$〈{\widehat{W}}_{\left|{\mathrm{\varphi }}^{+}\right.〉}〉=\frac{1}{4}-\frac{1}{4}\left(〈X_1{X}_2〉+〈Z_1{Z}_2〉\right)=-0.22\pm 0.09<0.(17)$

Therefore, since the measurement result is less than zero, we have experimentally shown that the prepared state is an entangled state.

3.2.2 Theoretical results from the density matrix obtained by QST

From the density matrix ${\rho }_{exp}$ of Eq. 12 obtained by QST, we have theoretically calculated the expectation value of ${\widehat{W}}_{\left|{\varphi }^{+}〉\right.}$:

$\mathrm{Tr}\left[{\widehat{W}}_{\left|{\varphi }^{+}⟩\right.}{\rho }_{\mathit{exp}}\right]=\frac{1}{4}-\frac{1}{4}\left(\mathrm{Tr}\left[{\rho }_{\mathit{exp}}{X}_1{X}_2\right]+\mathrm{Tr}\left[{\rho }_{\mathit{exp}}{Z}_1{Z}_2\right]\right)=-0.23\pm 0.01<0,(18)$

where $\mathrm{Tr}\left[{\rho }_{\mathit{exp}}\left(Z_1{Z}_2\right)\right]=0.97\pm 0.01$ and $\mathrm{Tr}\left[{\rho }_{\mathit{exp}}\left(X_1{X}_2\right)\right]=0.94\pm 0.03$. As a result, the experimentally obtained value of $〈{\widehat{W}}_{\left|{\varphi }^{+}〉\right.}〉$ agrees with the value $\mathrm{Tr}\left[{\widehat{W}}_{\left|{\varphi }^{+}〉\right.}{\rho }_{\mathit{exp}}\right]$ obtained by QST.

4 Conclusion

We have experimentally prepared a two-photon time-bin entangled state using an interferometer with fiber-based active feedback for thermal stabilization and SFWM. The entanglement of the prepared state has been verified by measuring the EW operator. This EW operator has been constructed with two local measurements on individual photons. Additionally, the entanglement was also verified by QST. Both EW and QST methods confirmed that the $\left|{\varphi }^{+}\right.〉$ state has been generated with high fidelity with the ideal state. Our experimental setup can generate any Bell state.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

KH: data curation, formal analysis, investigation, and writing—original draft. JS: conceptualization, data curation, and writing—review and editing. KP: data curation, investigation, and writing—review and editing. JK: data curation, investigation, and writing—review and editing. TP: conceptualization, data curation, formal analysis, and writing—review and editing. JB: conceptualization, formal analysis, and writing—review and editing. HS: funding acquisition, resources, supervision, and writing—review and editing.

Funding

This research was supported by the Institute for Information and Communications Technology Promotion (IITP) (2020-0-00947). JS and JB are supported by the National Research Foundation of Korea (NRF-2021R1A2C2006309, NRF2022M1A3C2069728) and the Institute for Information & Communication Technology Promotion (IITP) (RS-2023-00229524).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Werner RF. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys Rev A (1989) 40:4277–81. doi:10.1103/PhysRevA.40.4277

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys (2009) 81:865–942. doi:10.1103/RevModPhys.81.865

CrossRef Full Text | Google Scholar

3. Curty M, Lewenstein M, Lütkenhaus N. Entanglement as a precondition for secure quantum key distribution. Phys Rev Lett (2004) 92:217903. doi:10.1103/PhysRevLett.92.217903

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Acín A, Gisin N. Quantum correlations and secret bits. Phys Rev Lett (2005) 94:020501. doi:10.1103/PhysRevLett.94.020501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Gisin N, Ribordy G, Tittel W, Zbinden H. Quantum cryptography. Rev Mod Phys (2002) 74:145–95. doi:10.1103/RevModPhys.74.145

CrossRef Full Text | Google Scholar

6. Portmann C, Renner R. Security in quantum cryptography. Rev Mod Phys (2022) 94:025008. doi:10.1103/RevModPhys.94.025008

CrossRef Full Text | Google Scholar

7. Řeháček J, Hradil Z, Ježek M. Iterative algorithm for reconstruction of entangled states. Phys Rev A (2001) 63:040303. R). doi:10.1103/PhysRevA.63.040303

CrossRef Full Text | Google Scholar

8. Bengtsson I. Three ways to look at mutually unbiased bases. AIP Conf Proc (2007) 889:40–51. doi:10.1063/1.2713445

CrossRef Full Text | Google Scholar

9. Renes JM, Blume-Kohout R, Scott AJ, Carlton M. Symmetric informationally complete quantum measurements. Math Phys (2004) 45:2171–80. doi:10.1063/1.1737053

CrossRef Full Text | Google Scholar

10. Peres A. Separability criterion for density matrices. Phys Rev Lett (1996) 77:1413–5. doi:10.1103/physrevlett.77.1413

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Horodecki M, Horodecki P, Horodecki R. Separability of mixed states: Necessary and sufficient conditions. Phys Lett A (1996) 223:1–8. Issues 1–2. doi:10.1016/s0375-9601(96)00706-2

CrossRef Full Text | Google Scholar

12. Chruściński D, Sarbicki G. Entanglement witnesses: Construction, analysis and classification. J Phys A: Math Theor (2014) 47:483001. doi:10.1088/1751-8113/47/48/483001

CrossRef Full Text | Google Scholar

13. Lewenstein M, Kraus B, Cirac JI, Horodecki P. Optimization of entanglement witnesses. Phys Rev A (2000) 62:052310. doi:10.1103/PhysRevA.62.052310

CrossRef Full Text | Google Scholar

14. Barbara M. Terhal. Detecting quantum entanglement. Theor Comp Sci (2002) 289(1):313–35. doi:10.1016/s0304-3975(02)00139-1

CrossRef Full Text | Google Scholar

15. Bae J, Hiesmayr BC, McNulty D. Linking entanglement detection and state tomography via quantum 2-designs. New J Phys (2019) 21:013012. doi:10.1088/1367-2630/aaf8cf

CrossRef Full Text | Google Scholar

16. Bell JS. On the einstein podolsky rosen paradox. Phys Physique Fizika (1964) 1:195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195

CrossRef Full Text | Google Scholar

17. Clauser JF, Horne MA, Shimony A, Holt RA. Proposed experiment to test local hidden-variable theories. Rev Lett (1970) 24:880–4. doi:10.1103/PhysRevLett.23.880

CrossRef Full Text | Google Scholar

18. Bennet CH, Brassard G, Crepeau C, Josca R, Peres A, Wootters WK. Teleporting an unknown quantum state via dualclassical and Einstein–Podolsky–Rosen channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Barenco A, Deutsch D, Ekert A, Jozs R. Conditional quantum dynamics and logic gates. Phys Rev Lett (1995) 74:4083–6. doi:10.1103/PhysRevLett.74.4083

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kwiat PG, Mattle K, Weinfurter H, Zeilinger A, Sergienko AV, Shih Y. New high-intensity source of polarization-entangled photon pairs. Phys Rev Lett (1995) 75:4337–41. doi:10.1103/PhysRevLett.75.4337

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang W, Xu D, Chen L. Polarization entanglement from parametric down-conversion with an LED pump. Phys Rev (2023) 19:054079. doi:10.1103/PhysRevApplied.19.054079

CrossRef Full Text | Google Scholar

22. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature (2001) 412:313–6. doi:10.1038/35085529

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fadel M, Zibold T, Décamps B, Treutlein P. Spatial entanglement patterns and Einstein-Podolsky-Rosen steering in Bose-Einstein condensates. Science (2018) 360:409–13. doi:10.1126/science.aao1850

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Brendel J, Gisin N, Tittel W, Zbinden H. Pulsed energy-time entangled twin-photon source for quantum communication. Phys Rev Lett (1999) 82:2594–7. doi:10.1103/PhysRevLett.82.2594

CrossRef Full Text | Google Scholar

25. Tomasin M, Mantoan E, Jogenfors J, Giuseppe V, Larsson J-Å, Villoresi P. High-visibility time-bin entanglement for testing chained Bell inequalities. Phys Rev A (2017) 95:032107. doi:10.1103/PhysRevA.95.032107

CrossRef Full Text | Google Scholar

26. Rossi A, Vallone G, Chiuri A, De Martini F, Mataloni P. Multipath entanglement of two photons. Phys Rev Lett (2009) 102:153902. doi:10.1103/PhysRevLett.102.153902

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xia L, Lu L, Wang K, Jiang X, Zhu S, Ma X. Experimental optimal verification of three-dimensional entanglement on a silicon chip. New J Phys (2022) 24:095002. doi:10.1088/1367-2630/ac8a67

CrossRef Full Text | Google Scholar

28. Agrawal GP. Fiber-optic communication systems. Hoboken, New Jersey: wiley (1992).

Google Scholar

29. Boaron A, Boso G, Rusca D, Vulliez C, Autebert C, Caloz M, et al. Secure quantum key distribution over 421 km of optical fiber. Phys Rev Lett (2018) 121:190502. doi:10.1103/PhysRevLett.121.190502

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu X, Yao X, Wang H, Li H, Wang Z, You L, et al. Energy-time entanglement-based dispersive optics quantum key distribution over optical fibers of 20 km. Appl Phys Lett (2019) 114:141104. doi:10.1063/1.5089784

CrossRef Full Text | Google Scholar

31. Takesue H. Long-distance distribution of time-bin entanglement generated in a cooled fiber. Opt Express (2006) 14:3453–60. doi:10.1364/oe.14.003453

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Marcikic I, de Riedmatten H, Tittel W, Zbinden H, Legré M, Gisin N. Distribution of time-bin entangled qubits over 50 km of optical fiber. Phys Rev Lett (2004) 93:180502. doi:10.1103/PhysRevLett.93.180502

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Gühne O, Tóth G. Entanglement detection. Phys Rep (2009) 474:1–75. doi:10.1016/j.physrep.2009.02.004

CrossRef Full Text | Google Scholar

34. Barbara M. Terhal. Bell inequalities and the separability criterion. Phys Lett A (2000) 271:5–6. doi:10.1016/s0375-9601(00)00401-1

CrossRef Full Text | Google Scholar

35. Tóth G, Gühne O. Detecting genuine multipartite entanglement with two local measurements. Phys Rev Lett (2005) 94:060501. doi:10.1103/PhysRevLett.94.060501

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tóth G, Gühne O. Entanglement detection in the stabilizer formalism. Phys Rev A (2005) 72:022340. doi:10.1103/PhysRevA.72.022340

CrossRef Full Text | Google Scholar

37. Takesue H, Noguchi Y. Implementation of quantum state tomography for time-bin entangled photon pairs. Opt Express (2009) 17:10976–89. doi:10.1364/oe.17.010976

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Mo X-F, Zhu B, Han Z-F, Gui Y-Z, Guo G-C. Faraday–Michelson system for quantum cryptography. Opt Lett (2005) 30:2632–4. doi:10.1364/ol.30.002632

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cho S-B, Noh T-G. Stabilization of a long-armed fiber-optic single-photon interferometer. Opt Express (2009) 17:19027–32. doi:10.1364/oe.17.019027

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Altepeter JB, Branning D, Jeffrey E, Wei TC, Kwiat PG, Thew RT, et al. Ancilla-assisted quantum process tomography. Phys Rev Lett (2003) 90:193601. doi:10.1103/PhysRevLett.90.193601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. James DFV, Kwiat PG, Munro WJ, White AG. Measurement of qubits. Phys Rev A (2001) 64:052312. doi:10.1103/PhysRevA.64.052312

CrossRef Full Text | Google Scholar