- 1College of Materials Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, Jiangsu, China
- 2Aircraft Technology Branch of Hunan Aerospace Co., Ltd., Changsha, China
- 3China Aerospace Science and Industry Corporation, Beijing, China
Multi-scroll attractors have attracted attention because of their more complex topological structures and artificially controllable attractor structures. This paper proposes a new nonvolatile magnetic-controlled memristor and uses it to simulate the effect of membrane flux changes caused by neuronal exposure to electromagnetic radiation. A series of complex chaotic phenomena are found by plotting phase diagrams, bifurcation diagrams, attractor domains and 01 tests, including multi-scroll chaotic attractors controlled by memristors, symmetric bifurcation behavior, coexistence phenomena enhanced by initial offset. The mechanisms behind them are explained through equilibrium point analysis. A dual memristive HNN (MHNN) coupling synchronization model is proposed to simulate the synchronization between regions within the human brain. The Lyapunov function of the error is constructed to prove that this coupling synchronization scheme is ultimately bounded. The feasibility of this synchronization scheme is verified by establishing a Simulink model and conducting simulation experiments.
1 Introduction
Numerous neurophysiological and neuroanatomical studies have shown that human brain activity is closely related to the dynamic behavior of biological neurons and neural networks. In order to reveal the mystery of how the brain processes, manipulates and accesses information, scientists have conducted long-term research on the structure and working mechanism of biological neural networks and established various artificial neuron and neural network models [1–10]. Hopfield neural networks (HNN) have been widely studied for their simple mathematical form and rich dynamical behavior. Liang et al. investigated the long time behavior of the mild solution to delayed reaction-diffusion HNNs driven by infinite dimensional Wiener processes. They analyzed the existence, uniqueness, and stability of this system under the local Lipschitz function by constructing an appropriate Lyapunov-Krasovskii function and utilizing the semigroup theory. Pu et al. proposed to introduce fractional calculus to implement HNN. They implemented the fractional HNN by utilizing fractor in the form of an analog circuit and the fractional steepest descent approach. In addition, they construct the Lyapunov function to prove the stability of fractional HNN and analyze its attractors [11]. Danca et al. unveiled the existence of hidden chaotic sets in a simplified HNN with three neurons. They proved that besides two stable cycles, the system also has hidden chaotic attractors and hidden chaotic transients, which converge to regular motions along the stable cycles after a relatively long lifetime [12]. In order to make HNN generate more rich and complex brain-like dynamical behaviors, more and more scholars introduce the brain-like element memristor into them [13–19].
A memristor is a nonlinear circuit element whose resistance changes in response to the current flowing through it or the voltage at both ends [20–23]. This nonlinear behavior is very similar to the plasticity of synapses in the human brain [24]. In the process of transferring action potentials, the properties of synapses also change dynamically. Therefore, in recent years, many scholars have used memristors to replace the invariant synaptic weights in HNN and proposed a series of memristive HNN (MHNN) [25–28]. For example, Leng et al. proposed a new circuit to emulate the Coupled Hyperbolic Memristors and utilized it to simulate the synaptic crosstalk of a HNN. With various crosstalk strengths, multi-stability, asymmetry attractors, and anti-monotonicity are observed in this MHNN [29]. Dong et al. proposed a novel memristive synaptic HNN with time delay, which used a memristor synapse to simulate the electromagnetic induced current caused by the membrane potential difference between two adjacent neurons. By choosing time delay and the coupling strength of memristors as bifurcation parameters, they obtained sufficient conditions of zero bifurcation and zero-Hopf bifurcation [26]. Besides simulating synapses, memristors are also used to simulate the effects of electromagnetic radiation on neurons. With the popularity of electronic products, electromagnetic radiation fills people’s daily lives. In order to explore the dynamical behavior of the human brain under electromagnetic radiation, more and more scholars introduce magnetically controlled memristors into HNN and propose a series of new MHNN [30–32]. For instance, Lin et al. studied the chaotic dynamics of a three-neuron HNN under electromagnetic radiation stimulation, and found hidden extreme multistability that includes hyperchaos and transient chaos. In addition, they also designed a circuit based on HNN composed of commercially available electronic components to verify the theoretical analysis [33]. Wan et al. investigated the hidden multistability and parallel bifurcation behaviors of a HNN under the simulation of external electromagnetic radiation and dual bias currents. They also designed an equivalent analog circuit and verified the numerical simulation results by Multisim simulation and hardware experiment based on discrete electronic components [34].
In recent years, various complex dynamical behaviors have been found in both memristive synaptic weight HNN and HNN under electromagnetic radiation, including multi-scroll or multistructure chaotic attractors. Compared with general chaotic attractors, they are more attractive for their more complex topological structure and artificially controllable attractor structure. Zhang et al. introduced a non-ideal magnetically controlled memristor model containing a sign function into HNN, and constructed a memristive HNN model with multiple double-scroll attractors. The odd and even numbers of double scrolls can be flexibly controlled by the internal parameters of the memristor. In particular, they found the coexisting behavior induced by the initial state offset of the memristor, and the number of coexisting attractors was closely related to the total number of scrolls, and eventually tended to infinity as the total number of scrolls increased [35]. Yu et al. proposed a locally active memristor containing a smooth sign function and established a MHNN satisfying the Lipschitz condition by replacing the synaptic weights of HNN. From it, they found controllable multi-scroll behavior and extreme multistability. In addition, they physically implemented this multi-scroll MHNN using FPGA technology and applied it to image encryption [36]. Lai et al. established a novel flux-controlled memristor model using hyperbolic function series. By taking the memristor as synapses in a HNN, they constructed three MHNNs. These MHNNs can generate multi-double-scroll chaotic attractors or grid multi-double-scroll chaotic attractors, and the number of double scrolls in the attractors is controlled by the memristor [37].
Inspired by the above research status, We propose a new model of MHNN under electromagnetic radiation, from which we discover the complex dynamic behavior. The main novelty and contributions of this study are summarized as follows:
1) We propose a new memristor model with controllable number of power interruption steady states, whose memductance does not contain any polynomials.
2) By using it to simulate the effects of membrane flux changes caused by electromagnetic radiation, a new model of MHNN under electromagnetic radiation is proposed
3) A series of complex chaotic phenomena are found, including memristor-controlled multi-scroll attractors, symmetric bifurcation behaviors, initial offset boosting coexistence.
4) Inspired by inter-brain region synchronization of the human brain, we propose a dual MHNN coupling synchronization model. Through Lyapunov function and Simulink experiments, the feasibility of this synchronization scheme is verified.
The rest of this article is organized as follows. In Section 2, the memristor model is constructed. In Section 3, a MHNN under electromagnetic are constructed and analyzed. In Section 4, The dynamic numerical simulation is carried out. In Section 5, an dual coupling synchronous model is designed and proved. Section 6 summarizes the paper.
2 Novel nonvolatile memristor
2.1 Construction of memristor model
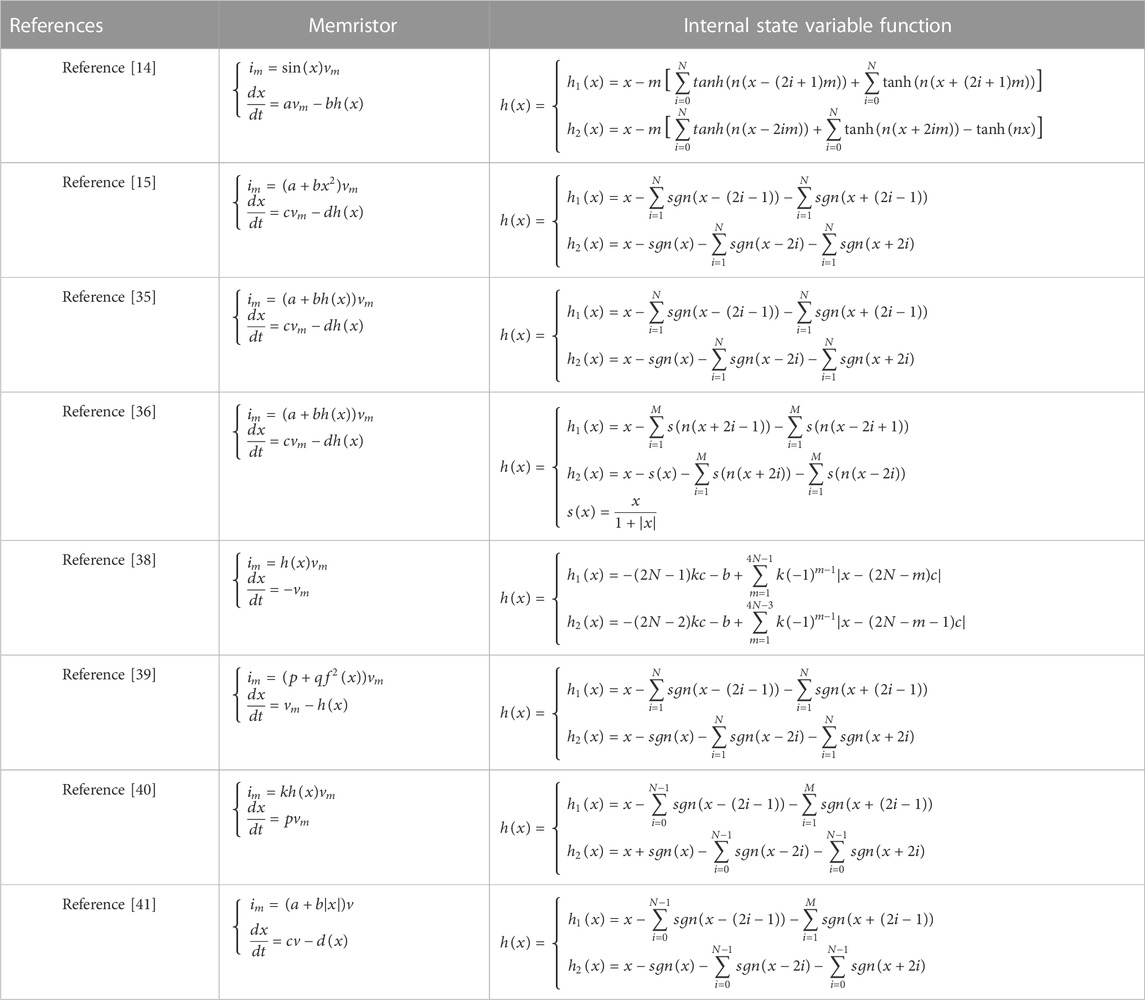
Over the past few years, a number of memristor models that can assist in the generation of multi-scroll attractors have been proposed one after another, and they are summarized in Table 1. Based on the general form of memristors, we propose a novel non-volatile memristor model that can induce controllable multi-scrolls in HNN. It can be expressed by the following equation:
where
and
where
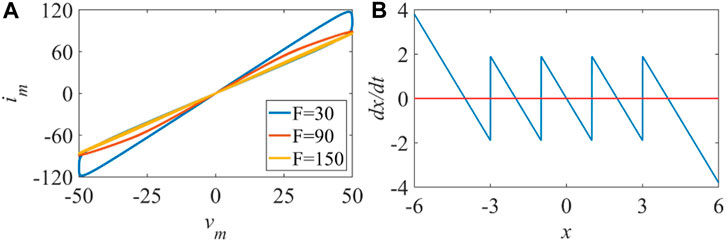
2.2 Hysteresis characteristics and non-volatility
For the proposed memristor model, we first need to verify whether it satisfies the three fingerprints of a memristor [42]. Let the parameters a, b, m and n in Eq. 1 be 2.1, 0.5, 4.5 and 1.9 respectively, and take
Taking the internal variable x as the horizontal axis and
3 MHNN under electromagnetic radiation
3.1 MHNN model construction
HNN has a simple mathematical form and complex dynamic behavior. In the study of chaotic dynamics, the membrane capacitance and membrane resistance of neurons are usually set to 1 to further simplify the dynamic equation of HNN. At this time, any HNN can be expressed by the following formula:
Where X is the neuron membrane potential vector, I is the external stimulus current vector, W is the weight matrix between neurons. In this paper, the weight matrix is:
The external stimulus current is uniformly set to zero. Let the initial membrane potentials of neuron one and neuron three be 0.1, and let the initial membrane potentials of neuron two be 1 and -1 respectively. The three-dimensional HNN can exhibit complex chaotic coexistence behavior at this time, and its phase diagram is shown in Figure 2A. By continuously changing the initial membrane potential of neuron 2, we can obtain the corresponding Lyapunov exponent spectrum diagram. Figure 2B shows that when the initial membrane potential of neuron 2 takes values in [-2, 2], it finally corresponds to a chaotic attractor.With the development of electronic products, people are exposed to electromagnetic radiation more and more frequently. According to Maxwell’s equations, the effect of electromagnetic radiation on a single neuron can be described by the fluctuation of magnetic flux on the cell membrane. The coupling between magnetic flux and membrane voltage can be realized by a magnetically controlled memristor [43]. Specifically for this paper, we add the memductance term of the memristor described by Eq. 1 to the dynamic equation of neuron 2 to simulate the effect of neuron 2 exposed to electromagnetic radiation. At this time, the dynamic equation of the original three-dimensional HNN becomes:
where k represents the intensity of electromagnetic radiation, a, b, m and n are memristor parameters.
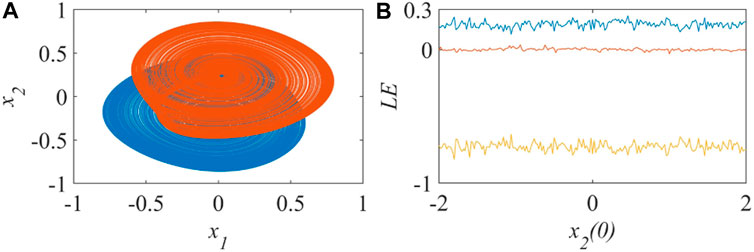
FIGURE 2. The coexistence (A) and the variation of Lyapunov exponent spectrum with the initial potential of neuron 2 (B) of the three-dimensional HNN.
3.2 Equilibrium analysis
Let the left side of Eq. 7 be zero, then we get the following system of equations:
After Gaussian elimination, it can be simplified to the following form:
After eliminating x1 and x2, we can use the graphical method to solve the equation. Let the roots obtained be
Substituting the equilibrium point
4 Kinetic analysis of MHNN
Let the parameters a = 2.1, m = 2, n = 1.9. Taking
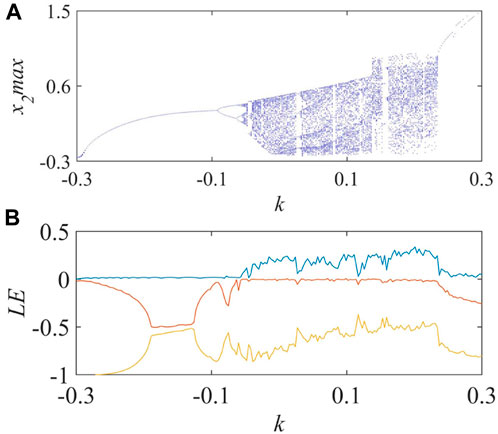
FIGURE 3. Bifurcation behavior of parameter k: (A) bifurcation diagram, (B) Lyapunov exponential spectrum.
In addition to parameter k, the bifurcation behavior of the MHNN with respect to parameter b is more interesting. Similarly, let parameter b continuously change in the interval [-10, 10], we can obtain the bifurcation diagram and the Lyapunov exponent spectrum diagram with respect to parameter b, as shown in Figure 4. In the interval (−10, −9.7), the system exhibits a period one. Near b = −9.7, the system bifurcates from period one to period two. Then near b = −7.9, the system evolves from period two to period four. Near b = −6.6, the system degenerates from period two to period one. Until near b = −4.05, the system again starts to change from period two to period four. After that, with the acceleration of period doubling, the system goes to chaos. In the interval [-3.85, 3.85], chaos and periodicity alternate. Near b = 4.05, the system degenerates from period four to period two. Near b = 6.6, the system evolves from period two to period four. Then near b = 7.9, the system degenerates from period four to period two, and finally degenerates to period one near b = 9.7. It is not difficult to find that the system evolves and degenerates at almost symmetrical positions. In addition, the Lyapunov exponent spectrum in Figure 4 is almost symmetrical about the vertical axis. In summary, the MHNN has a symmetrical bifurcation behavior with respect to parameter b.
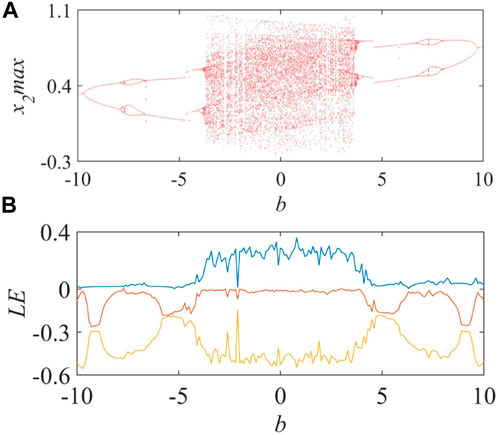
FIGURE 4. Bifurcation behavior of parameter b: (A) bifurcation diagram, (B) Lyapunov exponential spectrum.
4.1 Bifurcation behavior
4.1.1 Multi-scroll chaotic attractor
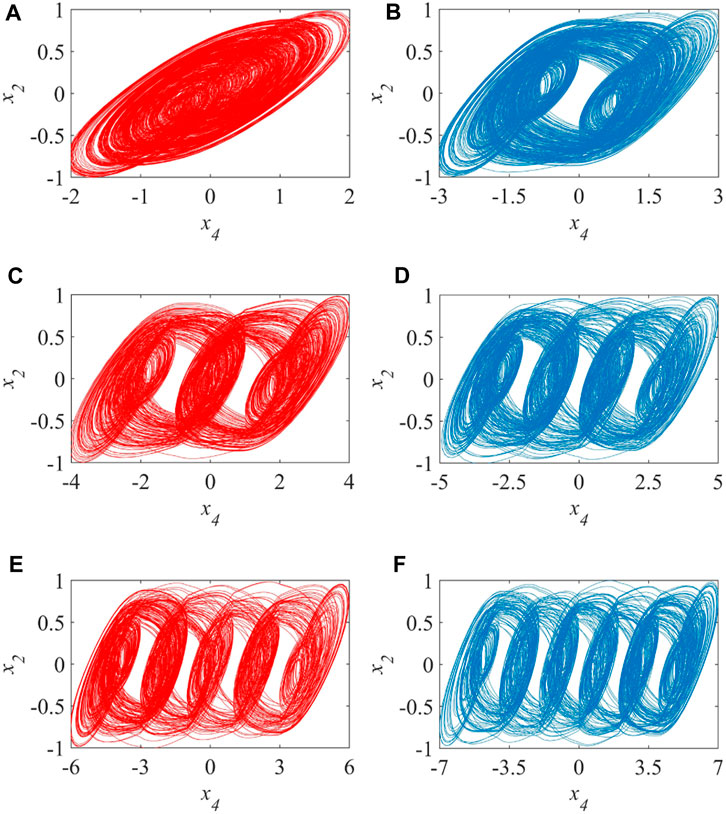
Due to the introduction of the memristor, the MHNN can exhibit multi-scroll behavior that does not exist in the general HNN. Let the parameters a = 2.1, b = 0.1, m = 5, n = 1.9 and k = 0.2 and the initial values be [0.1, 0.1, 0.1, 0.1]. First, we choose
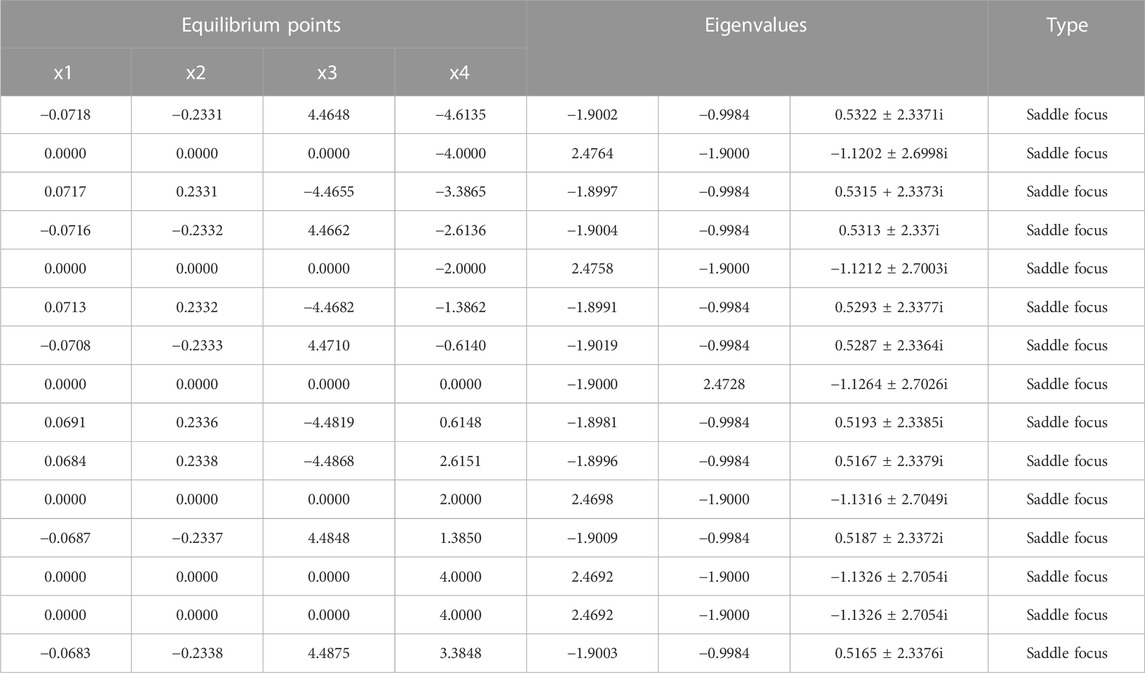
With the help of Shil’nikov’s theorem, the law behind this can be further explained. Taking the appearance of a five-scroll chaotic attractor as an example, according to the idea provided in Section 3.2, all the equilibrium points of the system at this time can be obtained. First, the graphical method is used to obtain the rough values of the roots. Using all the intersections in Figure 6 as a guide, numerical methods are used to obtain more accurate results of x3 and x4. Then the obtained results are substituted into Eq. 9 to obtain all the roots. Next, QR decomposition is used to obtain the eigenvalues corresponding to each equilibrium point, and the final results are shown in Table 2. Table 2 shows that for the MHNN that exhibits a five-scroll chaotic attractor, there are a total of 15 saddle-focus points at this time. And according to Shil’nikov’s theorem, there will be chaotic attractors near these equilibrium points, which is consistent with the simulation results in Figure 5. By observing the distribution of equilibrium points in Figure 6 and Table 2, it is not difficult to summarize that as the parameter M or N increases, the equilibrium points gradually extend along the direction of x4. That is to say, by changing the form of the internal variable function of the memristor and its parameters M or N, the number of equilibrium points of the MHNN can be easily controlled. And according to Shil’nikov’s theory, there will be chaotic attractors near these saddle-focus type equilibrium points. This directly makes the range of chaotic attractors of the MHNN also increase accordingly, which is specifically manifested as an increase in the number of scrolls in this section.
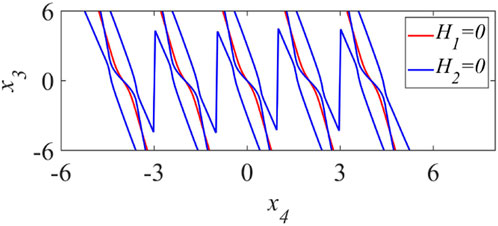
FIGURE 6. Trajectory diagram of the equation in Eq. 9.
4.1.2 Initial offset boosting coexistence
In addition to having complex topological structures of multiple scroll attractors, the MHNN also has complex coexistence behavior. Let the parameters of the MHNN be a = 2.1, b = 0.1, m = 2, n = 1.9 and k = 0.2. First, we choose
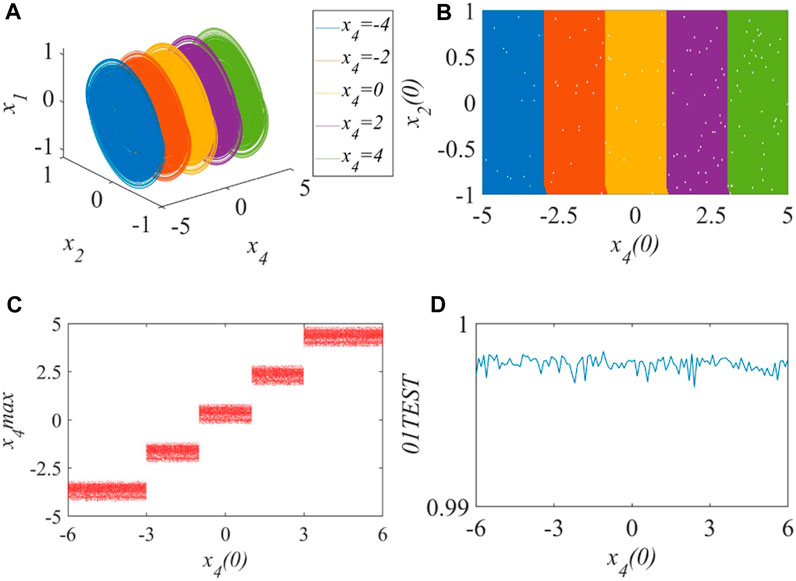
FIGURE 7. Initial offset boosting coexistence when h1(x) is selected and M = 2: (A) Phase diagram, (B) Attraction of basin, (C) Bifurcation diagram, (D) Result of 0–1 test.
In addition,
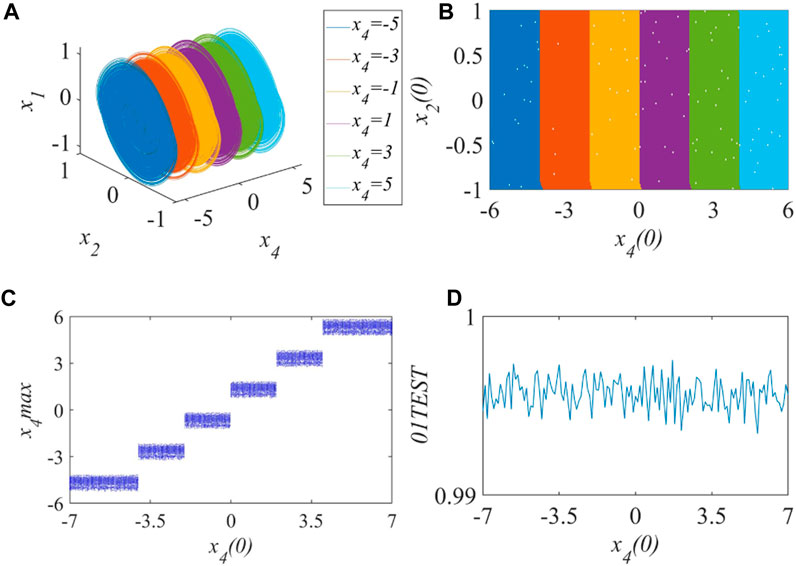
FIGURE 8. Initial offset boosting coexistence when h2(x) is selected and N = 2: (A) Phase diagram, (B) Attraction of basin, (C) Bifurcation diagram, (D) Result of 0–1 test.
From the analysis results of the previous section, it can be known that by choosing the form of the internal variable function of the memristor and its parameters M or N, the number of equilibrium points of the MHNN can be easily controlled. And there will be chaotic attractors near these saddle-focus type equilibrium points. Different from the previous section, the MHNN does not exhibit multi-scroll phenomena, but manifests as coexistence induced by initial position offset. By analogy with the change law of the number of scrolls of multi-scroll attractors, it can be inferred that when choosing
5 Coupling synchronization of MHNN
5.1 Dual coupling synchronous model
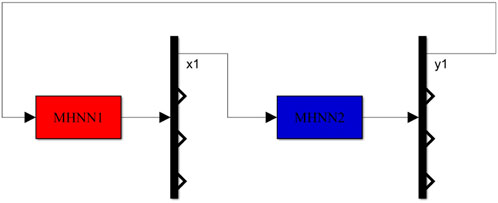
Studies have shown that synchronization plays an important role in memory processing. Synchronization between brain regions supports working memory and long-term memory by facilitating communication between neurons and enhancing neuronal plasticity [44]. Brain regions are synchronized through the connection of some neurons to form inter-regional neural networks, and thus complete the information transmission between different brain regions. Designing a suitable controller is one of the most fundamental methods for controlling complex systems to achieve synchronization, and many scholars have proposed different control strategies [45–55]. In this paper, we use two bounded sub-MHNNs to represent different brain regions. By coupling these two sub-neural networks with a single neuron, a dual-MHNN coupling model is established:
where p represents the coupling strength of the sub-neural networks. To make the two sub-neural networks successfully synchronized, the difference between their outputs needs to be zero, that is:
where i = 1, 2, 3. To prove the validity of the above equation, the following Lyapunov function can be constructed:
Then its derivative with respect to time is:
Since
Therefore, Eq. 14 can be further relaxed as:
Therefore, when 2p − 1 < 0 holds, Eq. 13 is ultimately uniformly bounded.
5.2 Simulink simulation
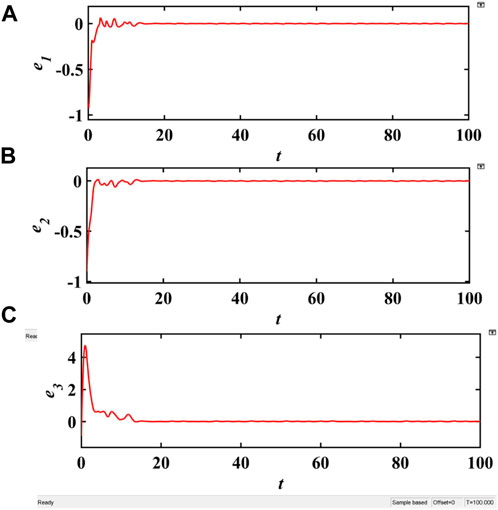
The schematic diagram of Simulink experiment is shown in Figure 9 and let the system parameters be a = 2.1, b = 0.1, m = 2, n = 1.9, k = 0.1. By building a Simlulink model, the coupling synchronization model described by Eq. 11 can be easily simulated. When the coupling strength p = −1, the simulation results are shown in Figures 10, 11. Figure 11 shows that after the two sub-memristive HNNs are coupled, the difference between the potentials on the corresponding neurons quickly drops to near zero. Figure 10 is the time domain diagram of the potentials on neuron 1 of the two sub-networks, which shows that they match well.
6 Conclusion
This paper has investigated the nonlinear dynamics and applications of a new non-volatile magnetic-controlled memristor. It is demonstrated that the memristor can simulate the effect of electromagnetic radiation on neuronal membrane flux. By introducing this memristor to a 3D HNN, a 4D MHNN under electromagnetic radiation is constructed. By plotting phase diagrams, bifurcation diagrams, basins of attraction and 01 tests, a series of complex chaotic phenomena are found, including memristor-controlled multi-scroll chaotic attractors, symmetric bifurcation behaviors, initial offset boosting coexistence. Through equilibrium point analysis, the mechanisms behind them are explained. Finally, a dual MHNN coupling synchronization model simulating the inter-brain region synchronization of the human brain is proposed. By constructing a Lyapunov function for the error, this coupling synchronization scheme is proved to be ultimately bounded. By building a Simulink model, we verify the feasibility of this synchronization scheme by simulation experiments. This study contributes to the understanding of memristive systems, synchronization of brain regions and their potential applications in engineering.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, SF and ZY; methodology, SF; software, SF and XW; validation, SF, XW, and HG; formal analysis, SF and ZY; investigation, XC; resources, ZY; data curation, SF; writing—original draft preparation, SF; writing—review and editing, SF, XW, and ZY; visualization, HG; supervision, ZY; project administration, ZY and SF; funding acquisition, SF and ZY. All authors contributed to the article and approved the submitted version.
Funding
This paper was supported by the Integrated Innovation Project of the Group Company under Grant 2023-JC-13.
Conflict of interest
SF, XW, and XC were employed by the Aircraft Technology Branch of Hunan Aerospace Co., Ltd. SF and HG were employed by the China Aerospace Science and Industry Corporation.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (1952) 117:500–44. doi:10.1113/jphysiol.1952.sp004764
2. Nagumo J, Arimoto S, Yoshizawa S. An active pulse transmission line simulating nerve axon. Proc IRE (1962) 50:2061–70. doi:10.1109/jrproc.1962.288235
3. Deng Z, Wang C, Lin H, Sun Y. A memristive spiking neural network circuit with selective supervised attention algorithm. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2022) 42:2604–17. doi:10.1109/TCAD.2022.3228896
4. Izhikevich EM. Simple model of spiking neurons. IEEE Trans Neural networks (2003) 14:1569–72. doi:10.1109/tnn.2003.820440
5. Hindmarsh JL, Rose R. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond Ser B. Biol Sci (1984) 221:87–102. doi:10.1098/rspb.1984.0024
6. Chua LO, Yang L. Cellular neural networks: Theory. IEEE Trans circuits Syst (1988) 35:1257–72. doi:10.1109/31.7600
7. Chen Z, Liang Q, Wei Z, Chen X, Shi Q, Yu Z, et al. An overview of in vitro biological neural networks for robot intelligence. Cyborg Bionic Syst (2023) 4:0001. doi:10.34133/cbsystems.0001
8. Hopfield JJ. Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci (1984) 81:3088–92. doi:10.1073/pnas.81.10.3088
9. Lin H, Wang C, Yu F, Hong Q, Xu C, Sun Y. A triple-memristor hopfield neural network with space multi-structure attractors and space initial-offset behaviors. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2023) 1. doi:10.1109/TCAD.2023.3287760
10. Xu Q, Wang Y, Iu HH-C, Wang N, Bao H. Locally active memristor-based neuromorphic circuit: Firing pattern and hardware experiment. IEEE Trans Circuits Syst Regular Pap (2023) 70:3130–41. doi:10.1109/TCSI.2023.3276983
11. Pu Y-F, Yi Z, Zhou J-L. Fractional hopfield neural networks: Fractional dynamic associative recurrent neural networks. IEEE Trans Neural Networks Learn Syst (2017) 28:2319–33. doi:10.1109/tnnls.2016.2582512
12. Danca M-F, Kuznetsov N. Hidden chaotic sets in a Hopfield neural system. Solitons and Fractals (2017) 103:144–50. doi:10.1016/j.chaos.2017.06.002
13. Yu F, Yu Q, Chen H, Kong X, Mokbel AAM, Cai S, et al. Dynamic analysis and audio encryption application in iot of a multi-scroll fractional-order memristive hopfield neural network. Fractal and Fractional (2022) 6:370. doi:10.3390/fractalfract6070370
14. Lai Q, Wan Z, Zhang H, Chen G. Design and analysis of multiscroll memristive hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans Neural Networks Learn Syst (2022) 2022:1. doi:10.1109/tnnls.2022.3146570
15. Yu F, Shen H, Yu Q, Kong X, Sharma PK, Cai S. Privacy protection of medical data based on multi-scroll memristive hopfield neural network. IEEE Trans Netw Sci Eng (2023) 10:845–58. doi:10.1109/tnse.2022.3223930
16. Wan Q, Li F, Chen S, Yang Q. Symmetric multi-scroll attractors in magnetized Hopfield neural network under pulse controlled memristor and pulse current stimulation. Solitons and Fractals (2023) 169:113259. doi:10.1016/j.chaos.2023.113259
17. Yu F, Chen H, Kong X, Yu Q, Cai S, Huang Y, et al. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. The Eur Phys J Plus (2022) 137:434. doi:10.1140/epjp/s13360-022-02652-4
18. Chen C, Min F, Hu F, Cai J, Zhang Y. Analog/digital circuit simplification for Hopfield neural network. Solitons and Fractals (2023) 173:113727. doi:10.1016/j.chaos.2023.113727
19. Chen C, Min F, Zhang Y, Bao H. ReLU-type Hopfield neural network with analog hardware implementation. Solitons and Fractals (2023) 167:113068. doi:10.1016/j.chaos.2022.113068
20. Chua L. Memristor-the missing circuit element. IEEE Trans Circuit Theor (1971) 18:507–19. doi:10.1109/tct.1971.1083337
21. Xu Q, Wang Y, Chen B, Li Z, Wang N. Firing pattern in a memristive Hodgkin–Huxley circuit: Numerical simulation and analog circuit validation. Solitons and Fractals (2023) 172:113627. doi:10.1016/j.chaos.2023.113627
22. Liu X, Mou J, Zhang Y, Cao Y. A new hyperchaotic map based on discrete memristor and meminductor: Dynamics analysis, encryption application, and dsp implementation. IEEE Trans Ind Elect (2023) 2023:1–10. doi:10.1109/TIE.2023.3281687
23. Yu F, Xu S, Xiao X, Yao W, Huang Y, Cai S, et al. Dynamics analysis, fpga realization and image encryption application of a 5d memristive exponential hyperchaotic system. Integration (2023) 90:58–70. doi:10.1016/j.vlsi.2023.01.006
24. Jo SH, Chang T, Ebong I, Bhadviya BB, Mazumder P, Lu W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett (2010) 10:1297–301. pMID: 20192230. doi:10.1021/nl904092h
25. Chen C, Chen J, Bao H, Chen M, Bao B. Coexisting multi-stable patterns in memristor synapse-coupled hopfield neural network with two neurons. Nonlinear Dyn (2019) 95:3385–99. doi:10.1007/s11071-019-04762-8
26. Eftekhari L, Amirian MM. Stability analysis of fractional order memristor synapse-coupled hopfield neural network with ring structure. Cogn Neurodynamics (2023) 17:1045–59. doi:10.1007/s11571-022-09844-9
27. Huang L-L, Zhang Y, Xiang J-H, Liu J. Extreme multistability in a hopfield neural network based on two biological neuronal systems. IEEE Trans Circuits Syst Express Briefs (2022) 69:4568–72. doi:10.1109/tcsii.2022.3183340
28. Lin H, Wang C, Yu F, Sun J, Du S, Deng Z, et al. A review of chaotic systems based on memristive hopfield neural networks. Mathematics (2023) 11:1369. doi:10.3390/math11061369
29. Leng Y, Yu D, Hu Y, Yu SS, Ye Z. Dynamic behaviors of hyperbolic-type memristor-based Hopfield neural network considering synaptic crosstalk. Interdiscip J Nonlinear Sci (2020) 30:033108. doi:10.1063/5.0002076
30. Chen C, Min F, Zhang Y, Bao B. Memristive electromagnetic induction effects on hopfield neural network. Nonlinear Dyn (2021) 106:2559–76. doi:10.1007/s11071-021-06910-5
31. Chen M, Chen C-j., Bao B-c., Xu Q. Multi-stable patterns coexisting in memristor synapse-coupled hopfield neural network. In: Mem-elements for neuromorphic circuits with artificial intelligence applications. Amsterdam, Netherlands: Elsevier (2021). p. 439–59.
32. Hu Z, Wang C. Hopfield neural network with multi-scroll attractors and application in image encryption. Multimedia Tools Appl (2023) 2023. doi:10.1007/s11042-023-15670-w
33. Lin H, Wang C, Tan Y. Hidden extreme multistability with hyperchaos and transient chaos in a hopfield neural network affected by electromagnetic radiation. Nonlinear Dyn (2020) 99:2369–86. doi:10.1007/s11071-019-05408-5
34. Wan Q, Yan Z, Li F, Liu J, Chen S. Multistable dynamics in a hopfield neural network under electromagnetic radiation and dual bias currents. Nonlinear Dyn (2022) 109:2085–101. doi:10.1007/s11071-022-07544-x
35. Zhang S, Zheng J, Wang X, Zeng Z, He S. Initial offset boosting coexisting attractors in memristive multi-double-scroll hopfield neural network. Nonlinear Dyn (2020) 102:2821–41. doi:10.1007/s11071-020-06072-w
36. Yu F, Kong X, Mokbel AAM, Yao W, Cai S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive hopfield neural network with a novel local active memeristor. IEEE Trans Circuits Syst Express Briefs (2023) 70:326–30. doi:10.1109/tcsii.2022.3218468
37. Lai Q, Wan Z, Kuate PDK. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans Circuits Syst Regular Pap (2023) 70:1324–36. doi:10.1109/tcsi.2022.3228566
38. Wang C, Liu X, Xia H. Multi-piecewise quadratic nonlinearity memristor and its 2 n-scroll and 2 n+ 1-scroll chaotic attractors system. Chaos (2017) 27:033114. doi:10.1063/1.4979039
39. Xia X, Zeng Y, Li Z. Coexisting multiscroll hyperchaotic attractors generated from a novel memristive jerk system. Pramana (2018) 91:82–14. doi:10.1007/s12043-018-1657-3
40. Zhang S, Zheng J, Wang X, Zeng Z. Multi-scroll hidden attractor in memristive hr neuron model under electromagnetic radiation and its applications. Chaos (2021) 31:011101. doi:10.1063/5.0035595
41. Lin H, Wang C, Sun Y, Wang T. Generating n-scroll chaotic attractors from a memristor-based magnetized hopfield neural network. IEEE Trans Circuits Syst Express Briefs (2023) 70:311–5. doi:10.1109/tcsii.2022.3212394
42. Adhikari SP, Sah MP, Kim H, Chua LO. Three fingerprints of memristor. IEEE Trans Circuits Syst Regular Pap (2013) 60:3008–21. doi:10.1109/tcsi.2013.2256171
43. Lin H, Wang C, Deng Q, Xu C, Deng Z, Zhou C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn (2021) 106:959–73. doi:10.1007/s11071-021-06853-x
44. Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat Rev Neurosci (2011) 12:105–18. doi:10.1038/nrn2979
45. Tan F, Zhou L, Lu J, Quan H, Liu K. Adaptive quantitative control for finite time synchronization among multiplex switched nonlinear coupling complex networks. Eur J Control (2023) 70:100764. doi:10.1016/j.ejcon.2022.100764
46. Zhang C, Yan L, Gao Y, Wang W, Li K, Wang D, et al. A new adaptive iterative learning control of finite-time hybrid function projective synchronization for unknown time-varying chaotic systems. Front Phys (2023) 11:1127884. doi:10.3389/fphy.2023.1127884
47. Yao W, Wang C, Sun Y, Gong S, Lin H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Networks (2023) 164:67–80. doi:10.1016/j.neunet.2023.04.024
48. Zhou L, Huang M, Tan F, Zhang Y. Mean-square bounded synchronization of complex networks under deception attacks via pinning impulsive control. Nonlinear Dyn (2023) 111:11243–59. doi:10.1007/s11071-023-08448-0
49. Lin L, Zhuang Y, Xu Z, Yang D, Wu D. Encryption algorithm based on fractional order chaotic system combined with adaptive predefined time synchronization. Front Phys (2023) 11:1202871. doi:10.3389/fphy.2023.1202871
50. Ma M-L, Xie X-H, Yang Y, Li Z-J, Sun Y-C. Synchronization coexistence in a rulkov neural network based on locally active discrete memristor. Chin Phys B (2023) 32:058701. doi:10.1088/1674-1056/acb9f7
51. Xu Q, Liu T, Ding S, Bao H, Li Z, Chen B. Extreme multistability and phase synchronization in a heterogeneous bi-neuron rulkov network with memristive electromagnetic induction. Cogn Neurodynamics (2023) 17:755–66. doi:10.1007/s11571-022-09866-3
52. Zhang C, Zhang C, Zhang X, Wang F, Liang Y. Dynamic event-triggered control for intra/inter-layer synchronization in multi-layer networks. Commun Nonlinear Sci Numer Simulation (2023) 119:107124. doi:10.1016/j.cnsns.2023.107124
53. Yu Y, Xiang L, Liu B, Xia C. Moment-based analysis of pinning synchronization in complex networks with sign inner-coupling configurations. Front Phys (2023) 11:1179469. doi:10.3389/fphy.2023.1179469
54. Zhou L, Lin H, Tan F. Fixed/predefined-time synchronization of coupled memristor-based neural networks with stochastic disturbance. Solitons and Fractals (2023) 173:113643. doi:10.1016/j.chaos.2023.113643
Keywords: memristor, Hopfield neural network (HNN), multi-scroll, multistability, synchronization
Citation: Fu S, Wang X, Gu H, Cao X and Yao Z (2023) Multi-scroll Hopfield neural network under electromagnetic radiation and its brain-like coupling synchronization. Front. Phys. 11:1252568. doi: 10.3389/fphy.2023.1252568
Received: 04 July 2023; Accepted: 15 August 2023;
Published: 25 August 2023.
Edited by:
Viet-Thanh Pham, Ton Duc Thang University, VietnamReviewed by:
Fuhong Min, Nanjing Normal University, ChinaHilaire Fotsin, University of Dschang, Cameroon
Junwei Sun, Zhengzhou University of Light Industry, China
Copyright © 2023 Fu, Wang, Gu, Cao and Yao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhengjun Yao, eWFvempAbnVhYS5lZHUuY24=
 Sen Fu
Sen Fu Xia Wang2
Xia Wang2