- 1Department of Medical Biophysics, The University of Western Ontario, London, ON, Canada
- 2Robarts Research Institute and Lawson Health Research Institute, London, ON, Canada
- 3Department of Medical Imaging, The University of Western Ontario, London, ON, Canada
CT perfusion (CTP)-derived quantitative maps of hemodynamic parameters have found important clinical applications in stroke, cancer, and cardiovascular disease. Blood flow, blood volume, transit time, and other perfusion parameters are sensitive markers of pathophysiology with impaired perfusion. This review summarizes the basic principles of CTP including image acquisition, tracer kinetic modeling, deconvolution algorithms, and diagnostic interpretation. The focus is on practical and theoretical considerations for accurate quantitative parametric imaging. Recommended CTP scan parameters to maintain CT number accuracy and optimize radiation dose versus image noise are first reviewed. Tracer kinetic models, which describe how injected contrast material is distributed between blood and the tissue microenvironment by perfusion and bidirectional passive exchange, are then derived. Deconvolution algorithms to solve for hemodynamic parameters of kinetic models are discussed and their quantitative accuracy benchmarked. The applications and diagnostic interpretation of CTP in stroke, cancer, and cardiovascular disease are summarized. Finally, we conclude with a discussion of future directions for CTP research, including radiation dose reduction, new opportunities with novel CT hardware, and emerging diagnostic applications.
1 Introduction
CT perfusion (CTP) is a functional imaging technique used to generate quantitative maps of hemodynamic parameters such as blood flow, blood volume, and mean transit time. Normal vascular perfusion underpins normal tissue function, and its disruption may be an indicator of underlying disease. Since the first demonstration of brain CTP by Leon Axel in 1980 [1], the field has rapidly grown to encompass specific diagnostic applications in various diseases such as acute ischemic stroke, cancer, and cardiovascular disease. Specifically, CTP may be used to non-invasively diagnose and characterize diseases with impaired tissue perfusion, monitor disease progression, and distinguish viable from non-viable tissue. Decisions on the management and treatment of patients can be informed by CTP.
A notable diagnostic application of CTP is in acute ischemic stroke. CTP was used to select patients with large vessel ischemic stroke for endovascular stroke treatment in multiple randomized controlled trials [2–4]. Post-processing and analysis of brain CTP imaging was fully automated, and imaging-based assessment of treatment eligibility was available within minutes of acquisition. Patients who received endovascular stroke treatment based on a favorable CTP profile had greatly improved 90-day functional outcomes compared to those not receiving treatment. The therapeutic benefit persisted beyond the 6-h onset-to-treatment time window normally recommended for patients selected without perfusion imaging. CTP is a validated and automated treatment decision assistance tool in acute ischemic stroke and played an important role in demonstrating that endovascular stroke treatment was safe and effective beyond the standard therapeutic time window.
A CTP study is normally performed as follows. An iodinated contrast agent is intravenously injected into the patient, and following a short delay (<10 s) for the contrast agent to arrive at the organ of interest, CT scans are serially acquired for ≈1 to 3 min. Time–density (attenuation) curves (TDCs) derived from the acquired serial (dynamic) contrast-enhanced CT images describe how the contrast agent washes in and out from tissue by blood flow. Hemodynamic parameters such as blood flow (F), blood volume (Vb), mean transit time (MTT), artery-to-tissue contrast delay time (T0), and time-to-maximum of the residue function (Tmax, a composite index of delay, dispersion, and MTT) [5] can be estimated by analyzing the acquired TDCs. Specifically, the arterial TDC, which estimates the arterial contrast concentration, is deconvolved from tissue TDCs to estimate an impulse residue function (IRF). The perfusion parameters of interest are derived from the IRF, which describes the hemodynamic response if a unit mass of contrast was injected into the arterial inlet of the tissue. Calculation of the IRF for each tissue voxel leads to quantitative maps of perfusion parameters from which regional impairment of perfusion can be visualized.
This review summarizes the basic principles of CTP, methods to estimate perfusion parameters, diagnostic applications, and emerging research, with a focus on quantitative parametric imaging.
2 The quantitative capability of CT
CT images are cross-sectional, quantitative maps of the linear attenuation coefficient (expressed as CT number) of tissue. Due to the small differences in the linear attenuation coefficient between water, blood, and soft tissue in the diagnostic X-ray energy range (≤150 keV) [6, 7], blood cannot be distinguished from soft tissue with CT to estimate perfusion. In contrast, iodine has a much greater attenuation coefficient than that of soft tissue [6, 7]. Intravenous injection of an iodine contrast agent allows the contrast agent to circulate throughout the organ of interest. If the patient is scanned serially with fixed CT protocols as in a CTP study, the contrast-induced changes in CT number reflect the same in iodine concentration in vessels and tissue in a linear fashion and can be quantified as TDCs. Furthermore, an iodine contrast agent is inert, extracellular, and does not bind to any target nor does it enter a cell; it remains either in the intravascular or interstitial space [8]. As such, contrast transport principles, which are described in Section 3, can be applied to describe TDCs obtained from CTP.
The linear relationship between CT number and contrast concentration is a notable advantage of CTP compared to perfusion magnetic resonance imaging (MRI). In dynamic susceptibility contrast perfusion MRI, a tissue-dependent scaling factor must be accounted to convert T2* signal change to gadolinium concentration [9, 10]. As such, absolute measurements of blood flow and blood volume cannot be obtained without knowledge of these tissue-dependent scaling factors. The relative blood flow and volume obtained by normalizing by mean blood flow or volume in a reference region are used for perfusion MRI in clinical practice due to this limitation. While perfusion imaging with positron emission tomography and flow-specific radiotracers is the clinical gold standard for absolute perfusion measurements, it is often impractical due to its long scan time and high resource requirement (e.g., availability of a cyclotron and flow-specific radiotracers such as 15O-water or 13N-NH3, which are short-lived tracers with additional logistical problems, unlike off-the-shelf stable contrast agents used in CTP).
2.1 CT perfusion scan protocol
In designing a CTP scan protocol, the goal is to balance the radiation dose to the patient versus the signal-to-noise ratio (SNR) of TDCs required to generate diagnostic quality perfusion maps. The following scan parameters are of significance in CTP: X-ray tube voltage, tube current-exposure time, scan interval, contrast injection volume and rate, axial coverage, and scan duration.
Tube voltage determines the energy spectrum of the incident X-ray beam and sensitivity to the iodine contrast agent. For CTP, to balance the iodine contrast-to-noise ratio and radiation dose, a tube voltage of 80 kV is used for most diagnostic applications [11, 12], though higher tube voltages (100 or 120 kV) may be appropriate in thoracic and abdominal CTP, where there may be greater attenuation of X-rays due to the larger scan object.
At a fixed tube voltage, photon fluence is determined by the tube current-exposure time product (referred to by its unit, mAs). Photon fluence and radiation dose are linearly proportional to mAs, and the noise level is inversely proportional to the square root of the mAs. The mAs is an important factor, besides kV, in determining the TDC SNR. The recommended mAs for brain CTP ranges between 100 mAs and 200 mAs per dynamic image at a tube voltage of 80 kV [13, 14]. The optimal mAs for other anatomical applications has not yet been established, but can range from tens of mAs to up to 200 mAs per dynamic image. The choice of mAs also depends on the number of dynamic CTP images acquired to balance the radiation dose.
The recommended CTP temporal resolution is ≤ 3 s between dynamic images [13–16]. This range has mainly been determined empirically and depends on other scan parameters such as contrast volume and injection rate, patient cardiac output, desired brain coverage versus scanner axial coverage, and radiation dose [17, 18]. A uniform scan interval of 3 s with a 40-mL bolus injection at 4 mL/s was found to balance the radiation dose and perfusion parameter accuracy [17]. Non-uniform scan intervals have also been used to sample the slower venous/wash-out phase of TDCs at prolonged intervals to assess blood–brain barrier permeability [19] or to optimize the radiation dose [15, 20].
The minimum scan interval can also be limited by the desired anatomical coverage versus the axial coverage provided by the scanner. In CT scanners with less whole organ coverage (<8 cm axially), a toggling table [21, 22] or periodic spiral [23] technique is often used to increase coverage. The toggling table technique (also called step-and-shoot or shuttle mode) increases the axial coverage by acquiring two “slabs” of the object at two “toggled” table positions. Here, the table is stopped during the scan, and this process is repeated over the prescribed scan duration [21, 22]. In the periodic spiral technique, the object is scanned continuously while the patient table smoothly moves in and out of the gantry (i.e., a continuous helical or spiral CT scan). The scan interval is therefore limited by the inter-scan time required due to table movement and the desired axial coverage.
CTP scan duration should be chosen such that at least the first pass of contrast through the vasculature is fully captured, which normally takes 45–60 s after contrast injection [24]. Following the first pass of contrast (the intravascular phase), the TDC signal is mainly from the influx and efflux of contrast through the blood–tissue barrier by passive diffusion (interstitial phase). Therefore, a longer scan duration of 120–150 s may be prescribed to assess vessel permeability and other kinetic parameters with model-dependent deconvolution [15, 19, 25]. Scan duration must otherwise be balanced against radiation dose. If a CTP study is too short, the full wash-out phase of the contrast agent may not be sampled, especially in diseased regions where the transit time may be prolonged. This so-called truncation of TDCs is known to cause an underestimation of CBV, MTT, and Tmax and, accordingly, may lead to an inaccurate diagnosis [26]. Tolerance to TDC truncation may depend on the deconvolution algorithm used to generate perfusion parametric maps [27]. Of note, an iodinated contrast material is diffusion-limited with respect to perfusion in blood–tissue exchange, particularly in the case of an intact blood–brain barrier. This contrasts with xenon, which is not diffusion-limited in all tissues. Tracers that are not diffusion-limited are freely diffusible.
2.2 CT artifacts
A select number of relevant CT artifacts that affect the estimation of perfusion are reviewed here. The key idea is to mitigate CT artifacts such that the linear relationship between the change in CT number and the change in iodine concentration is maintained. As such, for CTP, the consistency of the CT number between images is arguably more important than absolute CT number accuracy. Representative examples of CT artifacts discussed in this article are illustrated in Figure 1.
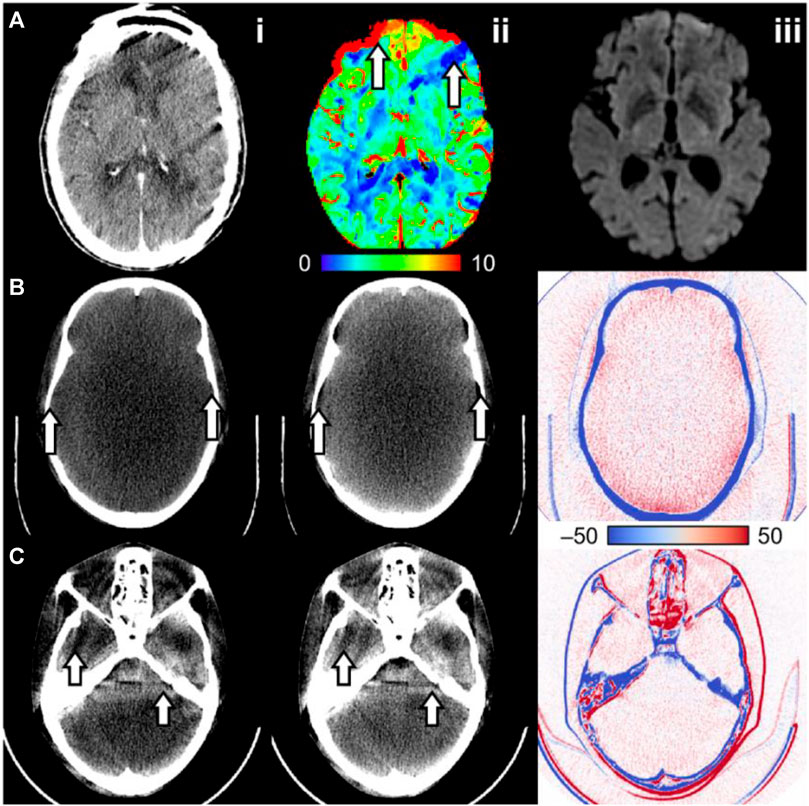
FIGURE 1. Examples of CT artifacts that may affect CT number consistency in CT perfusion. (A) Intra-scan motion artifact in a CT perfusion dynamic image. (A.ii) The cerebral blood volume map shows regions of increased and decreased blood volume (arrows), where the decrease suggests an ischemic core. (A.iii) Follow-up diffusion-weighted imaging does not show an infarct in that region. (B) An anthropomorphic head phantom reconstructed (B.i) with and (B.ii) without beam hardening correction and (B.iii) the difference image (without minus with correction). The image without beam hardening correction has cupping artifacts and a poor bone–brain interface (arrows). (C) An anthropomorphic head phantom scanned at (C.i) 20 mm and (C.ii) 40 mm beam collimation width. (C.iii) The difference image (40 mm minus 20 mm) shows increased intracranial CT number at 40 mm relative to 20 mm collimation width, possibly due to scattering overcorrection. The arrows also show beam hardening shading artifacts due to the different attenuation characteristics of bone compared to the intracranial material.
2.2.1 Patient motion
Two types of patient motion can be identified for CTP: (1) inter-scan motion, which misaligns tissue voxels between dynamic images, and (2) intra-scan motion, or motion during the scanning of an image, which often causes dark shading artifacts. Moderate-to-severe patient motion may be seen in up to 25% of patients receiving brain CTP [28]. A secondary analysis of a randomized clinical trial of endovascular stroke treatment revealed that ≈10% of patients who received brain CTP had motion artifacts, which rendered the CTP study unanalyzable [29]. Inter-scan motion can mostly be corrected by co-registering (spatially aligning) all dynamic images to a reference dynamic image in the CTP study [30]. Motion correction by image registration is automated and available in all commercial CTP software. Intra-scan motion artifact is difficult to correct retrospectively, and dynamic images showing severe intra-scan motion artifacts may need to be selectively excluded from CTP post-processing. Motion artifacts can cause both erroneous increases and decreases in estimated perfusion depending on the context. For example, intra-scan motion shading may decrease the amplitude of TDCs and erroneously introduce a low-blood flow region. In contrast, inter-scan motion may cause blurring of inter-organ boundaries (e.g., the bone–brain interface) and cause artificial increases or decreases in the measured TDC value. Motion is a major challenge for myocardial CTP imaging in which the beating heart undergoes nonrigid movement. These challenges are mitigated by electrocardiogram gating, fast gantry rotation time to minimize intra-scan motion, and nonrigid motion correction post-reconstruction [31]. Figure 1A illustrates the effect of intra-scan motion on a CTP cerebral blood volume map.
2.2.2 Beam hardening
Beam hardening refers to an increase in mean X-ray energy (“hardening”). Generated X-rays are polyenergetic, and low-energy photons are disproportionately attenuated compared to high-energy photons when passing through an object [6, 32]. X-rays that pass through a greater length of the attenuating material will proportionally have greater hardening. Non-uniform energy attenuation results in inconsistent X-ray energy distributions between detectors and projections, which causes a shift in the CT number, wherein beams with greater hardening have a lower CT number. Furthermore, streaking and shading artifacts may occur at cross-sections with heterogenous bone structures, such as at the posterior fossa of the head [6, 32]. This occurs due to inconsistent levels of beam hardening between projections. All commercial CT systems have methods to correct for these artifacts, but the discussion of specific methods is outside the scope of this review. Without proper correction, the linear relationship between CT number and iodine concentration is not maintained, thereby compromising the accuracy of perfusion parameter estimations. Beam hardening artifacts are illustrated in Figure 1B and Figure 1C.
2.2.3 X-ray scattering
Compton scattering is one of the main modes of interaction between X-ray photons and tissue at diagnostic X-ray energy levels [6]. As a result, the measured CT detector signal can be from primary photons (directly from the incident X-ray) or a scattered photon (deflected at a random angle from within the scanned object). Scattering increases with greater beam collimation width as the volume of the irradiated material and detector coverage are increased. Scattering can be modeled as a low-frequency additive bias to the true primary detector signal, which may cause streaking artifacts and CT number bias in the reconstructed image [6]. Because scattering induces a greater measured detector signal, the projections are seemingly less attenuated, causing a reduction in CT number [33]. Software correction methods [34, 35] or a post-patient collimator that rejects scattered photons [36] can reduce the effects of scattering. However, suboptimal scattering correction or scattering overcorrection may result in increased CT number [36]. In CTP, an inconsistent level of scattering between dynamic images may cause CT number inconsistency, which would invalidate the linear relationship between CT number and iodine concentration. The accuracy of estimated perfusion parameters would accordingly be affected. Figure 1C illustrates how CT number consistency may be impacted by differing levels of scattering due to protocols using different beam collimation widths.
2.3 CT perfusion radiation dose
2.3.1 CT perfusion dose reduction
Radiation dose levels used for CTP imaging likely do not increase the risk of cancer mortality substantially, relative to the natural prevalence rate. Concerns with CTP radiation dose are, therefore, with respect to the potential diagnostic benefit that is provided and whether the same diagnostic information can be reliably abstracted from a lower scan dose. Given a low enough scan dose, radiation risk-to-diagnostic benefit criteria may be favorable for CTP.
The most straightforward dose reduction technique is to reduce the mAs or kV. Dose scales linearly with mAs and by a power law with kV [6]. CTP image and TDC SNR suffer with lower mAs as noise increases proportionally to the inverse square root of mAs. The estimated blood flow becomes overestimated at lower mAs than at higher mAs, and similar biases are observed for other estimated CTP parameters [37]. The relationship between kV and the TDC SNR is more complex: while noise increases with lower kV by a power law [6], the sensitivity to iodine concentration also increases due to a greater proportion of the X-ray energy spectrum being closer to the K edge of iodine.
Dose reduction by reducing mAs and kV has mainly been investigated empirically. Murphy et al. found no significant differences in CBF, CBV, and Tmax estimated from brain CTP studies of patients with acute ischemic stroke acquired at 50 mAs versus 100 mAs at otherwise fixed protocols, potentially offering dose reduction by 50% [38]. Li et al. demonstrated that low-dose CTP acquired at 70 kV did not compromise the image quality of generated perfusion maps compared to 80 kV, resulting in a reduction of the effective dose from 4.7 to 3.0 mSv [39]. A low-dose 70 kV and 120 mAs CTP protocol was also superior to an 80 kV and 100 mAs protocol for CTP imaging of the pancreas, resulting in a lower effective dose of 3.60 versus 4.88 mSv [40]. The minimum image and TDC SNR required for reliable detection of disease at CTP is not yet known. A model relating the TDC SNR to lesion detectability may help determine the minimum required scan dose for the diagnosis.
3 Theory of contrast transport
This section describes the principles of contrast transport used to estimate perfusion parameters with dynamic contrast-enhanced CT imaging.
3.1 Fick principle
We begin with the Fick principle, which considers a control volume,
where
which states that perfusion is the ratio of the maximum tissue TDC value and the area of the arterial curve until
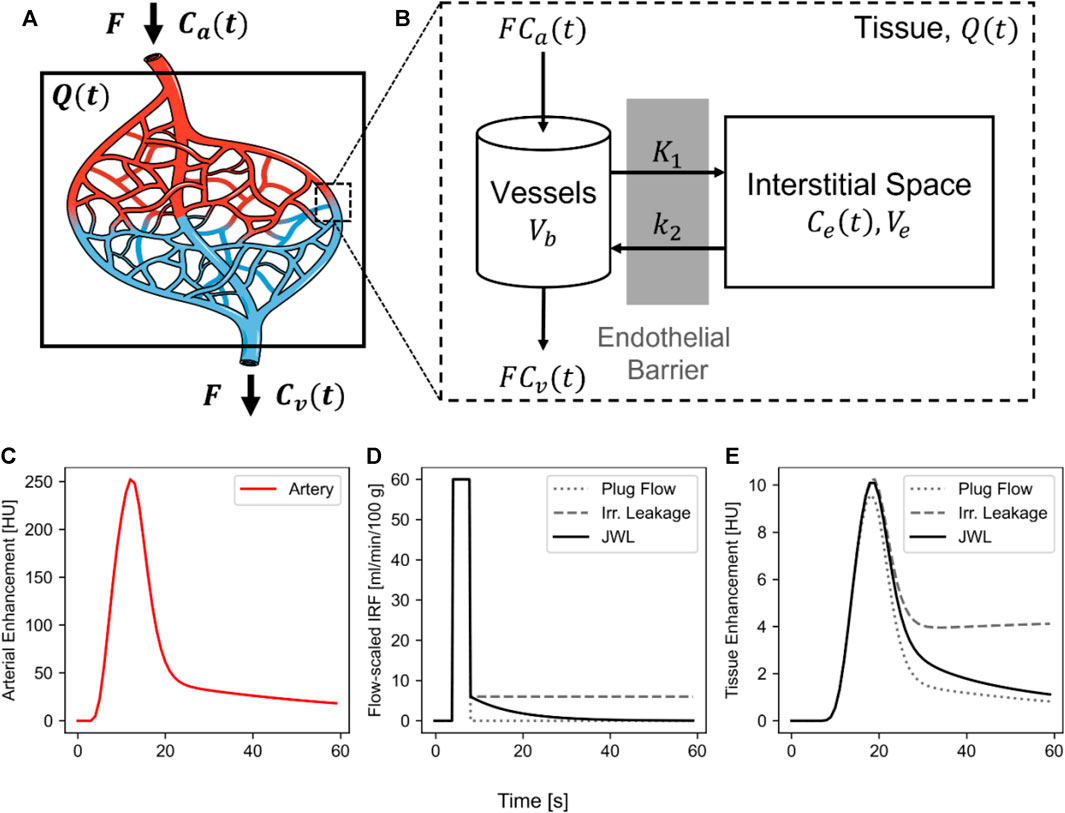
FIGURE 2. Contrast transport in CT perfusion. (A) Schematic of a tissue volume,
Eq. 3.3, the differential form of the Fick principle, is the basis for the maximum front slope method [41], which states that blood flow is the quotient of the maximum slope of
3.2 Impulse residue function
Meier and Zierler [42] formalized the work by Stewart [43] to describe an alternative impulse residue function (IRF)-based formulation to contrast transport. Consider a network of capillaries with contrast delivery via blood flow by an arterial inlet and a venous outlet (Figure 2A). The transit time of contrast from the arterial inlet to the venous outlet can be modeled by a probability distribution function or a transit time spectrum,
where
Defining the IRF,
Eq. 3.1 can be reformulated using (3.4) and (3.6) to arrive at the form:
The tissue TDC is the convolution of the arterial curve and the IRF scaled by blood flow. A flow-scaled IRF,
The IRF describes a theoretical tissue response function if a unit mass of bolus was instantaneously injected into the arterial inlet (i.e.,
3.3 Central volume principle
The central volume principle [42] describes the relationship between blood flow (
Therefore, the central volume principle states that the blood volume is the product of the blood flow and the MTT:
Meier and Zierler also showed that the area underneath
Of note, the central volume principle made no assumptions on the shape of
3.4 Tracer kinetic modeling
So far, the properties of the contrast agent were not considered, and no assumptions were made about underlying hemodynamic processes that determine the functional form of the transit time spectrum,
The Johnson–Wilson–Lee (JWL) model is a kinetic model that can describe the equilibration of contrast through the blood–tissue barrier between intra- and extra-vascular space [12, 44, 45], which accounts for the perfusion of contrast through the vasculature as well as its bidirectional permeation across the blood–tissue barrier. Note that because both perfusion and permeation are explicitly accounted for, the JWL model is valid independent of the relative rates of perfusion (
3.4.1 Johnson–Wilson–Lee model
The flow-scaled IRF of the JWL model is given by
where
For the JWL model, St Lawrence and Lee showed that [45]
where
By using Eq. 3.10 and (3.7), a closed-form solution to
where
The standard interpretation of the JWL model is that all vessels in a tissue volume are fused into a single tube and, therefore, has a uniform transit time. In this case, the minimum transit time
A modified interpretation of the JWL model may instead consider the exponential decay as a measure of dispersion due to varying vessel path lengths. In this interpretation, the contrast fully remains in the intravascular space and
3.4.2 Special case of the Johnson–Wilson–Lee model: irreversible leakage (k2 = 0)
A special case of the JWL model arises when the contrast leaks into the extravascular space but does not leak back into the intravascular space (
and the closed-form solution,
As with the JWL model, this special case can also be interpreted such that
3.4.3 Patlak graphical analysis
The special case of the JWL model with irreversible leakage is similar to the Patlak graphical analysis method when taking
where the area underneath the Dirac delta function is
Dividing both sides by
The Patlak parameters
3.4.4 Special case of the Johnson–Wilson–Lee model: intravascular plug flow (FE = 0, k2 = 0)
Another special case arises when there is no leakage of contrast to the extravascular space (i.e., the contrast fully remains in the intravascular space) and the vascular transit time is uniform. As mentioned previously, this is the so-called “plug flow” model. The resulting IRF,
and the closed-form solution,
Here,
4 Deconvolution methods
Deconvolution aims to “invert” the convolution in Eq. 3.7 to recover the flow-scaled IRF from the measured arterial (
4.1 Model-independent deconvolution
First, the convolution in Eq. 3.7 can be discretized as
where
are vectorized forms of
The discrete convolution in Eq. 3.14 can be formulated as a matrix multiplication:
where
Model-independent deconvolution methods therefore aim to non-parametrically recover
4.1.1 Singular value decomposition
One of the most commonly used approaches to recover
where
where + indicates the pseudoinverse and
Eq. 3.14 can then be solved by the pseudoinverse with the SVD:
where
However, since
where
These filters can be incorporated into Eq. 4.4:
where
where
Standard SVD deconvolution is considered delay-sensitive; that is,
The second case, in which the contrast arrives at
4.1.2 Block-circulant singular value decomposition
Wu et al. described a delay-insensitive deconvolution method by performing the SVD with a block-circulant matrix of
where
Block-circulant SVD deconvolution can be performed using
4.1.3 Fourier transform deconvolution
The Fourier transform-based method of deconvolution utilizes the convolution theorem, which states that a convolution in the time domain is a product in the frequency domain. Applying the Fourier transform to both sides of Eq. 3.7 results in
where
The Fourier transform method of deconvolution is mathematically equivalent to the block-circulant SVD method [50, 53]. It follows that
where
where
As such, with careful filtering to not modify the zero-frequency value during Fourier transform deconvolution, blood volume estimates will be unaffected by regularization.
4.1.4 Bayesian deconvolution
Applying Bayesian deconvolution to estimate hemodynamic parameters in patients starts with the assumption that each patient can be specified by two types of events (characteristics)—CTP TDCs and the model represented by the flow-scaled IRF,
where
Eq. 4.9 shows that
If
Eq. 4.11 shows that the Bayesian deconvolution or maximum a posteriori (MAP) is equivalent to the maximum likelihood estimation of
Assuming that the measured
Substituting Eq. 4.13 into (4.12) results in
Therefore, the MAP
When a priori knowledge of
If
One useful a priori constraint on
The marginal a posteriori distribution of
which is a definite integral in the
The marginal a posteriori distribution of
The Bayesian deconvolution-estimated IRF,
which is a definite integral in the
where
However, calculations of both marginal distributions and their means can be time-consuming as they involve evaluating up to
The right side of Eq. 4.16 suggests that Bayesian deconvolution with a priori knowledge of
for imposing a priori smoothness constraint on
4.2 Johnson–Wilson–Lee model-dependent deconvolution
Model-dependent deconvolution based on the JWL model will be described in this section. The special cases of the JWL model as described previously simplify parameter estimation by reducing the number of unknowns.
The closed-form solution of the JWL tissue curve,
where
Note that
Alternatively, the estimation of
As can be seen, the number of NNLS required can be large depending on the number of grid search combinations. Advanced optimization methods, such as using a dynamic grid search step size, may be required to reduce the grid search combinations for efficient application in practice. Alternatively, the grid search can be greatly accelerated by assuming a simplified model as described in Section 3.4.2 and Section 3.4.4.
Using the irreversible leakage model described in Section 3.4.2, it is assumed that
A further simplification is to assume no leakage and a uniform vascular transit time as in the plug flow model described in Section 3.4.4. Here,
where
While the appeal of the simplified models is their fast computation, their assumptions may not hold in general, especially in highly diseased conditions.
4.3 Comparison of deconvolution methods
We compared the quantitative accuracy of five deconvolution algorithms: two model-independent (SVD and Fourier transform) and three model-dependent (plug flow, irreversible leakage, and JWL) deconvolution methods. Block-circulant SVD was omitted as it produced the same results as the Fourier transform method when using equivalent regularization filters. Details of the methods are provided in Section 4.1 and Section 4.2. Specifically, SVD was not delay-corrected and regularized by truncating the smallest 15% of the largest singular value as described in Eq. 4.5. Fourier transform deconvolution used a Wiener-like regularization filter with 15% regularization as described in Eq. 4.6. The plug flow and irreversible leakage model deconvolution methods were the simplified cases of the JWL model as described in Section 4.2 and used a grid search of
4.3.1 Ground truth versus deconvolution-estimated blood flow
Correlation plots comparing ground truth versus mean estimated blood flow over 1,024 trials for each deconvolution method are shown in Figure 3. Simulation of routine-dose noise (
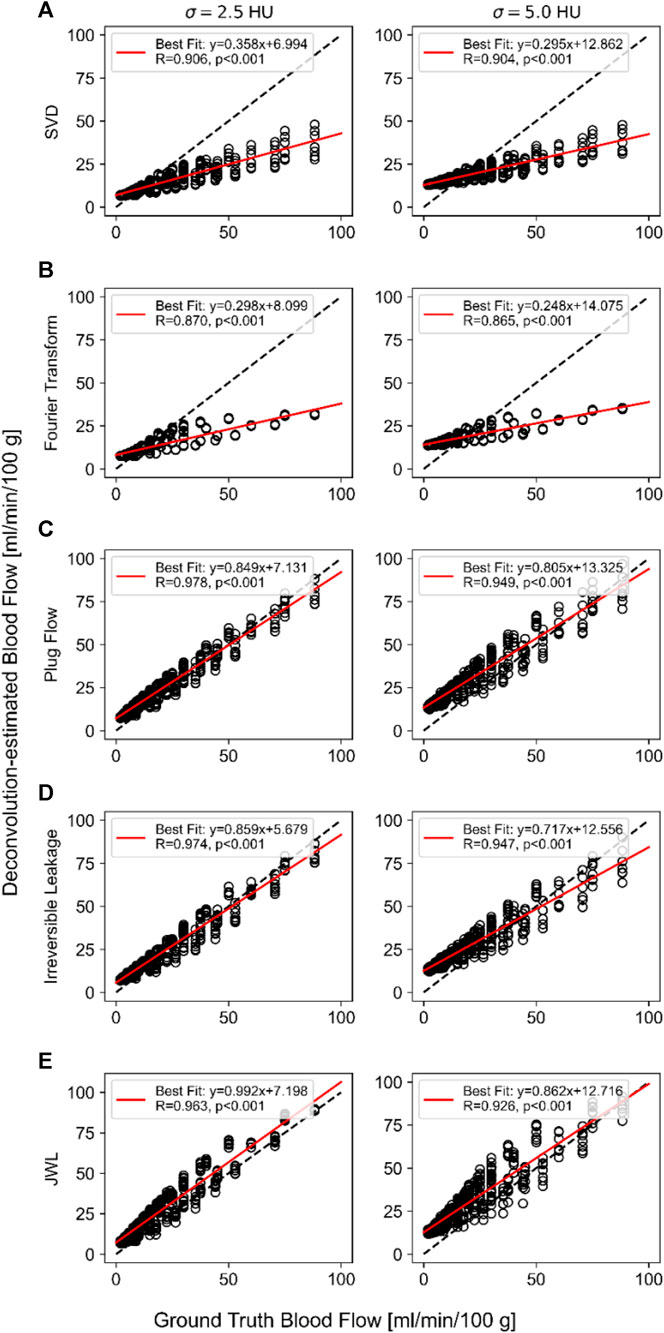
FIGURE 3. Ground truth versus deconvolution-estimated blood flow using (A) singular value decomposition (SVD), (B) Fourier transform, (C) plug flow, and (D) irreversible leakage. (E) Johnson–Wilson–Lee (JWL) model deconvolution at routine-dose noise (σ = 2.5 HU; left) and low-dose noise (σ = 5.0 HU; right) levels. The linear regression equation and Pearson’s correlation are indicated in the inset of each plot.
As shown in the correlation plots, all deconvolution methods have a positive vertical axis intercept that is similar in value and overestimates very low true blood flow values (e.g., <8 mL/min/100 g). The regression intercept has greater deviation from the origin at the low-dose noise level compared to the routine-dose noise level. Notably, the model-independent methods have shallower regression slopes that substantially underestimate higher true blood flow values, whereas the regression slopes of model-dependent methods are closer to 1. This indicates that despite the difference in the simulated model IRF versus those used in model-dependent deconvolution methods, (1) the model-dependent deconvolution methods investigated here are better able to estimate absolute blood flow than model-independent methods and (2), as a result, can better quantify differences between low and high ground truth blood flow values. In addition, the regression slope became shallower with greater noise for all methods, indicating that blood flow quantification worsens with greater noise.
The trade-off for better absolute agreement (lower bias) between ground truth and estimated blood flow with model-dependent methods is that they have higher variance than model-independent methods. The mean and standard deviation of deconvolution-estimated perfusion parameters over 1,024 trials for a single set of ground truth parameters at routine-dose noise levels (
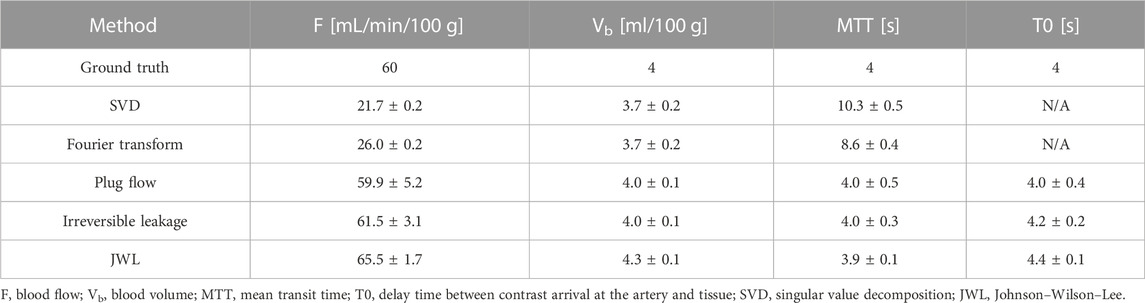
TABLE 1. Mean and standard deviation of deconvolution-estimated perfusion parameters over 1,024 noise trials for a set of ground truth perfusion parameters.
Figure 4 shows a comparison of the mean deconvolution-estimated flow-scaled IRF and their corresponding fitted tissue TDCs overlaid on their respective ground truths for the parameter set listed in Table 1. For the model-independent methods, the estimated flow-scaled IRFs were averaged and the fitted TDC was then computed with Eq. 4.2. For the model-dependent methods, the means of the estimated model parameters were first computed and then substituted into Equation 3.10 and 4.18 to evaluate the mean estimated flow-scaled IRFs and fitted TDCs, respectively. Despite applying regularization and averaging over 1,024 trials, the model-independent flow-scaled IRFs are oscillatory and fail to recover the sharp initial peak in the true flow-scaled IRF. The corresponding fitted tissue TDCs also contain oscillations, indicating that the model-independent deconvolution methods overfitted to noise. While the flow-scaled IRFs for the model-dependent methods did not match the shape of the ground truth, they better reproduced the sharp peak required for accurately estimating blood flow. The fitted tissue TDCs do not show oscillations and arguably agree better with those of the ground truth in this example.
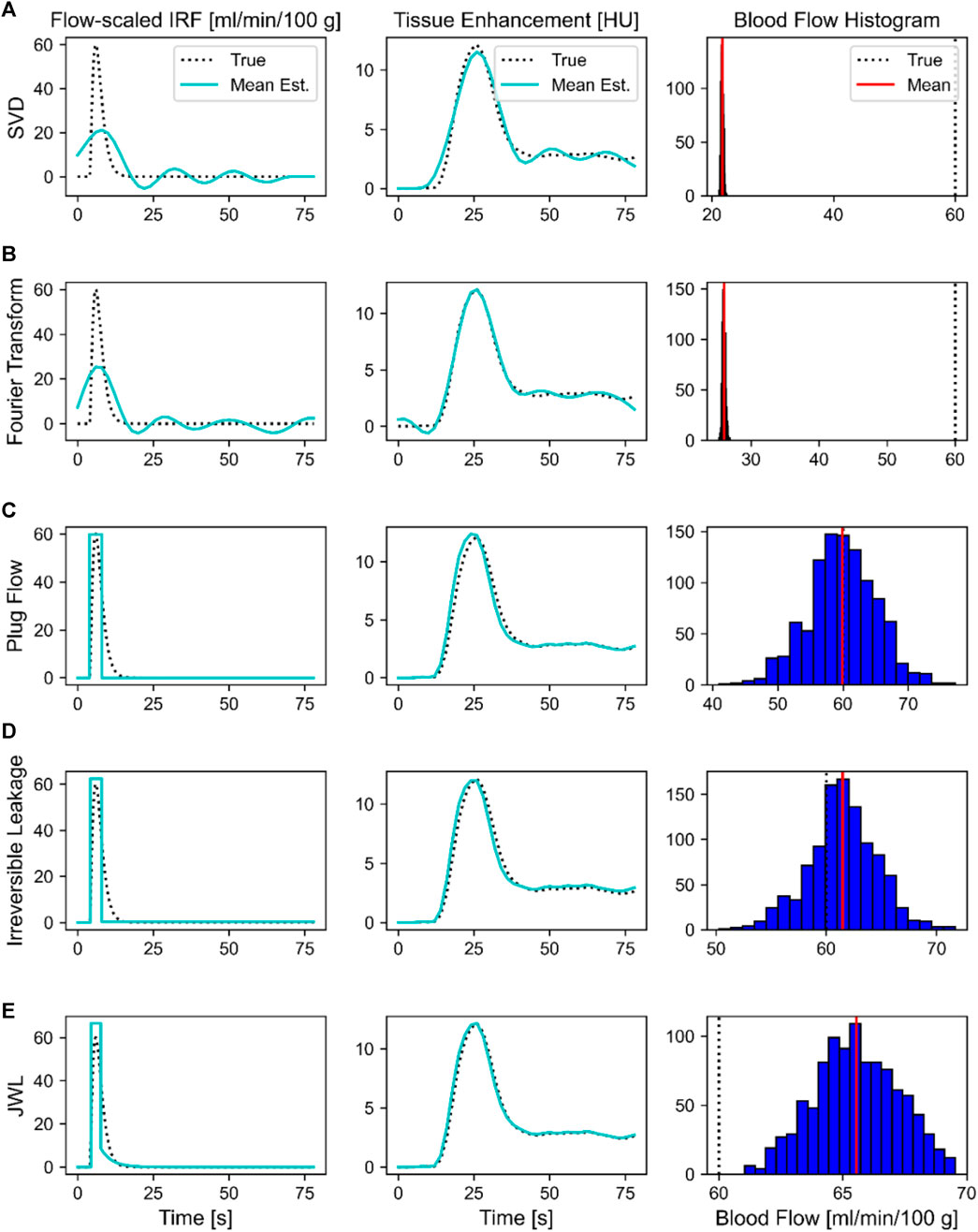
FIGURE 4. Comparison of deconvolution methods for a single set of ground truth parameters: blood flow, 60 mL/min/100 g; blood volume, 4 mL/100 g; mean transit time, 4 s; T0, 4 s. Deconvolution methods were (A) singular value decomposition (SVD), (B) Fourier Transform, (C) plug flow, (D) irreversible leakage, and (E) Johnson-Wilson-Lee (JWL) model. The mean deconvolution-estimated flow-scaled impulse residue function (IRF) and fitted tissue time–density curve over 1,024 trials are overlaid on their respective ground truths in the left and middle columns, respectively. Histograms showing the distribution of deconvolution-estimated blood flow values over 1,024 trials are shown in the rightmost column, where the solid red line indicates the mean and the dotted black line is the ground truth.
The rightmost column of Figure 4 shows the distribution of blood flow values estimated over 1,024 trials with each deconvolution method. All methods produced approximately a unimodal normal distribution of estimated blood flow values. The model-independent methods produced a very narrow distribution, whereas the model-dependent methods had a broader distribution. The standard deviations of estimated blood flow values are accordingly greater with model-dependent deconvolution. However, the mean of the distribution better converges to the true value with the model-dependent methods. As such, model-independent deconvolution methods are more precise at the expense of accuracy, whereas model-dependent methods are more accurate but are less precise.
Though not investigated in this experiment, model-dependent methods can also provide hemodynamic parameters that are unavailable with model-independent methods, such as those related to vessel permeability.
5 Applications of CT perfusion
5.1 Acute ischemic stroke
Acute ischemic stroke is mainly caused by a clot that limits blood flow to the brain. Reperfusion treatments including intravenous thrombolysis (IV-tPA) and endovascular thrombectomy (EVT) are highly effective if administered early after stroke onset (<4.5 h for IV-tPA and <6 h for EVT). However, randomized controlled trials demonstrated that the therapeutic time window can be extended up to 9 h after stroke onset for IV-tPA and 16–24 h for EVT with selection by CTP [2–4, 70]. Treatment selection was based on a target mismatch profile defined as a small volume of irreversible brain injury (infarct or ischemic core) relative to a large salvageable region (penumbra). Specifically, the target mismatch profile in the DEFUSE-3 late-window EVT trial (6–16 h after stroke onset) was defined as an ischemic core volume <70 mL, penumbra volume ≥15 mL, and a mismatch ratio (quotient of penumbra and core volume) ≥ 1.8 [4]. Anterior large vessel ischemic stroke patients receiving late-window EVT based on this target mismatch profile had significantly greater rates of good 90-day functional outcome compared to best medical therapy [4]. As of 2022, CTP is one of two imaging-based selection methods (alongside diffusion-weighted imaging and perfusion magnetic resonance imaging) approved by the American Heart Association best practice guidelines for EVT selection between 6 and 16 h after stroke onset [71]. CTP played a major role in demonstrating that the therapeutic window of reperfusion treatments can be extended based on tissue status rather than strict time thresholds. An example CTP study of a patient with large vessel ischemic stroke is shown in Figure 5.
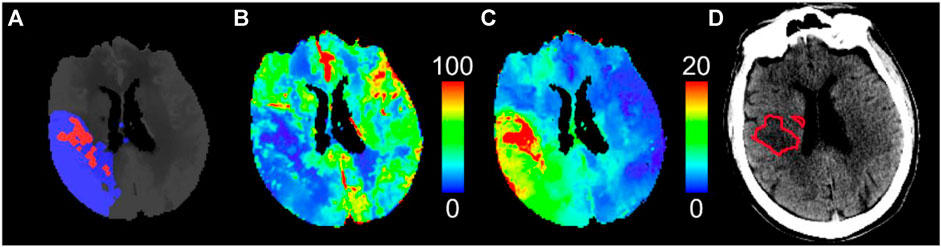
FIGURE 5. CT perfusion study of a patient with large vessel ischemic stroke who achieved early quality recanalization at endovascular thrombectomy. (A) Predicted pre-treatment ischemic core (red) and penumbra (blue) by thresholding (B) cerebral blood flow and (C) Tmax maps, respectively, using the optimal thresholds for this software package (CT Perfusion 4D, GE Healthcare). The small ischemic core relative to the large penumbra indicates a target mismatch profile suitable for endovascular thrombectomy. (D) Follow-up infarct (red outline) delineated on non-contrast CT shows good agreement with the ischemic core predicted by pre-treatment CT perfusion. Cerebral blood flow is in units of mL/min/100 g, and Tmax is in units of seconds.
As such, the main role of CTP is to measure the ischemic core and penumbral volumes and quantify mismatch profiles. Modern CTP software is automated and can provide diagnostic information within minutes of image acquisition [72]. Ischemic core and penumbra volumes are mainly measured by thresholding perfusion parameters. CBF is often used to detect the ischemic core, and Tmax is often used for the penumbra [73–75]. The randomized controlled trials that validated the diagnostic utility of CTP used a single software package (RAPID CTP, RapidAI, Menlo Park, CA), which used CBF<30% relative to that in the normal tissue to detect the ischemic core and Tmax>6 s for the penumbra [2–4, 70]. Of note, RAPID perfusion imaging software uses Fourier Transform deconvolution as described by Straka et al. [65], which may have limited absolute agreement with ground truth blood flow, as we have shown in Section 4.3.1. This demonstrates that absolute accuracy and quantification of blood flow may not be required specifically for determining target mismatch profiles, which may have implications for CTP scan protocol design and radiation dose reduction.
Optimal stroke lesion thresholds, however, differ between CTP software packages, which has raised doubts about its widespread deployment across institutions using different software platforms [76]. One of the potential reasons that stroke lesion thresholds differ between CTP software is that each software may use different deconvolution algorithms. As shown in Section 4.3, each deconvolution algorithm has different biases and variances in estimating blood flow, and optimal lesion thresholds may accordingly differ. Chung et al. found that linear regression relationships of ground truth versus estimated perfusion parameters determined from simulated CTP data (as in Section 4.3.1) may help guide the calibration of optimal stroke lesion thresholds between software packages [77]. Threshold calibration and demonstration of equivalence between other CTP software and RAPID CTP have also been shown empirically [78–81]. Nonetheless, CTP requires better standardization between software packages such that reliable diagnostic criteria can be deployed between institutions using different platforms.
CTP has also demonstrated potential for detecting hemorrhagic transformation in ischemic stroke [19, 82]. Hemorrhagic transformation is a brain bleed caused by a complete breakdown of the blood–brain barrier due to sustained severe ischemia and is associated with high rates of mortality when symptomatic [83, 84]. According to the Heidelberg Bleeding Classification [85], there are two main types of hemorrhagic transformation following ischemia: hemorrhagic infarct (HI1 and HI2) and parenchymal hemorrhage (PH1 and PH2). Symptomatic hemorrhage, which causes an increase in the National Institutes of Health Stroke Scale (NIHSS), is usually associated with PH and not HI.
Measures of vessel permeability as determined with model-dependent deconvolution methods have been found to identify patients likely to undergo hemorrhagic transformation. Aviv et al. found that patients with larger permeability surface area products (PS, Eq. 3.11) within the ischemic region at admission CTP were associated with hemorrhagic transformation [19]. In a voxel-wise analysis of CTP maps of 1,407 patients with acute ischemic stroke, Bivard et al. found that an extraction fraction (E, Eq. 3.11) threshold of 30% relative to the contralateral hemisphere optimally distinguished between patients who did and did not develop any form of hemorrhagic transformation [82]. Both studies by Bivard et al. and Aviv et al. showed that increased PS or E is associated with hemorrhagic transformation, but differentiation of PH from HI is an ongoing research issue. Nonetheless, Bivard et al. showed that the severity of hemorrhage increased with larger volumes of tissue with E > 30%.82 Neither study included patients treated with EVT and only included patients who were considered for IV-tPA. CTP measures of vessel permeability may therefore help identify patients at risk of hemorrhagic transformation. Validation of CTP permeability measures in predicting hemorrhagic transformation after EVT is still required. Specifically, a useful application may be to predict hemorrhagic transformation in large vessel ischemic stroke patients presenting with a large ischemic core or beyond 24 h after stroke onset, who have been found to have high rates of hemorrhage after EVT [86, 87].
5.2 Solid tumor
Tumor angiogenesis fosters the microenvironment required for tumor growth and metastasis [88]. Tumor perfusion and vessel permeability are therefore associated with tumor grades, prognosis, and treatment response [89, 90]. Therefore, the main role of CTP in evaluating solid tumors is to supplement histological assessment of the tumor with non-invasive imaging of tumor perfusion and vessel permeability.
5.2.1 Brain tumors
Gliomas are highly heterogeneous brain tumors that are the most common type of neoplasm in adults [91]. The malignancy of glioma is graded according to WHO tumor classification using a tumor sample taken from a brain biopsy or surgery [92]. However, the acquisition and utility of sampling the tumor is problematic due to the highly heterogeneous nature of glioma cells and the limited obtainable samples, meaning that the histopathological results may be under-graded [93, 94]. An alternative to this invasive and limited procedure is in vivo perfusion imaging, such as CTP. Perfusion parameters such as blood volume, blood flow, and PS are associated with angiogenesis, which underpins tumor growth. In current practice, perfusion imaging supplements histological evaluation of tumor grading, prognosis, and monitoring treatment response. Histological assessment is nonetheless still required as CTP lacks the spatial resolution required for assessing tumor microenvironments (i.e., CT resolution is approximately 0.5 mm, whereas microvasculature is on the order of μm) [89].
Perfusion parameters such as blood volume, blood flow, and PS are associated with the tumor vasculature and have demonstrated predictive value in glioma grading, prognosis, and treatment response [89, 90]. Studies have suggested that blood volume may potentially be a good biomarker for microvascular density (MVD), which is associated with angiogenesis and, therefore, the aggressiveness of the tumor [95–98]. Vascular endothelial growth factor (VEGF) is an additional biomarker that shows a positive correlation with hypoxic and hypoglycemic permeable blood vessels. It is used to judge the potential for neoangiogenesis, aiding in the histological grading process [99]. CTP PS could replace the need to sample for VEGF as well as be used to study treatment response [100]. This may help design more effective therapies based on the underlying mechanisms of permeability and the blood–brain barrier [99]. Jain et al. reported that in a study of 23 brain tumor patients with various tumor grades, CBV and PS showed a significant positive correlation with MVD (Pearson’s correlation, r = 0.596, p < 0.001) and microvascular cellular proliferation (MVCP) (r = 0.546, p = 0.001), respectively, as well as a significant correlation with WHO-defined tumor grade for CBV (r = 0.373, p = 0.031) and PS (r = 0.452, p = 0.039) [95]. Ellika et al. found that in a cohort of 19 patients with glioma, CTP had higher sensitivity and specificity than conventional MRI in classifying patients into low-grade and high-grade glioma (92.9% and 100% for CTP versus 85.7% and 60% for MRI, respectively) [90]. Therefore, CTP-derived parameters can be used in combination with biopsy to non-invasively differentiate tumor grades and elucidate different characteristics of tumor proliferation. Overall, CTP may have the potential to non-invasively track relevant biomarkers for tumor grading and angiogenesis associated with treatment planning and response.
5.3 Cardiovascular disease
The main role of CTP in cardiovascular disease is to determine regions of ischemic myocardial tissue using functional information on blood flow, blood volume, MTT, and other hemodynamic parameters.
5.3.1 Ischemic heart disease
Although coronary CT angiography (CCTA) is the main imaging tool used to define coronary artery disease (CAD) that causes myocardial ischemia, invasive fractional flow reserve (FFR) is currently the gold standard for the identification of significant CAD requiring revascularization [101–104]. CCTA provides morphological information on the degree of stenosis but lacks functional information on myocardial perfusion, leading to suboptimal positive predictive value and specificity for significant CAD [104–106]. FFR is a diagnostic measure that assesses the relative pressure difference across stenotic coronary arteries, providing guidance for revascularization decisions. It exhibits a diagnostic accuracy of over 90% when using a relative pressure threshold of ≤0.8 [102]. Treatment for significant CAD involves either enlarging the narrowed artery by percutaneous transluminal coronary angioplasty or stenting or bypassing blockages by grafts [103].
Despite diagnostically validated non-invasive FFRCT technology [107–110], FFRCT still does not provide quantitative data in the myocardium, such as with CTP. The principal role of CTP in CAD is non-invasively providing functional information on ischemic myocardial tissue while maintaining a similar diagnostic value to FFRCT. Using CTP-derived functional maps of blood flow, blood volume, and mean transit time, occluded major vessels can be determined by referencing ischemic regions segmented according to the AHA 17 segment model [111]. CTP, either dynamic or static, has been shown to have utility in isolation [104, 112] but has the most impact when combined with other modalities such as CCTA [113, 114]. Using their PERFECTION study data with CCTA-derived FFRCT, Pontone et al. showed that CCTA + CTP had similar diagnostic performance per vessel determination of significant CAD as CCTA + FFRCT in terms of the area under its receiver operating characteristic curve (CCTA + CTP AUC = 0.876 with 95% confidence interval: 0.832 to 0.919, and CCTA + FFRCT AUC = 0.878 with 95% confidence interval: 0.833–0.923) [113].
5.3.2 Cardiac sarcoidosis
Sarcoidosis is a disease where a number of granuloma cells accumulate within the tissue of any organ in the body, and in 2011, it was reported to affect about 10–40 in 100,000 Americans [115]. Cardiac sarcoidosis (CS) accounts for approximately 20%–30% of all sarcoidosis cases in the United States and can lead to sudden death without any admissible symptoms [115]. Silverman et al. found that there were a significant number of CS patients who were clinically silent [116]. Diagnostic imaging via 18F-FDG PET or gadolinium-based cardiac MRI has substantially improved the detection of sarcoidosis. Corticosteroid therapy is currently the only treatment for CS, though its benefit requires validation in randomized controlled trials [117]. Imaging may guide the management of CS symptoms and potentially decisions for corticosteroid treatment, but this requires validation in future studies [118]. So et al. demonstrated the potential utility of CTP to identify scar tissue in a CS patient using myocardial blood flow and extravascular contrast distribution volume imaging [119]. More studies are needed to validate the diagnostic potential of CTP in identifying CS patients, but if successful, myocardial CTP may prove to be a more accessible imaging modality than cardiac MRI and 18F-FDG PET for diagnosing CS.
6 Discussion
6.1 Radiation dose reduction
6.1.1 Low-dose CT perfusion denoising
Dose reduction by reducing mAs comes at the expense of lower CTP image SNRs and TDC SNRs. The lower limit for recommended mAs has mainly been established empirically. Further dose reduction may be possible with post-processing or advanced CT reconstruction techniques that improve image and TDC SNRs. In simulation studies, spatiotemporal filtering of dynamic CTP images demonstrated potential for dose reduction by leveraging spatial and temporal relationships between CTP TDCs to improve TDC SNRs [120–123]. An ultra-low-dose brain CTP protocol (effective dose: 1.2 mSv) with statistical iterative reconstruction (ASIRv, GE Healthcare) allowed the evaluation of blood–brain barrier permeability in thrombotic thrombocytopenic purpura [124]. Statistical iterative reconstruction has also been applied for 20
6.1.2 Low-temporal resolution CT perfusion
Radiation dose can be reduced by acquiring fewer dynamic CTP images at the expense of temporal resolution or scan duration. Van Ommen et al. demonstrated that certain deconvolution methods for brain CTP tolerated a scanning interval of up to 5 s while still adequately distinguishing between ischemic and normal brain tissue [129]. Chung et al. found that tailored sampling of four dynamic CTP images (pre-contrast baseline, arterial peak, and two additional delayed images at 8-s intervals) had diagnostic potential in identifying mismatch profiles in acute ischemic stroke [130]. While the quantitative accuracy of estimated perfusion parameters may decrease with fewer acquired dynamic images, perfusion map quality may be sufficient for diagnosis. Deep learning methods to interpolate missing dynamic images or directly predict perfusion maps from low-temporal resolution CTP studies may also be viable [131, 132].
6.1.3 Future outlook
Demonstration of low-dose CTP has mainly been with simulation studies or animal models. Prospective acquisition of low-dose CTP in humans has been hampered by ethical and safety considerations or concerns of diagnostic reliability. Studies reporting the prospective application of low-dose CTP are required. These data may then support the wider deployment of low-dose CTP in practice. In addition, a theoretical model relating the radiation dose and image/TDC SNR to the detectability of disease in CTP parametric maps may be helpful in guiding the selection of low-dose protocols. Future studies should also consider diagnostic task-based metrics rather than intermediate measures, such as the accuracy of estimated perfusion parameters. Absolute agreement between regular-dose and low-dose CTP parameters may not be important so long as diagnosis is reliable. For better inter-study comparison, dose reduction studies should also report dosage in more comparable absolute measures, such as the dose-length product (mGy cm), CTDI100 dose (mGy), or effective dose (mSv), in addition to relative measures of dose reduction compared to routine levels.
Ongoing work in CTP dose reduction may facilitate its broader clinical application. For example, perfusion imaging of pediatric stroke patients is garnering interest to validate the translation of diagnostic and therapeutic stroke paradigms from adults to children [133], but pediatric perfusion imaging studies have mainly used MRI in part due to the lack of ionizing radiation [134]. Therefore, ultra-low-dose CTP protocols may provide a broad opportunity to better characterize pediatric cerebrovascular disease and identify pediatric-specific imaging profiles suitable for stroke reperfusion therapies.
6.2 New CT technology
6.2.1 Photon-counting detector CT
Current clinical CT scanners use energy-integrating detectors (EIDs), which comprise scintillators to convert X-rays to light and light to electrical signals via photodiodes. The generated electrical signal is proportional to the sum of energies of all transmitted X-rays. Photon-counting detector (PCD) CT is an emerging technology that instead uses semiconductors to produce an electrical signal directly proportional to the energy of each incident X-ray photon. Electronic noise, which may be prevalent at low-fluence scans with EIDs, can therefore be minimized by setting an energy floor required for photon detection [135, 136]. PCD elements are much smaller than EID elements, ranging from 0.11
PCDs provide several advantages over EIDs: (1) spectral energy resolution from a single X-ray source, (2) higher spatial resolution, (3) beam hardening and metal artifact reduction, and (4) radiation dose efficiency. These have meaningful implications for PCD-CT perfusion. First, multi-energy resolution may improve the iodine contrast-to-noise ratio [135] and thus improve the CTP TDC SNR. Radiation dose reduction may be possible if sufficient TDC SNRs can be achieved at lower doses with spectral imaging. Second, smaller perfusion deficits, such as lacunar or watershed infarcts [137], may be better visualized with the higher spatial resolution afforded by PCD-CT. Last, artifact reduction may improve perfusion map quality in previously problematic anatomical locations and scan conditions. For example, CTP is less reliable in quantifying stroke lesion volumes for posterior circulation ischemic strokes compared to anterior circulation [30]. This may be in part due to beam hardening and photon starvation artifacts at the posterior fossa obscuring CTP TDCs.
6.3 New applications
6.3.1 Lung perfusion CT
In contrast to brain perfusion imaging, where deconvolution techniques are commonly employed, lung perfusion imaging predominantly utilizes either the peak enhancement method (Eq. 3.2) or the maximum front slope method (Eq. 3.3) [138–141]. These methods are applied under the assumption of no venous outflow and have the advantage that the numerical computation is simpler to implement. Nevertheless, the requirement of no venous outflow means the perfusion values will be dependent on injection rate and the viscosity of the contrast agent, as investigated by Xin et al. [141] They found that compared to invasive measurement of cardiac output by thermal dilution at the pulmonary artery, applying Eq. 3.3 to data acquired with diluted contrast (Isovue-370 and saline in the ratio of 3:2) calculated more accurate lung perfusion than applying Eq. 3.2. In contrast to Equation 3.2, Equation 3.3 also provided more comparable lung perfusion values when comparing the rapid injection rate (8 mL/s) with the slower rate (4 mL/s) of diluted contrast.
To circumvent the assumption of zero venous outflow, two approaches have been employed. The first approach involved utilizing the irreversible leakage model, as outlined in Section 3.4.3 and Eq. 3.16 [142]. The second approach used the model-independent regularized deconvolution method, as described in Section 4.1 [143]. The justification for irreversible leakage lies in the fact that CTP acquisition for lung perfusion usually lasts less than 20–30 s, primarily due to the necessity of breath holding. Consequently, any potential backflux of leaked contrast from tissue to blood can be disregarded. Nonetheless, as discussed in Section 3.4.1, the value of
Due to tumor-associated angiogenesis, the blood supply to lung cancer transitions from a single input solely from the pulmonary artery to a dual input from both the pulmonary and bronchial arteries. To account for this change, Yabuuchi et al. [145] expanded the application of the maximum front slope method to accommodate dual-input scenarios. By utilizing the dual-input maximum front slope method, Ohno et al. [146] demonstrated that dual-input total perfusion outperformed pulmonary arterial perfusion and the single-input perfusion obtained through the single-input maximum slope method in predicting treatment response and recurrence following chemo-radiotherapy for non-small-cell lung cancer.
The requirement of breath holding during lung CT perfusion restricts the acquisition time to a maximum of 20–30 s. Consequently, the analysis of lung CTP studies is currently limited to the simple models discussed above, namely, peak enhancement and maximum front slope, operating under the assumptions of no venous outflow or irreversible leakage. To advance lung CTP techniques, future developments can explore acquiring studies with shallow breathing and subsequently employing non-rigid registration to align the images. This approach has the potential to extend the acquisition time to 2–3 min. With these extended data, in addition to perfusion and blood volume, parameters such as PS can be determined as in solid tumors (Section 5.2).
7 Conclusion
CTP has demonstrated diagnostic utility in numerous clinical applications due to its relative accessibility and low cost compared to other perfusion imaging modalities. This review provided a summary of CTP scan protocols, theory of contrast transport, deconvolution methods, applications, and future opportunities for research and application. With further reductions to radiation dose and improvements in hardware and software methods to acquire and generate perfusion maps, CTP is poised to become an integral component of the diagnosis and management of patients with perfusion injuries.
Author contributions
KJC: conceptualization, data collection and analysis, investigation, methodology, software, validation, visualization, and writing. DDS: conceptualization, investigation, and writing. T-YL: conceptualization, investigation, methodology, project administration, and writing. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the Canadian Institutes of Health Research (CIHR, Grant Number 168945), the Canada Foundation for Innovation (CFI, Project Number 30954), the Ontario Research Fund (ORF, Project Number 30954), and the Heart and Stroke Foundation of Canada (Grant # G-19-0024345). KJC was supported in part by a CIHR Canada Graduate Scholarship–Doctoral Research Award.
Conflict of interest
T-YL licenses CT Perfusion software to GE HealthCare and Neusoft (Shenyang, China).
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1246973/full#supplementary-material
References
1. Axel L. Cerebral blood flow determination by rapid-sequence computed tomography: theoretical analysis. Radiology (1980) 137(3):679–86. doi:10.1148/radiology.137.3.7003648
2. Campbell BCV, Mitchell PJ, Kleinig TJ, Dewey HM, Churilov L, Yassi N, et al. Endovascular therapy for ischemic stroke with perfusion-imaging selection. N Engl J Med (2015) 372(11):1009–18. doi:10.1056/NEJMoa1414792
3. Nogueira RG, Jadhav AP, Haussen DC, Bonafe A, Budzik RF, Bhuva P, et al. Thrombectomy 6 to 24 hours after stroke with a mismatch between deficit and infarct. N Engl J Med (2018) 378(1):11–21. doi:10.1056/NEJMoa1706442
4. Albers GW, Marks MP, Kemp S, Christensen S, Tsai JP, Ortega-Gutierrez S, et al. Thrombectomy for stroke at 6 to 16 hours with selection by perfusion imaging. N Engl J Med (2018) 378(8):708–18. doi:10.1056/NEJMoa1713973
5. Calamante F, Christensen S, Desmond PM, Østergaard L, Davis SM, Connelly A. The physiological significance of the time-to-maximum (tmax) parameter in perfusion MRI. Stroke (2010) 41(6):1169–74. doi:10.1161/STROKEAHA.110.580670
6. Hsieh J. Computed tomography: principles, design, artifacts, and recent advances. 2. Hoboken: Wiley Interscience; SPIE Press (2009).
7. Seltzer S. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients, NIST standard reference database 126 (1995). Published online 1995. doi:10.18434/T4D01F
8. Christiansen C. X-ray contrast media—an overview. Toxicology (2005) 209(2):185–7. doi:10.1016/j.tox.2004.12.020
9. Copen WA, Schaefer PW, Wu O. MR perfusion imaging in acute ischemic stroke. Neuroimaging Clin N Am (2011) 21(2):259–83. doi:10.1016/j.nic.2011.02.007
10. Boxerman JL, Hamberg LM, Rosen BR, Weisskoff RM. MR contrast due to intravascular magnetic susceptibility perturbations. Magn Reson Med (1995) 34(4):555–66. doi:10.1002/mrm.1910340412
11. Wintermark M, Maeder P, Verdun FR, Thiran JP, Valley JF, Schnyder P, et al. Using 80 kVp versus 120 kVp in perfusion CT measurement of regional cerebral blood flow. AJNR Am J Neuroradiol (2000) 21 (10):1881–1884.
12. Lee TY, Yang DM, Li F, Marants R. CT perfusion techniques and applications in stroke and cancer. In: E Samei, and NJ Pelc, editors. Computed tomography: approaches, applications, and operations. Springer International Publishing (2020). p. 347–65. doi:10.1007/978-3-030-26957-9_19
13. Wintermark M, Albers GW, Alexandrov AV, Alger JR, Bammer R, Baron JC, et al. Acute stroke imaging research roadmap. Stroke (2008) 39(5):1621–8. doi:10.1161/STROKEAHA.107.512319
14. The Alliance for Quality Computed Tomography. Adult brain perfusion CT protocols (2016). Available at: https://www.aapm.org/pubs/CTProtocols/documents/AdultBrainPerfusionCT.pdf (Accessed January 1, 2023).
15. Kim SH, Kamaya A, Willmann JK. CT perfusion of the liver: principles and applications in oncology. Radiology (2014) 272(2):322–44. doi:10.1148/radiol.14130091
16. Patel AR, Bamberg F, Branch K, Carrascosa P, Chen M, Cury RC, et al. Society of cardiovascular computed tomography expert consensus document on myocardial computed tomography perfusion imaging. J Cardiovasc Comput Tomogr (2020) 14(1):87–100. doi:10.1016/j.jcct.2019.10.003
17. Wintermark M, Smith WS, Ko NU, Quist M, Schnyder P, Dillon WP. Dynamic perfusion CT: optimizing the temporal resolution and contrast volume for calculation of perfusion CT parameters in stroke patients. AJNR Am J Neuroradiol (2004) 25 (5):720–729.
18. Wiesmann M, Berg S, Bohner G, Klingebiel R, Schöpf V, Stoeckelhuber BM, et al. Dose reduction in dynamic perfusion CT of the brain: effects of the scan frequency on measurements of cerebral blood flow, cerebral blood volume, and mean transit time. Eur Radiol (2008) 18(12):2967–74. doi:10.1007/s00330-008-1083-x
19. Aviv RI, d’Esterre CD, Murphy BD, Hopyan JJ, Buck B, Mallia G, et al. Hemorrhagic transformation of ischemic stroke: prediction with CT perfusion. Radiology (2009) 250(3):867–77. doi:10.1148/radiol.2503080257
20. Lin L, Bivard A, Krishnamurthy V, Levi CR, Parsons MW. Whole-brain CT perfusion to quantify acute ischemic penumbra and core. Radiology (2016) 279(3):876–87. doi:10.1148/radiol.2015150319
21. Roberts HC, Roberts TPL, Smith WS, Lee TJ, Fischbein NJ, Dillon WP. Multisection dynamic CT perfusion for acute cerebral ischemia: the ‘“Toggling-table”’ technique (2001). p. 4. Published online.
22. Youn SW, Kim JH, Weon YC, Kim SH, Han MK, Bae HJ. Perfusion CT of the brain using 40-mm-Wide detector and toggling table technique for initial imaging of acute stroke. Am J Roentgenol (2008) 191(3):W120–6. doi:10.2214/AJR.07.2519
23. Haberland U, Klotz E, Abolmaali N. Performance assessment of dynamic spiral scan modes with variable pitch for quantitative perfusion computed tomography. Invest Radiol (2010) 45(7):378–86. doi:10.1097/RLI.0b013e3181dfda9f
24. Miles K, Eastwood JD, König M. Multidetector computed tomography in cerebrovascular disease: CT perfusion imaging. London, United Kingdom: Informa Healthcare (2007).
25. Yeung TPC, Yartsev S, Bauman G, He W, Fainardi E, Lee TY. The effect of scan duration on the measurement of perfusion parameters in CT perfusion studies of brain tumors. Acad Radiol (2013) 20(1):59–65. doi:10.1016/j.acra.2012.08.013
26. Copen WA, Deipolyi AR, Schaefer PW, Schwamm LH, González RG, Wu O. Exposing hidden truncation-related errors in acute stroke perfusion imaging. Am J Neuroradiol (2015) 36(4):638–45. doi:10.3174/ajnr.A4186
27. Bennink E, Oosterbroek J, Kudo K, Viergever MA, Velthuis BK, de Jong HWAM. Fast nonlinear regression method for CT brain perfusion analysis. J Med Imaging (2016) 3(2):026003. doi:10.1117/1.JMI.3.2.026003
28. Fahmi F, Beenen LFM, Streekstra GJ, Janssen N, de Jong H, Riordan A, et al. Head movement during CT brain perfusion acquisition of patients with suspected acute ischemic stroke. Eur J Radiol (2013) 82(12):2334–41. doi:10.1016/j.ejrad.2013.08.039
29. Borst J, Berkhemer OA, Roos YBWEM, van Bavel E, van Zwam WH, van Oostenbrugge RJ, et al. Value of computed tomographic perfusion–based patient selection for intra-arterial acute ischemic stroke treatment. Stroke (2015) 46(12):3375–82. doi:10.1161/STROKEAHA.115.010564
30. Vagal A, Wintermark M, Nael K, Bivard A, Parsons M, Grossman AW, et al. Automated CT perfusion imaging for acute ischemic stroke: pearls and pitfalls for real-world use. Neurology (2019) 93:888–98. Published online. doi:10.1212/WNL.0000000000008481
31. So A. CT myocardial perfusion imaging. In: E Samei, and NJ Pelc, editors. Computed tomography. Cham: Springer International Publishing (2020). p. 367–93. doi:10.1007/978-3-030-26957-9_20
32. Barrett JF, Keat N. Artifacts in CT: recognition and avoidance. RadioGraphics (2004) 24(6):1679–91. doi:10.1148/rg.246045065
33. Siewerdsen JH, Jaffray DA. Cone-beam computed tomography with a flat-panel imager: magnitude and effects of x-ray scatter. Med Phys (2001) 28(2):220–31. doi:10.1118/1.1339879
34. Ning R, Tang X, Conover D. X-ray scatter correction algorithm for cone beam CT imaging. Med Phys (2004) 31(5):1195–202. doi:10.1118/1.1711475
35. Siewerdsen JH, Daly MJ, Bakhtiar B, Moseley DJ, Richard S, Keller H, et al. A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT: X-ray scatter correction. Med Phys (2005) 33(1):187–97. doi:10.1118/1.2148916
36. Endo M, Mori S, Tsunoo T, Miyazaki H. Magnitude and effects of x-ray scatter in a 256-slice CT scanner: X-ray scatter in a 256-slice CT. Med Phys (2006) 33(9):3359–68. doi:10.1118/1.2239366
37. Murase K, Nanjo T, Ii S, Miyazaki S, Hirata M, Sugawara Y, et al. Effect of x-ray tube current on the accuracy of cerebral perfusion parameters obtained by CT perfusion studies. Phys Med Biol (2005) 50(21):5019–29. doi:10.1088/0031-9155/50/21/005
38. Murphy A, So A, Lee TY, Symons S, Jakubovic R, Zhang L, et al. Low dose CT perfusion in acute ischemic stroke. Neuroradiology (2014) 56(12):1055–62. doi:10.1007/s00234-014-1434-z
39. Li Zlin, Li H, Zhang K, Li W, Chen X, Wu B, et al. Improvement of image quality and radiation dose of CT perfusion of the brain by means of low-tube voltage (70 KV). Eur Radiol (2014) 24(8):1906–13. doi:10.1007/s00330-014-3247-1
40. Li Hou, Sun C, Xu Zdong, Miao F, Zhang D, Chen J, et al. Low-dose whole organ CT perfusion of the pancreas: preliminary study. Abdom Imaging (2014) 39(1):40–7. doi:10.1007/s00261-013-0045-1
41. Klotz E, König M. Perfusion measurements of the brain: using dynamic CT for the quantitative assessment of cerebral ischemia in acute stroke. Eur J Radiol (1999) 30(3):170–84. doi:10.1016/S0720-048X(99)00009-1
42. Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol (1954) 6(12):731–44. doi:10.1152/jappl.1954.6.12.731
43. Stewart GN. Researches on the circulation time in organs and on the influences which affect it: parts I.-III. J Physiol (1893) 15(1-2):1–89. doi:10.1113/jphysiol.1893.sp000462
44. Johnson J, Wilson T. A model for capillary exchange. Am J Physiol-leg Content (1966) 210(6):1299–303. doi:10.1152/ajplegacy.1966.210.6.1299
45. Lawrence KSS, Lee TY. An adiabatic approximation to the tissue homogeneity model for water exchange in the brain: II. Experimental validation. J Cereb Blood Flow Metab (1998) 18(12):1378–85. doi:10.1097/00004647-199812000-00012
46. Patlak CS, Blasberg RG. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. Generalizations. J Cereb Blood Flow Metab (1985) 5(4):584–90. doi:10.1038/jcbfm.1985.87
47. Kudo K, Christensen S, Sasaki M, Østergaard L, Shirato H, Ogasawara K, et al. Accuracy and reliability assessment of CT and MR perfusion analysis software using a digital phantom. Radiology (2013) 267(1):201–11. doi:10.1148/radiol.12112618
48. Kudo K, Sasaki M, Ogasawara K, Terae S, Ehara S, Shirato H. Difference in tracer delay–induced effect among deconvolution algorithms in CT perfusion analysis: quantitative evaluation with digital phantoms. Radiology (2009) 251(1):241–9. doi:10.1148/radiol.2511080983
49. Østergaard L, Weisskoff RM, Chesler DA, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part I: mathematical approach and statistical analysis. Magn Reson Med (1996) 36(5):715–25. doi:10.1002/mrm.1910360510
50. Wu O, Østergaard L, Weisskoff RM, Benner T, Rosen BR, Sorensen AG. Tracer arrival timing-insensitive technique for estimating flow in MR perfusion-weighted imaging using singular value decomposition with a block-circulant deconvolution matrix: technique for Estimating CBF in PWI. Magn Reson Med (2003) 50(1):164–74. doi:10.1002/mrm.10522
51. Østergaard L, Sorensen AG, Kwong KK, Weisskoff RM, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part II: experimental comparison and preliminary results. Magn Reson Med (1996) 36(5):726–36. doi:10.1002/mrm.1910360511
53. Golub GH, Van Loan CF. Matrix computations. 3. Maryland, United States: Johns Hopkins University Press (1996).
54. Gill PE, Murray W, Wright MH. Practical optimization. Massachusetts, United States: Academic Press (1981).
55. Fieselmann A, Kowarschik M, Ganguly A, Hornegger J, Fahrig R. Deconvolution-based CT and MR brain perfusion measurement: theoretical model revisited and practical implementation details. Int J Biomed Imaging (2011) 2011:1–20. doi:10.1155/2011/467563
56. Tikhonov AN. On the solution of ill-posed problems and the method of regularization. Proc USSR Acad Sci (1963) 151(3):501–4.
57. Li K, Chen G. Statistical properties of cerebral CT perfusion imaging systems. Part II. Deconvolution-based systems. Med Phys (2019) 46(11):4881–97. doi:10.1002/mp.13805
58. Lee TY. Method And Apparatus For Calculating Blood Flow Parameters. Published online May (2005) 24:18.
59. Lee TY, Murphy B. Implementing deconvolution analysis for perfusion CT. In: Multidetector computed tomography in cerebrovascular disease. Florida, United States: CRC Press (2007). p. 29–45. Available at: https://www.taylorfrancis.com/books/9780203008584/chapters/10.3109/9780203008584-7 (Accessed January 1, 2023).
60. Smith MR, Lu H, Trochet S, Frayne R. Removing the effect of SVD algorithmic artifacts present in quantitative MR perfusion studies: SVD Deconvolution Artifacts. Magn Reson Med (2004) 51(3):631–4. doi:10.1002/mrm.20006
61. Calamante F, Gadian DG, Connelly A. Delay and dispersion effects in dynamic susceptibility contrast MRI: simulations using singular value decomposition. Magn Reson Med (2000) 44(3):466–73. doi:10.1002/1522-2594(200009)44:3<466::AID-MRM18>3.0.CO;2-M
62. Ibaraki M, Shimosegawa E, Toyoshima H, Takahashi K, Miura S, Kanno I. Tracer delay correction of cerebral blood flow with dynamic susceptibility contrast-enhanced MRI. J Cereb Blood Flow Metab (2005) 25(3):378–90. doi:10.1038/sj.jcbfm.9600037
63. Oppenheim AV, Schafer RW, Buck JR. Discrete-time signal processing. 2. Hoboken, New Jersey: Prentice Hall (1999).
64. Gobbel GT, Fike JR. A deconvolution method for evaluating indicator-dilution curves. Phys Med Biol (1994) 39(11):1833–54. doi:10.1088/0031-9155/39/11/004
65. Straka M, Albers GW, Bammer R. Real-time diffusion-perfusion mismatch analysis in acute stroke. J Magn Reson Imaging (2010) 32(5):1024–37. doi:10.1002/jmri.22338
66. Gershenfeld NA. The nature of mathematical modeling. Cambridge: Cambridge University Press (1999).
67. Boutelier T, Kudo K, Pautot F, Sasaki M. Bayesian hemodynamic parameter estimation by bolus tracking perfusion weighted imaging. IEEE Trans Med Imaging (2012) 31(7):1381–95. doi:10.1109/TMI.2012.2189890
68. Bennink E, Riordan AJ, Horsch AD, Dankbaar JW, Velthuis BK, de Jong HW. A fast nonlinear regression method for estimating permeability in CT perfusion imaging. J Cereb Blood Flow Metab (2013) 33(11):1743–51. doi:10.1038/jcbfm.2013.122
69. Axel L. Tissue mean transit time from dynamic computed tomography by a simple deconvolution technique. Invest Radiol (1983) 18(1):94–9. doi:10.1097/00004424-198301000-00018
70. Ma H, Campbell BCV, Parsons MW, Churilov L, Levi CR, Hsu C, et al. Thrombolysis guided by perfusion imaging up to 9 hours after onset of stroke. N Engl J Med (2019) 380(19):1795–803. doi:10.1056/NEJMoa1813046
71. Powers WJ, Rabinstein AA, Ackerson T, Adeoye OM, Bambakidis NC, Becker K, et al. Guidelines for the early management of patients with acute ischemic stroke: 2019 update to the 2018 guidelines for the early management of acute ischemic stroke: a guideline for healthcare professionals from the American Heart Association/American Stroke Association. Stroke (2019) 50(12):e344–e418. doi:10.1161/STR.0000000000000211
72. Campbell BCV, Yassi N, Ma H, Sharma G, Salinas S, Churilov L, et al. Imaging selection in ischemic stroke: feasibility of automated CT-perfusion analysis. Int J Stroke (2015) 10(1):51–4. doi:10.1111/ijs.12381
73. Campbell BCV, Christensen S, Levi CR, Desmond PM, Donnan GA, Davis SM, et al. Cerebral blood flow is the optimal CT perfusion parameter for assessing infarct core. Stroke (2011) 42(12):3435–40. doi:10.1161/STROKEAHA.111.618355
74. Cereda CW, Christensen S, Campbell BC, Mishra NK, Mlynash M, Levi C, et al. A benchmarking tool to evaluate computer tomography perfusion infarct core predictions against a DWI standard. J Cereb Blood Flow Metab (2016) 36(10):1780–9. doi:10.1177/0271678X15610586
75. Olivot JM, Mlynash M, Thijs VN, Kemp S, Lansberg MG, Wechsler L, et al. Optimal tmax threshold for predicting penumbral tissue in acute stroke. Stroke (2009) 40(2):469–75. doi:10.1161/STROKEAHA.108.526954
76. Kamalian S, Kamalian S, Maas MB, Goldmacher GV, Payabvash S, Akbar A, et al. CT cerebral blood flow maps optimally correlate with admission diffusion-weighted imaging in acute stroke but thresholds vary by postprocessing platform. Stroke (2011) 42(7):1923–8. doi:10.1161/STROKEAHA.110.610618
77. Chung KJ, De Sarno D, Lee TY. CT perfusion stroke lesion threshold calibration between deconvolution algorithms. Sci Rep (Forthcoming 2023). doi:10.1038/s41598-023-48700-6
78. Koopman MS, Berkhemer OA, Geuskens RREG, Emmer BJ, van Walderveen MAA, Jenniskens SFM, et al. Comparison of three commonly used CT perfusion software packages in patients with acute ischemic stroke. J Neurointerventional Surg (2019) 11(12):1249–56. doi:10.1136/neurintsurg-2019-014822
79. Rava RA, Snyder KV, Mokin M, Waqas M, Allman A, Senko J, et al. Assessment of a bayesian vitrea CT perfusion analysis to predict final infarct and penumbra volumes in patients with acute ischemic stroke: a comparison with rapid. Am J Neuroradiol (2020) 41(2):206–12. doi:10.3174/ajnr.A6395
80. Rava RA, Snyder KV, Mokin M, Waqas M, Zhang X, Podgorsak AR, et al. Assessment of computed tomography perfusion software in predicting spatial location and volume of infarct in acute ischemic stroke patients: a comparison of Sphere, Vitrea, and RAPID. J Neurointerventional Surg (2021) 13(2):130–5. doi:10.1136/neurintsurg-2020-015966
81. Muehlen I, Sprügel M, Hoelter P, Hock S, Knott M, Huttner HB, et al. Comparison of two automated computed tomography perfusion applications to predict the final infarct volume after thrombolysis in cerebral infarction 3 recanalization. Stroke (2022) 53(5):1657–64. doi:10.1161/STROKEAHA.121.035626
82. Bivard A, Kleinig T, Churilov L, Levi C, Lin L, Cheng X, et al. Permeability measures predict hemorrhagic transformation after ischemic stroke. Ann Neurol (2020) 88(3):466–76. doi:10.1002/ana.25785
83. Simard JM, Kent TA, Chen M, Tarasov KV, Gerzanich V. Brain oedema in focal ischaemia: molecular pathophysiology and theoretical implications. Lancet Neurol (2007) 6(3):258–68. doi:10.1016/S1474-4422(07)70055-8
84. Seet RCS, Rabinstein AA. Symptomatic intracranial hemorrhage following intravenous thrombolysis for acute ischemic stroke: a critical review of case definitions. Cerebrovasc Dis (2012) 34(2):106–14. doi:10.1159/000339675
85. Von Kummer R, Broderick JP, Campbell BCV, Demchuk A, Goyal M, Hill MD, et al. The Heidelberg bleeding classification: classification of bleeding events after ischemic stroke and reperfusion therapy. Stroke (2015) 46(10):2981–6. doi:10.1161/STROKEAHA.115.010049
86. Yoshimura S, Sakai N, Yamagami H, Uchida K, Beppu M, Toyoda K, et al. Endovascular therapy for acute stroke with a large ischemic region. N Engl J Med (2022) 386(14):1303–13. doi:10.1056/NEJMoa2118191
87. Sarraj A, Kleinig TJ, Hassan AE, Portela PC, Ortega-Gutierrez S, Abraham MG, et al. Association of endovascular thrombectomy vs medical management with functional and safety outcomes in patients treated beyond 24 hours of last known well: the SELECT late study. JAMA Neurol Published Online December (2022) 27:172. doi:10.1001/jamaneurol.2022.4714
89. Jain R, Gutierrez J, Narang J, Scarpace L, Schultz L, Lemke N, et al. In vivo correlation of tumor blood volume and permeability with histologic and molecular angiogenic markers in gliomas. Am J Neuroradiol (2011) 32(2):388–94. doi:10.3174/ajnr.A2280
90. Ellika SK, Jain R, Patel SC, Scarpace L, Schultz L, Rock J, et al. Role of perfusion CT in glioma grading and comparison with conventional MR imaging features. Am J Neuroradiol (2007) 28(10):1981–7. doi:10.3174/ajnr.A0688
91. McFaline-Figueroa JR, Lee EQ. Brain tumors. Am J Med (2018) 131(8):874–82. doi:10.1016/j.amjmed.2017.12.039
92. Louis DN, Perry A, Wesseling P, Brat DJ, Cree IA, Figarella-Branger D, et al. The 2021 WHO classification of tumors of the central nervous system: a summary. Neuro-Oncol. (2021) 23(8):1231–51. doi:10.1093/neuonc/noab106
93. Chandrasoma PT, Smith MM, Apuzzo MLJ. Stereotactic biopsy in the diagnosis of brain masses: comparison of results of biopsy and resected surgical specimen. Neurosurgery (1989) 24(2):160–5. doi:10.1227/00006123-198902000-00002
94. Jackson RJ, Fuller GN, Abi-Said D, Lang FF, Gokaslan ZL, Shi WM, et al. Limitations of stereotactic biopsy in the initial management ofgliomas. Neuro-Oncol (2001) 3(3):193–200. doi:10.1093/neuonc/3.3.193
95. Jain R. Perfusion CT imaging of brain tumors: an overview. Am J Neuroradiol (2011) 32(9):1570–7. doi:10.3174/ajnr.A2263
96. Leon SP, Folkerth RD, Black PML. Microvessel density is a prognostic indicator for patients with astroglial brain tumors. Cancer (1996) 77(2):362–72. doi:10.1002/(SICI)1097-0142(19960115)77:2<362::AID-CNCR20>3.0.CO;2-Z
97. Li VW, Yu ABC, Folkman J, Yu C, Rupnick M, Barnes P, et al. Microvessel count and cerebrospinal fluid basic fibroblast growth factor in children with brain tumours. The Lancet (1994) 344(8915):82–6. doi:10.1016/S0140-6736(94)91280-7
98. Weidner N. Intratumor microvessel density as a prognostic factor in cancer. Am J Pathol (1995) 147(1):9–19.
99. Provenzale JM, Mukundan S, Dewhirst M. The role of blood-brain barrier permeability in brain tumor imaging and therapeutics. Am J Roentgenol (2005) 185(3):763–7. doi:10.2214/ajr.185.3.01850763
100. Ma SH, Le HB, Jia Bhui, Wang ZX, Xiao ZW, Cheng XL, et al. Peripheral pulmonary nodules: relationship between multi-slice spiral CT perfusion imaging and tumor angiogenesis and VEGF expression. BMC Cancer (2008) 8(1):186. doi:10.1186/1471-2407-8-186
101. Tonino PAL, Fearon WF, De Bruyne B, Oldroyd KG, Leesar MA, Ver Lee PN, et al. Angiographic versus functional severity of coronary artery stenoses in the FAME study. J Am Coll Cardiol (2010) 55(25):2816–21. doi:10.1016/j.jacc.2009.11.096
102. Tonino PAL, De Bruyne B, Pijls NHJ, Siebert U, Ikeno F, van `t Veer M, et al. Fractional flow reserve versus angiography for guiding percutaneous coronary intervention. N Engl J Med (2009) 360(3):213–24. doi:10.1056/NEJMoa0807611
103. Virani SS, Alonso A, Benjamin EJ, Bittencourt MS, Callaway CW, Carson AP, et al. Heart disease and stroke statistics—2020 update: a report from the American heart association. Circulation (2020) 141(9):e139–e596. doi:10.1161/CIR.0000000000000757
104. Yun CH, Hung CL, Wen MS, Wan YL, So A. CT assessment of myocardial perfusion and fractional flow reserve in coronary artery disease: a review of current clinical evidence and recent developments. Korean J Radiol (2021) 22(11):1749. doi:10.3348/kjr.2020.1277
105. Budoff MJ, Dowe D, Jollis JG, Gitter M, Sutherland J, Halamert E, et al. Diagnostic performance of 64-multidetector row coronary computed tomographic angiography for evaluation of coronary artery stenosis in individuals without known coronary artery disease: results from the prospective multicenter ACCURACY (Assessment by Coronary Computed Tomographic Angiography of Individuals Undergoing Invasive Coronary Angiography) trial. J Am Coll Cardiol (2008) 52(21):1724–32. doi:10.1016/j.jacc.2008.07.031
106. Meijboom WB, Meijs MFL, Schuijf JD, Cramer MJ, Mollet NR, van Mieghem CAG, et al. Diagnostic accuracy of 64-slice computed tomography coronary angiography: a prospective, multicenter, multivendor study. J Am Coll Cardiol (2008) 52(25):2135–44. doi:10.1016/j.jacc.2008.08.058
107. Min JK, Taylor CA, Achenbach S, Koo BK, Leipsic J, Nørgaard BL, et al. Noninvasive fractional flow reserve derived from coronary CT angiography. JACC Cardiovasc Imaging (2015) 8(10):1209–22. doi:10.1016/j.jcmg.2015.08.006
108. Cook CM, Petraco R, Shun-Shin MJ, Ahmad Y, Nijjer S, Al-Lamee R, et al. Diagnostic accuracy of computed tomography-derived fractional flow reserve: a systematic review. JAMA Cardiol (2017) 2(7):803–10. doi:10.1001/jamacardio.2017.1314
109. Fujimoto S, Kawasaki T, Kumamaru KK, Kawaguchi Y, Dohi T, Okonogi T, et al. Diagnostic performance of on-site computed CT-fractional flow reserve based on fluid structure interactions: comparison with invasive fractional flow reserve and instantaneous wave-free ratio. Eur Heart J - Cardiovasc Imaging (2019) 20(3):343–52. doi:10.1093/ehjci/jey104
110. Siogkas PK, Anagnostopoulos CD, Liga R, Exarchos TP, Sakellarios AI, Rigas G, et al. Noninvasive CT-based hemodynamic assessment of coronary lesions derived from fast computational analysis: a comparison against fractional flow reserve. Eur Radiol (2019) 29(4):2117–26. doi:10.1007/s00330-018-5781-8
111. Cerqueira M. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: a statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. J Nucl Cardiol (2002) 9(2):240–5. doi:10.1067/mnc.2002.123122
112. Mushtaq S, Conte E, Pontone G, Baggiano A, Annoni A, Formenti A, et al. State-of-the-art-myocardial perfusion stress testing: static CT perfusion. J Cardiovasc Comput Tomogr (2020) 14(4):294–302. doi:10.1016/j.jcct.2019.09.002
113. Pontone G, Baggiano A, Andreini D, Guaricci AI, Guglielmo M, Muscogiuri G, et al. Dynamic stress computed tomography perfusion with a whole-heart coverage scanner in addition to coronary computed tomography angiography and fractional flow reserve computed tomography derived. JACC Cardiovasc Imaging (2019) 12(12):2460–71. doi:10.1016/j.jcmg.2019.02.015
114. Pontone G, Baggiano A, Andreini D, Guaricci AI, Guglielmo M, Muscogiuri G, et al. Stress computed tomography perfusion versus fractional flow reserve CT derived in suspected coronary artery disease. JACC Cardiovasc Imaging (2019) 12(8):1487–97. doi:10.1016/j.jcmg.2018.08.023
115. Sekhri V, Sanal S, DeLorenzo LJ, Aronow WS, Maguire GP. Cardiac sarcoidosis: a comprehensive review. Arch Med Sci (2011) 4:546–54. doi:10.5114/aoms.2011.24118
116. Silverman KJ, Hutchins GM, Bulkley BH. Cardiac sarcoid: a clinicopathologic study of 84 unselected patients with systemic sarcoidosis. Circulation (1978) 58(6):1204–11. doi:10.1161/01.CIR.58.6.1204
117. Sadek MM, Yung D, Birnie DH, Beanlands RS, Nery PB. Corticosteroid therapy for cardiac sarcoidosis: a systematic review. Can J Cardiol (2013) 29(9):1034–41. doi:10.1016/j.cjca.2013.02.004
118. Youssef G, Beanlands RSB, Birnie DH, Nery PB. Cardiac sarcoidosis: applications of imaging in diagnosis and directing treatment. Heart (2011) 97(24):2078–87. doi:10.1136/hrt.2011.226076
119. So A, Lee TY, Tzemos N. Myocardial perfusion and scar assessment in cardiac sarcoidosis with functional computed tomography imaging. Circ Cardiovasc Imaging (2020) 13(4):e010046. doi:10.1161/CIRCIMAGING.119.010046
120. Mendrik AM, Vonken Ejan, van Ginneken B, de Jong HW, Riordan A, van Seeters T, et al. TIPS bilateral noise reduction in 4D CT perfusion scans produces high-quality cerebral blood flow maps. Phys Med Biol (2011) 56(13):3857–72. doi:10.1088/0031-9155/56/13/008
121. Pisana F, Henzler T, Schönberg S, Klotz E, Schmidt B, Kachelrieß M. Noise reduction and functional maps image quality improvement in dynamic CT perfusion using a new k-means clustering guided bilateral filter (KMGB). Med Phys (2017) 44(7):3464–82. doi:10.1002/mp.12297
122. Yeung TPC, Dekaban M, De Haan N, Morrison L, Hoffman L, Bureau Y, et al. Improving quantitative CT perfusion parameter measurements using principal component analysis. Acad Radiol (2014) 21(5):624–32. doi:10.1016/j.acra.2014.01.015
123. Zhao C, Martin T, Shao X, Alger JR, Duddalwar V, Wang DJJ. Low dose CT perfusion with K-space weighted image average (KWIA). IEEE Trans Med Imaging (2020) 39(12):3879–90. doi:10.1109/TMI.2020.3006461
124. Huang SHS, Pavenski K, Lee TY, Jurkiewicz MT, Bharatha A, Thiessen JD, et al. Blood–brain barrier permeability in survivors of immune-mediated thrombotic thrombocytopenic purpura: a pilot study. Blood Adv (2021) 5(20):4211–8. doi:10.1182/bloodadvances.2021005317
125. Tao Y, Chen GH, Hacker TA, Raval AN, Van Lysel MS, Speidel MA. Low dose dynamic CT myocardial perfusion imaging using a statistical iterative reconstruction method: low dose myocardial perfusion CT using SIR. Med Phys (2014) 41(7):071914. doi:10.1118/1.4884023
126. Wu D, Ren H, Li Q. Self-supervised dynamic CT perfusion image denoising with deep neural networks. IEEE Trans Radiat Plasma Med Sci (2021) 5(3):350–61. doi:10.1109/TRPMS.2020.2996566
127. Kadimesetty VS, Gutta S, Ganapathy S, Yalavarthy PK. Convolutional neural network-based robust denoising of low-dose computed tomography perfusion maps. IEEE Trans Radiat Plasma Med Sci (2019) 3(2):137–52. doi:10.1109/TRPMS.2018.2860788
128. Li S, Zeng D, Bian Z, Li D, Zhu M, Huang J, et al. Learning non-local perfusion textures for high-quality computed tomography perfusion imaging. Phys Med Biol (2021) 66(11):115007. doi:10.1088/1361-6560/abfc90
129. Ommen F, Kauw F, Bennink E, Dankbaar JW, Viergever MA, Jong HWAM. Effect of prolonged acquisition intervals for CT-perfusion analysis methods in patients with ischemic stroke. Med Phys (2019) 46(7):3156–64. doi:10.1002/mp.13559
130. Chung KJ, Khaw AV, Pandey SK, Lee DH, Mandzia JL, Lee TY. Feasibility of deconvolution-based multiphase CT angiography perfusion maps in acute ischemic stroke: simulation and concordance with CT perfusion. J Stroke Cerebrovasc Dis (2022) 31(12):106844. doi:10.1016/j.jstrokecerebrovasdis.2022.106844
131. Wang C, Shi Z, Yang M, Huang L, Fang W, Jiang L, et al. Deep learning-based identification of acute ischemic core and deficit from non-contrast CT and CTA. J Cereb Blood Flow Metab (2021) 41(11):3028–38. doi:10.1177/0271678X211023660
132. Qiu W, Kuang H, Ospel JM, Hill MD, Demchuk AM, Goyal M, et al. Automated prediction of ischemic brain tissue fate from multiphase computed tomographic angiography in patients with acute ischemic stroke using machine learning. J Stroke (2021) 23(2):234–43. doi:10.5853/jos.2020.05064
133. Lee S, Jiang B, Heit JJ, Dodd RL, Wintermark M. Cerebral perfusion in pediatric stroke: children are not little adults. Top Magn Reson Imaging (2021) 30(5):245–52. doi:10.1097/RMR.0000000000000275
134. Lee S, Mlynash M, Christensen S, Jiang B, Wintermark M, Sträter R, et al. Hyperacute perfusion imaging before pediatric thrombectomy: analysis of the save ChildS study. Neurology (2023) 100(11):e1148–58. doi:10.1212/WNL.0000000000201687
135. Willemink MJ, Persson M, Pourmorteza A, Pelc NJ, Fleischmann D. Photon-counting CT: technical principles and clinical prospects. Radiology (2018) 289(2):293–312. doi:10.1148/radiol.2018172656
136. Danielsson M, Persson M, Sjölin M. Photon-counting x-ray detectors for CT. Phys Med Biol (2021) 66(3):03TR01. doi:10.1088/1361-6560/abc5a5
137. Sotoudeh H, Bag AK, Brooks MD. “Code-Stroke” CT perfusion; challenges and pitfalls. Acad Radiol (2019) 26(11):1565–79. doi:10.1016/j.acra.2018.12.013
138. Sun H, Gao F, Li N, Liu C. An evaluation of the feasibility of assessment of volume perfusion for the whole lung by 128-slice spiral CT. Acta Radiol (2013) 54(8):921–7. doi:10.1177/0284185113490151
139. Mirsadraee S, Reid JH, Connell M, MacNee W, Hirani N, Murchison JT, et al. Dynamic (4D) CT perfusion offers simultaneous functional and anatomical insights into pulmonary embolism resolution. Eur J Radiol (2016) 85(10):1883–90. doi:10.1016/j.ejrad.2016.08.018
140. Zhao Y, Hubbard L, Malkasian S, Abbona P, Molloi S. Dynamic pulmonary CT perfusion using first-pass analysis technique with only two volume scans: validation in a swine model. PLOS ONE (2020) 15(2):e0228110. doi:10.1371/journal.pone.0228110
141. Xin Y, Kim T, Winkler T, Brix G, Gaulton T, Gerard SE, et al. Improving pulmonary perfusion assessment by dynamic contrast-enhanced computed tomography in an experimental lung injury model. J Appl Physiol (2023) 134(6):1496–507. doi:10.1152/japplphysiol.00159.2023
142. Sitartchouk I, Roberts HC, Pereira AM, Bayanati H, Waddell T, Roberts TP. Computed tomography perfusion using first pass methods for lung nodule characterization. Invest Radiol (2008) 43(6):349–58. doi:10.1097/RLI.0b013e3181690148
143. Jimenez-Juan L, Mehrez H, Dey C, Homampour S, Salazar-Ferrer P, Granton JT, et al. Quantitative assessment of pulmonary artery occlusion using lung dynamic perfusion CT. Sci Rep (2021) 11(1):483. doi:10.1038/s41598-020-80177-5
144. Ohno Y, Nishio M, Koyama H, Fujisawa Y, Yoshikawa T, Matsumoto S, et al. Comparison of quantitatively analyzed dynamic area-detector CT using various mathematic methods with FDG PET/CT in management of solitary pulmonary nodules. Am J Roentgenol (2013) 200(6):W593–W602. doi:10.2214/AJR.12.9197
145. Yabuuchi H, Kawanami S, Iwama E, Okamoto I, Kamitani T, Sagiyama K, et al. Prediction of therapeutic effect of chemotherapy for NSCLC using dual-input perfusion CT analysis: comparison among bevacizumab treatment, two-agent platinum-based therapy without bevacizumab, and other non-bevacizumab treatment groups. Radiology (2018) 286(2):685–95. doi:10.1148/radiol.2017162204
146. Ohno Y, Koyama H, Fujisawa Y, Yoshikawa T, Seki S, Sugihara N, et al. Dynamic contrast-enhanced perfusion area detector CT for non-small cell lung cancer patients: influence of mathematical models on early prediction capabilities for treatment response and recurrence after chemoradiotherapy. Eur J Radiol (2016) 85(1):176–86. doi:10.1016/j.ejrad.2015.11.009
Keywords: perfusion imaging, computed tomography, tracer kinetic modeling, deconvolution, radiation dose reduction, acute ischemic stroke, cancer, cardiovascular disease
Citation: Chung KJ, De Sarno D and Lee T-Y (2023) Quantitative functional imaging with CT perfusion: technical considerations, kinetic modeling, and applications. Front. Phys. 11:1246973. doi: 10.3389/fphy.2023.1246973
Received: 25 June 2023; Accepted: 27 November 2023;
Published: 19 December 2023.
Edited by:
Ewald V. Moser, Medical University of Vienna, AustriaReviewed by:
Giovanni Di Domenico, University of Ferrara, ItalyChristian Nasel, University Hospital Tulln, Austria
Copyright © 2023 Chung, De Sarno and Lee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ting-Yim Lee, dGxlZUB1d28uY2E=
 Kevin J. Chung
Kevin J. Chung Danny De Sarno2
Danny De Sarno2 Ting-Yim Lee
Ting-Yim Lee