A review of the shear rheology of carbon black suspensions

The microstructural link to the rheology of carbon black suspensions has recently become clear as a result of advances in computational and experimental methods. This understanding reveals the important role of the restructuring, build-up, and break-up of carbon black agglomerates in simple shear, rationalized by a dimensionless balance of the hydrodynamic forces acting to break the agglomerates apart against the cohesive forces holding them together (i.e., the Mason number). The Mason number not only can predict the origin of reversible thixotropy seen in carbon black suspensions observed at higher shear intensities, but can also be used to rationalize the evolution of microstructure at lower shear intensities. This review focuses on carbon black suspension behavior, but the insights derived from carbon black suspensions are broadly applicable to a diverse class of soft matter including colloidal gels relevant to a variety of applications.

1 Introduction

Carbon black is one of the most abundant nanomaterials in use today because its properties can be engineered for targeted applications including batteries [1], fuel cell electrodes [2], conductive inks [3], and polymer composites [4]. In many of these applications, carbon black must be formulated and processed while suspended in a liquid. These suspensions are soft solids commonly known as colloidal gels. The macroscopic behavior of colloidal gels is intimately connected with their microstructure and their rheology must be controlled during processing to yield useful products. With a total global market for carbon black valued at $ 12.61 billion in 2021, understanding how to process and control the rheological behavior of carbon black suspensions is key to enabling a variety of emerging technologies.

The complex rheological behavior of carbon black is a direct result of the suspension microstructure which evolves in flow. This microstructure is hierarchical [5] and the forces of flow cause physical changes to occur that impact the microstructure on many length scales. The hierarchy originates from the manufacturing of carbon particles which involves the partial combustion of oils into solid primary particles. These primary particles are typically tens of nanometer in length scale and have internal pores that act as a sponge to soak up bulk solvent, thereby modifying the suspension rheology at relatively low weight loading. These primary particles are fused to form primary aggregates that can be described by a fractal dimension, D_f, and a primary aggregate radius, a. These aggregates are the colloidal building blocks of the suspension. While carbon blacks from a given manufacturer can be further milled to reduce the aggregate size and density, it is generally assumed that once formulated in suspension the stresses experienced in flow are insufficient to change the primary aggregate structure. Finally at the largest length scales in suspension, the aggregates flocculate or cluster to form agglomerates whose size and number distribution depend on the balance of attractive and repulsive forces acting between primary aggregates and forces acting on the agglomerates as a result of flow. While surface modification of neat carbon black particles can significantly influence the pair potential between primary aggregates (ex., [6-8]), the focus of this review is on suspensions that are formulated using carbon blacks that exhibit strongly attractive interactions where the agglomerates grow in size to exceed several microns and exhibit a macroscopic yield stress.

While our understanding of carbon black suspension rheology has matured in the last decade as a consequence of the incorporation of carbon blacks in lithium-ion battery slurries and fuel cell catalyst inks, there remain important unanswered questions for the prediction of the suspension flow behavior. This review will outline the current state-of-the-art understanding of the physical processes that determine the evolution of carbon black agglomerates in steady and transient shear flow and highlight areas of ongoing work that are important to predict the flow behavior in coating flows.

2 Quiescent rheology of carbon black suspensions

Rheological measurements of carbon black suspensions are frequently used to understand how to engineer its processing. Such measurements require first suspending the carbon black into a liquid of interest. This is generally accomplished by blending the dry carbon black powder with a liquid and subjecting that mixture to a high shear intensity for several minutes. This high shear mixing is essential to not only homogeneously disperse the carbon black in the liquid, but also to ensure all carbon surfaces are uniformly wet by the suspending medium. For example, in lithium-ion battery slurry processing [9], high-intensity dispersing equipment, including hydrodynamic shear-based mixers and kneaders, are applied to suspensions containing carbon black [10, 11] to ensure homogeneous dispersion and minimal aggregations. Similarly, in fuel cell ink suspensions, ultrasonic bath is generally used with tuned parameters to achieve the desired dispersion of carbon black agglomerates. The oil adsorption number (OAN), typically measured according to ASTM D2414-01, indicates the amount of suspending liquid that can be added to the dry carbon black powder before a torque-sensing system observes a significant increase in viscosity. The OAN gives some indication about the internal porosity of the carbon black particle (i.e., the higher the oil adsorption number the more solvent can be imbibed by the primary aggregate). Formulating a suspension (as opposed to a paste) requires that there be a sufficient amount of the suspending liquid present to fully wet all the carbon surfaces. The OAN gives a good estimate for the maximum solid weight fraction of the carbon black particles in the suspending liquid.

Carbon black suspension rheology is performed using a variety of rheological accessories including plate-plate, cone-plate, and Couette style devices. Typically, the as-mixed sample is loaded onto the rheometer and then conditioned on the geometry prior to any rheological test to erase the memory of the high shear mixing step. Suspensions are usually measured shortly after preparation as their properties change in time. Suspensions left to stand on the benchtop will frequently sediment over several days. This sedimentation is accelerated if the suspension is mixed at a lower shear rate (ex. on a roll-mixer). Once loaded onto the rheometer, a typical shear protocol consists of a high shear intensity step followed by small amplitude oscillatory shear (SAOS). Carbon black gels are fragile and therefore the strain amplitude of the SAOS test is typically below 0.3%. One such example from Trappe et al. [12] illustrates (shown in Figure 1A) the fluid-solid transition in a carbon black suspension as a function of volume fraction determined using SAOS. The sample consisted of carbon black suspended in mineral oil. As the volume fraction increased, there was a divergence of the viscosity, η, at a critical volume fraction, and at this same critical volume fraction the onset of a finite elasticity as indicated by the increase in storage modulus, G′, as shown in Figure 1A. The critical volume fraction is identified by assuming critical scaling of the modulus and viscosity given as:

$\eta ={\eta }_s{\left({\varphi }_c-\varphi \right)}^{-v};G^{\prime }=G_0{\left(\varphi -{\varphi }_c\right)}^p$

where G₀ is the modulus intercept, η_s is the solvent viscosity, and p and v are the critical exponents. Fitting these forms identifies the concentration of carbon black where a stress-bearing network can form, which is commonly referred to as a colloidal gel. In the gel phase, the value of the critical exponent, p, depends on the nature of local mechanical contacts of the stress-bearing bonds, and both G₀ and p are thought to originate from local network rigidity and topology.[13] These quantities are thus intimately linked with the microstructure of the network building blocks. While it is commonly assumed that these building blocks are the primary particles, gels of carbon blacks frequently form as a result of the arrest of clusters/agglomerates and not as a consequence of the dynamic arrest of the primary aggregates themselves. [14] Understanding the fluid-cluster-gel transition remains an outstanding challenge in colloidal science and is outside of the scope of this review [15, 16].

FIGURE 1

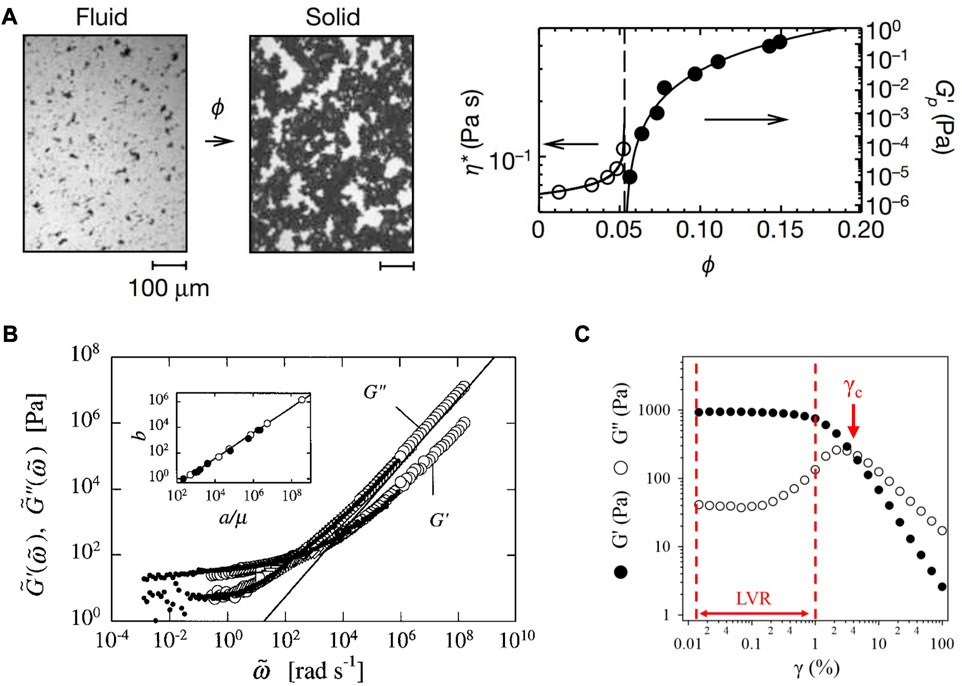
FIGURE 1. (A) Figure 2 from [12]¹ shows optical microscopy images (left) of carbon black agglomerates suspended in basestock oil forming a mechanically percolated network with increasing volume fraction, ϕ. The fluid-solid transition manifests microscopically as the divergence of the zero-shear viscosity, η, and the onset of a plateau modulus, $G_p^{\prime }$, with critical scalings of $\eta \sim {({\varphi }_c-\varphi )}^{-v}$ and $G_p^{\prime }\sim {(\varphi -{\varphi }_c)}^p$ (right). The vertical dashed line indicates the critical volume fraction, ϕ_c, associated with the transition. (B) Figure 2 from [17]² shows the scaled storage, ${\tilde{G}}^{\prime }$, and loss, ${\tilde{G}}^{\prime \prime }$, moduli versus frequency, $\tilde{\omega }$. The inset shows the shift factors applied to collapse the curves as a function of carbon black volume fraction. (C) Figure 2.3 from [20]³ where an amplitude sweep is performed on a gelled suspension of carbon black in propylene carbonate. The linear viscoelastic region (LVR) is marked by the vertical red lines and the critical strain, γ_c, is identified as the cross-over of the moduli prior to the transition to flow.

At low frequencies, the elastic modulus is a weak function of frequency in the gel phase. This reflects the highly arrested nature of the carbon black particles, which cannot relax on time-scales accessible to the rheometer. [17] observed that at high frequencies both the storage and loss moduli, G″, increased with increasing frequency and that the loss modulus crossed-over the storage modulus. They identified the cross-over frequency, shifted the modulus and the frequency to form scaled moduli, ${\tilde{G}}^{\prime }=b{G}^{\prime }$ and ${\tilde{G}}^{\prime \prime }=b{G}^{\prime \prime }$ and a scaled frequency, $\tilde{\omega }=af$. Using this scaled representation of the SAOS spectra, they observed collapse of the curves as a function of carbon black volume fraction and that ${\tilde{G}}^{\prime \prime }\sim \tilde{\omega }$, as shown in Figure 1B with the shift factors shown in the inset. They also observed that high frequency response was independent of carbon black volume fraction, which implied that it is associated with the suspending fluid’s viscosity. Dagès et al. [18] recently performed SAOS at different shear histories, and while the plateau modulus was sensistive to the preshear history, the scaled moduli superimposed with the results of Trappe et al. [17]. The similarity of the SAOS curves across the wide range of frequencies implies that there is structural similarity between carbon black gels prepared with different shear histories and different carbon black loadings. Legrand et al. [19] recently showed that such similarity is violated upon addition of adsorbing polymer to the suspending medium or when the carbon black in the suspension is concentrated such that it forms a paste which incorporates capillary interfaces homogeneously distributed throughout its volume.

SAOS is conducted in the linear viscoelastic region (LVR) where the microstructure remains unaltered by deformation. However, non-linear behavior can be explored by conducting an amplitude sweep. In an amplitude sweep the strain amplitude, γ, is increased at a fixed frequency and the storage and loss mudulus are determined from the transient oscillatory response. In the LVR (shown in Figure 1C), the storage and loss modulus are independent of frequency, but as the strain amplitude is increased beyond a critical strain, an increase in the loss modulus is generally observed before the gel network transitions to non-linear flow. An example amplitude sweep from a carbon black gel in propylene carbonate from Hipp et al. [20] is shown in Figure 1C. Increasing the strain amplitude beyond the critical strain causes the suspension to fully fluidize. The yielding of the elastic carbon black network is still poorly understood [21] and additional experiments that probe the microscopic response of the carbon black network during dynamic yielding and after cessation of flow are needed [22].

3 Rheology of carbon black suspensions under flow

A variety of shear protocols are utilized to characterize the rheology of carbon black suspensions including flow sweeps [23], flow ramps [24], step-up and step-down shear tests [25-27], and large amplitude oscillatory rheology [28]. In general, the goal of these tests is to understand how the viscosity, η, of the suspension depends on shear rate, $\dot{\gamma }$, and time, t. As carbon black suspensions fall into the category of yield stress fluids, their rheological behavior is quite complex. The complexities of yield stress fluids has been reviewed elsewhere [29-32]. In this section, we focus on observations specific to carbon black suspensions, which share many features in common with other yield stress fluids.

The rheology of carbon black suspensions is bifurcated. Ovarlez et al. and Coussot et al. [33,27] showed that this bifurcation manifests in a sensitivity of the flow curve to the preshear history. In Figure 2A the dependence of the shear stress, σ, on $\dot{\gamma }$ is shown as a function of preshear condition superimposed on the steady state flow curve. At high shear intensities, all the curves have the same stress and the stress is not a strong function of time. However, at low shear intensities, the flow curve is sensitive to the preshear history. This behavior is quite universal to carbon black suspensions and conveniently divides the rheological behavior into two flow regimes: 1) A strong flow regime where the suspension exhibits reversible thixotropy, and 2) a weak flow regime where the suspension exhibits a rheopectic response. Hipp et al. [26] identified the division of the strong and weak flow regimes based on the observation of the transient stress observed during step-down shear tests performed after imposition of high shear preshear step. In this way, they identified an apparent yield stress, σ_y, from the flow curve of a suspension of carbon black in mineral oil that matched well with the yield stress determined from creep measurements of the presheared sample [34]. Hipp et al. used this apparent yield stress to divide the flow curve based on the inverse Bingham number, Bi⁻¹ = σ/σ_y. When Bi⁻¹ ≫ 1, they defined the suspension in the strong flow regime. When Bi⁻¹ ≤ 1, the suspension was associated with the weak flow regime. This is shown in Figure 2B. The following two sections discuss important experimental results associated with linking microstructure to macroscopic rheology in the two flow regimes.

FIGURE 2

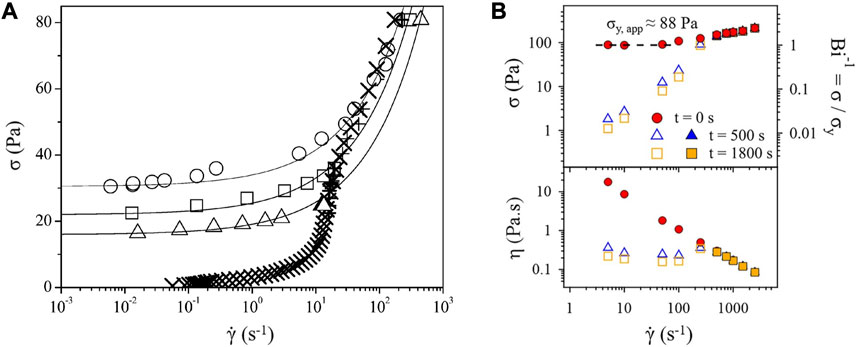
FIGURE 2. (A) Figure 4 from [27]⁴ shows the stress, σ, as a function of the shear rate, $\dot{\gamma }$, for flow curves constructed from different preshear conditions with circles, squares, and triangles corresponding to decreasing preshear stress respectively. The crosses represent the flow curve determined at steady state and the lines are Hershel-Bulkley fits to the “intrinsic” flow curves. (B) Figure 3 from [26]⁵ shows the time evolution, t, of a flow curve undergoing steady shear presented as shear stress and viscosity, η. The apparent yield stress, σ_y,app, is indicated by the horizontal dashed line and taken as the initial stress determined from the stress after a step-down in shear rate. The implication of the inverse Bingham number, Bi⁻¹, is discussed in the text. As indicated by the legend, the response changes in time resulting in an apparent shear thickening behavior commonly associated with carbon black gels. The preshear condition for these flow curves was the highest shear rate tested, 2,500 s⁻¹.

3.1 Reversible thixotropy in the strong-flow limit: The Mason number

In his seminal review, Barnes [30] defined thixotropy as associated with the reversible change from a “flowable fluid to a solid-like elastic gel.” He further associated this change with the microstructural evolution of a flocculated particle suspension whose structure can be modified in flow via the build-up and break-up of the microstructure in time. This generally occurs in materials where viscoelastic effects are marginal. Reversible thixotropy is a more specific class of thixotropic behavior. It is characterized by the ability to reversibly break-up and recover the microstructure in the rheometer, which can be identified by measurements of the viscosity. Dullaert et al. [25] identified reversible thixotropy as the decrease in viscosity in time upon a step-up in shear rate and an increase in viscosity in time upon a step-down in the shear rate applied to the suspension. This idea applied to a carbon black suspension [35] suspended in a mixture of paraffin oil and poly (isobutylene) produced a reversible thixotropic suspension that exhibited slow build-up and break-up kinetic, slow enough that transient microstructural changes in viscosity could be observed and modeled with a structural kinetics model. Structural kinetics models are popular for extracting rate constants associated with the build-up and break-up of structure and predicting more complex flows based on rheological tests. Larson et al. [36] has recently reviewed these approaches and their summary is outside the scope of this review. Nonetheless, for carbon black suspensions the origin of this time-dependent rheological response is the changing average size of carbon black agglomerates, which at higher shear intensity erode to smaller size resulting a lower suspension viscosity [37,38]. Similarly, at lower shear intensity agglomerates grow in size resulting in a larger viscosity. As the transition to different agglomerate sizes upon step-change in shear rate take a finite time to occur, a suspension can if left to stand eventually form an elastic gel with a finite yield stress and elasticity.

In the strong flow limit, the change in viscosity is directly linked to the change in microstructure [39, 40] by assuming that the break up of agglomerates is controlled by the hydrodynamic stress, which for fractal agglomerates is given as:

${\varphi }_a={\varphi }_p{\left(\frac{\eta \dot{\gamma }}{{\sigma }_m}\right)}^{\left(D_f-3\right)/3}$

and the viscosity given by the Kriegher-Dougherty equation:

$\eta ={\eta }_s{\left(1-\frac{{\varphi }_a}{{\varphi }_{\mathit{max}}}\right)}^{-2.5{\varphi }_{\mathit{max}}}$

where ϕ_a is the volume fraction of agglomerates, D_f is the fractal dimension, ϕ_p is the volume fraction of the primary particles, η_s is the viscosity of the carrying fluid, ϕ_max is the maximum packing volume fraction of the equivalent sphere, and σ_m is the stress associated with the bond strength holding the agglomerates together. These two equations predict that if the fractal dimension is held constant, shear thinning originates from the reduction in the effective volume fraction of the agglomerates. Harshe et al. [38] used Stokesian dynamics simulations to examine the break up of fractal agglomerates in simple shear and found that individual clusters restructure in flow and evolve toward a common fractal dimension depending on the stress. They observed a fractal dimension D_f = 2.4–2.6 depending on the initial cluster configuration and a reduction in agglomerate size with increasing stress. Based on these results, shear thinning should be enhanced as the hydrodynamic forces acting on the particles is increased. This can be accomplished by increasing the shear rate or the suspending medium’s viscosity. This idea built on the work by Sonntag et al. [41] which showed that the break-up of dilute flocs in shear flow is governed by the balance of hydrodynamic stress to the cohesive stress holding the flocs together. Sonntag collapsed this break up with the ratio, $\frac{{\eta }_s\dot{\gamma }}{{\sigma }_m}$, a dimensionless group balancing the shear stress acting on an agglomerate against the bond strength holding the agglomerates together.

Evidence confirming this microstructural picture applied to carbon black suspensions emerged first with experiments by Osuji et al. [42] using rheo-microscopy. In these experiments, a dilute carbon black suspension in mineral oil subjected to steady shear was observed to undergo three characteristic flow regimes, as shown in the inset in Figure 3A. In the strong-flow regime large carbon black agglomerates transformed into smaller ones reversibly. This microstructural transition coincided with strong shear thinning. Hipp et al. [26] confirmed this for carbon black suspensions using ultra-small angle neutron scattering (USANS) experiments where at high shear intensities, a reduction in agglomerate size occurred with increasing shear rate. Further, they observed that this reduction in agglomerate size occured with a constant fractal dimension, D_f ∼ 2.5. This value agrees closely with the simulated values from Harshe et al. [38]. By expanding this study [43] to various solvent types and carbon black volume fractions, they collapsed (as shown in Figure 3) the normalized agglomerate size, $R_g^a/a$, with an empirical scaling law $R_g^a/a=25.4M{n}^{-1}$ with the Mason number given as:

$Mn=6\pi \frac{\eta \dot{\gamma }{\varphi }_p^2}{{\sigma }_y}$

FIGURE 3

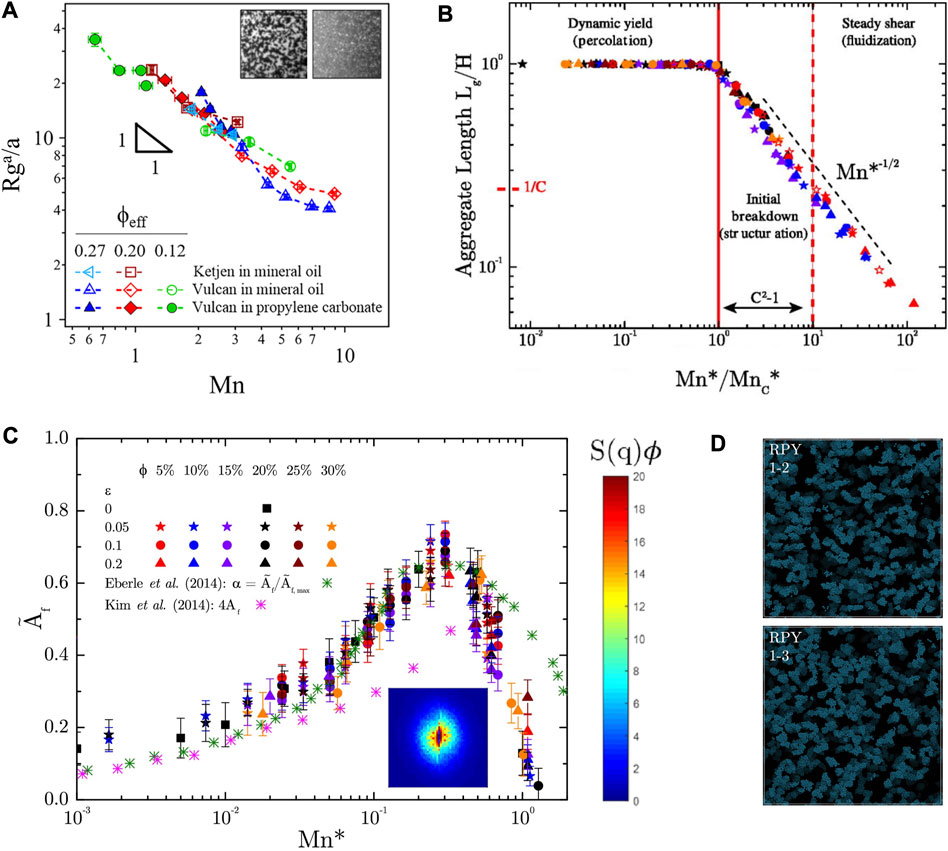
FIGURE 3. (A) Figure 7 from [43]⁶ shows the collapse of normalized agglomerate size, $R_g^a/a$ versus the modified Mason number, Mn. The data are measured for different solvent types and carbon black volume fractions. The inset image is Figure 7 from [54]⁷, both 1.5 × 1.5 mm in area, showing micrographs of carbon black suspensions under flow. The left image is at lower shear intensity $(\dot{\gamma }=1331/s)$ and the right image is at higher shear intensity $(\dot{\gamma }=13301/s)$. (B) Figure 6 from [45]⁸ of the aggregate length, L_g, normalized to box size, H, versus the Mason number normalized to a critical value, Mn_c. Aggregated colloidal suspensions of various volume fractions and attractive strength collapse on a single mastercurve. Three shear regimes are indicated: dynamic yield, initial breakdown, and steady shear. The black dashed line indicates the scaling of agglomerate size with Mason number (C) Figure 9 from [45] shows the simulated and experimental anisotropy factor, ${\tilde{A}}_f$, versus the Mason number, Mn, for attractive colloidal dispersions. The inset image is Figure 3 from [45] which shows an example of the 2-D Fourier transform of the structure factor along the one to two plane. (D) Figure 11 from [45] shows the final structure of colloidal agglomerates along the 1–2 (top) and 1–3 (bottom) plane. Images were generated from simulations using the Rotne-Prager-Yamakawa (RPY) approximation that accounts for long-range hydrodynamic interactions and scales with the particle size.

The Mason number has a form similar to that proposed by Potanin with a subtle modification that the cohesive force acting to hold the agglomerate together is estimated from the apparent yield stress defined by the flow curve, ${\sigma }_y=\frac{{\varphi }^2}{a^2{(d\mathrm{\Phi }/dr)}_{\mathit{max}}}$, as assumed by Eberle et al. [44] and that the hydrodynamic stress included the particle stress. The utility of this representation is that the Mason number can be determined solely from the flow curve without the need for other measurements and used to predict the agglomerate size at a given flow condition. A key picture that emerges from the assumption of the self-similar break-up (i.e., constant fractal dimension) is that the agglomerates reversibly transition from one size to the next based solely on the magnitude of the hydrodynamic stress in a given suspension. This is microscopic origin of the reversible thixotropic response.

While our current understanding of the rheology of carbon black suspensions in the strong flow limit is quite advanced, there remain significant areas where experiments and theory can contribute. For example, Stokesian dynamics by Varga et al. [45] show that the Mason number controls the size of agglomerates and their structural erosion leads to strong shear thinning which agrees with experiments as shown in Figure 3B. However, they also show large scale anisotropic structures that form under these same flow conditions that contribute to the shear thinning observed. They compute the anisotropy factor, A_f, as a function of the Mason number shown in Figure 3C. Anisotropy in flocculated suspensions of spherical nanoparticles is well known (ex., [44, 46]). However, a quantitative framework for predicting the degree of alignment of carbon black agglomerates or their direct observation in the strong-flow limit is not yet accessible to experiments. Nonetheless, the qualitative similarity between the microstructure observed in Figure 3D and the data from Osuji et al. [42] indicate that these simulations accurately capture the evolution of microstructure in shear flow. While advanced theoretical frameworks (ex., [47, 48, 36]) are emerging to develop broadly applicable physical models which predict the thixotropic nature of carbon black rheology, experiments that can quantify anisotropy in sheared carbon black suspensions are needed to confirm these models. Some progress in this direction comes from Wang et al. [49] who used orthogonal superposition (OSP) rheometry to quantify the development of anisotropy in carbon black suspensions in mineral oil and found that the transient orthogonal storage and loss moduli could be probed during step-down flow tests and that these values were not equal in the presheared state. This is consistent with Negi et al. [50] who found that residual stresses remain post-shear in gels of flocculated laponite. Nonetheless, questions remain. Directly measuring this anisotropy in the strong flow regime and developing physical insight into its scaling with the Mason number is critical to designing processes which control the microstructure of carbon black suspensions.

3.2 Rheopexy in the weak flow limit

Build-up and break-up of carbon black agglomerates do not always lead to a reversible thixotropic response in suspensions. A second category of behavior occurs in the “weak flow limit” where a slow decrease in viscosity is observed in time upon a step-down in shear rate or stress and an increase in viscosity is observed in time when the shear rate is returned to a high shear intensity [51, 52]. This phenomena is the opposite of a thixotropic response and is often called rheopexy or “antithixotropy”. Experimentally, a suspension will appear to shear thicken with increasing shear rate during a flow sweep test ([23, 53–55]). The extent of shear thickening will depend sensitively on the duration of the test, the range of shear rates probed, the shear history, and the nature of the agglomerates. Furthermore, suspensions may exhibit hidden shear thickening which is usually masked by the yield stress [56]. Ovarlez et al. [27] observed this shear thickening behavior in suspensions of carbon black and showed that the duration of flow and the shear intensity not only determined the extent of shear thinning upon step-down in shear rate, but also the suspensions retained memory of their shear history manifest as an apparent decrease in the yield stress of the material. They noted that the material became softer as a consequence of the shear history and remarked that the yield stress was controlled by the preshear stress imposed on the sample. A similar observation had been noted by Helal et al. [24], who also observed in rheo-electric measurements a strong dependence of the suspension conductivity on the shear history.

As observed by Osuji et al. [42] the transition from strong to weak flow leads to the formation of large and dense agglomerates, which under certain conditions flow align in the vorticity direction. This third category of rheological behavior is shown in Figure 4A [26] and occurs at relatively low shear rates in the weak flow regime. At higher shear rates in the weak flow regime, Hipp et al. [26] showed that the agglomerates formed in the strong flow regime densify and grow in size when the shear stress approaches the yield stress. Unlike the agglomerates formed at high shear intensities (D_f ≈ 2.5), these agglomerates exceed tens of microns in size are not fractal as shown in Figure 4B. Harshe et al. [37] used Stokesian dynamics simulations on fractal agglomerates to show that a critical stress must be exceeded to cause break-up of agglomerates. Below that critical stress, the agglomerates do not break-up but instead restructure. These restructured agglomerates remain suspended in the fluid for some time in shear flow but because of their higher densities will slowly sediment. The sedimentation of agglomerates leads to an apparent shear thinning in a Couette rheometer [57] as the suspended particles migrate out of the gap. Acrivos et al. [58] predicted the extent of shear thinning caused by sedimendation at a given shear rate to be controlled by the Shields number, a dimensionless balance between the viscous forces and buoyant forces given as:

$A=\frac{9{\eta }_s\dot{\gamma }}{2Lg\mathrm{\Delta }\rho }$

where L is the gap, Δρ is the density contrast, and g is the gravitational constant. Hipp et al. [26] confirmed that the Shields number accurately predicted the transition from sedimenting agglomerates to homogeneously dispersed agglomerates by directly measuring the distribution of carbon black in a Couette rheological accessory. The depletion of carbon black in the Couette accessory was probed using neutron scattering and the carbon was observed to migrate axially, L/L₀, toward the bottom of the Couette accessory with time as shown in Figure 4C. Regardless of the migration, the sample could be reversibly restored through shear rejuvenation in the strong flow regime.

FIGURE 4

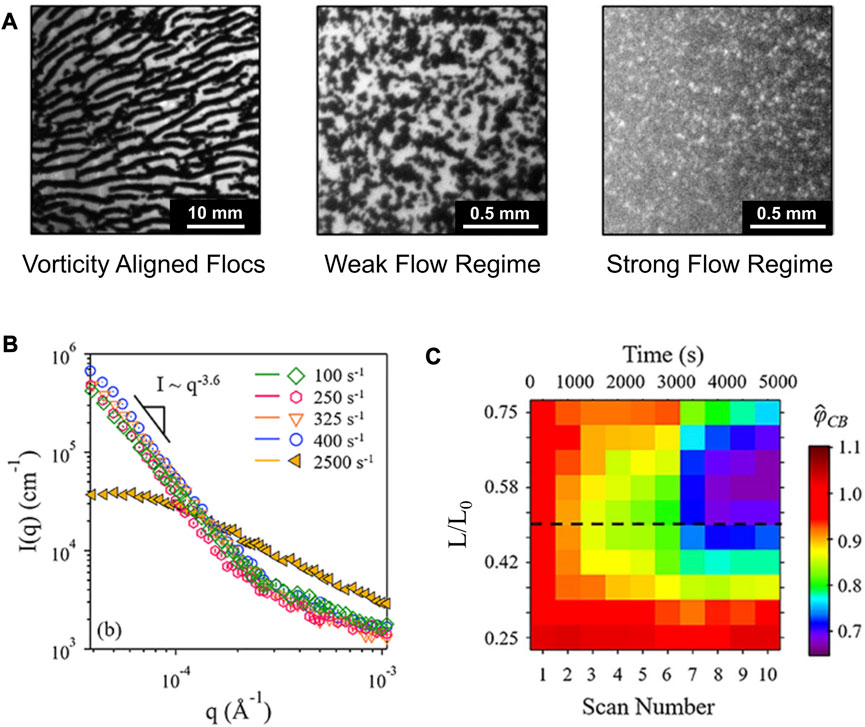
FIGURE 4. (A) Figure 2 from [42]⁹ shows rheo-optical images of carbon black suspensions undergoing shear deformation. Three flow regimes were observed: vorticity aligned flocs (left), a weak flow regime (middle), and a strong flow regime (right). (B) Figure 7 from [26]¹⁰ shows desmeared ultra-small angle neutron scattering (USANS) for a carbon black suspension in mineral oil. The scattering intensity, I(q), is plotted over the scattering wavevector, q, for several shear intensities. At low shear rates, the agglomerates densify to form non-fractal agglomerates whose size exceeds the length scale accessible with USANS (C) Figure 8 from [26] shows the normalized invariant, ${\widehat{\phi }}_{CB}$, as a function of normalized Couette height, L/L₀, for the carbon black suspension of (B) sheared at 400 s⁻¹. Sedimentation is observed over time in the Couette geometry of a rheo-SANS instrument.

At lower shear rates in the weak flow regime, the transition to vorticity aligned agglomerates occurs. This is a direct result of the confinement of these dense agglomerates in the gap of the rheometric accessory. In confinement, these agglomerates trigger the formation of viscous eddies that maintain periodic spacing within the gap, which orients the agglomerates to form vorticity aligned flocs [42, 59, 60], These “log-rolling” structures shown in the inset of Figure 4 are maintained under steady flow with a conserved wavelength and diameter. These structures have a striking appearance as they align in the neutral plan of flow and are maintained under steady shearing conditions. Time resolved measurements [59] of their formation indicated an increase in viscosity with time resulting from their formation. Grenard et al. [60] showed that a critical shear rate predicted the transition from dense agglomerates to vorticity aligned agglomerates based on the interaction potential between agglomerates given as:

$\dot{\gamma }=\frac{U}{{\eta }_s}\delta h^{D_f-3}$

where U is the depth and δ is the range of attractive well-depth of the carbon-carbon pair potential, and h is rheometer gap as shown in Figure 5A. Using this critical shear rate, a state diagram predicting the transition from dense agglomerates to vorticity aligned agglomerates was predicted across a range of weight fractions and gap heights. Varga et al. [61] later showed that this critical shear rate is equivalent to the Mason number and found therefore that a critical Mason number $M{n}_c=2.5{(h/R_g^a)}^{-1.4}$ predicted the transition from aligned to unaligned agglomerates, as shown in Figure 5B. This indicates that the degree of confinement determines the onset of the formation of vorticity aligned agglomerates. As long as the Mason number is larger than the critical Mason number (Mn > Mn_c), then vorticity aligned agglomerates will not form.

FIGURE 5

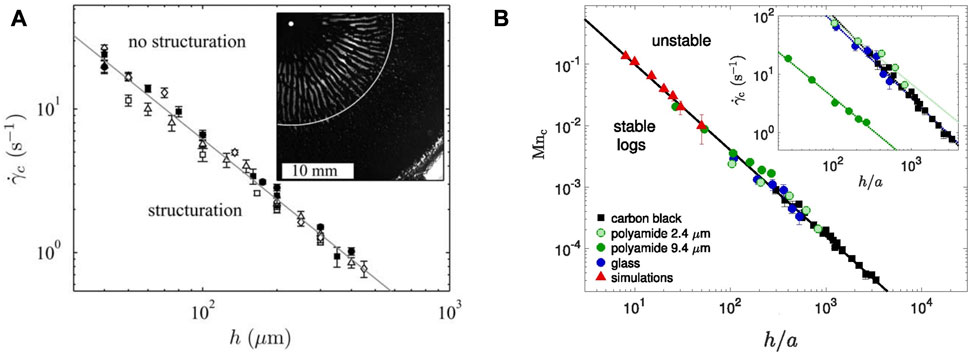
FIGURE 5. (A) Figure 13 from [60]¹¹ shows the state diagram from rheo-optics experiments delineating vorticity aligned flocs from agglomerates that exhibit no structuration. There is a critical shear rate, ${\dot{\gamma }}_c$, at a specific gap height, h, where this transition takes place regardless of carbon black volume fraction. The inset shows a representative image of the vorticity aligned flocs in a cone geometry. (B) Figure 5 from [61] shows results of a positively split Ewald (PSE) discrete element simulations that include the Rotne-Prager-Yamakawa (RPY) approximation to account for long-range hydrodynamic interactions between particles. The simulations predict the same transition in (A) mapped to the critical Mason number, Mn_c, as a function of the dimensionless gap size, h/a. The inset shows the critical shear rate corresponding to the critical Mason number.

4 Ongoing experimental and computational needs

The rheological phenomena described here are quite universal and impact the processing of suspensions containing carbon black including those used for battery coatings and fuel cell electrodes. It therefore remains relevant to continue to develop techniques to quantify and directly measure the evolution of carbon black agglomerates in shear flow. A particular need is the ability to resolve spatial heterogeneity on the agglomerate length scale, which spans 100 nm–100 μm, in steady and transient flow. This is particularly challenging for existing experiments. Traditional rheo-optical techniques are restricted to relatively slow flows. However, counter-rotating plates [62-64] permit access to a stagnation plane in the middle of the gap that permits the examination of structural changes of soft materials under simple shear, but with no translation in the laboratory reference frame. Challenges remain as these techniques cannot yet penetrate through optically dense samples, like carbon black suspensions, with the required resolution. Small angle neutron and X-ray scattering are also promising tools for evaluating structure and dynamics on these length scales. However, current instruments with the necessary spatial resolution are line-collimated, which severely limits information about anisotropy, heterogeneity, and orientation. Point collimated ultra-small angle X-ray scattering (USAXS) [65] and very-small angle neutron scattering (VSANS) [43] measurements in principle have access to the necessary spatial resolution, but the collimation of these instruments needs to be improved in order to access larger length scales $(>1\mu m)$.

In many ways simulations are outpacing experiments [37, 38, 45]. Accelerated Stokesian dynamics [66, 67] are making accurate computations of many thousands of particles in flow routine. Because they accurately and efficiently compute realistic hydrodynamic interactions between the particles, these simulation tools provide a way to computationally access quantities experiments cannot. A recent review [68] summarizes succinctly the differences between various computational tools applied to colloidal suspensions. Developing quantitative matching between information that is easy to access in simulations and experimentally accessible information will likely bridge the gap in existing measurement capabilities. Extending these measurements and simulations to predictive constitutive models that can be used to capture realistic process flows remains an important challenge that must be overcome. Incorporating advanced computational tools including neural networks [69] and machine learning may make this process computationally more efficient in the future.

Finally, in many emerging applications where carbon black suspensions are found, their electrical properties are particularly important. Rheo-electric measurements have emerged as a powerful tool to not only quantify how the imposition of flow modifies the electrical properties of the suspension, but also to characterize the performance of flowing electrochemical systems that incorporate carbon black as a conductive additive. Rheo-electric measurements of carbon black suspensions were pioneered by Mewis et al. [70], where they showed that the electrical conductivity is highly sensitive to the shear intensity. Mewis et al. speculated that the imposition of shear induced a complex microstructural change, which resulted in a nontrivial correlation between the electric properties and the rheology. They extended this work [71] to interrogate the dynamics of carbon black in flow and found that the electrical response originated from hopping conduction between carbon black agglomerates. Amari et al. [72] similarly used rheo-electric measurements to study shear thinning of carbon black suspensions in linseed oil and found a direct correlation between the conductivity of the suspension and its viscosity, implying a deep microstructural connection between the two properties. More recent work has focused on transient rheo-electric measurements. For example, Helal et al. [24] studied the evolution conductivity of carbon black gels in mineral oil cessation of shear at different ramp rates. They found a direct correlation between the rate of cessation, the resulting modulus, and the conductivity of the quiescent gel. They speculated that slowing the ramp rate caused topological rearrangement of the network structure affecting both the mechanical strength of the gel and its ability to transport charge. Recently, Liu et al. [73] demonstrated that the dielectric strength obtained from simultaneous rheo-electric measurements can serve as a proxy to the carbon black agglomerate size under flow. In addition to probing the structure of carbon black, rheo-electric measurements have also been successfully used to evaluate the performance of flowing electrochemical systems [8, 23], enabling the fast optimization of these systems by tuning the formulations and operating conditions. Enhanced understanding of the underlying physics of electron transport in these suspensions is needed if rheo-electric properties are used to predict process-property relationships in emerging applications. For example, in the manufacturing of solid-state energy storage systems slurries containing, carbon blacks are utilized. These energy storage systems, such as lithium-ion battery [74] and fuel cell [75] electrodes, have a process-dependent microstructure that needs to be sensitively controlled to achieve high performance. Characterizing both the rheological and electrical properties of electrode slurries may be used to the predictions of processed electrodes’ microstructure and electric properties. If done accurately, rheo-electric measurements promise to accelerate the speed of optimizing the processing conditions of these energy-storage systems from a fundamental understanding of materials properties.

5 Conclusion

In summary, the rheology of carbon black suspensions continues to be a topic of intense interest as the behavior is both complex and relevant to existing and emerging applications in energy storage. From the past 3 decades, a clear picture has emerged that links the underlying microstructure of these suspensions to their macroscopic behavior in flow. In particular, the suspension viscosity is extremely sensitive to the size and fractal dimension of the agglomerates, which can change during rheological tests. In all cases, the evolution of microstructure can be predicted using the Mason number, a dimensionless balance between the hydrodynamic forces acting to break the agglomerates apart and the cohesive forces holding them together. At low shear intensity, the Mason number predicts the formation of stable and unstable vorticity-aligned structure, while at high shear intensity, carbon black agglomerates undergo self-similar breakup and the Mason number predicts the agglomerate size. There are further opportunities for new experiments to probe both spatial anisotropy of the agglomerates in flow, currently inaccessible to existing experiments. Simulations will be particularly relevant therefore, in the near term to filling the gap left by experiments.

Author contributions

JR, QL, and PR contributed to conception and design of the review. All authors contributed to the article and approved the submitted version.

Funding

QL was funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Energy Frontier Research Centers program under Award No. DE-SC-0022119. QL acknowledged that this research was supported in part by an appointment to the Oak Ridge National Laboratory GRO Program, sponsored by the U.S. Department of Energy and administered by the Oak Ridge Institute for Science and Education. PR was funded by the National Science Foundation under Grant Nos. CBET-2047365 and DMR-1720139-006. JR recieved partial funding from the National Science Foundation and the Department of Energy.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Used with permission of Springer Nature, from V. Trappe et al., Nature, 411, 772—775; permission conveyed through Copyright Clearance Center, Inc.

²Reprinted Figure 2 with permission from V. Trappe et al, Phys Rev letter, 85, 449—452, 2000. Copyright 2000 by the American Physical Society.

³This material is used with permission from author J. Hipp; Structure, rheology, and electrical conductivity of high-structured carbon black suspensions; 2021. Further reproduction, distribution or transmission is prohibited, except as otherwise permitted by law.

⁴Used with permission of Royal Society of Chemistry, from Rheopexy and tunable yield stress of carbon black suspensions, G. Ovarlez et al., 9, 2013; permission conveyed through Copyright Clearance Center, Inc.

⁵Reprinted with permission from Structure-property relationships of sheared carbon black suspensions determined by simultaneous rheological and neutron scattering measurements, J. Hipp et al., J Rheology, 63. Copyright 2019, The Society of Rheology.

⁶Reprinted with permission from Direct measurements of the microstructural origin of shear-thinning in carbon black suspensions, J. Hipp et al., J Rheology, 65. Copyright 2021, The Society of Rheology.

⁷Reprinted Figure 7 with permission from C. Osuji et al., Phys Rev E, 77, 060402, 2008. Copyright 2008 by the American Physical Society.

⁸Reprinted with permission from Large scale anisotropies in sheared colloidal gels, Z. Varga et al., J Rheology, 62, 2018. Copyright 2018, The Society of Rheology.

⁹Used with permission of Royal Society of Chemistry, from Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system, C. Osuji et al., 4, 2008; permission conveyed through Copyright Clearance Center, Inc.

¹⁰Reprinted with permission from Structure-property relationships of sheared carbon black suspensions determined by simultaneous rheological and neutron scattering measurements, J. Hipp et al., J Rheology, 63. Copyright 2019, The Society of Rheology.

¹¹Used with permission of Royal Society of Chemistry, from Shear-induced structuration of confined carbon black gels: steady-state features of vorticity-aligned flocs, V. Grenard et al., 7, 2011; permission conveyed through Copyright Clearance Center, Inc.

References

1. Spahr ME, Goers D, Leone A, Stallone S, Grivei E. Development of carbon conductive additives for advanced lithium ion batteries. J Power Sourc (2011) 196:3404–13. doi:10.1016/j.jpowsour.2010.07.002

CrossRef Full Text | Google Scholar

2. Banham D, Ye S. Current status and future development of catalyst materials and catalyst layers for proton exchange membrane fuel cells: An industrial perspective. ACS Energ Lett (2017) 2:629–38. doi:10.1021/acsenergylett.6b00644

CrossRef Full Text | Google Scholar

3. Camargo JR, Orzari LO, Araújo DAG, de Oliveira PR, Kalinke C, Rocha DP, et al. Development of conductive inks for electrochemical sensors and biosensors. Microchemical J (2021) 164:105998. doi:10.1016/j.microc.2021.105998

CrossRef Full Text | Google Scholar

4. Fan Y, Fowler GD, Zhao M. The past, present and future of carbon black as a rubber reinforcing filler – A review. J Clean Prod (2020) 247:119115. doi:10.1016/j.jclepro.2019.119115

CrossRef Full Text | Google Scholar

5. Richards JJ, Hipp JB, Riley JK, Wagner NJ, Butler PD. Clustering and percolation in suspensions of carbon black. Langmuir (2017) 33:12260–6. doi:10.1021/acs.langmuir.7b02538

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hatzell KB, Hatzell MC, Cook KM, Boota M, Housel GM, McBride A, et al. Effect of oxidation of carbon material on suspension electrodes for flow electrode capacitive deionization. Environ Sci Tech (2015) 49:3040–7. doi:10.1021/es5055989

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sobolev AA. Structural, rheological, and electrical properties of suspensions of carbon black with different oxidation degrees in polar and apolar dielectric dispersion media. Colloid J (2015) 77:341–52. doi:10.1134/S1061933X15030175

CrossRef Full Text | Google Scholar

8. Ramos PZ, Call CC, Simitz LV, Richards JJ. Evaluating the rheo-electric performance of aqueous suspensions of oxidized carbon black. J Colloid Interf Sci (2023) 634:379–87. doi:10.1016/j.jcis.2022.12.017

CrossRef Full Text | Google Scholar

9. Kraytsberg A, Ein-Eli Y. Conveying advanced li-ion battery materials into practice the impact of electrode slurry preparation skills. Adv Energ Mater (2016) 6:1600655. doi:10.1002/aenm.201600655

CrossRef Full Text | Google Scholar

10. Wang M, Park JH, Kabir S, Neyerlin KC, Kariuki NN, Lv H, et al. Impact of catalyst ink dispersing methodology on fuel cell performance using in-situ x-ray scattering. ACS Appl Energ Mater (2019) 2:6417–27. doi:10.1021/acsaem.9b01037

CrossRef Full Text | Google Scholar

11. Pollet BG, Goh JT. The importance of ultrasonic parameters in the preparation of fuel cell catalyst inks. Electrochimica Acta (2014) 128:292–303. doi:10.1016/j.electacta.2013.09.160

CrossRef Full Text | Google Scholar

12. Trappe V, Prasad V, Cipelletti L, Segre PN, Weitz DA. Jamming phase diagram for attractive particles. Nature (2001) 411:772–5. doi:10.1038/35081021

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Shih W-H, Shih WY, Kim S-I, Liu J, Aksay IA. Scaling behavior of the elastic properties of colloidal gels. Phys Rev A (1990) 42:4772–9. doi:10.1103/physreva.42.4772

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Whitaker KA, Varga Z, Hsiao LC, Solomon MJ, Swan JW, Furst EM. Colloidal gel elasticity arises from the packing of locally glassy clusters. Nat Commun (2019) 10:2237. doi:10.1038/s41467-019-10039-w

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kroy K, Cates ME, Poon WC. Cluster mode-coupling approach to weak gelation in attractive colloids. Phys Rev Lett (2004) 92:148302. doi:10.1103/PhysRevLett.92.148302

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nabizadeh M, Jamali S. Life and death of colloidal bonds control the rate-dependent rheology of gels. Nat Commun (2021) 12:4274. doi:10.1038/s41467-021-24416-x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Trappe V, Weitz DA. Scaling of the viscoelasticity of weakly attractive particles. Phys Rev Lett (2000) 85:449–52. doi:10.1103/physrevlett.85.449

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Dagès N, Bouthier LV, Matthews L, Manneville S, Divoux T, Poulesquen A, et al. Interpenetration of fractal clusters drives elasticity in colloidal gels formed upon flow cessation. Soft Matter (2022) 18:6645–59. doi:10.1039/d2sm00481j

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Legrand G, Manneville S, McKinley GH, Divoux T. Dual origin of viscoelasticity in polymer-carbon black hydrogels: A rheometry and electrical spectroscopy study. Macromolecules (2023) 56:2298–308. doi:10.1021/acs.macromol.2c02068

CrossRef Full Text | Google Scholar

20. Hipp JB. Structure, rheology, and electrical conductivity of high-structured carbon black suspensions. United States: University of Delaware (2020).

Google Scholar

21. Bouthier L-V, Gibaud T. Three length-scales colloidal gels: The clusters of clusters versus the interpenetrating clusters approach. J Rheology (2023) 67:621–33. doi:10.1122/8.0000595

CrossRef Full Text | Google Scholar

22. Donley GJ, Singh PK, Shetty A, Rogers SA, Weitz DA. Elucidating the g overshoot in soft materials with a yield transition via a time-resolved experimental strain decomposition. Proc Natl Academies Sci (2020) 117:21945–52. doi:10.1073/pnas.2003869117

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Youssry M, Madec L, Soudan P, Cerbelaud M, Guyomard D, Lestriez B. Non-aqueous carbon black suspensions for lithium-based redox flow batteries: Rheology and simultaneous rheo-electrical behavior. Phys Chem Chem Phys (2013) 15:14476–86. doi:10.1039/c3cp51371h

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Helal A, Divoux T, McKinley GH. Simultaneous rheoelectric measurements of strongly conductive complex fluids. Phys Rev Appl (2016) 6:064004. doi:10.1103/PhysRevApplied.6.064004

CrossRef Full Text | Google Scholar

25. Dullaert K, Mewis J. Stress jumps on weakly flocculated dispersions: Steady state and transient results. J Colloid Interf Sci (2005) 287:542–51. doi:10.1016/j.jcis.2005.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Hipp JB, Richards JJ, Wagner NJ. Structure-property relationships of sheared carbon black suspensions determined by simultaneous rheological and neutron scattering measurements. J Rheology (2019) 63:423–36. doi:10.1122/1.5071470

CrossRef Full Text | Google Scholar

27. Ovarlez G, Tocquer L, Bertrand F, Coussot P. Rheopexy and tunable yield stress of carbon black suspensions. Soft Matter (2013) 9:5540–9. doi:10.1039/c3sm27650c

CrossRef Full Text | Google Scholar

28. Armstrong MJ, Beris AN, Rogers SA, Wagner NJ. Dynamic shear rheology and structure kinetics modeling of a thixotropic carbon black suspension. Rheologica Acta (2017) 56:811–24. doi:10.1007/s00397-017-1038-8

CrossRef Full Text | Google Scholar

29. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield stress materials in soft condensed matter. Rev Mod Phys (2017) 89:035005. doi:10.1103/RevModPhys.89.035005

CrossRef Full Text | Google Scholar

30. Barnes HA. Thixotropy a review. J Non-Newtonian Fluid Mech (1997) 70:1–33. doi:10.1016/s0377-0257(97)00004-9

CrossRef Full Text | Google Scholar

31. Nelson AZ, Ewoldt RH. Design of yield-stress fluids: A rheology-to-structure inverse problem. Soft Matter (2017) 13:7578–94. doi:10.1039/c7sm00758b

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Mewis J, Wagner NJ. Thixotropy. Adv Colloid Interf Sci (2009) 147-148:214–27. doi:10.1016/j.cis.2008.09.005

CrossRef Full Text | Google Scholar

33. Coussot P, Nguyen QD, Huynh HT, Bonn D. Viscosity bifurcation in thixotropic, yielding fluids. J Rheology (2002) 46:573–89. doi:10.1122/1.1459447

CrossRef Full Text | Google Scholar

34. Gibaud T, Frelat D, Manneville S. Heterogeneous yielding dynamics in a colloidal gel. Soft Matter (2010) 6:3482–8. doi:10.1039/c000886a

CrossRef Full Text | Google Scholar

35. Dullaert K, Mewis J. A structural kinetics model for thixotropy. J Non-Newtonian Fluid Mech (2006) 139:21–30. doi:10.1016/j.jnnfm.2006.06.002

CrossRef Full Text | Google Scholar

36. Larson RG, Wei Y. A review of thixotropy and its rheological modeling. J Rheology (2019) 63:477–501. doi:10.1122/1.5055031

CrossRef Full Text | Google Scholar

37. Harshe YM, Lattuada M. Breakage rate of colloidal aggregates in shear flow through stokesian dynamics. Langmuir (2012) 28:283–92. doi:10.1021/la2038476

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Harshe YM, Lattuada M. Universal breakup of colloidal clusters in simple shear flow. J Phys Chem B (2016) 120:7244–52. doi:10.1021/acs.jpcb.6b03220

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Rooij RD, Potanin AA, Ende DVD, Mellema J. Steady shear viscosity of weakly aggregating polystyrene latex dispersions. J Chem Phys (1993) 99:9213–23. doi:10.1063/1.465537

CrossRef Full Text | Google Scholar

40. Potanin AA, Rooij RD, Ende DVD, Mellema J. Microrheological modeling of weakly aggregated dispersions. J Chem Phys (1995) 102:5845–53. doi:10.1063/1.469317

CrossRef Full Text | Google Scholar

41. Sonntag RC, Russel WB. Structure and breakup of flocs subjected to fluid stresses: I. Shear experiments. J Colloid Interf Sci (1986) 113:399–413. doi:10.1016/0021-9797(86)90175-X

CrossRef Full Text | Google Scholar

42. Osuji CO, Weitz DA. Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system. Soft Matter (2008) 4:1388–92. doi:10.1039/b716324j

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Hipp JB, Richards JJ, Wagner NJ. Direct measurements of the microstructural origin of shear-thinning in carbon black suspensions. J Rheology (2021) 65:145–57. doi:10.1122/8.0000089

CrossRef Full Text | Google Scholar

44. Eberle AP, Martys N, Porcar L, Kline SR, George WL, Kim JM, et al. Shear viscosity and structural scalings in model adhesive hard-sphere gels. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2014) 89:050302. doi:10.1103/PhysRevE.89.050302

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Varga Z, Swan JW. Large scale anisotropies in sheared colloidal gels. J Rheology (2018) 62:405–18. doi:10.1122/1.5003364

CrossRef Full Text | Google Scholar

46. Min Kim J, Eberle APR, Kate Gurnon A, Porcar L, Wagner NJ. The microstructure and rheology of a model, thixotropic nanoparticle gel under steady shear and large amplitude oscillatory shear (Laos). J Rheology (2014) 58:1301–28. doi:10.1122/1.4878378

CrossRef Full Text | Google Scholar

47. Jariwala S, Wagner NJ, Beris AN. A thermodynamically consistent, microscopically-based, model of the rheology of aggregating particles suspensions. Entropy (2022) 24:717. doi:10.3390/e24050717

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Mwasame PM, Beris AN, Diemer RB, Wagner NJ. A constitutive equation for thixotropic suspensions with yield stress by coarse-graining a population balance model. AIChE J (2017) 63:517–31. doi:10.1002/aic.15574

CrossRef Full Text | Google Scholar

49. Wang Y, Ewoldt RH. New insights on carbon black suspension rheology—Anisotropic thixotropy and antithixotropy. J Rheology (2022) 66:937–53. doi:10.1122/8.0000455

CrossRef Full Text | Google Scholar

50. Negi AS, Osuji CO. Physical aging and relaxation of residual stresses in a colloidal glass following flow cessation. J Rheology (2010) 54:943–58. doi:10.1122/1.3460800

CrossRef Full Text | Google Scholar

51. Potanin A. Thixotropy and rheopexy of aggregated dispersions with wetting polymer. J Rheology (2004) 48:1279–93. doi:10.1122/1.1807844

CrossRef Full Text | Google Scholar

52. Narayanan A, Mugele F, Duits MH. Mechanical history dependence in carbon black suspensions for flow batteries: A rheo-impedance study. Langmuir (2017) 33:1629–38. doi:10.1021/acs.langmuir.6b04322

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Kawaguchi M, Okuno M, Kato T. Rheological properties of carbon black suspensions in a silicone oil. Langmuir (2001) 17:6041–4. doi:10.1021/la010560r

CrossRef Full Text | Google Scholar

54. Osuji CO, Kim C, Weitz DA. Shear thickening and scaling of the elastic modulus in a fractal colloidal system with attractive interactions. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2008) 77:060402. doi:10.1103/PhysRevE.77.060402

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Grenard V, Divoux T, Taberlet N, Manneville S. Timescales in creep and yielding of attractive gels. Soft Matter (2014) 10:1555–71. doi:10.1039/c3sm52548a

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Brown E, Forman NA, Orellana CS, Zhang H, Maynor BW, Betts DE, et al. Generality of shear thickening in dense suspensions. Nat Mater (2010) 9:220–4. doi:10.1038/nmat2627

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Wolthers W, van den Ende D, Duits MHG, Mellema J. The viscosity and sedimentation of aggregating colloidal dispersions in a Couette flow. J Rheology (1996) 40:55–67. doi:10.1122/1.550784

CrossRef Full Text | Google Scholar

58. Acrivos A, Fan X, Mauri R. On the measurement of the relative viscosity of suspensions. J Rheology (2002) 38:1285–96. doi:10.1122/1.550544

CrossRef Full Text | Google Scholar

59. Das M, Chambon L, Varga Z, Vamvakaki M, Swan JW, Petekidis G. Shear driven vorticity aligned flocs in a suspension of attractive rigid rods. Soft Matter (2021) 17:1232–45. doi:10.1039/d0sm01576h

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Grenard V, Taberlet N, Manneville S. Shear-induced structuration of confined carbon black gels: Steady-state features of vorticity-aligned flocs. Soft Matter (2011) 7:3920–8. doi:10.1039/c0sm01515f

CrossRef Full Text | Google Scholar

61. Varga Z, Grenard V, Pecorario S, Taberlet N, Dolique V, Manneville S, et al. Hydrodynamics control shear-induced pattern formation in attractive suspensions. Proc Natl Acad Sci USA (2019) 116:12193–8. doi:10.1073/pnas.1901370116

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Collin V, Boudimbou I, Peuvrel-Disdier E. New insights in dispersion mechanisms of carbon black in a polymer matrix under shear by rheo-optics. J Appl Polym Sci (2013) 127:2121–31. doi:10.1002/app.37769

CrossRef Full Text | Google Scholar

63. Liu W, Tarabukina E, Navard P. Influence of the elasticity of cellulose solutions on the dispersion of carbon black agglomerates. Cellulose (2013) 20:1679–90. doi:10.1007/s10570-013-9969-4

CrossRef Full Text | Google Scholar

64. Yearsley KM, Mackley MR, Chinesta F, Leygue A. The rheology of multiwalled carbon nanotube and carbon black suspensions. J Rheology (2012) 56:1465–90. doi:10.1122/1.4751871

CrossRef Full Text | Google Scholar

65. Ehrburger-Dolle F, Hindermann-Bischoff M, Livet F, Bley F, Rochas C, Geissler E. Anisotropic ultra-small-angle x-ray scattering in carbon black filled polymers. Langmuir (2001) 17:329–34. doi:10.1021/la001184y

CrossRef Full Text | Google Scholar

66. Fiore AM, Swan JW. Fast stokesian dynamics. J Fluid Mech (2019) 878:544–97. doi:10.1017/jfm.2019.640

CrossRef Full Text | Google Scholar

67. Elfring GJ, Brady JF. Active stokesian dynamics. J Fluid Mech (2022) 952:A19. doi:10.1017/jfm.2022.909

CrossRef Full Text | Google Scholar

68. Park JD, Myung JS, Ahn KH. A review on particle dynamics simulation techniques for colloidal dispersions: Methods and applications. Korean J Chem Eng (2016) 33:3069–78. doi:10.1007/s11814-016-0229-9

CrossRef Full Text | Google Scholar

69. Mahmoudabadbozchelou M, Caggioni M, Shahsavari S, Hartt WH, Em Karniadakis G, Jamali S. Data-driven physics-informed constitutive metamodeling of complex fluids: A multifidelity neural network (MFNN) framework. J Rheology (2021) 65:179–98. doi:10.1122/8.0000138

CrossRef Full Text | Google Scholar

70. Mewis J, De Groot L, Helsen J. Dielectric behaviour of flowing thixotropic suspensions. Colloids Surf (1987) 22:249–69. doi:10.1016/0166-6622(87)80225-1

CrossRef Full Text | Google Scholar

71. Genz U, Helsen JA, Mewis J. Dielectric spectroscopy of reversibly flocculated dispersions during flow. J Colloids Interf Sci (1994) 165:212–20. doi:10.1006/jcis.1994.1221

CrossRef Full Text | Google Scholar

72. Amari T, Watanabe K. Flow properties and electrical conductivity of carbon black–linseed oil suspension. J Rheology (1990) 34:207–21. doi:10.1122/1.550124

CrossRef Full Text | Google Scholar

73. Liu Q, Richards JJ. Rheo-electric measurements of carbon black suspensions containing polyvinylidene difluoride in N-methyl-2-pyrrolidone. J Rheology (2023) 67:647–59. doi:10.1122/8.0000615

CrossRef Full Text | Google Scholar

74. SarakaSamantha RMLM, TangAlvarez MHNJ, Alvarez NJ. Correlating processing conditions to short- and long-range order in coating and drying lithium-ion batteries. ACS Appl Energ Mater. (2020) 3:11681–9. doi:10.1021/acsaem.0c01305

CrossRef Full Text | Google Scholar

75. Pan W, Chen Z, Yao D, Chen X, Wang F, Dai G. Microstructure and macroscopic rheology of microporous layer nanoinks for pem fuel cells. Chem Eng Sci (2021) 246:117001. doi:10.1016/j.ces.2021.117001

CrossRef Full Text | Google Scholar