Status of experimental knowledge on the unbound nucleus 13Be

The structure of the unbound nucleus ¹³Be is important for understanding the Borromean, two-neutron halo nucleus ¹⁴Be. The experimental studies conducted over the last four decades are reviewed in the context of the beryllium chain of isotopes and some significant theoretical studies. The focus of this paper is the comparison of new data from a ¹²Be(d,p) reaction in inverse kinematics, which was analyzed using Geant4 simulations and a Bayesian fitting procedure, with previous measurements. Two possible scenarios to explain the strength below 1 MeV above the neutron separation energy were proposed in that study: a single p-wave resonance or a mixture of an s-wave virtual state with a weaker p- or d-wave resonance. Comparisons of recent invariant mass and the (d,p) experiments show good agreement between the transfer measurement and the two most recent high-energy nucleon removal measurements.

1 Introduction

With just four protons, the particle-bound members of the beryllium chain of isotopes stretch from ⁷Be (N/Z = 0.75) on the proton-rich side of stability to ¹⁴Be (N/Z = 2.5), the two-neutron halo on the neutron-rich side. Adding a single neutron to ⁷Be results in the ⁸Be system of two α particles which is unbound by only 92 keV. Adding a second neutron produces ⁹Be, the only beryllium isotope that is stable against β decay. This stability is a product of two phenomena that occur across the beryllium chain of isotopes, molecular structures [1]; [2]; [3], and core excitation [4]. The molecular structure is closely connected to the Borromean nature of ⁹Be; the three-body system of α − α − n is bound despite the two-body subsystems, α − n and α − α, being unbound. The delocalized neutron in ⁹Be can be viewed as being exchanged between α particles [5]. Analogous to atomic molecules, the neutron in the ground state of ⁹Be is well understood as being in a π-type orbital, whereas the first excited state may be better described with a neutron in the σ-type orbital. These molecular orbits are intimately related to the prolate nature of the two-α cluster structure [6].

The cluster structure appears to weaken in ¹⁰Be, as evidenced by the reduced size of its charge radius [7]; [8]. The two-α plus two-neutron structure is more apparent in excited states closer to the α and neutron separation energies, such as the isomeric second 0⁺ state at E_x = 6.179 MeV, which has a small γ branch to the more compact first 2⁺ state [5].

Adding another neutron makes the archetypal one-neutron halo nucleus ¹¹Be. A 16% core-excited component in the ground state of ¹¹Be was required to reproduce the results from the ¹¹Be(p,d)¹⁰Be reaction [9]. This is less than that of ⁹Be, where the core-excited component was calculated as approximately half of the ground-state wave function [4]. Additionally, dynamical core excitation needs to be included in the calculations of both transfer [10] and breakup [11] reactions.

The parity inversion in ¹¹Be, where the 1/2⁺ ground state decreases 320 keV below the only other bound state with J^π = 1/2⁻, along with larger collectivity in ¹⁰Be, led to the questioning about the robustness of the N = 8 shell closure at ¹²Be. Using a three-body model with core excitation, Nunes et al. were able to show an increased sphericity in the core ¹⁰Be within ¹²Be compared to that observed in ¹¹Be [12]. This in turn led to greater mixing between p- and sd-shell valence neutron states and a melting of the N = 8 shell closure. The coupling of a d-wave neutron with the excited 2^{+ 10}Be core severely restricts the formation of a halo in ¹²Be [13]. Notably, ¹²Be is not Borromean, as the n-¹⁰Be system is bound but is still well described by three-body models.

The N = 10 isotope ¹⁴Be presents the heaviest particle-stable beryllium isotope. The naive shell model would predict a d_5/2-dominated ground-state wave function for ¹⁴Be. However, with the level inversion seen in the other neutron-rich beryllium isotopes, some low-lying s_1/2 strength is expected. With two neutrons in the halo and with significant ℓ > 0 components of the wave function, the halo of ¹⁴Be is much more contained than that of ¹¹Be, despite being closer to the drip line. It would seem natural to study ¹⁴Be in a three-body model, with ¹²Be as the core and two valence neutrons [14]; [15]. Thompson and Zhukov found that adding an s-wave virtual state below the well-known ${\frac{5}{2}}^{+}$ state bound ¹³Be, in contradiction to its non-observance in fragmentation reactions. Reducing the energy, i.e., increasing the scattering length, of the virtual state resulted in the binding energy of ¹⁴Be being too low. The three-body approach of Descouvemont found that only 66% of the ground-state wave function of ¹⁴Be could be described as ¹²Be +n + n [14]. Labiche et al. [16], using the model of Vinh Mau and Pacheco [17], found that assuming a ${\frac{1}{2}}^{-}$ ground state for ¹³Be, consistent with the melting of the N = 8 shell closure observed in ¹¹Be and ¹⁰Li, could reproduce the measured properties of ¹⁴Be.

Beyond the neutron drip line, ¹⁵Be has been observed to decay to ¹²Be through unbound states in ¹⁴Be [18]. The last isotope to be observed is ¹⁶Be, which is bound with respect to one neutron emission, but unbound to the emission of two neutrons [19]. The two neutrons from the decay were observed in a small emission angle.

2 The unbound nucleus ¹³Be

Theoretical studies of ¹³Be have used the shell model [20] or a potential model [21], the Nilsson model [22], microscopic cluster models [23], antisymmetrized molecular dynamics [24], and relativistic mean-field theory [25]. As shown in Table 1, with the exception of the earliest work, the calculations agree on the existence of a 5/2⁺ resonance between 2 and 2.5 MeV above the neutron threshold. However, the location of the ground state relative to the neutron threshold is disputed, as is the parity of the ground state. There have also been reaction theory studies of, and comparing to, experimental data, for example, the work of Bonaccorso [26] and references therein. Casal et al. [27] used a transfer to the continuum model including deformation in the ¹²Be + n potential, following the prescription in Thompson et al. [28], to interpret the data obtained from Corsi et al. [29]. This work indicates a p-wave resonance at between 0.4 and 0.5 MeV above the threshold.

TABLE 1

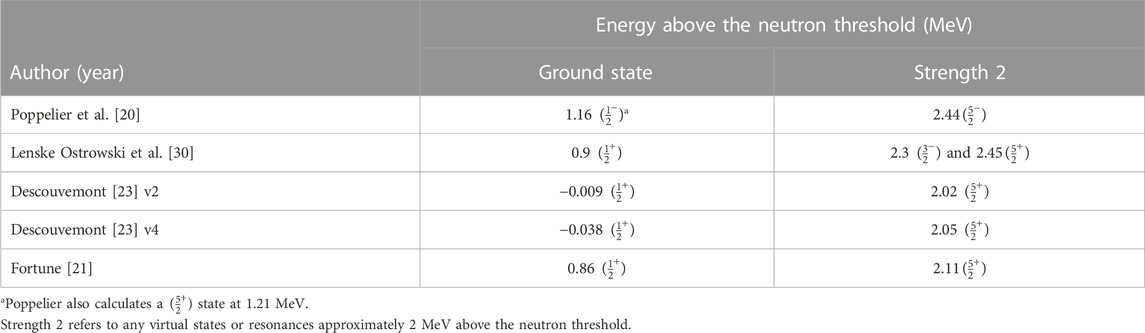
TABLE 1. Energy (and J^π assignments) of low-lying states in ¹³Be according to a selection of theoretical studies.

There have been many experiments on ¹³Be since the first discovery of a resonance [31] at 1.8 MeV above the neutron threshold. Some of the experimental results from the last four decades are shown in Table 2. The reactions used to probe the structure of halo nuclei can be broadly divided into missing mass and invariant mass techniques. Transfer reactions, where excitation energies are found from the reaction Q-values, fall into the missing mass category. Knockout, breakup, and Coulomb dissociation, where the final state is reconstructed from two or more fragments, represent invariant mass techniques. In the case of ¹³Be, the fragments are ¹²Be and a neutron. The early measurements, e.g., [31]; [30]; [32]; and [33], mostly populated ¹³Be through multinucleon transfer reactions. An exception is the ¹²Be(d,p) experiment performed in [34] at RIKEN. At a beam energy of 55 AMeV, the conditions are not well matched to observe low ℓ transfer, and the carbon in the target largely masked any structure below 2 MeV. Indeed, none of the experiments before the fragmentation experiment at the National Superconducting Cyclotron Laboratory [35] revealed any structure below the ${\frac{5}{2}}^{+}$ resonance at 2 MeV.

TABLE 2

TABLE 2. Previous studies of the low-lying structure of ¹³Be, up to approximately 2.5 MeV above the neutron threshold.

Most of the more recent experiments used invariant mass techniques at energies between 40 and 400 AMeV. Of these, all except one employed nucleon removal, either a neutron from ¹⁴Be [37]; [38]; [39]; and [29] or a proton from ¹⁴B [36]; [40]; and [42]. In [41], a nucleon exchange reaction was used to populate unbound states in ¹³Be from a ¹³B beam. Spectra from invariant mass methods contain information relating to the initial state of the target (the beam in an inverse kinematics reaction) and reflect final state interactions between outgoing fragments. There can also be complications relating to the reaction mechanism, which can be diffractive or absorptive.

3 Recent transfer reaction measurement

The most recent experiment, [44]; [43], used a ¹²Be beam from ISAC-II and the solid deuterium target and detector system IRIS [45] to perform a one-neutron transfer reaction. The advantages of using the (d,p) reaction at low energy (E_beam = 9.5 AMeV) are that the energy and angular momentum-matching conditions are ideal for populating low-ℓ, near-threshold states. The non-Gaussian experimental response caused by increasingly poor resolution for lower-energy protons exiting the solid deuterium target necessitated an analysis technique that included both simulation and Bayesian fitting methods, as demonstrated in [46]. The initial analysis included the ${\frac{5}{2}}^{+}$ resonance at approximately 2 MeV and a single s-, p-, or d-wave virtual state or resonance closer to the threshold, referenced as “single” in Table 2. Additionally, mixes of two out of s-, p-, and d-wave strengths were included to allow for two resonances or a resonance and a virtual state below the 2 MeV d-wave resonance, referenced as “mixed” in Table 2. The fits with the lowest χ²/NDF for the region below 1 MeV in resonance energy, for both the single and mixed cases, are the ones shown in Table 2. The rest of this paper relates to the findings in [43], including the comparisons with recent invariant mass measurements [38]; [40]; [42]; [29].

A comparison of the transfer measurement (for the case assuming a single state below 2 MeV) with some recent invariant mass measurement results is shown in Figure 1. Discrepancies clearly persist in the low-lying structure of ¹³Be, even between recent measurements. The ${\frac{5}{2}}^{+}$ state is in a similar position in all the measurements; however, the width is much larger according to the works in [38] and [40]. Similarly, in [40] and [42], a broad ${\frac{1}{2}}^{+}$ structure below 1 MeV was shown, whereas [38] and [29] agree on an s-wave virtual state. There is some consistency in the presence of a p-wave resonance of approximately 0.5 MeV, with the exception of [40]. This resonance is noticeably narrower (Γ = 0.11 MeV) in the work in [43].

FIGURE 1

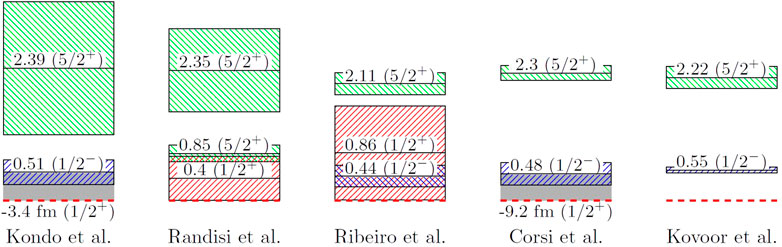
FIGURE 1. Comparison of the low-lying structure in ¹³Be according to recent invariant mass measurements [38]; [40]; [42]; [29] and a recent transfer reaction measurement [43]. Only the case with a pure p-wave is shown for [43], as the position of the waves in the mixtures could not be resolved. Red, blue, and green lines depict s, p, and d waves, respectively. Red-dashed lines show the threshold. Gray-shaded region shows the presence of a virtual state.

The mixed case in [43] is not shown in Figure 1 as the ordering of the s- and p-wave strength cannot be extracted from the data, only the relative intensities. The lowest χ²/NDF was found for a mixture of $s-\left(70_{-6}^{+8}\%\right)$ and $p-\left(30_{-8}^{+6}\%\right)$ wave strengths. It should be noticed that the χ²/NDF (3.87) for the $s-\left(93_{-2}^{+2}\%\right)$ and $d-\left(7_{-2}^{+2}\%\right)$ wave mixture below 1 MeV is similar to that for the s- and p-wave mixture (3.32). Therefore, the initial conclusion of the study was that the near-threshold strength was either a pure p wave or a mixture dominated by an s-wave strength, with a weaker resonance of either a p- or d-wave nature.

To make a more robust comparison between the recent invariant-mass measurements and the transfer reaction, the resonance parameters extracted from [38], [29], [40], and [42] were used as inputs for the Geant4 [47] simulation, as shown in Figure 2. The centroid energies and widths from the analyses were used, and the relative intensities of the resonances and virtual states were fitted as free parameters. A relatively poor fit to the data from the ¹²Be(d,p) reaction experiment was produced from the simulations using resonance parameters from [38] (χ²/NDF = 5.51). Using the parameters from [40] provided a better fit (χ²/NDF = 3.47), and those from [39] (not shown) provided a fit with χ²/NDF = 3.18. The parameters that provided the best fit from the literature were those from [29] (χ²/NDF = 2.62), closely followed by those from [42] (χ²/NDF = 2.76). These can all be compared to the Bayesian fit of the data with a single p-wave resonance along with the well-known d-wave resonance of approximately 2 MeV. This fit allowed the locations and widths of the two resonances to vary along with the intensities. The parameters shown in Table 2 resulted in a χ²/NDF of 2.02. The single p wave below the 2 MeV ${\frac{5}{2}}^{+}$ resonance is the scenario that best agrees with these data. This dominance of p-wave strength near the particle threshold is in agreement with the results of [27].

FIGURE 2

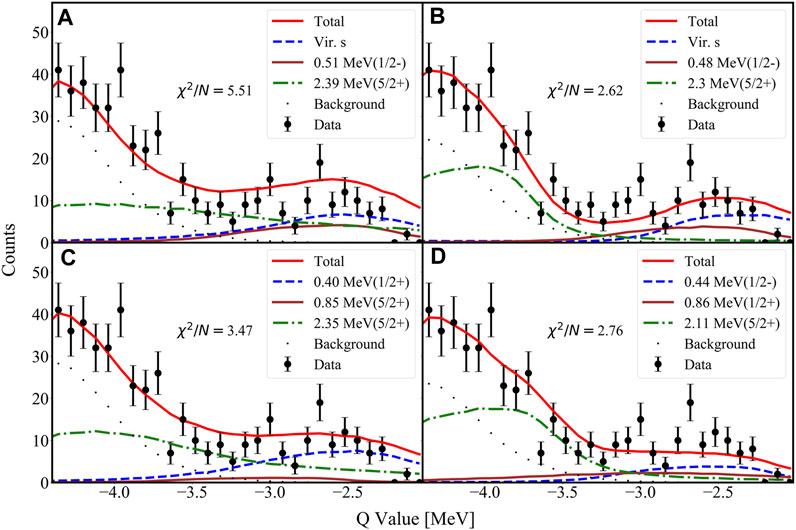
FIGURE 2. Data fitted with Geant4 simulations with energy and widths obtained from (A) [38], (B) [29], (C) [40], and (D) [42]. Amplitudes of the states were used from the angular distributions. Global fit is shown as the red line, and the background is denoted as black dots. Lowest-lying strength is shown as a blue-dashed line irrespective of its nature. Higher-lying states are depicted as solid brown and green dot–dashed lines.

4 Summary

The beryllium chain of isotopes displays various clustering phenomena including molecular structures and one- and two-neutron halos in ¹¹Be and ¹⁴Be, respectively. The isotope ¹³Be is an unbound subsystem of the Borromean nucleus ¹⁴Be. Its structure has been investigated experimentally for 40 years using both missing mass and invariant mass techniques. However, with the exception of the 2 MeV ${\frac{5}{2}}^{+}$ resonance, the low-lying structure is still disputed. A new single-neutron transfer reaction experiment has brought new data and a new analysis technique involving Geant4 simulations and a Bayesian fitting routine. The best fit of the Q-value data was obtained with a narrow 0.55 MeV p-wave resonance and the d-wave resonance located at 2.22 MeV. Adding either a virtual state or a second resonance below 1 MeV produced somewhat poorer fits (χ²/NDF = 3.0–3.4) that were dominated by the s-wave contribution (61%–89%) with a small p-wave (39%) or d-wave (11%) resonance. Using the resonance parameters from either [29] or [42] produced better fits to the new data from the literature. The literature resonance parameters producing poorer fits were those with a broader ${\frac{5}{2}}^{+}$ resonance [38]; [40].

Author contributions

KJ was the spokesperson for the new ¹²Be + ²H experiment and wrote the first draft of this manuscript. JK analyzed the data and produced the figures from the new ¹²Be + ²H experiment. RK was the co-spokesperson for the new ¹²Be + ²H experiment and was instrumental in the design and running of the experiment. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the U.S. Department of Energy, the Office of Science, the Office of Nuclear Physics under contract Nos DE-FG02-96ER40963 (UTK). The authors are grateful for the support from the NSERC, Canada Foundation for Innovation and Nova Scotia Research and Innovation Trust, and RCNP, the grant-in-aid program of the Japanese government. TRIUMF is supported by a contribution from the National Research Council, Canada.

Acknowledgments

The authors would like to acknowledge the collaborators on the TRIUMF ¹²Be + ²H experiment and the beam delivery team for providing the ¹²Be beam, and DE-AC05-00OR22725 (ORNL), and the U. S. National Science Foundation under Award Numbers PHY-1404218 (Rutgers) and PHY-2011890 (Notre Dame). This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) grant nos 2020R1A2C1005981 and 2016R1A5A1013277. This work was partially supported by STFC grant no. ST/L005743/1 (Surrey).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. von Oertzen W. Two-center molecular states in ⁹B, ⁹Be, ¹⁰Be, and ¹⁰B. Z Phys (1996) 354:37–43. doi:10.1007/s002180050010

CrossRef Full Text | Google Scholar

2. von Oertzen W. Dimers based on the α + α potential and chain states of carbon isotopes. Z Phys (1997) 357:355–65. doi:10.1007/s002180050255

CrossRef Full Text | Google Scholar

3. Seya M, Kohno M, Nagata S. Nuclear binding mechanism and structure of neutron-rich Be and B isotopes by molecular-orbital model. Prog Th Phys (1981) 65:204–23. doi:10.1143/PTP.65.204

CrossRef Full Text | Google Scholar

4. Parfenova Y, Leclercq-Willain C. Hyperfine anomaly in be isotopes in the cluster model and the neutron spatial distribution. Phys Rev C (2005) 72:024312. doi:10.1103/PhysRevC.72.024312

CrossRef Full Text | Google Scholar

5. Freer M, Horiuchi H, Kanada-En’yo Y, Lee D, Meißner U-G. Microscopic clustering in light nuclei. Rev Mod Phys (2018) 90:035004. doi:10.1103/RevModPhys.90.035004

CrossRef Full Text | Google Scholar

6. Canavan R, Freer M. Demonstration of the universality of molecular structures in prolate deformed nuclei. J Phys G (2020) 47:095102. doi:10.1088/1361-6471/ab96b3

CrossRef Full Text | Google Scholar

7. Nörtershäuser W, Tiedemann D, Žáková M, Andjelkovic Z, Blaum K, Bissell ML, et al. Nuclear charge radii of ^7,9,10Be and the one-neutron halo nucleus ¹¹Be. Phys Rev Lett (2009) 102:062503. doi:10.1103/PhysRevLett.102.062503

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Krieger A, Blaum K, Bissell ML, Frömmgen N, Geppert C, Hammen M, et al. Nuclear charge radius of ¹²Be. Phys Rev Lett (2012) 108:142501. doi:10.1103/PhysRevLett.108.142501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fortier S, Pita S, Winfield J, Catford W, Orr N, de Wiele V, et al. Core excitation in ¹¹Be_gs via the p(¹¹Be,¹⁰Be)d reaction. Phys Lett (1999) B461:22–7. doi:10.1016/S0370-2693(99)00825-4

CrossRef Full Text | Google Scholar

10. Deltuva A, Ross A, Norvaišas E, Nunes FM. Role of core excitation in (d, p) transfer reactions. Phys Rev C (2016) 94:044613. doi:10.1103/PhysRevC.94.044613

CrossRef Full Text | Google Scholar

11. Moro AM, Crespo R. Core excitation effects in the breakup of the one-neutron halo nucleus ¹¹be on a proton target. Phys Rev C (2012) 85:054613. doi:10.1103/PhysRevC.85.054613

CrossRef Full Text | Google Scholar

12. Nunes FM, Thompson IJ, Tostevin JA. Core excitation in ¹²Be. Nucl Phys (2002) A703:593–602. doi:10.1016/S0375-9474(01)01667-0

CrossRef Full Text | Google Scholar

13. Nunes FM. Valence pairing, core deformation and the development of two-neutron halos. Nucl Phys (2005) A757:349–59. doi:10.1016/j.nuclphysa.2005.04.005

CrossRef Full Text | Google Scholar

14. Descouvemont P. Halo structure of ¹⁴Be in a microscopic ¹²Be+n+n cluster model. Phys Rev C (1995) 52:704–10. doi:10.1103/PhysRevC.52.704

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Thompson IJ, Zhukov MV. Structure and reactions of the ^12,14Be nuclei. Phys Rev C (1996) 53:708–14. doi:10.1103/PhysRevC.53.708

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Labiche M, Marqués FM, Sorlin O, Vinh Mau N. Structure of ¹³Be and ¹⁴Be. Phys Rev C (1999) 60:027303. doi:10.1103/PhysRevC.60.027303

CrossRef Full Text | Google Scholar

17. Vinh Mau N, Pacheco JC. Structure of the ¹¹Li nucleus. Nucl Phys (1996) A607:163–77. doi:10.1016/0375-9474(96)00246-1

CrossRef Full Text | Google Scholar

18. Spyrou A, Smith JK, Baumann T, Brown BA, Brown J, Christian G, et al. Search for the ¹⁵be ground state. Phys Rev C (2011) 84:044309. doi:10.1103/PhysRevC.84.044309

CrossRef Full Text | Google Scholar

19. Spyrou A, Kohley Z, Baumann T, Bazin D, Brown BA, Christian G, et al. First observation of ground state dineutron decay: ¹⁶Be. Phys Rev Lett (2012) 108:102501. doi:10.1103/PhysRevLett.108.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Poppelier N, Wood L, Glaudemans P. Properties of exotic p-shell nuclei. Phys Lett B (1985) 157:120–2. doi:10.1016/0370-2693(85)91529-1

CrossRef Full Text | Google Scholar

21. Fortune HT. Update on energies and widths in ¹³Be. Phys Rev C (2019) 99:014304. doi:10.1103/PhysRevC.99.014304

CrossRef Full Text | Google Scholar

22. Macchiavelli AO, Crawford HL, Campbell CM, Clark RM, Cromaz M, Fallon P, et al. Analysis of spectroscopic factors in ¹¹Be and ¹²Be in the Nilsson strong-coupling limit. Phys Rev C (2018) 97:011302. doi:10.1103/PhysRevC.97.011302

CrossRef Full Text | Google Scholar

23. Descouvemont P. Evidence for particle stability of ¹³Be in a microscopic cluster model. Phys Lett B (1994) 331:271–5. doi:10.1016/0370-2693(94)91050-2

CrossRef Full Text | Google Scholar

24. Kanada-En’yo Y. Breaking of N=8 magicity in ¹³Be. Phys Rev C (2012) 85:044320. doi:10.1103/PhysRevC.85.044320

CrossRef Full Text | Google Scholar

25. Ren Z, Chen B, Ma Z, Xu G. Level inversion of N=9 isotones in the relativistic mean-field theory. Z Phys A (1997) 357:137–41. doi:10.1007/s002180050228

CrossRef Full Text | Google Scholar

26. Bonaccorso A. Unbound nuclei studied by projectile fragmentation. Physica Scripta (2012) 2012:014008. doi:10.1088/0031-8949/2012/t150/014008

CrossRef Full Text | Google Scholar

27. Casal J, Gómez-Ramos M, Moro A, Corsi A. Exploring continuum structures in reactions with three-body nuclei. J Phys Conf Ser (2020) 1643, 012075. doi:10.1088/1742-6596/1643/1/012075

CrossRef Full Text | Google Scholar

28. Thompson I, Nunes F, Danilin B. FaCE: A tool for three body faddeev calculations with core excitation. Comp Phys Commun (2004) 161:87–107. doi:10.1016/j.cpc.2004.03.007

CrossRef Full Text | Google Scholar

29. Corsi A, Kubota Y, Casal J, Gómez-Ramos M, Moro A, Authelet G, et al. Structure of ¹³Be probed via quasi-free scattering. Phys Lett B (2019) 797:134843. doi:10.1016/j.physletb.2019.134843

CrossRef Full Text | Google Scholar

30. Ostrowski AN, Bohlen HG, Demyanova AS, Gebauer B, Kalpakchieva R, Langner C, et al. Mass spectroscopy of ¹³Be. Z Phys (1992) A343:489–90. doi:10.1007/BF01289828

CrossRef Full Text | Google Scholar

31. Aleksandrov DV, Ganza EA, Glukhov YA. Observation of the isotope ¹³Be in the reaction ¹⁴C(⁷Li, ⁸B). Sov J Nucl Phys (1983) 37:474–5.

Google Scholar

32. von Oertzen W, Bohlen H, Gebauer B, von Lucke-Petsch M, Ostrowski A, Seyfert C, et al. Nuclear structure studies of very neutron-rich isotopes of ⁷⁻⁻¹⁰He, ⁹⁻¹¹Li and ¹²⁻¹⁴Be via two-body reactions. Nucl Phys A (1995) 588:c129–34. Proceedings of the Fifth International Symposium on Physics of Unstable Nuclei. doi:10.1016/0375-9474(95)00111-D

CrossRef Full Text | Google Scholar

33. Belozyorov A, Kalpakchieva R, Penionzhkevich Y, Dlouhý Z, Piskor S, Vincour J, et al. Spectroscopy of ¹³Be. Nucl Phys A (1998) 636:419–26. doi:10.1016/S0375-9474(98)00217-6

CrossRef Full Text | Google Scholar

34. Korsheninnikov A, Nikolskii E, Kobayashi T, Aleksandrov D, Fujimaki M, Kumagai H, et al. Spectroscopy of ¹²Be and ¹³Be using a ¹²Be radioactive beam. Phys Lett B (1995) 343:53–8. doi:10.1016/0370-2693(94)01435-F

CrossRef Full Text | Google Scholar

35. Thoennessen M, Yokoyama S, Hansen PG. First evidence for low lying s-wave strength in ¹³Be. Phys Rev C (2000) 63:014308. doi:10.1103/PhysRevC.63.014308

CrossRef Full Text | Google Scholar

36. Lecouey JL. Experimental studies of unbound neutron-rich nuclei. Few-Body Syst (2004) 34:21–6. doi:10.1007/s00601-004-0029-3

CrossRef Full Text | Google Scholar

37. Simon H, Meister M, Aumann T, Borge M, Chulkov L, Pramanik UD, et al. Systematic investigation of the drip-line nuclei ¹¹Li and ¹⁴Be and their unbound subsystems ¹⁰Li and ¹³Be. Nucl Phys A (2007) 791:267–302. doi:10.1016/j.nuclphysa.2007.04.021

CrossRef Full Text | Google Scholar

38. Kondo Y, Nakamura T, Satou Y, Matsumoto T, Aoi N, Endo N, et al. Low-lying intruder state of the unbound nucleus ¹³Be. Phys Lett B (2010) 690:245–9. doi:10.1016/j.physletb.2010.05.031

CrossRef Full Text | Google Scholar

39. Aksyutina Y, Aumann T, Boretzky K, Borge MJG, Caesar C, Chatillon A, et al. Structure of the unbound nucleus ¹³Be: One-neutron knockout reaction data from ¹⁴Be analyzed in a holistic approach. Phys Rev C (2013) 87:064316. doi:10.1103/PhysRevC.87.064316

CrossRef Full Text | Google Scholar

40. Randisi G, Leprince A, Al Falou H, Orr NA, Marqués FM, Achouri NL, et al. Structure of ¹³Be probed via secondary-beam reactions. Phys Rev C (2014) 89:034320. doi:10.1103/PhysRevC.89.034320

CrossRef Full Text | Google Scholar

41. Marks BR, DeYoung PA, Smith JK, Baumann T, Brown J, Frank N, et al. Population of ¹³Be in a nucleon exchange reaction. Phys Rev C (2015) 92:054320. doi:10.1103/PhysRevC.92.054320

CrossRef Full Text | Google Scholar

42. Ribeiro G, Nácher E, Tengblad O, Díaz Fernández P, Aksyutina Y, Alvarez-Pol H, et al. Structure of ¹³Be studied in proton knockout from ¹⁴B. Phys Rev C (2018) 98:024603. doi:10.1103/PhysRevC.98.024603

CrossRef Full Text | Google Scholar

43. Kovoor J, et al. Structure studies of ¹³Be accepted. Phys Rev C (2023).

Google Scholar

44. Kovoor JM. Study of one-nucleon transfer reactions. Phd dissertation. Knoxville: University of Tennessee (2022).

Google Scholar

45. Kanungo R. Iris: The ISAC charged particle reaction spectroscopy facility for reaccelerated high-energy ISOL beams. Hyperfine Interactions (2014) 225:235–40. doi:10.1007/s10751-013-0904-8

CrossRef Full Text | Google Scholar

46. Hooker J, Kovoor J, Jones K, Kanungo R, Alcorta M, Allen J, et al. Use of Bayesian Optimization to understand the structure of nuclei. Nucl Instrum Methods B (2022) 512:6–11. doi:10.1016/j.nimb.2021.11.014

CrossRef Full Text | Google Scholar

47. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4-a simulation toolkit. Nucl Instrum Methods A (2003) 506:250–303. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar