Sensor data reduction with novel local neighborhood information granularity and rough set approach

Data description and data reduction are important issues in sensors data acquisition and rough sets based models can be applied in sensors data acquisition. Data description by rough set theory relies on information granularity, approximation methods and attribute reduction. The distribution of actual data is complex and changeable. The current model lacks the ability to distinguish different data areas leading to decision-making errors. Based on the above, this paper proposes a neighborhood decision rough set based on justifiable granularity. Firstly, the rough affiliation of the data points in different cases is given separately according to the samples in the neighborhood. Secondly, the original labels are rectified using pseudo-labels obtained from the label noise data that has been found. The new judgment criteria are proposed based on justifiable granularity, and the optimal neighborhood radius is optimized by the particle swarm algorithm. Finally, attribute reduction is performed on the basis of risky decision cost. Complex data can be effectively handled by the method, as evidenced by the experimental results.

1 Introduction

In sensor data processing systems, researchers are often confronted with large amounts of multimodal and complex sensing data. To deal with these sensing data, data description and data reduction are pivotal process. For data acquisition, rough sets based models are considered as effective approaches in recent years [1, 2]. Rough set theory [3] was proposed in 1982 by Pawlak as a mathematical tool for analyzing and handling imprecise, inconsistent, and incomplete information. Traditional rough set theory lacks fault tolerance and does not take errors in the classification process into account at all. Pawlak et al. proposed the probabilistic rough set model to improve rough set theory using probabilistic threshold [4]. A probabilistic rough set model has been introduced to Bayesian decision theory by [5]. Further, Yao proposed a three-way decision theory on the basis of decision rough set theory [6].

Currently, many scholars have been improving the research on decision rough sets from different aspects. [7] proposed the theoretical framework of local rough set. [8] proposed local neighborhood rough set, which integrated the neighborhood rough set and local rough set. [9] combined Lebesgue and entropy measure, and proposed a novel attribute reduction approach. [10] introduced the pseudo-label into rough set, and proposed a pseudo-label neighborhood relationship, which can distinguish samples by distance measure and pseudo-labels.

As mentioned above, scholars proposed equivalent modifications to the neighborhood decision rough set approach from multiple perspectives. However, for complex sensor data processing, neighborhood decision rough set methods still face some challenges. For example, in practical applications, complex data distribution is often uneven. In addition, the presence of abnormal data can also greatly weaken the performance of rough models and cannot correctly classify abnormal data points. For the issues mentioned above, this paper proposes a local strategy to improve the calculation process of rough membership. Additionally, the neighborhood of sample is optimized by the particle swarm optimization method (PSO algorithm) to offer the optimal neighborhood granularity for the model and carry out attribute reduction.

The remainder of this paper is structured as follows. Section 2 introduces the relevant basic theories. Section 3 presents a decision rough calculation method based on justifiable granularity. Six datasets are chosen in Section 4 to evaluate the suggested methodology. Section 5 summarizes the full text.

2 Preliminary notion

2.1 Neighborhood relation and rough set

The construction of equivalence relations for numerical type data first requires the discretization of the original data, and this method will inevitably cause the loss of information. On the basis of neighborhood relations, a neighborhood rough set model was proposed by Hu et al. [11–13].

Assume that information system is expressed as $S=\left(U,AT=C\cup D,f,V\right)$.Among them, U = {x₁, x₂, … , x_n} represents a collection of non-empty limited objects, AT stands for the set of attributes, containing conditional attribute set C and decision attribute set D.

Definition 1. Suppose the information system is $S=\left(U,AT=C\cup D,f,V\right)$, $\forall x\in U$, $B\subseteq C$, the $\delta$-neighborhood of x in B is defined as:

${\delta }_B\left(x\right)=\left\{y\in U|di{s}_B\left(x,y\right)\le \delta ,\delta >0\right\}(1)$

where dis (•) represents the distance between any objects, using Euclidean distance commonly.

Definition 2. Suppose the information system is $S=\left(U,AT=C\cup D,f,V\right)$, $\forall x\in U$, $X\subseteq U$, $B\subseteq C$, the rough affiliation ${\mu }_B\left(x\right)$ of x to X in B is defined as:

${\mu }_B\left(x\right)=P\left(X|{\delta }_B\left(x\right)\right)=\frac{\left|X\cap {\delta }_B\left(x\right)\right|}{\left|{\delta }_B\left(x\right)\right|}(2)$

where $P\left(X|{\delta }_B\left(x\right)\right)$ represents the conditional probability of classification, and $\left|•\right|$ represents the number of elements in the combination.

Definition 3. Suppose the information system is $S=\left(U,AT=C\cup D,f,V\right),X\subseteq U,B\subseteq C$, the lower and upper approximations of the decision D in B are defined as:

$\overline{{\delta }_B}\left(X\right)=\left\{x\in U|{\delta }_B\left(x\right)\cap X\ne \varnothing \right\}(3)$

$\underset{¯}{{\delta }_B}\left(X\right)=\left\{x\in U|{\delta }_B\left(x\right)\subseteq X\right\}(4)$

The following definitions apply to the positive, negative, and boundary regions of X in B:

$PO{S}_B\left(X\right)=\underset{¯}{{\delta }_B}\left(X\right)=\left\{x\in U\left|P\left(X|{\delta }_B\left(X\right)\right)\right.=1\right\}(5)$

$NE{G}_B\left(X\right)=U-\underset{¯}{{\delta }_B}\left(x\right)=\left\{x\in U\left|P\left(X|{\delta }_B\left(x\right)\right)\right.=0\right\}(6)$

$BN{D}_B\left(X\right)=\overline{{\delta }_B}\left(x\right)-\underset{¯}{{\delta }_B}\left(x\right)=\left\{x\in U\left|0<P(X\right|{\delta }_B\left(x\right)<1\right\}(7)$

From the above definition, it can be found that the conditions on which the neighborhood rough set is based in taking both acceptance and rejection decisions are too severe and lack a certain degree of fault tolerance. Only elements that are completely correctly classified are grouped into the positive domain. Alternatively, only elements that are completely misclassified are classified in the negative domain. The result of such a definition makes the boundary domain too large.

2.2 Rough set with neighborhood decision

The rough set model for decision-making put forth by Yao et al. [5] lacks the ability to directly process numerical data. In order to address this weakness, a rough set model of decision theory based on neighborhood was proposed by Li et al. [14] through the integration of the neighborhood rough set and the decision rough set.

The decision rough set has two important elements: $\mathrm{\Omega }=\left\{X,\sim X\right\}$ and $Action=\left\{a_P,a_B,a_N\right\}$. When different decision-making actions are taken, different losses will occur. ${\lambda }_{PP}$, ${\lambda }_{BP}$, ${\lambda }_{NP}$ respectively represent the cost of $a_P,a_B$ and $a_N$ when X owns the object, ${\lambda }_{PN}$, ${\lambda }_{BN}$, ${\lambda }_{NN}$ respectively represent the cost of $a_P,a_B$ and $a_N$ when X is not the owner of the object. Through cost risk analysis, the solution formula of $\left(\alpha ,\beta \right)$ is given [5] as follows:

$\alpha =\frac{{\lambda }_{PN}-{\lambda }_{BN}}{\left({\lambda }_{PN}-{\lambda }_{NN}\right)+\left({\lambda }_{BP}-{\lambda }_{PP}\right)}(8)$

$\beta =\frac{{\lambda }_{BN}-{\lambda }_{NN}}{\left({\lambda }_{BN}-{\lambda }_{NN}\right)+\left({\lambda }_{NP}-{\lambda }_{BP}\right)}(9)$

In addition, Yao proposed three decision theories based on decision rough set model [5], including P rule, N rule and B rule.

Definition 4. Suppose the information system $S=\left(U,AT=C\cup D,f,V\right)$, $X\subseteq U$, $B\subseteq C$, then the P, B, and N rules of X on $\delta$-neighborhood under attribute set B are defined as:P rule: if $x\in U$, $P\left(X|{\delta }_B\left(X\right)\right)\ge \alpha$, then $x\in PO{S}_B\left(X\right)$;B rule: if $x\in U$, $\beta <P\left(X|{\delta }_B\left(X\right)\right)<\alpha$, then $x\in BN{D}_B\left(X\right)$;N rule: if $x\in U$, $P\left(X|{\delta }_B\left(X\right)\right)\le \beta$, then $x\in NE{G}_B\left(X\right)$.

3 Neighborhood decision rough set model based on justifiable granularity

To solve the problems discussed above, this article first introduces the local neighborhood rough set model to eliminate the interference of some noise data on the approximate set.

3.1 Local rough neighborhood decision model

Definition 5. Suppose the information system $S=\left(U,AT=C\cup D,f,V\right)$, $X\subseteq U$, $B\subseteq C$, then the X of the attribute set B is related to the upper and lower approximation sets of the $\delta$-neighborhood based local rough set, which are defined as:

$\overline{{\delta }_B^L}\left(X\right)=\left\{x\in X|P\left(X|{\delta }_B\left(x\right)\right)>\beta \right\}(10)$

$\underset{¯}{{\delta }_B^L}\left(X\right)=\left\{x\in X|P\left(X|{\delta }_B\left(x\right)\right)\ge \alpha \right\}(11)$

The following definitions apply to the positive, negative, and boundary regions of X in B:

$PO{S}_B\left(X\right)=\underset{¯}{{\delta }_B^L}\left(X\right)=\left\{x\in X\left|P\left(X|{\delta }_B\left(X\right)\right)\right.\ge \alpha \right\};(12)$

$NE{G}_B\left(X\right)=U-\underset{¯}{{\delta }_B^L}\left(x\right)=\left\{x\in X\left|P\left(X|{\delta }_B\left(x\right)\right)\right.\le \beta \right\};(13)$

$BN{D}_B\left(X\right)=\overline{{\delta }_B^L}\left(x\right)-\underset{¯}{{\delta }_B^L}\left(x\right)=\left\{x\in X\left|\beta <P(X\right|{\delta }_B\left(x\right)<\alpha \right\}.(14)$

The most significant difference between the local neighborhood rough set model and the neighborhood rough set model is the different search scope when finding the upper and lower approximation sets. In the neighborhood rough set model, finding the approximation set for each decision category requires traversing all the data points in the data set. However, in the local neighborhood rough set model, the focus is on the data points of the same category, and only the data points of the same decision category need to be traversed. This greatly reduces the computational effort and increases the computational speed [14]. This model not only improves computational efficiency, but also eliminates the interference of noisy points.In addition, the traditional method of calculating rough affiliation does not take into account the complexity of the data. In this paper, the calculation process of affiliation degree is improved for the affiliation degree, and the process is as follows:Suppose $S=\left(U,AT=C\cup D,f,V\right)$ is a decision system, $U/D=\left\{X_1,X_2,...,X_d\right\}$ is the decision attribute of all objects U in the decision attribute set D, $\forall x\in U$, the neighborhood of x is expressed as $\delta \left(x\right)$, the decision value of the information system is $L=\left\{\mathrm{1,2},...,d\right\}$. Now suppose that the decision value of the sample x to be investigated is q.

(1) $\left|\delta \left(x\right)\right|\le N$ (N represents a small positive integer), this paper sets rough membership degree to $P\left(X|\delta \left(x\right)\right)=e^{-5}$.

(2) $L_x=q$, $\forall x_i\in \delta \left(x\right)$, $\left|L_{x_i}\right|=1$ and $L_{x_i}=q$, this paper sets rough membership degree to $\min \left[1,p_0+s\times \left(\left|\delta \left(x\right)\right|-N\right)\right]$, where $p_0$ represents the initial probability value and N represents the minimum number of neighborhoods, s represents the search step.

(3) $L_x=q$, $\forall x_i\in \delta \left(x\right)-x_i$, $\left|L_{x_i}\right|=1$ and $\left|L_{x_i}\right|\ne q$, rough membership degree is set to $P\left(X|\delta \left(x\right)\right)=0$.

Depending on which of the data points in the neighborhood information granularity are specifically situated, above rules is used to define the rough membership function for each category of data points.Based on the above discussion, this paper designs the following Algorithm 1 to calculate the upper and lower approximation sets and identify the anomalous data. Different from the classical method that only considers the upper and lower approximation sets, Algorithm 1 not only identifies label noise data points and outlier data points based on the neighborhood information, making the upper and lower approximation sets more accurate. It also appends category information to the label noise data, which is referred to as pseudo-tagging in this paper.

Algorithm 1. The upper and lower approximation sets of local neighborhood rough set.

Input: $S=\left(U,AT=C\cup D\right)$, neighborhood radius $\delta$, cost matrix $\lambda$.

Output: lower approximate $\underset{\_}{\delta }\left(X_q\right)$, upper approximate $\overline{\delta }\left(X_q\right)$, outlier points set $\mathrm{{\rm O}}$, labeled noise points set $Noise$, and predicted pseudo-labels set $Nois{e}^{\prime }$.

1:  Segmentation of the entire dataset by tag categories $U/D=\left\{X_1,X_2,...,X_d\right\}$.

2:  Using the cost matrix, the threshold value $\alpha$ and $\beta$ are calculated according to Eqs 8, 9.

3:  For $\forall x_i\in X_q$

4:   Compute the $\delta$-neighborhood $\delta \left(x_i\right)$ of $x_i$ on the conditional attribute set C and obtain the label category $L_{\delta \left(x_i\right)}=\left\{\mathrm{1,2},...,d\right\}$.

5:  end

6:  If $\left|\delta \left(x_i\right)\right|\le N$

7:   $P\left(X_q|\delta \left(x_i\right)\right)=e^{-5}$.

8:   $\mathrm{{\rm O}}=\mathrm{{\rm O}}\cup \left\{x_i\right\}$.

9:  End

10:  If $\left|L_{\delta \left(x_i\right)}\right|=1$& $L_{x_i}=q$

11:   $P\left(X_q|\delta \left(x_i\right)\right)=0$.

12:   $Noise=Noise\cup \left\{x_i\right\}$.

13:   $Nois{e}^{\prime }=Nois{e}^{\prime }\cup \left\{x_i\right\}$

14:  End

15:  If $1<\left|L_{\delta \left(x_i\right)}\right|<d$

16:   $P\left(X_q|\delta \left(x_i\right)\right)=\frac{\left|\delta \left(x_i\right)\cap X_q\right|}{\left|\delta \left.\left(x_i\right)\right|\right.}$.

17:  End

18:  If $P\left(X_q|\delta \left(x_i\right)\right)\ge \alpha$

19:   $\underset{\_}{\delta }\left(X_q\right)=\underset{\_}{\delta }\left(X_q\right)\cup \left\{x_i\right\}$.

20:   If $P\left(X_q|\delta \left(x_i\right)\right)>\beta$

21:    $\overline{\delta }\left(X_q\right)=\overline{\delta }\left(X_q\right)\cup \left\{x_i\right\}$.

22:   End

23:  End

24:  Return $\underset{\_}{\delta }\left(X_q\right)$, $\overline{\delta }\left(X_q\right)$, $\mathrm{{\rm O}}$, $Noise$, $Nois{e}^{\prime }$.

Algorithm 1 detects outliers and labeled noisy points, as well as enables the detection of data points for high-density areas. In fact, some samples are not always considered as outlier data or noise, and their decisions sometimes depend on the choice of neighborhood radius.

3.2 Selection of neighborhood information granularity based on justifiable granularity

According to the above-mentioned rough set model, a smaller neighborhood radius contains very little information, while a larger radius may cause the next approximate set to be an empty set. This paper introduces the justifiable granularity criterion [15, 16]. There are generally two functions in the construction of information granules, namely, covering function and particularity function.

The coverage function describes how much data is in the constructed information granule. This paper designs the coverage index function as shown below:

$\mathrm{c}\mathrm{o}\mathrm{v}\left(\delta \right)=\max \left[0,F_1+F_2\right](15)$

where $F_1=\frac{1}{\left|X_q\right|}\left({\displaystyle \sum _{x\in X_q}}\left(\left|{\delta }_q\left(x\right)\right|-\underset{\begin{array}{l}j=1,\dots ,d\\ j\ne q\end{array}}{\max }\left|{\delta }_j\left(x\right)\right|\right)\right)$ and $F_2=\frac{1}{\left|\delta \left(x\right)\right|}$(|POS($X_q$)|-|BND($X_q$)|).

The coverage index function mentioned above is considered from two perspectives, namely, neighborhood information granularity and approximate set. In terms of specificity criteria, the smaller the neighborhood radius, the better. Therefore, the specificity function can be designed as: $\mathrm{s}\mathrm{p}\left(\delta \right)=1-\delta$.

Obviously, the two are contradictory. Therefore, the function for optimized performance can be written as the multiplication of specificity and coverage, which is: $Q=\mathrm{c}\mathrm{o}\mathrm{v}\left(\delta \right)\times \mathrm{s}\mathrm{p}\left(\delta \right)$.

In this way, the optimal neighborhood about $X_q$ can be obtained. To further elaborate, the cumulative behavior can be represented in terms of the decision partition set $U/D=\left\{X_1,X_2,...,X_d\right\}$ as follows: $Q=Q_1+Q_2+...+Q_d$, where $Q_1$, $Q_2$,…, $Q_d$ correspond to the optimized value of each decision class.

To achieve the optimal $Q$ value and the corresponding optimal neighborhood radius. In this paper, PSO algorithm is used for optimization [17, 18], which is an evolutionary algorithm based on population intelligence, proposed by Drs. Kennedy and Eberhart in 1995. In this paper, we use the PSO algorithm to intelligently optimize the selection of neighborhoods and select the appropriate granularity as a way to improve the accuracy of decision making.

Moreover, to update the dataset, one can utilize the noise identification strategy along with the set of predicted pseudo-decision labels. The main steps are described in Algorithm 2.

Algorithm 2. Update of rough approximation set in label noise injection environment.

 1: Obtain the optimal neighborhood radius $\delta$ using PSO optimization algorithm;

 2: Execute Algorithm 1 to obtain the approximation set, the set of outlier points, the set of labeled noise points, and the pseudo-tags of labeled noise points;

 3: Updating decision labels for noisy data based on pseudo-labels;

 4: Update the approximation set using the modified decision system.

3.3 Attribute reduction based on neighborhood decision rough set model

In this paper the risky decision cost will be used to reduce the attributes. It comes from the Bayesian decision process, which is comparable to the classical rough set. Risky decision costs for P, N and B rule can be separately expressed as:

$\mathit{COS}{T}_{POS}={\displaystyle \sum _{X_j\in U/D}}{\displaystyle \sum _{x\in POS\left(X_j\right)}}{\displaystyle \sum _{k=1}^m}\left({\lambda }_{PP}^k•P\left(X_j|{\left[x\right]}_{C_k}\right)+{\lambda }_{PN}^k•P\left(\sim X_j|{\left[x\right]}_{C_k}\right)\right)(16)$

$\mathit{COS}{T}_{NEG}={\displaystyle \sum _{X_j\in U/D}}{\displaystyle \sum _{x\in NEG\left(X_j\right)}}{\displaystyle \sum _{k=1}^m}\left({\lambda }_{NP}^k•P\left(X_j|{\left[x\right]}_{C_k}\right)+{\lambda }_{NN}^k•P\left(\sim X_j|{\left[x\right]}_{C_k}\right)\right)(17)$

$\mathit{COS}{T}_{BND}={\displaystyle \sum _{X_j\in U/D}}{\displaystyle \sum _{x\in BND\left(X_j\right)}}{\displaystyle \sum _{k=1}^m}\left({\lambda }_{BP}^k•P\left(X_j|{\left[x\right]}_{C_k}\right)+{\lambda }_{BN}^k•P\left(\sim X_j|{\left[x\right]}_{C_k}\right)\right)(18)$

As discussed above, the cost of making a risky decision for all decision rules can be obtained as:

$\mathit{COS}{T}_B=\mathit{COS}{T}_{POS}+\mathit{COS}{T}_{NEG}+\mathit{COS}{T}_{BND}(19)$

Obviously, the higher $\mathit{COS}{T}_B$, the greater the significance of the attribute becomes evident.

Definition 6. Suppose the information system $S=\left(U,AT=C\cup D,f,V\right)$, $B\subseteq C$, $a\notin B$, the significance of an attribute is defined as:

$sig\left(a,B,D\right)=\mathit{COS}{T}_{B\cup a}\left(D\right)-\mathit{COS}{T}_B\left(D\right)(20)$

A scheme based on neighborhood decision rough sets is designed for forward search to achieve the optimal reduction. Its specific steps are shown in Algorithm 3.

Algorithm 3. Attribute reduction based on neighborhood decision rough set model.

 1:  RED = $\varnothing$.

 2:  For $a_i\in C-RED$

 3:   Calculate $sig\left(a_i,B,D\right)=\mathit{COS}{T}_{RED\cup a_i}\left(D\right)-\mathit{COS}{T}_{RED}\left(D\right)$.

 4:  End

 5:  Select $a_k$ which satisfies $sig\left(a_k,B,D\right)={\max }_i\left(sig\left(a_i,RED,D\right)\right)$.

 6:  If $sig\left(a_k,B,D\right)>0$

 7:   $RED=RED\cup \left\{a_k\right\}$.

 8:  Else

 9:   Break.

 10:  End

 11:  Return RED

3.4 Evaluation index

To assess the effectiveness of the suggested approach, this article discusses the following two evaluation indicators: the lower approximation and information granularity.

Approximation quality (AQ): Given decision information system $S=\left(U,AT=C\cup D,f,V\right)$, $A\subseteq C$, the approximate quality of A relative to D [19] is defined as:

$\gamma =\frac{\left|\cup \underset{\_}{{\delta }_A\left(X_q\right)}\right|}{\left|U\right|},\left(q=\mathrm{1,2},...,d\right)(21)$

The $\gamma$ value is expressed as the ratio of the number of objects correctly classified by the conditional attribute set A to the number of all objects in the decision information system. The performance of the proposed granularity description is evaluated in terms of the lower approximation.

Neighborhood number(NN): $x\in U$, suppose $x\in X_q$. ${\delta }_q\left(x\right)$ is the set of data points with decision label q in the neighborhood of x. Therefore, the categories of similar decision label data and different data in the neighborhood can be described as:

$NN={\displaystyle \sum _{x\in X_q}}\left(\left|{\delta }_q\left(x\right)\right|-{\displaystyle \sum _{j=1,j\ne q}^d}\left|{\delta }_j\left(x\right)\right|\right)(22)$

The larger value of $NN$ indicates that the information granularity provides greater information value to the decision maker and more reasonable granularity.

4 Experiment analysis

In this section, six UCI datasets are utilized to illustrate the feasibility and validity of the suggested methodology. Table 1 describes the relevant information of the datasets.

TABLE 1

TABLE 1. Dataset description.

Parameter setting of PSO algorithm, initialize the particle swarm size to 300, a maximum of 100 iterations is permitted, the individual experience learning factor $c_1=1.49445$, the social experience learning factor $c_2=1.49445$, the top flight speed of the particle is 0.5 and the allowable error is set to 0.1. For the purpose of assessing the effectiveness of the inertia weight w, consider the use of a linear differential decreasing inertia weight [20], which is expressed as:

$\frac{dw}{dk}=-\frac{2\left(w_{start}-w_{end}\right)}{T_{\max }^2}\times k(23)$

$w\left(k\right)=w_{start}-\frac{\left(w_{start}-w_{end}\right)}{T_{\max }^2}\times k^2(24)$

where $w_{start}$ represents the initial inertia weight, $w_{end}$ represents the inertia weight when the iteration reaches the maximum number, k represents the current iteration number, and $T_{\max }$ is the maximum iteration number. Set $w_{start}=0.9$ and $w_{end}=0.4$.

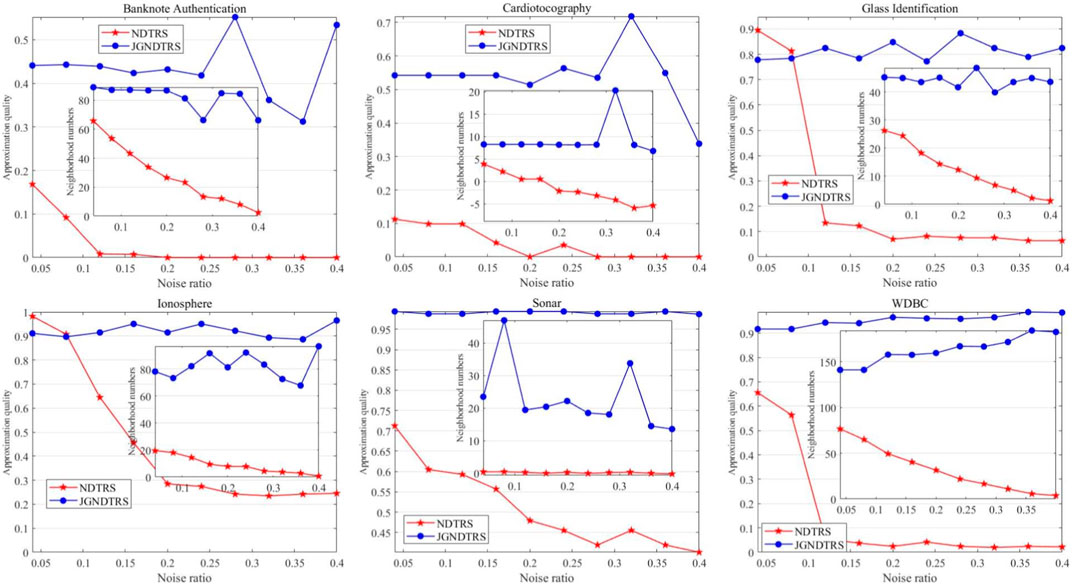
Figure 1 show the performance of $\gamma$ and NN respectively. The neighborhood decision rough set model based on reasonable granularity proposed in this paper is abbreviated as JGNDTRS, and NDTRS stands for traditional neighborhood decision rough set. Various noise ratios are represented on the x-axis of each subfigure, which corresponds to a dataset. It can be seen intuitively from the figure that as the noise ratio increases, the approximate quality and NN of NDTRS both show a downward trend. Regarding various noise ratios, the JGNDTRS can obtain the best and relatively stable values of $\gamma$ and NN in all datasets. Furthermore, JGNDTRS has remarkable performance in identifying anomalous data such as high-density and sparse-density region data points as well as label noise points.

FIGURE 1

FIGURE 1. Comparison of AQ and NN with different noise ratios.

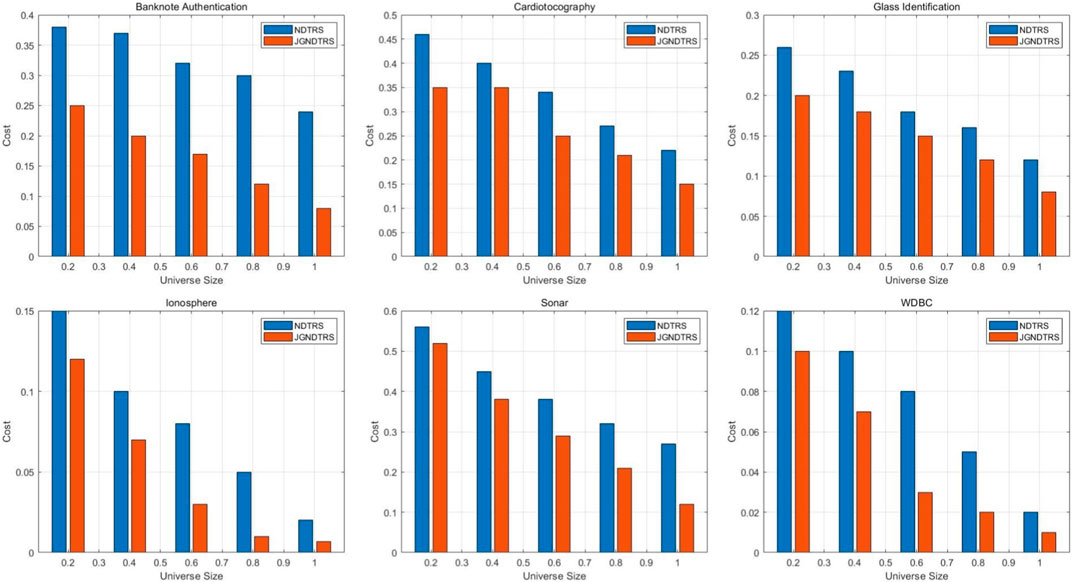
Figure 2 shows the comparison of the cost of JGNDTRS and NDTRS when performing attribute reduction. A dataset is represented by each subplot, and various Universe sizes are shown on the x-axis. Through closer observation, we can conclude that the decision cost of both JGNDTRS and NDTRS shows a decreasing trend as the size of Universe increases. In each dataset, the decision cost of JGNDTRS is always lower than that of NDTRS, regardless of the value of the Universe size. This indicates that JGNDTRS has a superior performance with less cost used in performing attribute reduction.

FIGURE 2

FIGURE 2. The cost of attribute reduction comparison under different universe sizes.

5 Conclusion

The proposed neighborhood decision rough set model compensates the lack of fault tolerance of classical rough sets. However, there are some challenges in the existing models when dealing with complex data. In this paper, we propose a neighborhood decision rough set model based on justifiable granularity. Firstly, the calculation of rough affiliation is improved according to the number of data points in the neighborhood and the corresponding decision label categories. Secondly, to rectify the original labels, provide pseudo-labels for the noisy data points that are found. A justifiable granularity criterion is introduced and the optimal neighborhood radius is obtained by PSO algorithm. Finally, the risky decision cost is used for attribute reduction. The results of the experiments demonstrate that the neighborhood decision rough set model based on justifiable granularity has significant performance in identifying abnormal data points and can enhance classification performance. In the future work, the attribute reduction of the neighborhood decision rough set based on justifiable granularity will be further investigated.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

The idea was proposed by PG and HJ; XF and XM simulated the algorithm, wrote the paper and polish the English, TC and YS analysed the data designed the experiments. All authors contributed to the article and approved the submitted version.

Funding

This work was supported the National Natural Science Foundation of China under Grant 62006128, Jiangsu Innovation and Entrepreneurship Program.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Liu J, Lin Y, Du J, Zhang H, Chen Z, Zhang J . Asfs: A novel streaming feature selection for multi-label data based on neighborhood rough set. Appl Intell (2023) 53:1707–24. doi:10.1007/s10489-022-03366-x

CrossRef Full Text | Google Scholar

2. Wang W, Guo M, Han T, Ning S. A novel feature selection method considering feature interaction in neighborhood rough set. Intell Data Anal (2023) 27:345–59. doi:10.3233/IDA-216447

CrossRef Full Text | Google Scholar

3. Pawlak Z. Rough sets. Int J Parallel Program (1982) 11:341–56. doi:10.1007/BF01001956

CrossRef Full Text | Google Scholar

4. Pawlak Z, Wong S, Ziarko W. Rough sets: Probabilistic versus deterministic approach. Int J Man Mach Stud (1988) 29:81–95. doi:10.1016/S0020-7373(88)80032-4

CrossRef Full Text | Google Scholar

5. Yao Y, Wong S. A decision theoretic framework for approximating concepts. Int J Man Mach Stud (1992) 37:793–809. doi:10.1016/0020-7373(92)90069-W

CrossRef Full Text | Google Scholar

6. Yao Y. Three-way decisions with probabilistic rough sets. Inf Sci (2010) 180:341–53. doi:10.1016/j.ins.2009.09.021

CrossRef Full Text | Google Scholar

7. Qian Y, Liang X, Wang Q, Liang J, Liu B, Skowron A, et al. Local rough set: A solution to rough data analysis in big data. Int J Approx Reason (2018) 97:38–63. doi:10.1016/j.ijar.2018.01.008

CrossRef Full Text | Google Scholar

8. Wang Q, Qian Y, Liang X, Guo Q, Liang J. Local neighborhood rough set. Knowl Based Syst (2018) 153:53–64. doi:10.1016/j.knosys.2018.04.023

CrossRef Full Text | Google Scholar

9. Sun L, Wang L, Ding W, Qian Y, Xu J. Neighborhood multi-granulation rough sets-based attribute reduction using lebesgue and entropy measures in incomplete neighborhood decision systems. Knowl Based Syst (2020) 192:105373. doi:10.1016/j.knosys.2019.105373

CrossRef Full Text | Google Scholar

10. Yang X, Liang S, Yu H, Gao S, Qian Y. Pseudo-label neighborhood rough set: Measures and attribute reductions. Int J Approx Reason (2019) 105:112–29. doi:10.1016/j.ijar.2018.11.010

CrossRef Full Text | Google Scholar

11. Hu Q, Liu J, Yu D. Mixed feature selection based on granulation and approximation. Knowl Based Syst (2008) 21:294–304. doi:10.1016/j.knosys.2007.07.001

CrossRef Full Text | Google Scholar

12. Hu Q, Yu D, Liu J, Wu C. Neighborhood rough set based heterogeneous feature subset selection. Inf Sci (2008) 178:3577–94. doi:10.1016/j.ins.2008.05.024

CrossRef Full Text | Google Scholar

13. Lin Y, Hu Q, Liu J, Chen J, Duan J. Multi-label feature selection based on neighborhood mutual information. Appl Soft Comput (2016) 38:244–56. doi:10.1016/j.asoc.2015.10.009

CrossRef Full Text | Google Scholar

14. Li W, Huang Z, Jia X, Cai X. Neighborhood based decision-theoretic rough set models. Int J Approx Reason (2016) 69:1–17. doi:10.1016/j.ijar.2015.11.005

CrossRef Full Text | Google Scholar

15. Pedrycz W, Homenda W. Building the fundamentals of granular computing: A principle of justifiable granularity. Appl Soft Comput (2013) 13:4209–18. doi:10.1016/j.asoc.2013.06.017

CrossRef Full Text | Google Scholar

16. Wang D, Liu H, Pedrycz W, Song W, Li H. Design Gaussian information granule based on the principle of justifiable granularity: A multi-dimensional perspective. Expert Syst Appl (2022) 197:116763. doi:10.1016/j.eswa.2022.116763

CrossRef Full Text | Google Scholar

17. Cui Y, Meng X, Qiao J. A multi-objective particle swarm optimization algorithm based on two-archive mechanism. Appl Soft Comput (2022) 119:108532. doi:10.1016/j.asoc.2022.108532

CrossRef Full Text | Google Scholar

18. Deng H, Liu L, Fang J, Yan L. The application of SOFNN based on PSO-ILM algorithm in nonlinear system modeling. Appl Intell (2023) 53:8927–40. doi:10.1007/s10489-022-03879-5

CrossRef Full Text | Google Scholar

19. Hu X, Cercone N. Learning in relational databases: A rough set approach. Comput Intell (1995) 11:323–38. doi:10.1111/j.1467-8640.1995.tb00035.x

CrossRef Full Text | Google Scholar

20. Salgotra R, Singh U, Singh S, Mittal N. A hybridized multi-algorithm strategy for engineering optimization problems. Knowl Based Syst (2021) 217:106790. doi:10.1016/j.knosys.2021.106790

CrossRef Full Text | Google Scholar