Kaonic atoms at the DAΦNE collider: a strangeness adventure

Kaonic atoms are an extremely efficient tool to investigate the strong interaction at the low energy Frontier, since they provide direct access to the K⁻N interaction at threshold, eliminating the necessity for extrapolation, unlike in the case of scattering experiments. During the 1970s and 1980s, extensive studies were performed on kaonic atoms spanning across a broad spectrum of elements in the periodic table, ranging from lithium to uranium. These measurements provided inputs and constraints for the theoretical description of the antikaon-nuclei interaction potential. Nevertheless, the existing data suffer from significant experimental uncertainties, and numerous measurements have been found to be inconsistent with more recent measurements that utilize advanced detector technology. Furthermore, there remain numerous transitions of kaonic atoms that have yet to be measured. For these reasons, a new era of kaonic atoms studies is mandatory. The DAΦNE electron-positron collider at the INFN Laboratory of Frascati (INFN-LNF) stands out as a unique source of low-energy kaons, having been utilized by Collaborations such as DEAR, SIDDHARTA, and AMADEUS for groundbreaking measurements of kaonic atoms and kaon-nuclei interactions. Presently, the SIDDHARTA-2 experiment is installed at DAΦNE, aiming to perform the first-ever measurement of the 2p → 1s x-ray transition in kaonic deuterium, a crucial step towards determining the isospin-dependent antikaon-nucleon scattering lengths. Based on the experience gained with the SIDDHARTA experiment, which performed the most precise measurement of the kaonic hydrogen 2p → 1s x-ray transition, the SIDDHARTA-2 setup is now fully equipped for the challenging kaonic deuterium measurement. In this paper, we present a comprehensive description of the SIDDHARTA-2 setup and of the first kaonic atoms measurements performed during the commissioning phase of the DAΦNE collider. We also outline a proposal for future measurements of kaonic atoms at DAΦNE beyond SIDDHARTA-2, which is intended to stimulate discussions within the broad scientific community performing research, directly or indirectly, related to this field.

1 Introduction

The measurements of the x-rays emitted by kaonic atoms allow to investigate the strong kaon-nuclei interaction at the low-energy Frontier ([1]). A kaonic atom is formed when a K⁻ meson, stopped in a target material, is captured in an atomic system through its electromagnetic interaction with the nucleus. The captured K⁻ meson replaces an electron in a highly excited atomic level, followed by an electromagnetic cascade process which can bring it to the innermost atomic level, where the strong interaction between the kaon and the atomic nucleus induces a shift and broadening of the ground state with respect to the purely electromagnetic values, which become detectable with advanced x-ray spectroscopy techniques. The measurements of the 2p → 1s transitions in Kaonic Hydrogen (KH) and Kaonic Deuterium (KD) allow to extract the energy shift and width of the 1s levels resulting from the strong kaon-nucleon interaction. From their values, one can extract the antikaon-nucleon isospin-dependent scattering lengths ([2–4]).

The DAΦNE electron-positron collider, located at the INFN National Laboratory of Frascati (LNF-INFN), Italy, represents a unique facility, suitable to investigate the strong interaction in the strangeness sector at low energies ([5]). This facility produces low-momentum (∼127 MeV/c) and nearly monochromatic kaons, through the decay of the ϕ-resonance, which is formed in electron-positron annihilation. This excellent quality kaon source, combined with remarkable advancements in fast spectroscopic x-ray detector systems, has propelled unprecedented progresses in the field of strangeness studies. A crucial pioneering role was played by the DEAR ([6]) and the SIDDHARTA ([7–9]) experiments. These experiments achieved the most precise measurement of kaonic hydrogen transitions to the ground level, the first measurement of kaonic helium-3 (K⁻-³He) transitions to the 2p level, and the measurements of the kaonic helium-4 (K⁻-⁴He) transitions to the 2p level ([7–9]) in gas. Currently, the SIDDHARTA-2 experiment is set up to perform the challenging measurement of KD transitions to the ground level, not yet detected, since their yields are expected to be about ten times lower and their widths at least two times larger than the KH ones ([1, 10]). During the commissioning phase of the DAΦNE collider, the SIDDHARTA-2 Collaboration carried out several measurements of kaonic atoms with a higher yield than deuterium, to optimize and test the performance of the experimental apparatus. Among them, we performed the most precise measurement of the transitions towards the 2p level in gaseous K⁻-⁴He ([11, 12]), and the precision spectroscopic measurement of high-n transitions in kaonic carbon (KC), oxygen (KO), aluminium (KAl) and nitrogen (KN) ([13]).

These measurements enrich the kaonic atoms database with new accurate data. Several measurements of kaonic atoms date back to the 70s and 80s ([14–25]) and are affected by significant experimental uncertainties, or are inconsistent with more recent measurements ([26]). Moreover, many more kaonic atoms transitions are not yet measured ([26, 27]). Beyond SIDDHARTA-2, systematic measurements of kaonic atoms transitions can provide important inputs for theoretical models describing the strong interaction at low energies. In the specific, they are fundamental to address kaon-nuclei potential and chiral models around the K⁻-N threshold, and the nature of the still ambiguous Λ(1405) structure ([28–36]). The Λ(1405) is a K⁻-N system ([37, 38]) currently interpreted as a dynamically generated molecular state with two poles coupling to the K⁻-N and the Σπ channels. It is the only accepted molecular state ([39]) of the hadron spectrum, and confirmed as 4 “stars” resonances by Particle Data Group since 2021 ([40]). The kaonic atoms measurements provide precise data about K⁻-N strong interaction at threshold energy, which represents a crucial input for different theoretical approaches below threshold, thus allowing to pin down the characteristics of this exotic state.Further experimental investigations may also have impacts in many fields, from nuclear interaction ([28–30]) to neutron stars ([31–36, 41–43]): The core of the neutron stars would be populated with particles with strangeness. This hypothesis is being cross-checked with the data extracted by recent astrophysical measurements, including the observation of gravitational waves, that constrain mass and dimensions of the neutron stars ([44–46]). Recent studies on kaon condensation revealed that both hyperons and/or delta baryons could play a catalytic role in the formation of this highly dense state of matter ([47–51]). A more accurate comprehension of the mechanisms ruling the interaction between hadrons containing the strange quark, and its extrapolation in dense baryonic environments, is fundamental for the construction of a model describing the interior of the neutron stars which agrees with astrophysical observations ([44–46]). During the KD run, the SIDDHARTA-2 Collaboration plans to develop and test various x-ray detection systems, to put forward a scientific program for kaonic atoms measurements, going from the very light (Li) nuclei to the heaviest ones (U).

The SIDDHARTA-2 apparatus and plans are described in Section 2. The recently obtained results running SIDDHARTA-2 during the DAΦNE commissioning phase are also included. In Section 3 future plans beyond SIDDHARTA-2, i.e., the EXKALIBUR project, are briefly introduced. Conclusions and future perspectives are presented in Section 4.

2 The SIDDHARTA-2 experiment

The main goal of the SIDDHARTA-2 experiment is to measure the 2p → 1s atomic transition in KD ([52]) and to extract the energy shift and width of the 1s atomic level, generated by the strong K⁻-N interaction. Below 1 GeV, the strong interaction cannot be described using Quantum Chromodynamics (QCD) in a perturbative approach. For that reason, various phenomenological models have been developed. In [53] a comparative analysis of the most advanced theoretical models is presented. Most of these models exploit dimensional regularization to manage the ultraviolet divergences, as the Bonn ([54, 55]), Murcia ([56]), and Kyoto-Munich ([57]) models. Other models use off-shell form factors, as the Prague model ([53, 58–60]). All these models contain free parameters, which are adjusted to the low-energy experimental data for K⁻p, obtained by the SIDDHARTA experiment ([7]). Recent effective field theory models ([61]) predict a very large width for the kaonic deuterium fundamental level. Substantial disagreements persist in the K⁻n scattering length predictions, with models exhibiting significant differences in both the real and imaginary parts. See also relative Refs. [1, 53]. The only way to address this issue is through the measurement of kaonic deuterium, the primary goal of the SIDDHARTA-2 experiment.

2.1 The SIDDHARTA-2 apparatus

The SIDDHARTA-2 apparatus is presently installed in the Interaction Region (IR) of the DAΦNE e⁺e⁻ collider at LNF-INFN. DAΦNE is a ϕ-factory, where electron and positron beams collide with momenta of 510 MeV/c, thus producing ϕ-mesons that decay into low-energy back-to-back K⁺K⁻ pairs with a branching ratio of 49.1% ± 0.5%. The K⁻s are produced by DAΦNE with a momentum of 127 MeV/c and a low energy spread of Δp/p ≃ 0.1%, making DAΦNE an ideal low-energy kaon source for kaonic atom measurements. The experimental target of SIDDHARTA-2 is a cylindrical cell with 144 mm diameter and 125 mm height. It has walls made of 150 μm thick Kapton layers on aluminum support and is filled with the target gas in which kaonic atoms are formed. The cylindrical target is surrounded by 384 large-area monolithic Silicon Drift Detectors (SDDs), specially developed for kaonic atoms x-ray spectroscopy, providing a high energy efficiency ($>$ 98%) for x-ray energies between 5 keV and 12 keV (see Figure 1).

FIGURE 1

FIGURE 1. Left: Picture of the SIDDHARTA-2 cylindric target cell. Right: SDD detectors arrays. Reproduced from [62].

Each SDD has an active area of 0.64 cm² and is 450 μm thick. The detectors are organized in arrays of eight SDDs, placed in two rows of four cells each (2 × 4 matrix), as shown in Figure 2. The silicon wafers are glued on an alumina carrier, and fixed to an aluminium support. The polarization of the SDD cells is provided through an external voltage. When an x-ray is absorbed within the silicon bulk, the central anode collects the generated charges. Each detector unit is closely bonded to a C-MOS charge-sensitive amplifier ([63]). The signals are then processed using a dedicated ASIC chip called SFERA ([64, 65]). The resolution of the SIDDHARTA-2 SDDs is $157.8\pm 0.3{(stat)}_{-0.2}^{+0.2}(syst)$ eV at 6.4 keV, with a linearity below 2–3 eV, measured in the commissioning phase at DAΦNE ([66, 67]). The target and the SDDs are placed inside a vacuum chamber, evacuated below 10^–5 mbar, and the target cell is cooled down to about 25 K by a closed-cycle helium refrigerator. The SDD calibration is performed in situ with two x-ray tubes which excite titanium and copper foils placed close to the detectors. Plastic scintillators, read by pairs of silicon photo-multipliers (SiPMs), are placed inside the vacuum chamber, displaced radially outside the cylindrical gas target, for external background identification (Veto-2 system) [68]. Twelve plastic scintillators, read by pairs of photo-multiplier tubes (PMTs), are placed radially around the target (Veto-1 system), outside the vacuum chamber. The VETO systems are used to suppress the background produced by the interactions of the kaons with the setup materials, decays and nuclear absorption (synchronous background), and by the electromagnetic showers due to the particles lost by the beams and crossing the setup (asynchronous background) [69].

FIGURE 2

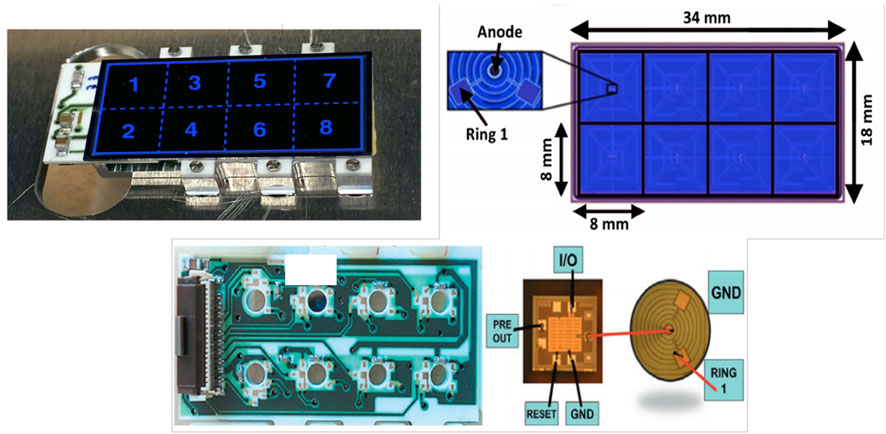
FIGURE 2. Top left: Picture of the SDD array; Top right: Schematic view of the SDD array; Bottom: The ceramic support on which the SDD cells are mounted. Reproduced from [62].

A lead shielding is placed around the vacuum chamber, downstream and upstream of the setup, to reduce the background from electrons and positrons lost from the accelerator. Additionally, two lead walls are installed along the beamline in both directions, externally to the setup, to protect the apparatus from particles (primarily minimum ionizing particles MIPs), lost from the beams due to the Touschek effect and beam-beam interactions. A Mylar degrader is placed between the target and the Interaction Point (IP) of the DAΦNE accelerator to optimize the kaon stopping power, decreasing the K⁻ momentum and centering the Bragg peak inside the target, as estimated with the MC simulations and confirmed by the measurements of the kaonic atoms x-ray rates as function of the degrader thickness ([11]). The experimental setup includes a Kaon Trigger (KT) which consists of a pair of plastic scintillators read out by photo-multipliers positioned above and below the IR. Its purpose is to identify K⁻ emitted back-to-back from the decay of the ϕ-meson in the IR, directed towards the target cell in the vertical direction, employing the Time of Flight (ToF) technique. This system allows for a drastic reduction of the background by 10⁵ thanks to the identification of the signal events, when a charged kaon enters the target cell ([62]). The SIDDHARTA-2 luminometer, based on the J-PET technology ([70–72]), is placed near the IR and consists of a pair of plastic scintillators read out by photomultipliers, positioned in the longitudinal plane. The luminometer measures the rate of kaons in the horizontal direction ([69]). The entire geometry was optimized using a GEANT4 simulation ([73]). A schematic diagram of the SIDDHARTA-2 setup is shown in Figure 3.

FIGURE 3

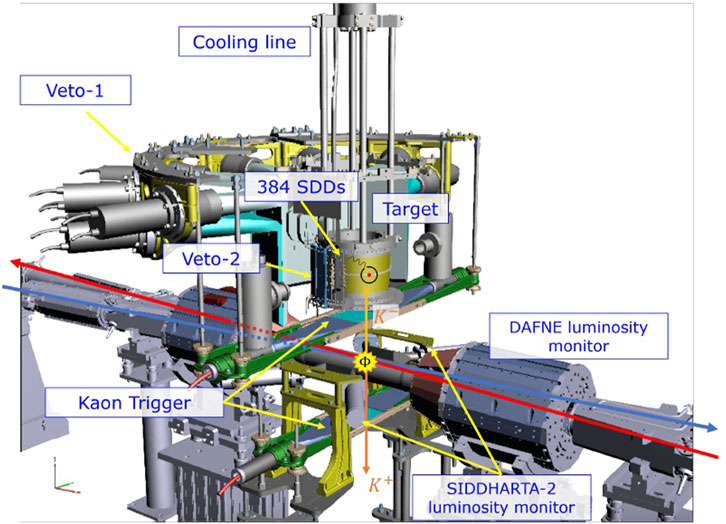
FIGURE 3. Schematic view of the SIDDHARTA-2 apparatus installed at the DAΦNE Interaction Point (reproduced from [62]).

2.2 Light kaonic atoms measured by SIDDHARTA-2

During the commissioning phase of the DAΦNE collider, in 2021, a reduced version of the SIDDHARTA-2 setup was installed at the IP of the collider, that we call the SIDDHARTINO setup. The goal was to optimize the experimental apparatus through the measurement of kaonic helium transitions to the 2p level, in a ⁴He gaseous target. These transitions have a significantly higher yield compared to the KD transition to the 1s level, and are therefore ideal for the optimization of the setup. The SIDDHARTINO apparatus was very similar to the SIDDHARTA-2 one. The most relevant difference was that it was equipped with 64 SDDs only, instead of the 384 actually used in SIDDHARTA-2. In June 2021, 26 pb⁻¹ of data were collected in about 20 days, which allowed to obtain the most precise measurement of the shift and width of the 2p atomic level in gaseous K⁻-⁴He [11]. Of these 26 pb⁻¹ of data, 16.5 pb⁻¹ were collected with 1.5% Liquid Helium Density (LHeD) and 9.5 pb⁻¹ were collected with 0.73% LHeD. The transitions yields for various densities in gaseous K⁻-⁴He were also measured [12]. In Figure 4, the spectrum collected by SIDDHARTINO of the x-ray transitions to the 2p level in K⁻-⁴He is shown. The strong interaction induced shift and width extracted by the fit for K⁻-⁴He are:

${\epsilon }_{2p}=0.2\pm 2.5\left(stat\right)\pm 2.0\left(syst\right)eV(1)$

${\mathrm{\Gamma }}_{2p}=8\pm 10\left(stat\right)eV(2)$

A detailed description of the SIDDHARTINO experiment and its results is provided in [11, 12]. The full SIDDHARTA-2 setup was installed in DAΦNE in autumn 2021, and the experiment took data with kaonic helium and other light kaonic atoms (See Figure 5) in 2022 ([62, 74]). The results of the measurements are reported in [13]. These first kaonic atoms data provided by SIDDHARTA-2 have already stimulated further theoretical activity in this area, leading to a better comprehension of strong interactions involving strangeness and the role of multi-nucleon absorption processes ([26, 28]).

FIGURE 4

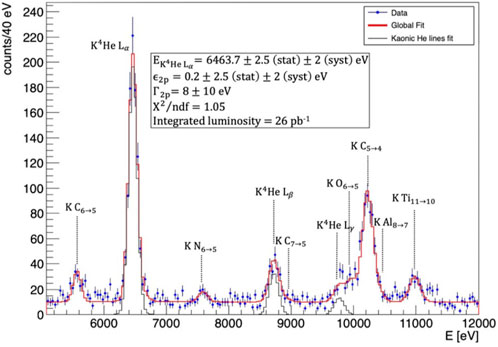
FIGURE 4. Spectrum collected by the SIDDHARTINO experiment measuring K⁻-⁴He transitions to the 2p energy level (reproduced from [12]). The data selection, based on the kaon trigger and the VETO systems was applied to suppress the synchronous and asynchronous backgrounds. The red line represents the global fit of the spectrum. Kaonic helium L_α, L_β and L_γ x-ray transitions are shown. The KN, KC, KAl and KTi lines are produced by kaons stopped in kapton walls of the target and in other elements of the setup (more details are reported in the text).

FIGURE 5

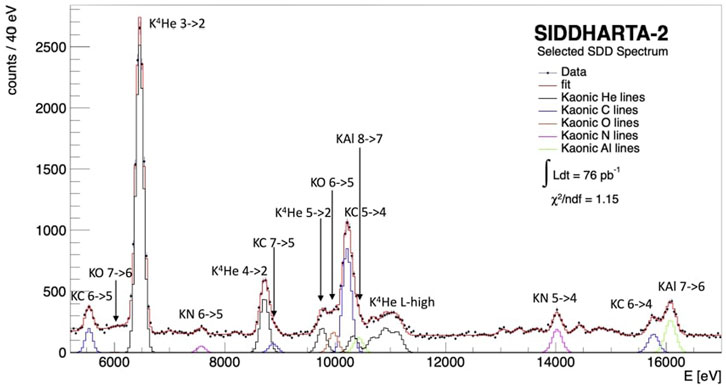
FIGURE 5. Spectrum of SIDDHARTA-2 and SIDDHARTINO summed data, after background suppression performed with kaon trigger and VETO systems. The line in red is the fit of the energy spectrum. The L_α, L_β and L_γ peaks are visible in the spectrum (black lines). KN, KC, KO, KAl, peaks (pink, blue, brown and green lines, respectively) are produced by the kaons stopped in the Kapton (C₂₂H₁₀O₅N₂) walls of the target cell and in other parts of the setup (reproduced from [13]).

2.3 Next step: The kaonic deuterium measurement

In May 2023, the SIDDHARTA-2 experiment started the measurement of the 2p → 1s transition in KD. This measurement, the first ever performed, is challenging due the very small KD x-ray yield, the even larger 1s widths of the K-lines than in KH [1] and the high-radiation environment of the DAΦNE accelerator. More than 10 years ago, SIDDHARTA made an exploratory measurement with a deuterium target ([75]). The limited statistics and the high background made the measurement of the strong interaction shift and width of the 1s level, needed for the first experimental determination of the isospin-dependent antikaon–nucleon scattering lengths, impossible. However, the data allowed to set an upper limit for the KD-lines x-ray yields: the total yield was less than 0.0143 and the K_α yield was less than 0.0039 ([76]). A Monte Carlo (MC) simulation, developed including the SIDDHARTA-2 experimental parameters and the DAΦNE background conditions, predicted the spectrum obtainable by the SIDDHARTA-2 experiment, for 800 pb⁻¹ of data with a deuterium target (see Figure 6). The assumed values of the 1s shift and width for KD were −800 eV and 750 eV, respectively. The yields ratios K_α: K_β: K_total were the same as for KH, with ${\mathrm{K}}_{\alpha }^D$ = 10^–3 per stopped kaons in gas target. Based on these MC, the shift and width of the 1s KD atomic level can be determined with precision of about 30 eV and 80 eV, respectively. The SIDDHARTA-2 data taking will go on until the end of 2024.

FIGURE 6

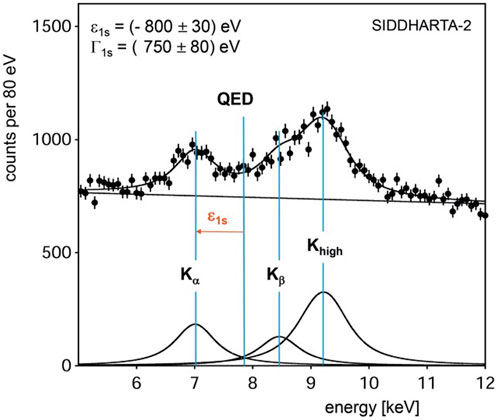
FIGURE 6. Monte Carlo simulation of the SIDDHARTA-2 kaonic deuterium spectrum for an integrated luminosity of 800 pb⁻¹. The values of the 1s shift and width for KD were −800 eV and 750 eV, respectively. The yields ratio K_α: K_β: K_total have been assumed the same for KH, with ${\mathrm{K}}_{\alpha }^D$ = 10^–3 (reproduced from [75]).

3 Beyond SIDDHARTA-2: EXKALIBUR, a proposal for future kaonic atoms measurements at DAΦNE

Kaonic atoms are a fundamental source of information for a better understanding of the strong interaction at low energies. The measurements performed so far, while significant and essential, represent only a small fraction of the vast amount of measurable kaonic atoms. Intermediate and high-Z kaonic atoms provide important insights about the in-medium kaon potential and multi-nucleonic absorption ([77]), where the chirally motivated models fail in the kaonic atoms description. The measurement of kaonic atoms, from the lightest to the heaviest ones, requires different technologies. The characteristics of the targets and the use of detectors, due to the various energy ranges of the transitions to be measured, has led to the design of a series of apparata. The Collaboration is preparing new experimental kaonic atoms measurements, with impact in various fields of physics: from providing a new precise measurement of the K⁻-mass to the investigation of nuclear resonance effects, to kaon multi-nucleon interactions and to the structure of the Λ(1405). The following subsections briefly discuss the EXKALIBUR proposal (EXtensive Kaonic Atoms research: from LIthium and Beryllium to URanium), i.e., various measurements of kaonic atoms proposed by the Collaboration, and their related apparata.

3.1 Light kaonic atoms measurements with 1 mm SDD detectors

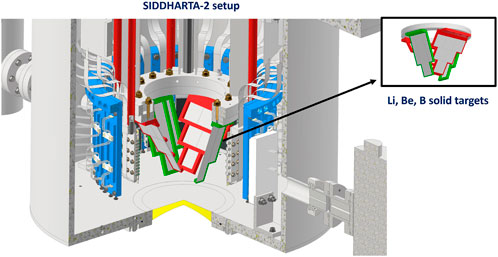
The first measurements of the K⁻-³He and K⁻-⁴He (2p → 1s) transitions, in the energy range of 30 keV, could provide stronger constraints on theoretical models describing the kaon-nucleon interaction in systems with more than two nucleons ([41]). The yields of such transitions are extremely low, but the optimal performances provided by the SIDDHARTA-2 experiment and by the DAΦNE collider, could be the key to perform such measurements. Information on the Λ(1405) can be obtained from the upper-level transitions of different isotopes of KLi, KBe, and KB ([28]). The Collaboration plans to perform high precision measurements of K⁻-³He and K⁻-⁴He (2p → 1s) transition, and several light elements, like ^6,7Li, ⁹Be, ⁹B. For these isotopes, the transitions to be measured, laying in the 10–40 keV range, are: 4 → 3 and 3 → 2 for K⁻−^6,7Li, and 5 → 4, 4 → 3 and 3 → 2 for K⁻−⁹Be and K⁻−⁹B. These measurements are planned to be performed with new 1 mm thick SDDs recently developed by POLIMI in collaboration with the Bruno Kessler Foundation (FBK) and currently being tested at POLIMI, in Milan. Such detectors provide large efficiencies in the 10–40 keV range and resolutions of 150–200 eV (FWHM), which are ideal parameters for high precision measurements. These measurements can be performed with a SIDDHARTA-2-like apparatus, where for KLi, KBe and KB a system of three solid targets will be used (see Figure 7). The energy measurements of light kaonic atoms transitions for Li, Be and B can reach a precision below 2–3 eV for an integrated luminosity of about 150 pb⁻¹. These measurements are estimated to be performed in 2–3 months, including the installations of 1 mm SDDs and of the targets, brief tests and an initial phase of debugging, followed by the data taking campaign.

FIGURE 7

FIGURE 7. Schematic view of the SIDDHARTA-2 apparatus with Li, Be and B targets.

3.2 Intermediate kaonic atoms measurements with cadmium-zinc-telluride detectors

In the ‘70s and ’80s, pioneering measurements of kaonic atoms were performed ([1]), which have been used to determine parameters of the kaon-nuclei interaction, ([27]). The most recent results on light kaonic atoms ([7–9, 78, 79]) proved that part of these old measurements are questionable. For example, recent theoretical models developed to describe the kaon-nuclei interaction and based on the data collected so far, could not fit the data, in particular when trying to accommodate transitions from kaonic sulfur ([80]). Beyond improving the quality of the kaonic atom database, measurements of several transitions in the same element are also strategic to tune the QED cascade models used to determine the purely electromagnetic energies of the kaonic atoms levels. These models are, in fact, refined and optimized using high precision kaonic atoms data ([81–83]). The Collaboration plans to measure atomic transitions towards low-n levels in several elements like carbon, aluminium and sulfur with cadmium-zinc-telluride (CdZnTe) detectors. The energy range of these transitions are between 30 and 300 keV, for which CdZnTe detectors provide a high detection efficiency (100% at 63 keV and 70% at 162 keV) and a resolution of few percent. In June 2022, a first prototype of a quasi-hemispherical CdZnTe detector system, manufactured by the IMEM-CNR of Parma, in collaboration with LNF-INFN and University of Palermo, was installed near the IP of the DAΦNE collider to test its performances in a high electromagnetic and hadronic background. The CdZnTe detector had an active surface of 1 cm² and a thickness of 5 mm. The system was vertically aligned with the SIDDHARTA-2 Luminosity Monitor ([69]), at a distance of 43 cm. The prototype was enclosed in a light-tight box with a 1 mm thick aluminium entrance window, matching the detector active surface. On the top of the box, a²⁴¹Am radioactive source was placed, producing a 500 Hz signal in the CdZnTe detector, to provide calibration peaks. The obtained spectrum, without any data selection requirement, is shown in Figure 8. The measured peak resolutions are 6% at 60 keV and 2.2% at 511 keV. Moreover, the trigger system based on the SIDDHARTA-2 Luminosity Monitor showed a rejection factor of 10^5–6 for the background suppression; more details are provided in [84].

FIGURE 8

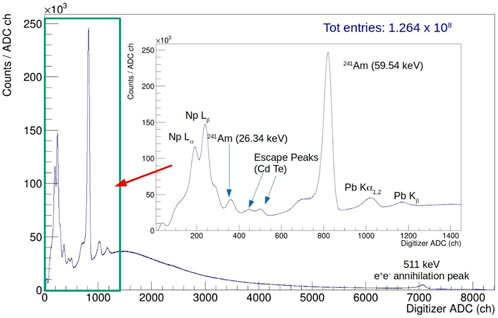
FIGURE 8. Spectrum acquired with the CdZnTe detector test system at the DAΦNE collider in 2022 (reproduced from [84]).

This very promising result encourages the SIDDHARTA-2 Collaboration to include, in its future data-taking, measurements of radiative transitions from several further intermediate and high mass kaonic atoms with dedicated CdZnTe detectors, exploiting kaons delivered from DAΦNE in the horizontal plane. The final configuration of the setup will be similar to that depicted in Figure 9. In future, the luminosity monitor of SIDDHARTA-2 will be used as trigger for the CdZnTe detectors in the same way as the Kaon Trigger acts for the SDDs, a degrader and a target will be placed after the scintillators (with dimensions optimized by Monte Carlo simulations [84]) and a third scintillator could be placed after the detectors to act as anticoincidence for the MIPs passing through the Cd(Zn)Te detectors and triggering a fake signal.

FIGURE 9

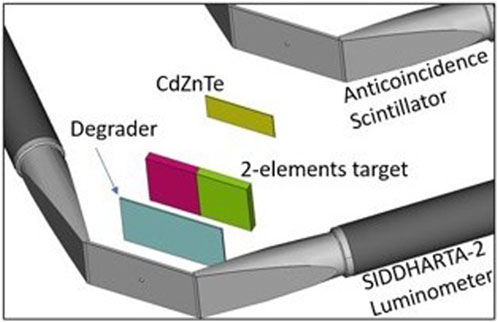
FIGURE 9. Schematic representation of the planned setup for kaonic atoms measurements with CdZnTe detection system at the DAΦNE collider.

With a similar setup, measurements of several transitions in intermediate mass kaonic atoms, like carbon, sulfur or aluminum, could be obtained in a few months with precisions of 10 eV and 20 eV for the shift and the width, respectively.

3.3 Heavy kaonic atoms measurements with high purity germanium detectors

Precision measurements of heavy kaonic atoms transitions have significant impact in two main fields: (i) to solve the charged kaon mass puzzle, namely, understanding the striking difference between the most precise measurements existing in literature ([42]), and (ii) the investigation of in-medium effects related to multi-nucleon interaction of kaons ([41, 83]). High-Z targets can be utilized to measure transitions to both low and high n-levels, where, in the former case, results about multi-nucleon interactions can be obtained, and, in the latter case, since high n-level transitions are purely QED, the charged kaon mass problem could be addressed ([40, 42]). Simultaneous measurements of atomic transitions from various n-levels and with different Δn for a single target will also help in minimizing systematic errors and provide useful information about the cascade processes in heavy kaonic atoms. Kaonic lead (KPb) is an ideal target for a precision measurement of the charged kaon mass and to investigate QCD at low energies. Moreover, the systematic uncertainty of the D⁰ meson mass can be reduced with a more precise measurement of the K⁻ mass ([29]), also impacting on the masses of the excited charmed mesons D₁ (2420)⁰. ${\mathrm{D}}_2^{*}{(2460)}^0$ and D_s1 (2536)^±. The masses of these excited charmed mesons are determined from the fit based on high-precision measurements of mass and mass difference of the D⁰, D^± and ${\mathrm{D}}_s^{\pm }$ ([40]). The precision on the D⁰ mass also impacts on the mixing parameters of the D⁰-${\bar{D}}^0$ system ([29]). The SIDDHARTA-2 Collaboration plans to measure KPb (9, 8, 7, 6 → 8, 7, 6, 5) atomic transitions with high precision ($<$ 5 eV), using a High Purity p-type Germanium Detector (HPGe), designed by Baltic Scientific Instruments. Such a detector is able to work under high-rate conditions (up to 150 kHz) and is ideal to perform measurements in the DAΦNE environment. The HPGe detector has a cylindrical active volume 59.3 mm height and 59.8 mm base diameter. The energy resolutions, tested with ¹³³Ba and ⁶⁰Co sources (activity $<$ 1 µCi), are 0.87 keV at 81 keV, 1.06 keV at 302.9 keV ([42]). The measurements can be performed by positioning the HPGe detector near the DAΦNE IP and maximizing its geometrical efficiency with appropriate shielding and according to MC simulations. The high rate capability is achieved by using a transistor reset preamplifier and a fast pulse digitizer, which processes signals directly from the preamplifier, rather than using a conventional amplifier and ADC data processing chain. An exploratory measurement is being conducted at the DAΦNE collider to test the in-beam behavior and evaluate the machine background, in parallel with the SIDDHARTA-2 experiment, but exploiting the horizontally emitted K⁻ ([42]). A schematic view of the setup is shown in Figure 10. With a MC simulation, we estimate that a precision of a few eV can be achieved with a total delivered integrated luminosity of 360 pb⁻¹. More precise information will be provided by the ongoing measurement. A similar setup will allow the measurements of other heavy kaonic atoms (as Mo, Se, Zr, Ta, etc.).

FIGURE 10

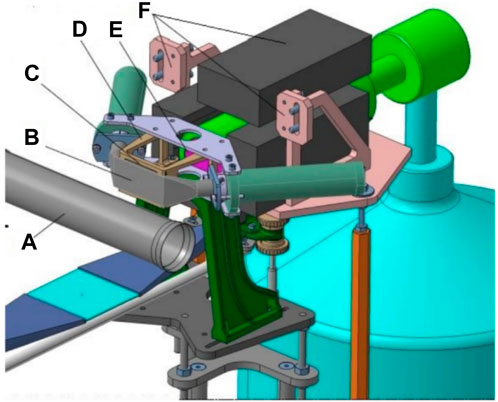
FIGURE 10. Sketch of the setup proposed by the SIDDHARTA Collaboration for the heavy kaonic atom measurement at the DAΦNE collider. The schematic view includes the active part of the HPGe detector (E), the target (C) and its holder (D), part of the mechanical support, lead shielding (F), the SIDDHARTA-2 luminosity monitor to be used as a trigger (B), and the DAΦNE beam pipe (A).

3.4 A special case: KAMEO, measurements of the E2 nuclear resonance effects in kaonic atoms

The E2 nuclear resonance occurs whenever a nuclear excitation energy closely matches an atomic de-excitation energy [85]. The resonance produces a mixing of an atomic state (n, ℓ, 0⁺) and an excited nuclear state (n, ℓ-2,2⁺), due to the electric quadrupole interaction between the kaon and the nucleus. In kaonic atoms, the rate of nuclear absorption of the kaon increases significantly for each unit of decreasing in orbital angular momentum ℓ. In resonant kaonic atoms, the E2 nuclear resonance can lead to a significant attenuation of the kaonic x-ray line and of any lower lines. Several kaonic atoms are predicted to be resonant. Among them, four isotopes of kaonic molybdenum ${\left(\right.}_{42}^{94}$Mo${\text{,\hspace{0.17em}}}_{42}^{96}$Mo${\text{,\hspace{0.17em}}}_{42}^{98}$Mo, ${\text{and\hspace{0.17em}}}_{42}^{100}$Mo) [85, 86] may provide insights about the properties of deeply bound kaonic atoms levels, which are otherwise difficult to access through K⁻ cascades, due to the nuclear absorption. Moreover, a comparison between the measurements performed on these isotopes, could reveal information about the strong nuclear potential and investigate variations in the resonance’s parameters with increasing the neutron number along the molybdenum isotopes. The E2 nuclear resonance effects were already measured in other exotic atoms, g. e. pionic atoms [87] and anti-protonic atoms [88]. Even-A antiprotonic Tellurium isotopes have been utilized to study the characteristics of the neutron density in the nuclear periphery of Te isotopes, as shown in [88]. Similarly, this investigation can be conducted on kaonic molybdenum isotopes to reveal the parameters and properties of the neutron density in the nuclear periphery. In 1975, G. L. Goldfrey, G. K. Lum, and C. E. Wiegand performed an experiment to measure the E2 nuclear resonance effect in ${\mathrm{K}}^{-}{-}_{42}^{98}$Mo at the Lawrence Berkeley Laboratory (LBL) in California [89], but the amount of data taken was not sufficient to provide conclusive results.

In KMo A = 94, 96, 98, and 100, the E2 nuclear resonance effect mixes the (6h, 0⁺) and (4f, 2⁺) states. A schematic representation of the E2 nuclear resonance effect ${\text{in\hspace{0.17em}}}_{42}^{98}$Mo is presented in Figure 11. The estimated parameters of the effect can be found in [85]. The KAMEO (Kaonic Atoms Measuring Nuclear Resonance Effects Observables) experiment plans to perform conclusive and precise measurements of the E2 nuclear resonance effects in KMo isotopes ([43]). We plan to expose to the kaons five solid target strips of enriched Mo isotopes ($>$99%) ${\text{:\hspace{0.17em}}}_{42}^{94}$Mo${\text{,\hspace{0.17em}}}_{42}^{96}$Mo${\text{,\hspace{0.17em}}}_{42}^{98}$Mo${\text{,\hspace{0.17em}}}_{42}^{100}$Mo ${\text{and\hspace{0.17em}}}_{42}^{92}$Mo (the latter used as the reference for standard transition not affected by the E2 nuclear resonance) in order to measure the x-ray transitions with the HPGe detector described in subsection 3.3. A MC simulation will be used to estimate the dimensions of the solid target strips, to maximize the efficiency of kaonic Mo isotope production and the measured x-ray transitions. The MC simulation, in parallel with the analysis of the spectra collected with the HPGe detector during the commissioning phase of DAΦNE, for background evaluation, will allow to estimate the required integrated luminosity for measurements of the effect. Further information about the KAMEO proposal can be found in [43].

FIGURE 11

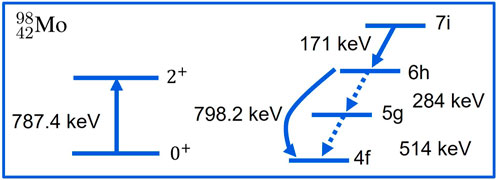
FIGURE 11. Excitation scheme of the E2 nuclear resonance effect in ${\mathrm{k}\mathrm{a}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{c}}_{42}^{98}$Mo. The resonance mixes the (6 h, 0⁺) and (4f, 2⁺) states, attenuating the 6 h→4f transition line and any lower lines with respect to a non-resonant molybdenum isotope.

3.5 Ultra-high precision kaonic atoms measurements

A more comprehensive understanding of the strong kaon-nuclei interaction, with high impact in theoretical models, could be provided by extreme precision (sub-eV) measurements of kaonic atoms transition energies. For example, the measurement of the relative difference of the 3d → 2p transition in K⁻-³He and K⁻-⁴He (isotopic shift) and of their relative widths in a gaseous target, with a precision below 1 eV, might have an important impact in the field, similar to that of the recent measurement on liquid helium ([90]). The most established technique to perform sub-eV precision x-ray measurements is the Bragg spectroscopy which, however, is limited by a very small geometrical acceptance and by the requirement of targets of a few hundreds microns. In recent years, the VOXES Collaboration at LNF-INFN developed a Highly Annealed Pyrolitic Graphite (HAPG) mosaic crystal based Von Hamos spectrometer, which has demonstrated exceptional resolution and efficiency, also when used to measure millimetric sources. This opens the door to possible future applications of such a technique to kaonic atoms spectroscopy ([91–94]). Examples of spectra obtained by the VOXES Collaboration are shown in Figure 12, where excellent resolutions are obtained also for source sizes (S₀’) of a few mm. A possible experimental setup to be used for such purposes is shown in Figure 13, with 8 spectrometer arms, each dedicated to a specific energy range. Kaons emitted from the DAΦNE IP are first detected using a scintillator and SiPM-based trigger system. They subsequently enter a target surrounding the beam pipe, where they form kaonic atoms. A spectrometer with a resolution of few eV measures the x-rays emitted during the transitions. With a similar apparatus, simultaneous measurements of K⁻-³He and K⁻-⁴He (7, 6, 5, 4, 3 → 2) transitions (see Figure 14) and KN (12, 11, 10, 9, 8, 7, 6 → 7, 6, 5) transitions could be, for example, achieved. The first ones would improve our knowledge of the isotopic shifts ([40, 42]), while the second set of measurements would contribute to a precise determination of the K⁻ mass ([83]). Both sets of measurements would also provide a wealth of data for studying electromagnetic kaon cascade processes, testing QED at the sub-eV level.

FIGURE 12

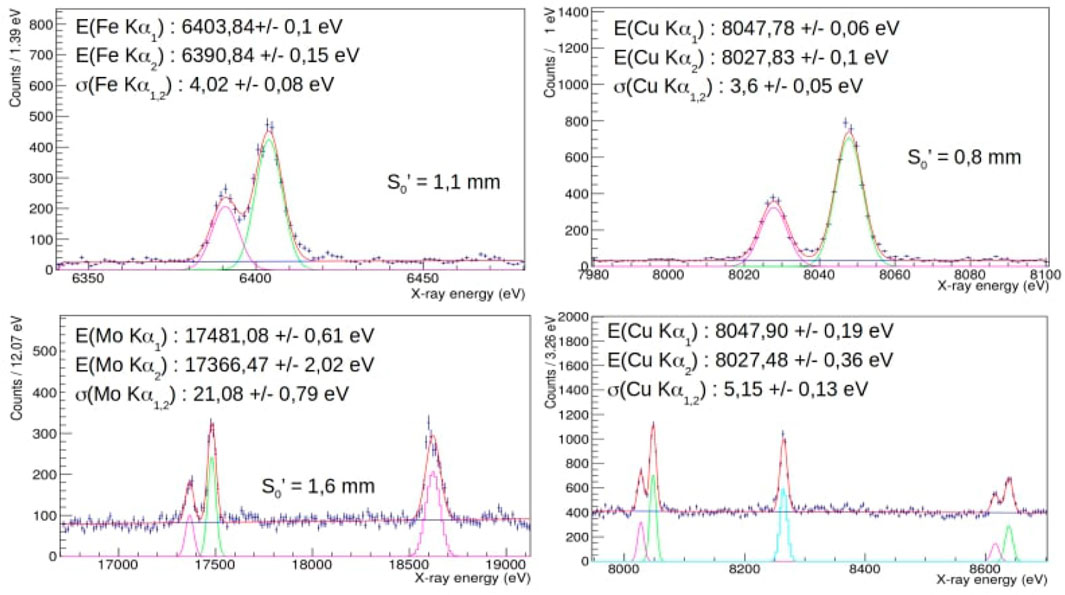
FIGURE 12. X-rays spectra from atomic transitions in Fe, Cu and Mo atoms, with VOXES setup at LNF (reproduced from [91]).

FIGURE 13

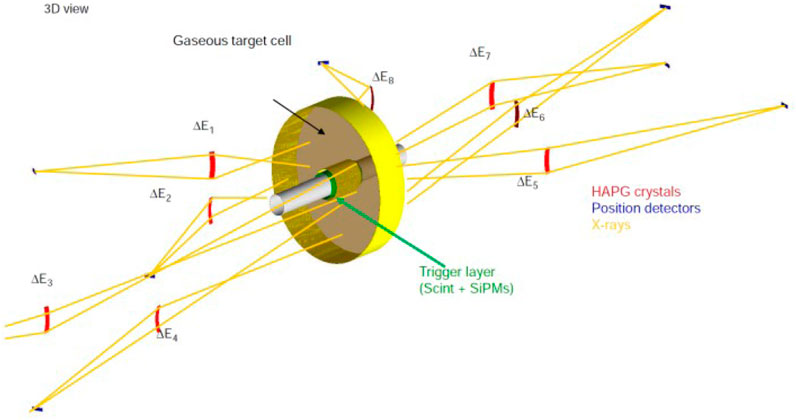
FIGURE 13. Schematic drawing of a possible experimental setup to perform ultra-high kaonic atoms measurements at the DAΦNE collider, LNF-INFN, Frascati (Italy).

FIGURE 14

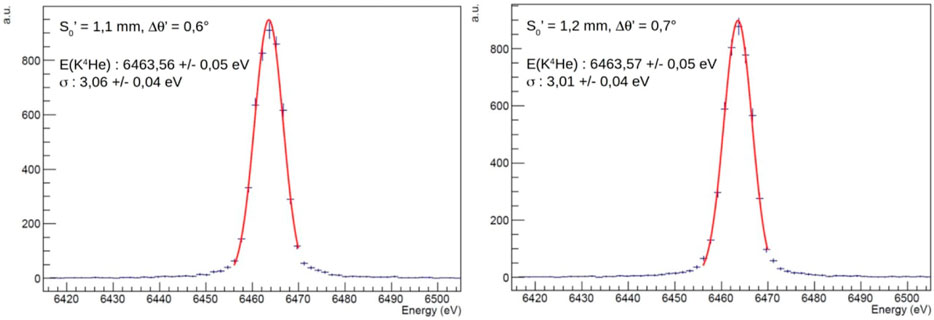
FIGURE 14. Simulated spectra of the K⁻-⁴He 3d →2p measurement achievable with the Highly Annealed Pyrolitic Graphite mosaic crystal based x-ray detection system developed by the VOXES at LNF-INFN (reference from [93]).

4 Conclusions and future perspectives

The kaonic atoms are essential tools to understand aspects of the strong interaction in low-energies regime, with implications going from particle and nuclear physics to astrophysics and cosmology. The DAΦNE collider of LNF-INFN is the ideal kaon source to perform high-precision kaonic atoms measurements. Presently, the SIDDHARTA-2 experiment is starting the kaonic deuterium measurement, aiming at a similar precision as that obtained for kaonic hydrogen performed by the SIDDHARTA experiment more than a decade ago. While preparing this delicate measurement, in the commissioning phase of the machine SIDDHARTA-2, the most precise measurement of kaonic helium 4 transitions to the 2p level in gas, and a series of unique measurements in light and intermediate kaonic atoms transitions were performed.

Beyond SIDDHARTA-2, the EXKALIBUR (EXtensive Kaonic Atoms research: from LIthium and Beryllium to URanium) proposal plans kaonic atoms measurements ([95]). The aim of EXKALIBUR is to perform unique kaonic atom measurements along the whole periodic table, to build a solid basis for all theories and models relying on kaonic atoms. These measurements will expand the database and put constraints for theoretical models which aim to describe the strong kaon-nuclei interaction at low energies. Moreover, EXKALIBUR aims to clarify discrepancies among old and recent kaonic atoms measurements, to provide new and more precise measurements and to solve the charged kaon mass puzzle ([42]) with a high precision measurement of the K⁻ mass through heavy kaonic atoms transitions measurements.

We aim to stimulate discussions and interest in the community and, in this regard, we welcome all those potentially interested to take part in the adventure of strangeness physics.

Author contributions

CC main author and group leader LD, FS, and MT corresponding authors and experimental physics working on the SIDDHARTA-2 setup FSi technical responsible and coordinator of SIDDHARTA-2 MI DAQ responsible of SIDDHARTA-2 MBa electronic engeneer responsible of SIDDHARTA-2 ASc Responsible for VOXES, experimental physics in SIDDHARTA-2 and CdZnTe detectors LA, AZ, MBe, AB, and FP responsible for CdZnTe detectors DB and IF responsible of HPGe detectors CF group leader responsible for SFERA chips and SDDs detectors production GD, MCarm, and GB engeneers for SDDs test and debug DS and KD built Monte Carlo simulation of SIDDHARTA-2 JZ responsible for installation of VETO-1 in SIDDHARTA-2 AC responsible for vacuum and cooling systems SIDDHARTA-2 YS, CY, HO, and KT responsible for kaon detector installation in SIDDHARTA-2 PM, MSk, MSi, SN, and AK responsible for VETO-2 and luminomter installations FN and OD Data analysts CG, CA, MBr, MCarg, RD, MIw, SM, JM, MM, KP, HS, and ASp, revisited critically the paper for important intellectual content. All authors contributed to the article and approved the submitted version.

Funding

Part of this work was supported by the Austrian Science Fund (FWF): [P24756-N20 and P33037-N] and FWF Doctoral program No. W1252-N27; the EXOTICA project of the Minstero degli Affari Esteri e della Cooperazione Internazionale, PO22MO03; the Croatian Science Foundation under the project IP-2018–01-8570; the EU STRONG-2020 project (Grant Agreement No. 824093); the EU Horizon 2020 project under the MSCA (Grant Agreement 754496); the Japan Society for the Promotion of Science JSPS KAKENHI Grant No. JP18H05402; the Polish Ministry of Science and Higher Education Grant No. 7150/E-338/M/2018 and the Polish National Agency for Academic Exchange (Grant No. PPN/BIT/2021/1/00037); the EU Horizon 2020 research and innovation programme under project OPSVIO (Grant Agreement No. 101038099).

Acknowledgments

We thank C. Capoccia from LNF-INFN and H. Schneider, L. Stohwasser, and D. Pristauz-Telsnigg from Stefan Meyer-Institut for their fundamental contribution in designing and building the SIDDHARTA-2 setup. We thank as well the DAΦNE staff for the excellent working conditions and permanent support. The authors acknowledge support from the SciMat and qLife Priority Research Areas budget under the program Excellence Initiative—Research University at the Jagiellonian University. Catalina Curceanu acknowledge University of Adelaide, where part of this work was done (under the George Southgate fellowship, 2023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Curceanu C, Guaraldo C, Iliescu M, Cargnelli M, Hayano R, Marton J, et al. The modern era of light kaonic atom experiments. Rev Mod Phys (2019) 91:025006. doi:10.1103/revmodphys.91.025006

CrossRef Full Text | Google Scholar

2. Gal A, Hungerford E, Millener D. Strangeness in nuclear physics. Rev Mod Phys (2016) 88:035004. doi:10.1103/revmodphys.88.035004

CrossRef Full Text | Google Scholar

3. Horiuchi W, Hyodo T, Weise W. Kaonic deuterium from realistic antikaon-nucleon interaction. EPJ Web of Conferences (2019) 199:03003. doi:10.1051/epjconf/201919903003

CrossRef Full Text | Google Scholar

4. Curceanu C, Guaraldo C, Sirghi D, Amirkhani A, Baniahmad A, Bazzi M, et al. Kaonic atoms to investigate global symmetry breaking. Symmetry (2020) 12:547. doi:10.3390/sym12040547

CrossRef Full Text | Google Scholar

5. Milardi C, Alsiene D, Biagini ME, Bonii R, Bossi F, Bosccolo M, et al. Results from the daΦne high luminosity test. Nuovo Cim (2009) 32:379.

Google Scholar

6. Beer G, Bragadireanu AM, Cargnelli M, Curceanu-Petrascu C, Egger JP, Fuhrmann H, et al. Measurement of the kaonic hydrogen x-ray spectrum. Phys Rev Lett (2005) 94:212302. doi:10.1103/physrevlett.94.212302

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bazzi M, Beer G, Bombelli L, Bragadireanu A, Cargnelli M, Corradi G, et al. A new measurement of kaonic hydrogen x-rays. Phys Lett B (2011) 704:113–7. doi:10.1016/j.physletb.2011.09.011

CrossRef Full Text | Google Scholar

8. Bazzi M, Beer G, Bombelli L, Bragadireanu A, Cargnelli M, Corradi G, et al. First measurement of kaonic helium-3 x-rays. Phys Lett B (2011) 697:199–202. doi:10.1016/j.physletb.2011.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bazzi M, Beer G, Bombelli L, Bragadireanu A, Cargnelli M, Corradi G, et al. Kaonic helium-4 x-ray measurement in siddharta. Phys Lett B (2009) 681:310–4. doi:10.1016/j.physletb.2009.10.052

CrossRef Full Text | Google Scholar

10. Napolitano F, Sgaramella F, Bazzi M, Bosnar D, Bragadireanu M, Carminati M, et al. Kaonic atoms at the daΦne collider with the siddharta-2 experiment. Phys Scr (2022) 97:084006. doi:10.1088/1402-4896/ac7fc0

CrossRef Full Text | Google Scholar

11. Sirghi DL, Sirghi F, Sgaramella F, Bazzi M, Bosnar D, Bragadireanu M, et al. A new kaonic helium measurement in gas by siddhartino at the daϕne collider. J Phys G: Nucl Part Phys (2022) 49:055106. doi:10.1088/1361-6471/ac5dac

CrossRef Full Text | Google Scholar

12. Sirghi DL, Shi H, Guaraldo C, Sgaramella F, Amsler C, Bazzi M, et al. New measurements of kaonic helium-4 l-series x-rays yields in gas with the siddhartino setup. Nucl Phys A (2023) 1029:122567. doi:10.1016/j.nuclphysa.2022.122567

CrossRef Full Text | Google Scholar

13. Sgaramella F, Tüchler M, Amsler C, Bazzi M, Bosnar D, Bragadireanu M, et al. Measurements of high-n transitions in intermediate mass kaonic atoms by SIDDHARTA-2 at DAΦNE. Eur Phys J A (2023) 59:56. doi:10.1140/epja/s10050-023-00976-y

CrossRef Full Text | Google Scholar

14. Batty C, Biagi S, Hoath S, Sharman P, Davies J, Pyle G, et al. Measurement of kaonic and pionic x-rays from liquid helium. Nucl Phys A (1979) 326:455–62. doi:10.1016/0375-9474(79)90403-2

CrossRef Full Text | Google Scholar

15. Batty C, Biagi S, Blecher M, Riddle R, Roberts B, Davies J, et al. Measurement of kaonic x-rays from li, lih and be. Nucl Phys A (1977) 282:487–92. doi:10.1016/0375-9474(77)90072-0

CrossRef Full Text | Google Scholar

16. Batty C, Biagi S, Blecher M, Hoath S, Riddle R, Roberts B, et al. Measurement of strong interaction effects in kaonic atoms. Nucl Phys A (1979) 329:407–28. doi:10.1016/0375-9474(79)90384-1

CrossRef Full Text | Google Scholar

17. Batty C, Biagi S, Riddle R, Roberts B, Pyle G, Squier G, et al. Nuclear quadrupole deformation effects on pionic and kaonic x-rays. Nucl Phys A (1981) 355:383–402. doi:10.1016/0375-9474(81)90534-0

CrossRef Full Text | Google Scholar

18. Wiegand CE, Pehl RH. Measurement of kaonic x rays from he-4. Phys Rev Lett (1971) 27:1410–2. doi:10.1103/PhysRevLett.27.1410

CrossRef Full Text | Google Scholar

19. Wiegand CE, Godfrey G. Measurements of x rays and γ rays from stopped kaons. Phys Rev A (1974) 9:2282–305. doi:10.1103/physreva.9.2282

CrossRef Full Text | Google Scholar

20. Backenstoss G, Bamberger A, Bergström I, Bunaciu T, Egger J, Hagelberg R, et al. K- mass and k-polarizability from kaonic atoms. Phys Lett B (1973) 43:431–6. doi:10.1016/0370-2693(73)90391-2

CrossRef Full Text | Google Scholar

21. Backenstoss G, Egger J, Koch H, Povel H, Schwitter A, Tauscher L. Intensities and strong interaction attenuation of kaonic x-rays. Nucl Phys B (1974) 73:189–201. doi:10.1016/0550-3213(74)90014-5

CrossRef Full Text | Google Scholar

22. Barnes P, Eisenstein R, Lam W, Miller J, Sutton R, Eckhause M, et al. Measurement of kaonic x-rays from al, si, ni and cu. Nucl Phys A (1974) 231:477–92. doi:10.1016/0375-9474(74)90511-9

CrossRef Full Text | Google Scholar

23. Kunselman R. Kaon mass measurement from kaonic atom x-ray energies; the 4f-3d kaonic transition in chlorine. Phys Lett B (1971) 34:485–7. doi:10.1016/0370-2693(71)90660-5

CrossRef Full Text | Google Scholar

24. Kunselman R. Negative - kaon mass. Phys.Rev C (1974) 9:2469–70. doi:10.1103/physrevc.9.2469

CrossRef Full Text | Google Scholar

25. Cheng S, Asano Y, Chen M, Dugan G, Hu E, Lidofsky L, et al. K- mass from kaonic atoms. Nucl Phys A (1975) 254:381–95. doi:10.1016/0375-9474(75)90224-9

CrossRef Full Text | Google Scholar

26. Friedman E, Gal A, Batty CJ. Density-dependent k⁻¹ nuclear optical potentials from kaonic atoms. Nucl Phys A (1994) 328:518–38. doi:10.1016/0375-9474(94)90921-0

CrossRef Full Text | Google Scholar

27. Batty CJ, Friedman E, Gal A. Strong interaction physics from hadronic atoms. Phys Rep (1997) 287:385–445. doi:10.1016/S0370-1573(97)00011-2

CrossRef Full Text | Google Scholar

28. Wycech S, Loiseau B. An advantage of ``Upper levels''. Acta Phys Polon B (2020) 51:109. doi:10.5506/aphyspolb.51.109

CrossRef Full Text | Google Scholar

29. Lees JP. Measurement of the mass of the d⁰ meson. Phys Rev D (2013) 88:071104.

Google Scholar

30. Prevoslek S. Hadron spectroscopy and interactions from lattice qcd. EPJ Web Conf (2016) 129:00018. doi:10.1051/epjconf/201612900018

CrossRef Full Text | Google Scholar

31. Lonardoni D, Pederiva F, Gandolfi S. Accurate determination of the interaction between λ hyperons and nucleons from auxiliary field diffusion Monte Carlo calculations. Phys Rev C (2014) 89:014314. doi:10.1103/physrevc.89.014314

CrossRef Full Text | Google Scholar

32. Drago A, Lavagno A, Pagliara G, Pigato D. Early appearance of δ isobars in neutron stars. Phys Rev C (2014) 90:065809. doi:10.1103/physrevc.90.065809

CrossRef Full Text | Google Scholar

33. Tolos L, Centelles M, Ramos A. The equation of state for the nucleonic and hyperonic core of neutron stars. Publ Astron Soc Austral (2017) 34:e065. doi:10.1017/pasa.2017.60

CrossRef Full Text | Google Scholar

34. Ramos A, Schaffner-Bielich J, Wambach J. Kaon condensation in neutron stars. Lect.Notes Phys (2001) 578:175.

CrossRef Full Text | Google Scholar

35. Ribes P, Ramos A, Tolos L, Gonzalez-Boquera C, Centelles M. Interplay between delta particles and hyperons in neutron stars. ApJ (2019) 883:168. doi:10.3847/1538-4357/ab3a93

CrossRef Full Text | Google Scholar

36. Bonanno L, Sedrakian A. Composition and stability of hybrid stars with hyperons and quark color-superconductivity. Astron Astrophys (2012) 539:A16. doi:10.1051/0004-6361/201117832

CrossRef Full Text | Google Scholar

37. Dalitz RH, Tuan SF. Possible resonant state in pion-hyperon scattering. Phys Rev Lett (1959) 2:425–8. doi:10.1103/PhysRevLett.2.425

CrossRef Full Text | Google Scholar

38. Dalitz RH, Tuan SF. The phenomenological representation of - scattering and reaction amplitudes. Ann Phys (1960) 10:307–51. doi:10.1016/0003-4916(60)90001-4

CrossRef Full Text | Google Scholar

39. Hall JMM, Kamleh W, Leinweber DB, Menadue BJ, Owen BJ, Thomas AW, et al. Lattice qcd evidence that the λ(1405) resonance is an antikaon-nucleon molecule. Phys Rev Lett (2015) 114:132002. doi:10.1103/PhysRevLett.114.132002

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Workman RL. Particle data group. Prog Theor Exp Phys (2022) 2022:083C01.

Google Scholar

41. Curceanu C, Guaraldo C, Scrado A, Sirghi D. Strong interaction with strangeness@lnf: A unique opportunity (2021). arXiv.

Google Scholar

42. Bosnar D, Bazzi M, Cargnelli M, Clozza A, Curceanu C, Del Grande R, et al. Revisiting the charged kaon mass. Acta Phys Polon B (2020) 51:115. doi:10.5506/aphyspolb.51.115

CrossRef Full Text | Google Scholar

43. De Paolis L, Bazzi M, Bosnar D, Bragadireanu M, Cargnelli M, Carminati M, et al. Investigating the e2 nuclear resonance effect in kaonic atoms. J Phys Conf Ser (2023) 2446:012038. doi:10.1088/1742-6596/2446/1/012038

CrossRef Full Text | Google Scholar

44. Weissenborn S, Chatterjee D, Schaffner-Bielich J. Hyperons and massive neutron stars: The role of hyperon potentials. Nucl Phys A (2012) 881:62–77. doi:10.1016/j.nuclphysa.2012.02.012

CrossRef Full Text | Google Scholar

45. Lonardoni D, Lovato A, Gandolfi S, Pederiva F. Hyperon puzzle: Hints from quantum Monte Carlo calculations. Phys Rev Lett (2015) 114:092301. doi:10.1103/PhysRevLett.114.092301

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Gerstung D, Kaiser N, Weise W. Hyperon–nucleon three-body forces and strangeness in neutron stars. Eur Phys J A (2020) 56:175. doi:10.1140/epja/s10050-020-00180-2

CrossRef Full Text | Google Scholar

47. Adam C, Garcìa Martìn-Caro A, Huidobro M, Vàzquez R, Wereszczynski A. Kaon condensation in skyrmion matter and compact stars. Phys Rev D) (2023) 107:074007. doi:10.1103/PhysRevD.107.074007

CrossRef Full Text | Google Scholar

48. Kumari M, Kumar A. Antikaon condensation in magnetized neutron stars. Int J Mod Phys E (2022) 31:2250050. doi:10.1142/S0218301322500501

CrossRef Full Text | Google Scholar

49. Ma F, Wu C, Guo W. Kaon-meson condensation and δresonance in hyperonic stellar matter within a relativistic mean-field model. Phys Rev C (2023) 107:045804. doi:10.1103/PhysRevC.107.045804

CrossRef Full Text | Google Scholar

50. Ma F, Guo W, Wu C. Kaon meson condensate in neutron star matter including hyperons. Phys Rev C (2022) 105:015807. doi:10.1103/PhysRevC.105.015807

CrossRef Full Text | Google Scholar

51. Muto T, Maruyama T, Tatsumi T. Effects of three-baryon forces on kaon condensation in hyperon-mixed matter. Phys Lett B (2021) 820:136587. doi:10.1016/j.physletb.2021.136587

CrossRef Full Text | Google Scholar

52. De Paolis L. The siddharta-2 experiment: Preparation for the first kaonic deuterium measurement. PoS (2022) 414:1003.

Google Scholar

53. Cieplý A, Mai M, Meißner UG, Smejka J. On the pole content of coupled channels chiral approaches used for the kn system. Nucl Phys A (2016) 954:17–40. doi:10.1016/j.nuclphysa.2016.04.031

CrossRef Full Text | Google Scholar

54. Bruns PC, Mai M, Meißner UG. Chiral dynamics of the s₁₁(1535) and s₁₁(1650) resonances revisited. Phys Lett B (2011) 697:254–9. doi:10.1016/j.physletb.2011.02.008

CrossRef Full Text | Google Scholar

55. Mai M, Meißner UG. New insights into antikaon–nucleon scattering and the structure of the λ (1405). Nucl Phys A (2013) 900:51–64. doi:10.1016/j.nuclphysa.2013.01.032

CrossRef Full Text | Google Scholar

56. Guo Z, Oller JA. Meson-baryon reactions with strangeness -1 within a chiral framework. Phys Rev C (2013) 87:035202. doi:10.1103/physrevc.87.035202

CrossRef Full Text | Google Scholar

57. Ikeda Y, Hyodo T, Weise W. Chiral su(3) theory of antikaon–nucleon interactions with improved threshold constraints. Nucl Phys A (2012) 881:98–114. doi:10.1016/j.nuclphysa.2012.01.029

CrossRef Full Text | Google Scholar

58. Cieplý A, Friedman E, Gal A, Gazda D, Mareš J. Chirally motivated k⁻ nuclear potentials. Phys Lett B (2011) 702:402–7. doi:10.1016/j.physletb.2011.07.040

CrossRef Full Text | Google Scholar

59. Cieplý A, Friedman E, Gal A, Gazda D, Mareš J. K⁻ nuclear potentials from in-medium chirally motivated models. Phys Rev C (2011) 84:045206. doi:10.1103/physrevc.84.045206

CrossRef Full Text | Google Scholar

60. Cieplý A, Smejkal J. Chirally motivated kn amplitudes for in-medium applications. Nucl Phys A (2012) 881:115–26. doi:10.1016/j.nuclphysa.2012.01.028

CrossRef Full Text | Google Scholar

61. Liu Z, Wu JJ, Leinweber DB, Thomas AW. Kaonic hydrogen and deuterium in Hamiltonian effective field theory. Phys Lett B (2020) 808:135652. doi:10.1016/j.physletb.2020.135652

CrossRef Full Text | Google Scholar

62. De Paolis L, Bazzi M, Bosnar D, Bragadireanu M, Cargnelli M, Carminati M, et al. Trigger rejection factor in the first kaonic helium run with the complete siddharta-2 setup. EPJ Web Conf (2022) 270:00028. doi:10.1051/epjconf/202227000028

CrossRef Full Text | Google Scholar

63. Bombelli L. Low-noise cmos charge preamplifier for x-ray spectroscopy detectors. IEEE Nucl Sci Symposuim Med Imaging Conf (2010) 135.

CrossRef Full Text | Google Scholar

64. Quaglia R, Schembari F, Bellotti G, Butt A, Fiorini C, Bombelli L, et al. Development of arrays of silicon drift detectors and readout asic for the siddharta experiment. Nucl Instrum Meth A (2016) 824:449–51. doi:10.1016/j.nima.2015.08.079

CrossRef Full Text | Google Scholar

65. Schembari F, Quaglia R, Bellotti G, Fiorini C. Sfera: An integrated circuit for the readout of x and γ-ray detectors. IEEE Trans Nucl Sci (2016) 63:1797–807. doi:10.1109/tns.2016.2565200

CrossRef Full Text | Google Scholar

66. Miliucci M, Iliescu M, Sgaramella F, Bazzi M, Bosnar D, Bragadireanu M, et al. Large area silicon drift detectors system for high precision timed x-ray spectroscopy. Meas Sci Technol (2022) 33:095502. doi:10.1088/1361-6501/ac777a

CrossRef Full Text | Google Scholar

67. Miliucci M, Iliescu M, Amirkhani A, Bazzi M, Curceanu C, Fiorini C, et al. Energy response of silicon drift detectors for kaonic atom precision measurements. Condens Matter (2019) 4:31. doi:10.3390/condmat4010031

CrossRef Full Text | Google Scholar

68. Tuchler M, Sirghi F, Bazzi M, Bosnar D, Bragadireanu M, Carminati M, et al. Main features of the siddharta-2 apparatus for kaonic deuterium x-ray measurements. EPJ Web Conf (2022) 7:01016. doi:10.1051/epjconf/202226201016

CrossRef Full Text | Google Scholar

69. Skurzok M, Scordo A, Niedzwiecki S, Baniahmad A, Bazzi M, Bosnar D, et al. Characterization of the siddharta-2 luminosity monitor. JINST (2020) 15:P10010. doi:10.1088/1748-0221/15/10/p10010

CrossRef Full Text | Google Scholar

70. Moskal P, Dulski K, Chug N, Curceanu C, Czerwiński E, Dadgar M, et al. Positronium imaging with the novel multiphoton pet scanner. Sci Adv (2022) 7:eabh4394. doi:10.1126/sciadv.abh4394

CrossRef Full Text | Google Scholar

71. Moskal P, Gajos A, Mohammed M, Chhokar J, Chug N, Curceanu C, et al. Testing cpt symmetry in ortho-positronium decays with positronium annihilation tomography. Nat Commun (2021) 12:5658. doi:10.1038/s41467-021-25905-9

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Niedźwiecki S, Białas P, Curceanu C, Czerwiński E, Dulski K, Gajos A, et al. J-Pet: a new technology for the whole-body pet imaging. Acta Phys Pol B (2017) 48:1567. doi:10.5506/aphyspolb.48.1567

CrossRef Full Text | Google Scholar

73. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—A simulation toolkit. Nucl Inst Meth Phys Res Sect A (2003) 506:250–303. doi:10.1016/s0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

74. Sgaramella F, Bazzi M, Bosnar D, Bragadireanu M, Cargnelli M, Carminati M, et al. Kaonic atoms measurements with siddharta-2. J Phys Conf Ser (2023) 2446:012023. doi:10.1088/1742-6596/2446/1/012023

CrossRef Full Text | Google Scholar

75. Curceanu C, Amirkhani A, Baniahmad A, Bazzi M, Bosnar D, Bragadireanu M, et al. Kaonic deuterium measurement with siddharta-2 on daϕne. Acta Phys Pol B (2020) 51:251. doi:10.5506/aphyspolb.51.251

CrossRef Full Text | Google Scholar

76. Bazzi M, Beer G, Berucci C, Bombelli L, Bragadireanu A, Cargnelli M, et al. Preliminary study of kaonic deuterium x-rays by the siddharta experiment at daΦne. Nucl Phys A (2013) 907:69–77. doi:10.1016/j.nuclphysa.2013.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Obertovà J, Friedman E, Mareš J. First application of a microscopic k-nn absorption model in calculations of kaonic atoms. Phys Rev C (2022) 106:065201. doi:10.1103/PhysRevC.106.065201

CrossRef Full Text | Google Scholar

78. Iwasaki M, Hayano RS, Ito TM, Nakamura SN, Terada TP, Gill DR, et al. Observation of kaonic hydrogen k_α x rays. Phys Rev Lett (1997) 78:3067–9. doi:10.1103/physrevlett.78.3067

CrossRef Full Text | Google Scholar

79. Okada S, Beer G, Bhang H, Cargnelli M, Chiba J, Choi S, et al. Precision measurement of the 3d → 2p x-ray energy in kaonic 4he. Phys Lett B (2007) 653:387–91. doi:10.1016/j.physletb.2007.08.032

CrossRef Full Text | Google Scholar

80. Curceanu C, Guaraldo C, Scrado A, Sirghi D, Bosnar D, Amsler C, et al. Fundamental physics at the strangeness frontier at daΦne workshop (2021). arXiv.

Google Scholar

81. Batty CJ. Exotic atoms. Sov J Part Nucl (1982) 13:71.

Google Scholar

82. Ishiwatari T, Beer G, Bragadireanu A, Cargnelli M, Curceanu Petrascu C, Egger JP, et al. Kaonic nitrogen x-ray transition yields in a gaseous target. Phys Lett B (2004) 593:48–54. doi:10.1016/j.physletb.2004.04.055

CrossRef Full Text | Google Scholar

83. Koike J. Cascade calculation of exotic atoms with many electrons. electron population during the cascade of kaonic nitrogen atoms. Genshikaku Kenkyu (2005) 49:159.

Google Scholar

84. Abbene L. New opportunities for kaonic atoms measurements from cdznte detectors (2023). p. 12253. Arxiv.

Google Scholar

85. Leon M. Hadronic atoms and ticklish nuclei: The e2 nuclear resonance effect. Nucl Phys A (1976) 260:461–73. doi:10.1016/0375-9474(76)90057-9

CrossRef Full Text | Google Scholar

86. Leon M. Quadrupole mixing in hadronic atoms: An additional probe of the hadron-nucleus interaction. Phys Lett B (1974) 50:425–8. doi:10.1016/0370-2693(74)90251-2

CrossRef Full Text | Google Scholar

87. Bradbury JN, Leon M, Daniel H, Reidy JJ. Observation of the e2 nuclear resonance effect in pionic cadmium. Phys Rev Lett (1975) 34:303–6. doi:10.1103/physrevlett.34.303

CrossRef Full Text | Google Scholar

88. Klos B, Wycech S, Trzcińska A, Jastrzȩbski J, Czosnyka T, Kisieliński M, et al. Strong interaction and e2 effect in even-a antiprotonic te atoms. Phys Rev C (2004) 69:044311. doi:10.1103/physrevc.69.044311

CrossRef Full Text | Google Scholar

89. Goldfrey GL, Lum GK, Wiegand CE. Observation of dynamic e2 mixing via kaonic x-ray intensities. Phys Lett B (1976) 61:45–6. doi:10.1016/0370-2693(76)90557-8

CrossRef Full Text | Google Scholar

90. Hashimoto T, Aikawa S, Akaishi T, Asano H, Bazzi M, Bennett D, et al. Measurements of strong-interaction effects in kaonic-helium isotopes at sub-ev precision with x-ray microcalorimeters. Phys Rev Lett (2022) 128:112503. doi:10.1103/physrevlett.128.112503

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Scordo A, Breschi L, Curceanu C, Miliucci M, Sirghi F, Zmeskal J. High resolution multielement xrf spectroscopy of extended and diffused sources with a graphite mosaic crystal based von hamos spectrometer. J Anal Spectrom (2020) 35:155–68. doi:10.1039/c9ja00269c

CrossRef Full Text | Google Scholar

92. Scordo A, Curceanu C, Miliucci M, Sirghi F, Zmeskal J. High precision x-ray measurements. Condensed Matter (2019) 4:59. doi:10.3390/condmat4020059

CrossRef Full Text | Google Scholar

93. Scordo A. Hapg mosaic crystal von hamos spectrometer for high precision kaonic atoms spectroscopy. Particles and Nuclei (2021) 5:10.

Google Scholar

94. Scordo A, De Leo V, Curceanu C, Miliucci M, Sirghi F. Efficiency measurements and simulations of a hapg based von hamos spectrometer for large sources. J Anal Spectrom (2021) 36:2485–91. doi:10.1039/d1ja00214g

CrossRef Full Text | Google Scholar

95. Curceanu C. Siddharta-2 status report. Sci Com LNF-INFN (2023) 2023.

Google Scholar