DilatedFormer: dilated granularity transformer network for placental maturity grading in ultrasound

Placental maturity grading (PMG) is often utilized for evaluating fetal growth and maternal health. Currently, PMG often relied on the subjective judgment of the clinician, which is time-consuming and tends to incur a wrong estimation due to redundancy and repeatability of the process. The existing methods often focus on designing diverse hand-crafted features or combining deep features and hand-crafted features to learn a hybrid feature with an SVM for grading the placental maturity of ultrasound images. Motivated by the dominated performance of end-to-end convolutional neural networks (CNNs) at diverse medical imaging tasks, we devise a dilated granularity transformer network for learning multi-scale global transformer features for boosting PMG. Our network first devises dilated transformer blocks to learn multi-scale transformer features at each convolutional layer and then integrates these obtained multi-scale transformer features for predicting the final result of PMG. We collect 500 ultrasound images to verify our network, and experimental results show that our network clearly outperforms state-of-the-art methods on PMG. In the future, we will strive to improve the computational complexity and generalization ability of deep neural networks for PMG.

1 Introduction

The placenta, an essential organ for fetal–placental blood circulation, gas exchange, nutrient supply, and fetal waste elimination, can serve as an immune barrier and minimize small gestational age (SGA), stillbirth, and pregnancy complications [1]. It cannot be emphasized more that placental development is indispensable for fetal growth and normal pregnancy, as well as closely related to the placental size, umbilical cord, and cord blood flow. The blood exchange between the mother and the fetus begins in the early embryo after the fourth week of pregnancy and may stop any time when approaching late pregnancy. Therefore, the correct identification of a mature placenta plays a key role in preventing fetal death by removing the fetus before placental senescence.

As a common medical modality for routine placental evaluation, ultrasound imaging has been widely adopted for prenatal diagnosis, prognosis, and evaluation of placental abnormalities [1–3], due to its non-radiation, convenience, and efficiency. Furthermore, ultrasound imaging can reflect the changes of the calcification degree from placental images without applying a contrast agent. These factors have successfully inspired many interests [1, 2, 4–6]. However, most existing placental maturity staging methods heavily depend on a doctor’s subjective measurement, which inevitably results in human error. Based on this, we argue that better and more consistent decisions can be obtained with an objective assessment. Hence, an automatic method for the objective assessment that complements the doctor’s subjective assessment would provide a more precise interpretation for placental evaluation [4, 5]. Although the challenging issues of placental maturity have been widely resolved, the changes in calcification and image quality limitations make subjective measurements uncompetitive [7]. Automatic computer-assisted diagnosis not only reduces errors caused by subjective judgment [8] but also provides an attractive and meaningful standardization tool [9–11] to improve the efficiency of diagnosis.

However, the existing automatic methods heavily relied on hand-crafted features to combine hand-crafted features with deep features from grayscale ultrasound images to evaluate placental maturity. It is time-consuming to design the specific hand-crafted features and inefficiency to deploy upon different datasets. Deep learning has shown tremendous potential in medical image analysis over the past decade. Medical images are complex and heterogeneous, and traditional machine learning algorithms struggle to accurately classify and segment them. Deep learning algorithms, on the other hand, have shown remarkable success in these tasks due to their ability to learn complex features from limited data [12–14]. One of the most popular deep learning architectures used in medical image classification and segmentation is convolutional neural networks (CNNs). CNNs are designed to automatically learn and extract features from images through layers of convolutional filters. They have been used successfully in a variety of medical imaging applications, including mammography [15], brain imaging [16], and prostate cancer detection [17].

Motivated by the dominant performance of CNNs, it is desirable to develop an end-to-end network for automatic placental maturity grading (PMG) from ultrasound images. In this work, we present a dilated granularity transformer network for staging placental maturity from ultrasound images by learning multi-scale long-range dependency features. To the best of our knowledge, our work is the first end-to-end network to grade placental maturity from ultrasound images. In our work, we devise a set of dilated transformer blocks to extract long-range dependency global features in a multi-scale manner from the input ultrasound image. Then, we progressively integrate these global features to predict the final result of the placental maturity grading. We collected 500 ultrasound images to evaluate the effectiveness of our method, and the experimental results show that our network clearly outperforms the state-of-the-art methods.

In summary, the contributions of our work have been summarized as follows:

• We devised a transformer-based pipeline to grade the placental maturity of the B-mode ultrasound image. To the best of our knowledge, our work is the first end-to-end network for addressing PMG from the ultrasound image.

• In our network, we devised a dilated transformer block to learn multi-scale transformer features and then integrate the obtained features at different convolutional layers for the reliable prediction of PMG.

• We collected 500 annotated ultrasound images, and experimental results show that our network clearly outperforms the state-of-the-art methods.

2 Related work

2.1 Placental maturity grading

Grannum et al. [6] presented the first PMG method on gray-scale ultrasound images to classify the chorionic plate, substance, and basal plate of the placenta into four grades, as shown in Figure 1. Although achieving promising results, this method largely relied on the visual inspection of ultrasound images to stage the placental maturity, which is subjective and time-consuming and lacks objective measurement. To alleviate this issue, many researchers have developed diverse automatic algorithms for grading placental maturity. Lei et al. [5] graded placental maturity by computing a fish vector (FV) and invariant descriptor based on local intensity, while Li et al. [4] adopted a dense DAISY [18] descriptor for staging placental maturity due to its superior performance over co-variant affine feature descriptors. Apart from the B-mode ultrasound (BUS) images, features are also computed from color Doppler energy (CDE) images for boosting the PMG performance. Lei et al. [19] utilized a hybrid learning framework to combine BUS images and CDE images, and later harnessed multi-view and multi-layout discriminative learning to fuse features extracted from BUS and CDE images in Eq. 3. Moreover, Lei et al. [20] proposed to integrate deep descriptors extracted from CNNs and hand-crafted features on BUS and CDE images to produce hybrid descriptors for boosting the grading performance. Despite achieving good performance in PMG, these methods are not effective to learn long-range context features, which has been proven to be an efficient manner as a self-attention mechanism [21] for booting network prediction performance than classical CNNs.

FIGURE 1

FIGURE 1. Cases of four levels of placental maturity are listed. (A) Grade 0; (B) Grade I; (C) Grade II; (D) Grade III.

2.2 Transformer

Transformer was first proposed for the machine translation task [22]. In the NLP domain, the transformer-based methods have achieved the state-of-the-art performance in various tasks [23]. ViT [24] first introduced transformer into visual tasks and achieved impressive performance because of the capacity for its global dependencies. Vision tasks developed a new stage inspired by ViT. For example, DeiT [25] explored the efficient training strategies for ViT, and the Swin transformer [26] was an effective hierarchical vision transformer, whose window-based mechanism enhances the locality of features. PVT [21] proposed a pyramid transformer with spatial reduction attention (SRA) to reduce the computational complexity, while MViT [27] created a multiscale pyramid of features to simultaneously model simple low-level visual information and complex high-dimensional features. For medical imaging tasks, TransUNet [28] combined the merits of transformer and U-net to construct a stronger alternative for medical image segmentation, while DS-TransUNet [29] incorporated the hierarchical Swin transformer into both the encoder and the decoder of the standard U-shaped architecture. Most works [30–34] in medical image classification jointly adopt the CNN and transformer model but did not develop a transformer-based backbone without convolutions to capture multi-granularity information in medical images.

3 Methods

The overall architecture of our designed DilatedFormer is illustrated in Figure 2. Given an input image with a spatial size of H × W × 3, we split it into the more informative token sequence with the length of $\frac{H}{4}\times \frac{W}{4}$ and the dimension of C by an improved overlapped patch embedding scheme. Our DilatedFormer network has four transformer stages to extract hierarchical feature maps, and each transformer stage stacks multiple dilated transformer blocks. An additional convolution layer with stride 2, i.e., linear embedding, is utilized between two stages to reduce a half size of the feature maps, and the size of feature maps S_i at the i-th (i = 1, 2, 3, 4) stages is $\frac{H}{2^{i+1}}\times \frac{W}{2^{i+1}}\times (C\times 2^{i-1})$. Finally, only the last three feature maps will be fed into our feature pyramid decoder to provide multi-resolution knowledge for predicting the output placental grading.

FIGURE 2

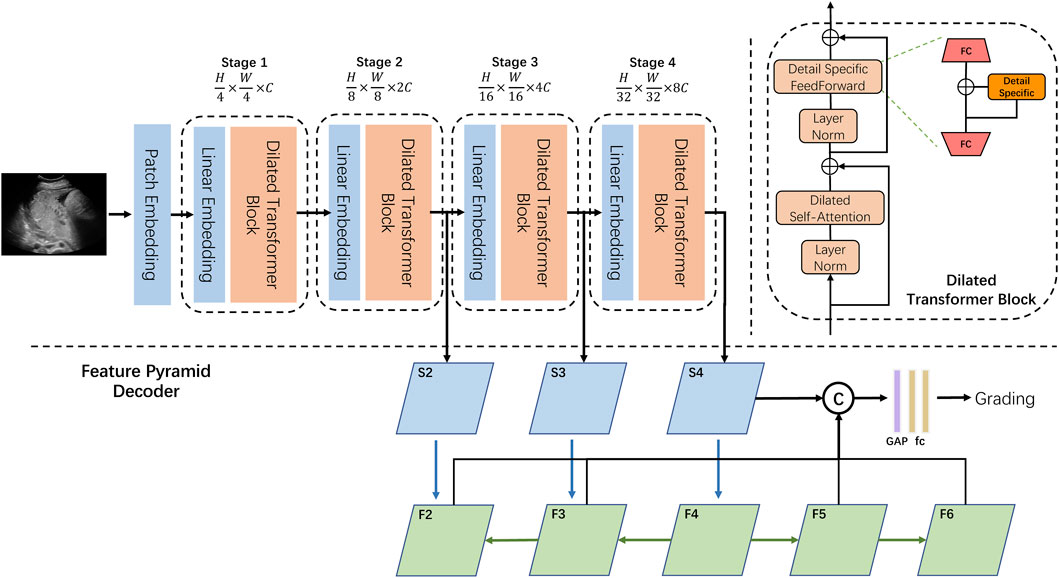
FIGURE 2. Overview of our DilatedFormer network. Top left: the encoder of our DilatedFormer network. Top right: details of the dilated transformer block. Bottom: the procedure of Feature Pyramid Decoder.

3.1 Dilated transformer block

As shown in Figure 2, our proposed dilated transformer block consists of a multi-head dilated self-attention (DSA) layer, a detail-specific feed-forward layer, and two layer normalization operations. To reduce the computational cost when processing high-resolution feature maps, PVT [21] adopted spatial reduction attention (SRA) to replace the vanilla multi-head self-attention (MSA). Since the pooled feature extracted by a single scale in PVT is less powerful, we equipped self-attention with parallel dilated convolutions with different dilated rates and scales to better detect multi-grain objects in one cohort.

What makes DSA blocks outperform the traditional self-attention blocks are the following: 1) DSA introduces a dilated convolutional mechanism to capture multi-scale information and integrate features of different sizes in one stage. 2) Weight-sharing dilated convolution boosts the model performance with a marginal increase in the number of parameters. 3) Detail-specific feed-forward network recovers local information, while DSA enhances its global counterpart. Furthermore, a feature pyramid decoder network is designed to grade the placental maturity, considering both high-resolution coarse features and low-resolution fine-grained features.

3.1.1 Dilated self-attention

Multi-scale features have shown superior performance in detecting objects with different grains [35]. Moreover, dilated convolution [36, 37] is proposed to capture the multi-scale context with the same amount of parameters as standard convolutions. Weight-sharing dilated convolution [38] is also designed to improve model performances without increasing the number of parameters. Different from local convolution operations, the self-attention mechanism learns long-range features by performing a weighted sum of the projected input vectors from all spatial locations and computing similarities between the queries and keys. To consider multi-scale information for computing weights of the self-attention mechanism, we used parallel dilated convolutions with different rates on the key and value. Specifically, given an input feature map X, we first downsample X to obtain two feature maps (H₁ and H₂) with a downsampling rate sr_i. It should be noted that the downsampling rate sr_i varying across attention heads in one layer further strengthens the ability to learn multi-granularity features. For example, as shown in Figure 3, attention heads are divided into two groups to emphasize the corresponding downsampling rate. Then, we apply three dilated convolutions on two downsampled features H₁ and H₂, respectively. These three dilated convolutions have different dilation rates dr but a shared 3 × 3 kernel to capture the multi-scale contexts after spatial reduction. After that, we added three dilated features from H₁ and H₂ by a self-calibration scheme (i.e., SiLU activation function [39]) to compute a feature map P:

$P=\sum _{dr\in \left\{\mathrm{1,3,5}\right\}}SiLU\left(Conv\left(\widehat{X},dr\right)\right),(1)$

$\widehat{X}=Conv\left(X,s{r}_i\right),(2)$

$SiLU\left(m\right)=m\cdot \sigma \left(m\right),(3)$

where SiLU denotes the SiLU activation function. σ(⋅), dr, and sr_i denote the Sigmoid activation function, the dilation rate, and the spatial downsampling rate in the ith head module, respectively. As shown in Figure 3, we can obtain two features (P₁ and P₂) from two groups of three dilated convolutions. This scheme provides the similarity calculation of the query and key between each pair of spatial locations with multi-scale information.

FIGURE 3

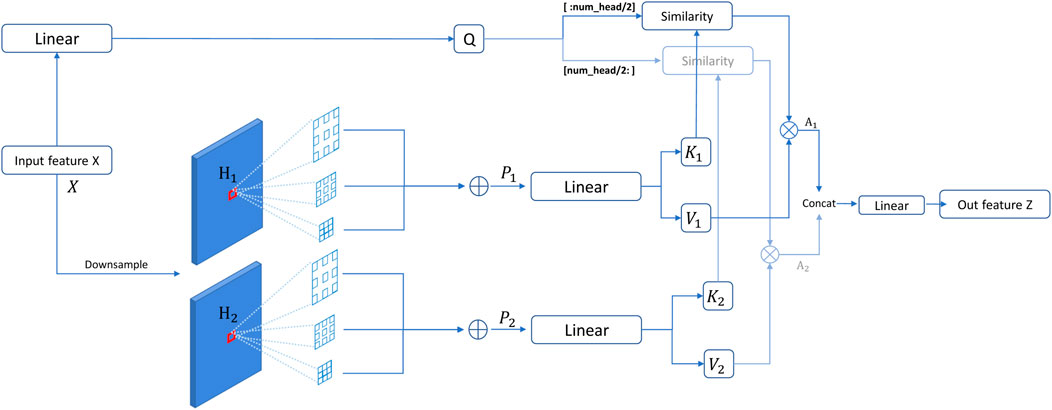
FIGURE 3. Overall procedure of our dilated self-attention (DSA). In such a setting, attention heads are divided into two groups, which focus on different downsampling rates. The corresponding outputs of similarity calculation are concatenated to be the final output of DSA.

Then, these two features (P₁ and P₂) are passed into a linear layer to obtain the key feature and value feature. Meanwhile, we apply a linear layer on the input feature to obtain a query feature map. For the ith head, we can compute the query, key, and value vectors:

$\left(Q,K_1,V_1\right)=\left(X{W}_q,P_1{W}_k,P_1{W}_v\right),V_1=V_1+DWConv\left(V_1\right),(4)$

$\left(Q,K_2,V_2\right)=\left(X{W}_q,P_2{W}_k,P_2{W}_v\right),V_2=V_2+DWConv\left(V_2\right),(5)$

where W_q, W_k, and W_v denote the weight matrices of linear transformations for generating the query, key, and value tensors in the ith head, respectively. DWConv(⋅) is depth-wise convolution to enhance the local details for the value vector. After that, Q, K₁, and V₁ are fed into the attention module to compute the self-attention feature map A₁, while Q, K₂, and V₂ are fed into the attention module to compute the self-attention feature map A₂. A₁ and A₂ are computed as follows:

$A_1=Softmax\left(\frac{Q{\left(K_1\right)}^T}{\sqrt{d_K}}\right)\times V_1,A_2=Softmax\left(\frac{Q{\left(K_2\right)}^T}{\sqrt{d_K}}\right)\times V_2,(6)$

where d_K is the channel dimension of K and $\sqrt{d_K}$ can serve as an approximate normalization operation. Then, we concatenate two self-attention features and pass the concatenation result into a 1 × 1 linear convolutional layer to compute the output feature map Z of our DSA module:

$Z=Conv\left(Concat\left(A_1,A_2\right)\right).(7)$

Each spatial location in different scales makes a diverse contribution to the feature response, according to the computed attention. Thanks to parallel dilated convolution, our DSA module conducts multi-scale-in-one-stage spirit and successfully provides at least 3× more scales than SRA with a marginal computational cost.

3.1.2 Detail-specific feed-forward network

The feed-forward network (FFN) is an essential component of transformers for feature enhancement [22]. The traditional transformers usually apply a point-wise fully connected layer as the FFN. To complement local information for the traditional FFN, we added a detail-specific layer between the two fully connected layers. Specifically, given an input feature map x, the output feature map y of the FFN with a detail-specific layer can be computed by the following equation:

$y=FC\left(GELU\left(x^{\prime }+DS\left(x^{\prime }\right)\right)\right),\mathit{\text{where}}{x}^{\prime }=FC\left(x\right),(8)$

where FC(⋅) denotes a fully connected layer, while GELU(⋅) represents the GELU activation function. DS(⋅) is the detail-specific layer, which is implemented by a depth-wise convolution.

3.2 Patch embedding

As is known, a conventional transformer is initially designed for handling sequential data in NLP, and how to map the image to a patch sequence is vital for a vision transformer. ViT [24] directly splits the input image into 16 × 16 non-overlap patches, while other recent works [40] find that convolution in patch embedding makes a significant contribution in mapping the image to a token sequence with higher quality. Following the existing works [21, 26] adopting overlapped patch embedding, we first take a 7 × 7 convolution layer with a stride of 2 as the first layer in the patch embedding, followed by an extra 3 × 3 convolution layer with a stride of 1. Finally, a non-overlapped projection layer with a stride of 2 is utilized to generate a patch sequence with the size of $\frac{H}{4}\times \frac{W}{4}$. It should be noted that linear embedding, a convolution layer with a stride of 2, is introduced to half the size of feature maps and connects two stages.

3.3 Feature pyramid decoder

The existing methods often utilize a single fully connected layer as the classification head [21, 24, 26], thereby generating less reliable prediction for dilated granularity grading. Inspired by [41], we introduced a feature pyramid decoder (FPD) to better aggregate multi-resolution features at different network levels for grading the placental maturity. Specifically, we first generate five feature maps (defined as {F₂, F₃, F₄, F₅, and F₆}; Figure 2) at different network levels. F₂, F₃, and F₄ are produced by passing feature maps S₂, S₃, and S₄ from the last three stages of our dilated transformer to a 1 × 1 convolutional layer with the top–down connections [41], while F₅ and F₆ are generated by a convolutional layer with the stride of 2 on F₄ and F₅, respectively. After that, we concatenate these five feature maps together and then pass the concatenation result into a global average pool (“GAP” of Figure 2) and two fully connected layers (“fc” of Figure 2) for predicting the final PMG result of the input ultrasound image.

3.4 Implementation details

For the model architecture, we adopt a standard four-stage design [21]. The first stage downsamples the image into stride-4 resolution. The other three stages downsample the feature maps to the resolution of stride-8, stride-16, and stride-32. The variants only come from the number of layers in different stages. Specifically, the number of blocks in each stage is set to 3, 4, 24, and 2, while the number of heads in each block is set to 2, 4, 8, and 16, respectively. The dilation rates are 1, 3, and 5 in each self-attention block, and the spatial reduction rate is empirically set as {8,4}, {4,2}, and {2,1} for two corresponding groups of attention heads in the first three stages inspired by multi-scale-in-one-stage spirit. Such a setting produces 6× more scales than PVT [21] in one stage.

For training details, our network is implemented on PyTorch [42] and trained using an Adam optimizer [43] with 80 epochs, an initial learning rate of 1 × 10⁻⁴, and a learning rate decay of 0.9 (every 5 epochs). The cross-entropy loss is empirically utilized to compute the predicted PMG error. The whole architecture is trained on one GeForce RTX 3090 GPU with a batch size of 16. The original ultrasound images are first cropped into a square region, resized into a spatial resolution of 224 × 224, and then augmented by using random horizontal flip and rotation before passing them to train our network for PMG.

4 Experiments

4.1 Dataset and evaluation setting

To evaluate the effectiveness of our method, we collect and annotate an ultrasound dataset for PMG. This dataset has 500 ultrasound images, comprising 128 ultrasound images with Grade I, 115 ultrasound images with Grade II, 122 images with Grade III, and 135 ultrasound images with Grade IV. All images are BUS and taken from the anterior wall placenta using a GE Voluson E8 Expert/Phillip EPIQ7 system. The image resolution ranges from 1136 × 852 to 1905 × 1183. The subjects involved in our dataset are pregnant women aged from 18 to 40 weeks. They are taken by ultrasound doctors with more than 5 years of clinical experience to ensure the image quality. For the whole dataset with 500 ultrasound images, 100 images are randomly selected as the test set (20% of the total data), while the remaining 400 images are used as the training set (80% of the total data).

The three widely used metrics are utilized for quantitatively comparing different PMG methods. They are accuracy, Cohen’s kappa coefficient, and F1-score. Cohen’s kappa coefficient is the standard evaluation metric for evaluating multi-category classification methods. Based on the confusion matrix, Cohen’s kappa coefficient takes its value in [−1, 1], usually greater than 0, and can provide more details about the classification results than accuracy.

4.2 Comparisons against state-of-the-art methods

To demonstrate the effectiveness and feasibility of our DilatedFormer network, we compare it against six state-of-the-art methods, which are ResNet [44], FCOS [45], vision transformer (ViT) [24], Swin transformer (Swin) [26], PVT [21], and MViT [27]. It should be noted that FCOS is a classical model for object detection with ResNet50 as the backbone and feature pyramid network as the decoder, and we replace the original head with a simple fully connected layer for grading. For providing a fair comparison, we obtain the classification results of all compared methods by exploiting their public implementations or implementing them by ourselves. We train these networks on our dataset and only set the batch size and epoch number to the same as ours. Table 1 reports the quantitative results of our network and compared methods. As shown in Table 1, our DilatedFormer network outperforms all these state-of-the-art methods in terms of three metrics, namely, accuracy, Cohen’s kappa, and F1-score. Among all compared methods, MViT and PVT have achieved the best accuracy score of 0.85, while MViT has the best Cohen’s kappa score of 0.9407 and the best F1-score of 0.8921. Compared with them, our method further improves the accuracy score from 0.85 to 0.89 while improving Cohen’s kappa score from 0.9407 to 0.9574 and F1-score from 0.8921 to 0.9022.

TABLE 1

TABLE 1. Quantitative comparisons of our network and compared methods on the collected ultrasound placental maturity dataset.

4.3 Ablation study

4.3.1 Effectiveness of each component

We conducted ablation study experiments to verify major modules in our DilatedFormer network. To do so, we first construct a baseline (denoted as “basic”) by removing DSA from all dilated transformer blocks and utilizing a vanilla classification head, and thus, the baseline is equal to PVT [21]. Then, we construct another three baseline networks from “basic” by progressively adding DSA into all dilated transformer blocks, replacing the vanilla classification head by using the feature pyramid network decoder, and incorporating a detail-specific layer into the traditional feed-forward network.

Table 2 reports metric scores of our network and compared methods in terms of accuracy and Cohen’s kappa. From these quantitative results, we can find that “basic +DSA” has an accuracy improvement of 0.02, a Cohen’s kappa improvement of 0.0115 over “basic,” and an F1-score improvement of 0.0060 (i.e., PVT [21]). Moreover, replacing the vanilla classification head with a feature pyramid network decoder (+FPD) incurs an accuracy improvement of 0.01, a Cohen’s kappa improvement of 0.0058, and an F1-score improvement of 0.0037, as shown in the quantitative comparisons between “basic +DSA” and “basic +DSA +FPD.” Finally, our method further outperforms “basic +DSA +FPD” in terms of three metrics. “basic +DSA +FPD” has an accuracy score of 0.88, a Cohen’s kappa score of 0.9538, and an F1-score of 0.9001, while the accuracy, Cohen’s kappa, and F1-score of our method are 0.89, 0.9574, and 0.9022, respectively.

TABLE 2

TABLE 2. Quantitative ablation study on major modules of our method. “FPD” denotes the feature pyramid network decoder, while “DS” represents the detail-specific layer in the feed-forward network (FFN) of our method.

4.3.2 Evaluation on dilation rates

As shown in Figure 3, the DSA block of our method leverages three dilated convolutions with different dilated rates to generate key and value features for computing the long-range dependency features via a self-attention mechanism. Here, we provide an ablation study experiment to discuss how to select specific dilated rates in these dilated convolutions.

As illustrated in Table 3, we quantitatively compare the accuracy, Cohen’s kappa, and F1-score of our method with different dilated rates in our DSA block and we utilize {1,2,3}, {1,3,5}, {1,6,10}, and {2,4,6} to assign the corresponding dilation rates for three weight-shared dilated convolutions, respectively. Apparently, our method with three dilated rates of {1,3, and 5} has the best accuracy, Cohen’s kappa, and F1-score. Hence, we empirically set the dilated rates of three dilated convolutions in DSA as 1, 3, and 5, respectively.

TABLE 3

TABLE 3. Quantitative comparisons on our DSA with three different dilation rates.

5 Conclusion

This work proposed an end-to-end deep learning-based pipeline, which presents a dilated granularity transformer network for boosting PMG in ultrasound images by learning multi-scale transformer features. The main idea is to devise dilated transformer blocks to learn multi-scale transformer features at each convolutional layer and then integrate them from all convolutional layers together to give the stronger constraint from multiple granularities for the more reliable prediction of the PMG result. We collect and annotate 500 ultrasound images for PMG. The experimental results show that our network outperforms the state-of-the-art methods in terms of three metrics in the PMG task.

However, we still have several limitations to be tackled in future work. First, we can develop a more lightweight model and improve the computational complexity based on this work. This will facilitate the deployment of our network onto clinical sites. Second, our model is trained by ultrasound images with the same intensity distribution in a fully supervised fashion. When generalized to other new clinical sites, the performance of our method may degrade due to the variability of vendors. In the future, we should devise a more generalizable deep learning algorithm for robust PMG. Third, to improve the data efficiency, we can incorporate multi-modality information, such as clinical data, into the deep learning model to support the grading from different perspectives.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YW and YY are responsible for writing the code and the draft paper. LZ, ZH, XX, and WW worked on pre-processing ultrasound images, providing supervisions on developing the physical-based deep model, revising the paper, and working on the experiments. HL collected and annotated the data for this work. All authors contributed to the article and approved the submitted version.

Acknowledgments

The work is supported by Henan Key Laboratory of Imaging and Intelligent Processing (HKLIIP2023-A07), the Hong Kong Metropolitan University (HKMU) Research Grant (No. PFDS/2022/05), the HKMU 2022/2023 S&T School Research Fund (R5108), and the “Double Hundred Plan” Fund of Nanchang Science and Technology Bureau.

Conflict of interest

Author XX was employed by the company Jiangxi Boku Information Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kellow ZS, Feldstein VA. Ultrasound of the placenta and umbilical cord: a review. Ultrasound Q (2011) 27:187–97. doi:10.1097/ruq.0b013e318229ffb5

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Moran M, Mulcahy C, Daly L, Zombori G, Downey P, McAuliffe FM. Novel placental ultrasound assessment: potential role in pre-gestational diabetic pregnancy. Placenta (2014) 35:639–44. doi:10.1016/j.placenta.2014.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lei B, Li W, Yao Y, Jiang X, Tan EL, Qin J, et al. Multi-modal and multi-layout discriminative learning for placental maturity staging. Pattern Recognition (2017) 63:719–30. doi:10.1016/j.patcog.2016.09.037

CrossRef Full Text | Google Scholar

4. Li X, Yao Y, Ni D, Chen S, Li S, Lei B, et al. Automatic staging of placental maturity based on dense descriptor. Bio-medical Mater Eng (2014) 24:2821–9. doi:10.3233/bme-141100

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lei B, Li X, Yao Y, Li S, Chen S, Zhou Y, et al. Automatic grading of placental maturity based on liop and Fisher vector. In: 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. (IEEE) (2014). p. 4671–4.

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Grannum PA, Berkowitz RL, Hobbins JC. The ultrasonic changes in the maturing placenta and their relation to fetal pulmonic maturity. Am J Obstet Gynecol (1979) 133:915–22. doi:10.1016/0002-9378(79)90312-0

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chou M, Ho E, Lee Y. Prenatal diagnosis of placenta previa accreta by transabdominal color Doppler ultrasound. Ultrasound Obstet Gynecol (2000) 15:28–35. doi:10.1046/j.1469-0705.2000.00018.x

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dubiel M, Breborowicz GH, Ropacka M, Pietryga M, Maulik D, Gudmundsson S. Computer analysis of three-dimensional power angiography images of foetal cerebral, lung and placental circulation in normal and high-risk pregnancy. Ultrasound Med Biol (2005) 31:321–7. doi:10.1016/j.ultrasmedbio.2004.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Goldenberg RL, Gravett MG, Iams J, Papageorghiou AT, Waller SA, Kramer M, et al. The preterm birth syndrome: issues to consider in creating a classification system. Am J Obstet Gynecol (2012) 206:113–8. doi:10.1016/j.ajog.2011.10.865

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhu X, Suk HI, Shen D. A novel matrix-similarity based loss function for joint regression and classification in ad diagnosis. NeuroImage (2014) 100:91–105. doi:10.1016/j.neuroimage.2014.05.078

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhu X, Suk HI, Wang L, Lee SW, Shen D, Initiative ADN, et al. A novel relational regularization feature selection method for joint regression and classification in ad diagnosis. Med image Anal (2017) 38:205–14. doi:10.1016/j.media.2015.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhou J, Wu Z, Jiang Z, Huang K, Guo K, Zhao S. Background selection schema on deep learning-based classification of dermatological disease. Comput Biol Med (2022) 149:105966. doi:10.1016/j.compbiomed.2022.105966

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Xu L, Magar R, Farimani AB. Forecasting covid-19 new cases using deep learning methods. Comput Biol Med (2022) 144:105342. doi:10.1016/j.compbiomed.2022.105342

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Liu G, Ding Q, Luo H, Sha M, Li X, Ju M. Cx22: a new publicly available dataset for deep learning-based segmentation of cervical cytology images. Comput Biol Med (2022) 150:106194. doi:10.1016/j.compbiomed.2022.106194

CrossRef Full Text | Google Scholar

15. Abdelhafiz D, Yang C, Ammar R, Nabavi S. Deep convolutional neural networks for mammography: advances, challenges and applications. BMC bioinformatics (2019) 20:281–20. doi:10.1186/s12859-019-2823-4

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hemanth DJ, Anitha J, Naaji A, Geman O, Popescu DE, Hoang Son L. A modified deep convolutional neural network for abnormal brain image classification. IEEE Access (2018) 7:4275–83. doi:10.1109/access.2018.2885639

CrossRef Full Text | Google Scholar

17. Yoo S, Gujrathi I, Haider MA, Khalvati F. Prostate cancer detection using deep convolutional neural networks. Scientific Rep (2019) 9:19518. doi:10.1038/s41598-019-55972-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tola E, Lepetit V, Fua P. Daisy: an efficient dense descriptor applied to wide-baseline stereo. IEEE Trans pattern Anal machine intelligence (2009) 32:815–30. doi:10.1109/tpami.2009.77

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lei B, Tan EL, Chen S, Li W, Ni D, Yao Y, et al. Automatic placental maturity grading via hybrid learning. Neurocomputing (2017) 223:86–102. doi:10.1016/j.neucom.2016.10.033

CrossRef Full Text | Google Scholar

20. Lei B, Jiang F, Zhou F, Ni D, Yao Y, Chen S, et al. Hybrid descriptor for placental maturity grading. Multimedia Tools Appl (2020) 79:21223–39. doi:10.1007/s11042-019-08489-x

CrossRef Full Text | Google Scholar

21. Wang W, Xie E, Li X, Fan DP, Song K, Liang D, et al. Pyramid vision transformer: a versatile backbone for dense prediction without convolutions. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (2021). p. 568–78.

CrossRef Full Text | Google Scholar

22. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. Adv Neural Inf Process Syst (2017) 30.

Google Scholar

23. Devlin J, Chang MW, Lee K, Toutanova K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018).

Google Scholar

24. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, et al. An image is worth 16x16 words: Transformers for image recognition at scale (2020). arXiv preprint arXiv:2010.11929.

Google Scholar

25. Touvron H, Cord M, Douze M, Massa F, Sablayrolles A, Jégou H. Training data-efficient image transformers & distillation through attention. In: International Conference on Machine Learning (PMLR) (2021). p. 10347–57.

Google Scholar

26. Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, et al. Swin transformer: hierarchical vision transformer using shifted windows. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (2021). p. 10012–22.

CrossRef Full Text | Google Scholar

27. Li Y, Wu CY, Fan H, Mangalam K, Xiong B, Malik J, et al. Mvitv2: improved multiscale vision transformers for classification and detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (2022). p. 4804–14.

CrossRef Full Text | Google Scholar

28. Chen J, Lu Y, Yu Q, Luo X, Adeli E, Wang Y, et al. Transunet: Transformers make strong encoders for medical image segmentation (2021). arXiv preprint arXiv:2102.04306.

Google Scholar

29. Lin A, Chen B, Xu J, Zhang Z, Lu G, Zhang D. Ds-transunet: dual swin transformer u-net for medical image segmentation. In: IEEE Transactions on Instrumentation and Measurement (2022).

CrossRef Full Text | Google Scholar

30. Yang H, Chen J, Xu M. Fundus disease image classification based on improved transformer. 2021 International Conference on Neuromorphic Computing (ICNC) (IEEE) (2021), 207–14.

CrossRef Full Text | Google Scholar

31. Gheflati B, Rivaz H. Vision transformers for classification of breast ultrasound images. 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (IEEE) (2022), 480–3.

CrossRef Full Text | Google Scholar

32. Jiang Z, Dong Z, Wang L, Jiang W. Method for diagnosis of acute lymphoblastic leukemia based on vit-cnn ensemble model. Comput Intelligence Neurosci (2021) 2021:1–12. doi:10.1155/2021/7529893

CrossRef Full Text | Google Scholar

33. Verenich E, Martin T, Velasquez A, Khan N, Hussain F. Pulmonary disease classification using globally correlated maximum likelihood: An auxiliary attention mechanism for convolutional neural networks (2021). arXiv preprint arXiv:2109.00573

Google Scholar

34. Costa GSS, Paiva AC, Junior GB, Ferreira MM. Covid-19 automatic diagnosis with ct images using the novel transformer architecture. Anais do XXI Simpósio Brasileiro de Computação Aplicada à Saúde (SBC) (2021) 293–301.

CrossRef Full Text | Google Scholar

35. Zhao H, Shi J, Qi X, Wang X, Jia J. Pyramid scene parsing network. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 2881–90.

CrossRef Full Text | Google Scholar

36. Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions (2015). arXiv preprint arXiv:1511.07122.

Google Scholar

37. Chen LC, Papandreou G, Schroff F, Adam H. Rethinking atrous convolution for semantic image segmentation. arXiv preprint arXiv:1706.05587 (2017).

Google Scholar

38. Qiao S, Chen LC, Yuille A. Detectors: detecting objects with recursive feature pyramid and switchable atrous convolution. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (2021). p. 10213–24.

CrossRef Full Text | Google Scholar

39. Hendrycks D, Gimpel K. Gaussian error linear units (gelus) (2016). arXiv preprint arXiv:1606.08415.

Google Scholar

40. Wang P, Wang X, Luo H, Zhou J, Zhou Z, Wang F, et al. Scaled relu matters for training vision transformers. In: Proc AAAI Conf Artif Intelligence, 36 (2022). p. 2495–503. doi:10.1609/aaai.v36i3.20150

CrossRef Full Text | Google Scholar

41. Tian Z, Shen C, Chen H, He T. Fcos: fully convolutional one-stage object detection. In: Proceedings of the IEEE/CVF international conference on computer vision (2019). p. 9627–36.

CrossRef Full Text | Google Scholar

42. Lin TY, Dollár P, Girshick R, He K, Hariharan B, Belongie S. Feature pyramid networks for object detection. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 2117–25.

CrossRef Full Text | Google Scholar

43. Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, et al. Pytorch: an imperative style, high-performance deep learning library. Adv Neural Inf Process Syst (2019) 32.

Google Scholar

44. Kingma DP, Ba J. Adam: A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.

Google Scholar

45. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2016). p. 770–8.

CrossRef Full Text | Google Scholar