Interpretation and prediction of optical properties: novel fluorescent dyes as a test case

The rapid development of modern quantum mechanical theories and computational resources facilitates extended characterization of molecular systems of increasing size and complexity, including chromophores of biochemical or technological interest. Efficient and accurate computations of molecular structure and properties in the ground and excited electronic states are routinely performed using density functional theory (DFT) and its time-dependent (TD-DFT) counterpart. However, the direct comparison with experiment requires simulation of electronic absorption or emission spectra, for which inclusion of vibrational effects leads to more realistic line shapes while at the same time allowing for more reliable interpretation and prediction of optical properties and providing additional information that is not available from experimental low-resolution UV-vis spectra. Computational support can help identify the most interesting chromophores among a large number of potential candidates for designing new materials or sensors, as well as unraveling effects contributing to the overall spectroscopic phenomena. In this perspective, recently developed viologen derivatives (1,1′-disubstituted-4,4′-bipyridyl cation salts, viol) are selected as test cases to illustrate the advantages of spectroscopic theoretical methodologies, which are still not widely used in “chemical” interpretation. Although these molecules are characterized by improved stability as well as the dual function of chromism and luminescence, their detailed spectroscopic characterization is hampered due to the availability of only low-resolution experimental spectra. DFT-based absorption and emission spectra are exploited in the analysis of optical properties, allowing detailed investigation of vibrational effects and gaining more insights on the structure–spectra relationship, which can be extended to develop further viologen dyes with improved optical properties.

1 Introduction

Photochromic molecular systems [1] undergo some chemical changes upon interaction with photons of suitable energy ranges. The optical properties of the product of light absorption are changing, either due to the modifications of its molecular structure [2,3] or the difference in the atomic valence state [4], leading to the variation in macroscopic properties such as color. The importance of color changing is related to the fact that these properties are easily “detected” by human vision. These properties are highly desired in “real-life” applications such as industrial [5] or biomedical [6] ones, which prompted extensive studies, leading in turn to the better understanding and development of novel photochromic compounds. Organic photochromic materials have high molar extinction coefficients; their production is also cost-effective and eco-friendly while at the same time allowing for a large versatility of possible new compounds and materials. For these reasons, organic photochromic materials have attracted considerable interest for practical applications [5–7].

Nowadays, theoretical and computational methodologies provide strong support for a better understanding of molecular system properties, including excited-state processes [8,9] and spectroscopic phenomena [10]. In this perspective, we focus on the simulations of absorption and emission spectra, which allow us for a better understanding or prediction of the structural and spectral properties of several types of organic and inorganic dyes of practical interest [10–16]. These computations become feasible due to advances within density functional theory (DFT) [17] and its time-dependent counterpart (TD-DFT) [18,19], which allowed relatively easy computations of molecular structure and properties [20,21], including molecular vibrations, in the excited electronic states [22]. Moving from the simplest vertical models, based on the computation of energy differences between the electronic states combined with phenomenological broadening, toward the simulation of realistic spectrum shapes accounting for vibrational effects highly increased the interpretative ability and accuracy of optical spectra simulations [23]. Indeed, spectra obtained experimentally often have unintelligible peaks that are difficult to interpret, while the first principle simulations allow for additional insights to accurately analyze the relevant properties. Therefore, computational studies can provide further insights into well-known molecular systems and are also crucial for the analysis of novel molecules.

4,4′-Bipyridyl salts, called as viologens ((C₅H₅NR)₂⁺ and Viol²⁺), are redox-active functional organic molecules composed of conjugated bi-/multi-pyridyl groups characterized by reversible two-step one-electron reductions related to significant visible color change toward a radical cation (Viol^+•) and then a neutral form (Viol⁰), which can occur under appropriate stimuli [24–26], such as, for instance, light irradiation. Due to these unique properties, viologens have been widely studied and applied in diverse fields such as electrochromic display [24], molecular electronics, solar energy conversion, and storage devices [24,25]. The wide applicability of viologens and possibility to derive several new chromophores are related to pyridyl groups, which are easily modified, so the properties of the organic photochromic molecules can be changed by modifying the ability to transfer intermolecular charge by varying the substituents. Viologen derivatives have also been exploited as building blocks in the metal–organic frameworks (MOFs), resulting in many synthetic multi-functional MOFs with varying colors [27], which show outstanding performance in many fields, such as gas storage and separation; they are also used to create devices with multiswitchable colors, representing a significant breakthrough toward full-color devices [28]. Redox properties of viologens have also been exploited in biosensing, which allows us to monitor in vivo spatiotemporal dynamics of metabolic fluctuations in chloroplasts and mitochondria, leading to a better understanding of the signaling events between subcellular compartments [29]. However, despite their wide use, there is still a need for chromophores with improved properties, particularly concerning their stability due to often rapid quenching of radicals by oxygen in air [26]. In this perspective, we focus on newly designed and synthesized viologen derivatives, which show enhanced stability combined with improved chromic and fluorescence properties and have been extensively studied from an experimental point of view [30] but still need to be better characterized to fully understand their spectral properties. In this work, computation of vibrationally resolved electronic spectra within the Franck–Condon (FC) approximation and considering the Duschinsky effects is used in order to decipher the origin of the experimentally observed broad spectral peaks. These computations yield absorption and emission spectra along with detailed information about the main vibronic transitions determining spectral shape, as well as about structural and electron density changes, upon electronic excitation. Such comprehensive analysis allows us to obtain information about the structural patterns of viologens which affect most of their optical properties while at the same time providing guidelines for the spectral simulations and the development of novel fluorescent dyes.

2 Computational details

The structural and spectroscopic properties of viologen cations (Viol²⁺) in the DMSO solvent environment have been simulated using the Gaussian 16 quantum chemistry package [31]. Geometry structure and vibrational frequency computations in the electronic ground state (S₀) have been performed using DFT, while the structure and vibrational frequencies in the first electronically excited state (S₁) have been computed using TD-DFT [22]. For the ground electronic state, the hybrid functional B3LYP [32] in conjunction with the SNSD basis set [33] is used. For the first electronic excited state, the TD-DFT computations are performed with the same basis set and the long-range-corrected CAM-B3LYP [34] hybrid functional which is more suitable for excited-state properties [35], including the magnetic properties needed for the computation of electronic circular dichroism spectra [36].

Moreover, due to the fact that traditional functionals, such as B3LYP and CAM-B3LYP, are lacking the description of the dispersion effect, the DFT-D3 (BJ) [37] correction has been added in all cases [37,38]. In order to match the experimental conditions, solvent effects have been considered using the polarizable continuum model in its conductor-like screening formulation, CPCM [39]. This computational model was shown to be suitable for the simulation of organic fluorophore optical properties in non-protic solvents [10,11].

Vibrationally resolved spectra of viologen derivative keto structures have been simulated considering the Franck–Condon approximation [40], along with mode-mixing Duschinsky [41] effects, within the adiabatic Hessian model, which hereafter is abbreviated as AH|FC, or the simpler FC spectrum. For the computations at the 0K and band assignments, we have resorted to the time-independent (TI, sum-over-states) algorithm [42], while path-integral time-dependent (TD) [43] computations have been used to simulate room-temperature spectra. Both algorithms use the same set of data and are implemented in the same code [31], facilitating integrated TI–TD studies [44]. These theoretical models and underlying approximations are extensively described in Refs [13,42] which also provide some practical guidelines on the computational procedures. Here, we only highlight that in the case of TI computations, the default number of FC integrals (10⁸) has been used, leading to the well-converged spectra (over 90% spectrum progression) in all cases. Moreover, for polyatomic molecules, the normal modes and vibrations change during the electronic transition; therefore, in order to compute FC overlaps, it is necessary to express both vibrational wave functions by the same set of coordinates, for example, by using the Duschinsky approximation [41,45], which is described as

$Q^{\prime }=JQ+K,$

where Q′ is the normal coordinate of the final state and Q is the normal coordinate of the initial state. The Duschinsky matrix J describes the linear transformation between the initial-state normal coordinates and the final-state normal coordinates. The shift vector K shows the displacement of normal modes between the initial and final states. Moreover, vibrational wave functions can be expressed by different types of coordinate systems. In this work, all computations are performed using the Cartesian coordinate system, but effective models for vibrationally resolved computations in various coordinate systems, taking into account the internal structure of molecules, have also been developed [13,46–49].

3 Results and discussion

The viologen derivatives are characterized by simultaneous emission and redox reactions, combined with structural changes after the photon emission. That process is necessary to reverse the redox reaction in order to return to the original structure and allow subsequent light emission. However, their strong radical character complicates their use in practical applications. The viologen derivatives studied in this work, 1,1′-disubstituted 4,4′-bipyridyl salts (see the inset of Figure 1A), include additional aromatic fluorophore substituents such as acetophenone (Viol1, 1,1′-di acetophenone 4,4′-bipyridyl, Viol1²⁺ cation with the chemical formula C₂₈H₂₄N₂O₂) (Supplementary Figure S1) or naphthophenone (Viol2, 1,1′-di naphthophenone 4,4′-bipyridyl, Viol2²⁺ cation with the chemical formula C₃₆H₂₈N₂O₂), allowing to increase the conjugated system, stabilize the molecular structure, and enhance fluorescence [30]. Crystallography experiments revealed that Viol1 may exist in two conformational forms, boat and chair (Supplementary Figures S2, S3), of equal stability based on the DFT computations (electronic + zero-point vibrational energies within 0.2 kJ mol⁻¹), while only one form has been observed for Viol2 (Supplementary Figure S4) [30]. Additionally, both Viol1 and Viol2 show excited-state keto-to-enol isomerization, which leads to significant discoloration reaction in the DMSO solution and changes in the emission spectra over the time. However, only the initial keto forms, which correspond to the emission spectra immediately after irradiation, as confirmed by FTIR and NMR experiments [30] and for which structures are obtained based on X-ray spectra, have been considered in this work for further theoretical characterization using tools available in user-friendly packages.

FIGURE 1

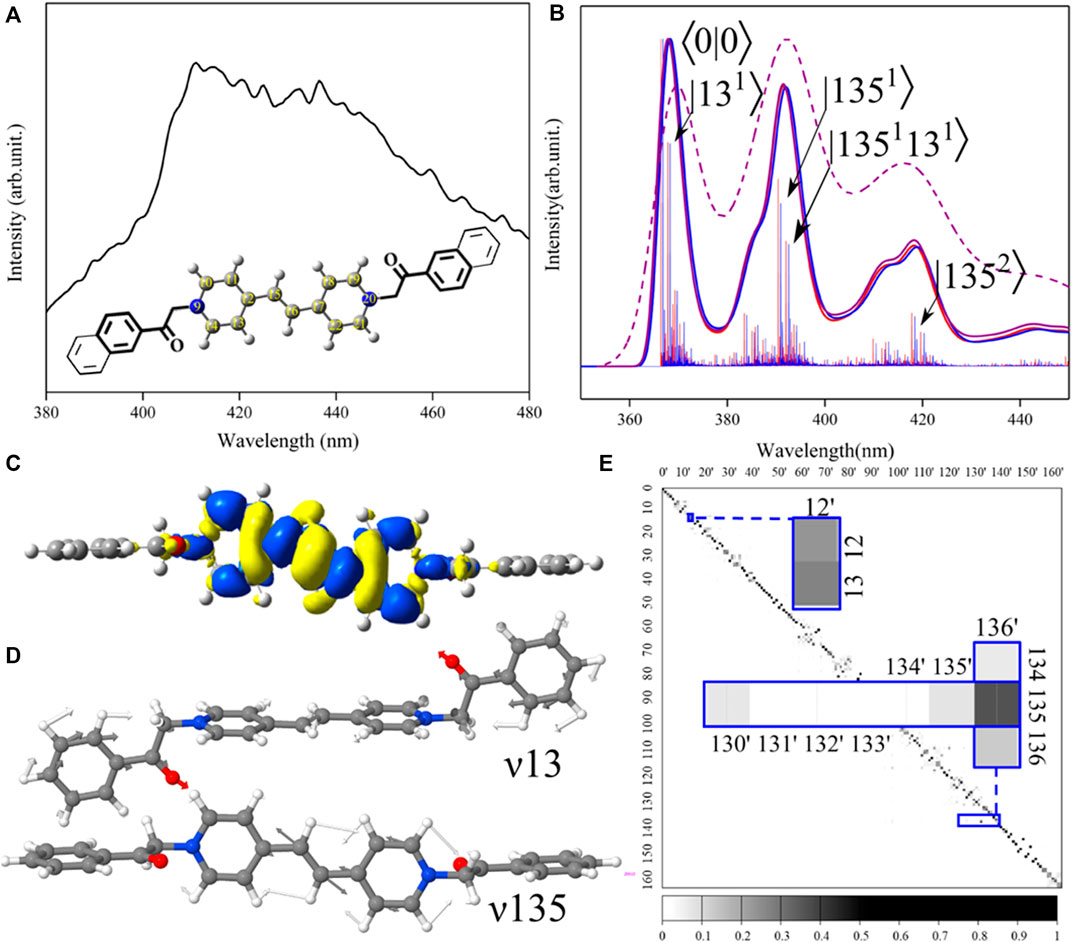
FIGURE 1. Connection between spectra and structure of viologens: insights from the theoretical analysis. (A) Experimental fluorescence spectrum recorded in the DMSO solvent immediately after irradiation by the UV light at 365 nm [30]. Inset demonstrates structures of Viol1 (bold lines) and Viol2 (thin lines) with the common bi-pyridinium unit reported as ball-sticks including atom labeling. (B) Theoretical vibrationally resolved TI-AH|FC emission spectra for Viol1-boat-keto (red) and Viol1-chair-keto (blue) as well as TD-AH|FC spectra for Viol1-boat-keto at 0 K (violet, solid line) and 298.5 K (violet and dashed-line). Individual TI vibronic transitions are shown as sticks and labeled (for Viol1-chair as an example) by the final vibrational state as |n^m⟩, where n corresponds to the mode number and m corresponds to the number of quanta. The overall spectrum shape has been obtained by convolution with Gaussian function with 135 cm⁻¹ half-width at half-maximum (HWHM). (C) Electron density difference (ELD) between the excited and ground states. The regions that have lost electron density as a result of excitation are shown in bright yellow, whereas the darker blue regions have gained electron density. ELD densities were plotted with an isovalue threshold of 0.001. (D) Representation of normal modes related to the most significant vibronic contributions to Viol1-chair-keto. (E) Duschinsky matrix for Viol1-chair-keto. Excited-state normal modes are listed in columns, while ground-state modes are listed in rows. Most significant modes are highlighted in the inset. The depth of the color represents the degree of coupling between the two vibration modes, for each element of the matrix (J²), from 0 (white) to 1 (black).

3.1 Ground- and excited-state structures and properties

Simulation of vibrationally resolved electronic spectra requires characterization of initial- and final-state structures and vibrational properties. Within the adiabatic Hessian model used in this work, the equilibrium structures in both states are obtained from unconstrained geometry optimizations, followed by molecular vibration computations within the harmonic approximation, at the DFT and TD-DFT levels, respectively. In such a way, both the ground and excited states are characterized at the same level of accuracy, and both absorption and emission vibrationally resolved electronic spectra are computed on the equal footing.

The optimized structures are reported in the Supplementary Material as the Cartesian coordinates, while the changes between the ground and excited states are analyzed in Supplementary Table S1 in terms of molecular parameters such as bond lengths, angles, and dihedral angles. Overall, Viol1-boat, Viol1-chair, and Viol2 show similar structures (Supplementary Figures S2–S7), with almost perpendicular relative orientations between fluorophore substituents and the central bipyridyl moiety (Figures 1C, D), as illustrated by the dihedral angle C7–C8–N9–C10 (Figure 1A) in the ground-state structures of 82°–89°. These orientations remain essentially unchanged upon electronic excitation, with maximum differences below 2°. This can be explained by the analysis of frontier molecular orbitals (Supplementary Figure S8), which are both localized on the central bipyridyl moiety. The structural changes upon electronic excitation are also localized mainly on the central part and can be correlated with the electron density differences (ELDs), as reported in Figure 1C; Supplementary Figures S9–S11, which are localized over atoms 9–22 and exhibit the same pattern of density loss/gain upon excitation in all cases. The largest differences are observed in the atoms linking two pyridyl rings (C12, C15, C16, and C17), with all of the molecules showing negative ELD (loose of electron density) on the central bond C15–C16, which leads to its elongation by approximately 0.075 Å, and positive ELD (gain of electron density) on C12–C15 and C16–C17, which leads to their shortening by 0.062 Å. These bond length variations are connected with the angles C12–C15–C16 and C15–C16–C17, which decrease by approximately 0.5°.

3.2 Absorption and emission spectra

When comparing with the experimental spectrum, theoretical simulation allows us to highlight and assign all specific spectral lines that contribute to the overall broad and unresolved experimental bands, which in turn gives insights into the specific structural patterns determining peaks with the highest intensity. This is clearly the case for studied viologens, for which very broad recorded spectra (Figure 1A) do not provide any specific information about vibronic transitions. In turn, simulated TI-FC absorption (Supplementary Figures S12–S14) and emission spectra (Supplementary Figures S15–S17) give insights into complex vibrational structure, which is responsible for the broadening and asymmetry of bands. Additionally, TD computations also allow accounting for the temperature effect, yielding spectra at the room temperature (Figure 1B). Let us first focus on the direct comparison between the experiment and simulation, which are reported in Figures 1A, B, respectively, for the fluorescence spectrum of Viol1. First, we can note a clear resemblance between the experiment and computation, with the intense transitions encompassing a rather broad wavelength range of over 60 nm. Theoretical analysis of TI and TD spectra highlights the two dominant bands, which can be assigned to specific vibronic transitions based on TI-FC computations. First band originates from the ⟨0|0⟩ and close-lying transitions, while the second, vibronic band, is red-shifted by approximately 1,700 cm⁻¹ (30 nm), and accompanied by a broad shoulder. Inclusion of hot bands appearing at room temperature by TD computations at 298.5 K leads to broader bands characterized by the same distinct vibronic features which better match the experiment. It should be noted that the simulated spectrum is red-shifted with respect to the experiment; the latter is characterized by λ_max of 410 nm, while for the simulated spectrum, the ⟨0|0⟩ transition is at approximately 370 nm and the λ_max is at 390 nm. This discrepancy can be potentially improved by the computation of electronic energies at a higher level of theory [36,50]; however, unfortunately, accurate computations of energies in excited states still represent a very challenging task for larger systems [51,52]. That major drawback in the predictive ability of TD-DFT-based computations can be potentially alleviated by benchmarking, aimed at specific classes of systems [44], which goes beyond the scope of the present work.

Moving to the more detailed analysis, it is noted that the spectra for two Viol1 conformers are essentially indistinguishable, so given their equal stability and the same property changes upon electronic excitation, only Viol1-chair-keto has been considered, as shown in Figures 1C–E, reporting electron density changes (ELDs) and the most important vibrations along with their coupling between two electronic states. Overall, the two most relevant vibrations (see Table 1), ν13 and ν135 (Figure 1D), are both related to the changes in the central part of the chromophore. For ν135, the main contribution is due to the C15–C16 stretch, which is coupled in the synchronized manner with C–C stretches from pyridyl rings, while ν13 can be described as the out-of-plane twisting of the C15–C16 bond coupled to phenyl ring rotations. Other distinct vibronic transitions are due to these modes two-quantum combinations, while the most distinct contribution to the shoulder is the overtone |135²⟩ at approximately −3,360 cm⁻¹ with respect to the origin. However, transitions up to two quanta yield only approximately 40% of the total spectrum intensity, highlighting the importance of many small contributions to the overall spectrum shape. Indeed, the TI spectrum computed using the default number of FC integrals (10⁸) is consistent with the fully converged TD spectrum at 0 K. The absorption spectra (Supplementary Figure S18) also show three distinct broad bands, with most intense peaks related to the transitions from the vibrational ground state of the electronic ground state to the vibrations, which are related to the peaks observed in the emission spectra (Supplementary Figure S19) via the Duschinsky matrix (Figure 1E; Supplementary Figures S20–S22). Notably, the excited state vibration ν12′ (Supplementary Figure S23) is a combination of ground-state modes ν12 and ν13, with the larger contribution of the latter, while in the higher energy range, the two excited state vibrational modes ν130′ (Supplementary Figure S24) and ν136′ (Supplementary Figure S25) can be distinguished, both having significant contributions from ν135. It should be noted that despite the close resemblance of the normal modes ν136′ and ν135, their wavenumbers vary between the two states, from 1,680 cm⁻¹ in the ground state to 1,734 cm⁻¹ in the excited state. These differences and overall mode-mixing contribute to the absorption–emission spectral asymmetry. All these spectral features can be clearly correlated with the changes in structure and properties between the two states.

TABLE 1

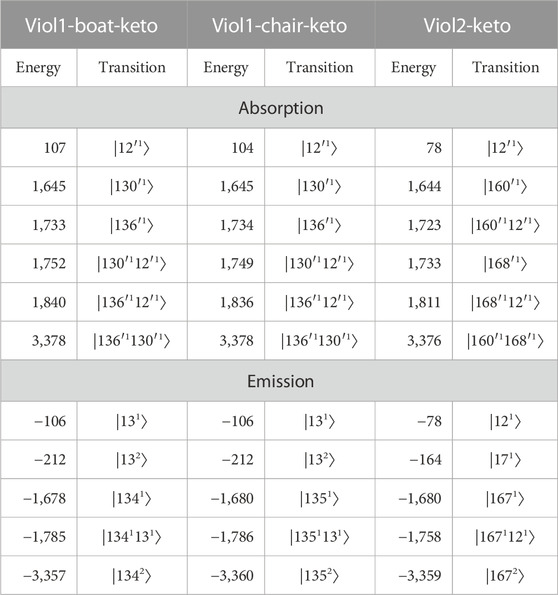
TABLE 1. Vibrational energies (in cm⁻¹) with respect to the ⟨0|0⟩ transition and band assignment of the most important vibronic transition to the simulated absorption and emission spectra of viologens. All transitions originate from the initial vibrational ground state and are labeled by the final vibrational state as |n^m⟩, where n corresponds to the mode number and m corresponds to the number of quanta.

Theoretical analysis provides a clear link between spectra, molecular properties, and their changes between electronic states. First, we note that the same vibrations show the largest vibronic contributions to the absorption/emission spectra of the two Viol1 conformers, which is expected as Viol1-boat-keto and Viol1-chair-keto are two very similar molecules. This indicates that the different orientation of substituent phenyl rings in the two structures has little influence on the vibrationally resolved spectrum of Viol1, simulations are in line with experimental observations for both absorption and fluorescence spectra. For the Viol2-keto molecule, it is observed that despite the larger number of transitions, the overall shapes of the emission and absorption spectra are similar compared to Viol1 (see Supplementary Figures S18, S19), with the main peaks related to the ⟨0|0⟩ transition and two additional bands (main one and the shoulder) due to vibronic effects.

Absorption and emission spectra assignment for all three molecules is reported in Table 1, with the energies of the main peaks relative to the ⟨0|0⟩ transition energy in order to facilitate comparison. Three absorption spectra show the most intense bands at approximately 1,645, 1,730, 1,810–1,840, and 3,378 cm⁻¹. Those transitions involve three modes, their overtones, and combinations. For example, transitions at the relative energies of 1,645 and 1,733/1,734 are described as |130′¹⟩ and |136′¹⟩ for Viol1 structures, while the corresponding transitions (|160′¹⟩ and |168′¹⟩) are at 1,644 cm⁻¹ and 1,733 cm⁻¹ for Viol2. Moreover, the transition at the relative energy of 1,752 cm⁻¹ of the Viol1-boat-keto molecule and the relative energy of 1,749 cm⁻¹ of the Viol1-chair-keto molecule are the two-quantum transitions involving |130′¹⟩ and |12′¹⟩ modes. For the emission spectra, the most intense bands involve two vibrations leading to transitions at approximately −1,680, −1,770, and −3,360 cm⁻¹, of which the former is the one-quantum transition involving |134¹⟩, |135¹⟩, and |167¹⟩ for Viol1-boat-keto, Viol1-chair-keto, and Viol2-keto, respectively. Detailed analysis indicates similar characters of normal modes contributing to the spectra in all cases (Figure 1D; Supplementary Figures S23–S25), which are mode ν13/ν12′ delocalized over the whole molecule and modes ν130′/160′ and ν136′/168′ localized on bipyridyl, which correlates with the ground-state modes ν134/135/167 for Viol1-boat-keto, Viol1-chair-keto, and Viol2-keto, respectively. These vibrations not only show similar patterns of atomic displacements but are also characterized by similar energy ranges and are clearly correlated with the structural changes upon electronic excitation. The most important contributions are from the C–C stretching in the linkage between two pyridyl rings, coupled to the synchronous stretch of all C–C bonds in the central part. These can be correlated with the structural changes at the linkage between two pyridyl rings C12–C15–C16–C17, such as the changes in C7–C8–N9, C12–C15–C16, and C15–C16–C17 angles by approximately 0.5°, as well as the C–C bond length deviations by over 0.05 Å. Moreover, the changes along these modes correspond to the shortening and elongations in the C–C bonds in the central part according to the alternate changes in the electron density upon excitation.

4 Conclusion and perspectives

Overall, detailed theoretical analysis indicated that spectral properties of Viol1 and Viol2 in their keto forms are largely determined by the central 4,4′-bipyridyl part, which is identical in all cases. This explains why both absorption and emission spectra are very similar for these three molecules, suggesting that larger modifications could be expected for asymmetric substitutions showing some push–pull characters or modifications within the central moiety or its linkage.

This example highlights that it is nowadays rather straightforward to simulate realistic vibrationally resolved spectra for semi-rigid molecules or moderately flexible systems for which there are no significant structural changes upon electronic excitation. However, analysis of more flexible systems or direct insights into excited-state processes are still significantly more challenging. Concerning the spectral simulation a viable route goes by resorting to the internal coordinate description [47–49,53], effective anharmonic treatments of some large amplitude degrees of freedom [13], or wavepacket dynamics [54]. Moreover, some improvements can also be made within vibronic harmonic models, such as AH|FC, by using the anharmonic corrections computed, for instance, by second-order vibrational theory. That is nowadays feasible due to the effective generalized VPT2 model [13,55,56] and the implementation of TD-DFT analytic second derivatives [57]; however, the accuracy of such obtained vibrational energies remain to be assessed. Finally, there is an issue of direct simulation of excited-state processes, such as, for instance, the keto-enol isomerization, which is instrumental for the improved fluorescence and stability of Viol1 and Viol2 molecules. These processes can be considered either by direct excited-state dynamics studies [8,58,59] or by static computations analyzing the relevant excited-state pathways [60], leading to the final full characterization of all the excited-state phenomena.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XL performed the quantum chemical calculations. XL and MB analyzed the data. XY and Y-LB designed the studied molecules. XL and MB wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 31870738) and European Cooperation in Science and Technology COST Action CA21101 “COSY.”

Acknowledgments

MB acknowledges the financial support from the National Natural Science Foundation of China (Grant No. 31870738). This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1236987/full#supplementary-material

References

1. Fihey A, Perrier A, Browne WR, Jacquemin D. Multiphotochromic molecular systems. Chem Soc Rev (2015) 44(11):3719–59. doi:10.1039/C5CS00137D

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kortekaas L, Browne WR. The evolution of spiropyran: Fundamentals and progress of an extraordinarily versatile photochrome. Chem Soc Rev (2019) 48(12):3406–24. doi:10.1039/c9cs00203k

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Png ZM, Wang C-G, Yeo JCC, Lee JJC, Surat'man NE, Tan YL, et al. Stimuli-responsive structure–property switchable polymer materials. Mol Syst Des Eng (2023). doi:10.1039/D3ME00002H

CrossRef Full Text | Google Scholar

4. Sato O. Dynamic molecular crystals with switchable physical properties. Nat Chem (2016) 8(7):644–56. doi:10.1038/nchem.2547

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ru Y, Shi Z, Zhang J, Wang J, Chen B, Huang R, et al. Recent progress of photochromic materials towards photocontrollable devices. Mat Chem Front (2021) 5(21):7737–58. doi:10.1039/D1QM00790D

CrossRef Full Text | Google Scholar

6. Cheng H, Yoon J, Tian H. Recent advances in the use of photochromic dyes for photocontrol in biomedicine. Coord Chem Rev (2018) 372:66–84. doi:10.1016/j.ccr.2018.06.003

CrossRef Full Text | Google Scholar

7. Berkovic G, Krongauz V, Weiss V. Spiropyrans and spirooxazines for memories and switches. Chem Rev (2000) 100(5):1741–54. doi:10.1021/cr9800715

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Mai S, González L. Molecular photochemistry: Recent developments in theory. Angew Chem Int Ed (2020) 59(39):16832–46. doi:10.1002/anie.201916381

CrossRef Full Text | Google Scholar

9. Robb MA. Theoretical chemistry for electronic excited states. London: The Royal Society of Chemistry (2018).

Google Scholar

10. Barone V, Alessandrini S, Biczysko M, Cheeseman JR, Clary DC, McCoy AB, et al. Computational molecular spectroscopy. Nat Rev Methods Primers (2021) 1(1):38. doi:10.1038/s43586-021-00034-1

CrossRef Full Text | Google Scholar

11. Barone V, Bellina F, Biczysko M, Bloino J, Fornaro T, Latouche C, et al. Toward the design of alkynylimidazole fluorophores: Computational and experimental characterization of spectroscopic features in solution and in poly(methyl methacrylate). Phys Chem Chem Phys (2015) 17(40):26710–23. doi:10.1039/C5CP03047A

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Barone V, Biczysko M, Latouche C, Pasti A. Virtual eyes for technology and cultural heritage: Towards computational strategy for new and old indigo-based dyes. Theor Chem Acc (2015) 134(12):145. doi:10.1007/s00214-015-1753-0

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bloino J, Baiardi A, Biczysko M. Aiming at an accurate prediction of vibrational and electronic spectra for medium-to-large molecules: An overview. Int J Quantum Chem (2016) 116(21):1543–74. doi:10.1002/qua.25188

CrossRef Full Text | Google Scholar

14. Ferrer FJA, Santoro F. Comparison of vertical and adiabatic harmonic approaches for the calculation of the vibrational structure of electronic spectra. Phys Chem Chem Phys (2012) 14(39):13549–63. doi:10.1039/c2cp41169e

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Jacquemin D, Perpète EA, Ciofini I, Adamo C. Accurate simulation of optical properties in dyes. Acc Chem Res (2009) 42(2):326–34. doi:10.1021/ar800163d

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Santoro F, Jacquemin D. Going beyond the vertical approximation with time-dependent density functional theory. Wires Comput Mol Sci (2016) 6(5):460–86. doi:10.1002/wcms.1260

CrossRef Full Text | Google Scholar

17. Burke K, Werschnik J, Gross EKU. Time-dependent density functional theory: Past, present, and future. J Chem Phys (2005) 123(6):062206. doi:10.1063/1.1904586

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Casida ME. Time-dependent density-functional theory for molecules and molecular solids. J Mol Struct THEOCHEM (2009) 914:3–18. doi:10.1016/j.theochem.2009.08.018

CrossRef Full Text | Google Scholar

19. Casida ME, Jamorski C, Casida KC, Salahub DR. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J Chem Phys (1998) 108(11):4439–49. doi:10.1063/1.475855

CrossRef Full Text | Google Scholar

20. Brémond E, Savarese M, Adamo C, Jacquemin D. Accuracy of td-dft geometries: A fresh look. J Chem Theor Comput. (2018) 14(7):3715–27. doi:10.1021/acs.jctc.8b00311

CrossRef Full Text | Google Scholar

21. Laurent AD, Adamo C, Jacquemin D. Dye chemistry with time-dependent density functional theory. Phys Chem Chem Phys (2014) 16(28):14334–56. doi:10.1039/C3CP55336A

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Scalmani G, Frisch MJ, Mennucci B, Tomasi J, Cammi R, Barone V. Geometries and properties of excited states in the gas phase and in solution: Theory and application of a time-dependent density functional theory polarizable continuum model. J Chem Phys (2006) 124(9):94107. doi:10.1063/1.2173258

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Barone V, Biczysko M, Borkowska-Panek M, Bloino J. A multifrequency virtual spectrometer for complex bio-organic systems: Vibronic and environmental effects on the uv/vis spectrum of chlorophyll a. Chem Phys Chem (2014) 15(15):3355–64. doi:10.1002/cphc.201402300

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ding J, Zheng C, Wang L, Lu C, Zhang B, Chen Y, et al. Viologen-inspired functional materials: Synthetic strategies and applications. J Mater Chem A (2019) 7(41):23337–60. doi:10.1039/C9TA01724K

CrossRef Full Text | Google Scholar

25. Kathiresan M, Ambrose B, Angulakshmi N, Mathew DE, Sujatha D, Stephan AM. Viologens: A versatile organic molecule for energy storage applications. J Mater Chem A (2021) 9(48):27215–33. doi:10.1039/D1TA07201C

CrossRef Full Text | Google Scholar

26. McCune JA, Kuehnel MF, Reisner E, Scherman OA. Stimulus-mediated ultrastable radical formation. Chem (2020) 6(7):1819–30. doi:10.1016/j.chempr.2020.05.005

CrossRef Full Text | Google Scholar

27. Sun JK, Yang XD, Yang GY, Zhang J. Bipyridinium derivative-based coordination polymers: From synthesis to materials applications. Coord Chem Rev (2019) 378:533–60. doi:10.1016/j.ccr.2017.10.029

CrossRef Full Text | Google Scholar

28. Alesanco Y, Vinuales A, Palenzuela J, Odriozola I, Cabanero G, Rodriguez J, et al. Multicolor electrochromics: Rainbow-like devices. ACS Appl Mater Inter (2016) 8(23):14795–801. doi:10.1021/acsami.6b01911

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ugalde JM, Fuchs P, Nietzel T, Cutolo EA, Homagk M, Vothknecht UC, et al. Chloroplast-derived photo-oxidative stress causes changes in h2o2 and egsh in other subcellular compartments. Plant Physiol (2021) 186(1):125–41. doi:10.1093/plphys/kiaa095

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yin X, Li X, Li X, Biczysko M, Zhu S, Xu J, et al. Isomerization-induced fluorescence enhancement of two new viologen derivatives: Mechanism insight and DFT calculations. Chem Sci (2023) 14:7016–25. doi:10.1039/D3SC02051G

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 16, revision C 01. Wallingford CT: Gaussian inc (2016).

Google Scholar

32. Becke AD. Density-functional thermochemistry. Iii. The role of exact exchange. J Chem Phys (1993) 98(7):5648–52. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

33. Barone V, Biczysko M, Bloino J. Fully anharmonic ir and Raman spectra of medium-size molecular systems: Accuracy and interpretation. Phys Chem Chem Phys (2014) 16:1759–87. doi:10.1039/C3CP53413H

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Chai JD, Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys Chem Chem Phys (2008) 10(44):6615–20. doi:10.1039/b810189b

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Yanai T, Tew DP, Handy NC. A new hybrid exchange–correlation functional using the coulomb-attenuating method (cam-b3lyp). Chem Phys Lett (2004) 393(1):51–7. doi:10.1016/j.cplett.2004.06.011

CrossRef Full Text | Google Scholar

36. Hodecker M, Biczysko M, Dreuw A, Barone V. Simulation of vacuum uv absorption and electronic circular dichroism spectra of methyl oxirane: The role of vibrational effects. J Chem Theor Comput. (2016) 12(6):2820–33. doi:10.1021/acs.jctc.6b00121

CrossRef Full Text | Google Scholar

37. Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (dft-d) for the 94 elements h-pu. J Chem Phys (2010) 132(15):154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Grimme S, Ehrlich S, Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J Comput Chem (2011) 32(7):1456–65. doi:10.1002/jcc.21759

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cossi M, Rega N, Scalmani G, Barone V. Energies, structures, and electronic properties of molecules in solution with the c-pcm solvation model. J Comput Chem (2003) 24(6):669–81. doi:10.1002/jcc.10189

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Franck J, Dymond EG. Elementary processes of photochemical reactions. Trans Faraday Soc (1926) 21:536–42. doi:10.1039/TF9262100536

CrossRef Full Text | Google Scholar

41. Duschinsky F. The importance of the electron spectrum in multiatomic molecules. Concerning the franck–condon principle. Acta Physicochim (1937) 7(4):551–66.

Google Scholar

42. Bloino J, Biczysko M, Santoro F, Barone V. General approach to compute vibrationally resolved one-photon electronic spectra. J Chem Theor Comput. (2010) 6(4):1256–74. doi:10.1021/ct9006772

CrossRef Full Text | Google Scholar

43. Baiardi A, Bloino J, Barone V. General time dependent approach to vibronic spectroscopy including franck-condon, herzberg-teller, and duschinsky effects. J Chem Theor Comput. (2013) 9:4097–115. doi:10.1021/ct400450k

CrossRef Full Text | Google Scholar

44. Barone V, Biczysko M, Bloino J, Carta L, Pedone A. Environmental and dynamical effects on the optical properties of molecular systems by time-independent and time-dependent approaches: Coumarin derivatives as test cases. Comput Theor Chem (2014) 1037:35–48. doi:10.1016/j.comptc.2014.03.027

CrossRef Full Text | Google Scholar

45. Herzberg G, Jones AV, Leitch LC. The photographic infrared spectrum of cd3cch and the structure of methyl acetylene. J Chem Phys (2004) 19(1):136–7. doi:10.1063/1.1747972

CrossRef Full Text | Google Scholar

46. Baker J. Techniques for geometry optimization: A comparison of cartesian and natural internal coordinates. J Comput Chem (1993) 14(9):1085–100. doi:10.1002/jcc.540140910

CrossRef Full Text | Google Scholar

47. Capobianco A, Borrelli R, Noce C, Peluso A. Franck–condon factors in curvilinear coordinates: The photoelectron spectrum of ammonia. Theor Chem Acc (2012) 131(3):1181. doi:10.1007/s00214-012-1181-3

CrossRef Full Text | Google Scholar

48. Cerezo J, Santoro F. Fcclasses3: Vibrationally-resolved spectra simulated at the edge of the harmonic approximation. J Comput Chem (2023) 44(4):626–43. doi:10.1002/jcc.27027

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Reimers JR. A practical method for the use of curvilinear coordinates in calculations of normal-mode-projected displacements and duschinsky rotation matrices for large molecules. J Chem Phys (2001) 115(20):9103–9. doi:10.1063/1.1412875

CrossRef Full Text | Google Scholar

50. Loos P-F, Lipparini F, Matthews DA, Blondel A, Jacquemin D. A mountaineering strategy to excited states: Revising reference values with eom-cc4. J Chem Theor Comput. (2022) 18(7):4418–27. doi:10.1021/acs.jctc.2c00416

CrossRef Full Text | Google Scholar

51. Liang J, Feng X, Hait D, Head-Gordon M. Revisiting the performance of time-dependent density functional theory for electronic excitations: Assessment of 43 popular and recently developed functionals from rungs one to four. J Chem Theor Comput. (2022) 18(6):3460–73. doi:10.1021/acs.jctc.2c00160

CrossRef Full Text | Google Scholar

52. Verma P, Truhlar DG. Status and challenges of density functional theory. Trends Chem (2020) 2(4):302–18. doi:10.1016/j.trechm.2020.02.005

CrossRef Full Text | Google Scholar

53. Baiardi A, Bloino J, Barone V. General formulation of vibronic spectroscopy in internal coordinates. J Chem Phys (2016) 144:084114. doi:10.1063/1.4942165

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Begušić T, Tapavicza E, Vaníček J. Applicability of the thawed Gaussian wavepacket dynamics to the calculation of vibronic spectra of molecules with double-well potential energy surfaces. J Chem Theor Comput. (2022) 18(5):3065–74. doi:10.1021/acs.jctc.2c00030

CrossRef Full Text | Google Scholar

55. Mendolicchio M, Bloino J, Barone V. Perturb-then-diagonalize vibrational engine exploiting curvilinear internal coordinates. J Chem Theor Comput. (2022) 18(12):7603–19. doi:10.1021/acs.jctc.2c00773

CrossRef Full Text | Google Scholar

56. Yang Q, Bloino J. An effective and automated processing of resonances in vibrational perturbation theory applied to spectroscopy. J Phys Chem A (2022) 126(49):9276–302. doi:10.1021/acs.jpca.2c06460

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Egidi F, Williams-Young DB, Baiardi A, Bloino J, Scalmani G, Frisch MJ, et al. Effective inclusion of mechanical and electrical anharmonicity in excited electronic states: Vpt2-tddft route. J Chem Theor Comput. (2017) 13(6):2789–803. doi:10.1021/acs.jctc.7b00218

CrossRef Full Text | Google Scholar

58. Raucci U, Perrella F, Donati G, Zoppi M, Petrone A, Rega N. Ab-initio molecular dynamics and hybrid explicit-implicit solvation model for aqueous and nonaqueous solvents: Gfp chromophore in water and methanol solution as case study. J Comput Chem (2020) 41(26):2228–39. doi:10.1002/jcc.26384

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Zhao L, Wildman A, Pavošević F, Tully JC, Hammes-Schiffer S, Li X. Excited state intramolecular proton transfer with nuclear-electronic orbital ehrenfest dynamics. J Phys Chem Lett (2021) 12(14):3497–502. doi:10.1021/acs.jpclett.1c00564

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Bil A, Latajka Z, Biczysko M. Hydrogen detachment driven by a repulsive 1πσ* state – An electron localization function study of 3-amino-1,2,4-triazole. Phys Chem Chem Phys (2018) 20(7):5210–6. doi:10.1039/C7CP06744E

PubMed Abstract | CrossRef Full Text | Google Scholar