- School of Physics and State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
Formation of neutron clusters from strongly correlated neutrons has become one of the hottest topics in nuclear physics. They lie at the heart of understanding the exotic structure of nuclei around the neutron drip line and provide an important basis for testing nuclear interactions due to the absence of Coulomb interaction and further developing theoretical models. Moreover, neutron clusters composed purely of neutrons could serve as a mini prototype of neutron matter to study the still elusive properties of the extremely neutron-rich nuclear matter, building a bridge between finite nuclei and neutron stars. In this paper, we will briefly review the recent highlights of experimental and theoretical works on neutron clusters.
1 Introduction
The nucleus, which is the heart of the atoms and determines to which chemical elements they belong, is basically composed of two constituents, protons and neutrons. So far, ∼300 stable nuclei and ∼3,000 radioactive isotopes have been discovered. While a particle-like system made of multiple protons is unlikely to exist owing to the repulsive Coulomb interaction, it has remained an open yet intriguing question as to whether a neutral cluster made purely of neutrons exists despite extensive experimental and theoretical efforts for more than half a century.
The properties of these chargeless systems serve as a stringent test for the underlying nuclear force, particularly for the isospin-dependent component. They also provide unique access to neutron-neutron and multi-neutron correlations, which is crucial for a deeper understanding of exotic phenomena emerging at the limit of nuclear stability. Furthermore, terrestrial experiments on neutron clusters can also help to bridge the gap between our current knowledge of the finite nuclei and the neutron-rich matter in the universe that makes up the neutron star. Neutron clusters and neutron-rich nuclei are predicted to exist in the crust of neutron stars [1, 2]. The formation of neutron clusters in neutron stars could further give rise to the condensation of neutron clusters [1] and the superfluidity of neutron matter [2]. This will in turn impact the properties of the neutron-rich matter which is generally described using the nuclear equation of state (EoS). A detailed knowledge of the nuclear equation of state is essential for modeling the structure and thermal properties of neutron stars [3].
Significant progress has been made on the dineutron cluster (2n) in the past decades. On the other hand, only a few experiments on the trineutron cluster (3n) and tetraneutron cluster (4n) were undertaken. In the multi-neutron study, researchers are confronted with two challenges: production and detection. For the production of such exotic systems, the double-charge-exchange (DCX) reaction, multinucleon-transfer reaction, and nucleon/cluster knockout reactions such as (p, 2p) (p, pα) (p, 3p) are currently utilized (see also Ref. [4] for more details). The multi-neutron detection efficiency decreases markedly as the number of neutrons increases since neutrons—unlike charged particles—hardly react with the detector material. Moreover, an advanced multi-neutron identification algorithm is indispensable for the correct identification of true neutron signals because a single neutron can induce multiple signals (so-called crosstalk) in the neutron detector array [5]. In this context, it should be very helpful to have complementary measurements based on the missing-mass spectroscopy without direct neutron detection, although such measurements are usually of worse resolution and more sensitive to the reaction mechanism of the selected reaction channel for the production (see, for example, Refs. [6, 7]). In this mini-review, we will focus on the recent progress on neutron clusters during the last 20 years.
2 Studies on dineutron
Dineutron (2n) [8] generally refers to a spatially compact neutron pair with a total spin of 0. Different nuclear reactions, as well as theoretical calculations, confirm that an isolated 2n cannot exist as a bound or resonant state. When going away from the valley of stability and approaching the limit of existence (the neutron drip line) in the nuclear chart, the weak binding results in the formation of halo. Two-neutron halo nuclei serve as an excellent candidate for investigating the 2n clusters since the neutron correlation and consequently the formation of 2n are expected to be enhanced in the dilute neutron matter of the halo [9].
The most notable example is 11Li, with a very small separation energy of S2n = 369 keV [9–11]. Its peculiar feature of being Borromean—namely, although 11Li is a bound three-body (9Li + n + n) system, its binary subsystems (10Li and 2n) are unbound—has attracted much attention, suggesting an essential role of the two-neutron correlation (dineutron correlation) in 11Li. The dineutron correlation can be probed by measuring the electric dipole (E1) response in the Coulomb dissociation experiment. For 11Li, the opening angle ⟨θ12⟩ of two valence neutrons with respect to the core is
In analogy to the α decay (the emission of preformed α clusters) in heavy nuclei, neutron cluster emission can be expected in nuclei at and beyond the neutron drip line. Two-neutron radioactivity is observed in unbound nuclei such as 10He [15], 13Li [15, 16], 16Be [17], and 26O [18, 19] and in the excited states of 8He [20] and 14Be [21, 22]. Among them, 16Be is an ideal candidate for search of direct dineutron emission since the sequential two-neutron emission through the intermediate system 15Be is energetically suppressed. In experiment, different two-neutron emission processes can be distinguished by comparing the observed n-n energy and angular correlation patterns with the model calculations. Following this methodology, A. Spyrou et al. reported the observation of direct dineutron decay in the ground state of 16Be [17]. However, Ref. [23] argued that the observed enhancement at low two-neutron relative energies or at small opening angles by Spyrou et al. could also be explained by the direct three-body breakup model incorporating the n-n FSI, as an alternative to the dineutron model of Ref. [17] assuming 16Be decays into 14Be and a quasi-bound 2n cluster. In the phenomenological n-n FSI model of Ref. [23], the effect of FSI was formulated by assuming a Gaussian-type source of the two-neutron emission and describing the n-n interaction using the s-wave scattering length [20, 24, 25]. Important progress has been achieved on a microscopic theoretical description of the two-neutron decay in recent years, such as the time-dependent approach based on the Gamow coupled-channel method [26]. In general, the correlation pattern observed in the final state should be determined by both the initial structure and the decay process (including the effect of FSI) as revealed in Ref. [26], but it has still remained a challenge for theoretical calculations to lift the effect of FSI from that of the initial 2n structure. As such, caution should always be taken when connecting the observed correlation patterns in experiment to 2n clusters in the initial state. It is thus very important to have high-quality two-neutron correlation data with high statistics and improved detector resolutions to benchmark the theoretical models. In this context, it is worthwhile to mention the dineutron study of 26O which has a near-threshold ground state (the two-neutron decay energy is only ∼18 keV) [18, 27]. A particularly designed high-resolution neutron detector array has been developed at RIKEN Nishina Center of Japan to achieve a high-resolution measurement of the dineutron decay in 26O. A similarly interesting process is the two-proton emission of nuclei beyond the proton drip line, and from the comparative study of the isobaric mirror pair such as 6He-6Be and 12Be-12O one can investigate the isospin symmetry breaking and the Thomas-Ehrman shift (see, e.g., Refs. [26, 28]).
3 Studies of multineutrons with focus on tetraneutron
Explorations on heavier neutron clusters (3n, 4n … ) are almost at the limits of present experimental capabilities due to the limited radioactive beam intensities and extremely low multi-neutron detection efficiency. In the early search for 3n and 4n using double-charge-exchange reactions (π−, π+) [29–31] and multi-nucleon-transfer reactions [32–35], strong neutron correlations within the populated multi-neutron systems could be inferred from the observed missing-mass spectrum, but these experiments fall short of being conclusive on the presence of neutron cluster states.
At the beginning of the new century, an experiment measuring the breakup reaction of the neutron-rich unstable nucleus 14Be based on the then emerging radioactive beam techniques was performed at GANIL [36, 37], which immediately triggered a boom in tetraneutron study. In that experiment, several peculiar events observed in the neutron detector array were found to be consistent with a bound tetraneutron cluster or a low-lying four-neutron resonant state at around 2 MeV. Many theories have since then attempted to explain the experimental result. The existence of a bound tetraneutron state has basically been ruled out [38–40]. Using the Green’s function Monte Carlo method (GFMC) and realistic nuclear force (AV18/IL2), S. C. Pieper revealed that drastic modifications of known nucleon-nucleon (NN) interactions were required to bind the four neutrons [38]. However, there is still no consensus on the existence of a resonant tetraneutron state [38, 39, 41]. A broad 4n resonance was predicted at around 2 MeV by the above mentioned GFMC calculation of S. C. Pieper [38]. By solving Faddeev-Yakubovsky (FY) equations in configuration space, Lazauskas et al. found that physically observable tetraneutron resonances could hardly exist based on the modern nuclear Hamiltonians [41]. Unfortunately, the follow-up experiments at GANIL using the same approach failed to catch the 4n signals.
In 2016, a new experiment at the Radioactive Ion Beam Factory (RIBF) of RIKEN revived the interest in this field [6]. This study utilized the DCX reaction 4He (8He, 8Be) with the intense 8He beam to populate 4n under the recoilless condition. The reaction channel of interest was selected by requesting the coincidence of two α particles from the decay of 8Be, and the energy of the four-neutron system was constructed using the missing-mass method. Prominent excess of events was observed near the breakup threshold, and was tentatively interpreted as a candidate resonant 4n state with a significance level of 4.9σ. The resonant energy was determined to be 0.83 ± 0.65 (stat) ± 1.25 (syst) MeV, while an upper limit of 2.6 MeV (FWHM) was estimated for the width. It is noteworthy that the possibility of tetraneutron being a bound state cannot be excluded due to the large experimental uncertainty.
Triggered by this intriguing experimental result, increasingly sophisticated theoretical works relevant to the tetraneutron have been undertaken. Based on the no-core shell model (NCSM) employing realistic two-body interaction JISP16, Shirokov et al. predicted the tetraneutron state with a resonant energy E4n = 0.84 MeV and width Γ = 1.38 MeV [42], which agreed well with the result of Kisamori et al. [6]. Later on, they incorporated the modern NN interactions Daejeon16 and chiral N3LO into NCSM [43]. As shown in Figure 1, the resonant energy and width from various NN interactions are similar, corroborating the conclusion of Refs. [41, 44] that 4n is not sensitive to the choice of NN interactions. In another work based on the ab initio no-core Gamow shell model (NCGSM) and the density matrix renormalization group method [44], a broad resonance-like four-neutron state with a width of Γ ≈ 3.7 MeV—much larger than the reported value of Ref. [6]—was reported, indicating that the tetraneutron was unlikely to be a narrow resonance and may thus be difficult to observe experimentally. The authors of Ref. [44] speculated that the low-energy peak could be attributed to a feature of the four-neutron scattering rather than a genuine nucleus (either bound or resonant). Interestingly, similar conclusions were also obtained recently by Deltuva using the Faddeev–Yakubovsky and Alt–Grassberger–Sandhas (AGS) formalisms [45] and by Higgins et al. within the adiabatic hyperspherical framework [46], both questioning the existence of a 4n resonance. Using the Gaussian Expansion Method, Hiyama et al. showed that an additional strongly attractive T = 3/2 isospin-dependent three-body force—that is remarkably inconsistent with the known properties of typical light nuclei—was required to generate an observable 4n resonant state [47].
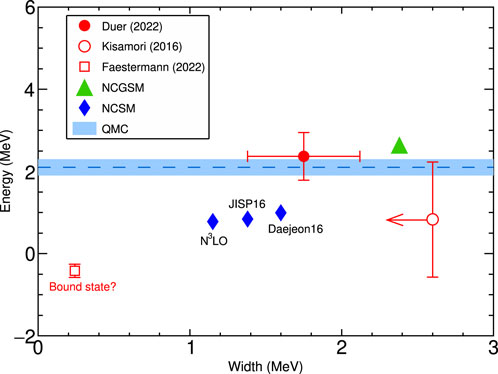
FIGURE 1. Energy versus width of the 4n resonance from experiments and theories. Experimental results of [6, 7, 51] are shown by red symbols, and for [6] the upper limit of the width is indicated by the arrow. For theoretical predictions, we include the results of NCGSM in [48] (green triangle), NCSM in [42, 43] (blue rhombuses), QMC in [53] (blue dashed line together with a shaded band showing the uncertainty). Theories that do not support the existence of a 4n resonance (e.g., [41, 45–47]) are not presented.
In a recent work published in Nature, Duer et al. reported the observation of a correlated four-neutron system using the quasi-free α-particle knockout reaction 8He (p, pα) [7]. The ground state of 8He has a well-developed cluster structure with an α particle plus four valence neutrons, providing unique access to the four-neutron system via the removal of the α particle. The detector setup was optimized in order that sufficient momentum was transferred to the α particle, ensuring its removal from the incident 8He under the quasi-free (p, pα) condition. The four-neutron system can thus be populated in an unperturbed way, and its energy was constructed using the missing-mass method. A resonance-like peak near the threshold was clearly observed, with a significance level well beyond 5σ. The extracted resonant energy (E4n) was 2.37 ± 0.38 (stat) ± 0.44 (syst) MeV and width (Γ) was 1.75 ± 0.22 (stat) ± 0.30 (syst) MeV, compatible with the previous experiment [6] but with significantly higher statistics. The experimental result was compared with state-of-the-art theoretical predictions and was in good agreement with the latest ab initio NCGSM predictions based on the chiral N3LO two-body nuclear force [48]. Another important ingredient of the NCGSM calculation is the treatment of the coupling to the continuum by using the Berggren basis [49], which is critical for the description of the resonant state.
Notably, subsequent theoretical research by Lazauskas et al. [50] proposed an alternative explanation for the prominent low-energy peak in the missing-mass spectrum of Duer et al. By constructing a reaction model based on the realistic nuclear forces such as AV18 and N3LO chiral nuclear force to describe the 8He (p, pα) reaction used by Duer et al., Lazauskas et al. attributed the observed sharp low-energy peak dominantly to the effect of the reaction mechanism (e.g, the final-state interaction among the four neutrons) rather than the formation of a four-neutron resonant state. Lazauskas et al. also pointed out that the initial dineutron cluster structure (α + 2n + 2n) of 8He was playing an important role and, accordingly, the energy distribution of the four-neutron system was strongly dependent on the n-n scattering length [50].
4 Outlook
Remarkable progress has been made on neutron clusters in the first 20 years of the new century, but more questions still remain to be answered. The most prominent one is the existence of a tetraneutron resonance. The current state of experimental and theoretical studies on tetraneutron is summarized in Figure 1. The supporting evidence has been provided by two missing-mass experiments [6, 7]. From the experimental point of view, new experiments using different production and measurement methods—particularly an invariant-mass measurement with the four constituent neutrons directly detected—are needed to reinforce or refute these positive evidences. A hint of positive signal was also reported recently by Faestermann et al. using the multi-nucleon-transfer reaction 7Li (7Li, 10C) [51]. From the theoretical point of view, the apparent discrepancies between many state-of-the-art models have to be resolved. It would also be important to go beyond the energy and width of the four-neutron system and peep into the internal neutron correlations. Such few-nucleon systems provide important benchmark information for the two-body and few-body interactions and the emergent correlations. In this respect, it is worthwhile to mention that, despite the conflicting results regarding the existence of a tetraneutron resonance, many theoretical models consistently find that the characteristics of the four-neutron system are insensitive to the three-body force [46, 48, 50], and Lazauskas et al. further pointed out that it can basically be determined by the n-n scattering length [50, 52]. Interestingly, a trineutron resonance has also been predicted by the ab initio calculations [48, 53]—both predicting a 3n resonance even lower than 4n, hinting at the working interactions or correlations beyond two neutrons. Such many-body interactions or correlations could be enhanced in a system with more neutrons and may thus give rise to more pronounced resonant structures in heavier neutron clusters (6n and 8n) or maybe a bound neutron cluster state at a certain number of neutrons.
It is also interesting to consider a multi-neutron cluster accommodated in a nuclear environment such as the low-density surface of neutron-rich nuclei. The neutron correlations are expected to be enhanced under such conditions [9, 13], and multiple dineutron clusters could form that can further lead to a condensate-like cluster state. For example, Refs. [54, 55] predicted a dineutron-condensate structure in the
The operating and forthcoming facilities worldwide, such as RIBF (Japan), FRIB (United States), HIAF (China), FAIR (Germany), and RAON (Korea), will provide massive opportunities to study the structure of neutron-rich systems, the neutron correlations, and multi-neutron clusters. With the operation of the next-generation neutron detector arrays (for example, NEBULA-Plus and NeuLAND [57]), direct detection on multiple neutrons will become feasible. New experiments with better resolution, higher statistics, or complementary reaction probes are under way. For example, the experiment on multi-neutron clusters using (p, 3p) reaction from He isotopes is now under plan at RIBF. The concerted effort of experiment and theory would eventually elucidate the nature of neutron clusters.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Key R&D Program of China (Grants No 2023YFE0101500 and 2022YFA1605100), the National Natural Science Foundation of China (Grant No. 12275006), and the State Key Laboratory of Nuclear Physics and Technology, Peking University (Grant No. NPT2022ZZ02).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ivanytskyi O, Ángeles Pérez-García M, Albertus C. Tetraneutron condensation in neutron rich matter. Eur Phys J A (2019) 55:184. doi:10.1140/epja/i2019-12900-6
2. Sedrakian A, Clark JW. Superfluidity in nuclear systems and neutron stars. Eur Phys J A (2019) 55:167–56. doi:10.1140/epja/i2019-12863-6
3. Oertel M, Hempel M, Klähn T, Typel S. Equations of state for supernovae and compact stars. Rev Mod Phys (2017) 89:015007. doi:10.1103/RevModPhys.89.015007
4. Marqués FM, Carbonell J. The quest for light multineutron systems. Eur Phys J A (2021) 57:105. doi:10.1140/epja/s10050-021-00417-8
5. Huang SW, Yang ZH, Marqués FM, Achouri NL, Ahn DS, Aumann T, et al. Experimental study of 4n by directly detecting the decay neutrons. Few Body Syst (2021) 62:102–7. doi:10.1007/s00601-021-01691-4
6. Kisamori K, Shimoura S, Miya H, Michimasa S, Ota S, Assie M, et al. Candidate resonant tetraneutron state populated by the 4He(8He,8Be) reaction. Phys Rev Lett (2016) 116:052501. doi:10.1103/PhysRevLett.116.052501
7. Duer M, Aumann T, Gernhäuser R, Panin V, Paschalis S, Rossi DM, et al. Observation of a correlated free four-neutron system. Nature (2022) 606:678–82. doi:10.1038/s41586-022-04827-6
9. Matsuo M. Spatial structure of neutron cooper pair in low density uniform matter. Phys Rev C (2006) 73:044309. doi:10.1103/PhysRevC.73.044309
10. Smith M, Brodeur M, Brunner T, Ettenauer S, Lapierre A, Ringle R, et al. First penning-trap mass measurement of the exotic halo nucleus 11Li. Phys Rev Lett (2008) 101:202501. doi:10.1103/PhysRevLett.101.202501
11. Tanihata I, Hamagaki H, Hashimoto O, Shida Y, Yoshikawa N, Sugimoto K, et al. Measurements of interaction cross sections and nuclear radii in the light p-shell region. Phys Rev Lett (1985) 55:2676–9. doi:10.1103/PhysRevLett.55.2676
12. Nakamura T, Vinodkumar AM, Sugimoto T, Aoi N, Baba H, Bazin D, et al. Observation of strong low-lying E1 strength in the two-neutron halo nucleus 11Li. Phys Rev Lett (2006) 96:252502. doi:10.1103/PhysRevLett.96.252502
13. Kubota Y, Corsi A, Authelet G, Baba H, Caesar C, Calvet D, et al. Surface localization of the dineutron in 11Li. Phys Rev Lett (2020) 125:252501. doi:10.1103/PhysRevLett.125.252501
14. Corsi A, Kubota Y, Casal J, Gómez-Ramos M, Moro AM, Authelet G, et al. Searching for universality of dineutron correlation at the surface of borromean nuclei. Phys Lett B (2023) 840:137875. doi:10.1016/j.physletb.2023.137875
15. Johansson HT, Aksyutina Y, Aumann T, Boretzky K, Borge MJG, Chatillon A, et al. Three-body correlations in the decay of 10He and 13Li. Nucl Phys A (2010) 847:66–88. doi:10.1016/j.nuclphysa.2010.07.002
16. Kohley Z, Lunderberg E, DeYoung PA, Volya A, Baumann T, Bazin D, et al. First observation of the 13Li ground state. Phys Rev C (2013) 87:011304. doi:10.1103/PhysRevC.87.011304
17. Spyrou A, Kohley Z, Baumann T, Bazin D, Brown BA, Christian G, et al. First observation of ground state dineutron decay: 16Be. Phys Rev Lett (2012) 108:102501. doi:10.1103/PhysRevLett.108.102501
18. Kondo Y, Nakamura T, Tanaka R, Minakata R, Ogoshi S, Orr NA, et al. Nucleus 26O: A barely unbound system beyond the drip line. Phys Rev Lett (2016) 116:102503. doi:10.1103/PhysRevLett.116.102503
19. Lunderberg E, DeYoung PA, Kohley Z, Attanayake H, Baumann T, Bazin D, et al. Evidence for the ground-state resonance of 26O. Phys Rev Lett (2012) 108:142503. doi:10.1103/PhysRevLett.108.142503
20. Laurent B, Marqués FM, Angulo C, Ashwood NI, Borge MJG, Bouchat V, et al. Chronology of the three-body dissociation of 8He. J Phys G: Nucl Part Phys (2019) 46:03LT02. doi:10.1088/1361-6471/ab02c3
21. Marqués FM, Labiche M, Orr NA, Angélique JC, Axelsson L, Benoit B, et al. Three-body correlations in borromean halo nuclei. Phys Rev C (2001) 64:061301. doi:10.1103/PhysRevC.64.061301
22. Aksyutina Y, Aumann T, Boretzky K, Borge MJG, Caesar C, Chatillon A, et al. Study of the 14Be continuum: Identification and structure of its second 2+ state. Phys Rev Lett (2013) 111:242501. doi:10.1103/PhysRevLett.111.242501
23. Marqués FM, Orr NA, Achouri NL, Delaunay F, Gibelin J. Comment on “first observation of ground state dineutron decay: 16Be”. Phys Rev Lett (2012) 109:239201. doi:10.1103/PhysRevLett.109.239201
24. Revel A, Marqués FM, Sorlin O, Aumann T, Caesar C, Holl M, et al. Strong neutron pairing in core+ 4n nuclei. Phys Rev Lett (2018) 120:152504. doi:10.1103/PhysRevLett.120.152504
25. Lednitski R, Lyuboshits VL. Final-state interaction effect on pairing correlations between particles with small relative momenta. Yadernaya Fizika (1982) 35:1316–30.
26. Wang SM, Nazarewicz W. Fermion pair dynamics in open quantum systems. Phys Rev Lett (2021) 126:142501. doi:10.1103/PhysRevLett.126.142501
27. Kohley Z, Baumann T, Christian G, DeYoung PA, Finck JE, Frank N, et al. Three-body correlations in the ground-state decay of 26O. Phys Rev C (2015) 91:034323. doi:10.1103/PhysRevC.91.034323
28. Grigorenko LV, Mukha IG, Thompson IJ, Zhukov MV. Two-proton widths of 12O,16Ne, and three-body mechanism of thomas-ehrman shift. Phys Rev Lett (2002) 88:042502. doi:10.1103/PhysRevLett.88.042502
29. Ungar JE, McKeown RD, Geesaman DF, Holt RJ, Specht JR, Stephenson KE, et al. Search for the tetraneutron by the double-charge-exchange of negative pions. Phys Lett B (1984) 144:333–6. doi:10.1016/0370-2693(84)91272-3
30. Gorringe TP, Ahmad S, Armstrong DS, Burnham RA, Hasinoff MD, Larabee AJ, et al. Search for the tetraneutron using the reaction 4He(π−, π+)4n. Phys Rev C (1989) 40:2390–3. doi:10.1103/PhysRevC.40.2390
31. Gräter J, Amaudruz PA, Bilger R, Camerini P, Clark J, Clement H, et al. Search for a bound trineutron with the 3He(π−, π+)nnn reaction. Eur Phys J A Hadron Nucl (1999) 4:5–7. doi:10.1007/s100500050196
32. Ohlsen GG, Stokes RH, Young PG. Search for states in the three-neutron and triton systems. Phys Rev (1968) 176:1163–5. doi:10.1103/PhysRev.176.1163
33. Cerny J, Weisenmiller RB, Jelley NA, Wilcox KH, Wozniak GJ. 7Li+7Li reaction studies leading to multi-neutron final states. Phys Lett B (1974) 53:247–9. doi:10.1016/0370-2693(74)90471-7
34. Belozyorov AV, Borcea C, Dlouhỳ Z, Kalinin AM, Chau NH, Penionzhkevich YE. Search for the tri- and tetra-neutron in reactions induced by 11B and 9Be ions on 7Li. Nucl Phys A (1988) 477:131–42. doi:10.1016/0375-9474(88)90365-X
35. Bohlen HG, Gebauer B, Kirchner T, von Lucke-Petsch M, Von Oertzen W, Ostrowski AN, et al. Study of light neutron-rich nuclei with 14C-induced reactions. Nucl Phys A (1995) 583:775–82. doi:10.1016/0375-9474(94)00757-E
36. Marqués FM, Labiche M, Orr NA, Angélique JC, Axelsson L, Benoit B, et al. Detection of neutron clusters. Phys Rev C (2002) 65:044006. doi:10.1103/PhysRevC.65.044006
37. Marqués FM, Orr NA, Falou HA, Normand G, Clarke NM. On the possible detection of 4n events in the breakup of 14Be (2005). arXiv preprint nucl-ex/0504009. doi:10.48550/arXiv.nucl-ex/0504009
38. Pieper SC. Can modern nuclear Hamiltonians tolerate a bound tetraneutron? Phys Rev Lett (2003) 90:252501. doi:10.1103/PhysRevLett.90.252501
39. Timofeyuk NK. Do multineutrons exist? J Phys G: Nucl Part Phys (2003) 29:L9–L14. doi:10.1088/0954-3899/29/2/102
40. Bertulani CA, Zelevinsky V. Is the tetraneutron a bound dineutron–dineutron molecule? J Phys G: Nucl Part Phys (2003) 29:2431–7. doi:10.1088/0954-3899/29/10/309
41. Lazauskas R, Carbonell J. Is a physically observable tetraneutron resonance compatible with realistic nuclear interactions? Phys Rev C (2005) 72:034003. doi:10.1103/PhysRevC.72.034003
42. Shirokov AM, Papadimitriou G, Mazur AI, Mazur IA, Roth R, Vary JP. Prediction for a four-neutron resonance. Phys Rev Lett (2016) 117:182502. doi:10.1103/PhysRevLett.117.182502
43. Shirokov AM, Kim Y, Mazur AI, Mazur IA, Shin IJ, Vary JP. Tetraneutron resonance: Theory. AIP Conf Proc (2018):020038. doi:10.1063/1.5078857
44. Fossez K, Rotureau J, Michel N, Płoszajczak M. Can tetraneutron be a narrow resonance? Phys Rev Lett (2017) 119:032501. doi:10.1103/PhysRevLett.119.032501
45. Deltuva A. Tetraneutron: Rigorous continuum calculation. Phys Lett B (2018) 782:238–41. doi:10.1016/j.physletb.2018.05.041
46. Higgins MD, Greene CH, Kievsky A, Viviani M. Nonresonant density of states enhancement at low energies for three or four neutrons. Phys Rev Lett (2020) 125:052501. doi:10.1103/PhysRevLett.125.052501
47. Hiyama E, Lazauskas R, Carbonell J, Kamimura M. Possibility of generating a 4-neutron resonance with a T = 3/2 isospin 3-neutron force. Phys Rev C (2016) 93:044004. doi:10.1103/PhysRevC.93.044004
48. Li JG, Michel N, Hu BS, Zuo W, Xu FR. Ab initio no-core gamow shell-model calculations of multineutron systems. Phys Rev C (2019) 100:054313. doi:10.1103/PhysRevC.100.054313
49. Berggren T. On the use of resonant states in eigenfunction expansions of scattering and reaction amplitudes. Nucl Phys A (1968) 109:265–87. doi:10.1016/0375-9474(68)90593-9
50. Lazauskas R, Hiyama E, Carbonell J. Low energy structures in nuclear reactions with 4n in the final state. Phys Rev Lett (2023) 130:102501. doi:10.1103/PhysRevLett.130.102501
51. Faestermann T, Bergmaier A, Gernhäuser R, Koll D, Mahgoub M. Indications for a bound tetraneutron. Phys Lett B (2022) 824:136799. doi:10.1016/j.physletb.2021.136799
52. Lazauskas R, Carbonell J. Three-neutron resonance trajectories for realistic interaction models. Phys Rev C (2005) 71:044004. doi:10.1103/PhysRevC.71.044004
53. Gandolfi S, Hammer HW, Klos P, Lynn JE, Schwenk A. Is a trineutron resonance lower in energy than a tetraneutron resonance? Phys Rev Lett (2017) 118:232501. doi:10.1103/PhysRevLett.118.232501
54. Kanada-En’yo Y. Dineutron structure in 8He. Phys Rev C (2007) 76:044323. doi:10.1103/PhysRevC.76.044323
55. Kobayashi F, Kanada-En’yo Y. Dineutron formation and breaking in 8He. Phys Rev C (2013) 88:034321. doi:10.1103/PhysRevC.88.034321
56. Tohsaki A, Horiuchi H, Schuck P, Röpke G. Colloquium: Status of α-particle condensate structure of the hoyle state. Rev Mod Phys (2017) 89:011002. doi:10.1103/RevModPhys.89.011002
Keywords: neutron cluster, neutron correlation, neutron-rich nuclei, dineutron, tetraneutron
Citation: Huang S and Yang Z (2023) Neutron clusters in nuclear systems. Front. Phys. 11:1233175. doi: 10.3389/fphy.2023.1233175
Received: 01 June 2023; Accepted: 27 June 2023;
Published: 11 July 2023.
Edited by:
Danyang Pang, Beihang University, ChinaReviewed by:
Georgios Souliotis, National and Kapodistrian University of Athens, GreeceCopyright © 2023 Huang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zaihong Yang, emFpaG9uZy55YW5nQHBrdS5lZHUuY24=
 Siwei Huang
Siwei Huang Zaihong Yang
Zaihong Yang