Adaptive consensus tracking control of non-affine non-linear MASs based on Taylor decoupling technology and an event-triggered design strategy

This research paper studies the consensus tracking control problem for a class of uncertain non-affine non-linear multi-agent systems (MASs). First, different from the separation design scheme using the mean value theorem in previous works, this research paper not only uses the mean value theorem but also introduces the Taylor decoupling method to decouple the complex unknown non-affine structure. Second, to solve the difficulty of unknown non-linear functions in non-linear MASs, an intelligent technique based on neural networks was used. In addition, compared with the existing traditional event-triggered control strategy based on the relative threshold, an improved event-triggered control strategy based on the decreasing function of error variables was introduced to reduce the waste of unnecessary resources. The theoretical result shows that the whole closed-loop system is stable under the action of the proposed control protocol. Finally, the simulation experiment verifies the effectiveness of our control method.

1 Introduction

In recent years, with the rapid development of computer technology, problems related to MASs have also been the focus of many scholars. The system is mainly used in the fields of robotics, transportation, and human–machine interactions [1–7]. Particularly, MASs have higher performance and efficiency compared with expensive single systems; however, their control is more complex. The large-scale complex control problem of MASs can be solved through information exchange and coordination among agents. One of the most significant and essential areas of study in MAS cooperative control is the consensus problem. Early studies conducted extensive research on the consensus tracking control of linear MASs [8–10]. However, in recent years, consensus tracking control of non-linear MASs has received increasing attention [11,12].

In real-world industrial production, many objects cannot be modeled as systems with affine forms; therefore, the control design of non-affine non-linear systems has always been a key problem [13–17]. Furthermore, due to the needs of some practical tasks, such as supersonic vehicles and magnetic levitation systems [18–20], theoretical research on non-affine non-linear MASs is more meaningful and some non-affine non-linear MAS control methods have been proposed. Using a new class of implicit function and fuzzy logic technology, under the condition of switching topologies, the containment control problem of uncertain non-affine non-linear MASs with many dynamic leaders has been addressed [21]. Regarding the control problem of non-affine non-linear MASs, Wang and Song [22] proposed a distributed neural adaptive control scheme under the condition that the control gain is uneven. The aforementioned research showed that the implicit function or median theorems are widely used for controller decoupling. In contrast, the Taylor method used in the present study provides a new approach for controller decoupling.

The previous literature has shown that the event-triggered control (ETC) strategy is a good way to reduce sample data and traffic to design control strategies. In recent years, many researchers have adopted the ETC strategy to design control strategies [23–28]. An ETC strategy that follows the switching threshold was introduced to save communication resources, and the tracking control problem for stochastic non-linear pure-feedback MASs was solved [29]. Wu et al [30] proposed an improved ETC strategy that included ETC input and tracking error reduction function to update the actual control input. However, the aforementioned event-triggered strategies do not take into account the triggering rate, which is worth considering in the development of more efficient ETC strategies, and which motivates our work.

Based on the aforementioned findings, this research paper focuses on the consensus tracking control problem for non-affine non-linear MASs. According to the Taylor decoupling technique, a scheme of control input separation design for non-affine non-linear MASs is proposed to ensure the boundedness of all signals and achieve good consensus tracking. By introducing an improved ETC strategy, unnecessary resource waste is reduced. The following is a summary of the contributions made by this research paper: 1) to solve the coupling problem of non-affine non-linear MASs, the Taylor decoupling technology was used to effectively decouple the non-linear coupling functions. In addition, an intelligent technology based on neural networks was used to approximate unknown non-linear functions. 2) The previous literature used the fixed threshold ETC strategy to change the size of the control amplitude, with a constant measurement error [31]; in contrast, the relative threshold ETC considered in this study can adjust the system performance more flexibly. This research paper adopts an improved relative threshold ETC strategy to design the controller for each agent and introduces a decreasing function of error variables, which improves the efficiency of the ETC strategy by reducing the waste of communication resources.

2 Problem formulation and preliminaries

2.1 Graph theory

Consider the topological structure of a MASs with one leader and multiple followers, which is represented by a $\widehat{G}=\left(\widehat{\mathcal{V}},\widehat{\mathcal{E}}\right)$ with $\widehat{\mathcal{V}}=\left\{v_0,v_1,\dots ,v_N\right\}$ representing the node set, where v₀ is an agent associated with the leader, and $\widehat{\mathcal{E}}=\widehat{\mathcal{V}}\times \widehat{\mathcal{V}}$ denoting the edge set. An edge $\left(i,j\right)\in \widehat{\mathcal{V}}$ in $\widehat{G}$ means that the agent i can get information from the agent j directly. The adjacency matrix is denoted as $A=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ with a_ij > 0. The set of neighbors of node i is denoted by $N_i=\left\{j=\left(j,i\right)\in \widehat{\mathcal{E}}\right\}$. The diagonal matrix $D=\mathit{diag}(d_1,d_2,\dots ,d_N)\in {\mathbb{R}}^{N\times N}$ is the definition of the in-degree matrix, where ${\tilde{d}}_i={\sum }_{j\in N_i}{a}_{ij}$. The Laplacian matrix is defined as L = D − A, where $L\in {\mathbb{R}}^{N\times N}$.

2.2 System formulation

We consider the following class of non-affine non-linear MASs:

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_{i,k}& =g_{i,k}\left({\mathrm{\Delta }}_{i,k}\right)x_{i,k+1}+f_{i,k}\left({\mathrm{\Delta }}_{i,k}\right)+{{\phi }_{i,k}}^T\left({\mathrm{\Delta }}_{i,k}\right){\eta }_{i,k},\hfill \\ \hfill {\dot{x}}_{i,n_i}& =f_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)+{{\phi }_{i,n_i}}^T\left({\mathrm{\Delta }}_i\right){\eta }_{i,n_i}+d_i\left(t\right),\hfill \\ \hfill y_i& =x_{i,1},\hfill \end{array}\hfill \end{array}(1)$

where ${\mathrm{\Delta }}_{i,k}={[x_{i,1},x_{i,2},\dots ,x_{i,k}]}^T\in {\mathbb{R}}^k$, ${\mathrm{\Delta }}_i={[x_{i,1},x_{i,2},\dots ,x_{i,n_i}]}^T\in {\mathbb{R}}^{n_i}$ are the system state vectors. $y_i\in \mathbb{R}$, $u_i\in \mathbb{R}$, $d_i\in \mathbb{R}$ are the control output, the input, and the additive disturbance, $f_{i,k}\left(\cdot \right)$; $g_{i,k}\left(\cdot \right):{\mathbb{R}}^k\to \mathbb{R}$ represents the known smooth functions, $f_{i,n_i}$; and ${\phi }_{i,k}\left(\cdot \right)$ represents the unknown smooth functions. ${\eta }_{i,k}\in {\mathbb{R}}^p$ denotes the unknown parameter vector.

Our goal is to ensure that: 1) all signals in the closed-loop system fall within the specified compact set; and 2) the system output tracking error e₁ = y − y_d converges to zero.

Assumption 1: The external disturbance d_i, the reference signal y_d, and its kth-order derivatives $y_d^{(k)}$, k = 1, 2, …, n, are all continuous and bounded. In addition, $\left|y_d\right|\le y_d^{*}$, $\left|y_d^{(k)}\right|\le y_d^{(k)*}$, and $\left|d_i\right|\le {d_i}^{*}$, where $y_d^{*},y_d^{(k)*}$ and ${d_i}^{*}$ are the unknown upper bounds.

Assumption 2: $\widehat{G}$ contains a spanning tree, the root which is called the leader y_d.

Assumption 3 [30]: Based on Assumption 1, for a given compact set ${\mathrm{\Omega }}_{\mathrm{\Delta }}\in {\mathbb{R}}^n$, there exist two positive constants $f_a^{*}$ and $f_b^{*}$ such that this research paper deals with a class of non-affine non-linear MASs tracking control systems with uncertainties

$0\le f_a^{*}\le \frac{\partial f_{i,n_i}\left(\mathrm{\Delta },0\right)}{\partial u}\le f_b^{*},(2)$

where arbitrary Δ ∈ Ω_Δ.

2.3 Preliminaries

Lemma1: Let Ω_Δ be given compact set of ${\mathbb{R}}^{n_i}$, then the non-linear coupling function $f_{i,n_i}({\mathrm{\Delta }}_i,u_i)$ can be changed into

$f_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)=f_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)+g_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)u_i.(3)$

Then, we use Taylor’s theorem to separate u_i from $g_{i,n_i}$

$\begin{array}{ll}\hfill g_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)& =g_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)+\frac{\partial g_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)}{\partial u_i}{u}_i+\frac{1}{2!}\frac{{\partial }^2{g}_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)}{\partial u_i^2}{u}_i^2+\cdots +\frac{1}{n_i!}\frac{{\partial }^n{g}_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)}{\partial u_i^n}{u}_i^n+{\mathfrak{R}}_{i,n_i+1}\left({\mathrm{\Delta }}_i,u_i\right),\hfill \end{array}(4)$

where $g_{i,n_i}({\mathrm{\Delta }}_i,u_i)=(\frac{\partial f({\mathrm{\Delta }}_i,u_i)}{\partial u_i}{\mid }_{u=u_c})$ with u_c = cu, c ∈ (0, 1) and ${\mathfrak{R}}_{i,n_i+1}({\mathrm{\Delta }}_i,u_i)=\frac{1}{(n_i+1)!}\frac{{\partial }^{n+1}{g}_{n_i}({\mathrm{\Delta }}_i,\zeta )}{\partial u_i^{n+1}}{u}_i^{n+1}$ with 0 < ζ < $u_i$.

Substituting Eq. 4 into Eq. 3, we obtain

$\begin{array}{ll}\hfill f_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)& =f_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)+g_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)u_i+m_{i,n_i}\left({\mathrm{\Delta }}_i,u_i\right)\hfill \\ \hfill & =g_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)u_i+C\left({\mathrm{\Delta }}_i\right),\hfill \end{array}(5)$

where $C({\mathrm{\Delta }}_i)=f_{i,n_i}({\mathrm{\Delta }}_i,0)+m_{i,n_i}({\mathrm{\Delta }}_i,u_i)$, $m_{i,n_i}({\mathrm{\Delta }}_i,u)=\frac{\partial g_{i,n_i}({\mathrm{\Delta }}_i,0)}{\partial u_i}{u}_i^2+\frac{1}{2!}\frac{{\partial }^2{g}_{i,n_i}({\mathrm{\Delta }}_i,0)}{\partial u_i^2}{u}_i^3+\cdots +\frac{1}{n_i!}\frac{{\partial }^n{g}_{i,n_i}({\mathrm{\Delta }}_i,0)}{\partial u_i^n}{u}_i^{n+1}+{\mathfrak{R}}_{i,n_i+1}({\mathrm{\Delta }}_i,u_i)u_i$.

Therefore, from Eqs 3–5, Eq. 1 can be rewritten in the following affine form:

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_{i,k}& =g_{i,k}\left(x_i\right)x_{i,k+1}+f_{i,k}\left(x_i\right)+{{\phi }_{i,k}}^T\left(x_i\right){\eta }_{i,k},\hfill \\ \hfill {\dot{x}}_{i,n_i}& =g_{i,n_i}\left({\mathrm{\Delta }}_i,0\right)u_i+C\left({\mathrm{\Delta }}_i\right)+{{\phi }_{i,n_i}}^T\left(x_i\right){\eta }_{i,n_i}+d_i\left(t\right),\hfill \\ \hfill y_i& =x_{i,1}.\hfill \end{array}\hfill \end{array}(6)$

Lemma 2 [32]: Define the diagonal matrix $\tilde{B}=\mathit{diag}\left\{{\tilde{b}}_i\right\}\in {\mathbb{R}}^{N\times N}$, then $L+\tilde{B}$ is non-singular.Lemma 3 [32]: Define $E_1={(e_{\mathrm{1,1}},e_{\mathrm{2,1}},\dots e_{N,1})}^T,Y={(y_1,y_2,\dots y_N)}^T,Y_c={(y_c,y_c,\dots y_c)}^T$, then

$‖Y-Y_c‖\le ‖E_1‖\underset{-}{\beta }\left(L+\tilde{B}\right),(7)$

where $\underset{-}{\beta }(L+\tilde{B})$ is the minimum singular value of $L+\tilde{B}$. Lemma 4 [32]: For any constant $\alpha \in \mathbb{R}$ and any variable ɛ > 0, the following inequality holds:

$0\le \left|\alpha \right|-\alpha \mathit{tanh}\left(\frac{\alpha }{\epsilon }\right)\le \kappa \epsilon ,(8)$

where κ = 0.2785.

2.4 Radial basis function neural networks

Radial basis function neural networks (RBFNNs) can approximate arbitrary non-linear functions [11,33–35]. Specifically, the unknown non-linear functions $F\left(\mathrm{\Gamma }\right)$ can be approximated over a compact set $\mathrm{\Gamma }\subset {\mathrm{\Omega }}_{\mathrm{\Gamma }}\subset {\mathbb{R}}^l$

$F\left(\mathrm{\Gamma }\right)={\mathrm{\Phi }}^{*T}\bar{S}\left(\mathrm{\Gamma }\right)+\delta \left(\mathrm{\Gamma }\right),(9)$

where ${\mathrm{\Phi }}^{*}={[{\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots ,{\mathrm{\Phi }}_l]}^T\in {\mathbb{R}}^l$ is the ideal weight vector, $\delta \left(\mathrm{\Gamma }\right)$ is the approximation error satisfying $\left|\delta (\mathrm{\Gamma })\right|\le \tau$ with a precision level τ > 0. $\bar{S}\left(\mathrm{\Gamma }\right)={\left[{\bar{S}}_1\left(\mathrm{\Gamma }\right),{\bar{S}}_2\left(\mathrm{\Gamma }\right),\dots ,{\bar{S}}_l\left(\mathrm{\Gamma }\right)\right]}^T\in {\mathbb{R}}^l$ is the basis function, where l > 1 is the node number of s RBFNNs. Particularly, the basis function can be chosen as

${\bar{S}}_i\left(\mathrm{\Gamma }\right)=\exp \left[-{\left(\mathrm{\Gamma }-{\xi }_i\right)}^T\left(\mathrm{\Gamma }-{\xi }_i\right)/{\eta }_i^2\right],i=1,\dots ,l,(10)$

where ${\xi }_i={\left[{\xi }_{i1},\dots ,{\xi }_{il}\right]}^T$ is the center of the receptive field center and η_i is the width of the Gaussian function.

3 Main result

This section provides an efficient adaptive ETC strategy based on the adaptive neural approximation technique and a backstepping scheme.

The following error variables are defined:

$e_{i,1}={\displaystyle \sum _{j=1}^N}{a}_{ij}\left(y_i-y_j\right)+{\tilde{b}}_i\left(y_i-y_d\right),(11)$

$e_{i,k}=x_{i,k}-u_{i,k-1},(12)$

where u_i,k−1 is the virtual controller designed in step k.

Step 1: First, the derivation of e_i,1 along (Eq. 11) is

$\begin{array}{ll}\hfill {\dot{e}}_{i,1}& =\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(g_{i,1}\left(x_i\right)x_{i,1}+f_{i,1}\left(x_i\right)+{\phi }_{i,1}^T\left(x_i\right){\eta }_{i,1}\right)\hfill \\ \hfill & -{\tilde{b}}_i{\dot{y}}_d-{\displaystyle \sum _{j=1}^N}{a}_{ij}\left(g_{j,1}\left(x_j\right)x_{j,1}+f_{j,1}\left(x_i\right)+{\phi }_{j,1}^T\left(x_j\right){\eta }_{j,1}\right).\hfill \end{array}(13)$

The Lyapunov function is

$V_{i,1}=\frac{1}{2}{e}_{i,1}^2+\frac{1}{2{\gamma }_{i,1}}{{\tilde{\theta }}_{i,1}}^2,(14)$

where γ_i,1 is a positive design parameter, ${\widehat{\theta }}_{i,1}$ is the estimation of θ_i,1, and ${\tilde{\theta }}_{i,1}={\theta }_{i,1}-{\widehat{\theta }}_{i,1}$.

From Eqs 13, 14, the derivative of V_i,1 is computed as

$\begin{array}{ll}\hfill {\dot{V}}_{i,1}=& e_{i,1}{\dot{e}}_{i,1}-\frac{{\tilde{\theta }}_{i,1}}{{\gamma }_{i,1}}{\dot{\widehat{\theta }}}_{i,1}\hfill \\ \hfill & =e_{i,1}\left[\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(g_{i,1}\left(x_i\right)x_{i,2}+f_{i,1}\left(x_i\right)+{\phi }_{i,1}^T\left(x_i\right){\eta }_{i,1}\right)\right.\hfill \\ \hfill & -{\tilde{b}}_i{\dot{y}}_d-{\displaystyle \sum _{j=1}^N}{a}_{ij}\left(g_{j,1}\left(x_j\right)x_{j,2}+f_{j,1}\left(x_i\right)\right.\hfill \\ \hfill & \left.\left.+{\phi }_{j,1}^T\left(x_j\right){\eta }_{j,1}\right)\right]-\frac{{\tilde{\theta }}_{i,1}}{{\gamma }_{i,1}}{\dot{\widehat{\theta }}}_{i,1}.\hfill \end{array}(15)$

Consequently, taking Eq. 15 into account yields

$\begin{array}{ll}\hfill {\dot{V}}_{i,1}& =e_{i,1}[\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(g_{i,1}\left(x_i\right)e_{i,2}+g_{i,1}\left(x_i\right)u_{i,1}\right)\hfill \\ \hfill & \left.+{\acute{F}}_{i,1}\left({\mathrm{\Gamma }}_i\right)-\frac{e_{i,1}}{2}\right]-\frac{{\tilde{\theta }}_{i,1}}{{\gamma }_{i,1}}{\dot{\widehat{\theta }}}_{i,1},\hfill \end{array}(16)$

where

$\begin{array}{ll}\hfill {\acute{F}}_{i,1}\left({\Gamma }_i\right)& =\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(f_{i,1}\left(x_i\right)+{\phi }_{i,1}^T\left(x_i\right){\eta }_{i,1}\right)-{\tilde{b}}_i{\dot{y}}_d\hfill \\ \hfill & -{\tilde{d}}_i\left(g_{j,1}\left(x_j\right)x_{j,2}+f_{j,1}\left(x_i\right)\right.\hfill \\ \hfill & \left.+{\phi }_{j,1}^T\left(x_j\right){\eta }_{j,1}\right)+\frac{e_{i,1}}{2}.\hfill \end{array}(17)$

Due to ${\acute{F}}_{i,1}({\mathrm{\Gamma }}_i)$ contains unknown functions. Hence, the RBFNN is introduced to approximate the unknown functions

$\begin{array}{c}\hfill {\acute{F}}_{i,1}\left({\mathrm{\Gamma }}_i\right)={\mathrm{\Phi }}_{i,1}^{{*}^T}{\bar{S}}_{i,1}\left({\mathrm{\Gamma }}_i\right)+{\delta }_{i,1}\left({\mathrm{\Gamma }}_i\right),\left|{\delta }_{i,1}\left({\mathrm{\Gamma }}_i\right)\right|\le {\tau }_{i,1},\hfill \end{array}(18)$

where τ_i,1 > 0, ${\mathrm{\Gamma }}_i={[x_{i,1}^T,x_{j,1}^T,y_d,{\dot{y}}_d]}^T\in \mathrm{\Omega }$.

Furthermore, combining Lemma 4 with Eq. 18 and Young inequality results in

$\begin{array}{c}\hfill e_{i,1}{\acute{F}}_{i,1}\left({\mathrm{\Gamma }}_i\right)\le \frac{{\theta }_{i,1}}{2c_{i,1}^2}{e}_{i,1}^2{\bar{S}}_{i,1}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,1}\left({\mathrm{\Gamma }}_i\right)+\frac{c_{i,1}^2}{2}+\frac{e_{i,1}^2}{2}+\frac{{\tau }_{i,1}^2}{2},\hfill \end{array}(19)$

where c_i,1 is a positive constant.

The virtual control u_i,1 is constructed as

$u_{i,1}=\frac{1}{\left({\tilde{b}}_i+{\tilde{d}}_i\right)g_{i,1}\left(x_i\right)}\left[-a_{i,1}{e}_{i,1}-\frac{{\widehat{\theta }}_{i,1}}{2{c^2}_{i,1}}{e}_{i,1}{\bar{S}}_{i,1}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,1}\left({\mathrm{\Gamma }}_i\right)\right],(20)$

where a_i,1 is a positive constant.

According to Assumption 3 and Eqs 17–20, we obtain

$\begin{array}{ll}\hfill {\dot{V}}_{i,1}& \le -a_{i,1}{e}_{i,1}^2+\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(g_{i,1}\left(x_i\right)e_{i,1}{e}_{i,2}\right)\hfill \\ \hfill & -\frac{{\tilde{\theta }}_{i,1}}{{\gamma }_{i,1}}\left(\frac{{\gamma }_{i,1}}{2{c^2}_{i,1}}{e}_{i,1}^2{\bar{S}}_{i,1}^T\left({\mathrm{\Gamma }}_{i,1}\right){\bar{S}}_{i,1}\left({\mathrm{\Gamma }}_{i,1}\right)-{\dot{\widehat{\theta }}}_{i,1}\right)\hfill \\ \hfill & +\frac{{c^2}_{i,1}}{2}+\frac{{{\tau }^2}_{i,1}}{2}.\hfill \end{array}(21)$

Then, the adaptive law ${\dot{\widehat{\theta }}}_{i,1}$ and the positive design parameters μ_i,1 are

${\dot{\widehat{\theta }}}_{i,1}=\frac{{\gamma }_{i,1}}{2{c^2}_{i,1}}{e}_{i,1}{\bar{S}}_{i,1}^T\left({\mathrm{\Gamma }}_{i,1}\right){\bar{S}}_{i,1}\left({\mathrm{\Gamma }}_{i,1}\right)-{\widehat{\theta }}_{i,1},(22)$

${\mu }_{i,1}=\frac{c_{i,1}^2}{2}+\frac{{\tau }_{i,1}^2}{2}+\frac{{{\theta }^2}_{i,1}}{2{\gamma }_{i,1}}.(23)$

Substituting Eqs 22, 23 into Eq. 21, we obtain

${\dot{V}}_{i,1}\le -a_{i,1}{e}_{i,1}^2+\left({\tilde{b}}_i+{\tilde{d}}_i\right)\left(g_{i,1}\left(x_i\right)e_{i,1}{e}_{i,2}\right)-\frac{{\tilde{\theta }}_{i,1}^2}{2{\gamma }_{i,1}}+{\mu }_{i,1}.(24)$

Step $k\left(2⩽k⩽n_i-1\right)$: We choose the Lyapunov function as

$V_{i,k}=V_{i,k-1}+\frac{1}{2}{e}_{i,k}^2+\frac{1}{2{\gamma }_{i,k}}{{\tilde{\theta }}_{i,k}}^2.(25)$

Similar to Eqs 14–17 in Step 1, the derivative of V_i,k can be computed as

$\begin{array}{ll}\hfill {\dot{V}}_{i,k}& ={\dot{V}}_{i,k-1}+e_{i,k}[g_{i,k}\left(x_i\right)x_{i,k+1}+f_{i,k}\left(x_i\right)+{\phi }_{i,k}^T{\eta }_{i,k}\hfill \\ \hfill & -{\displaystyle \sum _{l=1}^{k-1}}{\displaystyle \sum _{j\in N_j}}\frac{\partial u_{j,k-1}}{\partial x_{j,l}}\left(g_{j,l}\left(x_j\right)x_{j,l+1}+f_{j,l}\left(x_j\right)+{\phi }_{j,l}^T{\eta }_{j,l}\right)\hfill \\ \hfill & \left.-\frac{\partial u_{i,k-1}}{\partial y_d}{\dot{y}}_d-{\displaystyle \sum _{l=1}^{k-1}}\frac{\delta u_{i,k-1}}{\delta {\widehat{\theta }}_{i,l}}{\dot{\widehat{\theta }}}_{i,l}\right]-\frac{{\tilde{\theta }}_{i,k}}{{\gamma }_{i,k}}{\dot{\widehat{\theta }}}_{i,k},\hfill \end{array}(26)$

where γ_i,k is an arbitrary constant.

In the same way, as in Eq. 15, we get

$\begin{array}{ll}\hfill {\dot{V}}_{i,k}& ={\dot{V}}_{i,k-1}+e_{i,k}[g_{i,k}\left(x_i\right)\left(e_{i,k+1}+u_{i,k}\right)\hfill \\ \hfill & \left.+{\acute{F}}_{i,k}\left({\Gamma }_i\right)-\left({\widehat{b}}_i+{\widehat{d}}_i\right)g_{i,k-1}{e}_{i,k-1}-\frac{e_{i,k}}{2}\right]-\frac{{\tilde{\theta }}_{i,k}}{{\gamma }_{i,k}}{\dot{\widehat{\theta }}}_{i,k},\hfill \end{array}(27)$

where

$\begin{array}{ll}\hfill {\acute{F}}_{i,k}\left({\Gamma }_i\right)& =f_{i,k}\left(x_i\right)+{\phi }_{i,k}^T{\eta }_{i,k}\hfill \\ \hfill & -{\displaystyle \sum _{l=1}^{k-1}}{\displaystyle \sum _{j\in N_j}}\frac{\partial u_{j,k-1}}{\partial x_{j,l}}\left(g_{j,l}\left(x_j\right)x_{j,l+1}+f_{j,l}\left(x_j\right)\right.\hfill \\ \hfill & \left.+{\phi }_{j,l}^T{\eta }_{j,l}\right)-\frac{\partial u_{i,k-1}}{\partial y_d}{\dot{y}}_d-{\displaystyle \sum _{l=1}^{k-1}}\frac{\delta u_{i,k-1}}{\delta {\widehat{\theta }}_{i,l}}{\dot{\widehat{\theta }}}_{i,l}\hfill \\ \hfill & +\frac{e_{i,k}}{2}+\left({\acute{b}}_i+{\acute{d}}_i\right)g_{i,k-1}{e}_{i,k-1},\hfill \end{array}(28)$

where for k = 2, take $({\tilde{b}}_i+{\tilde{d}}_i)=({\acute{b}}_i+{\acute{d}}_i)$, and for 3 ≤ k ≤ n_i − 1, take ${\acute{b}}_i+{\acute{d}}_i=1$. Similar to Eq. 18, the equation ${\acute{F}}_{i,k}({\mathrm{\Gamma }}_i)={\mathrm{\Phi }}_{i,k}^{*}({\mathrm{\Gamma }}_i){\bar{S}}_{i,k}\left({\mathrm{\Gamma }}_i\right)+{\delta }_{i,k}({\mathrm{\Gamma }}_i),\left|{\delta }_{i,k}({\mathrm{\Gamma }}_i)\right|\le {\tau }_{i,k}$ can be obtained easily.

Therefore, we obtain

$e_{i,k}{\acute{F}}_{i,k}\left({\mathrm{\Gamma }}_i\right)\le \frac{{\theta }_{i,k}}{2c_{i,k}^2}{e}_{i,k}^2{\bar{S}}_{i,k}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,k}\left({\mathrm{\Gamma }}_i\right)+\frac{c_{i,k}^2}{2}+\frac{e_{i,k}^2}{2}+\frac{{\tau }_{i,k}^2}{2}.(29)$

Designing the virtual control u_i,k as

$u_{i,k}=\frac{1}{g_{i,k}\left(x_i\right)}\left[-a_{i,k}{e}_{i,k}-\frac{{\widehat{\theta }}_{i,k}}{2{c^2}_{i,k}}{e}_{i,k}{\bar{S}}_{i,k}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,k}\left({\mathrm{\Gamma }}_i\right)\right],(30)$

where c_i,k > 0 is the design constant.

We then get

$\begin{array}{ll}\hfill {\dot{V}}_{i,k}& \le -{\displaystyle \sum _{l=1}^k}{a}_{i,l}{e}_{i,l}^2+g_{i,k}\left(x_i\right)e_{i,k}{e}_{i,k+1}-{\displaystyle \sum _{l=1}^{k-1}}\frac{{{\tilde{\theta }}^2}_{i,l}}{2{\gamma }_{i,l}}\hfill \\ \hfill & -\frac{{\tilde{\theta }}_{i,k}}{{\gamma }_{i,k}}\left(\frac{{\gamma }_{i,k}}{2{c^2}_{i,k}}{e}_{i,k}^2{\bar{S}}_{i,k}^T\left({\mathrm{\Gamma }}_{i,k}\right){\bar{S}}_{i,k}\left({\mathrm{\Gamma }}_{i,k}\right)-{\dot{\widehat{\theta }}}_{i,k}\right)\hfill \\ \hfill & +{\displaystyle \sum _{l=1}^{k-1}}{\mu }_{i,k-1}+{\mu }_{i,k}.\hfill \end{array}(31)$

The adaptive law ${\dot{\widehat{\theta }}}_{i,k}$ and the positive design parameters μ_i,k are designed as

${\dot{\widehat{\theta }}}_{i,k}=\frac{{\gamma }_{i,1}}{2{c^2}_{i,k}}{e}_{i,k}{\bar{S}}_{i,k}^T\left({\mathrm{\Gamma }}_{i,k}\right){\bar{S}}_{i,k}\left({\mathrm{\Gamma }}_{i,k}\right)-{\widehat{\theta }}_{i,k},(32)$

${\mu }_{i,k}=\frac{c_{i,k}^2}{2}+\frac{{\tau }_{i,k}^2}{2}+\frac{{\theta }_{i,k}^2}{2{\gamma }_{i,k}}.(33)$

Substituting Eqs 28–33 into Eq. 31 yields

${\dot{V}}_{i,k}\le -{\displaystyle \sum _{l=1}^k}{a}_{i,l}{e}_{i,l}^2+g_{i,k}\left(x_i\right)e_{i,k}{e}_{i,k+1}-{\displaystyle \sum _{l=1}^k}\frac{{{\tilde{\theta }}^2}_{i,l}}{2{\gamma }_{i,l}}+{\displaystyle \sum _{l=1}^k}{\mu }_{i,l}.$

Step n_i: At this step, define $e_{i,n_i}=x_{i,n_i}-u_{i,n_{i-1}}$. We add an unidentified positive constant D such that $\left|C(x_i)+d_i\right|\le \left|C(x_i)\right|+\left|d_i\right|\le D$ for all Δ_i ∈ Ω_Δ.

The Lyapunov function is

$V_{i,n_i}=V_{i,n_i-1}+\frac{1}{2}{e}_{i,n_i}^2+\frac{1}{2{\gamma }_{i,n_i}}{{\tilde{\theta }}_{i,n_i}}^2.(34)$

Then,

$\begin{array}{ll}\hfill {\dot{V}}_{i,n_i}& \le {\dot{V}}_{i,n_i-1}+e_{i,n_i}\left(g_{i,n_i}\left(x_i,0\right)u_i+{\phi }_{i,n_i}^T\left(x_i\right){\eta }_{i,n_i}\right.\hfill \\ \hfill & \left.+D-{\dot{u}}_{i,n_{i-1}}\right)-\frac{{\tilde{\theta }}_{i,n_i}}{{\gamma }_{i,n_i}}{\dot{\widehat{\theta }}}_{i,n_i},\hfill \end{array}(35)$

where

$\begin{array}{ll}\hfill {\dot{u}}_{i,n_{i-1}}& ={\displaystyle \sum _{l=1}^{n-1}}\frac{\partial u_{i,n_i-1}}{\partial x_{i,l}}\left(g_{i,l}\left(x_i\right)x_{i,l+1}+f_{i,l}\left(x_i\right)+{\phi }_{i,l}^T{\eta }_{i,l}\right)\hfill \\ \hfill & +{\displaystyle \sum _{l=1}^{n-1}}{\displaystyle \sum _{j\in N_j}}\frac{\partial u_{j,n_i-1}}{\partial x_{j,l}}\left(g_{j,l}\left(x_j\right)x_{j,l+1}+f_{j,l}\left(x_j\right)\right.\hfill \\ \hfill & \left.+{\phi }_{j,l}^T{\eta }_{j,l}\right)+\frac{\partial u_{i,n_i-1}}{\partial y_d}{\dot{y}}_d+{\displaystyle \sum _{l=1}^{n-1}}\frac{\delta u_{i,n_i-1}}{\delta {\widehat{\theta }}_{i,l}}{\dot{\widehat{\theta }}}_{i,l}.\hfill \end{array}(36)$

From Eqs 35, 36, the derivative of ${\dot{V}}_{i,n_i}$is computed as

$\begin{array}{ll}\hfill {\dot{V}}_{i,n_i}& \le {\dot{V}}_{i,n_i-1}+e_{i,n_i}(g_{i,n_i}\left(x_i,0\right)u_i-g_{i,n_i-1}{e}_{i,n_i-1}\hfill \\ \hfill & \left.+{\acute{F}}_{i,n_i}\left(\mathrm{\Gamma }i\right)-\frac{e_{i,n_i}}{2}\right)-\frac{{\tilde{\theta }}_{i,n_i}}{{\gamma }_{i,n_i}}{\dot{\widehat{\theta }}}_{i,n_i},\hfill \end{array}(37)$

where

$\begin{array}{ll}\hfill {\acute{F}}_{i,n_i}\left({\mathrm{\Gamma }}_i\right)& ={\phi }_{i,n_i}^T\left(x_i\right){\eta }_{i,n_i}+D-\sum _{l=1}^{n-1}\frac{\partial u_{i,n_i-1}}{\partial x_{i,l}}\hfill \\ \hfill & \times \left(g_{i,l}\left(x_i\right)x_{i,l+1}+f_{i,l}\left(x_i\right)+{\phi }_{i,l}^T{\eta }_{i,l}\right)\hfill \\ \hfill & -{\displaystyle \sum _{l=1}^{n-1}}{\displaystyle \sum _{j\in N_j}}\frac{\partial u_{j,n_i-1}}{\partial x_{j,l}}\left(g_{j,l}\left(x_j\right)x_{j,l+1}+f_{j,l}\left(x_j\right)\right.\hfill \\ \hfill & \left.+{\phi }_{j,l}^T{\eta }_{j,l}\right)-\frac{\partial u_{i,n_i-1}}{\partial y_d}{\dot{y}}_d-\sum _{l=1}^{n-1}\frac{\delta u_{i,n_i-1}}{\delta {\widehat{\theta }}_{i,l}}{\dot{\widehat{\theta }}}_{i,l}\hfill \\ \hfill & +\frac{e_{i,n_i}}{2}+g_{i,n_i-1}{e}_{i,n_i-1}.\hfill \end{array}(38)$

Furthermore,

$e_{i,n_i}{\acute{F}}_{i,n_i}\left({\mathrm{\Gamma }}_i\right)\le \frac{{\theta }_{i,n_i}}{2c_{i,n_i}^2}{e}_{i,n_i}{\bar{S}}_{i,n_i}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,n_i}\left({\mathrm{\Gamma }}_i\right)+\frac{c_{i,n_i}^2}{2}+\frac{e_{i,n_i}^2}{2}+\frac{{\tau }_{i,n_i}^2}{2}.(39)$

Hence, the virtual control signal is designed as

$u_{i,n_i}=-a_{i,n_i}{e}_{i,n_i}-\frac{{\widehat{\theta }}_{i,n_i}}{2{c^2}_{i,n_i}}{e}_{i,n_i}{\bar{S}}_{i,n_i}^T\left({\mathrm{\Gamma }}_i\right){\bar{S}}_{i,n_i}\left({\mathrm{\Gamma }}_i\right),(40)$

where $a_{i,n_i}$ is the positive constant.

Substituting Eqs 34–40 into Eq. 35, we have

${\dot{V}}_{i,n_i}\le -{\displaystyle \sum _{l=1}^{n_i}}{a}_{i,l}{e}_{i,l}^2-{\displaystyle \sum _{l=1}^{n_i}}\frac{{{\tilde{\theta }}^2}_{i,l}}{2{\gamma }_{i,l}}+{\displaystyle \sum _{l=1}^{n_i}}{\mu }_{i,l}+e_{i,n_i}\left(g_{i,n_i}\left(x_i\right)u_i-u_{i,n_i}\right).(41)$

Furthermore, the actual ETC input strategy is as follows:

$\begin{array}{c}\hfill \begin{array}{cc}\hfill v_i\left(t\right)=& {\varsigma }_0^{-1}\left(1+{\varrho }_0\right)\left(u_{i,n_i}\mathit{tanh}\left(\frac{u_{i,n_i}{e}_{i,n_i}}{\epsilon }\right)\right.\hfill \\ \hfill & \left.+{\sigma }_1\mathit{tanh}\left(\frac{{\sigma }_1{e}_{i,n_i}}{\epsilon }\right)+e_n\mathit{tanh}\left(\frac{e_n{e}_{i,n_i}}{\epsilon }\right)\right),\hfill \end{array}\hfill \end{array}(42)$

$u_i\left(t\right)=v_i\left(t_k\right),\forall t\in \left[t_k,t_{k+1}\right),(43)$

$t_{k+1}=\inf \left\{t\in {\mathbb{R}}^{+}\mid \left|e_c\left(t\right)\right|\ge {\varrho }_0\left|u\left(t\right)\right|+{\omega }_0{e}_n+v_0\right\},(44)$

where e_c(t) = v(t) − u(t), $e_n=[1/\left(\right.{\sum }_{k-1}^n\left|e_k(t)\right|+{\kappa }_1]$ and κ₁ > 0, ς₀ > 0, 0 < ϱ₀ < 1, ω₀ > 0, and v₀ > 0 are positive design parameters such that ${\varsigma }_0\le f_a^{*},{\omega }_0{f}_b^{*}<1-{\varrho }_0,v_0{f}_b^{*}<{\sigma }_1(1-{\varrho }_0)$.

According to Eq. 44, $v(t)-u(t)={\lambda }_0(t)({\varrho }_0\left|u(t)\right|+{\omega }_0{e}_n(t)+v_0)$ where λ₀(t) is a continuous function and λ₀(t_k) = 0, λ₀(t_k+1) = ±1, λ₁(t) = ±λ₀(t), |λ₀(t)| ≤ 1, and |λ₁(t)| ≤ 1, $\forall t\in \left[\right.t_k,t_{k+1}\left.\right)$. Since $a\in \mathbb{R}$, ɛ > 0, $-a\tanh (\frac{a}{\epsilon })\le 0$, $e_{i,n_i}{v}_i(t)\le 0$, and $\frac{e_{i,n_i}{v}_i(t)}{1+{\lambda }_1(t){\varrho }_0}\le \frac{e_{i,n_i}{v}_i(t)}{1+{\varrho }_0}$.

Then,

$u_i\left(t\right)=\frac{v_i\left(t\right)}{1+{\lambda }_1\left(t\right){\varrho }_0}-\frac{{\lambda }_0\left(t\right){\varrho }_0{e}_0}{1+{\lambda }_1\left(t\right){\varrho }_0}-\frac{{\lambda }_0\left(t\right)v_0}{1+{\lambda }_1\left(t\right){\varrho }_0}.(45)$

Substituting Eqs 42–45 into Eq. 41, one obtains

$\begin{array}{ll}\hfill {\dot{V}}_{i,n_i}& \le -{\displaystyle \sum _{l=1}^{n_i}}{a}_{i,l}{e}_{i,l}^2-{\displaystyle \sum _{l=1}^{n_i}}\frac{{{\tilde{\theta }}^2}_{i,l}}{2{\gamma }_{i,l}}-\left|e_n\right|\left|e_{i,n_i}\right|-{\sigma }_1\left|e_{i,n_i}\right|\hfill \\ \hfill & +{\displaystyle \sum _{l=1}^{n_i}}{\mu }_{i,l}+\frac{f_b^{*}{\omega }_0\left|e_0\right|\left|e_{i,n_i}\right|}{1-{\varrho }_0}+\frac{f_b^{*}{v}_0\left|e_{i,n_i}\right|}{1-{\varrho }_0}+3\kappa \epsilon \hfill \\ \hfill & \le -{\displaystyle \sum _{l=1}^{n_i}}{a}_{i,l}{e}_{i,l}^2-{\displaystyle \sum _{l=1}^{n_i}}\frac{{{\tilde{\theta }}^2}_{i,l}}{2{\gamma }_{i,l}}+{\displaystyle \sum _{l=1}^{n_i}}{\mu }_{i,l}+3\kappa \epsilon .\hfill \end{array}(46)$

Remark 1: The newly introduced decreasing function e_n(t) gives a higher triggering threshold when the tracking error e_k, k = 1, 2, …, n is very small. According to $\left|e_c(t)\right|\ge {\varrho }_0\left|u(t)\right|+{\omega }_0{e}_n+v_0$, choosing the fixed threshold v₀ and parameters appropriately, ω₀ and ϱ₀ can achieve the expected tracking performance.

4 Stability analysis

We are now prepared to state the main results of this research after the analysis mentioned previously.

Theorem 1: Consider the non-linear MASs (Eq. 1) satisfying Assumption 2. For bounded initial conditions, the virtual control signals (Eqs 20, 30, 40), adaptive laws (Eqs 22, 31), and the tracking control protocol (Eq. 43) based on Assumptions 1–3 are obtained. The whole controller design process ensures that the signals of all closed-loop systems are bounded.

Proof: The derivative of $V_{I,n_i}$ is rewritten as

${\dot{V}}_{i,n_i}\le -{\varpi }_i{V}_{i,n_i}+{\beta }_i,(47)$

where ${\beta }_i={\displaystyle \sum _{l=1}^{n_i}}{\mu }_{i,l}+3\kappa \epsilon$, ${\varpi }_i=min\left\{2a_{i,l},{\gamma }_{i,l}\right\}$. The total Lyapunov candidate function V is $V={\sum }_{i=1}^N{V}_{i,n_i}$.

From Eq. 47, one obtains

$\dot{V}\le -\varpi V+\beta ,(48)$

where $\varpi =\min \left\{{\varpi }_i,i=\mathrm{1,2},\dots ,N\right\}$ and $\beta ={\sum }_{i=1}^N{\beta }_i$.

Furthermore, Eq. 48 satisfies

$0\le V\left(t\right)\le e^{\varpi t}V\left(0\right)+\frac{\beta }{\varpi }\left(1-e^{\varpi t}\right).(49)$

From Eq. 49,

${‖E_1‖}^2\le 2e^{-\varpi t}V\left(0\right)+\frac{2\beta }{\varpi }\left(1-e^{-\varpi t}\right).(50)$

Theoretically, the following inequality can be made to hold by choosing the design parameters a_i,k, c_i, γ_i correctly based on the definitions of ϖ and β

$\frac{\beta }{\varpi }\le \frac{{\varsigma }^2}{2}{\left(\underline{\beta }\left(L+\tilde{B}\right)\right)}^2,(51)$

where arbitrary ς > 0.

Lemma 3 states that the result lim_t→∞‖Y–Y_c‖ ≤ ς may be obtained by selecting the proper parameters, which implies that the system output is guaranteed to converge to a tiny finite error.

We can find t* > 0 such that the $\left\{t_{k+1}-t_k\right\}\ge t^{*}$, ∀k ∈ z⁺. For e_c(t) = v(t)– u(t), ∀t ∈ [t_k, t_k+1), we get

$\frac{\mathrm{d}}{\mathrm{d}t}\left|e_c\right|=\mathrm{sign}\left(e_c\right){\dot{e}}_c\le \left|\dot{v\left(t\right)}\right|.(52)$

We know that $\dot{v}(t)$ is continuously bounded. Consequently, there is a positive constant ν such that $\left|\dot{v}(t)\right|\le \nu$. Furthermore, e_c(t_k) = 0 and ${\lim }_{t\to t_k}{e}_c(t)=m$, the lower bound t* that satisfies $t^{*}\ge \frac{m}{\nu }$ can be obtained. The issue with the Zeno behavior is, therefore, resolved.

5 Simulation study

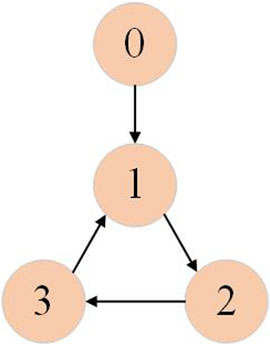
In this section, we will verify the effectiveness of the designed control strategy through a numerical example. Consider the following second-order non-affine non-linear system. The system’s communication structure is shown in Figure 1, where node 0 represents a virtual leader. It is obvious that only follower 1 is capable of receiving the leader’s signal. The system model is given by the following formula:

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_{i,1}& =g_{i,1}\left(x_i\right)x_{i,2}+f_{i,1}\left(x_i\right)+{\phi }_{i,1}^T\left(x_i\right){\eta }_{i,1}\hfill \\ \hfill {\dot{x}}_{i,2}& =f_{i,2}\left({\mathrm{\Delta }}_i,u_i\right)+{\phi }_{i,2}^T\left(x_i\right){\eta }_{i,2}+d_i\left(t\right)\hfill \\ \hfill y_i& =x_{i,1}.\hfill \end{array}\hfill \end{array}(53)$

FIGURE 1

FIGURE 1. Communications topology.

The aforementioned non-linear functions are g₁₁ = 1 + sin(x₁₁ + 1), f₁₁ = 0.6 cos(x₁₁), g₁₂ = 1 + sin(x₁₂), C₁ = 2 cos(x₁₂), d₁ = 0.1 sin(x₁₂), g₂₁ = sin(x₂₁ + 1), f₂₁ = 0.8 cos(x₂₁), g₂₂ = 1 − sin(x₂₂), C₂ = 0.8 cos(x₂₂), $d_2=0.1e^{-\frac{x_{22}}{2}}$, g₃₁ = sin(x₃₁ + 1), f₃₁ = 0.5 cos(x₃₁), g₃₂ = 1 + sin(x₃₂ + 1), C₃ = 0.5 cos(x₃₂), d₃ = 0.3 sin(x₃₂), and ${\phi }_{i,j}=e^{-x_{i,j}},i=\mathrm{1,2,3},j=\mathrm{1,2,3}$. The signal of the leader is chosen as y_d = 0.6 sin(t) + 1. We choose the initial values (0) = [1,1]^T, x₂(0) = [1,1]^T, x₃(0) = [1,1]^T, x₄(0) = [0,0]^T, x₅(0) = [0,0]^T, and x₆(0) = [1,1]^T. The design parameters are selected as a₁₁ = 1, a₁₂ = 10, a₂₁ = 1, a₂₂ = 1, a₃₁ = 1, a₃₁ = 1, γ_i,j = 1, i = 1, 2, 3, j = 1, 2, 3, k₁₁ = 30, k₁₂ = 40, k₂₁ = 28, k₂₂ = 35, k₃₁ = 40, and k₃₂ = 30.

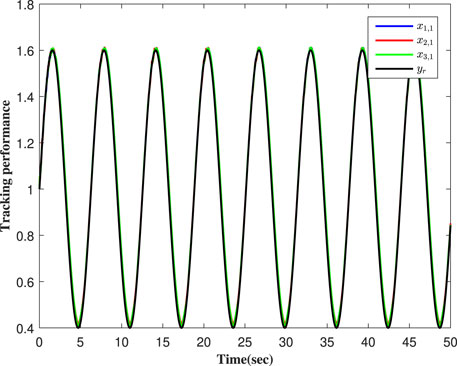
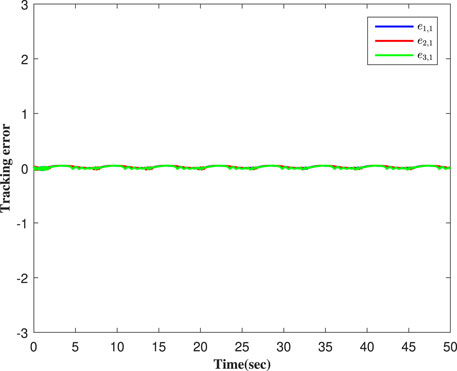
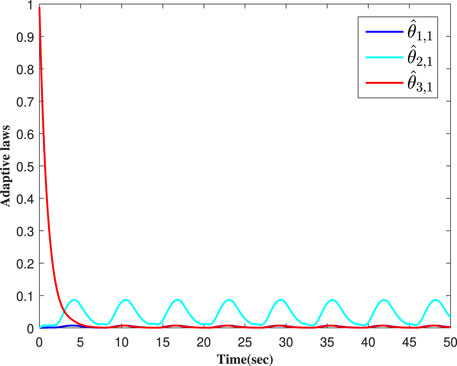
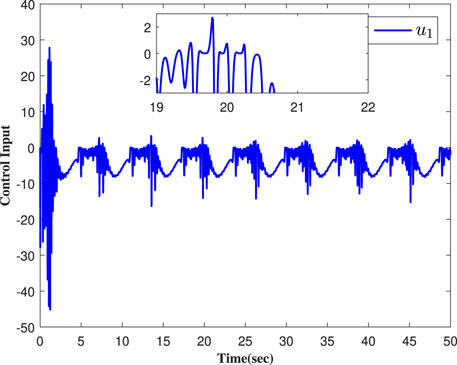
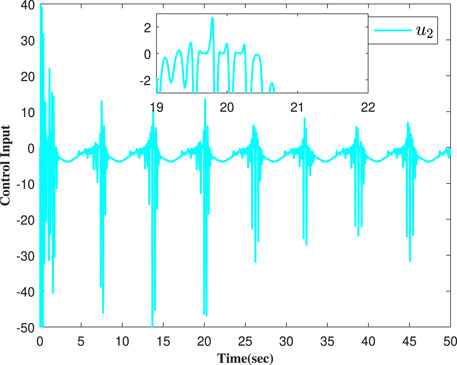
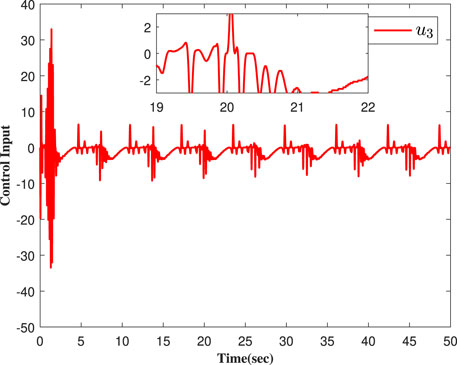
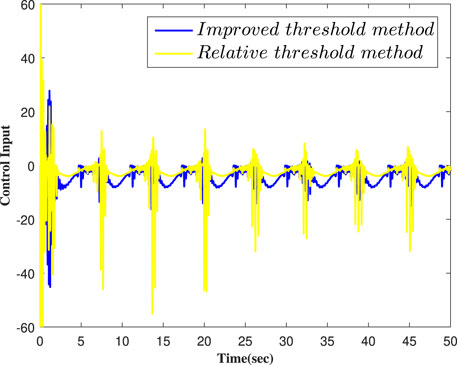
Concomitantly, we get the simulation results in Figures 2–7. Figure 2 shows that the actual output of the studies' systems can track well with the expected trajectory y_r. Figure 3 shows the error between the output signals and the expected signal. Figure 4 shows the adaptive parameter curves of each follower. The curves of the controller are shown in Figures 5–7. Figure 8 shows the event-triggered times and the threshold value comparisons of the two methods.

FIGURE 2

FIGURE 2. Output trajectories of the followers and leader.

FIGURE 3

FIGURE 3. Trajectories of the tracking error.

FIGURE 4

FIGURE 4. Trajectories of the adaptive law $\widehat{\theta }$.

FIGURE 5

FIGURE 5. Trajectories of the control input u₁.

FIGURE 6

FIGURE 6. Trajectories of the control input u₂.

FIGURE 7

FIGURE 7. Trajectories of the control input u₃.

FIGURE 8

FIGURE 8. Threshold value of the proposed improved method compared with those of other methods.

6 Conclusion

This research investigates the consensus tracking control problem for a class of non-affine non-linear MAS and proposes a design scheme for control input separation. The Taylor decoupling technology is used to successfully decouple the control inputs with the non-affine non-linear terms. Then, the unknown non-linear functions that exist in the non-affine non-linear MASs are approximated using RBFNNs. Moreover, an improved ETC strategy is proposed, which introduces a decreasing function to improve the performance of the ETC strategy. This ETC strategy significantly reduces the computational burden of the communication process and achieves better control objectives. The designed control strategy ensures the boundedness of all signals and achieves good consensus tracking performance. In the future, we will focus on extending the proposed method to MASs with more general structures and malicious attacks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

LW, ZS, and CL contributed to the study idea and design. LW wrote the first draft of the manuscript. LW organized the literature. ZS designed the figures. LC verified the experimental design. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhang Z, Hao F, Zhang L, Wang L. Consensus of linear multi-agent systems via event-triggered control. Int J Control (2014) 87:1243–51. doi:10.1080/00207179.2013.873952

CrossRef Full Text | Google Scholar

2. Zhou J, Wang Y, Zheng X, Wang Z, Shen H. Weighted $${\mathcal {H}}_{\infty }$$ H ∞ consensus design for stochastic multi-agent systems subject to external disturbances and ADT switching topologies. Nonlinear Dyn (2019) 96:853–68. doi:10.1007/s11071-019-04826-9

CrossRef Full Text | Google Scholar

3. Xiao H, Li Z, Chen CP. Formation control of leader–follower mobile robots’ systems using model predictive control based on neural-dynamic optimization. IEEE Trans Ind Elect (2016) 63:5752–62. doi:10.1109/tie.2016.2542788

CrossRef Full Text | Google Scholar

4. Alonso-Mora J, Montijano E, Nägeli T, Hilliges O, Schwager M, Rus D. Distributed multi-robot formation control in dynamic environments. Autonomous Robots (2019) 43:1079–100. doi:10.1007/s10514-018-9783-9

CrossRef Full Text | Google Scholar

5. Rossi E, Tognon M, Carli R, Schenato L, Cortés J, Franchi A. Cooperative aerial load transportation via sampled communication. IEEE Control Syst Lett (2019) 4:277–82. doi:10.1109/lcsys.2019.2924413

CrossRef Full Text | Google Scholar

6. Daugherty G, Reveliotis S, Mohler G. Optimized multiagent routing for a class of guidepath-based transport systems. IEEE Trans Automation Sci Eng (2018) 16:363–81. doi:10.1109/tase.2018.2798630

CrossRef Full Text | Google Scholar

7. Liu Y, Montenbruck JM, Zelazo D, Odelga M, Rajappa S, Bülthoff HH, et al. A distributed control approach to formation balancing and maneuvering of multiple multirotor uavs. IEEE Trans Robotics (2018) 34:870–82. doi:10.1109/tro.2018.2853606

CrossRef Full Text | Google Scholar

8. Hu J, Feng G. Distributed tracking control of leader–follower multi-agent systems under noisy measurement. Automatica (2010) 46:1382–7. doi:10.1016/j.automatica.2010.05.020

CrossRef Full Text | Google Scholar

9. Zhu W, Cheng D. Leader-following consensus of second-order agents with multiple time-varying delays. Automatica (2010) 46:1994–9. doi:10.1016/j.automatica.2010.08.003

CrossRef Full Text | Google Scholar

10. Hong Y, Chen G, Bushnell L. Distributed observers design for leader-following control of multi-agent networks. Automatica (2008) 44:846–50. doi:10.1016/j.automatica.2007.07.004

CrossRef Full Text | Google Scholar

11. Shang Y, Chen B, Lin C. Consensus tracking control for distributed nonlinear multiagent systems via adaptive neural backstepping approach. IEEE Trans Syst Man, Cybernetics: Syst (2018) 50:2436–44. doi:10.1109/tsmc.2018.2816928

CrossRef Full Text | Google Scholar

12. Liang H, Liu G, Zhang H, Huang T. Neural-network-based event-triggered adaptive control of nonaffine nonlinear multiagent systems with dynamic uncertainties. IEEE Trans Neural Networks Learn Syst (2020) 32:2239–50. doi:10.1109/tnnls.2020.3003950

CrossRef Full Text | Google Scholar

13. Liu Y-J, Wang W. Adaptive fuzzy control for a class of uncertain nonaffine nonlinear systems. Inf Sci (2007) 177:3901–17. doi:10.1016/j.ins.2007.03.005

CrossRef Full Text | Google Scholar

14. Wang M, Liu X, Shi P. Adaptive neural control of pure-feedback nonlinear time-delay systems via dynamic surface technique. IEEE Trans Syst Man, Cybernetics, B (Cybernetics) (2011) 41:1681–92. doi:10.1109/tsmcb.2011.2159111

CrossRef Full Text | Google Scholar

15. Na J, Ren X, Zheng D. Adaptive control for nonlinear pure-feedback systems with high-order sliding mode observer. IEEE Trans Neural networks Learn Syst (2013) 24:370–82. doi:10.1109/tnnls.2012.2225845

CrossRef Full Text | Google Scholar

16. Zhou J, Xu S. Curcumin-loaded porous scaffold: An anti-angiogenic approach to inhibit endochondral ossification. IEEE Trans Fuzzy Syst (2023) 2023:1–26. doi:10.1080/09205063.2023.2231663

CrossRef Full Text | Google Scholar

17. Wang D, Liu D, Wei Q, Zhao D, Jin N. Optimal control of unknown nonaffine nonlinear discrete-time systems based on adaptive dynamic programming. Automatica (2012) 48:1825–32. doi:10.1016/j.automatica.2012.05.049

CrossRef Full Text | Google Scholar

18. Zhang Q, Wang C. Robust adaptive backstepping control for a class of constrained non-affine nonlinear systems via self-organizing hermite-polynomial-based neural network disturbance observer. Adv Mech Eng (2017) 9:168781401770281. doi:10.1177/1687814017702811

CrossRef Full Text | Google Scholar

19. Zhang S, Wang Q, Dong C. Extended state observer based control for generic hypersonic vehicles with nonaffine-in-control character. ISA Trans (2018) 80:127–36. doi:10.1016/j.isatra.2018.05.020

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Boulkroune A, M’Saad M, Farza M. Fuzzy approximation-based indirect adaptive controller for multi-input multi-output non-affine systems with unknown control direction. IET Control Theor Appl (2012) 6:2619–29. doi:10.1049/iet-cta.2012.0565

CrossRef Full Text | Google Scholar

21. Wang W, Wang D, Peng Z. Distributed containment control for uncertain nonlinear multi-agent systems in non-affine pure-feedback form under switching topologies. Neurocomputing (2015) 152:1–10. doi:10.1016/j.neucom.2014.11.035

CrossRef Full Text | Google Scholar

22. Wang Y, Song Y. Fraction dynamic-surface-based neuroadaptive finite-time containment control of multiagent systems in nonaffine pure-feedback form. IEEE Trans Neural networks Learn Syst (2016) 28:678–89. doi:10.1109/tnnls.2015.2511005

CrossRef Full Text | Google Scholar

23. Zhou J, Xu D, Tai W, Ahn CK. Switched event-triggered $\mathcal {H}_{\infty }$ security control for networked systems vulnerable to aperiodic DoS attacks. IEEE Trans Netw Sci Eng (2023) 10:2109–23. doi:10.1109/tnse.2023.3243095

CrossRef Full Text | Google Scholar

24. Chen Z, Niu B, Zhao X, Zhang L, Xu N. Model-based adaptive event-triggered control of nonlinear continuous-time systems. Appl Math Comput (2021) 408:126330. doi:10.1016/j.amc.2021.126330

CrossRef Full Text | Google Scholar

25. Li H, Chen Z, Wu L, Lam H-K. Event-triggered control for nonlinear systems under unreliable communication links. IEEE Trans Fuzzy Syst (2016) 25:813–24. doi:10.1109/tfuzz.2016.2578346

CrossRef Full Text | Google Scholar

26. Xing L, Wen C, Liu Z, Su H, Cai J. Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans automatic Control (2016) 62:2071–6. doi:10.1109/tac.2016.2594204

CrossRef Full Text | Google Scholar

27. Hu X, Li Y-X, Hou Z. Event-triggered fuzzy adaptive fixed-time tracking controlfor nonlinear systems. IEEE Trans Cybernetics (2020) 52:7206–17. doi:10.1109/tcyb.2020.3035779

CrossRef Full Text | Google Scholar

28. Li Y-X, Hu X, Che W, Hou Z. Event-based adaptive fuzzy asymptotic tracking control of uncertain nonlinear systems. IEEE Trans Fuzzy Syst (2020) 29:3003–13. doi:10.1109/tfuzz.2020.3010643

CrossRef Full Text | Google Scholar

29. Liu C, Niu B, Liu L, Zhao X, Wang H, Duan H. Event-triggered adaptive bipartite asymptotic tracking control using intelligent technique for stochastic nonlinear multi-agent systems. IEEE Trans Artif Intelligence (2022) 2022:1–11. doi:10.1109/tai.2022.3214486

CrossRef Full Text | Google Scholar

30. Wu L-B, Park JH, Xie X-P, Gao C, Zhao N-N. Fuzzy adaptive event-triggered control for a class of uncertain nonaffine nonlinear systems with full state constraints. IEEE Trans Fuzzy Syst (2020) 29:904–16. doi:10.1109/tfuzz.2020.2966185

CrossRef Full Text | Google Scholar

31. Liu L, Li X, Liu Y-J, Tong S. Neural network based adaptive event trigger control for a class of electromagnetic suspension systems. Control Eng Pract (2021) 106:104675. doi:10.1016/j.conengprac.2020.104675

CrossRef Full Text | Google Scholar

32. Zhang H, Lewis FL, Qu Z. Lyapunov, adaptive, and optimal design techniques for cooperative systems on directed communication graphs. IEEE Trans Ind Electron (2011) 59:3026–41. doi:10.1109/tie.2011.2160140

CrossRef Full Text | Google Scholar

33. Shahvali M, Shojaei K. Distributed adaptive neural control of nonlinear multi-agent systems with unknown control directions. Nonlinear Dyn (2016) 83:2213–28. doi:10.1007/s11071-015-2476-4

CrossRef Full Text | Google Scholar

34. Wang X, Niu B, Wang X. Distributed adaptive bipartite consensus tracking of high-order nonstrict-feedback nonlinear multi-agent systems. J Control Decis (2022) 10:393–401. doi:10.1080/23307706.2022.2085196

CrossRef Full Text | Google Scholar

35. Zhao Y, Chen G. Distributed adaptive tracking control of non-affine nonlinear multi-agent systems. In: 2016 Chinese Control and Decision Conference (CCDC) (IEEE); 28-30 May 2016; Yinchuan, China (2016). p. 1518–23.

CrossRef Full Text | Google Scholar