A novel nussbaum functions based adaptive event-triggered asymptotic tracking control of stochastic nonlinear systems with strong interconnections

In this work, the issue of event-triggered-based asymptotic tracking adaptive control of stochastic nonlinear systems in pure-feedback form with strong interconnections is considered. First, a new decentralized control scheme is developed by introducing the new types of Nussbaum functions, which enables the output of each subsystem to asymptotically track the desired reference signal. Second, the nonaffine structures and the unknown control gains existing in the nonlinear systems are a part of the considered system model, which makes it more complicated to design the decentralized controllers. Therefore, the complexity caused by the nonaffine structures is faciliated by mean value theorem and the unknown control gains are handled by a novel Nussbaum function in our proposed design scheme. Meanwhile, the unknown nonlinearities of the system are approximated by using intelligent control technology. Furthermore, an event-triggered method is introduced in the design process to save communication resources effectively. It is shown that all signals of the closed-loop systems are bounded in probability and the tracking errors asymptotically converge to zero in probability. Finally, the simulation results illustrate the effectivity of the presented scheme.

1 Introduction

Stochastic external disturbances exist in many branches of science and industry such as unmanned air vehicles, intelligent home and distributed networks [1,2]. Seeing that stochastic nonlinear systems can model a mass of artificial or physical industrial platforms with stochastic external disturbances, it is necessary and beneficial to study them for the vast majority of researchers [3–5]. Recently, stability control of stochastic nonlinear systems with strict feedback or nonstrict feedback form has been the hot topic discussed by many researchers. Nevertheless, most of actual models do not satisfy strict-feedback and nonstrict-feedback form [6–9]. Therefore, numerous researchers have devoted themselves to the study of adaptive controller design for stochastic nonlinear systems in pure-feedback form such as mechanical and electrical systems, biochemical medical systems, and dynamic model systems in pendulum control. More researches on stochastic nonlinear systems with nonaffine structures have been explored, which were considered as complex and challenging themes such as state constraint, adaptive control, and output-feedback control. In [8], the finite-time tracking control problem was addressed for stochastic pure-feedback nonlinear systems by introducing the barrier Lyapunov functions, the mean value theorem, and the adaptive neural networks.

Furthermore, the interconnected systems composed of several subsystems are called large-scale systems. The large-scale systems have been extensively investigated because of their countless applications in power systems, mobile satellite communication systems, and multiagent systems. However, different from the existing literature [10,11], the interconnection terms of strongly interconnected nonlinear systems contain all the state variables of the other subsystems. There is no doubt that the design of the centralized controller of large-scale systems is difficult due to the existence of physical communication limitations among subsystems. Therefore, the decentralized control scheme was proposed in order to achieve the desired control goal of large-scale systems. For uncertain interconnected systems with dynamic interactions [10], presented a new decentralized adaptive backstepping-based control algorithm to deal with discontinuity caused by state-triggering. In [11], the decentralized event-triggered fault-tolerant control (FTC) scheme was proposed for the interconnected nonlinear systems with unknown strong coupling and actuator failures. Different from the centralized control, decentralized control not only mitigates computation burden, but also strengthens robustness of systems. Simultaneously, since event-triggered control (ETC) strategy can effectively reduce resources waste of unnecessary communication, it has become an attractive research orientation. The ETC strategy is that the control signal does not change in real time, but is restricted by the trigger condition. It only changes at the moment of trigger and remains stable within the trigger interval. So far, many meaningful results on ETC strategy have been obtained [12–14]. For asymptotic tracking of uncertain nonlinear systems [13], a novel adaptive event-triggered control framework was proposed to reduce the communication burden. Furthermore, the adaptive event-triggered tracking control problem was considered by relaxing the feasibility condition of the intermediate virtual controller for a class of stochastic nonlinear systems [14]. Although the ETC strategy has been employed to diversified nonlinear systems in aformentioned results, the ETC mechanism based on relative threshold for stochasitc interconnected pure-feedback nonlinear systems are yet to be investigated.

Moreover, the issue of adaptive control for nonlinear systems with stochastic disturbances has attracted extensive attention from innumerable scholars [15,16]. On the one hand, neural networks (NNs), which is identified as a powerful tool to approximate unknown nonlinearities, has been extensively used in the adaptive control. On the other hand, how to deal with the control gain of stochastic nonlinear systems is also a concern. As we all know, compared with the bounded and stable characteristics of stochastic nonlinear systems, how to realize asymptotic tracking control has more practical significance and research value. Therefore, a new type of Nussbaum function is applied to the adaptive controller design, which makes the nonlinear systems realize asymptotic tracking and eliminates the influence of the unknown control gains [17]. So far, although remarkable results have been obtained in the research of stochastic nonlinear systems by using Nussbaum function, there exist few results about how to construct event-triggered-based adaptive controllers for stochastic systems with nonaffine structures and strong interconnection terms, which motivates us for this study.

In this paper, an event-triggered based adaptive decentralized asymptotic tracking control scheme is proposed for stochastic nonlinear systems with nonaffine structures and strong interconnection terms. The main contributions of this work are three-fold: 1) One thing that needs to be stressed is that it is very complicated to design decentralized controllers for interconnected systems, especially for the interconnected systems with both stochastic terms and nonaffine structures. Thus, a new decentralized control scheme is first developed by introducing the new type of Nussbaum functions, which realizes the asymptotic tracking control in probability for stochastic interconnected pure-feedback systems. 2) Meanwhile, how to save the system-limited transmutation resource for nonlinear systems, especially for uncertain stochastic interconnected pure-feedback systems is also a crucial issue. Therefore, the ETC strategy based on relative threshold is developed and only an adaptive law needs to be designed for each n-order subsystem, which greatly conserves the communication resources. 3) The interconnected terms in the nonlinear systems considered are associated with all state variables, which makes the traditional decentralized control method unavailable. Hence, to solve the problem, a decentralized control scheme using variable separation technique is presented.

2 System description and preliminaries

Consider a stochastic nonlinear system:

$dx=f^u\left(x\right)dt+h^s\left(x\right)d\omega ,\forall x\in R^n,(1)$

where ω is standard Wiener process; x ∈ Rⁿ is the system state, f^u: Rⁿ → Rⁿ and h^s: Rⁿ → R^n×r are locally Lipschitz functions. Next, some necessary definitions are introduced into this paper.

Definition 1 [18]: Combining with the differential Eq. 1, for any given $V\left(x\right)\in C^2$, define the differential operator L as follows:

$LV=\frac{\partial V}{\partial x}{f}^u+\frac{1}{2}\text{Tr}\left\{{h^s}^T\frac{{\partial }^{2}V}{\partial x^2}{h}^s\right\}.(2)$

Definition 2 [18]: If the equality ${\lim }_{c\to \infty }{\sup }_{0⩽t⩽\infty }P\left\{\left|x\left(t\right)\right|>c\right\}=0$ holds, system 1) remains bounded in probability. Then, system 1) is identified as asymptotically stable in probability, if it satisfies that equality and $P\left\{\left|x\left(t\right)\right|=0\right\}=1$.

The stochastic interconnected pure-feedback nonlinear systems are described as:

$\begin{array}{c}\hfill \left\{\begin{array}{c}d{x}_{i,j}=f_{i,j}\left({\bar{x}}_{i,j},x_{i,j+1}\right)dt+h_{i,j}\left(X\right)dt+g_{i,j}^T\left(X\right)d{\omega }_i,\\ d{x}_{i,n_i}=f_{i,n_i}\left({\bar{x}}_{i,n_i},u_i\right)dt+h_{i,n_i}\left(X\right)dt+g_{i,n_i}^T\left(X\right)d{\omega }_i,\\ y_i=x_{i,1},\end{array}\right.\hfill \end{array}(3)$

where $X=\left[x_1^T,x_2^T,\dots ,x_N^T\right]$ represents interconnected terms of the nonlinear systems with $x_i={\bar{x}}_{i,n_i}={\left[x_{i,1},x_{i,2},\dots ,x_{i,n_i}\right]}^T\in R^{n_i}(i=\mathrm{1,2},\dots ,N)$ being state vector of the ith subsystem, u_i and y_i are the input and output of the ith subsystem, respectively. $f_{i,j}\left(\cdot \right)$ are smooth unknown functions. $h_{i,j}\left(\cdot \right)$ and $g_{i,j}\left(\cdot \right)$ represent smooth interconnected terms. Let ${\mathrm{\Phi }}_{i,j}\left({\bar{x}}_{i,j},{\bar{v}}_{i,j}\right)=\frac{\partial f_{i,j}\left({\bar{x}}_{i,j},x_{i,j+1}\right)}{\partial x_{i,j+1}}$, ${\mathrm{\Phi }}_{i,n_i}\left({\bar{x}}_{i,n_i},{\bar{v}}_{i,n_i}\right)=\frac{\partial f_{i,n_i}\left({\bar{x}}_{i,n_i},u_i\right)}{\partial u_i}$.

According to the properties of the mean value theorem [19], there must exist $x_{i,j+1}^0=0$ and $u_i^0=0$. There are point ${\bar{v}}_{i,j}$ between $x_{i,j+1}^0$ and x_i,j+1 and ${\bar{v}}_{i,n_i}$ between $u_i^0$ and u_i such that system 3) can be rewritten as:

$\begin{array}{c}\hfill \left\{\begin{array}{c}d{x}_{i,j}=\left(f_{i,j}\left({\bar{x}}_{i,j},0\right)+{\mathrm{\Phi }}_{i,j}\left({\bar{x}}_{i,j},{\bar{v}}_{i,j}\right)x_{i,j+1}+h_{i,j}\left(X\right)\right)dt+g_{i,j}^T\left(X\right)d{\omega }_i,\\ d{x}_{i,n_i}=\left(f_{i,n_i}\left({\bar{x}}_{i,n_i},0\right)+{\mathrm{\Phi }}_{i,n_i}\left({\bar{x}}_{i,n_i},{\bar{v}}_{i,n_i}\right)u_i+h_{i,n_i}\left(X\right)\right)dt+g_{i,n_i}^T\left(X\right)d{\omega }_i,\\ y_i=x_{i,1},\end{array}\right.\hfill \end{array}(4)$

where Φ_i,j and ${\mathrm{\Phi }}_{i,n_i}$ are unknown gain functions.

The control objective of this paper is to design decentralized adaptive controllers for system 3) so that the tracking errors between system outputs and reference signals asymptotically converge to zero in probability and all the signals are semiglobally uniformly ultimately bounded in probability. To realize the desired control objective, some lemmas and assumptions are showed below.

Assumption 1: The functions Φ_i,j (i = 1, … , N, j = 1, … , n_i) are bounded; there exist positive constants ς_m and ς_M such that $0<{\varsigma }_m⩽\left|{\mathrm{\Phi }}_{i,j}\left({\bar{x}}_{i,j},x_{i,j+1}\right)\right|⩽{\varsigma }_M<+\infty$. Moreover, all the signs of ${\mathrm{\Phi }}_{i,j}\left({\bar{x}}_{i,j},x_{i,j+1}\right)$ are getatable for overall design procedure. Without loss of generality, it is assumed ${\mathrm{\Phi }}_{i,j}\left({\bar{x}}_{i,j},x_{i,j+1}\right)⩾{\varsigma }_m>0$.

Assumption 2: The desired reference trajectories are represented as $y_{di}\left(t\right)$, where their cth derivative for c = 1, … , n_i is assumed to be continuous and bounded.

Assumption 3 [20]: There are strict increasing smooth functions ${\psi }_{i,j}\left(\cdot \right)$ satisfying $\left|h_{i,j}\left(X\right)\right|⩽{\psi }_{i,j}\left(‖X‖\right)$ with ${\psi }_{i,j}\left(0\right)=0$ for the unknown nonlinear interconnected terms $h_{i,j}\left(X\right)$.

Remark 1: If a_r⩾0, for r = 1, … , n_i, ${\psi }_{i,j}\left(\sum _{r=1}^{n_i}{a}_r\right)⩽\sum _{r=1}^{n_i}{\psi }_{i,j}\left(n_i{a}_r\right)$ can be employed due to the strict increasing property of ${\psi }_{i,j}\left(\cdot \right)$. Particularly, smooth functions ${\lambda }_{i,j}\left(s\right)$ are introduced such that ${\psi }_{i,j}\left(s\right)=s{\lambda }_{i,j}\left(s\right)$, which has

${\psi }_{i,j}\left(\sum _{r=1}^{n_i}{a}_r\right)⩽\sum _{r=1}^{n_i}{n}_i{a}_r{\lambda }_{i,j}\left(n_i{a}_r\right).(5)$

Assumption 4 [21]: There are strict increasing smooth functions ${\upsilon }_{i,j}\left(\cdot \right)$ satisfying $‖g_{i,j}\left(X\right)‖⩽{\upsilon }_{i,j}\left(‖X‖\right)$ with ${\upsilon }_{i,j}\left(0\right)=0$ for the unknown interconnected terms $g_{i,j}\left(X\right)$.

Remark 2: Apparently, there exist smooth functions ${\eta }_{i,j}\left(\cdot \right)$, we have

${\upsilon }_{i,j}\left(\sum _{r=1}^{n_i}{b}_r\right)⩽\sum _{r=1}^{n_i}n{b}_r{\eta }_{i,j}\left(n{b}_r\right),(6)$

where b_r⩾0.

Lemma 1 [22]: The Nussbaum function is given as ${\aleph }_{ms}\left({\phi }_{i,j}\right)=2e^{{\phi }_{i,j}^2}{\phi }_{i,j}$ if $LW\left(t\right)⩽-bW\left(t\right)-\sum _{j=1}^{n_i}{\varsigma }_{i,j}{\aleph }_{ms}({\phi }_{i,j}\left(t\right)){\dot{\phi }}_{i,j}\left(t\right)+\sum _{j=1}^{n_i}{\dot{\phi }}_{i,j}\left(t\right)+\eta$, where b is a positive constant, η is a bounded variable, and ς_i,j is an unknown but bounded positive constant. Moreover, φ_i,j and $W\left(t\right)$ must be bounded in probability.

Lemma 2 [23]: For the form of the dynamic system $\dot{\xi }(t)=-x\xi (t)+y\vartheta (t)$, if ϑ(t) is positive function, x and y are positive constants, and the initial value ξ(t₀) is non-negative, then the solution ξ(t)⩾0 can be obtained for ∀t⩾t₀.

Lemma 3 [24]: For any $\left(x^{*},y^{*}\right)$, one obtains

$x^{*}{y}^{*}⩽\frac{{\epsilon }^{p_c}}{p_c}{\left|x^{*}\right|}^{p_c}+\frac{1}{q_c{\epsilon }^{q_c}}{\left|y^{*}\right|}^{q_c},(7)$

where ɛ > 0, p_c > 1, q_c > 1, and $\left(p_c-1\right)\left(q_c-1\right)=1$.

Lemma 4 [25]: For any ϖ ∈ R and ɛ > 0, one has

$0⩽\left|\varpi \right|-\varpi \tanh \left(\frac{\varpi }{\epsilon }\right)⩽\delta \epsilon ,\delta =0.2785.(8)$

In this work, the radial basis function neural networks (RBFNNs) will be employed to estimate the unknown nonlinear functions $f\left(Z\right)$ such that

$f\left(Z\right)=W^{T}S\left(Z\right)+\delta \left(Z\right),(9)$

where Z ∈ R^q denotes input vector of the RBFNNs and q represents the dimension of the RBFNNs input. The estimation error is represented as $\delta \left(Z\right)$ with $\left|\delta \left(Z\right)\right|⩽\bar{\delta }$, where $\bar{\delta }$ is a positive constant. $W={\left[{\omega }_1,\dots ,{\omega }_l\right]}^T\in R^l$ denotes weight vector with l > 1 being the node number of RBFNNs. The basis vector of RBFNNs is denoted as $S\left(Z\right)={\left[s_1\left(Z\right),\dots ,s_l\left(Z\right)\right]}^T$. Besides, the basis functions $s_i\left(Z\right)$ are selected as

$s_i\left(Z\right)=\exp \left(-\frac{{\left(Z-{\mu }_i\right)}^T\left(Z-{\mu }_i\right)}{¯{\lambda }^2}\right),i=\mathrm{1,2},\dots ,l,(10)$

where ${\mu }_i=\left[{\mu }_{i1},{\mu }_{i2},\dots ,{\mu }_{iq}\right]$ is the center of the receptive field and ¯λ is the width of the Gaussian function. The ideal weight vector W is defined as

$W:=\arg \underset{W\in R^l}{\min }\left\{\sup \left|f\left(Z\right)-W^{T}S\left(Z\right)\right|\right\}.(11)$

Lemma 5 [26]: Consider a class of Gaussian function as basis function. Let $\rho :=\frac{1}{2}{\min }_{i\ne j}‖u_i-u_j‖$, the upper bound of $S\left(Z\right)$ is represented as $‖S\left(Z\right)‖⩽\sum _{k=0}^{\infty }3q{\left(k+2\right)}^{q-1}{e}^{-\frac{2{\rho }^2{k}^2}{{\eta }^2}}:=s$, where s is a limited constant.

In this section, the controllers design procedure based on the backstepping will be presented. The RBFNNs will be used to estimate the unknown nonlinearities. In addition, the virtual control signals and the adaptive laws are designed as follows:

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_{i,j}& ={\aleph }_{ms}\left({\phi }_{i,j}\right){\bar{\alpha }}_{i,j},\hfill \\ \hfill {\bar{\alpha }}_{i,j}& =-k_{i,j}{z}_{i,j}-\frac{1}{2a_{i,j}^2}{z}_{i,j}^3{\widehat{\theta }}_i{S}_{i,j}^T\left(Z_{i,j}\right)S_{i,j}\left(Z_{i,j}\right),\hfill \\ \hfill {\dot{\widehat{\theta }}}_i& =\sum _{j=1}^{n_i}\frac{{\gamma }_i}{2a_{i,j}^2}{z}_{i,j}^6{S}_{i,j}^T\left(Z_{i,j}\right)S_{i,j}\left(Z_{i,j}\right)-{\sigma }_i{\widehat{\theta }}_i,\hfill \end{array}\hfill \end{array}(12)$

where k_i,j, a_i,j, γ_i, and σ_i are positive design parameters and $Z_{i,j}=[{\bar{x}}_{i,j}^T,{\widehat{\theta }}_i,{\bar{y}}_{di}^{(j)}]$ with ${\bar{y}}_{di}^{(j)}=[y_{di},y_{di}^{(1)},\dots ,y_{di}^{(j)}](j=2,\dots ,n_i)$. In addition, ${\widehat{\theta }}_i$ is the estimation of θ_i with θ_i = max{‖W_i,j‖²; i = 1, 2, … , N, j = 1, 2, … , n_i}. Particularly, the error variables z_i,j satisfy the following variables transformation:

$z_{i,j}=x_{i,j}-{\alpha }_{i,j-1}.(13)$

Lemma 6 [27]: According to the variables transformation z_i,j = x_i,j − α_i,j−1, the strong interconnected term result can be obtained

$\Vert X\Vert ⩽\sum _{i=1}^N\sum _{j=1}^{n_i}{\chi }_{i,j}\left(z_{i,j},{\widehat{\theta }}_i\right)|z_{i,j}|+d^{*},(14)$

where d* being the sum of upper bound of y_di, ${\chi }_{i,j}(z_{i,j},{\widehat{\theta }}_i)=(k_{i,j}+1)+(1/2{a_{i,j}}^2){z_{i,j}}^2{s}^2{\widehat{\theta }}_i$, ${\chi }_{i,n_i}=1$, for i = 1, 2, … , N, j = 1, 2, … , n_i. In addition, to simplify the formula, ${\chi }_{m,l}(z_{m,l},{\widehat{\theta }}_m)$ will be denoted as χ_m,l.

3 Main result

For the sake of convenience, the state vector ${\bar{x}}_{i,j}$ and the time variable t will be omitted. Moreover, S_i,j (Z_i,j) will be denoted as S_i,j.

Step i, 1: Based on z_i,1 = x_i,1 − y_di, z_i,2 = x_i,2 − α_i,1, the derivative of z_i,1 is given by

$\begin{array}{c}\hfill d{z}_{i,1}=\left(f_{i,1}+{\mathrm{\Phi }}_{i,1}{x}_{i,2}+h_{i,1}\left(X\right)-{\dot{y}}_{di}\right)dt+g_{i,1}^T\left(X\right)d{\omega }_i.\hfill \end{array}(15)$

The Lyapunov function candidate V_i,1 is selected as

$V_{i,1}=\frac{1}{4}{z}_{i,1}^4+\frac{1}{2{\gamma }_i}{\tilde{\theta }}_i^2,(16)$

where γ_i > 0 is a positive constant and ${\tilde{\theta }}_i={\theta }_i-{\widehat{\theta }}_i$.

Differentiating V_i,1 yields

$L{V}_{i,1}=z_{i,1}^3\left(f_{i,1}+{\mathrm{\Phi }}_{i,1}{z}_{i,2}+{\mathrm{\Phi }}_{i,1}{\alpha }_{i,1}+h_{i,1}\left(X\right)-{\dot{y}}_{di}\right)+\frac{3}{2}{z}_{i,1}^2{g}_{i,1}^T\left(X\right)g_{i,1}\left(X\right)-\frac{1}{{\gamma }_i}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i.(17)$

By applying Assumption 3, 5), 7) and 14), we have

$\begin{array}{c}\hfill z_{i,1}^3{h}_{i,1}\left(X\right)⩽|z_{i,1}^3|{\psi }_{i,1}\left(\Vert X\Vert \right)⩽\frac{3}{4}M{z}_{i,1}^4+\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,1}^4+|z_{i,1}^3|{\psi }_{i,1}\left(\left(M+1\right)d^{*}\right),\hfill \end{array}(18)$

where $M=\sum _{m=1}^N{n}_m$ and ${\bar{\psi }}_{i,1}^4=\frac{1}{4}{(M+1)}^4{\chi }_{m,l}^4{\lambda }_{i,1}^4((M+1)|z_{m,l}|{\chi }_{m,l})$. Let K_i,1 = ψ_i,1 ((M + 1)d*).

Then, Lemma 4 is employed to K_i,1 yields

$|z_{i,1}^3|K_{i,1}-z_{i,1}^3{K}_{i,1}\tanh \left(\frac{z_{i,1}^3{K}_{i,1}}{{\epsilon }_{i,1}}\right)⩽0.2785{\epsilon }_{i,1}.(19)$

By using Assumption 4 and (6)–(14), we can obtain

$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{3}{2}{z}_{i,1}^2{g}_{i,1}^T\left(X\right)g_{i,1}\left(X\right)& ⩽\frac{3}{2}{z}_{i,1}^2{\upsilon }_{i,1}^2\left(\sum _{m=1}^N\sum _{l=1}^{n_m}{\chi }_{m,l}|z_{m,l}|+d^{*}\right)\hfill \\ \hfill & ⩽\frac{9}{8}{\left(M+1\right)}^2{z}_{i,1}^4{\upsilon }_{i,1}^4\left(\left(M+1\right)d^{*}\right)l_{i,\mathrm{1,1}}^{-2}+\frac{9}{8}{\left(M+1\right)}^{2}M{z}_{i,1}^4\hfill \\ \hfill & +\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,1}^4+\frac{1}{2}{l}_{i,\mathrm{1,1}}^2,\hfill \end{array}\hfill \end{array}(20)$

where l_i,1,1 is a positive constant and ${\bar{\upsilon }}_{i,1}^4=\frac{1}{2}{(M+1)}^4{\chi }_{m,l}^4{\eta }_{i,1}^4((M+1){\chi }_{m,l}|z_{m,l}|)$.

Submitting (18)–(20) into (17), we get

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{V}_{i,1}& ⩽z_{i,1}^3\left(f_{i,1}+{\mathrm{\Phi }}_{i,1}{z}_{i,2}+{\mathrm{\Phi }}_{i,1}{\alpha }_{i,1}-{\dot{y}}_{di}\right)+\frac{3}{4}M{z}_{i,1}^4+\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,1}^4+0.2785{\epsilon }_{i,1}\hfill \\ \hfill & +\frac{9}{8}{\left(M+1\right)}^{2}M{z}_{i,1}^4+z_{i,1}^3{K}_{i,1}\tanh \left(\frac{z_{i,1}^3{K}_{i,1}}{{\epsilon }_{i,1}}\right)+\frac{9}{8}{\left(M+1\right)}^2{z}_{i,1}^4{\upsilon }_{i,1}^4\left(\left(M+1\right)d^{*}\right)l_{i,\mathrm{1,1}}^{-2}\hfill \\ \hfill & +\frac{1}{2}{l}_{i,\mathrm{1,1}}^2-\frac{1}{{\gamma }_i}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i+\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,1}^4.\hfill \end{array}\hfill \end{array}(21)$

Step i, j: Define z_i,j = x_i,j − α_i,j−1 (2⩽j⩽n_i − 1), one can get the derivative of z_i,j

$\begin{array}{c}\hfill d{z}_{i,j}=\left(f_{i,j}+{\mathrm{\Phi }}_{i,j}{x}_{i,j+1}+h_{i,j}\left(X\right)-L{\alpha }_{i,j-1}\right)dt+{\left(g_{i,j}\left(X\right)-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\left(X\right)\right)}^{T}d{\omega }_i,\hfill \end{array}(22)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{\alpha }_{i,j-1}& =\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}+h_{i,k}\left(X\right)\right)+\sum _{k=0}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}\hfill \\ \hfill & +\frac{1}{2}\sum _{p,q=1}^{j-1}\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}{g}_{i,p}^T\left(X\right)g_{i,q}\left(X\right)+\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i.\hfill \end{array}\hfill \end{array}(23)$

Next, the Lyapunov function V_i,j is designed as $V_{i,j}=\frac{1}{4}{z}_{i,j}^4$, we further have

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{V}_{i,j}& =z_{i,j}^3\left(f_{i,j}+{\mathrm{\Phi }}_{i,j}{x}_{i,j+1}+h_{i,j}\left(X\right)-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}+h_{i,k}\left(X\right)\right)\right.\hfill \\ \hfill & -\left.\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i-\sum _{k=0}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}-\frac{1}{2}\sum _{p,q=1}^{j-1}\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}{g}_{i,p}^T\left(X\right)g_{i,q}\left(X\right)\right)\hfill \\ \hfill & +\frac{3}{2}{z}_{i,j}^2\Vert g_{i,j}\left(X\right)\Vert -\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}{g}_{i,k}\left(X\right){\Vert }^2.\hfill \end{array}\hfill \end{array}(24)$

By applying Assumptions 3, 4 and (5)–(14), one has

$\begin{array}{c}\hfill \begin{array}{cc}\hfill & -z_{i,j}^3\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}{h}_{i,k}\left(X\right)\hfill \\ \hfill & ⩽\frac{3}{4}M{z}_{i,j}^4\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^{\frac{4}{3}}+\sum _{k=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,k}^4+|z_{i,j}^3|\sum _{k=1}^{j-1}|\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}|{\psi }_{i,k}\left(\left(M+1\right)d^{*}\right),\hfill \\ \hfill & z_{i,j}^3{h}_{i,j}\left(X\right)⩽\frac{3}{4}M{z}_{i,j}^4+\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,j}^4+|z_{i,j}^3|{\psi }_{i,j}\left(\left(M+1\right)d^{*}\right),\hfill \\ \hfill & -\frac{1}{2}{z}_{i,j}^3\sum _{p,q=1}^{j-1}\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}{g}_{i,p}^T\left(X\right)g_{i,q}\left(X\right)\hfill \\ \hfill & ⩽\frac{1}{8}{\left(M+1\right)}^{2}M{z}_{i,j}^6\sum _{p=1}^{j-1}\sum _{q=1}^{j-1}{\left(\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}\right)}^2+\left(j-1\right)\sum _{q=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,q}^4+\frac{1}{2}\left(M+1\right)|\hfill \\ \hfill & z_{i,j}^3|\sum _{p=1}^{j-1}\sum _{q=1}^{j-1}|\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}|{\upsilon }_{i,q}^2\left(\left(M+1\right)d^{*}\right),\hfill \end{array}\hfill \end{array}(25)$

where for k = 1, 2, … , j, ${\bar{\psi }}_{i,k}^4=\frac{1}{4}{(M+1)}^4{\chi }_{m,l}^4{\lambda }_{i,k}^4((M+1)|z_{m,l}|{\chi }_{m,l})$. ${\bar{\upsilon }}_{i,q}^4=\frac{1}{2}{(M+1)}^4{\chi }_{m,l}^4{\eta }_{i,q}^4((M+1)|z_{m,l}|{\chi }_{m,l}),q=\mathrm{1,2},\dots j-1$. Let $K_{i,j}=\sum _{k=1}^{j-1}|\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}|{\psi }_{i,k}((M+1)d^{*})+{\psi }_{i,j}((M+1)d^{*})+\frac{1}{2}(M+1)\sum _{p=1}^{j-1}\sum _{q=1}^{j-1}|\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}|{\upsilon }_{i,q}^2((M+1)d^{*})$.

By using Lemma 4, one obtains

$|z_{i,j}^3|K_{i,j}-z_{i,j}^3{K}_{i,j}\tanh \left(\frac{z_{i,j}^3{K}_{i,j}}{{\epsilon }_{i,j}}\right)⩽0.2785{\epsilon }_{i,j}.(26)$

Next, we further obtain

$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{3}{2}{z}_{i,j}^2\Vert g_{i,j}\left(X\right)-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}{g}_{i,k}\left(X\right){\Vert }^2& ⩽\frac{9}{8}{z}_{i,j}^4{\left(M+1\right)}^2{j}^2{\upsilon }_{i,j}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,j}^{-2}+\frac{9}{8}{z}_{i,j}^4{j}^2{\left(M+1\right)}^2\hfill \\ \hfill & \times M+\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,j}^4+\frac{9}{8}{z}_{i,j}^4{\left(M+1\right)}^2{j}^2\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2\hfill \\ \hfill & \times {\upsilon }_{i,k}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,k}^{-2}+\frac{1}{2}\sum _{k=1}^j{l}_{i,j,k}^2+\frac{9}{8}{z}_{i,j}^4{\left(M+1\right)}^2{j}^{2}M\hfill \\ \hfill & \times \sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2+\sum _{k=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,k}^4,\hfill \end{array}\hfill \end{array}(27)$

where for k = 1, 2, … , j, l_i,j,k are positive constants, ${\bar{\upsilon }}_{i,k}^4=\frac{1}{2}{(M+1)}^4{{\chi }_{m,l}}^4{\eta }_{i,k}^4\left((M+1){\chi }_{m,l}|z_{m,l}|\right)$.

It follows from (Eqs 22–27) that

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{V}_{i,j}& ⩽z_{i,j}^3\left(f_{i,j}+{\mathrm{\Phi }}_{i,j}{x}_{i,j+1}-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}\right)-\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i\right.\hfill \\ \hfill & -\sum _{k=0}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}+\frac{3}{4}M{z}_{i,j}\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^{\frac{4}{3}}+\frac{3}{4}M{z}_{i,j}+\frac{1}{8}{\left(M+1\right)}^2\hfill \\ \hfill & \times M{z}_{i,j}^3\sum _{p=1}^{j-1}{\sum _{q=1}^{j-1}\left(\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}\right)}^2+K_{i,j}\tanh \left(\frac{z_{i,j}^3{K}_{i,j}}{{\epsilon }_{i,j}}\right)+\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^{2}M\hfill \\ \hfill & +\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^2{\upsilon }_{i,j}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,j}^{-2}+\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^2\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2\hfill \\ \hfill & \times \left.{\upsilon }_{i,k}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,k}^{-2}+\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^{2}M\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2\right)+\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,k}^4\hfill \\ \hfill & +\left(j-1\right)\sum _{q=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,q}^4+0.2785{\epsilon }_{i,j}+\frac{1}{2}\sum _{k=1}^j{l}_{i,j,k}^2+\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,k}^4.\hfill \end{array}\hfill \end{array}(28)$

Step i, n: Based on $z_{i,n_i}=x_{i,n_i}-{\alpha }_{i,n_i-1}$, the derivative of $z_{i,n_i}$ is given by

$d{z}_{i,n_i}=\left(f_{i,n_i}+{\mathrm{\Phi }}_{i,n_i}{u}_i+h_{i,n_i}\left(X\right)-L{\alpha }_{i,n_i-1}\right)dt+{\left(g_{i,n_i}\left(X\right)-\sum _{k=1}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}{g}_{i,k}\left(X\right)\right)}^{T}d{\omega }_i,(29)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{\alpha }_{i,n_i-1}& =\sum _{k=1}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}+h_{i,k}\left(X\right)\right)+\frac{\partial {\alpha }_{i,n_i-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i+\sum _{k=0}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}\hfill \\ \hfill & +\frac{1}{2}\sum _{p,q=1}^{n_i-1}\frac{{\partial }^2{\alpha }_{i,n_i-1}}{\partial x_{i,p}\partial x_{i,q}}{g}_{i,p}^T\left(X\right)g_{i,q}\left(X\right).\hfill \end{array}\hfill \end{array}(30)$

Next, consider a Lyapunov function as $V_{i,n_i}=\frac{1}{4}{z}_{i,n_i}^4$, the following result holds

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{V}_{i,n_i}& =z_{i,n_i}^3\left(f_{i,n_i}+{\mathrm{\Phi }}_{i,n_i}{u}_i+h_{i,n_i}\left(X\right)-\sum _{k=1}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}+h_{i,k}\left(X\right)\right)\right.\hfill \\ \hfill & -\left.\frac{\partial {\alpha }_{i,n_i-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i-\sum _{k=0}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}-\frac{1}{2}\sum _{p,q=1}^{n_i-1}\frac{{\partial }^2{\alpha }_{i,n_i-1}}{\partial x_{i,p}\partial x_{i,q}}{g}_{i,p}^T\left(X\right)g_{i,q}\left(X\right)\right)\hfill \\ \hfill & +\frac{3}{2}{z}_{i,n_i}^2\Vert g_{i,n_i}\left(X\right)-\sum _{k=1}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}{g}_{i,k}\left(X\right){\Vert }^2.\hfill \end{array}\hfill \end{array}(31)$

Repeating the same derivations as (25) and (27) yields

$\begin{array}{c}\hfill \begin{array}{cc}\hfill L{V}_{i,n_i}& ⩽z_{i,n_i}^3\left(f_{i,n_i}+{\mathrm{\Phi }}_{i,n_i}{u}_i-\sum _{k=1}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}\right)-\frac{\partial {\alpha }_{i,n_i-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i\right.\hfill \\ \hfill & -\sum _{k=0}^{n_i-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}+\frac{3}{4}M{z}_{i,n_i}\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^{\frac{4}{3}}+\frac{3}{4}M{z}_{i,n_i}\hfill \\ \hfill & +\frac{1}{8}{\left(M+1\right)}^{2}M{z}_{i,n_i}^3\sum _{p=1}^{n_i-1}{\sum _{q=1}^{n_i-1}\left(\frac{{\partial }^2{\alpha }_{i,n_i-1}}{\partial x_{i,p}\partial x_{i,q}}\right)}^2+\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^{2}M\hfill \\ \hfill & +K_{i,n_i}\tanh \left(\frac{z_{i,n_i}^3{K}_{i{n}_i}}{{\epsilon }_{i,n_i}}\right)+\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^2{\upsilon }_{i,n_i}^4\left(\left(M+1\right)d^{*}\right)l_{i,n_i,n_i}^{-2}\hfill \\ \hfill & +\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^2\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^2{\upsilon }_{i,k}^4\left(\left(M+1\right)d^{*}\right)l_{i,n_i,k}^{-2}\hfill \\ \hfill & +\left.\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^{2}M\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^2\right)+\sum _{k=1}^{n_i}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,k}^4+0.2785{\epsilon }_{i,n_i}\hfill \\ \hfill & +\frac{1}{2}\sum _{k=1}^{n_i}{l}_{i,n_i,k}^2+\left(n_i-1\right)\sum _{q=1}^{n_i-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,q}^4+\sum _{k=1}^{n_i}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,k}^4,\hfill \end{array}\hfill \end{array}(32)$

where for k = 1, 2, … n_i, $l_{i,n_{i,}k}$ are positive constants.

Combining with the whole design procedures from Step 1 to Step n_i, choose Lyapunov function for the ith subsystem as

$V_i=\sum _{j=1}^{n_i}{V}_{i,j}=\frac{1}{4}\sum _{j=1}^{n_i}{z}_{i,j}^4+\frac{1}{2{\gamma }_i}{\tilde{\theta }}_i^2.(33)$

Thus, the Lyapunov function of the nonlinear systems is designed as

$V=\sum _{i=1}^N\sum _{j=1}^{n_i}{V}_{i,j}=\sum _{i=1}^N\left(\frac{1}{4}{z}_{i,1}^4+\frac{1}{4}\sum _{j=2}^{n_i}{z}_{i,j}^4+\frac{1}{2{\gamma }_i}{\tilde{\theta }}_i^2\right).(34)$

Next, utilizing (21) (28), and (32), one obtains

$\begin{array}{c}\hfill \begin{array}{cc}\hfill LV& ⩽\sum _{i=1}^N{z}_{i,1}^3\left({\mathrm{\Phi }}_{i,1}{z}_{i,2}+{\mathrm{\Phi }}_{i,1}{\alpha }_{i,1}+{\mathrm{\Theta }}_{i,1}\right)+\sum _{i=1}^N\sum _{j=2}^{n_i-1}{z}_{i,j}^3\left({\mathrm{\Phi }}_{i,j}{z}_{i,j+1}+{\mathrm{\Phi }}_{i,j}{\alpha }_{i,j}+{\mathrm{\Theta }}_{i,j}\right)\hfill \\ \hfill & +\sum _{i=1}^N{z}_{i,n_i}^3\left({\mathrm{\Phi }}_{i,n_i}{u}_i+{\mathrm{\Theta }}_{i,n_i}\right)+\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,k}^4\hfill \\ \hfill & +\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,k}^4+\sum _{i=1}^N\sum _{j=1}^{n_i}\left(j-1\right)\sum _{q=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,q}^4\hfill \\ \hfill & +\sum _{i=1}^N\sum _{j=1}^{n_i}0.2785{\epsilon }_{i,j}+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j{l}_{i,j,k}^2-\sum _{i=1}^N\sum _{j=2}^{n_i}{z}_{i,j}^3\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i-\sum _{i=1}^N\frac{1}{{\gamma }_i}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i,\hfill \end{array}\hfill \end{array}(35)$

where

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{\Theta }}_{i,1}& =f_{i,1}-{\dot{y}}_{di}+\frac{3}{4}M{z}_{i,1}+K_{i,1}\tanh \left(\frac{z_{i,1}^3{K}_{i,1}}{{\epsilon }_{i,1}}\right)+\frac{9}{8}{\left(M+1\right)}^{2}M{z}_{i,1}\hfill \\ \hfill & +\frac{9}{8}{\left(M+1\right)}^2{z}_{i,1}{\upsilon }_{i,1}^4\left(\left(M+1\right)d^{*}\right)l_{i,\mathrm{1,1}}^{-2},\hfill \end{array}\hfill \end{array}(36)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{\Theta }}_{i,j}& =f_{i,j}-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}\right)-\sum _{k=0}^{j-1}\frac{\partial {\alpha }_{i,j-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}\hfill \\ \hfill & +\frac{3}{4}M{z}_{i,j}\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^{\frac{4}{3}}+\frac{3}{4}M{z}_{i,j}+\frac{1}{8}{\left(M+1\right)}^{2}M{z}_{i,j}^3\sum _{p=1}^{j-1}{\sum _{q=1}^{j-1}\left(\frac{{\partial }^2{\alpha }_{i,j-1}}{\partial x_{i,p}\partial x_{i,q}}\right)}^2\hfill \\ \hfill & +\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^2{\upsilon }_{i,j}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,j}^{-2}+\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^{2}M\hfill \\ \hfill & +\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^2\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2{\upsilon }_{i,k}^4\left(\left(M+1\right)d^{*}\right)l_{i,j,k}^{-2}+K_{i,j}\tanh \left(\frac{z_{i,j}^3{K}_{i,j}}{{\epsilon }_{i,j}}\right)\hfill \\ \hfill & +\frac{9}{8}{z}_{i,j}{j}^2{\left(M+1\right)}^{2}M\sum _{k=1}^{j-1}{\left(\frac{\partial {\alpha }_{i,j-1}}{\partial x_{i,k}}\right)}^2,j=\mathrm{2,3},\dots ,n_i-1,\hfill \end{array}\hfill \end{array}(37)$

$\begin{array}{c}\hfill {\mathrm{\Theta }}_{i,n_i}=f_{i,n_i}-\sum _{k=1}^{j-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\left(f_{i,k}+{\mathrm{\Phi }}_{i,k}{x}_{i,k+1}\right)+\frac{3}{4}M{z}_{i,n_i}\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^{\frac{4}{3}}\hfill \end{array}$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill & -\sum _{k=0}^{j-1}\frac{\partial {\alpha }_{i,n_i-1}}{\partial y_{di}^{\left(k\right)}}{y}_{di}^{\left(k+1\right)}+\frac{3}{4}M{z}_{i,n_i}+\frac{1}{8}{\left(M+1\right)}^{2}M{z}_{i,n_i}^3\sum _{p=1}^{n_i-1}{\sum _{q=1}^{n_i-1}\left(\frac{{\partial }^2{\alpha }_{i,n_i-1}}{\partial x_{i,p}\partial x_{i,q}}\right)}^2\hfill \\ \hfill & +K_{i,n_i}\tanh \left(\frac{z_{i,n_i}^3{K}_{i,n_i}}{{\epsilon }_{i,n_i}}\right)+\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^2{\upsilon }_{i,n_i}^4\left(\left(M+1\right)d^{*}\right)l_{i,n_i,n_i}^{-2}\hfill \\ \hfill & +\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^{2}M+\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^2\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^2{\upsilon }_{i,k}^4\left(\left(M+1\right)d^{*}\right)l_{i,n_i,k}^{-2}\hfill \\ \hfill & +\frac{9}{8}{z}_{i,n_i}{n_i}^2{\left(M+1\right)}^{2}M\sum _{k=1}^{n_i-1}{\left(\frac{\partial {\alpha }_{i,n_i-1}}{\partial x_{i,k}}\right)}^2.\hfill \end{array}\hfill \end{array}(38)$

By rearranging sequence for above terms, we have

$\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\psi }}_{i,k}^4=\sum _{i=1}^N\sum _{j=1}^{n_i}{z}_{i,j}^4\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\psi }}_{m,k}^4,(39)$

$\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,k}^4=\sum _{i=1}^N\sum _{j=1}^{n_i}{z}_{i,j}^4\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\upsilon }}_{m,k}^4,(40)$

$\sum _{i=1}^N\sum _{j=1}^{n_i}\left(j-1\right)\sum _{q=1}^{j-1}\sum _{m=1}^N\sum _{l=1}^{n_m}{z}_{m,l}^4{\bar{\upsilon }}_{i,q}^4=\sum _{i=1}^N\sum _{j=1}^{n_i}{z}_{i,j}^4\sum _{m=1}^N\sum _{l=2}^{n_m}\left(l-1\right)\sum _{q=1}^{l-1}{\bar{\upsilon }}_{m,q}^4.(41)$

By utilizing the adaptive laws (12), above rearranging sequence, and Lemma 5, the second-to-last term in (Eq. 35) is further handled, one has

$\begin{array}{c}\hfill \begin{array}{cc}\hfill -\sum _{i=1}^N\sum _{j=2}^{n_i}{z}_{i,j}^3\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\dot{\widehat{\theta }}}_i& ⩽\sum _{i=1}^N\sum _{j=2}^{n_i}{z}_{i,j}^3\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\sigma }_i{\widehat{\theta }}_i-\sum _{i=1}^N\sum _{j=2}^{n_i}{z}_{i,j}^3\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}\sum _{k=1}^{j-1}\frac{{\gamma }_i}{2a_{i,k}^2}\hfill \\ \hfill & \times z_{i,k}^6{S}_{i,k}^T{S}_{i,k}+\sum _{i=1}^N\sum _{j=2}^{n_i}\frac{{\gamma }_i}{2a_{i,j}^2}{s}^2{z}_{i,j}^6\left(\sum _{k=2}^j|z_{i,k}^3\frac{\partial {\alpha }_{i,k-1}}{\partial {\widehat{\theta }}_i}|\right).\hfill \end{array}\hfill \end{array}(42)$

Next, for j = 1, 2, … , n_i − 1, based on Assumption 1 and Lemma 3, we can obtain

$z_{i,j}^3{\mathrm{\Phi }}_{i,j}{z}_{i,j+1}⩽\frac{3}{4}{\varsigma }_M{z}_{i,j}^4+\frac{1}{4}{\varsigma }_M{z}_{i,j+1}^4.(43)$

Then, from (Eqs 39–43), Eq. 35 can be rewritten as

$\begin{array}{c}\hfill \begin{array}{cc}\hfill LV& ⩽\sum _{i=1}^N{z}_{i,1}^3\left({\mathrm{\Phi }}_{i,1}{\alpha }_{i,1}+{\bar{f}}_{i,1}\right)+\sum _{i=1}^N\sum _{j=2}^{n_i-1}{z}_{i,j}^3\left({\mathrm{\Phi }}_{i,j}{\alpha }_{i,j}+{\bar{f}}_{i,j}\right)+\sum _{i=1}^N{z}_{i,n_i}^3\left({\mathrm{\Phi }}_{i,n_i}{u}_i+{\bar{f}}_{i,n_i}\right)\hfill \\ \hfill & -\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{3}{4}{z}_{i,j}^4+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^{n_i}\sum _{k=1}^j{l}_{i,j,k}^2+\sum _{i=1}^N\sum _{j=1}^{n_i}0.2785{\epsilon }_{i,j}-\sum _{i=1}^N\frac{1}{{\gamma }_i}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i,\hfill \end{array}\hfill \end{array}(44)$

where

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\bar{f}}_{i,1}& =\frac{3}{4}{z}_{i,1}+\frac{3}{4}{\varsigma }_M{z}_{i,1}+{\mathrm{\Theta }}_{i,1}+z_{i,1}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\psi }}_{m,k}^4\left(z_{i,1},{\widehat{\theta }}_i\right)\hfill \\ \hfill & +z_{i,1}\sum _{m=1}^N\sum _{l=2}^{n_m}\left(l-1\right)\sum _{q=1}^{l-1}{\bar{\upsilon }}_{m,q}^4\left(z_{i,1},{\widehat{\theta }}_i\right)+z_{i,1}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\upsilon }}_{m,k}^4\left(z_{i,1},{\widehat{\theta }}_i\right),\hfill \end{array}\hfill \end{array}(45)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\bar{f}}_{i,j}& =\frac{3}{4}{z}_{i,j}+\frac{3}{4}{\varsigma }_M{z}_{i,j}+\frac{1}{4}{\varsigma }_M{z}_{i,j}+{\mathrm{\Theta }}_{i,j}+z_{i,j}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\psi }}_{m,k}^4\left(z_{i,j},{\widehat{\theta }}_i\right)\hfill \\ \hfill & +z_{i,j}\sum _{m=1}^N\sum _{l=2}^{n_m}\left(l-1\right)\sum _{q=1}^{l-1}{\bar{\upsilon }}_{m,q}^4\left(z_{i,j},{\widehat{\theta }}_i\right)+z_{i,j}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\upsilon }}_{m,k}^4\left(z_{i,j},{\widehat{\theta }}_i\right)+\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}{\sigma }_i{\widehat{\theta }}_i\hfill \\ \hfill & -\frac{\partial {\alpha }_{i,j-1}}{\partial {\widehat{\theta }}_i}\sum _{k=1}^{j-1}\frac{{\gamma }_i}{2a_{i,k}^2}{z}_{i,k}^6{S}_{i,k}^T{S}_{i,k}+\frac{{\gamma }_i}{2a_{i,j}^2}{s}^2{z}_{i,j}^3\left(\sum _{k=2}^j|z_{i,k}^3\frac{\partial {\alpha }_{i,k-1}}{\partial {\widehat{\theta }}_i}|\right),\hfill \end{array}\hfill \end{array}(46)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\bar{f}}_{i,n_i}& =\frac{3}{4}{z}_{i,n_i}+\frac{1}{4}{\varsigma }_M{z}_{i,n_i}+{\mathrm{\Theta }}_{i,n_i}+z_{i,n_i}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\psi }}_{m,k}^4\left(z_{i,n_i},{\widehat{\theta }}_i\right)\hfill \\ \hfill & +z_{i,n_i}\sum _{m=1}^N\sum _{l=2}^{n_m}\left(l-1\right)\sum _{q=1}^{l-1}{\bar{\upsilon }}_{m,q}^4\left(z_{i,n_i},{\widehat{\theta }}_i\right)+z_{i,n_i}\sum _{m=1}^N\sum _{l=1}^{n_m}\sum _{k=1}^l{\bar{\upsilon }}_{m,k}^4\left(z_{i,j},{\widehat{\theta }}_i\right)\hfill \\ \hfill & +\frac{\partial {\alpha }_{i,n_i-1}}{\partial {\widehat{\theta }}_i}{\sigma }_i{\widehat{\theta }}_i-\frac{\partial {\alpha }_{i,n_i-1}}{\partial {\widehat{\theta }}_i}\sum _{k=1}^{n_i-1}\frac{{\gamma }_i}{2a_{i,k}^2}{z}_{i,k}^6{S}_{i,k}^T{S}_{i,k}+\frac{{\gamma }_i}{2a_{i,n_i}^2}{s}^2{z}_{i,n_i}^3\left(\sum _{k=2}^{n_i}|z_{i,k}^3\frac{\partial {\alpha }_{i,k-1}}{\partial {\widehat{\theta }}_i}|\right).\hfill \end{array}\hfill \end{array}(47)$

The approximation ability of RBFNNs is applied to ${\bar{f}}_{i,j}$, we have

${\bar{f}}_{i,j}\left(Z_{i,j}\right)=W_{i,j}^T{S}_{i,j}\left(Z_{i,j}\right)+{\delta }_{i,j}\left(Z_{i,j}\right).(48)$

where $Z_{i,j}=[{\bar{x}}_{i,j}^T,{\widehat{\theta }}_i,y_{di},{\bar{y}}_{di}^{(j)}]$.

In addition, we can obtain below inequalities by using Young’s inequality

$z_{i,j}^3{\bar{f}}_{i,j}\left(Z_{i,j}\right)⩽\frac{1}{2a_{i,j}^2}{z}_{i,j}^6{\theta }_i{S}_{i,j}^T{S}_{i,j}+\frac{1}{2}{a}_{i,j}^2+\frac{3}{4}{z}_{i,j}^4+\frac{1}{4}{\bar{\delta }}_{i,j}^4,(49)$

where ${\theta }_i=\max \{{\Vert W_{i,j}\Vert }^2;i=\mathrm{1,2},\dots ,N,j=\mathrm{1,2},\dots ,n_i\}$.

Based on above overall backstepping design procedures, we construct the virtual controllers for ith subsystems as

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_{i,1}& ={\aleph }_{ms}\left({\phi }_{i,1}\right){\bar{\alpha }}_{i,1},\hfill \\ \hfill {\bar{\alpha }}_{i,1}& =-k_{i,1}{z}_{i,1}-\frac{1}{2a_{i,1}^2}{z}_{i,1}^3{\widehat{\theta }}_i{S}_{i,1}^T{S}_{i,1},\hfill \\ \hfill {\dot{\phi }}_{i,1}& =-P_{i,1}{z}_{i,1}^3{\bar{\alpha }}_{i,1},{\phi }_{i,1}\left(0\right)⩾0,\hfill \end{array}\hfill \end{array}(50)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_{i,j}& ={\aleph }_{ms}\left({\phi }_{i,j}\right){\bar{\alpha }}_{i,j},\hfill \\ \hfill {\bar{\alpha }}_{i,j}& =-k_{i,j}{z}_{i,j}-\frac{1}{2a_{i,j}^2}{z}_{i,j}^3{\widehat{\theta }}_i{S}_{i,j}^T{S}_{i,j},\hfill \\ \hfill {\dot{\phi }}_{i,j}& =-P_{i,j}{z}_{i,j}^3{\bar{\alpha }}_{i,j},{\phi }_{i,j}\left(0\right)⩾0,\hfill \end{array}\hfill \end{array}(51)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_{i,n_i}& ={\aleph }_{ms}\left({\phi }_{i,n_i}\right){\bar{\alpha }}_{i,n_i},\hfill \\ \hfill {\bar{\alpha }}_{i,n_i}& =-k_{i,n_i}{z}_{i,n_i}-\frac{1}{2a_{i,n_i}^2}{z}_{i,n_i}^3{\widehat{\theta }}_i{S}_{i,n_i}^T{S}_{i,n_i},\hfill \\ \hfill {\dot{\phi }}_{i,n_i}& =-P_{i,n_i}{z}_{i,n_i}^3{\bar{\alpha }}_{i,n_i},{\phi }_{i,n_i}\left(0\right)⩾0,\hfill \end{array}\hfill \end{array}(52)$

$\begin{array}{c}\hfill \begin{array}{cc}\hfill w_i\left(t\right)& =-\left(1+\beta \right)\left({\alpha }_{i,n_i}\tanh \left(\frac{z_{i,n_i}^3{\alpha }_{i,n_i}}{\varphi }\right)+{\bar{m}}_i\tanh \left(\frac{z_{i,n_i}^3{\bar{m}}_i}{\varphi }\right)\right),\hfill \\ \hfill u_i& =w_i\left(t_k\right)\forall t\in \left[t_k,t_{k+1}\right),\hfill \\ \hfill t_{k+1}& =\inf \left\{t\in \mathfrak{R}||e\left(t\right)|⩾\beta |u_i\left(t\right)|+m_i.\right\},\hfill \end{array}\hfill \end{array}(53)$

where e_i(t) = w_i(t) − u_i(t) denote errors. k_i,j, P_i,j, 0 < β < 1, ϕ, m_i > 0, and ${\bar{m}}_i>\frac{m_i}{1-\beta }$ are all positive parameters. In addition, κ_i,1t) and κ_i,2t) are time-varying parameters satisfying |κ_i,1t)|⩽1 and |κ_i,2t)|⩽1.

Thus, the controllers can be chosen as

$u_i\left(t\right)=\frac{w_i\left(t\right)-{\kappa }_{i,2}\left(t\right)m_i}{1+{\kappa }_{i,1}\left(t\right)\beta }.(54)$

Then, by substituting Eqs 50–54 into Eq. 44, one has

$\begin{array}{c}\hfill \begin{array}{cc}\hfill LV& ⩽\sum _{i=1}^N{z}_{i,1}^3\left({\mathrm{\Phi }}_{i,1}{\alpha }_{i,1}-{\bar{\alpha }}_{i,1}-k_{i,1}{z}_{i,1}+\frac{1}{2a_{i,1}^2}{z}_{i,1}^3{\tilde{\theta }}_i{S}_{i,1}^T{S}_{i,1}\right)+\sum _{i=1}^N\sum _{j=2}^{n_i-1}{z}_{i,j}^3\left({\mathrm{\Phi }}_{i,j}{\alpha }_{i,j}-{\bar{\alpha }}_{i,j}\right.\hfill \\ \hfill & -\left.k_{i,j}{z}_{i,j}+\frac{1}{2a_{i,j}^2}{z}_{i,j}^3{\tilde{\theta }}_i{S}_{i,j}^T{S}_{i,j}\right)+\sum _{i=1}^N{z}_{i,n_i}^3\left({\mathrm{\Phi }}_{i,n_i}{u}_i-{\mathrm{\Phi }}_{i,n_i}{\alpha }_{i,n_i}+{\mathrm{\Phi }}_{i,n_i}{\alpha }_{i,n_i}-{\bar{u}}_i-k_{i,n_i}{z}_{i,n_i}\right.\hfill \\ \hfill & +\left.\frac{1}{2a_{i,n_i}^2}{z}_{i,n_i}^3{\tilde{\theta }}_i{S}_{i,n_i}^T{S}_{i,n_i}\right)+\sum _{i=1}^N\sum _{j=1}^{n_i}\left(\frac{1}{2}\sum _{k=1}^j{l}_{i,j,k}^2+0.2785{\epsilon }_{i,j}+\frac{1}{2}{a}_{i,j}^2+\frac{1}{4}{\bar{\delta }}_{i,j}^4\right)-\sum _{i=1}^N\frac{1}{{\gamma }_i}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i,\hfill \end{array}\hfill \end{array}(55)$

where

$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{i=1}^N{z}_{i,n_i}^3{\mathrm{\Phi }}_{i,n_i}{u}_i-z_{i,n_i}^3{\mathrm{\Phi }}_{i,n_i}{\alpha }_{i,n_i}& ⩽-\sum _{i=1}^N{\mathrm{\Phi }}_{i,n_i}|z_{i,n_i}^3{\alpha }_{i,n_i}|-\sum _{i=1}^N{\mathrm{\Phi }}_{i,n_i}|z_{i,n_i}^3{\bar{m}}_i|+\sum _{i=1}^{N}0.557{\mathrm{\Phi }}_{i,n_i}{\epsilon }_{i,n_i}\hfill \\ \hfill & +\sum _{i=1}^N\frac{z_{i,n_i}^3{\mathrm{\Phi }}_{i,n_i}{m}_{i,1}}{1-\beta }-\sum _{i=1}^N{z}_{i,n_i}^3{\mathrm{\Phi }}_{i,n_i}{\alpha }_{i,n_i}⩽\sum _{i=1}^{N}0.557{\varsigma }_M{\epsilon }_{i,n_i}.\hfill \end{array}\hfill \end{array}(56)$

Next, substituting the designed controllers and Eq. 56 into Eq. 55, we have

$LV⩽\sum _{i=1}^N\sum _{j=1}^{n_i}\left(-k_{i,j}{z}_{i,j}^4\right)-\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\mathrm{\Phi }}_{i,j}\aleph {\dot{\phi }}_{i,j}+\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\dot{\phi }}_{i,j}+\mathrm{H}+\sum _{i=1}^N\frac{{\sigma }_i}{{\gamma }_i}{\tilde{\theta }}_i{\widehat{\theta }}_i,(57)$

where $\mathrm{H}=\sum _{i=1}^{N}0.557{\varsigma }_M{\epsilon }_{i,n_i}+\sum _{i=1}^N\sum _{j=1}^{n_i}(\frac{1}{2}\sum _{k=1}^j{l}_{i,j,k}^2+0.2785{\epsilon }_{i,j}+\frac{1}{2}{a}_{i,j}^2+\frac{1}{4}{\bar{\delta }}_{i,j}^4)$.

Furthermore, according to the inequality ${\tilde{\theta }}_i{\widehat{\theta }}_i⩽-\frac{1}{2}{\tilde{\theta }}_i^2+\frac{1}{2}{\theta }_i^2$, the below result holds

$LV⩽-\sum _{i=1}^N\left(\sum _{j=1}^{n_i}{k}_{i,j}{z}_{i,j}^4+\frac{{\sigma }_i}{2{\gamma }_i}{\tilde{\theta }}_i^2\right)-\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\mathrm{\Phi }}_{i,j}\aleph {\dot{\phi }}_{i,j}+\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\dot{\phi }}_{i,j}+\bar{H},(58)$

where $\bar{\mathrm{H}}=\mathrm{H}+\sum _{i=1}^N\frac{{\sigma }_i}{2{\gamma }_i}{\theta }_i^2$.

Theorem 1: Consider the stochastic interconnected nonlinear systems in pure-feedback form (Eq. 3), the adaptive laws (Eq. 13), the virtual controllers (Eqs 53, 54), and the actual control inputs (Eq. 55) based on Assumptions Eq. 1-4 are obtained. Above design procedures ensure that the signals of closed-loop remain semiglobally uniformly bounded in probability and z_i,1 is asymptotically converge to zero in probability. In addition, the tracking error z_i,j converge to compact set Ω_Z, which is defined as

${\mathrm{\Omega }}_Z=\left\{z_{i,j}|\sum _{i=1}^N\sum _{j=1}^{n_i}E\left[{|z_{i,j}|}^4\right]⩽4E\left[V\left(0\right)\right]+4\left(\frac{D}{c}\right)+4\left(\frac{b}{\underline{P}}\right)\right\},(59)$

where c = min{4k_i,j, σ_i, i = 1, 2, … , N, j = 1, 2, … , n_i}, $b=\sup \left\{|\right.\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\mathrm{\Phi }}_{i,j}{\aleph }_{ms}({\phi }_{i,j}){\dot{\phi }}_{i,j}-\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\dot{\phi }}_{i,j}|$, $i=\mathrm{1,2},\dots ,N,j=\mathrm{1,2},\dots ,\left.n_i\right\}$, $\underline{P}=\inf \{P_{i,j},\text{for}i=\mathrm{1,2},\dots ,N,j=\mathrm{1,2},\dots ,n_i\}$, and $D=\sum _{i=1}^N\frac{{\sigma }_i}{2{\gamma }_i}{\theta }_i^2+\sum _{i=1}^{N}0.557{\varsigma }_M{\epsilon }_{i,n_i}+\sum _{i=1}^N\sum _{j=1}^{n_i}(\frac{1}{2}\sum _{k=1}^j{l}_{i,j,k}^2+0.2785{\epsilon }_{i,j}+\frac{1}{2}{a}_{i,j}^2+\frac{1}{4}{\epsilon }_{i,j}^4)$.

Proof: Based on above design parameters $c,b,\underline{P}\text{and}D$ Eq. 58 is rewritten as follows:

$LV⩽-cV+D-\left(\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\mathrm{\Phi }}_{i,j}{\aleph }_{ms}\left({\phi }_{i,j}\right){\dot{\phi }}_{i,j}-\sum _{i=1}^N\sum _{j=1}^{n_i}\frac{1}{P_{i,j}}{\dot{\phi }}_{i,j}\right)(60)$

holds for ∀t⩾0. According to (12) and Lemma 2, ${\widehat{\theta }}_i\left(t\right)⩾0$ for t⩾0, when ${\widehat{\theta }}_i\left(0\right)⩾0$ for i = 1, 2, … , N. Hence, $\frac{1}{2a_{i,j}^2}{z}_{i,j}^6{\widehat{\theta }}_i{S}_{i,j}^T{S}_{i,j}⩾0$ for i = 1, 2, … , N, j = 1, 2, … , n_i. Furthermore, ${\dot{\phi }}_{i,j}$ must be non-negative so that φ_i,j and ${\aleph }_{ms}\left({\phi }_{i,j}\right)$ are non-negative with ${\phi }_{i,j}\left(0\right)⩾0$. Then, Eq. 60 is transformed into

$LV⩽-cV+D+\sum _{i=1}^N\sum _{j=1}^{n_i}\left(\frac{1}{P_{i,j}}{\dot{\phi }}_{i,j}-\frac{1}{P_{i,j}}{\underline{\mathrm{\Phi }}}_{i,j}{\aleph }_{ms}\left({\phi }_{i,j}\right){\dot{\phi }}_{i,j}\right),(61)$

where ${\underline{\mathrm{\Phi }}}_{i,j}$ is defined as ${\underline{\mathrm{\Phi }}}_{i,j}=\inf {\mathrm{\Phi }}_{i,j}({\bar{x}}_{i,j},x_{i,j+1})$, and it is an unknown constant. Then, we take the integration of Eq. 61

$E\left[V\left(t\right)\right]⩽E\left[V\left(0\right)\right]+\left(\frac{D}{c}\right)+\left(\frac{b}{\underline{P}}\right).(62)$

Furthermore, one obtains

$E\left[\sum _{i=1}^N\sum _{j=1}^{n_i}{z}_{i,j}^4\right]⩽4E\left[V\left(0\right)\right]+4\left(\frac{D}{c}\right)+4\left(\frac{b}{\underline{P}}\right),(63)$

such that z_i,j remain bounded for i = 1, 2, … , N, j = 1, 2, … , n_i. Based on Eq. 63, we can conclude that z_i,j eventually converge to compact set Ω_Z. Moreover, from Eqs 50, 51 and $\frac{1}{2a_{i,j}^2}{z}_{i,j}^6{\widehat{\theta }}_i{S}_{i,j}^T{S}_{i,j}⩾0$, it yields that

${\dot{\phi }}_{i,j}⩾k_{i,j}{P}_{i,j}{z}_{i,j}^4.(64)$

Hence, taking the integration of Eq. 64, we have

$E\left[{\int }_0^t{k}_{i,j}{P}_{i,j}{z}_{i,j}^4\left(v\right)dv\right]⩽E\left[{\phi }_{i,j}\left(t\right)-{\phi }_{i,j}\left(0\right)\right]<+\infty .(65)$

As a result, $k_{i,j}{P}_{i,j}{z}_{i,j}^4(t)$ is integrable in probability over [0, t_M]. Then, employing stochastic Barbalat’s theorem [28,29], we can see that $E[\underset{t\to \infty }{\lim }\left|z_{i,j}\right|]\to 0,j=\mathrm{1,2},\dots ,n_i$. Then, one has

$P\left\{\underset{t\to \infty }{\lim }\left|z_{i,1}\right|=0\right\}=1.(66)$

The proof is finished.

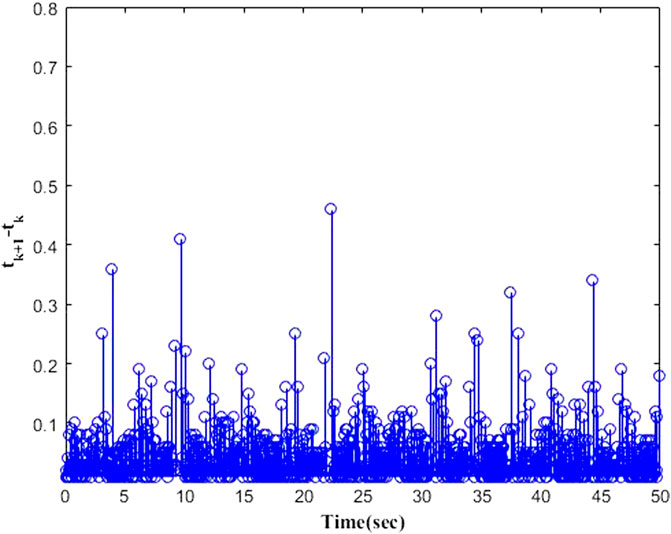
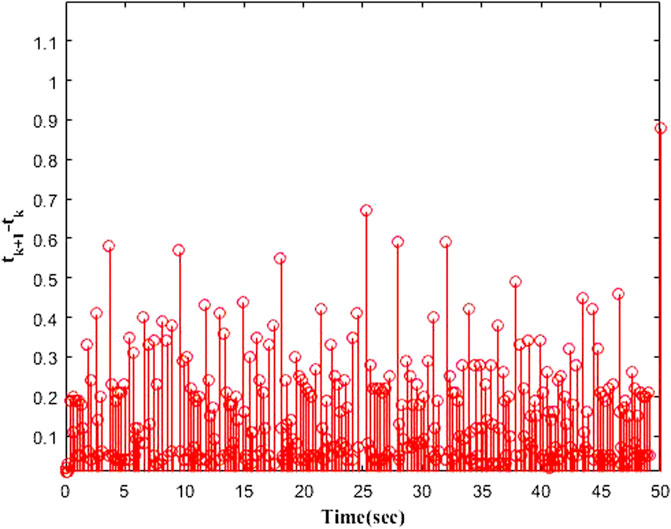
Finally, for relative threshold ETC strategy, the Zeno phenomenon is a problem that must not be ignored. Therefore, there is a ${\bar{t}}_Z>0$ such that $t_{k+1}-t_k>{\bar{t}}_Z$ for ∀k. According to the definition of e_i(t) = w_i(t) − u_i(t), we have

$\frac{d}{dt}|e_i\left(t\right)|=\text{sign}\left(e_i\left(t\right)\right)\dot{e_i}\left(t\right)⩽|{\dot{w}}_i\left(t\right)|.(67)$

We can know that w_i(t) is bounded due to the existence of bounded variable signals. Consequently, it can be realized that w_i(t) are smooth functions, thus ${\dot{w}}_i(t)$ are bounded. There must be a positive constant $\bar{b}$ such that ${\dot{w}}_i(t)⩽\bar{b}$. According to e_i(t) = 0, $\underset{t\to t_{k+1}}{\lim }{e}_i(t)=\beta |u_i(t)|+m_i$, the lower bound of ${\bar{t}}_Z$ is $\frac{\beta |u_i(t)|+m_i}{\bar{b}}$. As a result, we can always make sure that ${\bar{t}}_Z$ is not zero. The Zeno phenomenon would not be presented in our design process.

Remark 3: The previous analysis shows that the stability of the researched systems depends on the design parameters k_i,j, a_i,j, γ_i, ɛ_i,j and σ_i (i = 1, 2, … , N; j = 1, 2, … , n_i). By adjusting parameters ɛ_i,j, a_i,j, σ_i, γ_i to make the term D in Eq. 63 relatively small, and adjusting parameters k_i,j, σ_i to make the term c in Eq. 63 relatively large. Then the proposed control strategy can ensure the stability of the closed-loop system.

4 Simulation example

At this section, the simulation results of the stochastic interconnected pure-feedback systems including three subsystems show effectiveness of the control scheme

$\begin{array}{c}\hfill \left\{\begin{array}{c}d{x}_{\mathrm{1,1}}=\left(\left(1+\sin {\left(x_{\mathrm{1,1}}\right)}^2\right)x_{\mathrm{1,2}}+\sin \left(x_{\mathrm{1,1}}\right)x_{\mathrm{2,1}}{x}_{\mathrm{2,2}}\right)dt+0.001\left(\sin \left(x_{\mathrm{2,2}}^2\right)/\left(1+x_{\mathrm{2,2}}^2\right)\right)d{\omega }_1,\\ d{x}_{\mathrm{1,2}}=\left(\left(2+\text{cos}\left(x_{\mathrm{1,1}}{x}_{\mathrm{1,2}}^2\right)\right)u_1+\left(\left(\text{cos}{\left(x_{\mathrm{1,2}}\right)}^2+x_{\mathrm{2,2}}^2\right)/\left(1+\text{exp}\left(-x_{\mathrm{2,2}}^2\right)\right)\right)\right)dt\\ +0.001\left(\text{cos}\left(x_{\mathrm{2,2}}^2\right)/\left(1+x_{\mathrm{2,2}}^2\right)\right)d{\omega }_1,\\ y_1=x_{\mathrm{1,1}},\\ d{x}_{\mathrm{2,1}}=\left(\left(0.05\left(1+x_{\mathrm{2,1}}\right)x_{\mathrm{2,2}}\right)+\left(2\text{cos}\left(x_{\mathrm{1,1}}{x}_{\mathrm{1,2}}\right)x_{\mathrm{2,2}}\right)\right)dt+0.001\left(0.5x_{\mathrm{2,2}}^2{x}_{\mathrm{1,1}}^2\right)d{\omega }_2,\\ d{x}_{\mathrm{2,2}}=\left(2+\text{exp}\left(-x_{\mathrm{2,1}}{x}_{\mathrm{2,2}}\right)\right)u_2+\left(\text{cos}\left(x_{\mathrm{2,1}}\right)x_{\mathrm{1,1}}\right)+0.001x_{\mathrm{2,1}}^2\sin \left(x_{\mathrm{1,1}}\right)d{\omega }_2,\\ y_2=x_{\mathrm{2,1}},\\ d{x}_{\mathrm{3,1}}=\left(0.5\left(\sin \left(x_{\mathrm{3,1}}\right)+1\right)*x_{\mathrm{3,2}}+2\left(\text{cos}\left(x_{\mathrm{1,1}}{x}_{\mathrm{1,2}}\right)\right)x_{\mathrm{3,2}}\right)dt+0.001\left(0.5x_{\mathrm{3,2}}^2{x}_{\mathrm{1,1}}^2\right)d{\omega }_3,\\ d{x}_{\mathrm{3,2}}=\left(2+\text{exp}\left(-x_{\mathrm{3,1}}{x}_{\mathrm{3,2}}\right)\right)u_3+\left(\text{cos}\left(x_{\mathrm{3,1}}\right)x_{\mathrm{1,1}}\right)+0.001x_{\mathrm{3,1}}^2\sin \left(x_{\mathrm{1,1}}\right)d{\omega }_3,\\ y_3=x_{\mathrm{3,1}}.\end{array}\right.\hfill \end{array}(68)$

In simulation, the design parameters are defined as follows: γ₁ = 1, γ₂ = 1, γ₃ = 1, σ₁ = 0.1, σ₂ = 0.01, σ₃ = 0.1, a_1,1 = 0.01, a_1,2 = 0.01, a_2,1 = 2, a_2,2 = 1, a_3,1 = 0.1, a_3,2 = 0.5, P_1,1 = 0.01, P_1,2 = 0.01, P_2,1 = 0.001, P_2,2 = 0.001, P_3,1 = 1, P_3,2 = 1, k_1,1 = 7, k_1,2 = 12, k_2,1 = 6, k_2,2 = 8, k_3,1 = 5, k_3,2 = 1, β = 0.1, ϕ = 0.5, ${\bar{m}}_{\mathrm{1,1}}=4$, ${\bar{m}}_{\mathrm{2,1}}=4$, ${\bar{m}}_{\mathrm{3,1}}=4$, m_1,1 = 0.2, m_2,1 = 0.9, and m_3,1 = 0.5. Initial values are given as ${[x_{\mathrm{1,1}}(0),x_{\mathrm{1,2}}(0),x_{\mathrm{2,1}}(0),x_{\mathrm{2,2}}(0),x_{\mathrm{3,1}}(0),x_{\mathrm{3,2}}(0)]}^T={[\mathrm{0,0,0,0,0,0}]}^T,{[{\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\theta }}_3]}^T={[\mathrm{0,0,0}]}^T$, and $\left[{\phi }_{\mathrm{1,1}}\right.,{\phi }_{\mathrm{1,2}}$, ${\phi }_{\mathrm{2,1}},{\phi }_{\mathrm{2,2}},{\phi }_{\mathrm{3,1}},{\left.{\phi }_{\mathrm{3,2}}\right]}^T={[\mathrm{1,1},\text{0}\text{.}5,\text{0}\text{.}5,\text{0},\text{0}]}^T$ The desired signals are chosen as y_d1 = sin(t), y_d2 = cos(t), and y_d3 = cos(t).

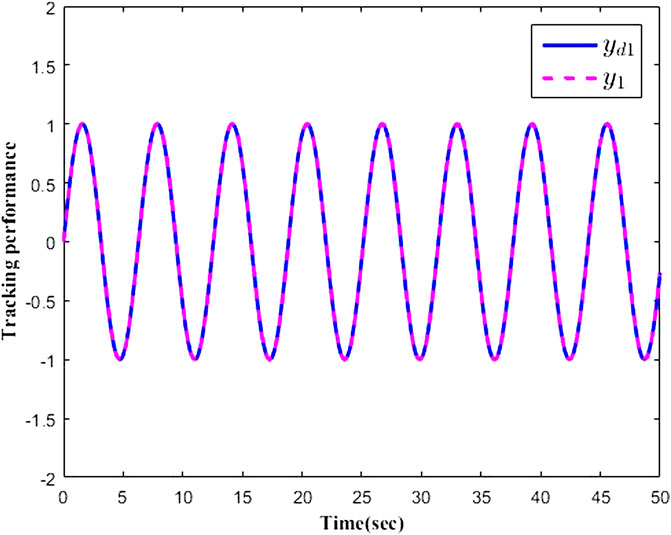
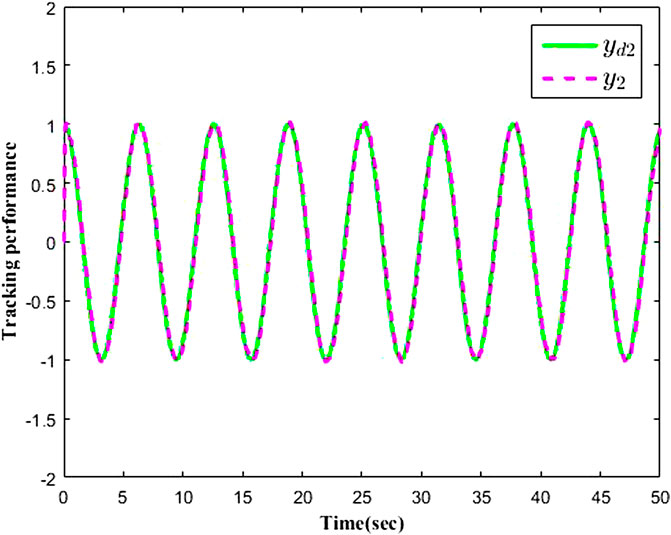
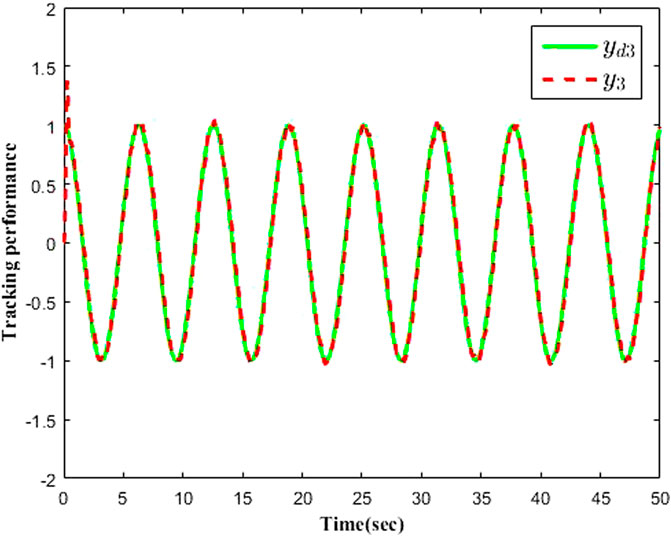
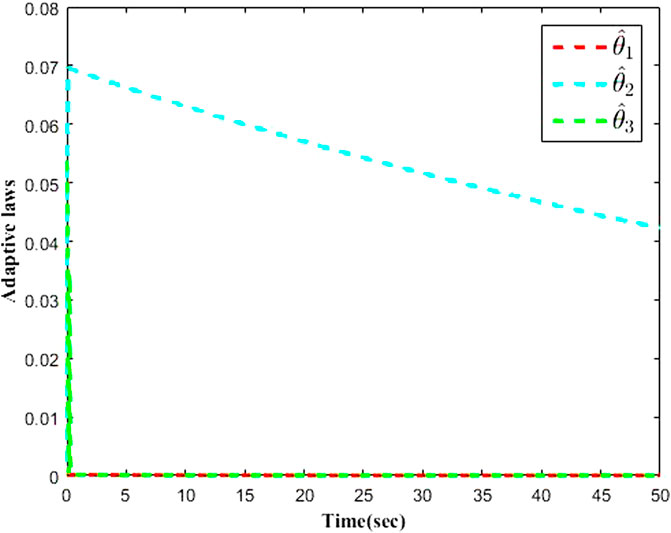
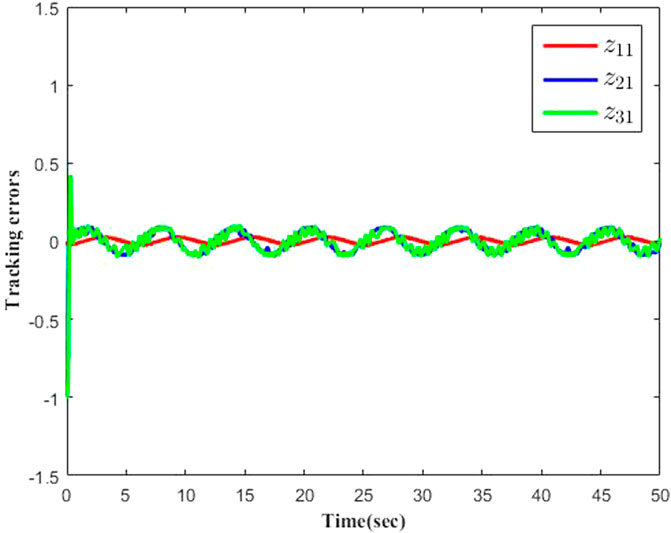
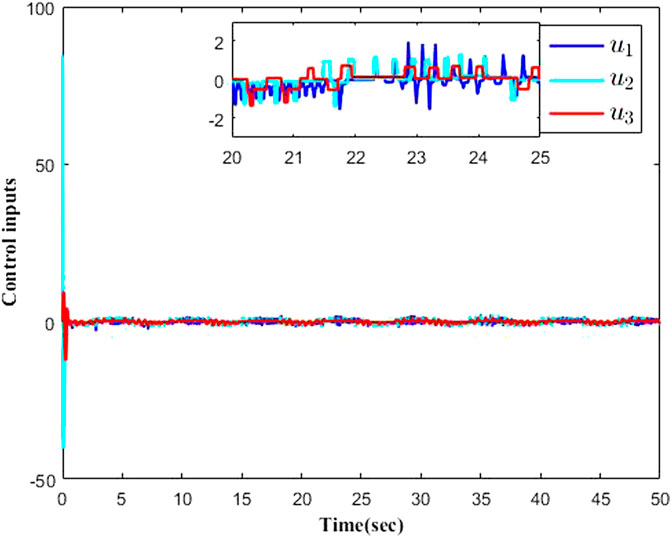
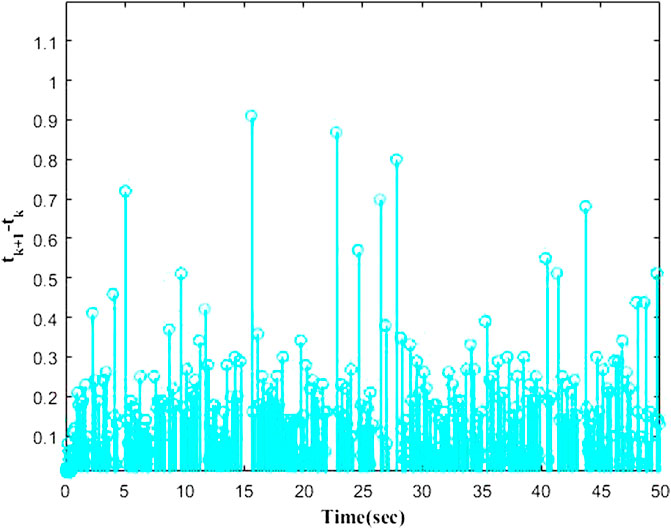
The simulation results are presented in Figures 1–9 by using the Matlab routine. Figures 1–3 show output signals y₁, y₂, y₃ and desired signals y_d1, y_d2, y_d3 respectively. As shown in Figures 1–3, the results demonstrate favourable tracking performances. Figure 4 shows the curves of adaptive laws ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$, and ${\widehat{\theta }}_3$. The tracking errors are presented in Figure 5 and converge to zero in probability. Figure 6 illustrates that control inputs u₁, u₂, and u₃ are bounded. Finally, the profiles of event-triggered times are provided in Figures 7–9.

FIGURE 1

FIGURE 1. The trajectories of y₁ and y_d1.

FIGURE 2

FIGURE 2. The trajectories of y₂ and y_d2.

FIGURE 3

FIGURE 3. The trajectories of y₃ and y_d3.

FIGURE 4

FIGURE 4. The trajectories of ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$ and ${\widehat{\theta }}_3$.

FIGURE 5

FIGURE 5. The trajectories of z₁₁, z₂₁ and z₃₁.

FIGURE 6

FIGURE 6. The trajectories of control inputs u₁, u₂ and u₃.

FIGURE 7

FIGURE 7. Triggering event subsystem₁.

FIGURE 8

FIGURE 8. Triggering event subsystem₂.

FIGURE 9

FIGURE 9. Triggering event subsystem₃.

5 Conclusion

This paper has proposed the event-triggered-based asymptotic tracking control scheme for a class of uncertain stochastic interconnected nonlinear systems in pure-feedback form. The effect caused by the unknown control gains and the nonaffine structures have been eliminated by using the new types of Nussbaum functions and the mean value theorem, respectively. Then, the decentralized controllers have been constructed to achieve desired tracking performance. Furthermore, it has been proved that the proposed controllers guarantee that all signals remain bounded in probability. The simulation example illustrates the effectivity of the proposed scheme. In future, we intend to extend the proposed scheme to multi-agent stochastic nonlinear systems with malicious attacks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YG, CL, ZG, BN, and BZ contributed the idea and design of the study. YG wrote the first draft of the manuscript. YG organized the literature. CL and ZG performed the design of figures. BN and BZ verified the experimental design. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shang Y, Chen B, Lin C. Consensus tracking control for distributed nonlinear multiagent systems via adaptive neural backstepping approach. IEEE Trans Syst Man, Cybernetics: Syst (2018) 50:2436–44. doi:10.1109/tsmc.2018.2816928

CrossRef Full Text | Google Scholar

2. Xie X, Duan N. Output tracking of high-order stochastic nonlinear systems with application to benchmark mechanical system. IEEE Trans Automatic Control (2010) 55:1197–202. doi:10.1109/tac.2010.2043004

CrossRef Full Text | Google Scholar

3. Li L, Fan M, Xia Y, Zhu C. Recursive distributed fusion estimation for nonlinear stochastic systems with event-triggered feedback. J Franklin Inst (2021) 358:7286–307. doi:10.1016/j.jfranklin.2021.07.036

CrossRef Full Text | Google Scholar

4. Ma H, Zhou Q, Bai L, Liang H. Observer-based adaptive fuzzy fault-tolerant control for stochastic nonstrict-feedback nonlinear systems with input quantization. IEEE Trans Syst Man, Cybernetics: Syst (2018) 49:287–98. doi:10.1109/tsmc.2018.2833872

CrossRef Full Text | Google Scholar

5. Liu H, Li X, Liu X, Wang H. Backstepping-based decentralized bounded-h adaptive neural control for a class of large-scale stochastic nonlinear systems. J Franklin Inst (2019) 356:8049–79. doi:10.1016/j.jfranklin.2019.06.043

CrossRef Full Text | Google Scholar

6. Wang H, Zou Y, Shan L (2017). Adaptive fuzzy control of pure-feedback stochastic nonlinear systems with hysteresis. In Proceedings of the 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS) Dalian, China, July 20147 91–5.

CrossRef Full Text | Google Scholar

7. Niu B, Duan P, Li J, Li X. Adaptive neural tracking control scheme of switched stochastic nonlinear pure-feedback nonlower triangular systems. IEEE Trans Syst Man, Cybernetics: Syst (2019) 51:975–86. doi:10.1109/tsmc.2019.2894745

CrossRef Full Text | Google Scholar

8. Liu Y, Zhu Q. Adaptive neural network finite-time tracking control of full state constrained pure feedback stochastic nonlinear systems. J Franklin Inst (2020) 357:6738–59. doi:10.1016/j.jfranklin.2020.04.048

CrossRef Full Text | Google Scholar

9. Niu B, Li H, Qin T, Karimi HR. Adaptive nn dynamic surface controller design for nonlinear pure-feedback switched systems with time-delays and quantized input. IEEE Trans Syst Man, Cybernetics: Syst (2017) 48:1676–88. doi:10.1109/tsmc.2017.2696710

CrossRef Full Text | Google Scholar

10. Zhang Z, Wen C, Zhao K, Song Y. Decentralized adaptive control of uncertain interconnected systems with triggering state signals. Automatica (2022) 141:110283. doi:10.1016/j.automatica.2022.110283

CrossRef Full Text | Google Scholar

11. Xu L, Wang Y, Wang X, Peng C. Decentralized event-triggered adaptive control for interconnected nonlinear systems with actuator failures. IEEE Trans Fuzzy Syst (2022) 31:148–59. doi:10.1109/tfuzz.2022.3183798

CrossRef Full Text | Google Scholar

12. Hu X, Li Y, Hou Z. Event-triggered fuzzy adaptive fixed-time tracking control for nonlinear systems. IEEE Trans Cybernetics (2020) 52:7206–17. doi:10.1109/tcyb.2020.3035779

CrossRef Full Text | Google Scholar

13. Li Y, Hu X, Che W, Hou Z. Event-based adaptive fuzzy asymptotic tracking control of uncertain nonlinear systems. IEEE Trans Fuzzy Syst (2020) 29:3003–13. doi:10.1109/tfuzz.2020.3010643

CrossRef Full Text | Google Scholar

14. Wang T, Wang N, Qiu J, Buccella C, Cecati C. Adaptive event-triggered control of stochastic nonlinear systems with unknown dead zone. IEEE Trans Fuzzy Syst (2022) 31:138–47. doi:10.1109/tfuzz.2022.3183763

CrossRef Full Text | Google Scholar

15. Song Y, Zhao K, Krstic M. Adaptive control with exponential regulation in the absence of persistent excitation. IEEE Trans Automatic Control (2016) 62:2589–96. doi:10.1109/tac.2016.2599645

CrossRef Full Text | Google Scholar

16. Wang H, Liu PX, Bao J, Xie X-J, Li S. Adaptive neural output-feedback decentralized control for large-scale nonlinear systems with stochastic disturbances. IEEE Trans Neural networks Learn Syst (2019) 31:972–83. doi:10.1109/tnnls.2019.2912082

CrossRef Full Text | Google Scholar

17. Chen C, Liu Z, Xie K, Liu Y, Zhang Y, Chen CP. Adaptive fuzzy asymptotic control of mimo systems with unknown input coefficients via a robust nussbaum gain-based approach. IEEE Trans Fuzzy Syst (2016) 25:1252–63. doi:10.1109/tfuzz.2016.2604848

CrossRef Full Text | Google Scholar

18. Liu S-J, Zhang J-F, Jiang Z-P. Decentralized adaptive output-feedback stabilization for large-scale stochastic nonlinear systems. Automatica (2007) 43:238–51. doi:10.1016/j.automatica.2006.08.028

CrossRef Full Text | Google Scholar

19. Ge SS, Wang C. Adaptive nn control of uncertain nonlinear pure-feedback systems. Automatica (2002) 38:671–82. doi:10.1016/s0005-1098(01)00254-0

CrossRef Full Text | Google Scholar

20. Chen B, Liu XP, Ge SS, Lin C. Adaptive fuzzy control of a class of nonlinear systems by fuzzy approximation approach. IEEE Trans Fuzzy Syst (2012) 20:1012–21. doi:10.1109/tfuzz.2012.2190048

CrossRef Full Text | Google Scholar

21. Wang H, Chen B, Lin C. Approximation-based adaptive fuzzy control for a class of non-strict-feedback stochastic nonlinear systems. Sci China Inf Sci (2014) 57:1–16. doi:10.1007/s11432-013-4785-x

CrossRef Full Text | Google Scholar

22. Chen C, Liu Z, Xie K, Zhang Y, Chen CP. Asymptotic fuzzy neural network control for pure-feedback stochastic systems based on a semi-nussbaum function technique. IEEE Trans Cybernetics (2016) 47:2448–59. doi:10.1109/tcyb.2016.2628182

CrossRef Full Text | Google Scholar

23. Wang M, Zhang S, Chen B, Luo F. Direct adaptive neural control for stabilization of nonlinear time-delay systems. Sci China Inf Sci (2010) 53:800–12. doi:10.1007/s11432-010-0075-z

CrossRef Full Text | Google Scholar

24. Deng H, Krstić M. Stochastic nonlinear stabilization—i: A backstepping design. Syst Control Lett (1997) 32:143–50. doi:10.1016/s0167-6911(97)00068-6

CrossRef Full Text | Google Scholar

25. Polycarpou MM, Ioannou PA (1993). A robust adaptive nonlinear control design. In Proceedings of the 1993 American control conference 1365–9. New Orleans, LA, USA, June 1993

CrossRef Full Text | Google Scholar

26. Kurdila A, Narcowich FJ, Ward JD. Persistency of excitation in identification using radial basis function approximants. SIAM J Control optimization (1995) 33:625–42. doi:10.1137/s0363012992232555

CrossRef Full Text | Google Scholar

27. Wang H, Liu X, Liu K. Robust adaptive neural tracking control for a class of stochastic nonlinear interconnected systems. IEEE Trans Neural Networks Learn Syst (2015) 27:510–23. doi:10.1109/tnnls.2015.2412035

CrossRef Full Text | Google Scholar

28. Yu X, Xie X. Output feedback regulation of stochastic nonlinear systems with stochastic iiss inverse dynamics. IEEE Trans Automatic Control (2009) 55:304–20. doi:10.1109/TAC.2009.2034924

CrossRef Full Text | Google Scholar

29. Wu Z, Cui M, Shi P, Karimi HR. Stability of stochastic nonlinear systems with state-dependent switching. IEEE Trans Automatic Control (2013) 58:1904–18. doi:10.1109/tac.2013.2246094

CrossRef Full Text | Google Scholar