Many-body theory calculations of positron scattering and annihilation in noble-gas atoms via the solution of Bethe–Salpeter equations using the Gaussian-basis code EXCITON+

Scattering phase shifts and annihilation rates for low-energy positrons interacting with noble gas atoms are calculated ab initio using many-body theory implemented in the Gaussian-orbital code EXCITON+. Specifically, we construct the positron–atom correlation potential (self-energy) as the sum of three classes of infinite series describing the screened polarization, virtual positronium formation, and positron-hole repulsion found via the solution of Bethe–Salpeter equations for the two-particle propagators. The normalization of the continuum states is determined using the shifted pseudostates method [A. R. Swann and G. F. Gribakin, Phys. Rev. A 101, 022702 (2020)]. Comparison with the previous sophisticated B-spline many-body approach, which is restricted to atoms [J. Ludlow, D. G. Green, and G. F. Gribakin, Phys. Rev. A 90, 032712 (2014)], validates the EXCITON+ code, which can be used for multicentered targets including molecules, clusters, and condensed matter. Moreover, the relative effects of higher-order diagrams are quantified. It is found that the screening of the electron–positron Coulomb interaction represented by the infinite ring-diagram series (random-phase approximation) is compensated effectively by the additional electron-hole attraction corrections to it (the Bethe–Salpeter equation approximation) and that the use of the screened Coulomb interaction (screened at BSE level) in place of the bare Coulomb interaction in the virtual positronium and positron-hole ladder diagrams has negligible effect on both the phase shifts and Z_eff. Our scattering length for Ne and Kr is in improved agreement with the convergent close-coupling result, and for Ar, the scattering length is in better agreement with the experiment compared with the previous B-spline many-body approach.

1 Introduction

Positrons are unique probes of matter with important applications in medical imaging (positron emission tomography [PET]) [1]; astrophysics (understanding the composition of the galaxy) [2]; materials science as ultrasensitive diagnostics of surfaces, defects, and porosity [3, 4]; molecular spectroscopy [5]; and key to the formation and exploitation of positronium [6, 7] and antihydrogen [8–14], which are used for tests of fundamental symmetries and gravity.

Proper interpretation of the fundamental experiments and materials science experiments, as well as development of the antimatter-based technologies (traps, accumulators, ultra-high energy resolution beams, and next-generation PET), relies on the theoretical understanding of positron interactions with atoms, molecules, and condensed matter. The positron–atom system is, however, characterized by strong many-body correlations [15, 16]. A powerful method that accurately describes positron–electron correlations in a systematic, intuitive, and computationally scalable way is the many-body theory [16–26]. It has provided a full ab initio description of positron scattering and annihilation rates in atoms [16, 18], annihilation γ spectra [27], and positron cooling in noble gas atoms [28, 29], solving a number of long-standing problems. Moreover, the approach enabled ab initio calculations of annihilation vertex enhancement factors that can be used to calculate core annihilation probabilities in condensed matter [24] and also enabled a many-body approach to calculations of Ps-atom scattering and pickoff annihilation [30, 31]. Most recently, we have developed the many-body theory for positron binding [32] in molecules, and extended to non-resonant scattering and annihilation [33] (in the fixed nuclei approximation) using a Gaussian-basis approach that constructed the positron–molecule correlation potential via a solution of the Bethe–Salpeter equations for the two-particle propagators, implemented in our code EXCITON+ [32], which is an extended version of the all-electron EXCITON code of Patterson [34, 35] that additionally handles positrons.

High-quality many-body theory calculations of positron scattering and annihilation in noble gas atoms were performed by Green, Ludlow, and Gribakin in 2014 employing a single-centered B-spline basis approach (which is restricted to atoms) [16]. In that work, the positron–atom correlation potential (self-energy) was calculated (with diagrams constructed from Hartree–Fock states obtained from an atomic code [36]) including the bare polarization diagram Σ⁽²⁾ but included screening corrections at third-order only. Moreover, the virtual positronium contribution Σ^(Γ) was calculated using bare Coulomb interactions in the ladder series. Extrapolation of observable quantities with respect to angular momenta of intermediate states included in the diagram sums was performed. Here, we applied our Gaussian-basis Bethe–Salpeter approach to calculate elastic scattering phase shifts, cross sections, and annihilation rates of positrons with noble gas atoms. The purpose is two-fold: first, comparison with the accurate B-spline results allows verification of the suitability of Gaussian-basis expansion and veracity of the EXCITON+ code (which is also applicable to molecules, clusters, and condensed matter); and second, to quantify the relative effects of the higher-order diagrams omitted in the previous B-spline-based study, including the infinite random-phase approximation and electron-hole attraction corrections to the polarization diagram (so called GW@BSE), and determining the virtual positronium and positron-hole ladder series using dressed Coulomb interactions rather than bare Coulomb interactions.

The outline of the remainder of the paper is as follows. Section 2 gives an overview of the many-body theory and its numerical implementation in the Gaussian-orbital code EXCITON+. Section 3 presents results for helium, neon, argon, and krypton, including scattering phase shifts, cross sections, and annihilation rates, before concluding with a summary.

We use atomic units (a.u.) unless otherwise stated.

2 Theory and numerical implementation

In the many-body theory approach, the positron quasiparticle wavefunction ψ_ɛ of energy ɛ is found from the solution of the Dyson equation [37, 38] as follows:

$\left(H^{\left(0\right)}+{\widehat{\mathrm{\Sigma }}}_{\epsilon }\right){\psi }_{\epsilon }\left(\mathit{r}\right)=\epsilon {\psi }_{\epsilon }\left(\mathit{r}\right),(1)$

where H⁽⁰⁾ is the zeroth-order Hamiltonian, which is taken to be that of the positron in the Hartree–Fock field of the ground-state atom, and ${\widehat{\mathrm{\Sigma }}}_{\epsilon }$ is a non-local, energy-dependent correlation potential (irreducible self-energy of the positron in the field of the atom). The self-energy is expanded in residual electron–electron and electron–positron interactions. Figure 1 shows the three infinite classes of diagrams considered, with the total self-energy given by their sum as Σ = Σ^GW + Σ^Γ + Σ^Λ. The GW diagram [Figure 1A, the product of the positron Green’s function G and the dressed Coulomb interaction W] describes the polarization of the electron cloud by the positron and screening, and electron-hole interaction corrections to it. It can be calculated at the bare (Σ⁽²⁾), random-phase approximation (RPA), time-dependent Hartree–Fock (TDHF), or Bethe–Salpeter equation approximations depending on the kernel K used in the calculation of the electron-hole propagator Π [Figures 1D–F and Figure 2]. In this work, we present results obtained using GW at either Σ⁽²⁾ or the BSE level. Figure 1B shows the infinite ladder series of (either bare or screened) electron–positron interactions, the “Γ-block,” which represents the non-perturbative process of virtual positronium formation. Finally, we also consider the infinite series of (either bare or screened) positron-hole Coulomb interactions Σ^Λ [Figure 1C].

FIGURE 1

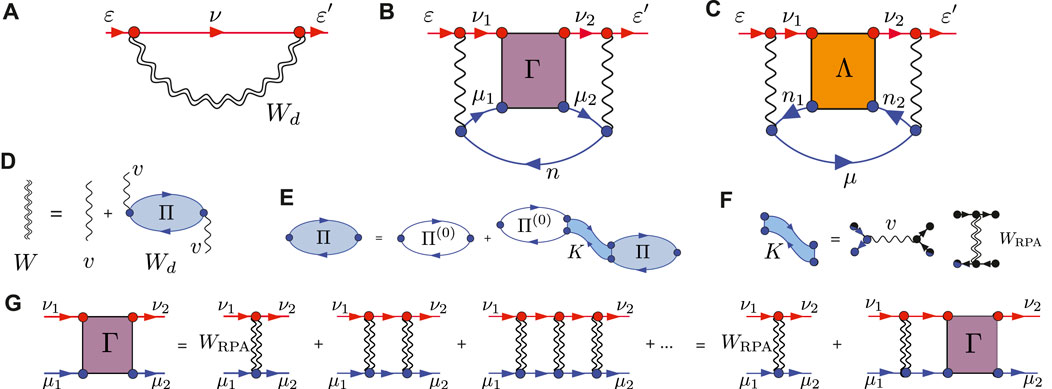
FIGURE 1. Main contributions to the positron–atom self-energy: (A) GW diagram, which describes polarization, and screening and electron-hole interaction corrections to it; (B,C) infinite ladder series of screened electron–positron interactions (“Γ-block”) and positron–hole interactions (“Λ-block”). Lines labeled ν (μ) [(n)] are excited positron (electron) [(hole)] propagators; a single (double) wavy line denotes a bare (dressed) Coulomb interaction. The GW diagram in (A) involves the positron Green’s function G_ν and the dynamic part (due to the absence of an electron–positron exchange interaction) of the screened Coulomb interaction W_d = vΠv, where Π is the electron-hole polarization propagator [see (D)]. It satisfies the Bethe–Salpeter equation [diagram (E)] with kernel K = v − W_RPA [diagram (F)], where W_RPA = v + W_d,RPA is the screened electron–hole Coulomb interaction calculated in the random-phase approximation. Setting K = 0 results in the bare polarization entering W only and gives the Σ⁽²⁾ approximation, so-called as it is a second-order diagram in the electron–positron Coulomb interaction. Setting K = v, the direct part of the Coulomb interaction only, gives the “random-phase approximation” (GW@RPA). Setting K = v − v_exch, i.e., including exchange, which gives rise to interactions within the bubbles and yields the “time-dependent Hartree–Fock” approximation (GW@TDHF). Using screened Coulomb interactions in the exchange term is “Bethe–Salpeter” approximation (GW@BSE). See Figure 2 for more details. Finally, (G) shows the summed infinite ladder diagram series of screened electron–positron interactions, the “Γ block in the virtual positronium contribution in (B).

FIGURE 2

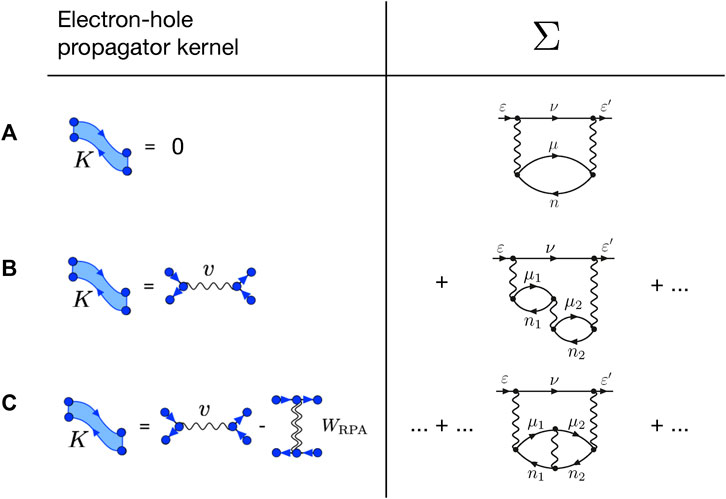
FIGURE 2. Different approximations to the positron GW self-energy diagram [Figure 1A] dependent on the choice of the kernel K of the electron-hole propagator: (A) setting K = 0 reduces the electron-hole propagator to the bare propagator Π⁽⁰⁾ and results in the second-order bare polarization self-energy diagram Σ⁽²⁾; (B) setting K = v, the direct part of the Coulomb interaction only gives in addition to the Σ⁽²⁾ diagram, the infinite series of connected ring diagrams, the random-phase approximation (GW@RPA); (C) setting K = v − v_exch, i.e., including exchange, additionally gives rise to diagrams beyond RPA that include interactions within the rings. When the bare Coulomb interaction is used as the intra-ring interaction, one obtains the time-dependent Hartree–Fock approximation (GW@TDHF). When one instead uses the screened Coulomb interaction W, one obtains the Bethe–Salpeter approximation (GW@BSE).

The EXCITON+ program employs distinct Gaussian-basis sets to expand the electron (−) and positron (+) Hartree–Fock orbitals ${\phi }_a^{\pm }(\mathit{r})$ as ${\phi }_a^{\pm }(\mathit{r})={\sum }_A^{N_c^{\pm }}{\sum }_{k=1}^{N_A^{\pm }}{C}_{aAk}^{\pm }{\chi }_{A_k}^{\pm }(\mathit{r})$, where A labels the $N_c^{\pm }$ basis centers and k labels the $N_A^{\pm }$ different Gaussians on center A, each taken to be of Cartesian type with angular momentum l^x + l^y + l^z, viz., ${\chi }_{A_k}(\mathit{r})={\mathcal{N}}_{A_k}{(x-x_A)}^{l_{Ak}^x}{(y-y_A)}^{l_{Ak}^y}{(z-z_A)}^{l_{Ak}^z}\exp \{-{\zeta }_{Ak}|{\mathbf{r}-\mathbf{r}}_A{|}^2\}$, where ${\mathcal{N}}_{A_k}$ is a normalization constant and C are the expansion coefficients. We use diffuse-function-augmented correlation-consistent polarized aug-cc-pVQZ (TZ on Kr) Dunning basis sets [39–41] centered on atomic nuclei, enabling the accurate determination of the electronic structure including polarizabilities. For the positron, we additionally use a much more diffuse even-tempered basis of the form 19s17p16d15f with exponents for the jth Gaussian for each angular momentum given as ${\zeta }_{Aj}={\zeta }_{A1}{\beta }^{j-1}(j=1,\dots ,N_A^{+l})$, with β = 2 and ζ_A1 = 10⁻⁵ for l = 0 − 1 and ζ_A1 = 10⁻⁴ for l = 2 − 3. Convergence tests were performed, varying ζ_A1, β, $N_A^{+0}$, and l_max for the positron basis on the atoms. Moreover, to more accurately describe the virtual positronium formation process, which takes place away from the atom and requires large angular momentum to resolve the electron–positron distance, for He and Ne, we placed 12 additional hydrogen type aug-cc-pVTZ basis sets symmetrically on a sphere of radius ∼ 1 a.u. from the atom (corresponding to the vertices of a regular icosahedron), and for Ar and Kr, 20 ghosts on a sphere of radius ∼ 2 a.u. (corresponding to the vertices of a regular dodecahedron), finding this to be sufficient for the convergence of the final eigenstates.

2.1 Scattering calculations

For the positron–atom system, the solution of the Dyson equation (Eq. 1) in a Gaussian basis yields a discrete set of n continuum pseudostates of energy ɛ_n, which decay exponentially rather than oscillate at large positron–atom separations, and are normalized to unity instead of to an asymptotic plane wave, as required by a true continuum state. Although these are not true continuum states, they can be used to extract information about positron elastic scattering from the target, as outlined in Swann and Gribakin [42]. First, we determine the s-type pseudostates¹ of a free positron, i.e., eigenstates of the positron kinetic energy Hamiltonian in the Gaussian basis, with energies ${\epsilon }_{n_0}^{(0)}$. Since these energies increase monotonically with n₀ (where n₀ = 1, 2, …), there exists an invertible function f such that

$f_0\left(n_0\right)={\epsilon }_{n_0}^{\left(0\right)}.(2)$

Then, we determine the phase shift for the s-type pseudostates of energy ${\epsilon }_{n_0}$ for the positron in the dressed field of the atom as follows:

${\delta }_0=\left[n_0-f_0^{-1}\left({\epsilon }_{n_0}\right)\right]\pi ,(3)$

where the inverse function $f_0^{-1}$ is constructed by the interpolation of integer n₀ against ${\epsilon }_{n_0}^{(0)}$. In practice, for even-tempered Gaussian-basis sets, the energies ${\epsilon }_{n_0}^{(0)}$ and ${\epsilon }_{n_0}$ grow approximately exponentially with n₀. It is, therefore, easier to determine function g by the interpolation of n₀ vs. $\ln ({\epsilon }_{n_0}^{(0)})$, making $g(\ln ({\epsilon }_{n_0}))=f_0^{-1}({\epsilon }_{n_0})$, which is nearly linear. The phase shift for positron energy ${\epsilon }_{n_0}$ is then given by

${\delta }_0=\left[n_0-g\left(\ln \left({\epsilon }_{n_0}\right)\right)\right]\pi .(4)$

The same procedure is used for p- and d-type pseudostates, utilizing p- and d-type free positron pseudostates to form invertible functions f₁(n₁) and f₂(n₂).

Since ${\widehat{\mathrm{\Sigma }}}_E$ depends on the energy E of the pseudostate involved and the pseudostate energies are not known a priori, we first calculate Σ_E on a dense energy grid and interpolate to the energy of the pseudostate. For all of our calculations, we use a linear energy mesh for the self-energy, typically using 30 points between 0 and 0.3 a.u. We also tested a denser exponential energy mesh but found negligible improvement in accuracy, owing to the weak energy (E) dependence of the eigenvalues.

In addition to scattering phase shifts, we determined the scattering length a from the effective-range expansion of the s-wave phase shift for momenta $k=\sqrt{2\epsilon }\to 0$ [43], independently fitting to each of

$k\cot {\delta }_0=-\frac{1}{a}+\frac{\pi \alpha }{3a^2}k,(\mathrm{5a})$

$k\cot {\delta }_0=-\frac{1}{a}+\frac{\pi \alpha }{3a^2}k+C_1{k}^2\ln C_{2}k,(\mathrm{5b})$

$\tan {\delta }_0=-ak{\left[1-\frac{\pi \alpha k}{3a}-\frac{4\alpha k^2}{3}\ln \left(C\frac{\sqrt{\alpha }k}{4}\right)\right]}^{-1},(\mathrm{5c})$

${\delta }_0=-ak-\frac{\pi \alpha k^2}{3}-\frac{4a\alpha k^3}{3}\ln \left(\frac{\sqrt{\alpha }k}{4}\right)+C{k}^3,(\mathrm{5d})$

where α is the static dipole polarizability of the atom determined by EXCITON+ at the BSE level of theory and C, C₁, and C₂ are constants. We use the first four or five lowest energy discrete datapoints of δ₀(k) for fitting. Finally, the elastic scattering cross section is obtained as a sum over the partial waves l = 0, 1, 2 (s, p, d − waves), which dominate at low positron energies [44]:

${\sigma }_{\text{el}}=\frac{4\pi }{k^2}{\displaystyle \sum _{l=0}^2}\left(2l+1\right){\sin }^2{\delta }_l\left(k\right).(6)$

2.2 Annihilation rates

For a gas of number density n_g, the positron annihilation rate is parametrized as $\lambda =\pi r_0^{2}c{n}_g{Z}_{\text{eff}}$, where r₀ is the classical electron radius, c is the speed of light, and Z_eff is the effective number of electrons that participate in the annihilation process. Formally, Z_eff is equal to the electron density at the positron,

$Z_{\text{eff}}\left(k\right)=\int {\displaystyle \sum _{i=1}^{N_e}}\delta \left(\mathit{r}-{\mathit{r}}_i\right)|{\mathrm{\Psi }}_{\mathbf{k}}\left({\mathit{r}}_1,\dots ,{\mathit{r}}_{N_e},\mathit{r}\right){|}^{2}d{\mathbf{r}}_1\dots d{\mathbf{r}}_{N_e}d\mathbf{r},(7)$

where Ψ_k is the total wavefunction of the system, with the electron coordinate r_i and positron coordinate r. It describes the scattering of the positron of momentum k by the atom and is normalized asymptotically to the product of the ground-state target atomic wavefunction and positron plane wave. Using the finite basis approach, it can be approximated by [42] Z_eff = 4πδ_epA⁻², with the normalization factor $A^2={(2l+1)}^{-1}2\sqrt{2\epsilon }\pi d\epsilon /dn$ [42], and the annihilation contact density in the independent-particle approximation is as follows:

${\delta }_{\text{ep}}=2{\displaystyle \sum _{i=1}^{N_e/2}}{\gamma }_i\int |{\phi }_i\left(\mathit{r}\right){|}^2|\psi \left(\mathit{r}\right){|}^{2}d\mathbf{r}.(8)$

The summation in Eq. 8 runs over all occupied electronic orbitals φ_i, including vertex enhancement factors ${\gamma }_i=1+\sqrt{1.31/|{\epsilon }_i|}+{\left(0.834/|{\epsilon }_i|\right)}^{2.15}$ for orbital i with energy ɛ_i (in a.u.) that account for the effects of short-range electron–positron Coulomb attraction [24, 27]. The integral in Eq. 8 is calculated as a four-centered overlap integral over pairs of electron and positron basis functions ${\chi }_i^{\pm }(\mathit{r}){\chi }_j^{\pm }(\mathit{r})$. To speed up calculations and reduce the memory cost, we employ density fitting (DF), which involves approximating the electronic density using N_aux auxiliary (corresponding aug-cc-pVTZ or QZ type) basis functions ${\{{\tilde{\chi }}_{\mu }^{-}(\mathit{r})\}}_{\mu =1}^{N_{\text{aux}}}$ such that ${\chi }_i^{-}(\mathit{r}){\chi }_j^{-}(\mathit{r})\approx {\sum }_{\mu }{d}_{\mu }^{i,j}{\tilde{\chi }}_{\mu }^{-}(\mathit{r})$ with optimal fitting coefficients $d_{\mu }^{i,j}$ determined using the Coulomb metric [35, 45–49]. The use of DF reduces four-centered integrals (which for basis size N requires memory ∼ N⁴) to products of three-centered integrals and matrix elements of the Coulomb operator in the auxiliary basis (of order N²N_aux, where N_aux ≳ N). We found DF implementation gives results within 0.5% of the exact calculation.

When analyzing the results of the many-body calculations, it is instructive to consider the physically motivated form of the s-wave Z_eff at low momenta k [16, 50]

$Z_{\text{eff}}\left(k\right)=\frac{F}{{\kappa }^2+k^2+A{k}^4}+B,(9)$

where F, B, A and κ are constants. We also compute the Maxwellian average Z_eff at room temperature:

${\bar{Z}}_{\text{eff}}={\int }_0^{\infty }{Z}_{\text{eff}}\left(k\right)\frac{\exp \left(-k^2/2k_{B}T\right)}{{\left(2\pi k_{B}T\right)}^{3/2}}4\pi k^{2}dk,(10)$

where k_B is the Boltzmann constant and k_BT = 9.28 × 10⁻⁴ a.u. at room temperature T = 293 K.

3 Results

3.1 Positron scattering on noble gas atoms

3.1.1 Benchmarking the Gaussian-basis approach against previous B-spline many-body theory calculations

First, we benchmark our method against the previous B-spline atomic MBT [16] at Σ⁽²⁾ and Σ^(2+Γ) levels of theory². Figure 3 shows comparisons of the s-, p-, and d-wave scattering phase shifts for the noble gas sequence He–Kr (He and Ne shown on top panels, and Ar and Kr shown on bottom panels). Overall, there is very good agreement. The Σ⁽²⁾ results are in excellent agreement, validating the Gaussian-basis many-body implementation and its combination with the shifted pseudostate method. The present Σ^(2+Γ) results are, in some cases, slightly less positive compared to the B-spline reference. Accurate calculation of the virtual positronium formation contribution to the correlation potential is perhaps the most challenging aspect of positron–atom calculations. In the previous atomic MBT B-spline method [16], B-spline basis functions were used for the expansion of the radial part of the positron wavefunction with angular integrations carried out analytically (via diagrammatic angular momentum algebra), reducing the numerics to a one-dimensional problem. Moreover, extrapolation to infinite angular momenta in the intermediate sums was performed via well-defined extrapolation formula (Eqs 22, 23 in [16]). In contrast, our Gaussian-basis approach is three-dimensional, currently making no use of the spherical symmetry, i.e., we use all the non-symmetry-adapted states at once; thus, the convergence with respect to the basis set size is relatively slower. Moreover, we do not perform an extrapolation to a complete basis set limit but only perform convergence checks by increasing the number of virtual states by adding multiple ghost centers, as explained previously. Agreement could be improved by including larger angular momentum functions in the Gaussian-basis approach³. With these considerations in mind, the overall agreement of the current Gaussian-basis implementation in EXCITON+ and the previous B-spline reference Σ^(2+Γ) results are excellent.

FIGURE 3

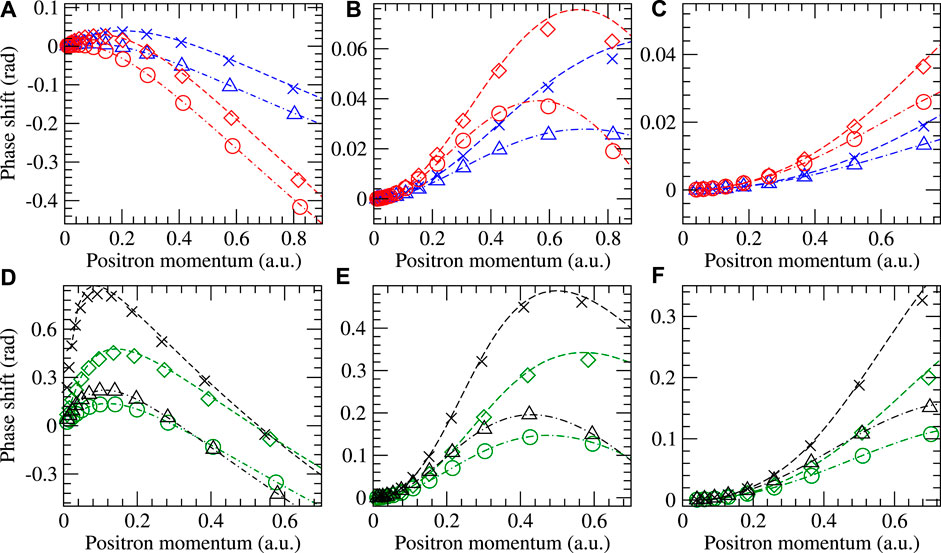
FIGURE 3. Comparison of the present calculated scattering phase shifts (symbols) with previous MBT B-spline results (lines) [16]. Panels (A–C) show s-, p-, and d-wave positron scattering phase shifts, respectively, for both helium (blue) and neon (red). Panels (D–F) show that for argon (green) and krypton (black). The present Σ⁽²⁾ results from EXCITON+ are shown as circles (Ne and Ar) and triangles (He and Kr), with the previous B-spline results shown as dot-dashed lines. The present Σ^(2+Γ) results from EXCITON+ are shown as diamonds (Ne and Ar) and crosses (He and Kr), with the previous B-spline results shown as dashed lines.

3.1.2 Effect of higher-order diagrams

With the EXCITON+ implementation validated, we now go beyond the previous B-spline study and consider the relative effects of higher-order diagrams, including Bethe–Salpeter equation treatment of screening of the electron–positron Coulomb interaction, and screening corrections to the ladder series in Γ and the inclusion of the Λ block (Figure 1).

Elastic scattering phase shifts for the noble gas atoms are shown in Figure 4 for different approximations: HF, Σ⁽²⁾, Σ^BSE, Σ^BSE+Γ, and Σ^BSE+Γ+Λ, with three alternative treatments of Γ and Λ terms: using unscreened (bare) Coulomb interaction; using screened Coulomb interaction; and using screened Coulomb interaction and GW instead of HF energies in the energy denominators (see also Table 1 for scattering lengths). For the ease of comparison, we also show in Figure 4 the previous B-spline MBT calculations, which were calculated at the Σ^2+3+Γ level, i.e., including the second-order bare polarization diagram, third-order screening diagrams, and the virtual positronium formation contribution. The general features of the phase shifts as functions of the positron momentum k are mostly the same for all studied atoms. In HF approximation, the phase shifts are negative and linear, indicating a repulsive electrostatic field, as expected for positrons. Inclusion of the second-order polarization diagram, Σ⁽²⁾ makes the phase shifts positive at low k, reaching a maximum and then fall off with increasing k and passing through zero (Ramsauer–Townsend effect). Going from Σ⁽²⁾ to GW@BSE increases the low-energy positive phase shifts for He and Ne; there is little difference between them in Ar, and the opposite is found in Kr. Compared to Σ⁽²⁾, GW@BSE includes, on one hand, the infinite random-phase approximation ring series of screening diagrams, and on the other hand, intra-ring attractive electron-hole dressed Coulomb interactions. Thus, we find that for the smaller atoms, the intra-ring electron-hole attractions give a larger effect than the repulsive screening effects from the ring series. The latter only start to dominate in krypton [Figure 4J]. The inclusion of virtual positronium (Σ^Γ) significantly increases the phase shifts of the BSE calculations by nearly a factor of 3 at the peak values. The inclusion of positron-hole repulsion (Σ^Λ) reduces the overall phase shifts, sitting between the results of BSE and BSE+Γ. There are also multiple ways to treat Σ^Γ and Σ^Λ (see [32] for more details): using screened interactions in the ladders reduces the strength of the dominant virtual positronium diagram and correspondingly reduces the phase shifts, but by a small amount. The effect of the screened ladders are, however, compensated and almost cancelled by the introduction of GW electronic energies in place of the HF energies in the construction of the diagrams. Overall, we find the full Σ^BSE+Γ+Λ results in good agreement with the Σ^2+3+Γ B-spline results across all atoms and partial waves, although our current results typically sit higher than the B-spline results. Given that our approach slightly underestimates the virtual positronium contribution, as discussed in the previous section, the overall effect of the higher-order diagrams has been to increase the strength of the attractive positron–atom potential. This has resulted from a delicate balance of attractive polarization, screening via the random phase approximation, intra-ring electron-hole attractive corrections to screening, attraction from the virtual positronium block, and repulsion from the positron-hole block.

FIGURE 4

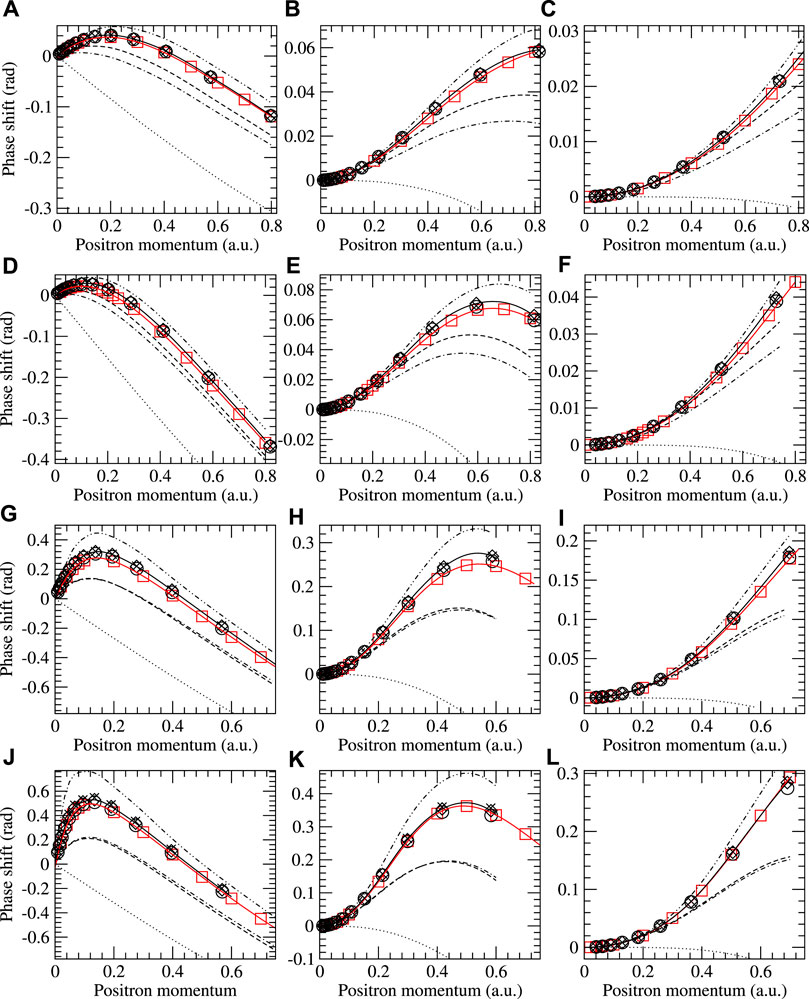
FIGURE 4. Scattering phase shifts for positron on helium (A–C), neon (D–F), argon (G–I), and krypton (J–L) with s- (A,D,G,J), p- (B,E,H,K), and d-wave (C,F,I,L) results shown. Previous MBT B-spline results [16] (red squares) and current MBT results with different approximations: HF (dotted lines), Σ⁽²⁾ (dot-dashed lines), Σ^BSE (dashed lines), Σ^BSE+Γ (dot-dot-dashed lines), and Σ^BSE+Γ+Λ with three alternative treatments of Γ and Λ terms: crosses, using unscreened (bare) Coulomb interaction; circles, using screened Coulomb interaction; and our most sophisticated approximation: solid lines with diamonds, using the screened Coulomb interaction and GW instead of HF energies in the energy denominators of the diagrams.

TABLE 1

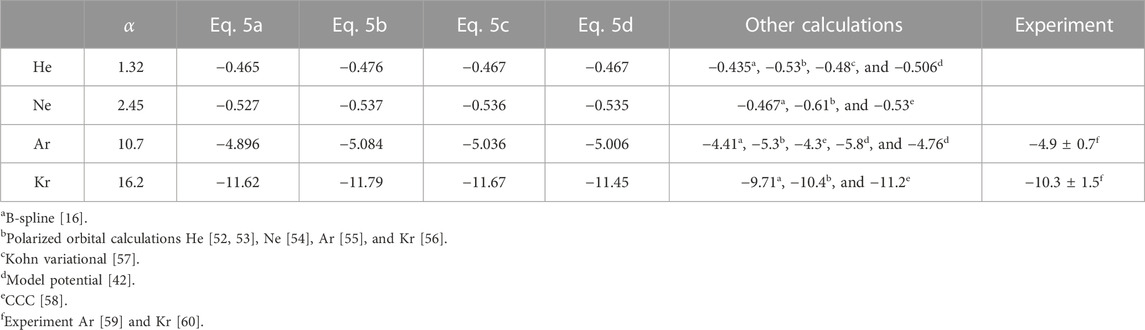
TABLE 1. Scattering lengths a (a.u.) at the Σ^BSE+Γ+Λ level of theory for the noble gas–atom sequence He–Kr determined using the fitting equations in Eq. 5. Here, α is the static dipole polarizability in a.u. computed at the BSE level of theory.

Table 1 compares the scattering lengths extracted from the s-wave phase shifts with other theoretical and experimental results. The scattering length increases along the noble gas atom sequence. The results of the fits to Eqs. 5a–d all agree within 5%. For neon and krypton, we observe very good agreement (notably closer than the previous B-spline result) with the convergent close-coupling (CCC) calculations [58]. Otherwise, our present results tend to be of larger magnitude than other theoretical predictions, including the previous many-body theory calculations [16]. The scattering length of argon is in better agreement (and within the error bars) with the experimental result [59], while the result for krypton is of slightly larger magnitude but within error bars of the measurement [60].

Although it is more illuminating to compare the results of the different self-energy approximations at the level of phase shifts, in panels A–D in Figure 5, for completeness, we also show the s-, p-, and d-wave partial-wave contributions to the elastic scattering cross section for He and their sum, using different approximations and corresponding to the phase shift results in Figure 4A–C. The HF s-wave cross section stands out as weakly energy-dependent and much larger than those calculated with higher-order approximations. Furthermore, one can see that the effect of the virtual positronium diagram with respect to Σ⁽²⁾ or BSE is to increase the s-wave cross section at energies below approximately 2.5 eV and decrease it above that threshold. For p- and d-waves, the cross sections closely mirror the phase shift data in Figures 4B, C. Our total elastic scattering cross sections for He–Kr are compared with previous results in Figure 5E, Figure 6–8, respectively. Of the theoretical reference data, our results are in very good overall agreement with, although slightly larger at small energy than, the previous B-spline MBT method [16]. For He and Ne, there is also close agreement with recent experimental measurements of [70, 75], which are recommended as the best in recent reviews [78, 79]. It should be noted that the Ramsauer–Townsend minimum, which is very prominent in He and Ne, is not visible in Ar and Kr. This is due to the shift of the minimum in the s-wave scattering cross section toward higher energies, where it combines with p and d partial wave contributions to produce a characteristic plateau in the cross section, which stretches from approximately 2 eV to 8–10 eV. For Ar, the present MBT results are very similar to the previous B-spline MBT, although slightly larger at small energy, and in good agreement with the CCC calculations [58] and more recent measurements of Refs. [59] and [70]. For Kr, the present results are in good agreement with the measurements of [77] at small energy and in good agreement with the CCC calculations. At the larger energies, where the higher partial waves contribute, our calculations are likely to be underconverged compared with the atomic B-spline MBT calculations, and thus underestimate experiment.

FIGURE 5

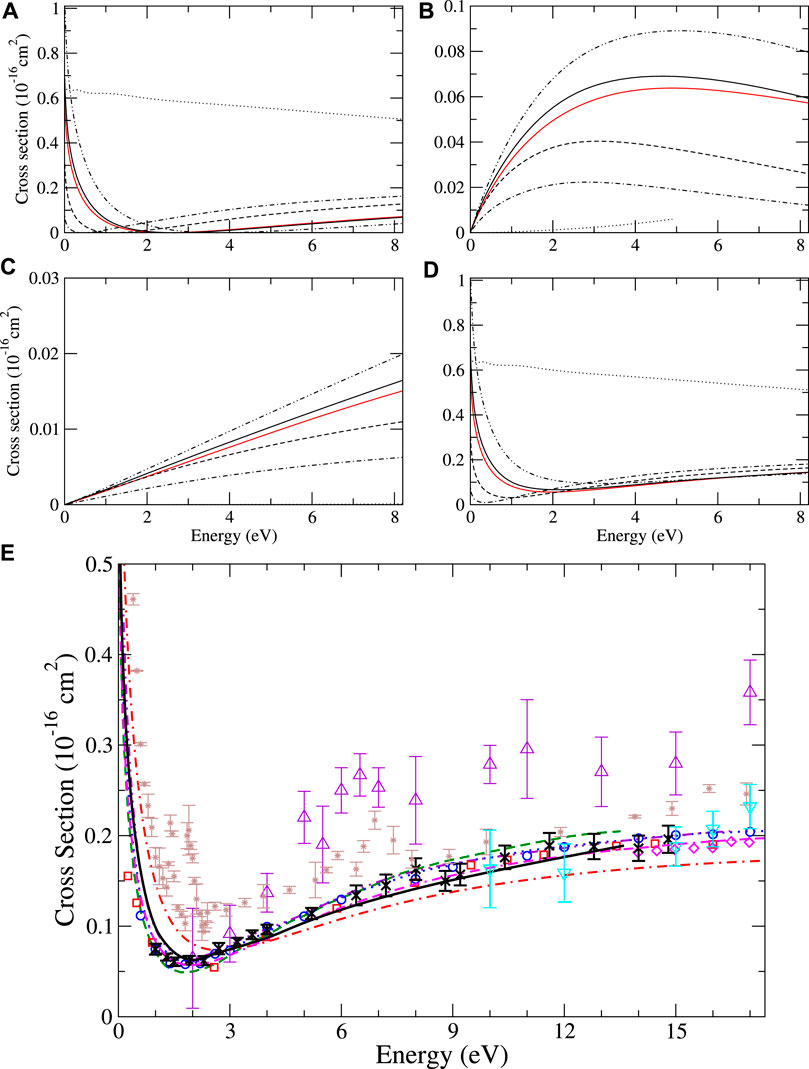
FIGURE 5. Elastic scattering cross sections for helium. Partial s-, p-, and d-wave contributions (A–C), and their sum (D), calculated presently using MBT in different approximations: HF (dotted lines), Σ⁽²⁾ (dot-dashed lines), Σ^BSE (dashed lines), Σ^BSE+Γ (dot-dot-dashed lines), and Σ^BSE+Γ+Λ, our most sophisticated approximation (solid lines). Previous MBT B-spline results [16] are shown as the red line. (E) Comparison of theory and the experiment. Previous calculations: present many-body theory (black solid line); previous B-spline MBT [16] (magenta dot-dash-dashed); polarized orbital [52, 53] (red dot-dashed); previous MBPT of [17] (green dashed); CCC [61] (blue dotted); and Kohn variational [62] (purple dot-dot-dashed). Experiment: [63] (red squares); [64] (blue circles); [65] (brown stars); [66] (magenta diamonds); [67] (black crosses); [68] (purple triangles up); and [69] (cyan triangles down).

FIGURE 6

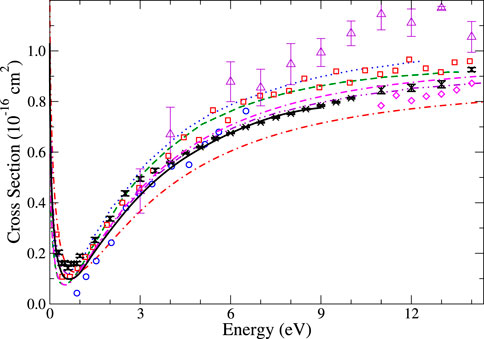
FIGURE 6. Elastic scattering cross section for neon. Theory: present many-body theory (solid black line); B-spline MBT [16] (magenta dot-dash-dashed); polarized orbital [54] (red dot-dashed); previous MBPT of [17] (green dashed); CCC [58] (blue dotted); and relativistic polarized orbital [70] (purple dot-dot-dashed). Experiment: [63] (red squares); [71] (blue circles); [66] (magenta diamonds); [70] (black crosses); and [72] (purple triangles).

FIGURE 7

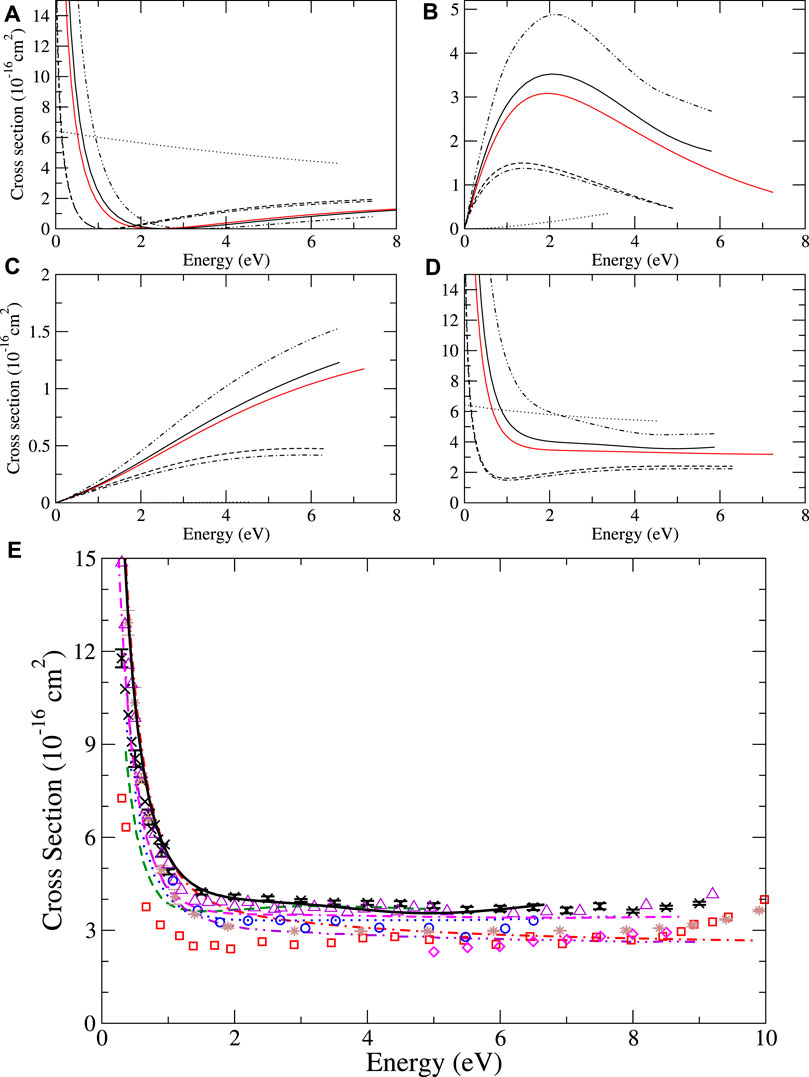
FIGURE 7. Elastic scattering cross section for argon. Partial s-, p-, and d-wave contributions (A–C), and their sum (D), calculated presently using MBT in different approximations: HF (dotted lines), Σ⁽²⁾ (dot-dashed lines), Σ^BSE (dashed lines), Σ^BSE+Γ (dot-dot-dashed lines), and Σ^BSE+Γ+Λ, our most sophisticated approximation (solid lines). Previous MBT B-spline results [16] are shown as the red line; (E) Comparison of theory and experiment. Previous calculations: present MBT (black solid line), B-spline MBT [16] (magenta dot-dash-dashed line), polarized orbital [55] (red dot-dashed line), previous MBPT of [17] (green dashed line), CCC [58] (blue dotted line), and relativistic polarized orbital [70] (purple dot-dot-dashed line). Experiment: [73] (red squares), [71] (blue circles), [74] (brown stars), [66] (magenta diamonds), [59] (purple up triangles), and [70] (black crosses).

FIGURE 8

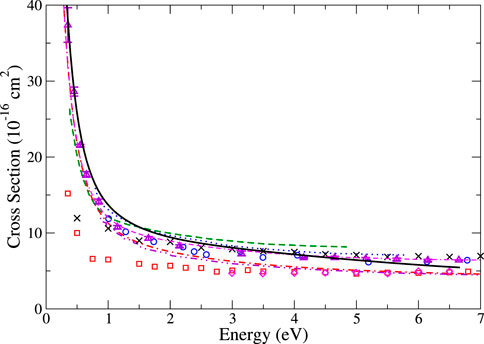
FIGURE 8. Elastic scattering cross section for krypton. Theory: present many-body theory (black solid line), B-spline [16] (magenta dot-dash-dashed line), polarized orbital [56] (red dot-dashed line), previous MBPT of [17] (green dashed line), CCC [58] (blue dotted line), and relativistic polarized orbital [75] (purple dot-dot-dashed line). Experiments: [76] (red squares), [71] (blue circles), [66] (magenta diamonds), [77] (purple up triangles), and [75] (black crosses).

3.2 Positron annihilation on noble gas atoms

Figure 9 shows Z_eff calculated for s-wave positron on He using the zeroth-order annihilation vertex [setting the enhancement factor γ_i = 1 in Eq. 8] for different approximations of the positron Dyson wave function: calculated at HF, Σ⁽²⁾ and Σ^2+Γ from the present Gaussian-based approach and the previous B-spline MBT approach. The HF results are in excellent agreement, confirming the veracity of the Gaussian basis combined with shifted pseudostate method (including the use of density fitting for the integrals, as described previously). The Σ⁽²⁾ and Σ^2+Γ annihilation rates are in good agreement, although the Gaussian-basis results are slightly smaller than the B-spline results, mirroring what was found previously for the phase shifts. Regardless, we can here assess the relative effect of the higher-order diagrams on Z_eff.

FIGURE 9

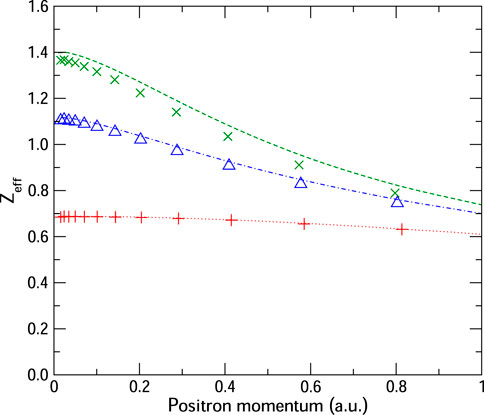
FIGURE 9. Normalized annihilation rate Z_eff for s-wave positron on He calculated in the independent-particle model vertex, i.e., using enhancement factors γ_i set to unity (Eq. 8), in different approximations to the positron wavefunction: Hartree–Fock (red), Σ² (blue), and Σ^2+Γ (green) approximations to the Dyson positron wavefunction, calculated using the present Gaussian-basis approach (symbols) and previous B-spline results (lines) [16].

Figures 10–13 show the s-, p-, and d-wave partial-wave contributions to the total momentum-dependent positron annihilation rate Z_eff for the sequence He–Kr. It should be noted that at low-positron momenta k, the s-wave contribution always dominates and the annihilation rates increase as one moves along the noble-gas sequence. The second-order diagram Σ⁽²⁾ provides the largest contribution to the s-wave Z_eff at low momenta for all atoms except for krypton. In all atoms except for helium, the BSE approximation lowers Σ⁽²⁾ Z_eff due to screening of electron-hole interactions. For helium p- and d-waves, the higher-order MBT diagrams modify Z_eff only slightly. The virtual positronium diagram increases the annihilation rates significantly, and it becomes more important as the atom size increases. In argon and krypton, it contributes more to low-energy Z_eff than the second-order Σ⁽²⁾ diagram (see [16] for more details). Finally, the positron-hole ladder series diagram decreases Z_eff in all cases. We found that (static) screening of the ladder diagrams has a negligible effect on the Z_eff results. Specifically, using dressed instead of bare Coulomb interactions in the ladders results in $<1\%$ decrease in ${\bar{Z}}_{\text{eff}}$ for He and Ne, and 6% and 10% decrease for Ar and Kr, respectively. However, using dressed (GW) energies instead of HF energies in the screening kernel mostly cancels out these changes (to within 2%). When compared with the previous B-spline results, our s-wave results are noticeably larger for all of the atoms. The opposite is true for d-wave and p-wave results (with the exception of neon). This is reflected in the total Z_eff results, with the current MBT results being higher at low k, but B-spline being higher as k increases (with the exception of neon, where the difference between the s-wave results are too much for the additional partial waves to overcome). When compared with the semi-empirical results of Ref. [84], He and Ne match the shape well but are noticeably larger (5% for He and 20% for Ne), Ar stays within 15%, and Kr matches the shape well but is about 25% lower.

FIGURE 10

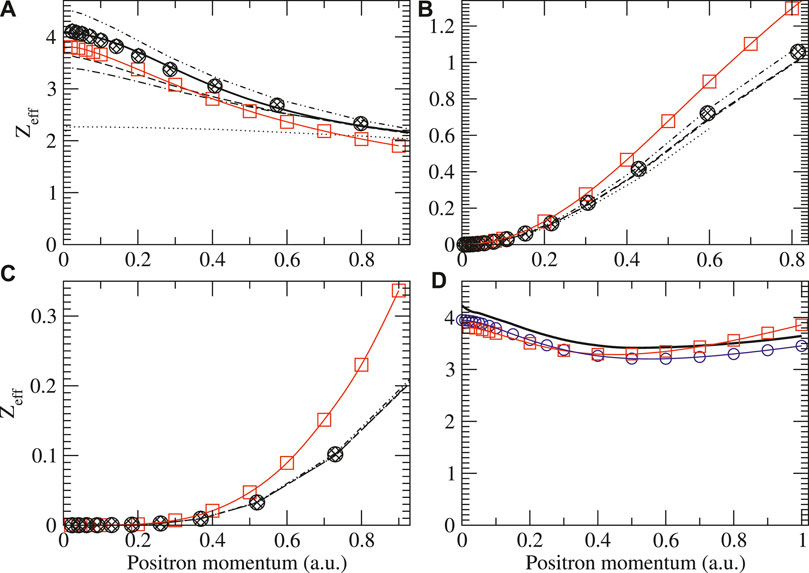
FIGURE 10. Z_eff for positrons on helium showing the s (A), p (B), and d (C) wave contributions to the total (D). Legend is the same as in Figure 4 with the addition of total results by Ref. [84] (blue circles). For the s-wave results, the solid line is the fit based in Eq. 9 and the parameters in Table 2.

FIGURE 11

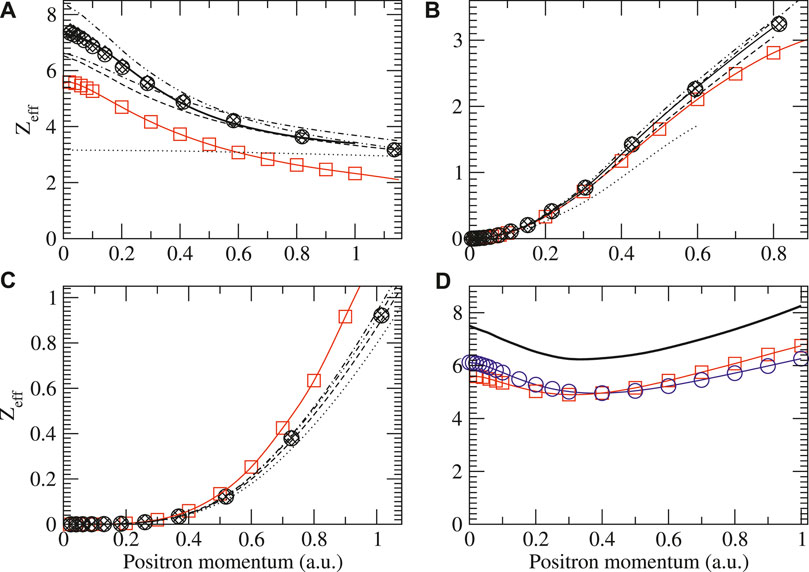
FIGURE 11. Z_eff for positrons on neon showing the s (A), p (B), and d (C) wave contributions to the total (D). Legend is the same as in Figure 4 with the addition of total results by Ref. [84] (blue circles). For the s-wave results, the solid line is the fit based on Eq. 9 and the parameters in Table 2.

FIGURE 12

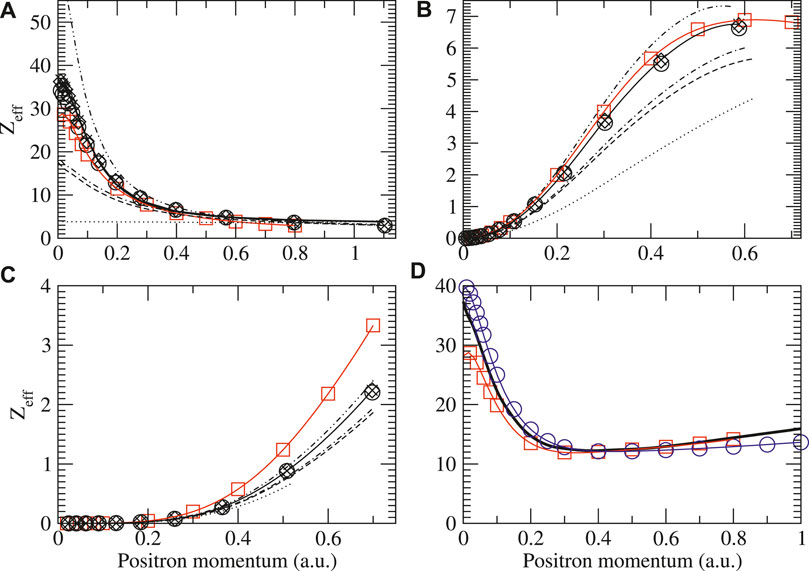
FIGURE 12. Z_eff for positrons on argon showing the s (A), p (B), and d (C) wave contributions to the total (D). Legend is the same as in Figure 4 with the addition of total results by Ref. [84] (blue circles). For the s-wave results, the solid line is the fit based on Eq. 9 and the parameters in Table 2.

FIGURE 13

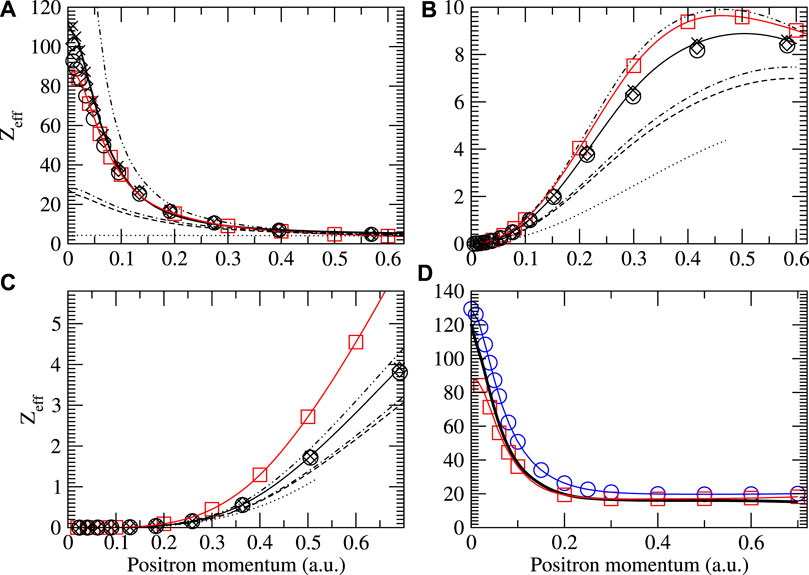
FIGURE 13. Z_eff for positrons on krypton showing the s (A), p (B), and d (C) wave contributions to the total (D). Legend is the same as in Figure 4 with the addition of total results by Ref. [84] (blue circles). For the s-wave results, the solid line is the fit based in Eq. 9 and the parameters in Table 2.

Table 2 shows the values of Z_eff at room temperature (k = 0.053 a.u.) and thermally averaged values using the fit in Eq. 9 for our best calculation (BSE + Γ + Λ) compared with the previous results. Overall, our thermalized Z_eff results tend to be higher than the previous theoretical data. Notably, the agreement with previous MBT results [16] is worse than in the case of phase shift results. This could be due to the (energy-dependent) enhancement factors that approximate the annihilation vertex correction. We note that a proper ab initio description of the annihilation vertex is beyond current capabilities of our approach. The calculated thermally averaged annihilation rate ${\bar{Z}}_{\text{eff}}$ is in excellent accord with a previous measurement of [81] for He (within 2.8%), while for neon, argon, and krypton, we calculate ${\bar{Z}}_{\text{eff}}$ values that are 20%, 16%, and 12% larger than measurements of [81, 82], respectively. However, our ${\bar{Z}}_{\text{eff}}$ results for Ar and Kr are lower than positron trap measurements of [83] by 8% and 18%, respectively.

TABLE 2

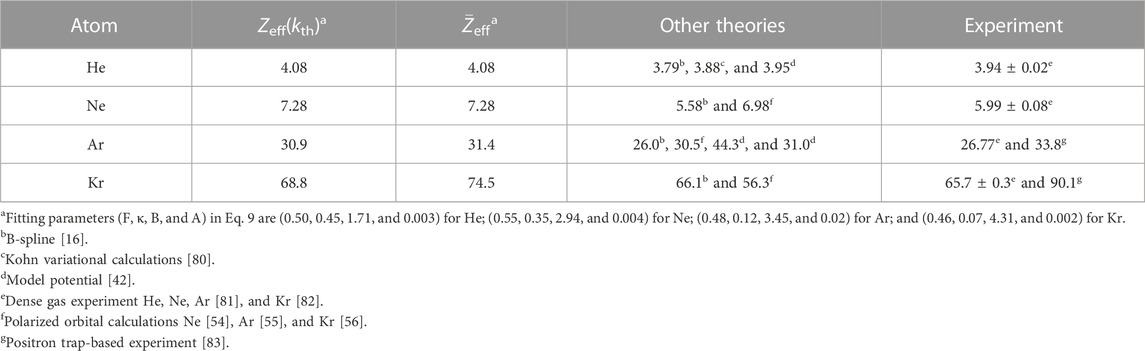
TABLE 2. Annihilation rates Z_eff both at room temperature and thermally averaged for noble gas atoms at the Σ^BSE+Γ+Λ level of theory, using enhancement factors to account for the short-range electron–positron attraction, compared with other theories and experiments.

4 Summary

Many-body theory calculations of positron scattering and annihilation in the noble gas atoms have been performed, using a Gaussian-basis approach implemented in the EXCITON+ program [32] combined with the recent shifted pseudostate method of [42]. The veracity of the EXCITON+ code was confirmed by comparing the scattering phase shifts calculated using bare polarization, and additionally including virtual positronium formation, with the previous atomic B-spline MBT method [16]. The previous B-spline approach included self-energy diagrams up to third order and additionally the infinite ladder series of electron–positron interactions that describe the virtual positronium contribution to the positron–atom correlation potential. We considered the relative effects of higher-order diagrams, going beyond the previous B-spline approach, including e.g., the infinite random-phase series of ring diagrams, dressed with intra-ring electron hole interactions, known as GW@BSE, calculated by solving the Bethe–Salpeter equation for the electron-hole propagator. We found that the screening of the infinite series of ring diagrams (random-phase approximation) was compensated by the electron-hole intra-ring attraction corrections (BSE) to it. We also found that using screened Coulomb interactions in the ladder series for the virtual positronium contribution and positron-hole interactions had negligible effects. The importance of the electron-hole intra-ring attraction leads to phase shifts that are larger than those calculated in the B-spline approach for all the atoms considered. For Ne and Kr, our calculated scattering length is in better agreement with the CCC [58] calculations than the previous B-spline MBT results, and for Ar, we find a scattering length in better agreement with the experiment, and ${\bar{Z}}_{\text{eff}}$ in better agreement with the trap-based measurement [83]. For Kr, our ${\bar{Z}}_{\text{eff}}$ is larger than the previous B-spline calculation and dense gas experiment [81] but is closer to the trap-based measurement [83]. Overall, as the various higher-order diagrams act to somewhat compensate, our results for the scattering lengths and Z_eff are in reasonable agreement with the previous B-spline values.

Ultimately, the spherical symmetry of the positron–atom problem is better suited for the B-spline approach, in which angular integrations can be carried out analytically. The present study, however, has demonstrated that the strong positron–atom and positron–electron many-body correlations can be described via a Gaussian-basis approach. The importance of the latter is that it can be used to calculate positron scattering and annihilation on molecules, clusters, and condensed matter, the multicentered nature of which makes a single-centered B-spline basis unsuitable.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.

Author contributions

JH and CR implemented the scattering and Z_eff routines incorporating the approach of [42] in the EXCITON+ many-body code developed by JH, CR, BC, and DG, based on the EXCITON all-electron code of Patterson [34, 35]. JH and CR performed the EXCITON+ calculations and data analysis. DW performed additional B-spline calculations. DG conceived and supervised the work. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the European Research Council, StG 804383 “ANTI-ATOM,” and used the Northern Ireland High-Performance Computing service funded by EPSRC (EP/T022175).

Acknowledgments

The authors thank Jack Cassidy, Sarah Gregg, Gleb Gribakin, Charles Patterson, and Andrew Swann for useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In selecting the s-type states, we look for states with L² < 1, i.e., l < 0.6. For p-type states, 1 < L² < 3, i.e., 0.6 < l < 1.3 and for d-type functions, 5 < L² < 7, i.e., 1.8 < l < 2.2.

²Both methods can calculate the self-energy at these levels, and so, they provide for faithful comparisons. Beyond those levels, the present method and B-spline calculations diverge in how they include screening effects, e.g., the B-spline method accounts only for third-order screening diagrams, while the current approach calculates the infinite ring series (random-phase approximation) and corrections to it, via a solution of the Bethe–Salpeter equation for the dressed electron-hole propagator.

³Including higher angular momentum functions is a major challenge: see the discussion in [51], where an efficient algorithm was recently proposed for 4-centered integrals only (i.e., not including 3-centered integrals, which are central to the density-fitting approach we use).

References

1. Wahal RL. Principles and practice of positron emission tomography. Philadelphia: Lippincott, Williams and Wilkins (2008).

Google Scholar

2. Prantzos N, Boehm C, Bykov A, Diehl R, Ferrière K, Guessoum N, et al. The 511 kev emission from positron annihilation in the galaxy. Rev Mod Phys (2011) 83:1001–56. doi:10.1103/RevModPhys.83.1001

CrossRef Full Text | Google Scholar

3. Tuomisto F, Makkonen I. Defect identification in semiconductors with positron annihilation: Experiment and theory. Rev Mod Phys (2013) 85:1583–631. doi:10.1103/RevModPhys.85.1583

CrossRef Full Text | Google Scholar

4. Hugenschmidt C. Positrons in surface physics. Surf Sci Rep (2016) 71:547–94. doi:10.1016/j.surfrep.2016.09.002

CrossRef Full Text | Google Scholar

5. Gribakin GF, Young JA, Surko CM. Positron-molecule interactions: Resonant attachment, annihilation, and bound states. Rev Mod Phys (2010) 82:2557–607. doi:10.1103/RevModPhys.82.2557

CrossRef Full Text | Google Scholar

6. Brawley SJ, Armitage S, Beale J, Leslie DE, Williams AI, Laricchia G. Electron-like scattering of positronium. Science (2010) 330:789. doi:10.1126/science.1192322

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Cassidy DB. Experimental progress in positronium laser physics. Eur J Phys D (2018) 72:53. doi:10.1140/epjd/e2018-80721-y

CrossRef Full Text | Google Scholar

8. Andresen GB, Ashkezari MD, Baquero-Ruiz M, Bertsche W, Bowe PD, Butler E, et al. Trapped antihydrogen. Nature (2010) 468:673–6. doi:10.1038/nature09610

PubMed Abstract | CrossRef Full Text | Google Scholar

9. collaboration TA. Confinement of antihydrogen for 1,000 seconds. Nat Phys (2011) 7:558–64. doi:10.1038/nphys2025

CrossRef Full Text | Google Scholar

10. Amole C, Ashkezari MD, Baquero-Ruiz M, Bertsche W, Butler E, Capra A, et al. An experimental limit on the charge of antihydrogen. Nat Comm (2014) 5:3955. doi:10.1038/ncomms4955

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Pérez P, Banerjee D, Biraben F, Brook-Roberge D, Charlton M, Cladé P, et al. The GBAR antimatter gravity experiment. Hyperfine Interact (2015) 233:21–7. doi:10.1007/s10751-015-1154-8

CrossRef Full Text | Google Scholar

12. Malbrunot C, Amsler C, Arguedas Cuendis S, Breuker H, Dupre P, Fleck M, et al. The asacusa antihydrogen and hydrogen program: Results and prospects. Philos Trans Roy Soc A (2018) 376:20170273. doi:10.1098/rsta.2017.0273

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Baker CJ, Bertsche W, Capra A, Cesar CL, Charlton M, Mathad AC, et al. Sympathetic cooling of positrons to cryogenic temperatures for antihydrogen production. Nat Commun (2021) 12:6139. doi:10.1038/s41467-021-26086-1

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Amsler C, Antonello M, Belov A, Bonomi G, Brusa RS, Caccia M, et al. Pulsed production of antihydrogen. Comm Phys (2021) 4:19. doi:10.1038/s42005-020-00494-z

CrossRef Full Text | Google Scholar

15. Surko CM, Gribakin GF, Buckman SJ. Low-energy positron interactions with atoms and molecules. J Phys B: Atomic, Mol Opt Phys (2005) 38:R57–R126. –R126. doi:10.1088/0953-4075/38/6/r01

CrossRef Full Text | Google Scholar

16. Green DG, Ludlow JA, Gribakin GF. Positron scattering and annihilation on noble-gas atoms. Phys Rev A (2014) 90:032712. doi:10.1103/PhysRevA.90.032712

CrossRef Full Text | Google Scholar

17. Dzuba VA, Flambaum VV, Gribakin GF, King WA. Many-body calculations of positron scattering and annihilation from noble-gas atoms. J Phys B (1996) 29:3151–75. doi:10.1088/0953-4075/29/14/024

CrossRef Full Text | Google Scholar

18. Gribakin GF, Ludlow J. Many-body theory of positron-atom interactions. Phys Rev A (2004) 70:032720. doi:10.1103/PhysRevA.70.032720

CrossRef Full Text | Google Scholar

19. Müller M, Cederbaum LS. Many-body theory of composite electronic-positronic systems. Phys Rev A (1990) 42:170–83. doi:10.1103/PhysRevA.42.170

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cederbaum LS. Optical potentials for elastic and inelastic scattering of non-electronic projectiles from electronic targets. Few-Body Syst (1996) 21:211–25. doi:10.1007/s006010050048

CrossRef Full Text | Google Scholar

21. Amusia MY, Cherepkov NA, Chernysheva LV. Elastic scattering of slow positrons on atoms. J Exp Theor Phys (2003) 97:34–41. doi:10.1134/1.1600794

CrossRef Full Text | Google Scholar

22. Bartlett RJ, Musiał M. Coupled-cluster theory in quantum chemistry. Rev Mod Phys (2007) 79:291–352. doi:10.1103/RevModPhys.79.291

CrossRef Full Text | Google Scholar

23. Dzuba VA, Flambaum VV, Gribakin GF. Detecting positron-atom bound states through resonant annihilation. Phys Rev Lett (2010) 105:203401. doi:10.1103/PhysRevLett.105.203401

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Green DG, Gribakin GF. Enhancement factors for positron annihilation on valence and core orbitals of noble-gas atoms. Concepts, Methods Appl Quan Syst Chem Phys Prog. Theor. Chem. Phys. (2018) 31:243. doi:10.1007/978-3-319-74582-4_14

CrossRef Full Text | Google Scholar

25. Amusia MY, Dolmatov VK, Chernysheva LV. Positron elastic scattering by a semifilled-shell atom. J Phys B (2021) 54:185003. doi:10.1088/1361-6455/ac2e49

CrossRef Full Text | Google Scholar

26. Cheng Y, Tang LY, Mitroy J, Safronova MS. All-order relativistic many-body theory of low-energy electron-atom scattering. Phys Rev A (2014) 89:012701. doi:10.1103/PhysRevA.89.012701

CrossRef Full Text | Google Scholar

27. Green DG, Gribakin GF. γ spectra and enhancement factors for positron annihilation with core electrons. Phys Rev Lett (2015) 114:093201. doi:10.1103/PhysRevLett.114.093201

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Green DG. Positron cooling and annihilation in noble gases. Phys Rev Lett (2017) 119:203403. doi:10.1103/PhysRevLett.119.203403

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Green DG. Probing positron cooling in noble gases via annihilation γ spectra. Phys Rev Lett (2017) 119:203404. doi:10.1103/PhysRevLett.119.203404

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Green DG, Swann AR, Gribakin GF. Many-body theory for positronium-atom interactions. Phys Rev Lett (2018) 120:183402. doi:10.1103/PhysRevLett.120.183402

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Swann AR, Green DG, Gribakin GF. Many-body theory of positronium scattering and pickoff annihilation in noble-gas atoms. Phys Rev A (2023) 107:042802. doi:10.1103/PhysRevA.107.042802

CrossRef Full Text | Google Scholar

32. Hofierka J, Cunningham B, Rawlins CM, Patterson CH, Green DG. Many-body theory of positron binding to polyatomic molecules. Nature (2022) 606:688–93. doi:10.1038/s41586-022-04703-3

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hofierka J, Rawlins CM, Cunningham B, Patterson CH, Green DG. Many-body theory calculations of positron scattering and annihilation in H2, N2, and CH4. Phys Rev Lett (2023) 130:263001. doi:10.1103/PhysRevLett.130.263001

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Patterson CH. Photoabsorption spectra of small Na clusters: TDHF and BSE versus CI and experiment. Phys Rev Mat (2019) 3:043804. doi:10.1103/PhysRevMaterials.3.043804

CrossRef Full Text | Google Scholar

35. Patterson CH. Density fitting in periodic systems: Application to TDHF in diamond and oxides. J Chem Phys (2020) 153:064107. doi:10.1063/5.0014106

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Waide DT, Green DG, Gribakin GF. BSHF: A program to solve the Hartree–Fock equations for arbitrary central potentials using a B-spline basis. Comp Phys Commun (2020) 250:107112. doi:10.1016/j.cpc.2019.107112

CrossRef Full Text | Google Scholar

37. Dickhoff WH, Neck DV. Many-body theory exposed! - propagator description of quantum mechanics in many-body systems. 2nd ed. Singapore: World Scientific (2008).

Google Scholar

38. Fetter AL, Walecka JD. Quantum theory of many-particle systems. New York: Dover (2003).

Google Scholar

39. Dunning TH. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J Chem Phys (1989) 90:1007–23. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

40. Woon DE, Dunning TH. Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J Chem Phys (1994) 100:2975–88. doi:10.1063/1.466439

CrossRef Full Text | Google Scholar

41. Kendall RA, Dunning TH, Harrison RJ. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J Chem Phys (1992) 96:6796–806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

42. Swann AR, Gribakin GF. Model-potential calculations of positron binding, scattering, and annihilation for atoms and small molecules using a Gaussian basis. Phys Rev A (2020) 101:022702. doi:10.1103/PhysRevA.101.022702

CrossRef Full Text | Google Scholar

43. Spruch L, O’Malley TF, Rosenberg L. Modification of effective-range theory in the presence of a long-range potential. Phys Rev Lett (1960) 5:375–7. doi:10.1103/PhysRevLett.5.375

CrossRef Full Text | Google Scholar

44. Landau LD, Lifshitz EM. Quantum mechanics (Non-relativistic theory) - third edition - course of theoretical Physics. Oxford: Pergamon (1977).

Google Scholar

45. Whitten JL. Coulombic potential energy integrals and approximations. J Chem Phys (1973) 58:4496–501. doi:10.1063/1.1679012

CrossRef Full Text | Google Scholar

46. Dunlap BI, Connolly JWD, Sabin JR. On the applicability of LCAO-Xα methods to molecules containing transition metal atoms: The nickel atom and nickel hydride. Int J Quan Chem. (1977) 12:81–7. doi:10.1002/qua.560120813

CrossRef Full Text | Google Scholar

47. Dunlap BI, Connolly JWD, Sabin JR. On some approximations in applications of Xα theory. J Chem Phys (1979) 71:3396–402. doi:10.1063/1.438728

CrossRef Full Text | Google Scholar

48. Baerends E, Ellis D, Ros P. Self-consistent molecular Hartree-Fock-Slater calculations I. The computational procedure. Chem Phys (1973) 2:41–51. doi:10.1016/0301-0104(73)80059-X

CrossRef Full Text | Google Scholar

49. Vahtras O, Almlöf J, Feyereisen M. Integral approximations for LCAO-SCF calculations. Chem Phys Lett (1993) 213:514–8. doi:10.1016/0009-2614(93)89151-7

CrossRef Full Text | Google Scholar

50. Gribakin GF. Mechanisms of positron annihilation on molecules. Phys Rev A (2000) 61:022720. doi:10.1103/PhysRevA.61.022720

CrossRef Full Text | Google Scholar

51. Asadchev A, Valeev EF. High-performance evaluation of high angular momentum 4-center Gaussian integrals on modern accelerated processors (2023). arXiv:2307.03452

Google Scholar

52. McEachran RP, Ryman AG, Stauffer AD, Morgan DL. Positron scattering from noble gases. J Phys B (1977) 10:663–77. doi:10.1088/0022-3700/10/4/018

CrossRef Full Text | Google Scholar

53. McEachran RP, Morgan DL, Ryman AG, Stauffer AD. Positron scattering from noble gases: corrected results for helium. J Phys B (1978) 11:951–3. doi:10.1088/0022-3700/11/5/527

CrossRef Full Text | Google Scholar

54. McEachran RP, Ryman AG, Stauffer AD. Positron scattering from neon. J Phys B (1978) 11:551–61. doi:10.1088/0022-3700/11/3/025

CrossRef Full Text | Google Scholar

55. McEachran RP, Ryman AG, Stauffer AD. Positron scattering from argon. J Phys B (1979) 12:1031. doi:10.1088/0022-3700/12/6/019

CrossRef Full Text | Google Scholar

56. McEachran RP, Stauffer AD, Campbell LEM. Positron scattering from krypton and xenon. J Phys B (1980) 13:1281–92. doi:10.1088/0022-3700/13/6/030

CrossRef Full Text | Google Scholar

57. Campeanu RI, Humberston JW. The scattering of s-wave positrons by helium. J Phys B (1977) 10:L153–8. –L158. doi:10.1088/0022-3700/10/5/007

CrossRef Full Text | Google Scholar

58. Fursa DV, Bray I. Convergent close-coupling method for positron scattering from noble gases. New J Phys (2012) 14:035002. doi:10.1088/1367-2630/14/3/035002

CrossRef Full Text | Google Scholar

59. Zecca A, Chiari L, Trainotti E, Fursa DV, Bray I, Sarkar A, et al. Positron scattering from argon: total cross sections and the scattering length. J Phys B (2011) 45:015203. doi:10.1088/0953-4075/45/1/015203

CrossRef Full Text | Google Scholar

60. Zecca A, Chiari L, Trainotti E, Fursa DV, Bray I, Brunger MJ. Experimental determination of the scattering length for positron scattering from krypton. Eur Phys J D (2011) 64:317–21. doi:10.1140/epjd/e2011-20333-7

CrossRef Full Text | Google Scholar

61. Wu H, Bray I, Fursa DV, Stelbovics AT. Low-energy positron–helium convergent close coupling calculations. J Phys B (2003) 37:L1–6. doi:10.1088/0953-4075/37/1/L01

CrossRef Full Text | Google Scholar

62. Reeth PV, Humberston JW. Elastic scattering and positronium formation in low-energy positron-helium collisions. J Phys B (1999) 32:3651–67. doi:10.1088/0953-4075/32/15/303

CrossRef Full Text | Google Scholar

63. Stein TS, Kauppila WE, Pol V, Smart JH, Jesion G. Measurements of total scattering cross sections for low-energy positrons and electrons colliding with helium and neon atoms. Phys Rev A (1978) 17:1600–8. doi:10.1103/PhysRevA.17.1600

CrossRef Full Text | Google Scholar

64. Mizogawa T, Nakayama Y, Kawaratani T, Tosaki M. Precise measurements of positron-helium total cross sections from 0.6 to 22 ev. Phys Rev A (1985) 31:2171–9. doi:10.1103/PhysRevA.31.2171

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Karwasz GP, Pliszka D, Zecca A, Brusa RS. Positron scattering in helium: Virtual-positronium resonances. Nucl Instr Methods Phys Res B (2005) 240:666–74. doi:10.1016/j.nimb.2005.04.115

CrossRef Full Text | Google Scholar

66. Jay PM, Coleman PG. Coupling between positronium formation and elastic positron-scattering channels in the rare gases. Phys Rev A (2010) 82:012701. doi:10.1103/PhysRevA.82.012701

CrossRef Full Text | Google Scholar

67. Sullivan JP, Makochekanwa C, Jones A, Caradonna P, Buckman SJ. High-resolution, low-energy positron scattering from helium: measurements of the total scattering cross section. J Phys B (2008) 41:081001. doi:10.1088/0953-4075/41/8/081001

CrossRef Full Text | Google Scholar

68. Nagumo K, Nitta Y, Hoshino M, Tanaka H, Nagashima Y. Measurements of total cross sections for positron scattering from he under magnetic-field-free conditions using an electrostatic high-brightness slow positron beam system. J Phys Soc Jpn (2011) 80:064301. doi:10.1143/JPSJ.80.064301

CrossRef Full Text | Google Scholar

69. Fayer SE, Loreti A, Andersen SL, Kover A, Laricchia G. Magnetic field-free measurements of the total cross section for positrons scattering from helium and krypton. J Phys B (2016) 49:075202. doi:10.1088/0953-4075/49/7/075202

CrossRef Full Text | Google Scholar

70. Jones ACL, Makochekanwa C, Caradonna P, Slaughter DS, Machacek JR, McEachran RP, et al. Positron scattering from neon and argon. Phys Rev A (2011) 83:032701. doi:10.1103/PhysRevA.83.032701

CrossRef Full Text | Google Scholar

71. Sinapius G, Raith W, Wilson WG. Scattering of low-energy positrons from noble-gas atoms. J Phys B (1980) 13:4079–90. doi:10.1088/0022-3700/13/20/020

CrossRef Full Text | Google Scholar

72. Nagumo K, Nitta Y, Hoshino M, Tanaka H, Nagashima Y. Magnetic-field-free measurements of the total cross sections for positron scattering from neon. Eur Phys J D (2012) 66:81. doi:10.1140/epjd/e2012-20624-5

CrossRef Full Text | Google Scholar

73. Kauppila WE, Stein TS, Jesion G. Direct observation of a Ramsauer-Townsend effect in positron-argon collisions. Phys Rev Lett (1976) 36:580–4. doi:10.1103/PhysRevLett.36.580

CrossRef Full Text | Google Scholar

74. Karwasz G, Pliszka D, Brusa R. Total cross sections for positron scattering in argon, nitrogen and hydrogen below 20ev. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2006) 247:68–74. doi:10.1016/j.nimb.2006.01.065

CrossRef Full Text | Google Scholar

75. Makochekanwa C, Machacek JR, Jones ACL, Caradonna P, Slaughter DS, McEachran RP, et al. Low-energy positron interactions with krypton. Phys Rev A (2011) 83:032721. doi:10.1103/PhysRevA.83.032721

CrossRef Full Text | Google Scholar

76. Dababneh MS, Kauppila WE, Downing JP, Laperriere F, Pol V, Smart JH, et al. Measurements of total scattering cross sections for low-energy positrons and electrons colliding with krypton and xenon. Phys Rev A (1980) 22:1872–7. doi:10.1103/PhysRevA.22.1872

CrossRef Full Text | Google Scholar

77. Zecca A, Chiari L, Sarkar A, Brunger MJ. Positron scattering from the isoelectronic molecules n2, co and c2h2. New J Phys (2011) 13:115001. doi:10.1088/1367-2630/13/11/115001

CrossRef Full Text | Google Scholar

78. Chiari L, Zecca A. Recent positron-atom cross section measurements and calculations. Eur Phys J D (2014) 68:297. doi:10.1140/epjd/e2014-50436-4

CrossRef Full Text | Google Scholar

79. Ratnavelu K, Brunger MJ, Buckman SJ. Recommended positron scattering cross sections for atomic systems. J Phys Chem Ref Data (2019) 48:023102. doi:10.1063/1.5089638

CrossRef Full Text | Google Scholar

80. Reeth PV, Humberston JW, Iwata K, Greaves RG, Surko CM. Annihilation in low-energy positron - helium scattering. J Phys B (1996) 29:L465–71. doi:10.1088/0953-4075/29/12/004

CrossRef Full Text | Google Scholar

81. Coleman PG, Griffith TC, Heyland GR, Killeen TL. Positron lifetime spectra for the noble gases. J Phys B (1975) 8:1734–43. doi:10.1088/0022-3700/8/10/021

CrossRef Full Text | Google Scholar

82. Wright GL, Charlton M, Griffith TC, Heyland GR. The annihilation of positrons and positronium formation in gaseous Kr and Xe. J Phys B (1985) 18:4327–47. doi:10.1088/0022-3700/18/21/019

CrossRef Full Text | Google Scholar

83. Iwata K, Greaves RG, Murphy TJ, Tinkle MD, Surko CM. Measurements of positron-annihilation rates on molecules. Phys Rev A (1995) 51:473–87. doi:10.1103/PhysRevA.51.473

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Mitroy J, Ivanov IA. Semiempirical model of positron scattering and annihilation. Phys Rev A (2002) 65:042705. doi:10.1103/PhysRevA.65.042705

CrossRef Full Text | Google Scholar