A switchable terahertz metamaterial absorber between ultra-broadband and dual bands

Based on the phase change properties of vanadium dioxide (VO₂), we propose a terahertz metamaterial absorber that can be switched flexibly between ultra-broadband and dual bands. The absorber consists of a resonator array above a conductive ground layer separated with a dielectric spacer, which includes four square-loop VO₂ resonators and a crossed gold resonator in each unit cell. By changing the conductivity of VO₂ through thermal control, the absorber can achieve the switching between ultra-broadband absorption and dual-band absorption. Simulation results show that at high temperature, the absorber realizes more than 90% absorption bandwidth in the range of 3.98 to 9.06 THz, which can be elucidated by the wave-interference theory and impedance matching theory. At low temperature, up to 95% of the dual-band absorption occurs at 5.95 and 6.95 THz, which originates the dipole mode and nonlocal surface-Bloch mode of metal resonators. In addition, the absorber has the advantages of polarization-independence and wide-angle absorption. Compared with previous studies, our design can switch between two absorption modes and its absorption performance is greatly improved. The proposed absorber design scheme is expected to expand terahertz devices and enable a variety of applications in the terahertz range, such as modulation, sensing, stealth, and switching devices.

1 Introduction

Terahertz (THz) technology, usually in the frequency range from 0.1 to 10 THz, has a wide range of potential applications in the fields of sensing, imaging, and communication, due to its distinctive features such as high security, strong penetration, high temporal resolution and low background noise [1–5]. However, due to the lack of natural materials with strong responses to THz waves, the full development and utilization of THz technology are greatly limited. Over the past dozen years, through the design of artificial metamaterial, many novel phenomena have been brought from the visible to the microwave bands [6–9]. The size of metaatom can control the response frequency of metamaterial, which provides a tremendous impetus for the development of THz technology [10–13]. Various THz functional devices based on metamaterials have been proposed, such as THz filters [14–16], THz absorbers [17–19], and THz polarization converters [20–22]. Among these functional devices, THz metamaterial absorbers (TMAs), as one of the key elements in the THz detection system, have attracted much attention. With the advantages of strong absorption, thin thickness, and light mass, TMAs have potential applications in thermal emitters [23–25], photovoltaic cells [26–28], and stealth technologies [29–31].

The first demonstration of TMAs was achieved in 2008 [32]. Subsequently, various high-performance TMAs were proposed, including polarization-independent absorption [33, 34], multi-band absorption or broadband absorption [17, 35], high absorption under wide-angle incidence [36, 37], etc. Once the structural parameters are determined in these TMA schemes, the absorption performance of TMAs cannot be changed, greatly limiting their practical application. Recently, TMAs combining functional materials have been proposed, including semiconductors [17, 38], liquid crystals [39–41], graphene [42–44], and phase-change materials (PCMs) [45–47], achieving the tunability of TMAs, which meets the development needs of THz absorbers.

PCMs now are widely used for their fast and reversible switching between two atomic states, which can be triggered by heat, light or electricity. One of the most commonly used PCMs is vanadium dioxide (VO₂). It exhibits reversible phase transition behavior between the insulator phase and the metallic phase [48], which facilitates allowing smaller effective lengths and reducing power consumption compared to other commonly used PCMs [47, 49]. The phase transition from insulator to metal can be tuned by increasing the temperature, accompanied by a steady increase in the conductivity of VO₂ from 2 × 10² S/m to 2 × 10⁵ S/m [50, 51]. Conversely, it can be tuned by cooling down, with the conductivity decreasing. Due to the flexibility of this electromagnetic characteristic modulation, some temperature-controlled tunable TMAs based on VO₂ have been proposed [52–55]. However, these TMA schemes focus more on broadband absorption performance at high temperatures, with little absorption effect at low temperatures, resulting in a single functionality. Functionally switchable TMAs can greatly expand their own available scenarios, in line with current development trends to address the scarcity of THz devices.

Recently, some VO₂-based TMAs integrated with PCMs or noble metals have been developed to achieve efficient absorption [43], beam steering [56], polarization conversion [21, 57], and electromagnetically induced transparency [58] at low temperatures. However, these designs increase the complexity of the structure or require simultaneous consideration of the phase transition conditions of other PCMs. Unlike previously reported studies, in this paper, we propose a TMA with simple structural design and polarization-independence that can be switched flexibly between ultra-broadband and dual bands by changing the conductivity of VO₂ through thermal control. The TMA consists of a resonator array above a conductive ground layer separated with a dielectric spacer, which includes four square-loop VO₂ resonators and a crossed gold (Au) resonator in each unit cell. When VO₂ is in the completely metallic state at high temperature, the TMA realizes more than 90% absorption bandwidth in the range of 3.98 to 9.06 THz which can be elucidated by the wave-interference theory and impedance matching theory. At low temperature where VO₂ is fully insulated, up to 95% of the dual-band absorption occurs at 5.95 and 6.95 THz, which originates the dipole mode and nonlocal surface-Bloch mode of metal resonators. Compared with previous studies, our design can switch between two absorption modes and its absorption performance is greatly improved. Meanwhile, the TMA has the advantages of simple structure, polarization-independence and wide-angle absorption. The proposed TMA design scheme is expected to expand THz devices and enable a variety of applications in the THz range, such as modulation, sensing, stealth, and switching devices.

2 Design and methods

The unit cell structure of the designed switchable TMA is shown in Figure 1. It consists of a resonator array above an Au conductive ground layer separated with a polyimide (PI) dielectric spacer, which includes four square-loop VO₂ resonators and a crossed Au resonator. As shown in Figure 1A, the period of the unit cell structure is P. The thickness of the resonators is t₁ for the Au resonator and t₂ for the four VO₂ resonators, respectively, and the thickness of the PI spacer is h. For the Au resonator, the length of the cross is l and the width is w, located in the middle of the resonator layer of each unit cell as shown in Figure 1B. Around it are four square-loop VO₂ resonators. Their side length is P₁, and the width of each side is w₁. The spacing between the VO₂ resonators in both x- and y-directions is d. The detailed structural parameters are set as: p = 40 μm, t₁ = 0.1 μm, t₂ = 0.2 μm, h = 6.4 μm, l = 12.5 μm, w = 1.1 μm, P₁ = 11.7 μm, w₁ = 1 μm, and d = 10.1 μm.

FIGURE 1

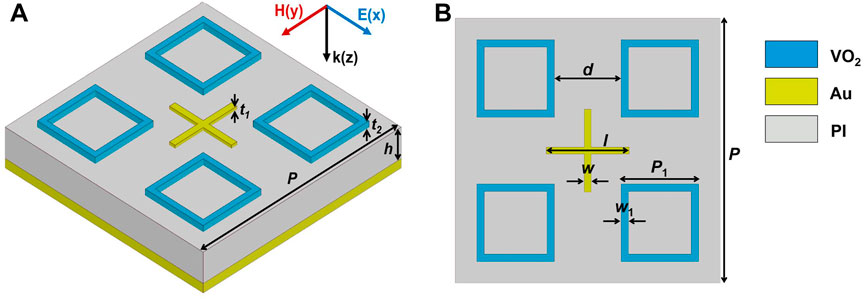
FIGURE 1. Schematic of the unit cell of the designed TMA under (A) the bird’s eye view and (B) the top view.

The electromagnetic response of the designed TMA is simulated by the finite element method (FEM). Periodic boundary conditions are applied in both x- and y-directions, and two perfectly matching layers are used in the z-direction to eliminate spurious reflections caused by any impedance mismatch at the two boundaries. In the simulation, the relative permittivity of PI is 3 with the loss angle tangent δ = 0.03 [59]. Due to the inherent loss of materials, it is helpful to improve the absorption performance of the designed TMA [60]. The relative permittivity of Au in the THz range can be described by the Drude dispersion model [61],

${\epsilon }_{\mathrm{A}\mathrm{u}}=1-\frac{{{\omega }_{\rho }}^2}{\left({\omega }^2+i{\gamma }_{\mathrm{A}\mathrm{u}}\omega \right)}(1)$

where the plasma frequency ω_ρ = 1.37 × 10¹⁶ rad/s, and the collision frequency γ_Au = 4.05 × 10¹³ rad/s [61]. Similarly, the dielectric dispersion of VO₂ in the THz range can also be expressed by the Drude model but with Lorentz correction [46],

${\epsilon }_{\mathrm{V}{\mathrm{O}}_{\mathrm{2}}}={\epsilon }_{\infty }-\frac{{{\omega }_{\rho }}^2\left(\sigma \right)}{\left({\omega }^2+i{\gamma }_{\mathrm{V}{\mathrm{O}}_{\mathrm{2}}}\omega \right)}(2)$

where ɛ_∞ = 12 is the high-frequency contribution to the relative permittivity, and the collision frequency ${\gamma }_{\mathrm{V}{\mathrm{O}}_{\mathrm{2}}}=5.75\times 10^{13}$ rad/s [46]. The plasma frequency of VO₂ is related to its conductivity σ, which can be expressed as [46],

${{\omega }_{\rho }}^2\left(\sigma \right)=\frac{\sigma }{{\sigma }_0}{{\omega }_{\rho }}^2\left({\sigma }_0\right)(3)$

where the fitted parameters σ₀ = 3 × 10⁵ S/m and ω_ρ(σ₀) = 1.4 × 10¹⁵ rad/s can match the dispersion measured in the experiment [46]. There is a thermal hysteresis line for the change in conductivity of VO₂, as shown in Figure 2. The conductivity of VO₂ can change rapidly with temperature heating or cooling, regardless of the speed of environmental temperature changes with negligible commutation time [62]. When the temperature rises from 298 K to 358 K, the conductivity increases from 2 × 10² S/m to 2 × 10⁵ S/m, corresponding to its phase transition from a complete insulator state to a fully metallic state [50, 51]. The phase transition is reversible. The opposite transition occurs when the temperature decreases, corresponding to a variation in conductivity between 2 × 10⁵ S/m (358 K) to 2 × 10² S/m (298 K).

FIGURE 2

FIGURE 2. Conductivity of VO₂ with temperature.

The absorbance A(ω), reflectance R(ω) and transmittance T(ω) can be calculated by the S-parameters obtained from the frequency domain solver in the FEM. The absorption equation can be expressed as,

$A\left(\omega \right)=1-R\left(\omega \right)-T\left(\omega \right)=1-{\left|S_{11}\left(\omega \right)\right|}^2-{\left|S_{21}\left(\omega \right)\right|}^2(4)$

where S₁₁ω) represents the reflectivity, and S₂₁ω) represents the transmissivity. In the simulation, the thickness of the conductive ground layer is greater than the skin depth of THz wave, resulting in a transmissivity of approximately 0. Thus, the absorbance A(ω) can be simplified as,

$A\left(\omega \right)=1-{\left|S_{11}\left(\omega \right)\right|}^2(5)$

3 Results and discussion

The simulated absorption and reflection spectra of the designed TMA are shown in Figure 3. When in a high-temperature state (358 K), VO₂ is in a completely metallic phase. At this time, the THz spectral response of the proposed TMA under normal incidence is shown in Figure 3A. The TMA has an absorption rate of more than 90% in the ultra-broadband range of 3.98 to 9.06 THz, with a bandwidth exceeding 5 THz. The THz spectral response of TMA under normal incidence at a temperature of 298 K (VO₂ is in a complete insulator state) is shown in Figure 3B. The THz spectral response exhibits a dual-band high absorption with the absorption rates of 97.2% at 5.95 THz and 95.4% at 6.95 THz. With the phase transition of VO₂, the TMA achieves the switching between ultra-broadband absorption and dual-band absorption. Moreover, the metaatom resonators in one unit cell are arranged in a two-dimensional symmetry, thus eliminating the polarization dependence of TMA on the incident THz wave. The results in Figures 3A, B can also confirm this point with TM polarization and TE polarization incident separately.

FIGURE 3

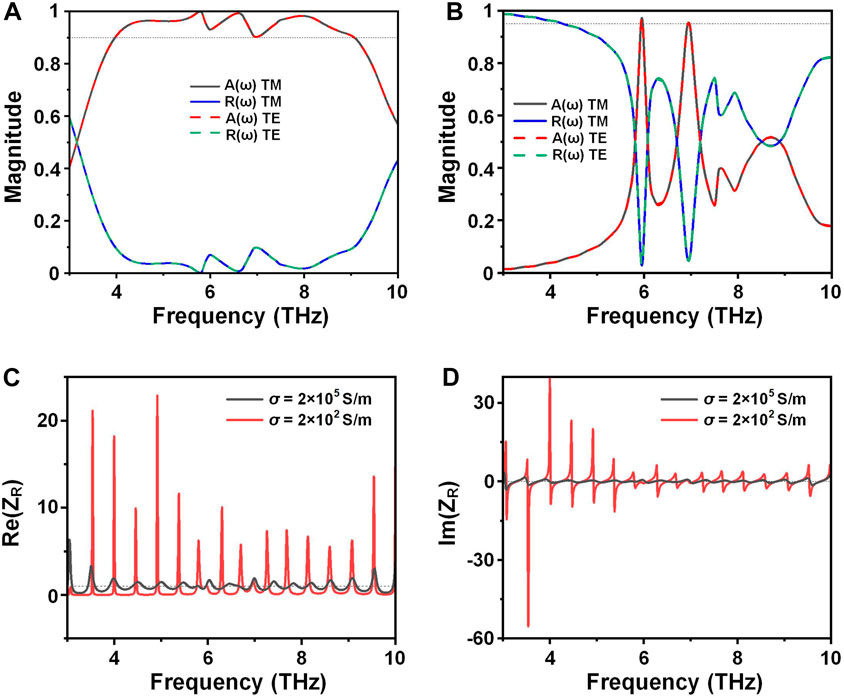
FIGURE 3. Reflection and absorption spectrums of the TMA at (A) high temperature (358 K) and (B) low temperature (298 K). (C) Real and (D) imaginary parts of the relative impedance between the TMA and the free space with VO₂ conductivity 2 × 10⁵ S/m (black line) and 2 × 10² S/m (red line).

The efficient absorption of TMA can be elucidated by the wave-interference theory and impedance matching theory. Obviously, in the absence of transmission, by minimizing the reflected waves through destructive interference, the absorption of TMA can be maximized. At this time, the effective permittivity and permeability of TMA can provide equivalent impedance to match the effective impedance in free space [63]. The relationship between absorption and relative impedance satisfies,

$A\left(\omega \right)=1-R\left(\omega \right)=1-\left|\frac{Z-Z_0}{Z+Z_0}\right|=1-\left|\frac{Z_R-1}{Z_R+1}\right|(6)$

$Z_R=\pm \sqrt{\frac{{\left(1+S_{11}\left(\omega \right)\right)}^2-{S_{21}}^2\left(\omega \right)}{{\left(1-S_{11}\left(\omega \right)\right)}^2-{S_{21}}^2\left(\omega \right)}}(7)$

where Z and Z₀ are the effective impedances of the TMA and the free space, respectively, and Z_R is the relative impedance between the TMA and the free space. When the impedances reach a perfect matching state, the real and imaginary parts of the relative impedance can be attained to 1 and 0. The calculated relative impedance results when the VO₂ at 358 K (σ = 2 × 10⁵ S/m) and 298 K (σ = 2 × 10² S/m) are shown in Figures 3C, D, respectively. When the real and imaginary parts of the relative impedance are around 1 and 0, respectively, the efficient absorption can be achieved, which corresponds to the state of impedance matching.

The absorption characteristics of our designed TMA are the combination of the absorption characteristics of Au and VO₂ resonators when they exist independently. These VO₂ resonators have different absorption characteristics at different temperatures, thus providing operability for the switching between broadband and dual-band absorption of our designed TMA. At the temperature where VO₂ is in a completely metallic phase, the absorption performance of a metamaterial absorber composed solely of Au or VO₂ resonators is shown in Figure 4A. It can be seen that the only VO₂ resonators provide a broadband absorption from 4.07 to 8.37 THz with three absorption peaks at f₁ = 4.63 THz, f₂ = 6.21 THz and f₃ = 7.54 THz, and a dual-band absorption is formed at f₄ = 6.02 THz and f₅ = 7.03 THz with only Au resonators. At the temperature where VO₂ is in a complete insulator phase, it can be seen from Figure 4B that the absorption drops sharply with only VO₂ resonators compared to the high temperature condition. But under this low temperature state, the absorption of the absorber composed of Au resonators remains unchanged. The absorption characteristics of our designed TMA is determined by the absorption characteristics of only Au and only VO₂ resonators. Therefore, the absorption characteristics of the combination of Au and VO₂ resonators can be switched between broadband and dual-band with the help of temperature control.

FIGURE 4

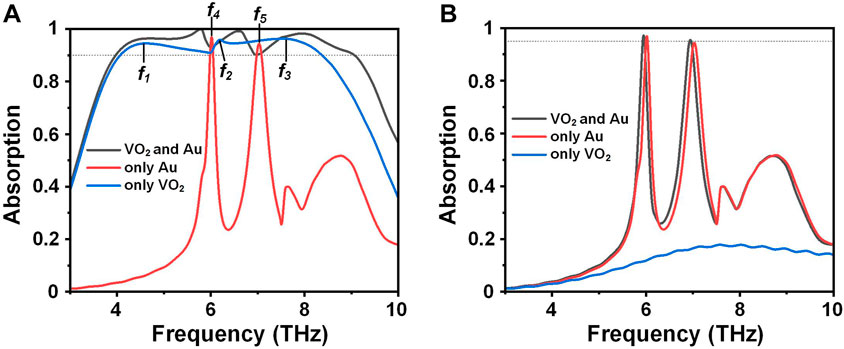
FIGURE 4. THz absorption spectra for TMA resonator array composed of hybrid VO₂ and Au resonators (black line), only Au resonators (red line) and only VO₂ resonators (blue line) at (A) high temperature (358 K) and (B) low temperature (298 K).

The broadband absorption effect of our proposed TMA is mainly provided by the VO₂ resonators. To further explore the physical origin of the designed TMA, the electric field distributions at the three absorption peaks in the presence of only VO₂ resonators are presented in Figure 5. Since our proposed TMA is polarization-independent, here, the electric field distributions are presented only under TM polarization incidence. It can be seen that the electric field distributions at f₁ = 4.63 THz and f₃ = 7.54 THz are similar with the positive charges concentrated on the left side of the square-loop and the negative charges concentrated on the right side. This indicates that both absorption peaks are caused by the excitation of electric dipole resonance, but the difference is that the intensity of charge accumulation is different. As for f₂ = 6.21 THz, in a unit cell with four square-loops, negative charges are induced on the two loops on the left, while positive charges are induced on the right. This suggests a dipole resonance that occurs between two adjacent loops in the horizontal direction. The local electric field intensity can reach 10⁶ V/m level, which can be explained by the coupled mode theory [64]. Therefore, electrical dipole resonances are responsible for all three absorption peaks and expand into broadband in the presence of only VO₂ resonators.

FIGURE 5

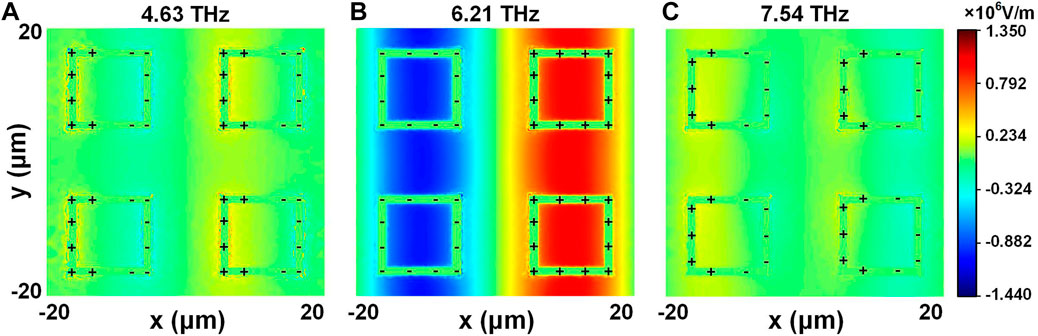
FIGURE 5. Electric field distributions (x-y plane) at the three absorption peaks in the presence of only VO₂ resonators in TMA. The peak frequencies are (A) f₁ = 4.63 THz (B) f₂ = 6.21 THz (C) f₃ = 7.54 THz, respectively.

In the presence of only Au resonators, the electric field distributions and magnetic field distributions at the two resonant peaks are shown in Figure 6. From the electric field distributions in the x-y plane, it can be seen that the electric field distributions at the two frequencies f₄ = 6.02 THz and f₅ = 7.03 THz are similar. However, combining the distributions of electric and magnetic fields in the y-z plane, it can be seen that there are significant differences between the two resonance modes. In these two resonances, the f₄ mode is a dark surface-Bloch mode related to the periodic constant [65]. If the period of the unit cell structure decreases to a certain value, the dark surface-Bloch mode resonance will disappear. In contrast, the electrical dipole resonance at the f₅ mode does not disappear with the decrease of the period. Thus, the dual-band absorption originates the electrical dipole mode and nonlocal surface-Bloch mode of metal resonators at low temperature (298 K).

FIGURE 6

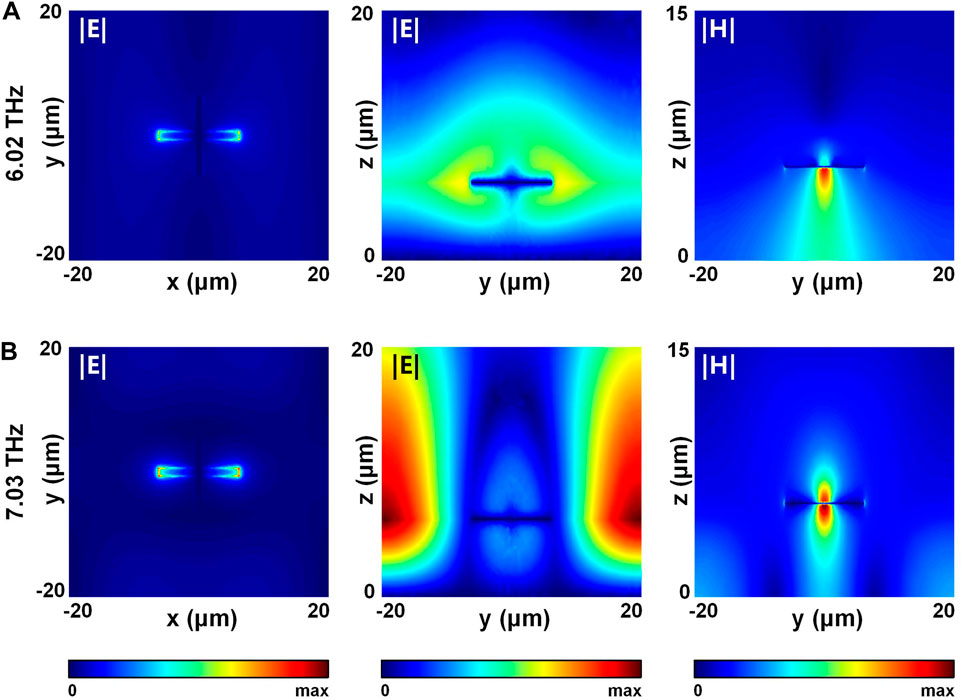
FIGURE 6. Electric field distributions and magnetic field distributions at the two resonant peaks in the presence of only Au resonators in TMA. The resonant peak frequencies are (A) f₄ = 6.02 THz (top row) (B) f₅ = 7.03 THz (bottom row), respectively. Left: electric field distributions (x-y plane), middle: electric field distributions (y-z plane), and right: magnetic field distributions (y-z plane).

The dependency of structural parameters is shown in Figure 7. Based on the designed parameters, each subgraph is obtained by ensuring that only one parameter is a variable. Among them, Figures 7A–D show the results obtained at the temperature of 358 K, while Figures 7E, F show the results obtained at 298 K. The simulation results show that the geometric parameters have a non-negligible influence on the absorption performance. Because our proposed TMA can be switch between ultra-broadband and dual-band, it is necessary to consider the influence of different parameters on the absorption rate at both low and high temperatures. Thus, the designed parameters are the optimized parameters obtained from our comprehensive consideration at both low and high temperature conditions.

FIGURE 7

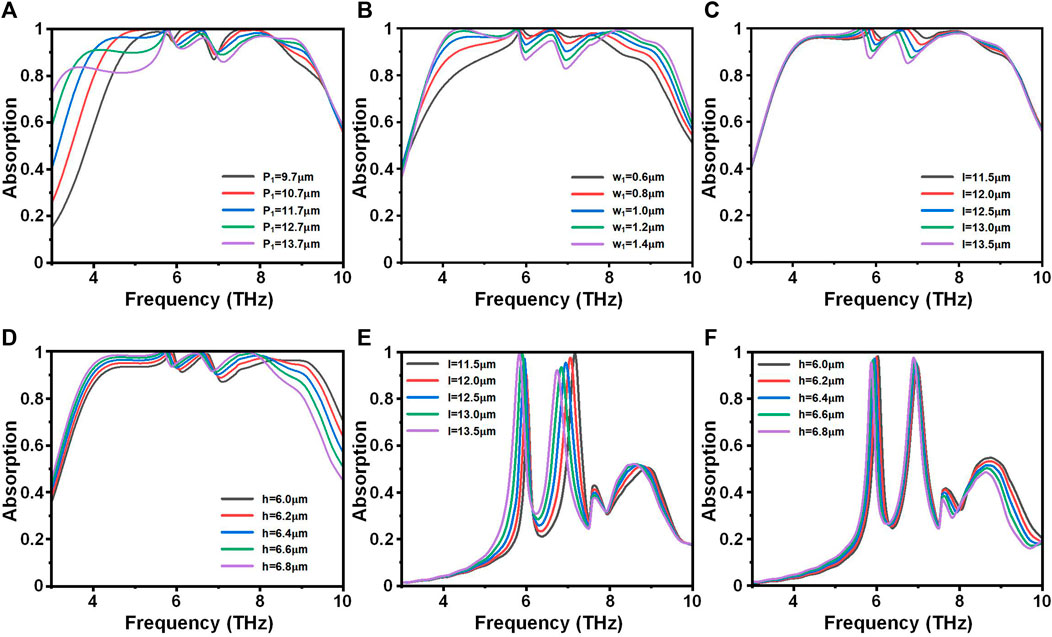
FIGURE 7. Dependency of structural parameters. Among them, (A–D) are at the temperature of T = 358 K, and (E) and (F) are at the temperature of T = 298 K.

The conductivity of VO₂ can vary with the temperature with a thermal hysteresis loop [62]. The change in conductivity caused by different temperatures leads to a change in the permittivity dispersion of VO₂. The real and imaginary parts of the relative permittivity under different conductivities are shown in Figures 8A, B. Thus, our designed TMA has the performance of continuously adjustable absorption efficiency with temperature. The absorption performance of TMA under different conductivities is shown in Figure 8C, and the absorption performance under continuous conductivity changes is presented in Figure 8D. It can be clearly seen that as the conductivity changes, the absorption performance transitions between dual-band absorption and ultra-broadband absorption.

FIGURE 8

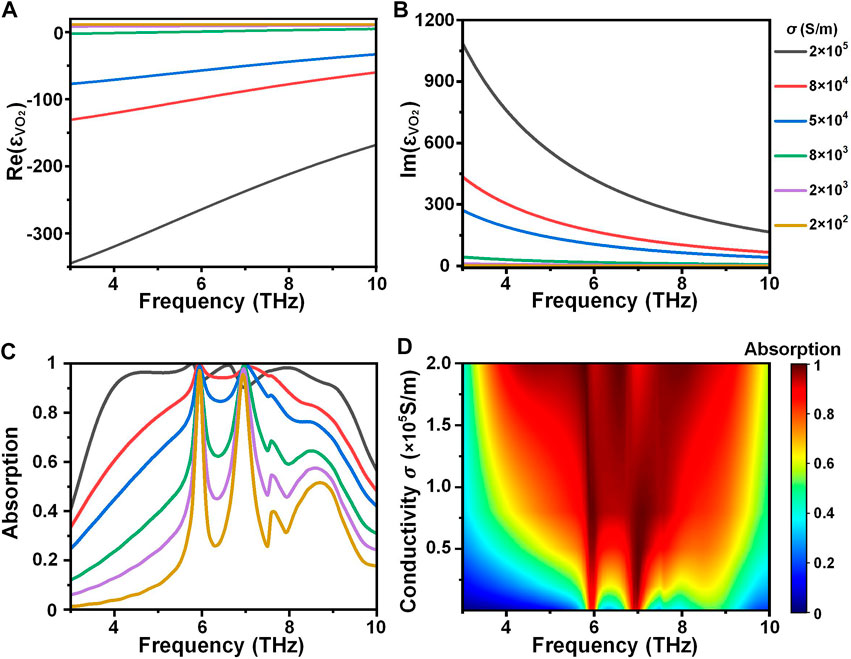
FIGURE 8. (A) Real and (B) imaginary parts of the relative permittivity of VO₂ under different conductivities. (C) Absorption performance of TMA under different conductivities. (D) Absorption performance as a function of the operating frequency and conductivity of VO₂.

Additionally, the broadband absorption spectra of TMA (at the temperature of 358 K) as a function of the operating frequency and incidence angle are discussed, under the incidence with TM and TE polarization states, respectively, as shown in Figures 9A, B, and the dual-band absorption spectra of TMA (at the temperature of 298 K) as a function of the operating frequency and incidence angle are shown in Figures 9C, D under the incidence with TM and TE polarization states, respectively. In Figures 9A, B, the red-highlighted area (within the black dashed line) indicates the broadband of angle-dependent absorption efficiency exceeding 80% level. It can be seen that the proposed TMA can work over a wide range of incident angles under both incidence cases with TM polarization state and TE polarization state. The frequency range of broadband absorption is basically unchanged. The effective working angles for broadband absorption with more than 80% absorption efficiency under oblique incidence can reach up to nearly 60° for TM polarization, and 50° for TE polarization. Due to the impedance mismatch and higher order scattering, the TMA broadband absorption tends to be deteriorated at a wider oblique incidence angle. In stark contrast, the dual-band absorption at 298 K is greatly affected by the incidence angle especially under TM polarization state, as shown in Figures 9C, D. However, in any case, there is a certain angle to meet the working conditions, which reduces the requirement for system alignment.

FIGURE 9

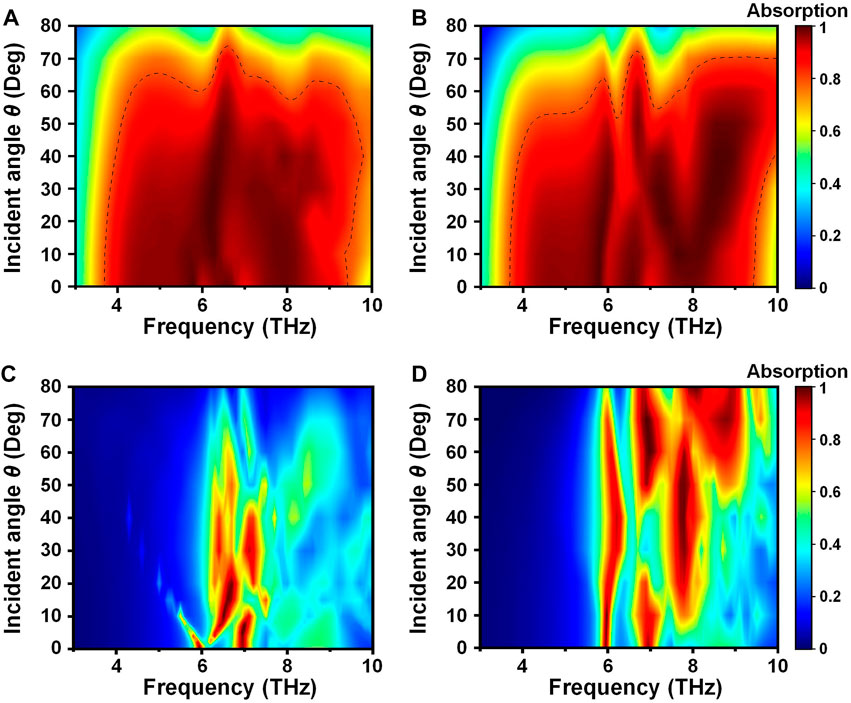
FIGURE 9. Broadband absorption spectra of TMA (at the temperature of 358 K) as a function of the operating frequency and incidence angle under the incidence with (A) TM and (B) TE polarization states, and dual-band absorption spectra of TMA (at the temperature of 298 K) as a function of the operating frequency and incidence angle under the incidence with (C) TM and (D) TE polarization states, respectively.

4 Conclusion

In conclusion, we have realized a TMA that can be switched flexibly between ultra-broadband and dual bands by changing the conductivity of VO₂ through thermal control. The TMA comprises a resonator array above a conductive ground layer separated with a dielectric spacer, which includes four square-loop VO₂ resonators and a crossed Au resonator in each unit cell. The TMA can achieve more than 90% absorption bandwidth in the range of 3.98 to 9.06 THz at high temperature (VO₂ is in the completely metallic state), which can be elucidated by the wave-interference theory and impedance matching theory. At low temperature where VO₂ is fully insulated, the TMA realizes a dual-band absorption with the absorption efficiency exceeding 95% at 5.95 and 6.95 THz, which originates the dipole mode and nonlocal surface-Bloch mode of metal resonators. The TMA has the advantage of polarization-independence, due to the two-dimensional symmetry of structural arrangement. In addition, the broadband absorbance can remain more than 80% over a wide range of incident angles, specifically up to nearly 60° for TM polarization, and 50° for TE polarization. Compared with previous studies, our design can switch between two absorption modes and its absorption performance is greatly improved. The proposed TMA design scheme is expected to expand THz devices and has many potential applications in the THz range, such as modulation, sensing, stealth, and switching devices.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZR, WW, and RW conceived and led the design. ZR, WW, SL, and RW finished the whole manuscript writing and manuscript modification. WW, YZ, SC, and GR performed the statistical analysis. WW and YZ performed image processing. ZR, WW, GR, SL, and RW contributed to the proofreading and revised the article format. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China (62205106), Fundamental Research Funds for the Central Universities (2022MS122 and 2019MS118), Natural Science Foundation of Hebei Province (A2019502044) and Program for New Century Excellent Talents in University (NCET-12-0844).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sengupta K, Nagatsuma T, Mittleman DM. Terahertz integrated electronic and hybrid electronic–photonic systems. Nat Elect (2018) 1:622–35. doi:10.1038/s41928-018-0173-2

CrossRef Full Text | Google Scholar

2. Zhang X, Xu Q, Xia L, Li Y, Gu J, Tian Z, et al. Terahertz surface plasmonic waves: A review. Adv Photon (2020) 2:014001. doi:10.1117/1.AP.2.1.014001

CrossRef Full Text | Google Scholar

3. Wang Y, Han Z, Du Y, Qin J. Ultrasensitive terahertz sensing with high-q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics (2021) 10:1295–307. doi:10.1515/nanoph-2020-0582

CrossRef Full Text | Google Scholar

4. Stantchev RI, Yu X, Blu T, Pickwell-MacPherson E. Real-time terahertz imaging with a single-pixel detector. Nat Commun (2020) 11:2535. doi:10.1038/s41467-020-16370-x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yang Y, Yamagami Y, Yu X, Pitchappa P, Webber J, Zhang B, et al. Terahertz topological photonics for on-chip communication. Nat Photon (2020) 14:446–51. doi:10.1038/s41566-020-0618-9

CrossRef Full Text | Google Scholar

6. Zhou Y, Qin Z, Liang Z, Meng D, Xu H, Smith DR, et al. Ultra-broadband metamaterial absorbers from long to very long infrared regime. Light: Sci Appl (2021) 10:138. doi:10.1038/s41377-021-00577-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yu H, Meng D, Liang Z, Xu H, Qin Z, Su X, et al. Polarization-dependent broadband absorber based on composite metamaterials in the long-wavelength infrared range. Opt Express (2021) 29:36111–20. doi:10.1364/OE.435579

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhao Y, Askarpour AN, Sun L, Shi J, Li X, Alù A. Chirality detection of enantiomers using twisted optical metamaterials. Nat Commun (2017) 8:14180. doi:10.1038/ncomms14180

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xu Q, Su X, Zhang X, Dong L, Liu L, Shi Y, et al. Mechanically reprogrammable pancharatnam–berry metasurface for microwaves. Adv Photon (2022) 4:016002. doi:10.1117/1.AP.4.1.016002

CrossRef Full Text | Google Scholar

10. Grady N, Heyes J, Chowdhury D, Zeng Y, Reiten M, Azad A, et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science (2013) 340:1304–7. doi:10.1126/science.1235399

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang R, Ansari MA, Ahmed H, Li Y, Cai W, Liu Y, et al. Compact multi-foci metalens spectrometer. Light: Sci Appl (2023) 12:103. doi:10.1038/s41377-023-01148-9

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang R, Ren G, Ren Z, Liu J, Li S, Chen X, et al. Reconstructing subwavelength resolution terahertz holographic images. Opt Express (2022) 30:7137–46. doi:10.1364/OE.453634

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang R, Intaravanne Y, Li S, Han J, Chen S, Liu J, et al. Metalens for generating a customized vectorial focal curve. Nano Lett (2021) 21:2081–7. doi:10.1021/acs.nanolett.0c04775

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Fu X, Cui T. Recent progress on metamaterials: From effective medium model to real-time information processing system. Prog Quan Elect (2019) 67:100223. doi:10.1016/j.pquantelec.2019.05.001

CrossRef Full Text | Google Scholar

15. Pitchappa P, Kumar A, Singh R, Wang N. Electromechanically tunable frequency-agile metamaterial bandpass filters for terahertz waves. Adv Opt Mater (2022) 10:2101544. doi:10.1002/adom.202101544

CrossRef Full Text | Google Scholar

16. Jung H, Jo H, Lee W, Kang MS, Lee H. Reconfigurable molecularization of terahertz meta-atoms. ACS Photon (2022) 9:1814–20. doi:10.1021/acsphotonics.2c00397

CrossRef Full Text | Google Scholar

17. Zhao X, Wang Y, Schalch J, Duan G, Cremin K, Zhang J, et al. Optically modulated ultra-broadband all-silicon metamaterial terahertz absorbers. ACS Photon (2019) 6:830–7. doi:10.1021/acsphotonics.8b01644

CrossRef Full Text | Google Scholar

18. Islam M, Sultana J, Biabanifard M, Vafapour Z, Nine M, Dinovitser A, et al. Tunable localized surface plasmon graphene metasurface for multiband superabsorption and terahertz sensing. Carbon (2020) 158:559–67. doi:10.1016/j.carbon.2019.11.026

CrossRef Full Text | Google Scholar

19. Yu P, Yang H, Chen X, Yi Z, Yao W, Chen J, et al. Ultra-wideband solar absorber based on refractory titanium metal. Renew Energ (2020) 158:227–35. doi:10.1016/j.renene.2020.05.142

CrossRef Full Text | Google Scholar

20. Wang R, Han J, Liu J, Tian H, Sun W, Li L, et al. Multi-foci metalens for terahertz polarization detection. Opt Lett (2020) 45:3506–9. doi:10.1364/OL.395580

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Song Z, Zhang J. Achieving broadband absorption and polarization conversion with a vanadium dioxide metasurface in the same terahertz frequencies. Opt Express (2020) 28:12487–97. doi:10.1364/OE.391066

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ren Z, Chang S, Li S, Wang R. Birefringent dielectric multi-foci metalens for polarization detection. Physica Scripta (2023) 98:045502. doi:10.1088/1402-4896/acbe35

CrossRef Full Text | Google Scholar

23. Sun K, Zhao Z, Cai Y, Levy U, Han Z. Ultra-narrowband and highly-directional thz thermal emitters based on the bound state in the continuum. Nanophotonics (2021) 10:4035–43. doi:10.1515/nanoph-2021-0380

CrossRef Full Text | Google Scholar

24. Zheng Z, Luo Y, Yang H, Yi Z, Zhang J, Song Q, et al. Thermal tuning of terahertz metamaterial absorber properties based on VO₂. Phys Chem Chem Phys (2022) 24:8846–53. doi:10.1039/d2cp01070d

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Torkaman P, Darbari S, Mohammad-Zamani M. Design and simulation of a piezotronic gan-based pulsed thz emitter. J Lightwave Tech (2018) 36:3645–51. doi:10.1109/JLT.2018.2844219

CrossRef Full Text | Google Scholar

26. Chai M, Wang Y, Chen C, Zhao Z, Jin M, He T. Metamaterials-based photoelectric conversion: From microwave to optical range. Laser Photon Rev (2022) 16:2100458. doi:10.1002/lpor.202100458

CrossRef Full Text | Google Scholar

27. Huang Y, Kaj K, Chen C, Yang Z, Ul Haque SR, Zhang Y, et al. Broadband terahertz silicon membrane metasurface absorber. ACS Photon (2022) 9:1150–6. doi:10.1021/acsphotonics.2c00166

CrossRef Full Text | Google Scholar

28. Obaidullah M, Esat V, Sabah C. Multi-band (9, 4) chiral single-walled carbon nanotube based metamaterial absorber for solar cells. Opt Laser Tech (2021) 134:106623. doi:10.1016/j.optlastec.2020.106623

CrossRef Full Text | Google Scholar

29. Chen H, Ma W, Huang Z, Zhang Y, Huang Y, Chen Y. Graphene-based materials toward microwave and terahertz absorbing stealth technologies. Adv Opt Mater (2019) 7:1801318. doi:10.1002/adom.201801318

CrossRef Full Text | Google Scholar

30. Shui W, Li J, Wang H, Xing Y, Li Y, Yang Q, et al. Ti₃C₂T_x MXene sponge composite as broadband terahertz absorber. Adv Opt Mater (2020) 8:2001120. doi:10.1002/adom.202001120

CrossRef Full Text | Google Scholar

31. Geng M, Liu Z, Chen H, Bao X, Yang X, Lu W. Flexible and dual-tunable radar absorber enabled by graphene. Adv Mater Tech (2022) 7:2200028. doi:10.1002/admt.202200028

CrossRef Full Text | Google Scholar

32. Tao H, Landy NI, Bingham CM, Zhang X, Averitt RD, Padilla WJ. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt Express (2008) 16:7181–8. doi:10.1364/OE.16.007181

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Huang X, He W, Yang F, Ran J, Gao B, Zhang WL. Polarization-independent and angle-insensitive broadband absorber with a target-patterned graphene layer in the terahertz regime. Opt Express (2018) 26:25558–66. doi:10.1364/OE.26.025558

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Wu X, Zheng Y, Luo Y, Zhang J, Yi Z, Wu X, et al. A four-band and polarization-independent bds-based tunable absorber with high refractive index sensitivity. Phys Chem Chem Phys (2021) 23:26864–73. doi:10.1039/d1cp04568g

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang B, Tang C, Niu Q, He Y, Chen T. Design of narrow discrete distances of dual-/triple-band terahertz metamaterial absorbers. Nanoscale Res Lett (2019) 14:1–7. doi:10.1186/s11671-019-2876-3

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Li Y, Gao W, Guo L, Chen Z, Li C, Zhang H, et al. Tunable ultra-broadband terahertz perfect absorber based on vanadium oxide metamaterial. Opt Express (2021) 29:41222–33. doi:10.1364/OE.444761

CrossRef Full Text | Google Scholar

37. Ding Z, Su W, Lu H, Wu H, Yao H. Terahertz absorber based on double-layer graphene metasurface with tunable absorption window and intensity. Opt Laser Tech (2023) 163:109446. doi:10.1016/j.optlastec.2023.109446

CrossRef Full Text | Google Scholar

38. Wang D, Xu KD, Luo S, Cui Y, Zhang L, Cui J. A high q-factor dual-band terahertz metamaterial absorber and its sensing characteristics. Nanoscale (2023) 15:3398–407. doi:10.1039/d2nr05820k

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang R, Li L, Liu J, Yan F, Tian F, Tian H, et al. Triple-band tunable perfect terahertz metamaterial absorber with liquid crystal. Opt Express (2017) 25:32280–9. doi:10.1364/OE.25.032280

CrossRef Full Text | Google Scholar

40. Zhang H, Wang Z, Hu C, Liu H. A tailored broadband terahertz metamaterial absorber based on the thermal expansion feature of liquid metal. Results Phys (2020) 16:102937. doi:10.1016/j.rinp.2020.102937

CrossRef Full Text | Google Scholar

41. Lari ES, Vafapour Z, Ghahraloud H. Optically tunable triple-band perfect absorber for nonlinear optical liquids sensing. IEEE Sensors J (2020) 20:10130–7. doi:10.1109/JSEN.2020.2989742

CrossRef Full Text | Google Scholar

42. Gong Y, Hu F, Jiang M, Zhang L, Zou Y, Jiang G, et al. Terahertz binary coder based on graphene metasurface. Carbon (2021) 184:167–76. doi:10.1364/OE.390835

CrossRef Full Text | Google Scholar

43. Zhang M, Song Z. Switchable terahertz metamaterial absorber with broadband absorption and multiband absorption. Opt Express (2021) 29:21551–61. doi:10.1364/OE.432967

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Qi L, Liu C, Shah SMA. A broad dual-band switchable graphene-based terahertz metamaterial absorber. Carbon (2019) 153:179–88. doi:10.1016/j.carbon.2019.07.011

CrossRef Full Text | Google Scholar

45. Liu M, Hwang HY, Tao H, Strikwerda AC, Fan K, Keiser GR, et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature (2012) 487:345–8. doi:10.1038/nature11231

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Huang J, Li J, Yang Y, Li J, Li J, Zhang Y, et al. Broadband terahertz absorber with a flexible, reconfigurable performance based on hybrid-patterned vanadium dioxide metasurfaces. Opt Express (2020) 28:17832–40. doi:10.1364/OE.394359

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wuttig M, Bhaskaran H, Taubner T. Phase-change materials for non-volatile photonic applications. Nat Photon (2017) 11:465–76. doi:10.1038/nphoton.2017.126

CrossRef Full Text | Google Scholar

48. Kübler C, Ehrke H, Huber R, Lopez R, Halabica A, Haglund R, et al. Coherent structural dynamics and electronic correlations during an ultrafast insulator-to-metal phase transition in VO₂. Phys Rev Lett (2007) 99:116401. doi:10.1103/PhysRevLett.99.116401

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Ko B, Badloe T, Rho J. Vanadium dioxide for dynamically tunable photonics. ChemNanoMat (2021) 7:713–27. doi:10.1002/cnma.202100060

CrossRef Full Text | Google Scholar

50. Qazilbash MM, Brehm M, Chae BG, Ho PC, Andreev GO, Kim BJ, et al. Mott transition in VO₂ revealed by infrared spectroscopy and nano-imaging. Science (2007) 318:1750–3. doi:10.1126/science.1150124

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chen L, Song Z. Simultaneous realizations of absorber and transparent conducting metal in a single metamaterial. Opt Express (2020) 28:6565–71. doi:10.1364/OE.388066

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Liu H, Wang ZH, Li L, Fan YX, Tao ZY. Vanadium dioxide-assisted broadband tunable terahertz metamaterial absorber. Scientific Rep (2019) 9:5751. doi:10.1038/s41598-019-42293-9

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Jiao XF, Zhang ZH, Li T, Xu Y, Song GF. Tunable dual broadband terahertz metamaterial absorber based on vanadium dioxide. Appl Sci (2020) 10:7259. doi:10.3390/app10207259

CrossRef Full Text | Google Scholar

54. Huang J, Li J, Yang Y, Li J, Zhang Y, Yao J, et al. Active controllable dual broadband terahertz absorber based on hybrid metamaterials with vanadium dioxide. Opt Express (2020) 28:7018–27. doi:10.1364/OE.387156

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Zheng Z, Zheng Y, Luo Y, Yi Z, Zhang J, Liu Z, et al. A switchable terahertz device combining ultra-wideband absorption and ultra-wideband complete reflection. Phys Chem Chem Phys (2022) 24:2527–33. doi:10.1039/d1cp04974g

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Liu W, Xu J, Song Z. Bifunctional terahertz modulator for beam steering and broadband absorption based on a hybrid structure of graphene and vanadium dioxide. Opt Express (2021) 29:23331–40. doi:10.1364/OE.433364

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Qiu Y, Yan DX, Feng QY, Li XJ, Zhang L, Qiu GH, et al. Vanadium dioxide-assisted switchable multifunctional metamaterial structure. Opt Express (2022) 30:26544–56. doi:10.1364/OE.465062

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Wang D, Sun S, Feng Z, Tan W. Enabling switchable and multifunctional terahertz metasurfaces with phase-change material. Opt Mater Express (2020) 10:2054–65. doi:10.1364/OME.397173

CrossRef Full Text | Google Scholar

59. Liu S, Chen H, Cui TJ. A broadband terahertz absorber using multi-layer stacked bars. Appl Phys Lett (2015) 106:151601. doi:10.1063/1.4918289

CrossRef Full Text | Google Scholar

60. Cunningham PD, Valdes NN, Vallejo FA, Hayden LM, Polishak B, Zhou XH, et al. Broadband terahertz characterization of the refractive index and absorption of some important polymeric and organic electro-optic materials. J Appl Phys (2011) 109:043505. doi:10.1063/1.3549120

CrossRef Full Text | Google Scholar

61. Ordal MA, Bell RJ, Alexander RW, Long LL, Querry MR. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl Opt (1985) 24:4493–9. doi:10.1364/ao.24.004493

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Zheng Z, Zheng Y, Luo Y, Yi Z, Zhang J, Liu L, et al. Terahertz perfect absorber based on flexible active switching of ultra-broadband and ultra-narrowband. Opt Express (2021) 29:42787–99. doi:10.1364/OE.445155

CrossRef Full Text | Google Scholar

63. Chen H. Interference theory of metamaterial perfect absorbers. Opt Express (2012) 20:7165–72. doi:10.1364/OE.20.007165

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Yong Z, Zhang S, Gong C, He S. Narrow band perfect absorber for maximum localized magnetic and electric field enhancement and sensing applications. Scientific Rep (2016) 6:24063. doi:10.1038/srep24063

CrossRef Full Text | Google Scholar

65. Wang J, Tian H, Wang Y, Li X, Cao Y, Li L, et al. Liquid crystal terahertz modulator with plasmon-induced transparency metamaterial. Opt Express (2018) 26:5769–76. doi:10.1364/oe.26.005769

PubMed Abstract | CrossRef Full Text | Google Scholar