A (t, n) threshold protocol of semi-quantum secret sharing based on single particles

Semi-quantum secret sharing is an important research issue in quantum cryptography. In this paper, we propose a (t, n) threshold semi-quantum secret sharing protocol, which combines the practicality of semi-quantum secret sharing protocols and the flexibility of (t, n) threshold quantum secret sharing protocols. Participants prepare and transmit single particles in a circular way, and then any t out of n participants can recover the secret according to Shamir’s secret sharing scheme. As quantum resources, single particles are easy to prepare. Furthermore, classical participants only need to possess the capability to prepare and insert particles. The security analysis shows our protocol has security against most attacks. Except decoy particles, all particles are useful to carry the secret message, so the efficiency of the proposed protocol can achieve 100%.

1 Introduction

Secret sharing is an important branch of modern cryptography. The concept of secret sharing is that the secret holder divides his secret into several pieces and each participant can obtain a piece from the holder. The threshold number of participants can recover the secret in collaboration with others.

The first classical secret sharing (CSS) protocol [1] was proposed by Shamir in 1979. However, if an eavesdropper, Eve, controls the communication channel, she can easily obtain the secret holder’s, Alice’s, secret [2]. Unfortunately, the physical properties of quantum mechanics mean that eavesdropping can be detected easily because eavesdropping may disturb quantum information, which induces errors. Therefore, quantum secret sharing (QSS) emerged based on security additional requirements. In 1999, Hillery et al. proposed the first QSS protocol [3]. Authors employed the three-particle and four-particle entangled Greenberger-Horne-Zeilinger (GHZ) state to share a secret message in their protocol. In 2003, Guo et al. proposed a more efficient QSS protocol [4] that only used product states. In 2008, Wang et al. put forward a QSS protocol [5] with higher efficiency and security based on single photons. After that, a huge number of QSS protocols [6–15] were proposed.

The above QSS protocols require all participants to possess full quantum capabilities, but not all participants are equipped with complete quantum devices. Fortunately, the concept of semi-quantum secret sharing (SQSS) was proposed. In a semi-quantum environment, some participants have limited quantum capabilities. They can cooperate with the participants with full quantum capabilities to complete tasks of secret distribution and reconstruction in SQSS protocols. In 2010, Li et al. proposed the first semi-quantum secret sharing protocol [16]. In the protocol, they used entangled GHZ-type states to share a secret message. In 2015, Xie et al. presented an efficient SQSS protocol [17] that can share a specific secret. In 2018, an SQSS protocol with limited resources was designed by Li et al. [18], which was more efficient compared with previous protocols. In 2021, Yin et al. proposed an SQSS protocol [19] based on GHZ-type states. The protocol adopted identity authentication to verify the identification of participants in communication. In recent years, more SQSS protocols [20, 21–27] were proposed.

However, all the above SQSS protocols are (n, n) threshold protocols. That is to say, the secret sharing tasks cannot be completed when there is someone unable to participate. So, we propose a (t, n) threshold SQSS protocol based on Shamir’s secret sharing scheme, in which any t out of n participants with limited quantum capabilities can recover the secret. All participants only use single particles, which are easier to prepare than other quantum resources. In our protocol, the initial particles prepared by Alice are sent to the first participant. Every participant inserts his particles and sends the new sequence to the next one until Alice receives the final sequence from the last participant. The sequence composed of particles is transmitted in a circular way. Due to the circular transmission mode, participants play the different roles. Furthermore, classical participants in our protocol are released from many quantum operations and they are only required to possess the capability to prepare and insert particles. Moreover, the qubit efficiency of our protocol can achieve 100% because all particles are used to carry the secret message except for decoy particles. As mentioned above, a flexible and efficient SQSS protocol is proposed in this paper. In addition, the security of our protocol can be proved under intercept-resend attack, measure-resend attack, entangle-measure attack, and collusion attack.

The rest of this paper is organized as follows. In Section 2, we present some preliminaries about the setting of SQSS and Shamir’s secret sharing. Then, in Section 3, we describe a (t, n) threshold SQSS protocol. An example of the proposed (t, n) threshold SQSS protocol is given in Section 4. In Section 5, we analyze the security of our protocol and give a comparison with some SQSS protocols. Finally, a conclusion is provided in Section 6.

2 Preliminaries

Here, to make our protocol easier to understand, we will briefly introduce some preliminaries about the setting of SQSS and Shamir’s secret sharing.

2.1 The setting of SQSS

In SQSS protocols, there are participants restricted to using only the quantum states in the fixed computational basis $\left\{\left|0\right.〉,\left|1\right.〉\right\}$, and they only have classical computing power. All participants of an SQSS protocol are required to perform the following operations only: (a) reflect the qubits undisturbed; (b) measure the qubits with the classical $\left\{\left|0\right.〉,\left|1\right.〉\right\}$ basis; (c) generate a (fresh) qubit with the classical $\left\{\left|0\right.〉,\left|1\right.〉\right\}$ basis and send it; and (d) reorder the qubits, so they can never prepare or measure qubits arbitrarily. The qubits with the classical basis are regarded as “classical bits”, and the participants restricted to performing the above operations are known as “classical participants”.

2.2 Shamir’s secret sharing

Shamir [1] proposed a (t, n) threshold scheme based on polynomial interpolation in 1979. According to the property of polynomial interpolation, this technique enables the construction of secret sharing schemes that can function even when fewer than n participants want to reconstruct the secret. Therefore, Shamir’s scheme has been widely used in the field of quantum cryptography, such as quantum secret sharing [28–30] and quantum key distribution [31].

Given that there is a secret holder Alice and n participants $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,...,{\mathrm{B}\mathrm{o}\mathrm{b}}_n\right\}$, Shamir’s secret sharing consists of two phases:

In the secret sharing phase, the secret holder Alice selects a polynomial of t–1 degree:

$f\left(x\right)=S+a_{1}x+a_2{x}^2+...+a_{t-1}{x}^{t-1}.(1)$

Here, S is Alice’s secret, t is the lower limit of the number of participants who can reconstruct Alice’s secret S, and $a_i\left(i=1,2,...,t-1\right)$ is the coefficient Alice picks. Alice selects n integers as $x_i$ and computes $f\left(x_i\right)$ as shadows. Then she distributes them among n participants. ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ only knows $x_i$ and $f\left(x_i\right)$, where $i=1,2,...,n$.

In secret reconstruction phase, t participants use the Lagrange interpolation formula and their shares to reconstruct the secret. The Lagrange interpolation formula is as follows:

$f\left(x\right)={\displaystyle \sum _{r=1}^t}f\left(x_r\right)\prod _{1\le j\le t,j\ne r}\frac{x-x_j}{x_r-x_j}.(2)$

Participants can calculate the polynomial under the condition that $x=0$ to obtain $f\left(0\right)$, which is just the secret S.

3 A (t, n) threshold SQSS protocol

In this section, we propose a (t, n) threshold SQSS protocol. Assume that the secret holder Alice wants to share her secret among n participants $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,...,{\mathrm{B}\mathrm{o}\mathrm{b}}_n\right\}$. Any t out of these n participants can recover Alice’s secret, and participants fewer than t cannot get information about the secret. The steps of the proposed (t, n) threshold SQSS protocol are described as follows:

Step 1. Alice picks a random polynomial:

$f\left(x\right)=S+a1x+a2x^2+...+a_{t-1}{x}^{t-1},(3)$

where S is Alice’s secret and $a_i\left(i=1,2,...,t-1\right)$ is a random coefficient.

Step 2. Alice randomly chooses an integer x_i and computes $f\left(x_i\right)$ for $Bo{b}_i\left(i=1,2,...,n\right)$ with $f\left(x_i\right)\in \left\{0,1,...,2^N-2,2^N-1\right\}$, meaning that the length of the binary sequence $f\left(x_i\right)$ is less than N bits.

Step 3. Alice randomly prepares N particles in one of the states $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$, which compose a sequence $S_0$. All particles in $S_0$ are used as decoy particles. Alice sends $S_0$ to ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$.

Step 4. After receiving $S_0$ from Alice, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ randomly chooses an N-bit binary sequence as his private key $b_1$. ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ prepares N new particles in $\left\{\left|0\right.〉,\left|1\right.〉\right\}$ according to his private key $b_1$. The binary bit “0” denotes $\left|0\right.〉$, and the binary bit “1” denotes $\left|1\right.〉$. According to the rule mentioned above, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ inserts the corresponding particles into $S_0$ randomly to form a new sequence $S_1$. $S_1$ is composed of 2N particles. Subsequently, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ sends $S_1$ to ${\mathrm{B}\mathrm{o}\mathrm{b}}_2$.

Step 5. ${\mathrm{B}\mathrm{o}\mathrm{b}}_i\left(i=2,3,...,n\right)$ repeats Step 4. Finally, ${\mathrm{B}\mathrm{o}\mathrm{b}}_n$ sends the sequence $S_n$ to Alice.

Step 6. Alice and ${\mathrm{B}\mathrm{o}\mathrm{b}}_i\left(i=1,2,...,n\right)$ perform the eavesdropping checking. Alice publicly announces that she has received $S_n$, which is composed of Alice’s decoy particles in $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$ and classical participants’ particles in $\left\{\left|0\right.〉,\left|1\right.〉\right\}$. Each participant announces the places where he inserts his particles. Then Alice knows the positions of her decoy particles in $S_n$. She uses the proper measurement basis to measure her particles. By comparing measurement results of decoy particles with the initial states, Alice can evaluate the error rate. If the error rate exceeds the predefined threshold value, Alice will restart the protocol.

Step 7. After the eavesdropping checks, Alice measures the remaining particles with Z basis. According to the measurement results, Alice can obtain the private key $b_i$ of ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$. Then, Alice computes $a_i=b_i\oplus c_i$. Here, $c_i$ is the binary bit string of $f\left(x_i\right)$. In this way, Alice can get a corresponding new binary sequence $K_A$, which is composed of $a_i$. Finally, Alice announces her new sequence $K_A$.

Step 8. Because all participants announce where they insert their particles in Step 6, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ knows the positions of his particles in $S_n$ and obtains his corresponding binary bit string $a_i$ from $K_A$. According to Step 7, $a_i=b_i\oplus c_i$. So, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ computes $c_i=b_i\oplus a_i$. After that, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ calculates an integer $f\left(x_i\right)$ by the binary bit string $c_i$ and successfully obtains his secret shadow. At least t participants use their secret shadows to recover Alice’s secret S through the Lagrange interpolation:

$f\left(0\right)={\displaystyle \sum _{r=1}^t}f\left(x_r\right)\prod _{1\le j\le t,j\ne r}\frac{-x_j}{x_r-x_j}.(4)$

4 An example

To give a clear explanation of our protocol, we will take a (3, 4) threshold protocol as an example in the following. Suppose the secret holder Alice wants to share her secret 00001 with the participants. Obviously, $S=1$.

4.1 Alice’s preparation

Alice picks a polynomial $f\left(x\right)=1+x+x^2$. She respectively announces $x_1=1,x_2=2,x_3=3,x_4=4$ to ${\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,{\mathrm{B}\mathrm{o}\mathrm{b}}_3,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{B}\mathrm{o}\mathrm{b}}_4$. Alice also computes $f\left(x_1\right)=3,f\left(x_2\right)=7,f\left(x_3\right)=13,f\left(x_4\right)=21$, which are the values Alice wants to distribute to classical participants.

Alice randomly prepares 5 decoy particles in one of the states $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$, which compose $S_0=\left\{{\left|0\right.〉}_A,{\left|1\right.〉}_A,{\left|+\right.〉}_A,{\left|-\right.〉}_A,{\left|0\right.〉}_A\right\}$.

4.2 Secret sharing

Alice sends $S_0$ to ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$. After that, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ creates a 5-bit private key $b_1=00000$ for himself. Therefore, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ prepares 5 particles in $\left|0\right.〉$ and inserts these particles into $S_0$ to form a new sequence $S_1=\left\{{\left|0\right.〉}_A,{\left|0\right.〉}_{B1},{\left|1\right.〉}_A,{\left|0\right.〉}_{B1},{\left|+\right.〉}_A,\right.\left.{\left|0\right.〉}_{B1},{\left|-\right.〉}_A,{\left|0\right.〉}_{B1},{\left|0\right.〉}_A,{\left|0\right.〉}_{B1}\right\}$. Then ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ sends $S_1$ to ${\mathrm{B}\mathrm{o}\mathrm{b}}_2$.

${\mathrm{B}\mathrm{o}\mathrm{b}}_2$ creates his private key $b_2=$ 01010. He prepares corresponding particles and inserts them into $S_1$. Therefore, the new sequence is $S_2=\left\{{\left|0\right.〉}_{B2},{\left|0\right.〉}_A,\right.{\left|0\right.〉}_{B1},{\left|1\right.〉}_A,\left.{\left|1\right.〉}_{B2},{\left|0\right.〉}_{B1},{\left|+\right.〉}_A,{\left|0\right.〉}_{B2},{\left|0\right.〉}_{B1},{\left|-\right.〉}_A,{\left|0\right.〉}_{B1},{\left|0\right.〉}_A,{\left|1\right.〉}_{B2},{\left|0\right.〉}_{B1},{\left|0\right.〉}_{B2}\right\}.$${\mathrm{B}\mathrm{o}\mathrm{b}}_3$’s private key is $b_3=$ 11100 and ${\mathrm{B}\mathrm{o}\mathrm{b}}_4$’s private key is $b_4=$ 11111. They do the operations similar to ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$ and ${\mathrm{B}\mathrm{o}\mathrm{b}}_2$. The final sequence received by Alice is $S_4$. Here, $\begin{array}{c}{S}_4=\left\{{\left|1\right.〉}_{B4},{\left|0\right.〉}_{B2},{\left|1\right.〉}_{B4},{\left|1\right.〉}_{B3},{\left|1\right.〉}_{B3},{\left|1\right.〉}_{B3},{\left|0\right.〉}_A,{\left|0\right.〉}_{B3},{\left|0\right.〉}_{B3},{\left|0\right.〉}_{B1},{\left|1\right.〉}_A,{\left|1\right.〉}_{B2},{\left|0\right.〉}_{B1},\right.\\ \left.{\left|+\right.〉}_A,{\left|0\right.〉}_{B2},{\left|0\right.〉}_{B1},{\left|-\right.〉}_A,{\left|0\right.〉}_{B1},{\left|0\right.〉}_A,{\left|1\right.〉}_{B2},{\left|0\right.〉}_{B1},{\left|0\right.〉}_{B2},{\left|1\right.〉}_{B4},{\left|1\right.〉}_{B4},{\left|1\right.〉}_{B4}\right\}.\end{array}$

For eavesdropping detection, participants announce where they insert their particles. Alice can obtain the positions of her particles. She measures these particles with proper measurement basis and checks the error rate. For example, if Alice prepares $\left|+\right.〉$ in $S_0$, she should measure the corresponding particle in $S_4$ with X basis after receiving the final sequence from ${\mathrm{B}\mathrm{o}\mathrm{b}}_4$. If there is no eavesdropper, the measurement result will be $\left|+\right.〉$. Once the result is different from $\left|+\right.〉$, there exists an eavesdropper. Then, Alice can evaluate the error rate. If the error rate exceeds the predefined threshold value, they will restart the protocol.

After eavesdropping detection, Alice measures the remaining particles with Z basis. Subsequently, she obtains $b_i$ of ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$. According to the relationship established in Step 7, Alice computes $a_i=b_i\oplus c_i$, where $c_i$ is the binary bit string of $f\left(x_i\right)$. She obtains a new binary sequence $K_A=00110001010101011010$, which is composed of $a_i$. Then Alice announces $K_A$.

All participants declare where they insert their particles in Step 6, so ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ knows the positions of his particles. ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ can obtain his $a_i$ from $K_A$ and calculate $c_i$, because $c_i=b_i\oplus a_i=b_i\oplus b_i\oplus c_i$. For ${\mathrm{B}\mathrm{o}\mathrm{b}}_1$, $c_1=a_1\oplus b_1=00011\oplus 00000=00011.\text{For}$ ${\mathrm{B}\mathrm{o}\mathrm{b}}_2$, $c_2=a_2\oplus b_2=01101\oplus 01010=00111.\text{For}$ ${\mathrm{B}\mathrm{o}\mathrm{b}}_3$, $c_3=a_3$ $\oplus b_3=10001\oplus 11100=01101.\text{For}$ ${\mathrm{B}\mathrm{o}\mathrm{b}}_4$, $c_4=a_4\oplus b_4=01010\oplus 11111=10101$

Finally, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ transforms the binary bit $c_i$ into the integer $f\left(x_i\right)$.

4.3 Secret recovery

Suppose three participants, ${\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{B}\mathrm{o}\mathrm{b}}_3$, try to recover Alice’s secret. According to the Lagrange interpolation,

$\begin{array}{l}S={\displaystyle \sum _{i=1}^t}f\left(x_i\right){\displaystyle \prod _{j=1,j\ne i}^t}\frac{x_j}{x_j-x_i}\\ =f\left(x_1\right)\cdot \frac{x_2}{x_2-x_1}\cdot \frac{x_3}{x_3-x_1}\cdot \frac{x_4}{x_4-x_1}+f\left(x_2\right)\cdot \frac{x_1}{x_1-x_2}\cdot \frac{x_3}{x_3-x_2}\cdot \frac{x_4}{x_4-x_2}\\ +f\left(x_3\right)\cdot \frac{x_1}{x_1-x_3}\cdot \frac{x_2}{x_2-x_3}\cdot \frac{x_4}{x_4-x_3}\\ =3\cdot \frac{2}{2-1}\cdot \frac{3}{3-1}\cdot \frac{4}{4-1}+7\cdot \frac{1}{1-2}\cdot \frac{3}{3-2}\cdot \frac{4}{4-2}+13\cdot \frac{1}{1-3}\cdot \frac{2}{2-3}\cdot \frac{4}{4-3}\\ =9-21+13=1.\end{array}(5)$

In this way, they complete a (3,4) threshold SQSS protocol and recover the secret shared by Alice.

5 Security analysis and comparison

In this section, we will analyze the security of our protocol and further compare our protocol with some SQSS protocols. An inside participant has a more powerful ability to eavesdrop on an SQSS protocol than an outside attacker. If a protocol can resist the attack from an inside participant, it is also secure for an outside attacker. Thus, in the following security analysis, we focus on the attack from an inside participant. The dishonest participant will try to steal Alice’s secret by using the following attack strategies.

5.1 Measure-resend attack

Suppose that ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ is the malicious participant. To obtain Alice’s shared integers ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ needs to intercept the sequence $S_n$ when ${\mathrm{B}\mathrm{o}\mathrm{b}}_n$ sends it to Alice. Then ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ measures all particles in $S_n$ with Z basis. After that, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ can get any participant’s private key $b_j$ after every participant announces where he inserts his particles. However, without knowing the positions of the particles prepared by Alice, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ would be detected by the security checks in Step 4. Concretely speaking, if Alice prepares $\left|0\right.〉$ or $\left|1\right.〉$, the state will not be changed. But if Alice prepares $\left|+\right.〉$ or $\left|-\right.〉$, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s attack will make the particle collapse into $\left|0\right.〉$ or $\left|1\right.〉$. For each decoy particle prepared in X basis, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s measure-resend attack on it will be detected by the security check with a probability of 50%. To sum up, the probability that Alice can detect ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s eavesdropping is $1-{\left(\frac{1}{2}\right)}^k$, where k represents the num of $\left|+\right.〉$ or $\left|-\right.〉$ in $S_0$. If k is large enough, the detection probability will approach to 100%. Therefore, $K_A$ will not be declared. According to $c_j=a_j\oplus b_j$, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ is unable to calculate any ${\mathrm{B}\mathrm{o}\mathrm{b}}_j$’s $c_j$ or $f\left(x_j\right)$ without $a_j$. Finally, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ cannot get Alice’s secret S.

5.2 Intercept-resend attack

To obtain Alice’s shared integers, the malicious participant ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ needs to intercept the sequence $S_n$ when ${\mathrm{B}\mathrm{o}\mathrm{b}}_n$ sends it to Alice. Afterward, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ keeps the (n+1)N particles in his hand and prepares (n+1)N fake particles with Z basis. Subsequently, he sends the fake sequence to Alice. However, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ does not know the positions of Alice’s particles. He replaces Alice’s particles with his fake particles. When Alice measures ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ fake particles in X basis in Step 6, she will obtain an incorrect result with a probability of 50%. Assume that there are k decoy particles prepared with X basis in $S_0$, the probability that ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ eavesdropping will be detected is $1-{\left(\frac{1}{2}\right)}^k$, which approaches 100%. So ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ cannot pass the security check. That is, Alice will not declare $K_A$, which makes it impossible for ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ to obtain Alice’s secret.

5.3 Entangle-measure attack

Suppose that ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ is the dishonest participant. He cannot discover the difference between the particles prepared by Alice and those prepared by other participants. Therefore, he has to entangle his auxiliary particles with all of them. ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ uses a unitary operation $U_E$ to entangle an ancillary particle on each of the transmitted particles and then measures the ancillary particles to obtain Alice’s shared secret information.

$U_E\left|0\right.〉\left|E\right.〉={\alpha }_0\left|0\right.〉\left|e_{00}\right.〉+{\beta }_0\left|1\right.〉\left|e_{01}\right.〉.(6)$

$U_E\left|1\right.〉\left|E\right.〉={\alpha }_1\left|0\right.〉\left|e_{10}\right.〉+{\beta }_1\left|1\right.〉\left|e_{11}\right.〉.(7)$

$\begin{array}{l}{U}_E\left|+\right.〉\left|E\right.〉=\frac{1}{\sqrt{2}}\left({\alpha }_0\left|e_{00}\right.〉+{\alpha }_1\left|e_{10}\right.〉\right)\left|0\right.〉+\frac{1}{\sqrt{2}}\left({\beta }_0\left|e_{01}\right.〉+{\beta }_1\left|e_{11}\right.〉\right)\left|1\right.〉\\ =\frac{1}{2}\left({\alpha }_0\left|e_{00}\right.〉+{\alpha }_1\left|e_{10}\right.〉+{\beta }_0\left|e_{01}\right.〉+{\beta }_1\left|e_{11}\right.〉\right)\left|+\right.〉\\ +\frac{1}{2}\left({\alpha }_0\left|e_{00}\right.〉+{\alpha }_1\left|e_{10}\right.〉-{\beta }_0\left|e_{01}\right.〉-{\beta }_1\left|e_{11}\right.〉\right)\left|-\right.〉.\end{array}(8)$

$\begin{array}{l}{U}_E\left|-\right.〉\left|E\right.〉=\frac{1}{\sqrt{2}}\left({\alpha }_0\left|e_{00}\right.〉-{\alpha }_1\left|e_{10}\right.〉\right)\left|0\right.〉+\frac{1}{\sqrt{2}}\left({\beta }_0\left|e_{01}\right.〉-{\beta }_1\left|e_{11}\right.〉\right)\left|1\right.〉\\ =\frac{1}{2}\left({\alpha }_0\left|e_{00}\right.〉-{\alpha }_1\left|e_{10}\right.〉+{\beta }_0\left|e_{01}\right.〉-{\beta }_1\left|e_{11}\right.〉\right)\left|+\right.〉\\ +\frac{1}{2}\left({\alpha }_0\left|e_{00}\right.〉-{\alpha }_1\left|e_{10}\right.〉-{\beta }_0\left|e_{01}\right.〉+{\beta }_1\left|e_{11}\right.〉\right)\left|-\right.〉.\end{array}(9)$

Here, ${\left|{\alpha }_0\right|}^2+{\left|{\beta }_0\right|}^2={\left|{\alpha }_1\right|}^2+{\left|{\beta }_1\right|}^2=1$. If ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ wants to avoid introducing an error, he must make his operation meet the following relations:

$\left\{\begin{array}{l}{U}_E\left|0\right.〉\left|E\right.〉=\left|0\right.〉\left|e_0\right.〉,\\ U_E\left|1\right.〉\left|E\right.〉=\left|1\right.〉\left|e_1\right.〉,\\ U_E\left|+\right.〉\left|E\right.〉=\left|+\right.〉\left|e_{+}\right.〉,\\ U_E\left|-\right.〉\left|E\right.〉=\left|-\right.〉\left|e_{-}\right.〉.\end{array}\right.(10)$

We can infer

$\left\{\begin{array}{l}{\beta }_0\left|e_{01}\right.〉=\mathbf{0},\\ {\alpha }_1\left|e_{10}\right.〉=\mathbf{0},\\ {\alpha }_0\left|e_{00}\right.〉+{\alpha }_1\left|e_{10}\right.〉-{\beta }_0\left|e_{01}\right.〉-{\beta }_1\left|e_{11}\right.〉=\mathbf{0},\\ {\alpha }_0\left|e_{00}\right.〉-{\alpha }_1\left|e_{10}\right.〉+{\beta }_0\left|e_{01}\right.〉-{\beta }_1\left|e_{11}\right.〉=\mathbf{0}.\end{array}\right.(11)$

Here, 0 denotes a column zero vector.

Then, the deduced results are as follows:

$\left\{\begin{array}{l}{\alpha }_1={\beta }_0=0,\\ {\alpha }_0={\beta }_1=1.\end{array}\right.(12)$

From Eq. 12, we can create Eq. 13:

$\left|e_{00}\right.〉=\left|e_{11}\right.〉.(13)$

In this way, the final results can be deduced as the following, Eq. 14:

$\left\{\begin{array}{l}{U}_E\left|0\right.〉\left|E\right.〉=\left|0\right.〉\left|e_{00}\right.〉=\left|0\right.〉\left|e_{11}\right.〉,\\ U_E\left|1\right.〉\left|E\right.〉=\left|1\right.〉\left|e_{11}\right.〉=\left|1\right.〉\left|e_{00}\right.〉.\end{array}\right.(14)$

So, ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ cannot distinguish $\left\{\left|0\right.〉,\left|1\right.〉\right\}$ without introducing an error. Once errors are found in the eavesdropping checks, Alice will abort the protocol, and ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ will obtain no information about Alice’s secret.

5.4 Collusion attack

Two or more dishonest participants may try to steal other participants’ secret shadows by stealing their private keys. First, we assume that ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}$ and ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$ are the ones who start the collusion attack to obtain ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s private key. After receiving the sequence $S_{i-1}$, ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}$ prepares fake particles and then sends the fake sequence to ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$. Then ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ inserts his particles into the fake sequence and sends it to ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$. ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}$ and ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$ try to perform measurement on the new sequence to steal ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s private key. Neither ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}$ nor ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$ knows the positions of ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s particles because the order is disrupted after ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ inserts his particles. That means it is impossible for ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$ to distinguish ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s particles from the fake particles after measuring all the particles with Z basis. So ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1}$ cannot obtain ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ private key without being detected in Step 6. If dishonest participants cannot pass through Alice’s check, Alice will not declare $K_A$. As a result, dishonest participants cannot get any information about ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ secret shadow.

Subsequently, we will discuss the situation where $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,\dots ,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}\right\}$ and $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1},{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+2},\dots ,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{B}\mathrm{o}\mathrm{b}}_t\right\}$ cooperate to steal ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ private key. Because of the collusion among $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_1,{\mathrm{B}\mathrm{o}\mathrm{b}}_2,\dots ,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}\right\}$, dishonest participants can master the positions of Alice’s decoy particles in $S_{i-1}$. ${\mathrm{B}\mathrm{o}\mathrm{b}}_{i-1}$ prepares a fake sequence and sends it to ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$. However, upon receiving the new sequence from ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$, $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1},{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+2},\dots ,{\mathrm{B}\mathrm{o}\mathrm{b}}_t\right\}$ are unable to know where ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$ inserts his particles. That is, $\left\{{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+1},{\mathrm{B}\mathrm{o}\mathrm{b}}_{i+2},\dots ,{\mathrm{B}\mathrm{o}\mathrm{b}}_t\right\}$ can no longer distinguish ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s particles from the fake particles. In this case, it is almost impossible for dishonest participants to steal ${\mathrm{B}\mathrm{o}\mathrm{b}}_i$’s private key and pass the security check. If the collusion attack is detected, Alice will not declare $K_A$, and dishonest participants cannot get any information about ${{\mathrm{B}\mathrm{o}\mathrm{b}}_i}^{\prime }\mathrm{s}$ secret shadow.

In this section, we prove that the proposed protocol is secure enough to resist measure-resend attack, intercept-resend attack, entangle-measure attack, and collusion attack.

5.5 Comparison

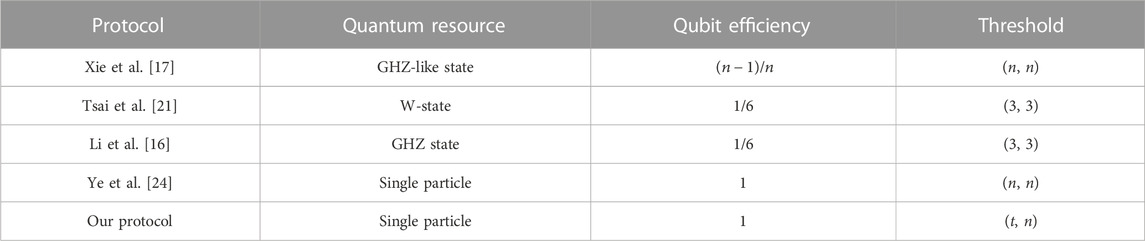
Here, we will give a comparison with some SQSS protocols. The comparison results are displayed in Table 1. The qubit efficiency is defined as $\eta =n/m$, where n denotes the number of the useful qubits, and m denotes the number of the qubits transmitted.

TABLE 1

TABLE 1. Comparison of the SQSS protocols.

In terms of the threshold structure, our protocol is (t, n) threshold protocol. That is, the proposed protocol is more flexible than the (n, n) threshold protocols in Refs. [17, 21, 16, 24]. For quantum resources, all participants in our protocol use single particles, which are easier to prepare than entangled states used in the protocols in Refs. [17, 21, 16]. Furthermore, in our protocol, except for the decoy particles, all particles prepared are used to carry the secret shadows in principle. Thus, the qubit efficiency of our protocol can achieve 100%. Therefore, our protocol has better qubit efficiency than the protocols in Refs. [17, 21, 16]. In summary, our protocol is efficient, and it is more flexible than these protocols.

6 Conclusion

In this paper, we have proposed a (t, n) threshold SQSS protocol. Different from previous SQSS protocols, any t out of n classical participants can recover the secret in our protocol. Next, as quantum resources, single particles used in our protocol are easy to prepare. Moreover, except decoy particles, all particles are useful to transmit secret shadows, so the qubit efficiency of our protocol can achieve 100%. In addition, for classical participants, only the capability to prepare and insert single particles is required in our protocol. On the whole, the protocol proposed in this paper is flexible and efficient.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial and intellectual contribution to this work and approved it for publication.

Funding

National Science Foundation of China (Grant No. 62272051) Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant No. 2019BDKFJJ014). Project supported by the National Key R&D Program of China (Grant No. 2020YFB1805405), the 111 Project (Grant No. B21049), the National Science Foundation of China (Grant No. 62272051), the Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant No. 2019BDKFJJ014), and the Fundamental Research Funds for the Central Universities, China (Grant Nos. 2020RC38, 2019XD-A02).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shamir A. How to share a secret. Commun ACM (1979) 22(11):612–3. doi:10.1145/359168.359176

CrossRef Full Text | Google Scholar

2. Yin A, Wang Z, Fu F. A novel semi-quantum secret sharing scheme based on Bell states. Mod Phys Lett B (2017) 31(13):1750150. doi:10.1142/S0217984917501500

CrossRef Full Text | Google Scholar

3. Hillery M, Bužek M, Berthiaume A. Quantum secret sharing. Phys Rev A (1999) 59(3):1829–34. doi:10.1103/PhysRevA.59.1829

CrossRef Full Text | Google Scholar

4. Guo GP, Guo GC. Quantum secret sharing without entanglement. Phys Lett A (2003) 310(4):247–51. doi:10.1016/S0375-9601(03)00074-4

CrossRef Full Text | Google Scholar

5. Wang T, Wen Q, Chen X, Guo F, Zhu F. An efficient and secure multiparty quantum secret sharing scheme based on single photons. Opt Commun (2008) 281(24):6130–4. doi:10.1016/j.optcom.2008.09.026

CrossRef Full Text | Google Scholar

6. Karimipour V, Bahraminasab A, Bagherinezhad S. Entanglement swapping of generalized cat states and secret sharing. Phys Rev A (2002) 65(4):042320. doi:10.1103/PhysRevA.65.042320

CrossRef Full Text | Google Scholar

7. Chau HF. Practical scheme to share a secret key through a quantum channel with a 27.6% bit error rate. Phys Rev A (2002) 66(6):060302. doi:10.1103/PhysRevA.66.060302

CrossRef Full Text | Google Scholar

8. Li Y, Zhang K, Peng K. Multiparty secret sharing of quantum information based on entanglement swapping. Phys Lett A (2004) 324(5-6):420–4. doi:10.1016/j.physleta.2004.03.034

CrossRef Full Text | Google Scholar

9. Wang HF, Ji X, Zhang S. Improving the security of multiparty quantum secret splitting and quantum state sharing. Phys Lett A (2006) 358(1):11–4. doi:10.1016/j.physleta.2006.04.110

CrossRef Full Text | Google Scholar

10. Lin S, Wen QY, Gao F, Zhu FC. Improving the security of multiparty quantum secret sharing based on the improved Boström–Felbinger protocol. Opt Commun (2008) 281(17):4553–4. doi:10.1016/j.optcom.2008.05.026

CrossRef Full Text | Google Scholar

11. Gao G. Improvement of efficient multiparty quantum secret sharing based on bell states and continuous variable operations. Int J Theor Phys (2014) 53(7):2231–5. doi:10.1007/s10773-014-2023-y

CrossRef Full Text | Google Scholar

12. Wang J, Zhang S, Zhang Q, Tang CJ. Semiquantum key distribution using entangled states. Chin Phys Lett (2011) 28(10):100301. doi:10.1088/0256-307X/28/10/100301

CrossRef Full Text | Google Scholar

13. Gao G. Secure multiparty quantum secret sharing with the collective eavesdropping-check character. Quan Inf Process (2013) 12(1):55–68. doi:10.1007/s11128-011-0351-x

CrossRef Full Text | Google Scholar

14. Rahaman R, Parker MG. Quantum scheme for secret sharing based on local distinguishability. Phys Rev A (2015) 91(2):022330. doi:10.1103/PhysRevA.91.022330

CrossRef Full Text | Google Scholar

15. Gao G, Wang Y, Wang D. Multiparty semiquantum secret sharing based on rearranging orders of qubits. Mod Phys Lett B (2016) 30(10):1650130. doi:10.1142/S021798491650130X

CrossRef Full Text | Google Scholar

16. Li Q, Chan WH, Long DY. Semiquantum secret sharing using entangled states. Phys Rev A (2010) 82(2):022303. doi:10.1103/PhysRevA.82.022303

CrossRef Full Text | Google Scholar

17. Xie C, Li L, Qiu D. A novel semi-quantum secret sharing scheme of specific bits. Int J Theor Phys (2015) 54(10):3819–24. doi:10.1007/s10773-015-2622-2

CrossRef Full Text | Google Scholar

18. Li Z, Li Q, Liu C, Peng Y, Chan WH. Limited resource semiquantum secret sharing. Quan Inf Process (2018) 17(10):285–11. doi:10.1007/s11128-018-2058-8

CrossRef Full Text | Google Scholar

19. Yin A, Chen T. Authenticated semi-quantum secret sharing based on GHZ-type states. Int J Theor Phys (2021) 60(1):265–73. doi:10.1007/s10773-020-04688-7

CrossRef Full Text | Google Scholar

20. Hu WW, Zhou RG, Luo J. Semi-quantum secret sharing in high-dimensional quantum system using product states. Chin J Phys (2022) 77:1701–12. doi:10.1016/j.cjph.2022.03.031

CrossRef Full Text | Google Scholar

21. Tsai CW, Yang CW, Lee NY. Semi-quantum secret sharing protocol using W-state. Mod Phys Lett A (2019) 34(27):1950213. doi:10.1142/S0217732319502134

CrossRef Full Text | Google Scholar

22. Cao G, Chen C, Jiang M. A scalable and flexible multi-user semi-quantum secret sharing. In: Proceedings of the 2nd International Conference on Telecommunications and Communication Engineering; November 2018; Beijing China (2018). p. 28–32. doi:10.1145/3291842.3291857

CrossRef Full Text | Google Scholar

23. Yin AH, Tong Y. A novel semi-quantum secret sharing scheme using entangled states. Mod Phys Lett B (2018) 32(22):1850256. doi:10.1142/S0217984918502561

CrossRef Full Text | Google Scholar

24. Ye CQ, Ye TY. Circular semi-quantum secret sharing using single particles. Commun Theor Phys (2018) 70(6):661. doi:10.1088/0253-6102/70/6/661

CrossRef Full Text | Google Scholar

25. Li XY, Chang Y, Zhang SB. Multi-party semi-quantum secret sharing protocol based on Bell states. In: Proceedings of the International Conference on Artificial Intelligence and Security; November 2020; Cham (2020). p. 280–8. doi:10.1007/978-3-030-57881-7_25

CrossRef Full Text | Google Scholar

26. Tian Y, Li J, Chen XB, Ye CQ, Li HJ. An efficient semi-quantum secret sharing protocol of specific bits. Quan Inf Process (2021) 20(6):217–1. doi:10.1007/s11128-021-03157-2

CrossRef Full Text | Google Scholar

27. Tian Y, Li J, Yuan KG, Li HJ, Chen XB. An efficient semi-quantum key distribution protocol based on EPR and single-particle hybridization. QUANTUM INFORMATION COMPUTATION (2021) 21(7-8):563–76. doi:10.26421/QIC21.7-8-3

CrossRef Full Text | Google Scholar

28. Yang YG, Wen QY. Threshold quantum secure direct communication without entanglement. Sci China Ser G: Phys Mech Astron (2008) 51(2):176–83. doi:10.1007/s11433-008-0028-3

CrossRef Full Text | Google Scholar

29. Qin HW, Dai YW. An efficient (t, n) threshold quantum secret sharing without entanglement. Mod Phys Lett B (2016) 30(12):1650138. doi:10.1142/S0217984916501384

CrossRef Full Text | Google Scholar

30. Lu CB, Miao FY, Meng KJ, Yu Y. Threshold quantum secret sharing based on single qubit. Quan Inf Process (2018) 17:64–13. doi:10.1007/s11128-017-1793-6

CrossRef Full Text | Google Scholar

31. Li L, Li Z. A multi-party quantum key agreement protocol based on Shamir’s secret sharing. Int J Theor Phys (2019) 58:3081–90. doi:10.1007/s10773-019-04187-4

CrossRef Full Text | Google Scholar