Moore–Gibson–Thompson model with the influence of moisture diffusivity of semiconductor materials during photothermal excitation

In the present work, the semiconductor material is used to study the moisture diffusivity when a modified Moore–Gibson–Thompson (MGT) model is taken into account. The influence of moisture concentration is included in the governing equations throughout the photothermal transfer process. Based on the dissimilar relaxation durations of the coupled optoelectronic and thermoelastic waves, the MGT model is used to investigate the issue at hand. The method of the Laplace transform is used to obtain analytical solutions for the physical quantities, constitutive relationships, elastic waves, carrier density, heat equation conduction, and moisture diffusivity for the thermo-elastic medium. To extract the primary physical quantities in the space–time domain, the boundary conditions, temperature, plasma, displacement, and mechanical stress are inverted numerically using the Laplace transform. The effect of the new parameter like the reference moisture parameter with various values is discussed graphically on the primary physical quantities. The comparison between silicon and germanium is taken into account to achieve numerical computations.

1 Introduction

The stress field is responsible for producing the temperature field, and the stress field modulates the strain and stress fields. Force loads and thermal stresses are common sources of damage to structural parts. A crack may occur if the strains are great enough or if the strains combine with mechanical stresses from external loads. Recently, many scientists have been concerned with semiconductor materials; this is due to their many modern applications, such as aircraft electronics and sensors. In semiconductors, some materials have unique properties like highly conductive materials such as copper. In semiconductors, the most important effect property in modern industries is the photothermal (PT) excitation process that happens when temperature increases to release electrons to the surface of the material, which makes the material a good conductor of electricity. The process of electrons gaining energy because of increasing temperature is called electronic deformation (plasma), and this process causes an electric current. Light absorbed by the material causes a local increase in temperature and pressure, and a proportional increase in volume, according to the PT effect.

Biot [1] was the first to highlight the solution for the coupled thermo-elasticity. The Fourier heat conduction theory is considered the basis for the conventional dynamic (CD) theory of the thermo-elasticity theory. The CD assumes that wave propagation can travel at an unlimited speed because of the parabolic form found in the governing equations, and this theory was unacceptable for the physical experiments. Because of this inconsistency, Lord and Shulman (LS) [2] introduced a new model by putting one relaxation time in the equations, which makes the system of equations take the hyperbolic form, making the thermal waves propagate at a finite speed. Green–Lindsay (GL) [3] modified a new model of thermoelasticity containing two relaxation times, which makes many researchers utilize this model to conduct numerous studies. Many authors [4, 5] have used the GL theory known as the generalized thermoelasticity theory. After adding the relaxation factor to the suggested heat equation to Green–Naghdi III (GN-III) by Abouelregal et al. [6], many authors tend to utilize the modified thermoelastic theory in the context of the MGT equation because of its importance in many applications and also it was derived using a third-order differential equation. Othman et al. [7] studied the transient disturbance according to the moving heat source in the generalized magneto-thermoelasticity theory. Quintanilla [8, 9] has developed thermoelastic MGT heat conduction. Marin et al. [10–13] analyzed the thermoelasticity theory in the context of the MGT model’s starting values, as set by the dipolar elastic property. Recent evidence [14] shows that the MGT equation may be used in a wide range of contexts. Using a thermoelastic semiconductor material, Lotfy et al. [15, 16] employed the MGT model to prove the stability of their analytical solutions.

We argue that the fundamental ideas behind heat transmission and moisture transport are similar. Mechanically induced stresses may have significant effects on how heat and moisture are distributed. Understanding the relationship between mechanical deformation and diffusion caused by temperature and moisture is so crucial. There are a wide variety of engineering problems where the correlation between humidity, temperature, and deformation may be seen. When a solid is subjected to both moisture and heat, a phenomenon known as hygro-thermoelasticity takes place. Szekeres [17, 18] published research discussing moisture’s impact on conventional heat transmission. More so than mechanical loadings, Gasch et al. [19] discussed temperature and moisture fluctuations. Szekeres and Engelbrecht [20] established a fundamental analogy between heat and moisture before proceeding with creating equations governing coupled hygro-thermoelasticity.

Semiconducting materials found widespread use in contemporary engineering because of technological advancements. There is both theoretical and practical usefulness in learning more about how waves travel through a semiconducting material. Unfortunately, the author was unable to find any previous documentation of the wave propagation issue in semiconducting media during a PT process. The fundamental principle shared by all PT techniques is the detection of short-lived thermal waves generated in the sample upon its absorption of modulated light. When an appropriate transducer picks up these pressure fluctuations in the surrounding gaseous medium, we obtain the photoacoustic (PA) signal. This happens because the absorbed energy is transformed into heat both in the bulk and on the surface of the sample. The PA technique uses a PA signal obtained experimentally to determine where the heat is coming from that is causing the thermal waves. So, in addition to the optical characteristics of the sample, we may also learn about its thermal parameters, structural formations, and inhomogeneities from the PA response. Several authors have created cutting-edge approaches to investigate the laser–semiconductor interaction in photoacoustic spectroscopy [21, 22]. Several physical studies using PT techniques [23–27] confirmed the accurate temperatures, internal displacements, thermal diffusion, and other electrical features of nano-composite semiconductor materials. Elastic oscillations in the atomic lattices of a material are directly responsible for the electronic deformation induced by light. Hobiny and Abbas [28] used a semiconductor-filled cylinder cavity to investigate PT waves in free space. When a semiconducting material is subjected to PT waves with hydrostatic stress, moisture diffusivity with non-local parameters, two temperatures, laser pulses, and the resulting strain stresses become problematic [29, 30]. Applying the photo-thermoelasticity hypothesis to the case of the Moore–Gibson–Thompson (MGT) stability model in a photonic semiconductor material subject to a two-temperature theory, Chteoui et al. [31] found support for their theory. On the other hand, Hobiny and Abbas [32–34] used a theoretical analysis to obtain the effect of a moving heat source with laser irradiation on skin tissue during thermal damage. Many applications according to the bioheat model based on the thermoelasticity theory are studied for living tissue [35–38].

In recent years, the MGT equation has gained a lot of attention because it may be used in a variety of contexts. Recent years have seen a rise in the profile of research into PT phenomena within the context of the subject of material science. It may be used in the evaluation of the thermal, optical, and electrical properties of various materials. In this research, moisture diffusivity is used to analyze the moisture and heat equation that occurs during the PT MGT process in one dimension when the mechanical force and moisture diffusivity are both in play. The issue is posed at the free surface of a semi-infinite semiconducting material in its most general form. To solve the system and obtain an analytical solution for the primary physical fields, the Laplace transform is used. To declare the physical numbers, the numerical inverse of the Laplace transform must be executed by utilizing a computer language. In conclusion, the results of all calculations regarding the distribution of temperature, carrier intensity, normal displacement, normal force stress, and moisture concentration are visually depicted.

2 Main equations

During the PT transport phase, the medium is analyzed with the overlapping processes of plasma–thermal and moisture diffusion in mind if the thermo-elastic semiconductor material exhibits linear elastic properties and is homogeneously transversely anisotropic. In this problem, the fundamental distributions in this problem are the carrier density (intensity) $N\left(r_i,t\right)$, moisture concentration $m\left(r_i,t\right)$, the temperature change of a material particle $T\left(r_i,t\right)$, and the displacement vector $u\left(r_i,t\right)$, ($r_i$ represents the position vector, and $t$ represents the time). Tensor forms of the equations for the interaction of plasma–thermal–elastic waves and moisture diffusion are given in [15, 16]:

$\frac{\partial \mathit{N}\left({\mathit{r}}_{\mathit{i}},\mathit{t}\right)}{\partial \mathit{t}}={\mathit{D}}_{\mathit{E}}{\mathit{N}}_{,\mathit{i}\mathit{i}}\left({\mathit{r}}_{\mathit{i}},\mathit{t}\right)-\frac{\mathit{N}\left({\mathit{r}}_{\mathit{i}},\mathit{t}\right)}{\mathit{\tau }}+\mathit{\kappa }\mathit{T}\left({\mathit{r}}_{\mathit{i}},\mathit{t}\right),(1)$

$\left.\begin{array}{l}\rho C_e\left(D_T\left(k\frac{\partial }{\partial t}+k^{*}\right)T_{,ii}\left(r_i,t\right)+\left(1+{\tau }_0\frac{\partial }{\partial t}\right)D_T^m{m}_{,ii}\left(r_i,t\right)\right)=\\ \left(1+{\tau }_0\frac{\partial }{\partial t}\right)\left(\rho C_e\frac{\partial \mathrm{T}\left(r_i,t\right)}{\partial t}+{\gamma }_t{T}_0\frac{\partial u_{i,j}\left(r_i,t\right)}{\partial t}-\frac{E_g}{\tau }N\left(r_i,t\right)\right)\end{array}\right\},(2)$

$\left.\begin{array}{l}{k}_m\left(D_m\left(k\frac{\partial }{\partial t}+k^{*}\right)m_{,ii}\left(r_i,t\right)+D_m^T{T}_{,ii}\left(r_i,t\right)\right)=\\ \left(k_m\frac{\partial m\left(r_i,t\right)}{\partial t}-\frac{E_g}{\tau }N\left(r_i,t\right)+{\gamma }_m{m}_0{D}_m\frac{\partial u_{i,j}\left(r_i,t\right)}{\partial t}\right)\end{array}\right\}.(3)$

In tensor form, the motion equation is similar to [1–3]:

$\rho \frac{{\partial }^2{u}_i\left(r_i,t\right)}{\partial t^2}={\sigma }_{ij,j}.(4)$

Both the displacement and strain tensor may be represented using the same equation:

${\epsilon }_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right).(5)$

With increasing humidity, the tensor form of stress, displacement, and plasma temperature is similar to the following equation:

${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}-{\beta }_{ij}\left({\alpha }_{t}T+d_{n}N\right)-{\beta }_{ij}^{m}m,i,j,k,l=\mathrm{1,2,3}.(6)$

In the aforementioned equations, the diffusivity parameters are $D_T$ and $D_m,$ which refer to the temperature diffusivity and the moisture diffusion coefficient, respectively. The coupled diffusivities are $D_T^m$ and $D_m^T$. On the other hand, $D_E$ represents the carrier diffusion coefficient, and $m_0$ refers to the reference moisture. The moisture diffusivity is $k_m$, $C_{ijkl}$ represents the isothermal parameter tensor of the medium, ${\epsilon }_{kl}$ represents the strain tensor, and ${\beta }_{ij}$ and ${\beta }_{ij}^m$ represent the isothermal thermoelastic coupling tensor material coefficients of moisture concentration. The thermal activation coupling parameter is $\kappa =\frac{\partial N_0}{\partial T}\frac{T}{\tau }$, and $N_0$ represents the equilibrium carrier concentration [10, 12]. The energy gap, the photogenerated carrier lifetime, the density, Lame’s elastic constants, the volume thermal expansion, and the absolute temperature of the medium are $E_g,\tau ,\rho ,\mu ,\lambda ,{\gamma }_t=\left(3\lambda +2\mu \right){\alpha }_T$ and $T_0$, respectively, where ${\alpha }_T$ represents the linear thermal expansion coefficient. The specific heat of the semiconductor is $C_e$, and ${\delta }_n$ represents the conductive deformation potential with the valence band, where $k^{*}$ represents the rate of thermal conductivity.

When the surface boundary conditions are thermally insulated, the rod representing the semiconductor elastic media is released from the constraints of the electrical short (closed circuit), isothermal, and stress loads. To that purpose, all analyses are performed along the $x$-axis (the direction of wave propagation is along the $x$-axis), and all physical values are arbitrary to the $yz$-coordinate system.

The following are the 1D descriptions of the physical quantities [30]:

$\frac{\partial N}{\partial t}=D_E\frac{{\partial }^{2}N}{\partial x^2}-\frac{N}{\tau }+\kappa T,(7)$

$\left(1+{\tau }_0\frac{\partial }{\partial t}\right)\left(\rho C_e\frac{\partial T}{\partial t}+{\gamma }_t{T}_0\frac{\partial e}{\partial t}-\rho C_e{D}_T^m\frac{{\partial }^{2}m}{\partial x^2}-\frac{E_g}{\tau }N\right)=\rho C_e{D}_T\left(k\frac{\partial }{\partial t}\frac{{\partial }^{2}T}{\partial x^2}+k^{*}\frac{{\partial }^{2}T}{\partial x^2}\right),(8)$

$\left(k_m\frac{\partial m}{\partial t}+{\gamma }_m{m}_0{D}_m\frac{\partial }{\partial t}\left(\frac{\partial u}{\partial x}\right)-k_m{D}_m\left(k\frac{\partial }{\partial t}+k^{*}\right)\frac{{\partial }^{2}m}{\partial x^2}\right)-\frac{E_g}{\tau }N=D_m^T{k}_m\frac{{\partial }^{2}T}{\partial x^2}.(9)$

For Eq. 4, we have

$\rho \frac{{\partial }^{2}u}{\partial t^2}=\left(2\mu +\lambda \right)\frac{{\partial }^{2}u}{\partial x^2}-{\gamma }_t\frac{\partial T}{\partial x}-{\delta }_n\frac{\partial N}{\partial x}-{\gamma }_m\frac{\partial m}{\partial x}.(10)$

Here, ${\gamma }_{t,m}=\beta {\alpha }_{t,m}$ and ${\delta }_n=\beta d_n,\beta =3\mu +2\lambda .$

In one dimension, the constitutive equation is similar to the following equation:

${\sigma }_{xx}=\left(2\mu +\lambda \right)\frac{\partial u}{\partial x}-\beta \left({\alpha }_{t}T+d_{n}N\right)-{\gamma }_{m}m=\sigma .(11)$

The MGT model according to the PT excitation can be expressed as a general form of the LS and GN-III models. In this case, the principal models of the photo-thermoelasticity theory under the MGT effect ($k$, $k^{*}$, and ${\tau }_0$ are non-negative) are reduced to the following cases [31]:

(i) When $k^{*}={\tau }_0=0$, the classical thermoelastic (CTE) model is obtained.

(ii) When $k^{*}=0$ only, the Lord and Shulman (LS) model is attained.

(iii) When $k={\tau }_0=0$, the GN-II model is observed.

(iv) When ${\tau }_0=0$, the GN-III model is obtained.

3 The mathematically formulized problem

The following non-dimensional variables are provided for convenience:

$\left(x^{\prime },u^{\prime }\right)=\frac{\left(x,u\right)}{C_T{t}^{*}},\left(t^{\prime },{{\tau }_0}^{\prime }\right)=\frac{\left(t,{\tau }_0\right)}{t^{*}},\left(T^{\prime },N^{\prime }\right)=\frac{\left({\gamma }_{t}T,{\delta }_{n}N\right)}{2\mu +\lambda },{\sigma }^{\prime }=\frac{\sigma }{\mu },e^{\prime }=e,m^{\prime }=m.(12)$

To simplify Eq. 7, Eq. 8, Eq. 9, Eq. 10, and Eq. 11, we may use Eq. 12 to remove the dashes and obtain

$\left(\frac{{\partial }^2}{\partial {\mathit{x}}^2}-{\mathit{q}}_1-{\mathit{q}}_2\frac{\partial }{\partial \mathit{t}}\right)\mathit{N}+{\mathit{\epsilon }}_1\mathit{T}=0,(13)$

$\left(k\frac{\partial }{\partial t}+t^{*}{k}^{*}\right)\frac{{\partial }^{2}T}{\partial x^2}-\left(1+{\tau }_0\frac{\partial }{\partial t}\right)\left(V_1\frac{\partial T}{\partial t}-V_2\frac{{\partial }^{2}m}{\partial x^2}-V_{3}N+V_4\frac{\partial e}{\partial t}\right)=0,(14)$

$\left(k\frac{\partial }{\partial t}+k^{*}{t}^{*}\right)\frac{{\partial }^{2}m}{\partial x^2}-a_4\frac{\partial m}{\partial t}+a_5\frac{{\partial }^{2}T}{\partial x^2}+a_{6}N-a_7\frac{{\partial }^{2}u}{\partial t\partial x}=0,(15)$

$\left(\frac{{\partial }^2}{\partial x^2}-\frac{{\partial }^2}{\partial t^2}\right)u-\frac{\partial T}{\partial x}-\frac{\partial N}{\partial x}-a_8\frac{\partial m}{\partial x}=0.(16)$

The 1D stress component takes the following form in the non-dimensional form:

${\mathrm{\sigma }}_{\mathrm{x}\mathrm{x}}=a_9\left(\frac{\partial u}{\partial x}-\left(T+N\right)\right)-a_{10}m=\mathrm{\sigma },(17)$

where $q_1=\frac{k{t}^{*}}{D_E\rho \tau C_e}$, $q_2=\frac{k}{D_E\rho C_e}$, ${\epsilon }_1=\frac{d_{n}k\kappa t^{*}}{{\alpha }_T\rho C_e{D}_E}$, $V_1=\frac{k{C}_T^2{t}^{*}}{D_T}$, $V_2=\frac{t^{*}{D}_T^m{\gamma }_t}{\rho C_e{D}_T\left(2\mu +\lambda \right)}$, $t^{*}=\frac{k}{\rho C_e{C}_T^2},V_3=\frac{{\alpha }_T{E}_g{t}^{*}}{\tau d_n\rho C_e{D}_T}$, $V_4=\frac{{\gamma }_t^2{T}_0{t}^{*}}{\rho C_e{D}_T}$, $a_4=\frac{C_T^2{t}^{*}}{D_m}$, $a_5=\frac{D_m^T\left(2\mu +\lambda \right)}{D_m{\gamma }_t}$, $a_6=\frac{E_g\left(2\mu +\lambda \right)t^{*}{a}_4}{k_m{\delta }_n\tau }$, $a_{10}=\frac{{\gamma }_m}{\mu },a_7=\frac{{\gamma }_m{m}_0{C}_T^2{t}^{*}}{k_m}$, $a_8=\frac{{\gamma }_m}{2\mu +\lambda }$, $a_9=\frac{2\mu +\lambda }{\mu }$, $C_T^2=\frac{2\mu +\lambda }{\rho }$, and ${\delta }_n=\left(2\mu +3\lambda \right)d_n$.

The coupled parameter ${\epsilon }_1$ is named the coupling thermoelectric coefficient.

According to the properties of homogeneity of the problem, the following initial conditions to solve the problem analytically are presented:

$\begin{array}{c}{\left.u\left(x,t\right)\right|}_{t=0}={\left.\frac{\partial u\left(x,t\right)}{\partial t}\right|}_{t=0}=0,{\left.T\left(x,t\right)\right|}_{t=0}={\left.\frac{\partial T\left.\left(x,t\right)\right|}{\partial t}\right|}_{t=0}=0,{\left.m\left(x,t\right)\right|}_{t=0}={\left.\frac{\partial m\left(x,t\right)}{\partial t}\right|}_{t=0}=0\\ {\left.\sigma \left(x,t\right)\right|}_{t=0}={\left.\frac{\partial \sigma \left(x,t\right)}{\partial t}\right|}_{t=0}=0,{\left.N\left(x,t\right)\right|}_{t=0}={\left.\frac{\partial N\left(x,t\right)}{\partial t}\right|}_{t=0}=0.\end{array}(18)$

4 The solution to the problem

Laplace transforms used, which are defined for any function $\mathrm{\Theta }\left(x,t\right),$ are as follows:

$L\left(\mathrm{\Gamma }\left(x,t\right)\right)=\overline{\mathrm{\Theta }}\left(x,s\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}}{\mathrm{e}}^{-st}\mathrm{\Theta }\left(x,t\right)dt.(19)$

Applying Eq. 19 to the main aforementioned Eqs 13–17, the following equations are obtained:

$\left({\mathit{D}}^2-{\mathit{\alpha }}_1\right)\overline{\mathit{N}}+{\mathit{\epsilon }}_1\overline{\mathit{T}}=0,(20)$

$\left(V_{10}{D}^2-{\alpha }_2\right)\overline{T}+{\alpha }_3{D}^2\overline{m}+{\alpha }_4\overline{N}-{\alpha }_{5}D\overline{u}=0,(21)$

$\left({\alpha }_6{D}^2-{\alpha }_7\right)\overline{m}+a_5{D}^2\overline{T}+{\alpha }_8\overline{N}-{\alpha }_{9}D\overline{u}=0,(22)$

$\left(D^2-s^2\right)\overline{u}-D\overline{T}-D\overline{N}-a_{8}D\overline{m}=0,(23)$

${\overline{\mathrm{\sigma }}}_{\mathrm{x}\mathrm{x}}=a_9\left(D\overline{u}-\left(\overline{T}+\overline{N}\right)\right)-a_{10}\overline{m},(24)$

where $D=\frac{d}{dx}$, ${\alpha }_1=q_1+q_{2}s$, $V_{10}=ks+k^{*}{t}^{*}$, ${\alpha }_2=\left(1+{\tau }_{0}s\right)s{V}_1$, ${\alpha }_3=\left(1+{\tau }_{0}s\right)V_2$, ${\alpha }_4=\left(1+{\tau }_{0}s\right)V_3$, ${\alpha }_5=\left(1+{\tau }_{0}s\right)s{V}_4$, ${\alpha }_6=V_{10}$, ${\alpha }_7=a_{4}s$, ${\alpha }_8=a_6$, and ${\alpha }_9=a_{7}s$.

Solving the converted Eqs 20–22 and Eq. 23 by the elimination technique between $\overline{T},\overline{u},\overline{N},$ and $\overline{m}$, the following equation is obtained:

$\left(D^8-{\prod }_1{D}^6+{\prod }_2{D}^4-{\prod }_3{D}^2-{\prod }_4\right)\left\{\overline{m},\overline{N},\overline{T},\overline{u}\right\}\left(x,s\right)=0,(25)$

where the main coefficients of Eq. 25 are given as follows:

$\left.\begin{array}{l}{\mathrm{\Pi }}_1=\frac{1}{\left(V_{10}{\alpha }_3-V_{10}{\alpha }_6\right)}(-(-s^2{V}_{10}{\alpha }_3+s^2{V}_{10}{\alpha }_6-V_{10}{a}_8{\alpha }_5+V_{10}{a}_8{\alpha }_9\\ -V_{10}{\alpha }_1{\alpha }_3+V_{10}{\alpha }_1{\alpha }_6+V_{10}{\alpha }_7+{\alpha }_2{\alpha }_6-{\alpha }_3{\alpha }_9+{\alpha }_5{\alpha }_6)),\\ {\mathrm{\Pi }}_2=\frac{1}{\left(V_{10}{\alpha }_3-V_{10}{\alpha }_6\right)}((s^2{V}_{10}{\alpha }_1{\alpha }_3-s^2{V}_{10}{\alpha }_1{\alpha }_6-s^2{V}_{10}{\alpha }_7\\ -s^2{\alpha }_2{\alpha }_6+V_{10}{a}_8{\alpha }_1{\alpha }_5-V_{10}{a}_8{\alpha }_1{\alpha }_9-V_{10}{\alpha }_1{\alpha }_7\\ -a_8{\alpha }_2{\alpha }_9-{\alpha }_1{\alpha }_2{\alpha }_6+{\alpha }_1{\alpha }_3{\alpha }_9-{\alpha }_1{\alpha }_5{\alpha }_6-{\alpha }_3{\alpha }_8{\epsilon }_3\\ +{\alpha }_3{\alpha }_9{\epsilon }_3+{\alpha }_4{\alpha }_6{\epsilon }_3-{\alpha }_5{\alpha }_6{\epsilon }_3-{\alpha }_2{\alpha }_7-{\alpha }_5{\alpha }_7)),\\ {\mathrm{\Pi }}_3=\frac{-1}{\left(V_{10}{\alpha }_3-V_{10}{\alpha }_6\right)}((s^2{V}_{10}{\alpha }_1{\alpha }_7+s^2{\alpha }_1{\alpha }_2{\alpha }_6+s^2{\alpha }_3{\alpha }_8{\epsilon }_3-s^2{\alpha }_4{\alpha }_6{\epsilon }_3\\ +s^2{\alpha }_2{\alpha }_7+a_8{\alpha }_1{\alpha }_2{\alpha }_9-a_8{\alpha }_4{\alpha }_9{\epsilon }_3+a_8{\alpha }_5{\alpha }_8{\epsilon }_9\\ +{\alpha }_1{\alpha }_2{\alpha }_7+{\alpha }_1{\alpha }_5{\alpha }_7-{\alpha }_4{\alpha }_7{\epsilon }_3+{\alpha }_5{\alpha }_7{\epsilon }_3)),\\ {\mathrm{\Pi }}_4=\frac{s^2{\alpha }_1{\alpha }_2{\alpha }_7-s^2{\alpha }_4{\alpha }_7{\epsilon }_3}{\left(V_{10}{\alpha }_3-V_{10}{\alpha }_6\right)}.\end{array}\right\}.(26)$

To solve the differential Eq. 25, the factorization method is given as follows:

$\left(D^2-m_1^2\right)\left(D^2-m_2^2\right)\left(D^2-m_3^2\right)\left(D^2-m_4^2\right)\left\{\overline{T},\overline{u},\overline{N},\overline{m}\right\}\left(x,s\right)=0.(27)$

The quantities $m_i^2\left(i=\mathrm{1,2,3,4}\right)$ are the roots that are chosen real and positive when $x\to \infty$. The linearity solution for thermal distribution according to the differential Eq. 27 can be written as follows:

$\overline{\mathrm{T}}\left(\mathrm{x},\mathrm{s}\right)={\displaystyle \sum _{\mathrm{i}=1}^4}{\mathrm{D}}_{\mathrm{i}}\left(\mathrm{s}\right){\mathrm{e}}^{-{\mathrm{m}}_{\mathrm{i}}\mathrm{x}}.(28)$

The other linear solutions of remain quantities are expressed in the following form:

$\overline{N}\left(x,s\right)={\displaystyle \sum _{i=1}^4}{D}_i^{\prime }\left(s\right)e^{-m_{i}x}={\displaystyle \sum _{i=1}^4}{H}_{1i}{D}_i\left(s\right)e^{-m_{i}x},(29)$

$\overline{u}\left(x,s\right)={\displaystyle \sum _{i=1}^4}{D_i}^{″}\left(s\right)\exp \left(-m_{i}x\right)={\displaystyle \sum _{i=1}^4}{H}_{2i}{D}_i\left(s\right)\exp \left(-m_{i}x\right),(30)$

$\overline{m}\left(x,s\right)={\displaystyle \sum _{i=1}^4}{D}_i^{‴}\left(s\right)\exp \left(-m_{i}x\right)={\displaystyle \sum _{i=1}^4}{H}_{3i}{D}_i\left(s\right)\exp \left(-m_{i}x\right),(31)$

$\overline{\sigma }\left(x,s\right)={\displaystyle \sum _{i=1}^4}{D}_i^{\left(4\right)}\left(s\right)\exp \left(-m_{i}x\right)={\displaystyle \sum _{i=1}^4}{H}_{4i}{D}_i\left(s\right)\exp \left(-m_{i}x\right).(32)$

Here, the parameters $D_i,D_i^{\prime },D_i^{″},$ and ${D_i}^{‴},i=\mathrm{1,2,3,4}$ can be determined when the elimination method between the main Eqs 25–30 is used. The following are the relationships between both of the unknown parameters $D_i,D_i^{\prime },D_i^{″},$ and ${D_i}^{‴}$:

$\begin{array}{c}{H}_{1i}=\frac{-{\epsilon }_3}{{m_i}^2-{\alpha }_1},H_{4i}=a_9\left(m_i{H}_{2i}+\left(1+H_{1i}\right)\right)+a_{10}{H}_{3i},\\ H_{2i}=\frac{-m\left(V_{10}{a}_8-{\alpha }_6\right)m_i^4+\left(-V_{10}{a}_8{\alpha }_1+{\alpha }_1{\alpha }_6+{\alpha }_6{\epsilon }_3+{\alpha }_7\right)m_i^2-{\alpha }_8{a}_8{\epsilon }_3-{\alpha }_7{\alpha }_1-{\epsilon }_3{\alpha }_7}{\left(m_i^2-{\alpha }_1\right)\left({\alpha }_6{m}_i^4+\left(-s^2{\alpha }_6-a_8{\alpha }_9-{\alpha }_7\right)m_i^2+{\alpha }_7{s}^2\right)},\\ H_{3i}=-\frac{m_i^6{V}_{10}+\left(-s^2{V}_{10}-V_{10}{\alpha }_1-{\alpha }_9\right)m_i^4+\left(s^2{V}_{10}{\alpha }_1+{\alpha }_1{\alpha }_9-{\alpha }_8{\epsilon }_3+{\alpha }_9{\epsilon }_3\right)m_i^2+s^2{\alpha }_8{\epsilon }_3}{m_i^6{\alpha }_6+\left(-s^2{\alpha }_6-a_8{\alpha }_9-{\alpha }_1{\alpha }_6-{\alpha }_7\right)m_i^4+\left(s^2{\alpha }_1{\alpha }_6-s^2{\alpha }_7+a_8{\alpha }_1{\alpha }_9-{\alpha }_1{\alpha }_7\right)m_i^2-s^2{\alpha }_1{\alpha }_7}.\end{array}$

The foregoing values provide the domain solution for Laplace’s main variable transformations in terms of unknown parameters $D_i\left(s\right)$, which are derived from the following boundary conditions.

5 Boundary conditions

Assume that the elastic semiconductor medium is subjected to mechanical, plasma, and thermal stresses, with the loss of control over these variables ($D_i$). These forces are imposed on the unconfined (external) surface of the material. Laplace transformations are used in all conditions.

(I) For $x=0$, we define the free-surface isothermal boundary condition (thermally isolated system) exposed to thermal shock as follows:

$\overline{T}\left(0,s\right)=T_{0}Z\left(s\right).(33)$

Accordingly,

${\displaystyle \sum _{n=1}^4}{D}_i\left(s\right)=\frac{T_0}{s}.(34)$

(II) Application of the Laplace transformation to the condition of mechanical normal stress (pressure) components at the free surface $x=0$ produces

${\overline{\sigma }}_{xx}\left(0,s\right)=-n.(35)$

Therefore,

${\displaystyle \sum _{\mathrm{i}=1}^4}\left\{{\mathrm{a}}_9\left({\mathrm{m}}_{\mathrm{i}}{\mathrm{H}}_{2\mathrm{i}}+\left(1+{\mathrm{H}}_{1\mathrm{i}}\right)\right)+{\mathrm{a}}_{10}{\mathrm{H}}_{3\mathrm{i}}\right\}\left({\mathrm{D}}_{\mathrm{i}}\right)=-\mathrm{n}.(36)$

(III) When the carrier density is diffusively transported and photosynthesized during recombination processes, the plasma boundary condition at the free surface ($x=0$) may be reformulated as follows using the Laplace transform:

$\overline{\mathrm{N}}\left(0,\mathrm{s}\right)=\frac{\mathrm{ƛ}}{\stackrel{\sim }{\mathrm{s}}{\mathrm{D}}_{\mathrm{E}}}\overline{\mathrm{R}}\left(\mathrm{s}\right).(37)$

The following equation is obtained:

${\displaystyle \sum _{i=1}^4}{H}_{1i}{D}_i\left(x,s\right)=\frac{\mathrm{ƛ}}{s\stackrel{\sim }{s}{D}_E}.(38)$

(IV) The free-surface displacement boundary condition is given as follows:

$\overline{\mathit{u}}\left(0,\mathit{s}\right)=\mathrm{l}.(39)$

On the other hand, the following relation is obtained:

${\displaystyle \sum _{i=1}^4}{H}_{2i}{D}_i\left(x,s\right)=n.(40)$

The quantities ($Z\left(s\right)$, $R\left(s\right)$), $n$, and $l$ are the Heaviside unit function, stress pressure, and roughness coefficient, respectively. The symbol $\mathrm{ƛ}$ is a chosen constant.

6 Inversion of the Fourier–Laplace transforms

Dimensionless physical fields in the time domain may be obtained by inversion of the Laplace transform. In this case, the Laplace transform may be approximated numerically using the Riemann sum method [39].

In the Laplace domain, the inverse of the function $\overline{\zeta }\left(x,s\right)$ may be expressed as follows:

$\zeta \left(x,t^{\prime }\right)=L^{-1}\left\{\overline{\zeta }\left(x,s\right)\right\}=\frac{1}{2\pi i}{\int }_{n-i\infty }^{n+i\infty }\overline{\zeta }\left(x,s\right){\mathrm{e}}^{s{t}^{\prime }}ds.(41)$

In this case, $s=n+i\mathrm{{\rm M}}$ ($n,\mathrm{{\rm M}}\in R$). Hence, we can rewrite the inverse Eq. 41 as follows:

$\zeta \left(x,t^{\prime }\right)=\frac{\exp \left(n{t}^{\prime }\right)}{2\pi }{\int }_{-\infty }^{\infty }\exp \left(i\beta t\right)\overline{\zeta }\left(x,n+i\beta \right)d\beta .(42)$

The following relation is obtained by expanding the Fourier series for the function $\zeta \left(x,t^{\prime }\right)$ in the closed interval $\left[0,2t^{\prime }\right]$:

$\zeta \left(x,t^{\prime }\right)=\frac{e^{n{t}^{\prime }}}{t^{\prime }}\left[\frac{1}{2}\overline{\zeta }\left(x,n\right)+Re{\displaystyle \sum _{k=1}^N}\overline{\zeta }\left(x,n+\frac{ik\pi }{t^{\prime }}\right){\left(-1\right)}^n\right].(43)$

Here, $i=\sqrt{-1}$, and $\mathrm{R}\mathrm{e}$ is the real part. The sufficient $N$ can be chosen in a large integer but can be selected in the notation $n{t}^{\prime }\approx 4.7$ [40].

7 Numerical results and discussion

To create the numerical simulation, the numerical parameters of the physical fields are used. These factors include temperature, moisture, normal stress, displacement, and carrier density. The simulation is carried out by using substances known as silicon (Si) and germanium (Ge). The following table presents the physical constants with their SI unit representations according to Table 1 [27–31]:

TABLE 1

TABLE 1. Physical constants of Si and Ge materials.

7.1 The moisture reference influence

Figure 1 (the first group) shows the semiconductor constants of silicon utilized to obtain the graph of the main physical quantities: thermal waves (thermal temperatures), normal stress (mechanical waves), plasma waves (carrier density), elastic waves (displacement distribution), and moisture field against the $x$-axis (distance). All calculations of the numerical results are made when the thermoelastic coupling parameters $V_4=0.678$ and the thermoelectric coupling parameters ${\epsilon }_1=-2.65·{10}^{-36}$. The first subfigure describes the positivity of the variation of the elastic waves with the $x$-axis; we noted that the displacement distribution begins from the maximum positive value and decreases sharply due to the moisture effect. Because of the increasing moisture effect, we noted the decreasing amplitude of the physical quantity. The second subfigure describes the plasma waves (carries density) against the $x$-axis; we noted that it starts from the maximum positive value in the three cases of the effect of moisture concentration and decreases gradually for a whole range which propagated in exponential behavior as it is mentioned in the plasma condition. Moreover, by increasing the moisture concentration, it shows the increasing curvature of the carrier density. The third subfigure shows the moisture concentration parameter (three values) effect that is utilized to mention the description of the thermal waves. The three cases describe the distribution of thermal waves that starts from the positive value on the surface and increases until the maximum value is reached after that decreasing in exponential behavior until arriving at the state of stability at the zero line inside the medium. The fourth subfigure describes the moisture concentration effect on the mechanical waves (normal stress distribution) against the $x$-axis, which satisfies the mechanical condition and begins from a negative value due to the moisture effect and stress pressure; the mechanical waves decrease sharply until it arrives at the minimum value in the three cases of increasing the values of reference moisture. After that, when observed far from the surface (within the semiconductor medium), the mechanical waves gradually increase until they reach the steady state with convergence from the zero line. The fifth subfigure represents the moisture field against the $x$-axis at different values for moisture concentration; we see that by increasing the value of moisture reference, the amplitude of the moisture field increases. The graph starts from the positive value and increases gradually in the three cases of the effect of moisture until it reaches the maximum value and decreases exponentially in its behavior until it arrives at the zero line. According to Liu et al. [41], the numerical results of photo-thermo-physical properties in this problem agree with the experimental results.

FIGURE 1

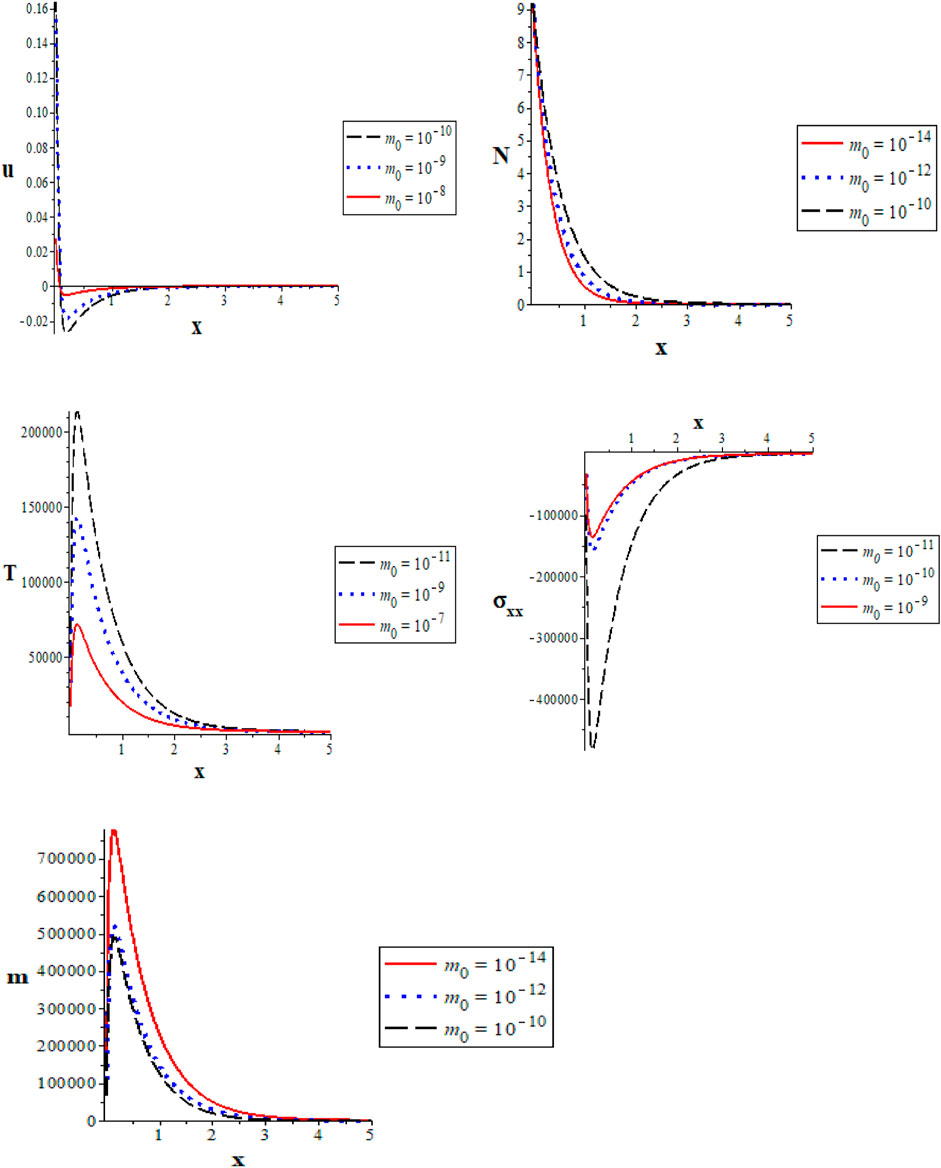
FIGURE 1. Representation of the variations of physical quantities with the x-axis (distance) under the effect of moisture diffusion at different values of reference moisture $m_0$.

7.2 The photo-thermoelastic model effect

The second kind of model depicts changes in photo-thermoelasticity models with increasing vertical distance, which may be used to investigate the effects of these variations on the basic dimensionless physical fields. Four different theories of photo-thermoelasticity are shown in Figure 2 (the second group) by showing the variations of the main physical field variables with distance (thermoelastic and photoelastic models). The outcomes fall within a range $0\le x\le 5$. For the Si medium, the full complement of computational findings was obtained in a relatively short time. Figure 2 shows the effect of varying the parameters of thermal memory on the distance against the propagation of non-dimensional thermal waves, plasma waves, mechanical waves, moisture concentration, and elastic waves. There is no discernible difference in the behavior between Figure 2 and Figure 1. Models of photo-thermoelasticity are generalized in the MGT PT model. The MGT PT model shows potential to fix some of the physical problems seen in older versions. To a large extent, all field distributions are affected by the MGT PT model.

FIGURE 2

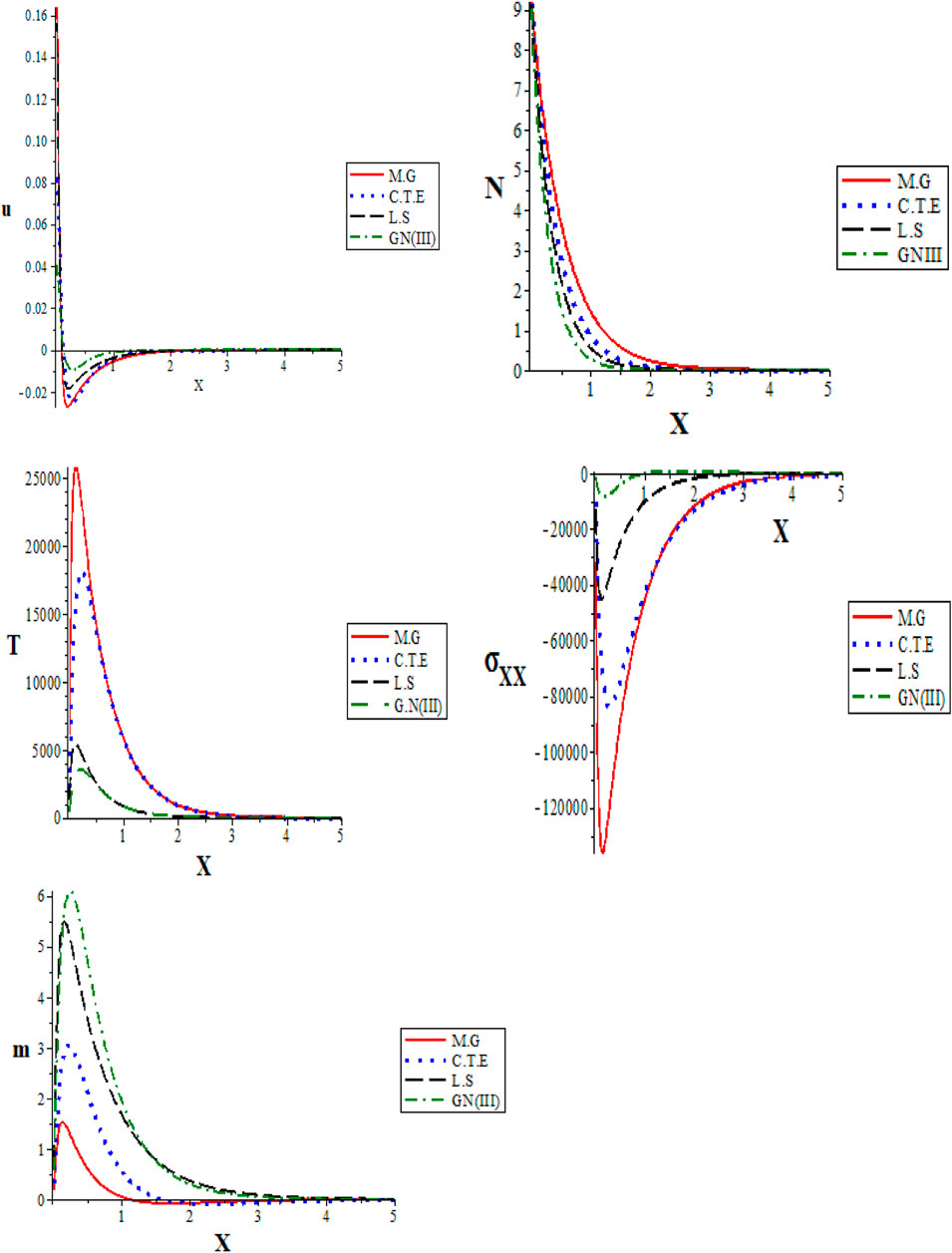
FIGURE 2. Representation of the variations of physical quantities with the x-axis (distance) for different photo-thermoelastic theories.

7.3 The comparison between two semiconductor materials

Silicon (Si) and germanium (Ge) are both semiconductor materials, and Figure 3 demonstrates the comparison when their physical constants are employed in the computations. All calculations are prepared according to the MGT model when $V_4=0.678$. It is evident from this figure that the results of numerical calculations on the propagation of waves in a semiconductor medium will rely on the numbers (input parameters) used in the computations.

FIGURE 3

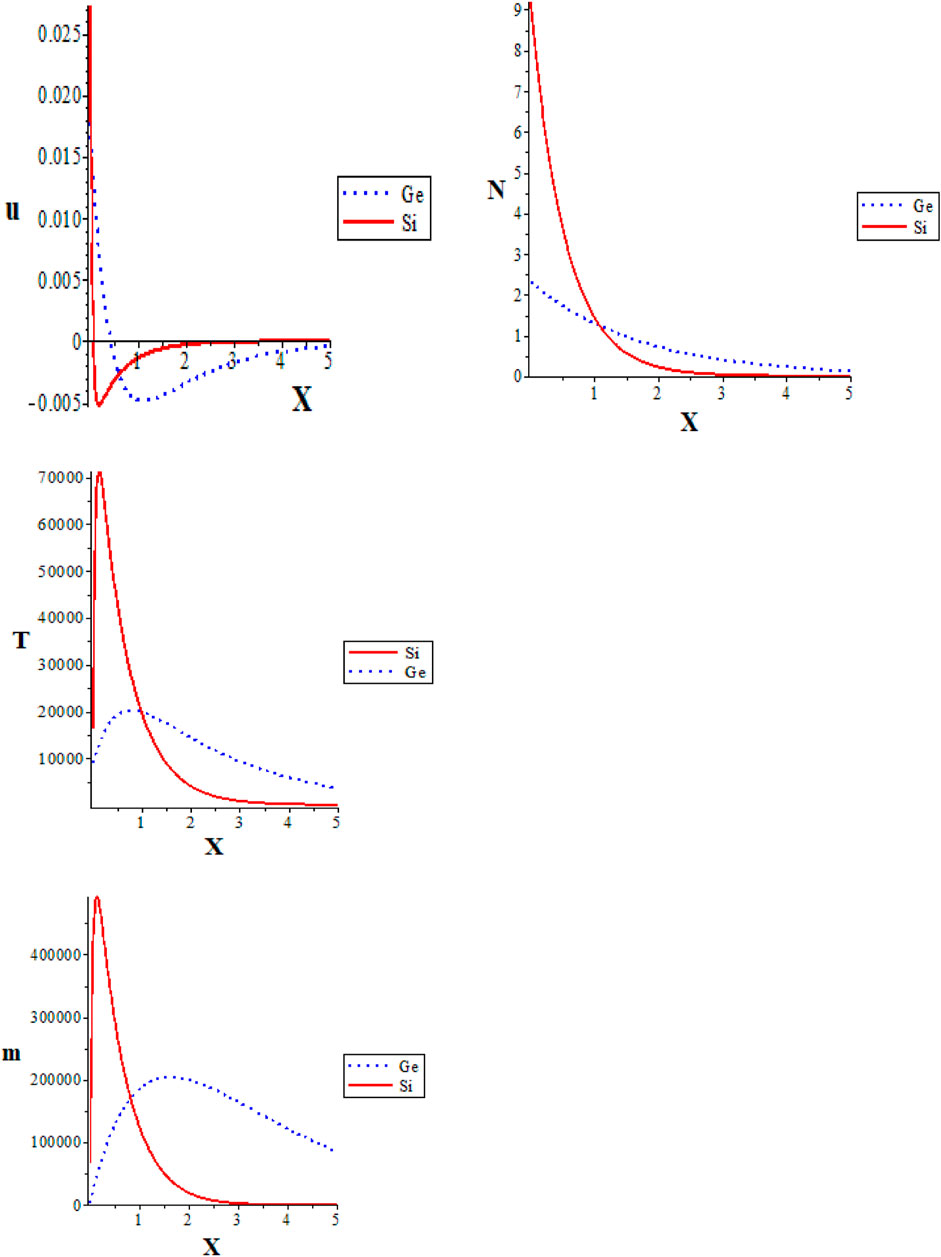
FIGURE 3. Representation of the variations of the main field with the x-axis (distance) for two different semiconductors.

8 Conclusion

This study offers an original account of the thermal and elastic relaxation time-dependent model applications (MG, GN(III), CTE, and LS) used to characterize the interference of elastic, thermal, and plasma waves in a semiconductor medium. Under the framework of MGT’s elasticity theory, the photo-thermoelastic interactions in an infinite semiconducting material have been investigated. A high quantity of moisture affects the semiconductor media. As various models have been developed to represent photo-thermoelasticity issues, the MGT model is a natural progression. The photo-thermoelastic models and the moisture diffusivity have drastically different standard deviations. The value of the moisture diffusivity parameter has a significant impact on the rate of change of the primary distribution variation. This means that the moisture content is a better indicator of heat transfer than it formerly was. The comparison of the wave propagations shows that the value of the physical parameters of the medium significantly affects the patterns of field distributions in this study. The physical assumptions are consistent with the notion that waves travel at limited speeds, as predicted by the MGT model and other photo-thermoelastic models.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KL: Conceptualization, Methodology, and Supervision. MS and ALB: Software, Data curation. AE-D: and Writing-Original draft preparation. SE-S: Visualization, Investigation, Software, Validation. NB and HC: Writing-Reviewing and Editing. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R154) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2023-0028”.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Biot MA. Thermoelasticity and irreversible thermodynamics. J Appl Phys (1956) 27:240–53. doi:10.1063/1.1722351

CrossRef Full Text | Google Scholar

2. Lord H, Shulman Y. A generalized dynamical theory of thermoelasticity. J.Mech Phys Sol (1967) 15:299–309. doi:10.1016/0022-5096(67)90024-5

CrossRef Full Text | Google Scholar

3. Green AE, Lindsay KA. Thermoelasticity J Elasticity (1972) 2(1):1–7. doi:10.1007/bf00045689

CrossRef Full Text

4. Abo-Dahab S, Lotfy K. Generalized magneto-thermoelasticity with fractional derivative heat transfer for a rotation of a fibre-reinforced thermoelastic. J Comput Theor Nanoscience (2015) 12(8):1869–81. doi:10.1166/jctn.2015.3972

CrossRef Full Text | Google Scholar

5. Othman M, Lotfy K. Two-dimensional problem of generalized magneto-thermoelasticity with temperature dependent elastic moduli for different theories. Multidiscipline Model Mater Structures (2009) 5(3):235–42. doi:10.1163/157361109789016961

CrossRef Full Text | Google Scholar

6. Aboueregal A, Sedighi H, Shirazi A, Malikan M, Eremeyev V. Computational analysis of an infinite magnetothermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach. Contin Mech Thermodyn (2022) 34:1067–85. doi:10.1007/s00161-021-00998-1

CrossRef Full Text | Google Scholar

7. Othman M, Lotfy K, Farouk R. Transient disturbance in a half-space under generalized magneto-thermoelasticity with internal heat source. Acta Physica Pol A (2009) 116(2):185–92. doi:10.12693/aphyspola.116.185

CrossRef Full Text | Google Scholar

8. Quintanilla R. Moore-Gibson-Thompson thermoelasticity. Math Mech Sol (2019) 24:4020–31. doi:10.1177/1081286519862007

CrossRef Full Text | Google Scholar

9. Quintanilla R. Moore-Gibson-Thompson thermoelasticity with two temperature. Appl Eng Sci (2020) 1:100006. doi:10.1016/j.apples.2020.100006

CrossRef Full Text | Google Scholar

10. Vlase S, Năstac C, Marin M, Mihălcică M. A method for the study of the vibration of mechanical bars systems with symmetries. Acta Tech Napocensis, Ser Appl Math Mech Eng (2017) 60(4):539–44.

Google Scholar

11. Abouelregal A, Marin M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics (2020) 8(7):1128. doi:10.3390/math8071128

CrossRef Full Text | Google Scholar

12. Abouelregal A, Marin M. The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry (2020) 12(8):1276. doi:10.3390/sym12081276

CrossRef Full Text | Google Scholar

13. Scutaru ML, Vlase S, Marin M, Modrea A. New analytical method based on dynamic response of planar mechanical elastic systems. Bound Value Problem (2020) 2020:104. doi:10.1186/s13661-020-01401-9

CrossRef Full Text | Google Scholar

14. Kaltenbacher B, Lasiecka I, Marchand R. Wellposedness and Exponential decay rates for the Moore–Gibson–Thompson equation arising in high intensity ultrasound. Control Cybernet (2011) 40:971–88.

Google Scholar

15. Lotfy K, Seddeek M, Hassanin W, El-Dali A. Analytical solutions of photo generated moore–gibson–thompson model with stability in thermoelastic semiconductor excited material. Silicon (2022) 14:12447–57. doi:10.1007/s12633-022-01927-w

CrossRef Full Text | Google Scholar

16. Lotfy K, Elidy E, Tantawi R. Piezo-photo-thermoelasticity transport process for hyperbolic two-temperature theory of semiconductor material. Int J Mod Phys C (2021) 32(7):2150088. doi:10.1142/S0129183121500881

CrossRef Full Text | Google Scholar

17. Szekeres A. Analogy between heat and moisture. Comput Structures (2000) 76:145–52. doi:10.1016/s0045-7949(99)00170-4

CrossRef Full Text | Google Scholar

18. Szekeres A. Cross-coupled heat and moisture transport: Part 1 theory. J Therm Stresses (2012) 35(1-3):248–68. doi:10.1080/01495739.2012.637827

CrossRef Full Text | Google Scholar

19. Gasch T, Malm R, Ansell A. A coupled hygro-thermo-mechanical model for concrete subjected to variable environmental conditions. Int J Sol Structures (2016) 91:143–56. doi:10.1016/j.ijsolstr.2016.03.004

CrossRef Full Text | Google Scholar

20. Szekeres A, Engelbrecht J. Coupling of generalized heat and moisture transfer. Periodica Polytechnica Ser Mech Eng (2000) 44(1):161–70.

Google Scholar

21. Gordon JP, Leite RCC, Moore RS, Porto SPS, Whinnery JR. Long-transient effects in lasers with inserted liquid samples. Bull Am Phys Soc (1964) 119:501. doi:10.1063/1.1713919

CrossRef Full Text | Google Scholar

22. Kreuzer LB. Ultralow gas concentration infrared absorption spectroscopy. J Appl Phys (1971) 42:2934–43. doi:10.1063/1.1660651

CrossRef Full Text | Google Scholar

23. Tam AC. Ultrasensitive laser spectroscopy. New York, NY: Academic Press (1983). p. 1–108.

CrossRef Full Text | Google Scholar

24. Tam AC. Applications of photoacoustic sensing techniques. Rev Mod Phys (1986) 58:381.

CrossRef Full Text | Google Scholar

25. Tam AC. Photothermal investigations in solids and fluids. Boston: Academic Press (1989). p. 1–33.

Google Scholar

26. Todorovic DM, Nikolic PM, Bojicic AI. Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J Appl Phys (1999) 85:7716–26. doi:10.1063/1.370576

CrossRef Full Text | Google Scholar

27. Song YQ, Todorovic DM, Cretin B, Vairac P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int J Sol Struct (2010) 47:1871–5. doi:10.1016/j.ijsolstr.2010.03.020

CrossRef Full Text | Google Scholar

28. Mahdy A, Lotfy K, El-Bary A, Sarhan H. Effect of rotation and magnetic field on a numerical-refined heat conduction in a semiconductor medium during photo-excitation processes. Eur Phys J Plus (2021) 136(5):553–63. doi:10.1140/epjp/s13360-021-01552-3

CrossRef Full Text | Google Scholar

29. El-Sapa S, Lotfy K, El-Bary A, Ahmed M. Moisture diffusivity and photothermal excitation in non-local semiconductor materials with laser pulses. Silicon (2023). doi:10.1007/s12633-023-02333-6

CrossRef Full Text | Google Scholar

30. Lotfy K. Photothermal waves for two temperature with a semiconducting medium under using a dual-phase-lag model and hydrostatic initial stress. Waves Ran Comp Med (2017) 27(3):482–501. doi:10.1080/17455030.2016.1267416

CrossRef Full Text | Google Scholar

31. Chteoui R, Lotfy K, Seddeek M, El-Dali A, Hassanin W. Moore–gibson–thompson stability model in a two-temperature photonic semiconductor excited medium affected by rotation and initial stress. Crystals (2022) 12(12):1720. doi:10.3390/cryst12121720

CrossRef Full Text | Google Scholar

32. Hobiny A, Abbas I. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int J Heat Mass Transf (2018) 124:1011–4. doi:10.1016/j.ijheatmasstransfer.2018.04.018

CrossRef Full Text | Google Scholar

33. Hobiny A, Abbas I. Nonlinear analysis of dual-phase lag bio-heat model in living tissues induced by laser irradiation. J Therm Stresses (2020) 43:503–11. doi:10.1080/01495739.2020.1722050

CrossRef Full Text | Google Scholar

34. Hobiny A, Abbas I. Analytical solutions of fractional bioheat model in a spherical tissue. Mech Based Des Struct Mach (2021) 49:430–9. doi:10.1080/15397734.2019.1702055

CrossRef Full Text | Google Scholar

35. Ghanmi A, Abbas I. An analytical study on the fractional transient heating within the skin tissue during the thermal therapy. J Therm Biol (2019) 82:229–33. doi:10.1016/j.jtherbio.2019.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zenkour A, Abbas I. Nonlinear transient thermal stress analysis of temperature-dependent hollow cylinders using a finite element model. Int J Struct Stab Dyn (2014) 14(7):1450025. doi:10.1142/s0219455414500254

CrossRef Full Text | Google Scholar

37. Alzahrani F, Abbas I. Analytical estimations of temperature in a living tissue generated by laser irradiation using experimental data. J Therm Biol (2019) 85:102421. doi:10.1016/j.jtherbio.2019.102421

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Saeed T, Abbas I. Finite element analyses of nonlinear DPL bioheat model in spherical tissues using experimental data. Mech Based Des Struct Mach (2020) 50:1287–97. doi:10.1080/15397734.2020.1749068

CrossRef Full Text | Google Scholar

39. Honig G, Hirdes U. A method for the numerical inversion of Laplace Transforms. Comp Appl Math (1984) 10(1):113–32. doi:10.1016/0377-0427(84)90075-x

CrossRef Full Text | Google Scholar

40. Brancik L. Programs for fast numerical inversion of Laplace transforms in MATLAB language environment. In: Proceedings of the 7th Conference. MATLAB’99; November 10, 1999; Czech Republic Prague (1999). p. 27–39.

Google Scholar

41. Liu J, Han M, Wang R, Xu S, Wang X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J Appl Phys (2022) 131:065107. doi:10.1063/5.0082014

CrossRef Full Text | Google Scholar