Continuum modeling for lithium storage inside nanotubes

Lithium storage and capture are of particular importance for the development of new technology in electric vehicles and portable electronics. Nanotubes (NTs) are among many porous nanomaterials offered as potential candidates for lithium storage. In this paper, we adopt a continuum approach together with the Lennard–Jones function to determine the minimum interaction energies for lithium atoms in boron nitride nanotubes (BNNTs) and carbon nanotubes (CNTs). By minimizing the interaction energies, we may obtain the preferred type and size of the nanotubes to encapsulate the lithium atoms. The results showed that BNNTs and CNTs are attractive candidates for lithium atom encapsulation, and the optimal nanotube to enclose lithium is the BNNT with a radius equal to 3.4 Å, and corresponding (5, 5) armchair nanotubes and (9, 0) zigzag nanotubes, where the minimum energy is obtained. The present computations observed that both nanotubes are promising candidates for lithium intercalation materials suitable for battery applications.

1 Introduction

Recently, with the rapid development of nanotechnology, nanomaterials represent a high level of importance in many applications, such as pharmaceuticals, electronic technology, energy applications, the biomedical sector, and environmental applications. They are used, for example, but not limited to the new generation of computer chips, harder and more durable cutting tools, removal of pollutants, very efficient batteries, magnets with high power, sensors with high sensitivity, automobiles, aerospace components, weapon platforms, long-lasting medical implants, and electrochromic display devices [1–3]. One of the most well-known and widely studied nanostructures in science is nanotubes (NTs), including boron nitride nanotubes (BNNTs) and carbon nanotubes (CNTs). Due to the distinctive structures and exceptional properties of nanotubes, they have attracted more interest in research and developing nanotechnology, and they are expected to be used in many new applications. CNTs have gained a wide range of theoretical and experimental research since their discovery in the 1990s [4]. They show a variety of captivating qualities, including exceptional electronic sensitivity, good mechanical strength, high surface area to volume ratios, high levels of flexibility, and exceptionally strong electro-catalytic activities, which enable them to find practical use in sensors, actuators, energy storage devices, etc. [5]. Until now, this field is still active and attractive to the interest of many researchers, and many distinguished and important applications of CNTs have emerged since their discovery. There are numerous studies on CNTs, and some authors highlight their applications in the field of electronics, sensing, and composite [6, 7].

Studies and research paid significant attention to the new material, BNNTs. Numerous accomplishments have allowed access to this material, and several applications have been implemented in this field since Chopra et al.’s invention of BNNTs in 1995. Both BNNTs and CNTs share some basic properties like outstanding mechanical properties and high heat conductivity. This is because of the similarity between the structures of BNNTs and CNTs, where boron and nitrogen atoms in BNNTs are replaced by carbon atoms in CNTs [8]. One exceptional physical feature of BNNTs is that they are an excellent insulator with a wide bandgap (5–6 eV), while CNTs are semiconducting materials. Moreover, they are not sensitive to the chirality and morphology of the tubes. BNNTs also have distinct characteristics such as high-temperature stability and neutron radiation shielding capability, which make them essential for use in sensors and devices in extreme environments [8]. The chiral vector C = ia₁ + ja₂ is used to classify the structure of the nanotubes, where a₁ and a₂ are the basis vectors of a hexagonal unit cell on layered inorganic sheets [such as hexagonal boron nitride (h-BN) and graphene (GRA)], and i and j are integers. Alternatively, the chiral vector may be indicated by (i, j), and the radii of the corresponding nanotubes are then given by $r=\ell \sqrt{3(i^2+j^2+ij)}/2\pi$, where ℓ denotes the bond length [3]. Although BNNTs and CNTs have structural similarities, the two nanotubes differ in some properties, which cause different behaviors for each. For example, the bond lengths of C–C bonds and B–N bonds are approximately 1.42 and 1.45 Å, respectively [9, 10].

The energy demand is increasing dramatically recently, and energy storage has become one of the major interests in technology and science. Due to climate change caused by global warming, researchers focus on developing systems of generating renewable energy and using electric motors in vehicles instead of the known engines [11, 12]. Sources of renewable energy like solar power generators also need batteries to store energy for later use [11, 12]. Therefore, improving battery technology requires materials with the ability to charge and recharge with high efficiency in order to be able to use energy resources successfully [11]. Owing to their advantages of excellent cyclic stability, lightweight, high capacity density, and high efficiency, lithium (Li) batteries have received considerable attention in many applications, such as electric vehicles, electric power grids, and portable electronics [12, 13].

One of the scientific challenges facing lithium batteries is their safety, which needs to be ensured before they can be widely used in everyday portable devices, and the most important factor that threatens the safety of the battery is the overheating of the cell, which results from a short circuit under a high temperature and high current environment. Since the separator plays an important role in avoiding short circuits, it is important that the separator be thermally stable [14]. Nanotubes can play an important role in energy storage systems, including the lithium battery, and they may protect against thermal shrinkage at high temperatures and high current operation, which improves the stability of the temperature in the polyolefin separator and then prevents battery short-circuits [12, 14]. Lithium batteries have offered great success for mobile electronics because of the progress in cell design and the manufacturing of lithium batteries with more efficient electrochemical performances regarding power densities and energy [15]. Further studies are required to improve the progress of these materials with the lithium battery technology. Moreover, nanomaterials, including nanotubes, might provide long-lasting separation of electron charges, and supramolecular nanoclusters can be supported, increasing the photoelectrochemical performance of photovoltaic cells [16]. Many experimental studies have worked on determining the lithium adsorption energetics in NTs. Theoretical studies have concentrated on the intercalation of Li atoms in nanotubes and the calculation of energy barriers for the entry and diffusion of Li inside the tubes.

Song et al. examined the intercalation and diffusion of Li ions in CNTs and found that lithium intercalation may cause deformation of CNTs [17]. Khantha et al. used density functional theory (DFT) to study the interaction of a single Li atom inside a (5, 5) CNT and reported that the lithium insertion capacities are dependent on the chirality and the equilibrium position of the Li atom on the tube axis, which provides strong binding energy, and is about 1.46 Å [18]. Zhong-Heng et al. used ab initio molecular dynamics (AIMD) simulations and first-principle calculations to probe the Li transport mechanism in armchair and zigzag CNTs, and their results showed a fast Li transport with an ultralow activation energy in the CNTs with a diameter of 5.5 Å, corresponding to (4, 4) and (7, 0) CNTs [19]. Meunier et al. found an equilibrium distance of 1.29 Å using ab initio simulations for Li inside the (5, 5) and (8, 0) CNTs [20]. Yanhong and Junwei have applied the DFT to investigate the adsorption of Li atoms in different CNTs [21]. Their results showed that a Li atom is steadily adsorbed inside the CNTs, and the strongest adsorption energy of the Li atom is obtained in the (6, 0) CNTs.

In addition, Rahman et al. presented a new separator coated by BNNTs with a thermal stability of up to 150°C for the safer operation of lithium batteries. Kim et al. investigated BNNT-based separators in lithium–sulfur batteries and showed the comparison of the electrochemical behavior of lithium–sulfur batteries with BNNTs and those without BNNTs [11]. They found that the BNNT-loaded polypropylene separator prevents the formation of dendrite on the Li metal anode, helps the ions move easily through the separator, and reduces the shuttle effect at the cathode compared to the ordinary polypropylene separator. Zhong et al. used the DFT method to investigate the interaction between (5, 0) BNNTs and lithium atoms, which is located near the open end of the tube [22]. Their results showed that the interaction between the lithium atom and the edge of BNNTs is around −30.05 (kcal/mol). Seif et al. performed the DFT method to study the effects of lithium doping on the properties of the electronic structure of (4, 4) BNNTs, and their results showed a heterogeneous electrostatic environment along the tube [23].

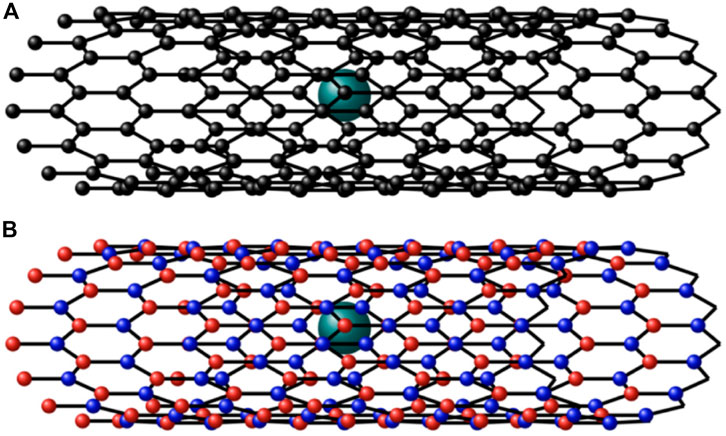
The investigation of the adsorption and encapsulation of lithium in different nanotubes is still active to improve the performance of lithium batteries. Experiments can be performed directly, but they are time-consuming and expensive. Mathematical modeling and simulation may be used as an alternative, complementary, and guiding method. Calculating the interaction energy between non-bonded atoms and molecules is usually performed by either the discrete method, which calculates the force for every non-bonded atom as a pair using molecular dynamics, or the continuum method, which approximates these atoms using geometric representation. Here, we apply the continuum approach with the Lennard–Jones (LJ) potential to calculate the van der Waals energies and the interaction between atoms and molecules. In this method, some simple geometric shapes with rotational symmetry are used to represent the molecular structures and the distance between them. These geometric shapes, like points and cylinders, with this geometric property are useful to simplify interaction expressions. In particular, we use this approach to determine the minimum interaction energies for lithium in two different nanotubes, namely, BNNTs and CNTs, as shown in Figure 1. By minimizing the interaction energies, we may obtain the preferred type and size of the nanotubes to encapsulate the lithium atoms.

FIGURE 1

FIGURE 1. Geometrical diagram of (A) Li in CNTs and (B) BNNTs.

2 Modeling approach

In this section, the interactions between Li atoms inside BNNTs and CNNTs are modeled. Predominantly, van der Waals forces are the forces present in physisorption, so we may use the Lennard–Jones potential to determine the interaction between lithium atoms and nanotubes, and it is given as

$P\left(\varrho \right)=-T{\varrho }^{-6}+R{\varrho }^{-12},$

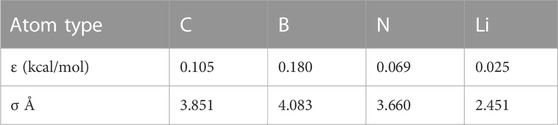
which evaluates the potential energy between two atoms at distance ϱ apart. The coefficients T and R are the attractive and repulsive parameters of the interaction, respectively, and their values might be obtained by applying the Lorentz–Berthelot mixing rule [24], where T = 4ɛσ⁶ and R = 4ɛσ¹². Furthermore, σ is the van der Waals diameter and ɛ is the well depth for Li, B, N, and C atoms, and their values are taken from Rappi et al. [25], as shown in Table 1. For two different atoms, they might be computed using σ₁₂ = (σ₁ + σ₂)/2 and ${\epsilon }_{12}=\sqrt{{\epsilon }_1{\epsilon }_2}$. As the nanotubes have cylindrical structures, we approximate them as continuum surfaces, where their atoms are uniformly distributed over their entire surfaces, and they are modeled continuously over their atoms by employing a typical surface element, dA. For such a problem, the hybrid discrete–continuum approach is used to obtain the interaction of an atom (i.e., a point) with the surface A (the cylinder), and it is given as

$E=\sum _i{\varpi }_j\int P\left(\varrho i\right)dA,(1)$

where P(ϱi) is the potential function, ϱ is the distance between an atom (point i) and the surface of nanotubes (BNNT and CNT), and ϖ_j (j ∈ {B, C}) is the atomic surface density of NTs, and their values are given by ϖ_B = 0.3661 and ϖ_C = 0.3812 Å⁻² [26, 27]. In the following subsections, we considered two factors affecting the interaction energies of lithium atoms and nanotubes.

TABLE 1

TABLE 1. Values of the well depth and van der Waals diameter used in this study.

2.1 Li atom entering nanotubes

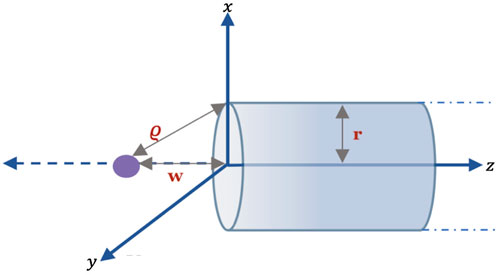
Here, we considered the entry of a Li atom in the nanotube, and the atom is assumed to be outside the tube. Figure 2 shows the Li atom as it enters an open-ended semi-infinite tube with the radius r. Thus, the NTs can be modeled as a cylinder, and their coordinates are (r cos u, r sin u, z), where −π ≤ u ≤ π and 0 < z < ∞, and the parametric equation of the atom is denoted by (0, 0, w), where w is the distance between the atom and the open end of the tube on the z-axis of the tube. The distance ϱ between the surface of the nanotube and the entering atom is given by

${\varrho }^2=r^2{\cos }^{2}u+r^2{\sin }^{2}u+{\left(z-w\right)}^2=r^2+{\left(z-w\right)}^2,$

FIGURE 2

FIGURE 2. Li atom entering the nanotube.

and the total interaction between the nanotube and the atom is given by

$E^{\mathit{tot}}=r{\varpi }_j{\int }_{-\pi }^{\pi }{\int }_0^{\infty }\left(-T{\varrho }^{-6}+R{\varrho }^{-12}\right)dzdu.(2)$

This integral may be rewritten as follows:

$E^{\mathit{tot}}=r{\varpi }_j\left(-T{Q}_3+R{Q}_6\right).(3)$

The integral Q_n (n = 3, 6) can be evaluated as follows:

$\begin{array}{ccc}\hfill Q_n& =\hfill & r{\int }_{-\pi }^{\pi }{\int }_0^{\infty }\frac{1}{{\left[r^2+{\left(z-w\right)}^2\right]}^n}dzdu\hfill \\ \hfill & =\hfill & 2\pi r{\int }_0^{\infty }\frac{1}{{\left[r^2+{\left(z-w\right)}^2\right]}^n}dz.\hfill \end{array}$

By using the change of variables t = z − w and the substitution t = r tan ϕ, we have

$Q_n=2\pi r^{2-2n}{\int }_{\arctan \left(-w/r\right)}^{\pi /2}{\sec }^{2-2n}\varphi d\varphi =2\pi r^{2-2n}{\int }_{\arctan \left(-w/c\right)}^{\pi /2}{\cos }^{2n-2}\varphi d\varphi .$

Now, using the formula, we obtain [∮2.512(2)] [28]. For n = 3 and 6, the integral, Q_n, is given by

$Q_3=\pi r^{-5}\left[\frac{3\pi }{8}+\frac{3}{4}\arctan \left(\frac{w}{r}\right)+\frac{3wr}{4\left(r^2+w^2\right)}+\frac{w{r}^3}{2{\left(r^2+w^2\right)}^2}\right],(4)$

and

$\begin{array}{ccc}\hfill Q_6=\pi r^{-11}\left[\frac{9\pi }{3840}+\frac{3}{640}\arctan \left(\frac{w}{r}\right)+\frac{w{r}^9}{5{\left(r^2+w^2\right)}^5}+\frac{9w{r}^7}{40{\left(r^2+w^2\right)}^4}\right.& \hfill & \hfill \\ \hfill +\frac{7w{r}^5}{60{\left(r^2+w^2\right)}^3}+\left.\frac{w{r}^3}{16{\left(r^2+w^2\right)}^2}+\frac{3wr}{80\left(r^2+w^2\right)}\right],& \hfill & \hfill \end{array}(5)$

and these expressions are completed (Eq. 3).

2.2 Preferred position of a Li atom inside nanotubes

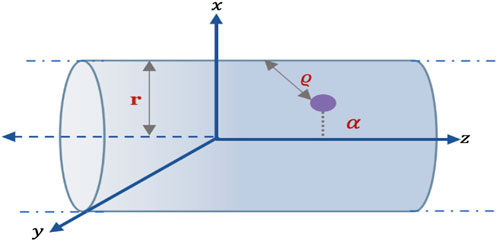
For a specific size nanotube, the preferred position of the Li atom inside the nanotube is determined with respect to the cross section of the tube, as shown in Figure 3. The atom is located at (α, 0, 0), where α is the distance of the offset atom (on the x-axis of the tube) from the central axis of the nanotube (z-axis), and the nanotubes are assumed to be of infinite length with a parametric equation, (r cos u, r sin u, z), where −π ≤ u ≤ π and −∞ < z < ∞. In this case, the distance ϱ is given by

$\begin{array}{ccc}\hfill {\varrho }^2& =\hfill & {\left(r\cos u-\alpha \right)}^2+r^2{\sin }^{2}u+z^2\hfill \\ \hfill & =\hfill & {\alpha }^2+r^2-2\alpha r\cos u+z^2\hfill \\ \hfill & =\hfill & {\left(r-\alpha \right)}^2+4r\alpha {\sin }^2\left(u/2\right)+z^2,\hfill \end{array}$

FIGURE 3

FIGURE 3. Offset distance of the Li atom in the nanotube.

and the total interaction of the Li atom in the nanotube is given by

$E^{\mathit{tot}}=r{\varpi }_j{\int }_{-\pi }^{\pi }{\int }_{-\infty }^{\infty }\left(-T{\varrho }^{-6}+R{\varrho }^{-12}\right)dzdu.(6)$

Again, these integrals can be written as

$E=r{\varpi }_j\left(-T{W}_3+R{W}_6\right),(7)$

where W_n is given by

$W_n=r{\int }_{-\pi }^{\pi }{\int }_{-\infty }^{\infty }\frac{1}{{\left[{\left(r-\alpha \right)}^2+4r\alpha {\sin }^2\left(u/2\right)+z^2\right]}^n}dzdu.(8)$

Here, these integrals can be solved by letting γ² = (r − α)² + 4rα sin²(u/2), and using the substitution z = γ tan θ, we obtain

$\begin{array}{ccc}\hfill W_n& =\hfill & r{\int }_{-\pi /2}^{\pi /2}{\cos }^{2n-2}\theta d\theta {\int }_{-\pi }^{\pi }\frac{1}{{\gamma }^{2n-1}}du.\hfill \\ \hfill & =\hfill & r\mathbf{B}\left(n-1/\mathrm{2,1}/2\right){\int }_{-\pi }^{\pi }\frac{1}{{\gamma }^{2n-1}}du,\hfill \end{array}$

where $\mathbf{B}\left(i^{*},j^{*}\right)$ is the beta function. By following the steps performed by Cox et al. in this work [29], the integral W_n became

$\begin{array}{ccc}\hfill W_n& =\hfill & \frac{2\pi r}{{\left(r-\alpha \right)}^{2n-1}}\mathbf{B}\left(n-1/\mathrm{2,1}/2\right)\hfill \\ \times \hfill & F\left(n-1/\mathrm{2,1}/2;1/2;1;4r\alpha /{\left(r-\alpha \right)}^2\right),\hfill \end{array}$

where F(a*, b*; c*, z*) indicates the usual hypergeometric function. Then, this expression is substituted in Eq. 7) in the cases of n = 3 and n = 6.

3 Numerical results

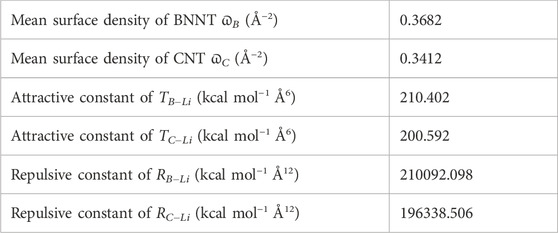
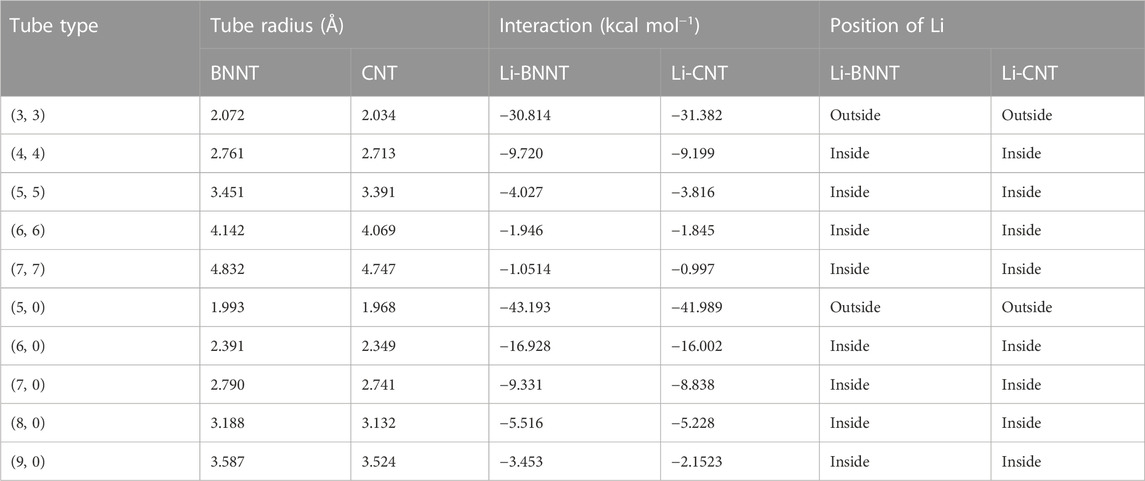
In this section, the interactions between the lithium atom and the nanotubes are presented numerically for various types of nanotubes by using the numerical values for the parameters associated with Li and nanotubes, which are given in Table 2. First, we determine the numerical solutions of the interactions of the Li atom entering various types of NTs. Figures 4, 5 show the results of the entry of the Li atom in CNTs and BNNTs. Moreover, by using the algebraic computer package Maple, in particular with optimization and then minimization, the minimal interaction energy values are obtained, as shown in Table 3. We comment that when the energies are lower in the +w tube side (i.e., inside the nanotube) than those in the −w tube side (i.e., outside the nanotube), Li is inserted in the tube. The results indicate that for both BNNTs and CNTs, the Li atom is accepted in all tubes except (3, 3) armchair and (5, 0) zigzag nanotubes. The results show that the interaction energies of the Li atom at the open end of the CNTs and BNNTs with a radius less than $\approx 2.2$ Å are highly positive, indicating that Li insertion is not feasible energetically due to the energy barrier. Moreover, Figures 4 and 5show that both tubes would not accept the Li atom from the rest because the suction energy is not sufficient to outdo the barrier energy at the opening of these tubes. Therefore, the interactions can exhibit two peaks [positive in the range (P₁, P₂) and negative in the range (P₂, ∞)], where it is possible for the Li atom to be inside these tubes when the curve of the energy crosses the horizontal axis at P2 as some additional energies are required. Our results for the interactions of Li with CNTs and BNNTs are in excellent agreement with the results given in [18–20] for the interactions of Li with CNTs and with those given in [22] for the interactions of Li with BNNTs. In addition, Table 4 summarizes the results for the relationship between the interaction energies and the offset position for Li inside (5, 5), (6, 6), (7, 7), (8, 8), and (9, 9) nanotubes. Our results show that the lowest energies for all CNTs and BNNTs considered in this study are obtained for the (5, 5) NTs with an equilibrium distance of 0 Å from the tube axis, assuming that the Li atom remains on the tube axis. These results differ from [18, 20], who used the ab initio simulations and the DFT method, and they showed that the equilibrium distance was between 1.29 and 1.46 Å inside the (5, 5) CNT. It is observed that the discrepancy between our results and these results may be attributed to the parameters which we have adopted here. In addition, our results are in excellent agreement with those performed by Yanhong and Junwei [21] using the DFT method, where their results showed that the strongest adsorption energy of the Li atom is obtained in the (6, 0) CNT. Finally, Figure 6 shows the preferred radii of both BNNTs and CNTs to encapsulate a Li atom, and the results show that the optimal radii are about 3.433 and 3.422 Å, corresponding to energies −2.476 and −2.217 kcal/mol, respectively. Our methods and results that are presented in this work yield the theoretical design of the interaction of a lithium atom stored in various types of nanotubes; moreover, further research should study the interaction energies and the changes in the electronic structure of the interaction configurations for lithium atoms interacting with nanotubes. In conclusion, the results are obvious that the BNNT and CNT are attractive candidates for Li atom encapsulation, and the best nanotubes are the BNNTs as the interaction between the Li atom and BNNT is slightly stronger than that between the Li atom and CNTs as the former gives the lowest minimum energy. We note that our approach can be used to investigate the interactions between the metal atoms with different types of nanotubes and nanomaterials such as fullerenes (see, for example, [30]).

TABLE 2

TABLE 2. Constants utilized in this study.

FIGURE 4

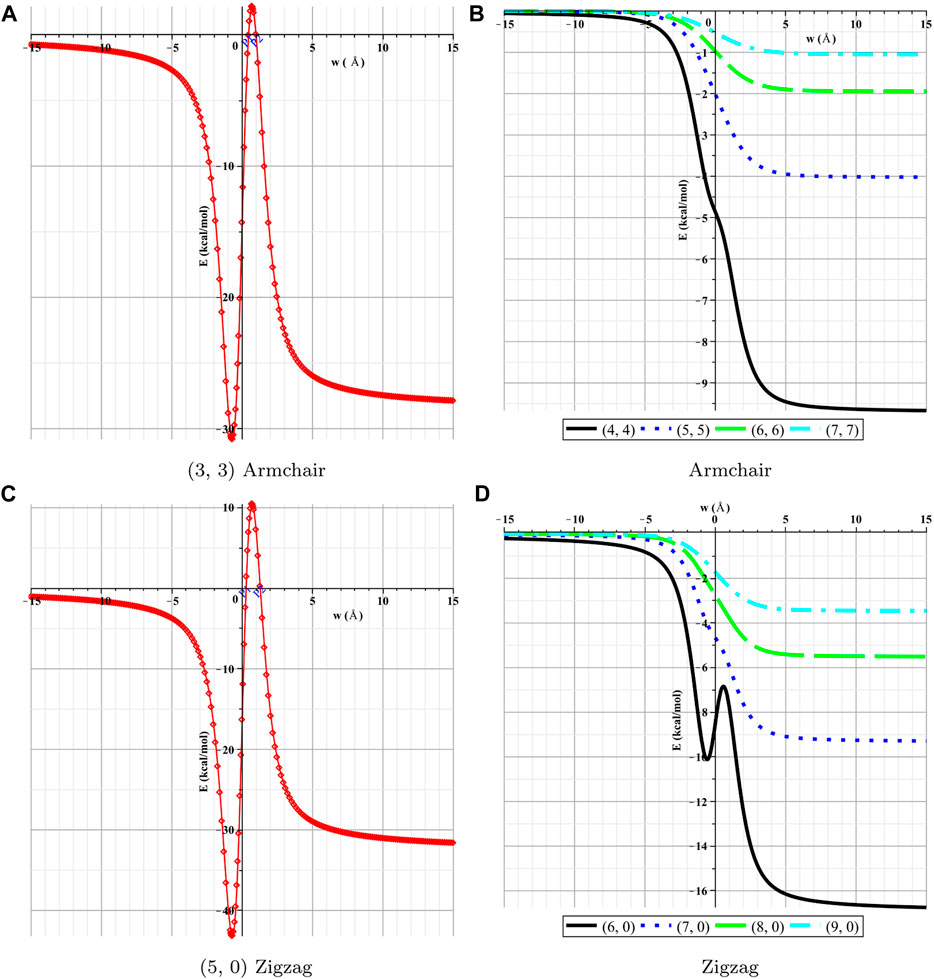
FIGURE 4. Interactions of Li and BNNTs with respect to w. (A) (3, 3) armchair, (B) armchair, (C) (5, 0) zigzag, and (D) zigzag.

FIGURE 5

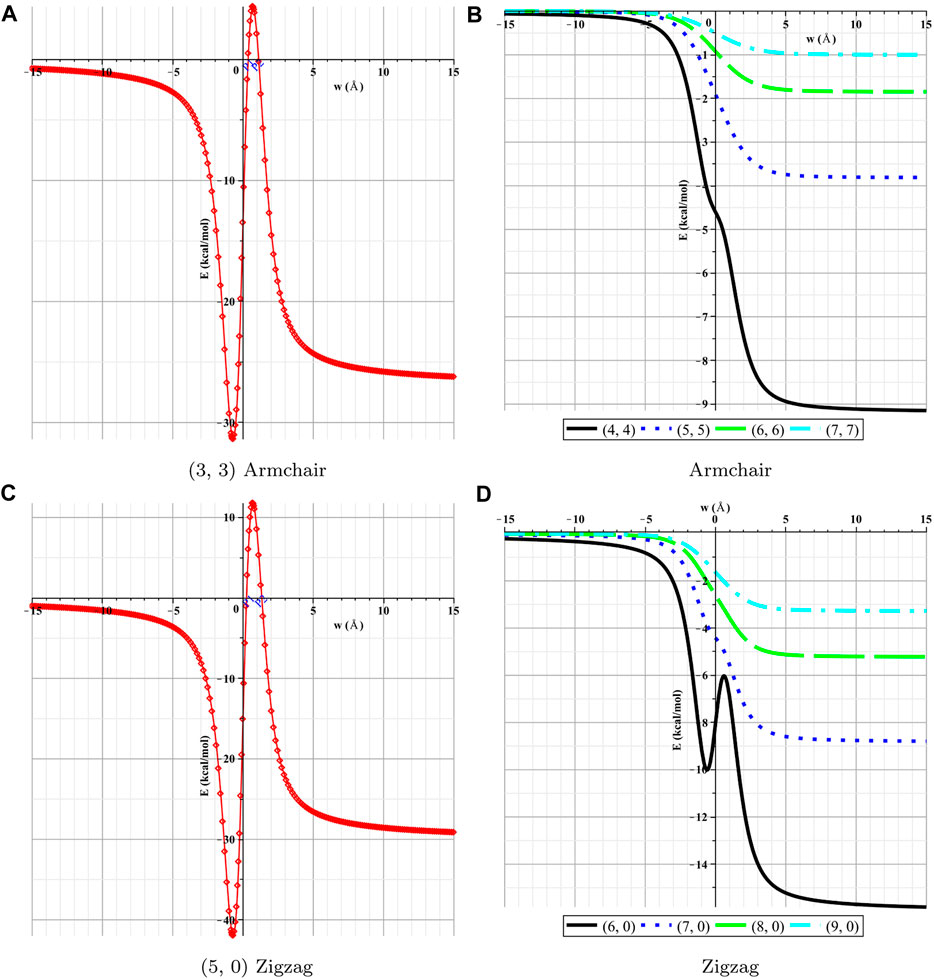
FIGURE 5. Interactions of Li and CNNTs with respect to w. (A) (3, 3) armchair, (B) armchair, (C) (5, 0) zigzag, and (D) zigzag.

TABLE 3

TABLE 3. Main results of the interactions of Li atoms with NTs.

TABLE 4

TABLE 4. Interaction energies of an offset Li atom inside NTs.

FIGURE 6

FIGURE 6. Interactions between the Li atom and nanotube as the function of tube radius r.

4 Summary

In this study, the Lennard–Jones potential, in conjunction with continuum modeling, has been used to investigate the interactions between a lithium atom and BNNTs and CNTs. First, calculations of the insertion of a Li atom at an open edge of nanotubes show that a lithium atom is attracted to the entrance open end of the tubes that have a radius larger than 2.2 Å. In addition, our results for (3, 3) and (5, 0) nanotubes showed that the lithium atom confronted a large energy barrier at the open end of these tubes, consequently, for the lithium atom to be enclosed into the nanotube with a radius less than 2.2 Å; some additional energy is also needed. Moreover, when the lithium atom is assumed to be inside the tube, our results indicate that the equilibrium distance from the tube axis depends on the size of the tube; as the radius gets larger, the position of the Li atom tends to be closer to the wall of the tube. By minimizing the interaction energy, we predicted that the preferred radii of both BNNTs and CNTs to encapsulate the Li atom are about 3.433 and 3.422 Å, respectively, with corresponding (5, 5) armchair nanotubes and (9, 0) zigzag nanotubes. Our results observed that both tubes are attractive candidates for Li atom encapsulation, and by minimizing the interaction energies, we obtained that the interaction between the Li atom and BNNTs is slightly stronger than that between the Li atom and CNTs. Overall, nanostructures, including CNTs and BNNTs, might offer a well-suited playground for optimizing rate performance nanomaterials and capacity for Li storage as an anode material in lithium batteries. Future work could involve a calculation on other nanotubes to enclose the lithium atoms as the particular architecture of nanotubes can offer a useful design idea for the electrode of next-generation lithium batteries.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This project was supported by the Researchers Supporting Project number (RSP2023R411), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sharma VP, Sharma U, Chattopadhyay M, Shukla V. Advance applications of nanomaterials: A review. Mater Today Proc (2018) 5:6376–80. doi:10.1016/j.matpr.2017.12.248

CrossRef Full Text | Google Scholar

2. Alshehri MH. Continuum modelling for encapsulation of anticancer drugs inside nanotubes. Mathematics (2021) 9:2469. doi:10.3390/math9192469

CrossRef Full Text | Google Scholar

3. Baowan D, Cox BJ, Hilder TA, Hill JM, Thamwattana N. Modelling and mechanics of carbon-based nanostructured materials. 1st ed. Norwich, NY, USA: William Andrew (2017).

Google Scholar

4. Iijima S. Helical microtubules of graphitic carbon. Nature (1991) 354:56–8. doi:10.1038/354056a0

CrossRef Full Text | Google Scholar

5. Zheng B, Dong H, Zhu J, Wang Y. Molecular dynamics study of lithium intercalation into -oh functionalized carbon nanotube bundle. Res Square (2022) 2022. doi:10.21203/rs.3.rs-1326366/v1

CrossRef Full Text | Google Scholar

6. Dresselhaus MS, Dresselhaus G, Avouris P. Carbon nanotubes: Synthesis, structure, properties, and applications. Berlin, Germany: Springer-Verlag (2000).

Google Scholar

7. Coleman JN, Khan U, Blau WJ, Gun’ko YK. Small but strong: A review of the mechanical properties of carbon nanotube-polymer composites. Carbon (2006) 44(9):1624–52. doi:10.1016/j.carbon.2006.02.038

CrossRef Full Text | Google Scholar

8. Kim JH, Pham TV, Hwang JH, Kim CS, Kim MJ. Boron nitride nanotubes: Synthesis and applications. Nano Convergence (2018) 5:17. doi:10.1186/s40580-018-0149-y

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Alshehri MH, Duraihema FZ, Aba Oud MA. Instability and translocation through nanopores of DNA interacting with single-layer materials. RSC Adv (2020) 10:36962–70. doi:10.1039/D0RA06359B

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Vovusha H, Sanyal B. Adsorption of nucleobases on 2D transition-metal dichalcogenides and graphene sheet: A first principles density functional theory study. RSC Adv (2015) 5:67427–34. doi:10.1039/C5RA14664J

CrossRef Full Text | Google Scholar

11. Kim HS, Kang HJ, Lim H, Hwang HJ, Park JW, Lee TG, et al. Boron nitride nanotube-based separator for high-performance lithium-sulfur batteries. Nanomaterials (2022) 12:11. doi:10.3390/nano12010011

CrossRef Full Text | Google Scholar

12. Yang F, Feng X, Glans PA, Guo J. MoS2 for beyond lithium-ion batteries. APL Mater (2021) 9:050903. doi:10.1063/5.0050118

CrossRef Full Text | Google Scholar

13. Landi BJ, Ganter MJ, Cress CD, DiLeoa RA, Raffaelle RP. Carbon nanotubes for lithium ion batteries. Energy Environ. Sci. (2009) 2:638–54. doi:10.1039/B904116H

CrossRef Full Text | Google Scholar

14. Rahman MM, Mateti S, Cai Q, Sultana I, Fan Y, Wang X, et al. High temperature and high rate lithium-ion batteries with boron nitride nanotubes coated polypropylene separators. Energ Storage Mater (2019) 19:352–9. doi:10.1016/j.ensm.2019.03.027

CrossRef Full Text | Google Scholar

15. Zhili X, Young SY, Hyoung-Joon J. Applications of carbon nanotubes for lithium ion battery anodes. Materials (2013) 6:1138–58. doi:10.3390/ma6031138

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ohkubo K, Kawashima Y, Fukuzumi S. Strong supramolecular binding of Li+@C60 with sulfonated meso-tetraphenylporphyrins and long-lived photoinduced charge separation. Chem Commun (2012) 48:4314–6. doi:10.1039/C2CC31186K

CrossRef Full Text | Google Scholar

17. Song B, Yang JW, Zhao JJ, Fang HP. Intercalation and diffusion of lithium ions in a carbon nanotube bundle by ab initio molecular dynamics simulations. Energ Environ. Sci. (2011) 4:1379–84. doi:10.1039/C0EE00473A

CrossRef Full Text | Google Scholar

18. Khantha M, Cordero NA, Alonso JA, Cawkwell M, Girifalco LA. Interaction and concerted diffusion of lithium in a (5,5) carbon nanotube. Phys Rev B (2008) 78:115430. doi:10.1103/PhysRevB.78.115430

CrossRef Full Text | Google Scholar

19. Zhong-Heng F, Xiang C, Nan Y, Le-Geng Y, Xin S, Shaochen S, et al. Diameter-dependent ultrafast lithium-ion transport in carbon nanotubes. J Chem Phys (2023) 158:014702. doi:10.1063/5.0131408

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Meunier V, Kephart J, Roland C, Bernholc J. Ab initio investigations of lithium diffusion in carbon nanotube systems. Phys Rev Lett (2002) 88:075506. doi:10.1103/PhysRevLett.88.075506

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yanhong Y, Junwei Y. Density functional theory study of lithium atom adsorbing in the interior and exterior of a series of carbon nanotubes. Adv Mater Res (2014) 1053:150–6. doi:10.4028/www.scientific.net/AMR.1053.150

CrossRef Full Text | Google Scholar

22. Rong-Lin Z, Hong-Liang X, Zhong-Min S. The interaction between Boron-carbon-nitride heteronanotubes and lithium atoms: Role of composition proportion. Chem Phys Lett (2016) 658:230–3. doi:10.1016/j.cplett.2016.06.054

CrossRef Full Text | Google Scholar

23. Seif A, Boshra A, Seif M. Lithium-doped (4,4) Boron nitride nanotube: Density functional theory study of N and B nuclear magnetic shielding and electric field gradient tensors. J Mol Struct THEOCHEM (2009) 895:82–5. doi:10.1016/j.theochem.2008.10.028

CrossRef Full Text | Google Scholar

24. Maitland GC, Rigby M, Smith EB, Wakeham WA. Intermolecular forces–their origin and determination. Oxford, UK: Clarendon Press (1981).

Google Scholar

25. Rappi AK, Casewit CJ, Colwell KS, Goddard WA, SkidUFF WM. A full periodic table force field formolecular mechanics and molecular dynamics simulations. J Am Chem Soc (1992) 114:10024–35. doi:10.1021/ja00051a040

CrossRef Full Text | Google Scholar

26. Hilder TA, Hill JM. Modelling the encapsulation of the anticancer drug cisplatin into carbon nanotubes. Nanotechnology (2007) 18:275704. doi:10.1088/0957-4484/18/27/275704

CrossRef Full Text | Google Scholar

27. Hilder TA, Hill JM. Theoretical comparison of nanotube materials for drug delivery. Micro Nano Lett (2008) 3:18–24. doi:10.1049/mnl:20070070

CrossRef Full Text | Google Scholar

28. Gradshteyn IS, Ryzhik IM. Table of integrals, series and products. 6th ed. San Diego, USA: Academic Press (2000).

Google Scholar

29. Barry JC, Ngamta T, James MH. Mechanics of atoms and fullerenes in single-walled carbon nanotubes. I. Acceptance and suction energies. Proc R Soc A (2007) 2007:463. doi:10.1098/rspa.2006.1771

CrossRef Full Text | Google Scholar

30. Alshehri MH. An analytical model for lithium storage in spherical fullerenes. Energies (2022) 15:7154. doi:10.3390/en15197154

CrossRef Full Text | Google Scholar